Вектор с началом в точке и концом в точке принято обозначать как
Download 342.76 Kb. Pdf ko’rish
|
1 2 3 4 5 6
Bog’liq
Вектор (геометрия) — Википедия
1-tajriba. Algoritm loyihalash, mantiq qonunlari. mantiq funksiyalari uchun chinlik jadvali tuzish, mantiq qonunlari. mantiq funksiyalari uchun chinlik jadvali tuzish, gazoanalizatorlar, gazoanalizatorlar, PUL BANK Yakuniy javoblari-1, Мехнат шартномаси, Simsiz tarmoq, 3, art003-definite-indefinite-articles, Baxtiyor.uz-Amaliy-xorijiy-tillar-testi, chizma 2 qavat
[1] . 
Вектор с началом в точке и концом в точке принято обозначать как . Векторы также могут обозначаться малыми латинскими буквами со стрелкой (иногда — чёрточкой) над ними, например . Другой распространённый способ записи: написание символа вектора прямым жирным шрифтом: . Вектор в геометрии естественно сопоставляется переносу ( параллельному переносу ), что, очевидно, проясняет происхождение его названия ( лат. vector, несущий). Итак, каждый направленный отрезок однозначно определяет собой какой-то параллельный
). 
Интерпретация вектора как переноса позволяет естественным и интуитивно очевидным способом ввести операцию сложения векторов — как композиции (последовательного применения) двух (или нескольких) переносов; то же касается и операции умножения вектора на число. Вектором называется направленный отрезок построенный по двум точкам, одна из которых считается началом, а другая концом. Координаты вектора определяются как разность координат точек его конца и начала. и , то координаты вектора будут: . Длиной вектора называется расстояние между двумя точками и , её обычно обозначают Роль нуля среди векторов играет нулевой вектор , у которого начало и конец совпадают ; ему, в отличие от других векторов, не приписывается никакого направления [2] . 
Основные понятия
Download 342.76 Kb. Do’stlaringiz bilan baham: |
1 2 3 4 5 6
Ma’lumotlar bazasi mualliflik huquqi bilan himoyalangan ©fayllar.org 2023
ma’muriyatiga murojaat qiling
Операции над векторами и их свойства. Особенности и правила умножения вектора на число
От-ме-тим, что сло-же-ние век-то-ров про-из-во-дит-ся ана-ло-гич-но пла-ни-мет-рии, толь-ко все дей-ствия вы-пол-ня-ют-ся в про-стран-стве.
Итак, пусть за-да-ны два про-из-воль-ных век-то-ра в про-стран-стве (рис. 1):
Рис. 1. Про-из-воль-ные век-то-ры в про-стран-стве
Опре-де-лим, что же на-зы-ва-ет-ся сум-мой двух этих век-то-ров.
Точно так же, как в пла-ни-мет-рии, из любой удоб-ной точки, на-зо-вем ее точ-кой А, можно един-ствен-ным об-ра-зом от-ло-жить век-тор, рав-ный век-то-ру .
Рис. 2. Сумма двух век-то-ров в про-стран-стве
Так, по-лу-че-но пра-ви-ло тре-уголь-ни-ка для сло-же-ния век-то-ров в про-стран-стве.
Пра-ви-ло тре-уголь-ни-ка
Из любой точки про-стран-ства (точка А) от-кла-ды-ва-ем пер-вый век-тор, из конца пер-во-го век-то-ра (точка В) от-кла-ды-ва-ем вто-рой век-тор и по-лу-ча-ем точку С. Век-тор, со-еди-ня-ю-щий на-ча-ло пер-во-го век-то-ра (точка А) и конец вто-ро-го (точка С), и будет ре-зуль-ти-ру-ю-щим.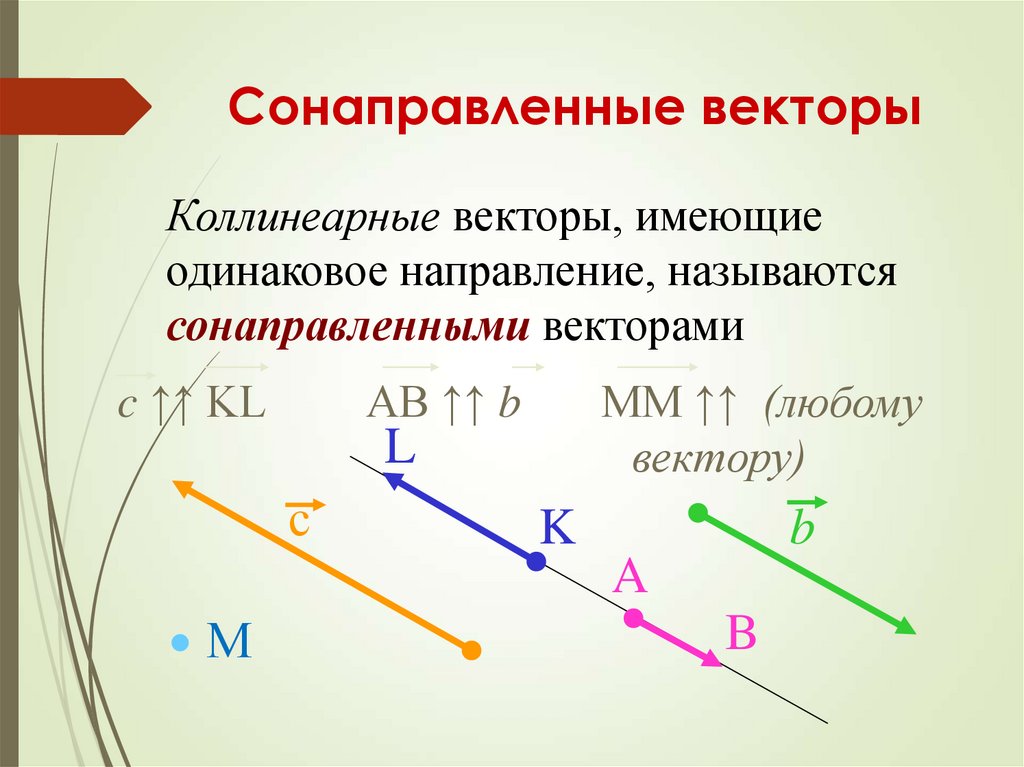
От-ме-тим, что ре-зуль-тат сло-же-ния век-то-ров не за-ви-сит от вы-бо-ра на-чаль-ной точки, су-ще-ству-ет со-от-вет-ству-ю-щая тео-ре-ма, ко-то-рая это до-ка-зы-ва-ет на ос-но-ва-нии того, что из точки можно от-ло-жить век-тор, рав-ный за-дан-но-му, един-ствен-ным об-ра-зом.
Опре-де-ле-ние
Раз-но-стью двух век-то-ров на-зы-ва-ет-ся такой тре-тий век-тор, ко-то-рый, бу-дучи сло-жен-ным со вто-рым век-то-ром, даст пер-вый век-тор.
Вве-дем раз-ность век-то-ров и , для этого сло-жим век-тор с про-ти-во-по-лож-ным век-то-ром :
Итак, из про-из-воль-ной точки А от-кла-ды-ва-ем век-тор , по-лу-ча-ем точку В. Чтобы по-лу-чить век-тор мы стро-им век-тор, рав-ный век-то-ру по длине, но про-ти-во-на-прав-лен-ный. По-лу-чен-ный век-тор от-кла-ды-ва-ем из точки В — по-лу-ча-ем точку D. Век-тор и будет ис-ко-мым век-то-ром раз-но-сти.
Про-ил-лю-стри-ру-ем (рис. 3):
Рис. 3. Вы-чи-та-ние двух век-то-ров в про-стран-стве
По-стро-им на за-дан-ных век-то-рах и па-рал-ле-ло-грамм (рис.
4):
Рис. 4. Па-рал-ле-ло-грамм на двух за-дан-ных век-то-рах
Т. к. век-тор ; ана-ло-гич-но .
По пра-ви-лу тре-уголь-ни-ка:
Так, одна из диа-го-на-лей па-рал-ле-ло-грам-ма, по-стро-ен-но-го на двух век-то-рах, со-от-вет-ству-ет сумме этих век-то-ров.
Рас-смот-рим раз-ность век-то-ров. По пра-ви-лу тре-уголь-ни-ка:
Так, вто-рая диа-го-наль па-рал-ле-ло-грам-ма, по-стро-ен-но-го на двух век-то-рах, со-от-вет-ству-ет раз-но-сти этих век-то-ров.
Для сло-же-ния и вы-чи-та-ния несколь-ких век-то-ров при-ме-ня-ет-ся пра-ви-ло мно-го-уголь-ни-ка. Пусть за-да-ны век-то-ры и :
Рис. 5. Три век-то-ра в про-стран-стве
Необ-хо-ди-мо по-стро-ить век-тор .
Видим, что перед неко-то-ры-ми век-то-ра-ми стоят чис-лен-ные мно-жи-те-ли. На-пом-ним, что при умно-же-нии век-то-ра на число по-лу-ча-ем со-на-прав-лен-ный век-тор, длина ко-то-ро-го — это длина ис-ход-но-го век-то-ра, умно-жен-ная на за-дан-ное число. По-лу-чим век-то-ры и .
Рис. 6. Умно-же-ние век-то-ра на число
При-сту-па-ем к сло-же-нию. Из про-из-воль-ной точки А от-кла-ды-ва-ем по-лу-чен-ный век-тор — по-лу-ча-ем точку В. Из точки В от-кла-ды-ва-ем век-тор — по-лу-ча-ем точку С. Из точки С от-кла-ды-ва-ем век-тор — по-лу-ча-ем точку D. Со-глас-но пра-ви-лу мно-го-уголь-ни-ка, век-тор со-от-вет-ству-ет ис-ко-мо-му век-то-ру :
Рис. 7. Сло-же-ние век-то-ров по пра-ви-лу мно-го-уголь-ни-ка
За-да-ча 1:
Задан тет-ра-эдр ABCD (ри-су-нок 8). До-ка-зать:
Рис. 8. Тет-ра-эдр, за-да-ча 1
Ре-ше-ние:
По пра-ви-лу тре-уголь-ни-ка:
В этой статье мы рассмотрим операции, которые можно производить с векторами на плоскости и в пространстве. Далее мы перечислим свойства операций над векторами и обоснуем их с помощью геометрических простроений.
Также покажем применение свойств операций над векторами при упрощении выражений, содержащих векторы.
Для более качественного усвоения материала рекомендуем освежить в памяти понятия, данные в статье векторы — основные определения .
Навигация по странице.
Операция сложения двух векторов — правило треугольника.
Покажем как происходит сложение двух векторов .
Сложение векторов и происходит так: от произвольной точки A откладывается вектор , равный , далее от точки B откладываеься вектор , равный , и вектор представляет собой сумму векторов и . Такой способ сложения двух векторов называется правилом треугольника .
Проиллюстрируем сложение не коллинеарных векторов на плоскости по правилу треугольника.
А на чертеже ниже показано сложение сонаправленных и противоположно направленных векторов.
Сложение нескольких векторов — правило многоугольника.
Основываясь на рассмотренной операции сложения двух векторов, мы можем сложить три вектора и более.
В этом случае складываются первые два вектора, к полученному результату прибавляется третий вектор, к получившемуся прибавляется четвертый и так далее.
Сложение нескольких векторов выполняется следующим построением. От произвольной точки А плоскости или пространства откладывается вектор, равный первому слагаемому, от его конца откладывается вектор, равный второму слагаемому, от его конца откладывается третье слагаемое, и так далее. Пусть точка B — это конец последнего отложенного вектора. Суммой всех этих векторов будет вектор .
Сложение нескольких векторов на плоскости таким способом называется правилом многоугольника . Приведем иллюстрацию правила многоугольника.
Абсолютно аналогично производится сложение нескольких векторов в пространстве.
Операция умножения вектора на число.
Сейчас разберемся как происходит умножение вектора на число .
Умножение вектора на число k соответствует растяжению вектора в k раз при k > 1 или сжатию в раз при 0
К примеру, при умножении вектора на число 2
нам следует вдвое увеличить его длину и сохранить направление, а при умножении вектора на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное.
Приведем для наглядности иллюстрацию этого случая.
Свойства операций над векторами.
Итак, мы определили операцию сложения векторов и операцию умножения вектора на число. При этом для любых векторов и произвольных действительных чисел можно при помощи геометрических построений обосновать следующие свойства операций над векторами . Некоторые из них очевидны.
Рассмотренные свойства дают нам возможность преобразовывать векторные выражения.
Свойства коммутативности и ассоциативности операции сложения векторов позволяют складывать векторы в произвольном порядке.
Операции вычитания векторов как таковой нет, так как разность векторов и есть сумма векторов и .
Учитывая рассмотренные свойства операций над векторами, мы можем в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования так же как и в числовых выражениях.
Разберем на примере.
Рассмотрим вектор v с начальной точкой в начале координат в любой координатной системе x-y и с конечной точкой в (a,b).
Мы говорим, что вектор находится в стандартном положении и ссылаемся на него как на радиус-вектор. Обратите внимание, что пара точек определяет этот вектор. Таким образом, мы можем использовать это для обозначения вектора. Чтобы подчеркнуть, что мы имеем в виду вектор, и, чтобы избежать путаницы, как правило, пишут:
v = .
Координата a есть скаляром горизонтальной компоненты вектора, и координата b есть скаляром вертикальной компоненты вектора. Под скаляром мы подразумеваем численное количество, а не векторную величину. Таким образом, это рассматривается как компонентная форма v. Обратите внимание, что a и b НЕ вектора и их не надо путать с определением компонента вектора.
Теперь рассмотрим с A = (x 1 , y 1) и C = (x 2 , y 2). Давайте рассмотрим, как найти радиус вектор, эквивалентный . Как Вы видите на рисунке внизу, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся вычитанием координат A из координат C.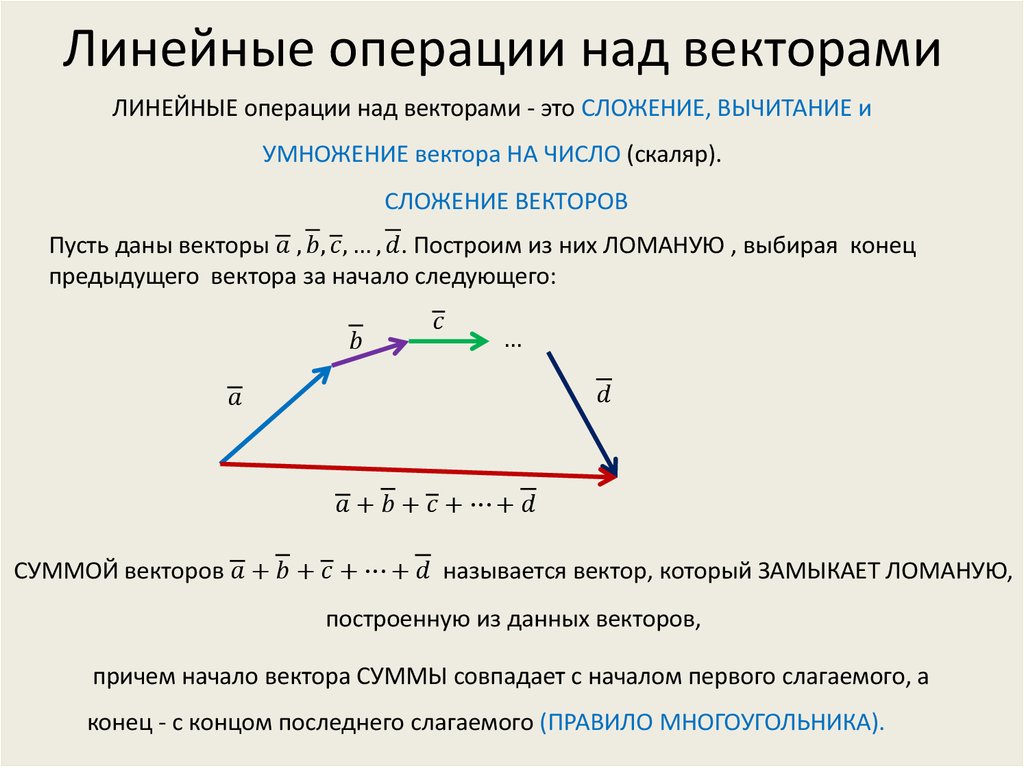
Таким образом, P = (x 2 — x 1 , y 2 — y 1) и радиус вектор есть .
Можно показать, что и имеют одну и ту же величину и направление, и поэтому эквивалентны. Таким образом, = = .
Компонентная форма с A = (x 1 , y 1) и C = (x 2 , y 2) есть
= .
Пример 1 Найдите компонентную форму если C = (- 4, — 3) и F = (1, 5).
Решение Мы имеем
= = .
Обратите внимание, что вектор есть равным радиус-вектору , как показано на рисунке вверху.
Теперь, когда мы знаем, как записать вектор в компонентной форме, давайте изложим некоторые определения.
Длину вектора v легко определить, когда известны компоненты вектора. Для v = , мы имеем
|v| 2 = v 2 1 + v 2 2 Используя теорему Пифагора
|v| = √v 2 1 + v 2 2
.
Длина , или величина ветктора v = находится как |v| = √v 2 1 + v 2 2 .
Два вектора равны или эквивалентны, если они имеют одну и ту же величину и одно и то же направление.
Пусть u = и v = . Tогда
= только если u 1 = v 1 and u 2 = v 2 .
Операции с векторами
Чтобы умножить вектор V на положительное число, мы умножаем его длину на это число. Его направление остается прежним. Когда вектор V умножается на 2, например, его длина увеличивается в два раза, но его направление не изменяется. Когда вектор умножается на 1,6, его длина увеличивается на 60%, а направление остается прежним. Чтобы умножить вектор V на отрицательное действительное число, умножаем его длину на это число и изменяем направление на противоположное. Например, Когда вектор умножается на (-2), его длина увеличивается в два раза и его направление изменяется на противоположное.
Так как действительные числа работают как скалярные множители в умножении векторов, мы называем их скаляры и произведение kv называется скалярные кратные v.
Для действительного числа k и вектора v = , скалярное произведение k и v есть
kv = k.
= .
Вектор kv есть скалярным кратным вектора v.
Пример 2 Пусть u = и w = . Найдите — 7w, 3u и — 1w.
Решение
— 7w = — 7. = ,
3u = 3. = ,
— 1w = — 1. = .
Теперь мы можем сложить два вектора, используя компоненты. Чтобы сложить два вектора в компонентной форме, мы складываем соответствующие компоненты. Пусть u = и v = . Тогда
u + v =
Например, если v = и w = , тогда
v + w = =
Если u = и v = , тогда
u + v = .
Перед тем, как мы определим вычитание векторов нам нужно дать определение — v. Противоположный вектору v = , изображенному внизу, есть
— v = (- 1).v = (- 1) =
Вычитание векторов, такое как u — v вовлекает вычитание соответствующих компонент. Мы покажем это представлением u — v как u + (- v). Если u = и v = , тогда
u — v = u + (- v) = + = =
Мы можем проиллюстрировать вычитание векторов с помощью параллелограмма, как мы это делали для сложения векторов.
Вычитание векторов
Если u = и v = , тогда
u — v = .
Интересно сравнить суммы двух векторов с разницей тех же двух векторов в одном параллелограмме. Векторы u + v и u — v есть диагоналями параллелограмма.
Пример 3 Сделайте следующие вычисления, где u = и v = .
a) u + v
b) u — 6v
c)3u + 4v
d)|5v — 2u|
Решение
a) u + v = + = = ;
b)u — 6v = — 6. = — = ;
c) 3u + 4v = 3. + 4. = + = ;
d) |5v — 2u| = |5. — 2.| = | — | = || = √(- 29) 2 + 21 2
= √1282
≈ 35,8
Прежде чем сформулировать свойства векторного сложения и умножения, мы должны дать определение еще одному специальному вектору — нулевому вектору. Вектор, чья начальная точка совпадает с конечной точкой, называется нулевым вектором , обозначается O, или. Его величина равна 0. В сложении векторов:
v + O = v. + =
Операции над векторами обладают те же самыми свойствами, что и операции над вещественными числами.
Для всех векторов u, v, и w, и для всех скаляров b и c:
1.
u + v = v + u.
2. u + (v + w) = (u + v) + w.
3. v + O = v.
4 1.v = v; 0.v = O.
5. v + (- v) = O.
6. b(cv) = (bc)v.
7. (b + c)v = bv + cv.
8. b(u + v) = bu + bv.
Орты
Вектор величиной, или длиной 1 называется орт . Вектор v = есть орт, потому что
|v| = || = √(- 3/5) 2 + (4/5) 2
= √9/25 + 16/25
= √25/25
= √1
= 1.
Пример 4 Найдите орт, который имеет то же самое направление, что и вектор w = .
Решение Найдем сначала длину w:
|w| = √(- 3) 2 + 5 2
= √34
. Таким образом, мы ищем вектор, с длиной 1/√34
от w и с таким же самым направлением, что и вектор w. Этот вектор есть
u = w/√34
= /√34
= 34, 5/√34
>.
Вектор u есть орт, потому что
|u| = |w/√34
| = = √9/34 + 25/34
= √34/34
= √1
= 1.
Если v есть вектор и v ≠ O, тогда
(1/|v|). v, or v/|v|,
есть орт в направлении v.
Хотя орты могут иметь любое направление, орты, параллельные осям x и y особенно полезны.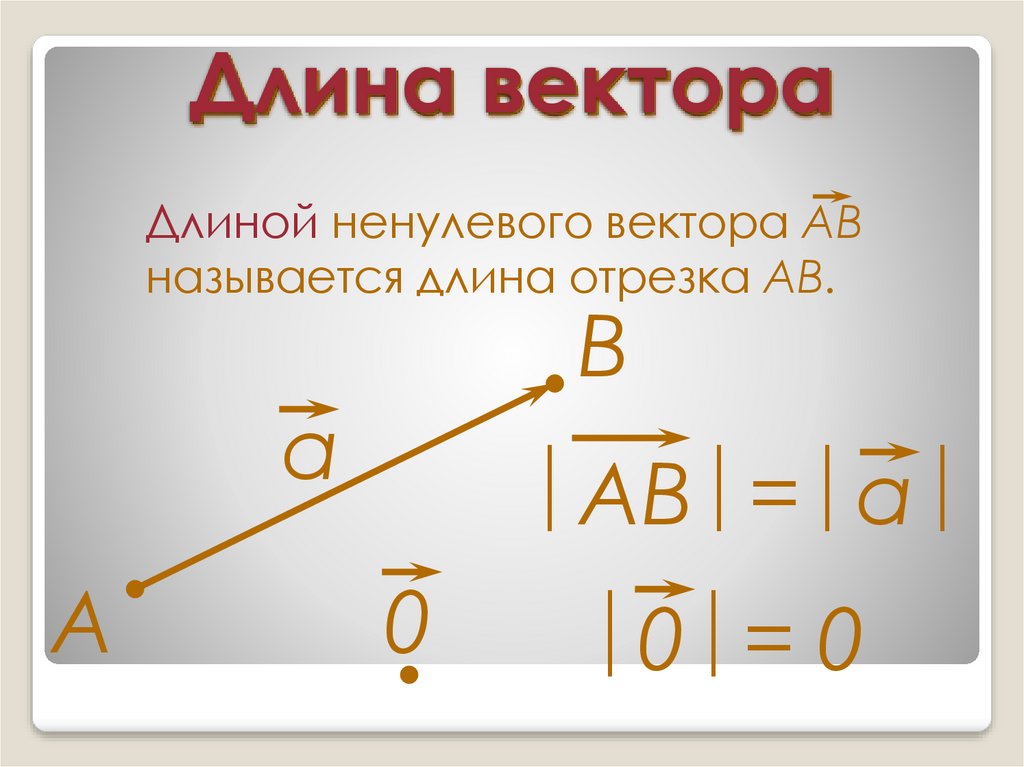
Они определяются как
i = and j = .
Любой вектор может быть выражен как линейная комбинация орта i и j. Например, пусть v = . Tогда
v = = + = v 1 + v 2 = v 1 i + v 2 j.
Пример 5 Выразите вектор r = как линейную комбинацию i и j.
Решение
r = = 2i + (- 6)j = 2i — 6j.
Пример 6 Запишите вектор q = — i + 7j в компонентной форме.
Решение q = — i + 7j = -1i + 7j =
Векторные операции могут быть также выполнены, когда векторы записаны как линейные i и j.
Пример 7 Если a = 5i — 2j и b = -i + 8j, найдите 3a — b.
Решение
3a — b = 3(5i — 2j) — (- i + 8j) = 15i — 6j + i — 8j = 16i — 14j.
Углы обзора
Конечная точка P орты в стандартной позиции есть точкой на единичной окружности, определенной (cosθ, sinθ). Таким образом, орт может быть выражен в компонентной форме,
u = ,
или как линейная комбинация орт i и j,
u = (cosθ)i + (sinθ)j,
где компоненты u есть функциями угла обзора θ измеряемого против часовой стрелки от оси x к этому вектору.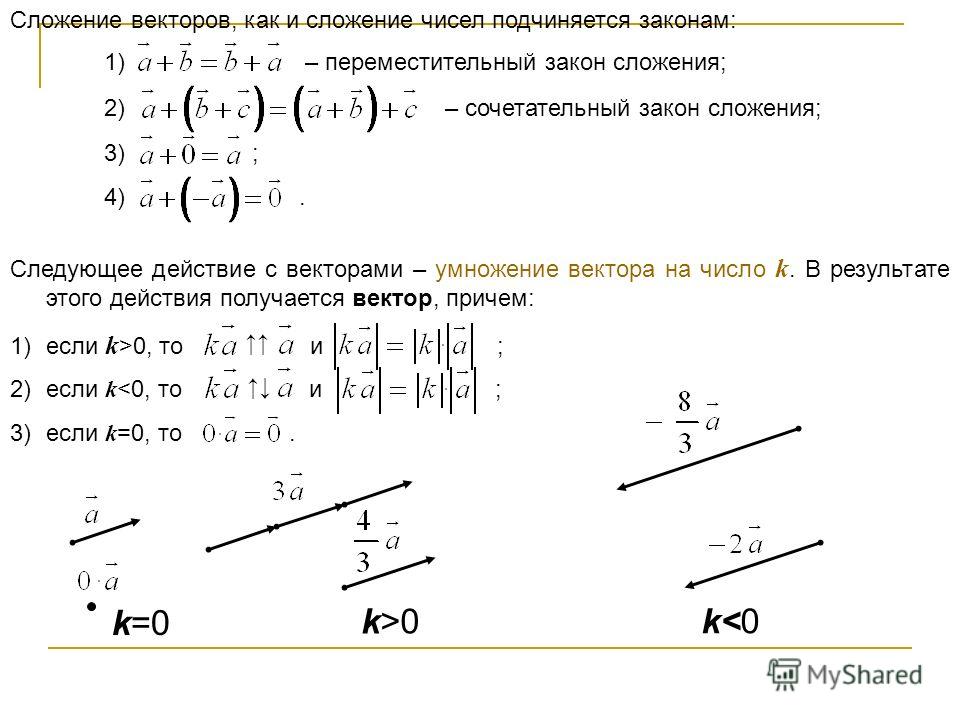
Так как θ изменяется от 0 до 2π, точка P отслеживает круг x 2 + y 2 = 1. Это охватывает все возможные направления ортов и тогда уравнение u = (cosθ)i + (sinθ)j описывает каждый возможный орт на плоскости.
Пример 8 Вычислите и сделайте эскиз орта u = (cosθ)i + (sinθ)j для θ = 2π/3. Изобразите единичную окружность на эскизе.
Решение
u = (cos(2π/3))i + (sin(2π/3))j = (- 1/2)i + (√3
/2)j
Пусть v = с углом обзора θ. Используя определение функции тангенса, мы можем определить угол обзора их компонент v:
Пример 9 Определите угол обзора θ вектора w = — 4i — 3j.
Решение Мы знаем, что
w = — 4i — 3j = .
Таким образом, имеем
tanθ = (- 3)/(- 4) = 3/4 и θ = tan — 1 (3/4).
Так как w находится в третьем квадранте, мы знаем, что θ есть углом третьего квадранта. Соответствующий угол есть
tan — 1 (3/4) ≈ 37°, и θ ≈ 180° + 37°, или 217°.
Это удобно для работы с прикладными задачами, а в последующих курсах, чтобы иметь способ выразить вектор так, чтобы его величина и направление могли быть легко определены или прочитаны.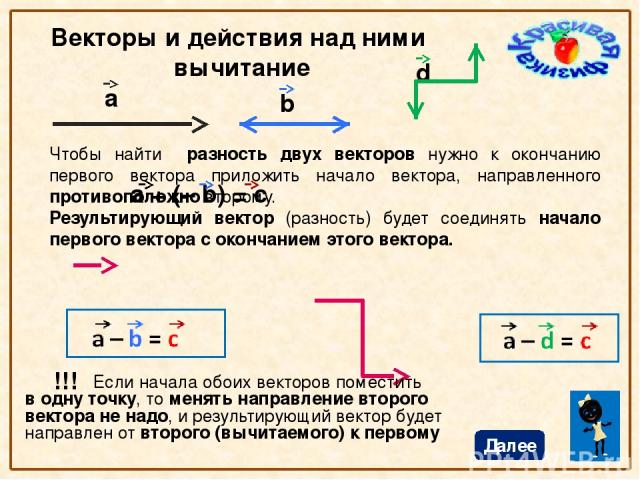
Пусть v это вектор. Тогда v/|v| есть орт в том же самом направлении, что и v. Таким образом, мы имеем
v/|v| = (cosθ)i + (sinθ)j
v = |v|[(cosθ)i + (sinθ)j] Умножая на |v|
v = |v|(cosθ)i + |v|(sinθ)j.
Углы между векторами
Когда вектор умножается на скаляр, результатом есть вектор. Когда складываются два вектора, результатом также есть вектор. Таким образом, мы могли бы ожидать, что произведение двух векторов есть вектор, но это не так. Скалярное произведение двух векторов есть действительное число или скаляр. Этот результат полезен в нахождении угла между двумя векторами и в определении, являются ли два вектора перпендикулярными.
Скалярное произведение двух векторов u = и v = is
u . v = u 1 .v 1 + u 2 .v 2
(Обратите внимание, что u 1 v 1 + u 2 v 2 есть скаляром , а не вектором.)
Пример 10 Найдите скалярное произведение, когда
u = , v = и w = .
a)u . w
b)w . v
Решение
a) u .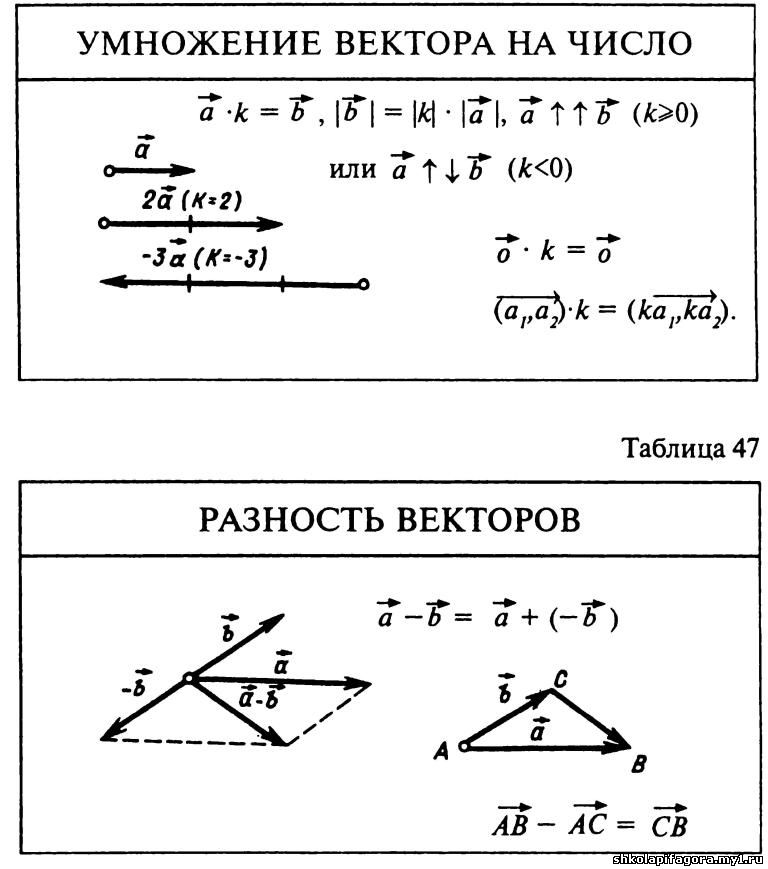
w = 2(- 3) + (- 5)1 = — 6 — 5 = — 11;
b) w . v = (- 3)0 + 1(4) = 0 + 4 = 4.
Скалярное произведение может быть использовано для нахождения угла между двумя векторами. Угол между двумя векторами это самый маленький положительный угол, образованный двумя направленными отрезками. Таким образом, θ между u и v это тот же самый угол, что и между v и u, и 0 ≤ θ ≤ π.
Если θ есть углом между двумя ненулевыми векторами u и v, тогда
cosθ = (u . v)/|u||v|.
Пример 11 Найдите угол между u = и v = .
Решение Начнем с нахождения u . v, |u|, и |v|:
u . v = 3(- 4) + 7(2) = 2,
|u| = √3 2 + 7 2
= √58
, and
|v| = √(- 4) 2 + 2 2
= √20
.
Tогда
cosα = (u . v)/|u||v| = 2/√58
.√20
α = cos — 1 (2/√58
.√20
)
α ≈ 86,6°.
Равновесие сил
Когда несколько сил действуют на одну и ту же точку на объекте, их векторная сумма должна быть равна нуля, для того, чтобы был баланс. Когда есть баланс сил, то объект является стационарным или движется по прямой линии, без ускорения.
Тот факт, что векторная сумма должна быть равна нулю вывода для получения баланса, и наоборот, позволяет решать нам многие прикладные задачи с участием сил.
Пример 12 Подвесной блок 350- фунтовый блок подвешен с помощью двух кабелей. осталось. В точке А есть три силы, действующие так: W блок тянет вниз, а R и S (два кабеля) тянут вверх и наружу. Найдите нагрузку каждого кабеля.
Решение Нарисуем диаграмму с начальными точками каждого вектора в начале кооординат. Для баланса, сумма векторов должна быть равна О:
R + S + W = О.
Мы можем выразить каждый вектор через его величину и угол обзора:
R = |R|[(cos125°)i + (sin125°)j],
S = |S|[(cos37°)i + (sin37°)j], и
W = |W|[(cos270°)i + (sin270°)j]
= 350(cos270°)i + 350(sin270°)j
= -350j cos270° = 0; sin270° = — 1.
Заменяя R, S, и W in R + S + W + O, мы имеем
[|R|(cos125°) + |S|(cos37°)]i + [|R|(sin125°) + |S|(sin37°) — 350]j = 0i + 0j.
Это дает нам систему уравнений:
|R|(cos125°) + |S|(cos37°) = 0,
|R|(sin125°) + |S|(sin37°) — 350 = 0.
Решая эту систему, мы получаем
|R| ≈ 280 и |S| ≈ 201.
Таким образом, нагрузка на кабели 280 фунтов и 201 фунт.
Пусть $\overrightarrow{a}$ и $\overrightarrow{b}$ — два вектора (рис.1, а).
Возьмем произвольную точку О и построим вектор $\overrightarrow{ОА} = \overrightarrow{a}$ . Затем от точки А отложим вектор $\overrightarrow{AB} = \overrightarrow{b}$. Вектор $\overrightarrow{OB}$, соединяющий начало первого слагаемого вектора с концом второго (рис.1, б), называется суммой этих векторов и обозначается $\overrightarrow{a} + \overrightarrow{b}$$ (правило треугольника ).
Ту же самую сумму векторов можно получить иным способом. Отложим от точки О векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{ОС} = \overrightarrow{b} $ (рис.1, в). Построим на этих векторах как на сторонах параллелограмм ОABC. Вектор $\overrightarrow{ОВ}$, служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов $\overrightarrow{a} + \overrightarrow{b}$ {правило параллелограмма ).
2} = \sqrt{9 + 16} = 5
\\ т.е.\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = 5.
$$
Понятие суммы векторов можно обобщить на случай любого конечного числа слагаемых векторов.
Пусть, например, даны три вектора $\overrightarrow{a}, \overrightarrow{b} \,и\, \overrightarrow{c}$ (рис.2).
Построив сначала сумму векторов $\overrightarrow{a} + \overrightarrow{b}$ , а затем прибавив к этой сумме вектор $\overrightarrow{c}$, получим вектор $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c}$ . На рисунке 2
$$ \overrightarrow{ОА} = \overrightarrow{a}\,; \overrightarrow{АВ} = b\,; \overrightarrow{ОВ} = \overrightarrow{a} + \overrightarrow{b}\,; \overrightarrow{BC} = \overrightarrow{c}
\\ и
\\ \overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС} = (\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c}
$$
Из рисунка 2 видно, что тот же вектор $\overrightarrow{ОС}$ мы получим, если к вектору $\overrightarrow{ОА} = \overrightarrow{a}$ прибавим вектор
$\overrightarrow{АВ} = \overrightarrow{b} + \overrightarrow{c}$ .
Таким образом, $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})$ , т. е. сумма векторов обладает сочетательным свойством.
Поэтому сумму трех векторов $\overrightarrow{a}\,\,\overrightarrow{b}\,\,\overrightarrow{c}$ записывают просто $\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}$ .
Разностью двух векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ называется третий вектор $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ , сумма которого с вычитаемым вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$. Таким образом, если $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}\,\, то\, \overrightarrow{c} + \overrightarrow{b} = \overrightarrow{a}$ .
Из определения суммы двух векторов вытекает правило построения вектора-разности (рис.3).
Откладываем векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{OB} = \overrightarrow{b}$ из общей точки О.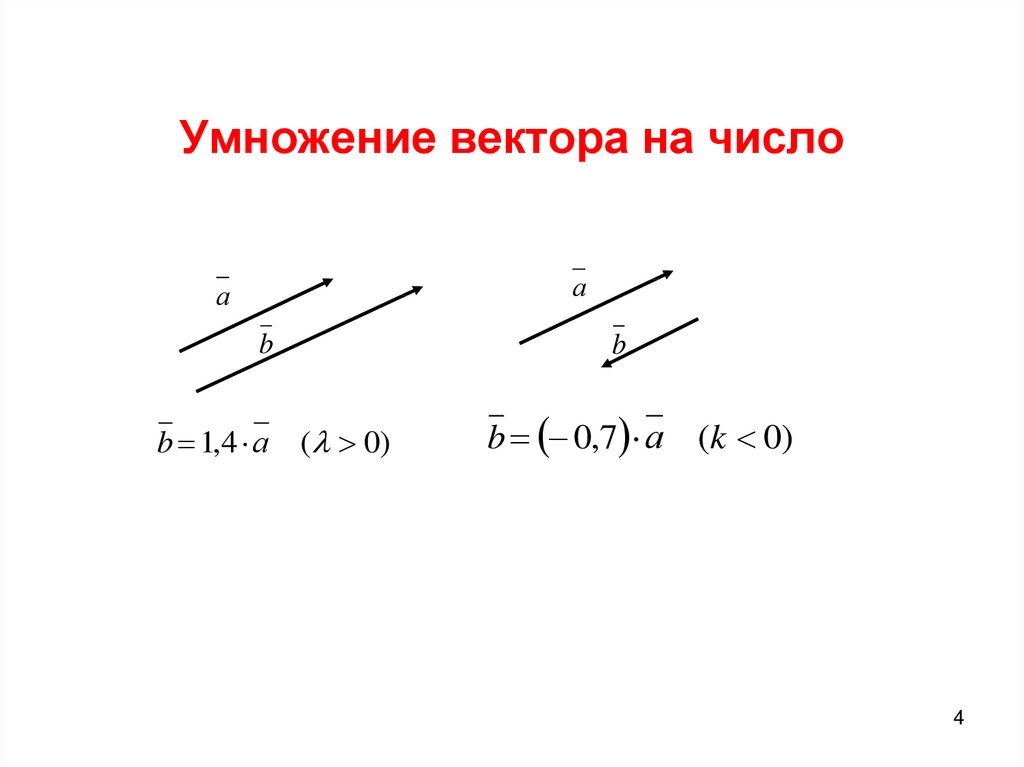
Вектор $\overrightarrow{BA}$ , соединяющий концы уменьшаемого вектора $\overrightarrow{a}$ и вычитаемого вектора $\overrightarrow{b}$ и направленный от вычитаемого к уменьшаемому, является разностью $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ . Действительно, по правилу
сложения векторов $\overrightarrow{ОВ} + \overrightarrow{ВА} = \overrightarrow{ОА} \text{ , или } \overrightarrow{b} + \overrightarrow{c} = \overrightarrow{a}$ .
Пример 2. Сторона равностороннего треугольника ABC равна а. Найти: $а) |\overrightarrow{ВА} — \overrightarrow{ВС}|\,;\,\ б)\,\,\ |\overrightarrow{АВ} — \overrightarrow{АС}|$ .
Решение а) Так как $\overrightarrow{ВА} — \overrightarrow{ВС} = \overrightarrow{СА}\text{ , а }|\overrightarrow{СА}| = а\text{ , то }|\overrightarrow{ВА} — \overrightarrow{ВС}| = а$ .
б) Так как $\overrightarrow{АВ} — \overrightarrow{АС} = \overrightarrow{СВ}\text{ , а }|\overrightarrow{СВ}| = а\text{ , то }|\overrightarrow{АВ} — \overrightarrow{АС}| = а$ .
Произведением вектора $\overrightarrow{a}$(обозначается $=\lambda\overrightarrow{a}$ или $\overrightarrow{a}\lambda$) на действительное число $\lambda$ называется вектор $\overrightarrow{b}$, коллинеарный вектору $\overrightarrow{a}$, имеющий длину, равную $|\lambda||\overrightarrow{a}|$, и то же направление, что и вектор $\overrightarrow{a}$, если $\lambda > 0$ , и направление, противоположное направлению вектора $\overrightarrow{a}$, если $\lambda
В случае, когда $\lambda = 0$ или $\overrightarrow{a} = 0$ , произведение $\lambda\overrightarrow{a}$ представляет собой нулевой вектор. Противоположный вектор $-\overrightarrow{a}$ можно рассматривать как результат умножения вектора $\overrightarrow{a}$ на $\lambda = -1$ (см. рис.4): $$ -\overrightarrow{a} = \ (-1)\overrightarrow{a} $$ Очевидно, что $\overrightarrow{a} + (-\overrightarrow{a}) = \overrightarrow{0}$ .
Пример 3. Доказать, что если О, А, В и С — произвольные точки, то $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{ВС} + \overrightarrow{СО} = 0$ .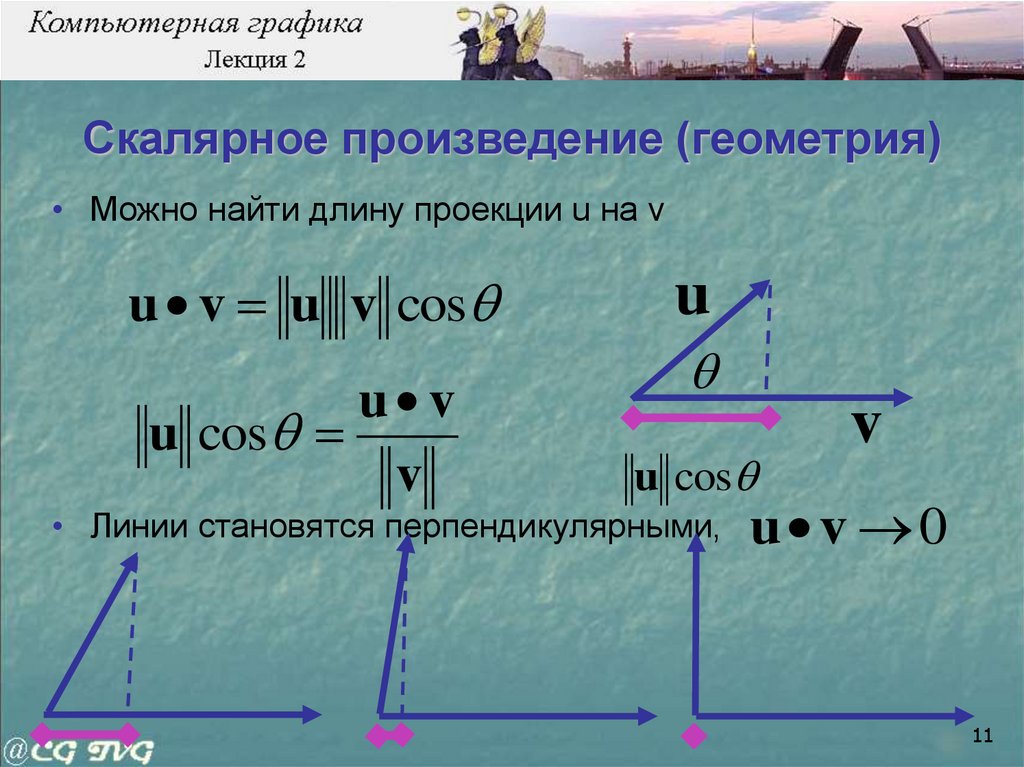
Решение. Сумма векторов $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{СВ} = \overrightarrow{ОС}$ , вектор $\overrightarrow{CO}$ — противоположный вектору $\overrightarrow{ОС}$ . Поэтому $\overrightarrow{ОС} + \overrightarrow{СО} = \overrightarrow{0}$ .
Пусть дан вектор $\overrightarrow{a}$. Рассмотрим единичный вектор $\overrightarrow{a_0}$ , коллинеарный вектору $\overrightarrow{a}$ и одинаково с ним направленный. Из определения умножения вектора на число следует, что
$$ \overrightarrow{a} = |\overrightarrow{a}|\,\ \overrightarrow{a_0} $$
, т.е. каждый вектор равен произведению его модуля на единичный вектор того же направления. Далее из того же определения следует, что если $\overrightarrow{b} = \lambda\overrightarrow{a}$ , где $\overrightarrow{a}$ — ненулевой вектор, то векторы $\overrightarrow{a} \,и\, \overrightarrow{b}$ коллинеарны. Очевидно, что и обратно, из коллинеарности векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ следует, что $\overrightarrow{b} = \lambda\overrightarrow{a}$.
Пример 4. Длина вектора AB равна 3, длина вектора AC равна 5. Косинус угла между этими векторами равен 1/15. Найдите длину вектора AB + AC.
Видео-решение.
Умножение скалярных векторов — проектирование цифровых систем
ДР. ШИРШЕНДУ РОЙ / 10 июня 2020 г. 19 февраля 2021 г. / Без рубрики
Умножение скаляра на вектор — очень важная арифметическая операция при реализации алгоритмов обработки сигналов или изображений. В этом уроке мы обсудим аппаратное обеспечение для умножения между матрицей 6X3 (A) и матрицей 3X1 (B), и результатом будет вектор-столбец 6X1 (C). Это умножение показано ниже на рисунке 1.
Рисунок 1: Умножение матрицы на вектор Это умножение может быть выполнено двумя способами: умножением вектора на вектор или умножением скаляра на вектор. При умножении на скалярный вектор один столбец матрицы и один элемент вектора-столбца B подаются на вычислительный процессор. Этот результат умножения суммируется с умножением 2-го столбца A и второго элемента B.
Таким образом, матричное и векторное умножение достигается путем скалярно-векторного умножения и накопления. Умножение между A и B может быть выражено как
Вычислительный блок разработан с использованием базового блока умножения и накопления (MAC). Эта единица умножает два элемента и накапливает. Схема этого блока MAC показана ниже на рисунке 2.
Рисунок 2: Схема MACОбщий вычислительный блок показан ниже на рисунке 3.
Рисунок 3: Умножитель скалярного вектораИспользуется шесть блоков MAC. Задержка блока MAC составляет два такта. Но после четырех тактов вычисляется вектор C. Вход сброса (первый) здесь очень важен. Регистр после сумматора в блоке MAC должен быть очищен перед умножением и перед запуском другого умножения. Временная диаграмма для вычисления блока MAC показана ниже на рисунке 4.
Рисунок 4: Выходной сигнал блока MAC по сравнению со статусом входа сброса Здесь P — выходной сигнал блока MAC. P1 — первый выход умножения, P2 — первый выход накопления, а P3 — конечный выход.
