Умножение вектора на число
Откладывание вектора от данной точки
Для того чтобы ввести понятие умножения вектора на число, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Определение 1
Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).

Рисунок 1. $\overrightarrow{a}$ отложенный от точки $A$
Введем следующую теорему:
Теорема 1
От любой точки $K$ можно отложить вектор $\overrightarrow{a}$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
Вектор $\overrightarrow{a}$ — нулевой.
В этом случае, очевидно, что искомый вектор — вектор $\overrightarrow{KK}$.
Вектор $\overrightarrow{a}$ — ненулевой.
Обозначим точкой $A$ начало вектора $\overrightarrow{a}$, а точкой $B$ — конец вектора $\overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)

Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Умножение вектора на число
Пусть нам дан вектор $\overrightarrow{a\ }$ и действительное число $k$.
Определение 2
Произведением вектора $\overrightarrow{a\ }$ на действительное число $k$ называется вектор $\overrightarrow{b\ }$ удовлетворяющий следующим условиям:
Длина вектора $\overrightarrow{b\ }$ равна $\left|\overrightarrow{b\ }\right|=\left|k\right||\overrightarrow{a\ }|$;
Векторы $\overrightarrow{a\ }$ и $\overrightarrow{b\ }$ сонаправлены, при $k\ge 0$ и противоположно направлены, если $k
Обозначение: $\ \overrightarrow{b\ }=k\overrightarrow{a\ }$.
Замечание 1
Отметим, что в результате произведения вектора на число всегда получается векторная величина.
Свойства произведения вектора на число
Произведение любого вектора с числом ноль равняется нулевому вектору.
Доказательство.
По определению 2, имеем $\left|\overrightarrow{b\ }\right|=\left|k\right|\left|\overrightarrow{a\ }\right|=0\cdot \left|\overrightarrow{a\ }\right|=0$, следовательно,$\overrightarrow{b\ }=k\overrightarrow{a\ }=\overrightarrow{0}$
Для любого вектора $\overrightarrow{a\ }$ и любого действительного числа $k$ векторы $\overrightarrow{a\ }$ и $k\overrightarrow{a\ }$ коллинеарны.
Доказательство.
Так как по определению 2, векторы $\overrightarrow{a\ }$ и $k\overrightarrow{a\ }$ сонаправлены или противоположно направлены (в зависимости от значения $k$), то они будут коллинеарны.
Для любых действительных чисел $m$ и $n$ и вектора $\overrightarrow{a\ }$ справедлив сочетательный закон:
\[\left(mn\right)\overrightarrow{a\ }=m(n\overrightarrow{a\ })\]Доказательство этого закона иллюстрирует рисунок 3.

Рисунок 3. Сочетательный закон
Для любых действительных чисел $m$ и $n$ и вектора $\overrightarrow{a\ }$ справедлив первый распределительный закон:
Доказательство этого закона иллюстрирует рисунок 4.

Рисунок 4. Первый распределительный закон
Для любого действительного числа $m$ и векторов $\overrightarrow{a\ }$ и $\overrightarrow{b\ }$ справедлив второй распределительный закон:
\[m\left(\overrightarrow{a\ }+\overrightarrow{b}\right)=m\overrightarrow{a\ }+m\overrightarrow{b\ }\]Доказательство этого закона иллюстрирует рисунок 5.

Рисунок 5. Второй распределительный закон
Пример задачи на использование понятия произведения вектора на число
Пример 1
Пусть $\overrightarrow{x}=\overrightarrow{a\ }+\overrightarrow{b}$, $\overrightarrow{y}=\overrightarrow{a\ }-\overrightarrow{b}$. Найти векторы:
$2\overrightarrow{x}+2\overrightarrow{y}$
$\overrightarrow{x}+\frac{1}{2}\overrightarrow{y}$
$-\overrightarrow{y}-\overrightarrow{x}$
Решение.
$2\overrightarrow{x}+2\overrightarrow{y}=2\left(\overrightarrow{a\ }+\overrightarrow{b}\right)+2\left(\overrightarrow{a\ }-\overrightarrow{b}\right)=2\overrightarrow{a\ }+2\overrightarrow{b}+2\overrightarrow{a\ }-2\overrightarrow{b}=4\overrightarrow{a\ }$
$\overrightarrow{x}+\frac{1}{2}\overrightarrow{y}=\overrightarrow{a\ }+\overrightarrow{b}+\frac{1}{2}\left(\overrightarrow{a\ }-\overrightarrow{b}\right)=\overrightarrow{a\ }+\overrightarrow{b}+\frac{1}{2}\overrightarrow{a\ }-\frac{1}{2}\overrightarrow{b}=\frac{3}{2}\overrightarrow{a\ }+\frac{1}{2}\overrightarrow{b}=\frac{3\overrightarrow{a\ }+\overrightarrow{b}}{2}$
$-\overrightarrow{y}-\overrightarrow{x}=-\left(\overrightarrow{a\ }-\overrightarrow{b}\right)-\left(\overrightarrow{a\ }+\overrightarrow{b}\right)=-\overrightarrow{a\ }+\overrightarrow{b}-\overrightarrow{a\ }-\overrightarrow{b}=-2\overrightarrow{a\ }$
Умножение вектора на число. Применение векторов к решению задач
На данном уроке мы рассмотрим новую операцию над векторами – умножение вектора на число. Кроме того, мы сформулируем законы умножения и научимся применять знания о векторах к решению различных задач.
На предыдущих уроках мы рассмотрели понятие вектора, ввели определения коллинеарных, сонаправленных, противонаправленных и равных векторов. Научились складывать и вычитать векторы, ввели законы сложения. Теперь нам нужно научиться умножать вектор на число. Особенность данной операции состоит в том, что число – это просто численная величина, не имеющая направления, а вектор – это направленный отрезок, имеющий численное измерение и направление.
Рассмотрим такую ситуацию: по дороге едут два автомобиля, скорость одного – 30 км/ч, а второго – 60 км/ч. Очевидно, что скорость второго автомобиля в два раза больше скорости первого, и скорость второго можно выразить через скорость первого, умножив скорость первого на два.
Определение
Произведение ненулевого вектора 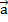 на число k – такой вектор
на число k – такой вектор 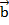 , длина которого равна
, длина которого равна 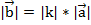
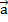 и
и 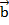 сонаправлены при
сонаправлены при 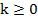 и противонаправлены при
и противонаправлены при 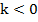 . Произведение нулевого вектора на любое число – это нулевой вектор.
. Произведение нулевого вектора на любое число – это нулевой вектор.Пусть задан вектор 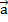 (см. Рис. 1). Вектор
(см. Рис. 1). Вектор 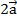 – это вектор, направленный в ту же сторону, но длина его в два раза больше.
– это вектор, направленный в ту же сторону, но длина его в два раза больше.
Вектор 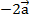 имеет длину, в два раза большую, чем вектор
имеет длину, в два раза большую, чем вектор  и ему противонаправлен.
и ему противонаправлен.
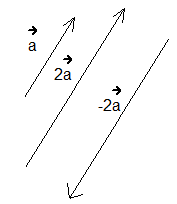
Рис. 1
Законы, которым подчиняется операция умножения вектора на число:
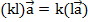 – сочетательный закон;
– сочетательный закон;
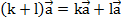 – первый распределительный закон;
– первый распределительный закон;
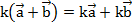 – второй распределительный закон.
– второй распределительный закон.
Анализ данных законов показывает, что действия с векторами аналогичны действиям с алгебраическими выражениями.
Пример 1 – упростить выражение:
Умножение вектора на число
Произведением вектора x на число β (x≠0, β≠0) называется вектор, модуль которого равен |x||β| и который направлен в ту же сторону, что и вектор x, если β>0, и в противоположную, если β<0. Если x=0 и (или) β=0, то βx=0.

Рис. 1
На рисунке Рис. 1 вектор x умножен на число 1.5. Полученный вектор y’ имеет то же направление, что и x т.к 1.5>0, и имеет длину 1.5 раз превысшающее длину x.
Вектор q имеет противополжное к p направление, т.к. вектор p умножено на отрицательное число -0.5, и имеет длину 2 раза меньше длины p.
Рассмотрим процесс умножения вектора на число.
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пусть имеется вектор

где  координаты вектора x, и пусть β некоторое число. Тогда
координаты вектора x, и пусть β некоторое число. Тогда

То есть для умножения вектора на число достаточно умножить каждый координат данного вектора на это число.
На рисунке Рис. 1 вектор x имеет координаты x=(6,4). Для умножения вектора x на число 1.5, умножим каждый координат вектора x на число 1.5:

Вариант 2. Начальные точки векторов произвольные.
Пусть имеется вектор x, с начальной точкой  и конечной точкой
и конечной точкой  . Умножим вектор x на число β. Для этого проще всего параллельно переместить вектор x на начало координат, умножить на число, после чего параллельно переместить началную точку полученного вектора на точку A.
. Умножим вектор x на число β. Для этого проще всего параллельно переместить вектор x на начало координат, умножить на число, после чего параллельно переместить началную точку полученного вектора на точку A.
Переместим вектор x на начало координат. Получим новый вектор x’ с начальными и конечными точками:
Умножим x’ на β:
  |
Параллельно переместив начальную точку вектора x’ на точку A, получим вектор x» с начальными и конечными точками:
На рисунке Рис. 1 вектор p=AB имеет координаты A(2,3) и B(8,1). Для умножения вектора p на число -0.5, сначала переместим параллельно вектор p так, чтобы начальная точка вектора p совпала с началом координат. Получим вектор p’=A’B’ с координатами A’(0,0) и B’(8-2, 1-3)=B’(6,-2). Умножим вектор p’ с числом -0.5:
  |
Перемесив начальную точку вектора q’ на точку A, получим вектор q=AE, где точка E имеет координаты:

Операция умножения вектора на число обладает следующими свойствами:
1.β(x+y)=βx+βy (дистрибутивность относительно сложения векторов).
2. (α+β)a=αa+βa (дистрибутивность относительно сложения чисел).
3. α(βa)=(αβ)a (ассоциативность).
4. 1·a=a (умножение на единицу).
Примеры умножения вектора на число
Пример 1. Умножить вектор y=(3,5,-6) на число 2.5.
Для умножения вектора y на число 2.5, просто умножаем каждый координат вектора y на данное число:  |
Пример 2. Умножить вектор x=AB на число 3, где A(2,2), B(7,6).
Переместим вектор AB на начало координат. Начальное и конечное точки перемещенного вектора будут:

Умножив полученный вектор на число 3, изменяется расположение конечной точки B’:
 .
.
Переместив вектор на точку A, получим вектор 3·x, со следующими начальной и конечной точками:

Сложение и вычитание векторов. Умножение вектора на число в координатах
На данном уроке мы рассмотрим технику выполнения действий над векторами в координатах. Мы сформулируем и докажем теоремы, рассмотрим конкретные примеры.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»
Ранее для выполнения действий с векторами мы применяли правило треугольника, правило параллелограмма, сжимали или растягивали вектор. Теперь мы научимся выполнять действия над векторами в координатах.
Пример
Даны векторы  ,
, 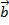 ,
, 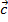 (см. рис. 1).
(см. рис. 1).
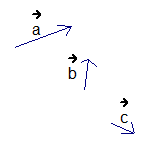
Рис. 1. Задача о сложении векторов
Найти: 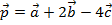
Решение
Из произвольной точки  строим вектор
строим вектор  . Далее из конца вектора
. Далее из конца вектора  строим вектор
строим вектор 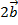 , он сонаправлен вектору
, он сонаправлен вектору 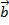 , а длина в два раза больше. Теперь из конца вектора
, а длина в два раза больше. Теперь из конца вектора 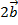 строим вектор
строим вектор  , он противоположно направлен вектору
, он противоположно направлен вектору 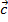 , а длина в 4 раза больше. Теперь соединяем точку
, а длина в 4 раза больше. Теперь соединяем точку  и конец вектора
и конец вектора  – получен ответ, вектор
– получен ответ, вектор 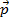 (см. рис. 2).
(см. рис. 2).
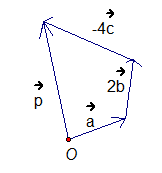
Рис. 2. Решение задачи
Пусть заданы два неколлинеарных вектора. Будучи отложены из одной точки, они задают косоугольную систему координат (см. рис. 3).
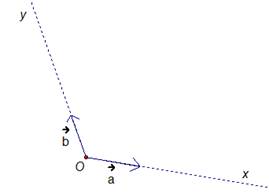
Рис. 3. Косоугольная система координат
Любой третий вектор однозначно выражается через векторы  ,
, 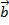
29.Умножение вектора на число. Свойства линейных операций над векторами.
Произведением
ненулевого вектора 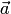 на
действительное число
на
действительное число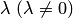 называется
вектор
называется
вектор ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
1) длина
вектора 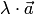 равна,
т.е.
равна,
т.е.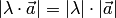 ;
;
2)
векторы 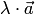 и
и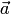 коллинеарные
коллинеарные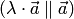 ;
;
3)
векторы 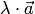 и
и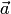 одинаково
направлены, если
одинаково
направлены, если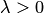 ,
и противоположно направлены, если
,
и противоположно направлены, если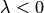 .
(рис. 9). Если среди сомножителей
.
(рис. 9). Если среди сомножителей 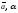 есть 0, то под произведением
есть 0, то под произведением понимается нулевой вектор.
понимается нулевой вектор.
Геометрический
смысл операции умножения вектора на
число следующий: если 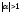 ,
то при умножении вектора
,
то при умножении вектора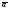 на число
на число вектор
вектор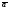 «растягивается» в
«растягивается» в раз, а если
раз, а если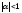 – «сжимается» в
– «сжимается» в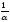 раз. На рис. 9 изображен случай
раз. На рис. 9 изображен случай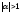 .
.
Утверждение
1. Если
векторы 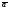 и
и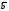 коллинеарны
и
коллинеарны
и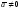 ,
то существует единственное число
,
то существует единственное число ,
что
,
что .
.
Свойства линейных операций над векторами
Сложение
векторов и умножение вектора на число
называются линейными
операциями над векторами.
Для любых векторов 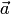 ,
,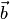 ,
,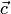 и
любых действительных чисел
и
любых действительных чисел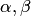 справедливы
равенства:
справедливы
равенства:
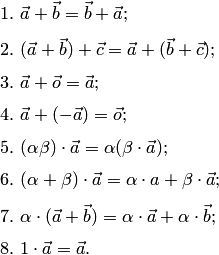
30.Угол между векторами. Скалярное произведение векторов

Скалярным
произведением двух
ненулевых векторов  и
и 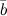 называется
число, равное произведению длин этих
векторов на косинус угла между ними:
называется
число, равное произведению длин этих
векторов на косинус угла между ними:
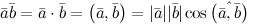

31. Составляющие вектора: на плоскости, по прямой и плоскости, по трем прямым
Проведём a и b,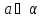 ,
, 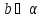 ,a
,a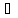 b,
b, 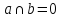 . Из точки О
отложим
. Из точки О
отложим 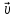 .По
правилу парал. сложения векторов устанав,
что
.По
правилу парал. сложения векторов устанав,
что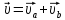 ,
где
,
где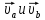 сост
вектора
сост
вектора 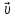 ,
леж на прямыхa и b,
соответственно. Предст вектора
,
леж на прямыхa и b,
соответственно. Предст вектора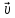 равенством назразлож
вектора
равенством назразлож
вектора 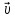 на
состав
на
состав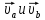 ,
леж на прямых a и b.Заданы
прямая
,
леж на прямых a и b.Заданы
прямая 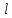 и плоскость
и плоскость 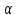 ,
причём
,
причём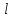 не лежит в
не лежит в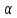 и не паралл
и не паралл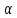 .
.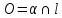 .
.
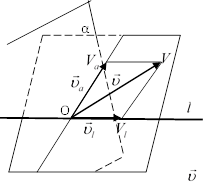
Возьмём 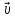 и отложим его от О. Получим
и отложим его от О. Получим .
Пусть точка
.
Пусть точка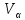 – проекцияV
на
– проекцияV
на  в направлении в направлении
в направлении в направлении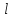 ,
то есть
,
то есть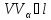 .
.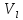 на
на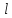 выбрана так, что
выбрана так, что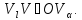
Тогда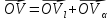 (1)
(1)
или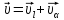 (2),где
(2),где явл сост
явл сост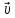 ,
леж на
,
леж на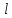 и на
и на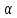 .Представление
.Представление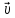 равенствами(1) или(2) назывразлож
равенствами(1) или(2) назывразлож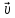 на
составл
на
составл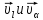 ,
леж на
,
леж на  и на
и на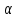 .Пусть
заданы три прямые a, b, c,
пересек в O
и не леж в одной плоскости.
.Пусть
заданы три прямые a, b, c,
пересек в O
и не леж в одной плоскости.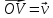 .
Разлаживаем
.
Разлаживаем  по прямa
и плосa:
по прямa
и плосa: 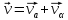
на
составляющие 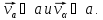 Теперь
Теперь 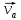 разложим на составляющие
разложим на составляющие 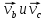 , леж наb
и c,
в a
:
, леж наb
и c,
в a
: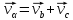 В
итоге имеем, что
В
итоге имеем, что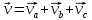 .где
.где 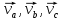 составляющиеv,леж
на a, b, c,соответственно.Представление
составляющиеv,леж
на a, b, c,соответственно.Представление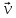 назыв разлож
назыв разлож 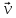 на сост
на сост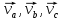 ,
леж наa, b, c.
,
леж наa, b, c.
Вопрос32. Разложение вектора по базису
Разложить 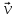 по базису
по базису 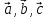 – это значит представить его
– это значит представить его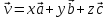 .Числкоэфx, y, zв
правой части равенства – координаты
.Числкоэфx, y, zв
правой части равенства – координаты 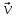 в базисе
в базисе 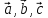 .Координаты
векторов (как и их сост.) обладают
след.св-ми (операции слож. векторов и
умн. на число): При
слож векторов их координаты
складываются. Разл.
вектора
.Координаты
векторов (как и их сост.) обладают
след.св-ми (операции слож. векторов и
умн. на число): При
слож векторов их координаты
складываются. Разл.
вектора 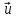 по базису
по базису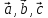 имеет вид
имеет вид
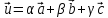 ,
где
,
где 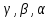 – действ.числа. Тогда сум.
– действ.числа. Тогда сум. ,
и предст. вектор
,
и предст. вектор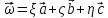 с координатами
с координатами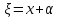 ,
,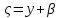 ,
, в базисе
в базисе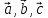
При
умнож.вектора на число его координаты
умнож. на это число.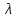 — действ. число. Разлож
— действ. число. Разлож по базису
по базису 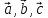 имеет вид
имеет вид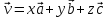 .
Тогда
.
Тогда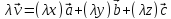 .Тройка
базисных векторов в пространстве наз.
Правой (левой), если эти векторы, отлож.
от одной точки, распол. так, как распол.
большой, указательный и средний пальцы
правой (левой) руки.
.Тройка
базисных векторов в пространстве наз.
Правой (левой), если эти векторы, отлож.
от одной точки, распол. так, как распол.
большой, указательный и средний пальцы
правой (левой) руки.
Вопрос33.Прямоугольные декартовы координаты в пространстве
Координатами
вектора 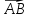 ,
начало кот. Точка А(
,
начало кот. Точка А(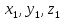 ),
а конец В(
),
а конец В(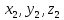 )
в прям. дек. системе координатOxyz
наз. числа
)
в прям. дек. системе координатOxyz
наз. числа 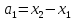 ,
,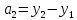 ,
,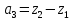 . Сначала фикс. в прям. дек. сист. координат
Охуz
точку А(х, у, z).
Потом строят точку В(х+
. Сначала фикс. в прям. дек. сист. координат
Охуz
точку А(х, у, z).
Потом строят точку В(х+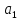 ,
у+
,
у+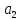 ,
z+
,
z+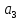 ).
Получаем
).
Получаем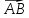 равн.
равн.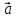 .
Радиусом-вектором – наз. вектор
.
Радиусом-вектором – наз. вектор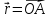 с точкой прилож. в нач. координат О, а
конец — в А.
с точкой прилож. в нач. координат О, а
конец — в А.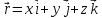 .
.
Умножение вектора на число [wiki.eduVdom.com]
Теорема 1. Два вектора $\overrightarrow{a}$ и $\overrightarrow{b}$ коллинеарны тогда и только тогда, когда имеет место равенство $\overrightarrow{b} = \lambda\overrightarrow{a}$ .
Умножение вектора на число обладает следующими основными свойствами.
Свойства. Для любых чисел k, l и любых векторов $\overrightarrow{a}\,, \overrightarrow{b}$ справедливы следующие равенства:
$(kl)\overrightarrow{a} = k(l\overrightarrow{a})$ {сочетательный закон).
$(k + l)\overrightarrow{a} = k\overrightarrow{a} + l\overrightarrow{a}$ {первыйраспределительный закон).
$k(\overrightarrow{a} + \overrightarrow{b}) = k\overrightarrow{a} + k\overrightarrow{b}$ {второй распределительный закон).
Рисунок 1 иллюстрирует сочетательный закон. На этом рисунке представлен случай, когда k = 2, l = 3.
Рис.1
Рисунок 2 иллюстрирует первый распределительный закон. На этом рисунке представлен случай, когда k = 3, l = 2.
Рис.2
Примечание. Рассмотренные свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например, выражение
$$ \overrightarrow{р} = 2(\overrightarrow{a} — \overrightarrow{b}) + (\overrightarrow{c} + \overrightarrow{a}) — 3(\overrightarrow{b} — \overrightarrow{c} + \overrightarrow{a}) $$
можно преобразовать так:
$$ \overrightarrow{р} = 2\overrightarrow{a} — 2\overrightarrow{b} + \overrightarrow{c} + \overrightarrow{a} — 3\overrightarrow{b} + 3\overrightarrow{c} — 3\overrightarrow{a} = — 5\overrightarrow{b} + 4\overrightarrow{c} $$
Пример 1. Коллинеарны ли векторы $2\overrightarrow{a} \,и\, -\overrightarrow{a}$ ?
Решение. Имеем $2\overrightarrow{a} = -2(-\overrightarrow{a})$ . Значит, данные векторы коллинеарны.
Пример 2. Дан треугольник ABC. Выразите через векторы $\overrightarrow{a} = \overrightarrow{АВ} \,и\, \overrightarrow{b} = \overrightarrow{АС}$ следующие векторы: $а)\, \overrightarrow{ВА}\text{ ; б) }\overrightarrow{СВ}\text{ ; в) }\overrightarrow{СВ} + \overrightarrow{ВА}$ .
Решение
а) Векторы $\overrightarrow{ВА} \,и\, \overrightarrow{АВ}$ — противоположные, поэтому $\overrightarrow{ВА} = -\overrightarrow{АВ}\text{ , или }\overrightarrow{ВА} = -\overrightarrow{a}$ .
б) По правилу треугольника $\overrightarrow{СВ} = \overrightarrow{СА} + \overrightarrow{АВ}$ . Но $\overrightarrow{СА} = -\overrightarrow{АС}$ , поэтому $\overrightarrow{СВ} = \overrightarrow{АВ} + (-\overrightarrow{АС}) = \overrightarrow{АВ} -\overrightarrow{АС} = \overrightarrow{a} — \overrightarrow{b}$ .
в) $\overrightarrow{СВ} + \overrightarrow{ВА} = \overrightarrow{СА} = -\overrightarrow{АС} = -\overrightarrow{b}$.
Умножение вектора на число
Векторы: \( \mathbf{u} \), \( \mathbf{v} \), \( \mathbf{w} \)
Нулевой вектор: \( \mathbf{0} \)
Координаты векторов: \( X \), \( Y \), \( Z \)
Действительные числа: \( \lambda \), \( \mu \)
Произведением вектора на число
Произведением вектора \( \mathbf{u} \ne \mathbf{0} \) на число \( \lambda \ne 0 \) называется вектор \( \mathbf{w} \), модуль которого равен \( \left| \lambda \right| \cdot \left| \mathbf{u} \right| \), направление которого совпадает с вектором \( \mathbf{u} \) при \( \lambda > 0 \) и противоположно ему при \( \lambda
\(\mathbf{w} = \lambda \mathbf{u},\;\;\left| \mathbf{w} \right| = \left| \lambda \right| \cdot \left| \mathbf{u} \right|\)
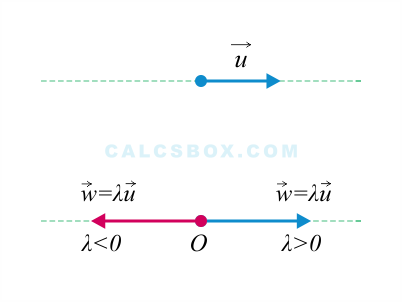
Произведение вектора \( \mathbf{u} \) на число \( \lambda \) при \( \lambda = 0 \) и/или \( \mathbf{u} = \mathbf{0} \) равно нулевому вектору \( \mathbf{0} \).
Операция умножения вектора на число обладает следующими линейными свойствами :
Коммутативность умножения вектора на число
\( \lambda \mathbf{u} = \mathbf{u}\lambda \)
Дистрибутивность умножения относительно сложения чисел
\( \left( {\lambda + \mu } \right)\mathbf{u} = \lambda \mathbf{u} + \mu \mathbf{u} \)
Дистрибутивность умножения относительно сложения векторов
\( \lambda \left( {\mathbf{u} + \mathbf{v}} \right) = \lambda \mathbf{u} + \lambda \mathbf{v} \)
Ассоциативность умножения вектора на число
\( \lambda \left( {\mu \mathbf{u}} \right) = \mu \left( {\lambda \mathbf{u}} \right) = \left( {\lambda \mu } \right)\mathbf{u} \)
Умножение вектора на единицу
\( 1 \cdot \mathbf{u} = \mathbf{u} \)
Умножение вектора на число в координатной форме
\( \lambda \mathbf{u} = \left( {\lambda X,\lambda Y,\lambda Z} \right) \)
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость





