Умножение вектора на число геометрия: Умножение вектора на число — урок. Геометрия, 9 класс. — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Умножение вектора на число Л.С. Атанасян «Геометрия 7-9» Савченко Е.М., учитель — презентация

Первый слайд презентации

Умножение вектора на число Л.С. Атанасян «Геометрия 7-9» Савченко Е.М., учитель математики, МОУ гимназия №, г. Полярные Зори, Мурманской обл.

Изображение слайда

Слайд 2

Прежде, чем ввести еще одно действие – умножение вектора на число, обратимся к примеру. Представим себе, что один автомобиль движется прямолинейно с постоянной скоростью, второй движется в том же направлении со скоростью, вдвое большей, а третий автомобиль движется им навстречу, т.е. в противоположном направлении, и величина его скорости такая же, как у второго автомобиля. ТАКСИ v 2v -2v Если мы изобразим скорость первого автомобиля вектором v, то естественно изобразить скорость второго автомобиля вектором, у которого направление такое же, как у вектора v, а длина в 2 раза больше, и обозначить этот вектор 2 v.

Скорость третьего автомобиля изобразиться вектором, противоположным вектору 2 v, т.е. вектором -2 v. Естественно считать, что вектор 2 v получается умножением вектора v на число 2, а вектор -2 v получается умножением вектора v на число -2. Этот пример показывает каким образом следует вести умножение вектора на число и что при умножении получается вектор.

Изображение слайда

Слайд 3

Умножение вектора на число. Произведением ненулевого вектора на число называется такой вектор, длина которого равна, причем векторы и сонаправлены при и притивоположно направлены при. a k a b a k k>0 b k<0 a 3 a 1 a 1 2 — 2 a

Изображение слайда

Слайд 4

Умножение вектора на число. a b 2b 2b b b 2b 2 = 2 a 1 2 a 1 a 2 a 1 a 2 1 =

Изображение слайда

Слайд 5

Умножение вектора на число.

Произведение любого вектора на число нуль есть нулевой вектор. o a o = Произведение нулевого вектора на любое число считается нулевой вектор. o o k = Для любого числа и любого вектора векторы и коллинеарны. a k a ka a — 2 a — a 1 2 1 a 1 2

Изображение слайда

Слайд 6

A B C D N M R E S F H J K L Z Q V T Y U Назовите вектор, который получится в результате умножения. I O P X G

Изображение слайда

Слайд 7

XT = XT х -4 4 1 – 4 3 – 0 СК = JO х A B C D N M R E S F H J K L Z Q V T Y U I O P X G JO = CK х XD = CK х NN = XD х ХТ = XD х х не существует 1 TX = XT х -1

Изображение слайда

Слайд 8

2 ВК = ОК х 3 A C O K T B О – точка пересечения медиан треугольника. 3 1 – К O = В K х ОВ = КО х

Изображение слайда

Слайд 9

х DO = KF –4 A C 7 T B AC = T В х 3 T В = 7 AC = 3 O D K F 10 2,5 DO = 10 KF = 2,5 7 3 TB = AC х 3 7 KF = DO х 4 1 –

Изображение слайда

Слайд 10

х D S L K SD = LK Длина вектора SD на 25% меньше длины вектора LK 1,25 A C T B ТВ = АС х Длина вектора TB на 25% больше длины вектора АС -0, 7 5

Изображение слайда

Слайд 11

BC = DA 8 В С ABCD – трапеция. А D 10 х –0,8 DA = BC х – 8 10

Изображение слайда

Слайд 12

– 3 8 В С ABCD – параллелограмм. CS : SB = 5 : 3 А D BS = DA х – 8 3 S х DA = BS

Изображение слайда

Слайд 13

Умножение вектора на число обладает следующими основными свойствами. k (l a) (kl)a = Сочетательный закон Первый распределительный закон Второй распределительный закон k (a + b) = ka + kb (k+l)a = ka + la Для любых, и любых чисел, справедливы равенства: a b b k l 1 2 3

Изображение слайда

Слайд 14

B O a Рисунок иллюстрирует сочетательный закон. Представлен случай, когда k = 2, l = 3. k (l a) (kl)a = Сочетательный закон 1 B O A O В = 2OA = 2( 3 ) a a a a O В = 6 a a a = (2 3 ) a a a a

Изображение слайда

Слайд 15

B Рисунок иллюстрирует первый распределительный закон.

Представлен случай, когда k = 3, l = 2. O a Первый распределительный закон 2 A ka l a OA = ka ; AB = la (k+l)a = ka + la OB = (k+l)a = ka + la

Изображение слайда

Слайд 16

O a Второй распределительный закон 3 A k (a + b) = ka + kb Рисунок иллюстрирует второй распределительный закон. На рисунке, коэффициент подобия ОАВ ОА 1 В 1 k A 1 B 1 B b a+b OA = ka k(a+b) kb AB = OB = ka+kb OB = OA + AB = С другой стороны, Таким образом, k(a+b) ka+kb =

Изображение слайда

Слайд 17

№ 781 Пусть х = m + n, y = m – n Выразите через и векторы m n 2х – 2у 2х + у 2 1 –х – у 3 1

Изображение слайда

Слайд 18

Задача Построить вектор С А В

Изображение слайда

Слайд 19

Задача Построить вектор С А В

Изображение слайда

Слайд 20

Задача Построить вектор.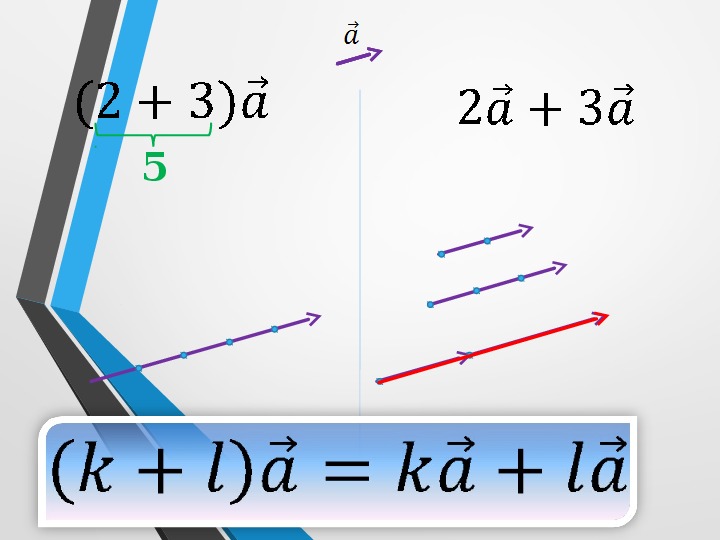 С А В = АВС D – параллелограмм. D CA AC

Изображение слайда

Слайд 21

Построить вектор. С А В D AC Задача АВС D – параллелограмм.

Изображение слайда

Слайд 22

B Точка С – середина отрезка АВ, а О – произвольная точка плоскости. Доказать, что Задача A O O А + АС O С = O В + ВС O С = + 2 O С = ОА + ОВ + АС + ВС 0 ( ) 2 O С = ОА + ОВ : 2 O С = (ОА + ОВ) 1 2 C

Изображение слайда

Слайд 23

2 NM = NB + NA + АС + В M + CM 0 ( ) A NB + BM NM = NM = + 2 NM = AC : 2 NM = AC 1 2 Задача Докажите теорему о средней линии треугольника. В С N M NA + A С + CM 0 ( ) NM = AC 1 2 NM AC

Изображение слайда

Слайд 24

Теорема Средняя линия трапеции параллельна основаниям и равна их полусумме. Дано: трапеция АВС D, MN — средняя линия Доказать:

Изображение слайда

Слайд 25

2 NM = NB + NA + B С + AD + CM +DM 0 ( ) Правило многоугольника 0 ( ) A NM = NM = + : 2 В С N M NA + AD + DM D NB + B С + СМ 2 NM = В C + AD NM = (BC+AD) 1 2 NM = BC+AD 1 2 NM BC AD; Доказать:

Изображение слайда

Слайд 26

Задача АВС D – ромб. Е ВС, ВЕ : ЕС = 3 : 1, К – середина DC, АВ =, AD =. Выразите через векторы и векторы: С А В a b a D b a b E K AE AK KE

Изображение слайда

Последний слайд презентации: Умножение вектора на число Л.С. Атанасян «Геометрия 7-9» Савченко Е.М., учитель

АВ — СВ = — ОА — РО = MN — RN = — KM + KM = — KM + OM = А S — С S = — MN — LM = RP — RP = — KZ + KZ = — ED + KD = MK + К O + OP + PR = SK + К V + VP + PM =

Изображение слайда

описание, примеры / Справочник :: Бингоскул

Основные свойства умножения вектора на число: описание, примеры добавить в закладки удалить из закладок

Содержание:

Изучающие математические науки и физику, начиная со старших классов, знакомятся с понятием «вектор». Это направленный отрезок, отличающийся от обычного (ненаправленного) рядом характеристик. Рассмотрим основные свойства умножения вектора на число. Ознакомимся с необходимыми для работы понятиями, приведём примеры задач.

Теория

Вектором называется отрезок, один конец которого указывает на направление, то есть это — ограниченное двумя точками пространство на прямой с указанным направлением. Является основой линейной алгебры. Векторы бывают коллинеарными – параллельными, причем могут лежать на одной прямой, неколлинеарными и нулевыми – начало совпадает с окончанием. Кроме направленности характеризуются длиной или модулем, который обозначается как |BC|.

Векторы применяются в геометрии, компьютерной графике, например, для создания карт освещения, прокладывания траекторий движения. Позволяют быстро вычислять площади геометрических фигур и объёмы тел. В физике векторами являются величины, имеющие направление: сила, ускорение. Обозначаются буквами с чёрточками, например, \overline{a}, \overline{b}, (\overline{c};\overline{d}) или \overline{A}B.

Умножение вектора на число

С направленным отрезком можно совершать ряд математических действий и преобразований. К таким относятся упрощение, суммирование, произведение. Сформулируем основные свойства умножения вектора на число, покажем, как их умножать в разнообразных ситуациях.

Произведением направленного отрезка ( \overline{c}; \overline{d}) на x называется величина ( \overline{x}c; \overline{x}d)=x*( \overline{c}; \overline{d}) .

При умножении пары чисел на вектор работают знакомые с начальных классов правила:

( a + b ) * \overline{x} = a \overline{x} + b \overline{x} ;

( \overline{a} + \overline{b} ) * x = \overline{a}x + \overline{b}x ; .

Особенности и закономерности произведения чисел и направленных отрезков:

При работе с отрицательным числом направление отрезка меняется на противоположное.

При константе между -1 и 1 модуль уменьшается.

Когда постоянная равна нулю, получим нулевой модуль.

Для умножения \overline{p} (x, y, z) на величину a находят произведение каждой координаты: \overline{p}1 (ax, ay, az).

Становится понятно, что произведением ненулевого вектора на число называется коллинеарный вектор. В геометрии:

с тем же направлением, что исходный, если умножаем на положительное число;

противоположно направленный, когда действие осуществляется с отрицательным числом,

длина которого равна произведению модуля изначального отрезка на модуль числа.

В алгебре следствием произведения будет тот же вектор, сдвинутый в координатной сетке на указанное число в направлении, которое зависит от его знака.

Физический смысл преобразования – инверсия направления величины (действия силы) в зависимости от знака числа (если отрицательное, меняется на противоположное) с изменением её значения в n (модуль) раз.

Модули можно возводить в степень, перемножать между собой.

Поделитесь в социальных сетях:

13 ноября 2021, 18:24

Геометрия

Could not load xLike class!

4.

5: Геометрический смысл скалярного умножения

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 14521

Кен Каттлер
Университет Бригама Янга via Lyryx 9{2}}\nonumber \] Таким образом, верно следующее. \[\| к \vec{u} \| =\левый\верт к \правый\верт \| \vec{u} \|\nonumber \] Другими словами, умножение на скаляр увеличивает или уменьшает длину вектора в \(\left\vert k \right\vert\). Если \(\left\vert k \right\vert > 1\), длина результирующего вектора будет увеличена. Если \(\left\vert k \right\vert <1\), длина результирующего вектора будет уменьшаться. Помните, что по определению абсолютного значения \(\left\vert k \right\vert >0\).
А как насчет направления? Нарисуйте изображение \(\vec{u}\) и \(k\vec{u}\), где \(k\) отрицательно. Обратите внимание, что это приводит к тому, что результирующий вектор указывает в противоположном направлении, в то время как если \(k>0\), он сохраняет направление, на которое указывает вектор. Поэтому направление может либо измениться, если \(k < 0\), либо остаться прежним, если \(k > 0\).
Рассмотрим следующий пример.
Пример \(\PageIndex{1}\): графическое скалярное умножение
Рассмотрим векторы \(\vec{u}\) и \(\vec{v}\), нарисованные ниже.
Рисунок \(\PageIndex{1}\)
Рисование \(-\vec{u}\), \(2\vec{v}\) и \(-\frac{1}{2}\vec{ v}\).
Решение
Чтобы найти \(-\vec{u}\), мы сохраняем длину \(\vec{u}\) и просто меняем направление. Для \(2\vec{v}\) мы удваиваем длину \(\vec{v}\), сохраняя при этом направление. Наконец, \(-\frac{1}{2}\vec{v}\) можно найти, взяв половину длины \(\vec{v}\) и изменив направление. Эти векторы показаны на следующей диаграмме.
Рисунок \(\PageIndex{2}\) 9п\) есть сумма векторов, умноженных на скаляры.
В следующем примере мы исследуем геометрический смысл этого понятия.
Пример \(\PageIndex{2}\): построение графика линейной комбинации векторов
Рассмотрим следующее изображение векторов \(\vec{u}\) и \(\vec{v}\)
Рисунок \( \PageIndex{3}\)
Нарисуйте изображение \(\vec{u}+2\vec{v},\vec{u}-\frac{1}{2}\vec{v}.\)
Решение
Два вектора показаны ниже.
Рисунок \(\PageIndex{4}\)
Эта страница под названием 4.5: Геометрическое значение скалярного умножения распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
1. Наверх
- Была ли эта статья полезной?
1. Тип изделия
  Раздел или Страница
  Автор
  Кен Каттлер
  Лицензия
  СС BY
  Версия лицензии
  4,0
  Показать страницу TOC
  нет
2. Теги
  1. источник@https://lyryx. com/first-course-linear-алгебра
Векторная математика стала проще в Blender и узлах геометрии — CG Cookie
Давайте поговорим о том, что такое векторы, почему они так важны для понимания 3D-приложений и как использовать наиболее важные векторные математические операции визуальным и интуитивно понятным способом. что я не думаю, что вы забудете.
А вектор это просто набор цифр. В контексте Blender и 3D-графики мы обычно говорим о наборе из трех чисел — по одному для каждого измерения. Если вы нанесете эти три числа на трехмерный график, вы получите точку в пространстве.

Вы также можете думать о векторе как о стрелке, которая указывает от начала координат до этой точки в пространстве. И точка, и стрелка являются допустимыми способами визуализации вектора, но стрелка будет гораздо более интуитивно понятной.

Многие люди избегают использования математических операций в Blender. Я тоже делал это долгое время, потому что просто предполагал, что это для людей, которые более умны или технически подкованы. Если вы чувствуете то же самое, я не хочу, чтобы вы думали об этом с точки зрения чисел и уравнений.
Я уверен, что вам нужно было узнать, что такое скос и выдавливание, в какой-то момент, когда вы были новичком в 3D-моделировании, но, конечно, вам не нужно было знать алгоритмы, лежащие в основе инструментов, чтобы использовать их — это было бы смешно. Точно так же я хочу, чтобы вы думали об этих операциях с точки зрения изучения нового инструмента. Если вы можете просто связать название математической операции с эффектом, который она оказывает на стрелку, представляющую вектор, вы сможете сразу же начать интуитивно ее использовать.

Добавление векторов
Здесь я использовал узлы геометрии Blender для создания стрелки сетки, которая начинается в какой-то точке и показывает нам направление и длину любого вектора. Я создам стрелку для вектора A, другую стрелку для вектора B, а затем соединим их вместе. Как вы думаете, как будет выглядеть полученная стрелка, когда мы сложим два вектора?

Теперь я воспользуюсь векторным математическим узлом, чтобы сложить два вектора вместе и визуализировать это как вектор C. Результат находится где-то между первыми двумя, и я не нахожу его интуитивно понятным, пока мы не сделаем маленькая хитрость.

На уроках математики вы, возможно, узнали, что вектор имеет только размер и направление. Чтобы визуализировать его, мы должны дать ему некоторую точку в пространстве, с которой можно начать. В моих узлах со стрелками сетки все начальные точки в настоящее время равны [0,0,0], но мы можем изменить это на что угодно, и это не повлияет на сам вектор. Даже если я перемещаю начальные точки, вектор A плюс вектор B по-прежнему равен вектору C. Размеры и направления стрелок одинаковы независимо от того, где они находятся. Итак, если мы можем разместить их там, где хотим, мы можем также переместить их в любую конфигурацию, наиболее полезную для понимания результата.

Посмотрите, что произойдет, если я начну векторы A и C в начале координат, а вектор B начну с конца вектора A. Посмотрите, как результирующий вектор C указывает на конец вектора B. Я могу изменить любой вектор на любой набор из трех чисел, и так будет всегда.

Вы можете добавить столько векторов, сколько захотите, и результат всегда будет указывать от начала до конца, если вы сложите их вместе.

Если вы хотите выполнить математику, вы можете просто сложить все значения X вместе, значения Y вместе и все значения Z вместе.

Но визуально сложение — это просто наложение векторов друг на друга и сокращение от начала до конца.
Вычитание векторов
Вычитание — это просто сложение противоположного вектора.

Если бы мы перевернули вектор B, наш треугольник был бы завершен. Независимо от того, делаем ли мы это с одним числом или с набором из трех, вычитание всегда является просто сложением, но с противоположным числом. A — B такой же, как А + (-В) .
Начальные точки
В этот момент вам может быть интересно, как же можно произвольно перемещать вектор, когда мы также можем визуализировать его как точку в пространстве. Как можно переместить точку в пространстве туда, куда мы хотим? Что ж, на самом деле это основа того, как все работает в компьютерной графике: все относительно!
Сам вектор, набор из трех чисел, ничего не говорит вам о начальной точке, с которой он связан. Начальная точка, она же происхождение, и вектор — две разные вещи. Нам всегда нужны обе части информации, чтобы визуализировать вектор.
Начальная точка вершины будет исходной точкой объекта, начальной точкой дочернего объекта будет родительский объект, а начальной точкой любого объекта без родителя будет мировая исходная точка. Blender знает, где нарисовать вершину в окне просмотра, сложив все эти векторы вместе!

Перемещение путем добавления или вычитания
В узлах геометрии мы можем смещать элементы, добавляя или вычитая из их текущего положения. В приведенном ниже примере я могу заставить Мелвина двигаться влево или вправо от кривой, добавляя или вычитая нормаль кривой к его положению.

Таким же образом мы можем перемещать любую текстуру в редакторе шейдеров, добавляя или вычитая ее векторные координаты.

Везде, где вы видите векторы в Блендере, добавление и вычитание будет тем, как вы перемещаете точку в пространстве, на которую указывает вектор.
Масштабирование векторов
Интереснее становится умножение. Если вы попросите студента-математика умножить вектор, он может вернуться к вам с несколькими разными ответами, потому что умножение может означать несколько разных вещей, когда речь идет о наборах чисел.
Первое, о чем мы поговорим, это масштабирование вектора. Когда вы масштабируете вектор, он указывает в том же направлении, но становится длиннее или короче. Функция масштабирования на узле векторной математики — это то же самое, что и умножение вектора на одно число, поэтому мы могли бы точно так же использовать узел векторной математики, установленный для умножения, а затем ввести одно и то же значение для X, Y и Z. оси. Функция масштабирования предназначена только для удобства.

Blender также позволяет независимо масштабировать каждую ось, если вы хотите, используя эту функцию умножения. Здесь мы можем ввести второй вектор для масштабирования вектора A по оси X, оси Y или оси Z.

Это называется поэлементным умножением, и ниже показано, как выглядит это уравнение, если вам интересно.

Как видите, масштабирование объектов в 3D-виде работает точно так же. Если мы направим наш вектор на вершину куба, а затем масштабируем наш куб, нам просто нужно умножить наш вектор на ту же величину, на которую мы масштабировали куб, и мы всегда сможем указать прямо на эту вершину. Масштабирование объектов в 3D — это просто умножение их векторов.

Одной из полезных операций, связанных с масштабированием, является нормализация. Это возьмет любой вектор и установит его длину равной единице. Если нам нужно установить вектор какой-либо определенной длины, мы можем сначала нормализовать его, а затем масштабировать.

Чтобы найти длину вектора, мы можем использовать операцию длины.

Деление, в данном случае, является полной противоположностью нашего поэлементного умножения. При делении чем меньше значение, тем больше будет результат. По мере приближения к нулю шкала будет приближаться к бесконечности, поэтому будьте осторожны с маленькими числами. К счастью, Blender не позволит вам взорвать ваш компьютер делением на ноль.
Точно так же в редакторе шейдеров умножение и деление позволяют масштабировать координаты текстуры.

Короче говоря, везде, где вы видите векторы в Blender, умножение и деление — это то, как вы масштабируете их.
Вращение векторов
Теперь, когда мы рассмотрели перемещение и масштабирование, давайте рассмотрим вращение. Вращение вектора немного сложнее математически и могло бы стать темой для другого дня, но мы можем легко сделать это в Blender с помощью нода Vector Rotate.
Мы можем использовать его для поворота вектора вокруг глобальной оси X, глобальной оси Y, глобальной оси Z, эйлеровой комбинации всех трех, или, если мы установим его на угол оси, мы можем повернуть вектор вокруг любой другой вектор.

Чтобы узнать больше о том, как работает вращение Эйлера, посмотрите мое предыдущее видео об узле Выравнивание Эйлера по вектору.
Скалярное произведение
Ранее я упоминал, что существует больше способов умножения векторов, чем просто умножение каждой оси по отдельности. Двумя другими наиболее полезными типами умножения векторов являются скалярное произведение и векторное произведение. Эти две вещи часто упоминаются как сбивающие с толку, но на самом деле это не обязательно.
Скалярный продукт возвращает одно значение, которое полезно для сравнения того, насколько похожи два вектора. Если два нормализованных вектора указывают в одном направлении, т. е. параллельны, скалярное произведение равно 1. Если они указывают в противоположных направлениях, скалярное произведение равно -1. Если они перпендикулярны, скалярное произведение равно 0. Если векторы не нормализованы и не имеют длины 1, то результат может быть меньше -1 или больше +1, поэтому я обычно сначала нормализую их.

Это чрезвычайно полезно для определения того, указывают ли два объекта друг на друга или в разные стороны. В приведенном ниже примере я использую надстройку LibSM64, чтобы добавить играбельного Марио в мою сцену Blender. Я использовал скалярное произведение для управления персонажем Бу, который преследует Марио, когда он повернут спиной (скалярное произведение больше 0), но прячется, когда они смотрят друг на друга (скалярное произведение меньше 0).

Сравнение двух векторов также может быть полезно в редакторе шейдеров. В приведенном ниже примере я сравниваю обычные нормали сетки со скошенными нормалями, чтобы замаскировать скошенные части.

Фактическое уравнение просто умножает значения X, Y и Z вместе, а затем складывает результат.

Но все, что вам действительно нужно знать, чтобы использовать его, это то, что скалярный продукт сравнивает, насколько похожи два вектора, и, если вы сначала нормализуете векторы, результат всегда будет между -1 и +1.
Перекрестное произведение
Перекрестное произведение, с другой стороны, также является формой умножения, но оно возвращает новый вектор вместо одного числа. Все, что вам действительно нужно знать, это то, что новый вектор перпендикулярен двум входным данным. Если вектор A расположен вдоль оси X, а вектор B — вдоль оси Y, результат всегда будет равен оси Z. Или, если вы думаете, что вектор A и вектор B создают поверхность, векторное произведение будет нормалью этой поверхности. Перекрестное произведение дает вам трехмерное направление для работы, когда у вас есть только два.

Это особенно полезно при работе с кривыми. У нас есть нормаль и касательная для работы, но что, если нам нужно что-то переместить в этом третьем измерении? Ну, мы просто возьмем векторное произведение нормали и касательной, чтобы получить третью ось. Если вы хотите, чтобы он указывал в другую сторону, просто переключите входы.

Вы всегда можете запомнить векторное произведение, потому что результат указывает на двух входных данных.
Разное Операции
Есть еще несколько операций, о которых полезно знать.
Расстояние вычисляет длину прямой линии между точками двух векторов. Просто помните, что векторы всегда относятся к некоторой начальной точке, и эти операции будут вычислять их как исходящие из одной и той же точки. Вы можете перемещать визуализацию векторов куда угодно, но результирующее расстояние не изменится, потому что сами векторы, набор из трех чисел, не имеют начальной точки.

Проект берет вершину вектора A и находит, где вдоль вектора B он лежит перпендикулярно вектору B. Неважно, какой длины вектор B и в какую сторону он направлен. Если вы думаете о векторе B как о земле и представляете, что свет направлен прямо на него, результатом Project будет тень, отбрасываемая вектором A.

луч света, идущий от вершины вектора к началу координат, и вектор B как поверхность. Новый вектор будет таким, как он отскакивает, и входной угол всегда будет равен выходному углу.

Как следует из названия, вы можете использовать его для всех видов зеркальных эффектов. Просто отразите положение ваших вершин вокруг любой оси, которую вы хотите.

Faceforward немного странный, и, честно говоря, я никогда не использовал его в реальном проекте, но он может быть полезен для переворачивания чего-либо. Он работает на основе скалярного произведения, которое, если вы помните, просто сравнивает два вектора, чтобы увидеть, указывают ли они одинаково или нет. На узле лицом вперед два сравниваемых вектора называются инцидентным и эталонным. Все, что вам нужно знать, это то, что если эти две точки указывают в одинаковых направлениях, выражение «лицом вперед» вернет вектор, противоположный вектору А. Если они указывают в разных направлениях, выражение «лицом вперед» просто вернет вектор А. Это либо одно, либо другое, и нет никакого смешаться между ними.

Также полезно знать, что узел Mix Vector может плавно смешивать два вектора. Однако вы также можете переключить его на Цвет, чтобы использовать любой из режимов наложения. Я подробно рассказывал обо всех этих режимах наложения в курсе «Основы текстурирования». Узел Mix Color будет работать так же с информацией XYZ, как и с информацией RGB, поскольку они оба представляют собой просто наборы из трех чисел.

Мне больше всего нравится использовать только в узле Mix Color — Linear Light. Этот будет добавлять, если второе значение выше 0,5 и вычитать, если оно ниже 0,5. Я еще не использовал это в узлах геометрии, так как мы можем сделать что-то подобное со смещением в узле «Установить положение», но я довольно часто использую его в редакторе шейдеров, чтобы плавно деформировать или искажать одну текстуру на основе другой текстуры. Помните, что сложение и вычитание — это просто перемещение, поэтому текстура будет двигаться в положительном направлении, где вторая текстура светлая, но двигаться в другом направлении, где вторая текстура темная.

Что нужно помнить
Хорошо, этого должно быть достаточно для начала. Я знаю, что ближе к концу я слишком углубился в сорняки, но резюмирую важные части:
- Вектор в Blender — это просто набор из трех чисел.
- Вы можете думать о векторах как о стрелках, которые начинаются в начале координат и указывают на их координату XYZ.
- Добавление — это просто наложение векторов друг на друга и указание на результат.
- Сложение и вычитание — это то, как вы перемещаетесь туда, куда указывает стрелка.
- Умножение и деление — это то, как вы масштабируете стрелку.
- Скалярное произведение проверяет, насколько похожи два вектора.
- Перекрестное произведение — это третье направление, пересекающее первые два.
Если вы сможете запомнить эти несколько вещей, у вас все получится.
Надеюсь, это было полезно! Конечно, вы все еще можете в некоторой степени использовать узлы геометрии, не зная много о векторной математике, но базовое понимание ее — это то, что откроет для вас всю ее мощь.