Уде́льное электри́ческое сопротивле́ние, или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока.
Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
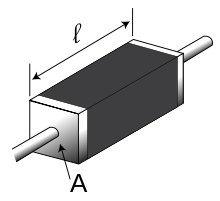
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле R = ρ ⋅ l S {\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ = R ⋅ S l . {\displaystyle \rho ={\frac {R\cdot S}{l}}.}
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Обобщение понятия удельного сопротивления
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E → ( r → ) {\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J → ( r → ) {\displaystyle {\vec {J}}({\vec {r}})} в данной точке r → {\displaystyle {\vec {r}}} . Указанная связь выражается законом Ома в дифференциальной форме:
- E → ( r → ) = ρ ( r → ) J → ( r → ) . {\displaystyle {\vec {E}}({\vec {r}})=\rho ({\vec {r}}){\vec {J}}({\vec {r}}).}
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρ i j {\displaystyle \rho _{ij}} . В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением
- E i ( r → ) = ∑ j = 1 3 ρ i j ( r → ) J j ( r → ) . {\displaystyle E_{i}({\vec {r}})=\sum _{j=1}^{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}
В анизотропном, но однородном веществе тензор ρ i j {\displaystyle \rho _{ij}} от координат не зависит.
Тензор ρ i j {\displaystyle \rho _{ij}} симметричен, то есть для любых i {\displaystyle i} и j {\displaystyle j} выполняется ρ i j = ρ j i {\displaystyle \rho _{ij}=\rho _{ji}} .
Как и для всякого симметричного тензора, для ρ i j {\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρ i j {\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρ i j {\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ 11 {\displaystyle \rho _{11}} , ρ 22 {\displaystyle \rho _{22}} и ρ 33 {\displaystyle \rho _{33}} . В этом случае, обозначив ρ i i {\displaystyle \rho _{ii}} как ρ i {\displaystyle \rho _{i}} , вместо предыдущей формулы получаем более простую
- E i = ρ i J i . {\displaystyle E_{i}=\rho _{i}J_{i}.}
Величины ρ i {\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.
Связь с удельной проводимостью
В изотропных материалах связь между удельным сопротивлением ρ {\displaystyle \rho } и удельной проводимостью σ {\displaystyle \sigma } выражается равенством
- ρ = 1 σ . {\displaystyle \rho ={\frac {1}{\sigma }}.}
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρ i j {\displaystyle \rho _{ij}} и тензора удельной проводимости σ i j {\displaystyle \sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
- J i ( r → ) = ∑ j = 1 3 σ i j ( r → ) E j ( r → ) . {\displaystyle J_{i}({\vec {r}})=\sum _{j=1}^{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
Из этого равенства и приведённого ранее соотношения для E i ( r → ) {\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
- ρ 11 = 1 det ( σ ) [ σ 22 σ 33 − σ 23 σ 32 ] , {\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}}[\sigma _{22}\sigma _{33}-\sigma _{23}\sigma _{32}],}
- ρ 12 = 1 det ( σ ) [ σ 33 σ 12 − σ 13 σ 32 ] , {\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}}[\sigma _{33}\sigma _{12}-\sigma _{13}\sigma _{32}],}
где det ( σ ) {\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σ i j {\displaystyle \sigma _{ij}} . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3[3].
Удельное электрическое сопротивление некоторых веществ
Металлические монокристаллы
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[4].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
|---|---|---|
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества
Тонкие плёнки
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», R S q . {\displaystyle R_{\mathrm {Sq} }.} Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: R S q = R W / L , {\displaystyle R_{\mathrm {Sq} }=RW/L,} где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в пленке неоднородное, используют метод ван дер Пау.
Примечания
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
См. также
Удельное сопротивление
Общая информация
Определение 1
Удельное сопротивление — это физическая величина, которая характеризует способность вещества препятствовать прохождению электрического тока.
Этот параметр обозначается греческой буквой $p$ (ро). Основой для расчета удельного сопротивления является эмпирическая формула, используемая для расчета электрического сопротивления, которую получил Георг Ом.
$R=p • l/S $
Чтобы получить формулу для расчета удельного сопротивления, нужно преобразовать формулу Ома:
$R =p · l/S$
$p • l/S=R$
$p/S=R/l $
$p=R • S/l $
Последний этап преобразования и есть нужная формула:
$p=R•S/l$, где
- $R$ — сопротивление, Ом;
- $S$ — площадь поперечного сечения, $мм^2$;
- $l$ — длина, м.
По международной системе СИ, удельное сопротивление выражается в $Ом•м$. На практике используется альтернативное выражение удельного сопротивления $Ом•мм^2/м$.
Рисунок 1. Удельное сопротивление отдельных материалов. Автор24 — интернет-биржа студенческих работ
Замечание 1
На рисунке изображены значения удельного сопротивления только для часто используемых материалов. Значения этого параметра для других материалов можно найти в соответствующих справочниках.
Готовые работы на аналогичную тему
Зависимость удельного сопротивления от температуры
Говоря об удельном сопротивлении, нельзя упомянуть о влиянии температуры окружающей среды на его значение. Однако, это влияние будет разным для каждого материала. Это объясняется одним важным параметром $α$ — температурным коэффициентом.
Температурный коэффициент используется в формула для расчета удельного сопротивления с учетом изменения температуры:
$ρ_t =ρ_0 • [1+α•(t-t_0)]$, где
- $ρ_0$ — удельное сопротивление при 20 С*,
- $α$ — температурный коэффициент,
- $t-t_0$ — разница температур.
Рисунок 2. Температурный коэффициент сопротивления. Автор24 — интернет-биржа студенческих работ
Рассчитаем удельное сопротивление меди при -30 C и +30 C .
Пример 1
Для расчета удельного сопротивления при +30 C*, нужно взять первую формулу и подставить известные значения:
$ρ_t=ρ_0 • [1+α•(t-t_0)]=0,017• [1+0,0039•(30-20)]=0,017•[1+(0,0039•10)]=0,0176 $
Для расчета удельного сопротивления при -30 C*, нужно взять вторую формулу и выполнить аналогичный расчет:
$ρ_t=ρ_0 • [1+α•(t-t_0)]=0,017 • [1+(0,0039 • (– 30 – 20)=0,0136$
Исходя из расчетов можно сделать вполне логичный вывод, который заключается в следующем.
Замечание 2
Чем выше температура окружающей среды, тем выше удельное сопротивление.
Практическое определение удельного сопротивления
Иногда, материал необходимый для работы бывает неизвестен. Из-за этого нет возможности использовать справочник и посмотреть значение удельного сопротивления. В этом случае, для определения необходимого параметра, нужно использовать расчетные формулы и ряд подручных инструментов: цифровой микрометр и мультиметр.
Определим удельное сопротивление проволоки из неизвестного материала длинной 3,5 м.
Включаем мультиметр и устанавливаем на нижний предел измерения сопротивления (200 Ом).
Подводим по одному щупу к каждому концу проволоки, проводим измерение и снимаем показания прибора, например, 75 Ом.
Берем микрометр и измеряем диаметр проволоки, например, 0,25 $мм^2$
Выпишем формулы для определения сечения провода и удельного сопротивления:
$S=π•d^2/4$;
$ρ=R•S/l$
Преобразуем формулу для нахождения удельного сопротивления с учетом новой формулы и подставим необходимы значения:
$ρ=R•S/l=R• π• d^2/4• l=75• 3,14• 0,25^2/4• 3,5=235,5• 0,25^2/4• 3,5=14,71/14=1,05$ $Ом• мм^2$
Откроем справочник и по найденному удельному сопротивлению определим материал (в данном случае это нихром).
формула удельного сопротивления и закон Ома
Закон Ома является основным законом электрических цепей. При этом он позволяет объяснять многие явления природы. Например, можно понять, почему электричество не «бьет» птиц, которые сидят на проводах. Для физики закон Ома является крайне значимым. Без его знания невозможно было бы создавать стабильно работающие электрические цепи или вовсе не было бы электроники.
Зависимость I = I(U) и ее значение
История открытия сопротивления материалов напрямую связана с вольт-амперной характеристикой. Что это такое? Возьмем цепь с постоянным электрическим током и рассмотрим любой ее элемент: лампу, газовую трубку, металлический проводник, колбу электролита и т. д.
Меняя напряжение U (часто обозначается как V), подаваемое на рассматриваемый элемент, будем отслеживать изменение силы тока (I), проходящего через него. Как итог, мы получим зависимость вида I = I (U), которая носит название «вольт-амперная характеристика элемента» и является прямым показателем его электрических свойств.
Вольт-амперная характеристика может выглядеть по-разному для различных элементов. Самый простой ее вид получается при рассмотрении металлического проводника, что и сделал Георг Ом(1789 — 1854).
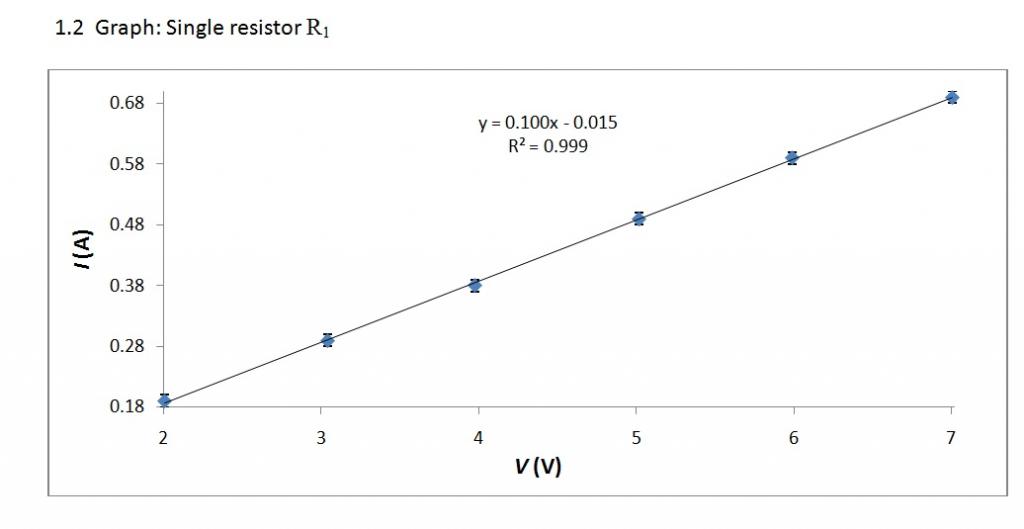
Вольт-амперная характеристика — это линейная зависимость. Поэтому ее графиком служит прямая линия.
Закон в простой форме
Исследования Ома по изучению вольт-амперных характеристик проводников показали, что сила тока внутри металлического проводника пропорциональна разности потенциалов на его концах (I ~ U) и обратно пропорциональна некоему коэффициенту, то есть I ~ 1/R. Этот коэффициент стал называться «сопротивление проводника», а единица измерения электрического сопротивления — Ом или В/А.
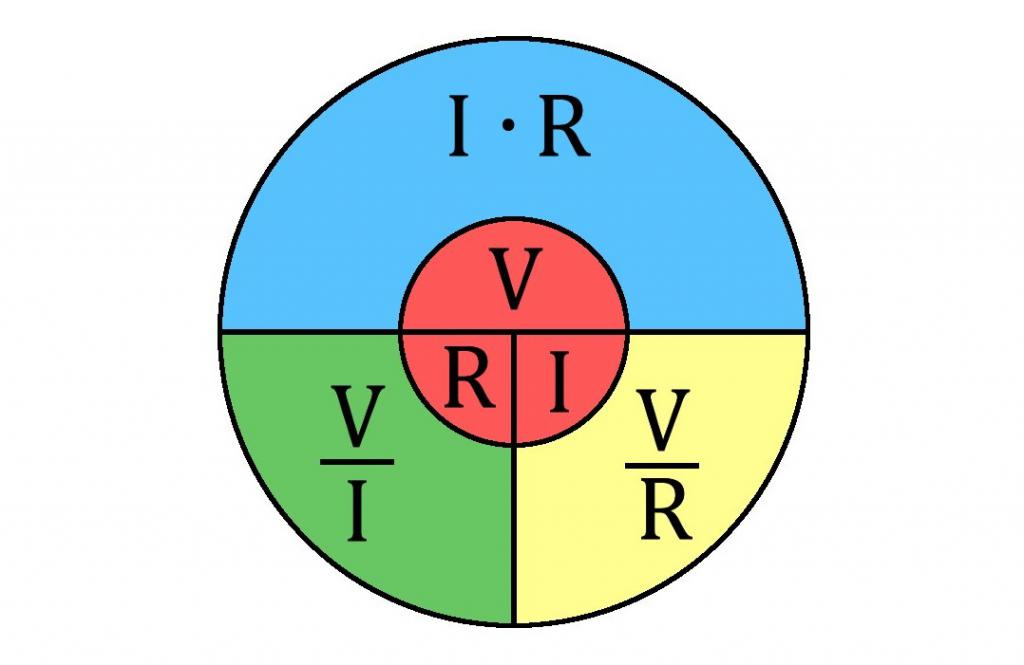
Стоит отметить еще вот что. Закон Ома часто используется для расчета сопротивления в цепях.
Формулировка закона
Закон Ома говорит, что сила тока (I) отдельно взятого участка цепи пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.
Следует заметить, что в таком виде закон остается верным только для однородного участка цепи. Однородной называется та часть электрической цепи, которая не содержит источника тока. Как пользоваться законом Ома в неоднородной цепи, будет рассмотрено ниже.
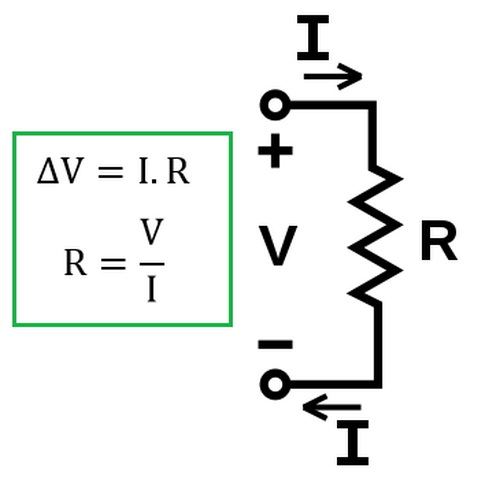
Позже опытным путем было установлено, что закон остается справедливым и для растворов электролитов в электрической цепи.
Физический смысл сопротивления
Сопротивление — это свойство материалов, веществ или сред препятствовать прохождению электрического тока. Количественно сопротивление в 1 Ом означает, что в проводнике при напряжении 1 В на его концах способен проходить электрический ток силой 1 А.
Удельное электрическое сопротивление
Экспериментальным методом было установлено, что сопротивление электрического тока проводника зависит от его размеров: длина, ширина, высота. А также от его формы (сфера, цилиндр) и материала, из которого он сделан. Таким образом, формула удельного сопротивления, например, однородного цилиндрического проводника будет: R = р*l/S.
Если в этой формуле положить s = 1 м2 и l = 1 м, то R численно будет равен р. Отсюда вычисляется единица измерения для коэффициента удельного сопротивления проводника в СИ — это Ом*м.

В формуле удельного сопротивления р — это коэффициент сопротивления, определяемый химическими свойствами материала, из которого изготовлен проводник.
Для рассмотрения дифференциальной формы закона Ома, необходимо рассмотреть еще несколько понятий.
Плотность тока
Как известно, электрический ток — это строго упорядоченное движение любых заряженных частиц. Например, в металлах носителями тока выступают электроны, а в проводящих газах — ионы.
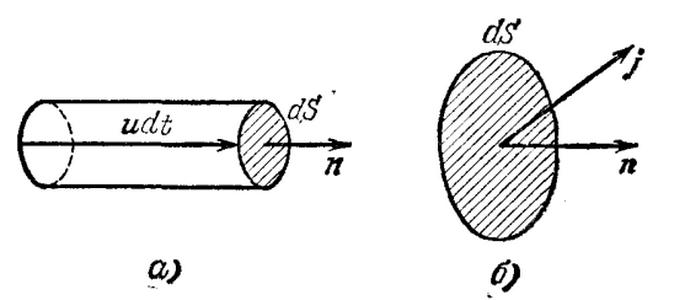
Возьмем тривиальный случай, когда все носители тока однородны — металлический проводник. Мысленно выделим в этом проводнике бесконечно малый объем и обозначим через u среднюю (дрейфовую, упорядоченную) скорость электронов во взятом объеме. Далее пусть n обозначает концентрацию носителей тока в единице объема.
Теперь проведем бесконечно малую площадь dS перпендикулярно вектору u и построим вдоль скорости бесконечно малый цилиндр с высотой u*dt, где dt — обозначает время, за которое все носители скорости тока, содержавшиеся в рассматриваемом объеме, пройдут сквозь площадку dS.
При этом электронами сквозь площадку будет перенесен заряд, равный q = n*e*u*dS*dt, где e — заряд электрона. Таким образом, плотность электрического тока — это вектор j = n*e*u, обозначающий количество заряда, переносимого в единицу времени через единицу площади.
Один из плюсов дифференциального определения закона Ома заключается в том, что часто можно обойтись без расчета сопротивления.
Электрический заряд. Напряженность электрического поля
Напряженность поля наряду с электрическим зарядом является фундаментальным параметром в теории электричества. При этом количественное представление о них можно получить из простых опытов, доступных школьникам.
Для простоты рассуждений будем рассматривать электростатическое поле. Это электрическое поле, которое не изменяется со временем. Такое поле может быть создано неподвижными электрическими зарядами.
Также для наших целей необходим пробный заряд. В его качестве будем использовать заряженное тело — настолько малое, что оно не способно вызывать какие-либо возмущения (перераспределение зарядов) в окружающих объектах.
Рассмотрим поочередно два взятых пробных заряда, последовательно помещенных в одну точку пространства, находящуюся под воздействием электростатического поля. Получается, что заряды будут подвергаться неизменному во времени воздействию с его стороны. Пусть F1 и F2 — это силы, воздействующие на заряды.
В результате обобщения опытных данных было установлено, что силы F1 и F2 направлены либо в одну, либо в противоположные стороны, а их отношение F1/F2 является независимым от точки пространства, куда были поочередно помещены пробные заряды. Следовательно, отношение F1/F2 является характеристикой исключительно самих зарядов, и никак не зависит от поля.
Открытие данного факта позволило охарактеризовать электризацию тел и в дальнейшем было названо электрическим зарядом. Таким образом, по определению получается q1/q2 = F1/F2, где q1 и q2 — величина зарядов, помещаемых в одну точку поля, а F1 и F2 — силы, действующие на заряды со стороны поля.
Из подобных соображений были экспериментально установлены величины зарядов различных частиц. Условно положив в соотношение один из пробных зарядов равным единице, можно вычислить величину другого заряда, измерив соотношение F1/F2.
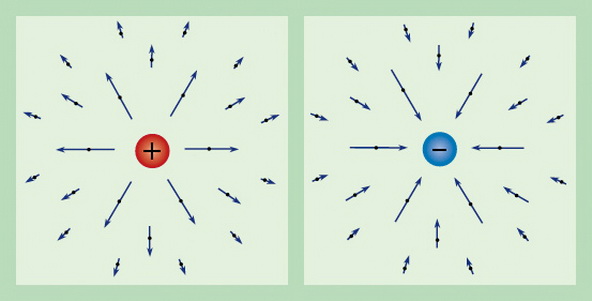
Через известный заряд можно охарактеризовать любое электрическое поле. Таким образом, сила, действующая на единичный пробный заряд, находящийся в состоянии покоя, называется напряженностью электрического поля и обозначается E. Из определения заряда получаем, что вектор напряженности имеет следующий вид: E = F/q.
Связь векторов j и E. Другая форма закона Ома
В однородном проводнике упорядоченное движение заряженных частиц будет происходить по направлению вектора E. А это значит, что векторы j и E будут сонаправлены. Как и при определении плотности тока, выделим в проводнике бесконечно малый цилиндрический объем. Тогда через поперечное сечение этого цилиндра будет проходить ток, равный j*dS, а напряжение, приложенное к цилиндру, будет равно E*dl. Также известна формула удельного сопротивления цилиндра.
Тогда, записав формулу силы тока двумя способами, получим: j = E/р, где величина 1/р носит название удельной электрической проводимости и является обратной к удельному электрическому сопротивлению. Ее принято обозначать σ (сигма) или λ (лямбда). Единицей измерения проводимости является См/м, где См — это Сименс. Единица, обратная Ом.
Таким образом, можно ответить на вопрос, поставленный выше, о законе Ома для неоднородной цепи. В таком случае на носителей тока будет действовать сила со стороны электростатического поля, которая характеризуется напряженностью E1, и другие силы, воздействующие на них со стороны другого источника тока, которые можно обозначить E2. Тогда Закон Ома применительно к неоднородному участку цепи будет иметь вид: j = λ(E1 + E2).
Подробнее о проводимости и сопротивлении
Способность проводника проводить электрический ток характеризуется его удельным сопротивлением, которое можно найти через формулу удельного сопротивления, или удельной проводимостью, рассчитывающейся как обратное проводимости. Величина данных параметров определяется как химическими свойствами материала проводника, так и внешними условиями. В частности температурой окружающей среды.
Для большинства металлов удельное сопротивление при нормальной температуре пропорционально ей, то есть р ~ T. Однако при низких температурах наблюдаются отклонения. У большого ряда металлов и сплавов при температурах, близких к 0°К, расчет сопротивления показывал нулевые значения. Это явление получило название сверхпроводимости. Таким свойством обладают, например, ртуть, олово, свинец, алюминий и др. Для каждого металла существует свое критическое значение температуры Tk, при которой наблюдается явление сверхпроводимости.
Также отметим, что определение удельного сопротивления цилиндра можно обобщить для проводов, состоящих из одного материала. В таком случае площадь поперечного сечения из формулы удельного сопротивления будет равна сечению провода, а l — его длине.
Уде?льное электри?ческое сопротивле?ние, или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока.
Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле  (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется
(при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется 
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1].
Из соотношения 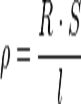 следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
ЭДС
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянногоили переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура[1].
По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил 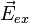 , под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд, к величине этого заряда. Тогда в замкнутом контуре
, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд, к величине этого заряда. Тогда в замкнутом контуре 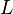 ЭДС будет равна:
ЭДС будет равна:

где 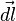 — элемент контура.
— элемент контура.
ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого? источника равна нулю.
ЭДС индукции
Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где 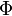 — поток магнитного поля через замкнутую поверхность
— поток магнитного поля через замкнутую поверхность 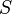 , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).
, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).
Т. Сопротивление — PhysBook
Сопротивление проводников. Удельное сопротивление
Как уже отмечалось, сила тока в цепи зависит не только от напряжения на концах участка, но также и от свойств проводника, включенного в цепь. Зависимость силы тока от свойств проводников объясняется тем, что разные проводники обладают различным электрическим сопротивлением.
Электрическое сопротивление R — физическая скалярная величина, характеризующая свойство проводника уменьшать скорость упорядоченного движения свободных носителей зарядов в проводнике. Обозначается сопротивление буквой R. В СИ единицей сопротивления проводника является ом (Ом).
1 Ом — сопротивление такого проводника, сила тока в котором равна 1 А при напряжении на нем 1 В.
Применяются и другие единицы: килоом (кОм), мегаом (МОм), миллиом (мОм): 1 кОм = 103 Ом; 1 МОм = 106 Ом; 1 мОм = 10-3 Ом.
Физическую величину G, обратную сопротивлению, называют электрической проводимостью\[~G = \frac 1R\].
Единицей электрической проводимости в СИ является сименс: 1 См — это проводимость проводника сопротивлением 1 Ом.
Проводник содержит не только свободные заряженные частицы — электроны, но и нейтральные частицы и связанные заряды. Все они участвуют в хаотическом тепловом движении, равновероятном в любых направлениях. При включении электрического поля под действием электрических сил будет преобладать направленное упорядоченное движение свободных зарядов, которые должны двигаться с ускорением и их скорость должна была бы со временем возрастать. Но в проводниках свободные заряды движутся с некоторой постоянной средней скоростью. Следовательно, проводник оказывает сопротивление упорядоченному движению свободных зарядов, часть энергии этого движения передается проводнику, в результате чего повышается его внутренняя энергия. Из-за движения свободных зарядов искажается даже идеальная кристаллическая решетка проводника, на искажениях кристаллической структуры рассеивается энергия упорядоченного движения свободных зарядов. Проводник оказывает сопротивление прохождению электрического тока.
Сопротивление проводника зависит от материала, из которого он изготовлен, длины проводника и площади поперечного сечения. Для проверки этой зависимости можно воспользоваться той же электрической схемой, что и для проверки закона Ома (рис. 2), включая в участок цепи ΜΝ различные по размерам проводники цилиндрической формы, изготовленные из одного и того же материала, а также из разных материалов.
Результаты эксперимента показали, что сопротивление проводника прямо пропорционально длине l проводника, обратно пропорционально площади S его поперечного сечения и зависит от рода вещества, из которого изготовлен проводник:
где ρ — удельное сопротивление проводника.
Удельное сопротивление проводника — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника, изготовленного из данного вещества и имеющего длину 1 м и площадь поперечного сечения 1 м2, или сопротивлению куба с ребром 1 м. Единицей удельного сопротивления в СИ является ом-метр (Ом·м).
Удельное сопротивление металлического проводника зависит от
- концентрации свободных электронов в проводнике;
- интенсивности рассеивания свободных электронов на ионах кристаллической решетки, совершающих тепловые колебания;
- интенсивности рассеивания свободных электронов на дефектах и примесях кристаллической структуры.
Наименьшим удельным сопротивлением обладает серебро и медь. Очень велико удельное сопротивление у сплава никеля, железа, хрома и марганца — «нихрома». Удельное сопротивление кристаллов металлов в значительной степени зависит от наличия в них примесей. Например, введение 1 % примеси марганца увеличивает удельное сопротивление меди в три раза.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 254-255.
* Удельное сопротивление полупроводников сильно зависит от наличия примесей в материале, что делает их полезными в твердотельной электронике. Рекомендации: 1. Джанколи, Дуглас С., Физика, 4-е издание, Прентис Холл, (1995). 2. CRC Справочник по химии и физике, 64-е изд. 3. Википедия, Удельное электрическое сопротивление и проводимость. | Указатель Таблицы Ссылка | ||||
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса 9
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agard Agard Agard Agard Agulis Class 12- Классы
- RS Решения Aggarwal класса 10
- RS Решения Aggarwal класса 11
- RS Решения Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Предыдущий год Вопросник
- CBSE Предыдущий год Вопросники Класс 10
- CBSE Предыдущий год Вопросник Класс 12
- HC Verma Solutions

- Полный курс физики — 11 класс
Предлагаемая цена: рупий2968
- Подробнее
Удельное сопротивление
Удельное сопротивление известно как удельное электрическое сопротивление или объемное удельное сопротивление.Его можно определить как внутреннее свойство данного материала, которое показывает, как оно противодействует потоку тока. Его также можно определить как сопротивление, предлагаемое проводником, имеющим единичную длину и единичную площадь поперечного сечения. Так что это не зависит от длины и площади поперечного сечения материала. Но сопротивление материала зависит от длины и площади поперечного сечения материала. Удельное сопротивление выражается как ρ = R A / L, где R — сопротивление в омах, A — площадь поперечного сечения в квадратных метрах, а L — длина в метрах.Единица удельного сопротивления — омметр.
Температурная зависимость удельного сопротивления
Удельное сопротивление материалов зависит от температуры. t = 0 [1 + α (T — T 0 ) — это уравнение, которое показывает связь между температурой и удельным сопротивлением материала. В уравнении ρ 0 — удельное сопротивление при стандартной температуре, ρ t — удельное сопротивление при t 0 C, T 0 — опорная температура, а α — температурный коэффициент удельного сопротивления.
Изменение удельного сопротивления в проводниках
Мы знаем, что ток — это движение свободных электронов от одного атома к другому, когда существует разность потенциалов. В проводниках нет запрещенной зоны между зоной проводимости и валентной зоной. Во многих случаях обе полосы перекрывают друг друга. Валентные электроны слабо связаны с ядром в проводниках. Обычно металлы или проводники имеют низкую энергию ионизации и поэтому очень легко теряют электроны.При подаче электрического тока делокализованные электроны могут свободно перемещаться внутри структуры. Это тот случай, когда это происходит при нормальной температуре.
Когда температура увеличивается, колебания ионов металлов в решетчатой структуре возрастают. Атомы начинают вибрировать с большей амплитудой. Эти колебания в свою очередь вызывают частые столкновения между свободными электронами и другими электронами. Каждое столкновение истощает некоторую энергию свободных электронов и делает их неспособными двигаться.Таким образом, он ограничивает движение делокализованных электронов. Когда происходит столкновение, дрейфовая скорость электронов уменьшается. Это означает, что удельное сопротивление металла увеличивается и, следовательно, ток в металле уменьшается. Увеличение удельного сопротивления означает, что проводимость материала уменьшается.
Для металлов или проводников говорят, что они имеют положительный температурный коэффициент. Значение α положительное. Для большинства металлов удельное сопротивление линейно возрастает с увеличением температуры в диапазоне 500К. Примеры для положительного температурного коэффициента включают серебро, медь, золото и т. Д.

Температурная зависимость от удельного сопротивления для металлов
Изменение удельного сопротивления в полупроводниках
Кремний — это полупроводник. В полупроводниках запрещенная щель между зоной проводимости и валентной зоной мала. При 0 К валентная зона полностью заполнена, и зона проводимости может быть пустой.Но когда прикладывается небольшое количество энергии, электроны легко перемещаются в зону проводимости. Кремний является примером для полупроводника. В обычных условиях кремний действует как плохой проводник. Каждый атом кремния связан с 4 другими атомами кремния. Связи между этими атомами представляют собой ковалентные связи, в которых электроны находятся в фиксированных положениях. Таким образом, при 0K электроны не движутся в структуре решетки.
![]()
Когда температура увеличивается, запрещенный зазор между двумя зонами становится очень меньше, и электроны перемещаются из валентной зоны в зону проводимости.Таким образом, некоторые электроны из ковалентных связей между атомами Si могут свободно перемещаться внутри структуры. Это увеличивает проводимость материала. Увеличение проводимости означает, что удельное сопротивление уменьшается. Таким образом, когда температура увеличивается в полупроводнике, плотность носителей заряда также увеличивается, и удельное сопротивление уменьшается. Говорят, что для полупроводников они имеют отрицательный температурный коэффициент. Таким образом, значение температурного коэффициента удельного сопротивления α является отрицательным.
Кривая нелинейная для широкого диапазона температур.
![]()
Температурная зависимость от удельного сопротивления для полупроводников
Изменение удельного сопротивления в изоляторах
В изоляторах запрещенная энергетическая щель между зоной проводимости и валентной зоной высока. Валентная зона полностью заполнена электронами. Запрещенный зазор между двумя зонами будет больше 3 е V. Таким образом, для перемещения валентного электрона в зону проводимости требуется большое количество энергии.Алмаз является примером для изолятора. Здесь все валентные электроны участвуют в образовании ковалентной связи и проводимости не происходит. Электроны тесно связаны с ядром.
Когда температура повышается, атомы материала вибрируют, и это заставляет валентные электроны, присутствующие в валентной зоне, сдвигаться в зону проводимости. Это, в свою очередь, увеличивает проводимость материала. Когда проводимость материала увеличивается, это означает, что удельное сопротивление уменьшается, и, следовательно, увеличивается ток.Таким образом, некоторые изоляторы при комнатной температуре превращаются в проводники при высокой температуре. Для изоляторов они имеют отрицательный температурный коэффициент. Таким образом, значение температурного коэффициента удельного сопротивления α является отрицательным.

Проводники и изоляторы
Сверхпроводники
Мы знаем, что когда электрический ток проходит через проводники, некоторая энергия теряется в виде тепла. Количество потерь энергии варьируется в зависимости от сопротивления материала.В 1911 году некоторые ученые охладили образец ртути до 4,2 ° выше абсолютного нуля. Таким образом сопротивление материала изменилось до нуля. Таким образом, был обнаружен первый сверхпроводник. Таким образом, ученые обнаружили, что при некоторых обстоятельствах некоторые материалы не проявляют никакого сопротивления. Материалы с нулевым сопротивлением называются сверхпроводниками. При нулевом сопротивлении материалы проводят ток без потери энергии. Когда температура таких материалов понижается, свободные электроны перестают сталкиваться с положительными ионами, и, таким образом, это оказывает нулевое сопротивление.Температура, при которой сопротивление падает до нуля, называется Критическая температура .
Когда сверхпроводник помещен в магнитное поле, магнитное поле огибает материал, поскольку оно не позволяет магнитному полю проходить через них. Когда напряженность магнитного поля увеличивается, в определенный момент поле может проникать через сверхпроводник, и, следовательно, его поведение нарушается.
Учтите, что электрический ток проходит через сверхпроводник.Предположим, что плотность тока увеличивается, при определенном значении плотности тока он теряет свою сверхпроводимость и, наконец, ведет себя как нормальный материал. Плотность тока, выше которой материал теряет сверхпроводимость, называется критической плотностью тока. Высокая температура, сильное магнитное поле и высокая плотность тока разрушат поведение сверхпроводимости материала. В наши дни эти материалы используются в машинах МРТ.
Другие материалы
Удельное сопротивление таких материалов, как нихром, манганин и константан, не сильно зависит от температуры и показывает очень низкую зависимость.Следовательно, эти материалы используются в стандартных резисторах с проволочной связью, так как изменение значения сопротивления незначительно при изменении температуры.
 |  |
| Манганин | Константин |
Факторы, влияющие на удельное сопротивление
Мы знаем, что удельное сопротивление, ρ = m / ne 2 where, где e — заряд электрона, ԏ — среднее время между каждым столкновением или временем релаксации электронов, а m — масса электрона, n — плотность заряда.Таким образом, это показывает, что удельное сопротивление зависит от ряда факторов, таких как время релаксации между столкновениями и плотность заряда. Из приведенных выше сценариев ясно, что при увеличении температуры средняя скорость электронов увеличивается и, следовательно, происходит большее столкновение. Таким образом время релаксации между каждым столкновением уменьшается.
В случае металлов плотность заряда в определенной степени не зависит от температуры. Таким образом, влияют другие факторы, такие как ԏ, что означает, что при повышении температуры среднее время между столкновениями уменьшается, что приводит к увеличению удельного сопротивления.
Для полупроводников и изоляторов плотность заряда n увеличивается при повышении температуры. Это компенсирует уменьшение значения ԏ. Следовательно, удельное сопротивление уменьшается при понижении температуры.
Резюме
Удельное сопротивление — это сопротивление, которое предлагает проводник, имеющий единицу длины и единицу площади поперечного сечения. Единица удельного сопротивления — омметр. Формула ρ = RA / L, где R — сопротивление в омах, A — площадь поперечного сечения в квадратных метрах, а L — длина в метрах.
ρ t = ρ 0 [1 + α (T — T 0 ) — это уравнение, которое показывает связь между температурой и удельным сопротивлением материала. ρ 0 — удельное сопротивление при стандартной температуре, ρ t — удельное сопротивление при t 0 C, T 0 — опорная температура, а α — температурный коэффициент удельного сопротивления.
Для металлов или проводников, когда температура увеличивается, а удельное сопротивление металла увеличивается и, следовательно, ток в металле уменьшается.Они имеют положительный температурный коэффициент. Значение α положительное.
Для полупроводников, когда температура увеличивается, проводимость материала увеличивается. Это означает, что удельное сопротивление материала уменьшается, и поэтому увеличивается ток. Для полупроводников они имеют отрицательный температурный коэффициент. Таким образом, значение температурного коэффициента удельного сопротивления α является отрицательным.
Для изоляторов проводимость материала увеличивается, когда температура увеличивается.Когда проводимость материала увеличивается, мы знаем, что удельное сопротивление уменьшается и, таким образом, увеличивается ток. Поэтому некоторые изоляторы при комнатной температуре превращаются в проводники при высокой температуре. Для изоляторов они имеют отрицательный температурный коэффициент. Значение температурного коэффициента удельного сопротивления, α отрицательно.
Материалы с нулевым сопротивлением называются сверхпроводниками. Температура, при которой сопротивление падает до нуля, называется критической температурой.Высокая температура, сильное магнитное поле и высокая плотность тока ослабят свойство сверхпроводимости материала. Меркурий является примером сверхпроводника.
Материалы, такие как нихром, манганин и константан, не сильно зависят от температуры. Таким образом, изменение удельного сопротивления материала при изменении температуры незначительно.
Смотрите это видео для получения дополнительной ссылки
Подробнее Чтения
Температурная зависимость удельного сопротивления

Особенности курса
- 101 видео лекций
- Редакция Примечания
- Документы за предыдущий год
- Mind Map
- Планировщик исследования
- NCERT Solutions
- Дискуссионный форум
- Тестовая бумага с Video Solution
,

