Логические операции — Студопедия
Поделись
1. Инверсия (отрицание). Это отрицание любого высказывания, простым языком — «неверно» или «не», а в программировании это «Not». Обозначается как
Таблица истинности для этой операции:
А B= не «А»
0 1
1 0
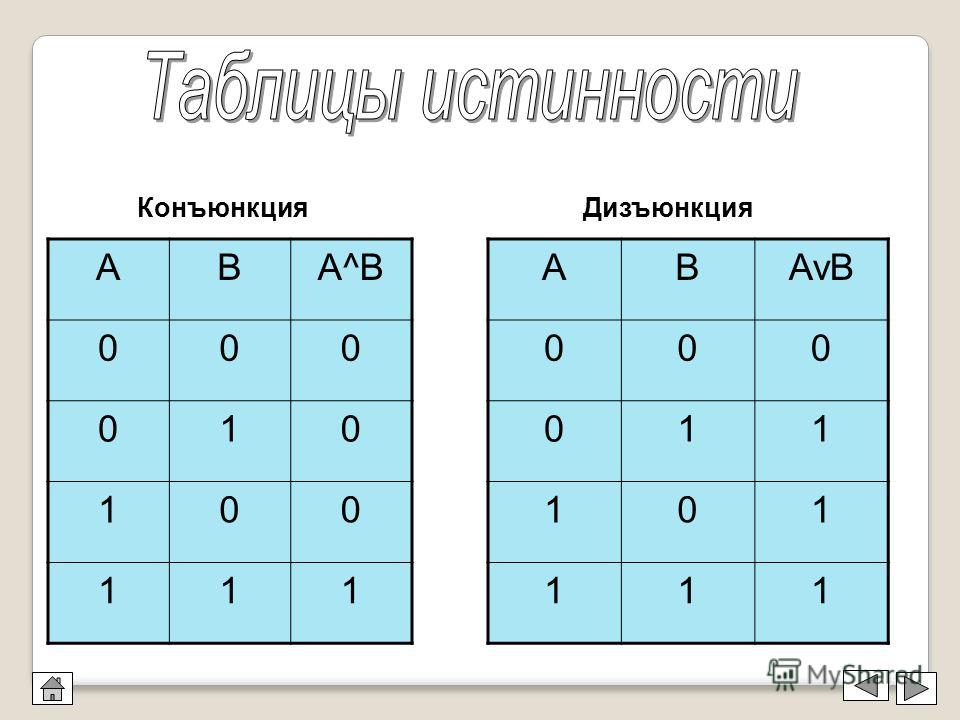
2. Операция КОНЪЮНКЦИЯ (логическое умножение). Конъюнкция — это составное высказывание, являющееся только тогда истинным, когда являются истинными простые высказывания, образующие это высказывание. На естественном языке обозначается союзом «и», в программировании как «And», а в записи логических функций это: & Можно записать одно и то же выражение по-разному, все варианты можно использовать в логических операциях:
Таблица истинности для конъюнкции :
А B А & B
000
100
111
Например: Перемножить логически два числа в двоичной системе счисления.
3. Операция ДИЗЪЮНКЦИЯ (логическое сложение). Дизъюнкция — это составное высказывание, являющееся только тогда истинным, когда хотя бы одно из образующих его высказываний является истинным.На естественном языке обозначается союзом «или», в программировании как «Or», а в записи логических функций как: V Также варианты записи:
Таблица истинности для дизъюнкции :
А B А v B
000
01
101
111
Пример: Теперь сложить логически два числа побитно.
4. Операция ИМПЛИКАЦИЯ (логическое следование).Импликация — это составное высказывание, являющееся ложным тогда и только тогда, когда первое высказывание истинно, а второе высказывание ложно. Естественным языком можно сказать как «если…, то …» , в программировании как «if», а в записи логических функций как: ⇒. Записываем так:
Записываем так:
…и это то же самое
Для операции импликация
А B А → B
001
011
100
111
Для операции импликация можно рассмотреть еще частный случай: обратная импликация, таблица истинности которой ниже:
А B А ← B
001
010
101
111
5. Операция ЭКВИВАЛЕНЦИЯ (логическая равнозначность). Эквиваленция — это составное высказывание, являющееся истинным тогда и только тогда, когда все простые высказывания, образующие его, одновременно истинны или одновременно ложны. Естественным языком можно сказать как
Для операции эквиваленция верна следующая таблица истинности :
А B А ↔ B
001
010
100
111
В конце можно привести пример, который может встретиться, например, в задании ЕГЭ:
«Для какого из указанных значений X истинно высказывание :
Варианты ответов: 1, 2, 3, 4.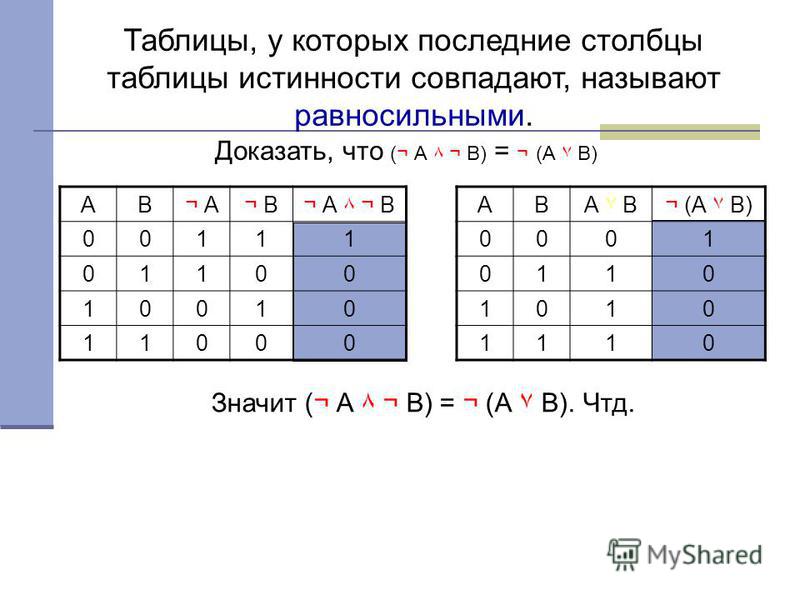
Решение в данном случае «лежит на поверхности»: действовать необходимо от обратного. Сначала, как видно из записи высказывания, идет операция отрицания, значит истинно высказывание будет тогда и только тогда, когда выражение под знаком отрицания будет ложным. Составное высказывание в скобках — это импликация из двух выражений сравнения. И, исходя из таблицы истинности импликации (см. п.4), значение «ложь» или «0», только когда первое высказывание ( X>2) «истинно», а второе (X>3) «ложь». Из предложенных вариантов значений подходит только значение
Ответ: 3.
|
Заглавная страница
КАТЕГОРИИ: Археология Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 15 из 19Следующая ⇒
Дизъюнкция (логическое сложение, ИЛИ) Равнозначность Импликация Функция Вебба (стрелка Пирса, ИЛИ-НЕ) Функция Шеффера (И-НЕ) Функция сложения по модулю два (полусумматор) Как можно представить логические функции с помощью электрических переключающих схем? Так как логические переменные могут иметь только два дискретных значения, то следует обратить внимание на схемы, которые могут находиться в двух легко различимых рабочих состояниях.
Можно условиться, что разомкнутый ключ эквивалентен логическому нулю, а замкнутый –логической единице. Таким образом, ключ реализует переменную х, если он замкнут при х = 1, и переменную , если он разомкнут при х = 1. Рассмотрим сначала, какая логическая функция будет реализована, если два ключа и соединить последовательно.
Значение зависимой переменной у характеризуется тем, будет ли замкнута или разомкнута составная коммутируемая цепь, расположенная между входными клеммами. Очевидно, что рассматриваемая цепь будет замкнута только тогда, когда и замкнуты, т.е. равны единице. Таким образом, последовательное включение ключей реализует функцию И. Функция ИЛИ может быть получена, если ключи включить параллельно. С помощью такой схемной логики можно наглядно показать справедливость ранее приведенных теорем. Рассмотрим это на примере правила повторения. На рис. показана реализация обеих частей выражения правила повторения с помощью коммутируемой цепи. Легко заметить, что рассматриваемое тождество выполняется, поскольку два включенных последовательно ключа, замыкание и размыкание которых происходит одновременно, воздействуют на внешние цепи как один такой ключ.
Другой возможностью представления логических переменных является электрическое напряжение, имеющее два различных уровня: высокий и низкий. Этим уровням можно поставить в соответствие логические состояния 1 и 0. Эта система обозначений: высокий = 1 и низкий = 0 – называется позитивной логикой. Но возможна также и обратная система обозначений: высокий = 0 и низкий = 1, которая называется негативной логикой. Основные логические функции могут быть реализованы с помощью соответствующих электронных схем. Эти схемы имеют один или несколько входов и один выход. Как правило, они называются логическими элементами. Уровень выходного напряжения определяется уровнями напряжения на входах и характером логической функции.
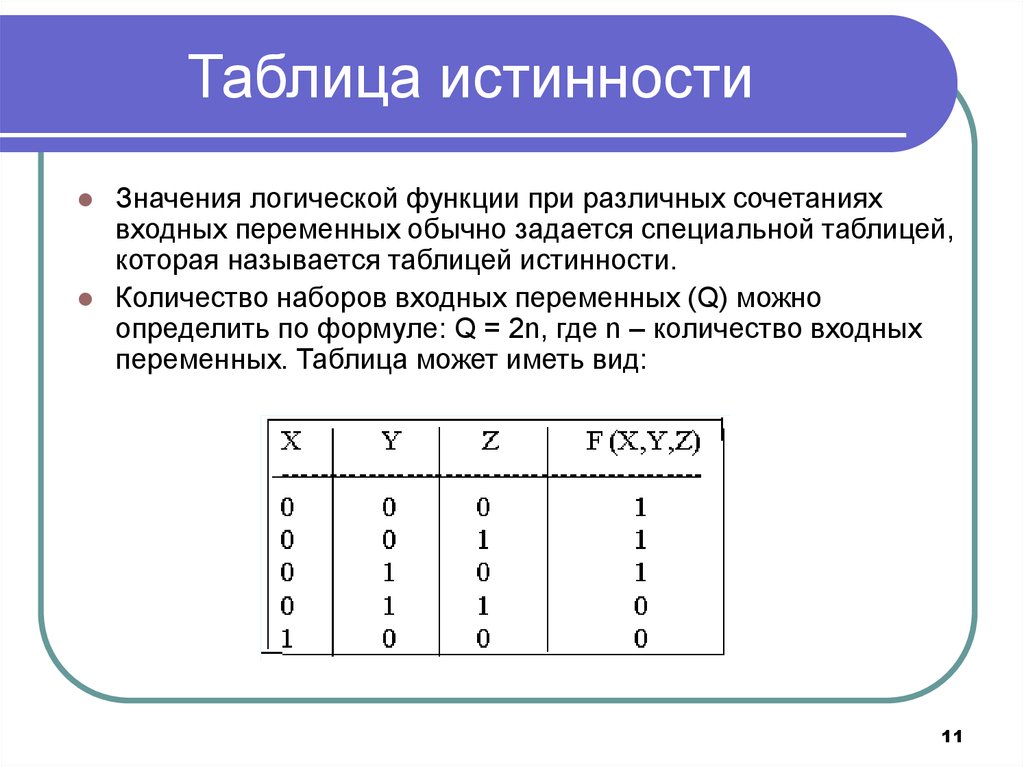
В цифровой технике задача, как правило, формулируется в форме таблицы переключений, которая называется также таблицей истинности. Прежде всего требуется найти такую логическую функцию, которая соответствовала бы этой таблице. На следующем этапе эту функцию преобразуют в простейшую форму, которую потом реализуют с помощью соответствующей комбинации базовых логических схем. Логические функции записывают, как правило, в дизъюнктивной совершенной нормальной форме (ДСНФ). При этом поступают следующим образом. 1. В таблице истинности выделяют строки, в которых выходная переменная у имеет значение 1. 2. Для каждой такой строки составляют конъюнкцию всех входных переменно причем записывают сомножитель , если рассматриваемая переменная принимает значение 1, в противном случае записывают . 3. Наконец, записывая логическую сумму всех найденных произведений, получают искомую функцию.
Формулы склеивания: Формулы поглощения:
Минимизация методом Карно При минимизации методом Карно логическую функцию в виде карты. При размещении различных комбинаций значений входных переменных следует выбирать таким, чтобы при переходе от одной ячейки к соседней изменялась только одна переменная (используют код Грэя). Склеивание возможно, если одинаковые значения функции располагаются рядом. Желательно образовывать контуры возможно большей протяженности. Контуры могут охватывать 1, 2, 4,8 и т.д. единиц (или нулей). В результате исчезает та переменная, которая меняет знак при обходе контура. При организации контуров следует считать, что карту можно навернуть на цилиндр. Если обхватывать контурами единицы, то результат получим в ДСНФ, если нули – то в КСНФ (конъюнктивная совершенная нормальная форма).
2-х разрядная карта Карно
Результат:
Элементарная база цифровых микросхем. Логические элементы И, ИЛИ, НЕ на диодах, биполярных и полевых транзисторах. Базовые логические элементы диодно-транзисторной, транзисторно-транзисторной, эмиттерно-связанной логики.
Эволюция цифровой логики: 1) РТЛ – резисторно-транзисторная логика. 2) ДТЛ – диодно-транзисторная логика. 3) ТТЛ –транзисторно-транзисторная логика. Элемент три «И-НЕ» на ДТЛ. Напряжение <0.4B считается логическим нулем, при U>2.4 – логическая единица. Элементы на основе ТТЛ. В основе – многоэммитерный транзистор. Серия 155. Если на всех входах «1» , то на коллекторе эмиттерный переход закрыт, а коллекторный открыт и напряжение на базе VT1=1.8 В. VT2 и VT5 открыты, VD4 –предназначен для надежного запирания VT4. R3, R4 и VT3 действуют как резистор и предназначены для увеличения помехоустойчивости. Если на любом из входов «0», то VT1 переключается из инверсного в активный режим и отпирается. R5 предназначен для защиты выходов при кратковременном замыкании на землю.
Серия повышенного быстродействия. VT1, VT2 – VT5 – используются транзисторы Шотке. Следующим шагом к повышению быстродействия стало использование транзистора Шотке.
Если на базу подать большое напряжение, то транзистор может войти в режим насыщения и его быстродействие уменьшается. У диода Шотке напряжение отпирания 0,3-0,4 В. Напряжение на базе транзистора Шотке не может превышать напряжение на его коллекторе более, чем на 0,4 В, т.е. коллекторный переход никогда полностью не открывается транзистор не заходит в режим насыщения, что резко увеличивает его быстродействие.
⇐ Предыдущая10111213141516171819Следующая ⇒ Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 665; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.) |
Logic 12 Функции истинности — ФУНКЦИИ ИСТИННОСТИ Вот некоторые вопросы, на которые мы ответим в этой лекции:
ФУНКЦИИ ИСТИННОСТИ
Вот некоторые вопросы, на которые мы ответим в этой лекции:
1. Что такое функция истинности? Переменная оператора?
2. Что такое таблица истинности? Как можно использовать таблицы истинности для определения логических операторов?
Что такое таблица истинности? Как можно использовать таблицы истинности для определения логических операторов?
3. Как можно вычислить истинностные значения сложных высказываний, если истина известна
значения составляющих их простых предложений?
4. Чем логические операторы (НЕ, И, ИЛИ, ЕСЛИ-ТО, РАВНО) отличаются от обычных английских
слов «не», «и», «или», «если-то» и « равно»?
ЧТО ТАКОЕ ФУНКЦИЯ ПРАВДЫ?
Функция истинности — это составное утверждение, истинность которого зависит только от истинностных значений составляющих его простых
утверждений. Ниже приведены примеры функций истинности:
1. «Гиганты — это футбольная команда, а Пэкерс — футбольная команда».
o Это состоит из двух простых утверждений G и P.
o Составное утверждение
истинно тогда и только тогда, когда G и B оба истинны.
2. «Дело не в том, что Баффи — вампир».
o Это состоит из одного простого утверждения B.
o Составное утверждение ~B истинно тогда и только тогда, когда B ложно.
3. «Если Фродо носит кольцо, то Фродо невидим».
oСостоит из двух простых операторов R и I.
oСоставное утверждение
истинно, если (a) R ложно или (b) I истинно. Оно ложно, только если R
истинно, а I ложно (т. е. Фродо носит кольцо, но его все еще видно).
Следующие составные утверждения НЕ являются функциями истинности:
1. «Келли считает Джейсона придурком».
а. Он состоит из простого утверждения J («Джейсон — придурок»).
б. Даже если мы знаем, придурок ли Джейсон (т. е. мы знаем, что J истинен), мы все равно не будем
способен определить, во что верит Кэлли. Выяснение того, является ли это утверждение истинным или ложным
, требует индуктивных рассуждений (и выходит за рамки пропозициональной логики, которая
касается дедуктивных аргументов).
2. «Если бы на выборах 2012 года победил Митт Ромни, США сейчас находились бы в состоянии войны с
Россией».
а. Он состоит из двух простых операторов R и W.
b. Даже если мы знаем истинное значение R (ложь) и W (ложь), мы не можем использовать это, чтобы вывести
истинное значение всего этого. Выяснение того, является ли это утверждение истинным или ложным
, требует индуктивных рассуждений.
ОПРЕДЕЛЕНИЕ ЛОГИЧЕСКИХ ОПЕРАТОРОВ С ИСПОЛЬЗОВАНИЕМ ТАБЛИЦ ИСТИННОСТИ
Таблица истинности показывает, как истинность составных утверждений определяется истинностью составляющих их
предложений для каждой возможной комбинации значений истинности. В таблицах истинности строчные буквы, такие как p, q, r,
,и т. д., называются операторными переменными. Они могут обозначать любое утверждение. Таблица истинности будет
содержат достаточно строк, чтобы показать все возможные комбинации значений переменной инструкции. Таким образом, если
есть ОДНА переменная оператора, будет ДВЕ строки (поскольку оператор имеет два возможных значения истинности
: ИСТИНА или ЛОЖЬ). Напротив, если есть ДВЕ переменные, вам нужно будет использовать ЧЕТЫРЕ строки (TT, TF,
FT и FF — все возможные комбинации). Для трех переменных потребуется восемь строк, для четырех переменных
Для трех переменных потребуется восемь строк, для четырех переменных
потребуется 16 строк и так далее.
Определение логических операторов. Таблицы истинности можно использовать для определения логических операторов.
Это потому, что таблица истинности может точно показать нам, как значение истинности составного утверждения изменяется
со значением истинности составных утверждений. Например, вот таблица истинности, определяющая НЕ
(или «~»). Обратите внимание, что поскольку имеется только одна переменная оператора (p), то и строк всего две.
ТАБЛИЦА ИСТИННОСТИ ДЛЯ «ОТРИЦАНИЯ»
Путеводитель по главам
Глава 7: Логика высказываний
Мы уже знаем, что каждое утверждение является предложением, которое либо истинно, либо ложно. То есть каждое утверждение является предложением со значением истинности. Понятие истинностного значения лежит в основе этой главы. Логика высказываний включает в себя изучение того, как сложные утверждения собираются и разбираются, а также то, как мы можем заменить одно утверждение другим, логически эквивалентным ему. Следующие концепции являются ключевыми для понимания систем, представленных в этой главе, а также в главах 8 и 9.: простое утверждение , составное (или сложное) утверждение и функция истинности .
Следующие концепции являются ключевыми для понимания систем, представленных в этой главе, а также в главах 8 и 9.: простое утверждение , составное (или сложное) утверждение и функция истинности .
Существует два типа выписки: простая и составная . Простой оператор — это оператор, который не содержит другого оператора в качестве компонента. Другой способ описать простое утверждение — сказать, что оно содержит подлежащее и глагол. Он также может содержать зависимые предложения, но основная идея заключается в том, что наименьшая грамматическая единица имеет истинностное значение. В обозначениях символической логики эти утверждения обозначаются заглавными буквами A–Z.
Составной оператор содержит по крайней мере один простой оператор в качестве компонента вместе со связкой . Есть пять связок: отрицание, союз, дизъюнкция, условное и биусловное. В нотации символической логики эти связки представлены операторами :
Обычный язык переводится в нотацию символической логики с помощью вышеупомянутых заглавных букв A–Z. Обычно мы переводим связки следующим образом:
Обычно мы переводим связки следующим образом:
При переводе сложных предложений с обычного языка в символическую логическую запись изолируйте простые предложения и связки.
Вот четыре правила, которые помогут организовать ваше мышление при переводе сложных утверждений:
3. Тильда никогда не ставится сама по себе между двумя утверждениями.
4. «Скобки, скобки и фигурные скобки необходимы для устранения двусмысленности в сложном выражении» (стр. 297). Рассмотрите любой тип вводных скобок как средство объединения сложного утверждения в единое целое как части более крупного сложного утверждения.
Каждый составной оператор, состоящий из простых операторов и двух или более операторов, управляется или управляется основным оператором . В любом составном операторе всегда есть только один основной оператор, и этот оператор является либо одним из четырех, которые появляются между операторами, либо тильдой, которая появляется перед оператором, который инвертируется.
C. Функции истинности
Мы знаем, что утверждение имеет значения истинности: оно либо истинно, либо ложно:
Составное утверждение также имеет истинностные значения. Это функции простых операторов в сочетании со значением данного оператора:
Отрицание говорит нам: «Дело не в том, что…»
Соединение говорит нам: «И то, и другое… имеет место».
Дизъюнкция говорит нам, что «по крайней мере один случай…»
Условное выражение отражает концепцию достоверности: если предпосылки верны, вывод не может быть ложным. Когда посылки верны, а заключение ложно, вывод недействителен.
Бикондиционал говорит нам, что «либо оба варианта имеют место, либо ни один из них…»
Когда мы строим таблицу истинности для определения возможных значений истинности данного утверждения, нам сначала нужно знать как минимум две вещи:
- Количество простых операторов в составном операторе.
 Количество строк таблицы истинности следует этой формуле: R = 2 количество простых утверждений .
Количество строк таблицы истинности следует этой формуле: R = 2 количество простых утверждений . - Главный оператор. Любой оператор, содержащий два или более оператора, будет вычисляться в соответствии с порядком операций. Главный оператор определяет окончательные значения истинности утверждения, и поэтому его значения вычисляются последними.
Когда предоставляются значения истинности, мы вычисляем главный оператор, используя тот же порядок операций, что и при вычислении всех возможных значений истинности. Если вам говорят, что P , Q и R имеют значения T, F и T соответственно, вы можете вычислить значение составного оператора P ⊃ (Q R) :
условное утверждение истинно* по крайней мере в одной строке таблицы истинности и ложно по крайней мере в одной строке таблицы истинности. Другими словами, такое утверждение иногда верно, а иногда ложно. А не зависящее от обстоятельств утверждение не зависит от истинностных значений составных частей. Такое утверждение либо всегда истинно ( тавтология ), либо всегда ложно ( самопротиворечиво ).
Такое утверждение либо всегда истинно ( тавтология ), либо всегда ложно ( самопротиворечиво ).
Два или более утверждений логически эквивалентны , если они имеют одинаковые значения* в каждой строке таблицы истинности. В главе 8 мы увидим, что правила замены основаны на таких эквивалентностях. Таблицы истинности для следующих пар утверждений покажут их логическую эквивалентность. Это всего лишь несколько из множества утверждений, функционально эквивалентных истине:
P ⊃ Q and ~ P v Q
P ⊃ Q and ~ Q ⊃ ~ P
~ (P Q) and ~ P v ~ Q
G. Противоречивые, непротиворечивые и противоречивые утверждения
Два утверждения являются противоречивыми , когда они никогда не бывают истинными или ложными* в одно и то же время в одной и той же строке таблицы истинности.
Два или более операторов равны соответствует , когда они верны* одновременно хотя бы в одной строке таблицы истинности.
Два или более утверждения являются противоречивыми , когда они неверны* одновременно даже в одной строке таблицы истинности.
*Под основным оператором.
Мы видели, что таблицы истинности могут быть построены для отдельных утверждений и пар утверждений. Таблица истинности позволяет нам классифицировать утверждения в соответствии с их значениями истинности под основным оператором. То же самое можно сделать для аргументов, чтобы определить действительность или недействительность.
Таблица истинности, в которой есть хотя бы одна строка аргумента, в которой все посылки верны, а заключение ложно, недействительна. Таблица истинности, в которой нет ни одной строки аргумента, в котором все посылки верны, а заключение ложно, является действительной.
Таблица косвенной истинности является мощным и удобным инструментом для проверки достоверности аргумента:
- Предположим, что посылки верны, а заключение ложно. Другими словами, предположим, что аргумент недействителен.





 Простейшим способом реализации логической переменной является ключ.
Простейшим способом реализации логической переменной является ключ.
 Для реализации одной и той же логической функции существует большое число различных электронных схем. Поэтому с целью упрощения документации были введены символы, которые обозначают лишь только логическую функцию и не раскрывают внутреннее строение схемы.
Для реализации одной и той же логической функции существует большое число различных электронных схем. Поэтому с целью упрощения документации были введены символы, которые обозначают лишь только логическую функцию и не раскрывают внутреннее строение схемы. Таким образом, составляется столько произведений, сколько имеется строк с у = 1.
Таким образом, составляется столько произведений, сколько имеется строк с у = 1.
 Логические элементы на однотипных и комплементарных МДП-транзисторах. Логические элементы с тремя выходными состояниями. Микросхемы с открытым коллектором. Совместное применение микросхем разных серий.
Логические элементы на однотипных и комплементарных МДП-транзисторах. Логические элементы с тремя выходными состояниями. Микросхемы с открытым коллектором. Совместное применение микросхем разных серий.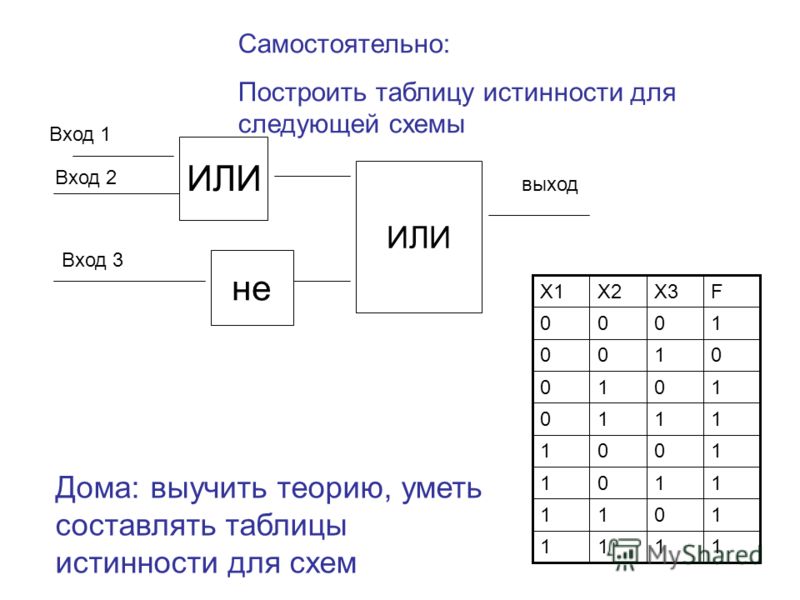 В этом случае напряжение на его коллекторе (0,8В) уже недостаточно для отпирания VT4 и VT5. VT4 при этом открыт и на выходе появляется логическая единица.
В этом случае напряжение на его коллекторе (0,8В) уже недостаточно для отпирания VT4 и VT5. VT4 при этом открыт и на выходе появляется логическая единица.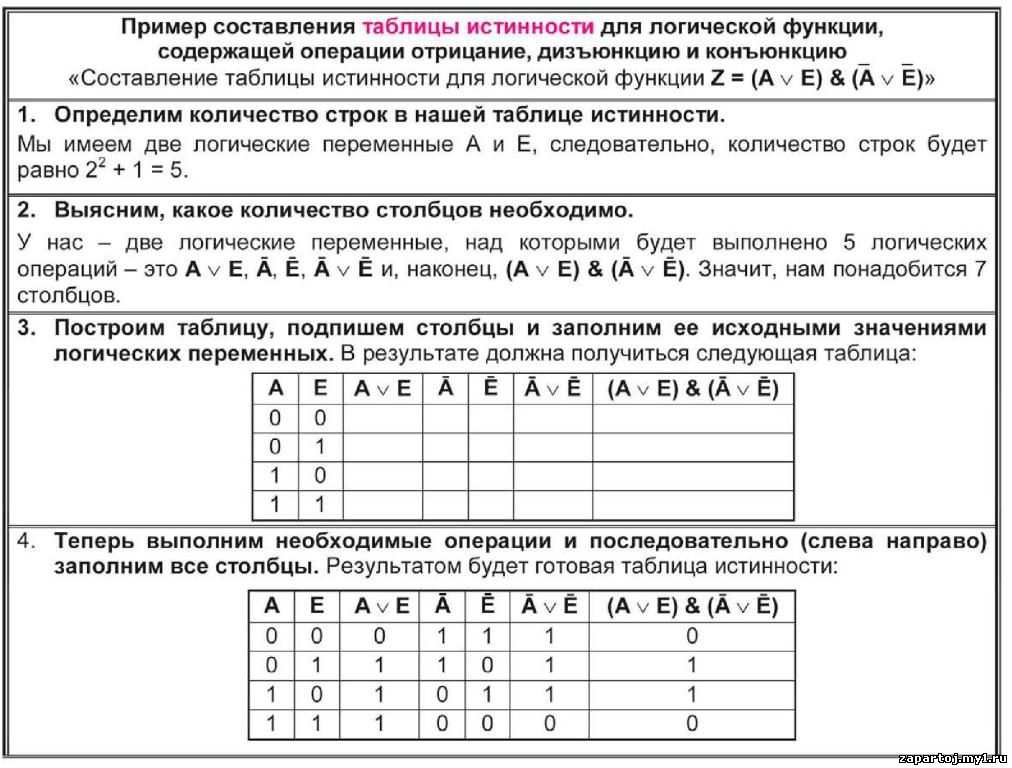 Сущность недвижимости
Сущность недвижимости Количество строк таблицы истинности следует этой формуле: R = 2 количество простых утверждений .
Количество строк таблицы истинности следует этой формуле: R = 2 количество простых утверждений .