2.2. Виды мощности. Треугольник мощностей

В цепях переменного тока различают три понятия мощности: активная Р, реактивная Q, полная S.

Соотношения между мощностями могут быть получены из треугольника мощностей, который образуется путем умножения всех сторон треугольника напряжений на значение тока I.

Рис.2.3. Треугольник мощностей

Здесь:

Q_L— реактивная индуктивная мощность,

Q_C — реактивная емкостная мощность.

Активная мощность [Вт] — характеризует необратимый процесс преобразования электромагнитной энергии источника в другие виды энергии: механическую, тепловую, световую и т.д.

Реактивная мощность [Вар] (вольт-ампер реактивный) — характеризует обратимый процесс преобразования электромагнитной энергии источника в энергию магнитного поля катушки и энергию электрического поля конденсатора.

Полная мощность [ВА] (вольт-ампер) — характеризует наибольшее значение активной мощности при заданных действующих значениях тока и напряжения.

Как видно из выражения активной мощности, если мощность, потребляемая приемником в данной цепи, является вполне определенной величиной, то при неизменном напряжении на зажимах цепи и с уменьшением ток нагрузки источника будет увеличиваться при одной и той же отдаваемой мощности.

.

(2.11.)

Поэтому даже при полной загрузке током источника, но при низком источник по мощности будет недогружен. Значениехарактеризует использование полной или установленной мощности источника и называется коэффициентом мощности.

Наибольшего значения активная мощность достигает при = 1, т.е. когда = 0, или, как следует из выражения (2. 10), когда . Такой режим работы называется резонансом напряжений. Явление резонанса напряжений как положительный эффект используется в технике слабых токов (в радиотехнике). В технике сильных токов резонанс напряжений является аварийным режимом, т.к. в этом случае напряжения на реактивных элементах могут достигать значений, намного превышающих приложенное напряжение, что может привести к пробою изоляции конденсаторов и катушек индуктивности.

Работа электрической цепи может быть описана, по крайней мере, тремя основными параметрами: напряжением (U), током (I) и активной мощностью (P). Произведение напряжения и тока в цепи дает нам полную мощность цепи (S = UI), а реактивную мощность (Q) можно найти из треугольника мощностей, зная полную и активную мощности.

Если активная мощность равна полной (P = S), то реактивная мощность обращается в ноль (Q = 0), тогда характер нагрузки является активным, а схема замещения цепи содержит только активное сопротивление.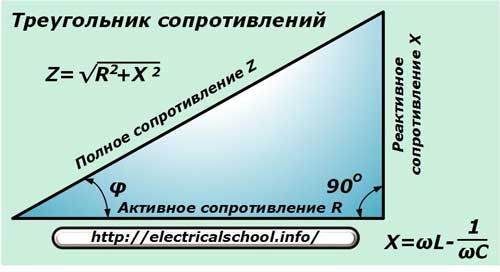

Если активная мощность в цепи равна нулю (P = 0), то полная мощность равна реактивной (Q = S), тогда характер нагрузки становится реактивным: или индуктивным (если в цепи содержится реактивное индуктивное сопротивление), или емкостным (если в цепи содержится реактивное емкостное сопротивление), а схема замещения содержит или индуктивность, или емкость.

Если активная мощность имеет значение отличное от нуля, но при этом меньше полной (0 < P < S), то мы имеем случай, когда характер нагрузки смешанный. Какой конкретно характер нагрузки будет, — зависит от разницы между реактивными сопротивлениями Х

L — Х_C. Если разница положительная (X_L > X_C ), то характер нагрузки активно-индуктивный, если отрицательная (X_L < X_C ) – активно-емкостной.

Таким образом характер нагрузки может быть определен, если известна структура цепи. Это легко сделать для простых электрических цепей. Для более сложных электрических цепей, содержащих большое количество электротехнических устройств, обычно используют фазометр, позволяющий определить угол сдвига фаз между напряжением и током и его характер: емкостной или индуктивный.

Реактивная и активная мощность — формула, как определить, коэффициент и баланс мощностей, потребление и нагрузка

Бытовая жизнь каждого из нас неразрывно связана с физикой, её остовыми законами и понятиями. Электронные приборы, без которых наша жизнь кажется невозможной, имеют определённую мощность. Именно понятие мощность, реактивная и активная, будет в дальнейшем рассмотрено для более глубокого понимания темы.

Содержание

Определения

Каждый электроприбор, который подключается к электрической сети, работает на базе переменного тока. Данное замечание важное, так как именно в таких условиях в дальнейшем будет разбираться «мощность».

Мощность — физическая величина, которая отображает скорость передачи или преобразования энергии электричества.

По-другому данный термин объясняют как соотношение работы к определённому промежутку времени, за который работа была совершена.

Более подробно понятие «мощность» можно разобрать на примере обычной лампочки накаливания. Лампочка потребляет электричество и то, с какой скоростью оно будет преобразовано в свет или тепло — и есть мощность лампочки.

Также из этого можно сделать следующий вывод: чем больше у электроприбора изначальная мощность (в нашем случае лампочка), тем большее количество электроэнергии он будет потреблять, а следовательно, даст больше света.

Активная мощность

Активная мощность — мощность, характеризующая конкретно процесс видоизменения энергии электричества во что-то другое. Измеряется в Ваттах (Вт) и обозначается буквой P.

Активная мощность встречается на ТЭС, АЭС, так как именно там вырабатывается напряжение, ведь потом именно оно поступает для потребления в наши дома и позволяет питать электричеством все электроприборы.

Реактивная мощность

Реактивная мощность — физическая величина, которая является характеристикой нагрузки, появляющейся в приборах электрической цепи из-за колебаний энергии электромагнитного поля.

Возникает данный феномен в цепи с переменным током. Из этого также выведена определенная зависимость: мощность равна произведению среднеквадратичных значений силы тока и напряжения. Представленная формула в последствии будет рассмотрена более подробно.

Самым важным отличием реактивной нагрузки является наличие индуктивности и ёмкости. Иными словами – это способность запасать энергию, для того чтобы позже передавать её в электрическую сеть.

Энергия электротока, которую преобразует индукционная нагрузка, сперва превращается в магнитное поле, а уже после в электрический ток. Пример: электромагниты, трансформаторы, асинхронные двигатели.

Ёмкостная нагрузка, аналогично индукционной, также преобразует энергию тока, однако не в магнитное поле, а в электрическое. Затем оно вновь превращается в электрический ток. Оба представленных процесса воспроизводятся за одну вторую полупериода. Примером могут послужить синхронные двигатели, батареи, конденсаторы.

По большей части, функция реактивной мощности заключается в блуждании от генератора электричества к потребителю и обратно. Однако, так как индуктивная нагрузка присутствует постоянно, то непременно появится и реактивный ток, который индукция потребляет.

По сути, данный процесс цикличен и, кажется, что бесконечен, но для того, чтобы электроны смогли постоянно двигаться по проводам – необходима активная энергия.

Физическое объединение реактивной и активной мощности

Существует такое понятие, как «полная мощность». Представленную величину можно вычислить геометрически — она равна корню суммы квадратов реактивной и активной мощностей. Обозначается такое понятие буквой S, а вычисляется она в Вольт-амперах (ВА).

В физике, для того чтобы зависимость между всеми мощностями была более понятна, существует «треугольник мощностей» ­­- соотношение активной, реактивной и полной мощности.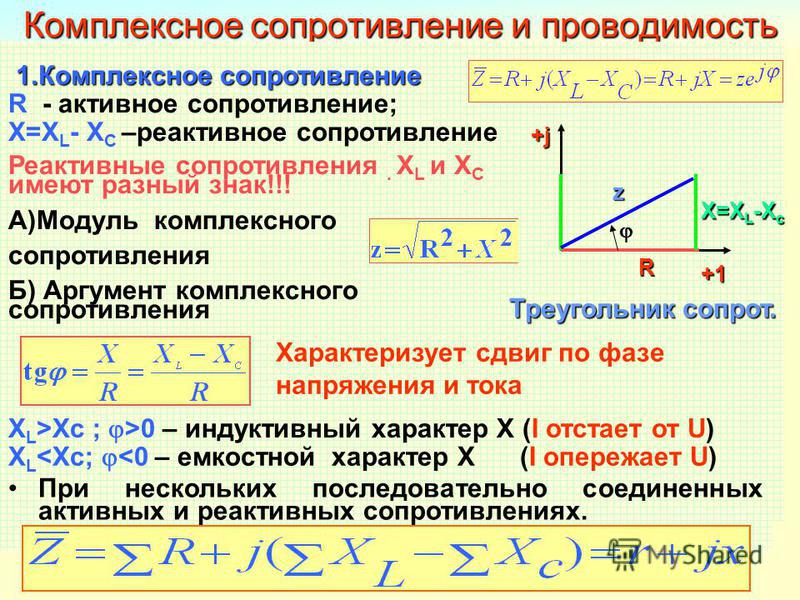

Сперва следует мысленно представить прямоугольный треугольник, где катеты – это активная и реактивная мощности, а гипотенуза – полная. Следуя геометрическим законам, косинус угла фи будет равен отношению реактивной и активной, другими словами – это коэффициент мощности.

Данный коэффициент исчисляется в пределе от нуля до единицы или же в процентах, от нуля процентов до ста. Чем больше активная мощность, тем больше коэффициент, а следовательно, лучше показатели электроприбора.

Формулы для нахождения мощностей

В большинстве случаев на электрических приборах указана активная мощность и числовое значение коэффициента косинуса фи. Когда есть подобные данные – далее рассчитать необходимые величины не представляет никакой сложности.

Расчётная формула полной мощности соответствует перемножению силы тока и напряжения:

• S = UxI, где
• S – полная мощность,
• U – электрическое напряжение,
• I – сила тока.

Реактивная мощность записывается буквой Р и исчисляется в Вольтах (Вт), и она вместе с активной при сложении образуют полную мощность:

S=P+Q

Однако на практике данная формула будет находится другим путём:

S= √(P2+Q2)

Порой, для нахождения мощностей могут понадобится емкостные и индуктивные нагрузки.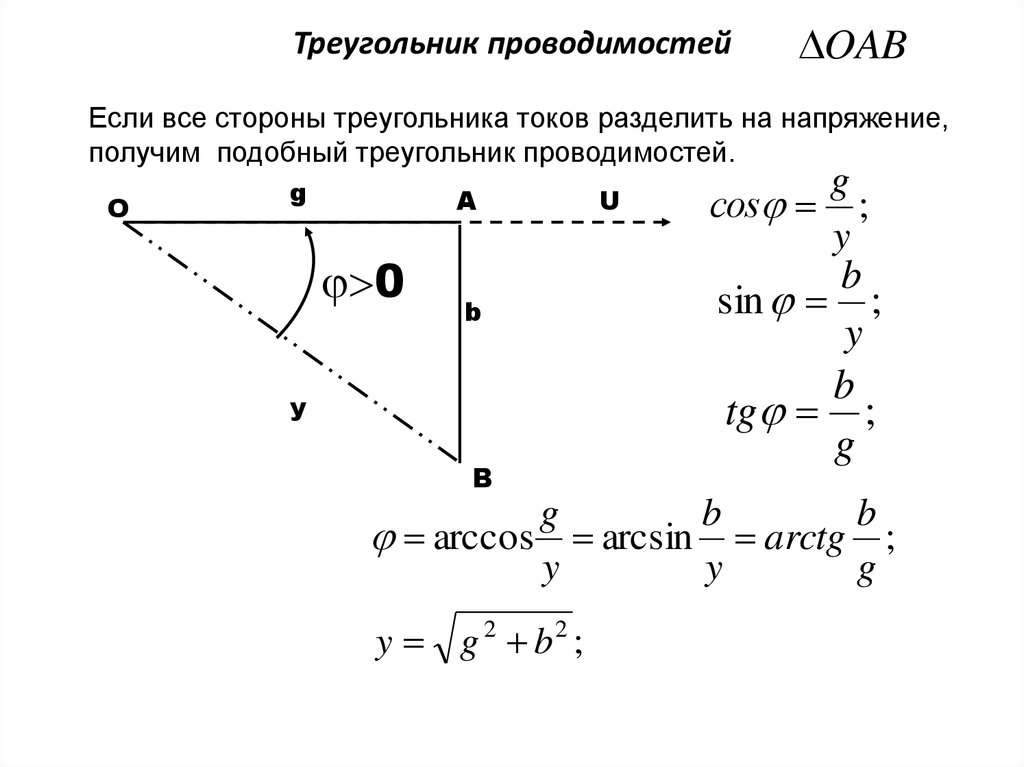 Для этого важно помнить о том, что при работе с индуктивной кривая точка всегда будет дальше от кривой напряжения на одну вторую полупериода. В это же время, при работе ёмкостной нагрузки кривая точка будет опережать кривую напряжения на одну вторую полупериода.

На практике коэффициента косинуса фи чаще всего указывают в описании электроприбора, но, если появляется необходимость самостоятельно измерить данную величину используется фазометр или цифровой ваттметр. Оба прибора значительно упрощают различные вычисления, хотя и рекомендуется пользоваться формулами для более точного теоретического расчёта.

Вычисление коэффициента мощности необходимо для того, чтобы скомпенсировать его недостаток путём включения в цепь дополнительных элементов.

Порой, появляется необходимость скомпенсировать реактивную мощность. Для этого в электрическую цепь включают реактивный прибор, который выполняет противоположную функцию к уже действующему электрическому объекту.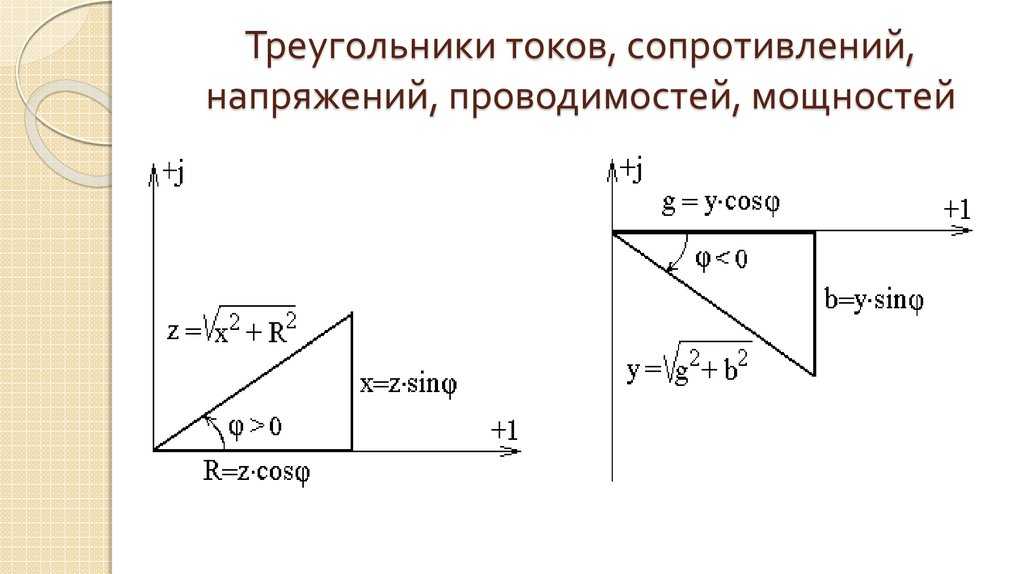 Например, чтобы скомпенсировать работу асинхронного двигателя — подключается в параллель конденсатор. Работа синхронного двигателя компенсируется электромагнитом.

Из изученного можно сделать вывод, что активная и реактивная мощность неразрывно связаны, однако не противоположны друг другу. Вместе они объединяются в другое понятие «полная мощность», а также позволяют вычислить коэффициент косинуса фи.

Мощность (активная, реактивная или полная) – наиважнейшее понятие в физике, как теоретической, так и практической. Знать, что эти величины обозначают, какими путями (через формулы или с помощью специальных приборов) их можно вычислить будет интересно и важно не только для обучающихся в школе или инженеров, но и для обычных людей, желающих развиваться всесторонне.

Фото реактивной и активной мощности

Автор статьи:

7.

3: Треугольник власти — Инженерные тексты LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

25281

• Джеймс М. Фиоре
• Муниципальный колледж Mohawk Valley

В предыдущем разделе было показано, что фазовый угол между током и напряжением нельзя игнорировать при расчете мощности. Например, если источник RMS на 120 вольт выдает ток 2 ампера, кажется, что он выдает 240 ватт. Это верно только в том случае, если нагрузка чисто резистивная. При комплексной нагрузке истинная мощность несколько меньше. На самом деле, как мы только что видели, если нагрузка является чисто реактивной, реальной мощности нагрузки вообще не будет.

Хотя построение кривых тока, напряжения и мощности является поучительным, оно может быть несколько громоздким. Вместо этого мы используем треугольник мощности, как показано на рисунке \(\PageIndex{1}\). Горизонтальная ось представляет реальную мощность, \(P\), в ваттах. Вертикальная ось представляет реактивную мощность \(Q\) в ВАр. Комбинация векторов \(P\) и \(Q\) дает полную мощность, \(S\), в ВА. Помните, что кажущаяся мощность является произведением величин тока и напряжения. Это то, чем «кажется» мощность на основе простых измерений тока и напряжения с помощью цифрового мультиметра по сравнению с надлежащим измерителем мощности. В резистивном случае реактивной мощности нет, поэтому \(S\) и \(P\) одинаковы. Следовательно, вектор \(S\) коллапсирует на вектор \(P\). В чисто реактивном случае истинной мощности нет и \(S\) и \(Q\) одинаковы; оба вектора идентичны и вертикальны. Для сложного случая \(S\) является векторной суммой \(P\) и \(Q\). Этот простой график хорошо иллюстрирует взаимосвязь между тремя векторами. Кроме того, при наличии любых двух из четырех частей (трех векторных величин и \(\тета\)) и с помощью небольшой тригонометрии можно найти две другие части.

Рисунок \(\PageIndex{1}\): треугольник власти.

Например, зная активную и реактивную мощности, можно найти полную мощность по теореме Пифагора. Точно так же, если известны кажущаяся мощность и угол, действительную и реактивную мощности можно найти с помощью синуса и косинуса. Помните, что кажущаяся мощность может быть найдена из произведения среднеквадратичных величин напряжения и тока для любого комплексного импеданса, а \(\theta\) совпадает с углом импеданса (т. е. угол напряжения минус угол тока). Для вашего удобства ниже перечислены некоторые полезные отношения треугольника мощности. 92} \метка{7.10} \]

Коэффициент мощности

Поскольку нас часто интересует истинная мощность, стоит отметить, что преобразование уравнения \ref{7.7} показывает, что отношение истинной мощности к кажущейся мощности равно косинусу угла импеданса, \(P /S = \cos\theta\). {\ circ}) = 86,6 \) Вт.

\[PF = \frac{P}{S} = \cos \theta \text{ (положительное значение запаздывает и является индуктивным)} \label{7.11} \]

Пример \(\PageIndex{1}\)

Найдите \(S\), \(P\) и \(Q\) в схеме на рисунке \(\PageIndex{2}\). \(E = 120\) вольт среднеквадратичное значение. Частота источника 60 Гц.

Рисунок \(\PageIndex{2}\): схема для примера \(\PageIndex{1}\).

Первым шагом является определение индуктивного сопротивления.

\[X_L = 2\pi f L \без номера \]

\[X_L = 2\pi 60 Гц 150 мГн \без номера \] 92}{160 \Omega} \nonumber \]

\[P = 90 Вт \nonumber \]

Треугольник мощности для этой схемы показан на рисунке \(\PageIndex{3}\).

Рисунок \(\PageIndex{3}\): треугольник мощности для схемы на рисунке \(\PageIndex{2}\).

Коррекция коэффициента мощности

Одна из проблем с реактивной нагрузкой заключается в том, что ток выше, чем необходимо для достижения определенной фактической мощности нагрузки. Это расточительно и потребует более крупных проводников. Чтобы решить эти проблемы, к нагрузке можно добавить противоположное реактивное сопротивление, чтобы результирующая нагрузка была чисто резистивной. Это можно реализовать, определив первоначальное значение \(Q\), а затем добавив реактивное сопротивление, достаточное для получения дополнительного \(Q\) противоположного знака, что приведет к нейтрализации. Оттуда, это короткий шаг, чтобы определить требуемый импеданс. Затем, зная частоту, можно найти требуемую емкость или индуктивность, используя соответствующую формулу реактивного сопротивления. Это показано в следующем примере. 9{\circ}\) пика вольт на частоте 10 кГц. Также найдите соответствующий компонент, который при размещении из узла \(a\) на землю приводит \(PF\) к единице.

Рисунок \(\PageIndex{4}\): Схема для примера \(\PageIndex{2}\).

Индуктивное сопротивление 1 мГн на частоте 10 кГц равно \(j62,83 \Омега\). Это параллельно резистору 100 Ом, который затем последовательно с резистором 20 Ом.

\[Z = 20\Омега +(100\Омега || j 62,83\Омега ) \без числа \]

\[Z = 20\Омега +(28,3+j 45\Омега ) \без числа \] 9{\circ} \nonumber \]

\[Q = 2,07 \text{ вар, индуктивная} \nonumber \]

Треугольник мощности для этой схемы показан на рисунке \(\PageIndex{5}\).

Рисунок \(\PageIndex{5}\): треугольник мощности для схемы на рисунке \(\PageIndex{4}\).

Для второй части, связанной с коррекцией коэффициента мощности, нам необходимо добавить реактивную мощность, равную по величине существующему значению, но противоположного знака. Это означает, что нам нужно добавить емкостное напряжение 2,07 ВАР. Новый треугольник мощности показан на рисунке \(\PageIndex{6}\). Вертикальные компоненты сокращаются, в результате чего кажущаяся мощность равна истинной мощности с \(PF = 1\).

Рисунок \(\PageIndex{6}\): треугольник мощности для схемы на рисунке \(\PageIndex{4}\) с коррекцией коэффициента мощности.

Мы можем разместить корректирующий конденсатор там, где это удобно с физической точки зрения, если мы добавим емкостное напряжение 2,07 ВАР. У нас нет физической цепи, так что это здесь не рассматривается. Удобным расположением было бы разместить его на существующей комбинации резистор-индуктор. Наша цель состоит в том, чтобы сначала найти требуемое реактивное сопротивление и, исходя из этого, определить требуемую емкость.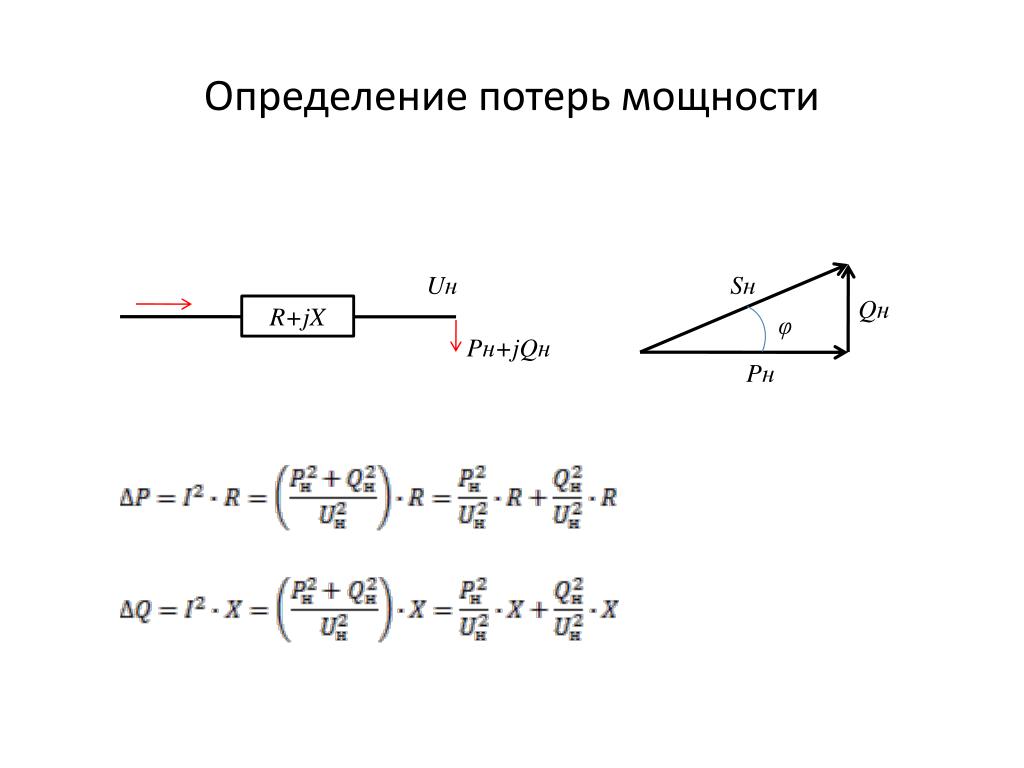 Мы сделаем это двумя разными способами. В первом случае заметим, что конденсатор появляется на единственном другом реактивном элементе в цепи. Следовательно, для того, чтобы они компенсировались, они должны иметь одинаковую величину реактивного сопротивления, и, таким образом, \(X_C\) должно равняться \(-j62,8 \Omega\). Но что, если в схеме было несколько реактивных элементов или если было бы нецелесообразно размещать компонент там, например, из-за нехватки места? В этом случае мы просто проработали бы соотношение сил в обратном порядке. Для сравнения предположим, что мы разместили конденсатор в том же месте; от узла \(a\) до земли. Делитель напряжения можно использовать для определения текущего значения \(v_a\). Это работает до 11,4 вольт RMS. Используя форму напряжения правила мощности: 92}{2.07VAR} \nonumber \]

\[X = 62.8\Omega \nonumber \]

В любом случае мы получим \(X_C\), теперь мы просто решим формулу емкостного реактивного сопротивления, чтобы найти \(C\) .

\[C = \frac{1}{2\pi f X_C} \nonumber \]

\[ C = \frac{1}{2\pi 10 kHz62. 8\Omega} \nonumber \]

\[C = 253,3 нФ \номер \]

Результирующая схема показана на рисунке \(\PageIndex{7}\).

Рисунок \(\PageIndex{7}\): Схема на рисунке \(\PageIndex{4}\) с коррекцией коэффициента мощности.

Компьютерное моделирование

Полезно видеть снижение потребляемой мощности, вызванное использованием коррекции коэффициента мощности. Таким образом, схема на рисунке \(\PageIndex{7}\) захвачена в симуляторе, как показано на рисунке \(\PageIndex{8}\).

Рисунок \(\PageIndex{8}\): Схема рисунка \(\PageIndex{7}\) в симуляторе.

Мы проведем два анализа переходных процессов, чтобы определить ток источника. Первая версия будет работать с оригинальной схемой без конденсатора. Второй запуск будет включать конденсатор. Для построения токов воспользуемся законом Ома. Сначала мы получаем напряжения в узлах 1 и 2. Затем, используя постпроцессор симулятора, мы вычитаем \(v_1\) из \(v_2\), что дает напряжение на резисторе 20 \(\Омега\). Эта величина затем делится на 20 \(\Омега\), чтобы получить входной ток.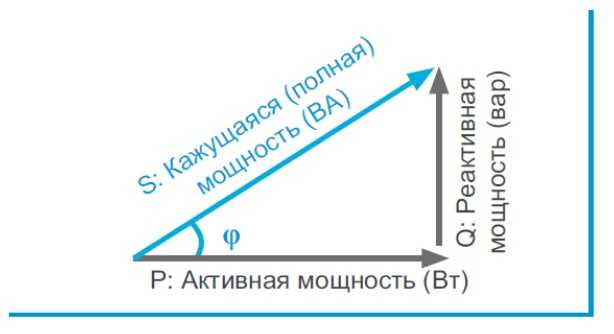 Это похоже на метод резистора измерения тока, использованный в предыдущих главах.

Результирующий ток для исходной цепи показан на рисунке \(\PageIndex{9}\). Обратите внимание, что пиковый ток составляет чуть более 300 миллиампер, рассчитанный на втором шаге примера.

Рисунок \(\PageIndex{9}\): результаты моделирования схемы на рисунке \(\PageIndex{8}\) без коррекции коэффициента мощности.

Второе моделирование показано на рисунке \(\PageIndex{10}\), теперь с коррекцией коэффициента мощности.

Рисунок \(\PageIndex{10}\): результаты моделирования схемы на рисунке \(\PageIndex{8}\) с коррекцией коэффициента мощности.

Амплитуда здесь сильно снижена, в диапазоне от 160 до 170 мА пик. При добавлении конденсатора два реактивных тока компенсируются, оставляя параллельное сопротивление всего 100 Ом. Это последовательно с резистором 20 \(\Омега\). Разделение 120 \(\Omega \) на пиковое напряжение источника 20 вольт дает пиковый ток приблизительно 167 мА, что соответствует моделированию. На компенсацию реактивных токов также указывает тот факт, что ток источника больше не находится в противофазе. На рисунке \(\PageIndex{10}\) текущий сигнал находится в фазе и начинается с нуля, как и ожидалось. Это подразумевает нагрузку, эквивалентную чистому сопротивлению. Напротив, график рисунка \(\PageIndex{9}\) показывает ток, который отстает примерно на половину деления, или примерно на 45 градусов, что неудивительно, что это приблизительное значение угла импеданса цепи. Очевидно, что этот комбинированный импеданс должен быть индуктивным.

Подводя итог, можно сказать, что коррекция коэффициента мощности используется для снижения потребления тока при сохранении постоянной мощности нагрузки. Если нагрузка фиксированная, этого можно добиться за счет использования конденсатора (для индуктивных нагрузок) или катушки индуктивности (для емкостных нагрузок). Если нагрузка является динамической, то требуется более сложная система, например, переключение через батарею конденсаторов для получения значения, близкого к точному значению, необходимому для этой конкретной нагрузки. Дополнительные примеры коррекции коэффициента мощности приведены в следующем разделе.

Ссылки

¹ Гипербола, похоже, работает в киноиндустрии.

---

Эта страница под названием 7.3: Power Triangle распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джеймс М. Фиоре

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. source@http://www.dissidents.com/resources/ACElectricalCircuitAnalysis.pdf

Что такое коэффициент мощности и треугольник мощности

Коэффициент мощности:

Коэффициент мощности определяется как косинус угла между током и напряжением. В противном случае отношение активной мощности к реактивной называется коэффициентом мощности.

Единица измерения: Поскольку коэффициент мощности является величиной отношения, поэтому он не имеет единиц измерения.

В общем случае мощность — это способность выполнять работу. В электрической области электрическая мощность — это количество электрической энергии, которое может быть передано в какую-либо другую форму (тепло, свет и т. д.) в единицу времени.

Математически это произведение падения напряжения на элементе и тока, протекающего через элемент, называется мощностью.

Сначала рассмотрим цепи постоянного тока, имеющие только источники постоянного напряжения (любой источник тока или источник напряжения), катушки индуктивности ведут себя как короткое замыкание, а конденсаторы ведут себя как разомкнутая цепь в установившемся режиме.

Следовательно, вся цепь ведет себя как резистивная цепь, и вся электрическая мощность рассеивается в виде тепла. Здесь напряжение и ток находятся в одной фазе, а общая электрическая мощность определяется выражением .

Но в системе переменного тока из-за переменного характера (частоты) катушка индуктивности и конденсатор обеспечивают определенное сопротивление цепи. Индуктивная цепь хранит энергию в виде магнитного поля.

Конденсатор хранит энергию в виде электрического поля. Но в резисторе работает так же, как цепи постоянного тока. Из-за индуктивного и емкостного действия возникает коэффициент мощности.

Треугольник мощности:

Отношения между активной мощностью P, реактивной мощностью Q, полной мощностью VI и углом мощности θ можно представить в виде треугольника мощности. Треугольник мощности показан на рисунке для индуктивной нагрузки и емкостной нагрузки, в этом случае θ и Q положительные, а Q отрицательные.

[wp_ad_camp_1]
Как правило, коэффициент мощности равен реальной или фактической мощности P в ваттах (Вт), деленной на кажущуюся мощность |S| в вольт-амперах (ВА) из треугольника мощности:

Как правило, коэффициент мощности говорит о соотношении фаз между напряжением и током. В идеальных условиях ток и напряжение находятся «в фазе», а коэффициент мощности равен «100 %». При наличии индуктивных нагрузок (двигателей) коэффициент мощности может быть менее 100 % (обычно от 80 до 90 %).

Низкий коэффициент мощности, с точки зрения электротехники, приводит к протеканию более сильного тока по линиям электропередачи для передачи заданного количества киловатт на электрическую нагрузку. Из-за этого нам приходится тратить ненужные затраты на электроэнергию в виде потери мощности и стоимости установки в виде увеличения мощности оборудования.

Коэффициент мощности резистивной цепи:

Рассмотрим треугольник мощности. Для чисто резистивной цепи угол мощности равен нулю, потому что напряжение и ток будут в фазе; следовательно, коэффициент мощности равен 1 (Cos0=1), так как реактивная мощность равна нулю. Здесь треугольник мощности будет выглядеть как горизонтальная линия, потому что противоположная сторона (реактивная мощность) будет иметь нулевую длину.

Чисто индуктивные цепи:

Для чисто индуктивных цепей, что означает, что цепь не должна иметь внутреннего сопротивления, поэтому ток отстает от напряжения на 90 град.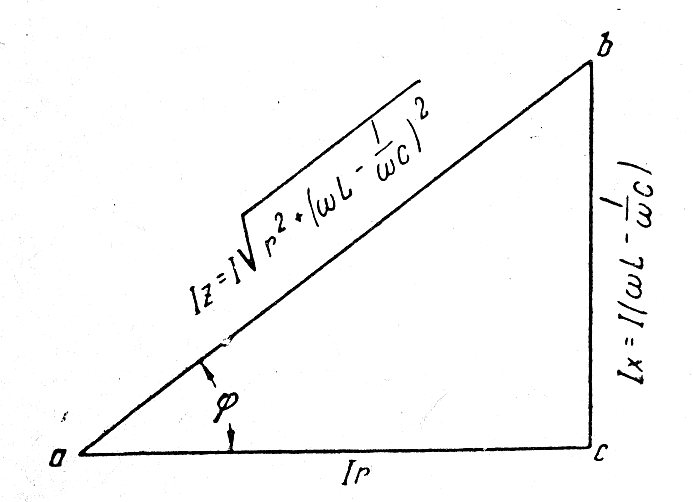 следовательно, коэффициент мощности равен нулю (Cos 90=0), поскольку истинная мощность равна нулю. Здесь треугольник мощности будет выглядеть как вертикальная линия, потому что смежная сторона (истинная мощность) будет иметь нулевую длину.

Чисто емкостные цепи:

То же самое можно сказать и о чисто емкостных цепях. Если в цепи нет диссипативных (резистивных) составляющих, то истинная мощность должна быть равна нулю, что делает любую мощность в цепи чисто реактивной. Треугольник мощности для чисто емкостной цепи снова будет вертикальной линией.

Также в чисто емкостной цепи ток опережает напряжение на 90 град. Это означает, что cos-90=-1
[wp_ad_camp_1]

Ключевые моменты:

• Косинус угла между напряжением и током называется коэффициентом мощности cos ϕ
• В индуктивной цепи коэффициент мощности в запаздывающем характере
• Здесь знак указывает на опережающий и отстающий характер коэффициента мощности.