Второй закон Кирхгофа — третий кит электротехники
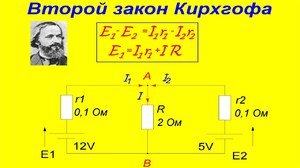Удивительно не то, как просто всё рассчитывается, когда знаешь два понятных всем правила расчёта — первый и второй Законы Кирхгофа, а то, как гениально это было придумано.
Ведь не было тогда бытовой электрической сети. Куда просто вкрутил лампочку, нажал выключатель, и всё — заработало напряжение, побежал ток, разогрелась спираль лампочки и засиял свет. Вот она, понятная работа электричества. Её нам сейчас ничуть не труднее осознать, чем бурчание воды в отоплении или гудение воздуха в инструменте трубача.
Закон Ома — первый кит электротехники
А когда Георг Симон Ом, изучая гальванические, как тогда называли, цепи, вывел своё простейшее соотношение, этого понять не мог никто, кроме немногих посвящённых. Просто потому, что обыденный мозг тогда сразу упирался в нечто невообразимое, а значит, непреодолимое: что это за течение такое, ток частиц, которых не то что пощупать, но и представить нельзя ввиду абсолютно исчезающей малости. Да ещё «текущих» в металле, твёрдом предмете. Уж не то, что попытаться составлять какие-либо точные формулы.
Теперь это соотношение кажется простым и ясным, как удар молнии. Видимо, он сумел почувствовать это явление — электрическое напряжение. Если цепь разомкнута, то тока ещё никакого нет, ничего не нагревается и не пузырится (как вода под током), а напряжение вот оно — попробуй, тронь! Видимо, как-то сумел гений потрогать и попробовать.
Собственно, вся любая электрическая цепь и описана законом Ома. Источник, дающий напряжение и нагрузка, подставляющая напряжению своё тело, отчего получается электрический ток. Соотношение простейшее — чем больше напряжение, тем больше ток. А конкретно каким он получится, определяет пропускная способность нагрузки, G, или проводимость.
I=U*G
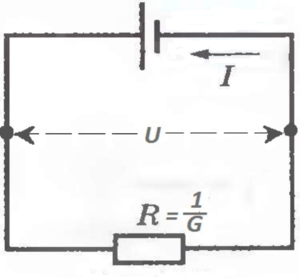
Удобнее и нагляднее оказалось вместо проводимости пользоваться понятием сопротивления, R, величиной обратной проводимости (R=1/G).
И обозначения на первой электросхеме самые простейшие: прямоугольничек — нагрузка, две линии поперёк тока — батарейка.
Самая первая электрическая схема
Видимо, и подключали поначалу что-то одно к чему-то одному. Но вот и эта схема «под напором реальности» усложняется. Во-первых, сама батарейка имеет сопротивление.
Как это изобразить, вот так?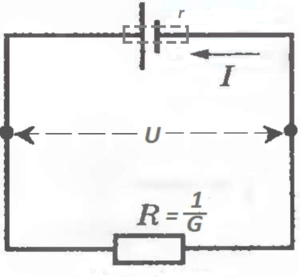 
Некрасиво.
Лучше располагать рядом так:
Есть искушение поставить этот прямоугольничек на другую сторону, рядом с нагрузкой, а нельзя, всё-таки батарейка и её внутреннее сопротивление — одно нераздельное физическое устройство.
Чтобы видеть действие тока, лучше в качестве нагрузки
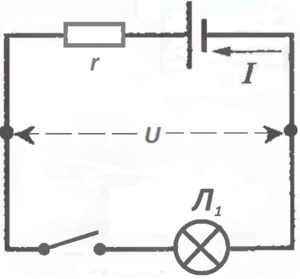
Мы получили последовательную цепочку.
Ток во всех её частях обязан быть одним и тем же, то есть одинаковый везде.
Это логично, и если включить выключатель, лампочка сразу загорится.
При этом никто и не задумывается, что если у нас через лампочку течёт ток всего в один ампер, то это значит, что каждую секунду через неё пробегает:
6 квинтиллионов 241 квадриллион 509 триллионов 125 миллиардов 493 миллиона 690 тысяч с небольшим электронов.
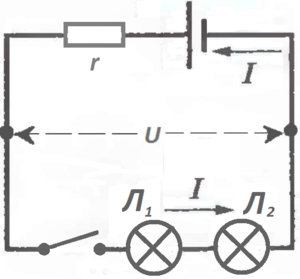
И все они вышли из небольшой батареечки и в неё же и вернутся с другой стороны.
Если поставить вместо одной лампочки две одинаковых, то они загорятся вполнакала, то есть ток I, протекающей последовательно из батарейки через выключатель сначала в лампочку Л1, потом в лампочку Л2 и снова в батарейку, станет меньше, чем был, когда стояла одна лампочка.
Это значит, что сопротивление стало больше: было R у одной лампочки, стало R+R, то есть 2R.
Токи и напряжения в сети
Точную величину тока можно подсчитать, если применить закон Ома ко всей нашей цепи, общее сопротивление которой есть сумма сопротивлений всех её нагрузок.
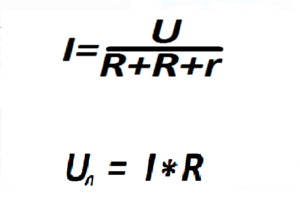
(1) А если оставить в формуле сопротивление только одной лампочки, то, зная, что ток у нас везде один и тот же, можно вычислить напряжение Uл конкретно для этого потребителя, лампочки.
Это напряжение, которое падает именно на нашу лампочку, так и называется «падение напряжения». Оно примерно вдвое меньше нашего напряжения питания U. Примерно — потому что в формуле (1) среди сопротивлений есть ещё небольшой довесок в виде
А теперь взглянем на нашу цепь как на единый контур, который можно обходить по часовой или против часовой стрелки. Ток наш идёт, как нарисовано, против часовой стрелки. Двинемся по этому направлению с любого места и пройдём всё, складываем падения напряжения на всех попадающихся по дороге приборах.
Для токов — узлы, для напряжений — контуры
Получится:
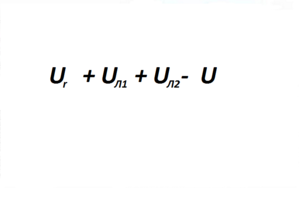
Последним напряжением добавлено то, которое вырабатывается батареей, только со знаком минус, так как оно работает не на потребление, а наоборот, вырабатывается и поставляется в сеть нашей героической батареей. И что у нас получилось?
Правило Кирхгофа для напряжений (2й закон)
А получилось ровно 0. Потому что вся энергия от батареи потребляется лампочками + внутреннее сопротивление батареи. И понятно, это есть высшая справедливость природы. То есть второй закон Кирхгофа в действии.
И вдруг у нас случился… прорыв.
Правило Кирхгофа для токов (1й закон)
К нам в двух точках — А и B — подключились неизвестные, скорее всего, инопланетяне.
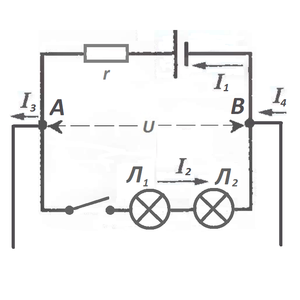
И начали качать от нас энергию. И теперь мы знаем, что ток I3 и ток I4 — не наши, они инопланетянские. И наша схема может быть безнадёжно испорчена.
Но!
А обойдём ка мы контур снова. Может быть, не всё ещё потеряно. И вот:
Ur=I1*r
Uл1=I2*R=Uл2
И, наконец:
U=Uг+Uл1+Uл2.
Потому что I1=I2+I3. И I1=I2+I4.
То есть сколько току вытекло в качестве тока I3 в точке А, столько его и вернулось к нам в точке B в виде тока I4. Высшая справедливость всё-таки восторжествовала. А помогло нам при этом здравое рассуждение, о том, что в любой точке цепи, где электрическая сеть разветвляется, общее количество тока, вытекающего из узла, то есть этой точки, равно количеству тока, втекающего в этот узел. Поэтому смело рисуем схему, зная, что нам помог уже первый, а не второй закон Кирхгофа:
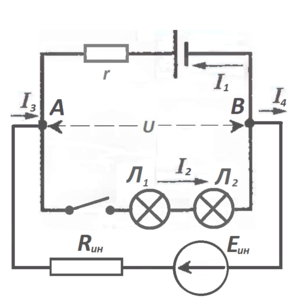Почему-то оказалось, что токи I3 и I4 оказались точно равными -I1, и значит… наши лампочки загорелись полным накалом.
Ох уж эти выдумки инопланетянские! С нашей стороны осталось только в схеме поставить стрелочки токов (и ЭДС у источника ЭДС Eин)
Расчёт цепи по законам Кирхгофа интуитивно понятен — правила позволяют рассчитывать электрические цепи, то есть определять все неизвестные параметры — токи, напряжения — любой, сколь угодно замысловатой цепи.
Применение законов Кирхгофа для расчёта сложных цепей
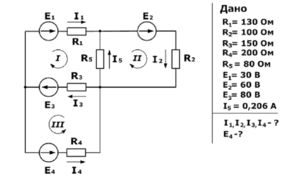
Цепь состоит из ветвей, соединяющихся в узлах. Ветвь — это несколько последовательно соединённых электрических приборов. В узлах могут соединяться три и более ветвей. Это значит, что через узел проходят токи, выходящие из ветвей, которые в нём соединяются.
Ну и теперь, вооружившись проверенными нами базовыми законами электротехники, решим пример, зная, что всё и для любой электрической цепи решаемо.
Смело решаем задачу.
Путь таков:
- Составляются уравнения для токов в узлах — работает первый закон Кирхгофа. Составляются уравнения для падений напряжений по всем независимым контурам — дело второго закона Кирхгофа.
- Уравнения сводятся в систему и решаются методами математики для системы из N линейных уравнений с N неизвестными.
- Делается проверка решения другим способом, например, подсчётом общей мощности сети
Составляем уравнения для токов, втекающих/вытекающих в узлы. Узлов сего три, значит, уравнений будет 3-1, то есть два.
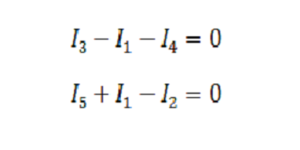
Теперь составляем уравнения для контуров и падений напряжения в них. Контуров у нас независимых три (в которых в каждом есть хотя бы одна ветвь, не встречающаяся в других).
Вот и получается три уравнения по второму закону Кирхгофа: Собрав все пять уравнений вместе, получаем систему из пяти уравнений с пятью неизвестными.
Остальное — дело королевы наук, то есть математики. Такие системы она щёлкает не глядя.
И получаются вполне похожие на правду ответы:
А мы знаем, хорош тот ответ, который поддаётся проверке.
Сделаем-ка мы расчёт мощности, выделяемой на всех устройствах данной схемы при полученной нами картине токов и напряжений двумя способами, пользуясь немного разными определениями для мощности:
- мощность как произведение тока на напряжение
- мощность, как квадрат силы тока, умноженный на сопротивление
Как видим, всё у нас правильно, задача нашего непростого примера решена.
Ответы Mail.ru: 2-ой закон кирхгофа
2-й закон Кирхгофа — сумма падений напряжения равна сумме ЭДС. не слушай верхнего !! «сушествует мнение», «бытует мнение»! I*R1 + R2*I = Uo U1+U2=Uo в основном применяется для расчёта сопротивления на том участке цепи где необходимо снизить напряжение U1= Uо-U2, U2= Uо-U1,
Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю: Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве, то она описывается уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными. Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно) , перепад напряжения считается положительным, в противном случае — отрицательным. Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения. Существует мнение, согласно которому «Законы Кирхгофа» следует именовать «Правилами Кирхгофа» , ибо они не отражают фундаментальных сущностей природы (и не являются обобщением большого количества опытных данных) , а могут быть выведены из других положений и предположений. [
Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю. Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве mi, то она описывается m-mi-(p-1) уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.
Лучше говорить: 2-е Правило Кирхгофа, потому что Закон Кирхгофа — это из области теории излучения. 2-е правило Кирхгофа: В любом замкнутом контуре, произвольно выбранном в разветвлённой электрической цепи, алгебраическая сумма произведений сил токов в отдельных участках контура на электрические сопротивления этих участков равна алгебраической сумме ЭДС всех источников электрической энергии, включённых в контур. Все токи, совпадающие с направлением обхода контура, считаются положительными. ЭДС считаются положительными, если они вызывают ток, совпадающий по направлению с обходом контура.
3.4. Законы Кирхгофа
В комплексном виде
| U m | U m |
| j( | u i ) | j |
|
| |
|
| 2 |
| ||||||
Z |
|
|
| e |
|
| xC e |
| jxC , |
Im |
| Im |
|
|
| ||||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| |
Z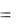 
jxC ,
т. е. комплексное сопротивление С-элемента является отрицательным мнимым числом, модуль которого равен xC .
В цепи с С-элементом не совершается работа, а происходит периодический обмен энергии между источником и электрическим полем.
Интенсивность этого обмена характеризуется реактивной емкостной мощностью QC, которая измеряется в тех же единицах, что и Q (вар).
QC 
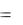UC IC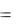 
xC IC2 
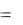UC2 / xC .
Если индуктивный и емкостной элементы соединены последовательно, то в моменты времени, когда энергия магнитного поля индуктивного элемента увеличивается, энергия электрического поля емкостного элемента уменьшается, и наоборот.
Следовательно, эти элементы могут обмениваться энергией не только с источником, но и друг с другом.
Законы Кирхгофа для цепей однофазного переменного тока записываются в комплексной форме или для мгновенных значений. Математическая формулировка зависит от выбранного способа представления синусоидальных величин, однако векторный и тригонометрический способы достаточно громоздкие.
I закон Кирхгофа – для мгновенных значений: алгебраическая сумма токов в любом узле электрической цепи в каждый момент времени равна нулю.
n
ik 0 ,
k 1
где n – число ветвей, сходящихся в узле.
В комплексной форме: алгебраическая сумма комплексных значений токов всех ветвей, сходящихся в каком-либо узле цепи синусоидального тока, равна нулю.
n
k 1 I k 0 .
II закон Кирхгофа – для мгновенных значений: алгебраическая сумма напряжений всех участков любого контура в каждый момент времени равна нулю.
m
uk 0,
k 1
где m – число участков контура.
Для контура, содержащего пассивные элементы (резистивные, индуктивные, емкостные) и источники ЭДС, формулировка II закона Кирхгофа следующая: в каждый момент времени алгебраическая сумма падений напряжений на пассивных элементах контура равна алгебраической сумме ЭДС в этом контуре.
В комплексной форме II закон Кирхгофа:
|
| n | m |
|
|
| U k | Ek . |
|
|
| k 1 | k 1 |
|
3.5. Неразветвленные электрические цепи | ||||
Рассмотрим цепь с последовательным соединением R-, L- и С- | ||||
элементов. |
|
|
|
|
Пусть | данная цепь | (рис. 19) подключена | к источнику тока | |
i Im sin ( t | i ). Необходимо определить напряжение на ее входе. | |||
R |
| По II закону Кирхгофа запишем: | ||
|
|
|
| |
|
| U | U R U L | UC , |
| L | где (из закона Ома): | ||
C |
| U R | R I ; U L | jxL I; |
|
|
|
| |
UC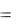 
jxC I .
Отсюда:
U I (R jxL jxC ) ,
где R j(xL xC ) Z – комплексное сопротивление всей цепи. Тогда для данной цепи:
U I Z .
При последовательном соединении элементов R, L и С эквивалентное комплексное сопротивление цепи равно сумме комплексных сопротивлении всех последовательно включенных элементов:
Z R jxL jxc .
Закон Ома для действующих значений и выражение полного сопротивления цепи будут иметь вид:
|
| U |
|
|
|
|
|
|
|
| |
I |
|
|
| ; | Z R2 ( x | L | x )2 . | ||||
|
|
|
|
| |||||||
|
|
|
|
| |||||||
|
| R2 ( x |
| x )2 |
|
| C | ||||
|
| L |
|
|
|
|
| ||||
|
|
| C |
|
|
|
|
| |||
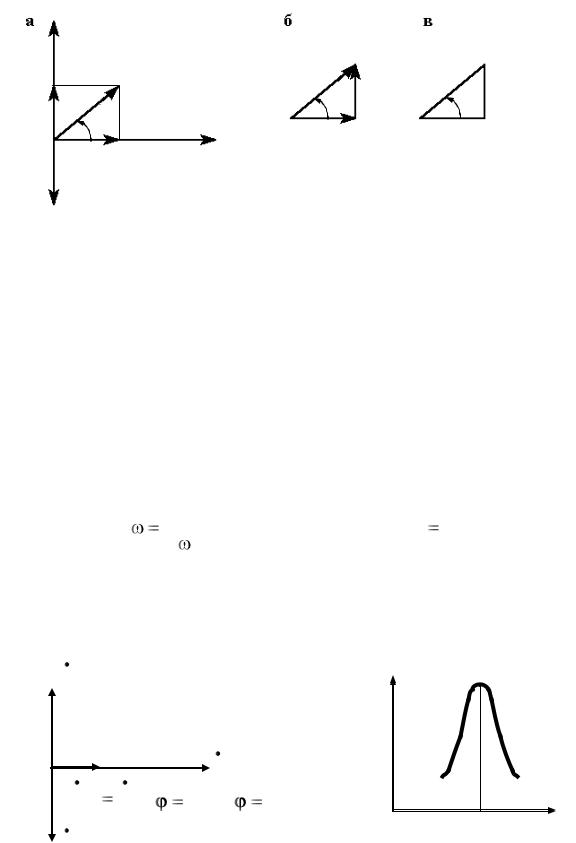
Рассмотрим векторные диаграммы.
При построении векторных диаграмм необходимо взять за основу какой-то базисный вектор, от которого и строить все другие векторы, при этом необходимо помнить, что за положительное направление вращения векторов принято вращение против часовой стрелки. При последовательном соединении элементов за исходный (основной) принимается вектор тока, так как во всех элементах цепи протекает один и тот же ток. Рассмотрим случай, когда индуктивное сопротивление катушки больше емкостного сопротивления конден-
сатора ( xL > xC ).
Векторная диаграмма будет иметь вид (рис. 20, а). Из векторной диаграммы можно выделить треугольник напряжений (рис. 20, б). Если стороны треугольника напряжений (мысленно) разделить на один и тот же ток получим подобный треугольник сопротивлений (рис. 20, в).
а |
|
| б |
| в |
|
|
|
| U L |
|
|
|
|
|
|
|
|
|
|
| U |
|
|
|
|
| U |
|
|
|
|
|
|
|
|
|
|
| Z |
| x | ||
|
|
|
| φ | ||||
|
|
|
| φ U L |
|
|
| |
| φ |
|
|
|
|
| R |
|
|
|
|
|
|
|
| ||
| U R |
|
| U R |
|
|
|
|
| I |
|
|
|
| |||
|
|
|
|
|
|
| ||
cos φ = R/Z
UC
Рис. 20
3.6. Резонанс напряжений
Электрический резонанс – совпадение частоты собственных электрических колебаний в замкнутом контуре с частотой колебаний электрического тока, передаваемого внешним источником энергии.
Резонансом напряжений называется режим, при котором в цепи с последовательным соединением индуктивного и емкостного сопротивлений напряжение на входе совпадает по фазе с током. Условие резонанса напряжений следующее:
L | 1 | или | xL xC | |
| ||||
C | ||||
|
|
|
При резонансе напряжений векторная диаграмма представлена на рис. 21, а, а график изменения тока от изменения емкости конденсатора (или индуктивности катушки) может иметь вид (рис. 21, б):
I
Cрез C
U C
Рис. 21
Как следствие из условия резонанса напряжений, можно отметить следующее:
–ток в цепи в точке резонанса – максимальный;
–угол сдвига фаз = 0, т. е. цепь ведет себя как цепь, имеющая только активное сопротивление;
– cos = 1;
– нaпpяжeния на отдельных участках цепи переменного тока с последовательным соединением L- и С-элементов могут значительно превышать напряжение на входе (что невозможно в цепях постоян-
ного тока), так | как напряжения на L- и С-элементах находятся в про- | ||
тивофазе ( | UC | U L | ) и их сумма меньше каждого в отдельности. |
|
| ||
В электроэнергетических устройствах в большинстве случаев резонанс напряжений – явление нежелательное именно потому, что входные напряжения установок могут в несколько раз превышать их рабочие напряжения; однако в радиотехнике и автоматике резонанс напряжений часто применяется для настройки цепей на заданную частоту.
3.7. Разветвлѐнные электрические цепи
Рассмотрим электрическую цепь, состоящую из двух параллельных ветвей, схема замещения которой представлена на рис. 22. Пусть цепь присоединена к источнику напряжения u Um sin t. Необходимо определить токи в ветвях и в неразветвлѐнной части це-
пи. Для узла «а» по I закону Кирхгофа можно записать: I |
|
| I1 I2 , но | |||||||||||||||||||||||||||||
по закону Ома: | I1 |
| U | ; | I2 | U | . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
| I |
|
|
| а |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
| Z1 |
|
| Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Тогда: | I | U | U | , |
|
|
|
|
|
|
|
|
|
|
|
|
| R1 |
|
|
|
|
| R2 |
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
| Z1 Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
| I1 |
|
|
|
|
|
|
|
| I2 |
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
где Z1 | R1 | jxL – комплексное |
| U |
|
|
|
|
|
|
|
| L |
|
|
|
|
|
|
| C |
| ||||||||||
|
|
|
|
|
|
|
|
|
|
| I2 |
| ||||||||||||||||||||
сопротивление |
|
| первой |
| ветви; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
Z 2 R2 jxC – комплексное сопротив- | б | |
|
| |
Рис. 22 |
| |
ление второй параллельной ветви. Ина- |
| |
|
| |
|
| |
че можно записать: |
|
|
|
|
|
|
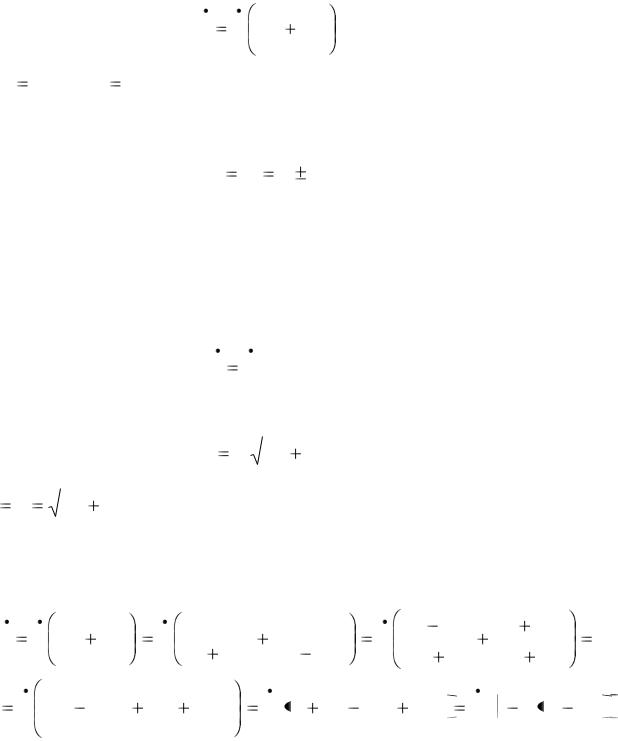
| I | U | 1 |
| 1 |
| , | |||
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
| Z 1 | Z 2 | |||||||
где | 1 | Y 1; | 1 | Y 2 | – комплексные проводимости ветвей. | |||||||||
|
| |||||||||||||
Z1 | Z 2 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||
| Комплексная проводимость всей цепи: |
| ||||||||||||
|
|
|
|
| Y | 1 |
| g | jb , |
| ||||
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
| Z |
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||
где g – активная проводимость, являющаяся действительной частью комплексного числа; b – реактивная проводимость, являющаяся мнимой частью комплексного числа ( может быть bL и bC ).
Закон Ома для цепи с параллельным соединением R- L- и С- элементов в комплексном виде
|
|
|
|
|
| I | U Y | ||
или для действующих значений |
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| I | U g 2 b2 , | ||
|
|
|
|
| |||||
где |
| Y |
| y | g 2 b2 – полная (действующая) проводимость цепи. | ||||
|
| ||||||||
Выразим проводимости ветвей через их сопротивления. Для схемы, представленной на рис. 22, можно записать закон Ома в следующем виде
1 | 1 |
|
|
|
| 1 |
|
|
| 1 |
|
|
| R1 | jxL |
| R2 | jxC |
| |||||||
I U |
|
|
|
|
|
|
| U |
|
|
|
|
|
| U |
|
|
|
|
|
| |||||
Z1 |
|
| Z 2 | R1 jxL |
| R2 | jxC | R2 | x2 |
| R2 | x2 |
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 | L | 2 |
| C |
| |
U | R1 |
| j | xL |
|
| R2 |
| j | xC |
| U g g | 2 | jb | L | jb | U g j b | L | b . | |||||||
|
|
|
|
|
|
| ||||||||||||||||||||
| Z12 |
|
| Z12 |
|
| Z22 |
| Z22 | 1 |
|
| C |
|
|
|
| C | ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
Из последнего выражения видно, что индуктивная проводимость – мнимая отрицательная часть комплексной проводимости с модулем, равным bL; емкостная проводимость – мнимая положи-
тельная
3.4. Законы Кирхгофа
В комплексном виде
| U m | U m |
| j( | u i ) | j |
|
| |
|
| 2 |
| ||||||
Z |
|
|
| e |
|
| xC e |
| jxC , |
Im |
| Im |
|
|
| ||||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| |
Z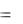 
jxC ,
т. е. комплексное сопротивление С-элемента является отрицательным мнимым числом, модуль которого равен xC .
В цепи с С-элементом не совершается работа, а происходит периодический обмен энергии между источником и электрическим полем.
Интенсивность этого обмена характеризуется реактивной емкостной мощностью QC, которая измеряется в тех же единицах, что и Q (вар).
QC 
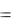UC IC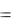 
xC IC2 
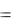UC2 / xC .
Если индуктивный и емкостной элементы соединены последовательно, то в моменты времени, когда энергия магнитного поля индуктивного элемента увеличивается, энергия электрического поля емкостного элемента уменьшается, и наоборот.
Следовательно, эти элементы могут обмениваться энергией не только с источником, но и друг с другом.
Законы Кирхгофа для цепей однофазного переменного тока записываются в комплексной форме или для мгновенных значений. Математическая формулировка зависит от выбранного способа представления синусоидальных величин, однако векторный и тригонометрический способы достаточно громоздкие.
I закон Кирхгофа – для мгновенных значений: алгебраическая сумма токов в любом узле электрической цепи в каждый момент времени равна нулю.
n
ik 0 ,
k 1
где n – число ветвей, сходящихся в узле.
В комплексной форме: алгебраическая сумма комплексных значений токов всех ветвей, сходящихся в каком-либо узле цепи синусоидального тока, равна нулю.
n
k 1 I k 0 .
II закон Кирхгофа – для мгновенных значений: алгебраическая сумма напряжений всех участков любого контура в каждый момент времени равна нулю.
m
uk 0,
k 1
где m – число участков контура.
Для контура, содержащего пассивные элементы (резистивные, индуктивные, емкостные) и источники ЭДС, формулировка II закона Кирхгофа следующая: в каждый момент времени алгебраическая сумма падений напряжений на пассивных элементах контура равна алгебраической сумме ЭДС в этом контуре.
В комплексной форме II закон Кирхгофа:
|
| n | m |
|
|
| U k | Ek . |
|
|
| k 1 | k 1 |
|
3.5. Неразветвленные электрические цепи | ||||
Рассмотрим цепь с последовательным соединением R-, L- и С- | ||||
элементов. |
|
|
|
|
Пусть | данная цепь | (рис. 19) подключена | к источнику тока | |
i Im sin ( t | i ). Необходимо определить напряжение на ее входе. | |||
R |
| По II закону Кирхгофа запишем: | ||
|
|
|
| |
|
| U | U R U L | UC , |
| L | где (из закона Ома): | ||
C |
| U R | R I ; U L | jxL I; |
|
|
|
| |
UC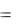 
jxC I .
Отсюда:
U I (R jxL jxC ) ,
где R j(xL xC ) Z – комплексное сопротивление всей цепи. Тогда для данной цепи:
U I Z .
При последовательном соединении элементов R, L и С эквивалентное комплексное сопротивление цепи равно сумме комплексных сопротивлении всех последовательно включенных элементов:
Z R jxL jxc .
Закон Ома для действующих значений и выражение полного сопротивления цепи будут иметь вид:
|
| U |
|
|
|
|
|
|
|
| |
I |
|
|
| ; | Z R2 ( x | L | x )2 . | ||||
|
|
|
|
| |||||||
|
|
|
|
| |||||||
|
| R2 ( x |
| x )2 |
|
| C | ||||
|
| L |
|
|
|
|
| ||||
|
|
| C |
|
|
|
|
| |||
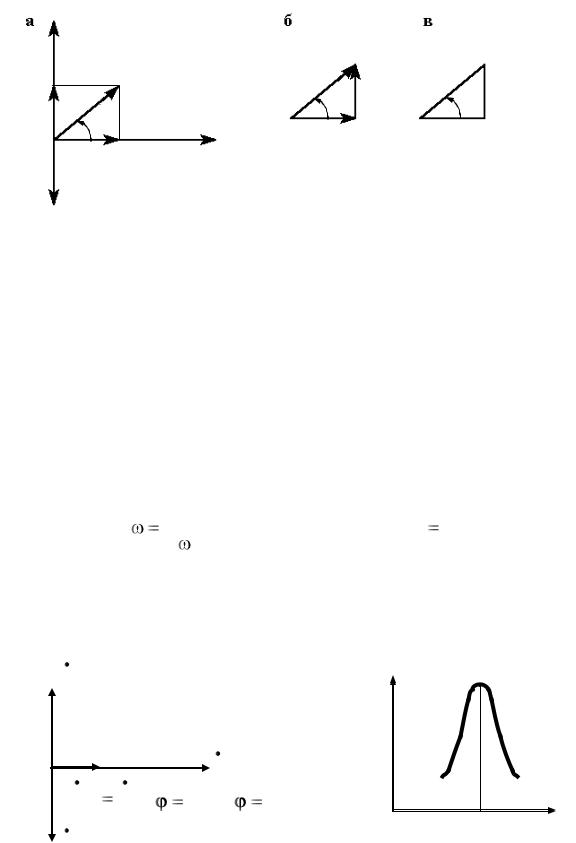
Рассмотрим векторные диаграммы.
При построении векторных диаграмм необходимо взять за основу какой-то базисный вектор, от которого и строить все другие векторы, при этом необходимо помнить, что за положительное направление вращения векторов принято вращение против часовой стрелки. При последовательном соединении элементов за исходный (основной) принимается вектор тока, так как во всех элементах цепи протекает один и тот же ток. Рассмотрим случай, когда индуктивное сопротивление катушки больше емкостного сопротивления конден-
сатора ( xL > xC ).
Векторная диаграмма будет иметь вид (рис. 20, а). Из векторной диаграммы можно выделить треугольник напряжений (рис. 20, б). Если стороны треугольника напряжений (мысленно) разделить на один и тот же ток получим подобный треугольник сопротивлений (рис. 20, в).
а |
|
| б |
| в |
|
|
|
| U L |
|
|
|
|
|
|
|
|
|
|
| U |
|
|
|
|
| U |
|
|
|
|
|
|
|
|
|
|
| Z |
| x | ||
|
|
|
| φ | ||||
|
|
|
| φ U L |
|
|
| |
| φ |
|
|
|
|
| R |
|
|
|
|
|
|
|
| ||
| U R |
|
| U R |
|
|
|
|
| I |
|
|
|
| |||
|
|
|
|
|
|
| ||
cos φ = R/Z
UC
Рис. 20
3.6. Резонанс напряжений
Электрический резонанс – совпадение частоты собственных электрических колебаний в замкнутом контуре с частотой колебаний электрического тока, передаваемого внешним источником энергии.
Резонансом напряжений называется режим, при котором в цепи с последовательным соединением индуктивного и емкостного сопротивлений напряжение на входе совпадает по фазе с током. Условие резонанса напряжений следующее:
L | 1 | или | xL xC | |
| ||||
C | ||||
|
|
|
При резонансе напряжений векторная диаграмма представлена на рис. 21, а, а график изменения тока от изменения емкости конденсатора (или индуктивности катушки) может иметь вид (рис. 21, б):
I
Cрез C
U C
Рис. 21
Как следствие из условия резонанса напряжений, можно отметить следующее:
–ток в цепи в точке резонанса – максимальный;
–угол сдвига фаз = 0, т. е. цепь ведет себя как цепь, имеющая только активное сопротивление;
– cos = 1;
– нaпpяжeния на отдельных участках цепи переменного тока с последовательным соединением L- и С-элементов могут значительно превышать напряжение на входе (что невозможно в цепях постоян-
ного тока), так | как напряжения на L- и С-элементах находятся в про- | ||
тивофазе ( | UC | U L | ) и их сумма меньше каждого в отдельности. |
|
| ||
В электроэнергетических устройствах в большинстве случаев резонанс напряжений – явление нежелательное именно потому, что входные напряжения установок могут в несколько раз превышать их рабочие напряжения; однако в радиотехнике и автоматике резонанс напряжений часто применяется для настройки цепей на заданную частоту.
3.7. Разветвлѐнные электрические цепи
Рассмотрим электрическую цепь, состоящую из двух параллельных ветвей, схема замещения которой представлена на рис. 22. Пусть цепь присоединена к источнику напряжения u Um sin t. Необходимо определить токи в ветвях и в неразветвлѐнной части це-
пи. Для узла «а» по I закону Кирхгофа можно записать: I |
|
| I1 I2 , но | |||||||||||||||||||||||||||||
по закону Ома: | I1 |
| U | ; | I2 | U | . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
| I |
|
|
| а |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
| Z1 |
|
| Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Тогда: | I | U | U | , |
|
|
|
|
|
|
|
|
|
|
|
|
| R1 |
|
|
|
|
| R2 |
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
| Z1 Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
| I1 |
|
|
|
|
|
|
|
| I2 |
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
где Z1 | R1 | jxL – комплексное |
| U |
|
|
|
|
|
|
|
| L |
|
|
|
|
|
|
| C |
| ||||||||||
|
|
|
|
|
|
|
|
|
|
| I2 |
| ||||||||||||||||||||
сопротивление |
|
| первой |
| ветви; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
Z 2 R2 jxC – комплексное сопротив- | б | |
|
| |
Рис. 22 |
| |
ление второй параллельной ветви. Ина- |
| |
|
| |
|
| |
че можно записать: |
|
|
|
|
|
|
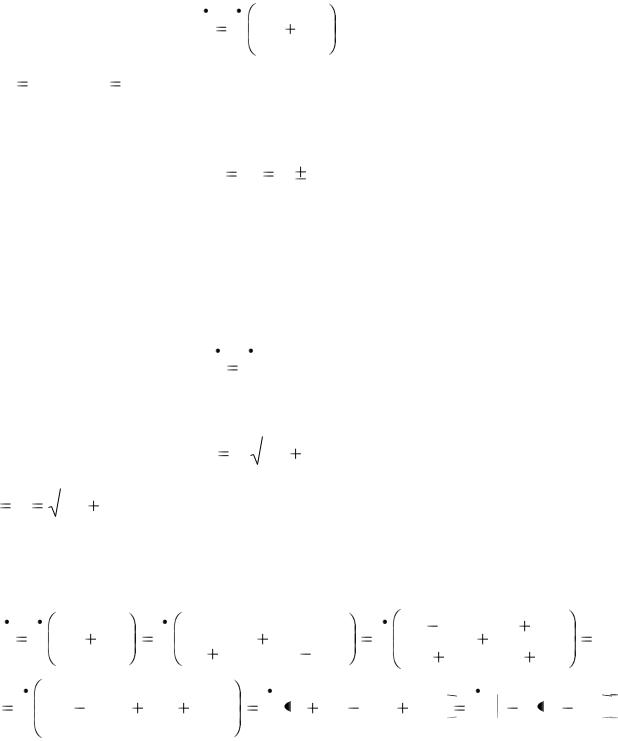
| I | U | 1 |
| 1 |
| , | |||
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
| Z 1 | Z 2 | |||||||
где | 1 | Y 1; | 1 | Y 2 | – комплексные проводимости ветвей. | |||||||||
|
| |||||||||||||
Z1 | Z 2 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||
| Комплексная проводимость всей цепи: |
| ||||||||||||
|
|
|
|
| Y | 1 |
| g | jb , |
| ||||
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
| Z |
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||
где g – активная проводимость, являющаяся действительной частью комплексного числа; b – реактивная проводимость, являющаяся мнимой частью комплексного числа ( может быть bL и bC ).
Закон Ома для цепи с параллельным соединением R- L- и С- элементов в комплексном виде
|
|
|
|
|
| I | U Y | ||
или для действующих значений |
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| I | U g 2 b2 , | ||
|
|
|
|
| |||||
где |
| Y |
| y | g 2 b2 – полная (действующая) проводимость цепи. | ||||
|
| ||||||||
Выразим проводимости ветвей через их сопротивления. Для схемы, представленной на рис. 22, можно записать закон Ома в следующем виде
1 | 1 |
|
|
|
| 1 |
|
|
| 1 |
|
|
| R1 | jxL |
| R2 | jxC |
| |||||||
I U |
|
|
|
|
|
|
| U |
|
|
|
|
|
| U |
|
|
|
|
|
| |||||
Z1 |
|
| Z 2 | R1 jxL |
| R2 | jxC | R2 | x2 |
| R2 | x2 |
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 | L | 2 |
| C |
| |
U | R1 |
| j | xL |
|
| R2 |
| j | xC |
| U g g | 2 | jb | L | jb | U g j b | L | b . | |||||||
|
|
|
|
|
|
| ||||||||||||||||||||
| Z12 |
|
| Z12 |
|
| Z22 |
| Z22 | 1 |
|
| C |
|
|
|
| C | ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
Из последнего выражения видно, что индуктивная проводимость – мнимая отрицательная часть комплексной проводимости с модулем, равным bL; емкостная проводимость – мнимая положи-
тельная
