Трение скольжения
Трением скольжения называют механический эффект, возникающий в зоне контакта взаимодействующих тел при их движении относительно друг друга.
Сила трения скольжения зависит от материалов и шероховатости контактирующих поверхностей тел, величины их давления друг на друга и скорости их относительного движения.
При определении сил трения используется известная из физики зависимость, показывающая, что сила трения пропорциональна нормальной реакции (закон Амонтона-Кулона).
При этом коэффициент пропорциональности зависит от материалов, физического состояния соприкасающихся поверхностей и называется коэффициентом трения скольжения (коэффициент трения обозначается f и является справочным материалом).
Геометрическая сумма нормальной реакции и силы трения представляет собой полную реакцию между соприкасающимися поверхностями.
Угол между полной реакцией R и нормальной составляющей называется углом трения (обычно обозначается греческой буквой ρ — рисунок 20а, в некоторых случаях – φ).
Из рисунка 20а:
Таким образом, между коэффициентом трения и углом трения очень простая однозначная зависимость, которая позволяет в равной степени пользоваться обоими параметрами для характеристики сил трения и получать наиболее удобные зависимости при расчетах.
При движении тела по поверхности в разных направлениях полная реакция меняет свое положение, а ее геометрическое место представляет собой конус, который называется конусом трения (см. рисунок 20б).
Заменим силы Q и F (рисунок 20а) результирующей силой FΣ ( рисунок 20в). На расчетной схеме обычно все силы прикладывают в центр ползуна, рассматривая сходящуюся систему сил для упрощения задачи и пренебрегая незначительным расстоянием от поверхности до центра ползуна.
Тело будет двигаться вдоль поверхности, если движущая сила Fдв будет больше силы сопротивления (в данном случае силы трения) или, в крайнем случае, равна ей. Из рисунка 20в:
Таким образом, тело будет двигаться вдоль поверхности в том случае, когда линия действия внешней результирующей силы, приложенной к этому телу, будет проходить вне конуса трения (ускоренное движение) или совпадать с его образующей (равномерное движение).
Если линия действия результирующей внешней силы проходит внутри конуса трения, то происходит
Трение на наклонной плоскости >
Курсовой проект по ТММ >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Заказать решение
Поиск формул и решений задач
Физика Сила трения.
 Трение покоя
Трение покояМатериалы к уроку
Конспект урока
Мы уже знаем, что причиной изменения скорости является сила трения.Мяч, скатившись с горки, движется по горизонтальному пути неравномерно, скорость его постепенно уменьшается, и через некоторое время он останавливается. Конькобежец, как только перестанет разгоняться, будет катиться довольно долго, но все равно остановится. Останавливается и автомобиль, после того, как двигатель перестанет работать.
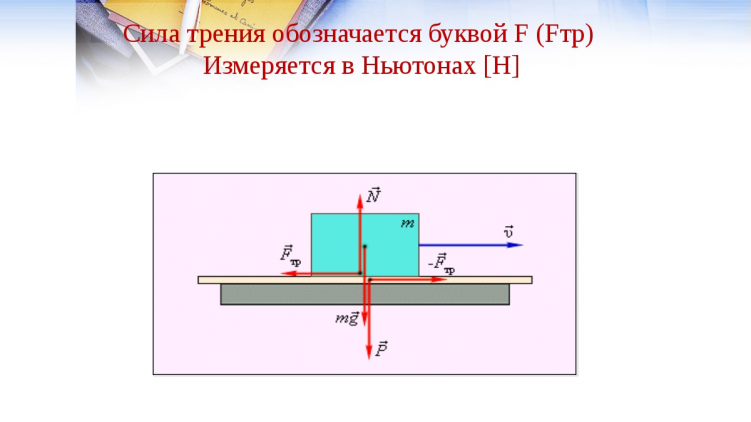
При соприкосновении поверхностей двух тел между ними возникает взаимодействие, которое начинает препятствовать их движению относительно друг друга. Это взаимодействие получило название трение. Сила, которая характеризует это взаимодействие, называется силой трения. Она обозначается буквой «эф» (F) с индексом: Fтp. .

Первая из причин, это шероховатость.Поверхности соприкасающихся тел, даже гладкие на вид, имеют неровности. Так при увеличении хорошо заметны неровности на лезвии бритвы. Рассмотрим под микроскопом лезвие бритвы, на котором лежит человеческий волос.Очевидно, что царапины и микронеровности очень малы, но при продвижении одного тела по поверхности другого, эти неровности, бугорки и впадинки, цепляясь друг за друга, создадут некоторую силу, задерживающую движение.
Существуют различные виды сухого трения:
1) трение покоя;
2) трение скольжения;
3) трение качения.
На полу стоит диван.
 Попробуем его передвинуть на другое место. Если подействовать на диван слабо, то он не сдвинется с места. Почему? ПАУЗА. В ответ на действие нашей силы резко возникает сила трения между полом и ножками дивана, уравновешивающая действие нашей силы.Когда тело находится в покое на наклонной плоскости, оно удерживается на ней силой трения. Однако если бы не было трения, то тело под действием силы тяжести начало бы скользить вниз по наклонной плоскости, как санки с горы. Так как эта сила существует между покоящимися друг относительно друга телами, то эту силу принято называть силой трения покоя. Благодаря трению покоя по ленточному транспортеру перемещают детали на производствах. Например, на картинке изображен транспортер, перемещающий отходы деревообрабатывающего производства. Сила трения покоя удерживает клин, вбитый в колоду; не дает развязаться ленте, завязанной на узел; удерживает крем для лица на коже, не давая ему соскользнуть и т.д.
Попробуем его передвинуть на другое место. Если подействовать на диван слабо, то он не сдвинется с места. Почему? ПАУЗА. В ответ на действие нашей силы резко возникает сила трения между полом и ножками дивана, уравновешивающая действие нашей силы.Когда тело находится в покое на наклонной плоскости, оно удерживается на ней силой трения. Однако если бы не было трения, то тело под действием силы тяжести начало бы скользить вниз по наклонной плоскости, как санки с горы. Так как эта сила существует между покоящимися друг относительно друга телами, то эту силу принято называть силой трения покоя. Благодаря трению покоя по ленточному транспортеру перемещают детали на производствах. Например, на картинке изображен транспортер, перемещающий отходы деревообрабатывающего производства. Сила трения покоя удерживает клин, вбитый в колоду; не дает развязаться ленте, завязанной на узел; удерживает крем для лица на коже, не давая ему соскользнуть и т.д.  Такое трение возникает, например, при движении коньков.
Такое трение возникает, например, при движении коньков.Если вместо лезвия конька будут колеса — то такое движение называют качение. Роликовые коньки катятся, а не скользят по поверхности земли. Трение, возникающее при этом, называют трением качения. Движение колес железнодорожного состава, перекатывание бревен, катушек с кабелем, скатывание шара по желобу – все это есть проявление силы трения качения.
Силу трения можно уменьшить во много раз, если ввести между трущимися поверхностями смазку. Соприкасаться будут не поверхности тел, а слои смазки. Трение слоев жидкой смазки меньше, чем твердых поверхностей. Например, слабое трение при катании на коньках по льду и на лыжах по снегу, можно объяснить действием смазки. Из-за сильного давления, между коньками и льдом, лыжами и снегом образуется тонкий слой воды.
На рисунке изображено тело, движущееся по наклонной плоскости.
 Вектор скорости указан рядом с телом.
Вектор скорости указан рядом с телом.Укажем направление силы трения. В обоих случаях трение будет направлено вдоль поверхности соприкосновения тел, в сторону, противоположную движению тела.
Рассмотрим, от чего зависит величина силы трения.
Проведем опыт.
К деревянному бруску прикрепим динамометр. Чтобы измерить силу трения скольжения деревянного бруска по гладкому столу и наждачной бумаге держим динамометр горизонтально, затем равномерно двигаем брусок: сначала по гладкому столу, потом по наждачной бумаге.
Значит, сила трения будет различной в зависимости от материалов трущихся поверхностей.
Опыт 2. К деревянному бруску прикрепим динамометр и измерим силу трения, равномерно двигая брусок по гладкому столу, держа динамометр горизонтально. Затем на брусок положим груз и аналогично измерим силу трения.
Сделаем вывод: чем больше вес тела, тем сила трения больше, при одинаковой поверхности соприкосновения.

Значит, сила трения зависит от силы, прижимающей тело к поверхности.
Опыт 3. Заменим трение скольжения на трение качения, положив деревянный брусок на круглые палочки. Измерим силу трения.
Сделаем вывод: при движении по шершавой поверхности, трение качения намного меньше силы трения скольжения.
Подведем итог.
Измеряя силу, с которой динамометр действует на тело при его равномерном движении, мы измеряем силу трения. Сила трения будет зависеть от:
— от материалов, трущихся поверхностей;
При равных нагрузках сила трения качения всегда меньше силы трения скольжения.
Остались вопросы по теме? Наши педагоги готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать педагогаОставить заявку на подбор
Трение скольжения: статическое и кинетическое трение — 1482 слов
Резюме
Трение препятствует скольжению и зависит от шероховатости контактирующих поверхностей. Эта пропорция называется «коэффициентом трения» и обозначается символом μ (произносится как «мяу»). Трение, противодействующее движению из состояния покоя, называется «статическим трением». Как только происходит скольжение, оказывается, что требуется меньшая сила, и это называется «кинетическим трением». Трение в основном зависит от характера поверхностей, а не от площади контакта между поверхностями.
Эта пропорция называется «коэффициентом трения» и обозначается символом μ (произносится как «мяу»). Трение, противодействующее движению из состояния покоя, называется «статическим трением». Как только происходит скольжение, оказывается, что требуется меньшая сила, и это называется «кинетическим трением». Трение в основном зависит от характера поверхностей, а не от площади контакта между поверхностями.
Эксперимент был проведен для определения того, как изменяется кинетическое и статическое трение и как изменяется коэффициент трения при увеличении нагрузки или давления на поверхность и типа используемого материала. Использовались деревянные, металлические и резиновые поверхности. Было обнаружено, что площадь контакта поверхностей и величина нормальной силы, приложенной к поверхностям, не влияют на трение; скорее, характер поверхностей, используемых для трения, был основным фактором, влияющим на значение коэффициента трения.
Экспериментальная цель
Целями этого эксперимента является проверка законов трения, различных типов трения (статическое и кинетическое трение) и того, как тип и природа поверхности, на которой происходит трение, определяют коэффициент трения. В частности, исследуются три поверхности. Это металл на металле, дерево на дереве и металл на резине.
В частности, исследуются три поверхности. Это металл на металле, дерево на дереве и металл на резине.
Теоретическая основа
Гладкие поверхности обычно характеризуются тем, что при соприкосновении они располагаются перпендикулярно своей касательной плоскости. Тем не менее, ни одна поверхность, какой бы гладкой она ни была, не лишена трения (CodeCogs Engineering, 2009).).
Трение можно определить как сопротивление скольжению, когда две или более поверхностей соприкасаются друг с другом. Сила трения – это сила, препятствующая относительному движению поверхностей. Неровные частицы между поверхностями являются основной причиной трения. Следовательно, чтобы произошло скольжение, эту силу необходимо преодолеть.
Существуют различные законы трения. Это:
- Величина трения между поверхностями не зависит от площади контакта.
- Коэффициент трения (μ), зависящий от состава или природы поверхностей (материалов, из которых они сделаны), имеет тенденцию ограничивать трение при приложении нормальной силы.

- Направление трения всегда противоположно направлению движения или направлению, в котором происходит скольжение, и не зависит от скорости тел.
- Силы трения обычно достаточно для предотвращения трения тел, находящихся в равновесии, и поэтому ее можно легко рассчитать с помощью условий равновесия (CodeCogs Engineering, 2009).).
Статическое трение определяется как трение, которое препятствует движению поверхностей из состояния покоя, в то время как кинетическое трение имеет место для поверхностей, уже находящихся в движении. Коэффициент статического трения обычно больше, чем коэффициент кинетического трения.
Трение имеет как положительные, так и отрицательные стороны. В частности, трение очень важно в тормозной системе транспортных средств. Однако это вызывает износ машин, заставляя их потреблять больше энергии.
Экспериментальные процедуры
Используемое оборудование: Фрикционное оборудование скольжения, фрикционная пластина и блок со шнуром, гайки с накаткой, грузовой крюк, пружинный баланс 10 Н, набор грузов, отвес и леска.
Установка оборудования: Монтажная панель была поставлена в вертикальное положение, а сборка плоскости установлена путем установки шпильки через отверстие h5, шпильки на стойке через С8 и закреплены гайками. Отвес был подвешен над центральным винтом транспортира, и плоскость гарантировалась горизонтальной. Центральная опора была отрегулирована. Фрикционный блок взвешивали с помощью пружинных весов и записывали его вес, затем помещали на левый конец плоскости деревянной поверхностью вниз и собирали трос на шкиве. Грузовой крюк 0,1 Н был прикреплен к концу шнура.
Процедуры
Испытание 1: Грузы (около 0,8 Н) были помещены на крюк, и каждый груз начал толкать блок до тех пор, пока вес не стал достаточным, чтобы тянуть блок вдоль плоскости с постоянной скоростью. Регистрировались вес фрикционного блока (R) и сила, необходимая для преодоления кинетического трения (Fk).
Тест 2: Процедура теста 1 была повторена, но блок не был протолкнут. Вместо этого на крюки помещали грузы примерно (0,1 Н) до тех пор, пока блок не начал двигаться только за счет натяжения шнура. Регистрировали силу на трущихся поверхностях (R) и силу, необходимую для преодоления статического трения (Fs).
Вместо этого на крюки помещали грузы примерно (0,1 Н) до тех пор, пока блок не начал двигаться только за счет натяжения шнура. Регистрировали силу на трущихся поверхностях (R) и силу, необходимую для преодоления статического трения (Fs).
Тест 3: Блок был повернут на узкую сторону и выполнена та же процедура, что и в тесте 1. Регистрировали силу на трущихся поверхностях и силу преодоления трения покоя Fs. Испытание повторяли с другой узкой стороной блока и регистрировали силу, необходимую для преодоления кинетического трения.
Испытание 4 (дерево по дереву): Фрикционный блок был установлен в исходное положение, как и для теста 1. К фрикционному блоку по очереди добавлялись нагрузки 0,5, 1, 2, 3 и 4 Н. Определены эквивалентные силы для преодоления кинетического трения. Затем результаты были сведены в таблицу и построен график зависимости R от Fk.
Испытание 5 (металл по металлу): Фрикционная пластина располагалась на плоскости между упорами металлической стороной вверх. Нагрузочный штифт на фрикционной колодке был перевернут и помещен на пластину металлической стороной вниз (чтобы обеспечить контакт металла по металлу). Нагрузки были добавлены, как и в испытании 4, и результаты были записаны и сведены в таблицу, а также построен график зависимости R от Fk.
Нагрузочный штифт на фрикционной колодке был перевернут и помещен на пластину металлической стороной вниз (чтобы обеспечить контакт металла по металлу). Нагрузки были добавлены, как и в испытании 4, и результаты были записаны и сведены в таблицу, а также построен график зависимости R от Fk.
Испытание 6 (металл на резине): Фрикционная пластина была повернута так, чтобы резиновая сторона была обращена вверх, чтобы обеспечить контакт металла с резиной. Блок перемещался с постоянной скоростью по длине плоскости примерно за 10 с. Нагрузки добавляли, как и в испытании 4, и результаты для Fk заносили в таблицу и строили график зависимости R от Fk.
Экспериментальные данные
- Испытание 1: R = 1 Н и Fk = 0,18 Н
- Испытание 2: R = 1 Н и Fs = 0,20 Н
- Испытание 3: R = 1 Н, Fs = 0,20 и Fk = 0,18 Н 9 0022
- Тест 4: Табличные результаты с R = добавленная нагрузка + вес блока
- Тест 5: Табличные результаты с R = добавленная нагрузка +1 Н
- Тест 6: Табличные результаты
Анализ данных
Тест 4: График R по сравнению с F для трения дерева по дереву Из графика получен градиент 0,2, который представляет собой коэффициент трения, когда поверхности представляют собой дерево по дереву.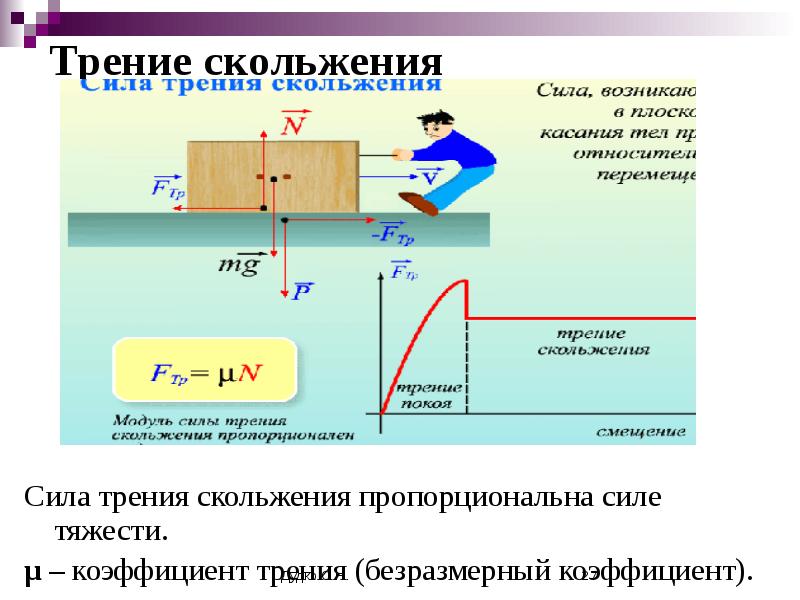
Fk = мкР
Y= mx; m=μ =Δy/Δx =1-0,4/(5-2) = 0,2
Из результатов следует, что коэффициент трения не меняется с нагрузкой (остается постоянным).
Тест 5: График зависимости R от F для трения металла о металлАналогично, градиент графика дает 0,2, что представляет собой коэффициент трения на металлических поверхностях. Коэффициент не меняется при добавлении нагрузки, а остается постоянным.
Fk = мкР
Y= mx; m=μ = Δy/Δx = 1-0,4/(5-2) = 0,2
Испытание 6: График зависимости R от Fk для металла на резинеИз графика видно, что градиент линии равен 0,514.
Обсуждение
В тестах 1 и 2 были получены значения статического и кинетического трения. В испытании 1 кинетическое трение оказалось равным 0,18 Н, а в испытании 2 статическое трение оказалось равным 0,20 Н. Из этих результатов видно, что статическое трение немного больше, чем кинетическое трение. В испытании 3 полученное кинетическое трение составило 0,18 Н, что не отличалось от значения, полученного в испытании 1. Это означает, что площадь контакта не влияет на трение. Испытания 4, 5 и 6 демонстрируют влияние природы поверхностей на коэффициент трения. Когда давление между поверхностями велико, коэффициент трения также велик (как видно из теста 6). Между поверхностями из подобных материалов коэффициент трения не очень велик (испытания 4 и 5).
Это означает, что площадь контакта не влияет на трение. Испытания 4, 5 и 6 демонстрируют влияние природы поверхностей на коэффициент трения. Когда давление между поверхностями велико, коэффициент трения также велик (как видно из теста 6). Между поверхностями из подобных материалов коэффициент трения не очень велик (испытания 4 и 5).
Фактический коэффициент трения между деревянными поверхностями составляет 0,2, что соответствует экспериментальным результатам. Точно так же между поверхностями металлов 0,2, что соответствует экспериментальным результатам. Для металлических/резиновых поверхностей фактический коэффициент >1, в то время как полученный в эксперименте коэффициент равен 0,51. Существует вариация из-за усталости поверхностей.
Выводы
Эксперимент смог продемонстрировать законы трения, которые можно переформулировать как:
- Площадь контакта между поверхностями не влияет на трение.
- Коэффициент трения зависит от природы используемых материалов (давления между поверхностями).

Были получены как статическое, так и кинетическое трение. Было обнаружено, что статическое трение больше, чем кинетическое трение.
Ссылки
CodeCogs Engineering. (2009). Законы трения . Веб.
Отрицательная сила трения, положительная нормальная сила
спросил
Изменено 7 лет, 3 месяца назад
Просмотрено 5к раз
$\begingroup$
Я понимаю, что формулы не всегда дают полную картину, но, похоже, в уравнении отсутствует некоторая информация: $F_f=\mu F_N$
Представьте, что мы говорим «вверх» и «вправо» — это положительно. Тогда, если объект движется по поверхности вправо, сила трения должна быть отрицательной (действующей против положительной приложенной силы), а нормальная сила должна быть положительной (действующей против силы тяжести).
Допустим: $F_N=882\ \text{N}$ и $\mu=0,600$, тогда: $F_f=0,600\times822=529\ \text{N}$, что положительно, хотя должно быть отрицательный.
Я понимаю, что эта формула выполняет преобразование между осями, поэтому не может быть надежного способа связать знаки, но тогда каково соглашение? Дает ли эта формула абсолютное значение трения, и вы можете установить его положительным или отрицательным, в зависимости от ситуации?
- силы
- трение
$\endgroup$
11
$\begingroup$
Вероятно, было бы разумнее сформулировать закон трения как:
$$|F_F|=\mu |F_N|$$
где $|F_N|$ обозначает модуль нормальной силы.
Теперь рассмотрим следующую схему:
Блоки и откосы идентичны.
- Слева: некоторая результирующая сила, действующая на блок, вызывает ускорение $a$ (влево и вверх).
 Сила трения $F_F$ направлена в противоположную сторону: она препятствует относительному движению.
Сила трения $F_F$ направлена в противоположную сторону: она препятствует относительному движению. - Справа: некоторая результирующая сила, действующая на блок, вызывает ускорение $a$ (вправо и вниз). Сила трения $F_F$ направлена в противоположную сторону: она препятствует относительному движению.
Таким образом, сила трения препятствует относительному движению поверхностей скольжения.
$\endgroup$
2
$\begingroup$
В соотношении $F_f = \mu F_{N}$ $F_f$ и $F_{N}$ являются величинами силы трения и нормальной силы, и обе они положительны. (Я предполагаю, что вы имеете в виду кинетическое трение.)
Сила трения направлена таким образом, что она препятствует относительному движению двух поверхностей. Этого нельзя вывести из $F_f = \mu F_{N}$.
$\endgroup$
6
$\begingroup$
Нет , знак минус , а не используется для указания направления.
Вектор — это просто направление и величина, и он не может быть отрицательным. Но это может быть 90 129, вычтенное из другого вектора, 90 130. Этот знак минус не показывает направление, а просто математическую процедуру.
Но получается что вычитание из вектора $\vec A$ образует другой вектор $\vec B$: $\vec A-\vec B$ равносильно добавлению вектора $\vec A$ к обращенному вектору $\ vec B$: $\vec A+(-1)*\vec B=\vec A+\vec B_{reverse}$
Это фундаментально (и довольно очевидно), но именно здесь начинается проблема. Знак минус — это , а не , определяющий направление вектора, но если он встречается в нашей математике, то может быть интерпретирован как перевернуть вектор вокруг.
В общем, в физике, особенно в отношении сил: если вы когда-нибудь получите знак минус в результате величины силы, это просто означает, что вектор перевернут по сравнению с тем направлением, которое вы определили для начала (если это направление каким-то образом включается в расчет). Если у вас нет знака минус, это вообще ничего не говорит о направлении.
Если у вас нет знака минус, это вообще ничего не говорит о направлении.
$\endgroup$
$\begingroup$
После обдумывания ответов и обсуждения я пришел к выводу, что проблема заключается именно в том, что использование знака для обозначения направления действительно работает только в одномерных задачах (если только вы не используете комплексные числа). Таким образом, решение состоит в том, чтобы использовать формулу $F_f=\mu F_f$ для обработки величина только , и при использовании обозначения со знаком вам просто нужно применить знак к полученной величине, поскольку это имеет смысл для сценария.
Обновление
Если немного подумать об этом, то стрелочная нотация на самом деле не лучше подходит для решения этой ситуации. Вы застрянете с одним и тем же решением применить стрелку в зависимости от направления движения.
Я думаю, что я не ясно дал понять в своем первоначальном вопросе, что я не просил разъяснений по поводу ситуации, я просто хотел проверить передовой опыт/конвенцию, поскольку у меня нет опыта.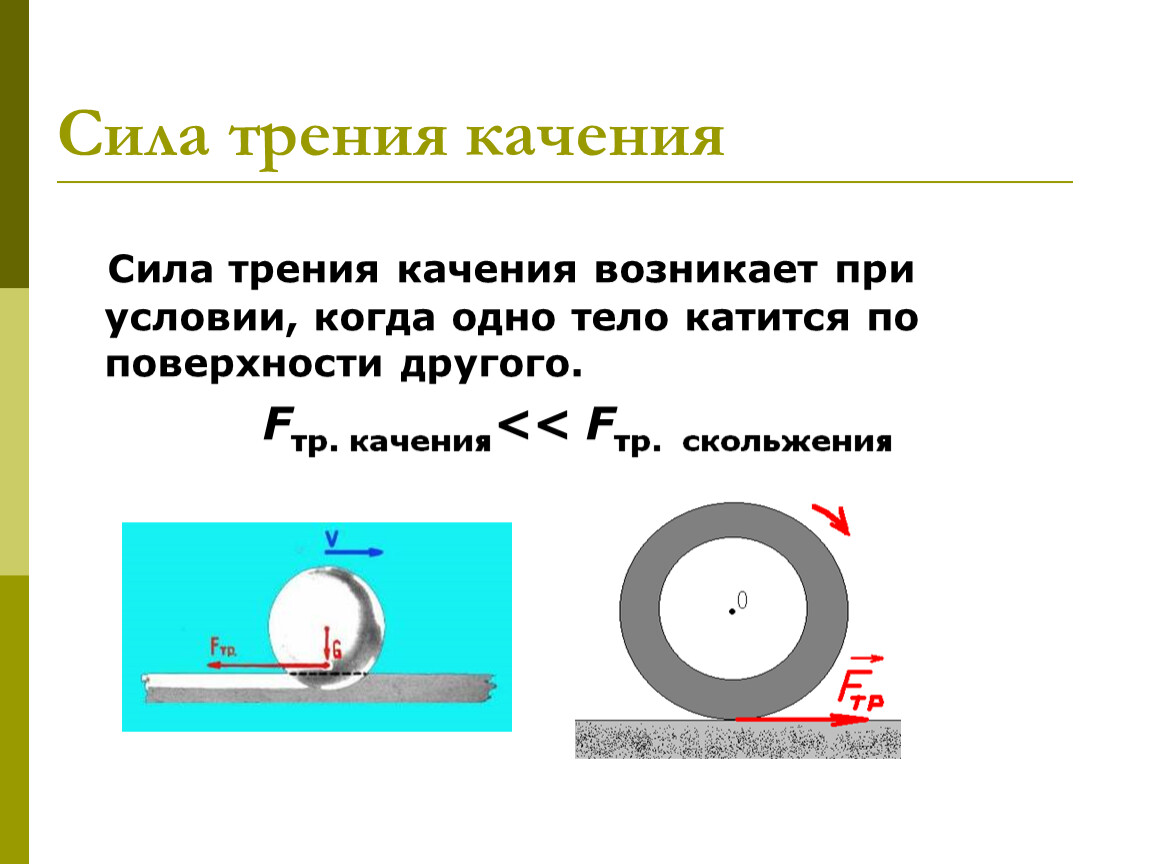



 Сила трения $F_F$ направлена в противоположную сторону: она препятствует относительному движению.
Сила трения $F_F$ направлена в противоположную сторону: она препятствует относительному движению.