Трехфазное электроснабжение частного дома. Фото, видео
Автор Alexey На чтение 6 мин Просмотров 3.9к. Опубликовано Обновлено
Содержание
- Разница между трехфазным и однофазным подключением
- Документация для подключения.
- Проект трехфазной сети.
- Как подключать?
Несмотря на, то строите ли вы новый дом или хотите модернизировать старый без электропроводки обойтись не получится, поскольку все приборы в доме потребляют электроэнергию в большей или меньшей мере. Подключение частного дома к электросети дело непростое и небыстрое.
Существует два типа электропитания одно- и трехфазный. Большинство используют однофазный тип и считают, что этого достаточно. Так и есть. Сейчас же все чаще выбирают трехфазный, поскольку он позволяет значительно снизить нагрузку на сеть равномерно распределив ее на три параллельные линии.
Большинство считают, что, перейдя на трехфазное подключение дома можно увеличить потребляемую мощность. Но это совсем не так. Такой вопрос следует решать с компанией, которая поставляет электричество.
В данном типе подключения используют 4 или 5 проводов. Три линии подачи тока (фаза), нулевой проводник (или просто ноль) и заземление, иногда ноль и заземление подключают одним проводом.
В таком случае можно примерно рассчитать количество приборов, которые можно одновременно включить в сеть на каждую линию чтобы не было перенапряжения. В однофазовом подключении используют 2 или 3 провода. Соответственно 1 фаза, 1 ноль и заземление.
Тогда все напряжение идет на одну линию и перегрузок просто не избежать.Силовой щиток однофазного электроснабжения частного дома немного меньше чем для трехфазного, и если нужно заменить один на другой, то придется добавить свободного места. Что касается использования домовой проводки, то и тут есть различия. В первом случае толщина жил кабеля значительно больше, чем во втором, поскольку и нагрузка тоже выше.
Документация для подключения.
Для того чтобы не было проблем с законом все нужно сделать как следует и подготовить необходимые документы и договора.
- Энергоснабжающая компания должна дать определенные условия эксплуатации.
- Проектная документация на снабжение здания электроэнергией.
- Акт разграничения по балансовой принадлежности.
- Акт лабораторных исследований схемы, которая собрана для определенного дома.
- Акт осмотра всего оборудования.
- Договор с энергосбытовой компанией.
Проект трехфазной сети.
Для начала нужно сделать проект, где будут учтены все особенности потребления электроэнергии. Чаще всего делают разделение на группы потребителей, то есть розетки отдельно подключаются, а освещение отдельно. Это дает возможность отключить отдельную группу для ремонтных работ и не доставлять неудобства в использовании другой группы.
Проект трехфазной сетиДля каждой рассчитывают максимальную мощность потребления электричества, и соответственно подбирают провода нужной толщины.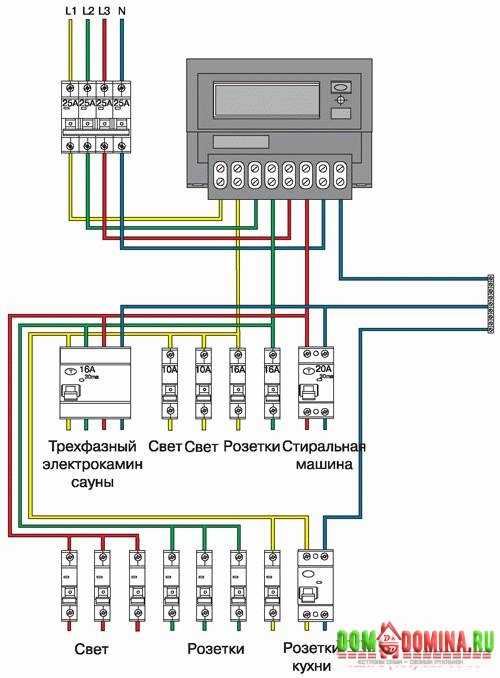
Например, для освещения чаще используют провод толщиной 1,5мм, а для розеток – 2,5 мм.
Для каждой группы нужно использовать приборы автоматического выключения тока, чтобы при коротком замыкании не возникло возгорание проводки.
Имея на руках проект подключения дома можно рассчитать количество необходимых материалов (проводов), приборов и даже планируемый размер силового щитка. А также можно наметить размещение розеток, выключателей и стабилизирующих устройств.
Как подключать?
Существует два вида подключения. Подземный и воздушный. Для частного дома используют преимущественно второй вариант, потому что:
- меньше времени тратиться на работу;
- есть возможность использования любых схем;
- стоимость подключения значительно ниже;
- при необходимости легче ремонтировать.
Нужно учитывать, что при воздушном подключении расстояние до ближайшего столба к частному дому должно быть не больше 15 м. Если же отрезок длиннее, нужно добавить дополнительный столб чтобы избежать сильного провисания или обрыва линии при плохих погодных условиях.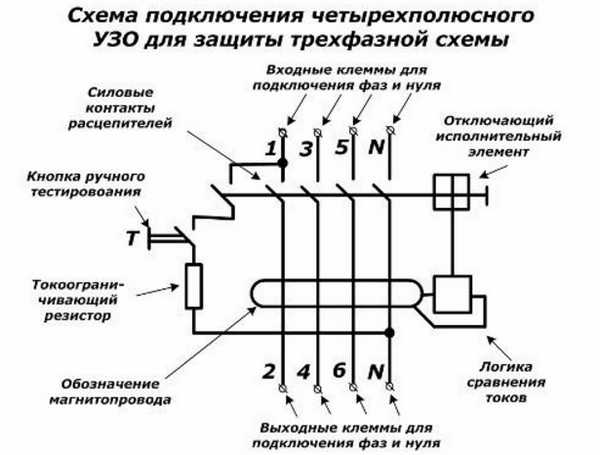
Вблизи не должно быть крупных деревьев или больших веток.А также провода не должны мешать перемещению транспортных средств или пешеходов
На частный дом трехфазная линия крепится на высоте не меньше чем 2,7м, а при необходимости и выше. Там помещают специальные изоляторы, к которым и присоединяется питание, а уже оттуда провода идут к силовому щиту.
Щиток лучше прикрепить на фасаде здания. Дальше от щитка по всему дому идут в нужных направлениях провода. Если есть пристройки где используется электричество, то к ним проводка идет тоже от щитка.
Счетчик для трехфазной линии.
Для особого подключения электричества нужен и особенный счетчик.
Трехфазный счетчикСчетчики для трехфазного подключения позволяют экономить электроэнергию, выбрать модель, подходящую именно потребителю, отслеживать перепады напряжения. Такие приборы есть трех видов:
- Прямого включения. Подключаются непосредственно к сети.
- Полукосвенного включения. Нужен трансформатор напряжения.
- Косвенного включения. Нужен трансформатор напряжения и силы тока. Подходит тем, кто подключается от высоковольтных линий электропередач. Чаще всего используют на предприятиях.
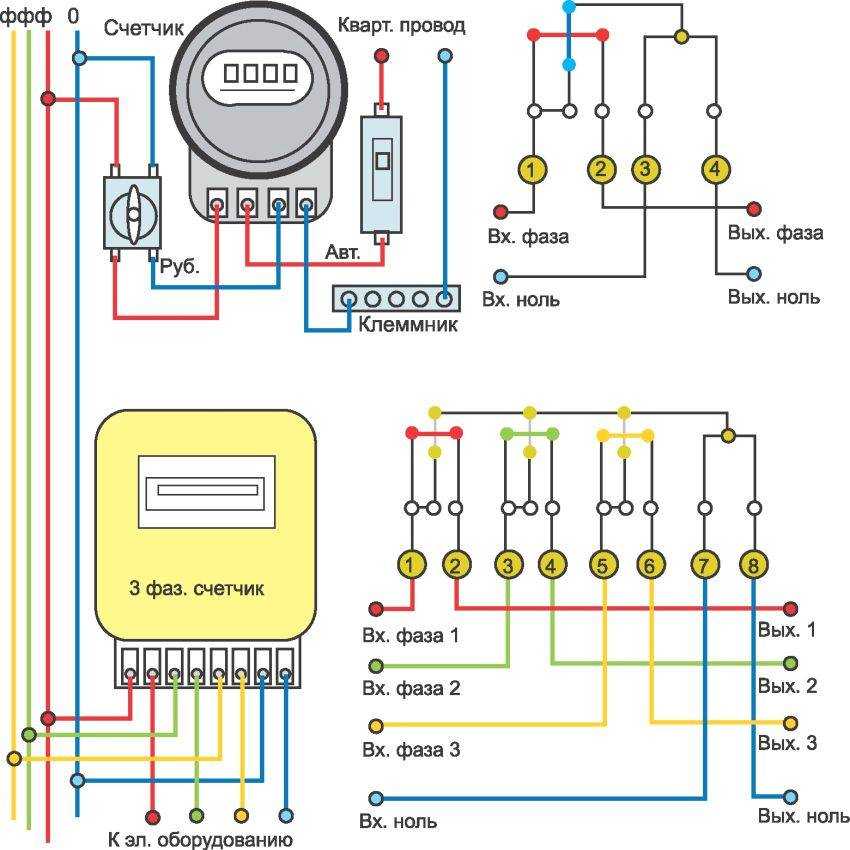
Для однофазного счетчика существует одна стандартная схема подключения, а для счетчиков трехфазной линии их много, поскольку видов несколько.
Устройства прямого включения имеют схему подключения немного схожую на схему однофазного счетчика. Обязательно следует учитывать порядок присоединения проводов в соответствии с цветом, который указан в схеме и не забывать, что четные номера — это нагрузка, а нечетные — цвет провода. Схема подключения размещена на задней крышке прибора, а также в паспорте.
Первая самая распространенная, поскольку самая простая. По данной схеме для каждой фазы используют три провода, которые присоединяются в строгом порядке, десятый провод — ноль. Всегда выбирается такая схема подключения счетчика, при которой можно легко отремонтировать ее любую часть.
Вы предоставляете план дома, указываете места где нужно разместить розетки, выключатели, где будут стоять котлы или бойлер, а квалифицированный специалист рассчитает длину проводов, их толщину, и подберет все необходимые приборы для безопасного использования электропроводки в частном доме. Подключение частного дома к электросети дело непростое и небыстрое.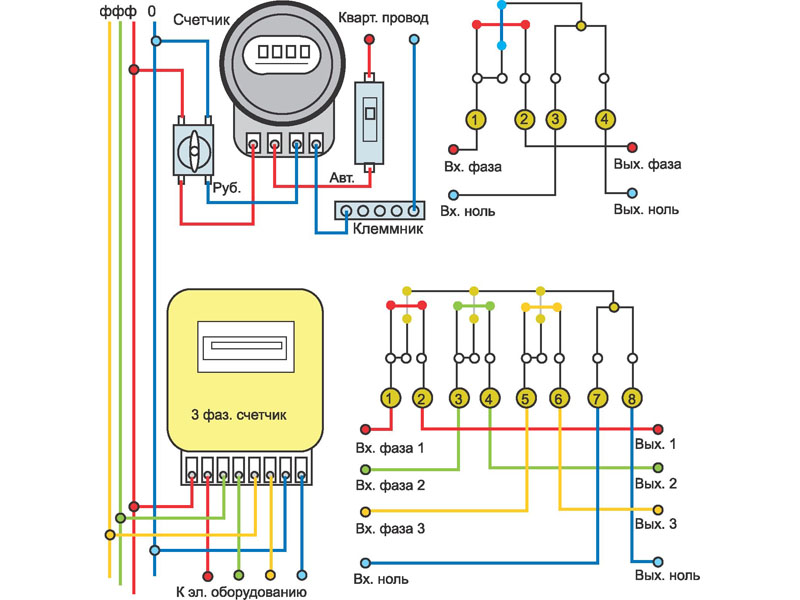
Что лучше для частного дома – однофазный или трехфазный ввод?
Главная
Обзоры и советы
Статьи
Что лучше для частного дома – однофазный или трехфазный ввод?
Если вы планируете подключить частный дом к электрическим сетям, то стает вопрос о том, какой ввод в дом выбрать. В данной статье рассмотрим, что лучше для частного дома – однофазный или трехфазный ввод.
Если сравнивать нагрузку современных бытовых электроприборов с нагрузкой электроприборов двадцатилетней давности, то можно сделать вывод, что количество потребляемой электроэнергии сегодня выросло в несколько раз. Причем наблюдается тенденция постоянного увеличения потребляемой электрической энергии на душу населения. Это связано, прежде всего, с тем, что в каждом доме появилось огромное количество бытовых электроприборов, характеризующихся большой мощностью и соответственно большим количеством потребляемой электрической энергии.
Преимущества трехфазного ввода в частном доме очевидны. Вы можете одну фазу использовать для питания электропроводки дома, вторую фазу для питания наиболее мощный бытовых приборов дома, например кухни, а третью для электроснабжения гаража и других вспомогательных помещений на территории частного дома.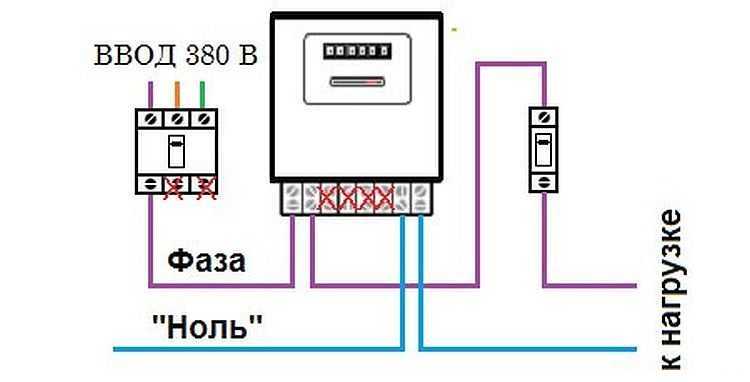
Как правило, степень защиты корпуса щитка, предназначенного для монтажа вне помещений – IP31 или IP54.
Для обеспечения удобства обслуживания электропроводки частного дома можно предусмотреть установку нескольких распределительных щитков. Например, на улице можно установить щиток типа ЩРУН-3/12, в котором будет расположен прибор учета электрической энергии, а также вводные аппараты защиты. В доме будет установлен небольшой пластиковый бокс Тусо 68112 СП 12, рассчитанный на 12 модульных мест, в котором будут расположены аппараты защиты линий электропроводки дома. В гараже или другом сооружении на территории частного дома может быть установлен еще одни аналогичный щиток. В общем, вы можете спроектировать схему электропроводки частного дома в соответствии со своими потребностями и удобством дальнейшего обслуживания.
Что касается лимитов потребляемой мощности, то в данном случае существует заблуждение о том, что трехфазный ввод – это значительно больший лимит потребляемой мощности. В данном случае все зависит от установленных норм энергоснабжающей компании, которая осуществляет подключение частных домов к электрическим сетям.
В соответствии с действующими техническими условиями подключения частных домов, может быть установлен одинаковый лимит потребления мощности, как для однофазного ввода, так и для трехфазного.
Какой все-таки выбрать ввод одно- или трехфазный? Если лимит потребления мощности одинаковый, как для однофазного, так и трехфазного ввода, то следует руководствоваться потребностью в использовании трехфазных бытовых электроприборов. Если в хозяйстве у вас нет трехфазных бытовых электроприборов, и в будущем вы не планируете их использовать, то проводить в дом трехфазный ввод не имеет смысла.
Кроме вышесказанного, следует отметить, что подключение трехфазного ввода – это довольно кропотливый процесс, который несколько сложнее процедуры подключения однофазного ввода электрической сети. Это, в первую очередь обусловлено тем, что использование трехфазного ввода предусматривает большие требования к пожарной безопасности дома и других сооружений на его территории.Подключение трехфазного оборудования
Трехфазная электроэнергия является распространенным методом производства, передачи и распределения электроэнергии переменного тока.
Это тип многофазной системы, который является наиболее распространенным методом, используемым сетями по всему миру для передачи электроэнергии. Он также используется для питания больших двигателей и других тяжелых нагрузок. Трехфазная система, как правило, более экономична, чем другие, поскольку в ней используется меньше материала проводника для передачи электроэнергии, чем в эквивалентных однофазных или двухфазных системах при том же напряжении. Трехфазная система была введена и запатентована Николой Теслой в период с 1887 по 1888 год.0003
В трехфазной системе по трем проводникам протекает три переменных тока (одной и той же частоты), мгновенные пиковые значения которых достигаются в разное время. Принимая за эталон один проводник, два других тока задерживаются во времени на одну треть и две трети одного цикла электрического тока. Эта задержка между фазами обеспечивает постоянную передачу мощности в каждом цикле тока, а также позволяет создавать вращающееся магнитное поле в электродвигателе.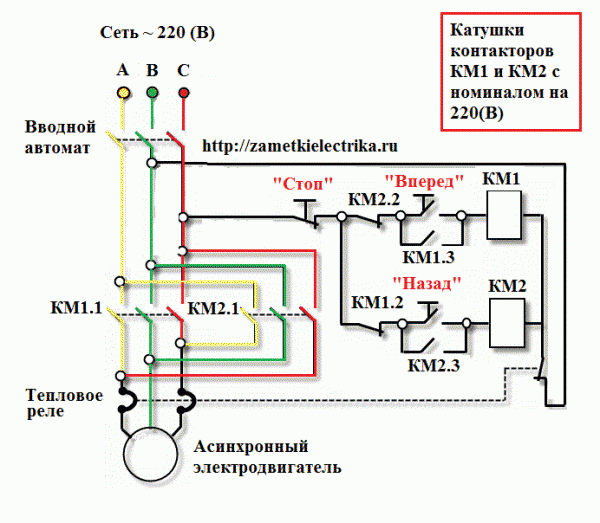
Трехфазные системы могут иметь нейтральный провод. Нейтральный провод позволяет трехфазной системе использовать более высокое напряжение, но при этом поддерживает однофазные приборы с более низким напряжением. В ситуациях распределения высокого напряжения обычно не используется нейтральный провод, поскольку нагрузки могут быть просто подключены между фазами (соединение между фазами).
Трехфазный ток обладает свойствами, которые делают его очень востребованным в системах электроснабжения:
Фазные токи имеют тенденцию компенсировать друг друга, суммируясь с нулем в случае линейной сбалансированной нагрузки. Это позволяет исключить или уменьшить размер нейтрального проводника; все фазные проводники пропускают один и тот же ток и поэтому могут быть одинакового размера для сбалансированной нагрузки.
Передача мощности на линейную сбалансированную нагрузку является постоянной, что помогает уменьшить вибрации генератора и двигателя.
Трехфазные системы могут создавать магнитное поле, которое вращается в заданном направлении, что упрощает конструкцию электродвигателей.
Именно по этой причине он так часто используется в коммерческой и промышленной недвижимости. Будь то ваш местный гараж, магазин, фабрика или офисный блок, вы чаще всего найдете 3-фазное питание 415 вольт. При работе с этой системой необходимо соблюдать особую осторожность, так как поражение электрическим током от 415 вольт довольно часто может привести к летальному исходу, тогда как 230/240 вольт, без защиты УЗО, в большинстве случаев просто даст вам жесткий ремень.
Третий — самый низкий фазовый порядок, демонстрирующий все эти свойства.
Три фазы обычно обозначаются цветами, которые различаются в зависимости от страны, но в Великобритании они выглядят следующим образом.
| Великобритания до апреля 2006 г. | |||||
Великобритания с апреля 2006 г. |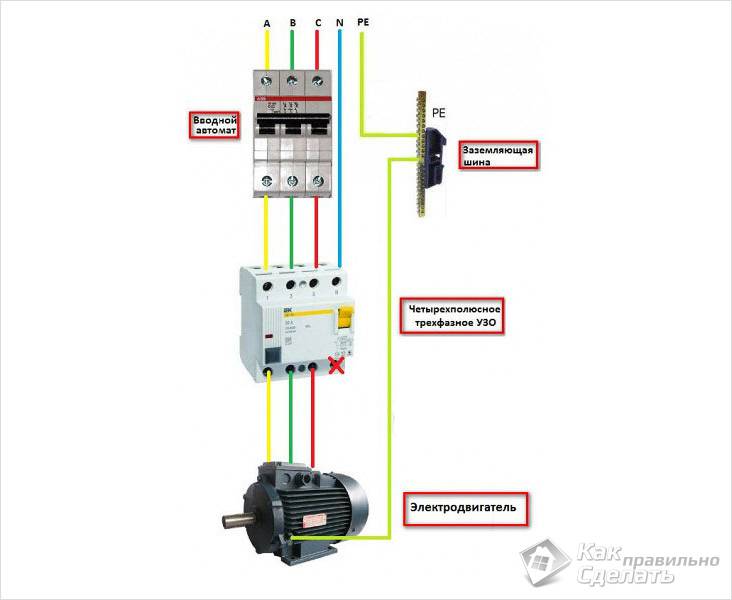
У нас работают надежные профессионалы, обученные устранять все аспекты электрических неисправностей. AA Electrical Services является авторитетной компанией по установке, ремонту и техническому обслуживанию, охватывающей юго-восточный регион. Наша команда электриков обеспечит вам техническое обслуживание вашей электроустановки и приборов, а также быстрое и надежное аварийное обслуживание. В соответствии с действующими британскими стандартами наши инженеры-электрики зарегистрированы в NICEIC, аккредитованы по части P и сертифицированы в соответствии со стандартом 17-го издания, сертифицированным Институтом инженеров-электриков (IEE). Это позволяет нам предлагать вам профессиональные услуги на самом высоком уровне.
9.3: Трехфазные соединения — технические библиотеки LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 25295
- Джеймс М. Фиоре
- Муниципальный колледж Mohawk Valley
ФиореВозможна конфигурация систем с использованием источников, соединенных треугольником или звездой, с нагрузками, соединенными треугольником или звездой. Следует отметить, что системы, соединенные треугольником, всегда представляют собой трехпроводные системы, в то время как системы, соединенные звездой, могут использовать четвертый нейтральный провод (общая точка, к которой подключаются все три источника).
Однородные системы
Наиболее простыми системами являются дельта-дельта и Y-к-Y. Мы будем называть их однородными системами, поскольку структуры генератора и нагрузки аналогичны. Примеры показаны на рисунках \(\PageIndex{1}\) и \(\PageIndex{2}\) соответственно.
Рисунок \(\PageIndex{1}\): Генератор, соединенный треугольником, с нагрузкой, соединенной треугольником (треугольник-треугольник). Рисунок \(\PageIndex{2}\): Генератор, соединенный звездой, с нагрузка (ГГ). Показан дополнительный четвертый нейтральный провод от центра к центру.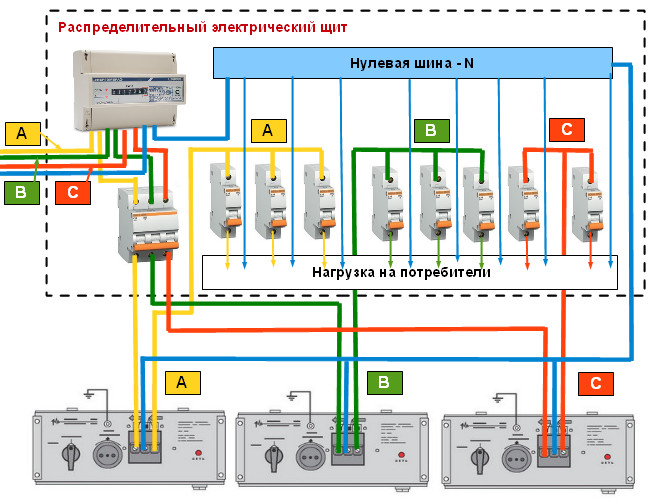
В этих конфигурациях каждая ветвь нагрузки совпадает с соответствующей ветвью генератора. В конфигурации «треугольник-треугольник» на рисунке \(\PageIndex{1}\) уже при осмотре должно быть очевидно, что напряжение на любой ветви нагрузки должно равняться напряжению соответствующей ветви генератора. Например, импеданс нагрузки, подключенный между \(A’\) и \(B’\), должен видеть напряжение, представленное генератором, расположенным между \(A\) и \(B\), потому что \(A\) непосредственно связан с \(A’\), как \(B\) с \(B’\). Точно так же для конфигурации Y-Y на рисунке \(\PageIndex{2}\) ток через любую ветвь нагрузки должен быть равен току, протекающему через связанную ветвь генератора, поскольку нет других путей для тока между \(A\) и \ (А’\), \(В\) и \(В’\), а также \(С\) и \(С’\).
Поскольку нагрузка сбалансирована и ветви генератора идентичны, за исключением их фаз, должно быть так, что напряжения и токи (и, следовательно, мощности) для каждой ветви нагрузки должны быть одинаковыми, за исключением фазы.
Это справедливо как для конфигурации Y-Y, так и для конфигурации дельта-треугольник. Сложность здесь заключается в разнице между током или напряжением источника (или нагрузки) и линейным током или напряжением.
\[\text{Линейное напряжение — это амплитуда напряжения между любыми двумя проводниками, соединяющими источник с нагрузкой, за исключением земли или общего провода.} \nonumber \]
\[\text{Линейный ток – это сила тока, протекающая по любому проводнику, соединяющему источник с нагрузкой, за исключением заземления или общего провода.} \nonumber \]
Рассмотрим систему треугольник-треугольник на рисунке \(\PageIndex{1 }\). Мы уже установили, что напряжение, развиваемое генератором \(A,B\), должно быть таким же, как и напряжение на нагрузке \(A’,B’\). Таким образом, напряжение, измеренное от проводника A, A’ до проводника B, B’, должно быть таким же, как напряжение источника и нагрузки. Другими словами, в конфигурации «треугольник-треугольник» напряжения источника, нагрузки и сети одинаковы.
Мы также обнаружили, что токи источника и нагрузки должны быть одинаковыми для конфигурации треугольник-треугольник, однако это не означает, что ток, протекающий по проводу, соединяющему \(A\) с \(A’\), должен быть такой же, как ток, протекающий через генератор или нагрузку. Ведь к \(A’\) подключаются два провода нагрузки, а не один. По определению, ток, протекающий по этому проводу, является линейным током, и, следовательно, в конфигурации треугольник-треугольник линейный ток не совпадает с током источника или нагрузки. Во избежание путаницы напряжение или ток, связанные с одной ветвью, называются фазным напряжением или током по отношению к линейному напряжению или току.
Обращаясь к конфигурации Y-Y на рисунке \(\PageIndex{2}\), мы видим противоположную ситуацию. Токи источника, нагрузки и линии будут одинаковыми. С другой стороны, линейное напряжение состоит из двух генераторов, а не одного (например, от \(A\) до \(B\) или от \(B\) до \(C\)). Таким образом, для конфигурации Y-Y напряжения источника и нагрузки одинаковы, но они не равны линейному напряжению (и не удваиваются благодаря фазовому сдвигу).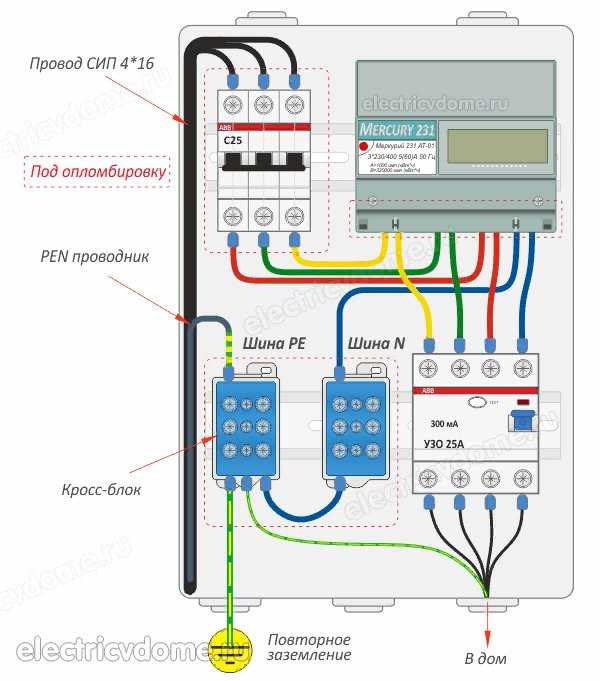
Определение линейного напряжения и тока
Чтобы определить линейное напряжение для генератора, подключенного по схеме «звезда» (и, аналогично, линейный ток для генератора, подключенного по схеме «треугольник»), полезно изучить векторный график напряжений отдельных генераторов. Это показано на рисунке \(\PageIndex{3}\). У нас есть три напряжения одинаковой амплитуды, единственная разница между ними заключается в их фазе. Каждый вектор отделен от других на 120 градусов. Далее каждая отдельная образующая соединяется из общей точки с одной из внешних точек \(А\), \(В\) и \(С\). Линейное напряжение определяется как потенциал, существующий между любыми двумя или этими тремя точками. Хотя можно просто вычесть одно напряжение генератора из другого, чтобы получить разницу, существует хорошее графическое решение, из которого мы можем получить точную формулу для линейного напряжения, учитывая напряжение генератора.
Рисунок \(\PageIndex{3}\): Векторная диаграмма Y-образного генератора Начнем с того, что сосредоточимся на втором и третьем квадрантах векторной диаграммы.
Этот раздел перерисован на рисунке \(\PageIndex{4}\). В действительности для следующего доказательства можно использовать любые два вектора, но эта пара оказывается особенно удобной по своей ориентации.
Для простоты использования нормируем величину напряжения генератора к единице. Мы видим, что векторы \(B\) и \(C\) идеально разделены горизонтальной осью; то, что находится над осью, идеально зеркально отражается под ней. В верхней части мы находим прямоугольный треугольник с гипотенузой, равной единице (темно-красный). Угол, который он образует с горизонтом, должен быть равен половине угла между ним и вектором \(C\). Это половина от 120 градусов или 60 градусов. Поскольку сумма внутренних углов треугольника должна быть 180 градусов, это означает, что третий угол должен быть равен 30 градусам. Горизонтальный катет треугольника (темно-желтый или, может быть, «пряно-горчичный») можно определить, потому что мы знаем и гипотенузу, и противолежащий угол.
92} \nonumber \]
\[\text{vertical} = \sqrt{\frac{3}{4}} \nonumber \]
\[\text{vertical} = \frac{1}{2} \sqrt{3} \nonumber \]
Вертикальная ножка точно зеркально отражена ниже горизонтальной оси. Таким образом, диапазон от \(B\) до \(C\) должен быть в два раза больше этого значения или \(\sqrt{3}\). Поскольку напряжение, развиваемое на каждой ветви генератора, называется фазным напряжением генератора, мы можем утверждать:
\[\text{Напряжение сети для генератора, подключенного по схеме Y, равно } \sqrt{3} \text{ раз его фазное напряжение.} \label{9.1} \]
Например, если фазное напряжение генератора, соединенного звездой, составляет 120 вольт, линейное напряжение будет в \(\sqrt{3}\) раз больше, или примерно 208 вольт.
Для генератора, соединенного треугольником, то же верно для фазного и линейного токов, доказательство оставлено в качестве упражнения. То есть,
\[\text{Сетевой ток для генератора, подключенного по схеме треугольника, в } \sqrt{3} \text{ умножается на его фазный ток.
} \label{9.2} \]
Те же самые отношения справедливы для нагрузки, а также источники, например, ток в ветви нагрузки, подключенной по схеме Y, будет таким же, как линейный ток, а ее фазное напряжение будет в \(\sqrt{3}\) раз меньше, чем линейное напряжение.
\[\text{ Подводя итог: для конфигураций треугольника (генератор или нагрузка) фазное напряжение равно линейному напряжению, а линейный ток больше фазного тока на } \sqrt{3} \text{. Для конфигураций Y фазный ток равен линейному току, а линейное напряжение } \sqrt{3} \text{ больше, чем фазное напряжение.} \nonumber \]
Для однородных систем, поскольку генератор и нагрузка распределяются При одинаковой конфигурации фазные напряжения и токи нагрузки должны быть такими же, как у генератора. Полезным помощником в запоминании является то, что мощность, рассеиваемая в системе, должна равняться генерируемой мощности.
Пример \(\PageIndex{1}\)
Трехфазный генератор, соединенный треугольником, питает трехфазную нагрузку, соединенную треугольником, как показано на рисунке \(\PageIndex{1}\).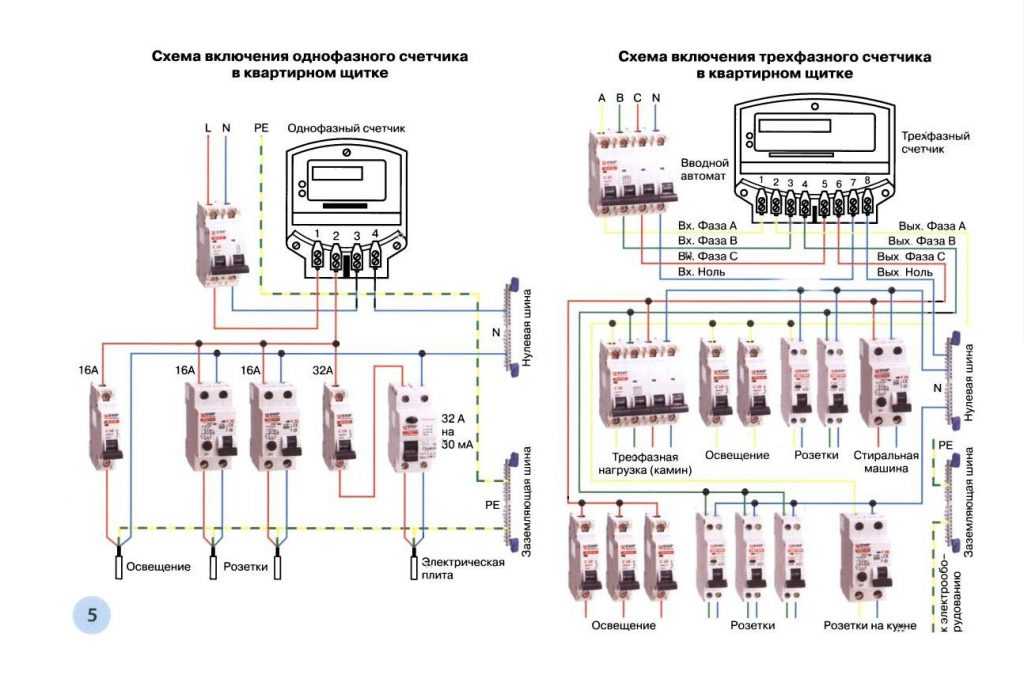
Предположим, что фазное напряжение генератора равно 120 В переменного тока (действующее значение). Груз состоит из трех одинаковых ветвей по 50 \(\Омега\) каждая. Определите линейное напряжение, фазное напряжение нагрузки, фазный ток генератора, линейный ток, фазный ток нагрузки и общую мощность, подаваемую на нагрузку.
Поскольку это однородная система (треугольник-треугольник), фазное напряжение и ток нагрузки такие же, как у генератора. Следовательно, фазное напряжение нагрузки также должно быть 120 вольт. Во-вторых, в конфигурации треугольника линейное напряжение равно фазному, опять же 120 вольт. Ток фазы нагрузки находится по закону Ома и будет среднеквадратичным значением, поскольку напряжение является среднеквадратичным:
\[i_{фаза} = \frac{v_{фаза}}{Z_{нагрузка}} \nonumber \]
\[i_{фаза} = \frac{120 В}{50 \Omega} \nonumber \ ]
\[i_{фаза} = 2,4 А \номер \]
Фазный ток генератора должен быть одинаковым, поскольку генератор и нагрузка имеют одинаковую конфигурацию.
Для конфигураций треугольником линейный ток в \(\sqrt{3}\) раз больше фазного тока, таким образом,
\[i_{line} = \sqrt{3}\times i_{phase} \nonumber \]
\[i_{line} = \sqrt{3}\times 2.4A \nonnumber \] 92\times 50 \Omega \nonnumber \]
\[P_{total} = 864 Вт \nonnumber \]
Это эквивалентно примерно 1,2 л.с. Мы также могли бы вычислить мощность фазы нагрузки, используя квадрат фазного напряжения, деленный на сопротивление нагрузки, или умножив фазное напряжение на фазный ток. Поскольку это чисто резистивная нагрузка, здесь нет фазового угла и, следовательно, нет коэффициента мощности, на который следует обращать внимание.
Пример \(\PageIndex{2}\)
Трехфазный генератор, соединенный звездой, питает трехфазную нагрузку, соединенную звездой, подобно системе, показанной на рисунке \(\PageIndex{2}\). Предположим, что фазное напряжение генератора составляет 220 В переменного тока (действующее значение). Груз состоит из трех одинаковых ветвей по 100 \(\Омега\) каждая.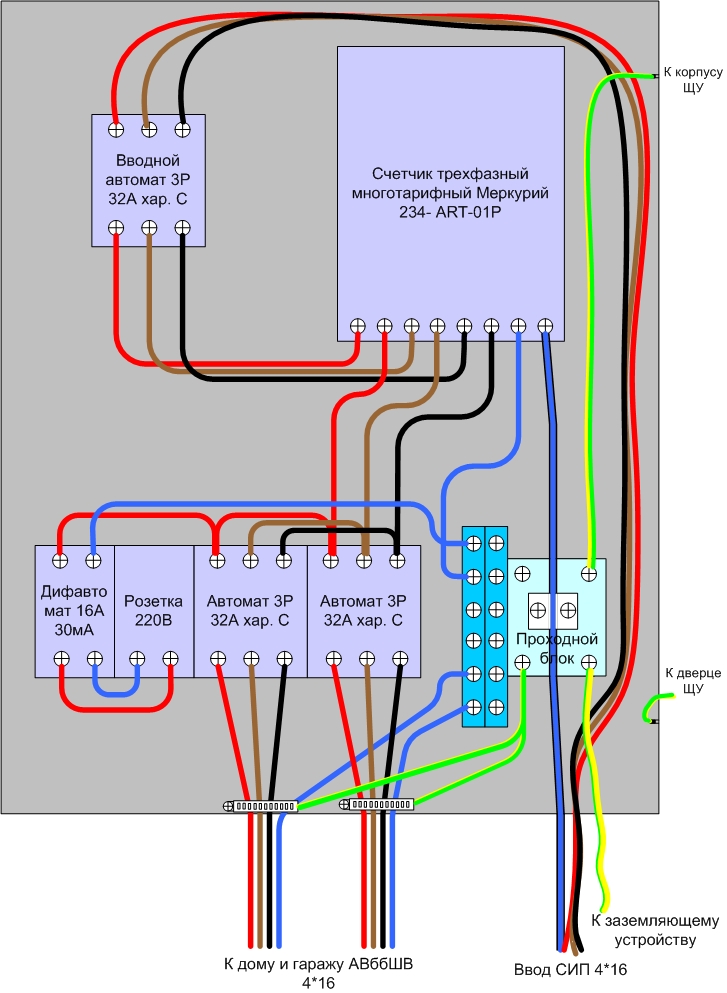
Определите линейное напряжение, фазное напряжение нагрузки, фазный ток генератора, линейный ток, фазный ток нагрузки и общую мощность, подаваемую на нагрузку.
Это однородная (Y-Y) система, поэтому фазное напряжение и ток нагрузки такие же, как у генератора. Следовательно, фазное напряжение нагрузки должно быть 220 вольт. В конфигурации Y линейное напряжение равно фазному напряжению, умноженному на \(\sqrt{3}\).
\[v_{линия} = \sqrt{3}\times v_{фаза} \nonnumber \]
\[v_{линия} = \sqrt{3}\times 220V \nonnumber \]
\[v_ {линия} \примерно 381 В \номер \]
Ток фазы нагрузки находится по закону Ома и будет представлять собой среднеквадратичное значение, поскольку напряжение является среднеквадратичным. Это то же самое, что и фазный ток генератора, а также линейный ток.
\[i_{фаза} = \frac{v_{фаза}}{Z_{нагрузка}} \nonumber \]
\[i_{фаза} = \frac{220 В}{100 \Omega} \nonumber \ ]
\[i_{фаза} = 2,2 А \номер \]
Полную мощность можно найти, используя базовый степенной закон, поскольку нагрузка является чисто резистивной, и у нас есть среднеквадратичные значения.
В этом случае мы будем использовать ток, умноженный на напряжение, для изменения темпа.
\[P_{total} = 3\times i_{phase} \times v_{phase} \nonumber \]
\[P_{total} = 3\times 2,2 A\times 220 V \nonumber \]
\[P_{total} = 1452 W \nonumber \]
Это всего лишь 2 HP. Еще раз, это чисто резистивная нагрузка и фазового угла нет. Таким образом, коэффициент мощности равен единице, при этом реальная и кажущаяся мощности одинаковы.
Пример \(\PageIndex{3}\)
Для системы, показанной на рисунке \(\PageIndex{5}\), определите полную кажущуюся и реальную мощность, подаваемую на нагрузку. Также найдите напряжение в сети. Фазное напряжение источника составляет 240 вольт среднеквадратичного значения при частоте 60 Гц.
Рисунок \(\PageIndex{5}\): Схема для примера \(\PageIndex{3}\). Учитывая тот факт, что все три опоры нагрузки находятся в одной общей точке (земля), это должна быть система Y-Y. Следовательно, мы знаем, что линейное напряжение должно быть в \(\sqrt{3}\) раз больше фазного напряжения генератора.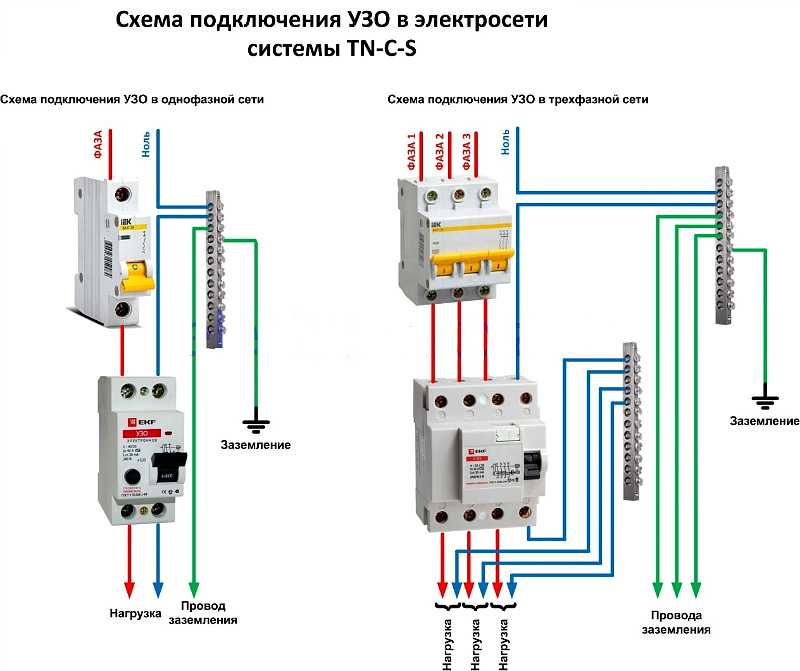
\[v_{линия} = \sqrt{3}\times v_{фаза} \без номера \]
\[v_{линия} = \sqrt{3}\times 240 В \без номера \]
\[ v_{line} \примерно 416 В RMS \nonumber \]
Это однородная система (Y-Y), поэтому мы также знаем, что напряжение нагрузки равно напряжению генератора или 240 вольт RMS. Отсюда мы можем найти ток нагрузки (линейный ток должен быть таким же, потому что это Y-образная нагрузка). 92\times R_{load} \nonumber \]
\[P = 3\times 4.8A 2\times 40 \Omega \nonumber \]
\[P = 2765W \nonumber \]
Компьютерное моделирование
Схема примера \(\PageIndex{3}\) достойна моделирования. Первое, что нужно сделать, это определить подходящее значение индуктивности для достижения реактивного сопротивления \(j40 \Омега\). При частоте источника 60 Гц получается примерно 80 мГн. Схема построена, как показано на рисунке \(\PageIndex{6}\). Среднеквадратичное значение фазового напряжения источника 240 вольт эквивалентно примерно 340 вольтам пикового значения.
Положения катушки индуктивности и резистора в каждом плече поменялись местами по причине, которая вскоре станет очевидной.
Непосредственный интерес представляет проверка временных сдвигов и амплитуд фазных напряжений. Они соответствуют узлам 1, 2 и 3. В этой конфигурации фазное напряжение нагрузки равно фазному напряжению генератора, поэтому они должны составлять 340 вольт пикового значения и быть разделены на 120 градусов или 1/3 цикла.
Выполняется анализ переходных процессов с нанесением интересующих узловых напряжений. Результат показан на рисунке \(\PageIndex{7}\). Напряжения точно такие, как ожидалось, и график идеально соответствует теоретическому графику на рисунке 9..2.4.
Рисунок \(\PageIndex{7}\): три напряжения нагрузки, смоделированные из рисунка \(\PageIndex{6}\). Теперь проверяем напряжение в сети. Это было рассчитано как среднеквадратичное значение 416 вольт или пиковое значение примерно 588 вольт. Постпроцессор используется для отображения результата напряжения узла 1 минус напряжения узла 2. Это показано на рисунке \(\PageIndex{8}\). Опять же, результаты, как и ожидалось, с пиком чуть ниже 600 вольт.
Наконец, мы исследуем реальную мощность нагрузки. Возможно, самый простой способ сделать это — определить напряжение на резистивной части нагрузки. Из предыдущей работы мы знаем, что истинная мощность связана только с сопротивлением, а не реактивным сопротивлением. Таким образом, все, что нам нужно сделать, это измерить пиковое напряжение на резисторе. Оттуда мы находим его эквивалент RMS, возводим его в квадрат и делим на номинал резистора. Это дает нам реальную мощность нагрузки на одну ногу. Для общей мощности мы просто утраиваем результат. Получить напряжение на резисторе легко, если резистор подключен к земле. В этом случае это просто напряжение в узле, к которому подключен резистор. Вот почему при моделировании местами индуктор и резистор были поменяны местами. Поскольку они соединены последовательно, это не влияет на общее сопротивление нагрузки, однако новое расположение позволяет нам получать напряжение резистора напрямую, вместо того, чтобы полагаться на дифференциальное напряжение, полученное через постпроцессор.
Выполняется еще один анализ переходных процессов, на этот раз на графике отображается напряжение на одном из нагрузочных резисторов; а именно узел 4. Результат показан на рисунке \(\PageIndex{9}\). Измеренное пиковое значение этой формы волны составляет 271,5 вольта или около 192 вольт среднеквадратичного значения. Возведение этого числа в квадрат и деление на 40 \( \Omega \) дает чуть более 921 Вт на ногу, что в сумме составляет около 2765 Вт, как и ожидалось.
Рисунок \(\PageIndex{8}\): одно из смоделированных значений линейного напряжения из рисунка \(\PageIndex{6}\).Рисунок \(\PageIndex{9}\): смоделированное напряжение на одном из нагрузочных резисторов на рисунке \(\PageIndex{6}\).Гетерогенные системы
Системы, сконфигурированные как дельта-Y и Y-дельта, кажутся немного более сложными, чем гомогенные системы. Мы будем называть их гетерогенными системами, поскольку структуры генератора и нагрузки противоположны. Примеры показаны на рисунках \(\PageIndex{10}\) и \(\PageIndex{11}\) соответственно.
Эти системы не так сложны, как думают некоторые; все, что вам нужно сделать, это запомнить операторы \ref{9.1} и \ref{9.2}. Действительно, здесь стоит повторить суммирование:
\text{Для схем треугольника (генератор или нагрузка) фазное напряжение равно линейному напряжению, а линейный ток больше фазного на } \sqrt{3} \ текст{. Для конфигураций Y фазный ток равен линейному току, а линейное напряжение } \sqrt{3} \text{ больше, чем фазное напряжение.} \nonumber \]
Анализ этих систем можно рассматривать как двухэтапный процесс. Сначала определите линейное напряжение и ток либо от генератора, либо от нагрузки; во-вторых, переход с линии на другую сторону (нагрузку или генератор). Если возникнет путаница, помните, что генерируемая мощность должна равняться рассеиваемой или отдаваемой мощности. {\circ}\) \( \Omega \), определите фазный ток генератора, линейное напряжение, фазное напряжение нагрузки, фазный ток нагрузки и общую мощность, подаваемую на нагрузка.
Генератор соединен треугольником, поэтому напряжение сети равно фазному напряжению генератора или 230 вольт. На нагрузке, подключенной по схеме Y, фазное напряжение будет уменьшено в \(\sqrt{3}\).
\[v_{нагрузка} = \frac{v_{линия}}{\sqrt{3}} \nonumber \]
\[v_{нагрузка} = \frac{230 В}{\sqrt{3}} \номер \]
\[v_{нагрузка} \приблизительно 132,8 В среднеквадратичного значения \неномер \]
Мы можем использовать закон Ома для определения фазного тока нагрузки.
\[i_{нагрузка} = \frac{v_{фаза}}{Z_{нагрузка}} \номер\] 9{\circ} \Omega} \nonumber \]
\[i_{load} \приблизительно 0,664 A RMS \nonumber \]
При соединении по схеме Y линейный ток должен быть таким же, как ток фазы нагрузки, или 0,664 ампер При соединении треугольником линейный ток в \(\sqrt{3}\) раз больше фазного тока, поэтому фазный ток генератора должен быть в \(\sqrt{3}\) раз меньше.
\[i_{gen} = \frac{i_{line}}{\sqrt{3}} \nonumber \]
\[i_{gen} = \frac{0.664A}{\sqrt{3}} \номер \]
\[i_{gen} \приблизительно 0,383 А среднеквадратичное значение \неномер \] 92 \times 200 \Omega \nonumber \]
\[P_{total} = 264 Вт \nonumber \]
В качестве перекрестной проверки получаем мощность:
\[P_{total} = 3\times i_{ gen} \times v_{gen} \nonumber \]
\[P_{total} = 3\times 0,383A\times 230 V \nonumber \]
\[P_{total} = 264 Вт \nonumber \]
Генерируемая мощность равна рассеиваемой мощности.
Пример \(\PageIndex{5}\)
Система Y-треугольник, подобная той, что показана на рисунке \(\PageIndex{11}\), имеет фазное напряжение генератора 100 вольт RMS при 60 Гц. Если нагрузка имеет величину 50 \( \Omega \) с отстающим коэффициентом мощности 0,8, определите фазный ток генератора, линейное напряжение, фазное напряжение нагрузки, фазный ток нагрузки и полную истинную мощность, отдаваемую в нагрузку. .
Генератор, соединенный звездой, создает линейное напряжение, равное фазному напряжению генератора, умноженному на \(\sqrt{3}\). Это также фазное напряжение нагрузки, так как оно соединено треугольником.
\[v_{линия} = \sqrt{3}\times v_{фаза} \номер \]
\[v_{линия} = \sqrt{3}\times 100 В \неномер \]
\[ v_{line} \примерно 173,2 В RMS \номер \]
На нагрузке, соединенной по схеме треугольник, фазное напряжение будет таким же, как и линейное, или 173,2 вольта. Отсюда мы можем определить ток нагрузки.
\[i_{нагрузка} = \frac{v_{фаза}}{Z_{нагрузка}} \nonumber \]
\[i_{нагрузка} = \frac{173.2V}{50 \Omega} \nonumber \ ]
\[i_{нагрузка} \приблизительно 3,464 A RMS \номер \]
Поскольку нагрузка соединена треугольником, линейный ток равен току нагрузки, умноженному на \(\sqrt{3}\). Фазный ток генератора будет таким же, как линейный ток.
\[i_{линия} = \sqrt{3}\times i_{фаза} \nonnumber \]
\[i_{line} = \sqrt{3}\times 3.464A \nonnumber \]
\[ i_{line} = 6 A RMS \nonumber \] 92\times 40 \Omega \nonumber \]
\[P_{total} = 1440 Вт \nonumber \]
Мы также можем найти полную мощность и использовать коэффициент мощности.
\[P_{total} = 3\times v_{load} \times i_{load} PF \nonumber \]
\[P_{total} = 3\times 173,2V\times 3,464 A\times 0,8 \nonumber \]
\[P_{total} = 1440 Вт \nonumber \]
В качестве перекрестной проверки сравните рассеиваемую мощность с генерируемой мощностью.
\[P_{всего} = 3\times v_{gen}\times i_{gen}\times PF \nonumber \]
\[P_{total} = 3\times 100V\times 6A\times 0.8 \nonumber \]
\[P_{total} = 1440 W \nonumber \]
Эта страница под названием 9.3: Three-Phase Connections распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Джеймс М.
