Когда возникает электрический ток в катушке?

Магазины › Магнит › Почему при приближении Магнита к катушке Магнитный поток пронизывающий эту катушку менялся?

Индукционный ток в катушке из металлической проволоки возникает при вдвигании магнита внутрь катушки и при выдвигании магнита из катушки, а также при изменении силы тока во второй катушке, магнитное поле которой пронизывает первую катушку.

Индукционный ток в катушке возникает при перемещении постоянного магнита относительно катушки; при перемещении электромагнита относительно катушки; при перемещении сердечника относительно электромагнита, вставленного в катушку; при регулировании тока в цепи электромагнита; при замыкании и размыкании цепи.

1. Когда появляется индукционный ток в катушке?
2. Чем можно вызвать появление индукционного тока?
3. В каком случае индукционный ток не возникает?
4. Где будет больше индукционный ток в катушке или Реостате?
5. Когда будет появляться индукционный ток?
6. Как возникает электромагнитная индукция?
7. Что порождает ток?
8. Чем отличается ток от индукционного тока?
9. Как и от чего зависит индукционный ток?
10. Почему катушка с током отталкивается от магнита?
11. Что такое индукция простыми словами?
12. В каком кольце возникает индукционный ток?
13. Что происходит при увеличении силы тока В катушке?
14. Как найти энергию В катушке?
15. Как направлен индукционный ток В катушке?
16. Почему в рамке возникает индукционный ток?
17. Когда возникает магнитное поле?
18. В каком случае наблюдается явление электромагнитной индукции?
19. В каком случае увеличивается сила индукционного тока?
20. Когда возникает явление самоиндукции?
21. В чем суть закона электромагнитной индукции?
22. Где есть магнитное поле?
23. Как получить индукционный электрический ток?
24. Можно ли получить индукционный ток?
25. Куда направлен ток самоиндукции?
26. Как изменяется магнитное поле при изменении силы тока В катушке?
27. Что такое Самоиндукция и индуктивность?
28. Как возникает вихревое электрическое поле?
29. Как понять индукционный?
30. Как определяется индукционный ток?
31. Как называется явление возникновения электрического тока в замкнутом пространстве?
32. Как определить куда направлен индукционный ток?
33. Почему индукционный ток является переменным?
34. В каком случае в кольце возникает индукционный ток?
35. Как направлен индукционный ток в катушке?
36. Какие факторы влияют на величину индукционного тока?

Когда появляется индукционный ток в катушке?

Индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении. Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Чем можно вызвать появление индукционного тока?

Практическое применение Если менять магнитное поле вблизи неподвижного замкнутого проводника, то причиной индукционного тока является вихревое электрическое поле. Если двигать замкнутый проводник вблизи неподвижного магнита, то причиной индукционного тока является сила Лоренца.

В каком случае индукционный ток не возникает?

При вращении рамки 1 (задача 23.1.5) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает.

В катушке индукционный ток будет значительно больше, чем в реостате, т. к. катушка имеет большее число витков и сердечник (обладает большей индуктивностью), чем реостат. Чем больше сила индукционного тока, тем большее противодействие он оказывает изменению силы тока, созданного источником.

Когда будет появляться индукционный ток?

Раз изменяется электрический ток, будет изменяться магнитное поле. В момент перемещения скользящего контакта реостата изменяется магнитное поле, что приводит к появлению индукционного тока.

Как возникает электромагнитная индукция?

Электромагнитная индукция это явление возникновения тока в замкнутом проводнике при прохождении через него магнитного потока, изменяющегося со временем. То есть благодаря этому явлению мы можем преобразовывать механическую энергию в электрическую, и это замечательно.

Что порождает ток?

Переменное магнитное поле создает переменное электрическое поле, которое, действуя на свободные заряды, создает электрический ток. Этот ток, будучи переменным, в свою очередь порождает переменное магнитное поле, создающее электрическое поле в том же проводнике, и т.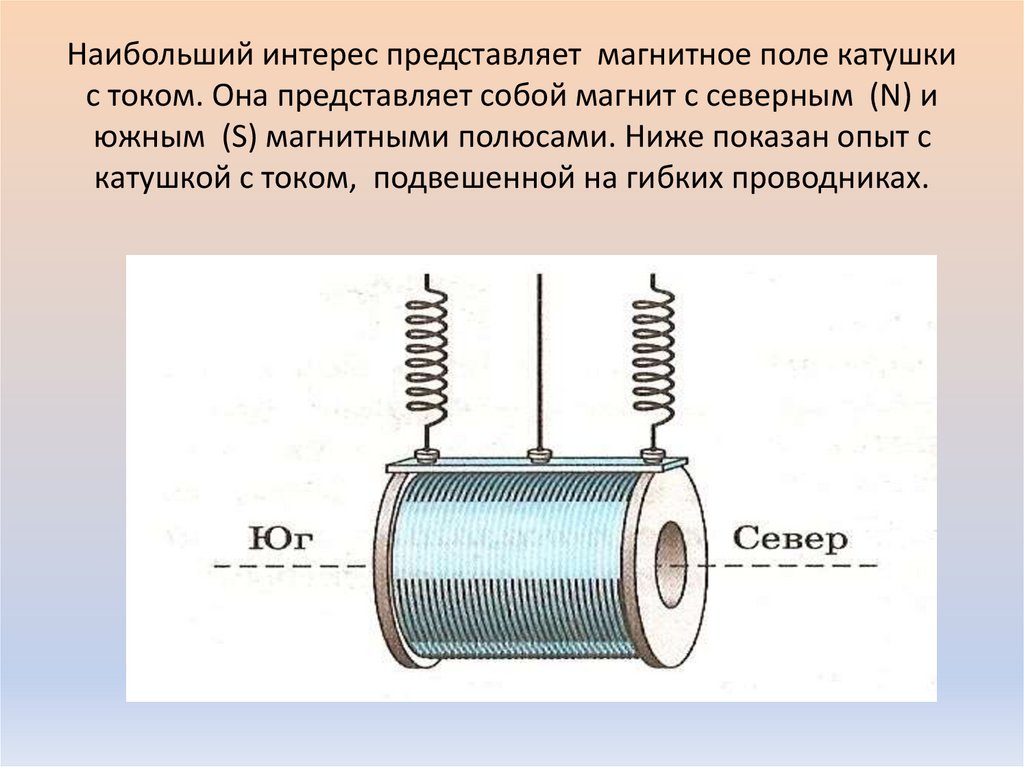

Чем отличается ток от индукционного тока?

Электрический ток в замкнутом контуре, возникающий при изменении магнитного поля, называется индукционным. Индукционный ток, так же как и ток от гальванического элемента или аккумулятора, представляет собой упорядоченное движение электронов.

Как и от чего зависит индукционный ток?

Сила индукционного тока зависит от скорости изменения магнитного потока. Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.

Почему катушка с током отталкивается от магнита?

Магнит будет взаимодействовать с катушкой либо притягиваясь, либо отталкиваясь от нее. Это будет возникать вследствие того, что катушка с проходящим по ней током, будет подобна магниту с двумя полюсами. Направление индуцируемого тока будет определять, где у катушки будет находиться какой из полюсов.

Что такое индукция простыми словами?

Индукция — это вид обобщения, связанный с предвосхищением результатов наблюдений и экспериментов на основе данных опыта. В индукции данные опыта «наводят» на общее, поэтому индуктивные обобщения рассматриваются обычно как опытные истины или эмпирические законы.

В каком кольце возникает индукционный ток?

При приближении магнита к кольцу без прорези возрастает магнитный поток сквозь площадь кольца. Так как кольцо замкнуто, то в нем возникает индукционный ток.

Что происходит при увеличении силы тока В катушке?

При увеличении тока в катушке на dI, пронизывающий ее поток возрастает на Электрический ток в газах. Вольтамперная характеристика (ВАХ) газового разряда и ее физический анализ. Виды электрического разряда в газе.

Как найти энергию В катушке?

Экспериментально выведена формула энергии магнитного поля катушки с током: E m = L I 2 2, где \(L\) — индуктивность катушки (Гн), \(I\) — сила тока в катушке (А). Энергия магнитного поля равна половине произведения индуктивности катушки на квадрат силы тока в ней.

Как направлен индукционный ток В катушке?

Направление индуцируемого тока будет определять, где у катушки будет находиться какой из полюсов. Если приближать к катушке магнит, то в ней будет возникать индукционный ток такого направления, что катушка обязательно будет отталкиваться от магнита.

Почему в рамке возникает индукционный ток?

Если ось вращения рамки будет перпендикулярна направлению силовых линий магнитного поля, то через рамку потечёт индукционный ток.

Когда возникает магнитное поле?

Магнитное поле создаётся (порождается) током заряженных частиц, или изменяющимся во времени электрическим полем, или собственными магнитными моментами частиц (последние для единообразия картины могут быть формальным образом сведены к электрическим токам).

В каком случае наблюдается явление электромагнитной индукции?

Рассмотрим случай, когда явление электромагнитной индукции наблюдается при изменении силы тока, проходящего через катушку с большим количеством витков. Если причина возникновения индукционного тока состоит в возрастании тока, то индукционный ток своим магнитным полем будет противодействовать этому возрастанию.

В каком случае увеличивается сила индукционного тока?

Если внешний ток увеличивается, то растёт создаваемое им магнитное поле и его поток, что приводит к появлению индукционного тока, уменьшающего это увеличение. В этом случае индукционный ток направлен в сторону, противоположную основному.

Когда возникает явление самоиндукции?

Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре (в цепи) при изменении протекающего через контур тока. При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром.

В чем суть закона электромагнитной индукции?

Закон гласит: Для любого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус. или другими словами: Генерируемая ЭДС пропорциональна скорости изменения магнитного потока.

Где есть магнитное поле?

Магнитное поле — это особый вид материи, который существует вокруг магнитов или движущихся зарядов.

Как получить индукционный электрический ток?

Способы получения индукционного тока: перемещение магнита и катушки относительно друг друга; перемещение одной катушки относительно другой; изменение силы тока в одной из катушек; замыкание и размыкание цепи; перемещение сердечника.

Можно ли получить индукционный ток?

Нельзя получить ни при каких условиях. Чтобы создать индукционный ток нужен замкнутый контур. Обязательно, чтобы он находился в изменяющемся магнитном поле. По причине того, что этот ток должен принимать разные значения.

Куда направлен ток самоиндукции?

При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный.

Как изменяется магнитное поле при изменении силы тока В катушке?

Действие магнитного поля катушки с током прямо пропорционально силе тока.

Что такое Самоиндукция и индуктивность?

Самоиндукцией называют явление возникновения ЭДС индукции в самом проводнике, по которому идет переменный ток. Эта ЭДС называется ЭДС самоиндукции. Величину L называют индуктивностью контура или его коэффициентом самоиндукции.

Как возникает вихревое электрическое поле?

Итак, сущность явления электромагнитной индукции заключается в том, что вихревое электрическое поле возникает в любой точке пространства, если в этой точке существует изменяющееся во времени магнитное поле, независимо от того, есть там проводящий контур или нет.

Как понять индукционный?

ИНДУКЦИО́ННЫЙ, -ая, -ое. Физ. Прил. к индукция (во 2 знач.), возникший вследствие индукции.

Как определяется индукционный ток?

Направление индукционного тока в контуре определяется правилом Ленца: Индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван.

Как называется явление возникновения электрического тока в замкнутом пространстве?

Возникновение электрического тока в замкнутом проводнике (замкнутой цепи) возможно при помощи обратного преобразования из магнитного потока в электрический. Это явление называется электромагнитной индукцией.

Как определить куда направлен индукционный ток?

Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.

Почему индукционный ток является переменным?

Это значит, что по катушке течёт индукционный ток, у которого изменяется как модуль, так и направление с течением времени. Такой ток называется переменным током. Переменный ток создаётся и в замкнутом контуре изменяющимся магнитным потоком, пронизывающим его площадь.

В каком случае в кольце возникает индукционный ток?

При приближении магнита к кольцу без прорези возрастает магнитный поток сквозь площадь кольца. Так как кольцо замкнуто, то в нем возникает индукционный ток.

Как направлен индукционный ток в катушке?

Направление индуцируемого тока будет определять, где у катушки будет находиться какой из полюсов.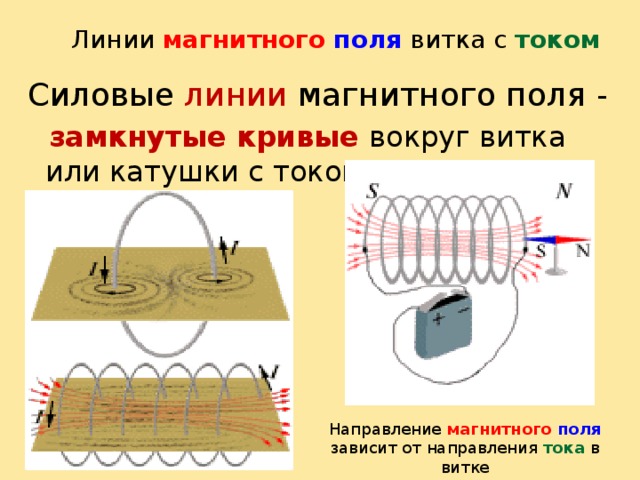 Если приближать к катушке магнит, то в ней будет возникать индукционный ток такого направления, что катушка обязательно будет отталкиваться от магнита.

Какие факторы влияют на величину индукционного тока?

Величина индукционного тока зависит от скорости изменения магнитного потока, пронизывающего катушку. Направление индукционного тока зависит от того, увеличивается или уменьшается магнитный поток, пронизывающий катушку. Направление индукционного тока зависит от направления магнитных линий, пронизывающих катушку.

Основы теории цепей

Основы теории цепей

Основы теории цепей. Учебник для вузов. Изд.4-е, переработанное. М., «Энергия», 1975. — 752 с. В книге излагаются общие методы анализа и синтеза и описание свойств линейных электрических цепей с сосредоточенными и распределенными параметрами при постоянных, переменных, периодических и переходных токах и напряжениях Рассматриваются свойства и методы расчета установившихся и переходных процессов в нелинейных электрических и магнитных цепях постоянного и переменного тока Все положения теории иллюстрируются практическими примерами. Третье издание книги выпущено в 1965 г. Книга является учебником для студентов электротехнических специальностей вузов. Оглавление ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ ВВЕДЕНИЕ Раздел первый. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ 1-1. Элементы электрических цепей и электрических схем 1-2. Эквивалентные схемы для источников энергии 1-3. Закон Ома для участка цепи с э. д. с. 1-4. Распределение потенциала вдоль неразветвленной электрической цепи 1-5. Баланс мощностей для простейшей неразветвленной цепи 1-6. Применение законов Кирхгофа для расчета разветвленных цепей 1-7. Метод узловых потенциалов 1-8. Метод контурных токов 1-9. Уравнения состояния цепи в матричной форме 1-10. Преобразование линейных электрических схем Глава вторая. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ 2-2. Свойство взаимности 2-3. Входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов 2-4. Применение топологических методов для расчета цепей 2-5. Топологические формулы и правила для определения передачи электрической цепи 2-6. Теорема о компенсации 2-7. Линейные соотношения между напряжениями и токами 2-8. Теорема о взаимных приращениях токов и напряжений 2-9. Общие замечания о двухполюсниках 2-10. Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей 2-11. Передача энергии от активного двухполюсника к пассивному Глава третья. ОСНОВНЫЕ ПОНЯТИЯ О ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА 3-2. Понятие о генераторах переменного тока 3-3. Синусоидальный ток 3-4. Действующие ток, э. д. с. и напряжение 3-5. Изображение синусоидальных функций времени векторами и комплексными числами 3-6. Сложение синусоидальных функций времени 3-7. Электрическая цепь и ее схема 3-8. Ток и напряжения при последовательном соединении сопротивления, Индуктивности и емкости 3-9. Сопротивления 3-10. Разность фаз напряжения и тока 3-11. Напряжение и токи при параллельном соединении сопротивления, индуктивности и емкости 3-12. Проводимости 3-13. Пассивный двухполюсник 3-14. Мощности 3-15. Мощности в сопротивлении, индуктивности и емкости 3-16. Баланс мощностей 3-17. Знаки мощностей и направление передачи энергии 3-18. Определение параметров пассивного двухполюсника при помощи амперметра, вольтметра и ваттметра 3-19. Условия передачи максимальной мощности от источника энергии к приемнику 3-20. Понятие о поверхностном эффекте и эффекте близости 3-21. Параметры и эквивалентные схемы конденсаторов 3-22. Параметры и эквивалентные схемы индуктивных катушек и резисторов Глава четвертая. РАСЧЕТ ЦЕПЕЙ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ 4-1. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока 4-2. Последовательное соединение приемников 4-3. Параллельное соединение приемников 4-4. Смешанное соединение приемников 4-5. Сложные разветвленные цепи 4-6. Топографические диаграммы 4-7. Дуальность электрических цепей 4-8. Сигнальные графы и их применение для расчета цепей Глава пятая. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ 5-2. Частотные характеристики неразветвленной цепи 5-3. Резонанс в цепи с двумя параллельными ветвями 5-4. Частотные характеристики параллельного контура 5-5. Понятие о резонансе в сложных цепях Глава шестая. ЦЕПИ С ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ 6-2. Электродвижущая сила взаимной индукции 6-3. Последовательное соединение индуктивно связанных элементов цепи 6-4. Параллельное соединение индуктивно связанных элементов цепи 6-5. Расчеты разветвленных цепей при наличии взаимной индуктивности 6-6. Эквивалентная замена индуктивных связей 6-7. Передача энергии между индуктивно связанными элементами цепи 6-8. Трансформатор без стального сердечника (воздушный трансформатор) Глава седьмая. КРУГОВЫЕ ДИАГРАММЫ 7-1. Комплексные уравнения прямой и окружности 7-2. Круговые диаграммы для неразветвленной цепи и для активного двухполюсника 7-3. Круговые диаграммы для любой разветвленной цепи Глава восьмая. МНОГОПОЛЮСНИКИ И ЧЕТЫРЕХПОЛЮСНИКИ ПРИ СИНУСОИДАЛЬНЫХ ТОКАХ И НАПРЯЖЕНИЯХ 8-1. Четырехполюсники и их основные уравнения 8-2. Определение коэффициентов четырехполюсников 8-3. Режим четырехполюсника при нагрузке 8-4. Эквивалентные схемы четырехполюсников 8-5. Основные уравнения и эквивалентные схемы для активного четырехполюсника 8-6. Идеальный трансформатор как четырехполюсник 8-7. Эквивалентные схемы с идеальными трансформаторами для четырехполюсника 8-8. Эквивалентные схемы трансформатора со стальным магнитопроводом 8-9. Расчеты электрических цепей с трансформаторами 8-10. Графы пассивных четырехполюсников и их простейшие соединения Глава девятая. ЦЕПИ С ЭЛЕКТРОННЫМИ И ПОЛУПРОВОДНИКОВЫМИ ПРИБОРАМИ В ЛИНЕЙНОМ РЕЖИМЕ 9-2. Эквивалентные схемы лампового триода 9-3. Транзисторы (полупроводниковые триоды) 9-4. Эквивалентные схемы транзисторов 9-5. Простейшие электрические цепи с невзаимными элементами и их направленные графы Глава десятая. ТРЕХФАЗНЫЕ ЦЕПИ 10-2. Соединения звездой и многоугольником 10-3. Симметричный режим трехфазной цепи 10-4. Некоторые свойства трехфазных цепей с различными схемами соединений 10-5. Расчет симметричных режимов трехфазных цепей 10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой 10-7. Напряжения на фазах приемника в некоторых частных случаях 10-8. Эквивалентные схемы трехфазных линий 10-9. Измерение мощности в трехфазных цепях 10-10. Вращающееся магнитное поле 10-11. Принципы действия асинхронного и синхронного двигателей Глава одиннадцатая. МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ 11-2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений 11-3. Сопротивления симметричной трехфазной цепи для токов различных последовательностей 11-4. Определение токов в симметричной цепи 11-5. Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи 11-6. Расчет цепи с несимметричной нагрузкой 11-7. Расчет цепи с несимметричным участком в линии Глава двенадцатая. НЕСИНУСОИДАЛЬНЫЕ ТОКИ 12-2. Разложение периодической несинусоидальной кривой в тригонометрический ряд 12-3. Максимальные, действующие и средние значения несинусоидальных периодических э. д. с., напряжений и токов 12-4. Коэффициенты, характеризующие форму несинусоидальных периодических кривых 12-5. Несинусоидальные кривые с периодической огибающей 12-6. Действующие значения э. д. с., напряжений и токов с периодическими огибающими 12-7. Расчет цепей с несинусоидальными периодическими э. д. с. и токами 12-8. Резонанс при несинусоидальных э. д. с. и токах 12-9. Мощность периодических несинусоидальных токов 12-10. Высшие гармоники в трехфазных цепях Глава тринадцатая. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 13-2. Переходный, принужденный и свободный процессы 13-3. Короткое замыкание цепи r, L 13-4. Включение цепи r, L на постоянное напряжение 13-5. Включение цепи r, L на синусоидальное напряжение 13-6. Короткое замыкание цепи r, С 13-7. Включение цепи r, С на постоянное напряжение 13-8. Включение цепи r, С на синусоидальное напряжение 13-9. Переходные процессы в неразветвленной цепи r, С 13-10. Апериодический разряд конденсатора 13-11. Предельный случай апериодического разряда конденсатора 13-12. Периодический (колебательный) разряд конденсатора 13-13. Включение цепи r, С на постоянное напряжение 13-14. Общий случай расчета переходных процессов классическим методом 13-15. Включение пассивного двухполюсника на непрерывно изменяющееся напряжение (формула или интеграл Дюамеля) 13-16. Включение пассивного двухполюсника на напряжение любой формы 13-17. Временная и импульсная переходные характеристики 13-18. Запись теоремы свертки при помощи импульсной переходной характеристики 13-19. Переходные процессы при скачках токов в индуктивностях и напряжений на конденсаторах 13-20. Определение переходного процесса и установившегося режима при воздействии периодических импульсов напряжения или тока Глава четырнадцатая. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 14-2. Законы Ома и Кирхгофа в операторной форме 14-3. Эквивалентные операторные схемы 14-4. Переходные процессы в цепях с взаимной индуктивностью 14-5. Сведение расчетов переходных процессов к нулевым начальным условиям 14-6. Определение свободных токов по их изображениям 14-7. Формулы включения 14-8. Расчет переходных процессов методом переменных состояния 14-9. Определение принужденного режима цепи при воздействии на нее периодического несинусоидального напряжения Глава пятнадцатая. ЧАСТОТНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ 15-2. Законы Ома и Кирхгофа и эквивалентные схемы для частотных спектров 15-3. Приближенный метод определения оригинала по вещественной частотной характеристике (метод трапеций) 15-4. О переходе от преобразований Фурье к преобразованиям Лапласа 15-5. Сравнение различных методов расчета переходных процессов в линейных электрических цепях Глава шестнадцатая. ЦЕПНЫЕ СХЕМЫ И ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ 16-2. Характеристическое сопротивление и постоянная передачи симметричного четырехполюсника 16-3. Вносимая и рабочая постоянные передачи 16-4. Цепные схемы 16-5. Частотные электрические фильтры 16-6. Низкочастотные фильтры 16-8. Полосные фильтры 16-11. Г-образный фильтр как пример несимметричного фильтра 16-12. Безындукционные (или r, C) фильтры Глава семнадцатая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 17-2. Передаточная функция четырехполюсника. Цепи минимальной фазы 17-3. Входные функции цепей. Положительные вещественные функции 17-4. Реактивные двухполюсники 17-5. Частотные характеристики реактивных двухполюсников 17-6. Синтез реактивных двухполюсников. Метод Фостера 17-7. Синтез реактивных двухполюсников. Метод Кауэра 17-8. Синтез двухполюсников с потерями. Метод Фостера 17-9. Синтез двухполюсников с потерями. Метод Кауэра 17-10. Понятие о синтезе четырехполюсников Раздел второй. ЛИНЕЙНЫЕ ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ Глава восемнадцатая. ГАРМОНИЧЕСКИЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 18-2. Уравнения однородной линии 18-3. Установившийся режим в однородной линии 18-4. Уравнения однородной линии с гиперболическими функциями 18-5. Характеристики однородной линии 18-6. Входное сопротивление линии 18-7. Коэффициент отражения волны 18-8. Согласованная нагрузка линии 18-9. Линия без искажений 18-10. Холостой ход, короткое замыкание и нагрузочный режим линии с потерями 18-11. Линии без потерь 18-12. Стоячие волны 18-13. Линия как четырехполюсник Глава девятнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 19-2. Общее решение уравнений однородной линии 19-3. Возникновение волн с прямоугольным фронтом 19-4. Общие случаи нахождения волн, возникающих при переключениях 19-5. Отражение волны с прямоугольным фронтом от конца линии 19-6. Общий метод определения отраженных волн 19-7. Качественное рассмотрение переходных процессов в линиях, содержащих сосредоточенные емкости и индуктивности 19-8. Многократные отражения волн с прямоугольным фронтом от активного сопротивления 19-9. Блуждающие волны Раздел III. НЕЛИНЕЙНЫЕ ЦЕПИ Глава двадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ 20-2. Графический метод расчета неразветвленных цепей с нелинейными элементами 20-3. Графический метод расчета цепей с параллельным соединением нелинейных элементов 20-4. Графический метод расчета цепей со смешанным соединением нелинейных и линейных элементов 20-5. Применение эквивалентных схем с источниками э. д. с. для исследования режима нелинейных цепей 20-6. Вольт-амперные характеристики нелинейных активных двухполюсников 20-7. Примеры расчета разветвленных электрических цепей с нелинейными элементами 20-8. Применение теории активных двухполюсника, четырехполюсника и шестиполюсника для расчета цепей с линейными и нелинейными элементами 20-9. Расчет разветвленных нелинейных цепей итерационным методом (методом последовательных приближений) Глава двадцать первая. МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ 21-2. Расчет неразветвленных магнитных цепей 21-3. Расчет разветвленных магнитных цепей 21-4. Расчет магнитной цепи кольцевого постоянного магнита с воздушным зазором 21-5. Расчет неразветвленной неоднородной магнитной цепи с постоянным магнитом Глава двадцать вторая. ОБЩАЯ ХАРАКТЕРИСТИКА НЕЛИНЕЙНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА И МЕТОДОВ ИХ РАСЧЕТА 22-1. Нелинейные двухполюсники и четырехполюсники при переменных токах 22-2. Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников 22-3. Явления в нелинейных цепях переменного тока 22-4. Методы расчета нелинейных цепей переменного тока Глава двадцать третья. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА ОДИНАКОВОЙ ЧАСТОТЫ 23-2. Форма кривой тока в цепи с вентилями 23-3. Простейшие выпрямители 23-4. Формы кривых тока и напряжения в цепях с нелинейными реактивными сопротивлениями 23-5. Утроители частоты 23-6. Формы кривых тока и напряжения в цепях с терморезисторами 23-7. Замена реальных нелинейных элементов условно-нелинейными 23-8. Учет реальных свойств стальных магнитопроводов 23-9. Расчет тока в катушке со стальным магнитопроводом 23-10. Понятие о расчете условно-нелинейных магнитных цепей 23-11. Явление феррорезонанса 23-12. Стабилизаторы напряжения Глава двадцать четвертая. НЕЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ Э. Д. С. И ТОКА РАЗЛИЧНЫХ ЧАСТОТ 24-1. Общая характеристика нелинейных цепей с источниками э. д. с. различных частот 24-2. Вентили в цепях с постоянными и переменными э. д. с. 24-3. Управляемые вентили в простейших выпрямителях и преобразователях постоянного тока в переменный 24-4. Катушки со стальными магнитопроводами в цепях с постоянными и переменными э. 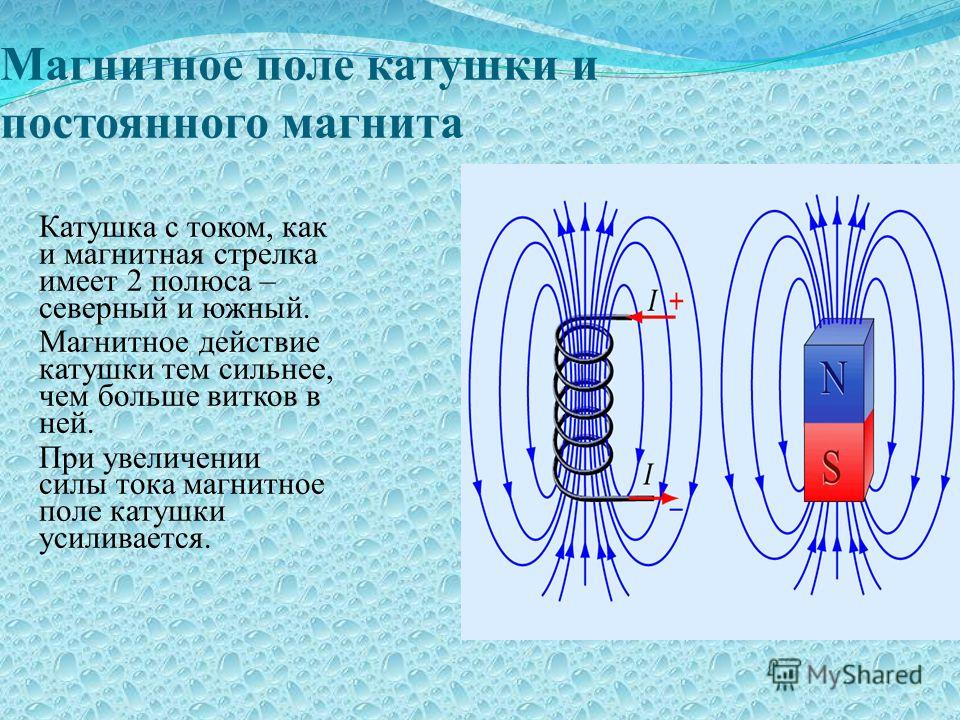д. с. 24-5. Удвоитель частоты 24-6. Метод гармонического баланса 24-7. Влияние постоянной э. д. с. на переменную составляющую тока в цепях с нелинейными безынерционными сопротивлениядли 24-8. Принцип получения модулированных колебаний 24-9. Влияние постоянной составляющей на переменную в цепях с нелинейными индуктивностями 24-10. Магнитные усилители мощности Глава двадцать пятая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ 25-2. Включение катушки со стальным магнитопроводом на постоянное напряжение 25-3. Включение катушки со стальным магнитопроводом на синусоидальное напряжение 25-4. Импульсное воздействие в цепях с неоднозначными нелинейностями 25-5. Понятие о простейших запоминающих устройствах 25-6. Изображение переходных процессов на фазовой плоскости 25-7. Колебательный разряд емкости через нелинейную индуктивность Глава двадцать шестая. АВТОКОЛЕБАНИЯ 26-1. Нелинейные резисторы со спадающим участком характеристики 26-2. Понятие об устойчивости режима в цепи с нелинейными резисторами 26-3. Релаксационные колебания в цепи с отрицательным сопротивлением 26-4. Близкие к синусоидальным колебания в цепи с отрицательным сопротивлением 26-5. Фазовые траектории процессов в цепи с отрицательным сопротивлением 26-6. Фазовые траектории процессов в генераторе синусоидальных колебаний 26-7. Определение амплитуды автоколебаний методом гармонического баланса Приложение 1. Разложение периодических функций в тригонометрический ряд Приложение 2. Таблица оригиналов и изображений (по Лапласу) Приложение 3. Таблица функций и их частных спектров Приложение 4. Таблица функций для трапеций СПИСОК ЛИТЕРАТУРЫ

Токовая катушка – определение, важные факторы и применение

Токовая катушка в основном представляет собой катушку, например, провод, намотанный на электрический проводник. Обычно катушка изготавливается из изолированного медного провода, а проводник представляет собой сердечник из мягкого железа. Когда катушка, намотанная на проводник, несет ток, было замечено, что катушка начинает вести себя как магнит. Это свойство проводника, намотанного на катушку с током, называется электромагнетизмом. Популярный физический эксперимент проводится с использованием того же явления. Когда гвозди кладут поперек стола с проводником, намотанным на провод с током, то гвозди стола прилипают к катушке. Причина, по которой эти гвозди приклеиваются к проводу, — электромагнетизм.

Катушка тока представляет собой электрический проводник, похожий на проволочную катушку. Рассмотрим катушку из изолированного медного провода, намотанную на сердечник из мягкого железа. Ставим на стол железный гвоздь, надеваем на гвоздь катушку и смотрим, что получится. Теперь мы можем подключить батарею 9 В к клеммам катушки и посмотреть, что произойдет. Катушка работает как по волшебству. Магнит притягивает железные гвозди, поэтому повторите этот эксперимент с большим количеством витков и более мощной батареей. Обратите внимание, как меняется интенсивность. Проводник в виде катушки действует как магнит, а свойство этого проводника называется электромагнитом. Сила электромагнита зависит от количества витков в катушке. Один провод не создает достаточного магнитного поля вокруг проводника, чтобы притянуть железный гвоздь на столе, поэтому он несколько раз наматывает проводник, чтобы создать индукционно-индукционное магнитное поле. Умножая на количество витков, сила наведенного магнитного поля также зависит от величины тока, протекающего через проводник.

Важные факторы для токовой катушки

Существует ряд факторов, от которых зависит сила электромагнетизма.

1. Первым фактором, определяющим силу тока катушки, является количество витков. Чем больше витков, тем больше ток в амперах. Магнитное поле также умножается на количество витков в катушке.

2. Вторым важным фактором является сила тока, протекающего по проводнику. Чем больше электрический ток, тем больше сила катушки тока.

3. Третий фактор – это материал, из которого изготовлен проводник. Обычно железо или железосодержащие материалы используются для улучшения электромагнетизма вокруг катушки с током. Кроме того, использование таких сплавов, как алюминий-никель-кобальт, также может создавать сильные магнитные поля.

4. Четвертый и последний фактор, который важен для катушки тока, это температура. Обнаружено, что токонесущая способность улучшается при более низких температурах. Причем самые сильные магниты сделаны из сверхпроводников, охлаждаемых жидким азотом или гелием.

Применение катушки тока

Благодаря своей уникальной способности создавать электромагнетизм, в реальном мире существует множество применений катушки тока.

• Известно, что токовая катушка используется в качестве дробилки консервных банок. Это приложение основано на электромагнитном поле, которое генерируется, когда банка помещается внутрь катушки, которая затем получает дополнительную энергию, чтобы согнуть и деформировать банку, сжав ее в плоский диск.

• Катушки тока также широко используются в качестве электромагнитов. Существуют также определенные типы электромагнитов, такие как соленоид, катушка Максвелла, звуковая катушка и катушка размагничивания.

• Другим распространенным применением токовой катушки являются магнитные краны. Мусор на свалках также содержит большое количество металлов, которые либо разлагаются годами, либо могут быть просто переработаны и использованы повторно. Электромагнит может быть большим помощником здесь. Гигантский электромагнит притягивает и приклеивает все металлические детали к мусору на свалках и свалках. Более того, эти металлические обрезки легко удаляются электромагнитом, когда он обесточен. Эта функция была невозможна с постоянными магнитами, и раньше людям приходилось убирать металлический лом вручную.

Обмотка катушки тока

Понятия электричества и магнетизма пересекаются при изучении физики. Пример катушки с током объясняет одновременное возникновение двух вышеупомянутых явлений, которые затем называются электромагнетизмом. Электромагнитное поле, создаваемое при прохождении тока через катушку с током, может служить нескольким целям. Некоторыми из этих реальных применений являются электромагниты, консервные дробилки и магнитные краны.

Технические характеристики электрической катушки

Электрическая катушка состоит из сердечника и проволоки, намотанной вокруг сердечника. Некоторые типы электрических катушек не имеют сердечника и просто намотаны обмотками.

• Катушка для проволоки

Форма и размеры проволоки, используемой в катушке, выбираются для конкретной функции. Индуктивность, рассеяние энергии, диэлектрическая прочность и напряженность магнитного поля являются ключевыми факторами при выборе проводки. Наиболее эффективные катушки ограничивают материал и объем. Между площадью электрического проводника и площадью обмотки существует зависимость, называемая рабочим циклом. Круглый провод всегда имеет некоторый зазор, который увеличивается за счет количества витков и зазора между слоями, создаваемого изолятором. Коэффициент заполнения всегда меньше 1 и находится в диапазоне от 0,01 до 0,05. Использование прямоугольной, квадратной и плоской проволоки позволяет увеличить коэффициент заполнения.

• Провод катушки  

В компании Sag Harbour Industries существует три типа рабочих циклов в зависимости от соотношения между площадью поперечного сечения детали и площадью поперечного сечения катушки. Расчет рабочего цикла колеблется от 0,1 до 0,5 с символическими высокими, средними и низкими рабочими циклами. Затягивание проволоки уменьшает пространство и увеличивает скорость заполнения. Это, в свою очередь, повышает эффективность электрического устройства и улучшает его проводимость. Наилучшей намоткой круглой проволоки является заполнение канавки на 300° ниже периметра катушки верхним слоем проволоки.

• Коэффициент заполнения зазора

Обмотка — это изолированный проводник, используемый для обмена электрической и магнитной энергией. В большинстве случаев провод покрыт тонким слоем меди или алюминия с тонкой многослойной изоляцией, что обычно является первым выбором для большинства электрических катушек при исследовании таких факторов, как химические, физические и механические свойства меди. Медь высокой чистоты используется в высокотемпературных или высокотемпературных системах или двигателях, использующих водород для охлаждения.

• Оцинкованная проволока

Оцинкованная проволока используется в средах, где условия могут ухудшить или повредить проводку. Оболочка провода бывает золотой, серебряной или никелевой различной толщины и покрыта изоляцией. Гальваника обеспечивает наилучшую защиту в суровых условиях. Покрытие провода значительно улучшает такие свойства, как проводимость.

• Тип изоляции

В электрических катушках используются различные изоляционные материалы в зависимости от диапазона рабочих температур. Типы материалов включают поливинилхлорид (ПВХ), полиуретан, полиэстер и различные формы полиимида. При выборе изоляционного материала используется полиимид, температура которого достигает 250 °С. В процессе намотки провод нагревается и изоляционный материал прилипает друг к другу.

Изоляция повышает термостойкость и защищает провода. Основной функцией изоляции проводов является предотвращение их соприкосновения с проводом. Это может вызвать короткое замыкание. Каждый тип изоляции имеет различные свойства, включая теплоемкость, толщину и область применения.

1. Полиэстер — Полиэстер обладает высокотемпературными свойствами и очень низкой хрупкостью. высокая износостойкость. Отличные свойства намотки, гибкость и устойчивость к нагреву и растворителям. Полиамидное покрытие на полиэстере улучшает свойства термопласта при сминании и текучести.

2. Полиимид — Полиимид является одним из наиболее широко используемых типов изоляции для электромагнитных катушек. Обладает отличными механическими свойствами и может эксплуатироваться при высоких температурах. Полиимиды представляют собой полимеры, состоящие из имидных мономеров с двумя ацильными группами, связанными с азотом. Благодаря механическим и термическим свойствам полиимида он может выдерживать температуры свыше 240 °C, и его использование с электромагнитными катушками расширилось.

Интересные факты

Разница между токовой катушкой и катушкой давления.

Катушка давления также известна как катушка напряжения и обычно используется в ваттметре. Существует заметная разница между катушкой тока и катушкой давления. Катушка тока всегда подключается последовательно. При этом катушка давления подключается параллельно нагрузке. Кроме того, токовая катушка измеряет ток, а катушка давления измеряет напряжение. Обе катушки используются в шкале ваттметра и для измерения тока или напряжения в линиях электропередач.

Заключение

Vedantu — это целостная учебная платформа, которая предоставляет экспертные знания по концептуальному обучению, чтобы помочь учащемуся лучше понять. В Vedantu вы можете найти все, что ищете, в одном месте в формате PDF. Эти PDF-файлы легко загружаются и бесплатны. Учащиеся могут внимательно изучить концепции, определения и вопросы и понять концепции, используемые для решения этих вопросов. Это очень поможет учащимся с экзаменационной точки зрения.

Возбуждение катушки

Возбуждение катушки

Катушка возбуждения

Плотность тока, протекающего в области катушки, вычисляется из сосредоточенной величины, которая составляет возбуждение катушки. Выбор этой величины можно сделать, установив параметр возбуждения катушки, при этом значение указывается в соответствующем текстовом поле. Все характеристики катушки могут быть возбуждены либо с возбуждением по току, возбуждением по напряжению, либо, в некоторых случаях, с возбуждением по мощности. Предоставленное значение или выражение переводится в плотность тока или электрическое поле, приложенное к домену, в соответствии с используемой моделью катушки. Элементы катушки также могут извлекать значение тока или напряжения из соединения цепи, если для параметра возбуждения катушки установлено значение Цепь (ток) или Цепь (напряжение) соответственно.

Возбуждение цепи (тока) работает аналогично возбуждению тока, но в этом случае входы обеспечиваются соединением цепи. Возбуждение по цепи (напряжению) работает аналогично возбуждению по напряжению, но в этом случае входы обеспечиваются подключением по цепи.

Текущее возбуждение

Катушка

с одним проводником, модель

При указании полного тока Icoil катушка прикладывает внешнее электрическое поле в направлении протекания тока, вычисляемое как:

(3-2)

, где L равно толщине физического интерфейса d для 2D-моделей, 2πr для 2D-аксиально-симметричных моделей и длине катушки в 3D-моделях. V — неизвестный приложенный потенциал. Потенциал V решается с использованием дополнительного уравнения, которое ограничивает общий интегрированный ток равным заданному значению тока Icoil, выступая в качестве регулятора.

Катушка

с гомогенизированным многооборотным витком Модель

При указании полного тока Icoil катушка применяет плотность внешнего тока в направлении проводов, как в уравнении 3-3, где N – это указанное количество витков, а A – общая площадь поперечного сечения домена катушки.

(3-3)

Режим группы катушек

При активации режима Coil Group в модель добавляются дополнительные уравнения для обеспечения равенства токов, протекающих в каждом домене или группе доменов.

Одновитковая катушка (в магнитном и электрическом полях)

При указании полного тока Icoil внеплоскостная составляющая плотности тока определяется как:

(3-4)

, где L равно толщине физического интерфейса d для 2D-моделей и 2πr для 2D-аксиально-симметричных моделей, а V — неизвестный приложенный потенциал. Потенциал V решается с использованием дополнительного алгебраического уравнения, которое ограничивает общий интегрированный ток равным заданному значению тока Icoil.

Напряжение возбуждения

Катушка

с одним проводником, модель

При указании полного напряжения Vcoil внешнее электрическое поле вычисляется как:

(3-5)

, где Vcoil — указанное приложенное напряжение, а L — толщина физического интерфейса d для 2D-моделей, 2πr для 2D-аксиально-симметричных моделей и длина катушки в 3D-моделях.

Катушка с гомогенизированным многооборотным двигателем, модель

При указании напряжения Vcoil составляющая плотности тока в направлении проводов определяется по уравнению 3-6 и уравнению 3-7.

(3-6)

, где Vcoil — указанное приложенное напряжение, A — общая площадь поперечного сечения области катушки, N — указанное количество витков, Rcoil — полное сопротивление катушки, рассчитанное как

(3-7)

, где L равно толщине физического интерфейса d для 2D-моделей, 2πr для 2D-аксиально-симметричных моделей и длине катушки в 3D-моделях. Выражение σcoilacoil представляет собой произведение объемной проводимости провода на площадь поперечного сечения провода. Vind — индуцированное напряжение, вычисляемое путем интегрирования электрического поля вдоль катушки.

Режим группы катушек

Когда режим Coil Group активирован, в модель добавляются дополнительные условия, чтобы сумма всех напряжений в доменах или группах доменов была равна указанному напряжению:

, где Vcoil — заданное пользователем падение напряжения на катушке, Vi — отдельные приложенные потенциалы, а N — количество витков в группе катушек.

Одновитковая катушка (в магнитном и электрическом полях)

При указании общего напряжения Vcoil катушка применяет внеплоскостную плотность внешнего тока, вычисляемую как:

(3-8)

, где Vcoil — указанное приложенное напряжение, а L — толщина физического интерфейса d для 2D-моделей и равна 2πr для 2D-аксиально-симметричных моделей.

Силовое возбуждение

В двухмерных и двухмерных осесимметричных моделях мощность является опцией, доступной для параметра возбуждения катушки. Когда выбрана мощность, физический интерфейс устанавливает уравнение, указанное в разделе «Токовое возбуждение», плюс ограничение между током катушки и напряжением:

в стационарных и зависящих от времени шагах исследования и

в частотной области (средний цикл). Выберите этот параметр, чтобы указать входную мощность для катушек. С этими настройками проблема становится нелинейной.