Занимательная математика: правило Гаусса

Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.

Первая статья из этого цикла посвящена правилу Гаусса.

Немного истории

Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.

Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:

Найти сумму всех натуральных чисел от 1 до 100.

Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.

Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.

Гаусс сгруппировал числа следующим образом:

(1+10) + (2+9) + (3+8) + (4+7) + (5+6)

Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо

5 * 11 = 55

Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:

1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100

1. Находим количество пар в ряде натуральных чисел. В данном случае их 50.

2. Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.

3. Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050

Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.

Задачи на использование правила Гаусса

А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.

Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.

В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.

Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.

Задача 1

Найти сумму чисел:

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
• 1 + 2 + 3 + … + 14 + 15 + 16;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.

Решение.

Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
• 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050

Задача 2

Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?

Решение.

С помощью правила Гаусса находим сумму всех весов:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)

Далее смотрим, можно ли этот вес разбить на три равных веса:

45 : 3 = 15 (г)

Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.

Один из вариантов:

• 9г, 6г
• 8г, 7г
• 5г, 4г, 3г, 2г, 1г

Другие возможные варианты найдите сами с ребенком.

Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).

Задача 3

Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?

Решение.

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

Значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.

Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.

Задача 4

Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?

Решение.

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.

Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.

Задача 5

Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?

Решение.

Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:

1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.

Задача 6

Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?

Решение.

Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:

• первая клетка — 1,
• вторая — 2,
• третья — 3,
• …
• восьмая — 8,
• девятая — 9.

Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.

Задача 7

Вычислить сумму, используя прием Гаусса:

• 31 + 32 + 33 + … + 40;
• 5 + 10 + 15 + 20 + … + 100;
• 91 + 81 + … + 21 + 11 + 1;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
• 1 + 2 + 3 + 4 + 5 + 6;
• 4 + 6 + 8 + 10 + 12 + 14;
• 4 + 6 + 8 + 10 + 12;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.

Решение.

• 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
• 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
• 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
• 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
• 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
• 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.

Задача 8

Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?

Решение.

Применяем правило Гаусса, чтобы найти общую массу гирек:

1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)

Вычисляем массу гирек, которые убрали:

78 : 3 = 26 (г)

Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.

Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.

Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):

1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.

Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.

Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.

Удачи в развитии Ваших детей.

Метод Гаусса — примеры c решением, теоремы и формулы

Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ

Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.

Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений. Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.

У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.

О чем статья

Определения и обозначения

Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.

Для начала систематизируем знания о системах линейных уравнений.

Обратите внимание!

СЛАУ в зависимости от её элементов может иметь:

1. Одно решение;
2. много решений;
3. совсем не иметь решений.

В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.

Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:

• перемена мест уравнений системы;
• почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
• сложение к обеим частям одного из уравнений определённых частей другого уравнения.

Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.

Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:

   

где а, в, с  – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.

Если = = = , тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.

Множественные числа , , называются решением СЛАУ, если при подстановке , , в СЛАУ получим числовые тождества.

Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:

– это основная матрица СЛАУ.

– матрица столбец неизвестных переменных.

– матрица столбец свободных членов.

Если к основной матрице добавить в качестве – ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой , а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов. То есть, расширенная матрица выглядит так:

Если квадратная матрица равна нулю, она называется

вырожденная, а если – матрица невырожденная.

Обратите внимание!

Если с системой уравнений:          

Произвести такие действия:

• умножать обе части любого из уравнений на произвольное и отличное от нуля число ;
• менять местами уравнения;
• к обеим частям любого из уравнений прибавить определённые части другого уравнения, которые умножаются на произвольное число ,

тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.

Теперь можно перейти непосредственно к методу Гаусса.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов).

Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Простейшие преобразования элементов матрицы

Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:

Из уравнения запишем расширенную матрицу:

Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.

Матрица системы – это матрица, которая составляется исключительно с коэффициентами при неизвестных. Что касается расширенной матрицы системы, так, это такая матрица, в которой кроме коэффициентов записаны ещё и свободные члены. Любую из этих матриц называют просто матрицей.

На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:

1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:

.

2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).

3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.

4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.

5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:

Для удобства умножаем первую строку на (-3):

Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:

В итоге получилось такое преобразование:

Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:

В матрице верхняя строка преобразовалась:

Первую строку делим на и преобразовалась нижняя строка:

И верхнюю строку поделили на то же самое число :

Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась. ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты.

Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:

.

Обратите внимание!

Если в примере приведены десятичные дроби, метод Гаусса в этом случае также поможет решить систему линейных алгебраических уравнений. Однако, не стоит забывать, что следует избегать приближённых вычислений, так как ответ будет неверным. Лучше всего использовать десятичные дроби, а от них переходить к обыкновенным дробям.

Алгоритм решения методом Гаусса пошагово

После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:

Шаг 1. Переписываем систему в виде матрицы

Записываем матрицу:

Шаг 2.

Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю

Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на .

Шаг 3. Приводим матрицу к ступенчатому виду

Теперь вторую строку можно поделить на 2 и получается:

Верхнюю строку делим на и приводим матрицу к ступенчатому виду:

Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.

Шаг 4. Записываем эквивалентную систему

После наших элементарных преобразований получилась эквивалентная система:

Шаг 5. Производим проверку (решение системы обратным путём)

Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки. :

находим : ,

,

.

После находим :

,

.

Тогда:

.

Как видим, уравнение решено правильно, так как ответы в системе совпадают.

Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений

Как мы уже упоминали, невырожденная матрица бывает тогда, когда . Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.

Дана система уравнений:

Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.

Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную :

Из последнего, третьего уравнения мы видим, что . Из второго уравнения находим . И последнее, находим первое уравнение .

Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.

Когда выражается через и в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:

• берём второе уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на ,
• берём третье уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на .

И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:

Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:

В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно , чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.

Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.

В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.

Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.

Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений

Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.

Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.

В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:

1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.

Например, вам попалась подобная система:

У нас получается такая ситуация

Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.

Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.

2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где – число, которое отличное от нуля.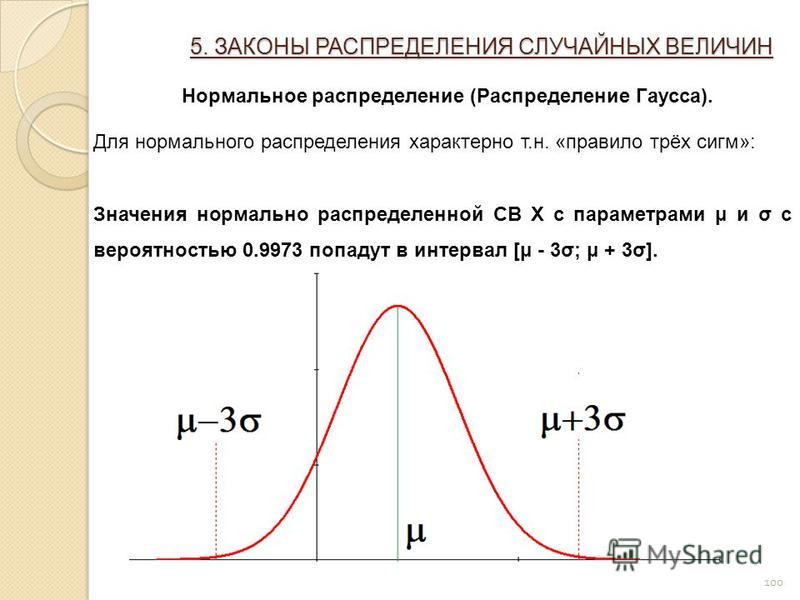 Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло  вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:

Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:

В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных , и , и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.

3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной . Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной . Если же  уже исключались, тогда переходим к ,  и т. д.

Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :

Такая система уравнений после преобразования выглядит так:

Вы наверное уже обратили внимание, что вместе с исключились и . Поэтому решение методом Гаусса продолжаем исключением переменной из всех уравнений системы, а начнём мы с третьего уравнения:

Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:

Допусти, что система уравнений стала:

В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:

В нашем примере это , и . В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:

Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: , , , где , ,  – произвольные числа.

Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.

В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении: , а из первого уравнения получаем:

= =

В итоге, получился результат, который можно и записать.

Ответ

,

,

,

,

,

.

Примеры решения методом Гаусса

Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.

Пример 1

Задача 

Решить систему линейных алгебраических уравнений методом Гаусса:

Решение

Выписываем матрицу, куда добавляем столбец свободных членов:

Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:

Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой превратился в . Для этого можно ко второй строке прибавить первую строку и умножить на .Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на (разрешающий элемент данного шага).

Соответственно, первая строка остаётся неизменной, а вторая поменяется:

Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на и только после этого ко второй строке прибавить изменённую после умножения на вторую строку. Вот что получилось:

. Теперь прибавляем со второй строки первую строку . У нас получился , который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:

Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.

Итак, у нас получился ступенчатый вид матрицы:

Записываем новую систему уравнений:

Для проверки решаем систему обратным ходом. Для этого находим сначала :

Так как найден, находим :

.

Подставляем в изначальную нашу систему уравнений найденные и :

и .

Как видите из решения, система уравнений решена верно. Запишем ответ.

Ответ

Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.

Пример 2

Задача

Решить систему уравнений методом Гаусса:

Решение

Составляем матрицу, куда вписываем и свободные члены:

Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку: . В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем , и . Аналогично, и . И умножаем свободный член . Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:

Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:

Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:

В результате получилась ступенчатая система уравнений:

Сначала находим : ,

.

Обратный ход:

Итак, уравнение системы решено верно.

Ответ

,

,

.

Пример 3

Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.

Задача

Решите систему уравнений методом Гаусса:

Решение                                                                

В уравнении , то есть – ведущий член и пусть  ≠ 0

Из данного уравнения составим расширенную матрицу:

Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: , , . Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в теперь стоит 0.

Поменяем вторую и третью строку местами и получим:

Получилось так, что = b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную из третьей и четвёртой строк:

Получилась такая матрица:

Также, учитывая, что  = , умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную и получаем новую систему уравнений:

Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,

из третьего: = = =

второе уравнение находим: = = = 2,

из первого уравнения: = .

Значит, решение системы такое: (1, 2, -1, -2).

Ответ

,

,

,

.

Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.

Пример 4

Задача

Решить систему уравнений методом Гаусса:

Решение

Записываем расширенную матрицу системы:

Сначала смотрим на левое верхнее число:

Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:

 

Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:

Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:

Получился ступенчатый вид уравнения:

Проверяем:

,

,

,

,

.

.

  Ответ

,

,

.

Заключение

Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.

Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.

Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.

Литература для общего развития:

Умнов А. Е. Аналитическая геометрия и линейная алгебра, изд. 3: учеб. пособие – М. МФТИ – 2011 – 259 с.

Карчевский Е. М. Лекции по линейной алгебре и аналитической геометрии, учеб. пособие – Казанский университет – 2012 – 302 с.

Закон Гаусса | Brilliant Math & Science Wiki

Агнишом Чаттопадхьяй, Абхиджит Ватс, Сатьябрата Даш, и

способствовал

Содержимое

• Утверждение теоремы
• Закрытые поверхности
• Поток векторного поля
• Дивергенция векторного поля.
• Закон Гаусса для электрического поля
• Закон Гаусса для других важных полей
• Эквивалентность с законом Кулона
• Приложения

Замкнутая поверхность — это поверхность, которая компактна и не имеет границы . Другими словами, замкнутая поверхность — это поверхность, которая делит пространство (за исключением самого себя) на две непересекающиеся части: внешнюю и внутреннюю. Некоторые простые примеры закрытых поверхностей включают неповрежденные пузыри, сферы Дайсона или корпус, внутри которого можно было бы оказаться, если бы они залезли в спальный мешок и зашили отверстие.

Лист бумаги Пустая бутылка из-под газировки Чаша Надувная трубка для плавания

Закон Гаусса — очень мощный метод определения электрического поля, обусловленного распределением зарядов. Математическое выражение для закона Гаусса:

\[ \int_{S} \vec{E} \cdot \vec{dA}=\frac{Q_{enc}}{\epsilon_0} ,\]

где \(S\) — поверхность, \(\vec{E}\) — вектор электрического поля, \(\vec{dA}\) — бесконечно малый элемент площади, \(Q_{enc}\) — заряд, заключенный в \(S,\), а \(\epsilon_0\) — константа.

Чтобы применить закон Гаусса, нам нужно понять, что означает каждая из частей этого выражения. Этот набор задач поможет вам понять каждый из компонентов. Начнем с \(S\). Вы можете быть более знакомы с интегралами как с пределом суммы функции на линейном интервале, который дает «площадь под кривой». Интеграл по поверхности функции — это просто сумма этой функции по всем точкам на поверхности.

Поверхность по закону Гаусса представляет собой замкнутую двумерную поверхность , такую ​​как поверхность сферы или поверхность куба. Замкнутая поверхность — это поверхность, которая делит пространство на внутреннее и внешнее, причем под делением мы понимаем, что нет пути, идущего изнутри наружу, который не проникал бы сквозь поверхность. Рассмотрим поверхность \(S\) объектов внизу. Для какого из объектов \(S\) является замкнутой поверхностью?

Грубо говоря, поток поля через поверхность — это суммарный поток через нее. Мы развиваем эту интуицию в примере ниже.

Подумайте об этой аналогии:

Предположим, вы поместили хлопчатобумажную мембрану в середину трубы, по которой течет вода. Какой поток воды через мембрану?

Конечно, ответом будет средняя нормальная составляющая скорости , умноженная на площадь мембраны .

Это то, что мы называем потоком через мембрану!

Почему мы берем нормальный компонент? Потому что выравнивание мембраны по направлению потока имеет значение. Что, если и мембрана, и поток выровнены горизонтально?

\[ \Phi = \oint_{\mathcal{S}} \overrightarrow{E} \cdot d \overrightarrow{A}.\]

Дивергенция векторного поля в точке — это величина источника или стока поля в этой точке. Конечно, это то же самое, что утверждать, что дивергенция представляет собой объемную плотность внешнего потока векторного поля из бесконечно малого объема вокруг данной точки.

Формально указанное выше переводится как

Дивергенция векторного поля \(\overrightarrow{E}\) в точке \(p\) определяется как предел чистого потока \(\overrightarrow{E}\) через гладкую границу трехмерной области \(V \) разделить на объем \(V\), поскольку \(V\) сжимается до \(p\):

\[\operatorname{div}\,\overrightarrow{E}(p) = \lim_{V \стрелка вправо \{p\}} \iint_{S(V)} {\overrightarrow{E}\cdot\widehat{n} \over |V| } \; дС, \]

, где \(|V|\) — объем \(V\), \(S(V)\) — граница \(V\), а интеграл — поверхностный интеграл с \(\widehat{ n}\) — внешняя единица нормали к этой поверхности.

Применение в декартовых координатах:

Если существует такое векторное поле, что

\[ \overrightarrow{E}(x \widehat{i} + y \widehat{j} + z \widehat{k}) = u \widehat{i} + v \widehat{j} + w \widehat{k }, \]

, затем

\[ \operatorname{div}\,\overrightarrow{E} = \nabla \cdot \overrightarrow{E} = \frac{\partial{u}}{\partial{x}}+\frac{\partial{v }}{\partial{y}}+\frac{\partial{w}}{\partial{z}} . \]

Интегральная форма
Если \(S\) является замкнутой поверхностью, в которой заключен заряд \(Q\), то поток \(\Phi_E\) через \(S\) определяется выражением

\[ \Phi_E = \ oint_{\mathcal{S}} \overrightarrow{E} \cdot d \overrightarrow{A} =\frac{Q}{\varepsilon_0}. \]

Дифференциальная форма
Если \( \rho \left(\overrightarrow{r}\right)\) объемная плотность заряда в точке \(\overrightarrow{r}\), то дивергенция электрическое поле \(\overrightarrow{E}\) в точке \(\overrightarrow{r}\) равно

\[ \nabla \cdot \overrightarrow{E}\left(\overrightarrow{r}\right) = \frac{\rho \left(\overrightarrow{r}\right) }{\varepsilon_0} .\]

Приведенное выше обсуждение потоков и дивергенций должно прояснить, почему эти две формы эквивалентны. Тем не менее эта эквивалентность вытекает из теоремы Гаусса или теоремы о расходимости.

Аналогичное утверждение, такое как электрический закон Гаусса, может быть сделано для нескольких других полей. Вот таблица таких выражений, где символы имеют свои обычные значения.

92\\ &= 4\пи\гамма\\ &= \frac{q}{\varepsilon_0}, \конец{выравнивание}\]

, что является законом Гаусса, как и хотелось. \(_\квадрат\).

Примечание : Предлагаемое доказательство работает только для сферических поверхностей; более общее доказательство заканчивается использованием векторного исчисления и функций Грина/Дельта. Не стесняйтесь делать снимок в общем случае.

Закон Гаусса — мощное утверждение о полях обратных квадратов. Он нашел свое место не только в решении задач, но и в четырех уравнениях Максвелла, а также в гравитации. 92}\]

Предположим, что бесконечно длинный прямой проводник с током имеет однородную линейную плотность заряда \(\lambda.\). Пусть этот провод лежит на оси \(y\) плоскости \(xy\), и пусть \( x > 0\) — расстояние между осью \(y\) и точкой \(P\) на плоскости \(xy\). Какова напряженность электрического поля в точке \(P?\)

Примечание: \(\epsilon_0 \) в приведенных ниже вариантах обозначает электрическую постоянную.

Гравитационный поезд — это гипотетическая идея, предложенная Робертом Гуком (известным автором закона Гука) Исааку Ньютону в 1600-х годах. Он состоит из простой идеи, которую трудно реализовать на практике. Выкопайте туннель, который проходит прямо через Землю между двумя точками на поверхности. Если вы сможете понять, как устранить трение и снизить сопротивление воздуха, у вас теперь есть механизм для чрезвычайно эффективного и быстрого перемещения между удаленными друг от друга точками. Просто бросьте что-нибудь в туннель с одного конца. Гравитация сначала будет тянуть его вниз через туннель, в конечном итоге достигая высоких скоростей. Как только объект окажется на полпути через туннель, гравитация теперь замедлит его обратно, так что вы сможете легко найти объект на другой стороне. 9{24}~\mbox{кг}\).

См. «Набор Давида» для ознакомления с теоремой Гаусса и ее приложениями.

Цитировать как: Закон Гаусса. Brilliant.org . Извлекаются из https://brilliant.org/wiki/gauss-law/

Закон Гаусса — приложения, вывод, задачи по теореме Гаусса

Закон Гаусса  утверждает, что полный электрический поток, выходящий из замкнутой поверхности, равен заключенному заряду разделить на диэлектрическую проницаемость. Электрический поток в области определяется как электрическое поле, умноженное на площадь поверхности, спроецированной на плоскость и перпендикулярную полю.

JEE Main 2021 LIVE Physics Paper Solutions 24 февраля Shift-1 На основе памяти

Содержание:

• Что такое закон Гаусса?
• Формула
• Теорема Гаусса
• Приложения
• Часто задаваемые вопросы
• Проблемы

 

Что такое закон Гаусса?

Согласно закону Гаусса, полный поток, связанный с замкнутой поверхностью, в 1/ε ₀ умножает на заряд, заключенный на замкнутой поверхности.

\(\begin{array}{l}\oint{\vec{E}.\vec{d}s=\frac{1}{{{\in}_{0}}}q}\end{массив } \)

Например, точечный заряд q помещен внутри куба с ребром «a». Теперь, согласно закону Гаусса , поток через каждую грань куба равен q/6ε ₀ .

Электрическое поле является основной концепцией знаний об электричестве. Как правило, электрическое поле поверхности рассчитывается с применением закона Кулона, но для расчета распределения электрического поля на замкнутой поверхности нам необходимо понимать концепцию закона Гаусса. Это объясняет электрический заряд, заключенный в замкнутом пространстве, или электрический заряд, присутствующий в замкнутой замкнутой поверхности.

Формула закона Гаусса

Согласно теореме Гаусса, общий заряд, заключенный в замкнутой поверхности, пропорционален полному потоку, заключенному в этой поверхности. Следовательно, если ϕ – это полный поток, а ϵ ₀   – электрическая постоянная, то общий электрический заряд Q, заключенный на поверхности, равен;

Q =  ϕ ϵ ₀

Формула закона Гаусса выражается формулой;

ϕ = Q/ϵ ₀

Где,

Q = общий заряд на данной поверхности,

ε ₀ = электрическая постоянная.

⇒ Читайте также:  Эквипотенциальная поверхность

Теорема Гаусса

Чистый поток через закрытую поверхность прямо пропорционален чистому заряду в объеме, ограниченном закрытой поверхностью.

Φ = → E.d → A = q _net /ε ₀

Проще говоря, теорема Гаусса связывает «поток» силовых линий электрического поля (поток) с зарядами внутри замкнутой поверхности. Если заряды не окружены поверхностью, то чистый электрический поток остается нулевым.

Это означает, что количество линий электрического поля, входящих в поверхность, равно количеству силовых линий, выходящих из поверхности.

Утверждение теоремы Гаусса также дает важное следствие:

Электрический поток от любой замкнутой поверхности возникает только из-за источников (положительных зарядов) и стоков (отрицательных зарядов) электрических полей, окруженных поверхностью. Любые заряды вне поверхности не вносят вклада в электрический поток. Кроме того, только электрические заряды могут выступать в качестве источников или поглотителей электрических полей. Изменение магнитных полей, например, не может действовать как источник или поглотитель электрического поля.

Закон Гаусса в магнетизме

Чистый поток для поверхности слева отличен от нуля, так как он содержит чистый заряд. Чистый поток для поверхности справа равен нулю, поскольку она не содержит никакого заряда.

⇒ Примечание: Закон Гаусса является лишь переформулировкой закона Кулона. Если вы примените теорему Гаусса к точечному заряду, заключенному в сферу, вы легко получите закон Кулона.

Применение закона Гаусса

1. 9{3/2}}}\end{массив} \)

. В центре x = 0 и E = 0.

2. В случае бесконечной линии заряда на расстоянии «r». E = (1/4 × πrε ₀ ) (2π/r) = λ/2πrε ₀ . Где λ — линейная плотность заряда.

3. Напряженность электрического поля вблизи плоского слоя заряда равна E = σ/2ε ₀ К, где σ — поверхностная плотность заряда.

4. Напряженность электрического поля вблизи плоского заряженного проводника E = σ/Kε ₀ в среде с диэлектрической проницаемостью K. Если диэлектрической средой является воздух, то E _air = σ/ε ₀ .

5 . Поле между двумя параллельными пластинами конденсатора равно E = σ/ε ₀ , где σ — поверхностная плотность заряда.

Применение закона Гаусса — Видеоурок

Электрическое поле, вызванное бесконечным проводом — применение закона Гаусса

Рассмотрим бесконечно длинную линию заряда с зарядом на единицу длины, равным λ. Мы можем воспользоваться цилиндрической симметрией этой ситуации. Согласно симметрии, все электрические поля направлены радиально от линии заряда, и нет компонента, параллельного линии заряда.

Мы можем использовать цилиндр (с произвольным радиусом (r) и длиной (l)) с центром на линии заряда в качестве нашей поверхности Гаусса.

Применение закона Гаусса – электрическое поле, создаваемое бесконечным проводом

Как вы можете видеть на приведенной выше диаграмме, электрическое поле перпендикулярно искривленной поверхности цилиндра. Таким образом, угол между электрическим полем и вектором площади равен нулю и cos θ = 1

Верхняя и нижняя поверхности цилиндра параллельны электрическому полю. Таким образом, угол между вектором площади и электрическим полем равен 90 градусов, а cos θ = 0,

Таким образом, электрический поток возникает только за счет искривленной поверхности

Согласно закону Гаусса,

Φ = → E.d → A

Φ = Φ _{изогнутая} + Φ _{верхняя} + Φ _нижняя

Φ знак равно → E . d → А знак равно ∫E . dA cos 0 + ∫E . dA cos 90° + ∫E . dA cos 90°

Φ знак равно ∫E . дА × 1

Из-за радиальной симметрии искривленная поверхность равноудалена от линии заряда, а электрическое поле на поверхности имеет постоянную величину повсюду.

Φ знак равно ∫E . dA знак равно E ∫dA знак равно E . 2πrl

Чистый заряд, заключенный в поверхности:

q _нетто = λ.l

Использование теоремы Гаусса,

Φ = E × 2πrl = q _net /ε ₀ = λl/ε ₀

E × 2πrl = λl/ε ₀

E = λ/2πrε ₀

⇒ Читайте также:  Электрическая Потенциальная Энергия

Задачи по закону Гаусса

Задача 1: В пространстве в направлении X существует однородное электрическое поле величиной E = 100 Н/Кл. Используя теорему Гаусса, вычислите поток этого поля через плоский квадрат со стороной 10 см, расположенный в плоскости Y-Z. Возьмите нормаль вдоль положительной оси X положительной.

Решение:

Поток Φ = ∫ E.cosθ ds.

Поскольку нормаль к площади указывает вдоль электрического поля, θ = 0,

Кроме того, E является однородным, поэтому Φ = E.ΔS = (100 Н/Кл) (0,10 м) ²  = 1 Н-м ² .

Задача 2:  Большой плоский слой заряда с поверхностной плотностью заряда σ = 2,0 × 10 ^-6 C-m ^-2  лежит в плоскости X-Y. Найти поток электрического поля через круглую площадку радиусом 1 см, лежащую полностью в области, где все x, y и z положительны, и с нормалью к ней, образуя угол 60 ⁰ с осью Z.

Решение:

Электрическое поле вблизи плоского слоя заряда равно E = σ/2ε ₀  в направлении от слоя. В данной области поле направлено по оси Z.

Площадь = πr ² = 3,14 × 1 см ²  = 3,14 × 10 ^-4 м ² .

Угол между нормалью к площади и полем равен 60 ⁰ .

Отсюда, согласно теореме Гаусса, поток 9{2})\frac{1}{2}\end{массив} \)

= 17,5 Н-м ² C ^-1 .

Задача 3: Заряд 4×10 ^-8 Кл равномерно распределен по поверхности сферы радиусом 1 см. Он покрыт концентрической полой проводящей сферой радиусом 5 см.

• Найти электрическое поле в точке на расстоянии 2 см от центра.
• На полую сферу помещен заряд 6 × 10 ^-8 Кл. Найти поверхностную плотность заряда на внешней поверхности полого шара.

Решение:

 

(а) Рассмотрим рисунок (i).

Предположим, нам нужно найти поле в точке P. Проведите концентрическую сферическую поверхность через точку P. Все точки на этой поверхности эквивалентны; по симметрии поле во всех этих точках будет одинаковым по величине и радиальным по направлению.

Поток через эту поверхность }\,}\конец{массив} \)

\(\begin{array}{l}=\oint{EdS}=E\oint{dS}\end{array} \)

= 4π x ²  E.

где x = 2 см = 2 × 10 ^-2 м.

По закону Гаусса этот поток равен заряду q, содержащемуся внутри поверхности, деленному на ε ₀ . Таким образом,

⇒ 4π x ²  E = q/ε ₀  или, E = q/4πε ₀ x ²

= ( 9 × 10 ⁹ ) × [(4 × 10 ^-8 )/(4 × 10 ^-4 )] = 9 × 10 ⁵ Н С ^-1 .

(б) Рассмотрим рисунок (ii).

Проведите поверхность Гаусса через материал полой сферы. Поскольку электрическое поле в проводящем материале равно нулю, поток }{\mathop{S}}\,}\end{array} \)

через эту гауссову поверхность равно нулю.

Согласно закону Гаусса, общий заключенный заряд должен быть равен нулю. Следовательно, заряд на внутренней поверхности полого шара равен 4 × 10 ^-8 С.

Но общий заряд, переданный этой полой сфере, равен 6 × 10 ^-8 Кл. Следовательно, заряд на внешней поверхности будет 10 × 10 ^-8 Кл.

Задача 4: На рисунке показаны три концентрические тонкие сферические оболочки A, B и C радиусов a, b и c соответственно. Оболочки A и C получают заряды q и -q соответственно, а оболочка B заземлена. Найдите заряды на поверхностях B и C.

 

Решение:

Как показано в предыдущем разработанном примере, внутренняя поверхность B должна иметь заряд -q по закону Гаусса. Предположим, что внешняя поверхность B имеет заряд q’.

Внутренняя поверхность C должна иметь заряд -q’ по закону Гаусса. Поскольку суммарный заряд C должен быть равен -q, его внешняя поверхность должна иметь заряд q’ – q. Распределение заряда показано на рисунке.

 

Потенциал на В,

• Благодаря заряду q на A = q/4πε ₀ б,
• Из-за заряда -q на внутренней поверхности B = -q/4πε ₀ б,
• Из-за заряда q’ на внешней поверхности B = q’/4πε ₀ b,
• За счет заряда -q’, на внутренней поверхности C = -q’/4πε ₀ c,
• За счет заряда q’ – q на внешней поверхности C = (q’ – q)/4πε ₀ в.

Суммарный потенциал, VB = q’/4πε ₀ b – q/4πε ₀ c

Должен быть равен нулю, так как корпус B заземлен. Таким образом, q’ = q × b/c

Заряды на различных поверхностях показаны на рисунке:

 

 

Задача 5: Частица массой 5 ​​× 10 ^-6 г удерживается над большим горизонтальным слоем заряда плотностью 4,0 × 10 ^-6 Кл/м ² (рисунок). Какой заряд нужно сообщить этой частице, чтобы при освобождении она не упала? Сколько электронов нужно удалить, чтобы получить этот заряд? Насколько масса уменьшилась из-за удаления этих электронов?

 

Решение:

Электрическое поле перед листом,

E = σ/2ε ₀  = (4,0 × 10 ^-6 )/(2 × 8,85 × 10 ^-12 ) = 2,26 × 10 ⁵ N/C

Если частице придан заряд q, электрическая сила qE действует в направлении вверх. Он уравновесит вес частицы, если

q × 2,26 × 10 ⁵  N/C = 5 × 10 ^-9 кг × 9,8 м/с ²

или, q = [4,9 × 10 ^-8 ]/[2,26 × 10 ⁵ ]С = 2,21 × 10 ^-13 С

Заряд одного электрона равен 1,6 × 10 ^-19 Кл. Количество электронов, которые необходимо удалить;

= [2,21 × 10 ^-13 ]/[1,6 × 10 ^-19 ] = 1,4 × 10 ⁶

Масса уменьшилась за счет удаления этих электронов = 1,4 × 10 ⁶ × 9,1 × 10 ^-31 кг = 1,3 × 10 ^-24 кг.

Задача 6: Две проводящие пластины, А и В, расположены параллельно друг другу. А получает заряд Q1, а В — заряд Q2. Найдите распределение зарядов на четырех поверхностях.

Решение:

 

Рассмотрим поверхность Гаусса, как показано на рисунке (а). Две грани этой замкнутой поверхности полностью лежат внутри проводника, где электрическое поле равно нулю.

Таким образом, поток через эти грани равен нулю. Остальные части замкнутой поверхности, находящиеся вне проводника, параллельны электрическому полю, поэтому поток на этих частях также равен нулю.

Таким образом, полный поток электрического поля через замкнутую поверхность равен нулю. По закону Гаусса полный заряд внутри замкнутой поверхности должен быть равен нулю. Заряд на внутренней поверхности А должен быть равен и противоположен заряду на внутренней поверхности В.

Распределение должно быть таким, как показано на рисунке (b). Чтобы найти значение q, рассмотрим поле в точке P внутри пластины A. Предположим, что площадь поверхности пластины (с одной стороны) равна A.

Используя уравнение E = σ/2ε ₀ , электрическое поле в точке P;

• За счет заряда Q1 – q = (Q1 – q)/2Aε ₀  (вниз),
• Из-за заряда +q = q/2Aε ₀ (вверх),
• За счет заряда -q = q/2Aε ₀  (вниз),
• За счет заряда Q2 + q = (Q2 + q)/2Aε ₀  (вверх).

Суммарное электрическое поле в точке P, создаваемое всеми четырьмя заряженными поверхностями, равно (в направлении вниз)

(Q1 – q)/2Aε ₀ – q/2Aε ₀ + q/2Aε ₀ – (Q2 + q)/2Aε ₀

Поскольку точка P находится внутри проводника, это поле должно быть равно нулю.

Следовательно, Q1 – q – Q2 – q = 0

или q = (Q1 – Q2)/2 . . . . . (и)

Таким образом, Q1 – q = (Q1 + Q2)/2 . . . . . . (ii)

и Q2 + q = [Q1 + Q]2/2

Используя эти уравнения, можно перерисовать распределение, показанное на рисунках (а, б), как на рисунке.

 

 

Этот результат является частным случаем следующего результата. Когда заряженные проводящие пластины размещаются параллельно друг другу, две крайние поверхности получают одинаковые заряды, а обращенные друг к другу поверхности получают равные и противоположные заряды.

Задача 7: Твердый проводящий шар с зарядом Q окружен незаряженной концентрической проводящей полой сферической оболочкой. Пусть разность потенциалов между поверхностью твердого шара и внешней поверхностью полой оболочки равна V. Какой будет новая разность потенциалов между теми же двумя поверхностями, если оболочке придать заряд -3Q?

Решение:

В случае заряженной проводящей сферы

 

В _дюймов = В _с = В _с = 1/4πε ₀

и V _из = 1/4πε ₀

Итак, если a и b — радиусы сферы и сферической оболочки соответственно, то потенциал на их поверхностях будет равен;

Vсфера = 1/4πε ₀  [Q/a] и Vshell = 1/4πε ₀  [Q/b] и так по заданной задаче;

V = V’сфера – V’оболочка = Q/4πε ₀  [1/a – 1/b] = V . . . . . . . (1)

Теперь, когда оболочке придан заряд (-3Q), потенциал на ее поверхности, а также внутри изменится на;

В ₀ = 1/4πε ₀  [ -3Q/b]

Так что теперь,

V’сфера = 1/4πε ₀  [Q/a + V ₀ ] и V’оболочка = 1/4πε ₀  [Q/b + V ₀ ]

Следовательно, V’сфера – V’оболочка = Q/4πε ₀  [1/a – 1/b] = V [из уравнения (1)]

т. е. если внешней оболочке придать какой-либо заряд, то разность потенциалов между сферой и оболочкой не изменится.

Это связано с тем, что при наличии заряда на внешней оболочке потенциал везде внутри и на поверхности оболочки изменится на одинаковую величину, и, следовательно, разность потенциалов между сферой и оболочкой останется неизменной.

Задача 8: Очень маленький шар массой 80 г, имеющий заряд q, удерживается на высоте 9 м вертикально над центром неподвижного непроводящего шара радиусом 1 м, несущего равный заряд q. Когда его отпускают, он падает до тех пор, пока не будет отброшен непосредственно перед тем, как вступит в контакт со сферой. Рассчитайте заряд q. [г = 90,8 м/с ² ]

Решение:

Имея в виду, что здесь меняется как электрическая, так и гравитационная потенциальная энергия, а для внешней точки заряженный шар ведет себя так, как если бы весь его заряд был сосредоточен в его центре.

Применяя закон сохранения энергии между начальным и конечным положением, мы имеем

 

1/4πε ₀  × (q. q/9) + мг × 9 = (1/4πε ₀ ) x(q ² /1) + мг × 1

или, q ² = (80 × 10 ^-3 × 9,8)/10 ⁹  = 28 мкКл.

Закон Гаусса и проводники – Краткие заметки для быстрого повторения

Закон Гаусса и его приложения – Видеоурок

Решенные вопросы по закону Гаусса

Как

закон Гаусса связан с законом Кулона ?

Одно из фундаментальных соотношений между двумя законами заключается в том, что закон Гаусса можно использовать для вывода Закон Кулона и наоборот. Далее мы можем сказать, что закон Кулона эквивалентен закону Гаусса, что означает, что они почти одно и то же. Хотя это соотношение широко обсуждается в электродинамике, мы рассмотрим его вывод на примере.

Возьмем точечный заряд q. Теперь, если мы применим закон Кулона, генерируемое электрическое поле определяется как:

E = ккв/р ²

, где k=1/4πϵ0. Если мы возьмем сферу радиуса (r) с центром на заряде q. Теперь для поверхности S этой сферы будем иметь:

В конце уравнения видно, что оно относится к закону Гаусса. В общем, мы можем определить связь между законом Гаусса и законом Кулона, выведя сферическую симметрию электрического поля и выполнив интегрирование.

Как выбрать подходящую поверхность Гаусса для различных случаев?

Чтобы выбрать подходящую гауссову поверхность, мы должны принять во внимание положение о том, что отношение заряда к диэлектрической проницаемости определяется (двумерным) поверхностным интегралом по симметрии электрического поля распределения заряда. Нам нужно знать три разных случая.

• Сферический, когда распределение заряда сферически симметрично.
• Цилиндрический, когда распределение заряда цилиндрически симметрично.
• Дот, когда распределение заряда имеет трансляционную симметрию вдоль плоскости.

Мы можем выбрать размер поверхности в зависимости от того, где мы хотим вычислить поле. Теорема Гаусса полезна для нахождения поля, когда существует определенная симметрия, поскольку она говорит нам, как поле направлено.

Как электрический поток связан с законом Гаусса?

Когда мы говорим о связи между электрическим потоком и законом Гаусса, закон гласит, что чистый электрический поток на замкнутой поверхности будет равен нулю, если объем, определяемый поверхностью, содержит чистый заряд.

Чтобы установить соотношение, мы сначала рассмотрим закон Гаусса.

Если мы возьмем закон Гаусса, он будет представлен как: 

Φ _E  = Q/ε _o

Здесь,

• Φ _E = электрический поток через замкнутую поверхность S, охватывающую любой объем V.
• Q = общий заряд, заключенный в V,
• ε _o = электрическая постоянная.

Между тем электрический поток Φ _E теперь можно определить как поверхностный интеграл электрического поля. Это дается как:

Φ _E = ∫∫ E . дА

Здесь,

• E = электрическое поле.
• dA = вектор, представляющий бесконечно малый элемент площади поверхности.

Примечательно, что поток рассматривается как интеграл электрического поля. Это отношение или форма закона Гаусса известна как интегральная форма.

Какова дифференциальная форма теоремы Гаусса?

Дифференциальная форма закона Гаусса связывает электрическое поле с распределением заряда в конкретной точке пространства. Чтобы уточнить, согласно закону, расходимость электрического поля (E) будет равна объемной плотности заряда (p) в конкретной точке. Он представлен как:

ΔE = ρ/ε _или

Здесь,

ε _o = диэлектрическая проницаемость свободного пространства.

Как найти электрическое поле по закону Гаусса?

Обычно закон Гаусса используется для определения электрического поля распределения заряда с симметрией. Есть несколько шагов, связанных с решением проблемы электрического поля с этим законом. Они следующие:

1. Во-первых, мы должны определить пространственную симметрию распределения заряда.
2. Следующий шаг включает в себя выбор правильной поверхности Гаусса с той же симметрией, что и распределение заряда. Следует также выявить его последствия.
3. Вычислить интеграл Φ _s E по поверхности Гаусса, а затем вычислить поток через поверхность.
4. Найдите количество заряда на поверхности Гаусса.
5. Оценить электрическое поле распределения заряда.

Однако учащиеся должны помнить о трех типах симметрии, чтобы определить электрическое поле. Типы симметрии:

• Сферическая симметрия
• Цилиндрическая симметрия
• Плоская симметрия

Расчеты неподходящих систем координат должны выполняться вместе с правильной гауссовой поверхностью для конкретной симметрии.

Часто задаваемые вопросы о законе Гаусса

Можно ли применить закон Гаусса ко всем поверхностям?

Для любой замкнутой поверхности и для любого распределения зарядов справедлив закон Гаусса.

Можно ли применить закон Гаусса к неоднородному электрическому полю?

Закон Гаусса можно применять к однородным и неоднородным электрическим полям.

Состояние Закон Гаусса.

Согласно закону Гаусса, суммарный поток электрического поля на замкнутой поверхности прямо пропорционален заключенному заряду.

От чего зависят линии электрического поля?

Закон Гаусса интерпретируется в терминах электрического потока через поверхность. Электрический поток через поверхность представляет собой число силовых линий, проходящих нормально через поверхность. Электрический поток зависит от заряда, окружающего поверхность.

Когда поток через поверхность считается положительным или отрицательным?

Поток через поверхность считается положительным, если линии потока направлены наружу, или отрицательным, если поток направлен внутрь.

Что называется поверхностью Гаусса?

Поверхность Гаусса – это поверхность, через которую рассчитывается электрический поток.

alexxlab

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт

Рубрики

• Прост
• Радио
• Разное
• Своими руками
• Советы
• Схем
• Схемы
• Транзист
• Транзисторы
• Электрон
• Электроника

Поле	Интегральная форма	Дифференциальная форма
Гравитационная\(\hspace{20mm}\)	\overcright 4 \pi G M\)\(\hspace{20mm}\)	\( \nabla \cdot \overrightarrow{g} =-4 \pi G \rho \)
Магнитный	\(\oint \ overrightarrow{B} \cdot d \overrightarrow{A} = 0\)	\(\nabla \cdot \overrightarrow{B} = 0 \)