феномен возникающий в индуцированном поле
Содержание
- 1 Обоснование явления
- 2 Направление действия магнитного поля
- 3 Явление самоиндукции
- 3.1 Общие положения
- 3.2 Основные величины и наименования измеряемых единиц
- 4 Общая теория электромагнитного поля
- 4.1 Фундаментальные основания
- 4.2 Работа, производимая силами в вихревом поле
- 5 Видео
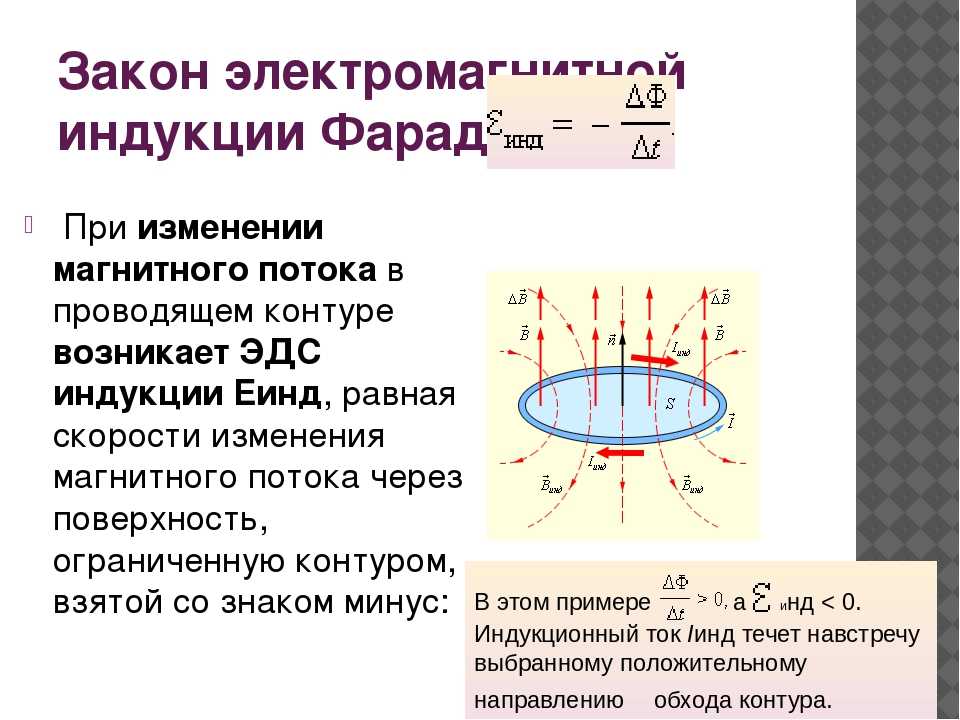
В начале 19-го века учёным М.Фарадеем при проведении опытов с проводящими материалами был открыт интересный феномен, который заключался в следующем. При размещении в магнитном поле проводящей рамки наблюдалось протекание тока в ней, величина которого возрастала по мере увеличения скорости её перемещения. Этот эффект был назван явлением электромагнитной индукции, а создаваемое проводником собственное поле – индуцированным.
Эффект индукции
Таким образом, явление электромагнитной индукции наблюдается всегда, когда замкнутый на нагрузку проводник перемещается во внешнем магнитном поле. Аналогичное явление можно было наблюдать, если оставить рамку неподвижной, а изменять величину внешнего магнитного поля электромагнитной индукции (подносить постоянный магнит к рамке или отодвигать его).
Аналогичное явление можно было наблюдать, если оставить рамку неподвижной, а изменять величину внешнего магнитного поля электромагнитной индукции (подносить постоянный магнит к рамке или отодвигать его).
Обоснование явления
В качестве теоретического обоснования того, в чем состоит явление электромагнитной индукции, открывшим его учёным М.Фарадеем была предложена следующая трактовка:
- При размещении рамки в поле магнита её начинают пронизывать линии, перпендикулярные её плоскости или направленные под определённым углом к ней;
- При её вращении число этих линий или напряжённость магнитного поля (его поток) изменяется, что приводит к появлению ЭДС на концах проводника;
- Величина этой силы прямо пропорциональна скорости перемещения проводящей рамки, а знак определяется направлением её вращения.
Изменять напряженность поля допускается и при неподвижной рамке, но для получения того же эффекта в этом случае придётся перемещать около неё сам магнит.
Направление индукционного тока
Для количественного представления открытого явления и оценке действующей магнитной силы учёным было введено понятие потока через заданную поверхность с общей площадью S. Оно вычисляется следующим образом:
F=B S cos а.
Обратите внимание! Вектор индукции магнитного поля всегда совпадает по направлению с указателем стрелки компаса, помещённого между полюсами.
Для оценки величины индукции «В» введена специальная единица измерения, имеющая в системе СИ наименование Тесла (по фамилии знаменитого естествоиспытателя). На основании всех приведённых ранее выкладок индукция определяется таким образом:
B=F/ S cos а.
Сравните её с приведённой выше формулой.
Направление действия магнитного поля
Линии магнитной индукции
Согласно проверенному на практике правилу (его называют правилом буравчика), определить направление действия вектора поля можно очень просто, если воспользоваться следующим простым пояснением.
Если вворачивать мнимый буравчик в сторону протекания тока в проводе, то вращающий импульс укажет искомое направление (эту закономерность называют иногда правилом «правой руки»).
Для данного эффекта справедливо и обратное утверждение: если правой рукой вращать буравчик в сторону действия магнитного потока, то вектор его вворачивания укажет направление потока электронов, который инициируется этим полем.
Правило «буравчика»
Ещё одна трактовка этой закономерности касается определения вектора силовых линий индуцированного током поля в соленоиде (обычной катушке с намотанной на сердечнике обмоткой). Это правило, подобно предыдущим, может быть представлено следующим образом.
Если сердечник обхватывается правой кистью так, чтобы пальцы ладони были направлены в сторону перемещения потока электронов, то большой палец укажет на вектор действия поля внутри катушки.
Явление самоиндукции
Общие положения
Помимо того, что в замкнутой рамке или проводнике при изменении магнитного потока появляется ЭДС, учёными был обнаружен ещё один эффект. Последний проявляется в том, что протекающий в рамке (витке) ток порождает собственное э/м поле, действующее в направлении, противоположном порождающему его полевому образованию. Это явление впервые было открыто российским учёным Э. X. Ленцем (1804-1865), предложившим ему следующую трактовку:
Последний проявляется в том, что протекающий в рамке (витке) ток порождает собственное э/м поле, действующее в направлении, противоположном порождающему его полевому образованию. Это явление впервые было открыто российским учёным Э. X. Ленцем (1804-1865), предложившим ему следующую трактовку:
- Под действием поля магнита в витке провода возникает так называемый «наведённый» ток;
- Сила индукционного тока и его направление определяются согласно рассмотренным выше правилам;
- Создаваемое током собственное магнитное поле, линии которого действуют через очерченную контуром или витком поверхность, всегда препятствует изменению породившего его поля.
Важно! Полученное в эксперименте явление было названо законом Ленца, являющегося прекрасным подтверждением принципа сохранения энергии.
Явление самоиндукции
Простыми словами открытие Ленца описывается следующим образом:
- При перемещении рамки определённой длины в магнитном поле с фиксированной индукцией на её провод воздействует ЭДС, которая разделяет подвижные электрические заряды;
- Вследствие этого в рамочном проводнике образуется рассчитываемая по закону Максвелла электродвижущая сила индукционного тока;
- Протекающий под её воздействием ток вызывает появление ещё одной ЭДС, направленной в противоположном направлении.
 При этом она препятствует изменению вызвавшего её тока.
При этом она препятствует изменению вызвавшего её тока.
Описанному выше явлению и было присвоено название самоиндукции, в простейшем выражении состоящей в появлении дополнительного поля.
Основные величины и наименования измеряемых единиц
Наведённый в витках катушки магнитный поток пронизывает её строго перпендикулярно и имеет величину, пропорциональную силе тока в ней. Величину, выражаемую как отношение потока поля к силе тока в исследуемом контуре, принято называть его индуктивностью.
За её единицу в классической системе СИ договорились принимать 1 генри. Иными словами, 1 Гн представляет собой индуктивность такого витка или обмотки, в которых при изменении тока на 1 Ампер за 1 секунду наводится ЭДС самоиндукции, по своей величине равная одному Вольту.
В последующие за открытиями М. Максвелла и Х. Ленца годы учёными предпринималось множество попыток объяснения всей совокупности обнаруженных э\м явлений и получения единой теории поля.
Общая теория электромагнитного поля
Фундаментальные основания
Что является источником магнитного поля
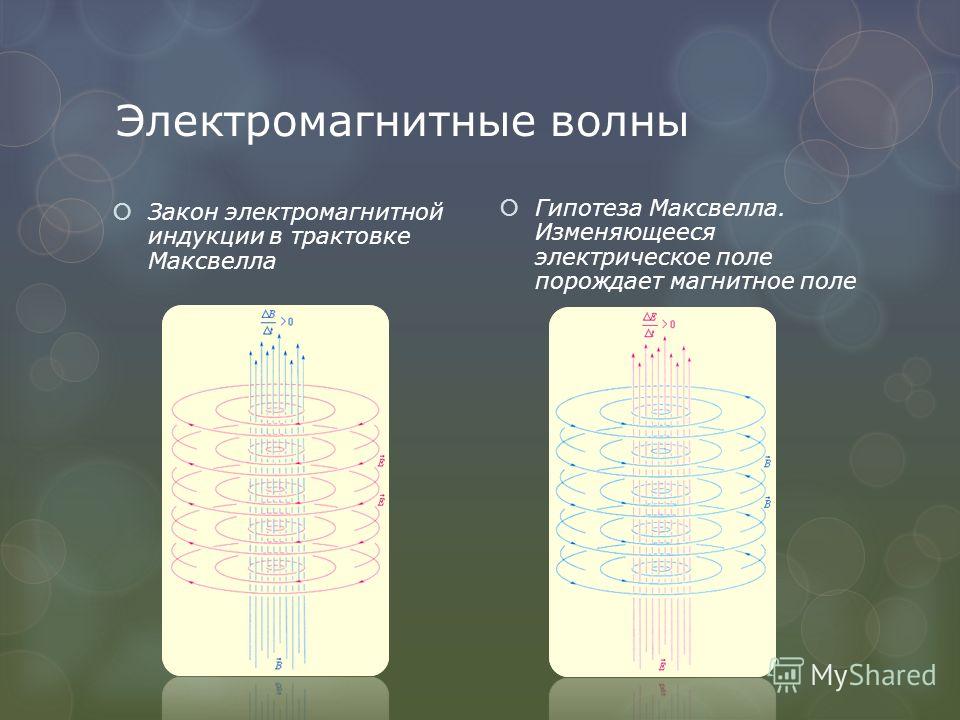
По итогам проведённых исследований Дж.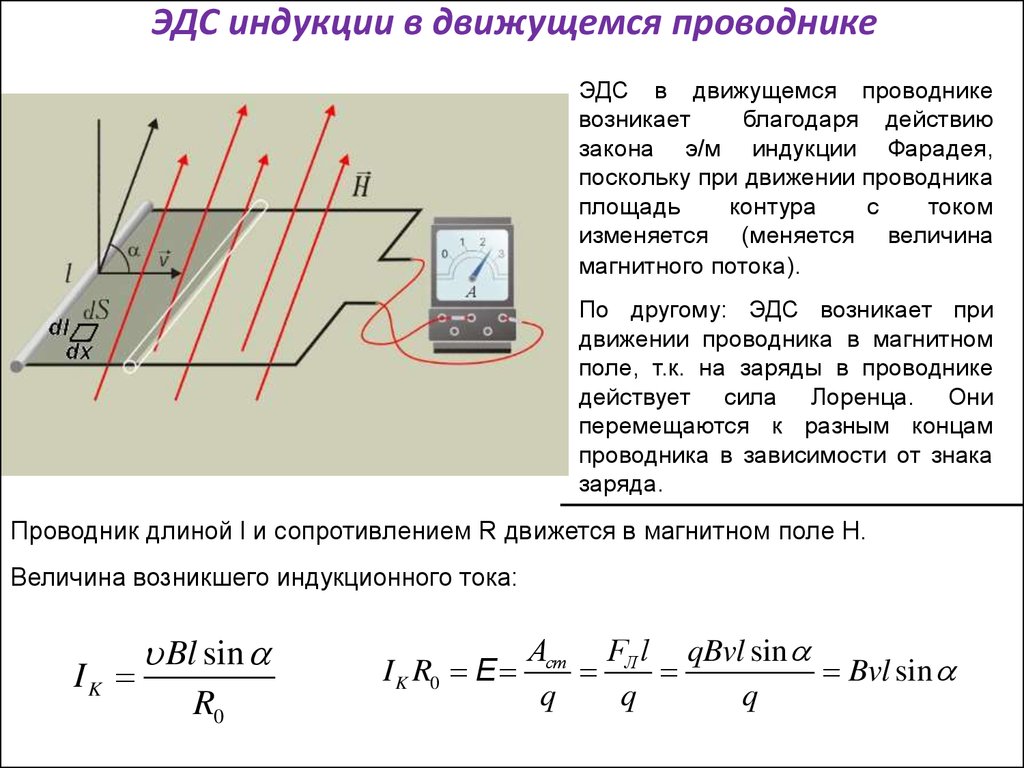 Максвеллом было сформулировано следующее основополагающее предположение, позволяющее разобраться с тем, в чем заключается явление электромагнитной индукции:
Максвеллом было сформулировано следующее основополагающее предположение, позволяющее разобраться с тем, в чем заключается явление электромагнитной индукции:
- Изменение во времени параметров магнитного поля порождает соответствующий этим переменам электрический полевой эффект;
- Такое образование имеет структуру, отличную от электростатического поля, создаваемого неподвижными зарядами;
- Линии напряженности порождённого током электрического образования (подобно тем же характеристикам для всех известных полей) являются замкнутыми;
Обратите внимание! В ряде источников это поле называют «вихревым», что при изучении материала не так важно для понимания его истинной сути.
- Оно воздействует на свободные электрические заряды подобно электростатическому полю, а сила индукционного тока в нём зависит от показателя напряжённости (E).
Работа, производимая силами в вихревом поле
В отличие от всех других электрических полевых образований, работа такого поля на всём протяжении замкнутого контура из проводников не равна нулю. Она имеет вполне конкретное положительное значение, вследствие чего его принято относить к потенциальным полевым структурам.
Она имеет вполне конкретное положительное значение, вследствие чего его принято относить к потенциальным полевым структурам.
Величина такой работы в простейшем случае может быть представлена как результат действия наведённой в замкнутом контуре ЭДС.
В заключение несколько слов о значимости рассмотренных выше открытий, позволяющих понять, что такое электромагнитная индукция. Рассмотренные феномены и явления широко применяются в практической электротехнике и позволяют изготавливать такие полезные для любого человека приборы, какими являются электродвигатели, генераторы и трансформаторы. Этот перечень может быть дополнен большим количеством наименований агрегатов и приборов, работающих за счёт рассмотренных ранее эффектов.
Видео
Явление резонанса
Оцените статью:
Что такое электромагнитная индукция. Закон электромагнитной индукции
История
Около 1830 г. Майкл Фарадей установили, что химические реакции на каждой из двух поверхностей раздела электрод-электролит обеспечивают «место действия ЭДС» для гальванического элемента. То есть эти реакции приводят в движение ток, а не являются бесконечным источником энергии, как предполагалось изначально. [11] В случае разомкнутой цепи разделение зарядов продолжается до тех пор, пока электрическое поле разделенных зарядов не станет достаточным для остановки реакций. Годами ранее, Алессандро Вольта, который измерял контактную разность потенциалов на границе металл – металл (электрод – электрод) своих ячеек, ошибочно полагал, что только контакт (без учета химической реакции) является источником ЭДС.
То есть эти реакции приводят в движение ток, а не являются бесконечным источником энергии, как предполагалось изначально. [11] В случае разомкнутой цепи разделение зарядов продолжается до тех пор, пока электрическое поле разделенных зарядов не станет достаточным для остановки реакций. Годами ранее, Алессандро Вольта, который измерял контактную разность потенциалов на границе металл – металл (электрод – электрод) своих ячеек, ошибочно полагал, что только контакт (без учета химической реакции) является источником ЭДС.
Явление электромагнитной индукции
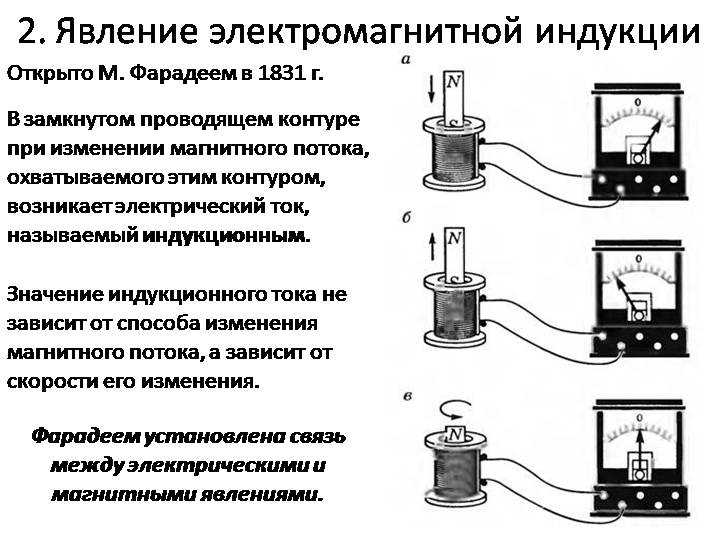
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока.
 При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении. - Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).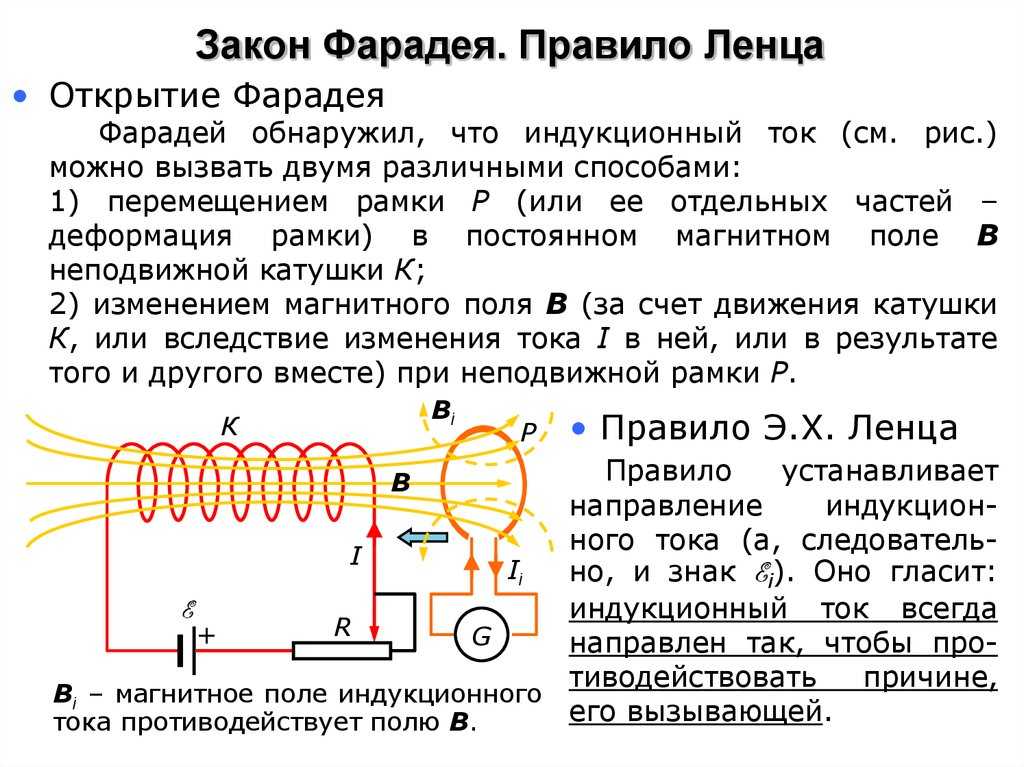
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
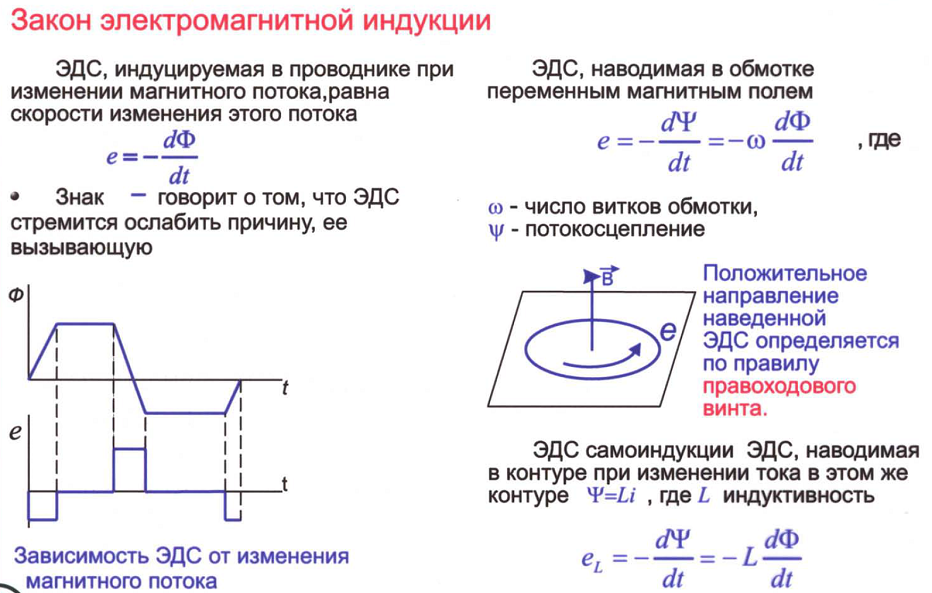
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
| Закон Фарадея Ɛi — ЭДС индукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] |
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
| Закон Фарадея для контура из N витков Ɛi — ЭДС индукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] N — количество витков [-] |
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
| Закон Ома для проводящего контура Ɛi — ЭДС индукции [В] I — сила индукционного тока [А] R — сопротивление контура [Ом] |
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
| ЭДС индукции для движущегося проводника Ɛi — ЭДС индукции [В] B — магнитная индукция [Тл] v — скорость проводника [м/с] l — длина проводника [м] |
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках.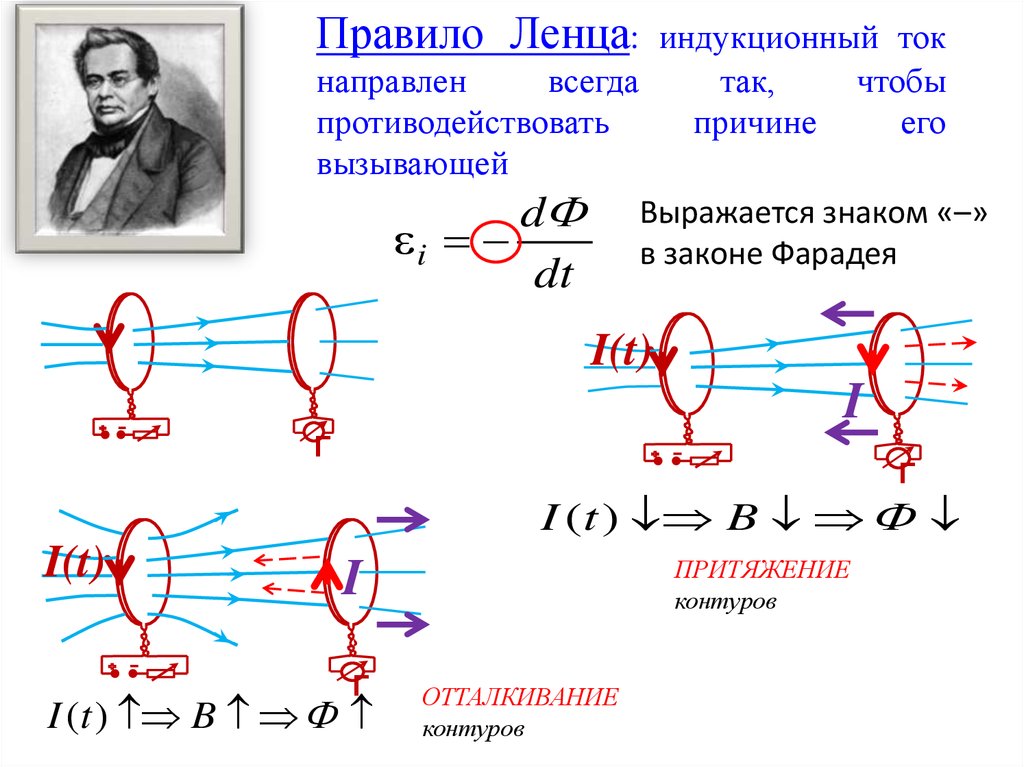 Сила Лоренца играет в этом случае роль сторонней силы.
Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Закон электромагнитной индукции Фарадея
Явление электромагнитной индукции описывается законом Фарадея, первооткрывателя и исследователя этого явления.
Представьте себе простейший контур с подвижной стороной, помещенный в магнитное поле так, чтобы поверхность контура была перпендикулярна линиям магнитного поля (рис.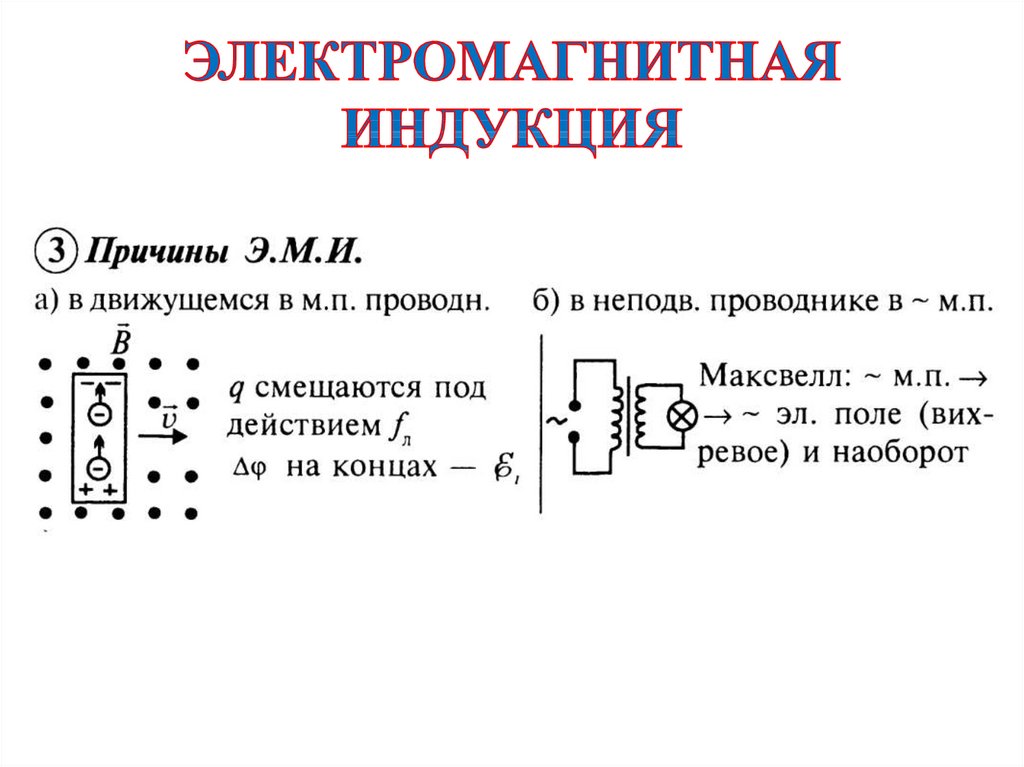 2.).
2.).
Рис. Контур с подвижной стороной (перекладиной)
Мы перемещаем контур со скоростью v вправо. Это изменяет поток магнитной индукции, пронизывающий поверхность, охватываемую контуром, обозначенным на рисунке более темным цветом.
Вспоминая определение магнитного потока индукции, мы можем понять, почему изменяется поток ФB (рис.) – потому что, значение площади S поверхности увеличивается .
Вследствие изменения потока магнитной индукции в рассматриваемой цепи возникнет электродвижущая сила индукции и, следовательно, потечет электрический ток.
Рис. Внешняя сила Fz уравновешивает электродинамическую силу Fed , действующую на контур, движущийся с постоянной скоростью v
В рассматриваемом нами случае легко вычислить работу внешней силы, предполагая постоянную скорость движения контура. Внешняя сила Fz действует в соответствии со смещением контура (и вектором скорости) и в любой момент уравновешивает электродинамическую силу (силу Ампера) Fed, действующую в противоположном направлении (рис. 3.). Согласно определению работы Az = F * Δx где Δx – смещение контура во времени Δt.
3.). Согласно определению работы Az = F * Δx где Δx – смещение контура во времени Δt.
Величина силы Fz равна величине электродинамической силы (силе Ампера) Fed, действующей на контур. Поэтому Az = I * L * B * Δx, где – I сила индукционного тока, протекающего в цепи (и в контуре), L – длина контура (той части, где протекает электрический ток), B – величина магнитной индукции. Давайте введем наше выражение в определение ЭДС индукции. Зная, что q = I * Δt, получаем:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * ΔS / Δt = dФB / dt.
Мы получили интересный результат. Абсолютное значение ЭДС индукции равно скорости изменения потока магнитной индукции.
В рассматриваемом здесь случае поток магнитной индукции изменяется равномерно во времени. В общем случае это совсем не обязательно. Вот почему мы пишем: εинд = ΔФB / Δt , где Δt → 0, который в сокращенном виде записывается как dФB / dt . Это производная магнитного потока по времени.
Хотя наш вывод формулы относится к одному примеру, оказывается, что выведенное отношение является общим. Необходимо сделать лишь небольшую поправку. Это знак минус, который связан с определенной условностью и принципом сохранения энергии.
Необходимо сделать лишь небольшую поправку. Это знак минус, который связан с определенной условностью и принципом сохранения энергии.
Таким образом, закон электромагнитной индукции Фарадея записывается следующим образом: εинд = – dФB / dt и формулируется так:
Для любого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус.
Знак “минус” означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт отражён в правиле Ленца.
Этот закон верен независимо от того, как изменяется поток магнитного поля; когда изменение вызвано относительным движением источника магнитного поля и контура, или когда движения вообще нет, но значение магнитной индукции меняется.
Закон Фарадея – это универсальный, всеобъемлющий и полный математический отчет о явлении электромагнитной индукции.
Вернемся на мгновение к нашему примеру и отметим, что скорость изменения потока, а значит и абсолютное значение ЭДС индукции, в данном случае равна произведению B*L*v.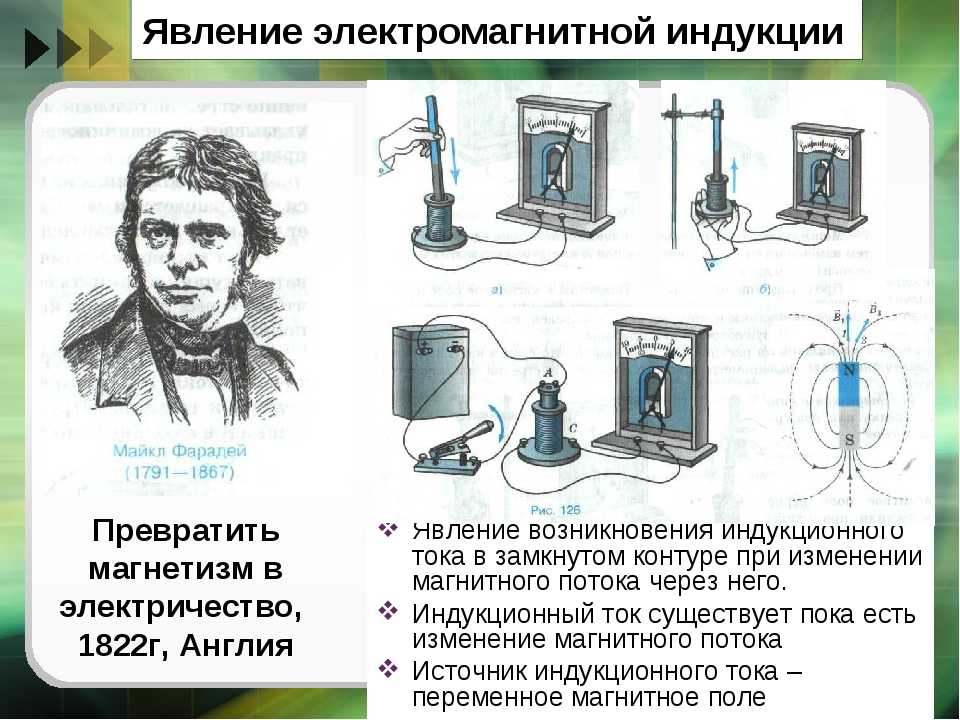 Это следует из ранее написанных соотношений, а именно:
Это следует из ранее написанных соотношений, а именно:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * L * ( Δx / Δt ) = B * L * v .
Правило Ленца.
Правило Ленца позволяет быстро и легко определить направление индукционного тока. Это действительно одна из форм принципа сохранения энергии. Правило гласит, что индукционный ток, наведенный в проводнике под действием переменного потока магнитной индукции, всегда имеет такое направление, что магнитное поле, создаваемое этим индукционным током, противодействует причине (т.е. изменению потока магнитного поля), которая его вызвала.
Обозначение и единицы измерения
Вектор магнитной индукции: формула
ЭДС в формулах обозначают вектором Е. Подразумевается напряженность, которую создают сторонние силы. Соответствующим образом эту величину можно оценивать по разнице потенциалов. По действующим международным стандартам (СИ), единица измерения – один вольт. Большие и малые значения указывают с применением кратных приставок: «микро», «кило» и др.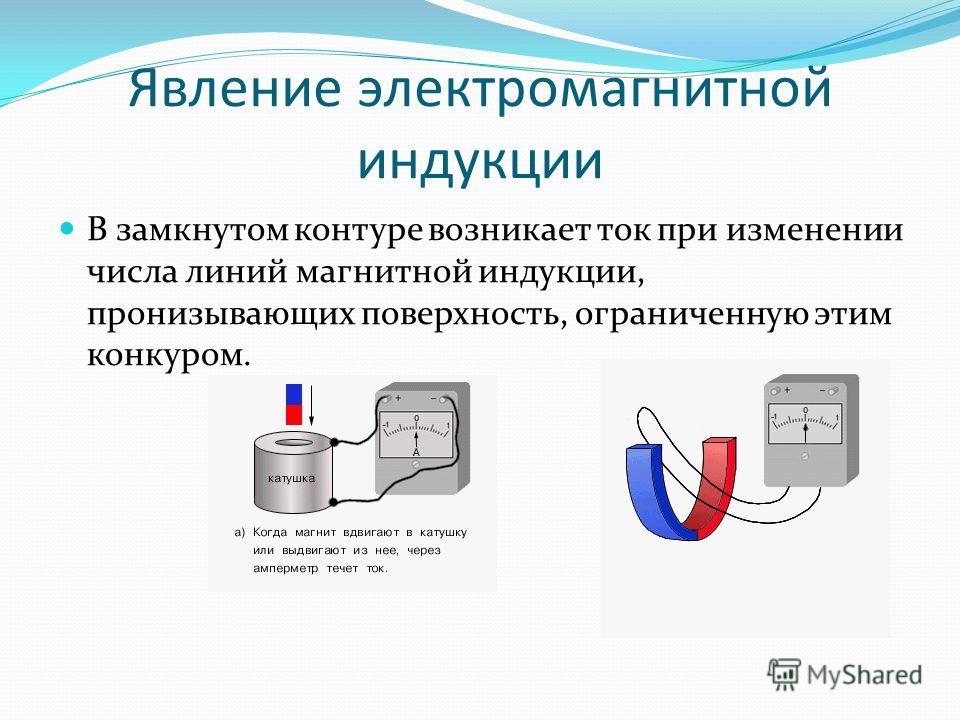
Движение провода в магнитном поле
Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.
Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.
Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.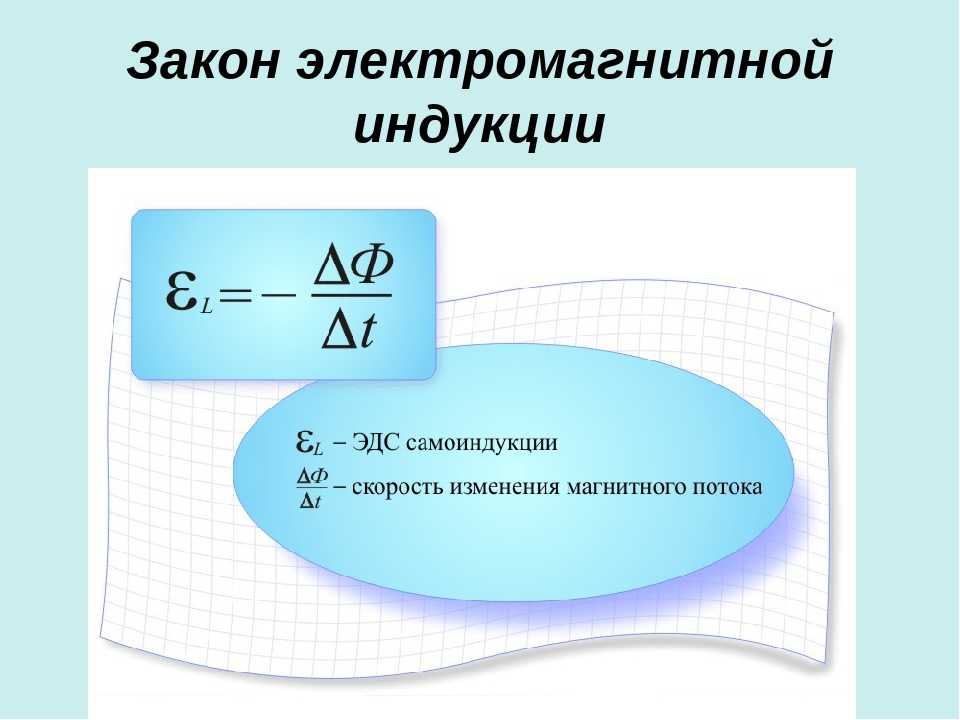
Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.
Вращающаяся катушка
Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).
Согласно формуле, на Ф воздействуют изменения в ситуациях:
- при изменении магнитного потока меняется вектор направления;
- изменяется площадь, заключенная в контур;
- меняется угол.

Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.
На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.
ЭДС самоиндукции
При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.
В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:
Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Где используются разные виды ЭДС
Перемещение проводника в магнитном поле применяют для генерации электроэнергии. Вращение ротора обеспечивают за счет разницы уровней жидкости (ГЭС), энергией ветра, приливами, топливными двигателями.
Различное количество витков (взаимоиндукцию) применяют для изменения нужным образом напряжения во вторичной обмотке трансформатора. В таких конструкциях взаимную связь увеличивают с помощью ферромагнитного сердечника. Магнитную индукцию применяют для возникновения мощной отталкивающей силы при создании ультрасовременных транспортных магистралей. Созданная левитация позволяет исключить силу трения, значительно увеличить скорость передвижения поезда.
Взаимодействие магнита с контуром
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.
Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.
Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .
Расположение полюсов магнита при этом роли не играет .
Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.
Вихревое электрическое поле
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.
Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора. Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.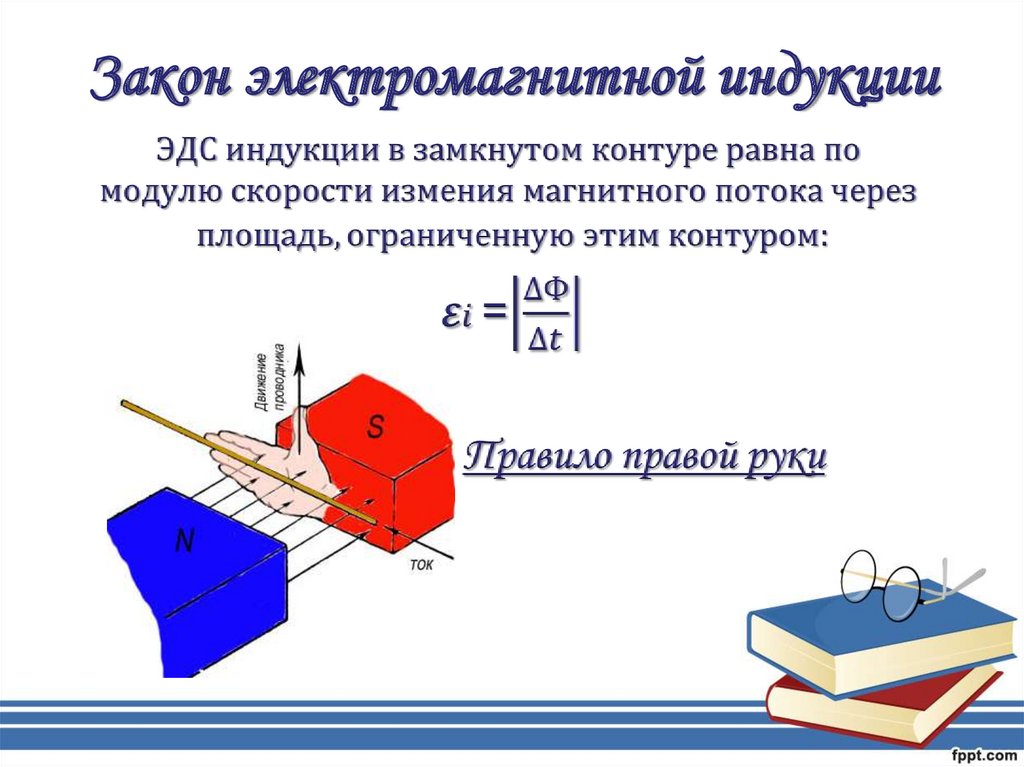
Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора.
Рис. Вихревое электрическое поле при увеличении магнитного поля
Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис).
Рис. Вихревое электрическое поле при уменьшении магнитного поля
Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.
Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.
1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .
Пример задачи
Дано:
Контур в форме квадрата со стороной d = 0,5 м “втягивается” с постоянной скоростью v = 4 м/с в область однородного магнитного поля, величина индукции которого B = 1 Тл (см. рис. 4). Электрическое сопротивление цепи равно R = 2 Ом.
Рис. . Пример задачи по электростатической индукции
Нам нужно найти ответы на следующие вопросы:
a) Когда (в какой момент/моменты) в рамке будет протекать электрический ток?
б) Определите направление этого электрического тока.
(в) Вычислите значение силы, действующей на рамку при ее перемещении в соответствии с направлением вектора скорости. Предположите отсутствие механического сопротивления движению.
Предположите отсутствие механического сопротивления движению.
Решение.
(a) Индукционный ток протекает при изменении потока магнитной индукции через поверхность, охваченную контуром. В ситуации, показанной на рисунке 4, магнитный поток равен нулю и будет оставаться таковым до тех пор, пока правый край контура не коснется границы области магнитного поля. Затем, по мере движения контура, он будет все больше и больше заполняться магнитным полем – магнитный поток будет увеличиваться. Поэтому выполняется условие электромагнитной индукции, т.е. начинает протекать индукционный ток. Как долго? Это легко вычислить, поскольку движение рамы равномерно:
t = d / v = 0,5 / 2 = 0,25 секунд
Ток будет течь до тех пор, пока весь квадрат не войдет в магнитное поле. Тогда поток будет ненулевым, но больше не будет меняться.
б) Воспользуемся правилом Ленца. Мы уже заметили, что поток магнитной индукции при “втягивании” контура в магнитное поле увеличивается. Поэтому индукционный ток будет протекать в таком направлении, чтобы противодействовать увеличению потока.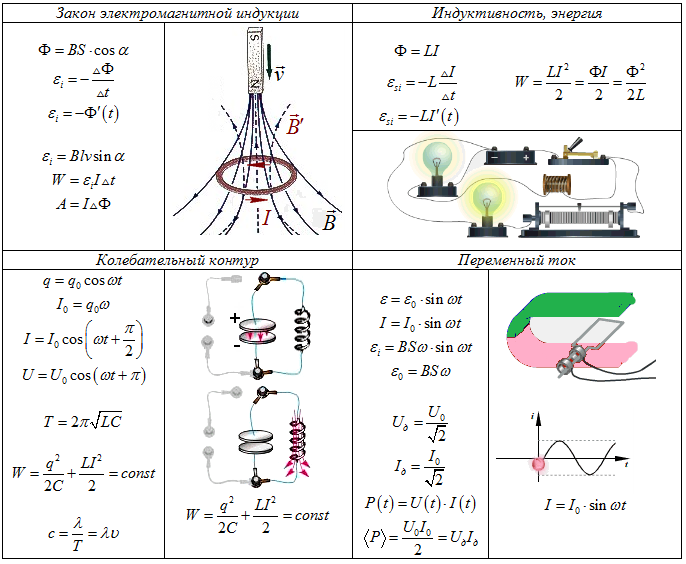
Магнитное поле, создаваемое индукционным током с вектором индукции Bинд, будет противоположно вектору B.
Таким образом, вектор Bинд направлен в нашу сторону. Если расположить таким образом большой палец правой руки, остальные согнутые пальцы покажут направление индукционного тока. Ток будет течь против часовой стрелки.
(в) Снова воспользуемся равномерностью движения рамы. Обратите внимание, что сила, которая действует на рамку при ее перемещении по вектору скорости (например, сила моей руки), не может быть единственной силой, действующей на квадрат. Если бы это было так, он бы двигался с ускорением. Поскольку движение равномерное, это означает, что в каждый момент времени существует сила, которая уравновешивает силу моей руки. Это и есть электродинамическая сила. Ведь теперь в рамке течет ток, и часть его протекает в магнитном поле (см. рис. 5).
Рис.
Красная стрелка показывает направление электрического тока. Электродинамическая сила (сила Ампера) действует слева (я определил ее с помощью правила трех пальцев).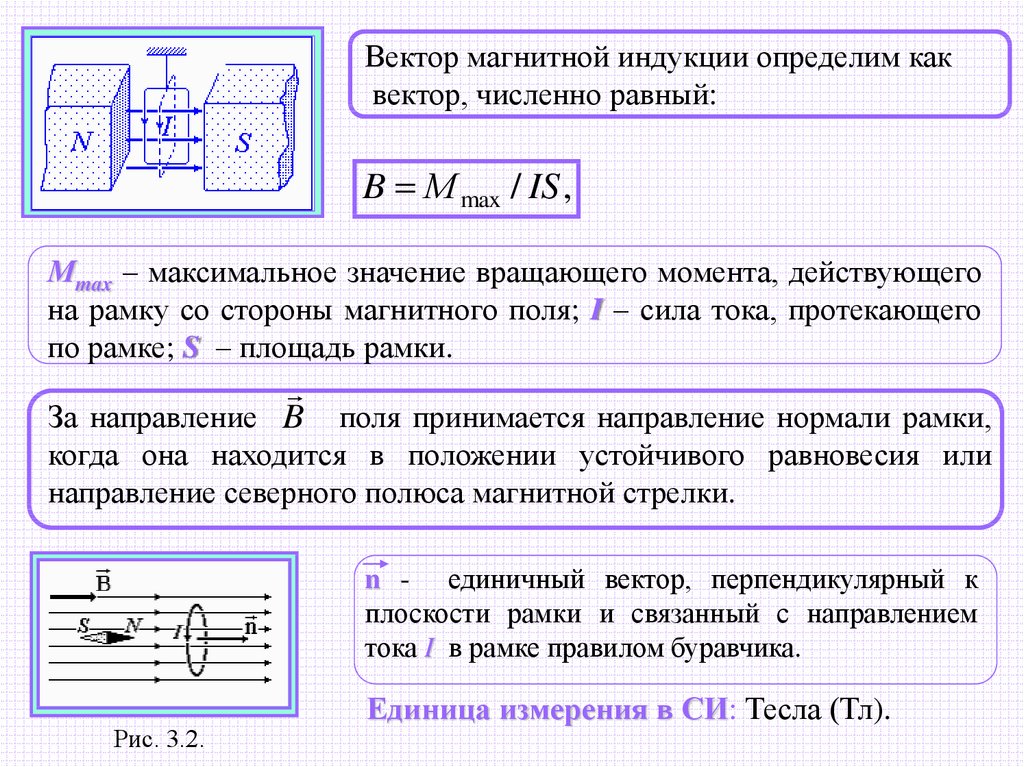 На верхнюю часть рамки и нижнюю часть также действуют электродинамические силы, но они аннулируют друг друга.
На верхнюю часть рамки и нижнюю часть также действуют электродинамические силы, но они аннулируют друг друга.
Подведем итог: электродинамическая сила уравновешивает силу моей руки. Таким образом, я могу сравнить значения обеих сил, то есть F = Fed = B * I * d, где I – сила индукционного тока. Теперь достаточно рассчитать значение силы этого тока. Мы будем использовать закон Фарадея и закон Ома для участка цепи. Давайте начнем с последнего: поскольку нас интересует только значение I, мы напишем
I = εинд / R .
| εинд | = ΔФB / Δt = Δx * d * B / Δt = ( Δx / Δt ) * d * B = v * d * B .
После подстановки в I получаем: I = εинд / R = v * d * B / R .
В конечном итоге искомое значение силы будет выражено через: Fed = B * I * d = ( B * d * v * d * B ) / R = ( B2 * d2 * v ) / R .
Подставляя численные значения получим: Fed = F = ( 12 * 0,52 * 4 ) / 2 = 0,5 Н .
Что мы узнали?
Кратко и понятно явление электромагнитной индукции можно описать, как возникновение электрического тока в проводящем контуре при изменении магнитного потока, проходящего через этот контур. При этом возникающий ток направлен так, чтобы противодействовать причине, его создавшей.
При этом возникающий ток направлен так, чтобы противодействовать причине, его создавшей.
Источники
- https://wikibgu.ru/wiki/Electromotive_Force
- https://fizi4ka.ru/egje-2018-po-fizike/jelektromagnitnaja-indukcija.html
- https://skysmart.ru/articles/physics/zakon-elektromagnitnoj-indukcii
- https://www.asutpp.ru/elektromagnitnaya-induktsiya.html
- https://amperof.ru/teoriya/formula-eds-indukcii.html
- https://odinelectric.ru/knowledgebase/chto-takoe-eds-induktsii-i-kogda-voznikaet
- https://ege-study.ru/ru/ege/materialy/fizika/elektromagnitnaya-indukciya/
- https://obrazovaka.ru/fizika/elektromagnitnaya-indukciya-formula.html
Как вам статья?
Павел
Бакалавр «210400 Радиотехника» – ТУСУР. Томский государственный университет систем управления и радиоэлектроники
Написать
Пишите свои рекомендации и задавайте вопросы
Электромагнитная индукция.Электромагнитные колебания и волны.
 Теория Максвелла
Теория Максвелла1. Индуктивность соленоида с числом витков 120, в котором при силе тока 8 А создается магнитный поток 2·10–3 Вб, равна …
1. 0,0025 2. 0,016 3. 0,03 4. 0,06 5. 0,075
2. Колебательный контур составлен из катушки с индуктивностью L и конденсатора с электроемкостью С = 4· 10-5 Ф. Конденсатор зарядили до напряжения u = 2 В, и он начал разряжаться. В некоторый момент времени энергия контура оказалась поровну распределенной между электрическим и магнитным полями, при этом сила тока в катушке равна I = 0,02 А. Индуктивность L катушки равна … мГн
1. 250 2. 200 3. 100 4. 50 5. 12,5
3. Через контур, индуктивность которого 0,02 Гн, течет ток, изменяющийся по закону . Амплитудное значение ЭДС самоиндукции, возникающей в контуре, равно … В.
1. 250 2. 5 3. 0,5 4. 0,02 5.
4. В однородном магнитном поле индукции 1 Тл поступательно и равномерно движется проводник длиной l = 4 см со скоростью υ = 2 м/с. Вектор скорости перпендикулярен направлению магнитного поля. Разность потенциалов на концах проводника равна … В.
1. 8 2. 0,8 3. 0,4 4. 0,08 5. 0,02
5. Колебательный контур имеет индуктивность L = 1,6 мГн, электроемкость С = 0,04 мкФ и максимальное напряжение на зажимах, равное 200 В. Максимальная сила тока в контуре равна … А.
1. 0,04 2. 0,2 3. 1,0 4. 2,0 5. 4,0
6. Напряженность электрического поля между пластинами воздушного конденсатора изменяется со скоростью 2,8·109 В/м·с. Если пластина конденсатора представляет собой квадрат со стороной 1 см, то величина тока смещения составляет … мкА.
1. 2,8 2. 2,5 3. 8,85 4. 7,85 5. 3,14
2,8 2. 2,5 3. 8,85 4. 7,85 5. 3,14
7. Напряжение на обкладках конденсатора в колебательном контуре изменяется по закону (В). Емкость конденсатора 10 мкФ. Индуктивность контура равна … мГн.
1. 1,0 2.2,75 3. 3,7 4. 5,0 5. 5,1
8. Система уравнений Максвелла для электромагнитного поля:
справедлива …
1. в отсутствие заряженных тел и токов проводимости
2. в отсутствие токов проводимости
3. в отсутствие заряженных тел
4. при наличии заряженных тел и токов проводимости
5. при наличии токов смещения
1. 1, 2 2. 2, 3 3. 3, 4 4. 4, 5 5. 3,5
1. 2.3.4.5.
2.3.4.5.
Обобщением основного закона электромагнитной индукции являются уравнения …
1. 5 2. 1 3. 2 и 3 4. 1 и 3 5. 1 и 2
10. Колебательный контур имеет электроемкость С = 25 мкФ, индуктивность L = 0,1 Гн максимальная сила тока в контуре 0,1 А. Максимальное напряжение на обкладках конденсатора … В.
1. 72,0 2. 100,5 3. 3,7 4. 4,5 5. 6,29
11. Конденсатору емкостью 0,4 мкФ сообщают заряд 10 мкКл, после чего он замыкается на катушку с индуктивностью 1 мГн. Максимальная сила тока в катушке равна … А.
1. 0,25 2.0,33 3. 1,25 4. 0,5 5. 0,75
12. Напряженность
электрического поля между пластинами
воздушного конденсатора изменяется со
скоростью 2,8·109 В/м·с.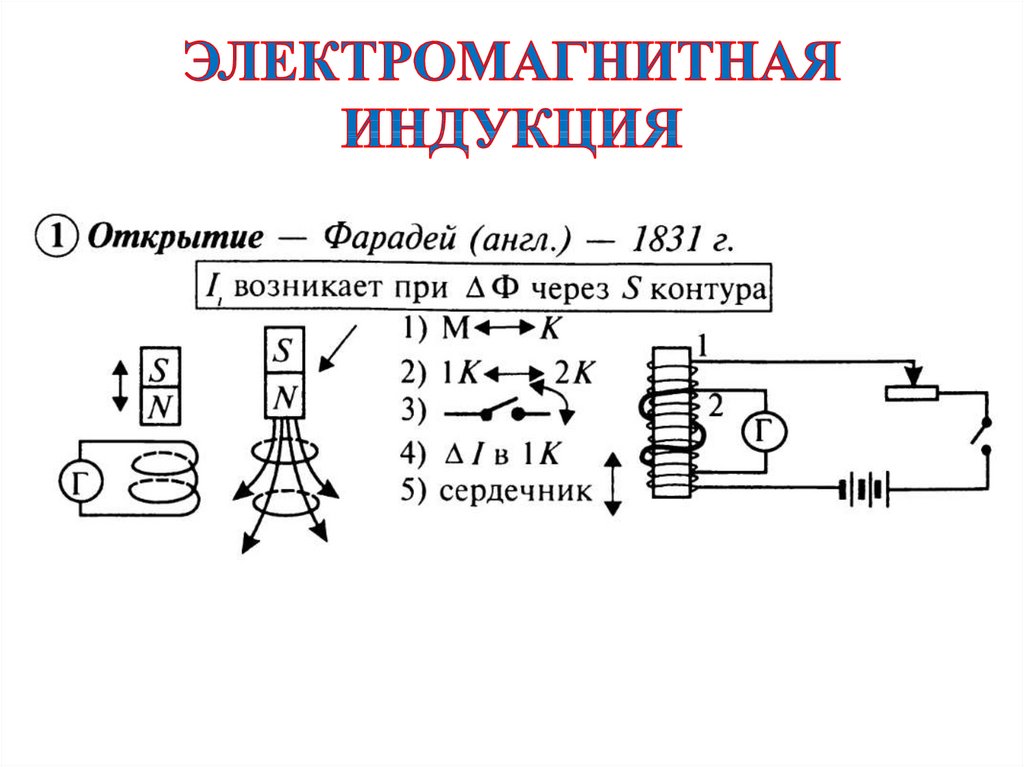 Плотность тока смещения составляет …
мА/м2.
Плотность тока смещения составляет …
мА/м2.
13. Проволочное кольцо радиуса лежит на столе. Сопротивление кольца, вертикальная составляющая индукции магнитного поля Земли –В. Если кольцо повернуть с одной стороны на другую, то заряд, прошедший по кольцу, равен …
1. 2.3.4.5. 0
14. Уравнение Максвелла для пространства имеют следующий вид:
1. 2.3.4.
В этом пространстве …
а. присутствуют токи смещения
б. присутствуют неподвижные электрические заряды
в. присутствует переменное магнитное поле
д. присутствует переменное электрическое поле
1. а, б
2. а, г 3. а, в,
д 4. а, в, г
5. в, б, г
а, г 3. а, в,
д 4. а, в, г
5. в, б, г
15. Колебательный контур состоит из катушки индуктивности L = 6 мкГн и конденсатора емкостью С = 40 пФ. Если максимальный заряд на конденсаторе равен 3·10-9 Кл, то максимальный ток, протекающий в схеме, равен … мА.
1. 124 2. 81 3. 194 4. 245 5. 158
16. Утверждение «В любой точке пространства изменяющееся электрическое поле возбуждает вихревое магнитное поле» раскрывает физический уравнений
1. 2.3.4.5.
1. 1, 2 2. 1, 3 3. 1, 4 4. 2, 3 5. 2, 5
17. Цепь
состоит из катушки индуктивности
и сопротивления 10 Ом. Источник тока
можно отключить, не разрывая цепи. Время,
по истечении которого сила тока уменьшится
до 0,001 первоначального значения, равно
… с.
1. 7 2. 1,4 3. 1 4. 0,7 5. 0,1
18. В кольцо из диэлектрика вдвигают магнит. В диэлектрике возникнут следующие изменения …
1. диэлектрик намагничивается
2. возбуждается вихревое электрическое поле
3. индуцируется электрический ток
4. возбуждается вихревое магнитное поле
5. никаких изменений не произойдет
1. 1, 2 2. 2, 3 3. 1, 4 4. 3, 4 5. 5
19. Изменение электрического заряда конденсатора в колебательном контуре происходит по закону . Колебания электрического тока происходят по закону …
1. 2.3.
4. 5.
20. Уравнения Максвелла для пространства имеют следующий вид
1. 2.3.4.
В этом пространстве
1. отсутствуют токи смещения
2. имеется
переменное магнитное поле
имеется
переменное магнитное поле
3. имеются электрические заряды
4. имеется переменное электрическое поле
5. имеются независимые друг от друга стационарные электрическое и магнитное поля
1. 1, 2 2. 3, 4 3. 3, 5 4. 1, 3, 5 5. 3, 4, 5
21. Индуктивность катушки равна L = 0,2 Гн. При протекании по ней постоянного тока энергия магнитного поля катушки составляет 0,9 Дж. Сила тока в катушке равна … А.
1. 1 2. 3 3. 2 4. 0,2 5. 0,3
22. Уравнение Максвелла для пространства имеют следующий вид…
1. 2.3.4.
В этом пространстве
1. отсутствуют электрические заряды
2. имеются токи смещения
3. имеется стационарное электрическое поле
4. имеется
стационарное магнитное поле
имеется
стационарное магнитное поле
5. имеется переменное магнитное поле
1. 1, 2 2. 1, 3 3. 2, 3, 4 4. 1, 4, 5 5. 3, 4, 5
23. Источник тока замкнут на катушку сопротивлением 10 Ом и индуктивности 1 Гн. При замыкании сети сила тока достигает 0,9 предельного значения через время … с.
1. 0,01 2. 0,1 3. 0,23 4. 0,46 5. 10
24. По двум вертикальным рельсам, верхние концы которых замкнуты резистором сопротивлением , начинает скользить проводящая перемычка массойи длиной. Система находится в магнитном поле. Вектор магнитной индукции перпендикулярен плоскости, в которой расположены рельсы. Сила трения пренебрежимо мала. Установившаяся скорость движения перемычки равна …
1. 2.3.4.5.
25. На рисунке показана ориентация векторов напряженности электрического и магнитногополей в электромагнитной волне. Вектор плотности потока энергии электромагнитного поля ориентирован в направлении …
1. 1 2. 2 3. 3 4. 4
1 2. 2 3. 3 4. 4
26. Вихревой характер магнитного поля выражается формулой …
1. 2.3.4.5.
1. 1, 2 2. 2, 3 3. 1, 2, 4 4. 2, 3, 4 5. 2, 3, 5
27. Индуктивность электромагнита L = 0,4 Гн. При равномерном возрастании силы тока в обмотке на Δ I = 2 А в течении Δ t = 0,04 с, в ней возбуждается среднее значение ЭДС индукции, по модулю равное … В.
1. 20 2. 10 3. 5 4.12,5 5. 7,5
28. Магнитный поток, пронизывающий контур, равномерно увеличился от 2 Вб до 8 Вб за 2 с. ЭДС индукции в контуре равна … В.
1. 53 2. 20 3. 3 4. 2 5. 7,0
29. Колебательный
контур индуктивностью 0,5 мГн резонирует
на длину волны 300 м, если емкость
контура равна … пФ.
1. 0,2 2. 3,02 3. 20 4. 25 5. 51
30. На концах крыльев самолета с размахом 20 м, летящего со скоростью 900 км/ч, возникает ЭДС индукции 0,06 В. Вертикальная составляющая напряженности магнитного поля Земли равна … А/м.
1. 15 2. 7,5 3. 9,6 4. 5,7 5. 8,3
31. Условием возникновения электромагнитных волн является …
1. наличие проводников
2. изменение во времени электрического поля
3. наличие электрического поля
4. наличие неподвижных заряженных частиц
5. изменение во времени магнитного поля
1. 1, 3 2. 3, 5 3. 1, 2, 4 4. 3, 5 5. 2, 5
32. Утверждение
«В любой точке пространства изменяющееся
магнитное поле возбуждает вихревое
электрическое поле» раскрывает физический
смысл уравнений …
Утверждение
«В любой точке пространства изменяющееся
магнитное поле возбуждает вихревое
электрическое поле» раскрывает физический
смысл уравнений …
1. 2.3.4.5.
1. 1, 2 2. 2, 3 3. 1, 2, 3 4. 1, 2, 4 5. 2, 3, 4
33. Магнитный поток, пронизывающий контур, равномерно увеличился от 2 Вб до 8 Вб за 2 с. ЭДС индукции в контуре равна … В.
1. 53 2. 20 3. 3,0 4. 2,5 5. 16,1
34. По обмотке соленоида индуктивностью L = 0,2 Гн течет ток I = 10 А. Энергия магнитного поля соленоида равна … Дж.
1. 5 2. 10 3. 15 4. 20 5. 25
35. Между
полюсами электромагнита создается
магнитное поле с индукцией В = 0,1 Тл.
По проводу длиной l = 70 см,
помещенному перпендикулярно к направлению
магнитного поля, течет ток I = 70 А.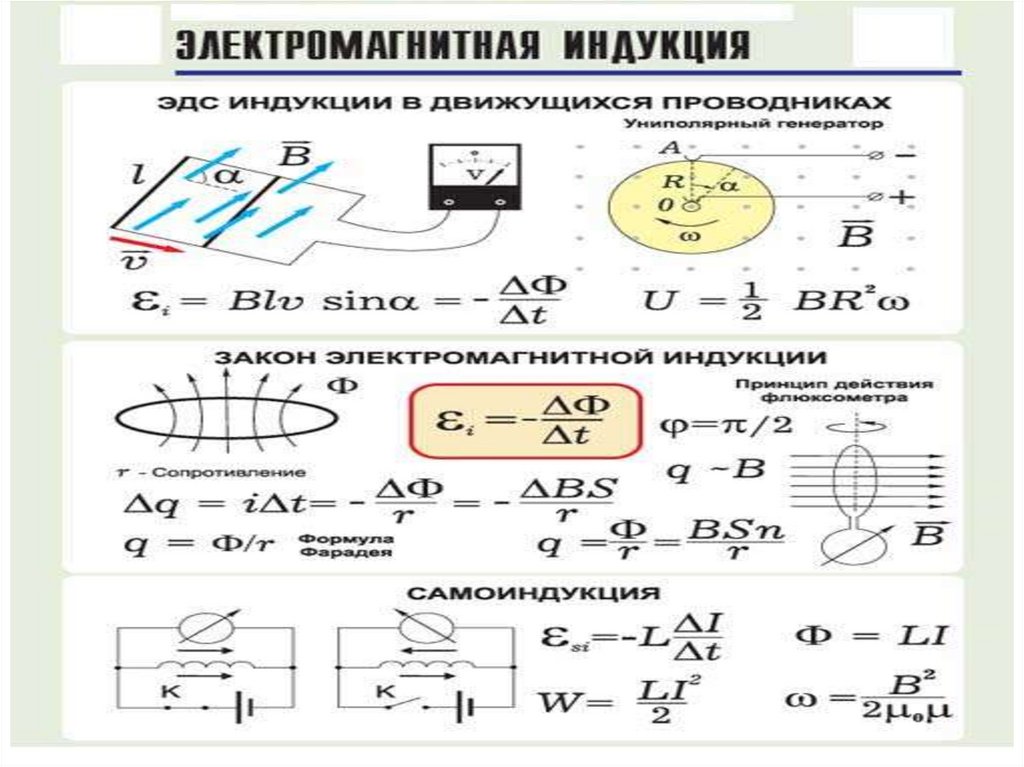 Сила FА,
действующая на провод с током, равна …
Н.
Сила FА,
действующая на провод с током, равна …
Н.
1. 4,9 2. 9,6 3. 10,5 4. 27,1 5. 8,4
36. Сколько витков имеет катушка индуктивность которой L = 1 мГн, если при токе I = 1 А магнитный поток сквозь катушку Ф = 2 мкВб?
1. 1000 2. 2000 3. 500 4. 1500 5. 200
37. Если емкость контура 10 мкФ, индуктивность 1 мГн, то сопротивление, при котором невозможны периодические электромагнитные колебания, равно … Ом.
1. 2 2. 3.4.5. 20
38. В магнитное поле, изменяющееся по закону , помещена квадратная рамка со сторонойа = 10 см. Нормаль к рамке совпадает с направлением изменения поля. ЭДС индукции , возникающая в рамке, изменяется по закону …
1. 2.3.4.5.
2.3.4.5.
39. Колебательный контур состоит из конденсатора емкости и катушки индуктивности. Контур настроен на длину волны … м.
1. 2500 2. 400 3. 250 4. 40 5. 25
40. С помощью реостата равномерно увеличивают силу тока в катушке на в 1 с. Индуктивность катушки. Среднее значение ЭДС самоиндукции равно … В.
1. 60 2. 40 3. 2,7 4. 3,1 5. 4,2
41. Колебательный контур содержит конденсатор емкостью и катушку индуктивностью. Длина волны излучения, генерируемого контуром равна …м.
1. 338 2. 527 3. 627 4. 843 5. 1884
42. Если при неизменном омическом сопротивлении в колебательном контуре увеличить в 2 раза индуктивность катушки, то время релаксации …
1. увеличится в 2 раза 2. уменьшится в 4 раза
3. увеличится в 4 раза 4. уменьшится в 2 раза
43. Амплитуда
колебаний ЭДС индукции, возникающей во
вращающей в магнитном поле проволочной
рамке, при увеличении индукции магнитного
поля в 2 раза и уменьшении угловой
скорости вращения в 2 раза …
Амплитуда
колебаний ЭДС индукции, возникающей во
вращающей в магнитном поле проволочной
рамке, при увеличении индукции магнитного
поля в 2 раза и уменьшении угловой
скорости вращения в 2 раза …
1. увеличится в 2 раза 2. уменьшится в 4 раза
3. уменьшится в 2 раза 4. увеличится в 4 раза 5. не изменится
44. Прямой провод длиной движется в однородном магнитном поле со скоростьюперпендикулярно линиям индукции. Разность потенциалов между концами провода равна. Индукциямагнитного поля равна … Тл.
1. 0,5 2. 0,1 3. 1,0 4. 0,5 5. 0,3
45. При уменьшении в 2 раза амплитуды колебаний векторов напряженностей электрического и магнитного полей плотность потока энергии …
1. уменьшится в 2 раза 2. уменьшится в 4 раза
3. увеличится в
2 раза 4. увеличится в 4 раза
5. останется неизменной
увеличится в
2 раза 4. увеличится в 4 раза
5. останется неизменной
46. Амплитуда колебаний ЭДС индукции, возникающей во вращающейся в магнитном поле проволочной рамке, при увеличении индукции магнитного поля в 2 раза и уменьшении угловой скорости вращения в 2 раза …
1. увеличится в 2 раза 2. уменьшится в 4 раза
3. уменьшится в 2 раза 4. увеличится в 4 раза 5. не изменится
47. В соленоиде сила тока равномерно возрастает от 0 до 100 А в течение 2 с и при этом индуцируется . Энергия магнитного поля соленоида равна … Дж.
1. 0 2. 20 3. 60 4. 80 5. 100
48. Магнитный поток, пронизывающий контур, равномерно увеличивается от 3 Вб до 9 Вб за 3 с. ЭДС индукции в контуре равна .. В.
1. 0 2. 0,3 3. 1,2 4. 2,0 5. 2,5
49. Напряжение
на обкладках конденсатора в колебательном
контуре изменяется по закону
.
Емкость конденсатора 10 мкФ. Индуктивность
контура равна … мГн.
Напряжение
на обкладках конденсатора в колебательном
контуре изменяется по закону
.
Емкость конденсатора 10 мкФ. Индуктивность
контура равна … мГн.
1. 3,0 2. 2,7 3. 2,1 4. 1,8 5. 1,0
50. При уменьшении в 2 раза амплитуды колебаний векторов напряженности электрического и магнитного полей плотность потока энергии …
1. уменьшится в 2 раза 2. уменьшится в 4 раза
3. увеличится в 2 раза 4. увеличится в 4 раза 5. остается неизменной
51. Индуктивность контура зависит от …
1. материала, из которого изготовлен контур
2. силы тока, протекающего в контуре
3. формы и размеров контура, магнитной проницаемости среды
4. скорости изменения магнитного потока сквозь поверхность, ограниченную контуром
52. Следующая система уравнений Максвелла:
справедлива для переменного электромагнитного поля …
1. при наличии
тел и токов проводимости
при наличии
тел и токов проводимости
2. в отсутствие токов проводимости
3. в отсутствие заряженных тел и токов проводимости
4. в отсутствие заряженных тел
53. По длинному соленоиду с немагнитным сердечником сечением , содержащемувитков, течет ток силой. Индукция магнитного поля в центре соленоида. Индуктивность соленоида равна … мГн.
1. 2,1 2. 3,4 3. 7,2 4. 5,5 5. 3,0
54. На рисунке представлены графики, отражающие характер зависимости величины намагниченности вещества (по модулю) от напряженности магнитного поля. Зависимость, соответствующую диамагнетикам …
1. 1 2. 2 3. 3 4. 4
Общая теория электромагнитной индукции в проводящем полупространстве | Международный геофизический журнал
Фильтр поиска панели навигации Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Дж. Т. Уивер
Т. Уивер
Дж. Т. Уивер
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
ОБЪЯВЛЕНИЯ
Geophysical Journal International , том 22, выпуск 1, январь 1971 г., страницы 83–100, https://doi.org/10.1111/j.1365-246X.1971.tb03584.x
Опубликовано:
1 января 1971 г.
История статьи
Получено:
06 июня 1970 г.
Опубликовано:
01 января 1971 г.
Фильтр поиска панели навигации Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Geophysical Journal InternationalЭтот выпускЖурналы РАНГеофизикаКнигиЖурналыOxford Academic Термин поиска на микросайте
Advanced Search
Резюме
Общая теория электромагнитной индукции в проводящем полупространстве внешним магнитным источником разработана по-новому, упрощая и обобщая классическую трактовку А. Т. Прайса. Новыми чертами теории являются систематическое применение интегральных преобразований и использование электрических и магнитных векторов Герца, выровненных по нормали к поверхности проводника. Показано, что решения, связанные с электрическим вектором Герца, соответствуют только свободному затуханию токов внутри проводника, так что вся теория задачи индукции развивается в терминах одной скалярной компоненты магнитного вектора Герца. Общее решение магнитного потенциала Герца, соответствующего индукции произвольным нестационарным источником, получается в виде замкнутого интеграла, включающего только одну неизвестную функцию, которая представляет собой преобразование Фурье магнитного потенциала Герца источника, оцененного на поверхности проводник. Развиты результаты, соответствующие частным случаям апериодических и периодических полей, а также получены явные выражения для векторов электрического и магнитного полей. Общая теория иллюстрируется рассмотрением трех конкретных источников: (i) апериодического магнитного диполя, нормального к поверхности проводника, (ii) периодического магнитного диполя, параллельного поверхности проводника, и (iii) периодического линейного тока, протекающего параллельно поверхности проводника.
Т. Прайса. Новыми чертами теории являются систематическое применение интегральных преобразований и использование электрических и магнитных векторов Герца, выровненных по нормали к поверхности проводника. Показано, что решения, связанные с электрическим вектором Герца, соответствуют только свободному затуханию токов внутри проводника, так что вся теория задачи индукции развивается в терминах одной скалярной компоненты магнитного вектора Герца. Общее решение магнитного потенциала Герца, соответствующего индукции произвольным нестационарным источником, получается в виде замкнутого интеграла, включающего только одну неизвестную функцию, которая представляет собой преобразование Фурье магнитного потенциала Герца источника, оцененного на поверхности проводник. Развиты результаты, соответствующие частным случаям апериодических и периодических полей, а также получены явные выражения для векторов электрического и магнитного полей. Общая теория иллюстрируется рассмотрением трех конкретных источников: (i) апериодического магнитного диполя, нормального к поверхности проводника, (ii) периодического магнитного диполя, параллельного поверхности проводника, и (iii) периодического линейного тока, протекающего параллельно поверхности проводника.
Ссылки
Бхаттачарья
Б.К.
,
1959
.
Электромагнитные поля переходного магнитного диполя на поверхности Земли
,
Геофизика
,
24
,
89
—
108
.
Черчилль
Р. В.
,
1944
.
Современная операционная математика в технике, раздел 71
,
McGraw-Hill Book Co. Inc.
,
Нью-Йорк
.
Эрдейи
А.
, (ред.),
1954
.
Таблицы интегральных преобразований
,
тт. I и II
,
McGraw-Hill Book Co. Inc.
,
Нью-Йорк
.
Гордон
А. Н.
,
1951
.
Электромагнитная индукция в однородном полубесконечном проводнике
,
Кварт. Дж. мех. приложение Мат.
,
4
,
116
–
128
.
Джонс
Д. С.
,
1964
.
Теория электромагнетизма, Раздел 1.10
,
Pergamon Press Ltd.
,
Оксфорд
.
Мейер
Дж.
,
1962
.
Electromagnetische Induktion eines vertikalen magnetischen Dipols über einem leitenden homogenen Halbraum
,
Mitt. Институт Макса Планка. Aeronomie
, Nr. 7.
Цена
А. Т.
,
1950
.
Электромагнитная индукция в полубесконечном проводнике с плоской границей
,
Кварт. Дж. мех. приложение Мат.
,
3
,
385
–
410
.
Цена
А. Т.
Т.
,
1962
.
Теория магнитотеллурических методов с учетом поля источника
,
J. geophys. Рез.
,
67
,
1907
–
1918
.
Куон
К.
,
1963
.
Электромагнитные поля приподнятых диполей на двухслойной Земле
,
Магистр наук. Диссертация
,
Университет Альберты
,
Эдмонтон
.
Подождите
Дж. Р.
,
1951
.
Магнитный диполь над горизонтально стратифицированной Землей
,
Can. Дж. Физ.
,
29
,
577
–
592
.
Подождите
Дж. Р.
,
1953
.
Наведение горизонтальным колеблющимся диполем над проводящей однородной Землей
,
Пер. Являюсь. геофиз. Союз
,
34
,
185
–
188
.
Уорд
С. Х.
,
1967
.
Электромагнитная теория для геофизических приложений
, в
Горная геофизика
,
Том. II
II
, edited by
Hansen
D. A.
Heinrichs
W. E.
Holmer
R. C.
MacDougall
R. E.
Rogers
G. R.
Summer
J. S.
Ward
S. H.
, гл. II (Часть А),
Общество геофизиков-исследователей
,
Талса, Оклахома
.
Этот контент доступен только в формате PDF.
Раздел выпуска:
Статьи
Скачать все слайды
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Оповещение о текущей проблеме
Оповещение о теме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Система астрофизических данных
Резюме объявленийСсылки на статьи по телефону
Последний
Самые читаемые
Самые цитируемые
Нишевая стратегия оптимизации роя частиц для мультимодальной инверсии поверхностных волн
Деформация бесконечного упругого конуса из-за точечного источника давления, закопанного на оси: влияние на вулканическую деформацию
Новые археомагнитные направления от стоянок позднего неолита в провинции Шаньдун, Китай
Гравитационный и магнитный метод быстрой инверсии с перекрестным градиентом на основе подбора функций
Эмпирические сценарии потрясений для Европы: технико-экономическое обоснование
Реклама
Эпизод 414: Электромагнитная индукция | IOPSpark
У учащихся уже есть представление об электромагнитной индукции. В этом эпизоде ваша задача состоит в том, чтобы разработать картину индукции, в которой разрезание линий потока проводником приводит к индуцированной ЭДС или току.
В этом эпизоде ваша задача состоит в том, чтобы разработать картину индукции, в которой разрезание линий потока проводником приводит к индуцированной ЭДС или току.
Краткий обзор урока
Эксперимент для учащихся: провод, магнит, метр
Начните с простого эксперимента, включающего катушку провода и вольтметр. Это даст вам возможность оценить знания, которые учащиеся привнесли в этот раздел.
Эпизод 414-1: Закон Фарадея (Word, 26 КБ)
Обсуждение и демонстрации: эффекты индукции
Хорошей отправной точкой является повторение представлений об электромагнитной индукции, которые должны быть у ваших учащихся до 16-го уровня.
Первые две демонстрации включают перемещение провода в магнитном поле, а затем постоянного магнита в маленькую катушку и из нее. В обоих случаях важно подчеркнуть, что:
Представьте идею резки флюса
. Используйте свои пальцы, чтобы изобразить линии потока; показать, как проводник движется так, чтобы перерезать линии потока.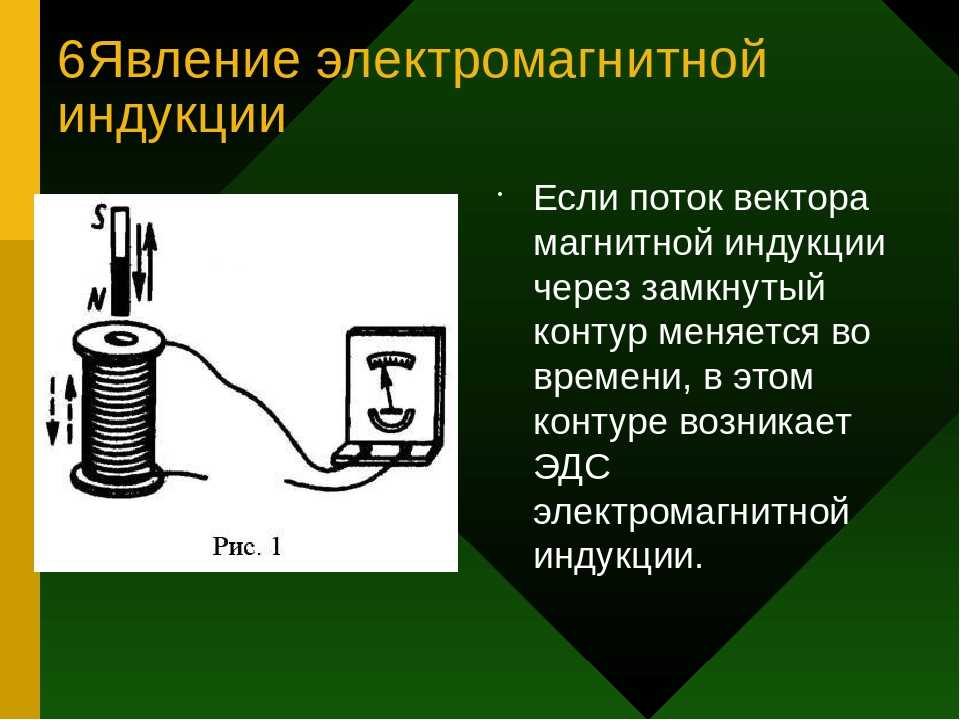 Если вы переместите проводник вдоль линий потока ток не индуцируется.
Если вы переместите проводник вдоль линий потока ток не индуцируется.
Третья демонстрация показывает, что движение не является существенным и что изменение поля вблизи катушки имеет тот же эффект, что и движущийся магнит.
(Демонстрация с динамо-машиной мало что добавляет на данном этапе и может быть отложена до дальнейшего обсуждения генераторов.)
Эпизод 414-2: Электромагнитная индукция (Word, 62 КБ)
Обсуждение: Как
производится электричество?
Демонстрации показали, что , создающий
электричество, использует магнитные поля, но что происходит на самом деле? Ваши ученики уже знают, что на заряды, движущиеся поперек магнитного поля, действует сила (сила B I L ). Теперь металл проводника содержит подвижные заряды, электроны проводимости. Что произойдет с ними, если проводник будет перемещаться поперек магнитного поля?
Рассмотрим проводящий стержень PQ, движущийся с постоянной скоростью v перпендикулярно полю с плотностью потока Б . Электрон (отрицательный заряд 90 565 e 90 566 ) в стержне будет испытывать силу ( 90 565 B 90 566 90 565 e 90 566 90 565 v 90 566 ) (правило левой руки Флеминга), которая подтолкнет его к концу Q. То же верно и для других электронов в стержне. стержень, поэтому конец Q станет отрицательно заряженным, а P останется с положительным зарядом. В результате электрическое поле E накапливается до тех пор, пока сила, действующая на электроны в стержне из-за этого электрического поля ( E e ), не уравновесит силу из-за магнитного поля.
Электрон (отрицательный заряд 90 565 e 90 566 ) в стержне будет испытывать силу ( 90 565 B 90 566 90 565 e 90 566 90 565 v 90 566 ) (правило левой руки Флеминга), которая подтолкнет его к концу Q. То же верно и для других электронов в стержне. стержень, поэтому конец Q станет отрицательно заряженным, а P останется с положительным зарядом. В результате электрическое поле E накапливается до тех пор, пока сила, действующая на электроны в стержне из-за этого электрического поля ( E e ), не уравновесит силу из-за магнитного поля.
E e = B e v
so
E = B v
For a rod of length L
E = V L
Следовательно, ЭДС индукции
E = B L v
Очевидно, что мы не имеем здесь полного тока видим, что более быстрое движение дает большую индуцированную ЭДС.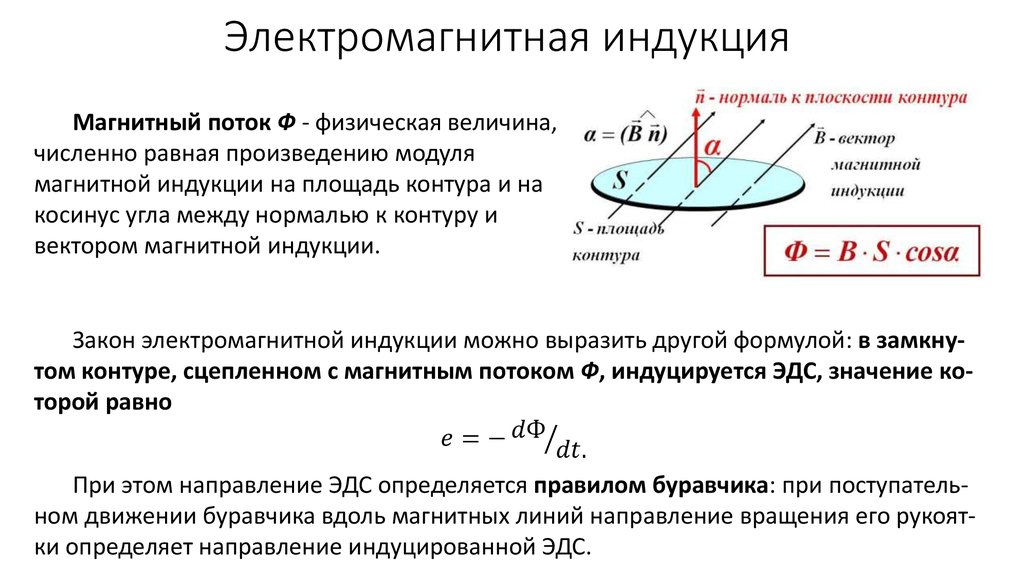
Теперь рассмотрим, что происходит, когда ЭДС вызывает ток во внешней цепи. Для этого представьте, что стержень движется по паре параллельных проводников, которые подключены к внешней цепи.
Теперь ЭДС вызовет протекание тока во внешнем резисторе R. Это означает, что аналогичный ток протекает через сам стержень, создавая магнитную силу BIL влево.
(L теперь представляет собой расстояние между двумя проводниками, вдоль которых движется стержень PQ.) Необходима равная и противоположная сила (справа), чтобы поддерживать движение PQ с постоянной скоростью.
Работа, совершаемая при перемещении стержня, равна энергии, рассеиваемой на резисторе.
За время t стержень проходит расстояние d = v × t
Work done on the rod = B I L v t
Energy dissipated in R = power × time
Energy dissipated in R = ЭДС v t
дающая
B I L V T = EMF V T
или, как и ранее,
E = B
666666666666. что электрическая цепь окружает больше магнитного поля по мере движения стержня и что за одну секунду дополнительная замкнутая площадь составит
что электрическая цепь окружает больше магнитного поля по мере движения стержня и что за одну секунду дополнительная замкнутая площадь составит
v × l .
т.е. ЭДС индукции, E = B × площадь, заметаемая в секунду
E = B A t
Мы уже назвали B плотностью потока, поэтому неудивительно, что величину B × × A можно назвать магнитным потоком Ф .
Таким образом ЭДС индуцирования = F t
ЭДС индуцирования = скорость изменения потока
И в более общем случае
E = d Φ 6 5 t
Как увеличить ЭДС индукции? Обсуждение должно привести к:
Но есть еще одна возможность, это увеличить количество витков провода N в нашей схеме. При этом поток не изменится, но потокосцепление (N × 90 565 F 90 566 ) увеличится. Следовательно, правильнее сказать, что
ЭДС индукции = скорость изменения потокосцепления
E = N × d F d t
Это соотношение известно как закон Фарадея: при изменении цепи индуцированная ЭДС пропорциональна скорости изменения потокосцепления.
Наконец, напомните своим ученикам, что магнитная сила на нашем простом генераторе (a) (b) была направлена так, что стержень замедлился бы, если бы не действовала внешняя сила. Это пример закона Ленца: — направление индуцированной ЭДС таково, что она имеет тенденцию противодействовать движению или изменению, вызывающему его.
Чтобы включить эту идею в нашу формулу, необходимо ввести знак минус, давая;
E = − N × d F d t
Обсуждение: Подробнее о потоке и потокосцеплении
У нас есть две формулы:
Flux, F = B × A
Потокосцепление N F = N B A
При использовании этих формул важно понимать, что B должны располагаться под прямым углом к площади A . Если это не так, то следует использовать составляющую поля, перпендикулярную A .
Единицы:
Напомним, что тесла (T) определяется из F = B I L , поэтому
1 T = 1 N A -1 м -1 .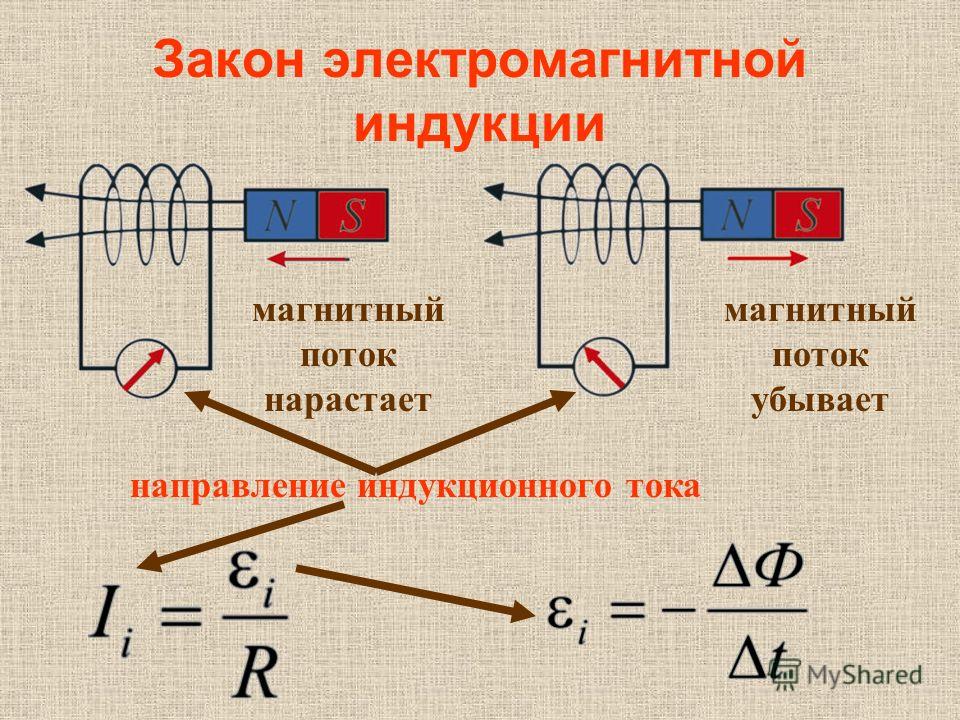
Таким образом, единицами потока являются N A -1 м. Эта единица известна как Вебер (Вб).
Потокосцепление измеряется в витках Вебера (Wb-витках).
Вопросы учащихся: О потокосцеплении
Хотя лучше отложить вопросы о законе Фарадея до тех пор, пока не будет проведена дополнительная экспериментальная работа, взаимосвязь между потоком, плотностью потока и потокосцеплением следует подкрепить парой вопросов.
Эпизод 414-3: Зарисовка структур потока (Word, 269 КБ)
Студенческие эксперименты: исследование индукции
Для подтверждения теории важно, чтобы учащиеся рассмотрели электромагнитную индукцию экспериментально более подробно, чем это было показано в начальной демонстрации. . То, что вы решите делать, будет зависеть от того, какой аппарат доступен.
Предлагаемый здесь эксперимент основан на катушках (120/240 витков), соединенных железными сердечниками. Снова показаны основы закона Фарадея, и есть очень сильное преимущество в трансформаторах.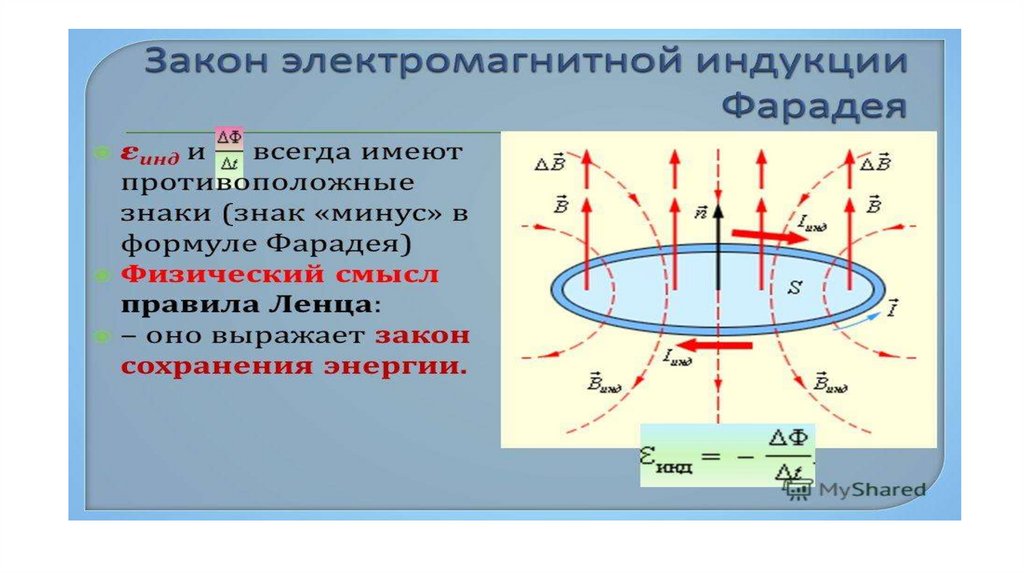
Эпизод 414-4: Изучение электромагнитной индукции (Word, 219 КБ)
Можно провести простой эксперимент (или демонстрацию), пропуская постоянный магнит через катушку провода, подключенную к регистратору данных.
Это ясно показывает, что при движении магнита в катушке на короткое время генерируется ЭДС.
Эпизод 414-5: Магнит, падающий через катушку (Word, 27 КБ)
Демонстрация: Связанные эффекты
Несколько идей для быстрой демонстрации эффектов, связанных с электромагнитной индукцией.
Эпизод 414-6: Быстрая демонстрация электромагнитной индукции (Word, 39 КБ)
Вопросы учащихся: Наведенные ЭДС
Первая ссылка включает в себя качественную работу, наброски графиков и эксперимент с падающим магнитом
Эпизод 414-7: Скорость изменения (Word, 198 КБ)
Некоторые простые расчеты.
Эпизод 414-8: ЭДС в авиалайнере (Word, 34 КБ)
Обсуждение и демонстрации: Вихревые токи
До сих пор индуцированные эффекты наблюдались в проводах с соответствующим изменением потока. Но должен ли дирижер быть
Но должен ли дирижер быть провод
? Ответ заключается в том, что индуцированные токи будут возникать всякий раз, когда изменяется поток, связанный с проводником любой формы или размера. Если проводник не является проводом, то эти наведенные токи называются вихревыми токами
.
Несколько демонстраций показывают эффект. Из этих экспериментов должно стать ясно, что действует закон Ленца, т. е. индуцированные эффекты противодействуют движению, которое их производит. Одним из основных применений вихревых токов является электромагнитное торможение.
При протекании вихревых токов в резистивном металле возникает вихретоковый нагрев. Он находит хорошее практическое применение, т.е. в производстве чистых сплавов, где вихретоковый нагрев металлического тигля заменяет грязную печь
. Чаще всего нагрев доставляет неудобства, так как в электромагнитных машинах расходуется энергия.
Эпизод 414-9: Введение в вихревые токи (Word, 49 КБ)
Эпизод 414-10: Дальнейшие демонстрации вихревых токов (Word, 48 КБ)
Вопросы учащихся: Вихревые токи и закон Ленца
Некоторые описательные работы могут укрепить эти идеи.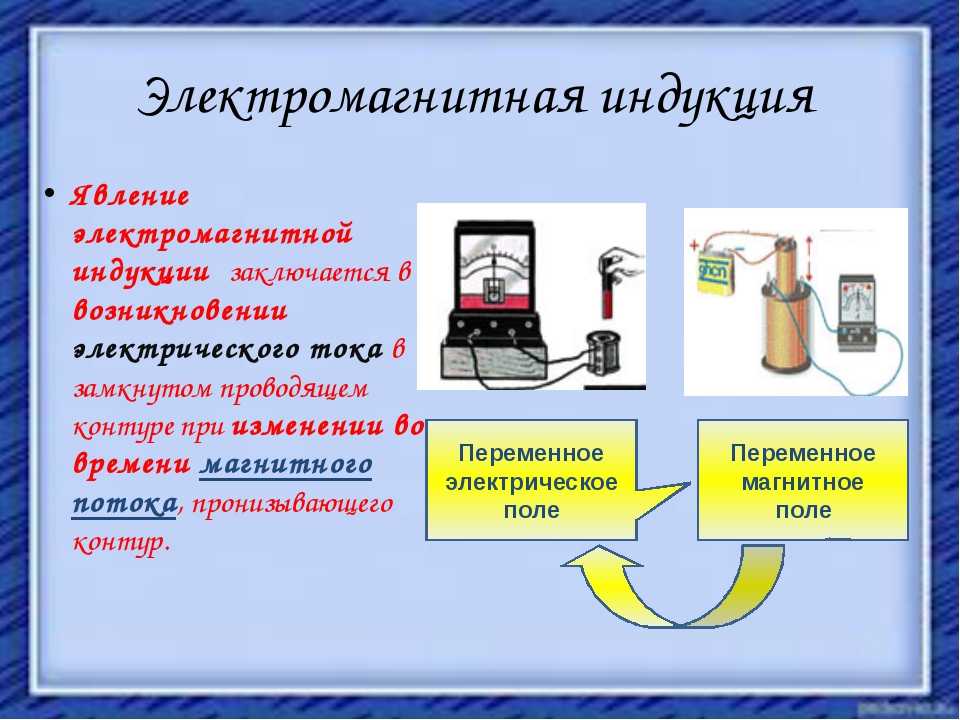
Эпизод 414-11: Вихревые токи и закон Ленца (Word, 69 КБ)
Скачать этот эпизод
Эпизод 414 — Электромагнитная индукция.doc
Электромагнитная индукция | Aviation Pros
Авиационная промышленность всегда была сферой таинственности. В конце концов, это нарушает многие неизвестные. Даже по прошествии стольких лет мы по-прежнему называем наш самый основной принцип «Теорией полета», а не «Фактом полета». Атаки гремлинов часто заглушают наши самые блестящие умы, и такое явление, как огонь Святого Эльма, наблюдается регулярно. У меня даже были комментарии тех лет, когда я был старше, что авиация сегодня — это сплошной дым и зеркала. Я точно знаю, что эта предпосылка имеет некоторые достоинства, поскольку каждый раз, когда вы видите дым, вырывающийся из одного из этих новомодных черных ящиков, магия заканчивается.
Поскольку наша отрасль продолжает развиваться, электричество играет все более важную роль в работе авиационных систем. Это было не так много лет назад, когда механические устройства и соединения считались стандартами для управления реакцией двигателей или даже управления полетом.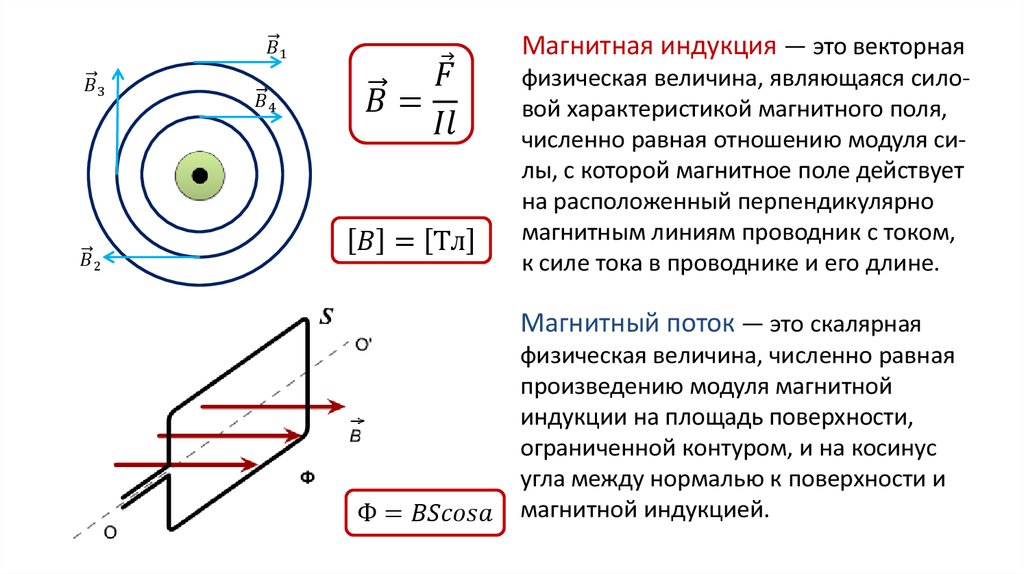 В современных самолетах компьютеры используются для регулирования тяги двигателя, а также для подачи сигналов сервоприводам, изменяющим положение самолета. Стимулирует ли использование этой технологии уверенность? Рассмотрим определение электричества, любезно предоставленное словарем Хоутона-Миффлина: Физические явления, возникающие в результате поведения электронов и протонов, вызванного притяжением частиц с противоположными зарядами и отталкиванием частиц с одинаковым зарядом.
В современных самолетах компьютеры используются для регулирования тяги двигателя, а также для подачи сигналов сервоприводам, изменяющим положение самолета. Стимулирует ли использование этой технологии уверенность? Рассмотрим определение электричества, любезно предоставленное словарем Хоутона-Миффлина: Физические явления, возникающие в результате поведения электронов и протонов, вызванного притяжением частиц с противоположными зарядами и отталкиванием частиц с одинаковым зарядом.
Если это не внушает доверия, я не знаю, что могло бы.
Магнетизм — еще одна тема, связанная с волшебниками и другими мистическими предметами, и снова следует отдать должное людям из Houghton Mifflin за их интерпретацию: класс явлений, демонстрируемых магнитным полем.
Что это такое
Электромагнитная индукция — это производство электродвижущей силы (ЭДС) в проводнике в результате изменения магнитного поля вокруг проводника. Концепция была определена в 1831 году Майклом Фарадеем и независимо Джозефом Генри.
Изменение поля вокруг электрического проводника может быть вызвано относительным движением между проводником и источником магнитного поля. Это принцип электрического генератора: изменяя силу поля вокруг проводника, можно поддерживать постоянное напряжение, которое компенсирует изменения электрической нагрузки или даже изменения относительного движения между проводником и полем.
Поскольку вокруг проводника с током создается магнитное поле, такое поле можно изменить, изменив силу тока. Если проводник, в котором должна быть наведена ЭДС, является частью электрической цепи, индукция может быть вызвана изменением тока в этой цепи; это называется самоиндукцией. Индуцированная ЭДС всегда такова, что противодействует вызывающему ее изменению, согласно закону Ленца.
Изменение тока в данной цепи также может индуцировать ЭДС в другой соседней цепи, не связанной с исходной. Этот тип электромагнитной индукции называется взаимной индукцией и является основой трансформатора, а также частой причиной аномалий в системах самолета.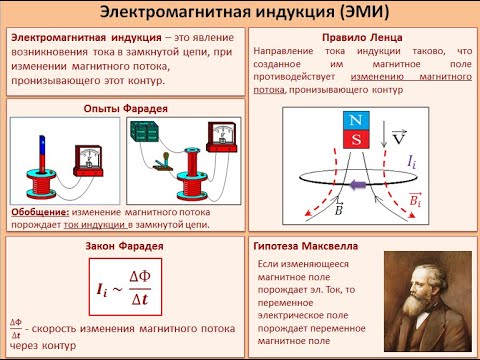 Электростатическая индукция возникает, когда неуравновешенный электрический заряд на ранее незаряженном металлическом теле возникает в результате приближения заряженного объекта без прикосновения. Если заряженное устройство положительно, электроны в незаряженном теле будут притягиваться к нему; если противоположный конец тела затем заземлен, электроны будут течь на него, чтобы заменить те, которые притянуты к другому концу, таким образом, тело приобретает отрицательный заряд после разрыва заземления.
Электростатическая индукция возникает, когда неуравновешенный электрический заряд на ранее незаряженном металлическом теле возникает в результате приближения заряженного объекта без прикосновения. Если заряженное устройство положительно, электроны в незаряженном теле будут притягиваться к нему; если противоположный конец тела затем заземлен, электроны будут течь на него, чтобы заменить те, которые притянуты к другому концу, таким образом, тело приобретает отрицательный заряд после разрыва заземления.
Аналогичную процедуру можно использовать для создания положительного заряда на незаряженном теле, когда к нему подносят отрицательно заряженный прибор. Магнитная индукция — это создание магнитного поля в куске ненамагниченного железа или другого железосодержащего вещества, когда рядом находится магнит. Магнит заставляет отдельные частицы железа, которые действуют как крошечные магниты, выстраиваться в линию, так что образец в целом становится намагниченным. Большая часть этого индуцированного магнетизма теряется, когда магнит, вызывающий его, удаляется.
Предупреждающие сигналы
По мере того, как сегодняшние самолеты становятся все более зависимыми от компьютеризированных или электронно-управляемых систем, обычно маломощные входы и, в некоторых случаях, выходы этих систем легко искажаются, когда нежелательные индуцированные электрические сигналы попадают в изолированные цепи. Сообщалось об одном таком происшествии с реактивным самолетом бизнес-класса, в котором использовался электрический стартер вместе с компьютером, который должен был получать все данные о двигателе от различных аналоговых или дискретных датчиков, оцифровывать все данные и затем передавать их на электронные дисплеи в кабине экипажа.
В некоторых случаях во время запуска двигателя экипаж сообщал о загорании сообщения «Засорен топливный фильтр». В каждом случае проверка топливного фильтра не выявила загрязнения. Также был заменен ЭБУ, получавший данные от датчика байпаса. Кроме того, проводка от датчика к компьютеру была тщательно проверена на предмет короткого замыкания на землю, но никаких проблем обнаружено не было. На проводе, идущем к датчику перепуска топливного фильтра, подавался дискретный сигнал (специфического типично низкого напряжения). Когда происходил фактический байпас, переключатель датчика закрывался, подавая электрическое заземление на компьютер, снижая дискретное напряжение почти до нуля вольт, что, в свою очередь, вызывало предупреждающее сообщение. Было замечено, что проблема исчезала после установки новых основных батарей и имела тенденцию к повторному возникновению, когда батареи находились в эксплуатации в течение нескольких месяцев.
На проводе, идущем к датчику перепуска топливного фильтра, подавался дискретный сигнал (специфического типично низкого напряжения). Когда происходил фактический байпас, переключатель датчика закрывался, подавая электрическое заземление на компьютер, снижая дискретное напряжение почти до нуля вольт, что, в свою очередь, вызывало предупреждающее сообщение. Было замечено, что проблема исчезала после установки новых основных батарей и имела тенденцию к повторному возникновению, когда батареи находились в эксплуатации в течение нескольких месяцев.
В конце концов, когда оператору надоело заменять детали, к датчику байпаса подключили осциллограф и инициировали запуск двигателя. Несмотря на отсутствие сообщения об обходе, технические специалисты заметили изменение напряжения на дискретном сигнале. Подумав, что, возможно, падение напряжения на шине, сопровождающее запуск, повредило компьютер, техники заглушили проблемный двигатель и запустили другой. Во время этого запуска они продолжали контролировать сигнал на проблемном датчике двигателя. На этот раз дискретное напряжение не изменилось. Затем они решили выключить работающий двигатель и перезапустить тот, который вызвал проблему. Следует отметить, что все пуски производились с основных батарей самолета.
На этот раз дискретное напряжение не изменилось. Затем они решили выключить работающий двигатель и перезапустить тот, который вызвал проблему. Следует отметить, что все пуски производились с основных батарей самолета.
Во время запуска проблемного двигателя появилось сообщение о засорении топливного фильтра, и снова техники заметили значительный скачок напряжения на разъеме датчика. В то время визуальный осмотр показал, что провод датчика был проложен в непосредственной близости от основного источника питания стартера. Было принято решение разъединить провода и был произведен еще один запуск, на этот раз заметного изменения напряжения на прицеле не наблюдалось, и на кабину экипажа не передавалось никаких сообщений.
Почему новые батареи решили проблему? С возрастом батареи имеют тенденцию терять некоторую емкость, что означает, что при значительной нагрузке, такой как запуск двигателя, можно ожидать большего падения напряжения, что, в свою очередь, приводит к более высокому току, подаваемому на стартер. Так как батареи в самолете со временем разлагаются, индуцированный всплеск напряжения будет увеличиваться по амплитуде и в конечном итоге достигнет критической точки, когда сенсорный компьютер обнаружит пороговое напряжение, при котором сработает схема сигнализации. Также так уж получилось, что проблемный двигатель был запущен последним в соответствии с процедурами контрольного списка, поэтому в повседневной жизни главные аккумуляторы были уже в несколько разряженном состоянии, когда пришло время запуска этого двигателя.
Так как батареи в самолете со временем разлагаются, индуцированный всплеск напряжения будет увеличиваться по амплитуде и в конечном итоге достигнет критической точки, когда сенсорный компьютер обнаружит пороговое напряжение, при котором сработает схема сигнализации. Также так уж получилось, что проблемный двигатель был запущен последним в соответствии с процедурами контрольного списка, поэтому в повседневной жизни главные аккумуляторы были уже в несколько разряженном состоянии, когда пришло время запуска этого двигателя.
В этом случае решением стало перемещение проводки, обеспечивающее достаточное разделение между фидером для стартера и меньшим проводом с дискретным датчиком для датчика байпаса топливного фильтра.
Сигналы системы переменного тока
Системы переменного тока (AC) часто являются источниками нежелательных наведенных электрических сигналов. Многие самолеты, использующие несколько электрических систем постоянной частоты, будут включать средства синхронизации. При этом оба источника питания переменного тока, такие как инверторы, будут работать в фазе. Электрические проводники, расположенные вместе, с меньшей вероятностью будут испытывать эффекты взаимной индукции, когда потенциал на обоих возрастает и падает одновременно.
При этом оба источника питания переменного тока, такие как инверторы, будут работать в фазе. Электрические проводники, расположенные вместе, с меньшей вероятностью будут испытывать эффекты взаимной индукции, когда потенциал на обоих возрастает и падает одновременно.
Один из примеров этого произошел в самолете с двумя независимыми системами переменного тока, питаемыми двумя работающими полупроводниковыми инверторами. В этом случае каждая инверторная система будет подавать питание независимо и, соответственно, на приборные системы пилота и второго пилота. Во время обычного полета было замечено, что система магнитного курса капитана (MHS) отклонилась примерно на 12 градусов от системы второго пилота. Наблюдение за другими приборами подтвердило, что неисправность была с левой стороны.
Во время устранения неполадок техник заметил, что, когда инвертор капитана работал в одиночку, система компаса показывала правильно. При включении второго инвертора произошло резкое смещение левых индикаторов компаса.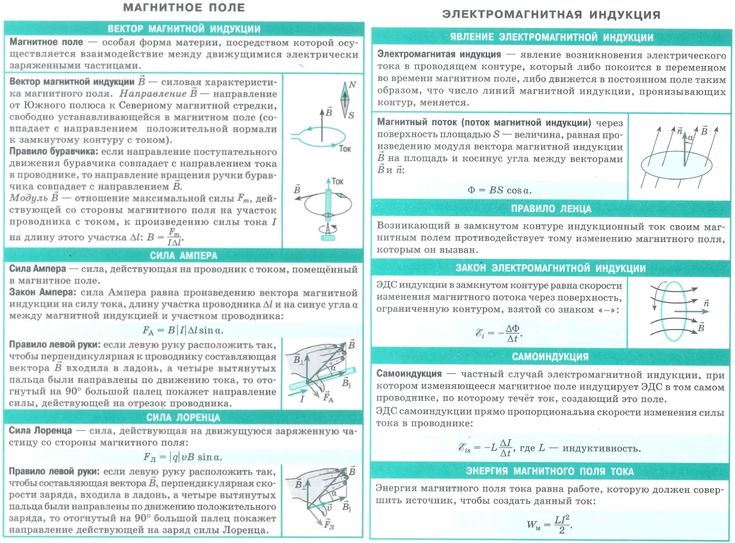 При просмотре руководств по подключению было обнаружено несколько областей, где провода от компаса № 1 и инвертора № 2 проходили в непосредственной близости. Но это был самолет 14-летней давности, почему проблемы только начинаются?
При просмотре руководств по подключению было обнаружено несколько областей, где провода от компаса № 1 и инвертора № 2 проходили в непосредственной близости. Но это был самолет 14-летней давности, почему проблемы только начинаются?
К счастью, в системе питания переменного тока был установлен третий инвертор, который использовался в качестве замены в полете в случае выхода из строя одного из двух первичных преобразователей. Затем было отмечено, что при выборе резервного инвертора вместо левого инвертора проблема с компасом исчезла. Инвертор № 1 был проверен, никаких отклонений не обнаружено, и заменен в качестве меры предосторожности. Проблема повторилась. Затем техник контролировал выходы обоих работающих инверторов с помощью осциллографа с возможностью одновременного отображения двух сигналов. Когда работали обычные инверторы, на их выходах наблюдалось заметное фазовое расщепление. Когда резервный инвертор был выбран с левой стороны, фазовый сдвиг исчезал.
Оказывается, несоответствие заключалось в обрыве провода от цепи синхронизации инвертора №1 в систему синхронизатора общего инвертора самолета.
Устранение эффектов индукции
В дополнение к обеспечению надлежащего расстояния между проводниками и работающими системами переменного тока в фазе, другие меры предосторожности, которые используются для устранения эффектов индукции, включают устройство, известное как клетка Фарадея.
Хорошим примером этого является металлическая коробка с заземлением корпуса, окружающая печатные платы, или, в более широком масштабе, правильно склеенный фюзеляж, окружающий внутреннее содержимое самолета. Цель здесь состоит в том, чтобы предотвратить воздействие паразитных зарядов на содержащиеся схемы. Металлический и заземленный экран, покрывающий провод, дает тот же результат. Ключевым моментом здесь является обеспечение герметичности системы. Если экранирование присутствует на всем протяжении провода и заканчивается в 6 дюймах от того места, где провод входит в разъем на переборке, образовался дверной проем, который может позволить паразитным сигналам либо войти, либо выйти.
Какие инструменты использовать
Итак, какие инструменты следует использовать в процессе обнаружения и устранения индуктивных аномалий? Как упоминалось ранее, осциллограф дает техническим специалистам возможность просматривать фактическое рабочее состояние схемы. Если наблюдаются электрические помехи, могут быть предприняты действия для идентификации источника. Стоимость прицела может быть нелегко оправдана для большинства технических специалистов, поэтому альтернативные способы устранения неполадок могут включать обертывание подозрительных участков алюминиевой фольгой и ее заземление для проверки воздействия зараженной системы. Этот метод, конечно, рекомендуется для устранения неполадок на земле.
Индуктивные тестеры, такие как «Лиса и гончая», являются более дешевыми и эффективными средствами для обнаружения электрических помех, а также определения места пробоя в экранах. Это устройство оснащено тональным генератором, который можно подключить к подозрительной цепи, а трассировщик сигнала держится в руке, пока техник перемещает датчик вдоль проводника.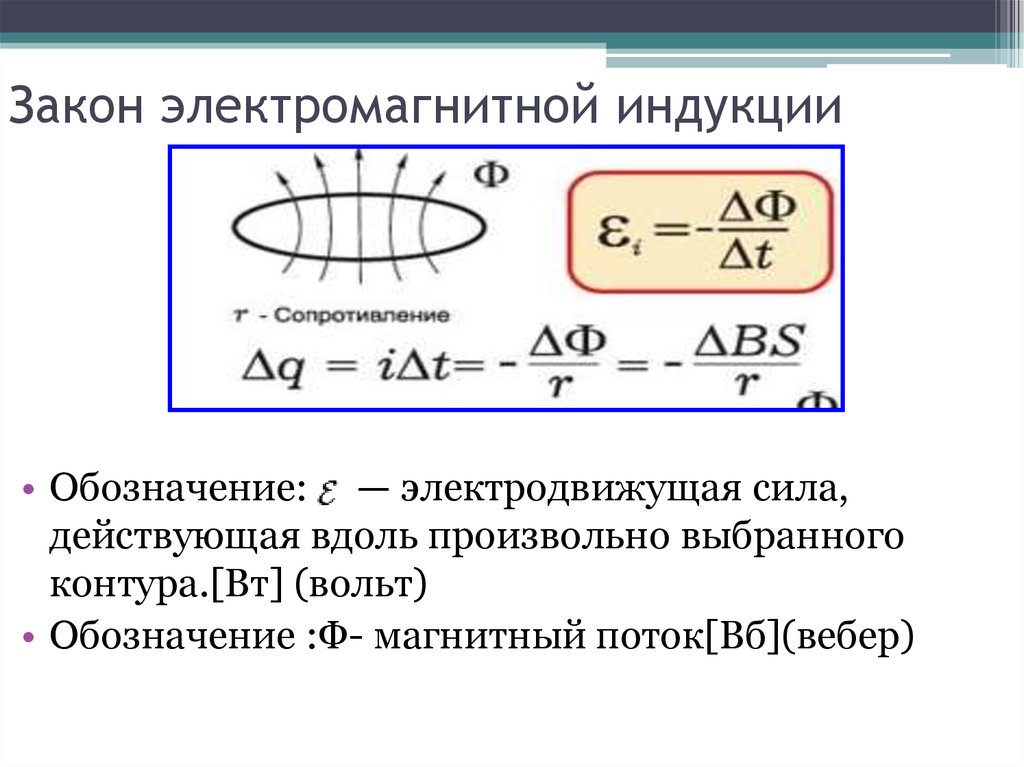


 При этом она препятствует изменению вызвавшего её тока.
При этом она препятствует изменению вызвавшего её тока.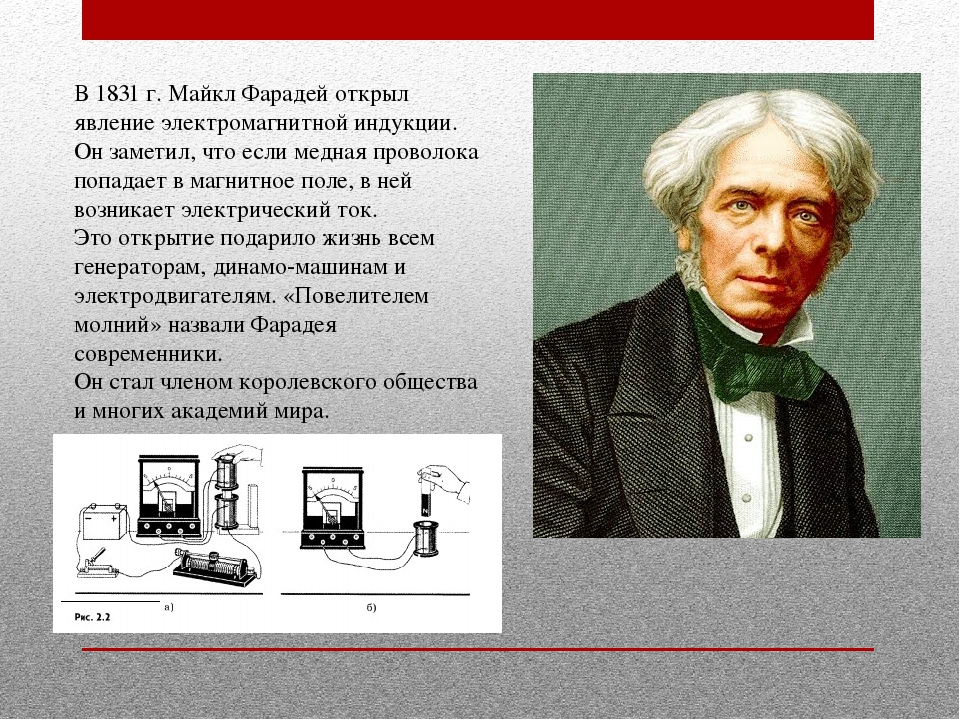 При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
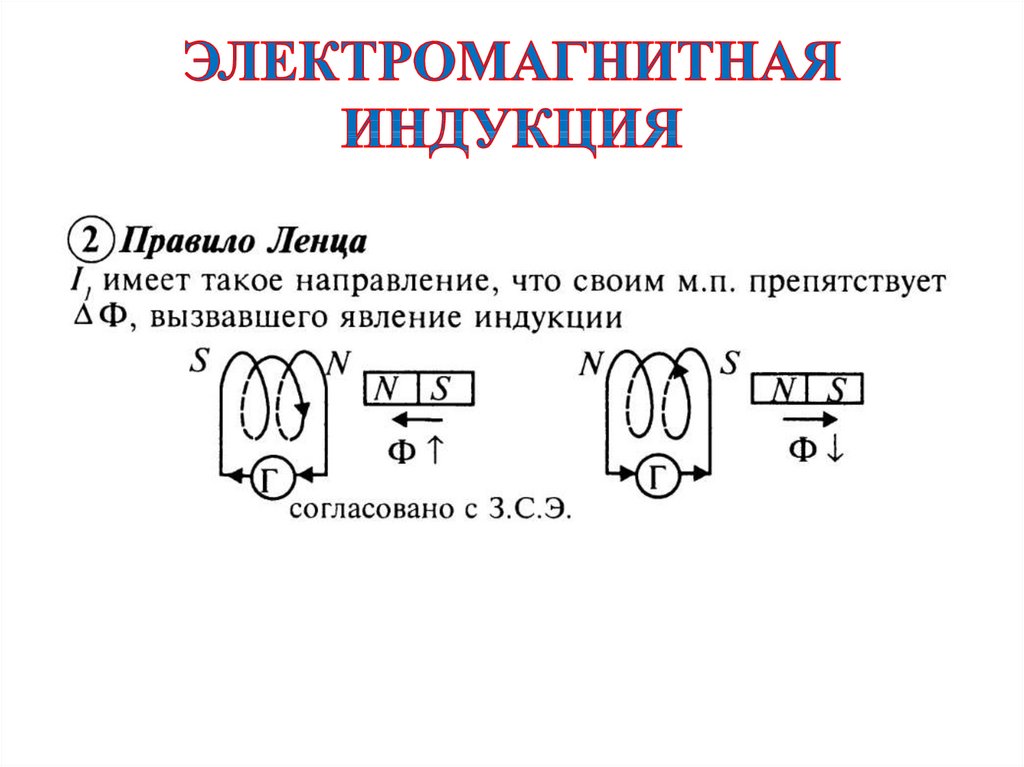
 Т. Уивер. Общая теория электромагнитной индукции в проводящем полупространстве. /j.1365-246X.1971.tb03584.x
Т. Уивер. Общая теория электромагнитной индукции в проводящем полупространстве. /j.1365-246X.1971.tb03584.x