Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика

Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика

Андронов В.В. Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика: Учебное пособие для студентов очного и заочного обучения. Спец. 260100 и 260200. 2-е изд., доп. и испр. — М: МГУЛ, 2003.- 137 с. Книга содержит материал лекций, которые автор читает в Московском государственном университете леса студентам технологических специальностей. Настоящая, первая часть книги, включает статику и кинематику. Для лучшего усвоения материала в конце каждой лекции приводятся вопросы для самопроверки и упражнения. В интересах студентов заочных форм обучения в книге большое внимание уделяется поясняющим примерам и решению задач. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ Момент силы относительно точки Алгебраический момент силы Основные типы связей и их реакции Упражнения ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ Сходящиеся силы. Приведение сходящихся сил к простейшему виду Вычисление и построение равнодействующей Условия равновесия сходящихся сил Теорема о трех силах Теорема Вариньона Пара сил и ее момент Приведение системы пар сил к простейшему виду или сложение пар сил Упражнения ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ Момент силы относительно оси Аналитический способ вычисления момента Геометрический способ вычисления момента Преобразование пространственной произвольной системы сил Приведение пространственной произвольной системы сил к данному центру. 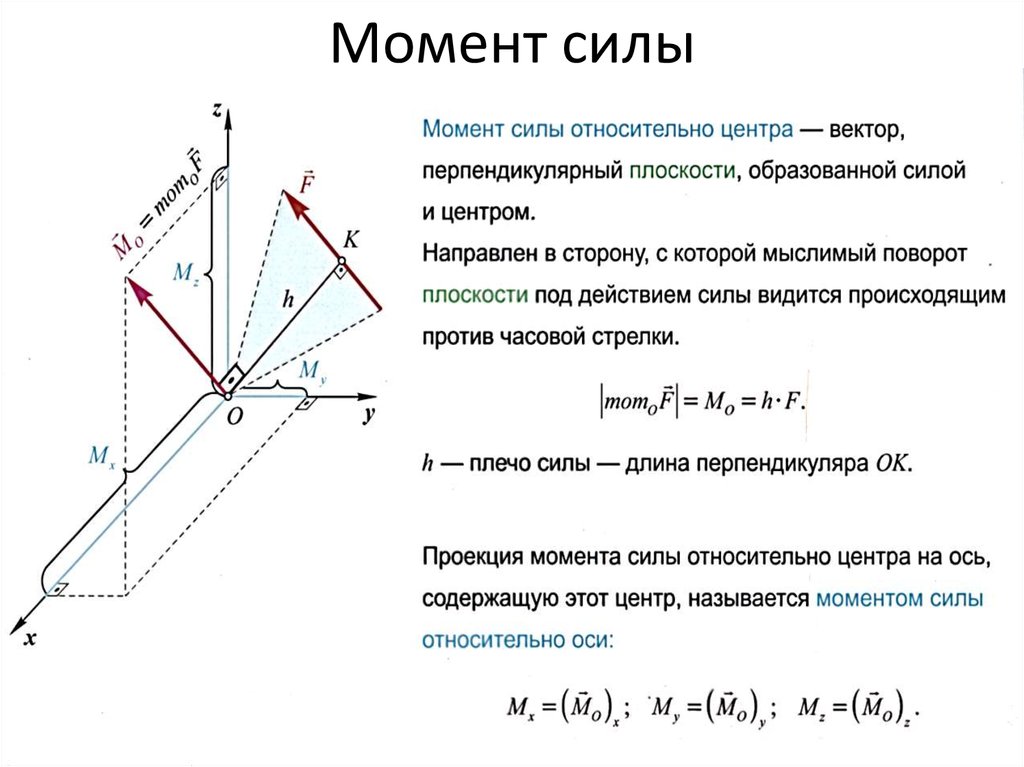Главный вектор и главный момент. Основная теорема статики Вычисление и построение главного вектора и главного момента Перемена центра приведения ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ Случаи приведения к простейшему виду Условия (уравнения) равновесия пространственной произвольной системы сил Частные случаи системы сил Плоская система сил Система параллельных сил Равновесие системы тел Вопросы для самопроверки ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ Центр параллельных сил Распределенные силы Центр тяжести Интегральные формулы для координат центра тяжести Метод разбиения Вопросы для самопроверки ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ Трение покоя и трение скольжения Трение качения Решение задач статики при учете сил трения Заклинивание Упражнения КИНЕМАТИКА ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ Способы задания движения точки Определение траектории, скорости и ускорения точки при векторном способе задания движения Определение траектории, скорости и ускорения точки при координатном способе задания движения Определение скорости и ускорения точки при естественном способе задания движения Естественные координатные оси и их орты Определение скорости Определение ускорения Вопросы для самопроверки ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА Поступательное движение Вращательное движение Уравнение вращательного движения. Угловая скорость и угловое ускорение тела Траектории, скорости и ускорения точек тела Векторы угловой скорости и углового ускорения тела Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела Вопросы для самопроверки ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА Уравнения движения Угловая скорость и угловое ускорение тела при плоскопараллельном движении Определение скоростей точек тела. Метод полюса Мгновенный центр скоростей Определение скоростей точек плоской фигуры через мгновенный центр скоростей Различные случаи определения положения мгновенного центра скоростей Определение ускорений точек тела Вопросы для самопроверки ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ Теорема сложения скоростей Теорема сложения ускорений Причины появления ускорения Кориолиса Вычисление и построение ускорения Кориолиса Вопросы для самопроверки ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ Схема и расчетная модель процесса фугования Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке Геометрические характеристики поверхности в случае многоножевой головки РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Момент силы относительно центра (точки)

1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА СТАТИКА

Лекция №2

2. 2.1 Момент силы относительно центра (точки)

3. Момент силы относительно центра

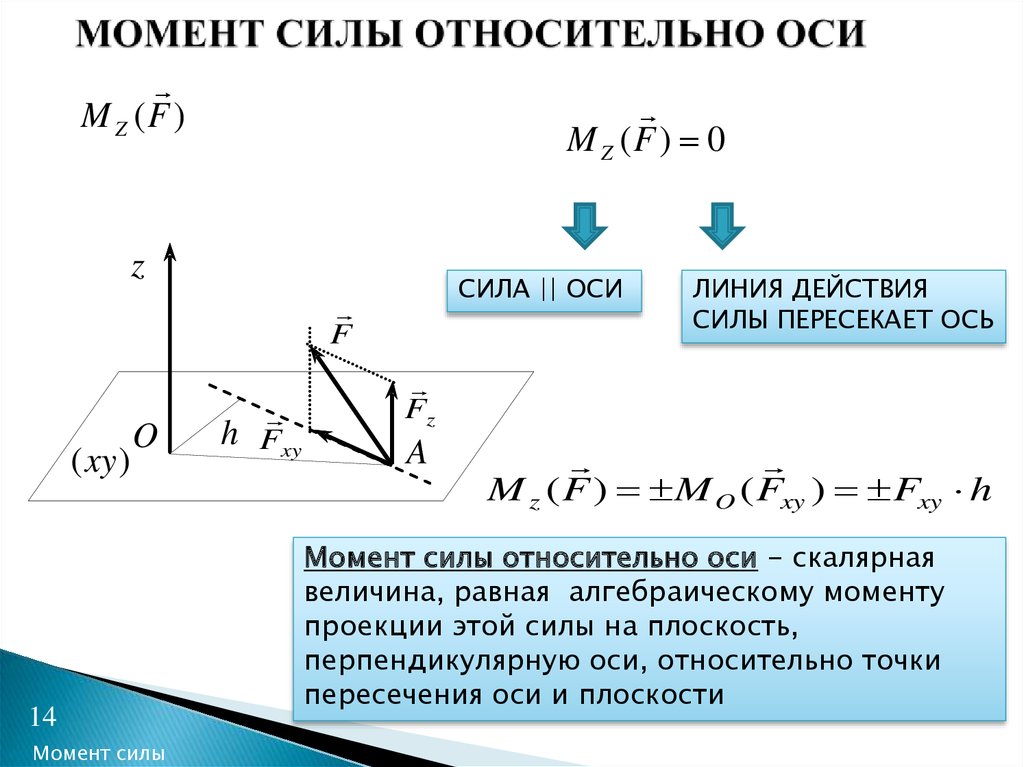
Z
mO r F
B
mO F h
F
mO
h
O
r
A
Моментом силы F относительно центра
(точки) О называется вектор mO F равный векторному произведению радиуса вектора r , проведенного из центра О в точку А приложения силы, и
вектора силы F :
mO F r F
B
Z
F
mO
h
A
r
O
Вектор mO F приложен в точке О и направлен плоскости, проходящей через центр О и силу F , в ту сторону, откуда сила видна стремящейся повернуть
тело вокруг центра О против хода часовой стрелки.
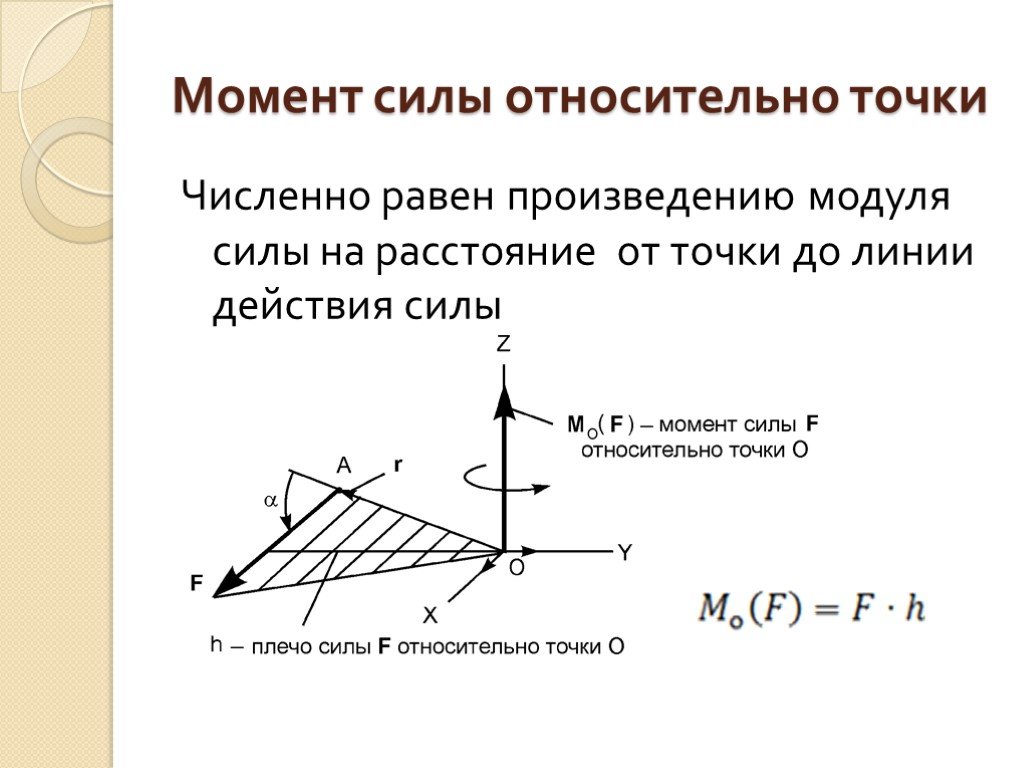
Модуль mO F равен произведению модуля силы F на плечо h:
mO
= F·h,
где плечо h перпендикуляр, опущенный из центра О на линию действия
силы F .
Момент mO F характеризует вращательный эффект силы
но центра (точки) О.
F
относитель-

5. Свойства момента силы:

Момент силы относительно центра не изменяется при переносе силы вдоль
линии ее действия в любую точку.
Если линия действия силы проходит через центр О (h = 0), то момент силы
относительно центра О равен нулю.
Для плоской системы сил при вычислении моментов сил относительно точки
(центра), находящейся в той же плоскости, пользуются понятием алгебраического момента силы относительно точки.
Алгебраический момент силы F относительно
точки О равен взятому с соответствующим знаком
произведению модуля силы на ее плечо:
mО( F ) = F h.
Момент считается положительным, если сила
стремится повернуть тело вокруг точки О против хода
часовой стрелки, и отрицательным по ходу часовой
стрелки:
mO ( F1 ) F1 h2 ;
mO ( F2 ) F2 h3 .
F1
h2 О
h3
F2
Р
F
О
Р
F

8. Пьер Вариньон

Пьер Вариньон (фр. Pierre Varignon, Кан, 1654 — 23 декабря, 1722,
Париж) — французский математик, член Парижской Академии наук,
профессор математики коллежа Мазарини (1688), профессор Коллеж де
Франс.[1] Обучался в иезуитском коллеже и университете в Кане, где стал
магистром в 1682 году.
Вариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад
Вариньон совершил в статику и механику; кроме того, труды Вариньона
посвящены анализу бесконечно малых, геометрии, гидромеханике. За
исключением Лопиталя, Вариньон был самым первым пропагандистом
дифференциального исчисления во Франции. В 1687 году в своей работе
«Проект новой механики…» Вариньон дал точную формулировку закона
параллелограмма сил, развил понятие момента сил и вывел теорему,
получившую имя Вариньона. В работе «Новая механика или статика,
проект которой был дан в 1687» (1725) Вариньон дал систематическое
изложение учения о сложении и разложении сил, о моментах сил и о
правилах оперирования ими. [1]

9. Теорема Вариньона

При определении алгебраического момента силы относительно
точки в случае, когда сложно найти плечо h, следует разложить
силу на составляющие, плечи которых найти проще, (часто параллельно осям координат), и применить теорему Вариньона:
если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки О равен
сумме моментов составляющих сил, относительно той же
точки
mO ( R ) mO ( Fk ), где R Fk .

10. 2.2 Теория пар сил, свойства пар сил

Парой сил называется система двух равных
по модулю, параллельных и направленных в
противоположные стороны сил ( F F ).
Плоскость, в которой лежат силы F и F , называется плоскостью пары, а кратчайшее расстояние d между линиями действия сил плечом пары.
Пара сил не может быть заменена одной эквивалентной ей силой, т.е. не имеет равнодействующей, так как R F F 0.
Пара может быть уравновешена только
другой парой сил.
Под действием пары сил тело вращается.
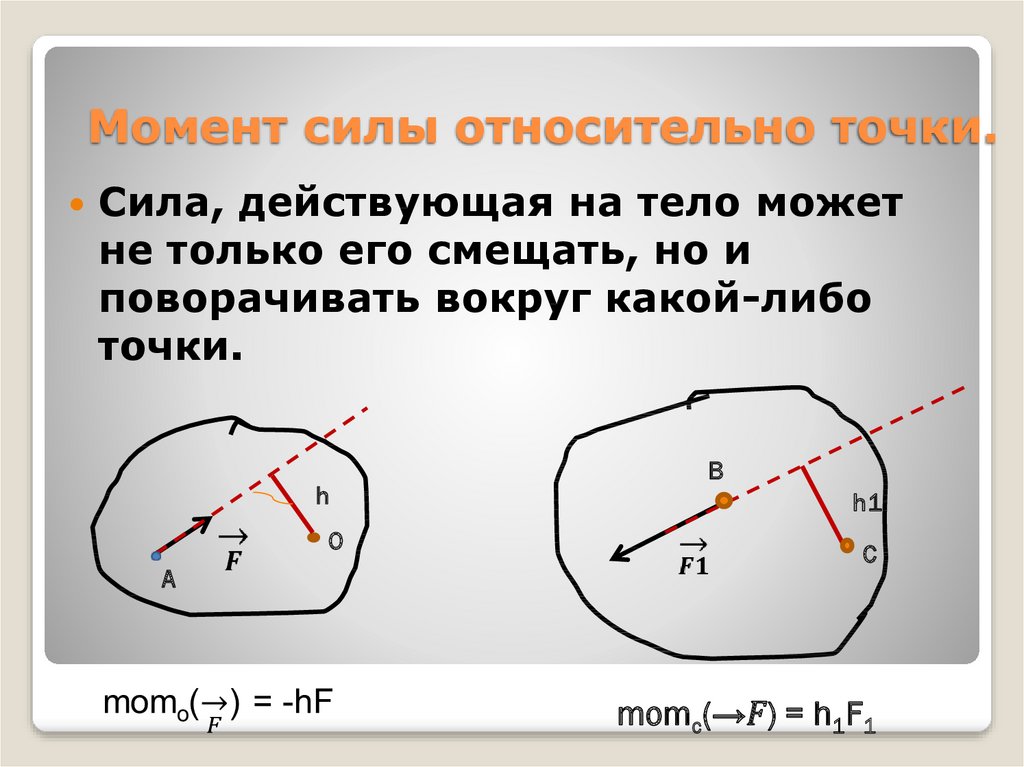
Вращательный эффект пары, характеризуется
моментом пары.
F
B
A
F
d

11. Момент пары сил

Моментом пары называется вектор равный векторному произведению
m r F
,
модуль которого равен произведению модуля одной из сил пары на ее плечо
m F d.
Вектор m направлен перпендикулярно
плоскости пары в ту сторону, откуда пара
видна стремящейся повернуть тело против
хода часовой стрелки. Момент пары m
свободный вектор, т. е. его можно прикладывать в любой точке тела.
m
B
F d
F
r
A

12. Свойства пар сил

1. Момент пары равен сумме моментов сил пары относительно произвольного центра (точки) О:
mO mO ( F ) mO ( F ) .
2. Момент пары относительно любого центра
F
mO равен моменту пары m:
mO F h F (h d ) F d m.
mO m
h
d
B
A
F
O
3. Момент пары равен моменту одной из сил пары относительно точки
приложения другой силы пары:
m mB ( F ) mA ( F ).
4. Теорема. Пары сил с равными моментами эквивалентны.
Следствия:
Пару сил, приложенную к твердому телу, можно заменить другой
парой в той же плоскости, если при такой замене не изменяется величина момента пары и его направление:
Пару сил можно переносить в плоскость, параллельную плоскости
пары.
5. Теорема. Совокупность нескольких пар с моментами m1 , m2, mn
эквивалентна одной паре, момент
сумме моментов данных пар:
m которой равен геометрической
m m1 m2 mn .
6. Если на тело действует пространственная система пар, то тело находится в равновесии, если векторная сумма моментов пар равна нулю:
m 0.
7. Если пары лежат в одной плоскости, то
момент пары считают величиной алгебраической,
так как в этом случае все вектора моментов пар
параллельны.
Алгебраический момент пары равен взятому
с соответствующим знаком произведению модуля
одной из сил пары на плечо пары:
Z
m1
mn
Y
X
m2
m F d .
Знак «+» соответствует повороту тела под действием пары против хода часовой
стрелки,
«─» по ходу часовой стрелки.
Пары сил на плоскости часто изображается
Y
дуговой стрелкой, показывающей направление
поворота тела парой.
8. Если на тело действует плоская система пар, то
тело находится в равновесии, если сумма моментов пар
равна нулю:
m
k
0.
m1
O
m2
X

16. 2.3 Приведение системы сил к заданному центру

Теорема Пуансо

17. Пуансо Луи

Пуансо (Poinsot) Луи (3.1.1777, Париж, —
5.12.1859, там же), французский математик
и механик, член Парижской АН с 1813.
Окончил
Политехническую
школу
в
Париже (1797), с 1809 профессор там же. В
период
Июльской
монархии
—
в
Министерстве народного образования. Пэр
Франции (1846), сенатор (1852). Первые
работы П. посвящены теории правильных
звездчатых
многогранников.
В
1803
опубликовал
«Элементы
статики»,
в
которых применил разработанные им
геометрические методы исследования к
учению о равновесии твёрдых тел и их
систем. В 1834 построил теорию вращения
твёрдого тела вокруг неподвижной точки.
Впервые
ввёл
понятие
эллипсоида
вращения.

18. Теорема1 — О параллельном переносе силы (лемма Пуансо):

силу F, не изменяя ее действия на
абсолютно твердое тело, можно
переносить из данной точки А в любую
другую точку О тела, прибавляя при
этом пару с моментом m равным
моменту переносимой силы
относительно точки О, в которую
переносится сила F.

19. Доказательство

mO (F )
Z
F
F F F
O
F
d
F
A
X
Y
mO (F )
Z
F
O
F
d
F
O
F
A
X
Y

21. Теорема 2 – О приведении системы сил к заданному центру (теорема Пуансо):

Любая система сил , действующая на
абсолютно твердое тело, при
приведении к произвольному центру О
заменяется главным вектором системы
сил, приложенным в центре О и парой
сил с моментом , равным главному
моменту системы сил относительно
центра О.

22. Доказательство

F1
Z
MO
F1 m1
m2
R
Fn
O
mn
X
Fn
F2
F2
Y
F1
Z
MO
F1
m1
m2
O
mn
X
Fn
R
Fn
F2
F2
Y
Используя теорему 1 перенесем все силы в
центр О прибавляя пары с моментами
равными моментам сил относительно
центра О. Сложив все силы и моменты
получим в центре О два вектора и равные:
k n
R F1 F2 Fn Fk ;
k 1
k n
M O M O F1 M O F2 M O Fn M O Fk .
k 1
Величина главного вектора
значение главного момента
может изменяться.
R не зависит от выбора центра О, а
M O при изменении положения центра О
k n
R F1 F2 Fn Fk ;
k 1
k n
M O M O F1 M O F2 M O Fn M O Fk .
Для плоской системы
сил главный вектор R
лежит в плоскости
действия сил, а главный
момент M Oперпендикулярен
этой плоскости. Поэтому
главный момент плоской
системы сил относительно
центра О определяется как
сумма алгебраических
моментов сил относительно
центра О и изображается
на плоскости дуговой
стрелкой.
k 1
Y
R XY
O
M O XY
Z
X

26. Частные случаи приведения системы сил:

R 0; M O 0
система сил
приводится к одной
паре, лежащей в
плоскости действия
сил с моментом M O
(причем это
свободный вектор).
MO
Z
X
O
Y
R 0; M O 0
система сил приводится
к равнодействующей ,
приложенной в центреО.
R 0; M O 0
система сил приводится
к равнодействующей ,
проходящей через точку
С, положение которой
определяется
равенством
OC d M O / R; OC R
R
Z
O
X
Y
Z
R
R
C
X
O
d
Y
R
R 0; M O 0
система сил уравновешена.
Теорема: Для равновесия любой
системы сил необходимо и достаточно,
чтобы главный вектор и главный
момент этой системы относительно
любого центра (точки) были равны
нулю.

29. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПЛОСКОЙ СИСТЕМЫ СИЛ

Необходимые и достаточные условия
равновесия твердого тела, находящегося под
действием произвольной плоской
системы сил в векторной форме имеют вид
R 0; M O O
Из этих векторных уравнений следуют три
формы аналитических условий
равновесия.

30. Основная форма условий равновесия

для сил, лежащих в плоскости ОХУ:
F
kX
0; FkY 0; mO ( Fk ) 0.
Для равновесия произвольной плоской
системы сил необходимо и достаточно,
чтобы сумма проекций сил на каждую из
координатных осей и сумма моментов сил
относительно любой точки, лежащей в
плоскости действия сил, были равны нулю.

31. Вторая форма условий равновесия:

F
kX
0; mA ( Fk ) 0; mB ( Fk ) 0,
OX не AB.
Для равновесия произвольной плоской
системы сил необходимо и достаточно,
чтобы суммы моментов всех сил
относительно двух точек А и В и сумма
их проекций на ось ОX,
не перпендикулярную прямой АВ,
были равны нулю.
AB не OX
правильно
Y
AB OX
R
Y
B
B
A
O
A
X
O
m
X
A
0; mB 0; FX 0,
но R 0, система не уравновешена!

33. Третья форма условий равновесия

m ( F ) 0; m ( F ) 0; m
A
k
B
k
C
( Fk ) 0,
точки A, B, C не лежат на одной прямой.
Для равновесия произвольной плоской
системы сил необходимо и достаточно,
чтобы суммы моментов всех сил
относительно любых трех точек А, В и
С, не лежащих на одной прямой,
были равны нулю.
A, B, C лежат на
A, B, C не лежат на
одной прямой
правильно
Y
B
A
O
одной прямой
R
Y
С
С
X
O
m
B
A
X
A
0; mB 0; mC 0,
но R 0, система не уравновешена!
Для проверки решения задачи
на равновесие плоской системы сил
составляют сумму моментов всех сил
относительно других точек или строят в
масштабе многоугольник всех сил,
действующих на тело. Если
проверочное уравнение обращается в
тождество, а многоугольник сил
замкнут, то задача решена верно.

классическая механика — Изменить точку измерения сил и моментов

Моменты говорят вам, где приложена сила. Вектор силы даст вам величину и направление силы, но не

, где является линией действия силы. {2}} \end{выровнено} $$ 9{2}}=\vec{M_{A}}\;\галочка \end{aligned}$$

классическая механика — Почему при расчете крутящего момента расстояние считается перпендикулярным направлению силы?

спросил 1 год, 9 месяцев назад

Изменено 1 год, 9 месяцев назад

Просмотрено 1к раз

$\begingroup$

По моему учебнику:

Момент силы = сила $\times$ перпендикулярное расстояние линии действия силы от точки опоры.

Я не понимаю, почему это так (особенно какая математика стоит за этим). Почему расстояние считается перпендикулярным направлению силы при расчете крутящего момента, независимо от его направления?

Например, в этом вопросе:

Ответ (данный по схеме маркировки) предположительно $240$ $\text{N}$ $\times 1. 2$ $\text{m}$ или $288$ $\ текст{Nm}$. Обычно я решаю подобные вопросы, разлагая вектор на его компоненты и умножая величину его вертикального вектора на расстояние.

Как работает метод, использованный выше в схеме маркировки? Есть ли доказательство того, что это так?

• классическая механика
• крутящий момент

$\endgroup$

4

$\begingroup$

Крутящий момент $\vec \tau$ от некоторой силы ${\bf \vec F}$ относительно оси вращения определяется как $$\boldsymbol {\vec \tau}={\bf \vec r}\times {\ bf \vec F}$$, где ${\bf \vec r}$ — вектор, идущий от точки вращения (точки опоры) к точке приложения силы.

Математически вы знаете, что величина векторного произведения двух векторов ${\bf \vec a}$ и ${\bf \vec b}$ определяется следующим образом: $$\left|{\bf \vec a} \times {\bf \vec b}\right| = ab\sin\theta$$, где $\theta$ — угол между векторами (измеряемый, когда векторы расположены хвост к хвосту).

Следовательно, величина крутящего момента равна $$\tau = F\underbrace{r \sin\theta}_\text{плечо рычага}$$

Теперь, благодаря тригонометрии, вы можете видеть, что $r \sin\theta$ — это выделенное вами расстояние в $1,2 \\rm$. См. ниже:

Вспомним, что $\sin(\pi — x)=\sin x$, и вы сможете понять вышеизложенное, чтобы понять, что плечо рычага действительно равно $r\sin(\pi-\theta)= г \ грех \ тета $.

$\endgroup$

$\begingroup$

Лучшим определением крутящего момента является работа на единицу угла поворота, которую может совершить сила, действующая таким образом, что она стремится вызвать вращение. Работу совершает та составляющая силы, которая направлена ​​по дуге в направлении движения. Этот компонент перпендикулярен радиусу. Для каждого небольшого пройденного расстояния длина дуги равна rθ. Таким образом, крутящий момент равен $F_θ$(rθ)/θ = $F_θ$(r).

$\endgroup$

$\begingroup$

Вы хотите рассчитать крутящий момент относительно точки B , вызванный общей силой $\vec{F}$, проходящей через точку A . Без ограничения общности разложим силу на три составляющие ($F_1$, $F_2$, $F_3$), одна из которых проходит по линии AB .

Теперь рассмотрим крутящий момент около B как сумму крутящих моментов трех компонентов.

Линия действия каждого компонента определяется точкой A и выбранным направлением. Для $F_3$ линия действия проходит через

A , как вы можете видеть выше (по задумке).

Это означает, что $F_3$ имеет нулевой крутящий момент относительно AB , а общий крутящий момент в B обусловлен исключительно перпендикулярными компонентами $F_1$ и $F_2$.

Математически это делается с помощью перекрестного произведения, которое игнорирует любые параллельные компоненты.

Также обратите внимание, что вы можете обратить указанную выше конструкцию и разложить вектор положения $\vec{r}_{A/B}$ по трем направлениям, одно из которых параллельно силе $\vec{F}$.