Теорема о свадьбах — Википедия

Материал из Википедии — свободной энциклопедии

Теорема о свадьбах (также теорема о мальчиках и девочках, теорема Холла) — утверждение о том, что если в двудольном графе для любого натурального k{\displaystyle k} любые k{\displaystyle k} вершин одной из долей связаны с по крайней мере с k{\displaystyle k} вершинами другой, то граф разбивается на пары.

Доказана в 1935 году Филиппом Холлом. Доказательство следует немедленно из венгерского алгоритма для поиска максимального паросочетания в графе; также утверждение легко выводится из теоремы Форда — Фалкерсона о разрезаниях транспортных сетей.

Из теоремы о свадьбах немедленно следует, что любой регулярный граф степени r⩾1{\displaystyle r\geqslant 1} допускает совершенное паросочетание.

Теорема обобщается на двудольные графы с бесконечным множеством вершин, при условии, что все вершины имеют конечную степень. Пример бесконечного двудольного графа, для которого теорема не верна — прямой цилиндрический стакан, который строится следующим образом: первая доля множества вершин — точки верхней окружности стакана и центр нижнего основания; вторая доля — точки окружности нижнего основания; рёбра графа — все радиусы нижнего основания и вертикальные отрезки боковой поверхности.

Обобщение теоремы о свадьбах на случай произвольных конечных, но необязательно двудольных, графов — теорема Татта о паросочетаниях.

Теорема Кёнига — близкое утверждение, связывающее нахождение наибольшего паросочетания и наименьшего вершинного покрытия в конечных графах.

Теорема Холла, или теорема о свадьбах

Филип Холл

Филип Холл (Philip Hall, 1904–1982) — английский математик, большая часть работ которого относится к теории групп и связанным с ней разделам алгебры. Так, первая теорема Холла относится к разрешимым группам. Теорема Холла о свадьбах, доказанная им в 1935 году, является одним из основных комбинаторных принципов. Возможно, самый важный его вклад в математику — полиномы Холла, которые играют важную роль в теории представлений групп.

В задаче о свадьбах требуется поженить каждую из девушек с одним из юношей. Каждая девушка (после долгих и изнурительных сомнений и обсуждений) представляет список юношей, которые ей нравятся. Мы также сделаем предположение, что все юноши достаточно благородны для того, чтобы не разбивать сердце девушки, которая выбрала его, своим отказом. Таким образом, хотя девушки проявляют инициативу, высказывая свои предпочтения, ситуация вполне симметричная и лучше всего представляется таблицей, состоящей из нулей и единиц.

Перенумеруем юношей и девушек числами от до . Номера девушек запишем по строкам, номера юношей — по столбцам. Элемент, стоящий в -й строке и -м столбце таблицы равен тогда и только тогда, когда брак между девушкой с номером и юношей с номером возможен, и в противном случае. Иногда все девушки могут выйти замуж, а иногда поженить всех невозможно.

Приведу пример такой таблицы. Пусть юношей четверо и девушек тоже четверо. Пусть первой девушке нравятся первый и третий юноши, второй — первый и второй, третьей — второй, третий и четвертый, четвертой — первый и четвертый.

   

В данном случае можно поженить девушек и юношей с одинаковыми номерами.

Условие, необходимое и достаточное для того, чтобы всех можно было поженить, можно сформулировать несколькими эквивалентными способами:

1. Каждым девушкам, нравятся по крайней мере юношей.

Возьмем любые строк. Найдем столбцы, которые содержат хотя бы одну в выбранных строках. Число таких столбцов не должно быть меньше, чем .

2. Каждым юношей нравятся по крайней мере девушек.

Возьмем любые столбцов. Найдем строки, которые содержат хотя бы одну в выбранных столбцах. Число таких строк не должно быть меньше, чем .

3. В таблице не содержится подтаблицы, состоящей из одних нулей, из строк и столбцов такой, что .

Если такая таблица существует, то некоторые девушек могут вступить в брак только с юношами вне подтаблицы. Так как , юношей слишком мало, чтобы выдать замуж всех девушек.

Теорема Холла. Условия 1, 2, 3 являются необходимыми и достаточными, чтобы можно было всех поженить.

Доказательство. Необходимость очевидна.

Достаточность докажем по индукции. В случае , когда есть всего одна пара и взаимная симпатия, требуется простая формальность, чтобы договориться о браке. Предположим теперь, что теорема верна для всех , таких что . В случае девушек и юношей может быть так, что каждым () девушкам нравятся больше юношей, а может быть, что им нравятся ровно юношей. В первом случае первая девушка может выйти замуж за любого из тех, кто ей нравится, и тогда условие теоремы по-прежнему будет выполняться, но уже для девушки и юноши. Действительно, пусть каждым девушкам нравятся больше, чем юношей. Один из этих юношей, возможно, был тот, кто женился на первой девушке. Но без него еще есть по крайней мере юношей, которые нравятся девушкам. Таким образом, после женитьбы любой пары остается девушка и юноша, для которых условие теоремы по-прежнему выполняется. По индукционному предположению, всех можно поженить.

Во втором случае есть девушек, которым нравятся ровно юношей. По индукционному предположению, мы можем выдать замуж этих девушек за тех юношей, которые им нравятся. Хитрость заключается в том, чтобы показать, что остальных девушек тоже можно выдать замуж за оставшихся юношей. Рассмотрим любых из оставшихся девушек. замужним девушкам плюс этим девушкам должны нравиться по крайней мере юношей, по условию теоремы. Так как замужним девушкам не нравятся другие юноши кроме тех , с которыми они состоят в браке, девушкам должны нравиться другие юноши, не те, что женаты. Таким образом, оставшиеся девушек могут заключить брак с неженатыми юношами, так как для них также выполнено условие теоремы. Тем самым, всех можно поженить.

Задачу о свадьбах можно также представить с помощью графа. Этот граф двудольный (все его вершины можно разбить на два множества так, что ребра соединяют только вершины из разных множеств). Девушек будут обозначать вершины в одном множестве, юношей — в другом, ребрами соединим вершины, соответствующие девушке и юноше, которые нравятся друг другу. Теперь нарисуем вместо таблицы, приведенной в начале статьи, граф:

Источник: http://www.cut-the-knot.org/arithmetic/elegant.shtml

Теорема Холла — это… Что такое Теорема Холла?

Теорема Холла (или теорема о свадьбах), утверждает, что если в двудольном графе для любого любые элементов одной из долей связаны по крайней мере с элементами другой, то граф разбивается на пары.

Названна в честь английского математика Филипа Холла (англ.).

Теорема обобщается на граф, имеющий произвольное (не обязательно конечное или счётное) множество долей.

Пусть мощность первой доли — . Сделаем из данного графа сеть. Для этого на каждом ребре введем пропускную способность по 1 в направлении от вершины первой доли к вершине второй. При этом создадим две дополнительные вершины — и , от первой проведем все стрелки в вершины первой доли, а из каждой вершины второй проведем стрелки во вторую добавленную вершину. Заметим, что получившаяся сеть — целочисленная, то есть в ней существует максимальный целочисленный поток, и что если мы сможем доказать, что пропускная способность минимального разреза равна , то по теореме Форда-Фалкерсона величина максимального потока равна пропускной способности минимального разреза, то есть тоже равна . Очевидно, что если в бинарной транспортной сети величина максимального потока равна , то существует непересекающихся по вершинам путей из истока в сток. Это следует из алгоритма для нахождения максимального целочисленного потока в целочисленном графе, а из каждого такого пути можно выбрать смежную пару вершин из разных долей исходного графа.

То, что мощность минимального разреза не превышает , очевидно — достаточно рассмотреть разрез, в котором множество содержит одну вершину .

Теперь рассмотрим произвольный разрез . Пусть в попали ровно вершин из первой доли и из второй.

1. Пусть . Тогда пропускная способность разреза складывается из рёбер, ведущих из в вершины первой доли, лежащие в и рёбер, ведущих из вершин второй доли, лежащих в , в . Суммируя, получаем: .
2. Иначе, . По условию теоремы, эти вершин связаны с вершинами второй доли, а так как , то они связаны хотя бы с вершинами во второй доле, попавшими во множество . Тогда пропускная способность разреза рассчитывается так же, как в предыдущем пункте, плюс рёбер из вершин первой доли, принадлежащих в вершины второй доли, принадлежащими . Итого, .

В обоих случаях величина максимального потока равна , что и требовалось доказать.

Ссылки

НОУ ИНТУИТ | Лекция | Паросочетания и свадьбы

Аннотация: Паросочетания и свадьбы. Теорема Холла о свадьбах. Приложение теоремы Холла. Латинские квадраты.

Паросочетания и свадьбы

Результаты этой главы носят более комбинаторный характер, чем результаты всех предыдущих глав, хотя они тесно связаны с теорией графов. Обсудим хорошо известную «теорему о свадьбах», принадлежащую Филиппу Холлу, и некоторые приложения этой теоремы, например, построение латинских квадратов.

Теорема Холла о свадьбах

Теорема о свадьбах, доказанная Филиппом Холлом в 1935 г., отвечает на следующий вопрос, известный под названием задачи о свадьбах: рассмотрим некоторое конечное множество юношей, каждый из которых знаком с несколькими девушками; спрашивается,

при каких условиях можно женить юношей так, чтобы каждый из них женился на знакомой ему девушке? (Будем считать, что полигамия не разрешена.) Например, если имеется четверо юношей и пять девушек , а отношения знакомства между ними показаны в таблице 1, то возможно следующее решение: женится на , — на , — , а — на .

Эту задачу можно представить графически, взяв двудольный граф с множеством вершин, разделенных на два непересекающихся подмножества , представляющих юношей и девушек, соответственно, и соединив ребром каждого юношу со знакомой ему девушкой.

Рис. 15.1.

Напомним определение двудольного графа. Допустим, что множество вершин графа можно разбить на два непересекающихся подмножества и так, что каждое ребро в соединяет какую-нибудь вершину из с какой-либо вершиной из , тогда называем двудольным графом. Такие графы иногда обозначают , если хотят выделить два указанных подмножества. Двудольный граф можно определить и по-другому в терминах раскраски его вершин двумя цветами, скажем, красным и синим. При этом граф называется двудольным, если каждую его вершину можно окрасить красным или синим цветом так, чтобы любое ребро имело один конец красный, а другой — синий. Следует подчеркнуть, что в двудольном графе совсем не обязательно каждая вершина из соединена с каждой вершиной из ; если же это так и если при этом граф , простой, то он называется полным двудольным графом и обычно обозначается , где — число вершин, соответственно, в и .

Совершенным паросочетанием из в в двудольном графе называется взаимно однозначное соответствие между вершинами из и подмножеством вершин из , обладающее тем свойством, что соответствующие вершины соединены ребром. Ясно, что задачу о свадьбах можно выразить в терминах теории графов следующим образом: если — двудольный граф, то при каких условиях в существует совершенное паросочетание из в ?

Используя прежнюю «матримониальную» терминологию, можно сформулировать следующее очевидное утверждение: необходимое условие для существования решения в задаче о свадьбах в том, что любые юношей из данного множества должны быть знакомы (в совокупности ), по меньшей мере, с девушками (для всех целых , удовлетворяющих неравенствам , где через обозначено общее число юношей). Необходимость этого условия сразу вытекает из того, что если оно не верно для какого-нибудь множества юношей, то мы не сможем женить требуемым способом даже этих юношей, не говоря уже об остальных.

Теорема Кёнига (комбинаторика) — Википедия

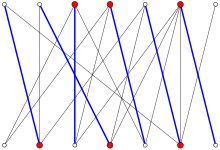Пример двудольного графа с наибольшим паросочетанием (выделено голубым) и наименьшим вершинным покрытием (выделено красным), оба имеют размер шесть.

В теории графов теорема Кёнига, доказанная Денешем Кёнигом в 1931, утверждает эквивалентность задач нахождения наибольшего паросочетания и наименьшего вершинного покрытия в двудольных графах. Это же было независимо открыто, в том же 1931, венгерским математиком Йенё Эгервари^[en] в несколько более общем виде для случая взвешенных графов.

Граф называется двудольным, если его вершины можно разбить на два множества так, что у каждого ребра конечные вершины принадлежат разным множествам.

Вершинное покрытие графа это множество вершин, такое, что любое ребро графа имеет хотя бы одну конечную вершину из этого множества. Вершинное покрытие называется наименьшим, если никакое другое вершинное покрытие не имеет меньшего числа вершин.

Паросочетанием в графе называется множество рёбер, не имеющих общих конечных вершин. Паросочетание называется наибольшим, если никакое другое паросочетание не содержит большего числа рёбер.

Теорема Кёнига утверждает, что в любом двудольном графе число рёбер в наибольшем паросочетании равно числу вершин в наименьшем вершинном покрытии.

Для графов, не являющихся двудольными, ситуация с задачами о наибольшем паросочетании и наименьшем вершинном покрытии совсем другая — наибольшее паросочетание можно найти за полиномиальное время для любого графа, в то время как поиск наименьшего вершинного покрытия является NP-полной задачей. Дополнение вершинного покрытия для любого графа — это независимое множество и поиск наибольшего независимого множества — это ещё одна NP-полная задача. Эквивалентность между паросочетаниями и покрытиями, выраженная в теореме Кёнига, позволяет найти наименьшее вершинное покрытие и наибольшее независимое множество за полиномиальное время для двудольных графов вопреки NP-полноте этой задачи для более общих семейств графов.

Теорема Кёнига эквивалентна массе других минимаксных теорем в теории графов и комбинаторике, таких как теорема Холла о свадьбах и теорема Дилуорса. Поскольку паросочетание в двудольных графах является частным случаем теоремы Форда — Фалкерсона, теорема Кёнига вытекает из теоремы Форда — Фалкерсона.

Теорема названа в честь венгерского математика Денеша Кёнига. Кёниг заявил о ней в 1914 и опубликовал в 1916 доказательство, что любой регулярный двудольный граф имеет совершенное паросочетание,^[1] и, обобщённо, что хроматический индекс любого двудольного графа (то есть наименьшее число паросочетаний, на которые можно разложить все дуги графа) равен максимальной степени^[2]. Последнее утверждение известно как теорема Кёнига о рёберной раскраске.^[3] Однако Бонди и Мерфи (Bondy, Murty, 1976) приписывают саму теорему более поздней работе Кёнига (1931). Согласно Бигу (Bigg) Кёниг приписывает идею изучения паросочетаний в двудольных графах своему отцу, математику Юлию Кёнигу^[en].

В любом двудольном графе число рёбер в наибольшем паросочетании равно числу вершин в наименьшем вершинном покрытии.

В русскоязычном интернете и научной литературе распространена следующая формулировка теоремы^[4]:

Если прямоугольная матрица составлена из нулей и единиц, то минимальное число линий, содержащих все единицы, равно максимальному числу единиц, которые могут быть выбраны так, чтобы никакие две из них не лежали на одной и той же линии (термин «линия» обозначает либо строку, либо столбец в матрице).^[5]

Данная формулировка легко переводится на язык двудольных графов:

Строки таблицы — это вершины одной части двудольного графа, столбцы — другой части.

Линии — это вершинное покрытие.

Единицы матрицы — рёбра. Требование, чтобы никакие две единицы не лежали на одной линии, соответствует паросочетанию.

Двудольный граф на рисунке вверху имеет 14 вершин, паросочетание с 6 рёбрами выделено синим цветом, а вершинное покрытие из шести вершин выделено красным. Нет меньшего по размеру вершинного покрытия, поскольку любая вершина должна включать по меньшей мере одну конечную вершину ребра паросочетания, так что это покрытие является наименьшим. Таким же образом, нет паросочетания большего размера, поскольку любое ребро паросочетания должно содержать по меньшей мере одну конечную вершину из вершинного покрытия, так что это паросочетание является наибольшим. Теорема Кёнига как раз и утверждает равенство размеров паросочетания и покрытия (в данном примере оба числа равны шести).

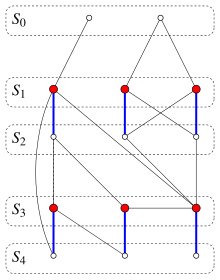Разделение вершин двудольного графа с паросочетанием на чётные и нечётные уровни для доказательства теоремы Кёнига.

Пусть задан двудольный граф G=(V,E){\displaystyle G=(V,E)}, и пусть V{\displaystyle V} делится на левое множество L{\displaystyle L} и правое R{\displaystyle R}.

Пусть M{\displaystyle M} — наибольшее паросочетание в G{\displaystyle G}.

По определению «паросочетания», никакая вершина не может принадлежать более чем одному ребру из M{\displaystyle M}. Таким образом, если вершинное покрытие с |M| вершинами может быть построено, оно наименьшее.

Если M{\displaystyle M} — совершенное паросочетание (что предполагает, что M{\displaystyle M} — наибольшее), то |L| = |R| = |M|. Поскольку каждое ребро G{\displaystyle G} сопряжено ровно с одной вершиной из L и ровно с одной вершиной из R, либо L, либо R является вершинным покрытием размера |M| и теорема доказана.

В противном случае используем построение чередующегося пути для построения наименьшего покрытия. При заданном M чередующимся путём называется путь, рёбра которого поочерёдно берутся из M и E \ M. Разделим вершины V графа G{\displaystyle G} на подмножества S_i, как описано ниже. Мы покажем, что объединение подмножеств с нечётными индексами является вершинным покрытием с |M| вершинами.

• Пусть S₀ состоит из всех вершин, не принадлежащих паросочетанию M.
• Для целого j ≥ 0, пусть S_2j+1 — множество всех вершин v, таких, что

1. v связано с некоторой вершиной из S_2j ребром из E \ M
2. v не входит ни в одно из ранее построенных множеств S_k, где k < 2j+1.

Если таких вершин нет, но остаются вершины, не содержащиеся в ранее построенных множествах S_k, выбираем произвольную из них и полагаем, что S_2j+1 состоит из этой единственной вершины.

• Для целого j ≥ 1, пусть S_2j — множество всех вершин u, таких, что u принадлежит некоторому ребру из M со второй вершиной из S_2j−1.

Заметим, что для любой v из S_2j−1 существует вершина u, в паре, с которой они входят в паросочетание, поскольку в противном случае v была бы в S₀. Таким образом, M устанавливает однозначное соответствие между вершинами из S_2j−1 и вершинами из S_2j.

Относительно последнего члена этого списка могут возникнуть сомнения — а не может ли случиться так, что вершина u, принадлежащая некоторому ребру из M с вершиной v в S_2j−1, будет также содержаться и в множестве S_i с индексом, меньшим 2j, откуда последует, что множество S_i не образует отдельной части. Мы покажем, что такого произойти не может.

• Вершина v, появившаяся по построению первый раз в S_2j−1, не может вместе с вершиной из S_2k с k < j принадлежать паросочетанию, поскольку вершины S_2k либо не содержатся ни в какой дуге паросочетания (при k = 0), либо образуют дугу паросочетания вместе с дугой из S_2k−1 (при k ≥ 1).
• Вершина v не может паросочетаться с вершиной u из S_2k-1 с k ≤ j. Заметим, во-первых, что вершины из S_2k−1 с k < j паросочетаются с вершинами из S_2k с 2k < 2j−1 и, поэтому, не могут паросочетаться с v. Во-вторых, предположим, что v паросочетается с u из S_2j−1. Построим чередующийся путь с началом в вершине v путём выбора ребра из E \ M, содержащего конечную вершину v и вторую вершину из S_2j−2, ребра из M, содержащего полученную вершину и вершину из S_2j-3, и так далее. Получим связи вершин из S_i с вершинами из S_i−1 рёбрами из E \ M при i нечётном и рёбрами из M при i чётном. Процесс будет продолжаться, пока либо не достигнем S₀, либо множество S_2h+1 будет содержать единственную вершину, не имеющую рёбер, соединяющих её с нижним уровнем S_2h. Построим такой же путь, начиная с u. Объединяя эти два пути ребром vu из M, получим более длинный чередующийся путь P. Путь P является простым, поскольку в случае наличия общей вершины w на уровне i, получили бы нечётной длины цикл, содержащий вершину w, что невозможно в двудольных графах. Как следствие, конечные вершины пути P должны быть различными вершинами из S₀. Поскольку первое и последнее ребро P принадлежат E \ M, P содержит на единицу больше рёбер из E \ M чем из M. Тогда, убирая рёбра P ∩ M из M и добавляя рёбра P ∩ (E \ M) к M мы получим паросочетание с большим числом рёбер, чем в M, что противоречит условию, что M наибольшее.

Мы показали, что каждая вершина множества V содержится ровно в одном множестве S_i. Отсюда следует, что рёбра M всегда соединяют вершины смежных уровней S_2j−1 и S_2j. Покажем, что никакое ребро E \ M не соединяет пару вершин, лежащих на чётных уровнях. Предположим, что ребро из E \ M соединяет вершину из S_2j с вершиной из S_2k при k ≤ j. Если v — вершина в S_2k с k < j, то любая вершина, сопряжённая с v ребром из E \ M, находится на уровне S_i с i ≤ 2k+1 < 2j, а потому v не может быть связано ребром из E \ M с вершиной из S_2j. С другой стороны, применяя тот же приём построения чередующегося пути, две вершины из S_2j не могут быть связаны друг с другом дугой из E \ M. Следовательно, любое ребро из M имеет в точности одну вершину в нечётном множестве и любое ребро из E \ M имеет по меньшей мере одну конечную вершину в нечётном множестве. Таким образом, объединение всех нечётных множеств даст вершинное покрытие с |M| вершинами.

Построение, описанное выше и используемое для доказательства теоремы, даёт алгоритм построения наименьшего вершинного покрытия по заданному наибольшему паросочетанию. Так, алгоритм Хопкрофта–Карпа^[en] для поиска наибольшего паросочетания в двудольных графах может быть использован для эффективного решения задачи о наименьшем вершинном покрытии.

Вопреки эквивалентности двух задач с точки зрения точного решения, они совершенно не эквивалентны для аппроксимационных алгоритмов. Задача о наибольшем паросочетании для двудольных графов может быть аппроксимирована с произвольной точностью за постоянное время с помощью распределённых алгоритмов^[en], в противоположность задаче о наименьшем вершинном покрытии, требующей как минимум логарифмического времени.^[6]

Говорят, что граф совершенен, если для любого порождённого подграфа его хроматическое число равно размеру максимальной клики. Любой двудольный граф совершенен, поскольку любой его подграф является либо двудольным, либо независимым. В двудольном графе, не являющемся независимым, хроматическое число и размер максимальной клики равны двум, в то время как для независимого множества оба этих числа равны единице.

Граф совершенен тогда и только тогда, когда его дополнение совершенно (Lovász 1972), и теорему Кёнига можно считать эквивалентом утверждения, что дополнение двудольного графа совершенно. Любые раскраски дополнения двудольного графа имеют размер максимум 2, а классы размера 2 образуют паросочетания. Клики в дополнении графа G — это независимое множество в G, и, как мы уже писали выше, независимое множество в двудольном графе G — это дополнение вершинного покрытия G. Таким образом, любое паросочетание M в двудольном графе G с n вершинами соответствует раскраске дополнения G с n-|M| цветами, что, ввиду совершенства дополнения двудольных графов, соответствует независимому множеству в G с n-|M| вершинами, что соответствует вершинному покрытию G |M| вершинами. Следовательно, теорема Кёнига доказывает совершенство дополнений двудольных графов, то есть результат, выраженный в более явной форме у Галаи (Gallai, 1958).

Можно связать также теорему Кёнига о рёберной раскраске с другим классом совершенных графов, рёберными графами двудольных графов. Для графа G рёберный граф L(G) имеет вершины, соответствующие рёбрам графа G, и рёбра для каждой пары смежных рёбер в G. Таким образом, хроматическое число L(G) равно хроматическому индексу G. Если G — двудольный, клики в L(G) — это в точности множества рёбер в G, имеющих общую конечную вершину. Теперь теорема Кёнига о рёберной раскраске, утверждающая, что хроматический индекс равен максимальной степени вершин в двудольном графе, может быть интерпретирована как утверждение, что рёберный граф двудольного графа совершенен.

Поскольку рёберные графы двудольных графов совершенны, дополнения рёберных графов двудольных графов тоже совершенны. Клика в дополнении рёберного графа для G — это просто паросочетание G. А раскраска дополнения рёберного графа для G, в случае, если G является двудольным, — это разбиение рёбер графа G на подмножества рёбер, имеющих общие вершины. Конечные вершины, являющиеся общими в этих подмножествах, образуют вершинное покрытие графа G. Таким образом, сама теорема Кёнига может быть также интерпретирована как утверждение, что дополнение рёберных графов двудольных графов совершенно.

1. ↑ На плакате, выставленном в 1998 на Международном конгрессе математиков в Берлине, а затем на Международной конференции по теории графов Bled’07, Геральд Гроп (Harald Gropp) указал на то, что тот же самый результат уже появлялся на языке конфигураций в 1894 в тезисах Эрнста Штайница.
2. ↑ Biggs, 1976.
3. ↑ Lovász, 1986, Theorem 1.4.17, с. 37.
4. ↑ Рыбников, 1972, с. 100.
5. ↑ Вопросы кибернетики. Тр. Семинара по комбинаторной математике. — М., 1973. — С. 185—99..
6. ↑ Göös, 2012.

• Biggs, N. L.; Lloyd, E. K.; Wilson, R. J. Graph Theory 1736–1936. — Oxford University Press, 1976. — С. 203–207. — ISBN 0-19-853916-9.

• J. A. Bondy, U. S. R. Murty. Graph Theory with Applications. — North Holland, 1976. — С. 74. — ISBN 0-444-19451-7.

• Gallai, Tibor. Maximum-minimum Sätze über Graphen // Acta Math. Acad. Sci. Hungar.. — 1958. — Т. 9, вып. 3-4. — С. 395–434. — DOI:10.1007/BF02020271.

• Mika Göös, Jukka Suomela. 26th International Symposium on Distributed Computing (DISC), Salvador, Brazil, October 2012. — 2012.

• Kőnig, Dénes. Gráfok és alkalmazásuk a determinánsok és a halmazok elméletére // Matematikai és Természettudományi Értesítő. — 1916. — Т. 34. — С. 104–119.

• Kőnig, Dénes. Gráfok és mátrixok // Matematikai és Fizikai Lapok. — 1931. — Т. 38. — С. 116–119.

• László Lovász, M. D. Plummer. Matching Theory. — North-Holland, 1986. — ISBN 0-444-87916-1.

Гипотеза Холла — Википедия

Гипотеза Холла — нерешённая на 2015 г. теоретико-числовая гипотеза об оценке сверху для решений диофантова уравнения Морделла y2=x3+k{\displaystyle y^{2}=x^{3}+k} при заданном k≠0{\displaystyle k\neq 0}. Имеет несколько формулировок разной силы. Была сформулирована Холлом в 1971 г.

Первоначальная формулировка такова:

Существует константа C>0{\displaystyle C>0}, такая что если y2=x3+k{\displaystyle y^{2}=x^{3}+k} для x,y,k∈Z{\displaystyle x,y,k\in \mathbb {Z} } и k≠0{\displaystyle k\neq 0}, то |x|⩽C|k|2{\displaystyle |x|\leqslant C|k|^{2}}.

Из конкретных решений разных уравнений для разных k{\displaystyle k} можно получать оценки снизу для C{\displaystyle C}. Наиболее сильный пример был найден Элкисом в 1998:

4478849284284020423079182−58538865167812233=−1641843{\displaystyle 447884928428402042307918^{2}-5853886516781223^{3}=-1641843}

Из него следует оценка C>2171{\displaystyle C>2171}. Это делает гипотезу неправдоподобной в такой формулировке, хотя эта формулировка и не опровергнута.

Старк и Троттер в 1980 предположили ослабленный вариант гипотезы Холла:

Для любого ϵ>0{\displaystyle \epsilon >0} существует константа C(ϵ)>0{\displaystyle C(\epsilon )>0}, такая что если y2=x3+k{\displaystyle y^{2}=x^{3}+k} для x,y,k∈Z{\displaystyle x,y,k\in \mathbb {Z} } и k≠0{\displaystyle k\neq 0}, то |x|⩽C(ϵ)|k|2+ϵ{\displaystyle |x|\leqslant C(\epsilon )|k|^{2+\epsilon }}.

Ввиду неправдоподобности первоначального варианта гипотеза Холла теперь гипотезой Холла называется её ослабленный вариант с ϵ{\displaystyle \epsilon }.

Доказано, что показатель 2 в оценке нельзя уменьшить — гипотеза становится неверной для оценки вида |x|⩽C|k|2−ϵ{\displaystyle |x|\leqslant C|k|^{2-\epsilon }} (Данилов, 1982).

Теорема Дэвенпорта — Аналог гипотезы Холла для многочленов[править | править код]

В 1965 Дэвенпорт доказал аналог гипотезы Холла для многочленов:

Если g(t)2=f(t)3+k(t){\displaystyle g(t)^{2}=f(t)^{3}+k(t)}, где k(t)≠const,f(t),g(t)≠0{\displaystyle k(t)\neq \mathrm {const} ,f(t),g(t)\neq 0}, то deg⁡f(t)⩽2(deg⁡k(t)−1){\displaystyle \deg f(t)\leqslant 2(\deg k(t)-1)}.

Эта теорема сразу следует из теоремы Мейсона — Стотерса^[en], аналога ABC-гипотезы для многочленов: Пусть a(t),b(t),c(t){\displaystyle a(t),b(t),c(t)} — попарно взаимно простые неконстантные многочлены, такие, что a+b=c{\displaystyle a+b=c}, тогда

max{deg⁡(a),deg⁡(b),deg⁡(c)}⩽deg⁡(rad⁡(abc))−1.{\displaystyle \max\{\deg(a),\deg(b),\deg(c)\}\leqslant \deg(\operatorname {rad} (abc))-1.}

Здесь rad(f){\displaystyle \mathrm {rad} (f)} — радикал многочлена, то есть произведение его различных простых множителей.

Подстановка c=g2{\displaystyle c=g^{2}}, a=f3{\displaystyle a=f^{3}}, b=k{\displaystyle b=k} даёт 2 неравенства:

3deg⁡f,2deg⁡g⩽deg⁡f+deg⁡g+deg⁡k−1{\displaystyle 3\deg f,2\deg g\leqslant \deg f+\deg g+\deg k-1},

из которых и получается теорема.

Гипотеза Холла следует из ABC-гипотезы. Из ABC-гипотезы сразу следует даже более сильная, т. н. радикальная гипотеза Холла:

Для любого ϵ>0{\displaystyle \epsilon >0} существует константа C(ϵ)>0{\displaystyle C(\epsilon )>0}, такая что если y2=x3+k{\displaystyle y^{2}=x^{3}+k} для x,y,k∈Z{\displaystyle x,y,k\in \mathbb {Z} } и k≠0{\displaystyle k\neq 0}, НОД(x,y)=1{\displaystyle {\text{НОД}}(x,y)=1} то |x|⩽C(ϵ)rad(k)2+ϵ{\displaystyle |x|\leqslant C(\epsilon )\mathrm {rad} (k)^{2+\epsilon }}.

Здесь rad(k){\displaystyle \mathrm {rad} (k)} — радикал целого числа k{\displaystyle k}.

Оказывается, из радикальной гипотезы Холла также следует ABC-гипотеза. Однако это утверждение нетривиально.^[1][2]

Обобщение гипотезы Холла на другие степени — это гипотеза Пиллаи.

Теория Холла — Википедия

Теория кодирования и декодирования Холла — критическая теория в области анализа приёма сообщений (англ. reception theory), сформулированная британским социологом Стюартом Холлом в труде «Encoding, decoding in the television discourse» (1973). В своих суждениях Холл основывался на примере телевидения, однако его подход применим и к другим масс-медиа.

Модель кодирования/декодирования поставила под вопрос конвенциональную модель коммуникации, представляющую собой линейную структуру: отправитель — сообщение — адресат. Согласно этой модели, отправитель создает сообщение, которое напрямую доходит до получателя, сохраняя свой первоначальный смысл. Холл счел этот процесс слишком изящным: он был скорее заинтересован тем, как зритель способен производить, а не обнаруживать истинное значение медиа-текста.

Эссе Холла бросает вызов всем трем компонентам массовых коммуникаций, утверждая, что:

• Значение сообщения не может быть четко зафиксировано отправителем
• Сообщение не может всегда нести очевидный и ясный смысл
• Аудитория не является пассивным приёмником сообщения

В качестве примера Холл приводит документальный фильм о просителях убежища. Он утверждает, что стремление создателей фильма вызвать сочувствие зрителей, не гарантирует, что аудитория действительно испытает это чувство. Для реализма и акцента на факты, документальная форма вынуждена обращаться к зрителю с помощью системы знака (аудиовизуальные признаки телевидения), что с одной стороны искажает намерения продюсера и режиссёра, а с другой —вызывает противоречивые чувства у аудитории.

Вместо того, чтобы назвать это искажение ошибкой или недостатком, Холл, напротив, встраивает его в систему коммуникационного обмена между моментом производства сообщения (кодированием) и моментом его приема (декодированием)

Согласно модели Холла, сообщения, получаемые аудиторией из телевидения и других СМИ, интерпретируются ею по-разному в зависимости от культурного бэкграунда человека, его экономического статуса, социального пространства, которое он занимает, и личного опыта. В отличие от других теорий СМИ, в которых роль зрителя сведена к нулю, Холл впервые выдвинул идею, что члены аудитории могут играть активную роль в расшифровке (декодировании) сообщений.

Именно в процессе декодирования осуществляется «семантическая герилья» против господствующей идеологии путём переосмысления преференциальных смыслов, заложенных в послание отправителями. Она возможна потому, что «не существует неизбежной зависимости между кодированием и декодированием: первое может попытаться навязать свои предпочтения, но не в состоянии предписать или гарантировать последнее, которое имеет собственные условия существования^[1]

.

Типы восприятия аудиторией медиасообщения[править | править код]

Как уже сказано, общий вывод Холла состоит в том, что декодированный смысл не всегда совпадает с тем смыслом, который был закодирован, так как зритель подходит к содержанию, предлагаемому медиа, с другими «смысловыми структурами», которые коренятся в его собственных идеях и опыте. Холл говорит, что предмет расшифровки может принять три различных положения:

• Доминирующая, либо желаемая реакция (англ. Dominant, or Preferred, Reading) — такая, какой её видит директор / создатель, когда хочет чтобы аудитория просмотрела медиатекст;
• Оппозиционное прочтение (англ. Opposition Reading) — аудитория отвергает предполагаемое создателем содержание и создаёт своё собственное;
• Согласованное прочтение (англ. Negotiated Reading) — компромисс между доминирующим и оппозиционным чтением, когда публика частично воспринимает мысли директора, но в то же время имеет свои собственные взгляды на текст.

Более свежие разработки в области анализа приема сообщений подчеркивают тот факт, что медиа-сообщения — это не просто закодированные языком смыслы, но смысловые конструкции, комбинирующие закодированный текст со смыслами, которые атрибутирует тексту его читатель^[2]. Согласно представлениям Джона Фиске («Television Culture», 1987), медиа-текст — это продукт его читателей. Он указывает, что (телевизионная) программа становится текстом именно в момент чтения, то есть когда её взаимодействие с одной из её многочисленных аудиторий активирует какие-нибудь смыслы, которые она способна вызвать»^[2]. Фиске вводит понятие «дискурс» и определяет его как «язык или систему репрезентации, которая развилась в ходе социальных процессов и которая создает и поддерживает когерентный набор смыслов относительно какого-то важного предмета». Определенное таким образом понятие дискурса весьма близко понятию смысловой структуры Холла (1980). По Фиске, множественность смыслов (полисемия) медиа-текстов — не просто демонстрируемый факт, но существенная характеристика средств медиа, делающая их популярными среди самых широких социальных слоев, и в разных социальных ситуациях.

В своей модели Фиске располагает смыслосодержащий текст на пересечении дискурсивного мира аудитории и дискурса, воплощенного в медиа-тексте. Телезритель вносит свой вклад в конструирование смысла текста, используя для этого свой собственный опыт. Важная переменная ТВ-дискурса — степень реализма. Чем «реалистичней» программа, тем более ограничены смыслы, которые могут быть сконструированы аудиторией. Чем более программа «полисемична», тем более она «открыта», тем больше разных текстов и альтернативных смыслов может быть сконструировано зрителями на её основе.

Исследователь Е.Г. Дьякова в своей работе «Семантическая герилья в Рунете как способ политической борьбы» рассматривает теорию Холла как «теоретическе обоснование практических попыток на основе семантической герильи дестабилизировать гегемонистский культурный порядок, будь то неоколониализм или патриархатное общество»^[3]. По её мнению, Холл с помощью своей теории научно обосновал тот факт, что гегемонистский культурный порядок не является всеобъемлющим. Сферу декодирования посланий E. Дьякова определяет как основное место борьбы за идеологическую гегемонию.

• Fiske, J. Television Culture. — London: Routledge, 1987
• Hall, S. Encoding, decoding in the television discourse. // Hall, S., Hobson, D. & Lowe, P. (eds). Culture, Media, Language. — London: Hutchinson, 1980
• Hall, S. / Encoding/decoding. In Centre for Contemporary Cultural Studies (Ed.): Culture, Media, Language: Working Papers in Cultural Studies — London: Hutchinson — 1972-1979 — C. 128—C. 138, (‘Encoding and Decoding in Television Discourse’, 1973)
• Proctor, James Stuart Hall // Routledge critical thinkers — 2004 — ISBN 978-0415262675
• McQual, D. & Windhal, S. / Communication Models for the Study of Mass Communication. 2nd Edition — London: Longman — 1993 — C. 146—C. 147 — ISBN 978-0582036505