30. Магнитный поток. Теорема Остроградского-Гаусса.

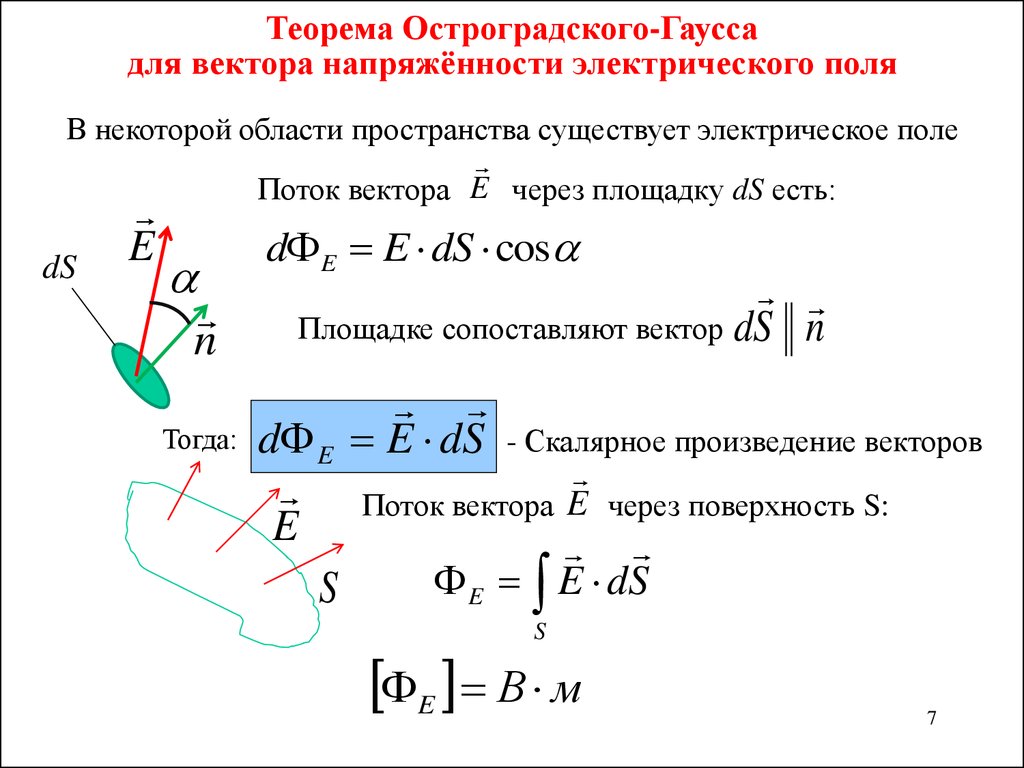
Магнитным потоком dФ (потоком вектора магнитной индукции) через площадку dS называется произведение площади этой площадки dS и проекции индукции B магнитного поля на направление внешней нормали n площадки dS.

Магнитный поток через поверхность S есть интеграл:

Если поле однородное =const., а поверхность плоская и магнитное поле перпендикулярное к поверхности, то:

Отсюда вытекает единица измерения магнитного потока в СИ.

[Ф]= Вебер (Вб)

Магнитный поток через поверхность равен одному веберу, если площадь поверхности равна одному квадратному метру, магнитное поле с индукцией 1 Тл перпендикулярно поверхности.

1 Вб = 1Тл × 1 м

Магнитный поток через поверхность численно равен числу магнитных силовых линий проходящих через эту поверхность или пропорционален числу магнитных силовых линий.

Теорема Остроградского — Гаусса: магнитный поток через любую замкнутую поверхность равна нулю, т.е.

Теорема Остроградского – Гаусса означает замкнутость магнитных силовых линий, т.е. отсутствие магнитных зарядов, на которых могли бы начинаться и кончаться магнитные силовые линии.

Рассмотрим доказательство теоремы Остроградского – Гаусса для магнитного поля на примере бесконечного прямолинейного проводника с током I.

В качестве поверхности S возьмем круговой цилиндр, с осью совпадающей с током.

Магнитные силовые линии такого тока есть концентрические окружности с центром на оси тока.

Тогда =0 (проекция на направление внешней нормали).

Очевидно, что:

Рассмотрим работу перемещения проводника с током в магнитном поле.

На проводник с током будет действовать сила Ампера и проводник передвинется.

Элементарная работа при перемещении проводника:

Конечная работа это:

Рассмотрим прямоугольную рамку с током I в однородном магнитном поле .

Покажем, что в общем случае рамка будет вращаться.

Это вид сбоку. Раз течет ток, то возникает сила Ампера.

Сила Ампера будет действовать на ребра

a перпендикулярные к ним и к магнитной индукции и будет только растягивать рамку.

Вид сверху:

Оказывается, что

Магнитное поле создаваемое самой рамкой будет совпадать с индукцией

Если контур повернется под действием сил на угол , то будет совершена работа этими силами.

(1)

С другой стороны, так как магнитный поток через плоскую поверхность ограничивается рамкой, магнитный поток есть:

, где S— площадь поверхности ограниченной рамкой.

(2)

Приравняем (1) и (2), получим:

получим максимальный момент

— определение магнитной индукции

1Тл =

Однако Тл это индукция такого однородного магнитного поля, которое создает максимальный вращательный момент на рамку с током в 1 ампер и площадью поверхности.

Поле должно быть однородным.

Если контур в неоднородном поле, то кроме вращательного момента возникает сила втягивающая рамку в область сильного поля.

| Теорема Остроградского-Гаусса для магнитного поля

Контрольные вопросы к главе 19

1. Какое время должен затратить протон в магнитном поле циклотрона, чтобы приобрести кинетическую энергию 10 МэВ, если при каждом обороте протон проходит между дуантами разность потенциалов 30 кВ? Магнитное поле циклотрона равно 1 Тл. (Ответ:

»3,47 мкс) (§19.1)

2. Тонкое металлическое кольцо быстро вращается вокруг вертикальной оси, проходящей через его диаметр и перпендикулярной однородному магнитному полю с индукцией 10-2 Тл. Пренебрегая трением в оси, определите, через какое время угловая скорость вращения уменьшается в е раз. (Ответ: »7,2 с) (§19.1)

3. По тонкому проводу в виде кольца радиусом 20 см течёт ток 100 А. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с индукцией 20 мТл.

Чему равна сила, растягивающая кольцо? (Ответ: 0,4 Н) (§19.3)

4. На оси контура с током, магнитный момент которого равен 10 мА×м2, находится такой же контур. Вектор магнитного момента второго контура перпендикулярен оси. Чему равен механический момент, действующий на второй контур? Расстояние между контурами равно 50 см. Размеры контуров малы по сравнению с расстоянием между ними. (Ответ: »0,16 нН×м) (§19.4)

5. Как будет себя вести изначально неподвижный магнитный момент, направленный по полю в представленном на рисунке магнитном поле? (Ответ: ускоренно двигаться влево) (§19.4)

6. Выполняется ли третий закон Ньютона при магнитном взаимодействии точечных зарядов? Возможна ли ситуация, когда первый заряд на второй действует, а второй на первый нет?

(§19.5)

7. Какова степень расстояния между источником и точкой наблюдения в зависимости модуля магнитной индукция от точки наблюдения? (§19. 7)

8. Магнитный момент, равный 1 А×м2, помещён в центр плоской петли радиуса 10 см на бесконечно длинном тонком проводе с силой тока 50 А, такой как показано на рисунке. Чему равен механический момент, действующий на магнитный? (Ответ: »214 мкН×м)

(§19.8)

9. Магнитный момент, равный 1 А×м2, помещён в центр плоской петли радиуса 10 см на бесконечно длинном тонком проводе с силой тока 50 А, такой как показано на рисунке. Чему равен механический момент, действующий на магнитный? (Ответ: »414 мкН×м) (§19.8)

10. Магнитные моменты из двух предыдущих задач перенесли на 5 метров из центров петель перпендикулярно проводу вверх. На сколько будут отличаться механические моменты первого и второго магнитного момента в новом положении? (Ответ: второй больше первого на »5нН×м) (§19.8)

Глава 20. МАГНЕТИЗМ.

ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ

§20.1. Теорема Остроградского-Гаусса для магнитного поля

Магнитным потоком Фm называется поток вектора магнитной индукции.

Теорема Остроградского-Гаусса для магнитного потока является обобщением опытных фактов:

магнитный поток через любую замкнутую поверхность равен 0.

Это означает, что силовые линии магнитного поля замкнуты, и в природе не существует магнитных зарядов — источников магнитного поля, из которых могли бы исходить силовые линии или на которых они обрывались бы.

Источниками магнитного поля являются токи, и силовые линии магнитного поля замыкаются вокруг них.

§20.2. Работа силы Ампера на перемещении проводника с током в постоянном магнитном поле

Рассмотрим элемент с током , ориентированный по току, движущийся со скоростью в постоянном магнитном поле с индукцией в месте нахождения . На один носитель заряда q0 в этом элементе со стороны магнитного поля действует сила, равная

,

где — дрейфовая скорость носителей относительно элемента .

Полная сила, действующая со стороны магнитного поля на совокупность носителей заряда в рассматриваемом элементе с током:

,

где dN — количество носителей в элементе. Тогда

С первым слагаемым мы уже сталкивались. Это — сила Ампера . Последнее слагаемое обозначим , то есть

.

Пусть dt — время, которое один носитель затрачивает на прохождение отрезка движущегося проводника. Тогда представляет собой перемещение всех рассматриваемых dN носителей относительно движущегося проводника. Обозначим элементарное перемещение проводника с током за время dt относительно неподвижного магнитного поля, как . Полное перемещение совокупности dN носителей относительно источников постоянного магнитного поля в соответствие с классической относительностью перемещения

.

Следовательно, работа магнитной силы на перемещении совокупности dN носителей

формально раскладывается на 4 слагаемых. Теперь проанализируем ситуацию с направлениями. Очевидно, что , поскольку . Очевидно, что , поскольку (рис.20.1).

Рис.20.1

Значит, из четырёх слагаемых элементарной работы магнитной силы два, и , равны 0. Оказывается, эта работа содержит всего два слагаемых:

.

Рассмотрим эти слагаемые по очереди.

Элементарная работа силы Ампера, действующей на элемент проводника с током

выражается через смешанное произведение трёх векторов, к которому применимо правило циклической перестановки:

Вектор является вектором элементарной площади, заметённой элементом при его поступательном движении (рис.20.2, левый).

SCIRP Открытый доступ

Издательство научных исследований

Журналы от A до Z

Журналы по темам

• Биомедицинские и биологические науки.
• Бизнес и экономика
• Химия и материаловедение.
• Информатика. и общ.
• Науки о Земле и окружающей среде.
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные науки. и гуманитарные науки

Журналы по тематике  

• Биомедицина и науки о жизни
• Бизнес и экономика
• Химия и материаловедение
• Информатика и связь
• Науки о Земле и окружающей среде
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные и гуманитарные науки

Публикация у нас

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Публикуйте у нас  

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Недавно опубликованные статьи

Недавно опубликованные статьи

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Бесплатные информационные бюллетени SCIRP

Copyright © 2006-2022 Scientific Research Publishing Inc. Все права защищены.

Вершина

Рассчитайте заряд монополя

Журнал физики высоких энергий, гравитации и космологии Vol.04 No.04 (2018), ID статьи:86538,7 страниц
10.4236/jhepgc.2018.44035

Закон Гаусса для магнетизма и закон универсального магнетизма: расчет заряда монополя Inc.

Эта работа находится под лицензией Creative Commons Attribution International License (CC BY 4. 0).

http://creativecommons.org/licenses/by/4.0/

Получено: 12 апреля 2018 г.; Принято: 5 августа 2018 г.; Опубликовано: 8 августа 2018 г.

АННОТАЦИЯ

В этой статье описывается математическое доказательство того, что закон Гаусса для магнетизма может быть получен из закона универсального магнетизма [1]. Второе обратное доказательство также показывает, что Закон универсального магнетизма может быть выведен из закона Гаусса для магнетизма. Эти два дополняющих друг друга доказательства подтверждают, что Закон Универсального Магнетизма является действительным уравнением, основанным на законе Гаусса. В статье также подтверждается теоретическое существование магнитного монополя и рассчитывается его магнитный заряд с использованием соотношения электромагнитного поля и скорости света. Используя отношение массы электрона к заряду, определяются масса и радиус магнитного монополя. Установлено, что монополь имеет тот же радиус, что и электрон, и его также можно найти в диапазоне электромагнитного спектра, известном как гамма-лучи. Молния является естественным источником гамма-лучей и может оказаться полезной для поиска монополей.

Ключевые слова:

Закон Гаусса для магнетизма, Закон универсального магнетизма, Плотность магнитного заряда, Проницаемость, Монополь

. В этой статье предлагается доказательство, чтобы определить, согласуется ли этот закон с законом Гаусса для магнетизма. Закон Гаусса для магнетизма является физическим применением теоремы Гаусса, также известной как теорема о дивергенции в исчислении, которая была независимо открыта Лагранжем в 1762 году, Гауссом в 1813 году, Остроградским в 1826 году и Грином в 1828 году [2].

Закон Гаусса для магнетизма — одно из четырех уравнений Максвелла, лежащих в основе классической электродинамики. Оно утверждает, что магнитное поле B имеет дивергенцию, равную нулю [3], является соленоидальным векторным полем и эквивалентно утверждению об отсутствии магнитных монополей [4]. Основным элементом магнетизма является не магнитные заряды, а магнитный диполь. Если бы существовали магнитные монополи, то закон Гаусса для магнетизма гласил бы, что расхождение B было бы пропорционально плотности магнитного заряда ρ _м , аналогично закону Гаусса для электрического поля. Если магнитных монополей не существует, то для нулевой суммарной плотности магнитного заряда (ρ _m = 0) результатом является исходная форма закона магнетизма Гаусса. Если монополии когда-нибудь будут найдены, закон Гаусса придется модифицировать, как описано в этой статье.

В 1894 г. Пьер Кюри указал, что магнитные монополи теоретически могут существовать, несмотря на то, что до сих пор их не наблюдали [5]. Физик Поль А. М. Дирак в 1931 году предложил квантовую теорию магнитного заряда, в своей работе Дирак показал, что если во Вселенной существуют какие-либо магнитные монополи, то весь электрический заряд во Вселенной должен быть квантован [6].

2. Вывод закона Гаусса для магнетизма из закона универсального магнетизма

Закон Гаусса для магнетизма не может быть выведен только из закона универсального магнетизма, поскольку закон универсального магнетизма определяет магнитное поле только благодаря индивидуальному магнитному заряду. Однако закон Гаусса для магнетизма можно доказать из закона универсального магнетизма, если предположить, кроме того, что магнитное поле подчиняется принципу суперпозиции. Принцип суперпозиции гласит, что результирующее поле представляет собой векторную сумму полей, создаваемых каждой частицей, или интеграл, если магнитные заряды распределены в пространстве плавно.

Закон Всемирного Магнетизма

Ф знак равно к е ЧАС 1 ЧАС 2 р 2 ϵ

Подстановка удельной орбитальной энергии квадратом скорости света ( ϵ ) получаем

Ф знак равно к е ЧАС 1 ЧАС 2 р 2 с 2

где,

F = сила (Ньютоны)

H ₁ и H ₂ = величины магнитных полюсов (амперметры) метр или ньютон/ампер ² )

r = расстояние (метр)

c ² = скорость света (м ² /с ² )

к е знак равно с 2 мю / 4 π

Замена в мю 0 4 π для постоянной Кулона к е с 2 , мы получаем классическую силу

уравнения притяжения между двумя магнитными полюсами, когда оба полюса достаточно малы, чтобы их можно было представить в виде точечных магнитных зарядов,

Ф знак равно мю ЧАС 1 ЧАС 2 4 π р 2

Закон универсального магнетизма гласит, что магнитное поле, создаваемое стационарным магнитным зарядом, равно:

Б ( р ) знак равно мю д м е р 4 π р 2

где,

е _р — радиальный единичный вектор,

q _м — магнитный заряд пробной частицы (единица СИ: амперметр),

μ — проницаемость промежуточной среды (единица СИ: тесла-метр на ампер, генри на метр или ньютон на ампер в квадрате),

r — расстояние (единица СИ: метр).

Используя закон универсального магнетизма, мы получаем полное поле в r, используя интеграл для суммирования поля в r из-за бесконечно малого изменения в каждой другой точке s пространства, чтобы получить:

Б ( р ) знак равно мю 4 π ∫ ​ р м ( с ) ( р − с ) | р − с | 3 д 3 с

где р м плотность магнитного заряда. Если взять расходимость обеих частей этого уравнения по r и воспользоваться известной теоремой [7]

∇ ⋅ ( р | р | 3 ) знак равно 4 π дельта (р)

где δ(r) — дельта-функция Дирака, результат равен

∇ ⋅ Б ( р ) знак равно ∫ ​ р ( с ) дельта ( р − с ) д 3 с

Используя свойство просеивания дельта-функции Дирака, мы получаем

∇ ⋅ Б ( р ) знак равно мю р м

где мю знак равно мю 0 вакуумная проницаемость,

∇ ⋅ Б ( р ) знак равно мю 0 р м

, что является дифференциальной формой закона Гаусса для магнетизма.

3. Вывод закона универсального магнетизма из закона Гаусса для магнетизма

Закон универсального магнетизма может быть доказан из закона Гаусса для магнетизма, если предположить, в дополнение к ротору поля B, что магнитное поле от магнитный заряд сферически симметричен. Это предположение, как и сам Закон Универсального Магнетизма, в точности верно, если магнитный заряд неподвижен, и приблизительно верно, если заряд находится в движении.

Взяв S в интегральной форме закона магнетизма Гаусса как сферическую поверхность радиуса r с центром в магнитном заряде q _м , мы получим

∮ с Б × д А знак равно мю д м

По предположению о сферической симметрии подынтегральная функция есть константа, которую можно вынести из интеграла. Результат 9представляет собой единичный вектор, направленный радиально от заряда. Опять же, согласно сферической симметрии, B указывает в радиальном направлении, поэтому мы получаем

. Б ( р ) знак равно мю д м е р 4 π р 2

, который по существу эквивалентен Закону Универсального Магнетизма. Таким образом, зависимость магнитного поля по закону обратных квадратов в Законе Вселенского Магнетизма следует из закона Гаусса для магнетизма.

4. Уравнение Максвелла

Уравнения электромагнетизма Максвелла связывают электрические и магнитные поля друг с другом и с движением электрических зарядов. Стандартные уравнения учитывают электрические заряды, но не предполагают магнитных зарядов. За исключением этой разницы, уравнения симметричны относительно перестановки электрического и магнитного полей. Фактически, симметричные уравнения Максвелла могут быть записаны, когда все заряды и, следовательно, электрические токи равны нулю, и именно так выводится уравнение электромагнитной волны.

Полностью симметричные уравнения Максвелла также могут быть записаны, если учесть возможность магнитных зарядов, аналогичных электрическим [8]. С учетом переменной плотности этих магнитных зарядов р м , в уравнениях также присутствует переменная плотность магнитного тока j _m .

Если магнитных зарядов не существует — или если они существуют, но не присутствуют в области пространства — тогда все новые члены в уравнениях Максвелла равны нулю, а расширенные уравнения сводятся к обычным уравнениям электромагнетизма, таким как

∇ ⋅ Б знак равно 0

, где ∇ = дивергенция и

B = магнитное поле B.

В уравнениях в таблице 1 ρ _м — плотность магнитного заряда, j _м — плотность магнитного тока и q _м — магнитный заряд пробной частицы, все они определены аналогично связанные величины электрического заряда и тока; v — скорость частицы, c — скорость света.

5. Рассчитать магнитный заряд монополя

Используя соотношение закона Гаусса и закона Гаусса о магнетизме, получаем,

∇ ⋅ Е ∇ ⋅ Б знак равно 4 π р е 4 π р м

Отношение электрического поля к магнитному в электромагнитной волне в свободном пространстве равно скорости света,

с знак равно р е р м

Рассчитать плотность магнитного заряда,

Таблица 1. Уравнения Максвелла и уравнение силы Лоренца с магнитными монополями (единицы Гаусса СГС) [9].

р м знак равно р е с знак равно 1,6 × 10 − 19С 3 × 10 8 м / с знак равно 5. 3 × 10 − 28 С ⋅ с / м

Отношение массы электрона к заряду (m/Q) — физическая величина, наиболее широко используемая в электродинамике заряженных частиц. Отношение массы к заряду для магнитного монополя неизвестно, поэтому мы будем использовать отношение массы к заряду электрона для последующих расчетов. Рекомендуемое значение CODATA 2014 для электрона составляет e/m 9.0236 e = −1,758820024 Кл/кг [10].

Предполагая, что монополь представляет собой магнитный заряд и массу электрона, тогда масса монополя равна,

монопольмасса знак равно 5.3 × 10 − 28 С ⋅ с / м 1,76 × 10 11 С / кг

монопольмасса знак равно 3. 0 × 10 − 39 кг ⋅ с / м

Коэффициент пересчета единиц СИ в натуральные единицы импульса,

1 ГэВ знак равно 5,39 × 10 − 19кг ⋅ м / с

Преобразование в единицы ГэВ,

Монополь Масса знак равно 3.0 × 10 − 39 кг ⋅ с / м 5,39× 10 − 19 кг ⋅ м / с

Монополь Масса знак равно 5,56 × 10 − 21 ГэВ / с 2

Решение для килограммов где,

1 ГэВ / с 2 знак равно 1,783 × 10 − 27 кг

Получаем,

Монополь Масса знак равно 9,9 × 10 − 48 кг

Для сравнения, масса электрона составляет 9,1 × 10 90 200 −31 90 201 кг.

Чтобы определить размер магнитного монополя, мы можем подставить заряд и массу монополя в классический расчет радиуса электрона:

р е знак равно 1 4 π ϵ 0 е 2 м е с 2

р м знак равно 2,8 × 10 − 15 м

Для сравнения, электрон имеет такой же радиус магнитного монополя 2,8 × 10 ⁻¹⁵ метра. Этот расчет подтверждает предположение Джакомелли и Патризила о свойствах магнитных монополей, где в их статье говорится, что радиус монополя и электрона совпадают [11].

Удвоив радиус, получим длину волны 5,6×10 ⁻¹⁵ метров, что соответствует v = f = 5,35×10 ²² Гц. Используя уравнение гипотезы Планка E = hv, мы получаем квантовую энергию магнитного монополя, равную 2,2 × 10 90 200 8 90 201 эВ, что соответствует 0,22 ГэВ. Низкая длина волны и высокая частота делают монополи состоянием гамма-лучей. Естественные источники гамма-лучей на Земле наблюдаются в гамма-распаде радионуклидов и вторичном излучении от взаимодействия атмосферы с частицами космических лучей. Существуют и другие земные естественные источники, такие как удары молнии и земные вспышки гамма-излучения.

6. Выводы

Магнитный монополь — гипотетическая элементарная частица в физике элементарных частиц, представляющая собой изолированный магнит только с одним магнитным полюсом. Магнитный монополь будет иметь чистый магнитный заряд, плюс или минус. Исходные уравнения Максвелла не допускают магнитных монополей. Однако, когда уравнения Максвелла переписываются с учетом магнитного заряда, существование монополей согласуется с обновленным уравнением. Современный интерес к этой концепции проистекает из теорий частиц, особенно теорий великого объединения и суперструн, которые предсказывают их существование.

В этой статье мы написали доказательство того, что закон Гаусса для магнетизма выводится из закона универсального магнетизма. Было также написано второе доказательство, доказывающее обратное, что закон универсального магнетизма может быть выведен из закона Гаусса для магнетизма. Два взаимных доказательства подтверждают закон универсального магнетизма, а также обеспечивают доказательство существования магнитного монополя. Закон Вселенского Магнетизма и монополии взаимозависимы.

Основываясь на размере радиуса магнитного монополя, мы пришли к выводу, что их можно найти в частотном диапазоне гамма-лучей или вблизи него. Молния — естественный источник высокочастотных гамма-лучей и отличное место для поиска магнитных монополей. Моделирование сильного короткого замыкания или короткого замыкания для имитации молнии в электрической лаборатории также должно приводить к возникновению монополей. В этой статье предполагается, что там, где есть большое количество электронов, мы должны найти и свободные монополи.

Благодарности

Автор выражает благодарность компании ASK Scientific (https://www.askscientific. com) за помощь в форматировании. Сердечно благодарю JHEPGC и их редакцию за предоставленную мне возможность опубликовать мои статьи.

Процитировать эту статью

Пул, Г. (2018) Закон Гаусса для магнетизма и закон универсального магнетизма: вычислить заряд монополя. Журнал физики высоких энергий, гравитации и космологии, 4, 581-587. https://doi.org/10.4236/jhepgc.2018.44035

Ссылки

1. 1. Пул Г. (2018) Закон универсального магнетизма. JHEPGC, в печати.


2. 2. Кац, В.Дж. (1979) История теоремы Стокса. Математический журнал. Математическая ассоциация Америки, 52, 146–156.


3. 3. Чоу Т.Л. (2006) Электромагнитная теория: современная перспектива. Jones and Bartlett, Boston, 134.


4. 4. Джексон, Дж. Д. (1999) Классическая электродинамика. 3-е издание, Wiley, Hoboken, 237.


5. 5. Кюри, П. (1894) Sur la possibilitéd’existence de la Conductibilitémagnétique et du magnétismelibre [О возможном существовании магнитной проводимости и свободного магнетизма. ] Séances de la Société FranÇaise de Physique, Paris, 76.


6. 6. Dirac, P. (1931) Квантованные особенности в электромагнитном поле. Proceedings of the Royal Society A (London), 133, 60.


7. 7. Griffiths, D.J. (2013) Введение в электродинамику. 4-е издание, Prentice Hall, Upper Saddle River, 50.


8. 8. http://www.ieeeghn.org/wiki/index.php/STARS:Maxwell%27s_Equations


9. 9. Новаковский М. и Келкар Н.Г. (2005) Закон Фарадея при наличии монополей. Europhysics Letters, 71, 346. arXiv:physics/0508099 [physics.class-ph]


10. 10. IUPAC (1997) Сборник химической терминологии. 2-е издание, «Золотая книга». Онлайн-исправленная версия: (2006-) «Отношение массы к заряду, m/z в масс-спектрометрии».


11. 11. Джакомелли Г. и Патрици Л. (2002) Поиски магнитных монополей. Dipartimento di Fisica dell’Universit`a di Bologna и INFN, Sezione di Bologna, Летняя школа по физике астрофизики и космологии ICTP, Триест, 17 июня – 5 июля 2002 г.