Задачи на закон Био Савара Лапласа с решением

Закон Био-Савара-Лапласа в магнитостатике – примерно то же самое, что и закон Кулона в электростатике. С помощью этого закона определяется индукция магнитного поля, созданного постоянным электрическим током. В сегодняшней статье разберем несколько примеров решения задач по магнитостатике на применение закона Био-Савара-Лапласа.

Присоединяйтесь к нам в телеграме, чтобы вовремя получать полезную рассылку и актуальные новости. А еще, не пропустите приятные скидки и акции на нашем втором канале.

Закон Био-Савара-Лапласа: решение задач

В нашем блоге есть материалы, которые помогут справиться с задачами по разным темам:

1. Общая памятка по решению физических задач.
2. Более 40 формул по физике. 

Задача на закон Био-Савара-Лапласа №1

Условие 

Прямой провод согнут в виде квадрата со стороной а=8 см. Какой силы ток надо пропустить по проводнику, чтобы напряженность магнитного поля в точке пересечения диагоналей была 20 А/м?

Решение

Согласно принципу суперпозиции напряженность магнитного поля в точке пересечения диагоналей квадрата будет равна сумме напряженностей, которые создают стороны.  Поскольку стороны одинаковые, то:

H=4h2=4B1μ0

Будем использовать формулу для магнитной индукции поля, создаваемого отрезком прямого провода с током (выводится из закона Био-Савара-Лапласа):

B=μ02πIr0cosαB1=μ02πIa2cosα=μ02πIacosα, α=45°

Тогда для напряженности в точке пересечения диагоналей получим:

Н=4πIacosα

Отсюда можем выразить ток:

I=πah5cosα=3,14×0,08×204cos45=1,78 А  

Ответ: 1,78 А.

Задача на закон Био-Савара-Лапласа №2

Условие

Используя закон Био-Савара-Лапласа, определите магнитную индукцию в вакууме B поля в центре кругового проводника радиусом 10 см, если сила тока в проводнике равна 5 A.

Решение

Модуль магнитной индукции в центре кругового тока вычисляется по формуле:

B=μ0μI2rμ=1 — магнитная проницаемость для вакуумаμ0=1,25×10-6 Гнм — магнитная постоянная

Вычислим индукцию:

В=1,25×10-6×1×52×0,1=3,1×10-5 Тл

Ответ: 0,31 мкТл.

Задача на закон Био-Савара-Лапласа №3

Условие

Используя закон Био-Савара-Лапласа выведите формулу для индукуии из предыдущей задачи.

Решение

Пусть ток идет по тонкому проводу в форме окружности, имеющей радиус R.

Разобъем провод на бесконечно малые элементы dl. Каждый такой элемент создает в центре окружности индукцию dB, направленную вдоль положительной нормали к контуру. По закону Био-Савара-Лапласа:

B=μ04πIdlsinαr2

Угол альфа между векторами r и Idl равен 90 градусам, а r=R. Тогда, можно записать:

Интегрируя это выражение по контуру, получим:

Ответ: см. выше.

Задача на закон Био-Савара-Лапласа №4

Условие

По квадратной рамке со стороной a=0,2 м течет ток 4 А. Определить напряженность и индукцию магнитного поля в центре рамки.

Решение

Будем рассматривать каждую из четырех сторон рамки, как отдельный проводник, создающий в ее центре магнитную индукцию. Направление векторно-магнитной индукции определяется по правилу правого винта: все векторы направлены в одну сторону, перпендикулярно рамке.

Найдем индукцию, создаваемую одной стороной рамки:

B1=μμ0I4πr(cosα1-cosα2)

r=a2α1=45°α2=135°В1=μμ0I2πa(cos45-cos135)

По принципу суперпозиции, запишем формулу для общей индукции в центре рамки и вычислим:

B=4B1=2μμ0Iπa(cos45-cos135)B=1×1,25×10-6×42×3,14×0,2(0,707+0,707)=22,6×10-6 Тл

Ответ: 22,6 мкТл.

Задача на закон Био-Савара-Лапласа №5

Условие

Проводник согнут в виде правильного треугольника со стороной а=20 см. Какой ток протекает по периметру треугольника, если в его центре напряженность поля равна Н = 71,64 А/м?

Решение

Условно разбиваем проводник на три проводника, каждый из которых создает магнитное поле. По закону Био – Савара – Лапласа элемент контура dl, по которому течет ток I, создает в некоторой точке А пространства магнитное поле напряженностью:

dH0=Isinα4πr2dl

r – расстояние от точки А до элемента тока dl, α – угол между радиус-вектором и элементом тока dl. Напряженность магнитного поля в точке О будет равна:

Н0=∫-∞+∞Isinα4πr2dl

Учтем, что:

l=b×ctgαdl=-bdαsin2αr=bsinα

Теперь выражение для напряженности можно переписать в следующем виде:

H0=-I4πb∫α1α2sinαdα=I4πbcosα1-cosα2b=a2tgαH0=I2π×a×tgαcosα1-cosα2

Из рисунка видно, что угол α1 равен 30 градусам, а угол α2 = 150. Очевидно, что результирующая напряженность:

Н=3Н0

Н=3I2π×a×tg30cos30-cos150

Отсюда найдем ток:

I=2πH×a×tg303(cos30-cos150)=2×3,14×71,64×0,2×0,5773(0,866+0,866)=10А

Ответ: 10 А.

Вопросы на закон Био-Савара-Лапласа

Вопрос 1. Сформулируйте закон Био-Савара-Лапласа

Ответ. Закон Био-Савара-Лапласа гласит:

Магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока.

B⇀=∑B⇀ii

Элементарный участок dl с током I создает магнитную индукцию:

B=μ04πIdlsinαr2

Здесь альфа — угол между радиусом-вектором и направлением тока в проводнике.

Вопрос 2. Что такое магнитная индукция?

Ответ. Магнитная индукция — векторная физическая величина, силовая характеристика магнитного поля. Определяет, с какой силой поле действует на заряд, движущийся в нем.

Вопрос 3. Сформулируйте теорему о циркуляции магнитной индукции.

Ответ. Циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи, прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур:

∮Вdl=μ0∑iIi

Вопрос 4. Как определяется направление вектора магнитной индукции?

Ответ. Направление вектора магнитной индукции определяется по правилу буравчика (правого винта):

Направление вращения головки винта дает направление вектора магнитной индукции, поступательное движение винта соответствует направлению тока в элементе.

Вопрос 5. Что такое напряженность магнитного поля?

Ответ. Напряженность — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. Связана с индукцией формулой:

H⇀=B⇀μ0

Нужна помощь в решении задач и выполнении других заданий? Профессиональный сервис для учащихся всегда к вашим услугам.

14.2. Закон Био-Савара-Лапласа. Магнитное поле прямолинейного и кругового токов.

Закон Био-Савара-Лапласа позволяет вычислить магнитную индукцию поля, созданного элементом тока

Id на расстоянии от него:

dB = ,(14-5)

т.е. индукция магнитного поля, создаваемого элементом тока Idточке А, (рис.14.3), на расстоянии r от него, пропорциональна ве­личине элемента тока и синусу угла , равного углу между направле­ниями элемента тока Id и , а также обратно пропорциональна квадрату расстояния между ними; Гн / м — магнитная посто­янная.

Закон Био — Савара — Лапласа в векторной форме имеет вид:

d=.

(14-6)

Закон Био — Савара — Лапласа позволяет вычислить магнитную индукцию поля любых систем токов, используя принцип суперпозиции магнитных поля

= . (14-7)

Применим закон Био — Савара — Лапласа и принцип суперпозиции (14-7) к расчету магнитных полей следующих токов:

1) Магнитное поле прямолинейного тока.

Из рис.14.4 с учетом (14-6) находим, что d плоскости, в которой лежат d и ; далее можно найти ,откуда, принимая во внимание, чтополучаем. С учетом этого из (14-5) находим:

интегрируя последнее равенство, получаем

(14-8)

Для бесконечно длинного проводника ,и из (8) следует, что

(14-9)

2) Магнитное поле кругового тока. Можно показать, что магнитная индукция поля, создан­ного круговым током радиуса R, на расстоянии r₀ вдоль перпендикуляра, восстановленного из центра контура, (рис.14.5), будет

(14-10)

В частности, в центре кругового тока ,

. (14-11)

Для плоской катушки, состоящей из N, витков магнитная индукция на оси катушки

. (14-12)

При больших расстояниях от контура, т. е. при r₀ >> R из (14-10) получим

(14-13)

Для электростатического поля

т

. е. циркуляция вектора вдоль замкнутого контура L равна нулю. Можно показать, что циркуляция вектора вдоль замкнутого контура L равна алгебраи­ческой сумме токов, охватываемых контуром, умноженной на ₀ , т. е.

(14-14) При этом токи будем считать положительными, если они совпадают с поступательным движением правого буравчика, рукоятка которого вращается по направлению обхода контура. Для нашего случая, (рис.14.6) это будут токи, текущие от нас и обозначенные . Токи, те­кущие в обратном направлении, будут считаться отрицательными. Для рис. 14.6, это будут токи, текущие на нас и обозначенные кружком с точкой в центре.

L

Поскольку , то магнитное поле не является потенциальным, оно называется вихревым или соленоидальным.

Применим теорему о циркуляции для вычисления индукции магнитного поля со­леноида и тороида.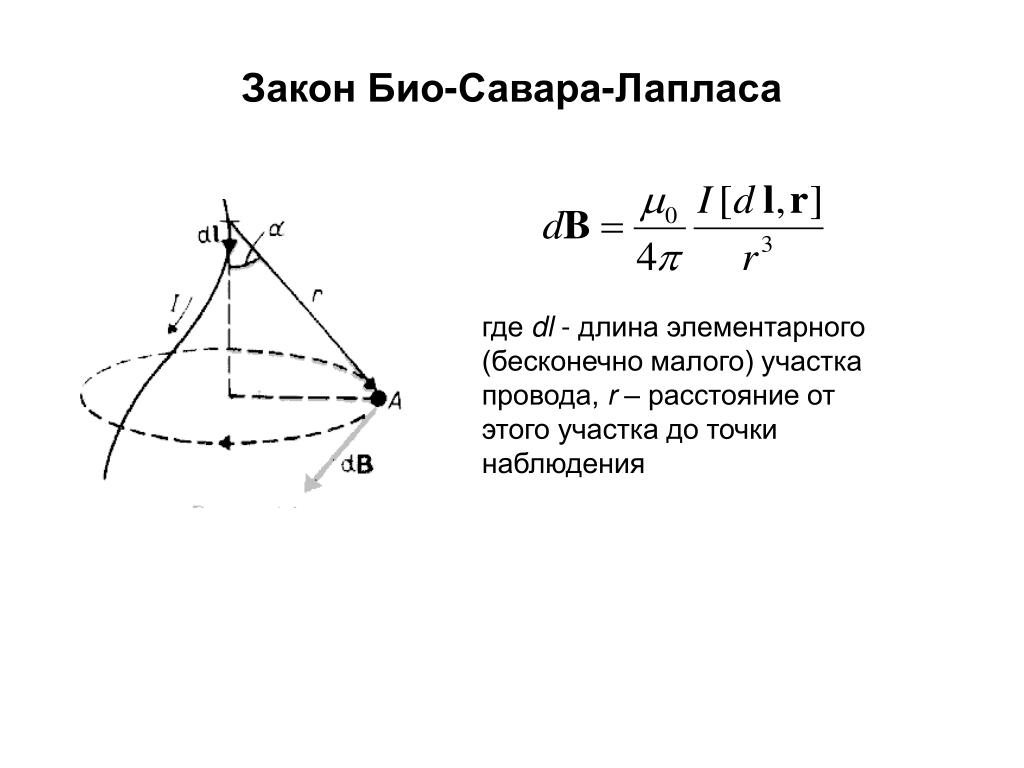

1) Поле соленоида

Соленоидом, (рис.14.7), называется цилиндрическая катушка, на которую вплотную намотано большое число витков провода. Пусть

N — число витков вдоль длины соленоида l, тогда , гдеL – контур 12341

или .

Интегралы на участках 1-2, 3- 4 равны нулю, т.к. d и d=Bdlcosπ/2 =0;

интеграл на участ­ке 4-1 равен нулю, т.к. вне соленоида индукция равна нулю. Поэтому , отсюда

B=, (14-15)

где n=N / l — число витков, приходящееся на единицу длины соленоида. Поле соленоида однородно.

2)Поле тороида

Тороид (рис. 14.8), представляет тонкий провод, плотно навитый на каркас, имеющий форму тора. Для него

где R — радиус средней линии тора, отсюда

B = (14-16)

Поле тороида неоднородно: оно уменьшается с увеличением r. Поле вне тороида рав­но нулю.

{3/2}} \ \hat{z} $$

интегрирование — Интеграл для закона Био-Савара на коробке

Я пытаюсь сделать базовую компьютерную модель стержневого магнита. В процессе я наткнулся на этот вопрос и ответ, который, кажется, имеет подходящее уравнение для меня. Я говорю «появляется», потому что мои знания по математике едва превышают уровень средней школы, и ответ останавливается здесь:

.

можно просто использовать закон Био-Савара для расчета магнитного поля: $$\mathbf B(\mathbf x) = \frac{\mu_0}{4\pi}\int_{\mathbb S}d\mathbf a’ \\mathbf K(\mathbf x’) \times \frac{\ mathbf{х-х’}}{|\mathbf{х-х’}|^3}$$ Я считаю, что вы можете взять его отсюда.

Итак, я понимаю, что в этом случае я могу использовать тот факт, что чистое магнитное поле (то, что я хочу смоделировать) состоит из суммы всех магнитных полей, созданных в этой ситуации. То есть мне нужно сложить поле, создаваемое каждым из граней относительно каждой точки, которую я хочу смоделировать.

Я также полагаю, что именно это пытается выразить та часть уравнения, которую я не понимаю, а именно раздел $\int_{\mathbb S}d\mathbf a’ \ \mathbf K(\mathbf x’ )$

Таким образом, в приведенном выше примере стержневой магнит моделируется следующим образом:

Стержневой магнит можно смоделировать прямоугольной коробкой с постоянной намагниченностью в одном направлении. Возьмем ящик $[0,a]\times[0,b]\times[0,c]$ с постоянной намагниченностью $\mathbf M(\mathbf x) = M_0 \\hat{\mathbf k}$ , где $\hat{\mathbf k}$ — единичный вектор в направлении $z$. Плотность связанного объема и поверхностного тока: $$\mathbf J_b(\mathbf x) = \boldsymbol{\nabla}\times\mathbf M(\mathbf x)$$ $$\mathbf K_b(\mathbf x) = \mathbf M(\mathbf x) \times \hat {\mathbf n}$$ Объемная плотность тока равна нулю, поскольку $\mathbf M$ постоянна.