Логические операции и таблицы истинности — Студопедия
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно. Обозначение: F = A & B.
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны. Обозначение: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Вопросы самоконтроля
1. Объясните состав ПК
2. Что такое Инверсия?
3. Что такое Импликация?
4. Что такое Дизъюнкция?
5. Опишите основные формы мышления
Базовые логические операции и схемы. Таблицы истинности — Студопедия
Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение
Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Таблица истинности для конъюнкции
Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Таблица истинности для импликации
Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Презентация к уроку информатики на тему «Логика и логические операции. Таблица Истинности.», 8 класс
Инфоурок › Информатика ›Презентации›Презентация к уроку информатики на тему «Логика и логические операции. Таблица Истинности.», 8 класс
Описание презентации по отдельным слайдам:
1 слайд
Логика и логические операции. Таблица Истинности.
2 слайд
Логика. Логика– наука о законах и формах мышления. Логика в информатике — это направления исследований и отраслей знания, где логика применяется в информатике и искусственном интеллекте. .
3 слайд
Описание слайда:
Описание слайда:Логические выражения. Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). Логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0)
5 слайд
Описание слайда:Логические операции и таблицы истинности. Бывает пять видов логических операций: Логическое умножение (конъюнкция) Логическое сложение (дизъюнкция) Логическое отрицание (инверсия) Логическое следование (импликация) 5) Логическая равнозначность (эквивалентность)
6 слайд
Описание слайда:Таблица истинности – таблица, содержащая все возможные комбинации входных переменных и соответствующее им значения на выходе. Таблица истинности содержит 2n строк, где n – число входных переменных, и n+m – столбцы, где m – выходные переменные.
7 слайд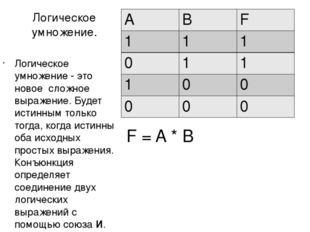
Описание слайда:Логическое умножение. Логическое умножение — это новое сложное выражение. Будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И. F = A * B A B F 1 1 1 0 1 1 1 0 0 0 0 0
8 слайд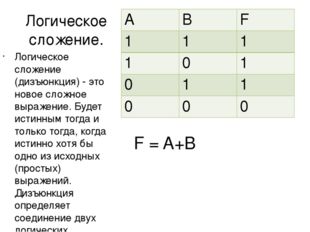
Описание слайда:Логическое сложение. Логическое сложение (дизъюнкция) — это новое сложное выражение. Будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ F = A+B A B F 1 1 1 1 0 1 0 1 1 0 0 0
9 слайд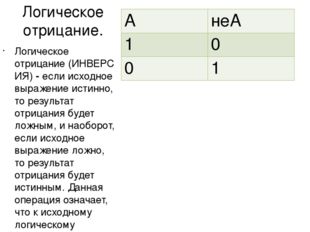
Описание слайда:Логическое отрицание. Логическое отрицание (ИНВЕРСИЯ) — если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным. Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО A неА 1 0 0 1
10 слайд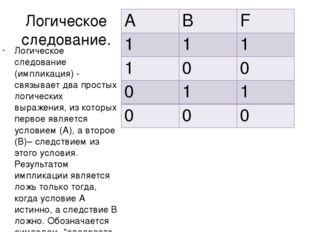
Описание слайда:Логическое следование. Логическое следование (импликация) — связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом импликации является ложь только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом «следовательно» и выражается словами если … , то … A B F 1 1 1 1 0 0 0 1 1 0 0 0
11 слайд
Описание слайда:Порядок выполнения логических операций в сложном логическом выражении: 1. инверсия 2. конъюнкция 3. дизъюнкция 4. импликация 5. эквивалентность Для изменения указанного порядка выполнения операций используются скобки.
12 слайд
Описание слайда:Построение таблиц истинности для сложных выражений: Количество строк = 2n + две строки для заголовка (n — количество простых высказываний) Количество столбцов = количество переменных + количество логических операций При построении таблицы надо учитывать все возможные сочетания логических значений 0 и 1 исходных выражений. Затем – определить порядок действий и составить таблицу с учетом таблиц истинности основных логических операций.
13 слайд
Описание слайда:Пример: составить таблицу истинности сложного логического выражения D = неA & ( B+C )
14 слайд
Описание слайда:Пример: составить таблицу истинности сложного логического выражения D = неA & ( B+C ) А,В, С — три простых высказывания, поэтому : количество строк = 23 +2 = 10 (n=3, т.к. на входе три элеманта А, В, С) количество столбцов : 1) А 2) В 3) С 4) не A это инверсия А (обозначим Y) 5) B + C это операция дизъюнкции (обозначим F) 6) D = неA & ( B+C ), т.е. D = E & F это операция конъюнкции
15 слайд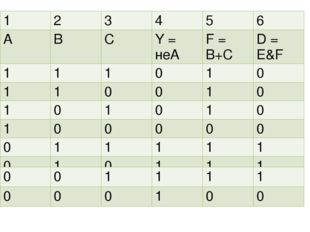
Описание слайда:1 2 3 4 5 6 A B C Y =неА F = B+C D = E&F 1 1 1 0 1 0 1 1 0 0 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 1 1 1 1 1 0 1 0 1 1 1 0 0 1 1 1 1 0 0 0 1 0 0
Курс профессиональной переподготовки
Учитель информатики
Курс профессиональной переподготовки
Учитель математики и информатики
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДБ-1192693
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Логические операции и таблицы истинности — Студопедия
F = A & B.
Логическое умножение КОНЪЮНКЦИЯ — это новое сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И.
F = A + B
Логическое сложение – ДИЗЪЮНКЦИЯ — это новое сложное выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ
Логическое отрицание : ИНВЕРСИЯ —если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным/ Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО
Логическое следование: ИМПЛИКАЦИЯ — связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом «следовательно» и выражается словами ЕСЛИ … , ТО …
Логическая равнозначность: ЭКВИВАЛЕНТНОСТЬ — определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом «эквивалентности»
Порядок выполнения логических операций в сложном логическом выражении:
1. инверсия
2. конъюнкция
3. дизъюнкция
4. импликация
5. эквивалентность
Для изменения указанного порядкавыполнения операций используются скобки.
Приоритеты выполнения логических операций.
Вычисление значений логических выражений выполняется в определенном порядке, согласно их приоритету:
— инверсия
— конъюнкция
— дизъюнкция
— импликация и эквивалентность
Операции одного приоритета выполняются слева направо. Для изменения порядкадейcтвий используются скобки.
ПРИМЕР 1: А V (B → C) & D = не(A)
Порядок выполнения:
Не(А) — инверсия
В→ С — импликация
(В → С) & D — конъюнкция
А V (B → C) & D — дизъюнкция
А V (B → C) & D = не(A)- эквивалентность
Построим таблицу истинности для высказывания
E = (A V не(B)) → не(C)
В высказывание Е входят три переменные: А, В, С (n=3 ) и четыре логические операции: инверсия В, инверсия С, дизъюнкция, импликация.
Таблица истинности будет состоять из 23 + 2 (заголовок) = 8 +2 = 10 строк и 3 + 4 = 7 столбцов
Логические выражения.
Логическое выражение — выражение, в котором операндами являются объекты, над которыми выполняются логические операции.
Результатом выполнения логического выражения является одно из двух логических значений: либо Истина, либо Ложь.
6.10.таблица истинности, алгоритм её построения.
Таблицу, показывающую, какие значения принимает функция при всех сочетаниях её агрументов, называют ТАБЛИЦЕЙ ИСТИННОСТИ составного высказывания.
Алгоритм построения таблицы истинности:
1)подсчитать количество переменных n в логическом выражении;
2) определить число строк в таблице, которое равно m = 2n;
3) подсчитать количество логических операций и количество столбцов в таблице, которое равно количеству переменных плюс количество операций;
4) ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
5) заполнить столбцы входных переменных наборами значений.
Что такое таблица истинности (диаграмма)? Определение Webopedia
Главная »СРОК» Т »Форрест Страуд
Таблица истинности — это математическая таблица, основанная на логике, которая иллюстрирует возможные результаты сценария. Таблица истинности содержит значения истинности, которые могут иметь место в условиях данного сценария. В результате таблица помогает визуализировать, является ли аргумент логичным (истинным) в сценарии.
Строки базовой таблицы истинности содержат истинные или ложные значения логической логики, а в столбцах перечисляются предпосылки сценария, а также заключение. Простая таблица истинности содержит единственный сценарий и перечисляет действительное утверждение и его отрицание.
Как создать таблицу истинности
Первый шаг в создании таблицы истинности — определить количество переменных и строк, необходимых для таблицы, а затем записать все возможные комбинации (обычно обозначенные как « p » и « q »).
Для создания базовой таблицы истинности «И» (соединения) мы будем использовать следующий пример:
«Если вас примут в государственный университет, вы получите работу с шестизначной суммой после его окончания».
В этом примере « p » представляет собой первую предпосылку, при которой вы поступаете в государственный университет, а « q » означает получение работы с шестизначной суммой после окончания университета.
В таблице истинности будет столбец для каждого из этих посылок и третий для логического заключения, причем каждая строка будет содержать логический результат комбинации двух посылок, как показано на иллюстрации ниже:
| p | q | Результат |
|---|---|---|
| т | т | т |
| т | Ф | Ф |
| Ф | т | Ф |
| Ф | Ф | Ф |
Пять основных операций в таблицах истинности
Таблицы истинности используют пять основных операций:
1. Соединение: Операция «И», в которой оба аргумента должны быть true , чтобы само утверждение было true
2. Дизъюнкция: Операция «или», в которой оба аргумента должны быть false , чтобы само утверждение было false
3. Отрицание: Операция «не» — это операция, противоположная (или дополняющая) исходному значению
.4.Условный: Операция «если — то», при которой утверждение неверно только тогда, когда первая предпосылка верна, а вторая ложна
5. Двуусловное: Операция «если и только если», в которой утверждение истинно только тогда, когда посылки имеют одно и то же значение истинности (они либо истинны, либо ложны)
НОВОСТИ ВЕБОПЕДИИ
Будьте в курсе последних событий в терминологии Интернета с помощью бесплатного информационного бюллетеня Webopedia.Присоединяйтесь, чтобы подписаться сейчас.
.{k} \ to \ mathbb {A},} где k {\ Displaystyle к \!} является целым неотрицательным числом и А {\ displaystyle \ mathbb {A}} это область логических значений { ложный , правда } . {\ displaystyle \ {\ operatorname {false}, \ operatorname {true} \}.} Имена логических значений или значений истинности обычно сокращаются в соответствии с уравнениями F знак равно ложный {\ displaystyle \ operatorname {F} = \ operatorname {false}} и Т знак равно правда .{k} \ to \ mathbb {B},} где k {\ Displaystyle к \!} является целым неотрицательным числом и B {\ displaystyle \ mathbb {B}} это логический домен { 0 , 1 } . {\ Displaystyle \ {0,1 \}. \!} В большинстве приложений ложный {\ displaystyle \ operatorname {false}} представлен 0 {\ displaystyle 0 \!} и правда {\ displaystyle \ operatorname {true}} представлен 1 {\ Displaystyle 1 \!} но возможно и обратное представление, в зависимости от общего представления функций истинности как булевых функций.Остальная часть этой статьи принимает обычное представление, принимая уравнения F знак равно 0 {\ displaystyle \ operatorname {F} = 0} и Т знак равно 1 {\ displaystyle \ operatorname {T} = 1} как должное.Логическое отрицание — это операция с одним логическим значением, обычно значением предложения, которая дает значение истинно, , когда его операнд ложно, и значение ложь, , когда его операнд истинен.
Таблица истинности НЕ п , {\ displaystyle \ operatorname {NOT} ~ p,} также написано ¬ п , {\ Displaystyle \ lnot p, \!} появляется ниже:
Отрицание предложения п {\ displaystyle p \!} могут быть отмечены различными способами в различных контекстах применения, часто просто для удобства типографского изображения.Среди этих вариантов можно выделить следующие:
Логическое соединение — это операция над двумя логическими значениями, обычно значениями двух предложений, которая дает значение истинно тогда и только тогда, когда оба его операнда истинны.
Таблица истинности п И q , {\ displaystyle p ~ \ operatorname {AND} ~ q,} также написано п ∧ q {\ displaystyle p \ land q \!} или п ⋅ q , {\ displaystyle p \ cdot q, \!} появляется ниже:
Логическая дизъюнкция , также называемая логическим чередованием , представляет собой операцию над двумя логическими значениями, обычно значениями двух предложений, которая производит значение false тогда и только тогда, когда оба его операнда ложны.
Таблица истинности п ИЛИ q , {\ displaystyle p ~ \ operatorname {OR} ~ q,} также написано п ∨ q , {\ displaystyle p \ lor q, \!} появляется ниже:
Логическое равенство — это операция над двумя логическими значениями, обычно значениями двух предложений, которая дает значение истина тогда и только тогда, когда оба операнда ложны или оба операнда истинны.
Таблица истинности п Эквалайзер q , {\ displaystyle p ~ \ operatorname {EQ} ~ q,} также написано п знак равно q , {\ Displaystyle р = д, \!} п ⇔ q , {\ displaystyle p \ Leftrightarrow q, \!} или п ≡ q , {\ Displaystyle п \ эквив д, \!} появляется ниже:
Исключительная дизъюнкция , также известная как логическое неравенство или симметричная разность , представляет собой операцию над двумя логическими значениями, обычно значениями двух предложений, которая дает значение истинное на случай, если ровно один из его операндов правда.
Таблица истинности п XOR q , {\ displaystyle p ~ \ operatorname {XOR} ~ q,} также написано п + q {\ Displaystyle р + д \!} или п ≠ q , {\ displaystyle p \ neq q, \!} появляется ниже:
Затем могут быть выведены следующие эквиваленты:
п + q знак равно ( п ∧ ¬ q ) ∨ ( ¬ п ∧ q ) знак равно ( п ∨ q ) ∧ ( ¬ п ∨ ¬ q ) знак равно ( п ∨ q ) ∧ ¬ ( п ∧ q ) {\ displaystyle {\ begin {matrix} p + q & = & (p \ land \ lnot q) & \ lor & (\ lnot p \ land q) \\ [6pt] & = & (p \ lor q) & \ земля & (\ lnot p \ lor \ lnot q) \\ [6pt] & = & (p \ lor q) & \ land & \ lnot (p \ land q) \ end {matrix}}} |
Связь логического импликации и материальная условная функция связаны с операцией над двумя логическими значениями, обычно значениями двух предложений, которая дает значение false тогда и только тогда, когда первый операнд истинен и второй операнд ложный.
Таблица истинности, связанная с материальной условной если п затем q , {\ displaystyle {\ text {if}} ~ p ~ {\ text {then}} ~ q, \!} символизированный п → q , {\ displaystyle p \ rightarrow q, \!} и логическое следствие п подразумевает q , {\ displaystyle p ~ {\ text {подразумевает}} ~ q, \!} символизированный п ⇒ q , {\ displaystyle p \ Rightarrow q, \!} появляется ниже:
Логическая И-НЕ — это операция над двумя логическими значениями, обычно значениями двух предложений, которая дает значение false тогда и только тогда, когда оба ее операнда истинны.Другими словами, он дает значение true тогда и только тогда, когда хотя бы один из его операндов ложен.
Таблица истинности п NAND q , {\ displaystyle p ~ \ operatorname {NAND} ~ q,} также написано
.Как работает логическая алгебра внутри FPGA
Булева алгебра лежит в основе работы FPGA. Булева алгебра описывает операции, в которых входы и выходы принимают значения истина или ложь (1 или 0 соответственно). Так что не волнуйтесь, если вы не очень хорошо разбираетесь в математическом анализе. Булева алгебра — это самая простая математика из возможных! Он был введен в 1854 году математиком Джорджем Бульем. С помощью правил, установленных булевой алгеброй, можно создать основу для выполнения всех основных логических операций.В этой статье будут обсуждаться следующие операции: AND, OR, NOT, XOR (исключающее или) и NAND (мой личный фаворит). Имея эти базовые строительные блоки цифровой логики, можно создавать гораздо более сложные операции, такие как сложение, вычитание, деление и т. Д. Однако сначала мы должны понять основы.
Первое понятие, которое необходимо понять, называется Таблица истинности . Таблица истинности — это таблица, которая описывает функциональные возможности на основе входных и выходных данных.Лучше всего это продемонстрировать, посмотрев на таблицу истинности для логического элемента И.
Логический элемент И имеет 2 входа и 1 выход. Каждый из них может иметь значение 0 или 1, а выходное значение зависит от 2 входных значений. Выход равен 1, когда оба входных значения равны 1. Ниже приведена таблица истинности для логического элемента И.
| Таблица истины — И ворота | ||
|---|---|---|
| Вход A | Вход B | Выход Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логический элемент ИЛИ имеет 2 входа и 1 выход.Выход равен 1, когда либо входных значений равны 1. Ниже приведена таблица истинности для логического элемента ИЛИ.
| Таблица истинности — OR Gate | ||
|---|---|---|
| Вход A | Вход B | Выход Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Элемент НЕ имеет 1 вход и 1 выход.Выходной сигнал противоположен входному значению. Ниже приведена таблица истинности для ворот НЕ.
| — НЕ Ворота | ||
|---|---|---|
| Вход A | Выход Q | |
| 0 | 1 | |
| 1 | 0 | |
Элемент XOR (исключающее ИЛИ) имеет 2 входа и 1 выход. Выход равен 1, когда или входных значений равны 1 , но не оба .Ниже приведена таблица истинности для ворот XOR.
| — XOR Gate | ||
|---|---|---|
| Вход A | Вход B | Выход Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Логический элемент И-НЕ имеет 2 входа и 1 выход.Вывод таблицы истинности противоположен выводу логического элемента И. Это только 0, когда оба входа установлены на 1, в противном случае — 1. Ниже приведена таблица истинности для логического элемента NAND.
| — NAND Gate | ||
|---|---|---|
| Вход A | Вход B | Выход Q |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Теперь, когда вы видите, как работают эти базовые вентили, давайте посмотрим на более сложную булеву алгебру с использованием таблиц поиска (LUT)
Помогите мне создавать отличный контент! Поддержите меня на Patreon! Купите доску Go!
Пожалуйста, включите JavaScript, чтобы просматривать комментарии от Disqus.
.
логических операторов, таблица истинности, Unicode
Автор Xah Lee. Дата: . Последнее обновление: .
истинная ложная амбиграммаТаблица истинности и возможные логические операторы
Вот определение оператора «и» с использованием черного треугольника ▲ для обозначения оператора:
И 0 ▲ 0 = 0 0 ▲ 1 = 0 1 ▲ 0 = 0 1 ▲ 1 = 1
Вот определение оператора «или», также с использованием черного треугольника ▲ для обозначения оператора:
Или 0 ▲ 0 = 0 0 ▲ 1 = 1 1 ▲ 0 = 1 1 ▲ 1 = 1
Рассмотрим их результаты, мы можем закодировать определение в сжатом виде кодом 0001
«Или», следовательно, 0111
Их можно рассматривать как 4-значные двоичные числа.4 = 16) Давайте посмотрим полный список того, что они собой представляют, и как они называются, и их символы, если таковые имеются.
Таблица истинности; Все возможные логические операторы
| Определение | Код | Название | Символ | Комментарий |
|---|---|---|---|---|
| 0 ▲ 0 = 0; 0 ▲ 1 = 0; 1 ▲ 0 = 0; 1 ▲ 1 = 0 | 0000 | ◇ | ◇ | ложно |
| 0 ▲ 0 = 0; 0 ▲ 1 = 0; 1 ▲ 0 = 0; 1 ▲ 1 = 1 | 0001 | и | ∧ | ◇ |
| 0 ▲ 0 = 0; 0 ▲ 1 = 0; 1 ▲ 0 = 1; 1 ▲ 1 = 0 | 0010 | ◇ | ◇ | |
| 0 ▲ 0 = 0; 0 ▲ 1 = 0; 1 ▲ 0 = 1; 1 ▲ 1 = 1 | 0011 | ◇ | ◇ | |
| 0 ▲ 0 = 0; 0 ▲ 1 = 1; 1 ▲ 0 = 0; 1 ▲ 1 = 0 | 0100 | ◇ | ◇ | |
| 0 ▲ 0 = 0; 0 ▲ 1 = 1; 1 ▲ 0 = 0; 1 ▲ 1 = 1 | 0101 | ◇ | ◇ | |
| 0 ▲ 0 = 0; 0 ▲ 1 = 1; 1 ▲ 0 = 1; 1 ▲ 1 = 0 | 0110 | xor | ⊻ | ◇ |
| 0 ▲ 0 = 0; 0 ▲ 1 = 1; 1 ▲ 0 = 1; 1 ▲ 1 = 1 | 0111 | или | ∨ | ◇ |
| 0 ▲ 0 = 1; 0 ▲ 1 = 0; 1 ▲ 0 = 0; 1 ▲ 1 = 0 | 1000 | или | ⊽ | ◇ |
| 0 ▲ 0 = 1; 0 ▲ 1 = 0; 1 ▲ 0 = 0; 1 ▲ 1 = 1 | 1001 | xnor | ⊻̅ | Этот символ представляет собой объединяющий символ в Юникоде. |
| 0 ▲ 0 = 1; 0 ▲ 1 = 0; 1 ▲ 0 = 1; 1 ▲ 1 = 0 | 1010 | ◇ | ◇ | |
| 0 ▲ 0 = 1; 0 ▲ 1 = 0; 1 ▲ 0 = 1; 1 ▲ 1 = 1 | 1011 | ◇ | ◇ | |
| 0 ▲ 0 = 1; 0 ▲ 1 = 1; 1 ▲ 0 = 0; 1 ▲ 1 = 0 | 1100 | ◇ | ◇ | |
| 0 ▲ 0 = 1; 0 ▲ 1 = 1; 1 ▲ 0 = 0; 1 ▲ 1 = 1 | 1101 | ◇ | ⇒ | |
| 0 ▲ 0 = 1; 0 ▲ 1 = 1; 1 ▲ 0 = 1; 1 ▲ 1 = 0 | 1110 | nand | ⊼ | |
| 0 ▲ 0 = 1; 0 ▲ 1 = 1; 1 ▲ 0 = 1; 1 ▲ 1 = 1 | 1111 | ◇ | ◇ | истинно |
Интересно отметить, что у половины из них нет названия.Википедия на Логическая связка дает название некоторым из них. Например, «0000» — это просто «ложь», «1111» — «истина», «1101» — «если / тогда». Хотя многие из этих имен довольно надуманные и не имеют особого смысла. Прежде всего, помните, что мы имеем дело с функциями от 2-х параметров (так называемые «бинарные операторы»). Термин «истина» обычно не рассматривается как бинарный оператор, и «если, то» и «не» здесь тоже не имеют смысла.
[см. Математические символы Unicode ∑ ∫ π² ∞]
Функциональная полнота
Набор (L) бинарных логических операторов является «функционально полным», если семантика любого из 16 возможных логических операторов может быть выражена комбинацией операторов в наборе L.
Мы знаем, что общее количество возможных двоичных функций в двоичном пространстве {1,0} равно 16 из приведенной выше таблицы истинности.
Итак, функционально полный набор функций — это такой, в котором любая из возможных функций в таблице истинности может быть выражена комбинацией функций в наборе.
Одна из функционально полного набора функций — это всего лишь одна функция, nand сама по себе.
Упражнение 1: выразите все возможные двоичные функции через nand.
Упражнение 2: напишите программу, которая перечисляет все возможные наборы двоичных логических операторов, которые являются функционально завершенными.
Если у вас есть вопросы, положите 5 долларов на patreon и напишите мне.
.