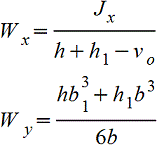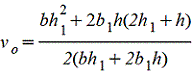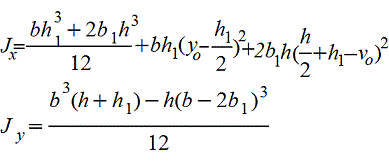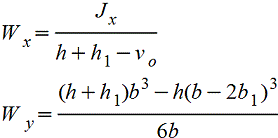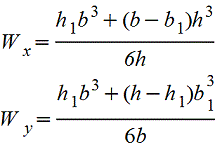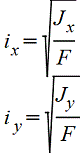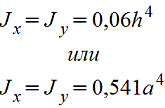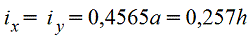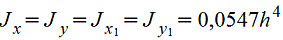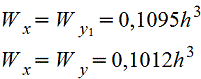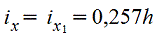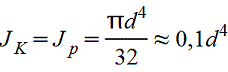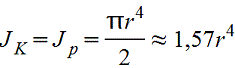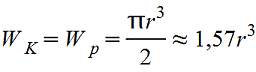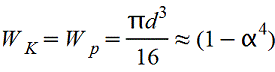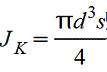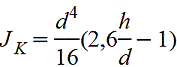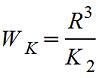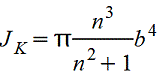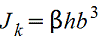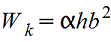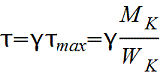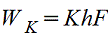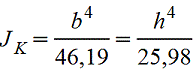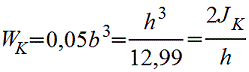Моменты инерции тел различной формы — Студопедия
Рассчитаем моменты инерции некоторых тел при различном расположении оси вращения.
1.Кольцо (тонкостенный цилиндр), ось вращения проходит через центр масс. (рис.3).


Рис.3а. Рис.3б.
Пусть кольцо (цилиндр) имеет радиус  и массу
и массу  . Для расчета используем формулу
. Для расчета используем формулу  . В этом случае
. В этом случае  для всех элементарных масс
для всех элементарных масс 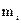
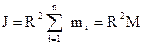 .
.2. Однородный стержень, ось вращения проходит через конец стержня.
Разобьем стержень на несколько частей длиной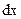 с массой
с массой , расположенных на разных расстояниях
, расположенных на разных расстояниях 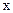 от оси вращения. Чем больше разбиений, тем точнее можно сосчитать момент инерции (рис.4). Поэтому удобней сумму заменить интегрированием:
от оси вращения. Чем больше разбиений, тем точнее можно сосчитать момент инерции (рис.4). Поэтому удобней сумму заменить интегрированием:
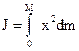
где 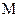 — масса всего стержня. Введем плотность и выразим через нее массу.
— масса всего стержня. Введем плотность и выразим через нее массу.

Рис.4.
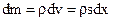 ,
,
где 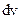 — объем элемента стержня площадью поперечного сечения
— объем элемента стержня площадью поперечного сечения 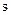 и длины
и длины 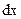
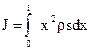 ,
,где 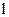 — длина стержня. После интегрирования получаем:
— длина стержня. После интегрирования получаем:
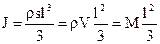 ,
,
где 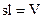 — объем всего стержня. Таким образом
— объем всего стержня. Таким образом
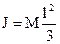 .
.
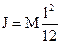 .
.
В таблице 1 приведены значения моментов инерции некоторых тел.
Таблица 1
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR2 |
| Сплошной цилиндр или диск радиусом R | Ось симметрии | (1/2)mR2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | (1/12)ml2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | (1/3)ml2 |
| Шар радиусом R | Ось проходит через центр шара | (2/5)mR2 |
Если известен момент инерции 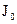 относительно оси проходящей через центр масс, то можно найти момент инерции относительно некоторых других осей по теореме Штейнера:
относительно оси проходящей через центр масс, то можно найти момент инерции относительно некоторых других осей по теореме Штейнера:
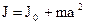 (15)
(15)Момент инерции твердого тела относительно любой оси равен моменту инерции относительно оси параллельной данной и проходящей через центр масс тела плюс произведение массы тела на квадрат расстояния между осями.

Рис.5.
Применим теорему Штейнера для определения момента инерции однородного стержня, длиной 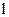 . Пусть
. Пусть 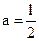 . Величина
. Величина 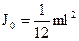

Рис.6.
 .
.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}Легенда:
|
Легенда:
|
||
|
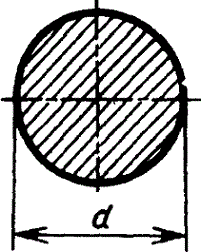
Форма поперечного сечения бруса |
Момент инерции при кручении J |
Момент сопротивления при кручении WK, см3 |
Положение точки, в которой возникает наибольшее напряжение τ=MK/WK |
|
Круглое |
или Полярный момент инерции Jp=2J |
или |
Наибольшее напряжение возникает во всех точках у наружного контура поперечного сечения |
|
Кольцо |
или |
или |
Наибольшее напряжение возникает во всех точках у наружного контура поперечного сечения |
|
Тонкостенное кольцо |
d — средний диаметр |
Все точки находятся в одинаковых условиях (приближенно) | |
| Незамкнутое тонкостенное кольцо | Наибольшее напряжение возникает в точках А. В точках В напряжение τ=0 | ||
|
Круглое сечение с лыской |
|||
Моменты инерции сечений простой формы — Студопедия
Теории прочности
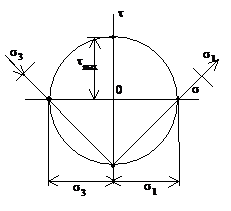
В общем случае опасное напряженное состояние элемента конструкции зависит от соотношения между тремя главными напряжениями (s1,s2,s3). Т.е., строго говоря, для каждого соотношения нужно экспериментально определять величину предельного напряжения, что нереально. Поэтому были приняты такие методы расчета прочности, которые позволяли бы оценить степень опасности любого напряженного состояния по напряжению растяжения – сжатия. Они называются теориями прочности (теории предельных напряженных состояний).
1-ая теория прочности (теория наибольших нормальных напряжений): причиной наступления предельного напряженного состояния являются наибольшие нормальные напряжения. smax= s1£ [s]. Главный недостаток: не учитываются два других главных напряжения. Подтверждается опытом только при растяжении весьма хрупких материалов (стекло, гипс). В настоящее время практически не применяется.
2-ая теория прочности (теория наибольших относительных деформаций): причиной наступления предельного напряженного состояния являются наибольшие удлинения. emax= e1£ [e]. Учитывая, что e1=  , m — коэффициент Пуассона, получаем условие прочности sэквII= s1 — m(s2 + s3)£ [s]. sэкв — эквивалентное (расчетное) напряжение. В настоящее время теория используется редко, только для хрупких материалов (бетон, камень).
, m — коэффициент Пуассона, получаем условие прочности sэквII= s1 — m(s2 + s3)£ [s]. sэкв — эквивалентное (расчетное) напряжение. В настоящее время теория используется редко, только для хрупких материалов (бетон, камень).
3-я теория прочности (теория наибольших касательных напряжений): причиной наступления предельного напряженного состояния являются наибольшие касательные напряжения tmax £ [t], tmax= 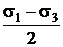 , условие прочности: sэквIII= s1 — s3£ [s]. Основной недостаток – не учитывает влияние s2. При плоском напряженном состоянии: sэквIII=
, условие прочности: sэквIII= s1 — s3£ [s]. Основной недостаток – не учитывает влияние s2. При плоском напряженном состоянии: sэквIII= 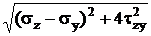 £ [s]. При sy=0 получаем
£ [s]. При sy=0 получаем 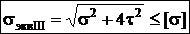 Широко используется для пластичных материалов.
Широко используется для пластичных материалов.
4-я теория прочности (энергетическая теория): причиной наступления предельного напряженного состояния являются величина удельной потенциальной энергии изменения формы. uф£[uф]. 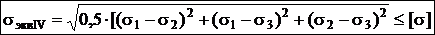 .
.
Учитывает, все три главных напряжения. При плоском напряженном состоянии: 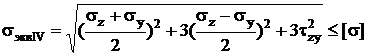 . При sy=0,
. При sy=0, 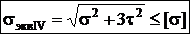
Широко используется для пластичных материалов.
Теория прочности Мора Получена на основе кругов напряжений Мора. 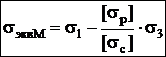 . Используется при расчетах хрупких материалов, у которых допускаемые напряжения на растяжение [sp] и сжатие [sс] не одинаковы (чугун).
. Используется при расчетах хрупких материалов, у которых допускаемые напряжения на растяжение [sp] и сжатие [sс] не одинаковы (чугун).
Для пластичных материалов [sp]=[sс] теория Мора превращается в 3-ю теорию.
Чистый сдвиг
 Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения
Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения  , где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: s1= — s3 = t; s2= 0. Главные площадки составляют с площадками чистого сдвига угол 45о.
, где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: s1= — s3 = t; s2= 0. Главные площадки составляют с площадками чистого сдвига угол 45о.
 При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. d — абсолютный сдвиг,
При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. d — абсолютный сдвиг,
g » 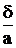 — относительный сдвиг или угол сдвига.
— относительный сдвиг или угол сдвига.
Закон Гука при сдвиге: g = t/G или t = G×g .
G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. 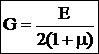 (Е — модуль упругости, m— коэффициент Пуассона).
(Е — модуль упругости, m— коэффициент Пуассона).
Потенциальная энергия при сдвиге:  .
.
 Удельная потенциальная энергия деформации при сдвиге:
Удельная потенциальная энергия деформации при сдвиге: 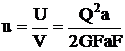 ,
,
где V=а×F — объем элемента. Учитывая закон Гука, 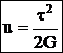 .
.
Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.
Круг Мора при чистом сдвиге.
Геометрические характеристики плоских сечений
Площадь: 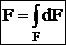 , dF — элементарная площадка.
, dF — элементарная площадка.
Статический момент элемента площади dF относительно оси 0x 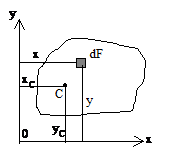 — произведение элемента площади на расстояние «y» от оси 0x: dSx = y×dF
— произведение элемента площади на расстояние «y» от оси 0x: dSx = y×dF
Просуммировав (проинтегрировав) такие произведения по всей площади фигуры, получаем статические моменты относительно осей y и x: 
 ;
;  [см3, м3, т.д.].
[см3, м3, т.д.].
Координаты центра тяжести: 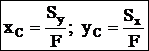 . Статические моменты относительно центральных осей (осей, проходящих через центр тяжести сечения) равны нулю. При вычислении статических моментов сложной фигуры ее разбивают на простые части, с известными площадями Fi и координатами центров тяжести xi, yi.Статический момент площади всей фигуры = сумме статических моментов каждой ее части:
. Статические моменты относительно центральных осей (осей, проходящих через центр тяжести сечения) равны нулю. При вычислении статических моментов сложной фигуры ее разбивают на простые части, с известными площадями Fi и координатами центров тяжести xi, yi.Статический момент площади всей фигуры = сумме статических моментов каждой ее части: 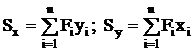 .
.
Координаты центра тяжести сложной фигуры: 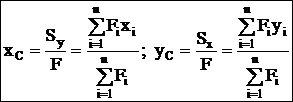
 Моменты инерции сечения
Моменты инерции сечения
Осевой (экваториальный) момент инерции сечения — сумма произведений элементарных площадок dF на квадраты их расстояний до оси.
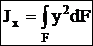 ;
; 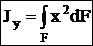 [см4, м4, т.д.].
[см4, м4, т.д.].
Полярный момент инерции сечения относительно некоторой точки (полюса) — сумма произведений элементарных площадок на квадраты их расстояний от этой точки.  ; [см4, м4, т.д.]. Jy + Jx = Jp .
; [см4, м4, т.д.]. Jy + Jx = Jp .
Центробежный момент инерции сечения — сумма произведений элементарных площадок на их расстояния от двух взаимно перпендикулярных осей.  .
.
Центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с осями симметрии, равен нулю.
Осевые и полярные моменты инерции всегда положительны, центробежные моменты инерции могут быть положительными, отрицательными или равными нулю.
Момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.
Моменты инерции сечений простой формы

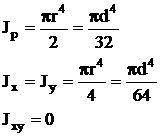
Прямоугольное сечение Круг

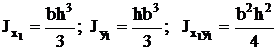

 Кольцо
Кольцо
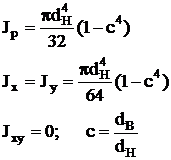
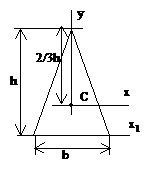 Треугольник
Треугольник

равнобедренный
Прямоугольный
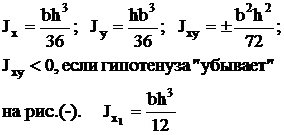
 треугольник
треугольник
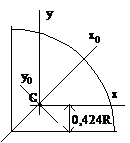 Четверть круга
Четверть круга
Jy=Jx=0,055R4
Jxy=±0,0165R4
на рис. (—)
Jx0=0,0714R4
Jy0=0,0384R4
Полукруг
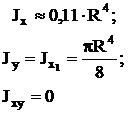
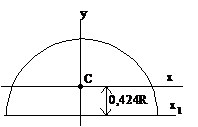 Моменты инерции стандартных профилей находятся из таблиц сортамента:
Моменты инерции стандартных профилей находятся из таблиц сортамента:

 ДвутаврШвеллерУголок
ДвутаврШвеллерУголок
 Моменты инерции относительно параллельных осей:
Моменты инерции относительно параллельных осей:
 Jx1=Jx + a2F;
Jx1=Jx + a2F;
Jy1=Jy + b2F;
момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. Jy1x1=Jyx + abF; («a» и «b» подставляют в формулу с учетом их знака).
Зависимость между моментами инерции при повороте осей:
 Jx1=Jxcos2a + Jysin2a — Jxysin2a; Jy1=Jycos2a + Jxsin2a + Jxysin2a;
Jx1=Jxcos2a + Jysin2a — Jxysin2a; Jy1=Jycos2a + Jxsin2a + Jxysin2a;
Jx1y1=  (Jx — Jy)sin2a + Jxycos2a ;
(Jx — Jy)sin2a + Jxycos2a ;
Угол a>0, если переход от старой системы координат к новой происходит против час.стр. Jy1 + Jx1= Jy + Jx
Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей: 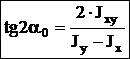 , если a0>0 Þ оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:
, если a0>0 Þ оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей: 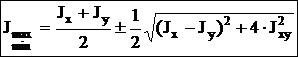
Jmax + Jmin= Jx + Jy. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям:
Jx1=Jmaxcos2a + Jminsin2a; Jy1=Jmaxcos2a + Jminsin2a; Jx1y1=  (Jmax — Jmin)sin2a;
(Jmax — Jmin)sin2a;
Конечной целью вычисления геометрических характеристик сечения является определение главных центральных моментов инерции и положения главных центральных осей инерции. 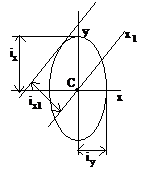 Радиус инерции —
Радиус инерции —  ; Jx=F×ix2, Jy=F×iy2.
; Jx=F×ix2, Jy=F×iy2.
Если Jx и Jy главные моменты инерции, то ix и iy — главные радиусы инерции. Эллипс, построенный на главных радиусах инерции как на полуосях, называется эллипсом инерции. При помощи эллипса инерции можно графически найти радиус инерции ix1 для любой оси х1. Для этого надо провести касательную к эллипсу, параллельную оси х1, и измерить расстояние от этой оси до касательной. Зная радиус инерции, можно найти момент инерции сечения относительно оси х1: 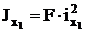 . Для сечений, имеющих более двух осей симметрии (например: круг, квадрат, кольцо и др.) осевые моменты инерции относительно всех центральных осей равны между собой, Jxy=0, эллипс инерции обращается в круг инерции.
. Для сечений, имеющих более двух осей симметрии (например: круг, квадрат, кольцо и др.) осевые моменты инерции относительно всех центральных осей равны между собой, Jxy=0, эллипс инерции обращается в круг инерции.
Моменты сопротивления.
Осевой момент сопротивления — отношение момента инерции относительно оси к расстоянию от нее до наиболее удаленной точки сечения. 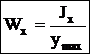 [см3, м3]
[см3, м3]
Особенно важны моменты сопротивления относительно главных центральных осей:
прямоугольник:  ; круг: Wx=Wy=
; круг: Wx=Wy= 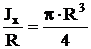 ,
,
трубчатое сечение (кольцо): Wx=Wy= 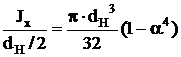 , где a= dН/dB.
, где a= dН/dB.
 Полярный момент сопротивления — отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения:
Полярный момент сопротивления — отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения: 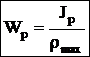 .
.
Для круга Wр= 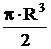 .
.
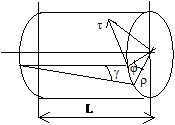
Кручение
Такой вид деформации, при котором в поперечных сечениях возникает только одни крутящие моменты — Мк. Знак крутящего момента Мк удобно определять по направлению внешнего момента. Если при взгляде со стороны сечения внешний момент направлен против час.стр., то Мк>0 (встречается и обратное правило). При кручении происходит поворот одного сечения относительно другого на угол закручивания -j. При кручении круглого бруса (вала) возникает напряженное состояние чистого сдвига (нормальные напряжения отсутствуют), возникают только касательные напряжения. Принимается, что сечения плоские до закручивания остаются плоскими и после закручивания — закон плоских сечений. Касательные напряжения в точках сечения изменяются пропорционально расстоянию точек от оси. Из закона Гука при сдвиге: t=gG, G — модуль сдвига, 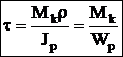 ,
,  — полярный момент сопротивления круглого сечения. Касательные напряжения в центре равны нулю, чем дальше от центра, тем они больше. Угол закручивания
— полярный момент сопротивления круглого сечения. Касательные напряжения в центре равны нулю, чем дальше от центра, тем они больше. Угол закручивания 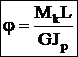 , GJp — жесткость сечения при кручении.
, GJp — жесткость сечения при кручении. 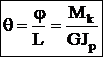 — относительный угол закручивания. Потенциальная энергия при кручении:
— относительный угол закручивания. Потенциальная энергия при кручении: 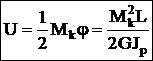 . Условие прочности:
. Условие прочности:  , [t] =
, [t] =  , для пластичного материала за tпред принимается предел текучести при сдвиге tт, для хрупкого материала – tв – предел прочности, [n] – коэффициент запаса прочности. Условие жесткости при кручении: qmax£[q] – допустимый угол закручивания.
, для пластичного материала за tпред принимается предел текучести при сдвиге tт, для хрупкого материала – tв – предел прочности, [n] – коэффициент запаса прочности. Условие жесткости при кручении: qmax£[q] – допустимый угол закручивания.
3. Моменты инерции тел различной формы.
Рассчитаем моменты инерции некоторых тел при различном расположении оси вращения.
1.Кольцо (тонкостенный цилиндр), ось вращения проходит через центр масс. (рис.3).


Рис.3а. Рис.3б.
Пусть кольцо (цилиндр) имеет радиус  и массу
и массу .
Для расчета используем формулу
.
Для расчета используем формулу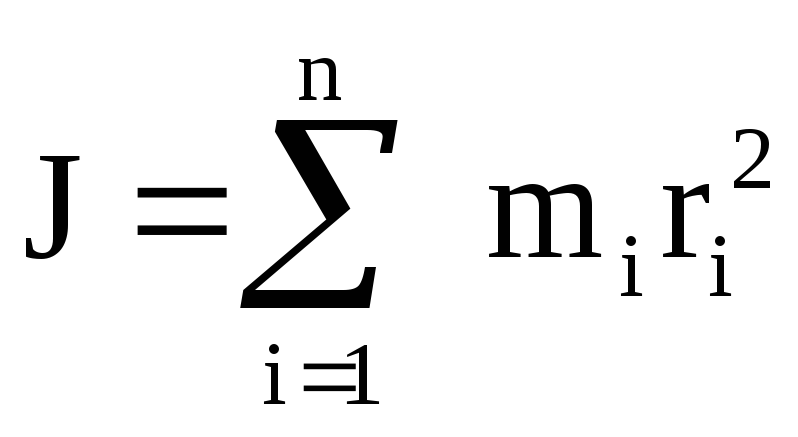 .
В этом случае
.
В этом случае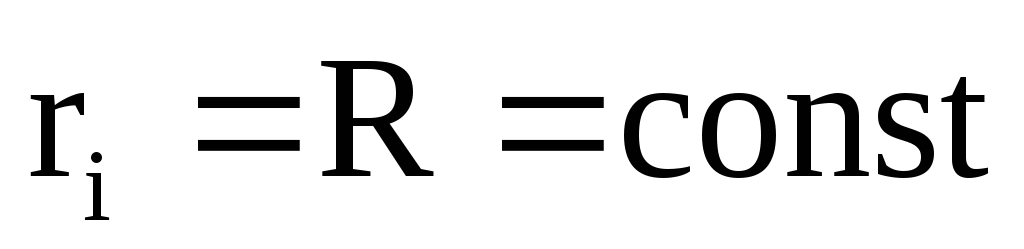 для
всех элементарных масс
для
всех элементарных масс .
Поэтому
.
Поэтому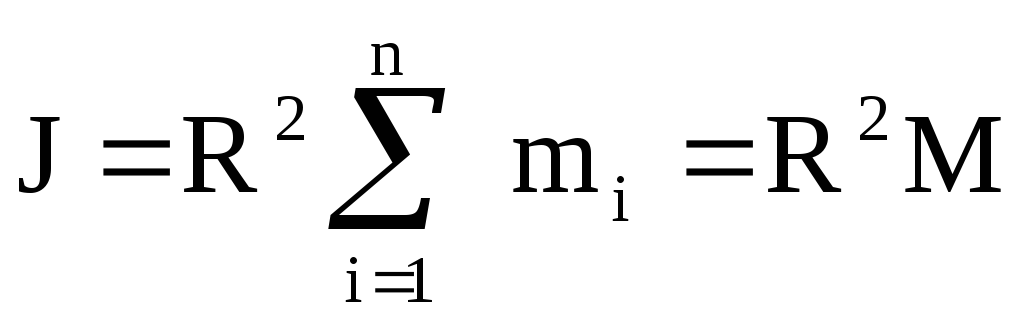 .
.
2. Однородный стержень, ось вращения проходит через конец стержня.
Разобьем стержень на несколько частей
длиной с
массой
с
массой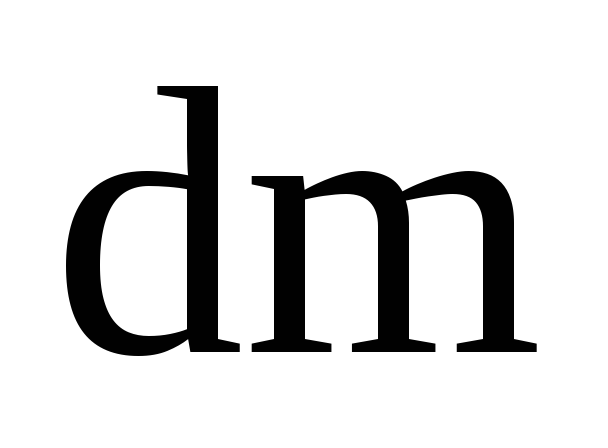 ,
расположенных на разных расстояниях
,
расположенных на разных расстояниях от оси вращения. Чем больше разбиений,
тем точнее можно сосчитать момент
инерции (рис.4). Поэтому удобней сумму
заменить интегрированием:
от оси вращения. Чем больше разбиений,
тем точнее можно сосчитать момент
инерции (рис.4). Поэтому удобней сумму
заменить интегрированием:
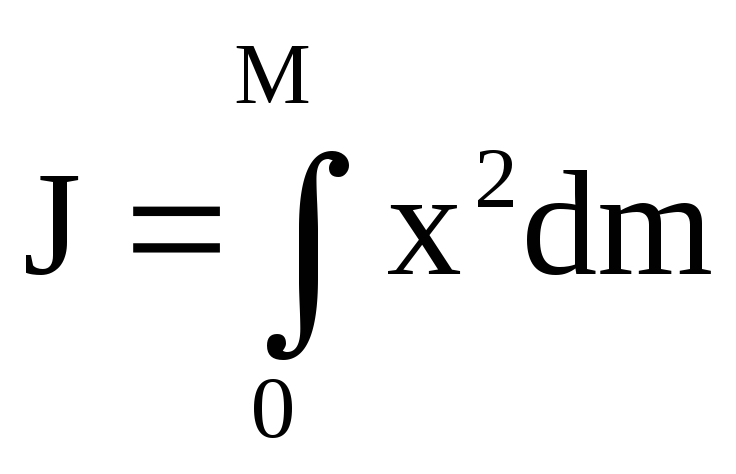
где  — масса всего стержня. Введем плотность
и выразим через нее массу.
— масса всего стержня. Введем плотность
и выразим через нее массу.

Рис.4.
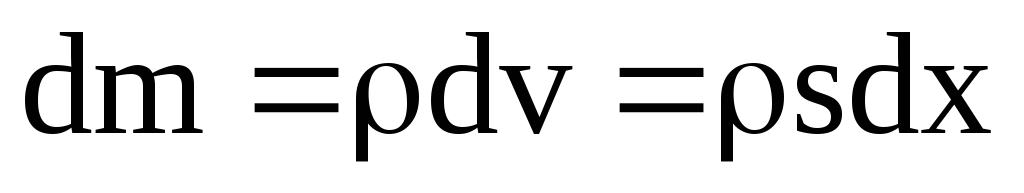 ,
,
где  — объем элемента стержня площадью
поперечного сечения
— объем элемента стержня площадью
поперечного сечения и длины
и длины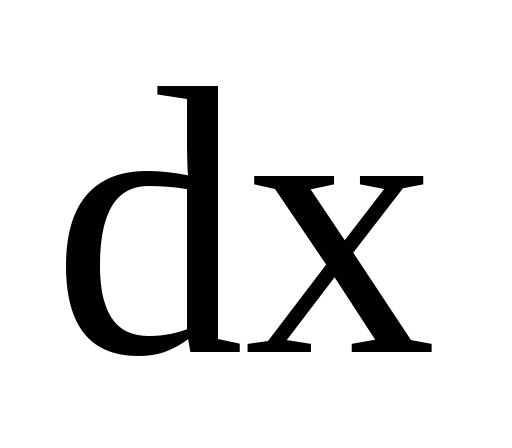 .
Тогда
.
Тогда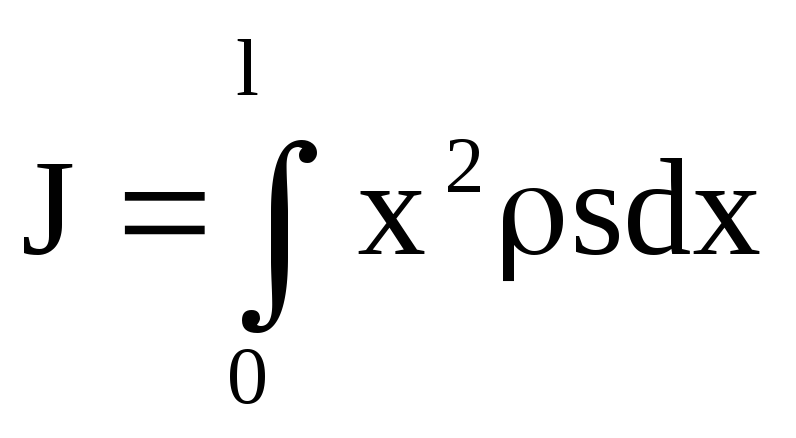 ,
,
где 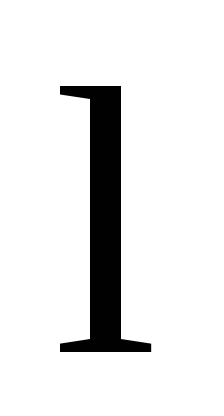 — длина стержня. После интегрирования
получаем:
— длина стержня. После интегрирования
получаем:
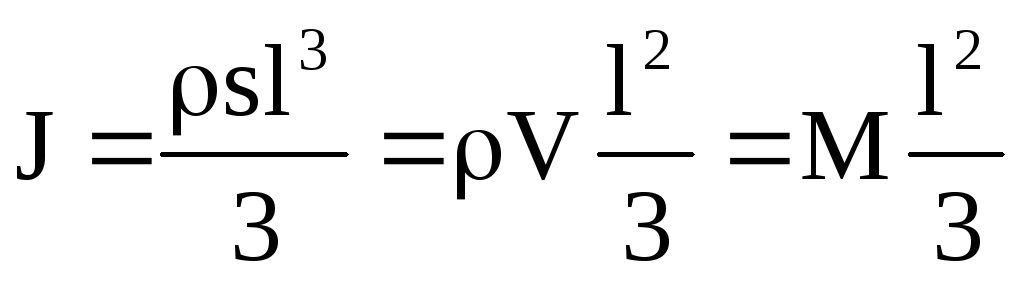 ,
,
где 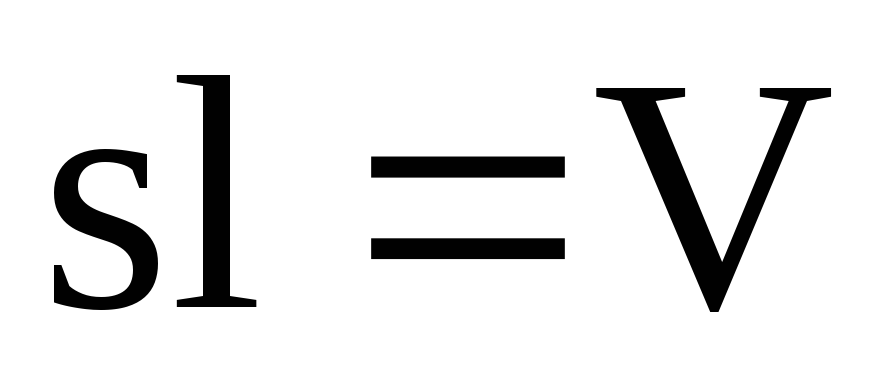 — объем всего стержня. Таким образом
— объем всего стержня. Таким образом
 .
.
Если ось вращения стержня проходит через центр масс стержня, то
 .
.
В таблице 1 приведены значения моментов инерции некоторых тел.
Таблица 1
Тело | Положение оси вращения | Момент инерции |
Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR2 |
Сплошной цилиндр или диск радиусом R | Ось симметрии | (1/2)mR2 |
Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | (1/12)ml2 |
Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | (1/3)ml2 |
Шар радиусом R | Ось проходит через центр шара | (2/5)mR2 |
Если известен момент инерции  относительно оси проходящей через центр
масс, то можно найти момент инерции
относительно некоторых других осей по
теореме Штейнера:
относительно оси проходящей через центр
масс, то можно найти момент инерции
относительно некоторых других осей по
теореме Штейнера:
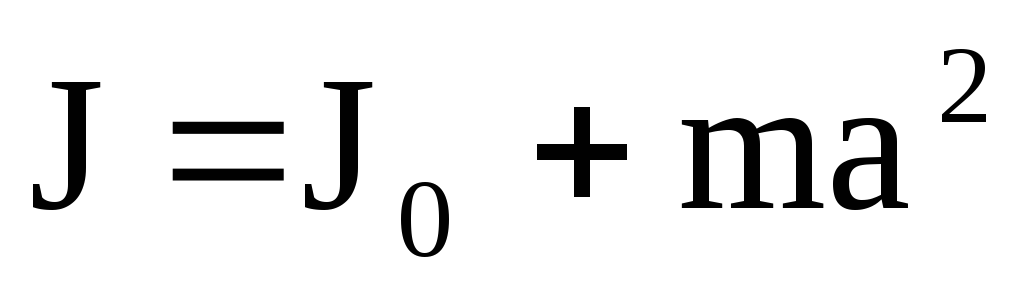 (15)
(15)
Момент инерции твердого тела относительно любой оси равен моменту инерции относительно оси параллельной данной и проходящей через центр масс тела плюс произведение массы тела на квадрат расстояния между осями.

Рис.5.
Применим теорему Штейнера для определения
момента инерции однородного стержня,
длиной  .
Пусть
.
Пусть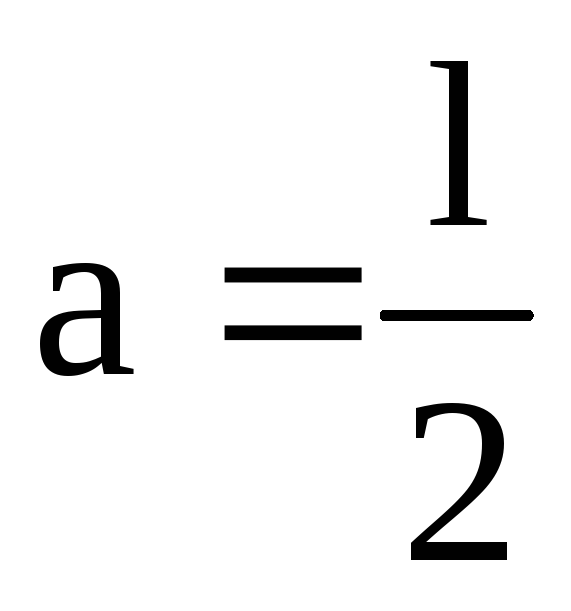 .
Величина
.
Величина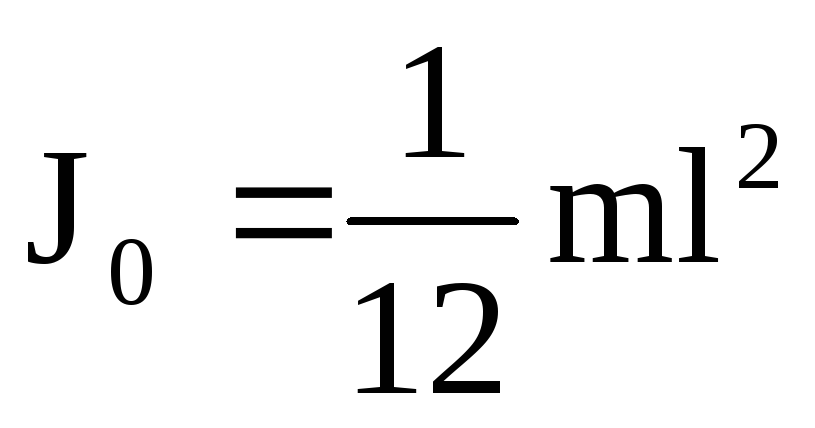 ( смотри таблицу). Тогда
( смотри таблицу). Тогда

Рис.6.
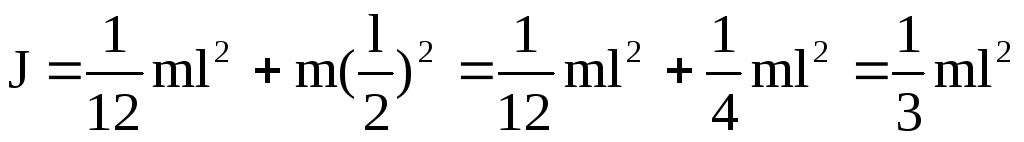 .
.
4. Момент силы относительно неподвижной точки.
Моментом силы  относительно неподвижной точки 0
называется физическая величина,
определяемая векторным произведением
радиуса-вектора
относительно неподвижной точки 0
называется физическая величина,
определяемая векторным произведением
радиуса-вектора ,
проведенного из точки 0 в точкуаприложения силы, на силу
,
проведенного из точки 0 в точкуаприложения силы, на силу
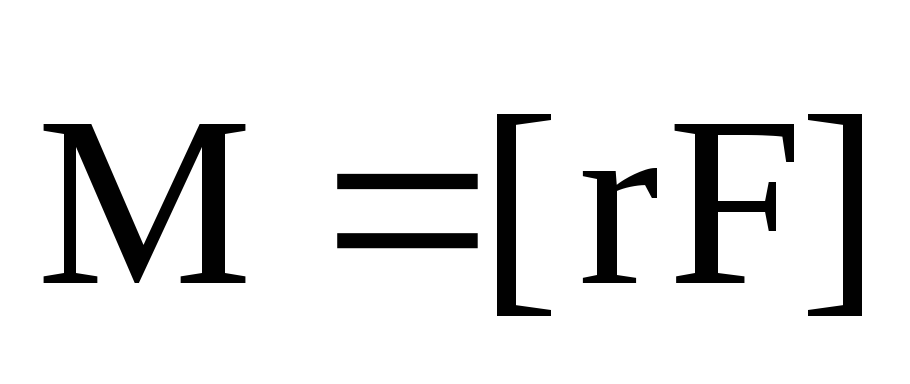 (16)
(16)

Рис.7.
Направление вектора  совпадает с направлением поступательного
движения правого винта при его вращении
от
совпадает с направлением поступательного
движения правого винта при его вращении
от к
к .
Модуль момента силы равен
.
Модуль момента силы равен
,
где  — угол между
— угол между и
и ,
а
,
а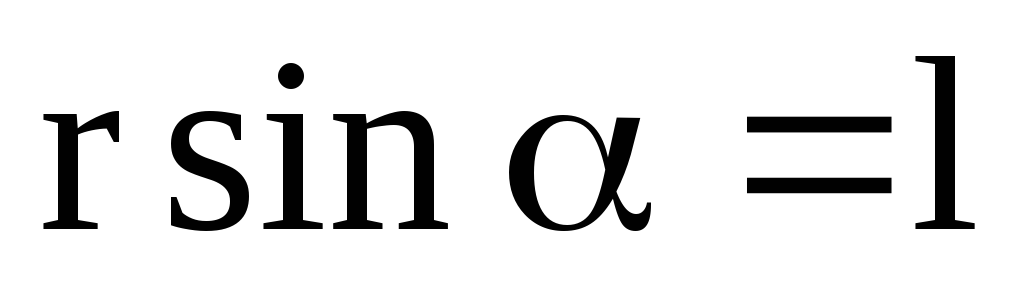 — кратчайшее расстояние между линией
действия силы и точкой 0 называется
плечом силы.
— кратчайшее расстояние между линией
действия силы и точкой 0 называется
плечом силы.
5. Момент силы относительно неподвижной оси.
Моментом силы относительно неподвижной
оси zназывается скалярная
величина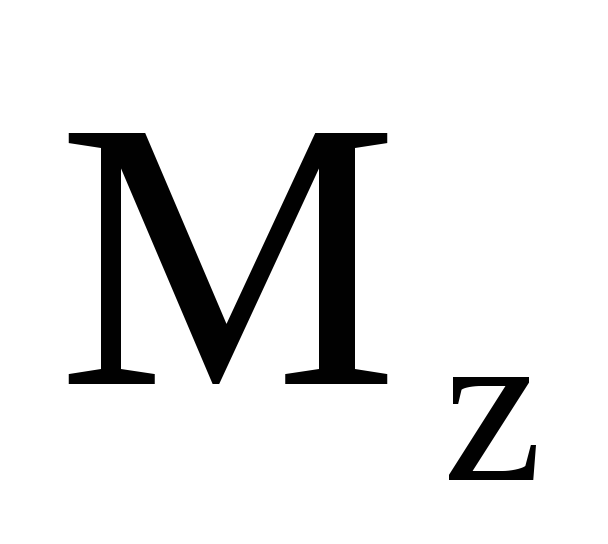 ,
равная проекции на эту ось вектора
момента силы
,
равная проекции на эту ось вектора
момента силы , определенного относительно произвольной
точки 0 данной осиz.
Значение момента
, определенного относительно произвольной
точки 0 данной осиz.
Значение момента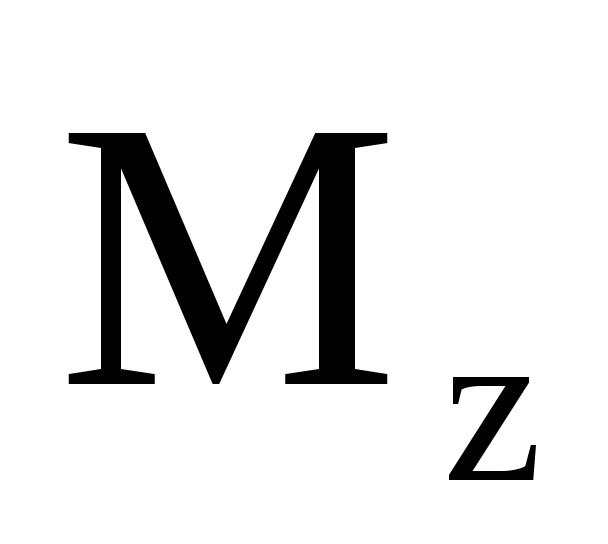 не зависит от выбора точки 0 на осиz.
не зависит от выбора точки 0 на осиz.

Рис. 8.
В частном случае, если ось zсовпадает с направлением вектора М, величина момента силы относительно точки, совпадает с моментом силы относительно оси.

Рассмотрим систему материальных точек, к которым приложены силы. Моментом всех сил, действующих на систему материальных точек относительно неподвижной точки, называется векторная сумма моментов отдельных сил относительно той же точки.
 (18)
(18)
Моментом всех сил, действующих на систему материальных точек относительно неподвижной оси называется алгебраическая сумма моментов отдельных сил относительно той же оси,
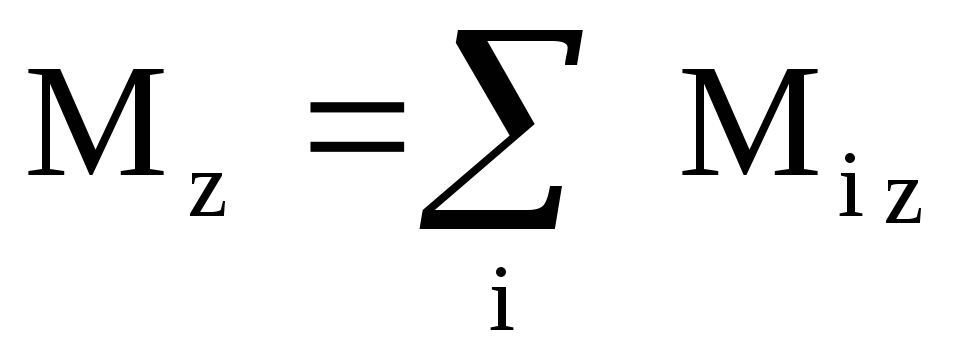 (19)
(19)
Легенда:
| Легенда: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Форма поперечного сечения | Осевой момент инерции, J, см4 | Момент сопротивления W, см3 | Радиус инерции i, см | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
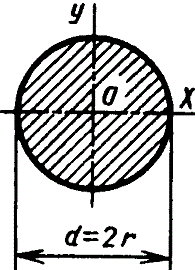
Круг |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
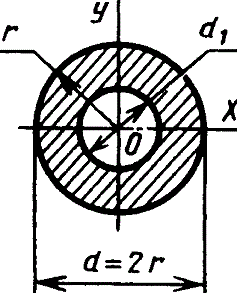
Кольцо |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тонкостенное
кольцо |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Полукруг |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Круговой
сегмент
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Круговой
сектор |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Круговое
полукольцо |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сектор
кругового кольца |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Профиль
с симметричными закруглениями |
|
| — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
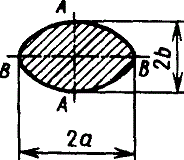
Эллипс
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
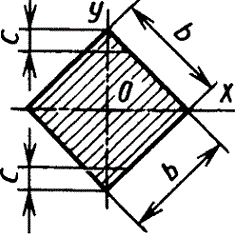
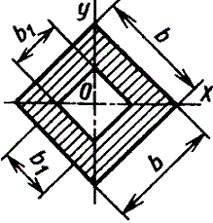
Квадрат
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Полый
квадрат |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
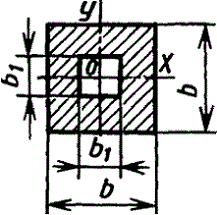
Полый тонкостенный квадрат s<(B/15) |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Квадрат,
поставленный на ребро |
| Срез верхнего и нижнего углов увеличивает Wx; при срезе углов на С=1/18 диагонали с каждой стороны момент сопротивления увеличивается до Wx=0,124b3 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Полый
квадрат, поставленный на ребро |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
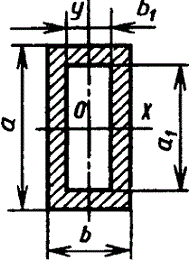
Прямоугольник
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Прямоугольник
повернутый |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Полый прямоугольник
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
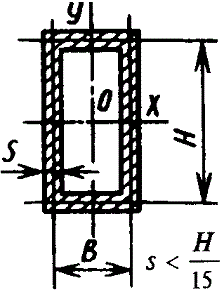
Полый тонкостенный прямоугольник
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сечение из двух равных прямоугольников
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Треугольник
|
| При
вычислении напряжения в вершине
треугольника |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Поставленный на ребро треугольник
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
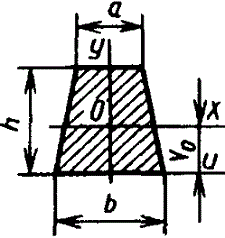
Трапеция
|
| При
вычислении напряжений в точках верхнего
основания |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Трапеция
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
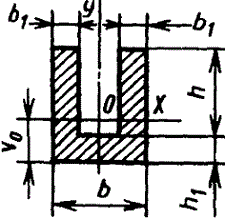
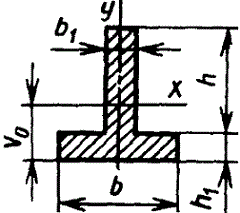
Тавр
|
| Для
нижних волокон |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Корытное сечение
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Крестообразное сечение
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Правильный шестиугольник
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
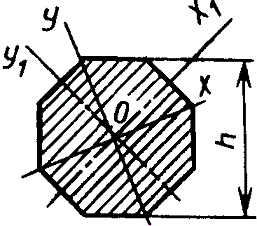
Правильный восьмиугольник
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Форма поперечного сечения бруса | Момент инерции при кручении JK, см4 | Момент сопротивления при кручении WK, см3 | Положение точки, в которой возникает наибольшее напряжение τ=MK/WK | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Круглое
| или Полярный момент инерции Jp=2J | или
| Наибольшее напряжение возникает во всех точках у наружного контура поперечного сечения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
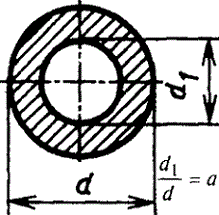
Кольцо
| или
| или
| Наибольшее напряжение возникает во всех точках у наружного контура поперечного сечения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
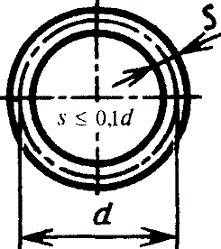
Тонкостенное кольцо
| d — средний диаметр |
| Все точки находятся в одинаковых условиях (приближенно) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
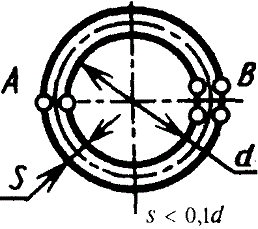
Незамкнутое
тонкостенное кольцо |
|
| Наибольшее напряжение возникает в точках А. В точках В напряжение τ=0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
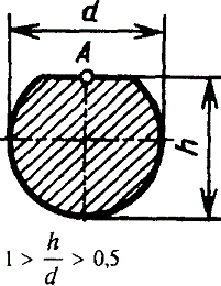
Круглое сечение с лыской
|
|
| Наибольшее напряжение возникает в середине плоского среза (точка А). В углах τ=0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Круглое с круговым вырезом
|
|
| Наибольшее напряжение возникает по дну канавки (точка А) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
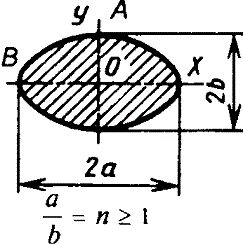
Значение коэффициентов K1 и K2 в зависимости от r/R
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сплошное эллиптическое | | Наибольшее напряжение в точках А. Напряжение в точках В | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
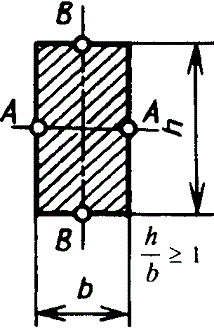
Прямоугольное | | Наибольшее напряжение возникает в серединах длинных сторон сечения (в точках А), в точках В напряжение | | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Значение коэффициентов α, β и γ в зависимости от h/b
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Правильный шести- или восьмиугольник | Для шестиугольника K’=0,133. Для восьмиугольника K’=0,130. F — площадь сечения | Для шестиугольника К=0,217 Для восьмиугольника К=0,233 | Наибольшее напряжение возникают в середине сторон в углах τ=0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Равносторонний треугольник | | | Наибольшие напряжения возникают в середине сторон. В углах τ=0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Момент инерции конуса
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- BNAT 000 NC
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы бумаги CBSE для класса 7
- Образцы бумаги CBSE для класса 8
- Образцы бумаги CBSE для класса 9
- Образцы бумаги CBSE для класса 10
- Образцы бумаги CBSE для класса 11
- Образцы бумаги CBSE чел для класса 12
- Классы
- CBSE Контрольный документ за предыдущий год
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- CBSE Notes
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции
- CBSE Class
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE
Дополнительные вопросы по математике для класса 10
- CBSE Class
- Дополнительные вопросы по науке, класс 10 по CBSE
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions For Класс 12 по физике
- Решения NCERT для химии класса 12
- Решения NCERT для класса 12 по биологии
- Решения NCERT для класса 12 по математике
- Решения NCERT Класс 12 Бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- Решения NCERT, класс 12 Экономика
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для социальных наук класса 6
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для класса 7 Наука
- Решения NCERT для класса 7 по социальным наукам
- Решения NCERT для класса 7 Английский
- Решения NCERT для класса 8 Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для социальных наук 8 класса
- Решение NCERT ns для класса 8 Английский
- Решения NCERT для социальных наук класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для Математика класса 9 Глава 2
- Решения NCERT для математики класса 9 Глава 3
- Решения NCERT для математики класса 9 Глава 4 Решения NCERT
- для математики класса 9 Глава 5
- Решения NCERT для математики класса 9 Глава 6
- Решения NCERT для Математика класса 9 Глава 7
- Решения NCERT для математики класса 9 Глава 8 Решения NCERT
- для математики класса 9 Глава 9 Решения NCERT
- для математики класса 9 Глава 10
- Решения NCERT для математики класса 9 Глава 11
- Решения NCERT для Математика класса 9 Глава 12
- Решения NCERT для математики класса 9 Глава 13 Решения
- NCERT для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для Науки Класса 9 Глава 4
- Решения NCERT для Науки Класса 9 Глава 5
- Решения NCERT для Науки Класса 9 Глава 6
- Решения NCERT для Науки Класса 9 Глава 7
- Решения NCERT для Класса 9 Наука Глава 8
- Решения NCERT для Науки Класса 9 Глава 9
- Решения NCERT для Науки Класса 9 Глава 10
- Решения NCERT для Науки Класса 9 Глава 12
- Решения NCERT для Науки Класса 9 Глава 11
- Решения NCERT для Класса 9 Наука Глава 13
- Решения NCERT для класса 9 Наука Глава 14
- Решения NCERT для класса 9 по науке Глава 15
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- Решения NCERT для математики класса 10 Глава 3
- Решения NCERT для математики класса 10 Глава 4
- Решения NCERT для математики класса 10 Глава 5
- Решения NCERT для математики класса 10 Глава 6
- Решения NCERT для математики класса 10 Глава 7
- Решения NCERT для математики класса 10 Глава 8
- Решения NCERT для математики класса 10 Глава 9 Решения NCERT
- для математики класса 10 Глава 10 Решения
- NCERT для математики класса 10 Глава 11
- Решения NCERT для математики класса 10 Глава 12
- Решения NCERT для математики класса 10 Глава 13
- NCERT Sol Решения NCERT для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки класса 10 Глава 1
- Решения NCERT для науки класса 10 Глава 2
- Решения NCERT для науки класса 10, глава 3
- Решения NCERT для науки класса 10, глава 4
- Решения NCERT для науки класса 10, глава 5
- Решения NCERT для науки класса 10, глава 6
- Решения NCERT для науки класса 10, глава 7
- Решения NCERT для науки 10 класса, глава 8
- Решения NCERT для науки класса 10 Глава 9
- Решения NCERT для науки класса 10 Глава 10
- Решения NCERT для науки класса 10 Глава 11
- Решения NCERT для науки класса 10 Глава 12
- Решения NCERT для науки 10 класса Глава 13
- Решения NCERT для науки 10 класса Глава 14
- Решения NCERT для науки 10 класса Глава 15
- Решения NCERT для науки 10 класса Глава 16
- Class 11 Commerce Syllabus
- ancy Account
- Программа бизнес-исследований 11 класса
- Учебная программа по экономике 11 класса
- Учебная программа по коммерции 12 класса
- Учебная программа по бухгалтерии 12 класса
- Учебная программа по бизнесу 12 класса
- Учебная программа по экономике
- 9000 9000
- Образцы документов по коммерции класса 11
- Образцы документов по коммерции класса 12
- TS Grewal Solutions
- TS Grewal Solutions Class 12 Accountancy
- TS Grewal Solutions Class 11 Accountancy
- Отчет о движении денежных средств
- Что такое Entry eurship
- Защита прав потребителей
- Что такое основной актив
- Что такое баланс
- Формат баланса
- Что такое акции
- Разница между продажами и маркетингом
- ICSE
- Документы
- ICSE
- Вопросы ICSE
- ML Aggarwal Solutions
- ML Aggarwal Solutions Class 10 Maths
- ML Aggarwal Solutions Class 9 Maths
- ML Aggarwal Solutions Class 8 Maths
- ML Aggarwal Solutions Class 7 Maths
- ML 6 Maths
- ML 6 Maths
- Selina Solutions
- Selina Solutions для класса 8
- Selina Solutions для Class 10
- Selina Solutions для Class 9
- Frank Solutions
- Frank Solutions для математики класса 10
- Frank Solutions для математики класса 9
- Класс ICSE 9000 2
- ICSE Class 6
- ICSE Class 7
- ICSE Class 8
- ICSE Class 9
- ICSE Class 10
- ISC Class 11
- ISC Class 12
- Exam
- IAS
- Civil
- Сервисный экзамен
- Программа UPSC
- Бесплатная подготовка к IAS
- Текущие события
- Список статей IAS
- Пробный тест IAS 2019
- Пробный тест IAS 2019 1
- Пробный тест IAS 2019 2
- Экзамен KPSC KAS
- Экзамен UPPSC PCS
- Экзамен MPSC
- Экзамен RPSC RAS
- TNPSC Group 1
- APPSC Group 1
- Экзамен BPSC
- WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
- Ключ ответов UPSC 2019
- IA S Coaching Бангалор
- IAS Coaching Дели
- IAS Coaching Ченнаи
- IAS Coaching Хайдарабад
- IAS Coaching Мумбаи
- BYJU’SEE
- 9000 JEE 9000 Основной документ JEE 9000 JEE 9000
- Вопросник JEE
- Биномиальная теорема
- Статьи JEE
- Квадратичное уравнение
- Программа BYJU NEET
- NEET 2020
- NEET Приемлемость 9000 Критерии 9000 NEET4 9000 Пример 9000 NEET 9000 9000 NEET
- Поддержка
- Разрешение жалоб
- Служба поддержки клиентов
- Центр поддержки
- GSEB
- GSEB Syllabus
- GSEB4
- GSEB3 Образец статьи 004
- MSBSHSE
- MSBSHSE Syllabus
- MSBSHSE Учебники
- Образцы статей MSBSHSE
- Вопросники MSBSHSE
- AP Board
- APSCERT
- APS4
- Syll
- AP
- Syll 9000SC4
- Syll
- AP 9000S4 9000 Syll
- Syll
- MP Board
- MP Board Syllabus
- MP Board Образцы документов
- Учебники MP Board
- Assam Board
- Assam Board Syllabus
- Assam Board Учебники 9000 9000 Board4
- Assam Board Учебники 9000 Board4 BSEB
- Bihar Board Syllabus
- Bihar Board Учебники
- Bihar Board Question Papers
- Bihar Board Model Papers
- BSE Odisha
- Odisha Board Syllabus
- Odisha Board Syllabus
- Программа PSEB
- Учебники PSEB
- Вопросы PSEB
- RBSE
- Rajasthan Board Syllabus
- RBSE Учебники
- RBSE Question Papers
- HPBOSE
- HPBOSE 000 Syllab HPBOSE
000 HPBOSE - JKBOSE
- Программа JKBOSE
- Образцы документов JKBOSE
- Шаблон экзамена JKBOSE
- TN Board
- TN Board Syllabus
- TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 Paper 9000 Paper JAC
- Программа JAC
- Учебники JAC
- Вопросники JAC
- Telangana Board
- Telangana Board Syllabus
- Telangana Board Учебники
- Papers Telangana Board Учебники
- KSEEB Syllabus
- Типовые вопросы KSEEB
- KBPE
- KBPE Syllabus
- Учебники KBPE
- KBPE Вопросы
- 9000 UPMSP Board 9000 UPMSP Board2
- Совет по Западной Бенгалии
- Учебный план Совета по Западной Бенгалии
- Учебники по Совету по Западной Бенгалии
- Вопросы для Совета по Западной Бенгалии
- UBSE
- TBSE
- Гоа Совет
- 000
- NBSE000
- Mega Board
- Manipur Board
- Haryana Board
- Банковские экзамены
- Экзамены SBI
- Экзамены IBPS
- Экзамены RBI
- IBPS
03
- Экзамены SSC
9SC2 - SSC GD
- SSC CPO 900 04
- SSC CHSL
- SSC CGL
- Экзамены RRB
- RRB JE
- RRB NTPC
- RRB ALP
- O Экзамены на страхование
- LIC4
- LIC4
- UPSC CAPF
- Список статей государственных экзаменов
- Класс 1
- Класс 2
- Класс 3
- Вопросы по физике
- Вопросы по химии
- Вопросы по химии
- Вопросы
- Вопросы по науке
- Вопросы для общего доступа
- Домашнее обучение
- BYJU’S CAT Program
- CAT3 9000 Предварительный курс CAT3 Экзамен 9000 9000 CAT3
Момент инерции. — ppt видео онлайн скачать
Презентация на тему: «Момент инерции». — Расшифровка презентации:
1
Момент инерции 
2 Тип момента инерции
Момент инерции площади Момент инерции массы Также известен как второй момент Зачем нужно рассчитывать момент инерции? Для измерения влияния формы поперечного сечения балки на сопротивление балки изгибающему моменту Применение Определение напряжений в балках и колоннах Символ I — символ области инерции Ix, Iy и Iz 
3 Применение: конструкционная сталь (свойства сечения)
4 Момент инерции области
yy dx dy dy hh C x C xbb Площадь закрашенного элемента, Площадь закрашенного элемента, Момент инерции относительно оси x Момент инерции относительно оси y Интегрирование от h / 2 до h / 2 Интеграция от b / 2 до b / 2 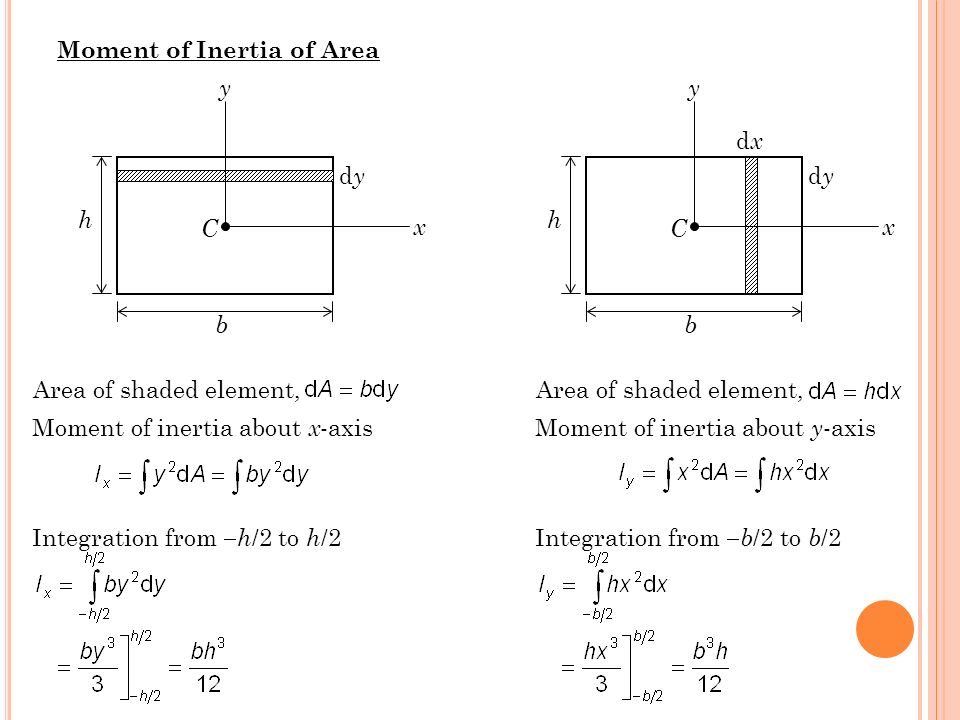
5 Дж = полярный момент инерции
Таблица 6.2. Момент инерции простых форм. Форма J = полярный момент инерции 1. Треугольник 2. Полукруг 3. Четверть круга 4. Прямоугольник 5. Окружность b h y x y x r y x r b h y x x y r
6 Параллельность — теорема осей
Существует взаимосвязь между моментом инерции относительно двух параллельных осей, которая не проходит через центр тяжести области. Из таблицы 6.1; Ix = и Iy = Центроид равен, (,) = (b / 2, h / 2) Момент инерции относительно оси xx, Ixx = Ix + Ady2, где dy — расстояние в центре тяжести y Момент инерции относительно оси yy, Iyy = Iy + Asx2, где sx — расстояние до центра тяжести xyxbh 
7 Определить центр тяжести комбинированной области
Пример 6.2 y 140 мм 60 мм 160 мм 60 мм xy 140 мм 1 3 2 60 мм x 60 мм 160 мм 60 мм Определить центр тяжести композитной области PART AREA (мм2) y (мм) x (мм) Ay (103) (мм3) Ax (103) (мм3) 1 60 (200) = 12000 200/2 = 100 60/2 = 30 1200 360 2 160 (60) = 9600 60 + [160/2] = 140 288 1344 3/2 = 250 3000 Σ: Σ: 2688 x 103 Σ: 4704 x 103 ![Example 6.2. y. 140 mm. 60 mm. 160 mm. 60mm. x. y. 140 mm mm. x. 60mm. 160 mm. 60 mm. Determine centroid of composite area. PART. AREA(mm2) y(mm) x(mm) Ay (103)(mm3) Ax (103) (mm3) 1. 60(200) = /2 = /2 = (60)= [160/2] = /2= Σ: Σ: 2688 x 103. Σ: 4704 x 103. Determine centroid of composite area](/800/600/https/slideplayer.com/slide/7596548/25/images/7/Determine+centroid+of+composite+area.jpg)
8 Второй момент инерции ЧАСТЬ ПЛОЩАДЬ (A) (мм2) Ix = bh4 / 12 (106) (мм4)
dy = | yy | (мм) Ady2 (106) (мм4) 1 60 (200) = 12000 60 (2003) ) / 12 = 40 | 100– 80 | = 20 4.8 2160 (60) = 9600 160 (603) / 12 = 2,88 | 30 — 80 | = 50 24 3 | 100 — 80 | = 20 Σ: [Ix + Ady2] 1 + [Ix + Ady2] 2 + [Ix + Ady2] 3 = [] x106 = x 106 мм4 ПЛОЩАДЬ ЧАСТИ (мм2) Iy = b3h / 12 (106) (мм4) Sx = | xx | (мм) Asx2 (106) (мм4) 1 60 (200) = 12000 603 (200) / 12 = 3,6 | 30-140 | = 110 145,2 2160 (60) = 9600 1603 (60) / 12 = 20,48 | 140 — 140 | = 0 3 | 250 — 140 | = 110 Σ: [Iy + As2] 1 + [Iy + As2] 2 + [Iy + As2] 3 = [] x106 = x 106 мм4


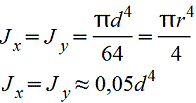
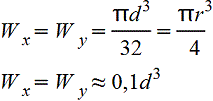
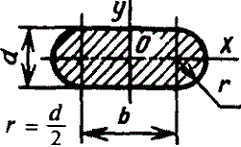
 c=d1/d
c=d1/d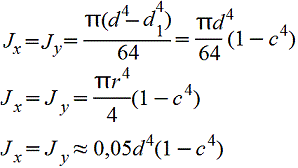
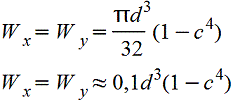
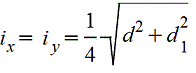
 s≤(D/10)
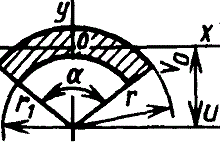
s≤(D/10)
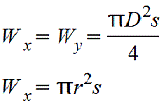

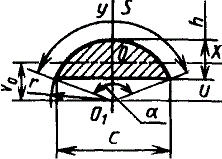
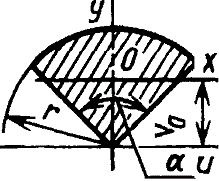
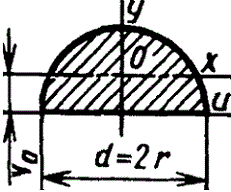 Vo=2d/3π=0,2122d=0,4244r
Vo=2d/3π=0,2122d=0,4244r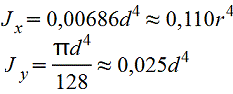

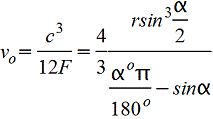


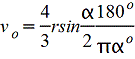

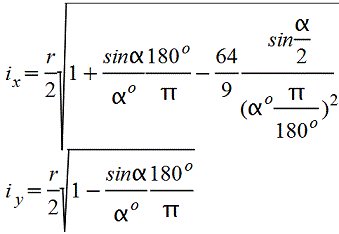


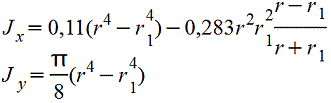
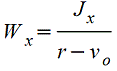
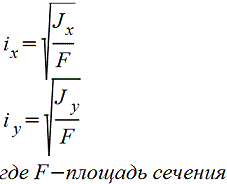
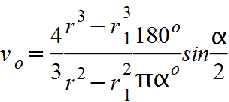
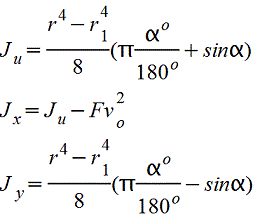
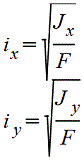

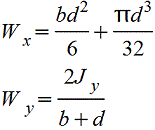
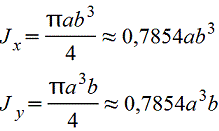

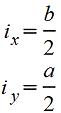


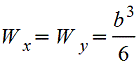
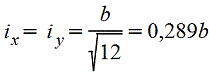

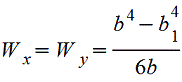
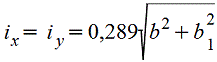
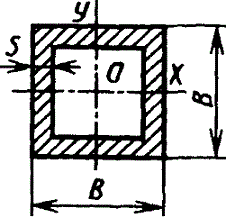
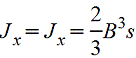

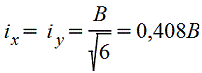
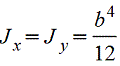
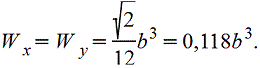
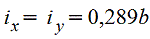
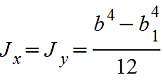
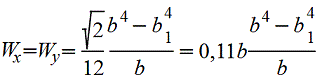
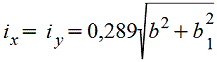
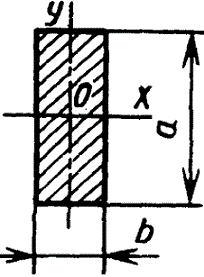




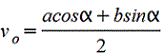
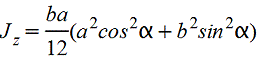

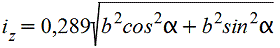

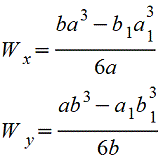
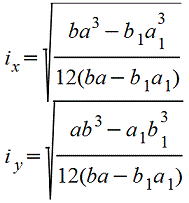

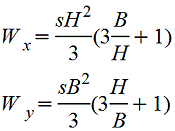
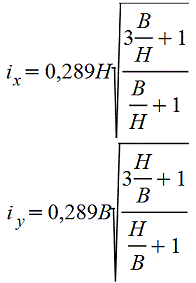
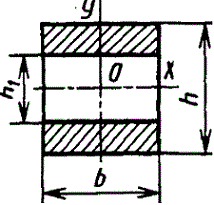
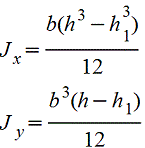
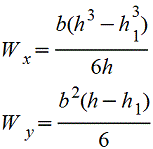
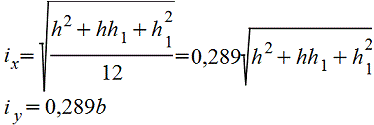



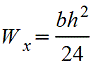 при
вычислении напряжения в точке основания
при
вычислении напряжения в точке основания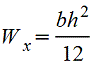
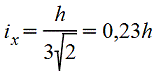

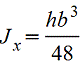

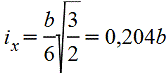
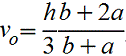
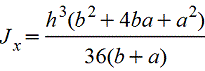
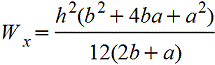 в
точках нижнего основания
в
точках нижнего основания 
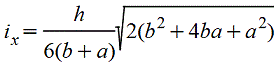

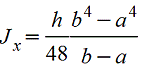
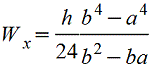
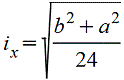
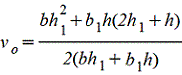

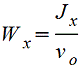 Для
верхних волокон
Для
верхних волокон