Логические функции — что это, определение и ответ
Математическая логика (она же булева алгебра) является неотъемлемым блоком знаний как в школьном курсе информатики, так и в ОГЭ.
Цель логики как науки – определить, истинно или ложно некоторое высказывание, а также прослеживать связь между высказываниями относительно друг друга. Высказывания обозначаются логическими переменными, которые могут принимать лишь два значения:
Истина = 1, Ложь = 0
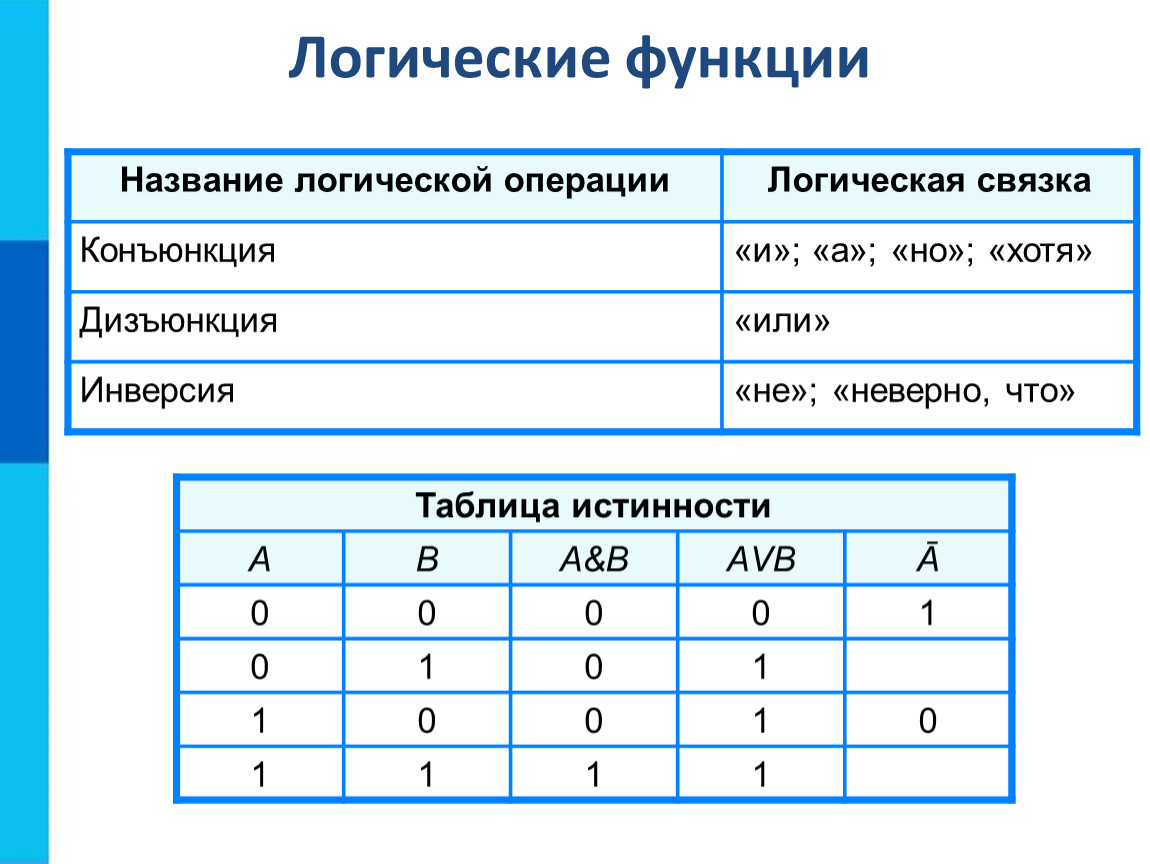
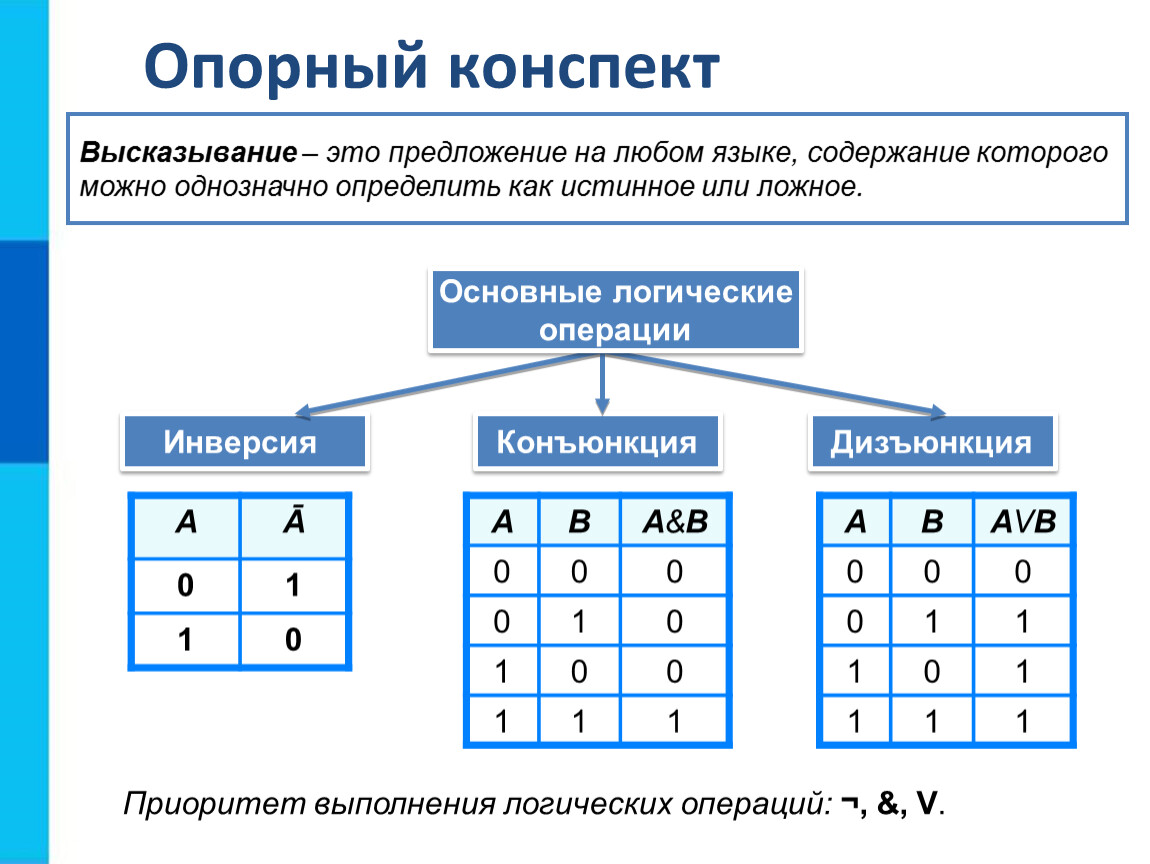
Логические выражения (которые состоят из более чем одного высказывания) на естественном языке образуются с помощью связок «И», «ИЛИ», «НЕ». В математической логике аналогом этих связок являются базовые логические операции — конъюнкция, дизъюнкция и инверсия.
Чтобы определить значение составного логического выражения, надо знать значения входящих в него логических переменных (высказываний). Чтобы рассмотреть все возможные случаи, в булевой алгебре есть специальный аппарат — таблица истинности.
Таблица истинности строится следующим образом: в столбцах записываются логические переменные и само выражение, а в строках — всевозможные комбинации переменных и соответствующий для них результат выражения.
Для выражения, содержащего n переменных, количество комбинаций для них будет равно 2n. Подробнее про таблицы истинности написано ниже.
Логическое умножение (И). Конъюнкция
Конъюнкция (логическое умножение, логическое «И») обозначает объединение двух или нескольких высказываний в одно таким образом, что результат будет истинным тогда и только тогда, когда истинны все входящие в него высказывания.
Пусть есть два высказывания:
Эти высказывания истинны. Значит, их объединение с помощью конъюнкции («В ЕГЭ по информатике есть программирование И логика») — истинно.
Операцию конъюнкции в булевой алгебре принято обозначать знаком « /\ » или, реже, « & » (амперсанд). Операция логического умножения, аргументами которой являются логические переменные А и В, записываются следующей формулой: A И B. Таблица истинности для конъюнкции:
| A | B | A И B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическое сложение (ИЛИ). Дизъюнкция
Дизъюнкция
Дизъюнкция (логическое сложение, логическое «ИЛИ») обозначает объединение двух или нескольких высказываний в одно таким образом, что результат будет истинным тогда, когда истинно хотя бы одно входящее в него высказывание.
Операцию дизъюнкции в булевой алгебре принято обозначать знаком « \/ ». Операция логического сложения, аргументами которой являются логические переменные А и В, записывается следующей формулой: A ИЛИ B. Таблица истинности для дизъюнкции:
| A | B | A ИЛИ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Логическое отрицание (НЕ). Инверсия
Инверсия (логическое отрицание, логическое «НЕ») получает из истинного высказывания ложное и, наоборот, из ложного — истинное.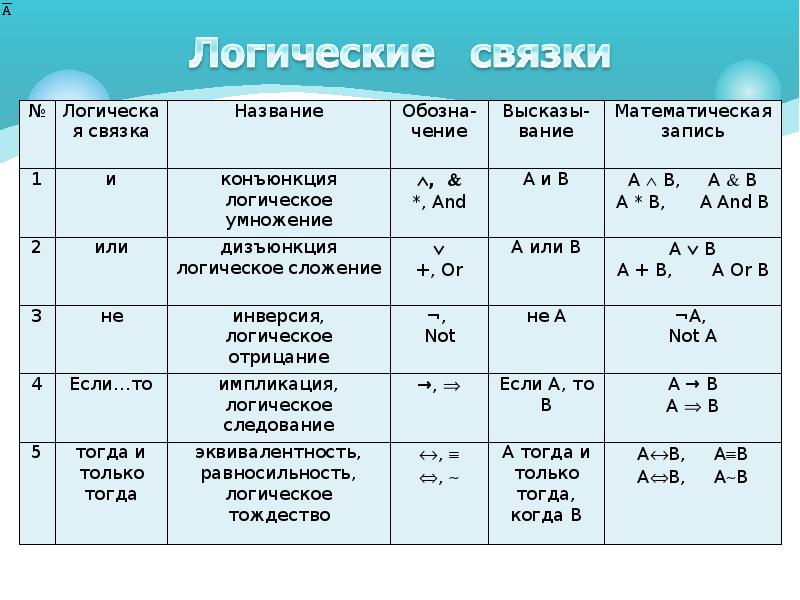
Например, высказывание «Москва — столица России» истинно, а данное высказывание, образованное с помощью логического отрицания («Москва — не столица России») — ложно. Ложное высказывание можно сделать истинным с помощью инверсии:
Операцию инверсии в булевой алгебре принято обозначать знаком « ¬ ». Операция логического отрицания, аргументом которой является логическая переменная А, записывается следующей формулой: НЕ (A). Результатом операции логического отрицания является Истина, когда аргумент Ложь, и значение Ложь, когда аргумент Истина. Таблица истинности для инверсии:
| A | НЕ (A) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Порядок выполнения логических операций
При вычислении значения логических выражений важно учитывать порядок действий аналогично вычислению математических примеров.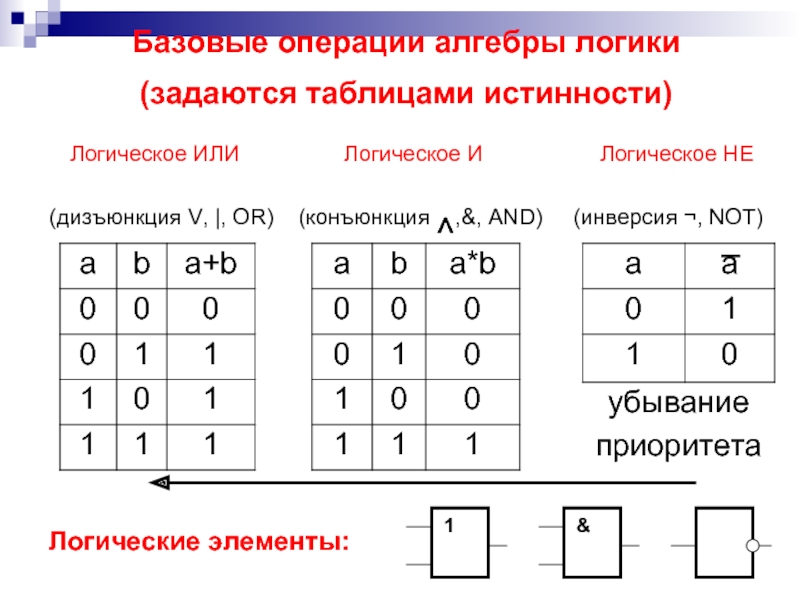 Порядок выполнения всех логических операций схож на логику математического порядка действий и выглядит так:
Порядок выполнения всех логических операций схож на логику математического порядка действий и выглядит так:
1. Инверсия (логическое отрицание, НЕ)
2. Конъюнкция (логическое умножение, И)
3. Дизъюнкция (логическое сложение, ИЛИ)
Скобки, разумеется, могут этот порядок менять.
Рассмотрим пример правильного порядка вычислений.
Определим значение выражения НЕ(А) ИЛИ B И (С ИЛИ D) при значениях переменных: A = 0, B = 1, C = 1, D = 0.Первыми выполнятся скобки: С ИЛИ D = 1 ИЛИ 0 = 1
Затем идёт отрицание: НЕ(А) = НЕ(0) = 1
Дальше идёт логическое умножение: B И (С ИЛИ D) = 1 И 1 = 1
Последним в данном примере будет логическое сложение: НЕ(А) ИЛИ B И (С ИЛИ D) = 1 ИЛИ 1 = 1
Построение таблиц истинности логических выражений
Для каждого логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений логических переменных. Алгоритм построения таблиц истинности:
Алгоритм построения таблиц истинности:
1. Определить количество строк, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение (если переменных n штук, то количество строк будет равно 2n). Еще одну строку стоит добавить для указания самих переменных, итого строк в таблице будет 2n + 1.
2. Определить количество столбцов, которое равно количеству логических переменных плюс количество логических операций. Это нужно для того, чтобы вычислять значение логического выражения поэтапно, последовательно выполняя все логические операции над исходными переменными.
3. Построить таблицу с указанным количеством столбцов и строк и внести всевозможные наборы логических переменных. Наборы входных переменных рекомендуется заполнять следующим образом:
a) разделить столбец значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю — единицами;
б) разделить столбец значений второй переменной на четыре части и заполнить четверти чередующимися группами нулей и единиц;
в) продолжать деление столбцов значений последующих переменных на 8, 16, 32 и т. д. частей.
д. частей.
4. Заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с таблицей истинности.
Ниже пример построения таблицы истинности для выражения: НЕ(А) ИЛИ B И С
В выражении содержится 3 переменных, значит есть 8 различных комбинаций их значений. С учётом шапки таблица истинности будет содержать 9 строк. В выражении 3 операции, значит столбцов потребуется 6.
| А | B | C | НЕ(А) | B И С | НЕ(А) ИЛИ B И С |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |
4.
 Логические выражения и таблицы истинности
Логические выражения и таблицы истинности13
4.1.Логические выражения
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание
«(2·2=5 или 2·2=4) и (2·2≠5 или 2·2≠4)».
Проанализируем составное высказывание. Оно содержит два простых высказывания:
А = «2•2=5»—ложно (0), В = «2•2=4»—истинно (1).
Тогда составное высказывание можно записать в следующей форме: «(А или В) и (Ā или В)».
Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:
инверсия, конъюнкция, дизъюнкция.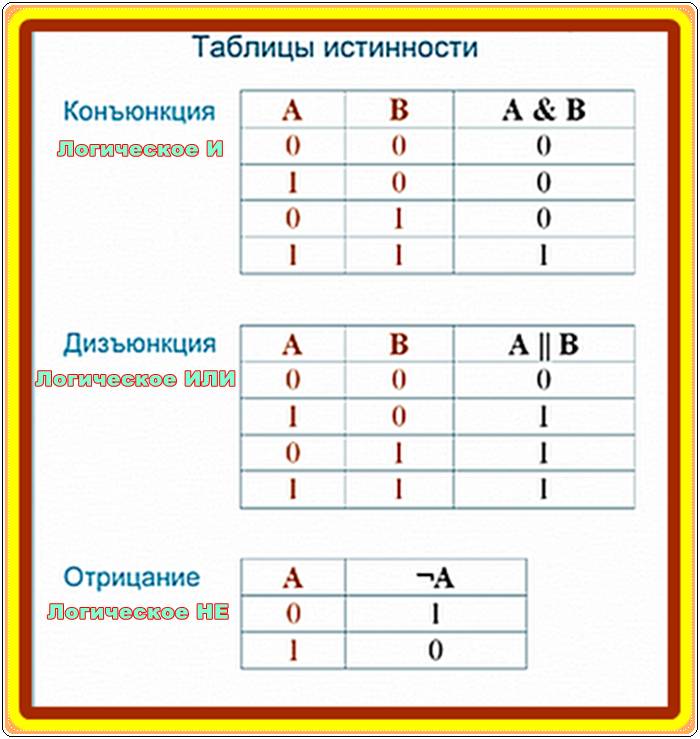
Для изменения указанного порядка могут использоваться скобки:
F = (A v В) & (Ā v В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F = (A v В) & (Ā v В) = (0 v 1) & (1 v 0) = 1 & 1 = 1.
14
4.2.Таблицы истинности
Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.
Простые высказывания обозначаются переменными (например, A и B).
При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:
1) необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
В нашем случае логическая функция имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;
2)необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;
3)необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;
4)необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
15
Таблица 8 – Таблица истинности логической функции
4.3.Равносильные логические выражения
Логические выражения, у которых последние столбцы таблиц истинности сов-
падают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Докажем, что логические выражения равносильны. Построим сначала таблицу истинности логического выражения (табли-
ца 9).
Таблица 9 – Таблица истинности логического выражения
А | В |
|
|
|
|
|
|
|
|
0 | 0 | 1 | 1 | 1 |
|
|
|
|
|
0 | 1 | 1 | 0 | 0 |
|
|
|
|
|
1 | 0 | 0 | 1 | 0 |
|
|
|
|
|
1 | 1 | 0 | 0 | 0 |
|
|
|
|
|
Теперь построим таблицу истинности логического выражения (таблица 10).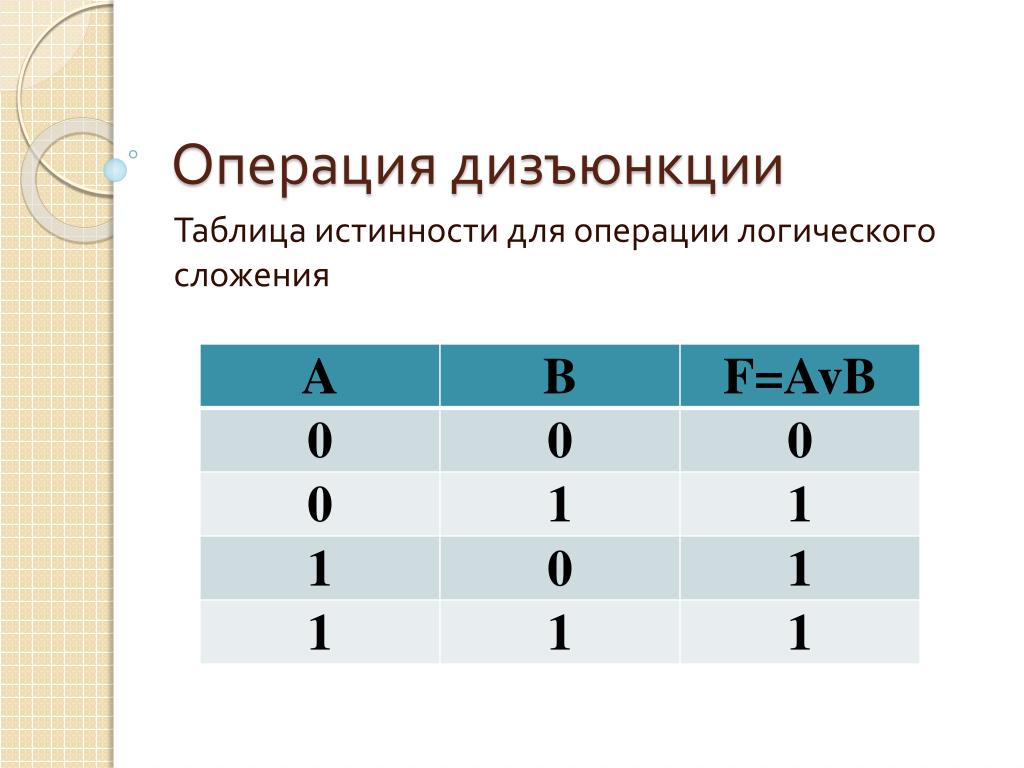
Таблица 10 – Таблица истинности логического выражения
А | В | А v В |
|
|
|
|
|
0 | 0 | 0 | 1 |
|
|
|
|
0 | 1 | 1 | 0 |
|
|
|
|
1 | 0 | 1 | 0 |
|
|
|
|
1 | 1 | 1 | 0 |
|
|
|
|
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:
=.
16
5. Построение таблиц истинности для сложных выражений
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений
переменных всего четыре: |
| ||
(0, 0), | (0, 1), | (1, 0), | (1, 1). |
Если формула содержит три переменные, то возможных наборов значений
переменных восемь: |
|
|
|
|
|
| |
(0, 0, 0), | (0, 0, 1), | (0, 1, 0), | (0, 1, 1), | (1, 0, 0), | (1, 0, 1), | (1, 1, 0), | (1, 1, 1). |
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Пример 1 1. Составим таблицу истинности для формулы, которая содержит две пере-
менные X и Y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 11:
Таблица 11 – Таблица истинности для формулы с переменными Х и У
Пример 2
Cоставить таблицу истинности сложного логического выражения: D = неA & (B+C).
А, В, С – три простых высказывания, поэтому:
количество строк = 23 +2 = 10 (n=3, т.к. на входе три элемента А, В, С) количество столбцов (таблица 12):
1)А,
2)В,
Математические/Сравнение/Логические операторы, Приоритет, Таблица истинности
Охватывает символы операций, используемые в
выражения сравнения. Включает порядок старшинства и таблицу истинности.
Включает порядок старшинства и таблицу истинности.
Следующая таблица истинности содержит все правила, необходимые для оценки
логические выражения.
| | Б | А И В | А ИЛИ В | НЕ |
| Т | Т | Т | Т | Ф |
| Ф | Т | Ф | Т | Т |
| Т | Ф | Ф | Т | Ф |
| Ф | Ф | Ф | Ф | Т |
Столбцы И и ИЛИ таблицы истинности можно резюмировать следующим образом:
- «А .
 И.В» истинно, только если истинны и А, и В.
И.В» истинно, только если истинны и А, и В. - «A .AND.B» ложно, если либо A, либо B ложны.
- «A .OR. B» истинно, если верно либо A, либо B.
- «A .OR. B» ложно, только если ложны и A, и B.
Символы логических операторов
Логические или логические операторы используются в логических (булевых) выражениях. (Пример: (А .И. Б .ИЛИ. В) ).
| Символ | Значение |
| НЕТ | Логическое НЕ |
| И | Логическое И |
| ИЛИ | Логическое ИЛИ |
Как и в математических выражениях, существует определенный порядок
приоритет для вычисления логических выражений, которые имеют более двух
операторы. Выражения внутри круглых скобок оцениваются первыми, а
логические операторы оцениваются в следующем порядке:
Выражения внутри круглых скобок оцениваются первыми, а
логические операторы оцениваются в следующем порядке:
- .НЕ.
- .И.
- .ИЛИ.
Пример: скобки в следующем примере означают два утверждения логически разные:
- А .И. Б .ИЛИ. С
- А .И. (Б.ИЛИ.С)
Символы математических операторов
Символы
| Символ | 9 | Возведение в степень |
| * | Умножение | |
| / | Разделение | |
| + | Добавление | |
| — | вычитание |
Порядок старшинства
 Приказ
приоритет для остальных математических операторов слева направо в
следующий порядок:
Приказ
приоритет для остальных математических операторов слева направо в
следующий порядок:- E возведение в степень
- M умножение и D ivision
- Дополнение A и удаление S
Следующая фраза полезна для запоминания порядка старшинства
для математических операторов. Просто обязательно осознайте, что умножение
не предшествует делению (они равны и выполняются слева направо
правильно, если нет круглых скобок) и сложение не приходит
перед вычитанием (они равны и выполняются слева направо, если нет
стоят скобки).
Символы операций со строками
Символы операций со строками показывают, как две или более строк символов
объединяются, операция, известная как конкатенация.
| Символ | Операция |
| + | Объединить две строки символов |
| — | Объединить две строки символов (конечные пробелы 1-й строки добавляются к концу результирующей строки) |
Пример (_ обозначает пробелы)
- «Здравствуйте____»+»Здесь.
 «=»Здравствуйте____Здесь.»
«=»Здравствуйте____Здесь.» - «Здравствуйте____»-«Туда.»=»ЗдравствуйтеТам.____»
Символы операторов сравнения
Операторы сравнения используются для сравнения математических,
символы или выражения даты. Они приводят к логическим значениям
True или False, как используется с булевой логикой.
| Символ | Значение |
| Меньше, чем | |
| > | Больше чем |
| «=» | Равно |
| <> или # | Не равно |
| Меньше или равно | |
| >= | Больше или равно |
| $ | Сравнение подстрок Пример, если A и B представляют собой строки из символов, A$B возвращает логическое значение True, если A либо идентично B , либо содержится внутри B.  |
Логические операторы | Python#
Логические операторы в Python используются для объединения истинных или ложных значений переменных (или выражений), чтобы вы могли определить их результирующее значение истинности. В Python доступны три логических оператора:
1. и – возвращает True , только если оба операнда истинны. В любом другом случае будет возвращено False . Например, следующее выражение будет иметь значение True: 5 < 7 и 5 > 3 , потому что 5 действительно меньше 7 и больше 3. Вот число 9.0334 и таблица истинности оператора (таблица, в которой перечислены все возможные входы и результаты для логических операторов):
| Первый операнд | Второй операнд | Результат |
|---|---|---|
| Правда | Правда | Правда |
| Правда | Ложь | Ложь |
| Ложь | Правда | Ложь |
| Ложь | Ложь | Ложь |
Вот несколько примеров:
>>> 5 < 7 и 5 > 3 Истинный >>> >>> 3 > 3 и 55 > 30 ЛОЖЬ >>> 15 / 3 >= 200 и 3 == 3 ЛОЖЬ >>> 55 == 55 и 3 <= 3 True
2. или – возвращает True , когда один или оба операнда истинны. Например, выражение 5 < 3 или 3 == 3 вернет True , поскольку второй операнд ( 3 == 3 ) оценивается как True . Только если оба операнда ложны, будет возвращено False . Таблица истинности для этого оператора выглядит так:
или – возвращает True , когда один или оба операнда истинны. Например, выражение 5 < 3 или 3 == 3 вернет True , поскольку второй операнд ( 3 == 3 ) оценивается как True . Только если оба операнда ложны, будет возвращено False . Таблица истинности для этого оператора выглядит так:
| Первый операнд | Второй операнд | Результат |
|---|---|---|
| Правда | Правда | Правда |
| Правда | Ложь | Правда |
| Ложь | Правда | Правда |
| Ложь | Ложь | Ложь |
Примеры:
>>> 3 == 3 или 5 < 3 Истинный >>> 15 < 3 или 5 > 3 Истинный >>> 12 <= 1 или 5 < 1 ЛОЖЬ >>> 20 + 3 >= 23 или 5 != 5 Правда
3. не — инвертирует значение истинности одного операнда. Другими словами, True становится False и наоборот. Таблица истинности здесь меньше, потому что используется только один операнд:
не — инвертирует значение истинности одного операнда. Другими словами, True становится False и наоборот. Таблица истинности здесь меньше, потому что используется только один операнд:
| Операнд | Результат | |
|---|---|---|
| Правда | Ложь | |
| Ложь | Правда |
Примеры:
>>> Неправда ЛОЖЬ >>> не неверно Истинный >>> не 5 > 3 ЛОЖЬ >>> нет (5 > 3 и 5 > 2) ЛОЖЬ >>> нет (5 > 3 и 5 < 33) ЛОЖЬ >>> нет (5 < 3 и 5 < 33) True
Разберем последний пример — not (5 < 3 и 5 < 33) — и почему он возвращает True . Просто сначала оцените выражение в скобках:
5 < 3 – 5 не меньше 3, поэтому это выражение ложно .
5 < 33 – 5 меньше 33, поэтому это выражение верно .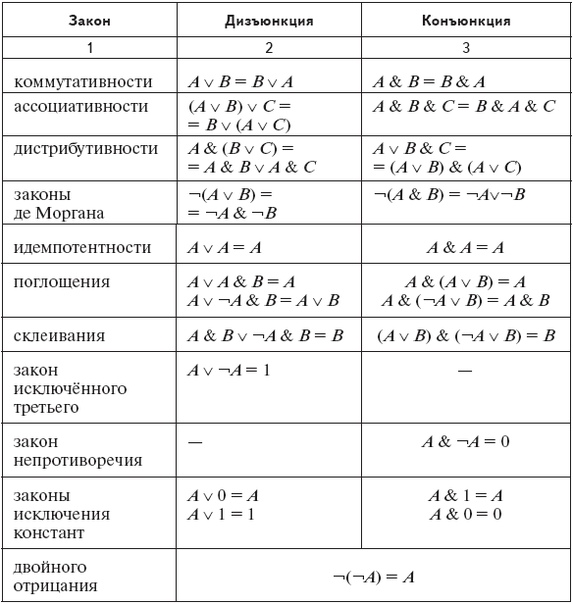


 И.В» истинно, только если истинны и А, и В.
И.В» истинно, только если истинны и А, и В.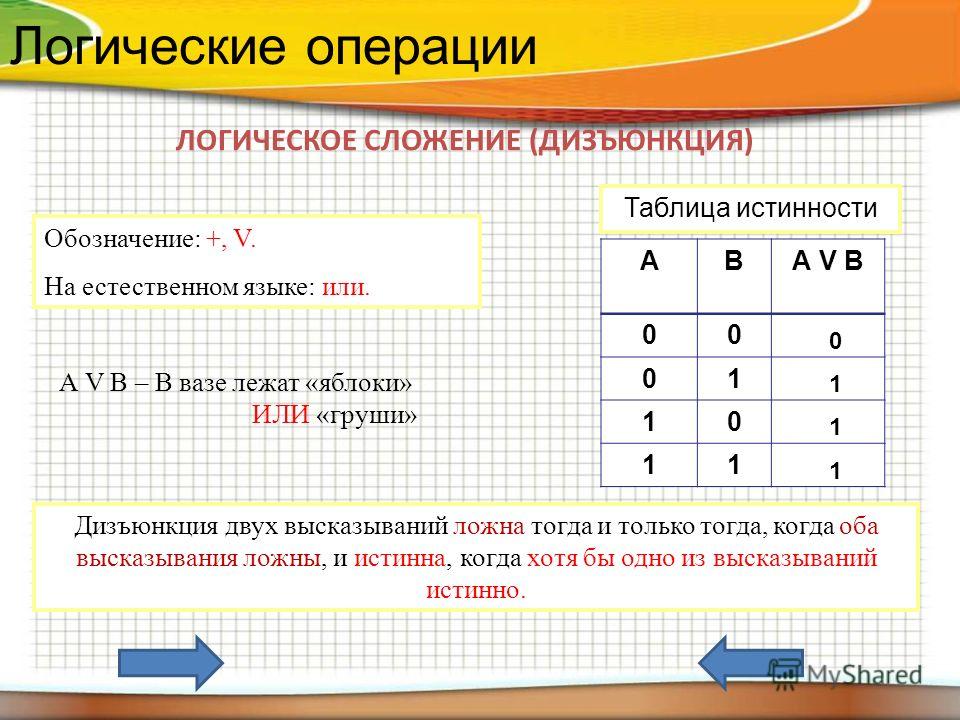 «=»Здравствуйте____Здесь.»
«=»Здравствуйте____Здесь.»