Логические выражения и таблицы истинности | Методическая разработка по информатике и икт (10 класс):
Методическая разработка уроков в 10 классе
по информатике и ИКТ
по теме «Логические выражения
и таблицы истинности».
Цель урока:
- Сформировать у учащихся навыки построения таблиц истинности и работы со сложными логическими выражениями.
- Проверка теоретических знаний по теме « Логические операции».
Ход урока.
Первый этап урока.
Проверка домашнего задания.
На предыдущем уроке ученики изучили:
- что изучает наука логика.
- что одним из понятий логики является высказывание.
- логическое умножение, логическое сложение, логическое отрицание.
Урок начинается с проверки домашнего задания.
№3.9
«Практикум по информатике и информационным технологиям»,
Н. Угринович, Л. Босова, Н.Михайлова; 2007, Москва БИНОМ. Лаборатория знаний.
Найдите значения логических выражений:
в) (0∨1)∨(1∨0)=1∨1=1
г) (0&1)&1=0&1=0
д) 1&(1&1)&1=1&1&1=1
ж) ((1&0)∨(1&0))∨1=(0∨0)∨1=0∨1=1
и) ((0&0)∨0)&(1∨1)=(0∨0)&1=0&1=0
№3.
10
Даны два простых высказывания:
А={2⋅2=4}, В={2⋅2=5}.
Какие из составных высказываний истинны:
а) ; б) ; в) А&В; г) А∨В.
Решение:
а) — ложное высказывание;
б) — истинное высказывание;
в) А&В – ложное высказывание;
г) А∨В – истинное высказывание.
Решение домашних примеров можно заранее записать на обратной части доски или вывести на экран с помощью проектора, заранее подготовив презентацию.
Второй этап урока.
Решение задач.
№1. Какое из следующих предложений является высказыванием?
- Ура!
- Светает.
- 3+4∙56
- Первый зимний месяц – декабрь.
№2. Из нижеприведённых фраз выберите ту, которая является истинным высказыванием.
- Все кошки серы.
- Познай самого себя.
- Талант всегда пробьёт себе дорогу.
- Число 7 – простое.
№3. Из нижеприведённых высказываний выберите логическую сумму.
- Хорошо, когда утро начинается с зарядки и обливания холодной водой.
- В салат можно положить или консервированные овощи, или сырые, или и те и другие.
- В холодный и пасмурный день хорошо сидеть дома.
- Мне предложили купить билеты в театр: или в партер, или в бельэтаж.
№4. Из приведённых высказываний выберите логическое умножение.
- За завтраком я выпиваю чашку кофе или чая.
- Без труда не выловишь и рыбку из пруда.
- На столе в беспорядке лежали книжки и тетрадки.
- Числа, кратные 4, кратны 2.
Эти задания выполняются устно. Необходимо как можно больше учеников подключить к обсуждению ответов. Условие этих задач напечатано на листах и раздаётся ученикам.
Решение:
№1. Первое предложение восклицательное. Про второе и третье высказывание нельзя сказать истинно оно или ложно. А вот четвёртое предложение — это истинное высказывание.
№2. Первое предложение – ложное высказывание. Второе – побудительное, третье – не всегда истинно. Истинным высказыванием является четвёртое предложение.
№3. Четвёртое сложное высказывание содержит логическую связку «или» в исключающем смысле, так как нельзя одновременно сидеть в партере и в бельэтаже. Первое и третье сложные высказывания представляют собой логическое произведение простых высказываний, так как содержат логическую связку «и». Правильный ответ под цифрой 2.
№4. Второе сложное высказывание является примером логического следования. Четвёртое предложение является простым высказыванием.
Первое предложение является сложным высказыванием, содержащим исключающее «или». Третье предложение относится к логическому умножению.
Так проходит совместное обсуждение решения логических задач. После того как учитель отвечает на все вопросы учеников, то можно и предложить выполнить самостоятельную работу на оценку.
Третий этап урока.
Самостоятельная работа.
№1. Какие из следующих предложений являются высказываниями? Определите их истинность.
а) Наполеон был французским императором.
б) Чему равно расстояние от Земли до Марса?
в) Всякий моряк умеет плавать.
г) Число 6 – чётное.
д) Внимание! Посмотрите направо.
е) Париж – столица Китая.
ж) Некоторые люди являются художниками.
з) Выразите 1 час 15минут в минутах.
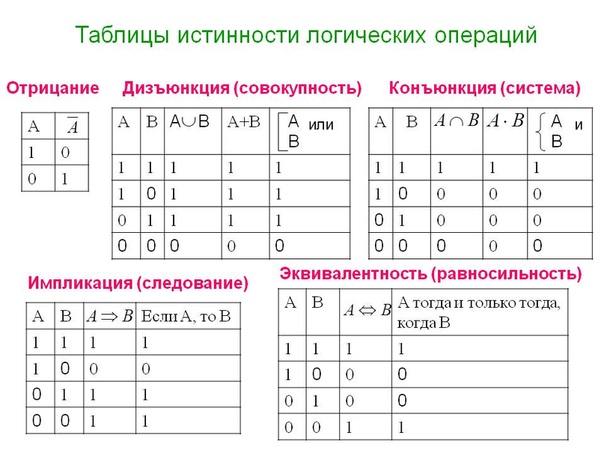
№2. Основные логические операции и соответствующие им таблицы истинности.
№3. Определите значение истинности следующих высказываний:
а) Приставка – это часть слова, и она пишется раздельно со словом.
б) Суффикс – это часть слова, и он стоит после корня.
в) Рыбу ловят сачком или ловят крючком, или мухой приманивают, или червячком.
г) Буква «а» — первая буква в слове «аист» или «сова».
д) Две прямые на плоскости параллельны или пересекаются.
е) Данное число чётно или число, больше его на единицу, чётно.
ж) х=3 и х>5.
В самостоятельной работе только один вариант. Ребятам можно предложить сесть по одному за партой, пересев на другое место.
Решение самостоятельной работы:
№1. Высказываниями являются следующие предложения:
а) Наполеон был французским императором.
в) Всякий моряк умеет плавать.
г) Число 6 – чётное.
е) Париж – столица Китая.
ж) Некоторые люди являются художниками.
Истинными высказываниями являются следующие предложения:
г) Число 6 – чётное.
ж) Некоторые люди являются художниками.
№2.
Логическое умножение (конъюнкция) – это объединение двух или нескольких высказываний с помощью союза «и».
Примеры:
1) 2⋅2=5 и 3⋅3=10. Ложь.
2) 2⋅2=5 и 3⋅3=9. Ложь.
3) 2⋅2=4 и 3⋅3=10. Ложь.
4) 2⋅2=4 и 3⋅3=9. Истина.
Таблица истинности:
А | В | А&В |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Логическое сложение (дизъюнкция) – это объединение двух или более высказываний с помощью «или».
Примеры:
1) 2⋅2=5 или 3⋅3=10. Ложь.
2) 2⋅2=5 или 3⋅3=9. Истина.
3) 2⋅2=4 или 3⋅3=10. Истина.
4) 2⋅2=4 или 3⋅3=9. Истина.
А | В | А∨В |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Логическое отрицание (инверсия) – это присоединение частицы «не» к высказыванию.
Примеры:
1) Семь умножить на два равно тринадцати.
(Ложь)
2) Семь умножить на два не равно тринадцати. (Истина)
А | |
0 | 1 |
1 | 0 |
№3.
а) Ложь.
б) Истина.
в) Истина.
г) Истина.
д) Истина.
е) Истина.
ж) Ложь.
Четвёртый этап урока.
После того как будут собраны самостоятельные работы учеников, можно проверить и обсудить решение №1 и №3.
Пятый этап урока.
Решение логических задач ЕГЭ.
На едином государственном экзамене по информатике встречаются задачи по теме «Логика». Можно рассмотреть решение таких задач.
ЕГЭ
- Для составления цепочек используются разные бусины,
которые условно обозначаются цифрами 1,2,3,4,5.
Каждая такая цепочка состоит из 4 бусин, при этом соблюдаются следующие правила построения цепочек:
На первом месте стоит одна из бусин 1,4 или 5.
После чётной цифры в цепочке не может идти снова чётная, а после нечётной — нечётная.
Последней цифрой не может быть цифра 3.
Какая из перечисленных цепочек создана по этим правилам?
- 4325 2) 4123 3) 1241 4) 3452
2) Для составления цепочек используются разноцветные бусины:
тёмные – синяя(С), зелёная(З) и светлые – жёлтая(Ж), белая(Б), голубая (Г). На первом месте в цепочке стоит бусина синего или жёлтого цвета. В середине цепочке – любая из светлых бусин, если первая бусина тёмная, и любая из тёмных бусин, если первая бусина светлая. На последнем месте – одна из бусин белого, голубого или зелёного цвета, не стоящая в цепочке в середине. Какая из перечисленных цепочек создана по этому правилу?
- ЖСГ 2) БГЗ 3) СГЖ 4) ЖБС
3) Символом R обозначено одно из указанных ниже логических выражений от трёх аргументов.
Используя фрагмент таблицы истинности, определите, чему равно R.
X | Y | Z | R |
0 | 0 | 0 | 0 |
1 | 1 | 0 | 1 |
1 | 0 | 0 | 1 |
- X&Y&Z 2)¬X∨Y∨¬Z 3) X&(Y∨Z) 4) (X∨Y)&¬Z
Решение:
№1.Правильный ответ под цифрой 1.
№2. Правильный ответ под цифрой 1.
№3. 1) X&Y&Z
X | Y | Z | X&Y&Z |
0 | 0 | 0 | 0 |
1 | 1 | 0 | 0 |
1 | 0 | 0 | 0 |
2) ¬X∨Y∨¬Z
Х | Z | ¬X | ¬Z | Y | ¬X∨Y∨¬Z |
0 | 0 | 1 | 1 | 0 | 1 |
1 | 0 | 0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 0 | 1 |
3) X&(Y∨Z)
X | Y | Z | Y∨Z | X&(Y∨Z) |
0 | 0 | 0 | 0 | 0 |
1 | 1 | 0 | 1 | 1 |
1 | 0 | 0 | 0 | 0 |
4) (X∨Y)&¬Z
X | Y | Z | X∨Y | ¬Z | (X∨Y)&¬Z |
0 | 0 | 0 | 0 | 1 | 0 |
1 | 1 | 0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 1 | 1 |
Правильный ответ под цифрой 4.
Шестой этап урока.
Составление таблиц истинности.
№1. F=(A∨B)&( ∨)
A | B | K=A∨B | M= ∨ | F=K&M | ||
0 | 0 | 0 | 1 | 1 | 1 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 0 | 0 |
№2.
R= &
A | B | R= & | ||
0 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 0 |
1 | 0 | 0 | 1 | 0 |
1 | 1 | 0 | 0 | 0 |
№3.
T=
A | B | A∨B | T= |
0 | 0 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 1 | 0 |
Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными.
№4. Записать составное высказывание
(2⋅2=4 и 3⋅3=9) или (2⋅2≠4 и 3⋅3≠9) в форме логического выражения. Построить таблицу истинности.
А={2⋅2=4}, В={3⋅3=9}
={2⋅2≠4}, ={3⋅3≠9}
F= (A&B)∨(&)
A | B | A&B | & | (A&B)∨(&) | ||
1 | 1 | 1 | 0 | 0 | 0 | 1 |
№5. Доказать, используя таблицы истинности, что логические выражения и А&В равносильны.
А | В | М=∨ | К= | ||
0 | 0 | 1 | 1 | 1 | 0 |
0 | 1 | 1 | 0 | 1 | 0 |
1 | 0 | 0 | 1 | 1 | 0 |
1 | 1 | 0 | 0 | 0 | 1 |
А | В | А&В |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Логические выражения, у которых последние столбцы таблиц истинности совпадают, являются равносильными.
Заключительный этап урока.
Домашнее задание.
№1. В процессе составления расписания учителя высказали свои пожелания. Учитель математики высказал пожелание проводить первый или второй урок, учитель информатики — первый или третий, а учитель физики- второй или третий урок. Сколько существует возможных вариантов расписания, и каковы они?
№2. Заполнить таблицы истинности:
а) А&, б) ∨В, в) (А∨) &(∨В).
№3. Доказать, используя таблицы истинности, что логические выражения равносильны и ∨.
Бывает так, что по школьному расписанию два урока информатики идут подряд в один день. Данная методическая разработка как раз и составлена для «сдвоенных» уроков информатики.
Логические операции (and, or, xor, not): таблицы истинности
Бит — это минимальная единица измерения объёма информации, так как она хранит одно из двух значений — 0 (False) или 1 (True). False и True в переводе на русский ложь и истина соответственно. То есть одна битовая ячейка может находиться одновременно лишь в одном состоянии из возможных двух.
Напомню, два возможных состояния битовой ячейки равны — 1 и 0.
Есть определённые операции, для манипуляций с битами. Эти операции называются логическими или булевыми операциями, названные в честь одного из математиков — Джорджа Буля (1815-1864), который способствовал развитию этой области науки.
Все эти операции могут быть применены к любому биту, независимо от того, какое он имеет значение — 0(нуль) или 1(единицу). Ниже приведены основные логические операции и примеры их использования.
Логическая операция И (AND)
Обозначение AND: &
Логическая операция И выполняется с двумя битами, назовем их a и b. Результат выполнения логической операции И будет равен 1, если a и b равны 1, а во всех остальных (других) случаях, результат будет равен 0. Смотрим таблицу истинности логической операции and.
| a(бит 1) | b(бит 2) | a(бит 1) & b(бит 2) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическая операция ИЛИ (OR)
Обозначение OR: |
Логическая операция ИЛИ выполняется с двумя битами (a и b).
b(бит 2)
Логическая операция НЕ (not)
Обозначение NOT: ~
Логическая операция НЕ выполняется с одним битом. Результат выполнения этой логической операции напрямую зависит от состояния бита. Если бит находился в нулевом состоянии, то результат выполнения NOT будет равен единице и наоборот. Смотрим таблицу истинности логической операции НЕ.
| a(бит 1) | ~a(отрицание бита) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Запомните эти 4 логические операции. Используя эти логические операции, мы можем получить любой возможный результат. Подробно об использовании логических операций в С++ читаем тут.
3.1: Предложения и логические операторы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 80504
- Al Doerr & Ken Levasseur
- Массачусетский университет Лоуэлл
Propositions
Определение \(\PageIndex{1}\): Proposition
Предложение — это предложение, к которому может быть осмысленно применено одно и только одно из условий true или false .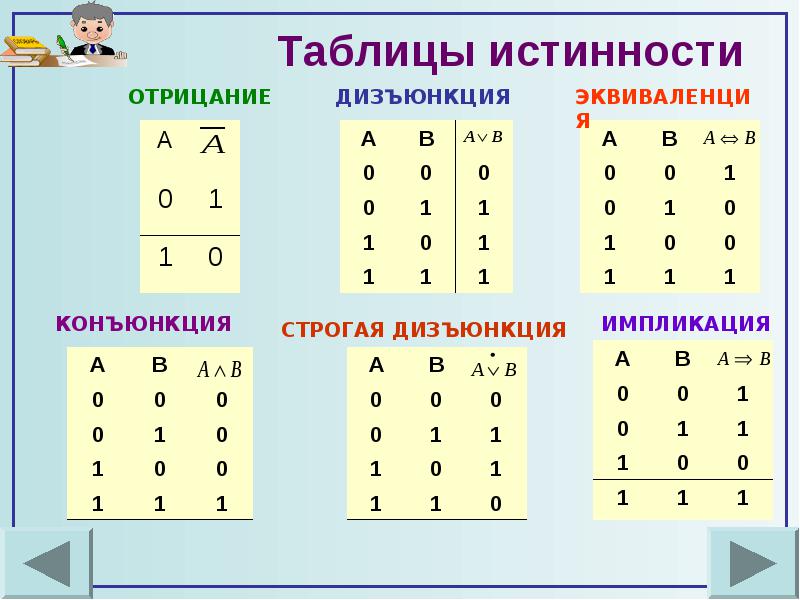
Пример \(\PageIndex{1}\): некоторые утверждения
«Четыре четные», «\(4 \in \{1,3, 5\}\)» и «\(43 > 21\) )» являются предложениями.
В традиционной логике декларативное утверждение с определенным значением истинности считается предложением. Хотя нашей конечной целью является обсуждение математической логики, мы не будем полностью отделяться от традиционной обстановки. Это естественно, потому что основные предположения или постулаты математической логики моделируются по образцу логики, которую мы используем в повседневной жизни. Поскольку в повседневной речи часто используются сложные предложения, мы ожидаем, что логические предложения содержат такие связки, как слово «и». Утверждение «Европа поддерживает жизнь или Марс поддерживает жизнь» является предложением и, следовательно, должно иметь определенное истинностное значение. Каким бы ни было это истинное значение, оно должно быть таким же, как истинное значение «Марс поддерживает жизнь или Европа поддерживает жизнь».
Логические операции
Существует несколько способов объединения простых операторов в составные. Слова/фразы и , или , не , если… то… , и …если и только если… можно добавить к одному или нескольким предложениям для создания новое предложение. Чтобы избежать путаницы, мы точно определим значение каждого из них и введем его стандартный символ. За исключением отрицания (
Определение \(\PageIndex{2}\): логическая конъюнкция
Если \(p\) и \(q\) являются высказываниями, их конъюнкция \(p \textrm{ и } q\) (обозначается \( p \land q\)) определяется таблицей истинности
\begin{equation*} \begin{array}{ccc} p & q & p\land q \\ \hline 0 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \\ \end{array} \end{equation*}
Примечание \(\PageIndex{1}\)
- Чтобы прочитать эту правду таблицы, вы должны понимать, что любая строка представляет случай: один возможный набор значений для \(p\) и \(q\text{. }\)
- Цифры 0 и 1 используются для обозначения ложных и истинных значений соответственно. Это согласуется со способом, которым многие языки программирования обрабатывают логические или логические переменные, поскольку один бит, 0 или 1, может представлять значение истинности.
- В каждом случае символ под \(p\) представляет истинное значение \(p\text{.}\) То же верно для \(q\text{.}\) Символ под \(p \ land q\) представляет его истинное значение для этого случая. Например, вторая строка таблицы истинности представляет случай, когда \(p\) ложно, \(q\) истинно, а результирующее значение истинности для \(p \land q\) ложно. Как и в повседневной речи, \(p \land q\) истинно только тогда, когда оба предложения истинны.
- Буквы \(x\text{,}\) \(y\) и \(z\) часто используются в алгебре для обозначения числовых переменных, \(p\text{,}\) \(q\ ) и \(r\) кажутся наиболее часто используемыми символами для логических переменных. Когда мы говорим, что \(p\) является логической переменной, мы имеем в виду, что любое предложение может занять место \(p\text{.
- И последнее замечание: порядок, в котором мы перечисляем случаи в таблице истинности, в этой книге стандартизирован. Если таблица истинности включает два простых предложения, числа под простыми предложениями можно интерпретировать как двузначные двоичные целые числа в возрастающем порядке: 00, 01, 10 и 11 для 0, 1, 2 и 3 соответственно.
}\)
Определение \(\PageIndex{3}\): Логическая дизъюнкция
Если \(p\) и \(q\) являются высказываниями, их дизъюнкция \(p \textrm{ или } q\) (обозначается \( p \lor q\)), определяется таблицей истинности
\begin{equation*} \begin{array}{ccc} p & q & p\lor q \\ \hline 0 & 0 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\ \end{массив} \end{уравнение*}
Определение \(\PageIndex{4}\): логическое отрицание
Если \ (p\) есть предложение, его отрицание, \(\textrm{not } p\text{,}\) обозначается \(\neg p\text{,}\) и определяется таблицей истинности
\begin{equation*} \begin{array}{cc} p & \neg p \\ \hline 0 & 1 \\ 1 & 0 \\ \end{array} \end{equation*}
Примечание \ (\PageIndex{2}\)
Отрицание — единственный стандартный оператор, который действует на одно предложение; следовательно, необходимы только два случая.
Рассмотрим следующие предложения из повседневной речи:
- Я уволюсь, если не получу повышения.
- Если я пройду финал, я закончу школу.
- Я пойду в кино, если моя машина заведется.
Все три суждения условны, их все можно переформулировать так, чтобы они соответствовали форме «Если Условие , то Заключение ». Например, первое утверждение можно переписать так: «Если я не получу повышения, я уволюсь».
Условное утверждение следует интерпретировать как гарантию; если условие истинно, то ожидается, что заключение будет истинным. Говорит не больше и не меньше.
Определение \(\PageIndex{5}\): условное выражение
Условное утверждение «Если \(p\), то \(q\text{,}\)», обозначаемое \(p \rightarrow q\text{,}\), определяется таблицей истинности
Таблица \(\ PageIndex{1}\: Таблица истинности для \(p\стрелка вправо q\)
| \(p\) | \(к\) | \(p\стрелка вправо q\) |
|---|---|---|
| \(0\) | \(0\) | \(1\) |
| \(0\) | \(1\) | \(1\) |
| \(1\) | \(0\) | \(0\) |
| \(1\) | \(1\) | \(1\) |
Пример \(\PageIndex{2}\): Анализ условного суждения
Предположим, ваш преподаватель сказал вам: «Если вы получите оценку 95 или выше на выпускном экзамене, вы получите пятерку на этом экзамене».
курс.» Ваш инструктор дал вам обещание. Если вы выполняете его условие, вы ожидаете, что вывод (получение пятерки) будет не за горами. Предположим, вам вернули итоговую оценку. Ваш инструктор сказал правду или он виновен во лжи?
Случай I: Ваш итоговый балл за экзамен был меньше 95 (условие ложно), и вы не получили пятерку (заключение ложно). Инструктор сказал правду.
Случай II: Ваш итоговый балл на экзамене был ниже 95, но вы получили пятерку за курс. Инструктор сказал правду. (Возможно, ваш общий средний балл по курсу был превосходным.)
Случай III: Ваш итоговый экзаменационный балл был выше 95, но вы не получили пятерку. Преподаватель солгал.
Случай IV: Ваш итоговый балл за экзамен был выше 95, и вы получили пятерку. Инструктор сказал правду.
Подводя итог, единственный случай, когда условное суждение ложно, это когда условие истинно, а заключение ложно.
Порядок условия и заключения в условном суждении важен. Если поменять местами условие и заключение, получится другое предложение.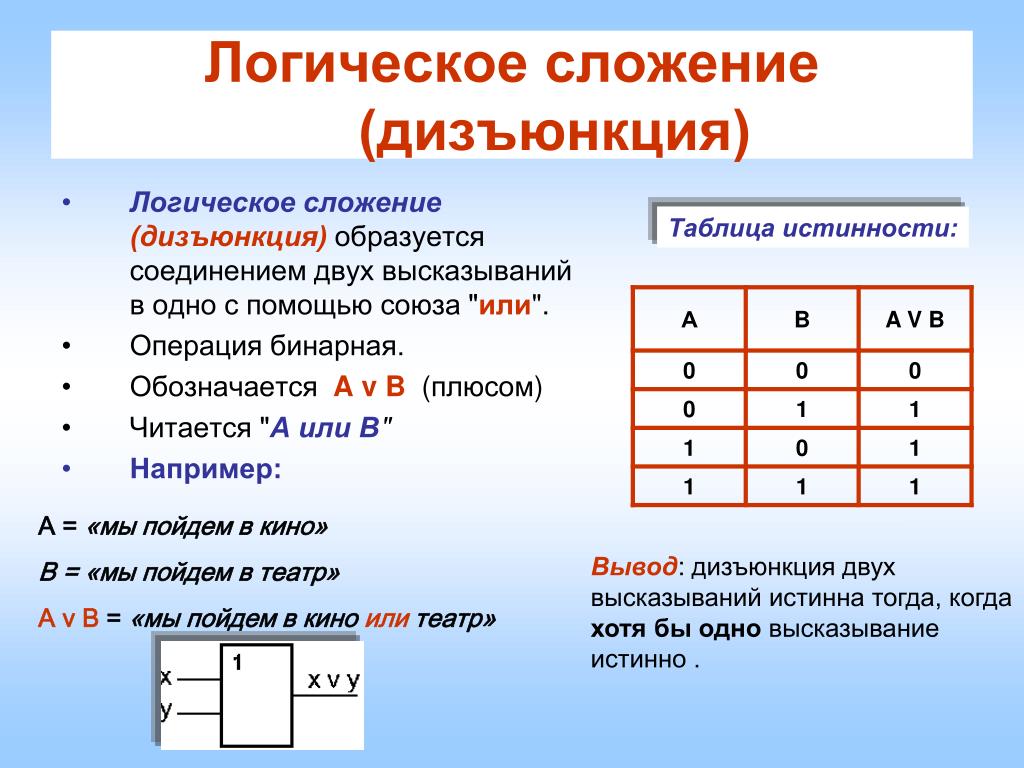
Определение \(\PageIndex{6}\): Обратное
Обратное предложение \(p \rightarrow q\) есть предложение \(q \rightarrow p\text{.}\)
Обратное выражение «Если вы получите оценку 95 или выше на выпускном экзамене, то вы получите пятерку по этому курсу»: «Если вы получите пятерку по этому курсу, то вы получите оценку 95 или выше. лучше на выпускном экзамене». Должно быть ясно, что эти два утверждения говорят о разных вещах.
Здесь есть предложение, связанное с \(p \rightarrow q\), которое имеет тот же логический смысл. Это противопоставление.
Определение \(\PageIndex{7}\): Противоположный
Противоположным высказыванию \(p \rightarrow q\) является высказывание \(\neg q \rightarrow \neg p\text{.}\)
Как мы увидим при обсуждении логических доказательств, мы можем доказать условное суждение, доказывая его противоположность, что может быть несколько проще.
Определение \(\PageIndex{8}\): Биусловное высказывание
Если \(p\) и \(q\) являются высказываниями, биусловное высказывание «\(p\) тогда и только тогда, когда \(q\text {,}\)», обозначаемый \(p \leftrightarrow q\text{,}\), определяется таблицей истинности
\begin{equation*} \begin{array}{ccc} p & q & p\leftrightarrow q \\ \hline 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \\ \end{массив} \end{уравнение*}
Обратите внимание, что \(p \leftrightarrow q\) истинно, когда \(p\) и \(q\) имеют одинаковые значения истинности.
Обычно «если и только если» сокращают до «iff».
Хотя выражения «если… то…» и «…если и только если…» часто используются в повседневной речи, существует несколько альтернативных форм, о которых вам следует знать. Они сведены в следующие списки.
Все следующие эквиваленты «Если \(p\), то \(q\)»:
- \(p\) подразумевает \(q\text{.}\)
- \(q\) следует из \(p\text{.}\)
- \(p\text{,}\) только если \(q\text{.}\)
- \(q\text{,}\) если \(p\text{.}\)
- \(p\) достаточно для \(q\text{.}\)
- \(q\) необходимо для \(p\text{.}\)
Все следующие эквиваленты «\(p\) тогда и только тогда, когда \(q\)»:
- \(p\) необходимо и достаточно для \(q\text{.}\)
- \(p\) эквивалентно \(q\text{.}\)
- Если \(p\text{,}\), то \(q\text{,}\), а если \(q\text{,}\), то \(p\text{.}\)
- Если \(p\text{,}\), то \(q\) и наоборот.
Упражнения
Упражнение \(\PageIndex{1}\)
Пусть \(d\) = «Мне нравятся дискретные структуры», \(c\) = «Я пройду этот курс» и \(s\) = «Я буду выполнять свои задания».
Выразите каждое из следующих утверждений в символической форме:
- Мне нравятся дискретные структуры, и я пройду этот курс.
- Я буду выполнять задания или не пройду этот курс.
- Неправда, что я люблю дискретные структуры и буду выполнять свои задания.
- Я не буду выполнять задание и не пройду этот курс.
- Ответить
- \(\displaystyle d\land c\)
- \(\displaystyle s\lor \neg c\)
- \(\displaystyle \neg (d\land s)\)
- \(\displaystyle \neg s\land \neg c\)
Упражнение \(\PageIndex{2}\)
Для каждого из следующих предложений определите простые предложения, выразите составное предложение в символической форме и определите, истинно оно или ложно:
- Мир плоский или ноль — четное целое число.
- Если 432 802 кратно 4, то 432 802 четно.
- 5 — простое число, а 6 не делится на 4.
- \(3 \in \mathbb{Z}\) и \(3 \in \mathbb{Q}\text{.}\)
- \(2/3 \in \mathbb{Z}\) и \(2/3 \in \mathbb{Q}\text{.}\)
- Сумма двух четных целых чисел четна, а сумма двух нечетных целых чисел нечетна.
Упражнение \(\PageIndex{3}\)
Пусть \(p =\)»\(2 \leq 5\)», \(q\) = «8 — четное целое число» и \(r \) = «11 — простое число». Выразите следующее в виде утверждения на английском языке и определите, верно оно или нет:
- \(\displaystyle \neg p \land q\)
- \(\displaystyle p\стрелка вправо q\)
- \(\displaystyle (p\land q)\to r\)
- \(\displaystyle p \rightarrow (q \lor (\neg r))\)
- \(\displaystyle p \rightarrow ((\neg q)\lor (\neg r))\)
- \(\displaystyle (\neg q) \rightarrow (\neg p)\)
- Ответить
- \(2>5\), а 8 — четное целое число. ЛОЖЬ.
- Если \(2\leqslant 5\), то 8 — четное целое число. Истинный.
- Если \(2\leqslant 5\) и 8 — четное целое число, то 11 — простое число. Истинный.
- Если \(2\leqslant 5\), то либо 8 — четное целое число, либо 11 — не простое число. Истинный.
- Если \(2\leqslant 5\), то либо 8 является нечетным целым числом, либо 11 не является простым числом. ЛОЖЬ.
- Если 8 не является четным целым числом, то \(2>5\text{.}\) Истинно.
- \(2>5\), а 8 — четное целое число.
ЛОЖЬ.Упражнение \(\PageIndex{4}\)
Перепишите каждое из следующих утверждений, используя другие условные формы:
- Если целое число кратно 4, то оно четное. 92\) является необходимым условием для \(x = y\text{.}\)
Упражнение \(\PageIndex{5}\)
Напишите обратное предложение из упражнения \(\PageIndex{4}\). Сравните истинность каждого предложения и его обратного.
- Ответить
Верно только обратное \(d\).
Эта страница под названием 3.1: Предложения и логические операторы распространяется по лицензии CC BY-NC-SA, автором, ремиксом и/или куратором этой страницы являются Эл Доерр и Кен Левассер.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Эл Дорр и Кен Левассер
- Лицензия
- СС BY-NC-SA
- Показать страницу TOC
- нет
- Теги
Таблицы истинности для унарных операций
Таблица истинности используется для логической спецификации в контексте булевой алгебры, логических функций и исчисления высказываний. Он устанавливает функциональные значения логических выражений с помощью логических операторов их функциональных аргументов. Он имеет столбец для каждой входной переменной и результирующий столбец, показывающий все возможные результаты логических операций. Он имеет четыре унарные операции: логическое истинное, логическое ложное, логическое тождество и логическое отрицание. Унарные операции — это такие операции, которые принимают только один ввод: оператор NULL и оператор NOT. Оператор NULL будет представлять тот же результат, что и ввод, но в случае оператора NOT он будет представлять противоположный результат.
Таблица истинности
Таблица истинности — это таблица, в которой логические операторы используются для оценки выражений.
В таблице истинности один столбец используется для каждого входа, а другой столбец представляет все возможные результаты логических операций. Таблица истинности — это таблица, которая разбивает логические функции, перечисляя все возможные значения. Таблица истинности может содержать несколько строк и столбцов. Верхняя строка представляет логические переменные и их комбинации. Логические вентили таблицы истинности дают нам всю информацию о комбинации входов и выходов для логической операции. В таблице истинности утверждение называется противоречием, если последний столбец этой таблицы истинности содержит только 0. Если последний столбец этой таблицы истинности содержит как 0, так и 1, это называется контингентностью или контингентностью. Таблица истинности показывает значения истинности формулы утверждения для каждой комбинации. Утверждение только с одним из двух возможных значений называется истинностным значением. Таблица истинности для унарных операций — это операция, которая имеет дело только с одним операндом.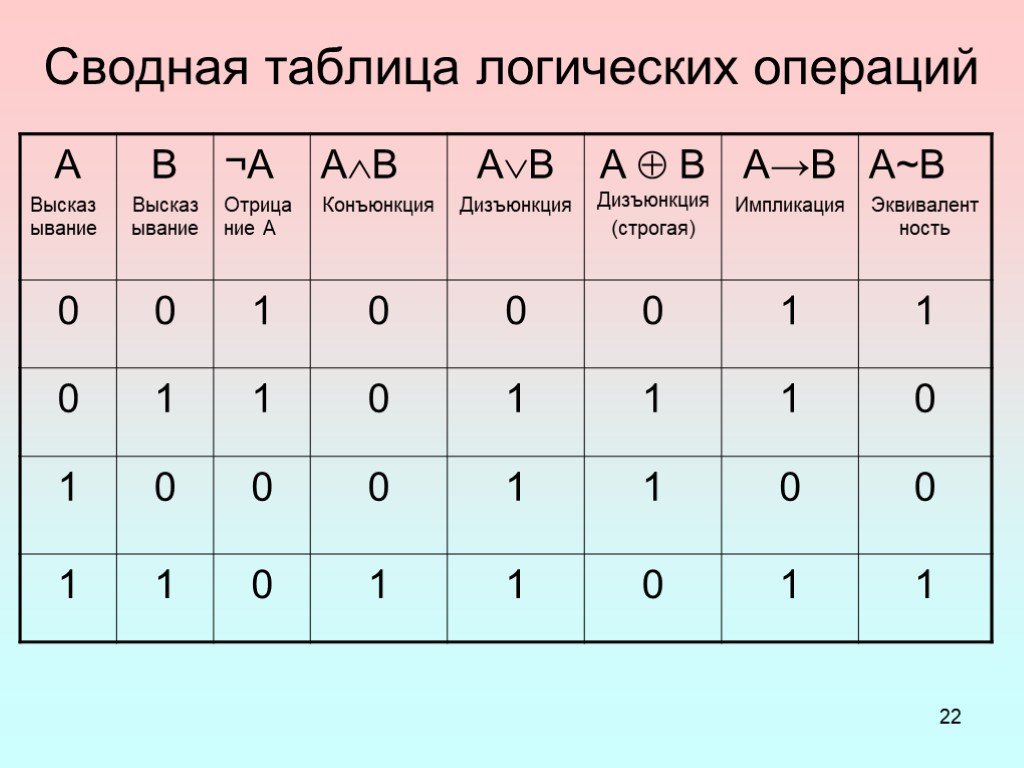
Где Двоичные операции — это такие операции, которые имеют дело с двумя операндами, но здесь мы просто обсуждаем унарные операции, то есть с одним или одним операндом. Прежде чем приступить к унарным операциям, мы должны разобраться с булевыми операторами. Итак, давайте узнаем о логических операторах.
Булевы операторы были изобретены математиком Джорджем Булем. Он изобрел булеву алгебру, математическую систему, лежащую в основе логики компьютеров. Булева алгебра — это раздел математики, который занимается различными операциями над логическими значениями. Три основные логические операции: И, ИЛИ, НЕ.
И:- Его основная работа заключается в удовлетворении обоих условий.
ИЛИ: — Его основная работа заключается в том, чтобы удовлетворить чье-либо условие, как если бы первое или второе любое из условий было истинным, оно сработает.
НЕ:- Меняет значение на противоположное. Если операнд ложный, он возвращает истину, а если истинный, возвращает ложь.
Существует четыре унарных операции:-
Логическая истина
В истинно логическом случае, каким бы ни был ввод, вывод всегда истинен, каким бы ни был ввод. Таблица истинности для логической истины: —
Логическая ложь
В логической ошибке выход всегда ложный, каким бы ни был вход. Таблица истинности для логической ошибки:
Логическая идентичность
В случае логической идентичности выходные данные остаются такими же, как и входные. Таблица истинности для логического тождества:
Логическое отрицание
В случае логического отрицания выходное значение противоположно входному (это означает, что в случае истинного входного значения выходное значение оказывается ложным, а в случае ложного входного значения выходное значение становится истинным).
Таблица истинности для логического отрицания is-
После обсуждения вышеперечисленных унарных операций теперь очередь операторов NOT и NULL.
Оператор NULL: — Если на входе значение A равно 0, NULL выдаст на выходе 0, а если на входе A будет 1, NULL выдаст 1.
Оператор НЕ:- Если на входе значение А равно 0, НЕ выдаст на выходе 1, а если на входе А будет 1, NULL выдаст 0.
Вход
Выход
А
НЕ
0
0
1
1
1
0
Заключение
Таблица истинности — это таблица, в которой логические операторы используются для оценки выражений.
