Метод цифровой логики
|
Страница 5 из 14 На основании эквивалентной таблицы истинности двоично-десятичного кода 8-4-2-1 (рис.7б) и эквивалентной таблицы истинности 4-хпозиционного кода У (рис.7в), представленные комбинациями цифр десятичного кода, построена структурная схема, преобразователя двоично-десятичного кода 8-4-2-1 в 4-хпозиционный код У (рис.7а). Функциональная зависимость начертания знаков от величины числа при формировании цифровых знаков (2,3,4,5 — 6,7,8,9) заключается в том, что большей измеряемой величине соответствует большее число зажженных сегментов (рис.7г) индикатора. При равном числе зажженных сегментов индикатора (цифровые знаки 2,3,4,5 – и 6,7,8,9 – рис.7г) начертание знака, отображающего большую величину 3, 4, 5 (7, 8, 9) повернуто по часовой стрелке на угол кратный 900 по отношению к начертанию знака (2 и 6, соответственно), отображающего меньшую величину (рис.7г). 3. Построение минимизированной структурной схемы преобразователя двоично-десятичного кода 8-4-2-1 в двоичный 9-ипозиционный код А (Патраль А.В. Патент № 2417455), предназначенной для управления элементами наименьшего матричного формата индикатора с видом матрицы 3х3 (рис.8а).
Наименьшее число позиционных (точечных), элементов используемых в формате матричного индикатора при формировании цифровых знаков позволяет осуществить индикацию как в динамическом режиме, так и в статическом режиме управления, при раздельной схеме включения позиционных элементов его. «ПерваяПредыдущая1234567891011121314СледующаяПоследняя» |
Есть вопрос? Задайте его Вашему персональному менеджеру.
Служба поддержки призвана помочь пользователям в решении любых проблем, связанных с вопросами публикации своих работ и другими аспектами работы издательства «Проблемы науки».
Интересная статья? Поделись ей с другими:
Добавить комментарий
Логические операции (and, or, xor, not): таблицы истинности
Бит — это минимальная единица измерения объёма информации, так как она хранит одно из двух значений — 0 (False) или 1 (True). False и True в переводе на русский ложь и истина соответственно. То есть одна битовая ячейка может находиться одновременно лишь в одном состоянии из возможных двух. Напомню, два возможных состояния битовой ячейки равны — 1 и 0.
Есть определённые операции, для манипуляций с битами. Эти операции называются логическими или булевыми операциями, названные в честь одного из математиков — Джорджа Буля (1815-1864), который способствовал развитию этой области науки.
Все эти операции могут быть применены к любому биту, независимо от того, какое он имеет значение — 0(нуль) или 1(единицу).
Ниже приведены основные логические операции и примеры их использования.
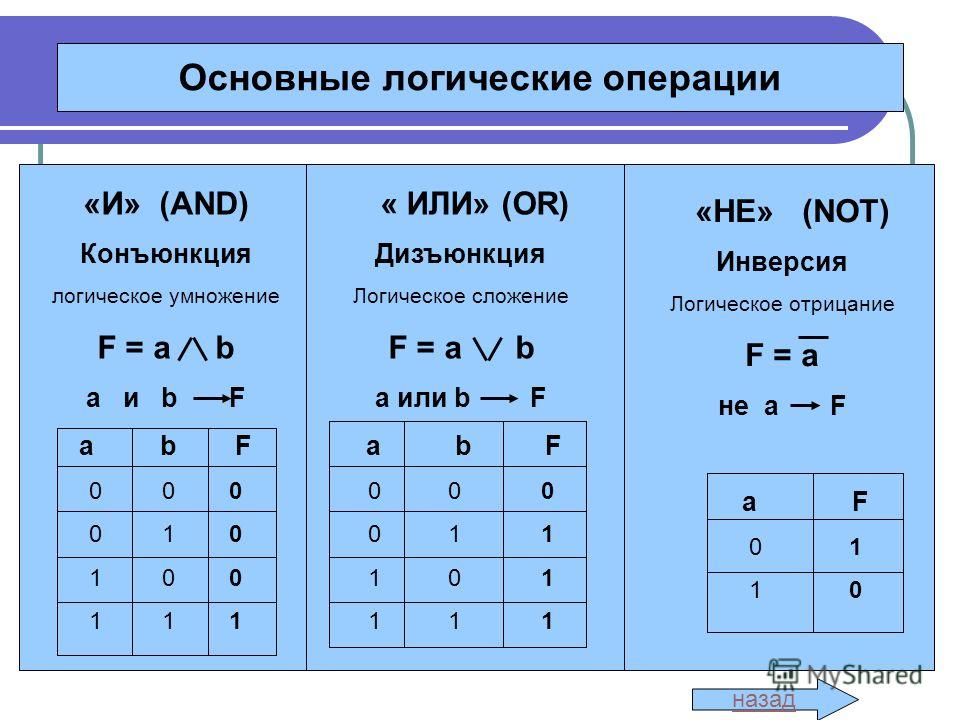
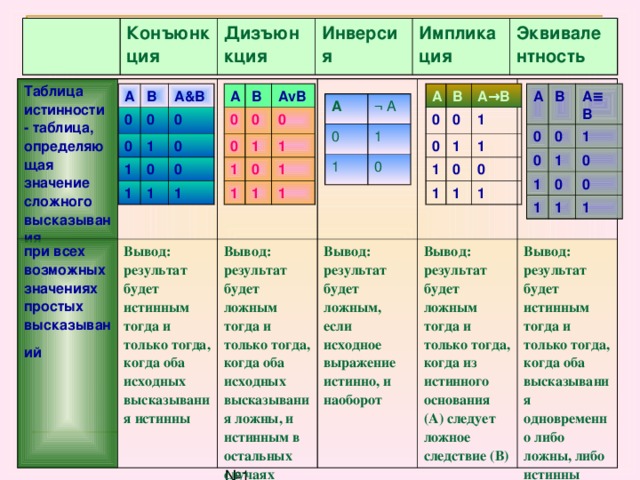
Логическая операция И (AND)
Обозначение AND: &
Логическая операция И выполняется с двумя битами, назовем их a и b. Результат выполнения логической операции И будет равен 1, если a и b равны 1, а во всех остальных (других) случаях, результат будет равен 0. Смотрим таблицу истинности логической операции and.
| a(бит 1) | b(бит 2) | a(бит 1) & b(бит 2) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическая операция ИЛИ (OR)
Обозначение OR: |
Логическая операция ИЛИ выполняется с двумя битами (a и b). Результат выполнения логической операции ИЛИ будет равен 0, если a и b равны 0 (нулю), а во всех остальных (других) случаях, результат равен 1 (единице). Смотрим таблицу истинности логической операции OR.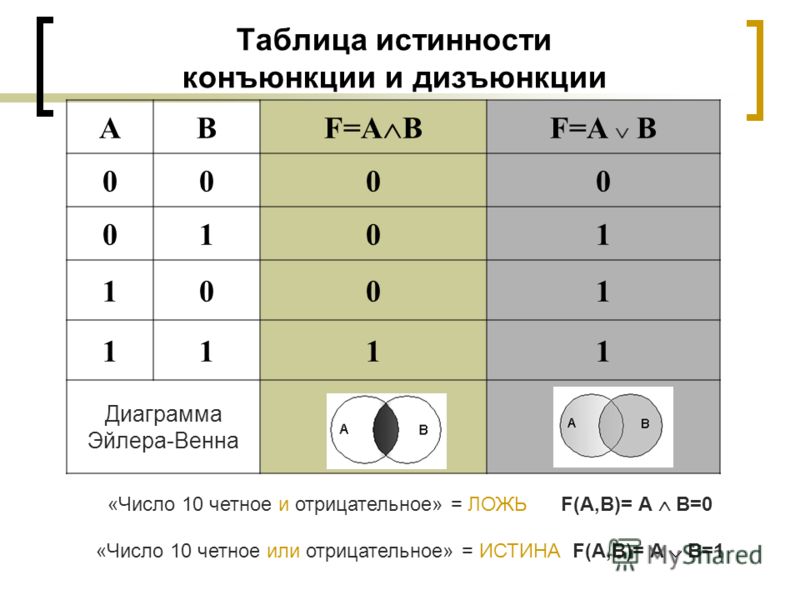
b(бит 2)
Логическая операция НЕ (not)
Обозначение NOT: ~
Логическая операция НЕ выполняется с одним битом. Результат выполнения этой логической операции напрямую зависит от состояния бита. Если бит находился в нулевом состоянии, то результат выполнения NOT будет равен единице и наоборот. Смотрим таблицу истинности логической операции НЕ.
| a(бит 1) | ~a(отрицание бита) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Запомните эти 4 логические операции. Используя эти логические операции, мы можем получить любой возможный результат. Подробно об использовании логических операций в С++ читаем тут.
исчисление высказываний — Логика — Что означает ∴ в таблице истинности?
спросил
Изменено 9 месяцев назад
Просмотрено 1к раз
$\begingroup$
Я вижу используемый символ, но я никогда не видел его логически определенным.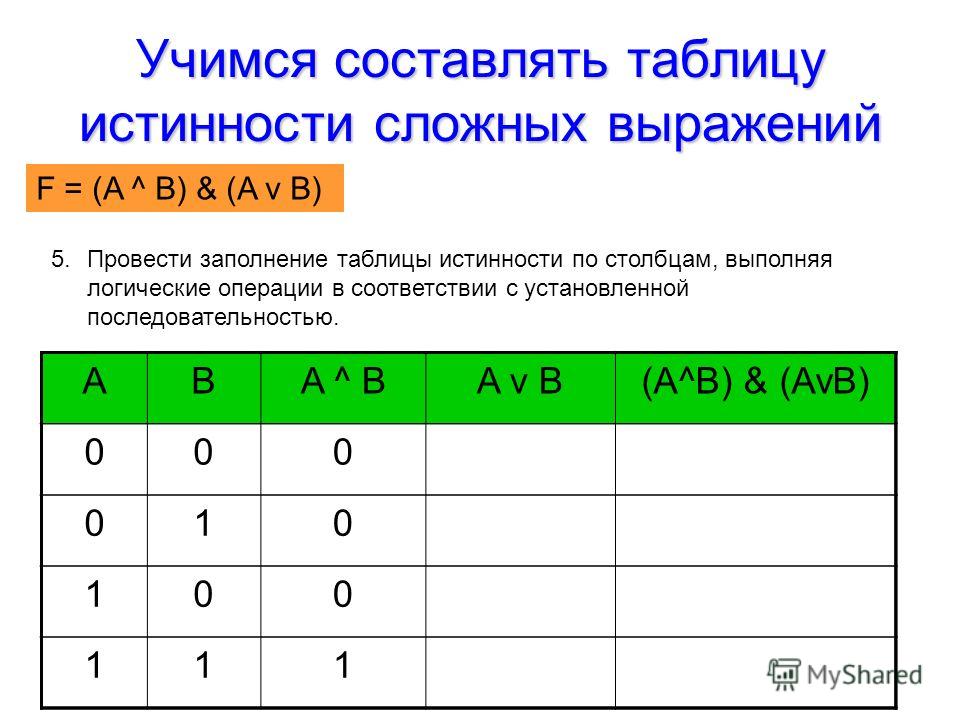
На словах это определяется как символ, означающий «поэтому». Из-за отсутствия определения я понятия не имею, почему это неверно: 9Б) -> С
то же, что и условное
Это ∴ то же, что и условное, только без истинностного значения, когда посылки ложны (выводы не могут основываться на ложных посылках) «А, следовательно, Б», возможно? Я читал, что действительный аргумент является таковым только в том случае, если (логически/символически/алгебраически) невозможно, чтобы вывод был ложным, учитывая, что предпосылка верна.
Я не уверен в этом, и буду признателен за любое исправление. Однако, тем не менее, я до сих пор не могу найти строгого, логического определения или эквивалента ∴, и дело не в том, что я не искал, кажется, что ∴ только когда-либо обсуждался, а не строго определялся.
- логика
- исчисление высказываний
$\endgroup$
$\begingroup$
Символ означает «поэтому».
В обычном использовании «следовательно» является более сильным утверждением, чем «если/то». Когда мы говорим «$p$, следовательно, $q$», мы имеем в виду и «если $p$, то $q$», и «$p$ истинно». Таким образом, мы гарантируем, что $q$ истинно, чего не делает одно утверждение «if/then». Математически:
$p \следовательно q \equiv ((p\стрелка вправо q) \land p)$
$\endgroup$
3
$\begingroup$
Это семантическое утверждение, а не синтаксическое. Синтаксис — это уровень исчисления высказываний, на котором живут $A,B, A\wedge B$. Семантика находится на более высоком уровне, где мы присваиваем значения истинности предложениям на основе их интерпретации в большей вселенной.
Ваш (1), $(A\клин B) \to C$, является предложением. Это может быть правдой или ложью. Однако $(A\wedge B) \следовательно C$ не может быть ложным.
Это может быть действительное доказательство или недействительное, что опять-таки находится на семантическом уровне, а не на синтаксическом.
Например, если выполняется $P$, то должно выполняться $\neg(\neg P)$. У нас есть $P \поэтому \neg(\neg P)$. Это значение отличается от значения $P\to \neg(\neg P)$, которое всегда оказывается верным (тавтология). Утверждая, что $P\to \neg(\neg P)$ логически эквивалентно тавтологии, эквивалентно $P \следовательно \neg(\neg P)$.
$\endgroup$
4
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
9Нотация 0000 — Таблица истинности и значение $\oplus$ в логике высказыванийспросил
Изменено 4 года, 9 месяцев назад
Просмотрено 1к раз
$\begingroup$
Кто-нибудь может показать мне таблицу истинности для этого предложения? Я думаю, что у меня есть последние два, но я не уверен, что это за символ в следующем: $$p\oplus (p\клин q)$$
- нотация
- исчисление высказываний
$\endgroup$
1
$\begingroup$
Первый символ, который появляется в так называемом «исключающем ИЛИ» или также известен как XOR
Исключающее ИЛИ оценивается как ложное, когда оба значения равны True или оба значения ложны.
