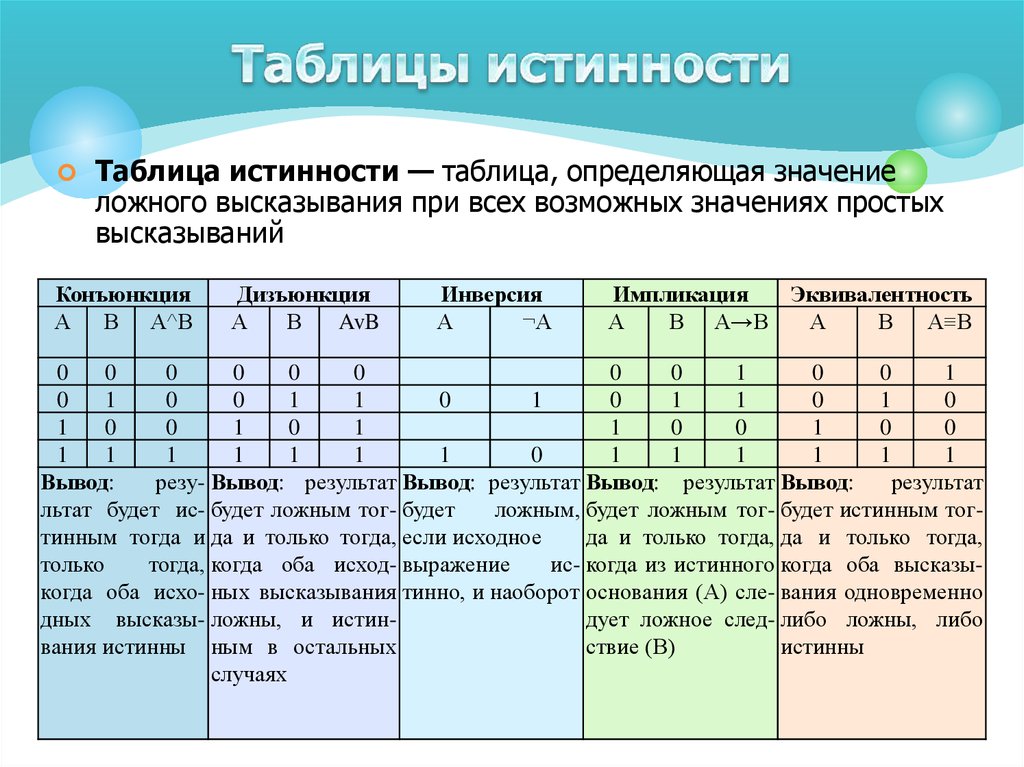
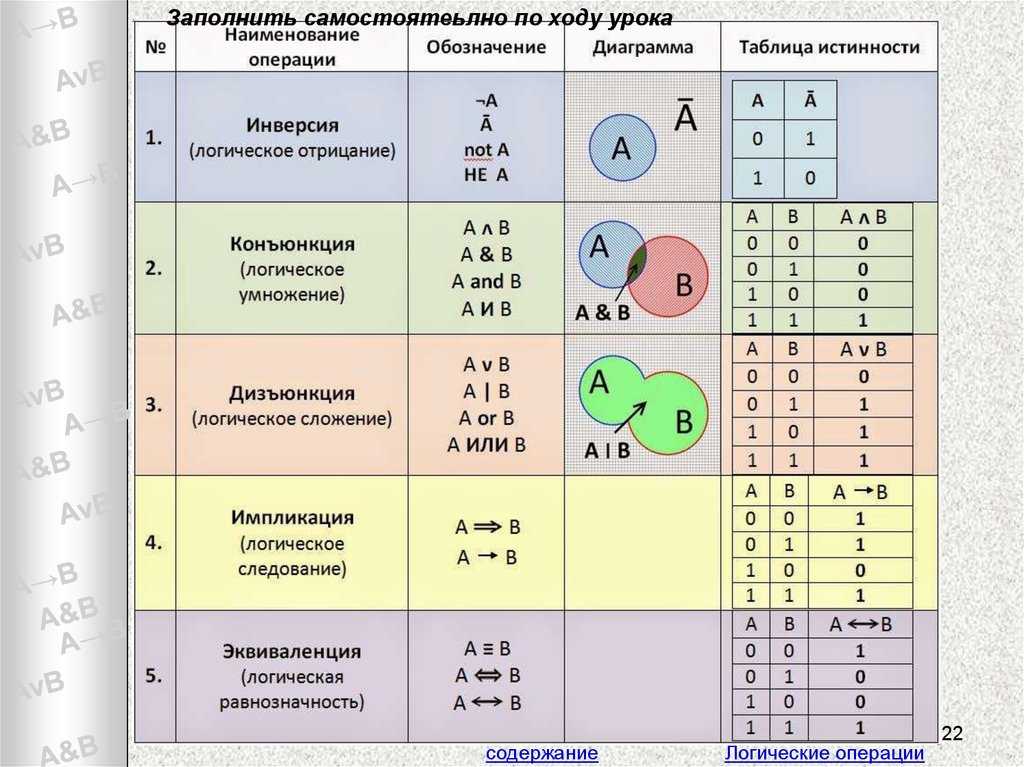
Таблица истинности и или не
Информатика онлайн Информатика онлайн Перевод чисел онлайн Таблица истинности онлайн Формат чисел с плавающей точкой Сложение двоичных чисел Умножение двоичных чисел Представление чисел в ЭВМ Курсы по информатике. Математика онлайн Математика онлайн Линейная алгебра Вычислительная математика Теория вероятностей и математическая статистика Статистика онлайн. Новые калькуляторы Построить график функции Точки разрыва функции Построение графика методом дифференциального исчисления Создание схемы логических элементов. Примеры решений Перевод в 8 систему Перевод в 10 систему.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Открытие окна Комбинационный анализ
- Редактор схемы логических элементов
- Основы логики. Логические операции и таблицы истинности
- лабы по информатике, егэ
- Основы формальной логики
- Логические схемы и таблицы истинности
- Логические элементы и таблицы истинности
- Составление таблиц истинности для логических высказываний нескольких переменных
youtube.com/embed/qrj6Ekwqr-c» frameborder=»0″ allowfullscreen=»»/>Открытие окна Комбинационный анализ
Русский: English:. Бесплатный архив статей статей в Архиве. Справочник бесплатно. Параметры радиодеталей бесплатно. Даташиты бесплатно. Прошивки бесплатно. Русские инструкции бесплатно. Стол заказов:. Бесплатная техническая библиотека, Энциклопедия радиоэлектроники и электротехники. Комментарии к статье. Абсолютно все цифровые микросхемы состоят из одних и тех же логических элементов — «кирпичиков» любого цифрового узла.
Вот о них мы и поговорим сейчас. Логический элемент — это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе. Итак, какие бывают элементы?
Элемент «И» AND. Иначе его называют «конъюнктор». Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов.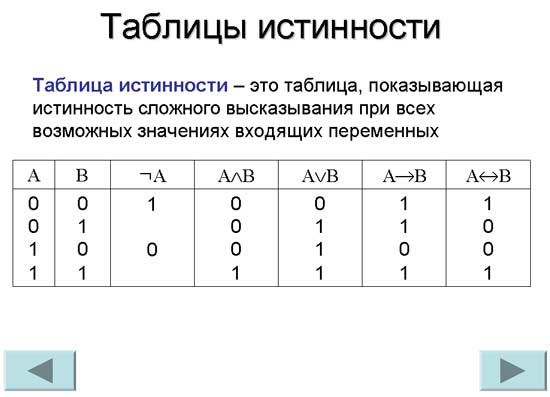
Такая таблица называется » таблица истинности «. Таблицы истинности широко применяются в цифровой технике для описания работы логических схем. Вот так выглядит элемент «И» и его таблица истинности: Поскольку вам придется общаться как с русской, так и с буржуйской тех.
Смотрим таблицу истинности, и проясняем в мозгу принцип. Понять его не сложно: единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.
Если посмотреть чуток иначе, то можно сказать так: на выходе элемента «И» будет ноль в том случае, если хотя бы на один из его входов подан ноль. Идем дальше. По другому, его зовут «дизъюнктор». Любуемся: Опять же, название говорит само за себя. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули.
Едем дальше. Дальше у нас очень простенький, но очень необходимый элемент.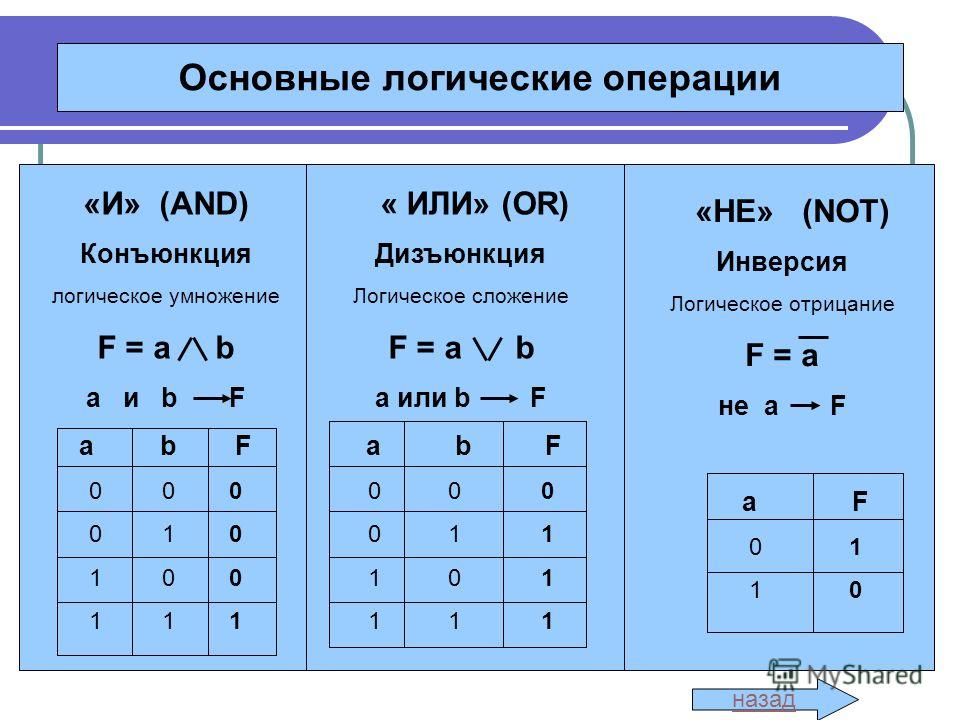
Чаще, его называют «инвертор». Надо чего-нибудь говорить по поводу его работы? Ну тогда поехали дальше. Следующие два элемента получаются путем установки инвертора на выход элементов «И» и «ИЛИ». Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» — единица. И наоборот. Та же история — элемент «ИЛИ» с инвертором на выходе. Он вот такой: Операция, которую он выполняет, часто называют «сложение по модулю 2».
На самом деле, на этих элементах строятся цифровые сумматоры. Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном — 1, на другом — 0. Вот такой он хитрый. Эквивалентная схема примерно такая: Ее запоминать не обязательно. Собственно, это и есть основные логические элементы. На их основе строятся абсолютно любые цифровые микросхемы. Даже ваш любимый Пентиум 4. Далее мы позанудствуем о том, как синтезировать цифровую схему, имея ее таблицу истинности.
Это совсем несложно, а знать надо, ибо пригодится еще как пригодится нам в дальнейшем.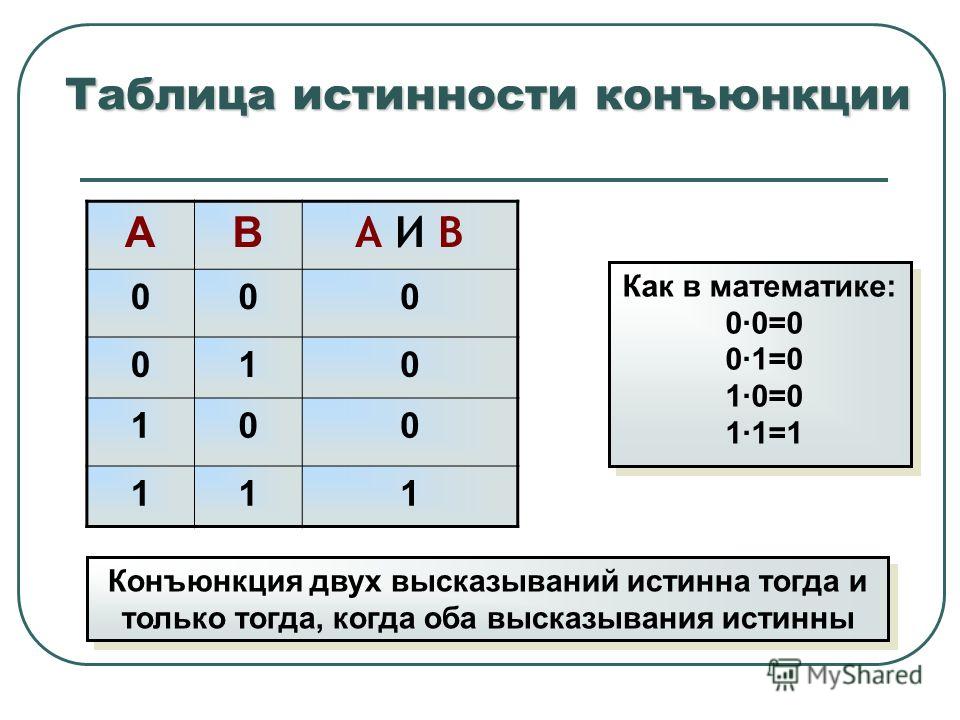
Найфельд М. Никольский И. Серия F.
Редактор схемы логических элементов
На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи. Таблица истинности операции ИЛИ дизъюнкция. Таблица истинности операции Импликация если…, то…. Таблица истинности операции Эквивалентность тогда и только тогда, …. О преобразованиях логических операций читайте здесь. Каждое из логических выражений F и G содержит 5 переменных.
Логические операции и таблицы истинности означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.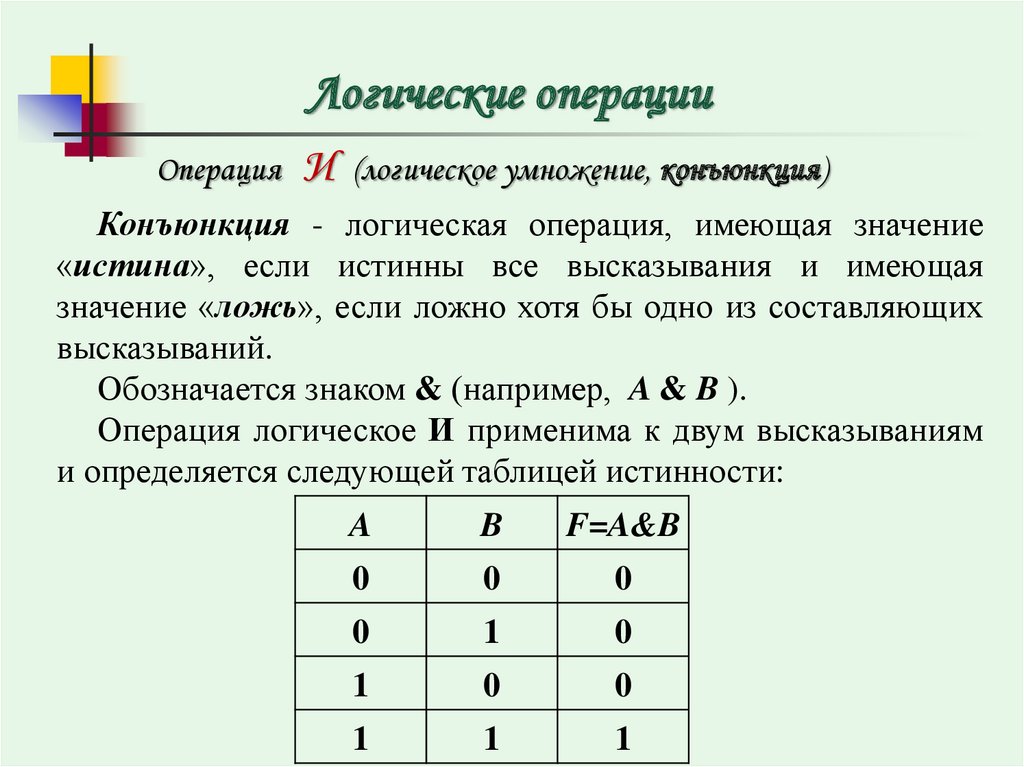
Основы логики. Логические операции и таблицы истинности
Библиотека: Базовые Введён в: 2. По умолчанию, неподключенные входы игнорируются — то есть, если входы действительно не имеют ничего подключенного к ним — даже провода. Таким образом, вы можете добавить 5-входовый элемент, но подключить только два входа, и он будет работать как 2-входовый элемент; это избавляет вас от необходимости беспокоиться о настройке количества входов каждый раз при создании элемента. Если все входы не подключены, то на выходе значение ошибки X. Некоторые пользователи, однако, предпочитают, чтобы Logisim настаивал, чтобы все входы были подключены, поскольку это соответствует реальным элементам. Но если входов с определённым значением больше двух, то элемент Исключающее ИЛИ будет давать на выходе 1, когда единица строго на одном входе, тогда как элемент Нечётность даст на выходе 1, когда единица на нечётном количестве входов. Элемент Исключающее ИЛИ-НЕ будет давать на выходе 1, когда входов с единицей строго не один, тогда как элемент Чётность даст 1, когда входов с единицей чётное количество.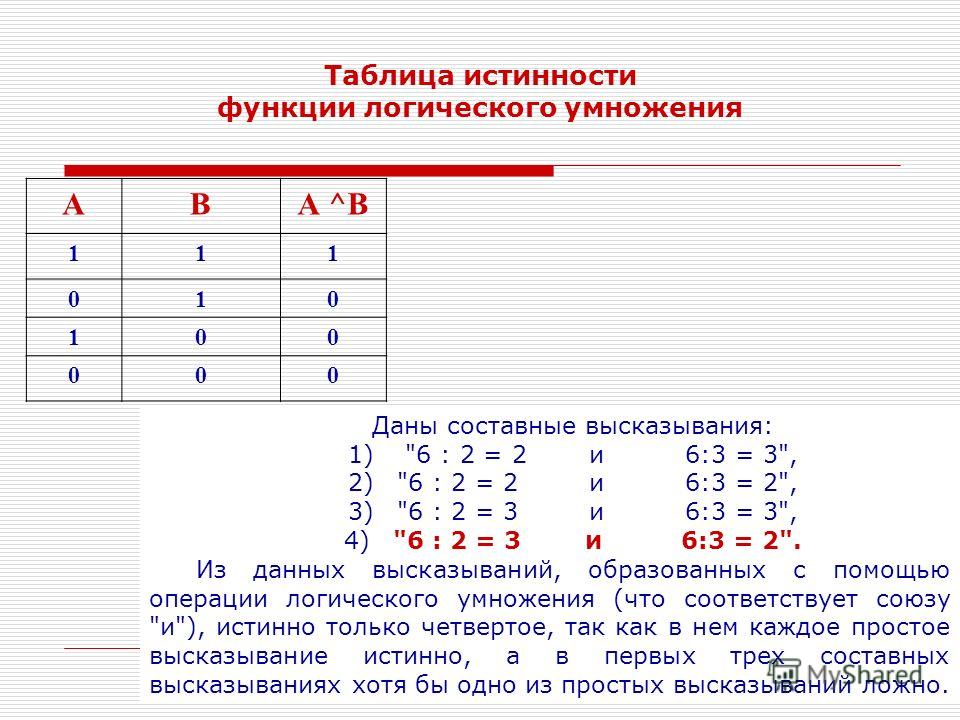
Если на каких-либо входах значение ошибки например, если противоречивые значения поступают на один и тот же провод или плавающее значение, то на выходе будет значение ошибки. Многобитные версии каждого элемента будут выполнять свои однобитные преобразования над входами поразрядно. Примечание: многие специалисты утверждают, что поведение фигурного элемента Исключающее ИЛИ должно соответствовать поведению элемента Нечётность, но по этому вопросу нет согласия.
лабы по информатике, егэ
Чаще всего существуют не отдельные схемы логического «И», а более сложные схемы, выполняющие одновременно логическую функцию «И» и логическую функцию «НЕ» Таблица истинности и изображение схемы, выполняющей логическую функцию «И-НЕ» изображены на рис 3 и 4 соответственно:. Точно также как не существует отдельных схем логического «И», выполненных по технологии ТТЛ, не существует отдельных схем логического «ИЛИ». Таблица истинности и изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ» изображены на рис 5 и 6 соответственно:.
Любая логическая схема без памяти полностью описывается таблицей истинности.
Таблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, у которой значения переменных и значение самой функции выражают истинность.
Основы формальной логики
В отличие от аналоговых электронных устройств, в цифровых устройствах ЦУ входные и выходные сигналы могут принимать ограниченное количество состояний. В соответствии с логическим соглашением ГОСТ 2. Такое соглашение называется положительной логикой. Обратное соотношение называется отрицательной логикой. Теоретической основой проектирования ЦУ является алгебра-логики или булева алгебра, оперирующая логическими переменными. Для логических переменных, принимающих только два значения,существуют 4 основных операции.
Логические схемы и таблицы истинности
Вот о них мы и поговорим сейчас. Логический элемент — это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.
Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Таблицы истинности широко применяются в цифровой технике для описания работы логических схем. Поскольку вам придется общаться как с русской, так и с буржуйской тех. Смотрим таблицу истинности, и проясняем в мозгу принцип. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.
Двухвходовая таблица истинности для элементов следующая. Элемент Исключающее ИЛИ-НЕ будет давать на выходе 1, когда входов с единицей.
Логические элементы и таблицы истинности
Логика — наука, изучающая законы и формы мышления; учение о способах рассуждений и доказательств. Законы мира, сущность предметов, общее в них мы познаем посредством абстрактного мышления. Основными формами абстрактного мышления являются понятия, суждения и умозаключения. Понятие — форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов.
Составление таблиц истинности для логических высказываний нескольких переменных
К основной части модуля Комбинационный анализ можно получить доступ через единственное окно с таким же именем, оно позволяет просматривать таблицы истинности и логические выражения. Это окно можно открыть двумя способами. Выберите Комбинационный анализ, и появится текущее окно Комбинационного анализа. Если вы ещё не рассматривали это окно прежде, открытое окно не будет представлять никакой схемы. Только одно окно Комбинационный анализ существует в Logisim, независимо от того, сколько проектов открыто.
Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений истинности или ложности и логических операций над ними.
Основные сведения. Логические значения, логические связки и логические выражения. Свойства логических выражений и таблиц истинности. Эквивалентные преобразования логических выражений. Такие высказывания утверждают что-то о свойствах объекта или об отношениях между объектами чаще всего — между двумя объектами.
Русский: English:. Бесплатный архив статей статей в Архиве. Справочник бесплатно. Параметры радиодеталей бесплатно.
Онлайн-уроки TutorOnline по информатике и ИКТ 11 класс
Русский языкРусская литератураАнглийский языкНемецкий языкМатематикаИстория РоссииОбществознаниеГеографияБиологияФизикаХимияИспанский языкФранцузский языкВсеобщая историяИнформатика и ИКТЛитературное чтениеВысшая математикаПольский языкТурецкий языкИтальянский языкКитайский языкРусский язык как иностранныйЭкономикаПрограммированиеЛогикаШахматыАнглийский язык IELTS TOEFLТеоретическая механикаМатематическая статистикаЭконометрикаМастерство актерскоеПравоЯпонский языкКорейский языкPhotoshopТеория вероятностейПодготовка к школеЖивописьРисованиеРКИ для детей-билингвовРиторикаЛогистикаПсихологияИгра на гитареИстория БеларусиУправление человеческими ресурсами
1 класс2 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс1 курс2 курсВзрослыйНе указан
Применить фильтр
Программирование, 27 номер ЕГЭ
Просмотреть
Поиск максимального и минимального элемента в массиве при сортировке методом прямого выбора.
Просмотреть
Подготовка к ЕГЭ. Алгоритмизация, основы программирования
Просмотреть
12. Нахождение НОД и НОК, факториал, разложение заданного числа на разряды
Просмотреть
9. Алгоритмы ввода, вывода и обработки массивов
Просмотреть
7. Повторение пройденного материала. Анализ полученного результата.
Просмотреть
6. Задачи повышенной сложности.
Просмотреть
5. Логика и теория множеств.
Просмотреть
7. Задачи повышенной сложности.
Просмотреть
4. Методы решения систем логических уравнений.
Просмотреть
6. Логика и теория множеств.
Просмотреть
3. Методы решения логических уравнений.
Просмотреть
Подготовка к ЕГЭ по информатике Вариант № 15
Просмотреть
2. Графическая интерпретация базовых логических операций и выражений.
Просмотреть
5. Методы решения систем логических уравнений.
Просмотреть
Анализ и составление таблиц истинности.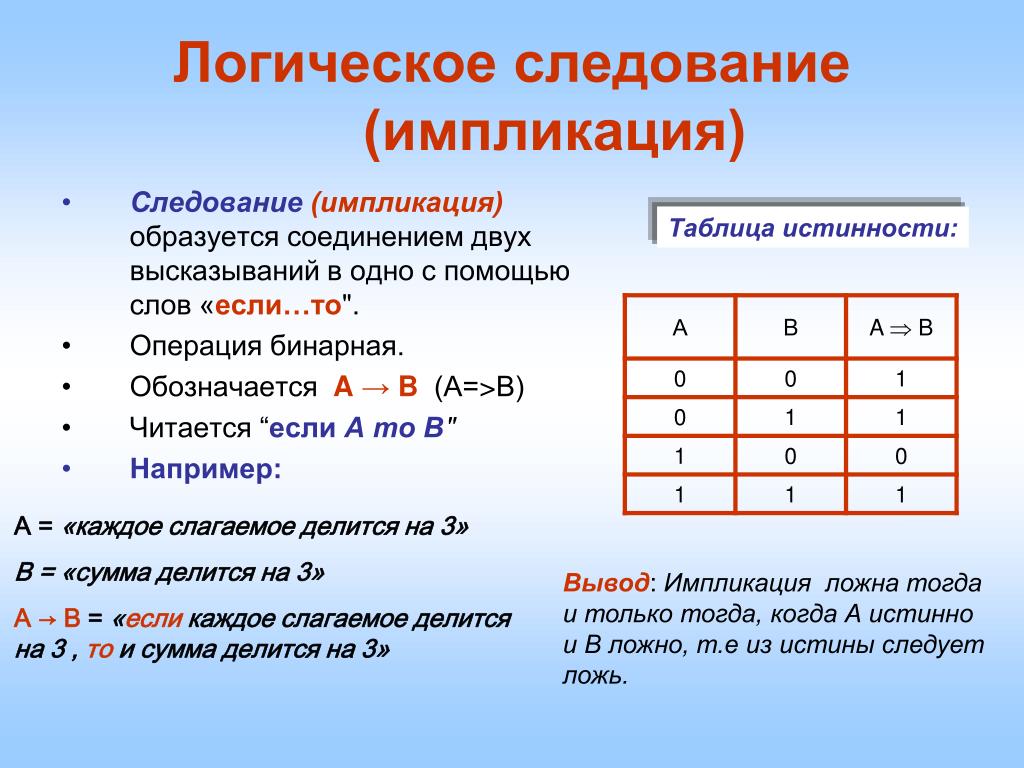
Основные законы логики. Решение задач.
Просмотреть
4. Методы решения логических уравнений.
Просмотреть
3. Графическая интерпретация базовых логических операций и выражений.
Просмотреть
2. Анализ и составление таблиц истинности. Решение задач.
Просмотреть
Написание программы для вычислений на Питоне.
Просмотреть
1. Представление о математической логике. Основные логические операции и их таблицы истинности. Основные законы логики.
Просмотреть
ЕГЭ по информатике 2 часть.
Просмотреть
2. Решение уравнений в различных С/С. Подсчет количества цифр.
Просмотреть
5. Неравномерные коды. Правило Фано. Формула Хартли для равнозначных событий, практическое применение её при решении задач.
Просмотреть
2.Свойства чисел в различных С/С и применение их при решении задач.
Просмотреть
Калькулятор таблицы истинности
Этот калькулятор создает таблица истинности для любого логического выражения.
Для начала введите логическое выражение в калькулятор.
Калькулятор поддерживает следующие логические операции:
Логическая операция «не» (отрицание, инверсия)
Эта операция обозначается символом
условное обозначение. Чтобы ввести его в наш калькулятор, можно использовать либо символ ¬, либо символ восклицательного знака (!). Операция отрицания является унарной (содержит только один операнд) и имеет наивысший приоритет среди логических операций.
Таблица истинности логической операции «не» имеет вид:
Логическая операция «и» (союз, логическое умножение)
Эта операция обозначается символом
условное обозначение. Чтобы ввести его в наш калькулятор, можно использовать либо символ ∧, либо два символа амперсанда (&&). Операция конъюнкции является бинарной (содержит два операнда).
Таблица истинности логической операции «и» имеет вид:
Логическая операция «или» (дизъюнкция, логическое сложение)
Эта операция обозначается символом
условное обозначение.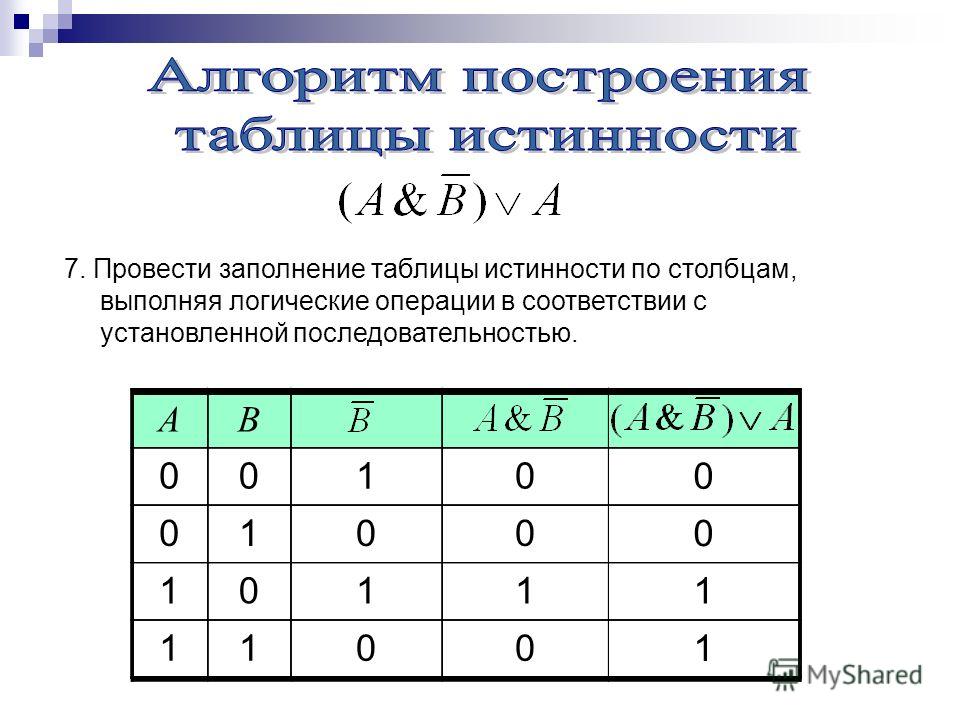
Чтобы ввести его в наш калькулятор, можно использовать либо ∨, либо два || символы. Операция дизъюнкции бинарна.
Таблица истинности логической операции «или» имеет вид:
Логическая операция «исключающее ИЛИ» (сложение по модулю 2)
Эта операция обозначается символом
условное обозначение. Чтобы ввести его в наш калькулятор, можно использовать либо символ ⊕, либо функцию
.
Таблица истинности логической операции «исключающее ИЛИ» имеет вид:
Логическая операция «не и» (Шрифт Шеффера)
Эта операция обозначается символом
условное обозначение. Чтобы ввести его в наш калькулятор, можно использовать либо ↑, либо | условное обозначение.
Таблица истинности логической операции «не и» имеет вид:
Логическая операция «не или» (стрелка Пирса)
Эта операция обозначается символом
условное обозначение.
Чтобы ввести его в наш калькулятор, можно использовать либо символ ↓, либо функцию
.
Таблица истинности логического «не или» имеет вид:
Логическая эквивалентность
Эта операция обозначается символом
условное обозначение. Чтобы ввести его в наш калькулятор, можно использовать либо символ ⇔, либо конструкцию (знак меньше, знак равенства, знак больше).
Таблица истинности логической эквивалентности имеет вид:
Логическая операция «исключающее не или»
Эта операция обозначается символом
условное обозначение. Чтобы ввести его в наш калькулятор, можно использовать либо символ ⊙, либо функцию
.
Таблица истинности логической операции «исключающее не или» имеет вид:
Следует отметить, что таблицы истинности для двоичный логические операции «эквивалентность» и «исключающее ИЛИ» совпадают.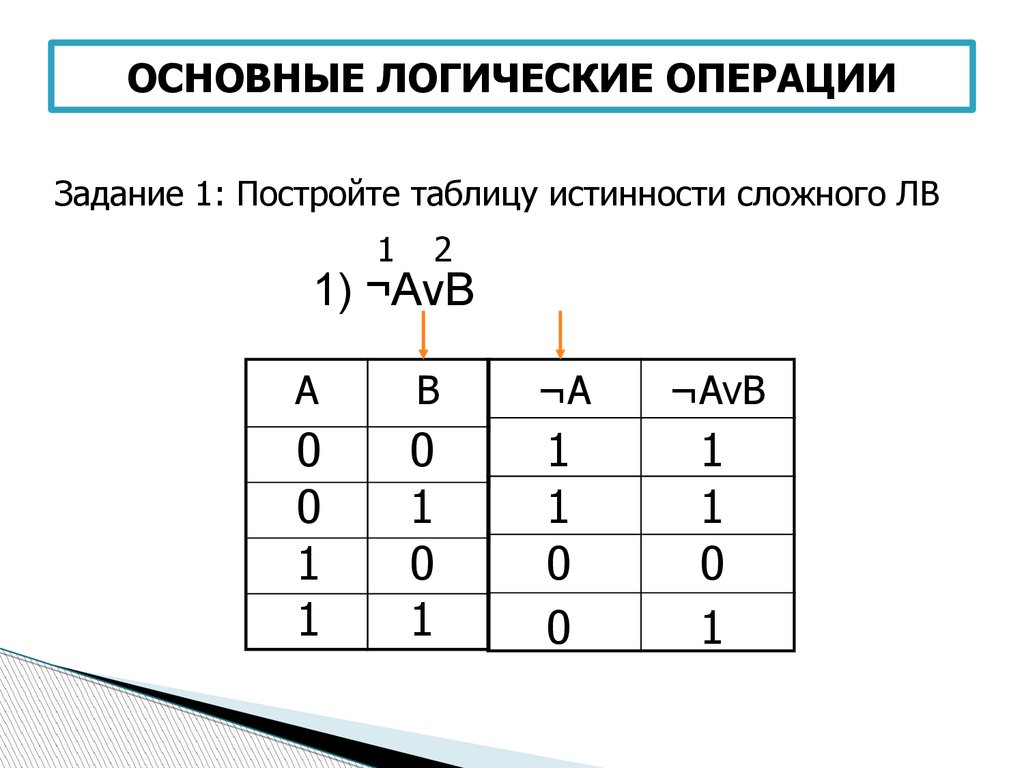
В случае, если указанные операции
-ары, их таблицы истинности отличаются. Обратите внимание, что
-арные операции можно вводить в наш калькулятор только как соответствующие функции, например
, и результат такого выражения будет отличаться от результата выражения
. Поскольку последнее интерпретируется как
, а в случае
— операция «эквивалентность» выполняется сразу с учетом всех ее аргументов.
Логическая операция «импликация»
Эта операция обозначается символом
условное обозначение. Чтобы ввести его в наш калькулятор, можно использовать либо символ ⇒, либо конструкцию => (знак равенства, знак больше).
Таблица истинности логической операции «импликация» имеет вид:
При создании таблицы истинности сложного (составного) логического выражения необходимо использовать приведенные выше таблицы истинности соответствующих логических операций.
2. Схемы и таблицы истинности — Сиреум Логика
В этой главе мы рассмотрим основные понятия о воротах и изучим взаимосвязь между схемами и компьютерными программами, основанными на назначениях. Это создает основу для анализа современных программ.
2.1. Гейтс и таблицы правды
Вот четыре основных врата:
П И К | ПОР К | НЕ П | P ИМПУЛЬС Q |
На приведенных выше рисунках входные провода обозначены именами P и Q .
Выходной сигнал, который вычисляется, испускается из крайнего правого провода, который выходит из
ворота. Для этих простых вентилей можно исчерпывающе протестировать каждую перестановку.
потенциальных входных данных и суммировать результаты в таблице, называемой таблицей истинности.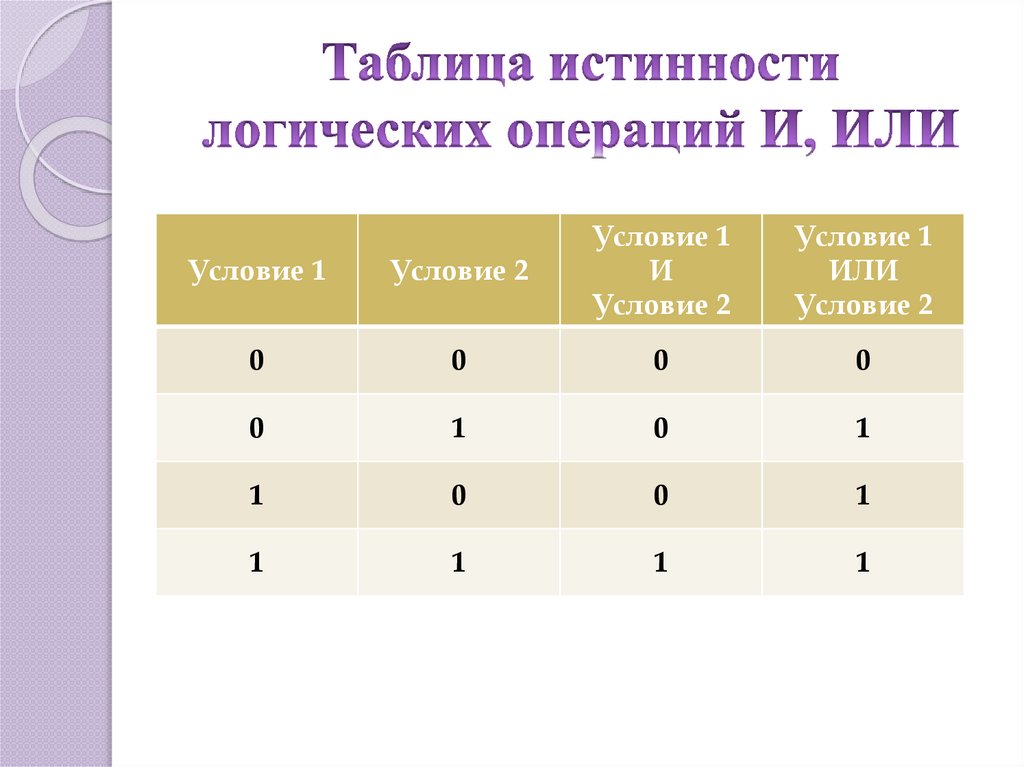
Давайте рассмотрим вентиль И. Логический элемент И излучает высокое напряжение ( 1 ) точно
при обнаружении высокого напряжения на входных проводах P и Q ; в противном случае
выдается низкое напряжение ( 0 ). Физическое поведение ворот резюмируется
в следующей таблице.:
И: П Q |
------------
1 1 | 1
1 0 | 0
0 1 | 0
0 0 | 0
В оставшейся части этого курса мы будем использовать T (читай «истинно») вместо 1 и F (читается как «ложь») вместо 0 .
Это потому, что мы будем исследовать приложения, выходящие далеко за рамки теории схем.
и арифметика с основанием два.
Вот таблицы истинности для логических элементов И, ИЛИ, НЕ и ПРЕДПОЛАГАЕТ:
Примечание
Заглавные буквы P и Q предназначены для заполнения, а не
переменные строго именуются P и Q. Их использование позволяет избежать многословия: «Правая рука».
Боковой операнд» и «Левый операнд».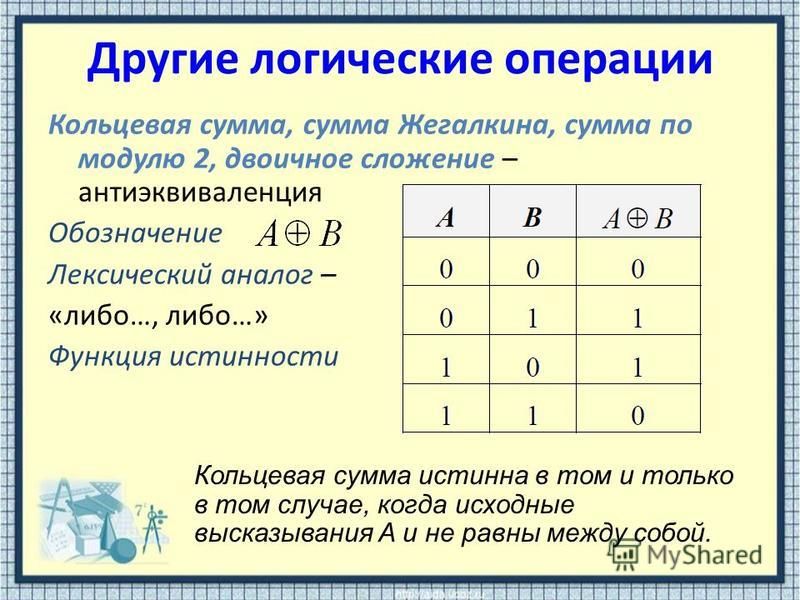
ИЛИ иногда называют «включающим ИЛИ», потому что до тех пор, пока один из его входные данные истинны, то его выходные данные истинны. Это отличается от обычных Соединенных Указывает использование английского языка. Как правило, в разговорном и письменном английском языке «или» несет в себе эксклюзивный оттенок. Если предлагается выбор «кофе или чай», это понимается что вы можете выбрать один, но не оба. Логическое «или» допускает возможность обоих. На английский язык более точно переводится как «и/или».
Значение ворот ПОДРАЗУМЕВАЕТСЯ будет раскрыто позже в этой главе. это включены сюда, поэтому вся информация о воротах консолидирована.
Стандартно записывать каждый вентиль в линейной записи, то есть вместо
рисунок, пишем P ∧ Q .
(Традиция написания линейных обозначений для представления двумерных
структур восходит к столетиям в физике и математике.)
Обозначения следующие (традиционные математические обозначения предусмотрены для
ваша ссылка.)
Ворота | ASCII-код | Математика | ЮНИКОД |
И | ∧ | ∧ | |
ИЛИ | v | ∨ | |
НЕ | ~ | ¬ | |
ПОДРАЗУМЕВАЕТСЯ | -> | ⇒ | . |
В этих примечаниях обычно используются обозначения UNICODE.
Мы также можем составить элементы для определения новых операций.
Например, эта схема, написанная ¬ (P ∧ Q) , определяет это
вычисление выходов:
П Q | ¬ (P ∧ Q) -------------- Т Т | Ф Т Ф | Т Ф Т | Т Ф Ф | Т
, который мы можем вычислить поэтапно, вот так:
Начнем с того, что запишем значение каждого набора входов слева под их
соответствующий символ справа. Далее мы применяем оператор (гейт) с
наивысший приоритет (рассматривается в разделе «Приоритет логических операторов» ниже). В нашем случае
«()» делает символ И ( ∧ ) самым высоким.
Присвоение истинности — это уникальная перестановка возможных входных данных для системы.
Для ∧-гейта это последовательность с двумя переменными. Рассматривая первую строку, мы видим
у нас есть «T ∧ T» — глядя на это в таблице истинности ∧-ворот, мы видим, что результат
также «T», и мы записываем это под символом «∧».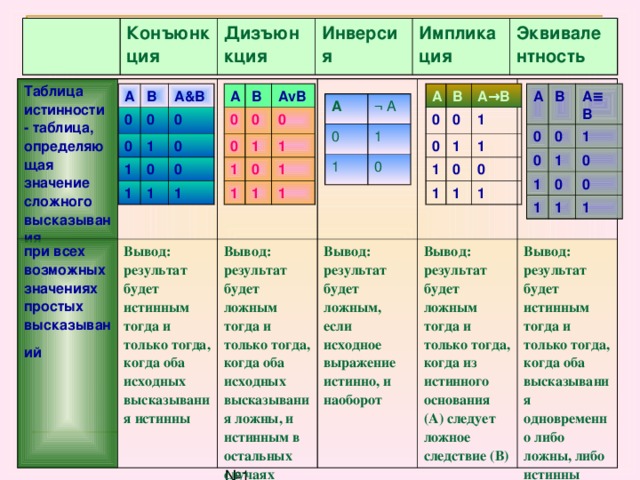
Мы делаем то же самое все
другие задания на правду.
После первоначальной расшифровки значений истинности под их соответствующие переменные, мы ищем значения истинности в таблицах вентилей, а не переменные. Также обратите внимание, что в то время как ∧ является симметричным, то есть «TF» == «FT» == «F» ворота IMPLY — нет.
Теперь ищем значение под символом «∧» в таблице ¬gate. Во-первых мы видим, что истинное назначение для первой строки, «T», равно «F», и записываем под символом «¬». Сделайте это для каждой строки, и мы закончили.
2.1.1. Характеристика таблиц истинности
В нашем изучении логики будет удобно характеризовать логическую формулу с помощью
описание их таблиц истинности. Если все назначения истинности для логической формулы
Верны, формула называется тавтологией. Формула p ∨ ¬ p — это
тавтология. В следующем примере * отмечает верхний или последний уровень.
оцененный оператор.
1 * 2------------ 3п | р ∨ ¬ р 4------------ 5Т | Т Т Ф Т 6F | Ф Т Т Ф 7------------ 8Тавтология
Формула, для которой каждое присваивание истинности равно False, называется противоречивой.
формула p ∧ ¬ p противоречива (или противоречие).
1 * 2------------ 3п | р ∧ ¬ р 4------------ 5Т | Т Ф Ф Т 6F | Ф Ф Т Ф 7------------ 8Противоречивый
Формула, для которой одни присваивания истинности являются ложными, а другие — истинными, называется
контингент. Уравнение p q | ¬ (q ∧ q) , сверху условно.
1 * 2--------------- 3п д | ¬ (р ∧ д) 4--------------- 5Т Т | Ф Т Т Т 6Т Ф | Т Т Ф Ф 7Ф Т | Т Ф Ф Т 8Ф Ф | Т Ф Ф Ф 9--------------- 10Контингент 11- Т : [ТФ] [ФТ] [ФФ] 12- Ф : [Т Т]
В этом разделе мы использовали таблицы истинности Logika. Они объясняются более подробно ниже. В этом классе, если вы создадите таблицу истинности как часть ответа, он должен соответствовать синтаксису Logika. 932 записи. Это займет немного (каламбур) более 1100 лет, чтобы написать вручную, если вы можете усреднить одно назначение истины в секунду.
Учитывая, что вас, вероятно, никогда не попросят написать реальное приложение
так же просто, как сложение целых чисел, легко сделать вывод, что это
невозможно доказать правильность программ с помощью таблиц истинности.
Неспособность
протестировать программу на
исчерпывающая проверка каждого входа или состояния известна как комбинаторный взрыв
проблема.
Ладно… тогда зачем мы заставляем вас учить таблицы истинности? Ну, даже когда более продвинутый методы применяются для доказательства логических утверждений, подтверждая обоснованность методов эти примитивные правила, которые легко выражаются и изучаются с помощью таблиц истинности.
2.2. Таблицы истинности Logika
С этого момента курс предполагает, что вы будете использовать формат Logika.
таблицы истинности. Таблица истинности логики для формулы ¬ (P ∧ Q) :
1 * 2------------ 3п | р ∨ ¬ р 4------------ 5Т | Т Т Ф Т 6F | Ф Т Т Ф 7------------ 8ТавтологияТаблицы истинности
Logika имеют стандартный формат (синтаксис) и семантическое значение. Все элементы таблицы истинности должны быть включены, чтобы считаться правильным.
Первая строка всегда будет содержать одну звездочку ( * ) над последним оцененным оператором
в формуле.
Это также может упоминаться как «высший уровень» или «самый низкий прецедент».
оператор. Почему его называют оператором «высшего уровня», будет рассказано
конец этой главы.
Далее идет строка из - (знак минус) символов, длина этих строк должна быть не меньше
в качестве третьей строки, чтобы избежать ошибок.
Третья строка содержит «переменные | формула». Поскольку в Logika используются заглавные буквы, зарезервированные слова, строчные буквы используются в качестве имен переменных. Кроме того, переменные должны быть перечислены в алфавитном порядке.
Четвертая строка — еще одна строка -- .
Далее идут задания на правду. Соглашение состоит в том, чтобы начать со всего True и прогрессировать
линейно ко всем False. Необходимо использовать Capital T и F . В задании правды
каждая переменная отображается либо в true, либо в false.
После заданий Правды идет еще ряд -.
Наконец идет стол.
Когда все присваивания истинности делают формулу истинной,
слово Тавтология используется без сопроводительной таблицы. Точно так же, когда
все присваивания истинности ложны, используется Contradictory . Все остальные результаты
являются Контингент , см. пример на рисунке выше.
Порядок приоритета логических операторов от высшего к низшему:
Скобки изменяют порядок операций, как в обычной алгебре. Выражения в скобках оцениваются от наиболее глубоко вложенных к наименее глубоко вложенные (внутри наружу).
2.3. Странный случай имплицитных ворот
Внимательный читатель заметит, что → таблицы истинности работают совсем не так, как ∧ и ∨ . Начнем с того, что ∧ и ∨ истинностные назначения симметричны;
если [T F] == F, то [F T] == F.
Это неверно по смыслу, потому что p → q является составным
утверждение, утверждающее, что p содержит знания, достаточные для вывода q.
Возьмем конкретный пример из K-State. Если я знаю, что вы специализируетесь по информатике (факт p), то я знаю, что вы специализируетесь на инженерии (факт q).
по специальности информатика → по специальности инженер
п → д
Однако наоборот, по специальности «Инженерное дело» → по специальности «Информатика» не обязательно верно.
Некоторые учащиеся склонны смешивать фразу «р содержит знания, достаточные для вывода q», что означает «p == q», и удивляются и возмущаются тем, что присваивание истины [F T] в ворота ПОДРАЗУМЕВАЕМЫЕ — Истина. p → q не означает p == q или q == p
В таблице истинности для p → q результат отражает существование последовательного
связь между p и q . Сначала p должно быть истинным, затем q тоже должно быть истинным
быть истинным, чтобы импликация была истинной.
Если оба верны, ссылка
верно, и импликация (отношение) между p и q верно.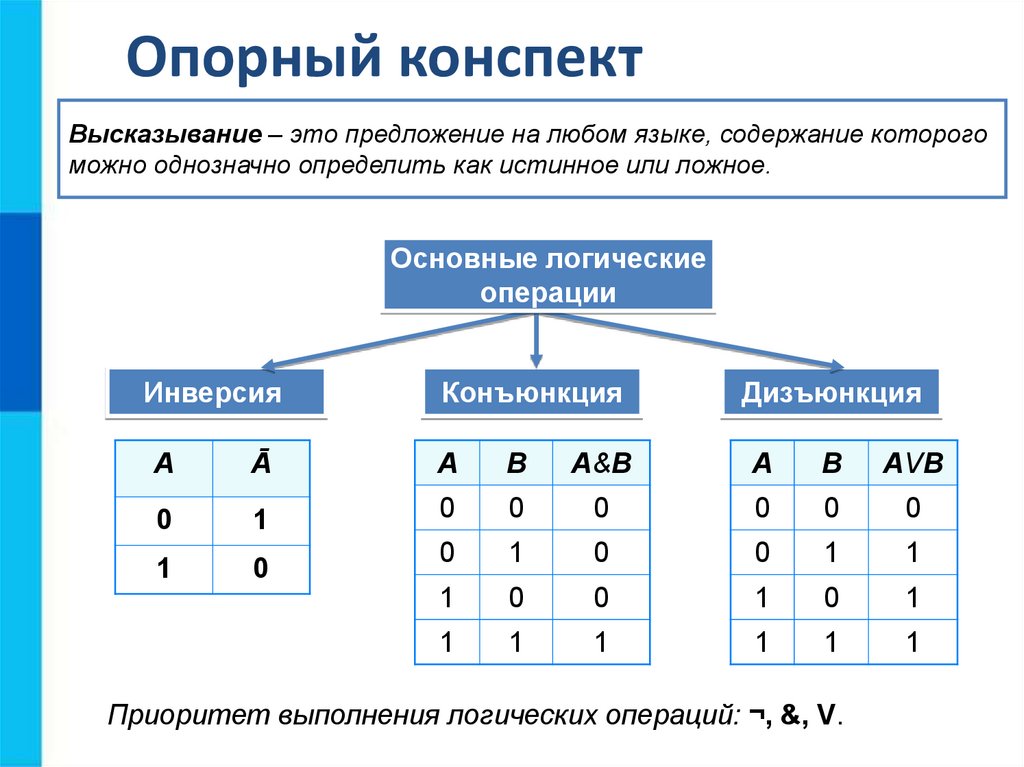
Если p истинно, а q ложно, то очевидно, что p не обладает достаточным знанием
вывести q, поэтому отношение не верно (ложно).
Наконец, если p неверно, нет никакого способа узнать, сохраняется ли связь. В этом случае импликация считается истинной или беспричинно истинной. Конечно нет доказательства, доказывающие, что это ложь.
Импликация в логике была формализована Уильямом Оккамом в его книге Summa Logicae в 14 веке. Эти несколько запутанные правила добавляют огромную выразительную силу логике и вычислениям. Без них в программах не было бы ветвлений (без IF, FOR, WHILE).
2.4. Общая логическая формула (схема) Эквивалентности
2.4.1. Равенство
Говорят, что два (или более) логических утверждения равны IFF (тогда и только тогда, когда ↔ ) они имеют
одно и то же значение истинности для каждого присваивания истинности; то есть их таблицы истинности
оценивают точно так же. Примером равенства являются q ∧ p и p ∧ (q ∧ p)
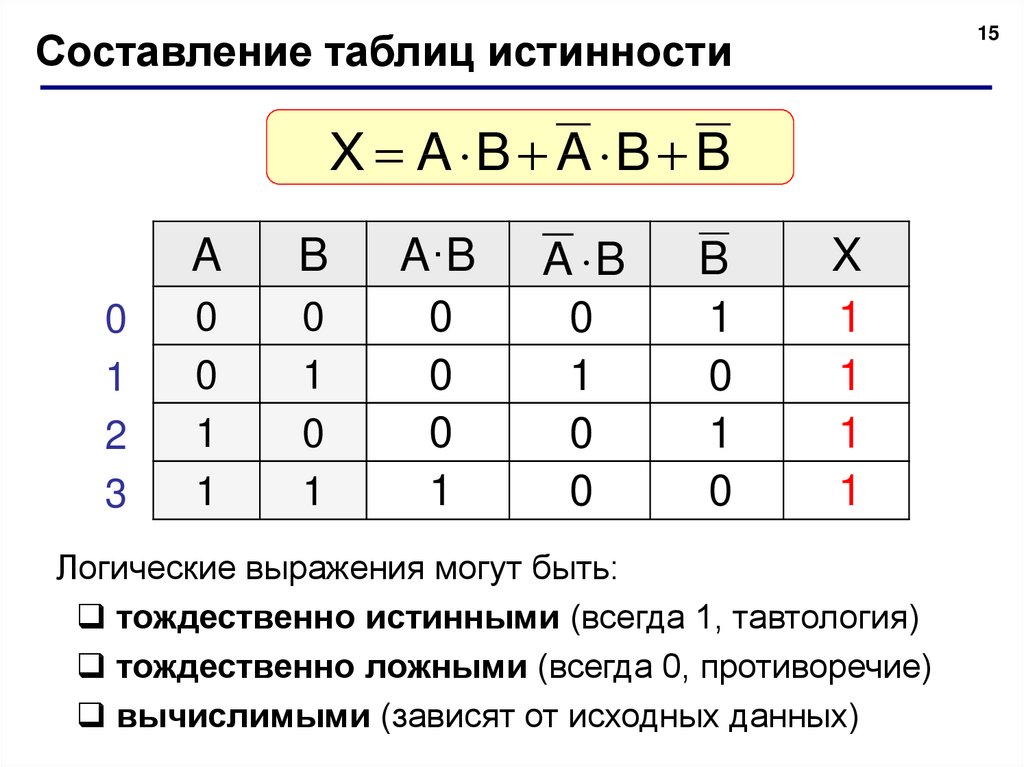
1 * 2-------------- 3п д | (р ∧ д) 4-------------- 5Т Т | Т Т Т 6Т Ф | Т Ф Ф 7Ф Т | Ф Ф Т 8Ф Ф | Ф Ф Ф 9--------------- 10Контингент 11- Т : [Т Т] 12- Ф : [Ф Ф] [Ф Т] [Т Ф]
1 * 2------------------- 3п д | р ∧ (д ∧ р) 4 -------------------- 5Т Т | Т Т Т Т Т 6Т Ф | Т Ф Ф Ф Т 7Ф Т | Ф Ф Т Ф Ф 8Ф Ф | Ф Ф Ф Ф Ф 9 -------------------- 10Контингент 11- Т : [Т Т] 12- Ф : [Ф Ф] [Ф Т] [Т Ф]
Нахождение эквивалентных логических операторов меньшего количества вентилей (состояний) важно для несколько полей. В компьютере науки, меньшее количество состояний может привести к меньшему объему памяти, меньшему количеству операций и программ меньшего размера. В компьютерная инженерия, меньше вентилей означает меньше цепей, меньше энергии и меньше тепла.
С технической точки зрения, биимпликация — это еще один способ выразить качество. Однако мы еще не ввели оператор «равно».
p = q ↔ (p → q) ∧ (q → p)
2.
4.2. Двойной негатив В логике и во многих логических приложениях двойное отрицание
эффективно компенсируют друг друга. Это не единственная возможная интерпретация ¬ ¬ p , но именно он реализован в Logika. Мы можем обсудить другие
интерпретации в разделе о логике высказываний.
¬ ¬ р ↔ р
2.4.3. Эксклюзивное ИЛИ (XOR)
Как обсуждалось ранее, в английском языке «или» используется в исключительном смысле. (p XOR q) можно выразить несколькими способами:
(p ∧ ¬ q) ∨ (¬p ∧ q) (p ∨ q) ∧ ¬ (p ∧ q)
В классе мы не примем использование оператора XOR, вы должны выразить все формулы в терминах И, ИЛИ, НЕ и ПОДРАЗУМЕВАЮТ.
2.4.4. Закон Де Моргана
Закон Де Моргана — это утверждение о взаимосвязи между И
и НЕ-ИЛИ (НИ) ( ¬ ( p ∨ q ) ). Конкретно:
p ∧ q ↔ ¬ (¬ p ∨ ¬ q)
p ∨ q ↔ ¬ (¬ p ∧ ¬ q)
Это имеет важное значение для вычислительной техники, позволяя
все логические конструкции должны быть выражены только двумя типами основных
ворота, И-НЕ и НЕ; значительно экономит интегрированное производство чипов.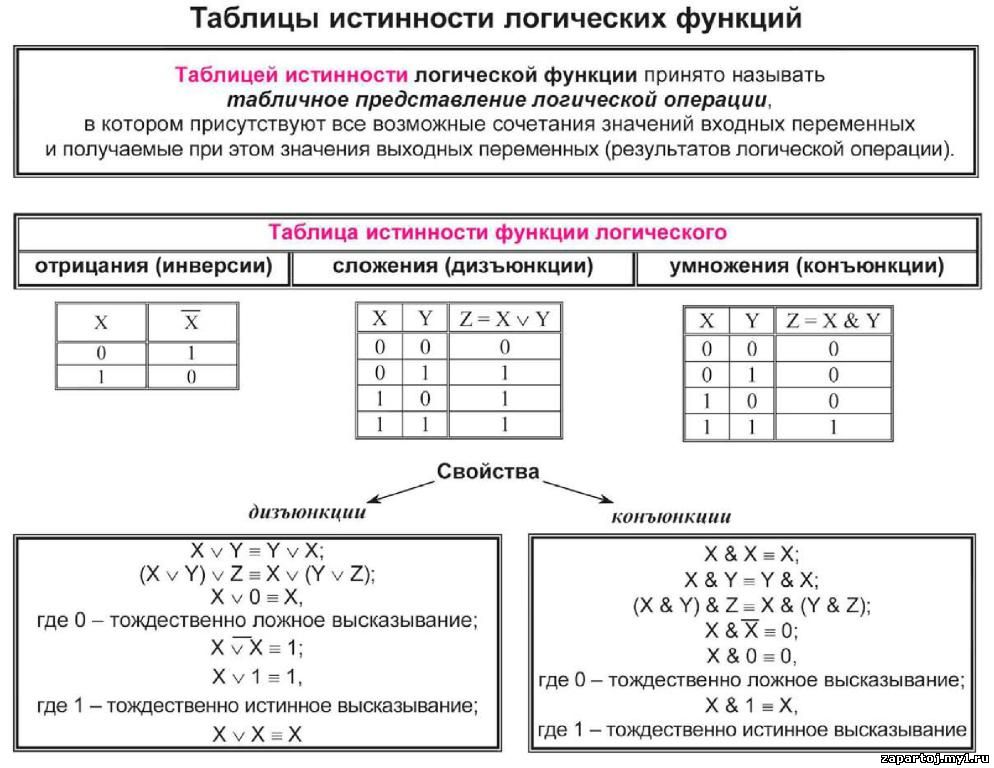
Август Де Морган также ввел термин «Математическая индукция» и дал строгую подход к его доказательству. Математическая индукция лежит в основе многих доказательства информатики в области алгоритмов, языков и вычислительная сложность.
2.4.5. Эквивалентности следствий
Наконец, импликация может быть выражена как отрицание и ИЛИ; или как его контрпозитивное утверждение.
(p → q) ↔ ¬ p ∨ q
(p → q) ↔ (¬ q → ¬ p) противоположное утверждение
Обратное следствие может быть истинным, а может и не быть
(р → к) ??? (q → p) обратное (НЕ ОБЯЗАТЕЛЬНО ЭКВИВАЛЕНТНОСТЬ)
Примечание
Хотя большая часть формул, представленных в этом разделе, верна
эквивалентности, ЕСЛИ вас просят доказать, что они равны по таблице истинности,
ожидается, что вы составите таблицу истинности для каждой стороны ↔ и покажите, что их значения совпадают для каждого присваивания истинности.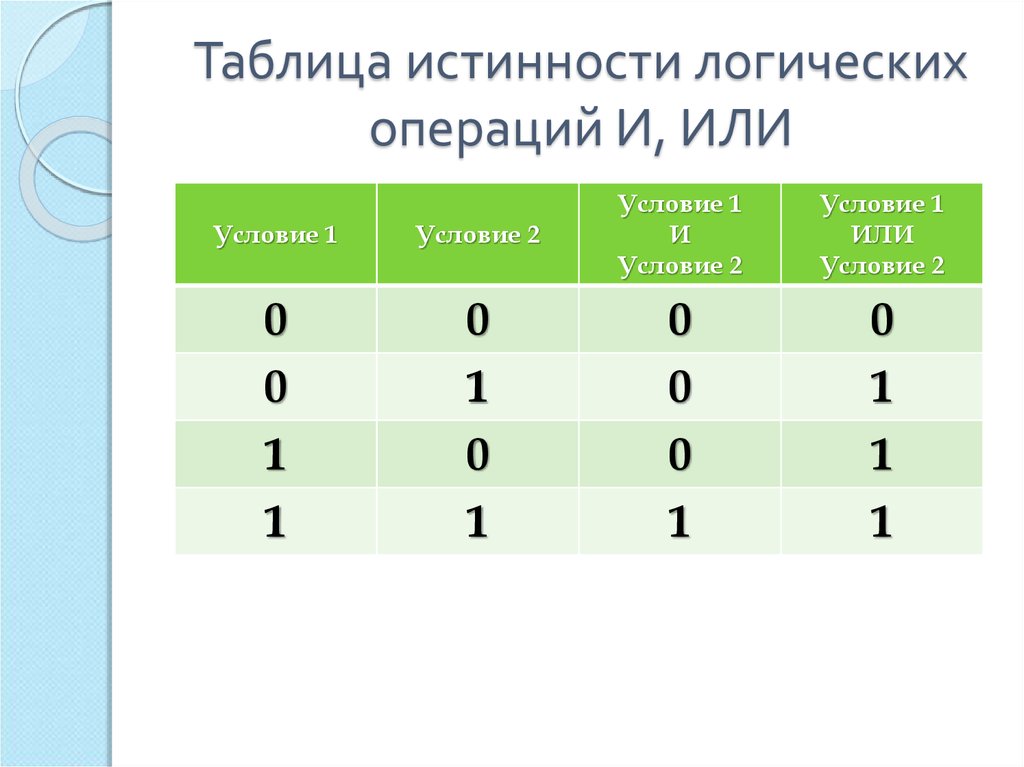
2.5. Почему его называют оператором «Верхнего уровня»
Вернемся к 2-разрядному сумматору и рассмотрим схему только для Q1. В цепи, можно сказать, что знания текут по проводам, где они трансформируются воротами, и новое знание распространяется на следующую точку.
В аннотированной выше схеме видно, какие знания (факты и выведенные факты) поток в каждом сегменте провода. Обычная математика, следовательно, информатика метод заключается в том, чтобы представить этот тип потока знаний в специализированном виде граф называется деревом. Дерево представлено набором узлов и ребер, один узел выбирается в качестве «корня», и все узлы имеют уникальный путь (набор ребер), ведущих к корневому узлу. По соглашению дерево рисуется перевернутым, с корнем вверху и листьями, свисающими снизу.
В информатике корень выбирается как узел, который обеспечивает
«окончательный ответ» на проблему. Как видите, ребра несут факты и узлы.
являются операторами, выводящими новые факты.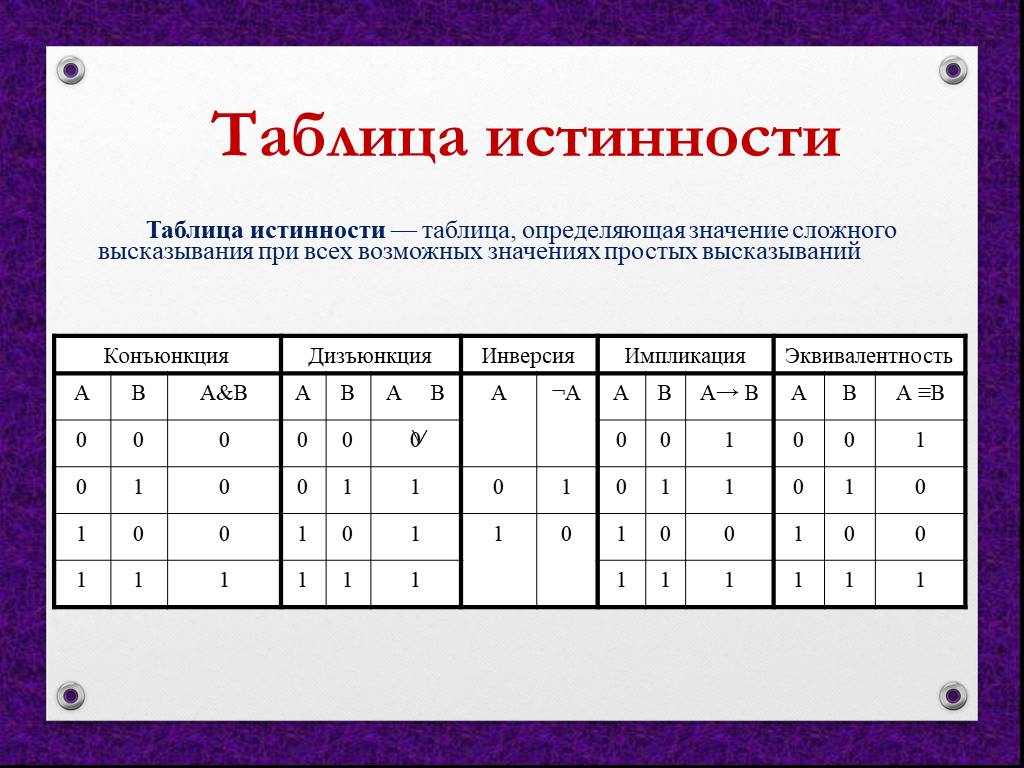
Древовидное представление компьютерной программы является фундаментальной абстракцией для специалист в области информатики. Современные компиляторы и интерпретаторы принимают программу, написанную на языке программирования высокого уровня и преобразовать его в абстрактное синтаксическое дерево (АСТ), что затем преобразованы в машинный код. Для языков функциональной парадигмы (C# и Java находятся в императивной и/или объектной парадигмах), существует сильная корреляция между структурой программы высокого уровня и структурой AST.
Когда мы сравниваем дерево с логическим оператором, мы видим самый низкий приоритет оператор — корень дерева; отсюда и термин «оператор верхнего уровня».
* (¬(A1 ∧ B1)) ∧ (A1 ∧ B1)
2.6. Знания путешествуют по проводам цепи
До сих пор мы делали вид, что уровни низкого и высокого напряжения проходят по проводке. цепи. Но на самом деле это знание путешествует по кругу. Это понятно по некоторым картинкам. Вот схема:
и вот его кодировка в уравнениях:
Р = Р ∧ Q S = R ∨ Q Т = ¬ S
Перерисуем схему по вертикали и положим рядом с заданием уравнения:
Каждому проводу в цепи присваивается имя.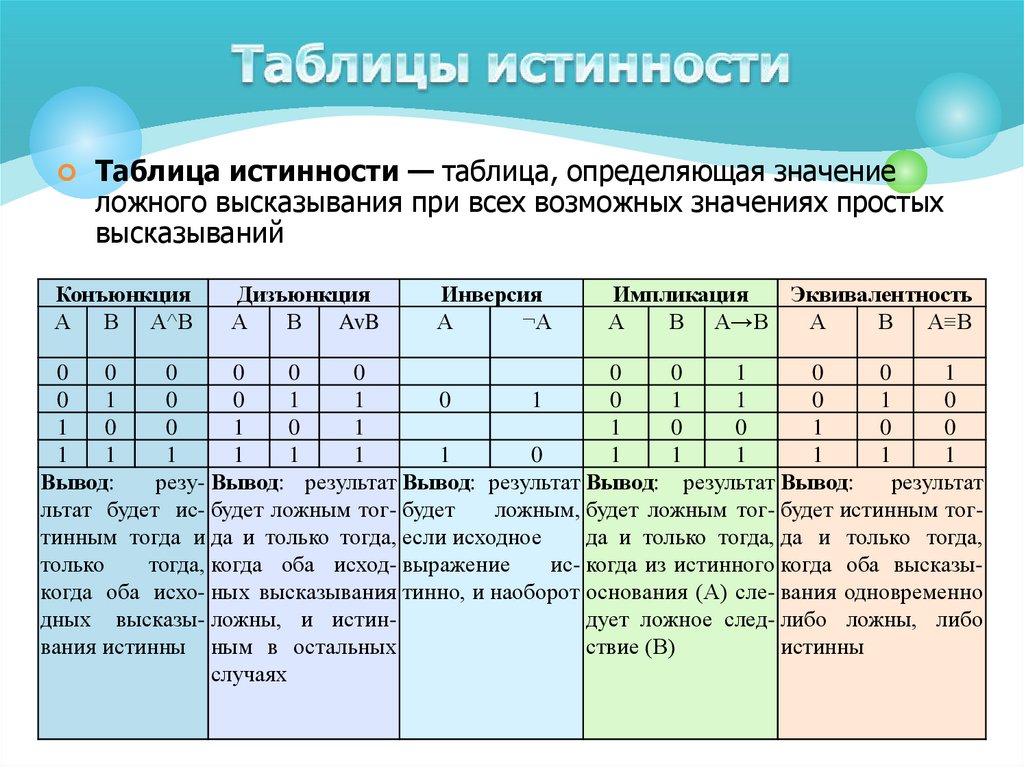
Это всего лишь имен переменных .
Действительно, первых (электронных) компьютерных программ в 1940-х годах были
описания электрических схем , как этот.
Современный компьютер с хранимой в памяти программой, разработанный Джоном фон Нейманом в 1950-х гг.
использовали регистры хранения для хранения значений имен переменных и использовали
процессор для вычисления значений уравнений.
Таким образом, процессор плюс регистры могут имитировать схему, и все компьютерные программы являются просто описаниями цепей, в которых информация
течет по проводам (переменным) .
Это источник компьютерного программирования, основанного на переменных и присваиваниях.
Теперь в каждой из программных точек по , отмеченных звездочками на приведенной выше диаграмме, что
информация распространяется по проводам?
Мы могли бы использовать схему с некоторыми входами, чтобы увидеть, «что происходит».
Допустим, мы поставляем true для P и false для В :
На схеме показаны значения на проводах с маркировкой P , Q , R и S по мере их прохождения по цепи. Но это просто отслеживание значений переменных в программе присваивания
мы написали!
«Выходная переменная»/запись с именем T имеет значение true .
Так же интересно, что мы можем проанализировать программу/схему до .
полностью протестировано.
Например, скажем, что схема будет вставлена в плату, где ее Р wire всегда будет получать t в качестве входных данных, но мы не знаем, что получит Q .
Что мы можем предсказать о поведении схемы после того, как она будет встроена в плату?
Это:
На диаграмме мы видим, что R = Q указано после вентиля И.
Откуда нам это знать?
Во-первых, мы знаем, что R = P ∧ Q . Но P = true .
Мы заменяем true на P и получаем R = true ∧ Q .
Далее мы делаем анализ случаев и рассматриваем случаи Q возможное значение:
Если Q равно true , то true ∧ Q равно true ∧ true , что упрощает до true ,
то есть к значению Q . Точно так же, когда Q равно false , тогда t ∧ Q также равно false .
Следовательно, в обоих случаях верно ∧ Q равно Q .
Приведенное выше рассуждение представляет собой вывод – мы вывели из фактов P = true и R = P ∧ Q что R = Q .
Весь смысл этого курса в том, чтобы научиться делать такие выводы.
Другие вычеты в примере рассчитываются с аналогичным использованием замена, упрощение и анализ случаев.
Суть предыдущего примера в том, что мы можем вывести (предсказать) свойства схему до ее использования. Эти выводы дополняют тестирование.
Далее скажем, что мы ничего не знаем о P и Q в качестве входов.
Что можно сказать о выходе схемы?
Ну, это:
Т = ¬((P ∧ Q) ∨ Q)
констатируя очевидное!
Но, внимательно изучив таблицы истинности, мы также можем утверждать, что Т = ¬Q .
