Основы логики и логические основы компьютера

1. Основы логики и логические основы компьютера

А(0,0,1,1)
В(0,1,0,1)
И
F(0,0,0,1)
A
F= Ā
0
1
1
0
Основы логики и логические
основы компьютера
по учебнику Н.Угриновича
Информатика и информационные
технологии 10-11 класс
S(1)
ИЛИ
1
НЕ
1
0
R
ИЛИ
0
НЕ
1
Q
2007

2. Содержание

1. Формы мышления
2. Алгебра высказываний
3. Логические выражения и таблицы
истинности
4. Логические функции
5. Логические законы и правила
преобразования лог.выражений
6. Логические основы устройства
компьютера

3. 1. Формы мышления

Логика – это наука о формах и способах мышления.
Основные формы мышления:
1. Понятие
2. Высказывание
3. Умозаключение
содержание

4. 1.1. Понятие

Понятие – это форма мышления,
фиксирующая основные, существенные
признаки объекта.
Понятие
Содержание
Объем
Совокупность
существенных
признаков объекта
Совокупность
предметов, на
которую
распространяется
понятие
содержание

5.

1.2. ВысказываниеВысказывание – это форма мышления, в которой чтолибо утверждается или отрицается о свойствах реальных
предметов и отношениях между ними.
Высказывание является повествовательным предложением.
Высказывание
Истинное
Ложное
Связь понятий
правильно отражает
свойства и отношения
реальных вещей
Высказывание не
соответствует реальной
действительности
Высказывание
Простое
Составное
содержание

6. 1.3. Умозаключение

Умозаключение – это форма мышления, с
помощью которой из одного или нескольких
суждений (посылок) может быть получено новое
суждение (заключение).
Посылки – только истинные суждения.
содержание

7. 2. Алгебра высказываний

Алгебра высказываний служит для
определения истинности или ложности
составных высказываний.
Высказывания обозначаются именами
логических переменных, которые могут
принимать лишь два значения:
«истина» (1) и «ложь» (0).
В языках программирования and;
Таблица истинности
A
B
F=A&B
0
0
0
1
0
0
1
1
0
1
0
1
содержание

10. 2.2. Логическое сложение (дизъюнкция)

Объединение двух (или нескольких) высказываний в одно с помощью
союза «или».
Составное высказывание истинно только тогда, когда истинно хотя бы одно
из двух простых высказывания.
Соответствует союзу ИЛИ
Обозначение V
В языках программирования or
Таблица истинности
A
B
F=AvB
0
0
0
1
0
1
1
1
0
1
1
1
содержание

11. 2.3. Логическое отрицание (инверсия)

Присоединение частицы «не» к высказыванию.
Инверсия делает истинное высказывание ложным и, наоборот.
Соответствует союзу НЕ
Обозначение Ā
В языках программирования not
Таблица истинности
A
F= Ā
0
1
1
0
содержание

12. 3. Логические выражения и таблицы истинности

Логическое выражение – формула, в которую входят логические
переменные и знаки логических операций.
Пример:
F ( A B) & ( A B)
Для логического выражения можно построить таблицу истинности, которая
определяет его истинность или ложность при всех возможных комбинациях
исходных значений простых высказываний.
содержание

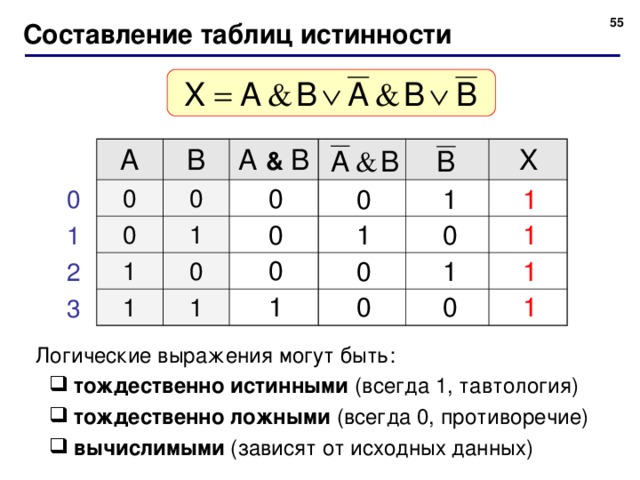
13. Построение таблицы истинности

1. Определить количество строк в таблице по формуле
2n, где n – количество логических переменных.
2. Определить количество столбцов таблицы:
количество логических переменных + количество
логических операций.
3. Построить таблицу истинности, обозначить столбцы,
внести всевозможные наборы исходных данных
логических переменных.
4. Заполнить таблицу истинности, выполняя базовые
логические операции в необходимой
последовательности.
содержание

14. Построение таблицы истинности для

F ( A B) & ( A B)
1. Количество строк таблицы 22 = 4, т.к. в формуле две переменные A и B.
2. Количество столбцов: 2 переменные + 5 логических операций = 7.
A
0
0
1
1
F (A
A BB) & ( A BF) ( A B) & ( A B)
B AvB
0
0
1 1
1
0
1
1
1 0
1
1
0
1
0 1
1
1
1
1
0 0
0
0
содержание

15.

Равносильные логические выраженияРавносильные логические выражения — это выражения, у которых последние
столбцы таблиц истинности совпадают, обозначают “=“.
Докажите равносильность выражений: A & B и A B
Таблица истинности
A & Bдля
и A B
A
0
0
1
1
B
0
1
0
1
AAvB
&B и A B
Таблица истинности для
A
0
0
1
1
B
0
1
0
1
A& B и A
A
&
A&B
и AB
A& BB ии
Проверить
Проверить
A& B и A B
Далее

16. 4. Логические функции

Любое составное высказывание можно
рассматривать как логическую функцию
F(X1, X2, …, Xn),
где X1, X2, …, Xn – простые высказывания.
Функция и аргументы могут принимать
только два различных значения:
«истина» (1) и «ложь» (0).
содержание

17. Таблицы истинности логических функций двух аргументов

Аргументы
A
B
Логические функции
F1
F2
F3
F4
F5
F6
F7
F8
F9
F10
F11
F12
F13
F14
F15
F16
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
содержание

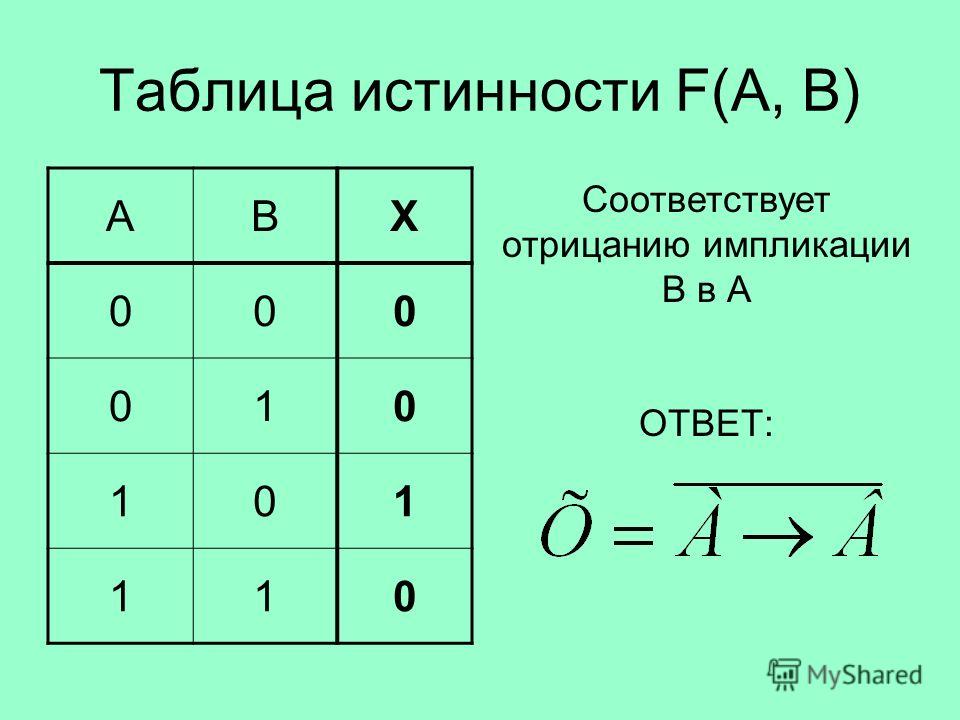
18.

Логическое следование (импликация)Импликация образуется соединением двух высказываний в одно с
помощью оборота речи «если…, то…».
Импликация ложна только тогда, когда из истинного первого
высказывания(предпосылки) следует ложный вывод (второе
высказывание).
Соответствует обороту Если…, то…
Обозначение А→В
В языках программирования if … then …
Таблица истинности
A
B
F14=A→B
0
0
1
1
0
1
0
1
1
1
0
1
содержание
Все логические функции путем логических преобразований можно свести к
трем базовым:
1. Логическому умножению
2. Логическому сложению
3. Логическому отрицанию
Методом сравнения таблиц истинности докажите: A B A B
Таблица истинности для A→B
A
0
0
1
1
B
0
1
0
1
Проверить
A→B
Таблица истинности
для
A B
A B
AA
0
0
&
A
A
BB и
B B
1
1
0
1
0
1
Проверить
Далее

20.

Логическое равенство (эквивалентность)Эквивалентность образуется соединением двух высказываний в одно с
помощью оборота речи «… тогда и только тогда, когда …».
Составное высказывание, образованное с помощью логической операции
эквивалентности истинно тогда и только тогда, когда оба высказывания
одновременно либо ложны, либо истинны.
Соответствует обороту тогда и только тогда, когда …
Обозначение А≡В, А~B
Таблица истинности
A
B
F10
0
0
1
1
0
1
0
1
1
0
0
1
содержание

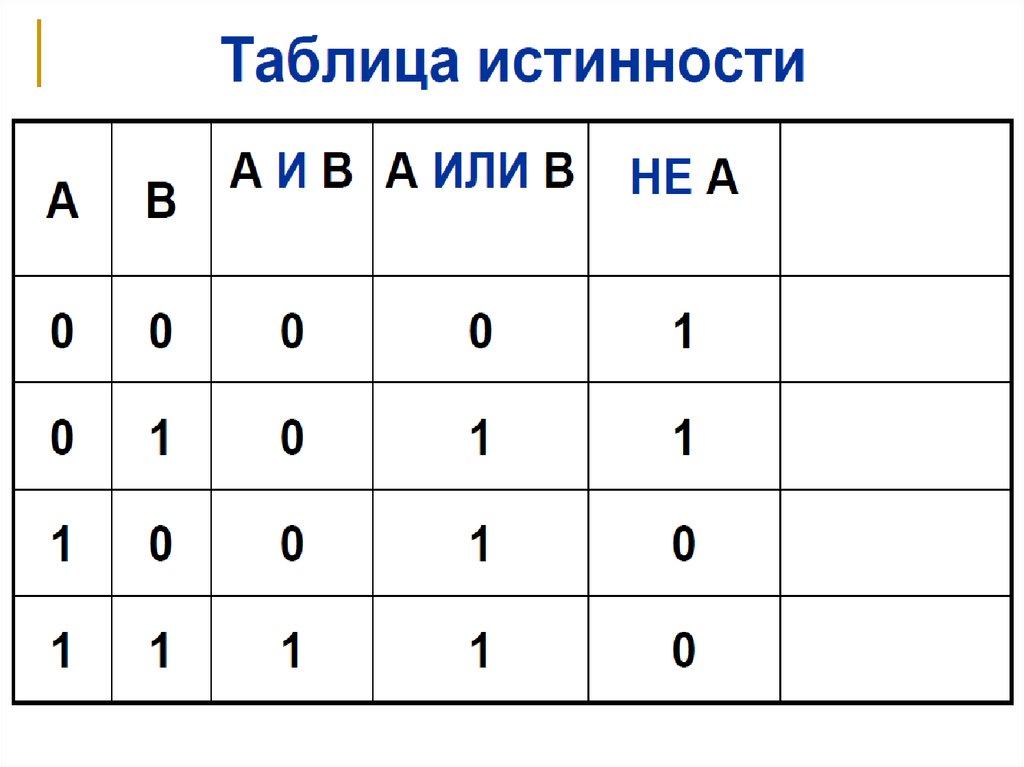
21. 5. Логические законы и правила преобразования логических выражений

Закон тождества.
Всякое высказывание тождественно самому себе.
А=А
Закон непротиворечия.
Высказывание не может быть одновременно истинным и ложным.
A A 1
Закон исключенного третьего.
Высказывание может быть либо истинным, либо ложным, третьего не дано.
A&A 0
Закон двойного отрицания.
Если дважды отрицать некоторое высказывание, то получим исходное
высказывание.
A A
содержание
Логические законы и правила
преобразования логических выражений
Законы де Моргана.
A B A&B
A&B A B
Закон коммутативности.
A&B=B&A
AvB=BvA
Закон ассоциативности.
(A & B) & C = A & (B & C)
(A v B) v C = A v (B v C)
Закон дистрибутивности.
(A & B) v (A & C) = A & (B v C)
(A v B) & (A v C) = A v (B & C)
содержание

23. Решение логических задач

1.
2.
3.
4.
5.
внимательно изучите условие;
выделить простые высказывания и обозначить их
латинскими буквами;
записать условие задачи на языке алгебры логики;
составить конечную формулу, для этого
объединить логическим умножением формулы
каждого утверждения, приравнять произведение
единице;
упростить формулу, проанализировать результат
или составить таблицу истинности, найти по
таблице значения переменных, для которых
результат равен 1, проанализировать результат.
содержание

24. 6. Логические основы устройства компьютера

Базовые логические элементы
Логический элемент
«И»
Логический элемент
«ИЛИ»
Логический элемент
«НЕ»
А(0,0,1,1)
В(0,1,0,1)
И
А(0,0,1,1)
ИЛИ
F(0,0,0,1)
F(0,1,1,1)
В(0,1,0,1)
А(0,1)
НЕ
F(1,0)
содержание

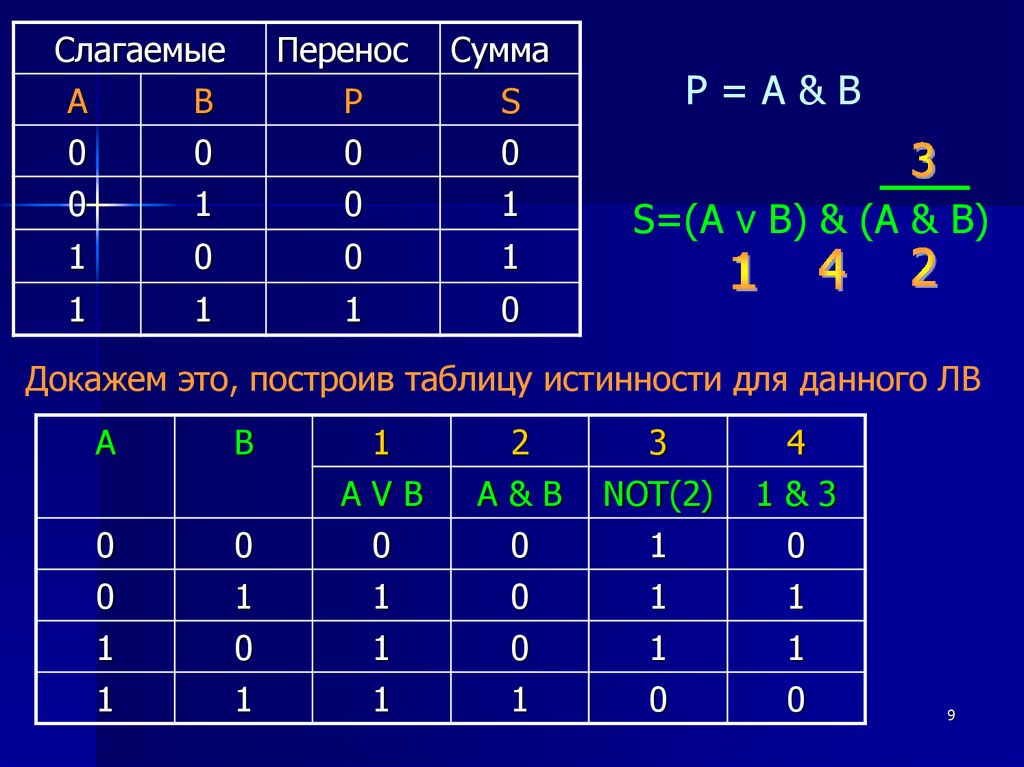
25. Логические основы устройства компьютера

Сумматор двоичных чисел
Полусумматор.
Слагаемые
A, B – слагаемые
P – перенос
S – сумма
Перенос
Сумма
A
B
P
S
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
P=A&B
S (A B) & (A & B)
содержание
Логические основы устройства
компьютера
Сумматор двоичных чисел
Полусумматор.
Таблица истинности логической функции
A
0
0
1
1
B
0
1
0
1
F (A B) & (A & B)
AvB
F) (A B) & (A & B)
F (AA&B
B) & (A & B
0
0
1
0
1
0
1
1
1
0
1
1
1
1
0
0
A
B
A&B
И
F (A B) & (A & B)
A&B
НЕ
ИЛИ
F (A B) & (A & B)
И
AvB
содержание
Логические основы устройства
компьютера
Имеет
Сумматор двоичных чисел
Полный одноразрядный сумматор
три входа: A, B – слагаемые, P0 – перенос из младшего разряда;
два выхода: S – сумму, P – перенос.
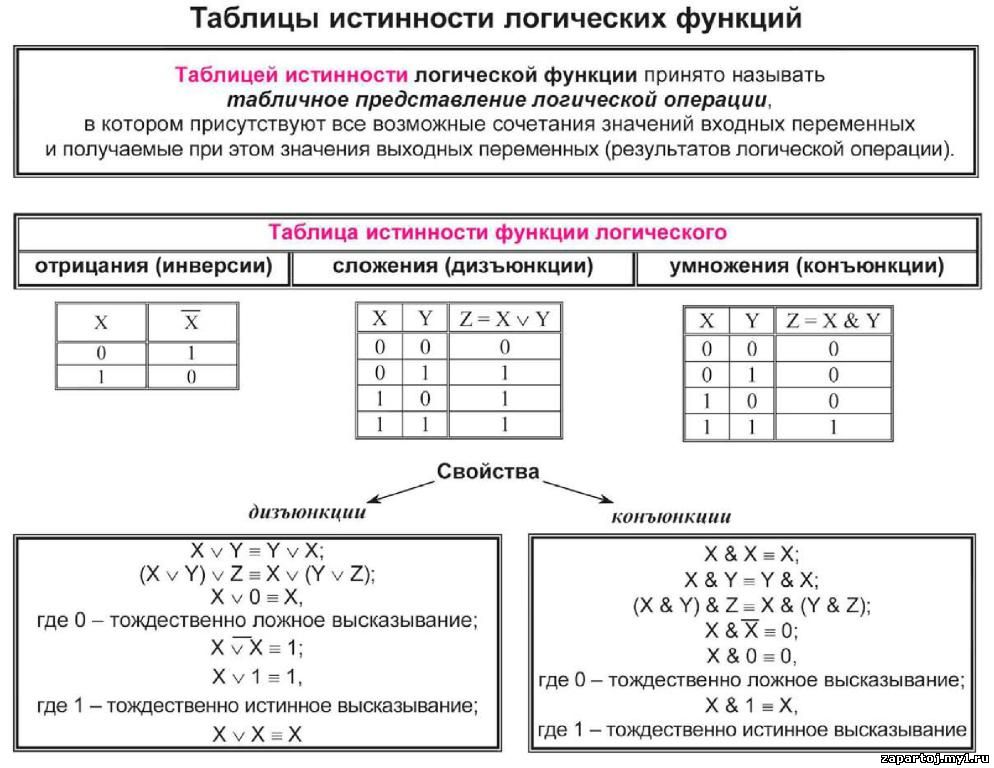
Таблица сложения
Слагаемые
Перенос из
младшего разряда
Перенос
Сумма
A
B
P0
P
S
0
0
0
0
0
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
1
0
1
0
1
1
1
0
1
0
1
1
0
1
1
1
1
1
P=(A&B)v(A&P0)v(B&P0)
S=(AvBvP0)&P0v(A&B&P0)
содержание
Логические основы устройства
компьютера
Триггер
Триггер позволяет запоминать, хранить, считывать информацию.
Триггер хранит 1 бит информации.
S(1)
1
1
ИЛИ
0
ИЛИ
R
НЕ
0
НЕ
1
Q
содержание

Таблицы истинности

Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).

Логические основы компьютера

В ЭВМ используются различные устройства, работу которых прекрасно описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры.

Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных.

Переключательные схемы

В ЭВМ применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае – ток проходит, во втором – нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах.

Вентили, триггеры и сумматоры

Вентиль представляет собой логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.

Триггеры и сумматоры – это относительно сложные устройства, состоящие из более простых элементов – вентилей.

Триггер способен хранить один двоичный разряд, за счет того, что может находиться в двух устойчивых состояниях. В основном триггеры используется в регистрах процессора.

Сумматоры широко используются в арифметико-логических устройствах (АЛУ) процессора и выполняют суммирование двоичных разрядов.

Изображения, использованные в статье

Таблицы истинности для конъюнкции, дизъюнкции и отрицания

Законы алгебры логики

Раздел: 

Логические основы компьютера

Номер темы: 

2

Для логических величин обычно используются три операции:

1. Конъюнкция– логическое умножение (И) –and, &, ∧.

2. Дизъюнкция

   – логическое сложение (ИЛИ) –or, |, v.

3. Логическое отрицание (НЕ) – not, ¬.

Логические выражения можно преобразовывать в соответствии с законами алгебры логики:

1. Законы рефлексивности a ∨ a = a a ∧ a = a

2. Законы коммутативностиa∨b = b∨a a∧b = b∧a

3. Законы ассоциативности(a∧b)∧c = a∧(b∧c) (a∨b)∨c = a∨(b∨c)

4. Законы дистрибутивностиa∧(b∨c) = a∧b∨a∧c a∨b∧c = (a∨b)∧(a∨c)

5. Закон отрицания отрицания

   ¬ (¬ a) = a

6. Законы де Моргана ¬ (a ∧ b) = ¬ a ∨ ¬ b ¬ (a ∨ b) = ¬ a ∧ ¬ b

7. Законы поглощения a ∨ a ∧ b = a a ∧ (a ∨ b) = a

Логические элементы. Вентили

Раздел: 

Логические основы компьютера

Номер темы: 

3

В основе построения компьютеров, а точнее аппаратного обеспечения, лежат так называемые вентили. Они представляют собой достаточно простые элементы, которые можно комбинировать между собой, создавая тем самым различные схемы. Одни схемы подходят для осуществления

арифметических операций, а на основе других строят различнуюпамятьЭВМ.

Простейший вентиль представляет собой транзисторный инвертор, который преобразует низкое напряжение в высокое или наоборот (высокое в низкое). Это можно представить как преобразование логического нуля в логическую единицу или наоборот. Т.е. получаем вентиль НЕ.

Соединив пару транзисторов различным способом, получают вентили ИЛИ-НЕиИ-НЕ. Эти вентили принимают уже не один, а два и более входных сигнала. Выходной сигнал всегда один и зависит (выдает высокое или низкое напряжение) от входных сигналов. В случае вентиля ИЛИ-НЕ получить высокое напряжение (логическую единицу) можно только при условии низкого напряжении на всех входах. В случае вентиля И-НЕ все наоборот: логическая единица получается, если все входные сигналы будут нулевыми.

Как видно, это обратно таким привычным логическим операциям как И и ИЛИ. Однако обычно используются вентили И-НЕ и ИЛИ-НЕ, т.к. их реализация проще: И-НЕ и ИЛИ-НЕ реализуются двумя транзисторами, тогда как логические И и ИЛИ тремя.

Выходной сигнал вентиля можно выражать как функцию от входных.

Транзистору требуется очень мало времени для переключения из одного состояния в другое (время переключения оценивается в наносекундах). И в этом одно из существенных преимуществ схем, построенных на их основе.

Изображения, использованные в статье

Схемы вентилей

Формальная логика — математические основы информатики

Логика — это систематический способ мышления. Мы, люди, постоянно получаем новую информацию, комбинируем ее с уже известной и строим новые идеи. Процесс объединения существующей информации для изучения новых вещей называется дедукция .

Самая удивительная идея в истории не помогает, если ее никто не понимает или не верит в нее.

Формальная логика дает нам согласованную основу для обмена идеями. Таким образом, мы можем записать наши рассуждения так, как это сделает любой, кто знаком с 9.0003 Формальная логика может понять.

Булева алгебра

Хорошо говорить о логике абстрактно, но нам нужна система для формального описания. Это позволяет нам общаться с другими и проверять наши рассуждения.

Утверждение — это предложение или выражение, которое равно True или False . Операторы будут записаны либо как отдельные переменные, либо как выражения, включающие переменные.

Мы присваиваем значение каждой из наших переменных.

Эти переменные могут иметь значение True или False . Наша

информация в начале задачи — это то, какие переменные мы знаем как True или False .

Мы можем объединять переменные с помощью операторов. Если бы хотел сказать

Идет дождь и облачно.

Мы можем использовать оператор И (\(\клин\)) для объединения двух переменных.

\( \начать{выравнивать} А\клин Б \end{выравнивание} \)

Три наиболее распространенных оператора используются в переходных английских словах.

• И использует символ \(\клин\) и формально называется соединением .

• ИЛИ использует символ \(\vee\) и формально называется дизъюнкцией

  .

• НЕ использует символ \(\neg\) и формально называется отрицанием .

У каждого оператора есть официальное имя. Это сделано для того, чтобы нам было легче сообщать о них. понятнее сказать

Три основных оператора булевой алгебры — это конъюнкция, дизъюнкция и отрицание.

вместо

Три основных оператора булевой алгебры — это и, или и не.

Оба предложения неверны, но второе гораздо более запутанно.

Соединение

Соединение позволяет нам объединить два выражения «и». Это означает, что мы хотим передать, что

оба значения должны быть истинными.

Мы описываем операторов, используя Таблицы истинности . Таблица истинности показывает входы функции и ее выходы. Поскольку каждая переменная может быть только True или False , таблица истинности может охватывать все возможные входные и выходные данные.

\(П\)	\(Q\)	\(P \клин Q\)
Т	Т	Т
Т	Ф	Ф
Ф	Т	Ф
Ф	Ф	Ф

В этой таблице показаны все возможные входы и выходы соединения. Мы можем применить его к конкретному случаю, выбрав строку из таблицы.

Нам нужна информация для вычисления выражения.

Утверждение \(A \клин B\) является сокращением от «Идет дождь и облачно».

Мы можем посмотреть каждую ситуацию в таблице истинности.

\(А\)	\(Б\)	\(А\клин Б\)	Значение
Т	Т	Т	Дождь и облачность одновременно.
Т	Ф	Ф	Дождь идет, но безоблачно.
Ф	Т	Ф	Облачно, но дождя нет.
Ф	Ф	Ф	Нет облачности и дождя.

Утверждение истинно только тогда, когда описываемая им ситуация действительно происходит. Соединение является только True , когда

оба входа равны True .

Дизъюнкция

Дизъюнкция позволяет нам «ИЛИ» два выражения вместе. Это означает, что мы хотим передать, что хотя бы одно из значений должно быть истинным.

Таблица истинности дизъюнкции приведена ниже.

\(П\)	\(Q\)	\(P \veeQ\)
Т	Т	Т
Т	Ф	Т
Ф	Т	Т
Ф	Ф	Ф

Нам нужна информация для вычисления выражения.

Утверждение \(A \vee B\) является сокращением от «Идет дождь или облачно».

Мы можем посмотреть каждую ситуацию в таблице истинности.

\(А\)	\(Б\)	\(А \вид Б\)	Значение
Т	Т	Т	Дождь и облачность одновременно.
Т	Ф	Т	Дождь идет, но безоблачно.
Ф	Т	Т	Облачно, но дождя нет.
Ф	Ф	Ф	Нет облачности и дождя.

Дизъюнкция равна True , если хотя бы один из двух входов равен True .

Отрицание

Отрицание позволяет нам «не» выражение. Это означает, что мы хотим передать, что противоположное значение должно быть истинным.

Таблица истинности для отрицания приведена ниже.

\(П\)	\(\отриц П\)
Т	Ф
Ф	Т

Нам нужна информация для вычисления выражения.

Утверждение \(\neg A\) является сокращением от «Дождя нет». Мы хотим, чтобы происходило противоположное дождю.

Отрицание равно True , когда его ввод равен False .

Примечание

Эти три оператора настолько распространены, что для них используется много разных символов в разных контекстах.

• Соединение: \(A \клин B\), \(A \шапка B\), \(A * B\), \(AB\), \(A \& B\), \(A \&\& Б\)

• Дизъюнкция: \(A \vee B\), \(A \cup B\), \(A + B\), \(A | B\), \(A || B\)

• Отрицание: \(\neg A\), \(\sim A\), \(-A\), \(\bar{A}\), \(!A\)

Таблицы истинности

Имея выражение, состоящее из переменных и операторов, мы можем всегда нарисовать таблицу истинности. Это покажет все возможные результаты. Затем мы можем выяснить, какая строка подходит для нашей ситуации, и определить результаты.

Таблица истинности для \(A \vee (\neg B \wedge C)\) приведена ниже. Частичные столбцы показаны для пояснения того, как был достигнут результат.

\(А\)	\(Б\)	\(С\)	\(\нег Б\)	\((\neg B \клин C)\)	\(A \vee (\neg B \клин C)\)
Т	Т	Т	Ф	Ф	Т
Т	Т	Ф	Ф	Ф	Т
Т	Ф	Т	Т	Т	Т
Т	Ф	Ф	Т	Ф	Т
Ф	Т	Т	Ф	Ф	Ф
Ф	Т	Ф	Ф	Ф	Ф
Ф	Ф	Т	Т	Т	Т
Ф	Ф	Ф	Т	Ф	Ф

Это выражение равно False в трех случаях и True в пяти. Это учитывает все возможные входные и выходные данные. Эта таблица истинности может действовать как доказательство . Это исчерпывающий список всех возможных входов и выходов. 9{n}\) бит. Если бы у нас была проблема с 45 переменными, это заняло бы 1 618 481 116 086 272 бита. Это 184 терабайта.

Хотя таблицы истинности всегда работают, они очень редко практичны.

Таблица истинности должна иметь одно из следующих трех свойств.

• Контингент : результат таблицы истинности зависит от значений входных переменных.

• Тавтология : результат всегда True независимо от входных данных.

• Противоречие : результат всегда False независимо от входных данных.

Условные операторы

Есть два дополнительных оператора, которые очень важны при написании доказательств. Первый — условный оператор . Это используется для создания связи между двумя переменными.

Следующий код Python содержит оператор if .

, если х > 10:
    у = 7
 

Этот код говорит нам, что когда x > 10 истинно, мы знаем, что y будет установлено кодом на 7. Мы можем присвоить их логическим переменным.

Тогда мы бы сказали, что этот код выполняется \(A \подразумевает B\). Символ \(\implies\) используется для условных выражений. Его также называют символом , означающим .

Таблица истинности условного оператора приведена ниже.

\(П\)	\(Q\)	\(P \подразумевает Q\)
Т	Т	Т
Т	Ф	Ф
Ф	Т	Т
Ф	Ф	Т

Таблица истинности содержит только Ложь в одной строке, строке \(T \подразумевает F\).

Думайте об условном выражении как о своего рода контракте. Это False , когда контракт нарушен . Это True , когда контракт не нарушен.

Начнем с реальной ситуации.

Если пробег вашего автомобиля менее 5000 миль, то весь ремонт оплачивает дилерский центр.

Мы можем определить переменные.

Оператор \(M \подразумевает W\).

Первая строка таблицы истинности — когда \(M=T\) и \(W=T\). В этой ситуации пробег автомобиля составляет менее 5000 миль. На машине ломается трансмиссия, и вы везете ее в автосалон. Дилер ремонтирует бесплатно, потому что на гарантии.

Вторая строка таблицы истинности — когда \(M=T\) и \(W=F\). В этой ситуации пробег автомобиля составляет менее 5000 миль. На машине ломается трансмиссия, и вы везете ее в автосалон. Дилер отказался установить его и вышвырнул вас. Дилер нарушил гарантийный договор, который они с вами заключили. Условное заявление является Ложным , потому что гарантия не действовала, как было согласовано. Вы можете подать в суд на дилера за нарушение контакта.

Третья строка таблицы истинности — когда \(M=F\) и \(W=T\). В этой ситуации пробег автомобиля составляет более 5000 миль. На машине ломается трансмиссия, и вы везете ее в автосалон. Дилерский центр сообщает вам, что у них был отзыв по этой части, и в любом случае соглашается починить машину бесплатно. Несмотря на то, что гарантия не действовала, дилерский центр все же решил оплатить весь ремонт. Тебе повезло, но никому разорвали их контракты.

Последняя строка таблицы истинности — когда \(M=F\) и \(W=F\). В этой ситуации пробег автомобиля составляет более 5000 миль. На машине ломается трансмиссия, и вы везете ее в автосалон. В дилерском центре говорят, что нужно платить за ремонт. Это разумно, ваша машина из гарантии. Вы должны заплатить за ремонт. Никто ничего плохого не делал, машина уже не на гарантии.

Биусловные операторы

Бикондициональные операторы используется, когда мы хотим сказать, что два значения одинаковы. Это логичный способ сказать «равно» или «эквивалентно». Английский эквивалент биусловного означает «если и только если».

Например,

X четно тогда и только тогда, когда \(X \mod 2 = 0\)

Эти два утверждения на самом деле одинаковы. Если \(X\) четно, то оно, очевидно, не имеет остатка при делении на два. Точно так же, если мы делим число на два и оно не имеет остатка, то оно должно быть четным. Они абсолютно одинаковы.

Таблица истинности для биусловного равна

\(P\)	\(Q\)	\(P \iff Q\)
Т	Т	Т
Т	Ф	Ф
Ф	Т	Ф
Ф	Ф	Т

Биусловное равно True , когда оба входа одинаковы. Это логическая версия эквивалентности.

Мы можем использовать таблицы истинности, чтобы доказать эквивалентность выражений. Если они есть, мы можем использовать их взаимозаменяемо.

Альтернативное определение условного подтверждается таблицей истинности.

\(А\)	\(Б\)	\(A \подразумевается B\)	\(\neg A \vee B\)	\((A \подразумевает B) \iff (\neg A \vee B)\)
Т	Т	Т	Т	Т
Т	Ф	Ф	Ф	Т
Ф	Т	Т	Т	Т
Ф	Ф	Т	Т	Т

Это выражение является тавтологией ! Это верно независимо от значений \(A\) и \(B\). Эти два выражения всегда эквивалентны.

Мы можем показать другую тавтологию , которая определяет биусловное в терминах двух условных предложений.

\(А\)	\(Б\)	\((A \подразумевается B) \клин (B \подразумевается A)\)	\(А \если только Б\)	\((A \подразумевает B) \клин (B \подразумевает A)) \iff (A \iff B)\)
Т	Т	Т	Т	Т
Т	Ф	Ф	Ф	Т
Ф	Т	Ф	Ф	Т
Ф	Ф	Т	Т	Т

Алгебра логических выражений

Мы можем использовать таблицы истинности для создания правил, а затем использовать правила для рассуждения о выражениях.

С помощью таблицы истинности мы показали следующие формулы. Символы равенства \(=\) используются, чтобы указать, что они доказываются одинаковыми по таблице истинности.

\( \начать{выравнивать} (P \ подразумевает Q) =& (\neg P \vee Q) & \text{Правило 1}\\ (P \iff Q) =& (P \подразумевает Q) \wedge (Q \подразумевает P) & \text{Правило 2} \end{выравнивание} \)

Мы можем использовать их для упрощения выражений

\( \начать{выравнивать} (P \iff Q) =& (P \предполагает Q) \клин (Q \подразумевает P) &\text{By R1} \\ =& (\neg P \vee Q) \wedge (Q \подразумевает P) &\text{By R2} \\ =& (\neg P \vee Q) \клин (\neg Q \vee P) &\text{By R2} \end{выравнивание} \)

Теперь мы можем указать

\( \начать{выравнивать} (P \iff Q) =& (\neg P \vee Q) \wedge (\neg Q \vee P) \end{выравнивание} \)

Это утверждение доказывается алгебраическими правилами.

Законы ДеМоргана

Законы ДеМоргана говорят нам, как распределить отрицание в конъюнкции или дизъюнкции. Они доказываются приведенной ниже таблицей истинности.

\( \начать{выравнивать} \neg ( P \vee Q) =& (\neg P) \wedge (\neg Q) & \text{DeMorgan 1} \\ \neg (P \wedge Q) =& (\neg P) \vee (\neg Q) & \text{ДеМорган 2} \end{выравнивание} \)

\(П\)	\(Q\)	\(\neg ( P \vee Q)\)	\((\neg P) \клин (\neg Q)\)	ДеМорган 1
Т	Т	Ф	Ф	Т
Т	Ф	Ф	Ф	Т
Ф	Т	Ф	Ф	Т
Ф	Ф	Т	Т	Т

\(П\)	\(Q\)	\(\neg ( P \клин Q)\)	\((\neg P) \vee (\neg Q)\)	ДеМорган 2
Т	Т	Ф	Ф	Т
Т	Ф	Т	Т	Т
Ф	Т	Т	Т	Т
Ф	Ф	Т	Т	Т

Логические основы киберфизических систем

Содержание Обзор Мультидинамические системы Избранные публикации

Обзор

Мое исследование разрабатывает логические основы для киберфизических систем (CPS), т. е. систем, которые сочетают в себе кибераспекты, такие как связь и управление компьютером, с физическими аспектами, такими как перемещение в пространстве. Приложений CPS предостаточно. Однако обеспечение их правильного функционирования является серьезной проблемой. Ученым и инженерам нужны аналитические инструменты, чтобы понять и предсказать поведение своих систем. Это ключ к разработке умного и надежного управления. Предоставляя такие аналитические основы, это исследование решает интеллектуальную грандиозную задачу, имеющую существенное научное, экономическое, социальное и образовательное влияние, возникающее благодаря преимуществам улучшенного анализа и дизайна CPS . Чтобы укротить их сложность, мы изучаем СУЗ как мультидинамические системы , т. е. с точки зрения элементарных динамических аспектов их частей.

Миссия или слайдов или Учебник или Книга или Курс или Инструмент

	Гибридные системы
Гибридные игры		Сточ. Гиб. Сис.

Отрасли с многомиллиардным оборотом тратят 50% стоимости разработки на проектирование и тестирование управляющего программного обеспечения. Это больше не может поддерживаться. Основы информатики произвели революцию в нашем обществе. Нам нужны еще более прочные основы, когда программное обеспечение проникает в наш физический мир.

Мультидинамические системы являются объединяющим принципом обучения и позволяют учащимся сосредоточиться на одном динамическом аспекте за раз, не упуская общей картины. Они преодолевают разрыв между информатикой и инженерией, который продолжает вызывать непримиримые разногласия между командами разработчиков. Этот проект разрабатывает межведомственные курсы для выпускников и студентов по логическим основам CPS в качестве ярких примеров интеграции STEM. Долгосрочные цели включают работу с K-12, которая вдохновляет молодежь на научную карьеру с ранним знакомством с математической красотой и интересными социальными проблемами. Основы CPS превосходно демонстрируют первостепенную важность дискретной и непрерывной математики, даже не как отдельных дисциплин, а хорошо интегрированных.

Мультидинамические системы

В этом исследовании принимается точка зрения, которую мы называем мультидинамическими системами [6,7,16], т. е. принцип понимания сложных систем как комбинации нескольких элементарных динамических аспектов. Этот подход помогает нам укротить сложность сложных систем, понимая, что их сложность просто возникает из-за объединения множества простых динамических аспектов друг с другом. Сама система в целом так же сложна, как и все приложение. Но поскольку дифференциальная динамическая логика и доказательства являются композиционными, мы можем использовать тот факт, что отдельные части системы проще, чем целое, и мы можем доказать свойства правильности всей системы путем сведения к более простым доказательствам ее частей. Этот подход демонстрирует, что целое может быть больше, чем сумма всех частей. Вся система сложна, но мы все же можем укротить ее сложность путем анализа ее более простых частей. Результаты полноты являются теоретическим обоснованием того, почему этот принцип мультидинамических систем работает. Мультидинамические системы — это динамические системы, которые могут сочетать дискретную динамику, непрерывную динамику, состязательную динамику, недетерминированную динамику и стохастическую динамику для моделирования киберфизических систем. Динамическая логика для мультидинамических систем охватывают основы и фундаментальные принципы рассуждений для этих мультидинамических систем.

Руководство или слайдов или Введение или Забронировать или Гибрид или Гибридные игры или Dist.Hyb. или Stoch.Hyb. или Курс

Избранные публикации

Очень удобочитаемый всеобъемлющий ресурс по логическим основам киберфизических систем можно найти в одноименном учебнике [20]. Общий обзор основополагающих принципов содержится в официальном документе IJCAR’16 [16]. Хороший технический обзор нескольких аспектов логических основ киберфизических систем и мультидинамических систем можно найти в приглашенном учебнике на LICS’12 [6] и в расширенной рукописи [7], а также в B.EATCS [10]. . Основные технические разработки ядерных мультидинамических систем находятся в литературе [1,4,5,14,17,23,27,31]. Также см. публикации по областям и руководство по чтению публикаций. Многие другие статьи развивают часть логических основ киберфизических систем. Полный список публикаций см.

1. Йонг Киам Тан и Андре Платцер .
   Аксиоматический подход к существованию и живучести дифференциальных уравнений.
   Формальные аспекты вычислений 33 (4), стр. 461-518, 2021.
   Спецвыпуск для избранных газет FM’19. © Авторы
   [нагрудник | ✂ | пдф | дои | arXiv | FM’19 | абстрактный]
2. Эндрю Согокон, Стефан Митч, Йонг Киам Тан, Кэтрин Кордуэлл и Андре Платцер .
   Pegasus: непрерывная генерация инвариантов звука.
   Формальные методы проектирования систем 58 (1), стр. 5–41, 2022 г.
   Спецвыпуск для избранных газет FM’19. © Авторы
   [нагрудник | ✂ | пдф | дои | инструмент | arXiv | FM’19 | абстрактный]
3. Брэндон Борер и Андре Платцер .
   Доработка конструктивных гибридных игр.
   Зена М. Ариола, редактор, 5-я Международная конференция по формальным структурам для вычислений и дедукции, FSCD 2020 , 29 июня — 5 июля, Париж, Франция, Proceedings , том 167 из LIPics , стр. 14:1-14:19. Schloss Dagstuhl — Leibniz-Zentrum für Informatik 2020. © Авторы
   [нагрудник | ✂ | пдф | дои | мой pdf | слайды | arXiv | абстрактный]
4. Брэндон Борер и Андре Платцер .
   Конструктивные гибридные игры.
   Николя Пельтье и Виорика Софрони-Стоккерманс, редакторы, Automated Reasoning, 10th International Joint Conference, IJCAR 2020 , Paris, France, Proceedings, Part I , том 12166 из LNCS , стр. 454-473. весна 2020. © Авторы
   [нагрудник | ✂ | пдф | дои | мой pdf | слайды | arXiv | абстрактный]
5. Андре Платцер и Йонг Киам Тан.
   Аксиоматизация инвариантности дифференциальных уравнений.
   J. ACM 67 (1), 6:1–6:66, 2020 г. © Авторы
   [нагрудник | ✂ | пдф | дои | мой pdf | слайды | видео | arXiv | абстрактный]
6. Эндрю Согокон, Стефан Митч, Йонг Киам Тан, Кэтрин Кордуэлл и Андре Платцер .
   Pegasus: платформа для непрерывной генерации инвариантов.
   В Морис тер Бик, Аннабель МакИвер и Хосе Н. Оливьера, редакторы, FM 2019 : Формальные методы — следующие 30 лет , том 11800 из LNCS , стр. 138-157. Спрингер, 2019. © Спрингер
   Награда FM за лучшую инструментальную бумагу .
   [нагрудник | ✂ | пдф | дои | слайды | орудие труда | ФМСД | абстрактный]
7. Андре Платцер .
   Единая замена одним махом.
   Паскаль Фонтейн, редактор, Международная конференция по автоматизированной дедукции, CADE-27 , Натал, Бразилия, Труды , том 11716 из LNCS , стр. 425-441. Спрингер, 2019. © Автор
   [нагрудник | ✂ | пдф | дои | мой pdf | слайды | Изабель | arXiv | абстрактный]
8. Брэндон Борер и Андре Платцер .
   Гибридная динамическая логика для гибридно-динамического потока информации.
   Ануй Давар и Эрих Грэдель, редакторы, Материалы 33-го ежегодного симпозиума ACM/IEEE по логике в компьютерных науках, ЛИКС’18 , стр. 115-124. АКМ 2018. © Авторы. Права на публикацию предоставлены ACM
   [нагрудник | ✂ | пдф | дои | слайды | ТР | абстрактный]
9. Андре Платцер и Йонг Киам Тан.
   Аксиоматизация дифференциальных уравнений:
   Впечатляющая сила дифференциальных призраков.
   Ануй Давар и Эрих Грэдель, редакторы, Материалы 33-го ежегодного симпозиума ACM/IEEE по логике в компьютерных науках, ЛИКС’18 , стр. 819-828. АКМ 2018. © Авторы
   [нагрудник | ✂ | пдф | дои | мой pdf | слайды | видео | arXiv | ЯКМ’20 | абстрактный]
10. Андре Платцер .
    Унифицированная замена логики дифференциальной игры.
    Дидье Гальмиш, Стефан Шульц и Роберто Себастьяни, редакторы, Automated Reasoning, 9th International Joint Conference, IJCAR 2018 , Oxford, UK, Proceedings г., том 10900 из LNCS , стр. 211-227. Весна 2018. © Спрингер
    [нагрудник | ✂ | пдф | дои | слайды | arXiv | абстрактный]
11. Брэндон Борер, Йонг Киам Тан, Стефан Митш, Магнус О. Майрин и Андре Платцер .
    VeriPhy: проверенные исполняемые файлы контроллера из проверенных киберфизических моделей системы.
    В Дэн Гроссманн, редактор, Материалы 39-й конференции ACM SIGPLAN по разработке и реализации языков программирования, PLDI 2018 , стр. 617-630. АКМ 2018. © Авторы
    [нагрудник | ✂ | пдф | дои | мой pdf | слайды | видео | орудие труда | абстрактный]
12. Андре Платцер .
    Логические основы киберфизических систем .
    Спрингер, Чам, 2018. 659 страниц. ISBN 978-3-319-63587-3.
    [нагрудник | ✂ | дои | слайды | видео | книга | сеть | опечатки | абстрактный]
13. Натан Фултон, Стефан Митч, Брэндон Борер и Андре Платцер .
    Беллерофонт: Тактическое доказательство теорем для гибридных систем.
    Маурисио Айяла-Ринкон и Сезар А. Муньос, редакторы, Интерактивное доказательство теорем, Международная конференция, ITP 2017 , том 10499 из LNCS , стр. 207-224. Спрингер, 2017. © Спрингер
    [нагрудник | ✂ | пдф | дои | слайды | кикс | абстрактный]
14. Андре Платцер .
    Дифференциальные гибридные игры.
    ACM Trans. вычисл. Журнал. 18 (3), стр. 19:1-19:44, 2017. © Автор
    [нагрудник | ✂ | пдф | дои | мой pdf | arXiv | абстрактный]
15. Андре Платцер .
    Полное унифицированное исчисление подстановок для дифференциальной динамической логики.
    Журнал автоматизированных рассуждений 59 (2), стр. 219-265, 2017. © Автор
    [нагрудник | ✂ | пдф | дои | мой pdf | arXiv | абстрактный]
16. Андре Платцер .
    Логика и доказательства для киберфизических систем.
    Никола Оливетти и Ашиш Тивари, редакторы, Automated Reasoning, 8th International Joint Conference, IJCAR 2016 , Coimbra, Portugal, Proceedings , том 9706 из LNCS , стр. 15-21. Спрингер, 2016. © Спрингер
    Приглашенный документ .
    [нагрудник | ✂ | пдф | дои | слайды | абстрактный]
17. Стефан Митч и Андре Платцер .
    ModelPlex: проверенная проверка во время выполнения проверенных киберфизических системных моделей.
    Формальные методы проектирования систем 49 (1), стр. 33-74. 2016.
    Спецвыпуск избранных статей РВ’14. © Авторы
    [нагрудник | ✂ | пдф | дои | мой pdf | РВ’14 | абстрактный]
18. Андре Платцер .
    Дифференциальная игровая логика.
    ACM Trans. вычисл. Журнал. 17 (1), стр. 1:1–1:52, 2015. © Автор
    [нагрудник | ✂ | пдф | дои | мой pdf | arxiv | опечатки | абстрактный]
19. Натан Фултон, Стефан Митч, Ян-Давид Кесел, Маркус Фёльп и Андре Платцер .
    KeYmaera X: аксиоматическое средство доказательства тактических теорем для гибридных систем.
    Эми П. Фелти и Аарт Мидделдорп, редакторы, Международная конференция по автоматизированной дедукции, CADE-25 , Берлин, Германия, Proceedings , том 9195 из LNCS , стр. 527-538. Спрингер, 2015. © Спрингер
    [нагрудник | ✂ | пдф | дои | слайды | постер | орудие труда | абстрактный]
20. Андре Платцер .
    Единое исчисление подстановок для дифференциальной динамической логики.
    Эми П. Фелти и Аарт Мидделдорп, редакторы, Международная конференция по автоматизированной дедукции, CADE-25 , Берлин, Германия, Proceedings , том 9195 из LNCS , стр. 467-481. Спрингер, 2015. © Спрингер
    [нагрудник | ✂ | пдф | дои | слайды | arXiv | январь 2017 г. | абстрактный]
21. Ян-Давид Кесель, Стефан Митч, Сара Лоос, Никос Арешига и Андре Платцер .
    Как моделировать и проверять гибридные системы с помощью KeYmaera: Учебник по технике безопасности.
    STTT 18 (1), стр. 67–91, 2016 г. © Авторы
    [нагрудник | ✂ | пдф | дои | мой pdf | абстрактный]
22. Андре Платцер .
    Аналоговые и гибридные вычисления: динамические системы и языки программирования.
    Бюллетень EATCS 114 , 2014 г. © Автор
    Приглашенная статья в колонке Юрия Гуревича «Логика в информатике».
    [нагрудник | ✂ | пдф | электронная печать | абстрактный]
23. Андре Платцер .
    Основы киберфизических систем .
    Конспект лекций, факультет компьютерных наук, Университет Карнеги-Меллона. 2014.
    [нагрудник | ✂ | пдф | учебник | курс]
24. Андре Платцер .
    Обучение основам CPS с контрактами.
    Первый семинар по обучению киберфизическим системам ( CPS-Ed 2013 ), стр. 7–10. 2013.
    [нагрудник | ✂ | пдф | электронная печать | слайды | постер | курс | абстрактный]
25. Андре Платцер .
    Динамическая логика динамических систем.
    arXiv:1205.4788, май 2012 г. Длинная версия приглашенного туториала LICS’12.
    [нагрудник | ✂ | пдф | arXiv | ЛИКС’12 | абстрактный]
26. Андре Платцер .
    Логика динамических систем.
    Симпозиум ACM/IEEE по логике в компьютерных науках, LICS 2012 , 25–28 июня 2012 г., Дубровник, Хорватия , стр. 13–24. ИЭЭЭ 2012. © IEEE
    Приглашенный документ .
    [нагрудник | ✂ | пдф | дои | слайды | абстрактный]
27. Андре Платцер .
    Полная теория доказательств гибридных систем.
    Симпозиум ACM/IEEE по логике в компьютерных науках, LICS 2012 , 25–28 июня 2012 г., Дубровник, Хорватия , стр. 541-550. ИЭЭЭ 2012. © IEEE
    [нагрудник | ✂ | пдф | дои | слайды | ТР | абстрактный]
28. Андре Платцер .
    Полная аксиоматизация количественной дифференциальной динамической логики для распределенных гибридных систем.
    Логические методы в информатике 8 (4), стр. 1–44, 2012.
    Специальный выпуск избранных статей CSL’10. © Автор
    [нагрудник | ✂ | пдф | дои | arXiv | CSL’10 | абстрактный]
29. Андре Платцер .
    Стохастическая дифференциальная динамическая логика для стохастических гибридных программ.
    Николаю Бьёрнеру и Виорике Софрони-Стоккерманс, редакторам, Международная конференция по автоматизированному дедукции, CADE-23 , Вроцлав, Польша, Proceedings , том 6803 из LNCS , стр. 446-460. Спрингер, 2011. © Спрингер
    [нагрудник | ✂ | пдф | дои | слайды | ТР | абстрактный]
30. Андре Платцер .
    Количественная дифференциальная динамическая логика для распределенных гибридных систем.
    Анудж Давар и Хельмут Вейт, редакторы, Логика компьютерных наук, 19-я ежегодная конференция EACSL, CSL 2010 , Брно, Чехия, 23–27 августа 2010 г. Труды , том 6247 из LNCS , стр. 469-483. Спрингер, 2010. © Спрингер
    [нагрудник | ✂ | пдф | дои | слайды | ТР | LMCS’12 | абстрактный]
31. Андре Платцер .
    Дифференциальная динамическая логика для гибридных систем.
    Journal of Automated Reasoning 41 (2), стр. 143–189, 2008 г. © Автор
    [нагрудник | ✂ | пдф | дои | мой pdf | изучение | абстрактный]

Любые высказанные мнения, выводы и выводы или рекомендации принадлежат автору (авторам) и не обязательно отражают взгляды какого-либо спонсирующего учреждения.