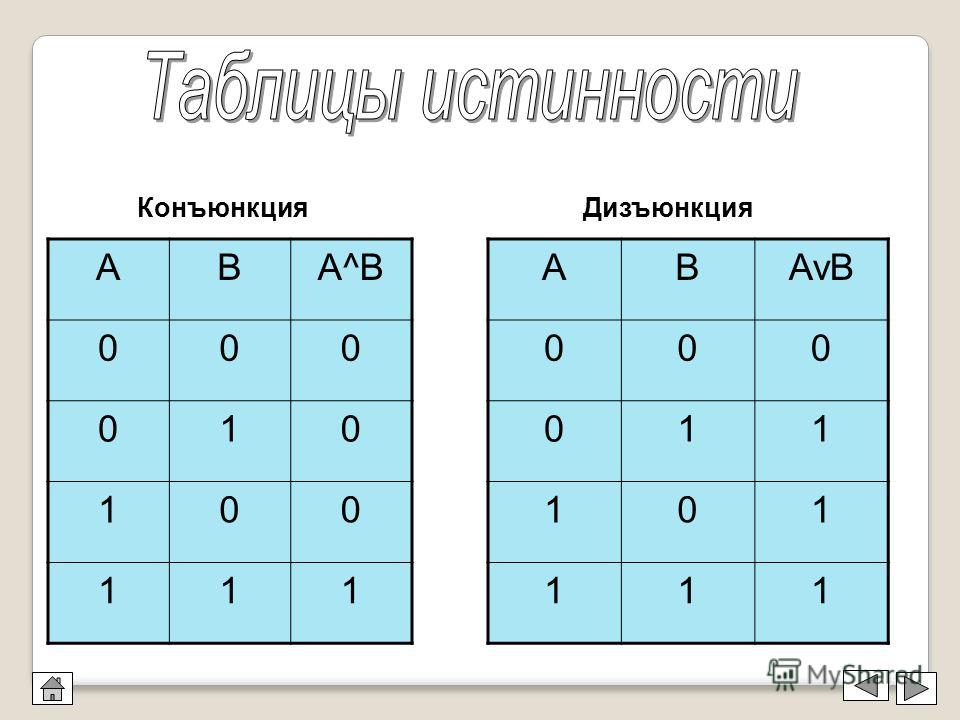
Таблица истинности логических элементов
Чаще всего существуют не отдельные схемы логического «И», а более сложные схемы, выполняющие одновременно логическую функцию «И» и логическую функцию «НЕ» Таблица истинности и изображение схемы, выполняющей логическую функцию «И-НЕ» изображены на рис 3 и 4 соответственно:. Точно также как не существует отдельных схем логического «И», выполненных по технологии ТТЛ, не существует отдельных схем логического «ИЛИ». Таблица истинности и изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ» изображены на рис 5 и 6 соответственно:. Любая логическая схема без памяти полностью описывается таблицей истинности. При построении сложных логических схем с произвольной таблицей истинности используется сочетание простейших схем «И» «ИЛИ» «НЕ». При построении схемы, реализующей произвольную таблицу истинности, каждый выход анализируется и строится схема отдельно.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Логические элементы и таблицы истинности
- Цифровые логические элементы
- Логические элементы и логические схемы компьютера. 10-й класс
- Логические схемы и таблицы истинности
- Логические элементы
- Редактор схемы логических элементов
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Конъюнкция, Дизъюнкция, Инверсия, Отрицание, Импликация, Следование. Таблица истинности
Логические элементы и таблицы истинности
Чаще всего существуют не отдельные схемы логического «И», а более сложные схемы, выполняющие одновременно логическую функцию «И» и логическую функцию «НЕ» Таблица истинности и изображение схемы, выполняющей логическую функцию «И-НЕ» изображены на рис 3 и 4 соответственно:.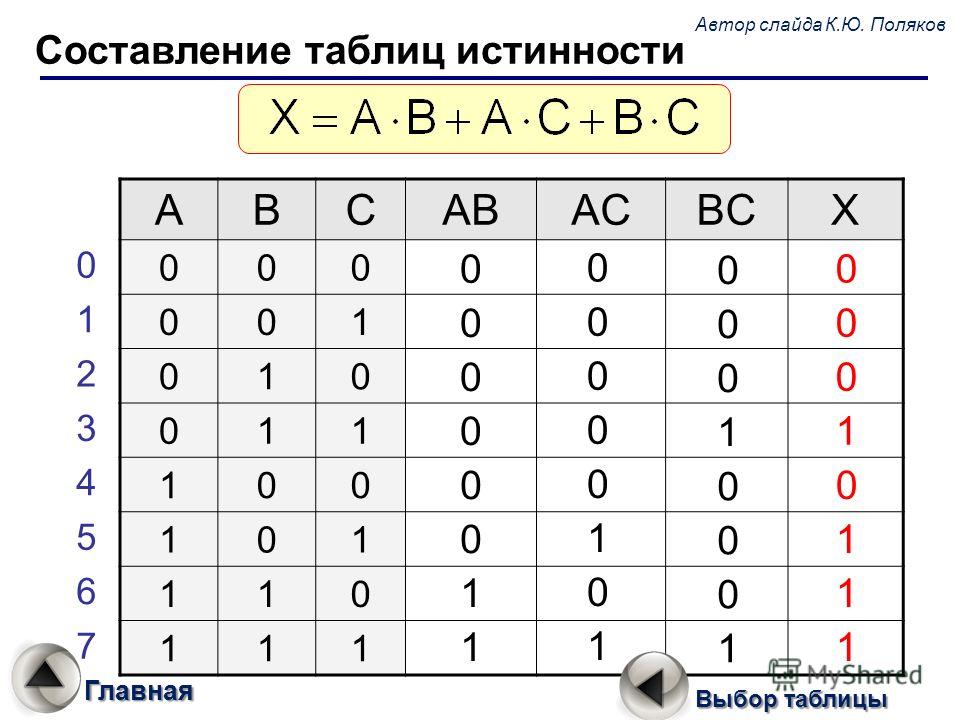 Точно также как не существует отдельных схем логического «И», выполненных по технологии ТТЛ, не существует отдельных схем логического «ИЛИ». Таблица истинности и изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ» изображены на рис 5 и 6 соответственно:.
Точно также как не существует отдельных схем логического «И», выполненных по технологии ТТЛ, не существует отдельных схем логического «ИЛИ». Таблица истинности и изображение схемы, выполняющей логическую функцию «ИЛИ-НЕ» изображены на рис 5 и 6 соответственно:.
Любая логическая схема без памяти полностью описывается таблицей истинности. При построении сложных логических схем с произвольной таблицей истинности используется сочетание простейших схем «И» «ИЛИ» «НЕ».
При построении схемы, реализующей произвольную таблицу истинности, каждый выход анализируется и строится схема отдельно. Для реализации таблицы истинности при помощи логических элементов «И» достаточно рассмотреть только те строки таблицы истинности, которые содержат логические «1» в выходном сигнале.
Строки, содержащие в выходном сигнале логический 0 в построении схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую «1», реализуется схемой логического «И» с количеством входов, совпадающим с количеством входных сигналов в таблице истинности.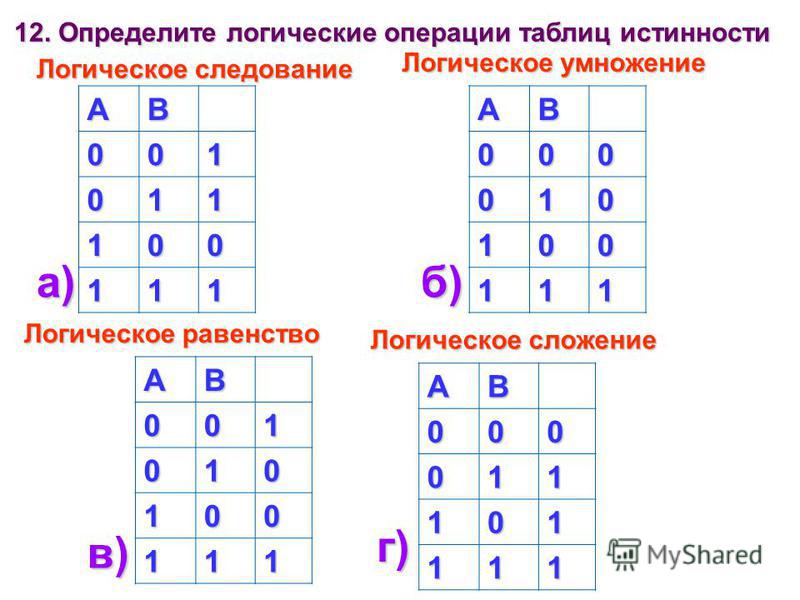
Входные сигналы, описанные в таблице истинности логической «1» подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логическим «0» подаются на вход через иверторы. Объединение сигналов с выходов схем, реализующих отдельные строки таблицы истинности, производится при помощи схемы логического ИЛИ.
Количество входов в этой схеме определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая «1». Рассмотрим конкретный пример.
Пусть необходимо реализовать таблицу истинности, приведенную на рисунке Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные красным цветом. Эти строки реализуются микросхемой D2 на рисунке 8. Эти строки реализуются микросхемой D3. Рисунок 8. Принципиальная схема, реализующая таблицу истинности, приведенную на рисунке 7. О нашем музее Вычисления в докомпьютерную эпоху История отечественной вычислительной техники История управляющей вычислительной техники История вычислительной техники за рубежом История развития электросвязи История развития программного обеспечения История отечественной электронной компонентной базы ЭКБ Галерея славы Технологии Документы и публикации Календарь событий Книги и компьютерная пресса История компьютерных игр IT энциклопедия Англо-русский компьютерный словарь Музеи и ВТ в Интернете Архив новостей Гостевая книга.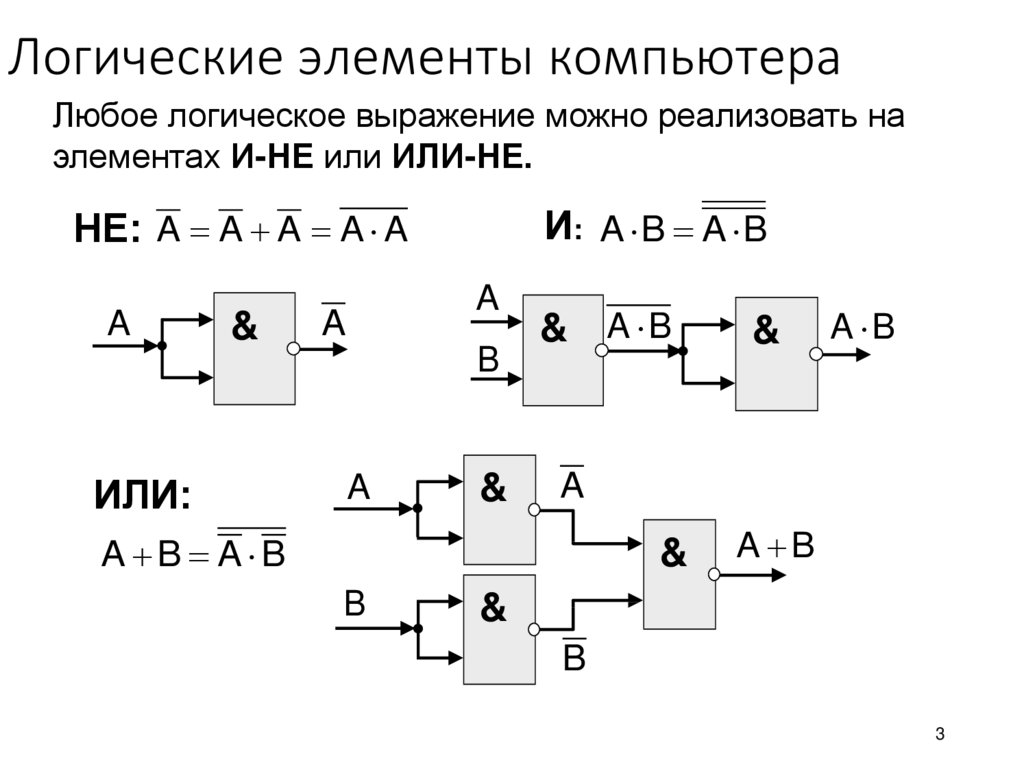
Чаще всего существуют не отдельные схемы логического «И», а более сложные схемы, выполняющие одновременно логическую функцию «И» и логическую функцию «НЕ» Таблица истинности и изображение схемы, выполняющей логическую функцию «И-НЕ» изображены на рис 3 и 4 соответственно: Рис 3 Таблица истинности схемы, выполняющей логическую функцию «И-НЕ».
Рис 4 Изображение схемы, выполняющей логическую функцию «И-НЕ». Построение произвольной таблицы истинности. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 7: Рисунок 7 Произвольная таблица истинности. Рис 3 Таблица истинности схемы, выполняющей логическую функцию «И-НЕ».
Цифровые логические элементы
Разделы: Информатика. Цель урока: дать учащимся представление о том, как в компьютере при помощи логических элементов выполняются арифметические и логические операции. Опорные понятия: логическая операция; сложное логическое выражение формула. Новые понятия: логический элемент, логическая схема.
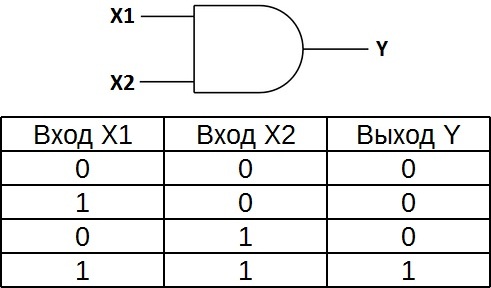
Для всех видов логических элементов, независимо от их физической природы, Таблица истинности для элемента 2И показывает, что на выходе.
Логические элементы и логические схемы компьютера. 10-й класс
Физически логические элементы могут быть выполнены механическими, электромеханическими на электромагнитных реле , электронными в частности, на диодах или транзисторах , пневматическими, гидравлическими , оптическими и другими. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами. Логические элементы выполняют логическую функцию операцию над входными сигналами операндами, данными. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы. Логические операции булева функция своё теоретическое обоснование получили в алгебре логики. Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками. Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Примечание 1.
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Примечание 1.
Логические схемы и таблицы истинности
Вот о них мы и поговорим сейчас. Логический элемент — это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе. Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов.
Решение: карта Карно представлена на рис.
Логические элементы
Табличное задание функций встречается не только в логике, но и в логических функциях. Таблицы оказались довольно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики. Материал из Википедии — свободной энциклопедии. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии , проверенной 7 октября ; проверки требуют 23 правки.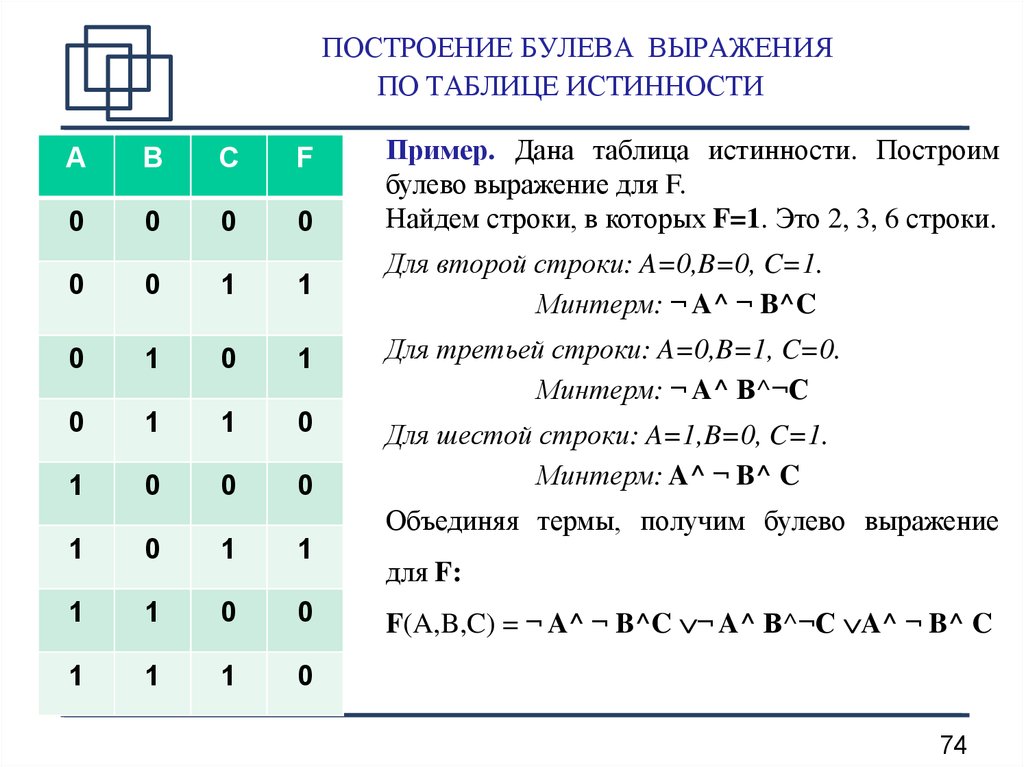 На эту тему нужна отдельная статья англ.
На эту тему нужна отдельная статья англ.
Редактор схемы логических элементов
В отличие от аналоговых электронных устройств, в цифровых устройствах ЦУ входные и выходные сигналы могут принимать ограниченное количество состояний. В соответствии с логическим соглашением ГОСТ 2. Такое соглашение называется положительной логикой. Обратное соотношение называется отрицательной логикой. Теоретической основой проектирования ЦУ является алгебра-логики или булева алгебра, оперирующая логическими переменными. Для логических переменных, принимающих только два значения,существуют 4 основных операции.
Как функция логических переменных дизъюнкция записывается следующим образом: .) 2. 1. 2. 1. 2.,. F x x. x x. = ∨. Таблица истинности операции.
И как вы догадались, я должен вам простым, а главное понятным языком рассказать о так называемых логических элементах. Их еще иногда называют вентилями. Начнем конечно же с некоего вступления, которое поможет понять работу этих самых логических элементов.
Главная Информатика и информационно-коммуникационные технологии Планирование уроков и материалы к урокам 9 классы Планирование уроков на учебный год Логические основы построения компьютера. Изучив эту тему, вы узнаете: — что изучает алгебра логики; — какие операции возможны над высказываниями; — как составляется таблица истинности; — каким законам подчиняются логические выражения; — что такое логические элементы компьютера. Некоторые законы булевой алгебры Существуют законы аксиомы , позволяющие преобразовывать сложные логические выражения с целью их упрощения. Некоторые из них приведены в таблице Таблица
Для добавления нового элемента нажмите на нужный, а затем щелкните левой кнопкой мыши на графическом поле.
Основы электроники. Электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными, называется логическим элементом. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное.
Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное.
Русский: English:. Бесплатный архив статей статей в Архиве. Справочник бесплатно. Параметры радиодеталей бесплатно.
|
Заглавная страница
КАТЕГОРИИ: Археология Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
Стр 1 из 5Следующая ⇒ Основные логические функции и элементы, их таблицы истинности, схемы и условно-графические обозначения. Основные законы и правила булевой алгебры логики. Логические схемы и их таблицы истинности, правила минимизации. 4. Основные термины и определения цифровой схемной логики.
Основные логические функции и элементы, их таблицы истинности, схемы и условно-графические обозначения
Уровни логических сигналов
Любая цифровая вычислительная машина состоит из логических схем – таких схем, которые могут находиться только в одном из двух возможных состояний – либо «логический ноль«, либо «логическая единица». За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как «истина» и «ложь«.
Рисунок 3.1 – Уровни логических сигналов на выходе цифровых ТТЛ-микросхем
Логические переменные и логические функции– это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1.
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1. В логических выражениях применяются обозначения: — либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое; — либо ; — либо ; — либо . Логическая функция и элемент ИЛИ-НЕ
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рисунке 3.6,а. Таблица истинности приведена на рисунке 3.6,б.
Рисунок 3.6 – Логический элемент ИЛИ-НЕ на два входа
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0. В логических выражениях применяются обозначения: — либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое; — либо .
Логические схемы и их таблицы истинности, Правила минимизации
Х переменных Рисунок 3.10 – Таблица истинности (а) и примеры заполнения карты Карно (б, в, г, д) для логической функции 3 переменных
Для функции четырех переменных карта Карно – это квадрат 4×4 клетки. В этих клетках размещаются 16 значений функции из последнего столбца таблицы истинности (рисунок 3.11). При разметке обеих осей нужно также четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы по одной оси соседними не оказались сочетания 00 и 11, либо 01 и 10, в которых одновременно меняются обе переменные. Для функции пяти переменных карта Карно представляет собой уже объемную фигуру – куб 4×4×4 клетки, поэтому для минимизации логических выражений она не применяется. В конкретных случаях вместо значений функций в общем виде в клетки карты проставляются конкретные значения (логические 0 и 1) из соответствующих строк таблицы истинности. 1. Контуры должны быть прямоугольными и содержать количество единиц, равное 2 n , где n – целое число. Таким образом, в контуре может быть либо одна, либо две, либо четыре, либо восемь единиц. 2. Количество единиц в контуре должно быть максимальным , при этом контуры могут пересекаться между собой. Нужно учитывать, что крайние строки являются соседними и крайние столбцы также являются соседними, поэтому контуры могут быть » разорванными «. 3. Количество контуров должно быть минимальным , но все единицы должны быть охвачены контурами. Нельзя забывать об отдельно стоящих единицах. Каждая такая единица – это контур, которому соответствует полное логическое произведение всех переменных. 4. После обведения контуров нужно записать минимальное выражение как логическую сумму логических произведений. Каждому произведению соответствует один контур карты Карно. В произведение входят только те переменные, которые остаются в данном контуре неизменными. При этом переменная входит в произведение с инверсией, если ее значение в данном контуре равно 0, и без инверсии, если ее значение равно 1.
Рисунок 3.11 – Таблица истинности (а) и примеры заполнения карты Карно (б, в) для логической функции 4 переменных
Пример 1. Написать минимальное выражение для таблицы истинности, представленной на рисунке 3.12,а и нарисовать по нему логическую схему. При одном варианте разметки осей (рисунок 3.12,б) первый контур, состоящий из четырех единиц, получается разорванным. Если же принять разметку, показанную на рисунке 3.12в, то контур будет иметь нормальные очертания, а выражение, ему соответствующее, останется без изменений. Первый контур охватывает четыре единицы, ему соответствует сумма минтермов: , в которой не изменяется только переменная «b». Второй контур охватывает две единицы. Ему соответствует сумма минтермов , в которой переменная «b» принимает оба возможных значения, а произведение остается неизменным. Таким образом, получаем минимальное выражение: (3.3)
Ему соответствует логическая схема на рисунке 3.12,г.
Рисунок 3.12 – Минимизация функции трех переменных
Для сравнения запишем максимальное выражение:
(3.
Разница между (3.3) и (3.4) очевидна и в комментариях не нуждается, за исключением того, что схема, реализованная по (3.4), будет на порядок сложнее и, соответственно, менее надежна, чем схема, показанная на рисунке 3.12,г. Пример 2. Написать минимальное выражение для таблицы истинности, представленной на рисунке 3.13,а, и нарисовать по нему логическую схему.
Рисунок 3.13 – Минимизация функции четырех переменных
При первоначально выбранной разметке осей (рисунок 3.13,б) первый контур, состоящий из четырех единиц с номерами 1.1, 1.2, 1.3 и 1.4, расположенных по углам карты, получается разорванным. Если же принять разметку, показанную на рисунке 3.14, то контур будет иметь очертания квадрата, а выражение, ему соответствующее, останется без изменений. Учитывая, что крайние столбцы являются соседними и крайние строки являются соседними, карту Карно для функции четырех переменных можно представить себе как торроид, развернутый на плоскости.
Рисунок 3.14 – К минимизации логической функции четырех переменных
Соответствующая ему схема приведена на рисунке 3.15. Рисунок 3.15 – Логическая схема для минимизированного Логического выражения 4. Основные термины и определения цифровой схемной логики.
ДНФ – дизъюнктивно-нормальная форма – представление логического выражения в виде суммы произведений. Инверсия – операция НЕ – логическое действие, при котором появление хотя бы одного логического нуля на входе даёт логический нуль на выходе. Инвертор – логический элемент, реализующий операцию НЕ. КНФ – конъюктивно-нормальная форма – представление логического выражения в виде произведения сумм. Логическая переменная – переменная, значение которой может быть равно либо логическому нулю, либо логической единице. Логическая схема – схема, состоящая из логических элементов. Логическая функция – функция, включающая в себя логические переменные, значение которой может быть равно либо логическому нулю, либо логической единице. Логический элемент – графическое представление элементарной логической функции. Логическое отрицание – операция НЕ, инверсия – логическое действие, при котором происходит изменение состояния на противоположное. Логическое сложение – операция ИЛИ, дизъюнкция – логическое действие, при котором появление хотя бы одной логической единицы на входе даёт логическую единицу на выходе. Логическое умножение – операция И, конъюнкция – логическое действие, при котором появление хотя бы одного логического нуля на входе даёт логический нуль на выходе. Таблица истинности – таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции. ДНФ– дизъюнктивно-нормальная форма – представление логического выражения в виде произведения сумм. КНФ– конъюнктивно-нормальная форма – представление логического выражения в виде суммы произведений. Минтерм– это полное произведение всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно логической 1. Каноническая сумма минтермов – это логическая сумма всех минтермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности. Карта Карно– графическое представление таблицы истинности. Макстерм– это сумма всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно 0. Переменная входит в макстерм с инверсией, если её значение в строке истинности равно 1. Каноническое произведение макстермов– это логическая сумма всех макстермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности.
Краткие итоги
Любая цифровая вычислительная машина состоит из логических схем. Работа логической схемы наиболее наглядно может быть описана с помощью таблицы истинности. Возможно и решение обратной задачи – по известной таблице истинности синтезировать логическое выражение и логическую схему. Для синтеза схем применяется метод минимизации с помощью карт Карно. Наиболее рациональная логическая схема может быть синтезирована по минимизированному логическому выражению.
Набор для практики Вопросы для самопроверки 1. Нарисуйте элементы И на два, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение. 2. Нарисуйте элементы ИЛИ на три, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение. 3. Нарисуйте элементы И-НЕ на два, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение. 4. Нарисуйте элементы ИЛИ-НЕ на три, четыре и пять входов, составьте для каждого из них таблицу истинности, напишите соответствующее каждому элементу логическое выражение. 5. Какой уровень сигнала является решающим для логического сложения? для логического умножения? для функции И-НЕ? для функции ИЛИ-НЕ?
Для логического сложения решающим является уровень логической 1. Уровень логического 0 является решающим для логического умножения. Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1. Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.
6. Что такое таблица истинности?
Таблица истинности – это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции. 7. Сколько строк в таблице истинности для 5-входовой логической схемы? для 4-входовой? для 2-входовой? 32, 16, 4
8. Функция скольких переменных описывается таблицей истинности длиной 4 строки? 64 строки? 512 строк? 2, 6, 9
Основные логические функции и элементы, их таблицы истинности, схемы и условно-графические обозначения. 12345Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Тактические действия в защите История Олимпийских игр История развития права интеллектуальной собственности |
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Базовые логические элементы и таблицы истинности
— Реклама —
Основы введения в логические элементы
Логические элементы являются основой всех цифровых систем, как комбинационных, так и последовательных, схема следует определенной логике. Проще говоря, логический элемент представляет собой цифровую схему с несколькими входами и одним выходом. Связь между входами и выходами логического элемента следует определенной логике. Эта логика придерживается правил булевой алгебры. Чтобы развить глубокое понимание логических элементов, мы должны понимать основы цифровых сигналов, двоичных систем счисления и булевой алгебры.
Рис.1 Логические элементы Основной вход Выход ПРИМЕЧАНИЕ: В логических схемах нет петли обратной связи или блока памяти.
Цифровой сигнал
Аналоговый сигнал представляет собой непрерывный изменяющийся во времени сигнал тока или напряжения, тогда как цифровой сигнал представляет собой пульсирующую форму волны с двумя дискретными значениями — высоким и низким. Эти два дискретных значения представлены двоичными числами 0 и 1. Цифровая схема — это электронная схема, которая обрабатывает цифровые сигналы.
— Реклама —
Просто это либо ДА , либо НЕТ , ничего между ними.
В цифровых схемах
0 = Нет, Ложь, Выключение, Разомкнутая цепь и Низкий уровень.
1 = Да, Истина, Включение, Замкнутая цепь и Высокий уровень.
Двоичные числа
Десятичная система имеет основание или основание 10, что означает, что число представлено десятью цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. двоичная система имеет основание или основание 2 только с двумя цифрами: 0 и 1.
Двоичная система счисления представляет число как 0 или 1. Любое число, представленное в двоичной форме, подвергается двоичному преобразованию.
Любое число, представленное в двоичной форме, подвергается двоичному преобразованию.
Пример: 1 – 001, 2 – 010, 3 – 011, 4 – 0100, 5 – 0101,… 15 – 1111 и так далее.
Булева алгебра
Ирландский математик Джордж Буль разработал математическую систему с использованием символов. Система ведет себя аналогично алгебре для решения бинарных или логических задач.
Уравнение, представленное символами, но подчиняющееся законам булевой алгебры, известно как логическое выражение.
В булевой алгебре используются три операции:
1) Операция ИЛИ
2) Операция И
3) Операция НЕ
Логические операции
1) Операция ИЛИ:
Операция ИЛИ представляет собой форму логического сложения знаком (+) с двумя или несколькими входами, производящими один выход. Операция ИЛИ выдает ВЫСОКИЙ уровень на выходе (1), только если один или все входы цифровой схемы имеют ВЫСОКИЙ уровень (1). Если оба входа имеют НИЗКИЙ уровень (0), выход цифровой схемы также будет НИЗКИМ (0).
Давайте разберем это на примере:
Рассмотрим схему с двумя переключателями, подключенными параллельно к светодиоду. Светодиод будет гореть, если через цепь протекает ток. Чтобы ток протекал, один из переключателей должен быть замкнут.
Рис.2 Логический вентиль или работаПРИМЕЧАНИЕ: МЫ ТАКЖЕ МОЖЕМ ИСПОЛЬЗОВАТЬ ЛАМПОЧКУ.
Случай 1:
Переключатель A=РАЗОМКНУТ, переключатель B=РАЗОМКНУТ
Если оба переключателя разомкнуты, ток в цепи не течет и светодиод не светится.
Случай 2:
Переключатель A=РАЗОМКНУТ, Переключатель B=ЗАМКНУТ
Благодаря параллельному соединению, даже если один из переключателей замкнут, а другой разомкнут, по цепи протекает ток. Это заставляет светодиод светиться.
Случай 3:
Переключатель A = ЗАКРЫТ, переключатель B = ОТКРЫТ
В цепи протекает ток, и светодиод горит ЗАКРЫТО
Если оба переключателя замкнуты, через цепь протекает сильный ток, и светодиод светится.
| СНО | ВЫКЛЮЧАТЕЛЬ А | ВЫКЛЮЧАТЕЛЬ B | Светодиод |
| КОРПУС 1 | ОТКРЫТЬ | ОТКРЫТЬ | ВЫКЛ |
| КОРПУС 2 | ОТКРЫТЬ | ЗАКРЫТО | НА |
| КОРПУС 3 | ЗАКРЫТО | ОТКРЫТЬ | НА |
| КОРПУС 4 | ЗАКРЫТО | ЗАКРЫТО | НА |
Логическое выражение для операции ИЛИ:
Y= A + B
Где Y= выход; А= Вход 1; B= Вход 2
2) Операция И:
Операция И представляет собой форму логического умножения, представленную знаком (.) с двумя или несколькими входами, дающими один выход. Операция И выдает ВЫСОКИЙ уровень на выходе (1) только в том случае, если все входы цифровой схемы имеют ВЫСОКИЙ уровень (1). Если один или оба входа имеют НИЗКИЙ уровень (0), выход цифровой схемы также будет НИЗКИМ (0).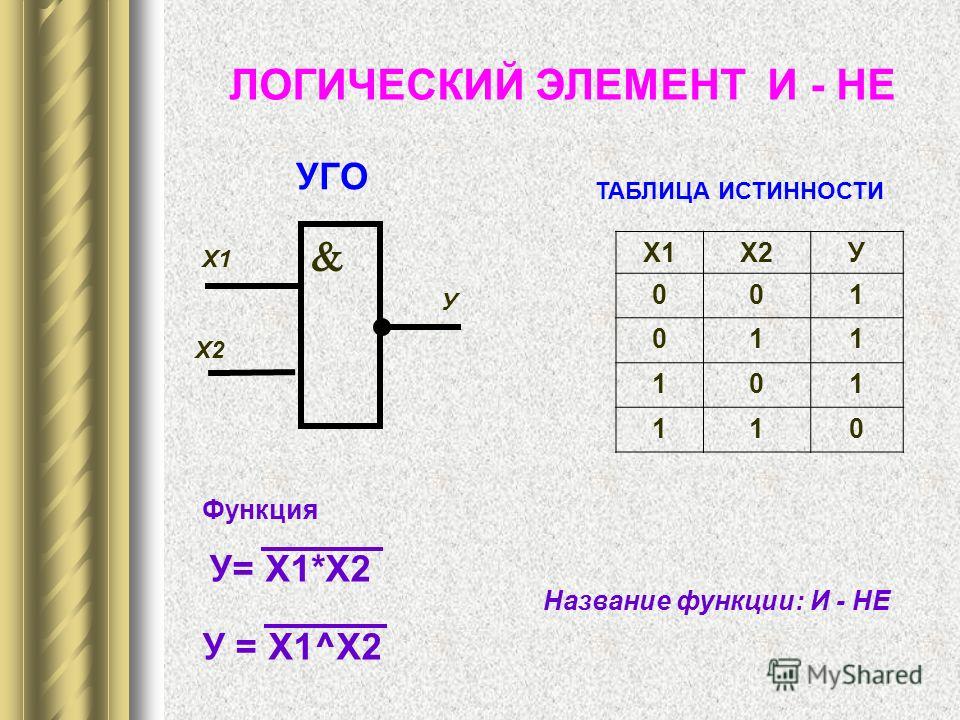
Давайте разберем это на примере:
Рассмотрим схему с двумя переключателями, последовательно соединенными со светодиодом. Светодиод будет гореть, если через цепь протекает ток. Чтобы ток протекал, оба переключателя должны быть замкнуты. Если один из переключателей разомкнут, ток не будет течь.
Рис.3 Логический вентиль И РаботаСлучай 1:
Переключатель A=ОТКРЫТ, переключатель B= ОТКРЫТ
Поскольку оба переключателя разомкнуты, ток не протекает через цепь и светодиод не светится. .
Случай 2:
Переключатель A=РАЗОМКНУТ, Переключатель B=ЗАКРЫТ
Если один из переключателей разомкнут в цепи последовательного соединения, протекание тока невозможно. Следовательно, светодиод не светится.
Случай 3:
Переключатель A = ЗАКРЫТ, переключатель B = РАЗОМКНУТ
Если один из переключателей разомкнут, ток в цепи не протекает и светодиод не светится.
Случай 4:
Переключатель A=ЗАКРЫТО, Переключатель B=ЗАКРЫТО
Если оба переключателя замкнуты, через цепь протекает сильный ток, и светодиод светится.
| СНО | ВЫКЛЮЧАТЕЛЬ А | ВЫКЛЮЧАТЕЛЬ B | Светодиод |
| КОРПУС 1 | ОТКРЫТЬ | ОТКРЫТЬ | ВЫКЛ |
| КОРПУС 2 | ОТКРЫТЬ | ЗАКРЫТО | ВЫКЛ |
| ДЕЛО 3 | ЗАКРЫТО | ОТКРЫТЬ | ВЫКЛ |
| КОРПУС 4 | ЗАКРЫТО | ЗАКРЫТО | НА |
Логическое выражение для операции И:
Y= A . B
В большинстве случаев точка (.) удалена
Y= AB
Где Y= Выход; А= Вход 1; B= Вход 2
3) Операция НЕ:
НЕ является операцией в форме логической инверсии, известной как дополнение. Существует единственный вход, производящий единственный выход. Операция НЕ создает ВЫСОКИЙ (1) выход для НИЗКОГО (0) входа и НИЗКИЙ (0) выход для ВЫСОКОГО (1) входа.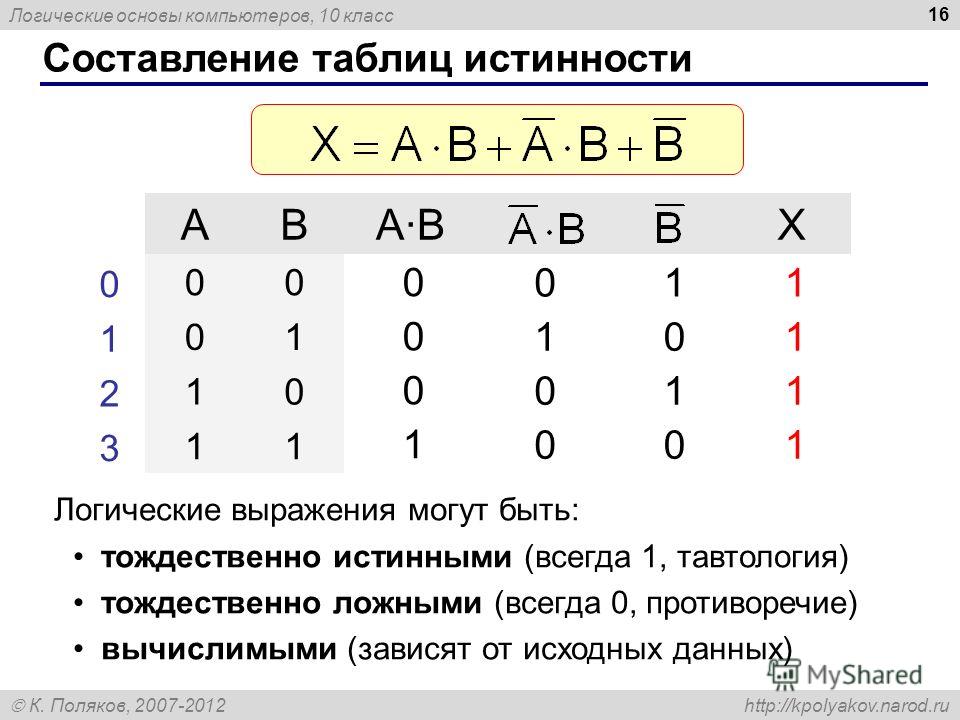
Представляется полосой ( ˉ ) над переменной.
Давайте разберем это на примере:
Рассмотрим групповой переключатель. Если один из переключателей разомкнут, другой автоматически закроется, и наоборот.
Рис.4 Логический вентиль НЕ работает| ПЕРЕКЛЮЧАТЕЛЬ A | ВЫКЛЮЧАТЕЛЬ B |
| ОТКРЫТЫЙ | ЗАКРЫТО |
| ЗАКРЫТО | ОТКРЫТЬ |
Логическое выражение для операции НЕ:
Y= A ˉ
Где Y= выход; A= Вход
Логические элементы
Логический элемент представляет собой цифровую схему с одним выходом, значение которого зависит от логической связи между входом(ами) и выходом. Проще говоря, связь между входными и выходными значениями основана на определенной «логике», поэтому эти схемы рассматриваются как логические вентили. Логические вентили имеют только один выход для одного входа или нескольких входов.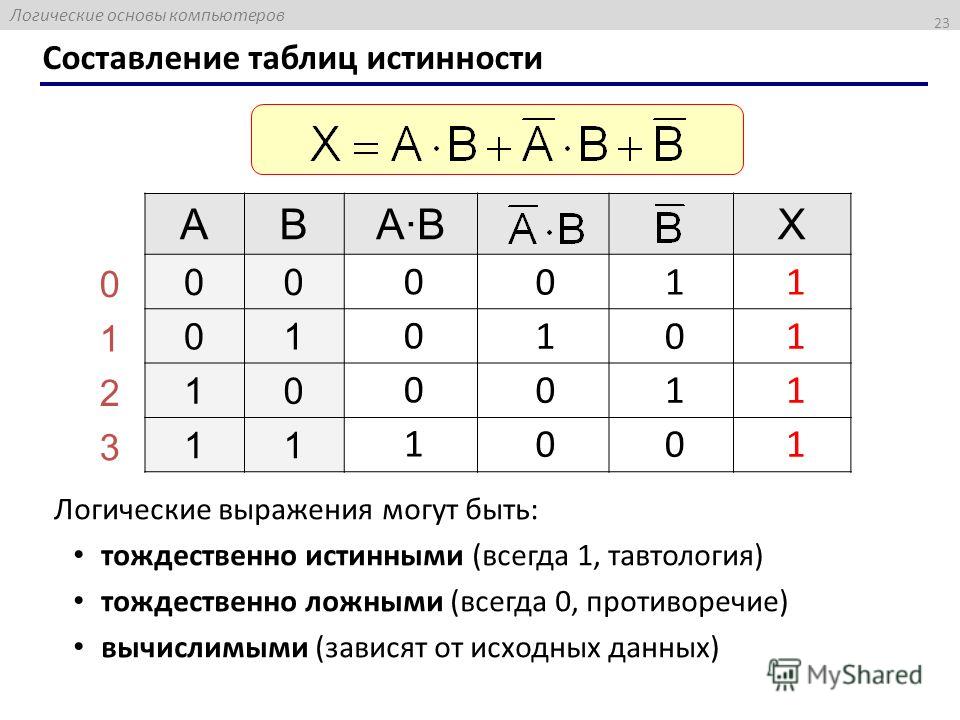 Чтобы понять работу логического вентиля, составляется таблица истинности, в которой указываются все комбинации входных данных вместе с выходными данными.
Чтобы понять работу логического вентиля, составляется таблица истинности, в которой указываются все комбинации входных данных вместе с выходными данными.
Существует 3 типа логических вентилей:
1) Базовые вентили: вентили ИЛИ, И и НЕ.
2) Универсальные вентили: вентили NAND и NOR.
3) Производные вентили: вентили XOR и вентили XNOR.
Давайте разберемся со всеми тремя логическими вентилями поглубже.
1) Базовые логические элементы
Существует три типа базовых логических вентилей: вентили ИЛИ, И и НЕ. Логический вентиль Basic ведет себя так же, как и соответствующий логический оператор.
- A) Логический элемент ИЛИ: Для двух или более входов вентиль ИЛИ выдает ВЫСОКИЙ (1) выходной сигнал, только если один или все входы имеют ВЫСОКИЙ (1) уровень. Это работает аналогично операции ИЛИ Логика.
Логическое выражение для вентиля ИЛИ:
Y= A ИЛИ B
Рис.5 Символ вентиля ИЛИСлучай 1: A= 0, B= 0; Y= 0
В этом случае оба входа имеют НИЗКИЙ уровень (0), поэтому логический элемент ИЛИ выдает НИЗКИЙ (0) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 1
В этом случае один из входов ВЫСОКИЙ (1), поэтому логический элемент ИЛИ выдает ВЫСОКИЙ (1) выход.
Случай 3: А= 1, В= 0; Y= 1
В этом случае один из входов имеет ВЫСОКИЙ уровень (1), поэтому логический элемент ИЛИ выдает ВЫСОКИЙ уровень (1) на выходе.
Случай 4: А= 1, В= 1; Y= 1
В этом случае оба входа имеют ВЫСОКИЙ уровень (1), поэтому логический элемент ИЛИ выдает ВЫСОКИЙ уровень (1) на выходе.
Таблица истинности шлюза OR:
| А | Б | Y=A ИЛИ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- B) Логический элемент И: Для двух или более входов логический элемент И выдает ВЫСОКИЙ (1) выходной сигнал, только если оба входа имеют ВЫСОКИЙ (1).
 Он выдает НИЗКИЙ (0) выход, даже если один из входов НИЗКИЙ (0). Работает аналогично логической операции AND 9.0388
Он выдает НИЗКИЙ (0) выход, даже если один из входов НИЗКИЙ (0). Работает аналогично логической операции AND 9.0388
Логическое выражение для вентиля И:
Y= A AND B
Рис. 6 Символ вентиля ИСлучай 1: A= 0, B= 0; Y= 0
В этом случае оба входа имеют НИЗКИЙ уровень (0), поэтому логический элемент И выдает НИЗКИЙ (0) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 0
В этом случае один из входов имеет НИЗКИЙ уровень (0), поэтому логический элемент И выдает НИЗКИЙ (0) выходной сигнал.
Случай 3: А= 1, В= 0; Y= 0
В этом случае один из входов НИЗКИЙ (0), поэтому логический элемент И выдает НИЗКИЙ (0) выход.
Случай 4: А= 1, В= 1; Y= 1
В этом случае оба входа имеют ВЫСОКИЙ уровень (1), логический элемент И выдает ВЫСОКИЙ уровень (1) на выходе.
И Таблица истинности шлюза:
| A | Б | Y=A И B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- C) Логический элемент НЕ: Для одного входа логический элемент НЕ создает выходной сигнал как дополнение к входному.
 Вентиль НЕ выдает ВЫСОКИЙ (1) выход, только если вход НИЗКИЙ (0), и НИЗКИЙ (0) выход, если вход ВЫСОКИЙ (1). Это работает аналогично логической операции НЕ.
Вентиль НЕ выдает ВЫСОКИЙ (1) выход, только если вход НИЗКИЙ (0), и НИЗКИЙ (0) выход, если вход ВЫСОКИЙ (1). Это работает аналогично логической операции НЕ.
Логическое выражение для шлюза НЕ:
Y=A ˉ
Рис. 7 Символ шлюза НЕСлучай 1: А=0; Y= 1
Вход вентиля НЕ НИЗКИЙ (0), выход становится ВЫСОКИЙ (1).
Случай 2: А=1; Y= 0
Вход вентиля НЕ ВЫСОКИЙ (1), поэтому выход становится НИЗКИМ (0).
Таблица истинности шлюза NOT:
| A | Y=A ˉ |
| 0 | 1 |
| 1 | 0 |
2) Универсальные логические элементы
Универсальные логические элементы могут реализовывать любое логическое выражение самостоятельно, это означает, что для их реализации не требуются никакие другие логические элементы. Один универсальный логический вентиль способен построить логическую схему.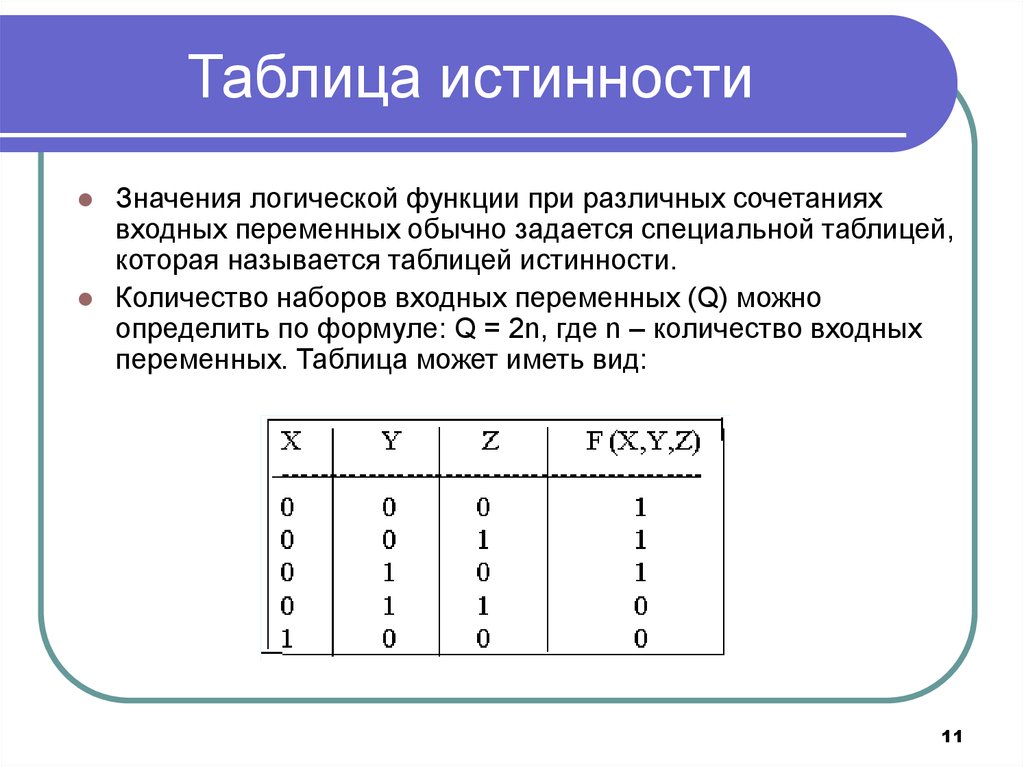 Существует два типа универсальных логических вентилей
Существует два типа универсальных логических вентилей
- A) NAND Gate
Логический элемент И-НЕ является дополнением вентиля И или просто комбинацией вентиля НЕ и вентиля И. Он называется И-НЕ, так как N означает НЕ, что означает НЕ-И-гейт. Для двух или более входов логический элемент И-НЕ выдает ВЫСОКИЙ (1) выходной сигнал, только если один из входов НИЗКИЙ (0).
Логическое выражение вентиля И-НЕ обозначается дополнением И.
Y= (AB) ˉ
Рис. 8 Символ вентиля И-НЕСлучай 1: A= 0, B= 0; Y= 1
В этом случае оба входа имеют НИЗКИЙ уровень (O), логический элемент И-НЕ выдает ВЫСОКИЙ (1) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 1
В этом случае один из входов НИЗКИЙ (0), вентиль И-НЕ выдает ВЫСОКИЙ (1) выход.
Случай 3: А= 1, В= 0; Y= 1
В этом случае один из входов НИЗКИЙ (0), вентиль И-НЕ выдает ВЫСОКИЙ (1) выход.
Случай 4: А= 1, В= 1; Y= 0
В этом случае оба входа имеют ВЫСОКИЙ (1), логический элемент И-НЕ выдает НИЗКИЙ (0) выходной сигнал.
Таблица истинности вентилей NAND:
| A | Б | Y=A НЕ-И B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- B) Ворота NOR
Шлюз НЕ-ИЛИ является дополнением шлюза ИЛИ или комбинацией шлюза НЕ и шлюза ИЛИ. Это называется ИЛИ, поскольку N означает НЕ, что означает ворота НЕ ИЛИ. Для двух или более входов логический элемент ИЛИ-НЕ выдает на выходе ВЫСОКИЙ (1); только оба входа имеют НИЗКИЙ уровень (0).
Логическое выражение NOR Gate обозначается дополнением OR.
Y= (A+B) ˉ
Рис.9 Символ вентиля НЕ-ИЛИСлучай 1: A= 0, B= 0; Y= 1
В этом случае оба входа имеют НИЗКИЙ уровень (O), логический элемент ИЛИ-НЕ выдает ВЫСОКИЙ (1) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 0
В этом случае, один из входов ВЫСОКИЙ (1), логический элемент ИЛИ-НЕ выдает НИЗКИЙ (0) выход.
Случай 3: А= 1, В= 0; Y= 0
В этом случае на одном из входов ВЫСОКИЙ уровень (1), логический элемент ИЛИ-НЕ формирует на выходе НИЗКИЙ уровень (0).
Случай 4: А= 1, В= 1; Y= 0
В этом случае оба входа имеют ВЫСОКИЙ уровень (1), логический элемент ИЛИ-НЕ формирует на выходе НИЗКИЙ уровень (0).
Таблица истинности шлюза NOR:
| A | Б | Y=A ИЛИ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
3) Производные логические элементы:
Производные или специальные элементы предназначены для конкретных приложений, таких как половинные сумматоры, полные сумматоры и вычитатели. Есть два производных логических элемента, сделанных из вентилей ИЛИ и НЕ.
Есть два производных логических элемента, сделанных из вентилей ИЛИ и НЕ.
- A) Исключающее ИЛИ, EX-OR или XOR Gate
Вентиль Ex-OR имеет два или более входа, но один выход. Логический элемент Ex-OR генерирует ВЫСОКИЙ (1) выход, если оба входа не находятся на одном и том же логическом уровне A≠B.
Рис. 10 Символ вентиля XORСлучай 1: A= 0, B= 0; Y= 0
В этом случае оба входа имеют НИЗКИЙ уровень (O) с одинаковым логическим уровнем. В результате вентиль Ex-OR выдает НИЗКИЙ (0) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 1
В этом случае один из входов НИЗКИЙ (0), а другой ВЫСОКИЙ (1). Следовательно, они не находятся на одном и том же логическом уровне. В результате вентиль Ex-OR выдает ВЫСОКИЙ (1) выходной сигнал.
Случай 3: A= 1, B= 0; Y= 1
В этом случае один из входов ВЫСОКИЙ (1), а другой НИЗКИЙ (0). Следовательно, они не находятся на одном и том же логическом уровне. В результате вентиль Ex-OR выдает ВЫСОКИЙ (1) выходной сигнал.
Случай 4: А= 1, В= 1; Y= 0
В этом случае оба входа имеют ВЫСОКИЙ уровень (1) с одинаковым логическим уровнем. В результате вентиль Ex-OR выдает НИЗКИЙ (0) выходной сигнал.
XOR Gate Truth Table:
| А | Б | Y=A Исключающее ИЛИ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- B) Исключительное ИЛИ, EX-NOR или XNOR Gate
Вентиль EX-NOR имеет два или более входа, но один выход. Логический элемент EX-NOR генерирует ВЫСОКИЙ (1) выход, если оба входа имеют одинаковый логический уровень A=B.
Рис. 11 Символ вентиля XNORСлучай 1: A= 0, B= 0; Y= 1
В этом случае оба входа имеют НИЗКИЙ уровень (O) с одинаковым логическим уровнем. В результате шлюз EX-NOR выдает ВЫСОКИЙ (1) выходной сигнал.
В результате шлюз EX-NOR выдает ВЫСОКИЙ (1) выходной сигнал.
Случай 2: А= 0, В= 1; Y= 0
В этом случае один из входов НИЗКИЙ (0), а другой ВЫСОКИЙ (1). Следовательно, они не находятся на одном и том же логическом уровне. В результате вентиль EX-NOR выдает НИЗКИЙ (0) выходной сигнал.
Случай 3: А= 1, В= 0; Y= 0
В этом случае один из входов ВЫСОКИЙ (1), а другой НИЗКИЙ (0). Следовательно, они не находятся на одном и том же логическом уровне. В результате шлюз EX-NOR выдает НИЗКИЙ (0) выходной сигнал.
Случай 4: А= 1, В= 1; Y= 1
В этом случае оба входа имеют ВЫСОКИЙ уровень (1) с одинаковым логическим уровнем. В результате шлюз EX-NOR выдает ВЫСОКИЙ (1) выходной сигнал.
Таблица истинности шлюза XNOR:
| A | Б | Y=A Исключающее ИЛИ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Надеемся, теперь у вас есть четкое представление обо всех логических элементах. Но если у вас есть какие-либо сомнения, не стесняйтесь комментировать ниже. Или вы можете использовать наш форум, чтобы связаться с нашими инженерами.
Но если у вас есть какие-либо сомнения, не стесняйтесь комментировать ниже. Или вы можете использовать наш форум, чтобы связаться с нашими инженерами.
Логические вентили и таблицы истинности – Mathigon
Обзор и цель
На этом уроке учащиеся изучают использование логических вентилей в разделе «Логика и вычисления» в Polypad. Если вы новичок в логических вентилях, этот учебник может быть полезен для чтения в первую очередь. Таблицы истинности часто используются для организации и передачи различных комбинаций входов и выходов через логические элементы.
Разминка
Предложите учащимся открыть холст Polypad и добавить два входа и один выход на холст. Предложите им посмотреть, могут ли они вызвать действие на выходе каждого из входов. Ниже приведен пример кнопки и выключателя, включающих свет:
После того, как учащиеся выполнили это задание, предложите им добавить вентиль ИЛИ между входами и выходами. Посмотрите, смогут ли они определить логику, когда включается свет.
Посмотрите, смогут ли они определить логику, когда включается свет.
Студенты, скорее всего, увидят, что свет включается, когда один или оба входа включены. Используйте эту информацию для создания таблицы истинности в качестве класса для вентиля ИЛИ . Расскажите учащимся, что верхний вход ворот — это A, нижний вход — B, а выход — Q.
В таблице истинности 0 означает ВЫКЛ, а 1 — ВКЛ. So the truth table for the OR gate is as follows:
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
В этой таблице численно показано, что только выход (Q) включен (1), а один или оба входа (A и B) включены (1).
Основное задание
Теперь учащиеся готовы приступить к созданию таблиц истинности для других логических элементов в Polypad. В зависимости от ваших предпочтений вы можете предложить учащимся составить таблицу истинности для всех ворот, позволить им выбрать некоторые ворота, поработать в группах, чтобы разделить задание и т. д.
В зависимости от ваших предпочтений вы можете предложить учащимся составить таблицу истинности для всех ворот, позволить им выбрать некоторые ворота, поработать в группах, чтобы разделить задание и т. д.
Учащиеся могут создавать свои таблицы непосредственно в Polypad, используя таблицы в разделе «Диаграммы и статистика» раздела «Вероятность и данные». Щелкните здесь, чтобы узнать о создании классов в Mathigon и о том, как учащиеся сохраняют свою работу.
Дайте учащимся достаточно времени для создания таблиц истинности. Ответы перечислены ниже.
Поддержка и расширение
Учащимся, нуждающимся в поддержке, может быть полезно выполнить еще один пример вместе. Наличие таблицы на холсте для записи результатов каждого испытания может помочь учащимся организовать свою работу.
Ниже ссылка на холст шаблона с таблицами, уже созданными для каждого логического элемента:
Шаблон логических элементов – Polypad
polypad. org/rDyyCfTiDg5KoA
org/rDyyCfTiDg5KoA
Когда учащиеся закончат, предложите им изучить комбинирование входов, выходов, и логические вентили, чтобы увидеть, что они могут создать. Некоторые примеры холстов находятся в разделе «Примеры и шаблоны» в меню «Файл» в Polypad. Предлагает учащимся изучить эти полотна. Кроме того, вы можете предложить учащимся объединить два логических вентиля и составить таблицу истинности для их комбинации.
Answers
AND
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
XOR
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
BUFFER
NAND
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
NOR
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
XNOR
| , | , | |
| , | , | |
| , | , | |
| , | , | |
| , | , |
NOT
Создать бесплатный аккаунт!
Бесплатные учетные записи Mathigon позволяют вам сохранять свою работу, настраивать классы и давать задания ученикам.


 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 В вычислительной технике логические 0 и 1 – это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 – это напряжение в диапазоне 0 + 0,4 В, а логическая 1 – это напряжение в диапазоне + 2,4…+5 В (рисунок 3.1). Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 – 1864 гг.), она является основой всех методов упрощения булевых выражений.
В вычислительной технике логические 0 и 1 – это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 – это напряжение в диапазоне 0 + 0,4 В, а логическая 1 – это напряжение в диапазоне + 2,4…+5 В (рисунок 3.1). Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 – 1864 гг.), она является основой всех методов упрощения булевых выражений.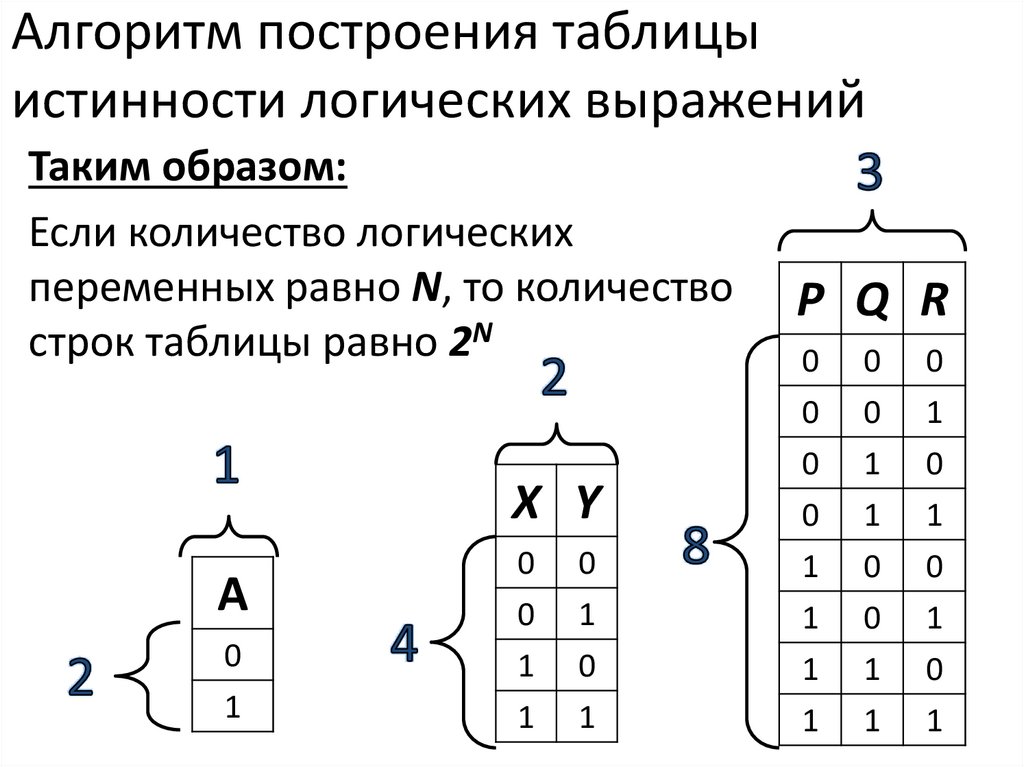
 Затем рассматриваются только те клетки, которые заполнены единицами. Все эти единицы должны быть обведены контурами по следующим правилам составления контуров:
Затем рассматриваются только те клетки, которые заполнены единицами. Все эти единицы должны быть обведены контурами по следующим правилам составления контуров:
 Учитывая, что при данном горизонтальном начертании карты Карно крайние столбцы являются соседними, ее можно представить себе как цилиндр, развернутый на плоскости. На рисунке 3.12б представлена развертка такого цилиндра, «разрезанная» между комбинациями «bc», равными 10 и 11. А на рисунке 3.12в представлена развертка этого же цилиндра, «разрезанная» между произведениями «bc», равными 11 и 01.
Учитывая, что при данном горизонтальном начертании карты Карно крайние столбцы являются соседними, ее можно представить себе как цилиндр, развернутый на плоскости. На рисунке 3.12б представлена развертка такого цилиндра, «разрезанная» между комбинациями «bc», равными 10 и 11. А на рисунке 3.12в представлена развертка этого же цилиндра, «разрезанная» между произведениями «bc», равными 11 и 01. 4)
4)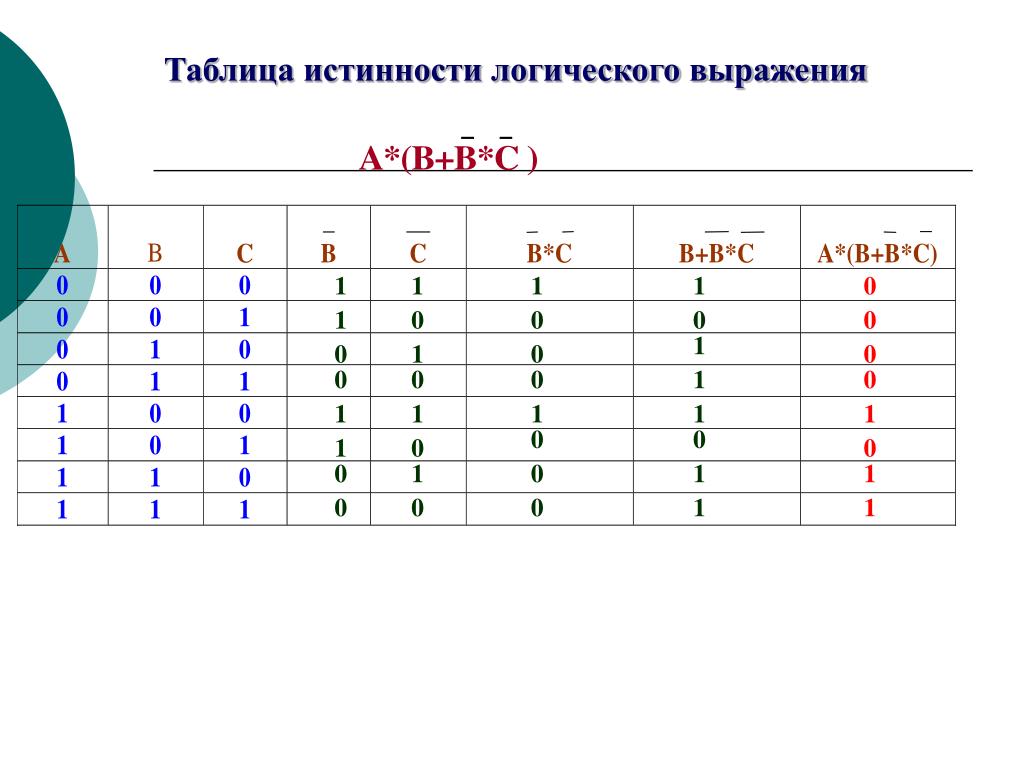 Проще представить себе обратный процесс получения торроида из плоской фигуры – квадрата. Для этого надо сначала соединить мысленно крайние строки – получим цилиндр. После этого основания цилиндров надо мысленно соединить. Получится торроид. На рисунке 3.136 б представлена развертка такого торроида, «разрезанная» между комбинациями , равными 01 и 00 и между сочетаниями , равными 10 и 00. А на рисунке 3.14 представлена развертка этого же торроида, «разрезанная» между комбинациями , равными 11 и 10 и между произведениями , равными 11 и 01. После анализа контуров получим минимальное выражение
Проще представить себе обратный процесс получения торроида из плоской фигуры – квадрата. Для этого надо сначала соединить мысленно крайние строки – получим цилиндр. После этого основания цилиндров надо мысленно соединить. Получится торроид. На рисунке 3.136 б представлена развертка такого торроида, «разрезанная» между комбинациями , равными 01 и 00 и между сочетаниями , равными 10 и 00. А на рисунке 3.14 представлена развертка этого же торроида, «разрезанная» между комбинациями , равными 11 и 10 и между произведениями , равными 11 и 01. После анализа контуров получим минимальное выражение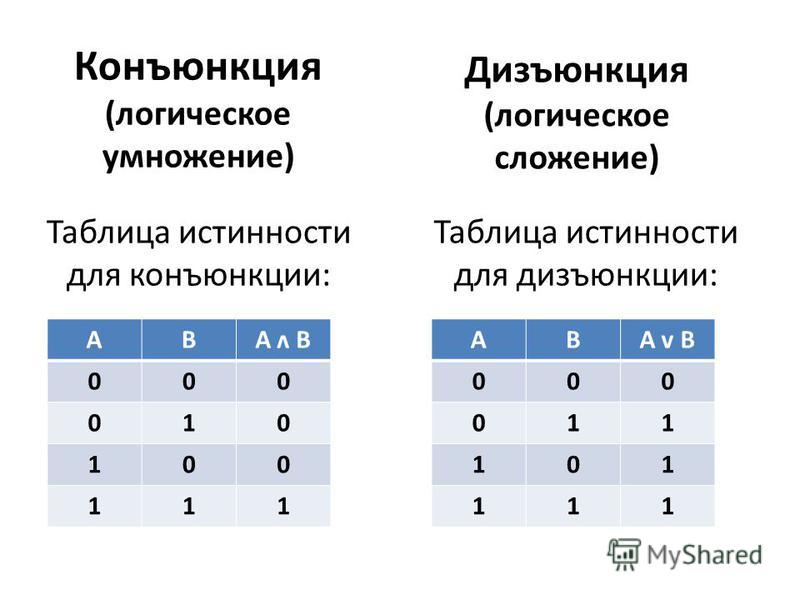
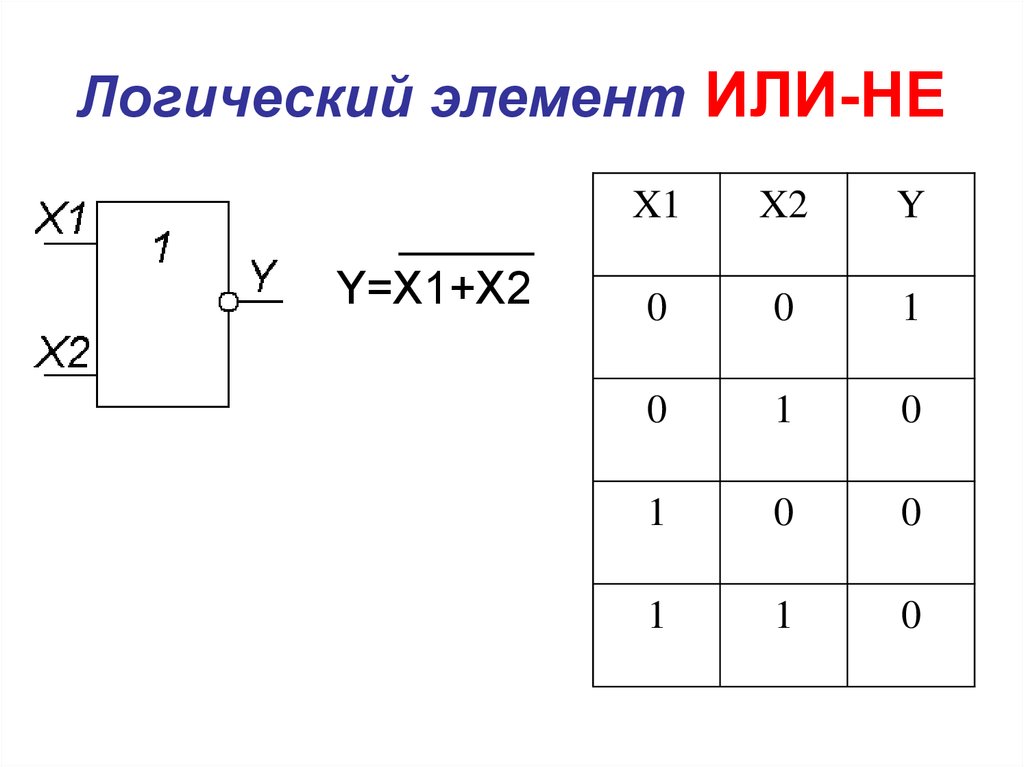
 Переменная входит в минтерм с инверсией, если её значение в строке истинности равно 0.
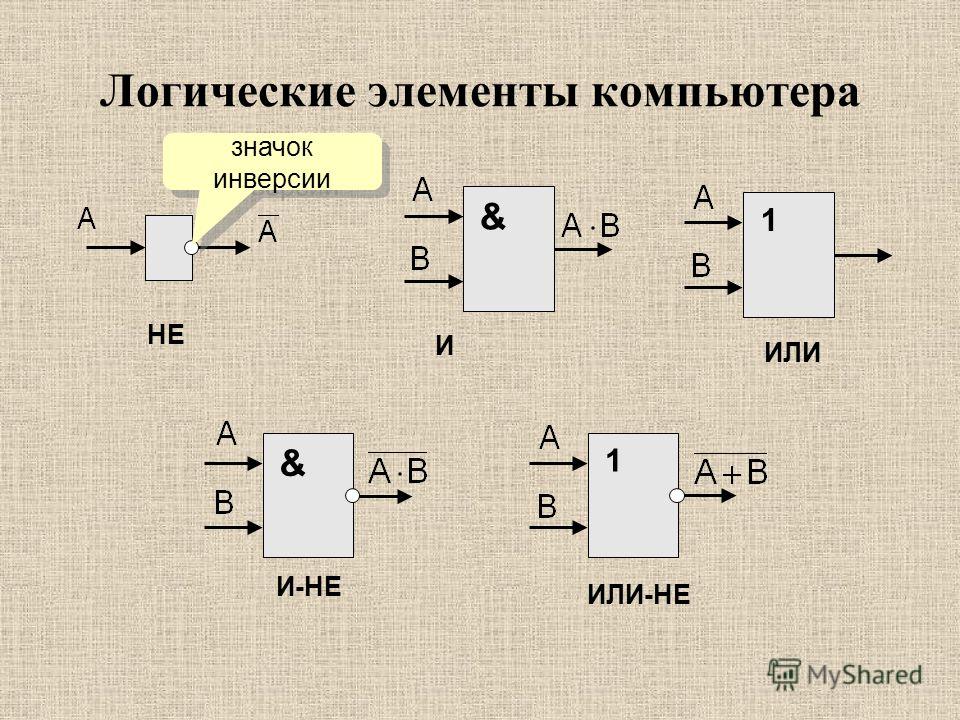
Переменная входит в минтерм с инверсией, если её значение в строке истинности равно 0.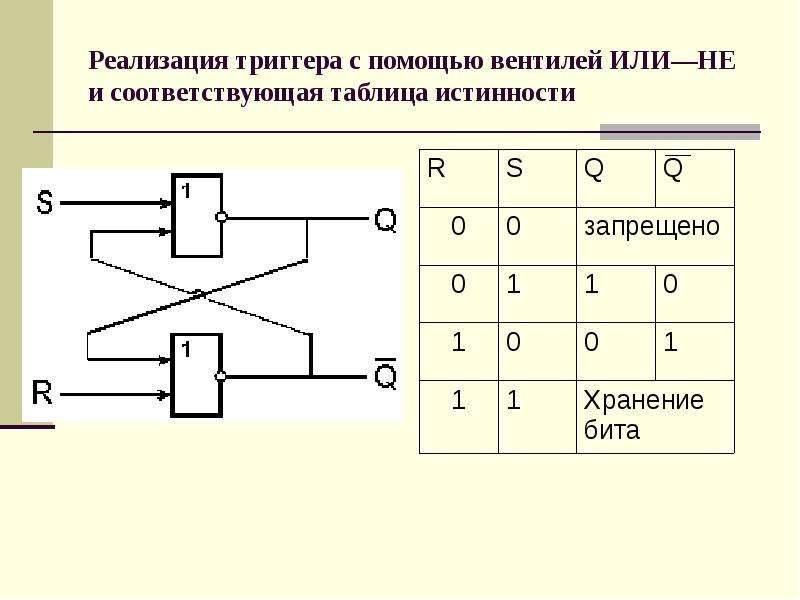 Логические схемы, в свою очередь, состоят из логических элементов. Самыми простыми логическими элементами являются элементы И, ИЛИ и НЕ. Им соответствуют функции логического умножения, сложения и инверсии.
Логические схемы, в свою очередь, состоят из логических элементов. Самыми простыми логическими элементами являются элементы И, ИЛИ и НЕ. Им соответствуют функции логического умножения, сложения и инверсии.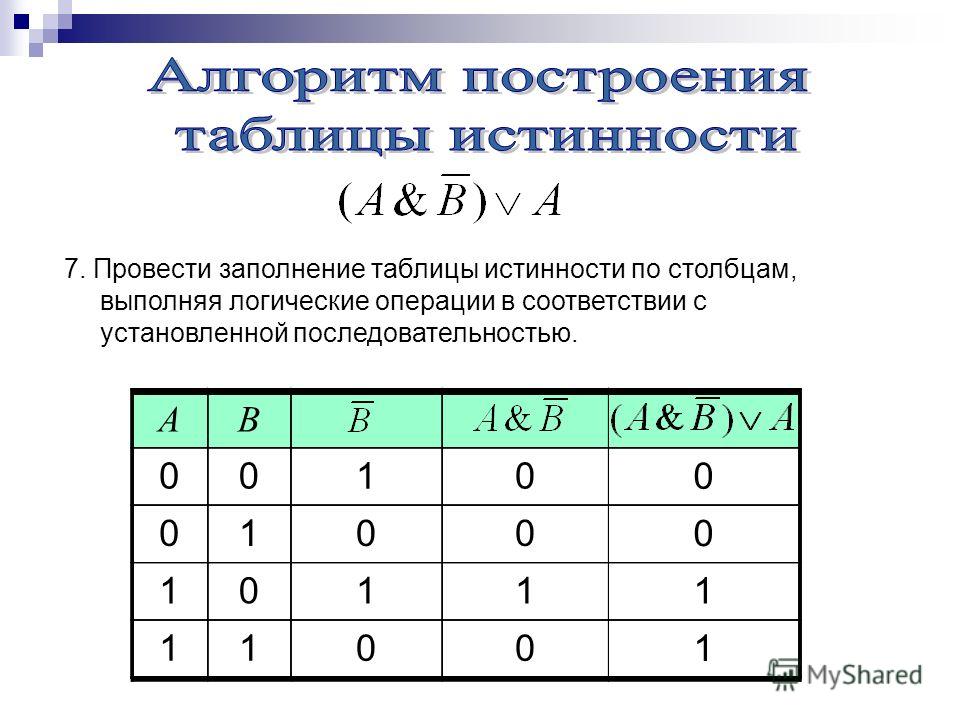
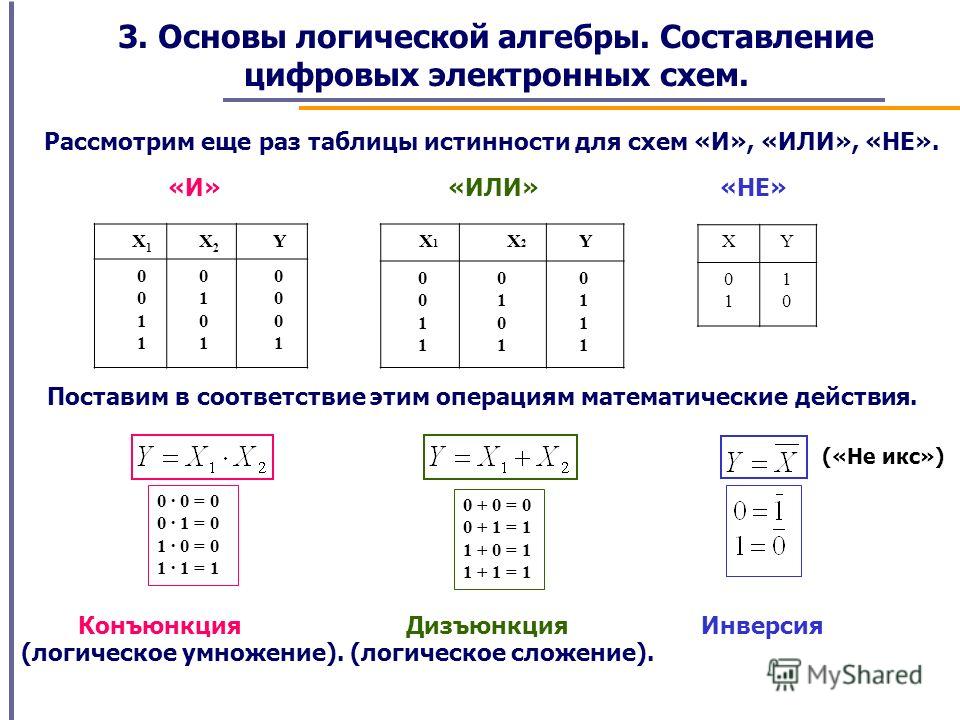
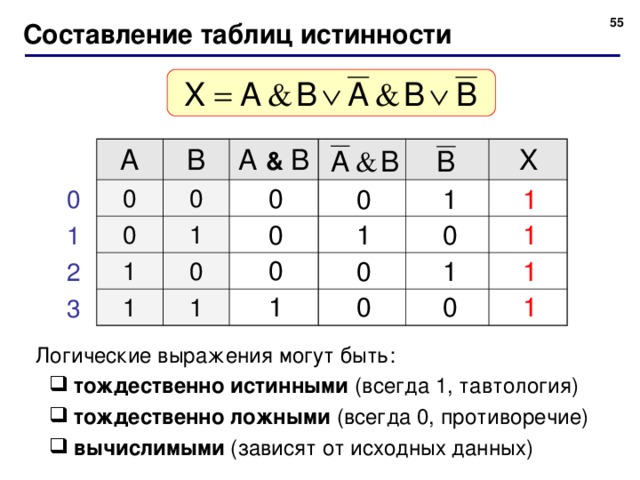 Он выдает НИЗКИЙ (0) выход, даже если один из входов НИЗКИЙ (0). Работает аналогично логической операции AND 9.0388
Он выдает НИЗКИЙ (0) выход, даже если один из входов НИЗКИЙ (0). Работает аналогично логической операции AND 9.0388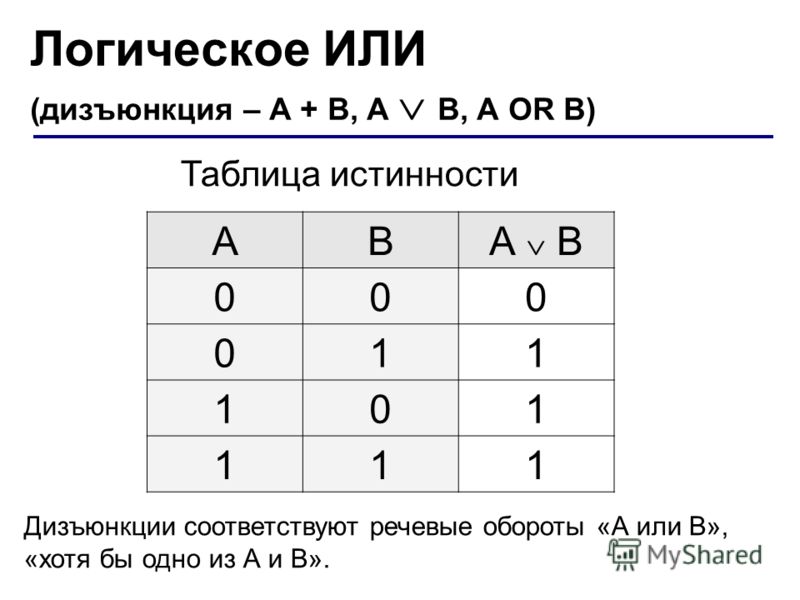 Вентиль НЕ выдает ВЫСОКИЙ (1) выход, только если вход НИЗКИЙ (0), и НИЗКИЙ (0) выход, если вход ВЫСОКИЙ (1). Это работает аналогично логической операции НЕ.
Вентиль НЕ выдает ВЫСОКИЙ (1) выход, только если вход НИЗКИЙ (0), и НИЗКИЙ (0) выход, если вход ВЫСОКИЙ (1). Это работает аналогично логической операции НЕ.