Таблица истинности логических операций — алгоритм построения » Kupuk.net
Используя таблицы истинности логических операций, можно точно определить, верна ли функция при определённых значениях. В перечень заносят всевозможные комбинации переменных появляющихся на входе и соответствующие им состояния на выходе. Чаще всего таблицы применяют при проектировании и анализе цифровых схем. При этом в интернете существуют сервисы, с помощью которых построить такого рода сводку не составит труда даже слабо разбирающемуся в этой сфере пользователю.
Определения и понятия
Под таблицей истинности понимают свод значений, которые может принять высказывание при сочетании различных входящих комбинаций. Другими словами, каждому набору функций или сигналам, присутствующим на входе чего-либо, соответствует строго определённые показатели на выходе. Все значения, являющиеся всевозможными высказываниями, называют логическими выражениями. Если в таблице последние столбцы логичных выражений идентичны, то рассматриваемый объект считается равносильным.
Любое выражение можно описать формулой, в которую будут включаться переменные, характеризующие состояния, и обозначающие функции знаки логических операций. Поэтому используя язык математики, в частности, алгебры, любое сложное высказывание можно разделить на несколько простых, а затем объединить логической связью.
Обычно значениями истинности описывают логическую функцию, у которой показатели параметров определяют верность. Раздел математики рассматривающий их на правдивость или ложность называется булевым. В 1854 году английский учёный Джордж Буль предложил метод, позволяющий проводить анализ классов и высказываний. Согласно ему, любое значение может принимать одно из двух состояний — истина или ложь.
Эти состояния принято обозначать арабскими цифрами один либо ноль или словами true и false. Это возможно из-за того, что для математики важна только истинность высказываний, а конкретное содержание второстепенно. Простые высказывания принято считать логическими переменными, а сложные — функциями логики.
Выражения для упрощения записи обозначают латинскими буквами A, B, C.
Применение двух цифр подчёркивает соответствие между двоичной системой счисления и математической логикой. В итоге с помощью последней стало удобным описывать работу цифровых схем радиоэлектронной аппаратуры, алгоритмы в программировании, проводить синтез и анализ результата выполнения операций.
Суждение о правильности построения таблиц истинности для логических выражений основано на учёте всех переменных и операций, последовательно выполняющихся в рассматриваемой функции. Обычно для начертания используют 2n+1 строк, где n обозначает количество входных переменных, и n+m столбцов, m — число значений на выходе.
Виды логических операций
В качестве наименьшей единицы измерения объёма данных принято считать бит. В него заносится одно из двух значений — ложь (0) или правда (1). Каждая ячейка, соответствующая биту, находится лишь в одном из этих состояний. Существуют определённые операции, используемые для действий с ячейками:
Каждая ячейка, соответствующая биту, находится лишь в одном из этих состояний. Существуют определённые операции, используемые для действий с ячейками:
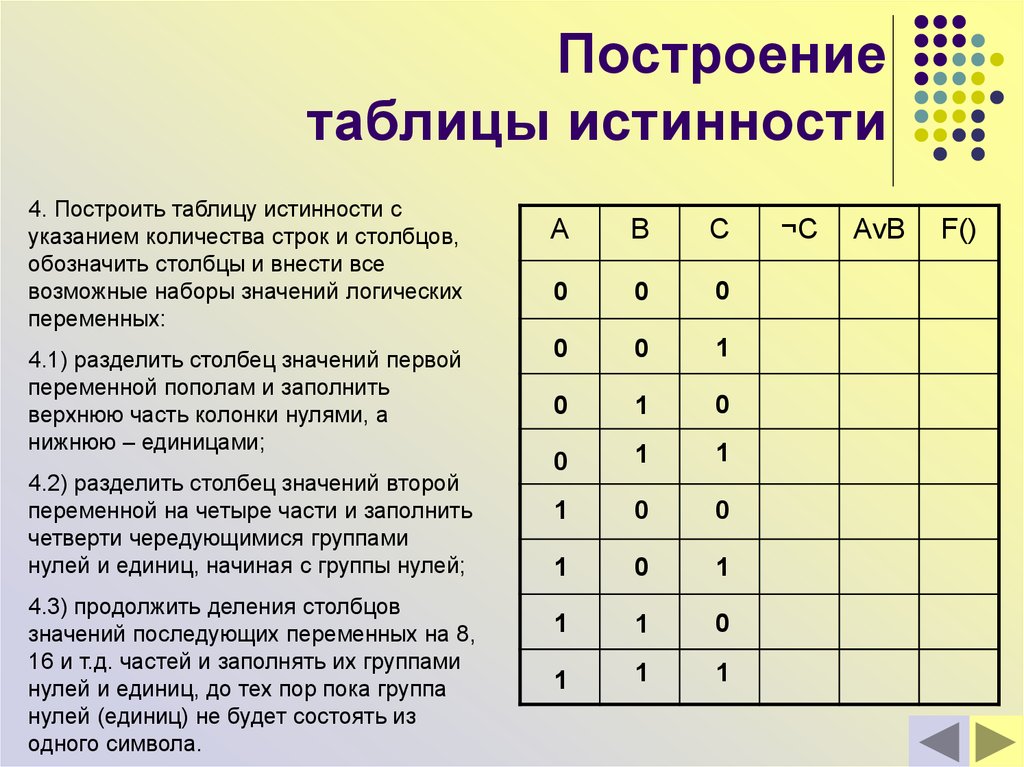
Эти операции являются основными элементами при составлении таблиц истинности и получения возможного результата. На основании их построена алгебра Буля. Некоторые элементы получаются путём объединения нескольких операций. Так, существует состояние: NAND (И-НЕ) и NOR (ИЛИ-НЕ). Первый элемент является инверсией операции «И», а второй — «ИЛИ». На основании рассмотренных операторов строится работа всех цифровых интегральных схем.
В информатике существует своя терминология, обозначающая то или иное логическое действие. Так, AND называют операцией конъюнкции, OR — дизъюнкции, XOR — сложение по модулю 2, NOT — отрицание. Задача инженера при анализе схем или алгоритма сводится к выполнению булевой арифметики и упрощению выражений. Для этого используют различные правила и положения не требующих доказательства.
Аксиомы и законы
Построение таблиц в удобной форме позволяет определить, когда определённое действие или высказывание принимает верное значение, а в каком случае нет.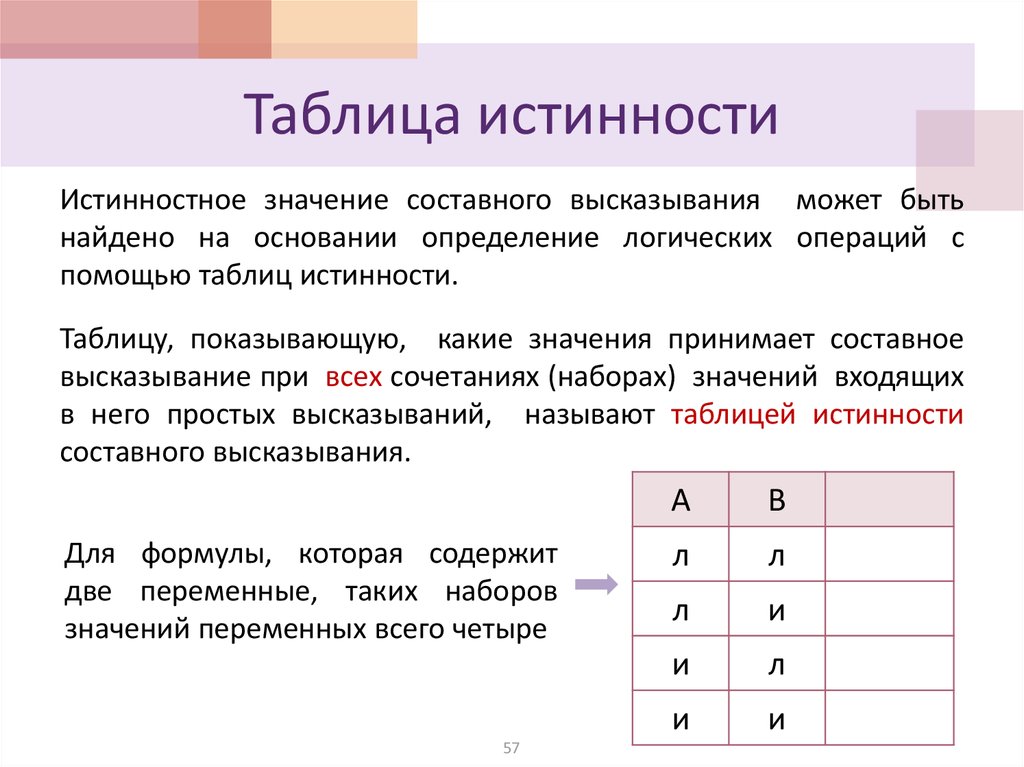 В верхней строчке записывают логическую форму высказывания, а в столбцах — истинные значения. Некоторые комбинации высказываний всегда будут истинными или ложными, независимо от содержания. Поэтому и были сформулированы следующие законы:
В верхней строчке записывают логическую форму высказывания, а в столбцах — истинные значения. Некоторые комбинации высказываний всегда будут истинными или ложными, независимо от содержания. Поэтому и были сформулированы следующие законы:
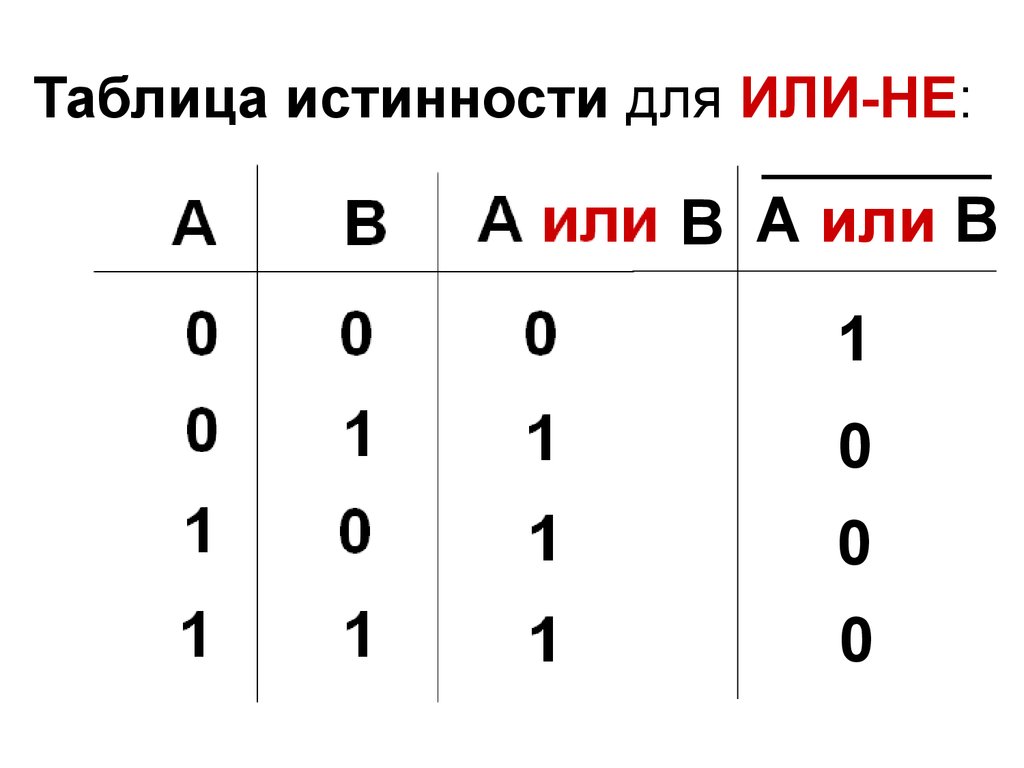 То есть третьего не дано.
То есть третьего не дано.Эти три закона фундаментальны. Без их соблюдения сделать любое правильное утверждение невозможно.
Для решения логических задач с помощью таблиц истинности используют различные формулы, соответствующие разного вида операциям. Одно из них логическое умножение (конъюнкция). В этом случае считается, что функция истинная лишь тогда, когда оба выражения являются верными: F = A & B. Другое логическое сложение (дизъюнкция). Оно гласит, что если оба выражения ложны, то и логическая функция будет неверной.
Кроме того, используется закон:
- инверсии (отрицания) — если логическое высказывание истинно, то отрицание его будет ложным выражением;
- импликации (следования) — для всегда истинного сложного логического выражения ложь будет тогда, когда из верности следует отрицание;
- эквивалентности (равнозначности) — выражение будет истинным лишь тогда, когда оба высказывания имеют одинаковое значение.

При построении таблиц нужно придерживаться установленного порядка выполнения упрощения операций. Вначале считают инверсию и конъюнкцию, а затем дизъюнкцию, импликацию и эквиваленцию. При изменении же порядка выполнения действий в описании логических операций используют скобки.
Алгоритм построения
Таблицы истинности показывают, какой вид может принять выражение при различных входящих в него значениях переменных. Для того чтобы их правильно построить и выполнить вычисление логического выражения нужно придерживаться установленного алгоритма. Построение таблиц выполняют в следующей последовательности:
- подсчитывают количество переменных n;
- вычисляют число строк для будущей таблицы используя формулу m = 2n+1;
- определяют число логических операций;
- устанавливают порядок выполнения операций в соответствии со скобками и приоритетами;
- строят таблицу с указанием столбцов и наборов значений, заданных логических операций;
- заполняют оставшиеся ячейки в таблице.

Для заполнения таблиц нужно упрощать выражения с учётом последовательности выполнения операций. При этом учитывать, что если значение какого-то из аргументов функции в соответствующей строке таблицы будет равное нулю, то записывать его нужно в виде отрицания.
Пример задания
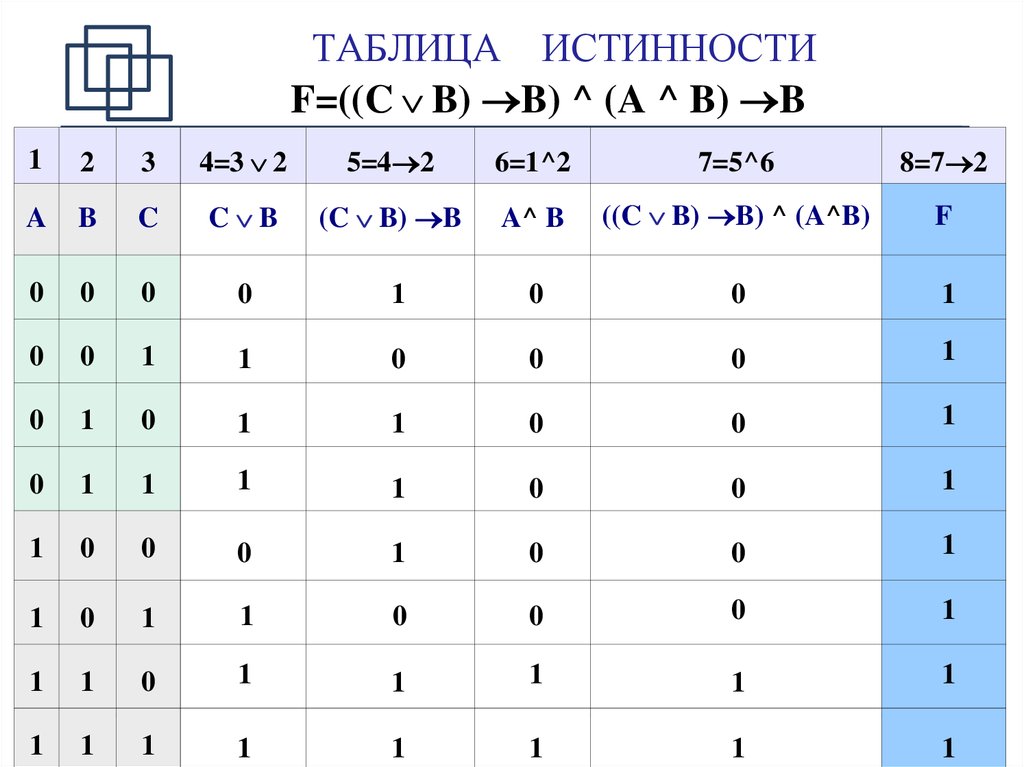
Пусть необходимо построить таблицу для логического выражения F = (A → B) * (A + B). Эта формула состоит из двух логических переменных A и B и нескольких операций. Начинают построение с определения строк. Используя формулу 2n+1 для рассматриваемого примера можно установить, что их число будет: x = 22 + 1 = 5.
Теперь следует определить число столбцов. Для этого используется формула, в которой учитывается количество переменных и операций. Последние можно просто посчитать, сложив количество разных знаков, используемых в записи формулы. Но правильней сначала расставить порядок операций, а затем посчитать. Согласно порядку действия над операциями их нумерацию можно представить в следующей очерёдности:
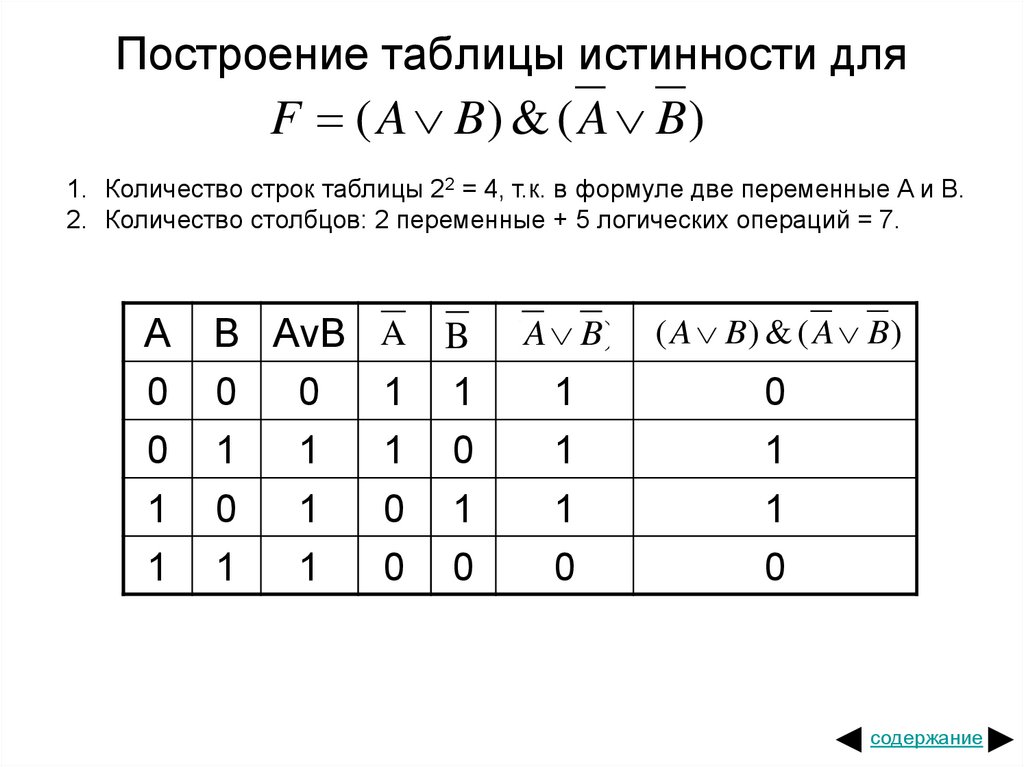
В итоге получится, что столбцов будет: Y = 2 + 5 = 7. Теперь нужно построить таблицу 7Х5. В шапку первого и второго столбца вписывают переменные, а затем операции над ними. Затем в строках, соответствующих A и B нужно записать всё, что с ними может произойти. В итоге останется только правильно посчитать последний столбец.
Для этого нужно использовать законы. Необходимо выполнить логическое умножение значений в скобках. Первой и второй строчке будет соответствовать операция произведения один на один, что в ответе даст единицу. Третьей и четвёртой — ноль на один, что в итоге даст ноль. Последний столбец является главным для рассматриваемой логической функции. По нему можно узнать значение логической функции для любых форм переменных A и B.
Это довольно простая задача, содержащая всего две переменных. Но в реальности, например, в программировании, их может быть намного больше. Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.
Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.
Например, заданно выражение (x + y + z) * (x + y). По сути, оно записано в совершенно нормальной конъюнктивной форме. Но для приведения его к этому виду нужно, чтобы во втором выражении стояла z. Для того чтобы её добавить необходимо обратить внимание на то, что внутри скобок стоит логическое сложение. Поэтому дописав к нему ноль, результат не изменится. Добавить ноль через z можно, как ноль умножить на НЕ z. В итоге получится выражение (x + y + z) * (x + y + z + z), для которого, используя алгоритм составить таблицу уже не так и сложно.
Вычисления онлайн
В интернете есть сервисы, автоматически строящие таблицы истинности. Такие сайты предлагают свои услуги бесплатно и доступны даже тем, кто слабо ориентируется в теме. С их помощью можно находить таблицы для довольно сложных выражений, решение которых требует скрупулёзности в расчёте. В основе онлайн-вычислений заложены принципы логических законов, поэтому за достоверность результата можно не переживать. Тем более расчёт занимает совсем небольшое количество времени.
В основе онлайн-вычислений заложены принципы логических законов, поэтому за достоверность результата можно не переживать. Тем более расчёт занимает совсем небольшое количество времени.
Для того чтобы воспользоваться сайтами-калькуляторами пользователю необходимо знать обозначение операций, иметь подключение к интернету и установленный веб-обозреватель, поддерживающий Flash-технологию. Регистрацию, указание личных данных сервисы, предлагающие такого рода услуги, не требуют.
Из различных порталов можно отметить три наиболее популярных калькулятора:
Эти сайты имеют интуитивно понятный интерфейс и что довольно полезно, на своих страницах содержат краткую теорию, используемую для составления таблиц истинности и даже примеры решений.
 ru 🎓
ru 🎓1
Первый слайд презентации
Что такое таблица истинности? Приведите примеры
Изображение слайда
2
Слайд 2: Пример:
Изображение слайда
3
Слайд 3: Логические схемы и выражения
Раздел 9.1А: Архитектура компьютера суббота, 22 сентября 2018 г.
Изображение слайда
4
Слайд 4: Цели обучения
9.4.2.1 строить логические схемы и логические выражения Критерии оценивания Знать обозначения и определение логических операций Уметь составлять таблицу истинности и строить схему по предложенному выражению Составлять выражение и таблицу истинности исходя из логической схемы
Изображение слайда
5
Слайд 5
Цель обучения
9. 4.2.1 строить логические схемы и логические выражения
Критерий оценивания:
Знать обозначения и определение логических операций
Задание 1. (И) Используя поисковую систему найдите определение и обозначения логическим операциям.
Оценивание : — Самооценивание. Отмечаем в листах самооценивания
— Взаимооценивание. оценка другой группе через комментарий **+ пожелание
Дескриторы :
Определяет логический элемент и обозначение
Определяет таблицу истинности
Записывает определение логической операции
Определяет логический элемент и обозначение
Использует
— предметную лексику : дизъюнкция, конъюнкция и инверсия;
— фразу для диалога :
К логическим функциям относятся…
4.2.1 строить логические схемы и логические выражения
Критерий оценивания:
Знать обозначения и определение логических операций
Задание 1. (И) Используя поисковую систему найдите определение и обозначения логическим операциям.
Оценивание : — Самооценивание. Отмечаем в листах самооценивания
— Взаимооценивание. оценка другой группе через комментарий **+ пожелание
Дескриторы :
Определяет логический элемент и обозначение
Определяет таблицу истинности
Записывает определение логической операции
Определяет логический элемент и обозначение
Использует
— предметную лексику : дизъюнкция, конъюнкция и инверсия;
— фразу для диалога :
К логическим функциям относятся…
Изображение слайда
6
Слайд 6
6 Элемент « Дизъюнктор » « ИЛИ» ( OR) Элемент « Конъюктор » «И » ( AND) Элемент «Инвертор» « НЕ» ( NOT)
Изображение слайда
7
Слайд 7
Цель обучения
9. 4.2.1 строить логические схемы и логические выражения
Критерий оценивания:
Уметь составлять таблицу истинности и строить схему по предложенному выражению
Задание 2. ( И,ф ) Построить таблицу истинности и логическую схему: (¬А v ¬ В) & С
Оценивание : — Самооценивание. Отмечаем в листах самооценивания
— Обратная связь учителя.
Дескриторы :
Правильно определил последовательность выполнения логических операции
Правильно заполнил таблицу истинности
Правильно построил схему
Проверил схему в онлайн симуляторе логических схем (www.logic.ly/ demo )
4.2.1 строить логические схемы и логические выражения
Критерий оценивания:
Уметь составлять таблицу истинности и строить схему по предложенному выражению
Задание 2. ( И,ф ) Построить таблицу истинности и логическую схему: (¬А v ¬ В) & С
Оценивание : — Самооценивание. Отмечаем в листах самооценивания
— Обратная связь учителя.
Дескриторы :
Правильно определил последовательность выполнения логических операции
Правильно заполнил таблицу истинности
Правильно построил схему
Проверил схему в онлайн симуляторе логических схем (www.logic.ly/ demo )
Изображение слайда
8
Слайд 8
Цель обучения
9.4.2.1 строить логические схемы и логические выражения
Критерий оценивания:
Составлять выражение и таблицу истинности исходя из логической схемы
Задание 3. ( И,ф ) По схеме напишите логическое выражение и постройте таблицу истинности.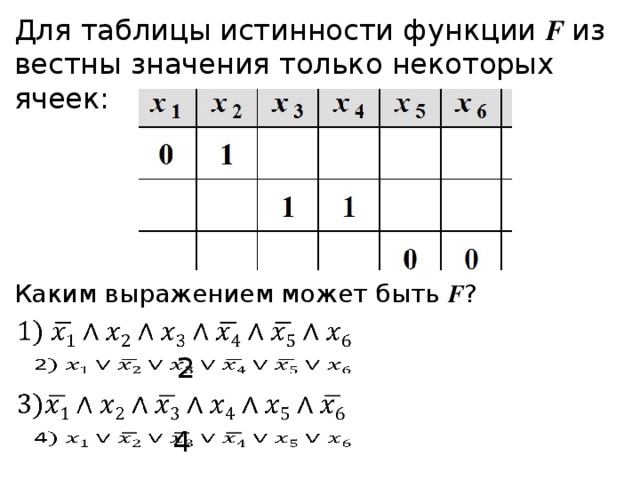
Изображение слайда
9
Слайд 9
Обозначьте своё мнение по изучению темы в свои индивидуальные листы
10
Слайд 10: Цели обучения
9.4.2.1 строить логические схемы и логические выражения Критерии оценивания Знать обозначения и определение логических операций Уметь составлять таблицу истинности и строить схему по предложенному выражению Составлять выражение и таблицу истинности исходя из логической схемы
Изображение слайда
11
Слайд 11
Изображение слайда
12
Слайд 12
Изображение слайда
13
Слайд 13: Логические схемы и выражения
Раздел 9. 1А: Архитектура компьютера
суббота, 22 сентября 2018 г.
1А: Архитектура компьютера
суббота, 22 сентября 2018 г.
Изображение слайда
14
Слайд 14: Цели обучения
9.4.2.1 строить логические схемы и логические выражения Критерии оценивания Составлять выражение и таблицу истинности исходя из логической схемы
Изображение слайда
15
Слайд 15: Повторение тем
5 (мин)
Изображение слайда
16
Слайд 16: Знакомство с рубрикой
2 мин
17
Слайд 17: СОР «Архитектура компьютера»
20 мин
Изображение слайда
18
Слайд 18: (И) Поиграйте в игру Logic Gate Puzzler в онлайн режиме, составляя логические схемы и изучая логические операции https://goo.
 gl/iWsPqA
gl/iWsPqA
Изображение слайда
19
Слайд 19
Обозначьте своё мнение по изучению темы в свои индивидуальные листы
Изображение слайда
20
Слайд 20: Цели обучения
9.4.2.1 строить логические схемы и логические выражения Критерии оценивания Составлять выражение и таблицу истинности исходя из логической схемы
Изображение слайда
21
Последний слайд презентации: Что такое таблица истинности? Приведите примеры: Подведение итогов урока
Рефлексия
Изображение слайда
Шифраторы.
 Составление таблиц истинности шифраторов
Составление таблиц истинности шифраторовЛабораторная работа 2.2 Шифраторы
Основные теоретические положения
Шифраторомназывается устройство, предназначенное для преобразования чисел, например, из десятичной системы в двоичную систему счисления. Основное применение шифраторов – это введение информации с клавиатуры. Обозначение CD(n—m), где n – количество входов, m – число выходов.
Схема и таблица истинности CD
Файлы для моделирования этих элементов расположены в папке Lab_2_2\Модели.
Таблица истинности CD(4 – 2) Таблица 1
Номер входа X ( | Выходной код Y (N2) | |
Y1 | Y0 | |
0 | 0 | 0 |
1 | 0 | 1 |
2 | 1 | 0 |
3 | 1 | 1 |
Рис.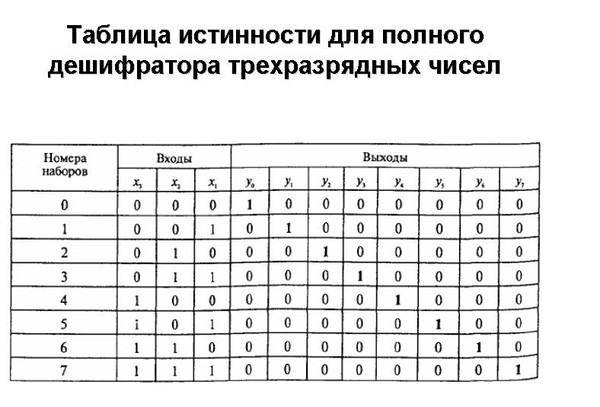 1 Шифратор CD(4-2) на логических элементах ИЛИ
1 Шифратор CD(4-2) на логических элементах ИЛИ
Уравнения работы шифратора CD(4-2):
Задание 1. С помощью комбинаций входных сигналов изучить работу CD(4-2) файл L2_CD_01.ewb, и его таблицу истинности.
Задание 2. Составить таблицу истинности (табл. 2) шифратора CD(4-2), изображенного на рис. 2.
Таблица истинности CD(4 – 2) Таблица 2
Номер входа X (N10) | Выходной код Y (N2) | |
Y1 | Y0 | |
0 | ||
1 | ||
2 | ||
3 | ||
Рис. 2 Шифратор CD(4-2) на логических элементах ИЛИ-НЕ (файл L2_CD_04.ewb)
2 Шифратор CD(4-2) на логических элементах ИЛИ-НЕ (файл L2_CD_04.ewb)
1 Приоритетный шифратор
Шифратор называют приоритетным, если он формирует код, определяющий номер единицы, стоящей в старшем разряде, из других имеющихся единиц.
Таким шифратором является CD(8-3) выполненный на микросхеме (рис. 3), файл L2_CD_02.ewb.
Шифратор имеет служебные входы и выходы:
- Разрешающий вход (инверсный) EI=0 – шифратор преобразует входной код, если EI =1, то на всех информационных выходах шифратора появляются единицы.
- Выход GS в данном шифраторе указывает на использование всех разрядов шифратора и его переполнение (все единицы).
- Выход EO= 1 определяет отсутствие сигналов на всех
информационных выходах.

Особенность данной схемы: номер старшей единицы преобразуется в код, если имеются единицы во всех младших разрядах. Область применения – аналого-цифровые преобразователи (АЦП).
Рис. 3 Приоритетный шифратор CD (8-3)
Задание 3. Заполнить таблицу истинности (табл. 3) приоритетного шифратора CD(8-3) используя модель: файл L2_CD_02.ewb.
Клетки таблицы в разделе «Информационные входы», где может находиться 0 или 1, не оказывая влияния на результат шифрации в разделе «Выходы», заполнить знаком «Х».
Таблица истинности CD(8 – 3) Таблица 3
№ | Служебный вход | Информационные входы | Выходы | ||||||||||
EI | X7 | X6 | X5 | X4 | X3 | X2 | X1 | X0 | EO | Y2 | Y1 | Y0 | |
0 | 0 | 1 | 0 | 0 | 0 | ||||||||
1 | 0 | 1 | 0 | 0 | 1 | ||||||||
2 | 0 | 1 | 0 | 1 | 0 | ||||||||
3 | 0 | 1 | 0 | 1 | 1 | ||||||||
4 | 0 | 1 | 1 | 0 | 0 | ||||||||
5 | 0 | 1 | 1 | 0 | 1 | ||||||||
6 | 0 | 1 | 1 | 1 | 0 | ||||||||
7 | 0 | 1 | 1 | 1 | 1 | ||||||||
8 | 0 | 0 | 1 | 1 | 1 | ||||||||
9 | 1 | 1 | 1 | 1 | |||||||||
Вывод:
— Если при
достижении амплитудного значения изменяющегося во времени аналогового сигнала
уровней 1, 2…7 (столбец «№» табл.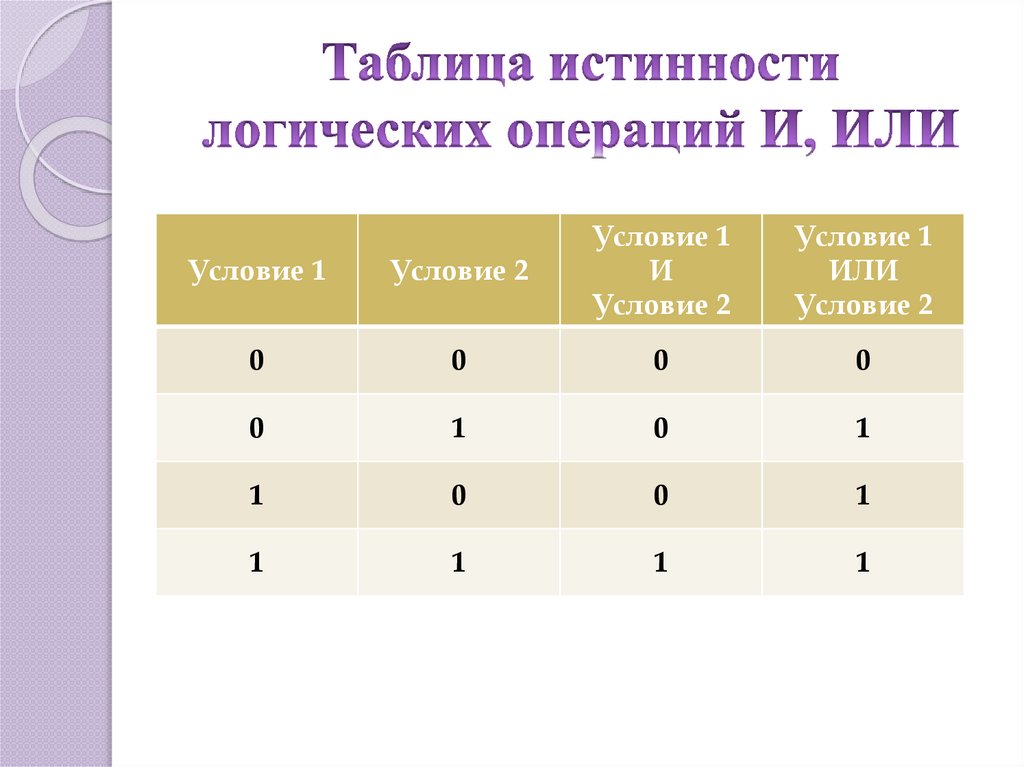 3) будет замыкаться соответствующий ключ – на
выходе приоритетного шифратора получим цифровой код для этого значения сигнала.
Этот принцип использован в параллельных АЦП.Вход EI в таблице 3 и модели инверсный.
3) будет замыкаться соответствующий ключ – на
выходе приоритетного шифратора получим цифровой код для этого значения сигнала.
Этот принцип использован в параллельных АЦП.Вход EI в таблице 3 и модели инверсный.
— Шифраторы являются преобразователями кодов, причем результирующий код более компактен, чем исходный.
2 Указатель старшей единицы
Приоритетный шифратор CD(8-3) выполнен на микросхеме (рис. 4), файл L2_CD_03.ewb. Шифратор выявляет старшую (левую) единицу, в отличие от предыдущей схемы в младших разрядах, при этом, могут быть также нули, и формирует двоичный код соответствующего единице десятичного номера.
Он называется указателем старшей единицы и исключает ошибки, например, при одновременном нажатии двух клавиш клавиатуры, применяется в работе светофоров и т.д.
Выход GSшифратора, указывает на наличие информационного сигнала хотя бы на
одном входе.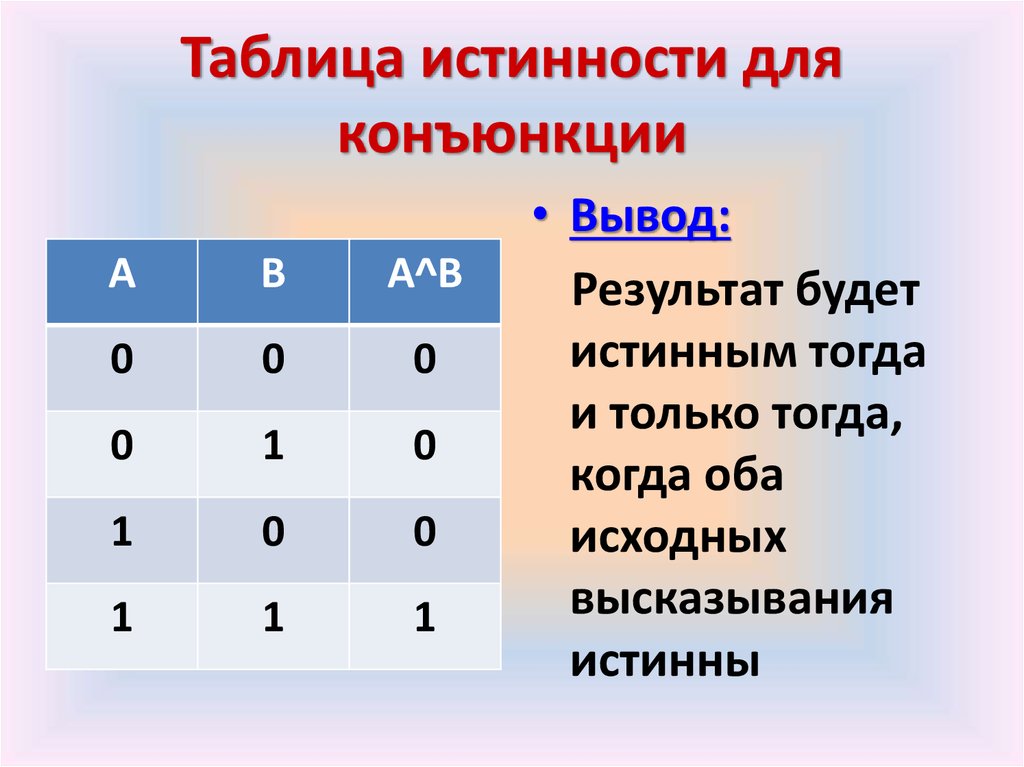 Для разрешения работы на вход подается единица EI=1.
Для разрешения работы на вход подается единица EI=1.
Рис. 4 Указатель старшей единицы CD (8-3)
Задание 4
Заполнить таблицу истинности (табл. 4) указателя старшей единицы CD(8-3), используя модель: файл L2_CD_03.ewb.
Клетки таблицы в разделе «Информационные входы», где может находиться 0 или 1, не оказывая влияния на результат шифрации в разделе «Выходы», заполнить знаком «Х».
Таблица истинности CD(8 – 3) Таблица 4
№ | Служебный вход | Информационные входы | Служебные выходы | Информационные выходы | ||||||||||
EI | X7 | X6 | X5 | X4 | X3 | X2 | X1 | X0 | EO | GS | Y2 | Y1 | Y0 | |
0 | 1 | 0 | 0 | 0 | ||||||||||
1 | 1 | 0 | 0 | 0 | ||||||||||
2 | 1 | 0 | 0 | 1 | ||||||||||
3 | 1 | 0 | 1 | 0 | ||||||||||
4 | 1 | 0 | 1 | 1 | ||||||||||
5 | 1 | 1 | 0 | 0 | ||||||||||
6 | 1 | 1 | 0 | 1 | ||||||||||
7 | 1 | 1 | 1 | 0 | ||||||||||
8 | 1 | 1 | 1 | 1 | ||||||||||
9 | 0 | |||||||||||||
Задание 5.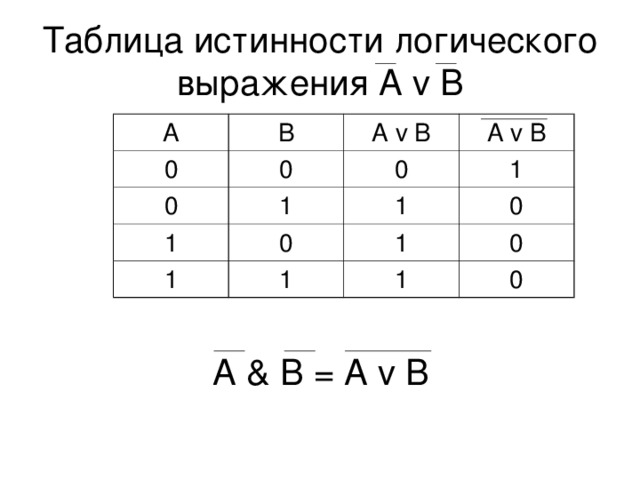 Перечислить,
где и для каких целей применяются шифраторы.
Перечислить,
где и для каких целей применяются шифраторы.
Выводы:
Шифраторы являются преобразователями кодов, причем результирующий код более компактен, чем исходный.
Служебные входы и выходы шифраторов используются для расширения их функциональных возможностей:
— вход EI(бывает прямым или инверсным) служит для определения момента времени, когда шифратор должен преобразовать код. Это позволяет согласовать его работу с другими устройствами, когда они готовы передавать и считывать информацию с шифратора.
— выходы GSи EO используются с целью увеличения разрядности путем выработки сигналов для подключения дополнительных шифраторов.
Шифраторы применяются, например, для преобразования
десятичного кода двоичный при вводе информации с клавиатуры в
компьютер (калькулятор, сотовый телефон), в аналового-цифровых преобразователях
и т.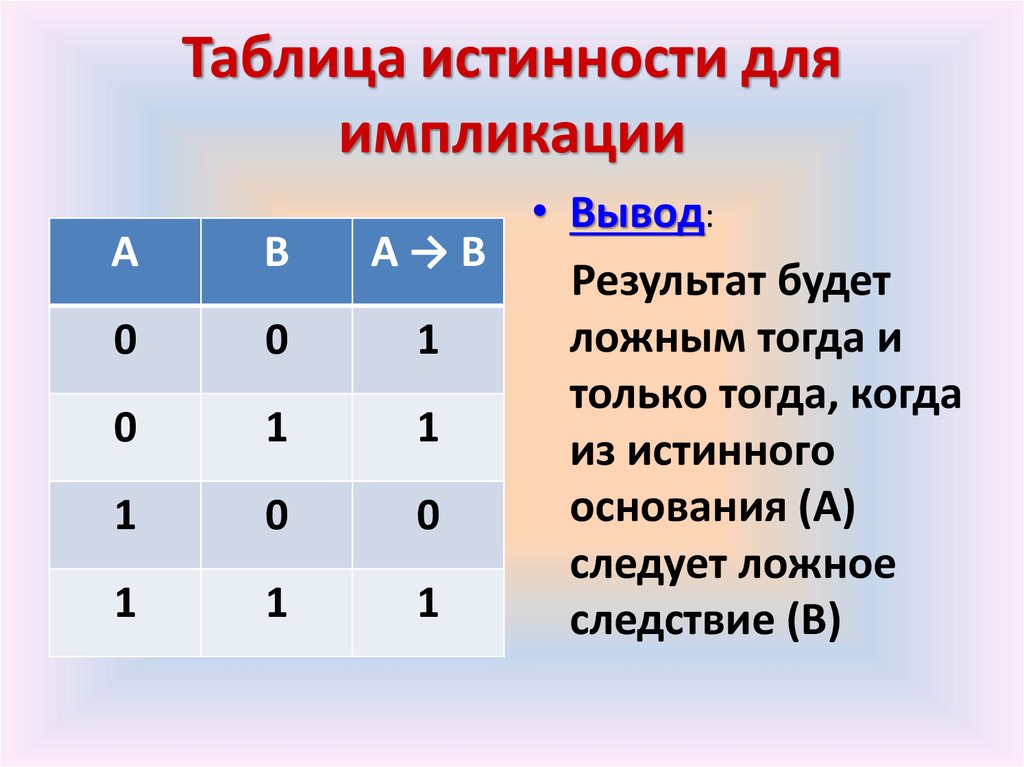 д.
д.
| Главная Другое |
страница 1страница 2страница 3страница 4 III. Изложение нового материала 1. Таблицы истинности Решение логических выражений принято записывать в виде таблиц истинности — таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных. Для составления таблицы необходимо:
Построим таблицу истинности для выражения F = (AvB)&(¬Av¬B). Количество строк = 22 (2 переменных) + 1 (заголовки столбцов) = 5. Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (v, &, ¬, v,) = 7. Расставим порядок выполнения операций: 1 5 2 4 3 (A v B) & (A vB) Построим таблицу:
Пример 2 Построим таблицу истинности для логического выражения X v Y& ¬ Z
3 2 1 X v Y&¬Z 4. Нарисуем и заполним таблицу:
2. Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 — 1933), кстати, несколько лет, работавший в России, писал еще в 1910 году: «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить: 1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции; 2) не содержит ли она излишних усложнений. Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе — система чисто качественных… «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?». Созданная позднее М.А.Гавриловым (1903 — 1979) теория релейно-контактных схем показала, что это вовсе не утопия. Посмотрим на микросхему. С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или его нет; электрическое напряжение есть или его нет… В связи с этим поговорим о различных вариантах управления включением и выключением обыкновенной лампочки (лампочка также работает на электричестве). Для этого рассмотрим электрические контактные схемы, реализующие логические операции. Пояснение: для наглядности приготовьте электрические схемы и продемонстрируйте их в действии. Для этого используйте: источник питания, лампочки, ключи, провода. На рисунках контакты обозначены латинскими буквами А и В. Введем обозначения: 1 -контакт замкнут, 0 — контакт разомкнут. Заполняем таблицу по ходу объяснения материала.
Докажем это, рассмотрев состояния схем при различных состояниях контактов. Схема 1 (составляем в основной таблице таблицу истинности).
Вывод: первая схема действительно реализует логическую операцию «И». Схема 2 (составляем в основной таблице таблицу истинности).
Вывод: вторая схема действительно реализует логическую операцию «ИЛИ». Схема 3 (составляем в основной таблице таблицу истинности). В этом устройстве в качестве переключателя используется автоматический ключ. когда тока на нем нет, пластинка замыкает контакты и лампочка горит. если на ключ подать напряжение, то вследствие явления электромагнитной индукции пластинка прижимается и цепь размыкается. Лампочка не горит. Вывод: третья схема действительно реализует логическую операцию «НЕ». Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключений в секунду. Именно такие электронные схемы нашли свое применение в качестве элементной базы ЭВМ. Вся теория, изложенная для контактных схем, была перенесена на электронные схемы. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента. Почему необходимо уметь строить логические схемы? Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом) таким образом, становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе. Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства. 3. Построение логических схем Правило построения логических схем:
Пример 1 Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X v Y & X.
2 1 X v Y & X. 3) Строим схему:
Пример 2 Постройте логическую схему, соответствующую логическому выражению F=X&Yv¬(YvX). Найдите значение логического выражения для X=1, Y=0.
1 4 3 2 X&Yv ¬ (YvX)
№1 Составьте таблицы истинности для следующих логических выражений:
№2 Заполните пустые ячейки таблицы истинности:
№3 Постройте логическое выражение по логической схеме:
Ответ:
№4 Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения:
Ответ: логические схемы:
V. Оцените работу класса и назовите учащихся, отличившихся на уроке. Домашнее задание Уровень знания: знать, что такое таблица истинности, логическая схема, что такое «вентиль», как его изобразить, почему необходимо уметь строить логические схемы, порядок построения схем. Уровень понимания: №1 Составьте таблицы истинности и определите истинность формулы: 1) F = ((Av B)→B)&(AvB). 2)F = ¬(AvB)≡(AvB).
№2 Составьте логические схемы к следующим логическим выражениям: A) F = Bv(C&A) v (A&B). B) F= ¬ (A&B) vC&D. №3 Постройте логические выражения к логическим схемам:
Уровень применения: составьте все возможные соединения в схеме следующих вентилей: назад к оглавлению Урок 3. Презентация Цели: познакомить учащихся с законами логики; сформулировать правила преобразования логических выражений; научить учащихся приводить логическое выражение к нормальной форме. Требования к знаниям и умениям: Учащиеся должны знать:
Программно-дидактическое обеспечение: ПК, карточки с заданиями, таблица с формулами преобразования. Ход урока I. Постановка целей урока
II.
Если логическое выражение содержит большое число операций, то составлять для него таблицу истинности достаточно сложно, так как приходится перебирать большое количество вариантов. В таких случаях формулы удобно привести к нормальной форме. Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, при этом знаки отрицания находятся только при логических переменных. Для приведения формулы к нормальной форме используют законы логики и правила логических преобразований. Смотрите также: Методическое пособие Электронный вариант Преподавателю и 737.68kb. 4 стр. Методическое пособие по дисциплине «Статистика» для специальности «Экономика и бухгалтерский учет (по отраслям): Методическое пособие /Под редакцией В. 1269.9kb. 12 стр. Практикум по курсу «Электронный маркетинг» Технологии создания Web-сайтов Москва 2003 Составители: Н. Б. Завьялова 643.92kb. 1 стр. Учебно-методическое пособие Ижевск 2012 резьбовые соединения учебно-методическое пособие Ижевск 2012 (075) 420.54kb. 3 стр. Методическое пособие для студентов высших и средних сельскохозяйственных заведений 1135.14kb. 6 стр. Методическое пособие по выполнению курсовых работ по курсу 153.17kb. 1 стр. Методическое пособие по курсам «Электрическая часть электростанций и подстанций» 344.65kb. 1 стр. Учебно-методическое пособие для курсового проектирования Барнаул 2009 (072) Скребковые конвейеры: Учебно-методическое пособие для курсовогоо проектирования / Сост. 403.45kb. 2 стр. Методическое пособие и описание лабораторной работы (препринт) Составители: д т. н. Кирьянов К. Г. аспирант Семенчуков И. В 326.55kb. 3 стр. Методическое пособие «От простого к сложному» 151.3kb. 1 стр. Учебно-методическое пособие москва военное издательство 1987 961.99kb. 6 стр. Учебно-методическое пособие Краснодар: Кубанский гос ун-т, 2004, 104 с 61.49kb. 1 стр. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица истинности логических операций — алгоритм построения
Используя таблицы истинности логических операций, можно точно определить, верна ли функция при определённых значениях. В перечень заносят всевозможные комбинации переменных появляющихся на входе и соответствующие им состояния на выходе. Чаще всего таблицы применяют при проектировании и анализе цифровых схем. При этом в интернете существуют сервисы, с помощью которых построить такого рода сводку не составит труда даже слабо разбирающемуся в этой сфере пользователю.
Чаще всего таблицы применяют при проектировании и анализе цифровых схем. При этом в интернете существуют сервисы, с помощью которых построить такого рода сводку не составит труда даже слабо разбирающемуся в этой сфере пользователю.
Содержание
- Определения и понятия
- Виды логических операций
- Аксиомы и законы
- Алгоритм построения
- Пример задания
- Вычисления онлайн
Определения и понятия
Под таблицей истинности понимают свод значений, которые может принять высказывание при сочетании различных входящих комбинаций. Другими словами, каждому набору функций или сигналам, присутствующим на входе чего-либо, соответствует строго определённые показатели на выходе. Все значения, являющиеся всевозможными высказываниями, называют логическими выражениями. Если в таблице последние столбцы логичных выражений идентичны, то рассматриваемый объект считается равносильным.
Любое выражение можно описать формулой, в которую будут включаться переменные, характеризующие состояния, и обозначающие функции знаки логических операций. Поэтому используя язык математики, в частности, алгебры, любое сложное высказывание можно разделить на несколько простых, а затем объединить логической связью.
Поэтому используя язык математики, в частности, алгебры, любое сложное высказывание можно разделить на несколько простых, а затем объединить логической связью.
Обычно значениями истинности описывают логическую функцию, у которой показатели параметров определяют верность. Раздел математики рассматривающий их на правдивость или ложность называется булевым. В 1854 году английский учёный Джордж Буль предложил метод, позволяющий проводить анализ классов и высказываний. Согласно ему, любое значение может принимать одно из двух состояний — истина или ложь.
Эти состояния принято обозначать арабскими цифрами один либо ноль или словами true и false. Это возможно из-за того, что для математики важна только истинность высказываний, а конкретное содержание второстепенно. Простые высказывания принято считать логическими переменными, а сложные — функциями логики. Выражения для упрощения записи обозначают латинскими буквами A, B, C.
Применение двух цифр подчёркивает соответствие между двоичной системой счисления и математической логикой.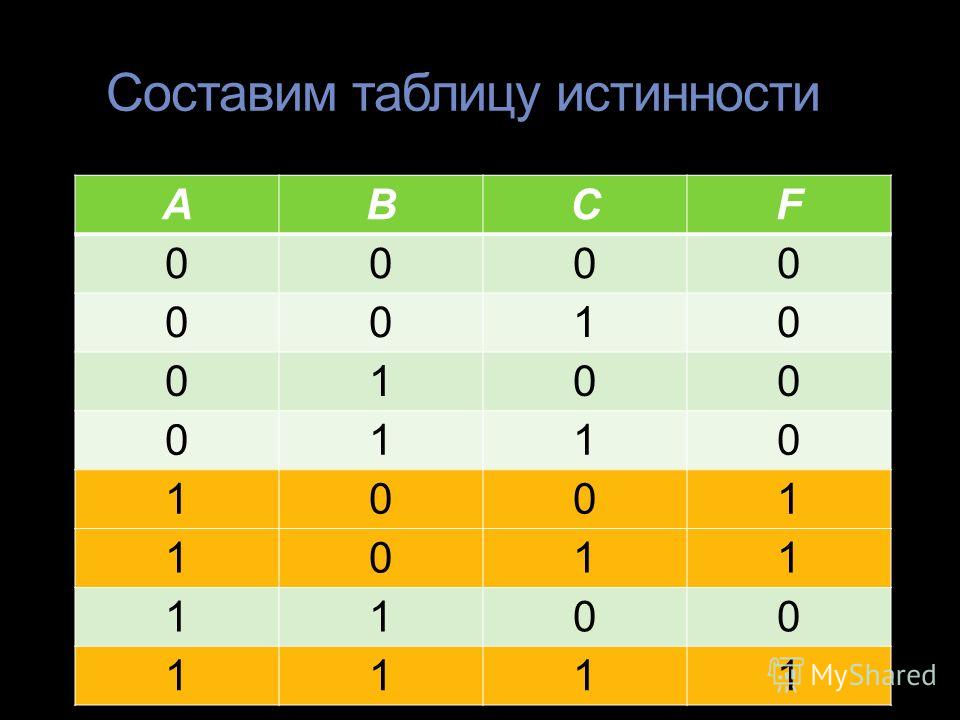 В итоге с помощью последней стало удобным описывать работу цифровых схем радиоэлектронной аппаратуры, алгоритмы в программировании, проводить синтез и анализ результата выполнения операций.
В итоге с помощью последней стало удобным описывать работу цифровых схем радиоэлектронной аппаратуры, алгоритмы в программировании, проводить синтез и анализ результата выполнения операций.
Суждение о правильности построения таблиц истинности для логических выражений основано на учёте всех переменных и операций, последовательно выполняющихся в рассматриваемой функции. Обычно для начертания используют 2n+1 строк, где n обозначает количество входных переменных, и n+m столбцов, m — число значений на выходе.
Виды логических операций
В качестве наименьшей единицы измерения объёма данных принято считать бит. В него заносится одно из двух значений — ложь (0) или правда (1). Каждая ячейка, соответствующая биту, находится лишь в одном из этих состояний. Существуют определённые операции, используемые для действий с ячейками:
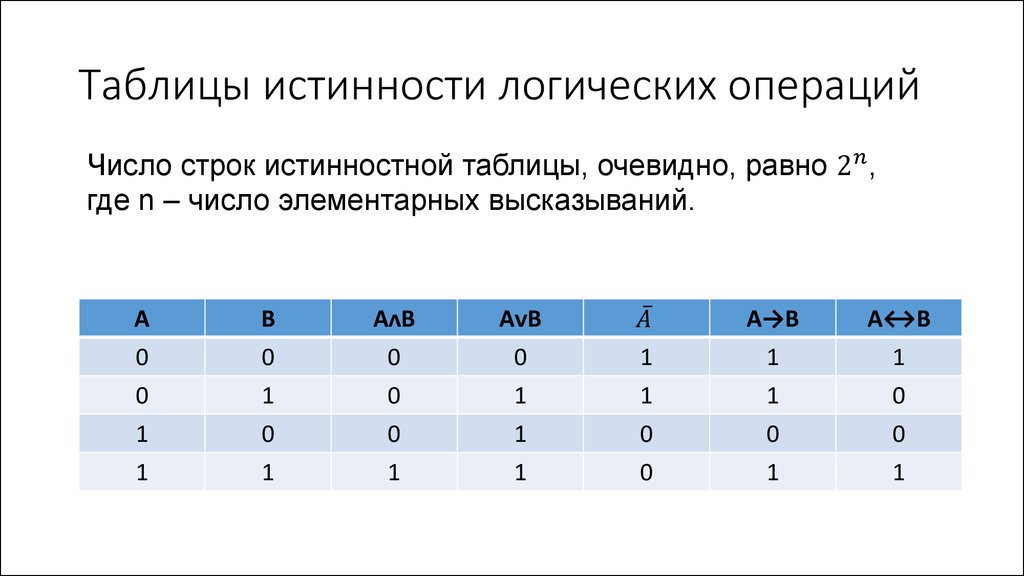 Результатом действия будет единица, но лишь в том случае, если значения двух ячеек одинаковое. При остальных вариантах итог будет иметь устойчивое нулевое состояние.
Результатом действия будет единица, но лишь в том случае, если значения двух ячеек одинаковое. При остальных вариантах итог будет иметь устойчивое нулевое состояние.Эти операции являются основными элементами при составлении таблиц истинности и получения возможного результата. На основании их построена алгебра Буля. Некоторые элементы получаются путём объединения нескольких операций.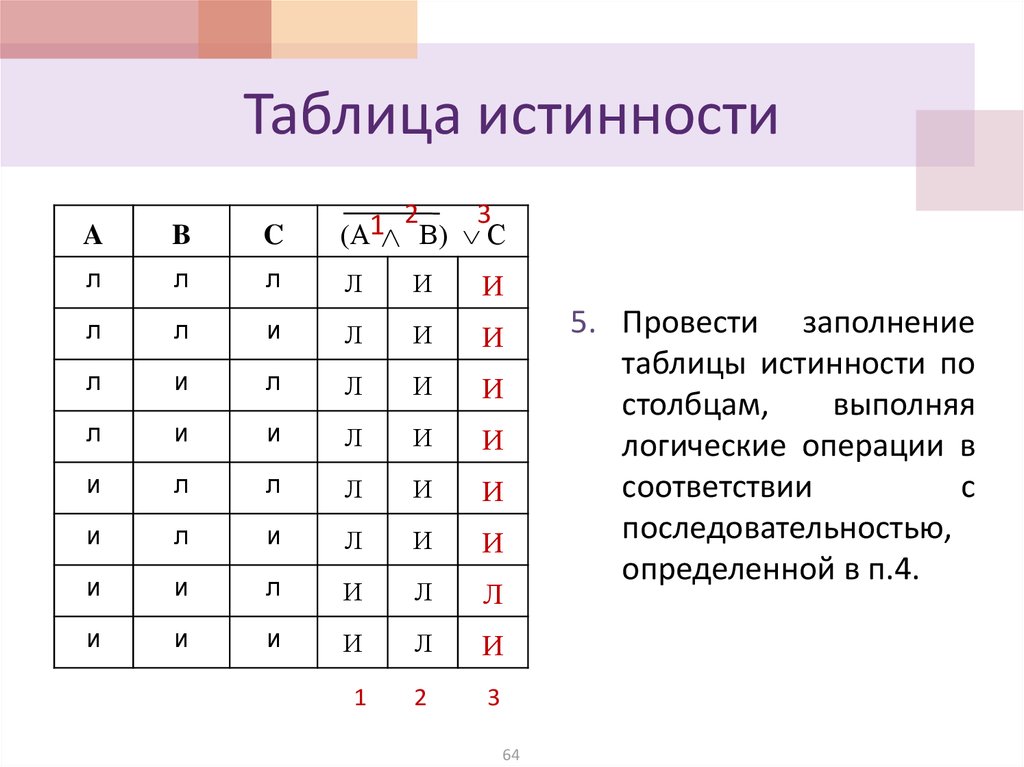 Так, существует состояние: NAND (И-НЕ) и NOR (ИЛИ-НЕ). Первый элемент является инверсией операции «И», а второй — «ИЛИ». На основании рассмотренных операторов строится работа всех цифровых интегральных схем.
Так, существует состояние: NAND (И-НЕ) и NOR (ИЛИ-НЕ). Первый элемент является инверсией операции «И», а второй — «ИЛИ». На основании рассмотренных операторов строится работа всех цифровых интегральных схем.
В информатике существует своя терминология, обозначающая то или иное логическое действие. Так, AND называют операцией конъюнкции, OR — дизъюнкции, XOR — сложение по модулю 2, NOT — отрицание. Задача инженера при анализе схем или алгоритма сводится к выполнению булевой арифметики и упрощению выражений. Для этого используют различные правила и положения не требующих доказательства.
Аксиомы и законы
Построение таблиц в удобной форме позволяет определить, когда определённое действие или высказывание принимает верное значение, а в каком случае нет. В верхней строчке записывают логическую форму высказывания, а в столбцах — истинные значения. Некоторые комбинации высказываний всегда будут истинными или ложными, независимо от содержания.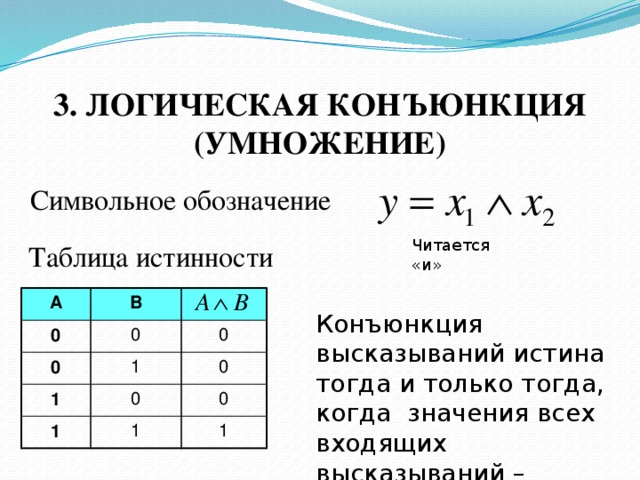 Поэтому и были сформулированы следующие законы:
Поэтому и были сформулированы следующие законы:
Эти три закона фундаментальны. Без их соблюдения сделать любое правильное утверждение невозможно.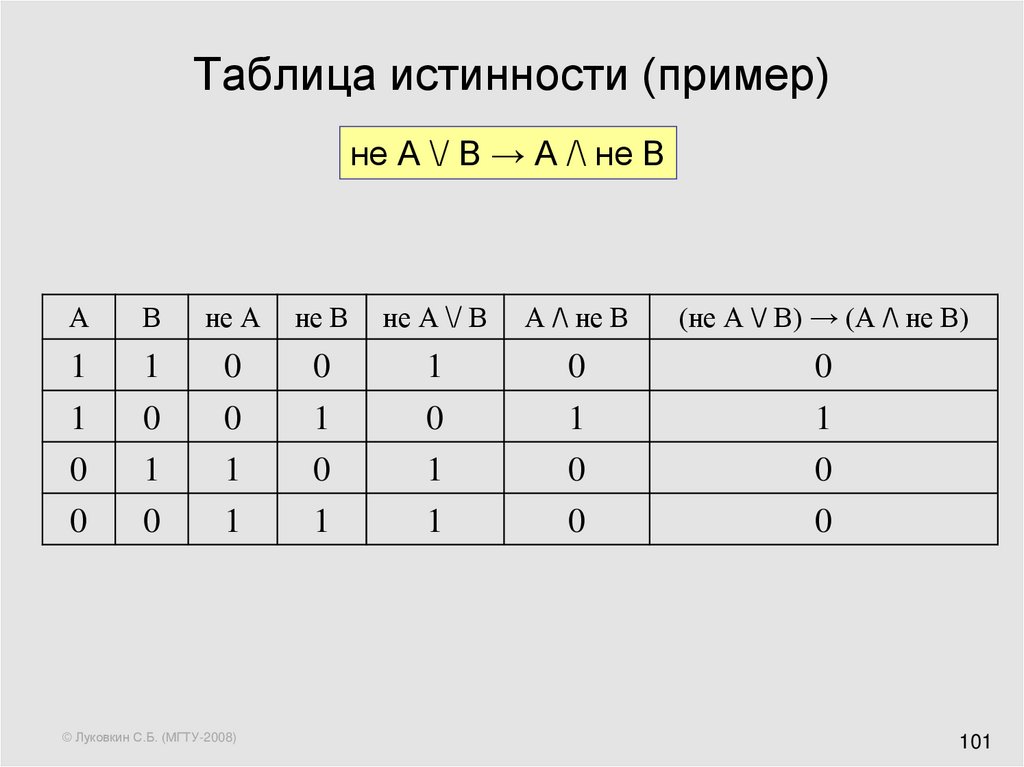
Для решения логических задач с помощью таблиц истинности используют различные формулы, соответствующие разного вида операциям. Одно из них логическое умножение (конъюнкция). В этом случае считается, что функция истинная лишь тогда, когда оба выражения являются верными: F = A & B. Другое логическое сложение (дизъюнкция). Оно гласит, что если оба выражения ложны, то и логическая функция будет неверной.
Кроме того, используется закон:
- инверсии (отрицания) — если логическое высказывание истинно, то отрицание его будет ложным выражением;
- импликации (следования) — для всегда истинного сложного логического выражения ложь будет тогда, когда из верности следует отрицание;
- эквивалентности (равнозначности) — выражение будет истинным лишь тогда, когда оба высказывания имеют одинаковое значение.
При построении таблиц нужно придерживаться установленного порядка выполнения упрощения операций. Вначале считают инверсию и конъюнкцию, а затем дизъюнкцию, импликацию и эквиваленцию.
При изменении же порядка выполнения действий в описании логических операций используют скобки.
Алгоритм построения
Таблицы истинности показывают, какой вид может принять выражение при различных входящих в него значениях переменных. Для того чтобы их правильно построить и выполнить вычисление логического выражения нужно придерживаться установленного алгоритма. Построение таблиц выполняют в следующей последовательности:
- подсчитывают количество переменных n;
- вычисляют число строк для будущей таблицы используя формулу m = 2n+1;
- определяют число логических операций;
- устанавливают порядок выполнения операций в соответствии со скобками и приоритетами;
- строят таблицу с указанием столбцов и наборов значений, заданных логических операций;
- заполняют оставшиеся ячейки в таблице.
Для заполнения таблиц нужно упрощать выражения с учётом последовательности выполнения операций.
При этом учитывать, что если значение какого-то из аргументов функции в соответствующей строке таблицы будет равное нулю, то записывать его нужно в виде отрицания.
Пример задания
Пусть необходимо построить таблицу для логического выражения F = (A → B) * (A + B). Эта формула состоит из двух логических переменных A и B и нескольких операций. Начинают построение с определения строк. Используя формулу 2n+1 для рассматриваемого примера можно установить, что их число будет: x = 22 + 1 = 5.
Теперь следует определить число столбцов. Для этого используется формула, в которой учитывается количество переменных и операций. Последние можно просто посчитать, сложив количество разных знаков, используемых в записи формулы. Но правильней сначала расставить порядок операций, а затем посчитать. Согласно порядку действия над операциями их нумерацию можно представить в следующей очерёдности:
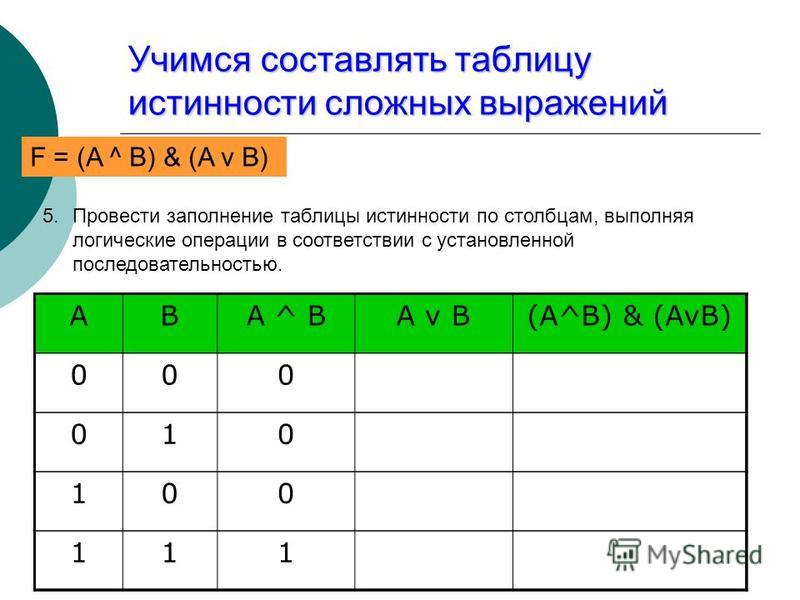
В итоге получится, что столбцов будет: Y = 2 + 5 = 7. Теперь нужно построить таблицу 7Х5. В шапку первого и второго столбца вписывают переменные, а затем операции над ними. Затем в строках, соответствующих A и B нужно записать всё, что с ними может произойти. В итоге останется только правильно посчитать последний столбец.
Для этого нужно использовать законы. Необходимо выполнить логическое умножение значений в скобках. Первой и второй строчке будет соответствовать операция произведения один на один, что в ответе даст единицу. Третьей и четвёртой — ноль на один, что в итоге даст ноль. Последний столбец является главным для рассматриваемой логической функции. По нему можно узнать значение логической функции для любых форм переменных A и B.
Это довольно простая задача, содержащая всего две переменных. Но в реальности, например, в программировании, их может быть намного больше. Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.
Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.
Например, заданно выражение (x + y + z) * (x + y). По сути, оно записано в совершенно нормальной конъюнктивной форме. Но для приведения его к этому виду нужно, чтобы во втором выражении стояла z. Для того чтобы её добавить необходимо обратить внимание на то, что внутри скобок стоит логическое сложение. Поэтому дописав к нему ноль, результат не изменится. Добавить ноль через z можно, как ноль умножить на НЕ z. В итоге получится выражение (x + y + z) * (x + y + z + z), для которого, используя алгоритм составить таблицу уже не так и сложно.
Вычисления онлайн
В интернете есть сервисы, автоматически строящие таблицы истинности. Такие сайты предлагают свои услуги бесплатно и доступны даже тем, кто слабо ориентируется в теме. С их помощью можно находить таблицы для довольно сложных выражений, решение которых требует скрупулёзности в расчёте. В основе онлайн-вычислений заложены принципы логических законов, поэтому за достоверность результата можно не переживать. Тем более расчёт занимает совсем небольшое количество времени.
В основе онлайн-вычислений заложены принципы логических законов, поэтому за достоверность результата можно не переживать. Тем более расчёт занимает совсем небольшое количество времени.
Для того чтобы воспользоваться сайтами-калькуляторами пользователю необходимо знать обозначение операций, иметь подключение к интернету и установленный веб-обозреватель, поддерживающий Flash-технологию. Регистрацию, указание личных данных сервисы, предлагающие такого рода услуги, не требуют.
Из различных порталов можно отметить три наиболее популярных калькулятора:
Эти сайты имеют интуитивно понятный интерфейс и что довольно полезно, на своих страницах содержат краткую теорию, используемую для составления таблиц истинности и даже примеры решений.
Предыдущая
ИнформатикаКак рисовать в Паскале АВС — команды, алгоритмы и примеры
Следующая
ИнформатикаРеляционные базы данных — определение, структура, примеры
Построение СКНФ и СДНФ по таблице истинности
- СКНФ
- СДНФ
Нормальной форме логической формулы не свойственна эквивалентность, отрицание формул неэлементарного типа и знаки импликации.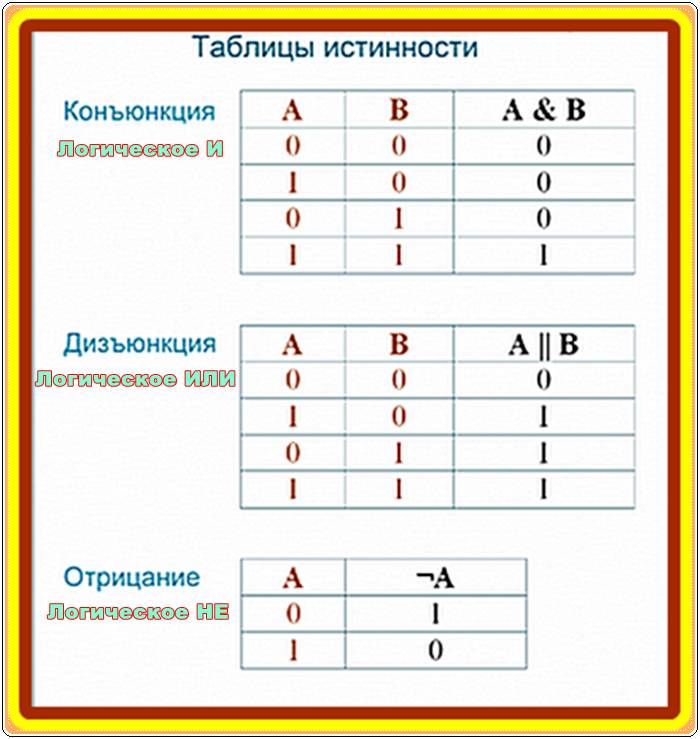
Выделяют такие виды формы нормального типа:
- КНФ (конъюнктивная нормальная форма), где подразумевается конъюнкция того или иного количества дизъюнкций, как пример, ;
- ДНФ (дизъюнктивная нормальная форма), где осуществляется дизъюнкция конъюнкций, как пример, .
СКНФ
Совершенная КНФ является разновидностью конъюнктивной нормальной формы, удовлетворяющей такие условия:
- отсутствие одинаковых элементарных дизъюнкций;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную НФ такого типа.
Построение СКНФ согласно таблице истинности
Если функция равна нулю, то в случае каждого набора записывают сумму, причем с отрицанием берутся те переменные, которые равны единице.
СДНФ
Совершенная ДНФ является разновидностью дизъюнктивной нормальной формы, удовлетворяющей следующие условия:
- отсутствие одинаковых элементарных конъюнкций;
- конъюнкции не свойственно обладать одинаковыми переменными;
в случае любой конъюнкции элементарного типа имеет место быть переменная, входящая в такую нормальную дизъюнктивную форму.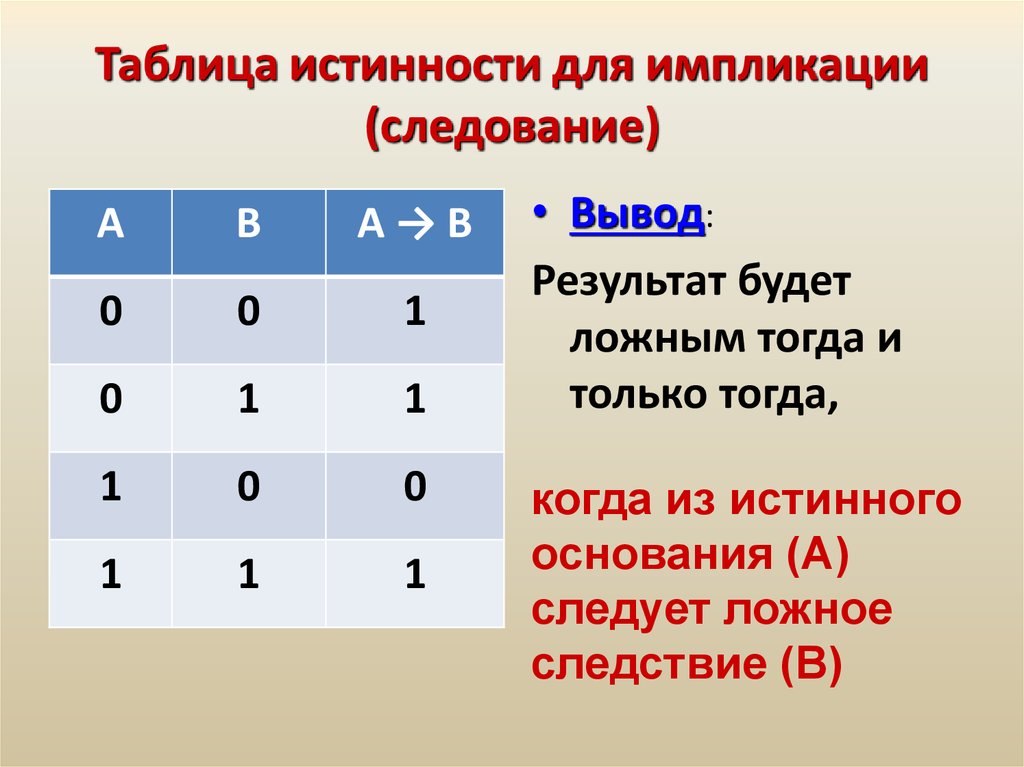 При этом в одинаковом порядке.
При этом в одинаковом порядке.
Все формулы булевого типа, которые не относятся к тождественно ложным, могут быть представлены в совершенной разновидности ДНФ, при этом в единственном возможном варианте.
Построение СДНФ согласно таблице истинности
Если функция соответствует единице, то в случае каждого набора записывается произведение, причем с отрицанием берутся те переменные, которые равны нулю.
Нахождение СКНФ и СДНФ: примеры
Пример
Согласно таблице истинности записать логическую функцию:
Рисунок 1.
Решение:
Прибегнем к правилу построения совершенной ДНФ
Рисунок 2.
Получаем такую СДНФ
Задействовав правило её построения:
Рисунок 3.
Получаем СКНФ:
Пример
Представить функцию как СДНФ и СКНФ, при том, что она задаётся таблицей истинности.
Рисунок 4.
РешениеДля начала нужно записать логическую функцию в СДНФ. Чтобы упростить решение, добавляем к таблице столбец. Прибегнув к правилу составления СДНФ, вводим знак отрицания для переменных с нулевым значением. Инвертирование нулевых значений переменных имеет большое значение, поскольку без этого значения конъюнкций будут преобразованы в нули ключевой функции.
Прибегнув к правилу составления СДНФ, вводим знак отрицания для переменных с нулевым значением. Инвертирование нулевых значений переменных имеет большое значение, поскольку без этого значения конъюнкций будут преобразованы в нули ключевой функции.
Рисунок 5.
Вычисленные конъюнкции из вспомогательного столбца необходимо объединить знаком дизъюнкции и получим необходимую логическую функцию, имеющую вид совершенной конъюнктивной формы нормального типа:
Запишем логическую функцию в СКНФ.
Прибегнув к правилу, по которому составляется СКНФ, нужно помнить о введения знака отрицания для переменных с единицей. Инвертирование единичных значений имеет большое значение, поскольку без этого значения дизъюнкций будут преобразованы в единицы ключевой функции.
Рисунок 6.
Вычисленные дизъюнкции из вспомогательного столбца необходимо объединить знаком конъюнкции, так как таким образом и можно получить необходимую логическую функцию, имеющую вид совершенной нормальной формы конъюнктивного типа.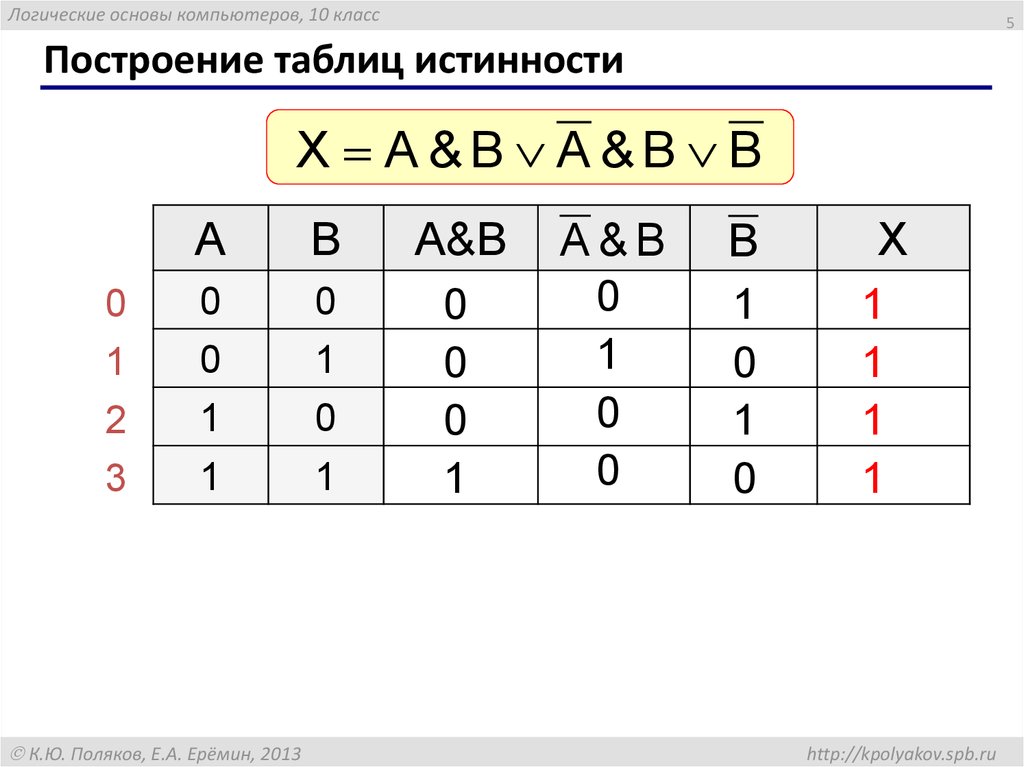
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Устройства хранения информации Алфавитный подход к оценке количества информации. Формула Хартли Информационные процессы и информация Прикладное программное обеспечение Архитектура персонального компьютера
Формула Хартли Информационные процессы и информация Прикладное программное обеспечение Архитектура персонального компьютера
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Как составить таблицу истинности
Как составить таблицу истинности
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашняя страница > Логика > Символическая логика > Таблицы истинности | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Философия 103: Введение в логику Как составить таблицу истинности Аннотация: Объясняются и иллюстрируются общие принципы построения таблиц истинности.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Отправляйте исправления или предложения по адресу [email protected] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Аргументы | Язык | Заблуждения | Предложения | Силлогизмы | Перевод | Символический | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
таблиц истинности
таблица истинностиМы научились брать предложения на английском языке и переводить их в логические утверждения, используя буквы и символы для логических связок. Мы говорили о том, когда утверждение, составленное из двух простых утверждений, соединенных одной логической связкой, истинно и когда ложно. Теперь нам нужен систематический способ найти истинностное значение более сложных утверждений, содержащих несколько логических символов. Итак, как мы это сделаем?
Прежде всего, нам нужен какой-то порядок операций: если у нас есть оператор с несколькими логическими символами, как мы узнаем, какой из них должен стоять первым? Логики решили использовать тот же порядок операций, который мы изучили в теории множеств.
Как и в теории множеств, нам обычно нужны круглые скобки, чтобы указать, что делать в первую очередь.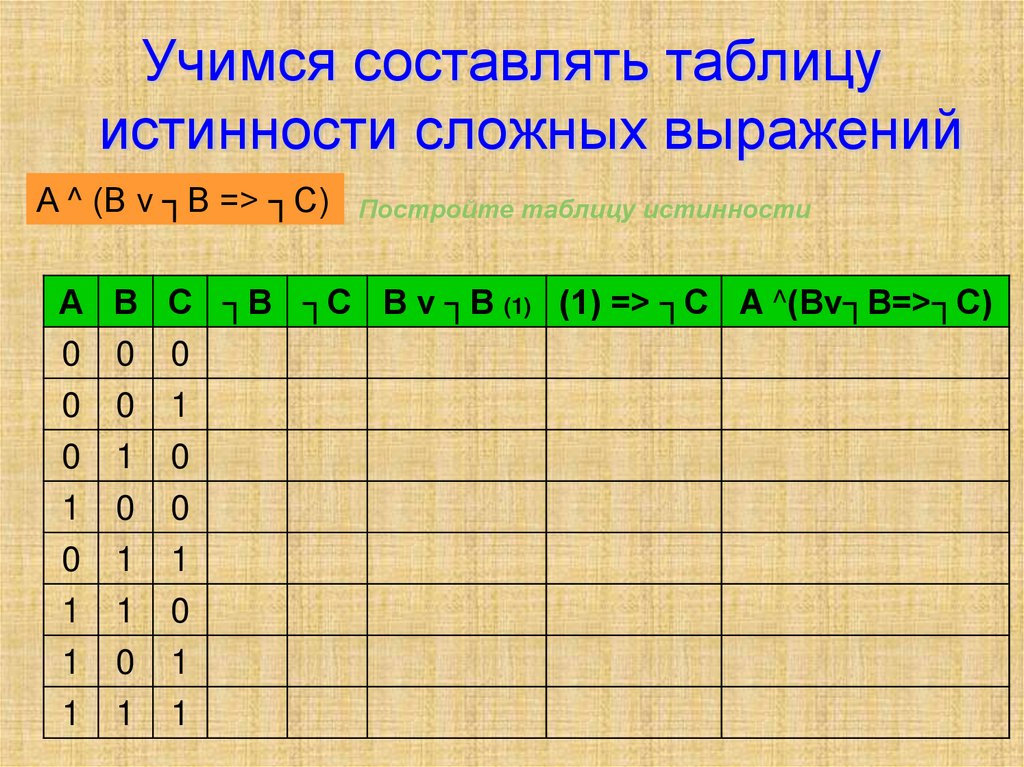 Итак, вот порядок, в котором мы должны делать что-то в логике:
Итак, вот порядок, в котором мы должны делать что-то в логике:
- Сначала делаем скобки, работая изнутри наружу.
- Внутри круглых скобок или после того, как круглые скобки исчезли, мы всегда делаем отрицание, прежде чем делать любую другую логическую связку.
- Если у нас есть какие-либо другие логические связки, у нас должны быть круглые скобки, говорящие нам, что делать в первую очередь.
Давайте рассмотрим пример:
(~ р ∧ к )∨ р
Если бы мы хотели посмотреть, какова истинность этого утверждения, когда с =T и q =F, то нам пришлось бы шаг за шагом выполнять оператор, выполняя каждый логический квантификатор один за другим.
Что бы мы сделали в первую очередь? Скобки.
Что делать в скобках? ~ р ∧ дИтак, что мы должны сделать первым, отрицание (~) или или (∨)?
Поскольку первыми всегда идут отрицания, мы начинаем с нахождения истинного значения ~ p .Если p =T, то должно быть ~ р =F.
Теперь, когда мы сделали ~ p , мы можем объединить его истинное значение с q истинным значением, чтобы найти истинное значение ~ p ∧ q .
(Помните, что оператор «и» истинен только тогда, когда оба утверждения по обе стороны от него истинны.)В этом случае у нас есть ~ p слева, что, как мы знаем, ложно, и q справа, что, как мы также знаем, ложно.
Итак, поскольку у нас нет утверждений по обе стороны от символа «и», которые оба верны, утверждение ~ p ∧ q неверно.
So ~ p ∧ q =F.
Теперь, когда мы знаем истинное значение всего в скобках (~ p ∧ q ), мы можем соединить это утверждение с ∨ p , чтобы получить окончательное утверждение (~ p ∧ q ). )∨ р .
Когда утверждение «или» верно?
Всякий раз, когда хотя бы одно из отдельных утверждений по обе стороны от него верно.
В этом случае два утверждения по обе стороны от знака или (~ p ∧ q ) и p .Мы знаем, что ~ p ∧ q ложно, и мы знаем, что p истинно.
Поскольку хотя бы одно из этих двух верно, мы знаем, что наше утверждение «или» (~ p ∧ q )∨ p должно быть истинным.
Так (~ p∧q ) ∨p =T.Другой способ пошаговой записи этой задачи будет выглядеть так:
(~ p∧q )∨ p
=(~T∧F)∨T
=(F∧F)∨T
=F∨T
=T
Мы часто хотим найти систематический способ найти все возможные значения истинности утверждения. Для этого составим таблицу истинности. Таблица истинности — это таблица, которая начинается со всех возможных комбинаций значений истинности для букв в составном утверждении; затем он разбивает составное утверждение и шаг за шагом определяет значения истинности для каждой из частей логического утверждения.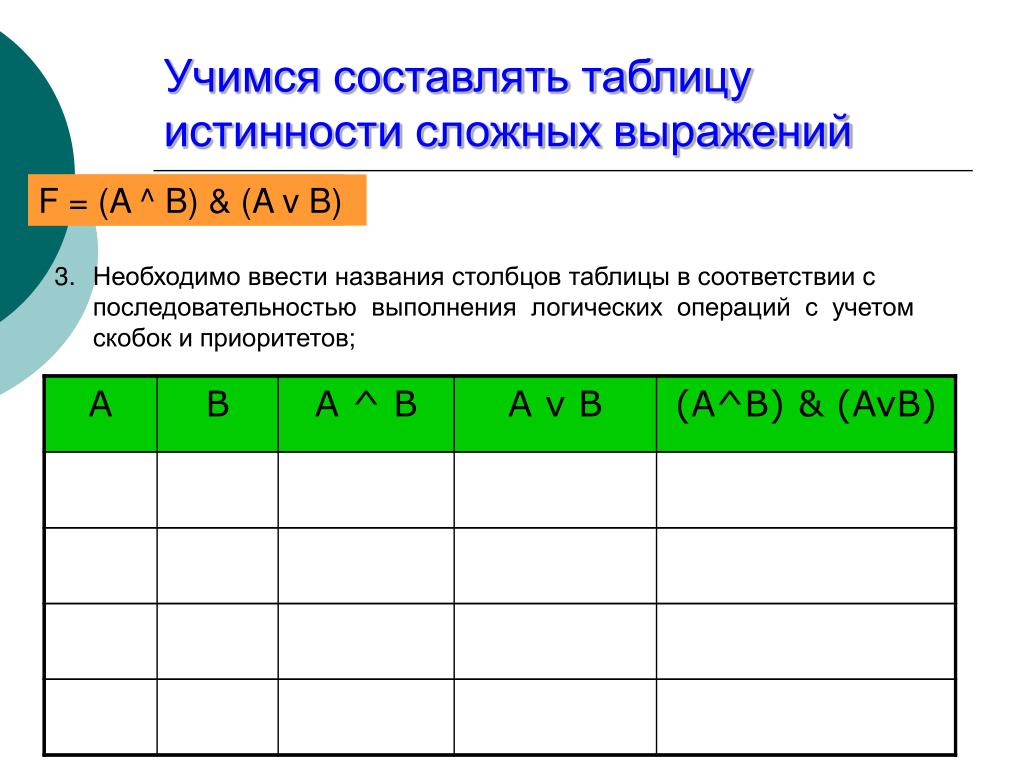
Давайте рассмотрим пример, чтобы это определение имело больше смысла:
Одна из простейших таблиц истинности, которые мы можем построить, — это таблица истинности для выражения ~ p .Вот как мы это делаем:
- Сначала мы начнем с построения таблицы с буквой p в верхней части первого столбца:
- Затем мы заполняем все возможные значения истинности p в этом столбце. Поскольку p может быть только истинным или ложным, столбец заполняется так:
- Затем мы помещаем выражение ~ p вверху следующего столбца.
р
~ р
Т
Ф
- Теперь смотрим на каждую строку; мы смотрим, каково значение истинности p в этой строке, а затем мы заполняем соответствующее значение истинности ~ p для данного значения истинности p .

- Если мы посмотрим на первую строку, истинное значение p равно T. Таким образом, в этой строке истинное значение ~ p должно быть F.
Чтобы понять, почему это так, просто вспомните определение отрицание ~. Подумайте об этом так: предположим, что p представляет утверждение «Идет дождь». Тогда ~ p представляет утверждение «Дождя нет». Всякий раз, когда правда, что идет дождь ( стр. =T), то должно быть ложным, что идет дождь , а не (~ p =F).р
~р
Т
Ф
Ф
Т
- Если мы посмотрим на вторую строку, истинное значение p равно F. Таким образом, в этой строке истинное значение ~ p должно быть T.

Чтобы понять, почему это так, просто вспомните определение отрицания ~. Подумайте об этом так: предположим, что p представляет утверждение «Идет дождь». Тогда ~ p представляет утверждение «Дождя нет». Всякий раз, когда ложно, что идет дождь ( p = F), тогда должно быть правдой, что идет , а не дождь (~ p = T).р
~р
Т
Ф
Ф
Т
- Если мы посмотрим на первую строку, истинное значение p равно T. Таким образом, в этой строке истинное значение ~ p должно быть F.
Итак, наша окончательная таблица истинности выглядит так:
р | ~р |
Т | Ф |
Ф | Т |
Теперь составим таблицу истинности для каждой из основных логических связок:
- р ∧ к Сначала настраиваем таблицу:
р
q
п∧q
Т
Т
Т
Ф
Ф
Т
Ф
Ф
Обратите внимание, что теперь, когда у нас есть две буквы, p и q , вместо одной буквы у нас есть четыре возможных комбинации значений истинности для p и q :
- p может быть правдой, а q может быть правдой
- p может быть правдой, а q может быть ложью
- p может быть ложным, а q может быть истинным
- p может быть ложным, а q может быть ложным
Мы знаем, что p ∧ q верно только тогда, когда оба p и q верны.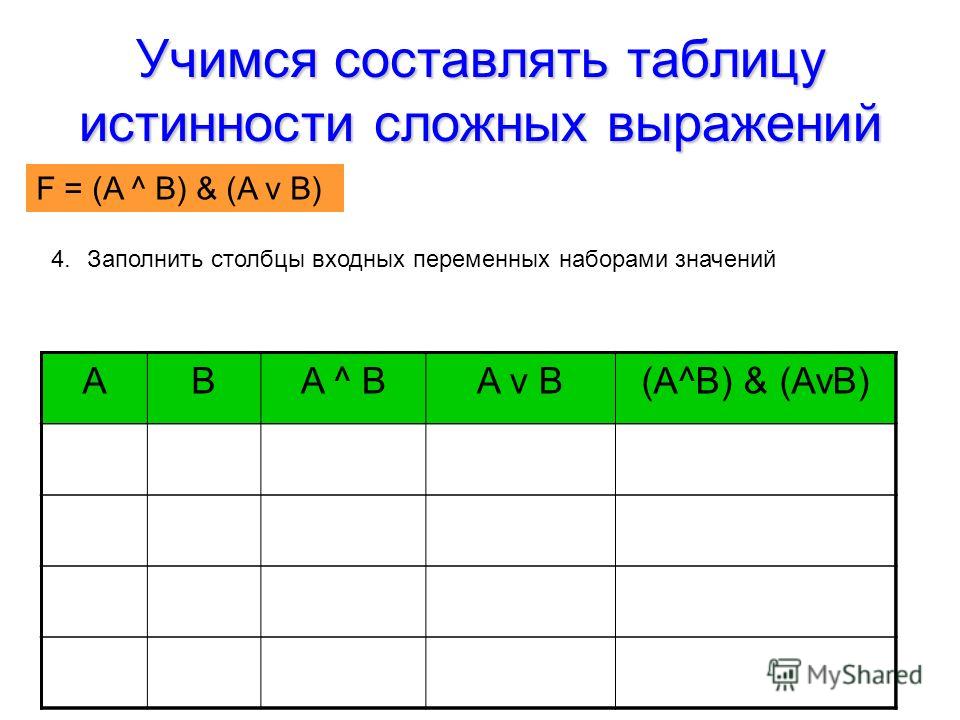
Итак, мы можем заполнить таблицу истинности следующим образом:
р | q | п∧q |
Т | Т | Т |
Т | Ф | Ф |
Ф | Т | Ф |
Ф | Ф | Ф |
- Когда p =T и q =T, тогда p∧q =T:
р
q
п∧q
Т
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Ф
Ф
Ф
- Когда p =T и q =F, тогда p∧q =F:
р
q
п∧q
Т
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Ф
Ф
Ф
- Когда p =F и q =T, тогда p∧q =F:
р
q
п∧q
Т
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Ф
Ф
Ф
- Когда p =F и q =F, тогда p∧q =F:
р
q
п∧q
Т
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Ф
Ф
Ф
р | q | п∧q |
Т | Т | Т |
Т | Ф | Ф |
Ф | Т | Ф |
Ф | Ф | Ф |
р | q | p∨q |
Т | Т | |
Т | Ф | |
Ф | Т | |
Ф | Ф |
Помните, что теперь, когда у нас есть две буквы, p и q , вместо одной буквы у нас есть четыре возможных комбинации значений истинности для p и q :
- p может быть правдой, а q может быть правдой
- p может быть истинным, а q может быть ложным
- p может быть ложным и q может быть правдой
- p может быть ложным, а q может быть ложным
Мы знаем, что p∨q истинно только тогда, когда хотя бы одно из p или q истинно.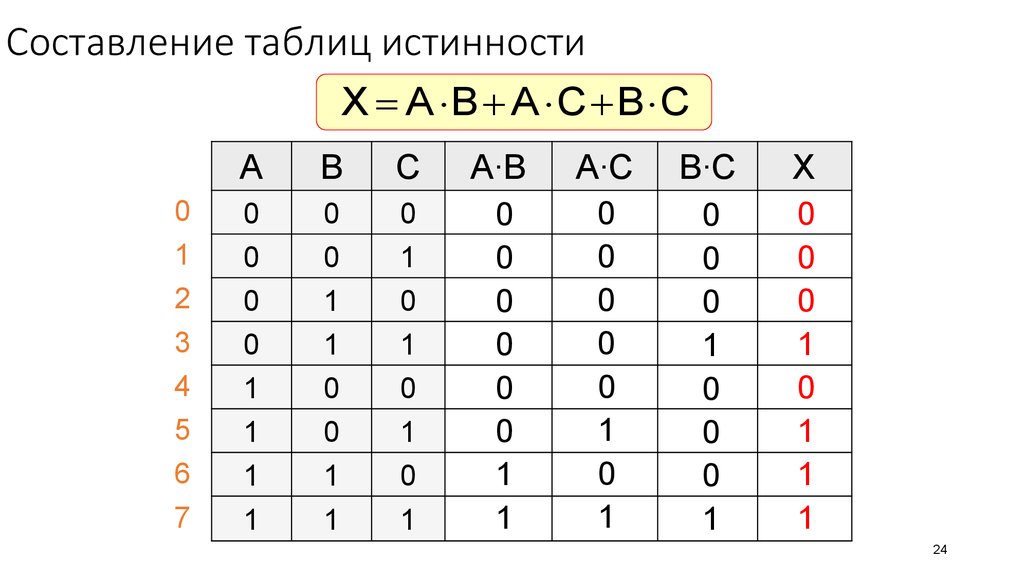
Итак, мы можем заполнить таблицу истинности следующим образом:
р | q | p∨q |
Т | Т | Т |
Т | Ф | Т |
Ф | Т | Т |
Ф | Ф | Ф |
- Когда p =T и q =T, тогда p∨q =T:
р
q
p∨q
Т
Т
Т
Т
Ф
Т
Ф
Т
Т
Ф
Ф
Ф
- Когда p =T и q =F, тогда p∨q =T:
р
q
p∨q
Т
Т
Т
Т
Ф
Т
Ф
Т
Т
Ф
Ф
Ф
- Когда p =F и q =T, тогда p∨q =T:
р
q
p∨q
Т
Т
Т
Т
Ф
Т
Ф
Т
Т
Ф
Ф
Ф
- Когда p =F и q =F, тогда p∨q =F:
р
q
p∨q
Т
Т
Т
Т
Ф
Т
Ф
Т
Т
Ф
Ф
Ф
р | q | p∨q |
Т | Т | Т |
Т | Ф | Т |
Ф | Т | Т |
Ф | Ф | Ф |
р | q | п→к |
Т | Т | |
Т | Ф | |
Ф | Т | |
Ф | Ф |
Мы знаем, что p→q только ложно , когда оба p верно и q ложно .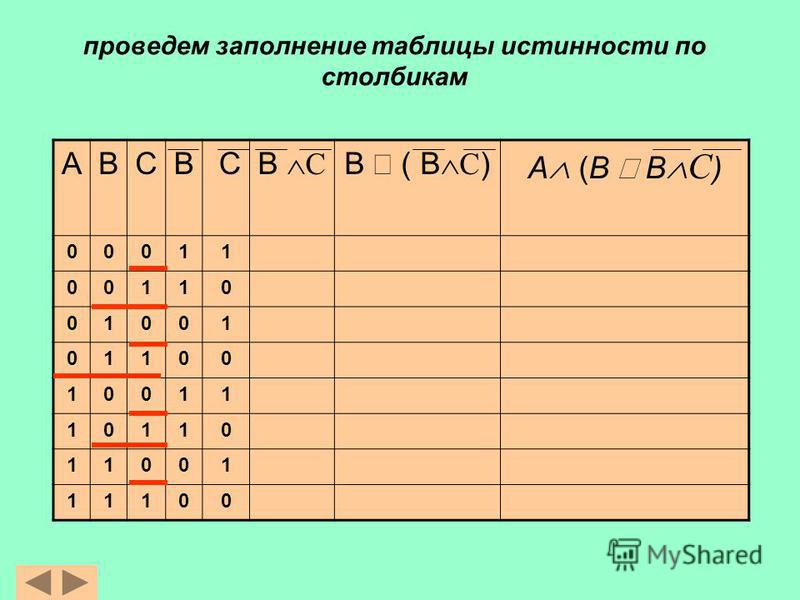
Итак, мы можем заполнить таблицу истинности следующим образом:
р | q | п→к |
Т | Т | Т |
Т | Ф | Ф |
Ф | Т | Т |
Ф | Ф | Т |
- Когда p =T и q =T, тогда p→q =T:
р
q
п→к
Т
Т
Т
Т
Ф
Ф
Ф
Т
Т
Ф
Ф
Т
- Когда p =T и q =F, тогда p→q =Ф:
р
q
п→к
Т
Т
Т
Т
Ф
Ф
Ф
Т
Т
Ф
Ф
Т
- Когда p =F и q =T, тогда p→q =T:
р
q
п→к
Т
Т
Т
Т
Ф
Ф
Ф
Т
Т
Ф
Ф
Т
- Когда p =F и q =F, тогда p→q =T:
р
q
п→к
Т
Т
Т
Т
Ф
Ф
Ф
Т
Т
Ф
Ф
Т
р | q | п→к |
Т | Т | Т |
Т | Ф | Ф |
Ф | Т | Т |
Ф | Ф | Т |
р | q | п↔к |
Т | Т | |
Т | Ф | |
Ф | Т | |
Ф | Ф |
Мы знаем, что p↔q верно только тогда, когда оба p и q верны или когда оба p и q являются ложными.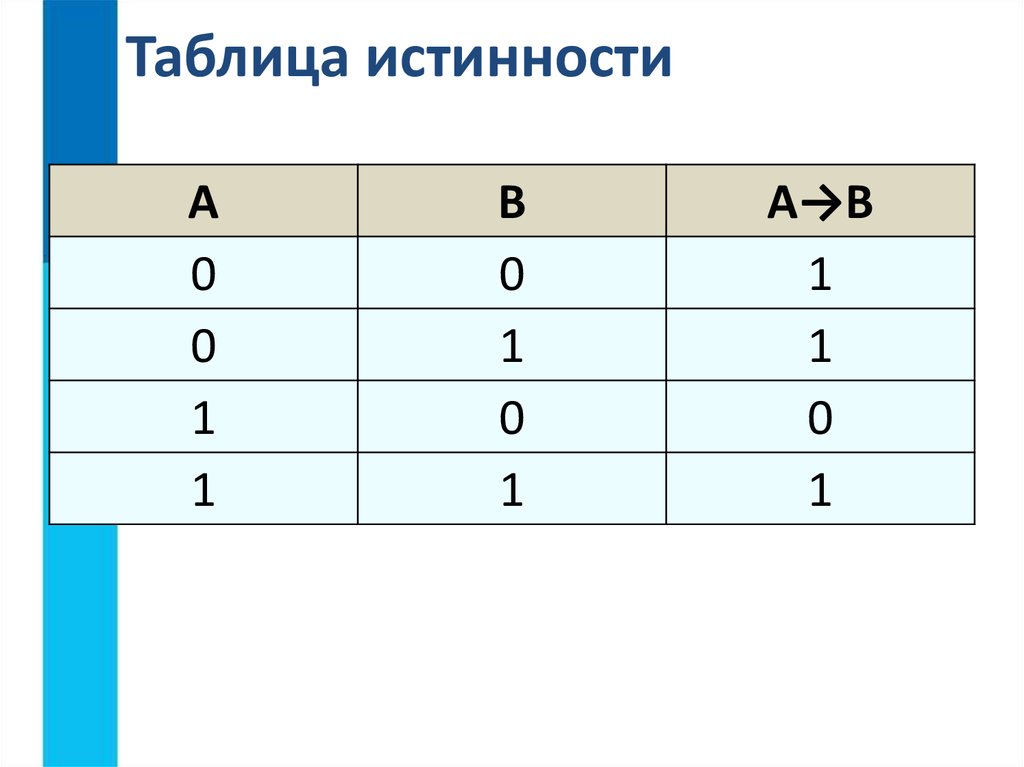
Итак, мы можем заполнить таблицу истинности следующим образом:
р | q | п↔к |
Т | Т | Т |
Т | Ф | Ф |
Ф | Т | Ф |
Ф | Ф | Т |
- Когда p =T и q =T, то p↔q =Т:
р
q
п↔к
Т
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Ф
Ф
Т
- Когда p =T и q =F, то p↔q =F:
стр.

q
п↔к
Т
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Ф
Ф
Т
- Когда p =F и q =T, то p↔q =F:
р
q
п↔к
Т
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Ф
Ф
Т
- Когда p =F и q =F, то p↔q =F:
р
q
п↔q
Т
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Ф
Ф
Т
р | q | п↔к |
Т | Т | Т |
Т | Ф | Ф |
Ф | Т | Ф |
Ф | Ф | Т |
Теперь наша конечная цель состоит в том, чтобы иметь возможность заполнять таблицы истинности большим количеством составных утверждений, содержащих более одной логической связки.
Выражения типа q→~s или (r∧~p)→r или (q&rarr~p)∧(p↔r) имеют несколько логических связок, поэтому нам нужно будет выполнять их по одному шагу за раз используя порядок операций, которые мы определили в начале этой лекции.
- q→~s
- Сначала мы начнем с написания таблицы со всеми возможными комбинациями значений истинности для каждой буквы в выражении. Поскольку здесь у нас есть 2 буквы, q и s, у нас будет 2 столбца в начале таблицы истинности, помеченные q и s:
- Потому что порядок операций гласит, что если у нас нет круглых скобок, мы всегда сначала делаем отрицание .

Итак, мы помечаем первый пустой столбец ~s.
Затем, поскольку s — единственная буква в выражении ~s, мы используем заданные значения истинности s в таблице, чтобы заполнить соответствующие значения истинности для ~s:q
с
Т
Т
Ф
Т
Ф
Т
Ф
Т
Ф
Ф
Ф
Т

- Первое истинное значение в столбце ~s равно F, потому что когда s=T, ~s=F.
- Вторым значением истинности в столбце ~s является T, потому что когда s=F, ~s=T.
- Третье истинное значение в столбце ~s равно F, потому что когда s=T, ~s=F.
- Четвертым значением истинности в столбце ~s является T, потому что, когда s=F, ~s=T.
- Теперь, когда мы позаботились о знаке ~ в выражении, осталось побеспокоиться только о символе → в q→~s. Символ → всегда объединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными утверждениями, но нас не волнует, насколько они сложны, до тех пор, пока у нас уже есть столбец в таблице истинности с этим логическим выражением вверху 9.0663 . В этом выражении символ → объединяет 2 выражения: q и ~s.
И q, и ~s находятся в верхней части столбцов таблицы истинности, поэтому мы можем использовать эти два столбца, чтобы заполнить столбец для q→~s, просто используя определение символа →:q
с
~с
Т
Т
Ф
Ф
Т
Ф
Т
Т
Ф
Т
Ф
Т
Ф
Ф
Т
Т
Когда вы работаете с условной связкой (→), вы должны отметить столбец, соответствующий первому утверждению иначе, чем так, как вы отмечаете второе колонка. При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора !
При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора !
В этих примерах мы различаем их, окрашивая столбец, содержащий , первый оператор , желтый , и столбец, содержащий , второй оператор , , голубой . Помните, что оператор, содержащий символ →, равен 9.0662 только ложь , если первое утверждение (то, что перед знаком →) является истинным , а второе утверждение (тот, что после знаком →) является ложным !- Первым значением истинности в столбце q→~s является F, потому что, когда q=T и ~s=F, q→~s=F.
- Вторым значением истинности в столбце q→~s является T, потому что, когда q=T и ~s=T, q→~s=T.
- Третьим значением истинности в столбце q→~s является F, потому что, когда q=F и ~s=T, q→~s=T.

- Четвертым значением истинности в столбце q→~s является T, потому что, когда q=F и ~s=T, q→~s=T.
Таким образом, окончательная таблица истинности для этого утверждения будет выглядеть так:
q
с
Т
Т
Т
Ф
Ф
Т
Ф
Ф
q
с
~с
q→~s
Т
Т
Ф
Ф
Т
Ф
Т
Т
Ф
Т
Ф
Т
Ф
Ф
Т
Т
- Потому что порядок операций гласит, что если у нас нет круглых скобок, мы всегда сначала делаем отрицание .
- (r∧~p)→r
- Сначала мы начнем с написания таблицы со всеми возможными комбинациями значений истинности для каждой буквы в выражении.
- Порядок операций гласит, что мы всегда делаем круглые скобки первыми .
 Итак, смотрим, что находится внутри скобок: r∧~p.
Итак, смотрим, что находится внутри скобок: r∧~p.
В скобках два символа: ∧ и ~.
Порядок операций гласит, что мы всегда делаем сначала отрицания .
с Поэтому мы помечаем первый пустой столбец как ~p. Затем, поскольку p — единственная буква в выражении ~p, мы используем заданные значения истинности p в таблице, чтобы заполнить соответствующие значения истинности для ~p:р
р
Т
Т
Ф
Т
Ф
Ф
Ф
Т
Т
Ф
Ф
Т

- Первым значением истинности в столбце ~p является F, потому что когда p=T, ~p=F.
- Вторым значением истинности в столбце ~p является T, потому что когда p=T, ~p=F.
- Третье истинное значение в столбце ~p равно F, потому что когда p=F, ~p=T.
- Четвертым значением истинности в столбце ~p является T, потому что когда p=T, ~p=F.
- Теперь, когда мы позаботились о знаке ~ в выражении внутри круглых скобок, все, о чем нам осталось позаботиться внутри круглых скобок, — это символ ∧ в r∧~p. Символ ∧ всегда соединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными операторами, но нам все равно, насколько они сложны, , если у нас уже есть столбец в таблице истинности с этим логическим выражением вверху . В этом выражении символ ∧ соединяет 2 выражения: r и ~p.
И r, и ~p находятся в верхней части столбцов таблицы истинности, поэтому мы можем использовать эти два столбца, чтобы заполнить столбец для r∧~p, просто используя определение символа ∧:р
р
~ стр.

Т
Т
Ф
Ф
Т
Ф
Ф
Ф
Ф
Т
Т
Т
Ф
Ф
Т
Ф
- Первым значением истинности в столбце r∧~p является F, потому что, когда r=T и ~p=F, r∧~p=F.

- Вторым значением истинности в столбце r∧~p является F, потому что, когда r=F и ~p=F, r∧~p=F.
- Третьим значением истинности в столбце r∧~p является T, потому что, когда r=T и ~p=T, r∧~p=T.
- Четвертым значением истинности в столбце r∧~p является F, потому что, когда r=F и ~p=T, r∧~p=F.
- Первым значением истинности в столбце r∧~p является F, потому что, когда r=T и ~p=F, r∧~p=F.
- Теперь, когда мы позаботились о скобках, все, о чем нам осталось побеспокоиться, это символ, оставшийся за скобками: символ → в (r∧~p)→r. Символ → всегда объединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными операторами, но нам все равно, насколько они сложны, , если у нас уже есть столбец в таблице истинности с этим логическим выражением вверху . В этом выражении символ → объединяет 2 выражения: r∧~p и r.
Оба r∧~p и r находятся в верхней части столбцов таблицы истинности, поэтому мы можем использовать эти два столбца, чтобы заполнить столбец для (r∧~p)→r, просто используя определение → символ:р
р
~ стр.

р∧~р
Т
Т
Ф
Ф
Т
Т
Ф
Ф
Ф
Т
Ф
Т
Т
Т
Т
Ф
Ф
Т
Ф
Т
Когда вы работаете с условной связкой (→), вы должны пометить столбец, соответствующий первому оператору иначе, чем пометку второго столбца . При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора !
При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора !
В этих примерах мы различаем их, окрашивая столбец, содержащий первый оператор желтый и столбец, содержащий второй оператор цвет морской волны . Помните, что утверждение, содержащее символ →, является ложным только тогда, когда первое утверждение (то, что перед знаком →) является истинным , а второе утверждение (то, что после знаком →) является ложь !- Первым значением истинности в столбце (r∧~p)→r является T, потому что, когда (r∧~p)=F и r=T, (r∧~p)→r=T.
- Вторым значением истинности в столбце (r∧~p)→r является T, потому что, когда (r∧~p)=F и r=F, (r∧~p)→r=T.
- Третьим значением истинности в столбце (r∧~p)→r является T, потому что, когда (r∧~p)=T и r=T, (r∧~p)→r=T.

- Четвертым значением истинности в столбце (r∧~p)→r является T, потому что, когда (r∧~p)=F и r=F, (r∧~p)→r=T.
Таким образом, окончательная таблица истинности для этого утверждения будет выглядеть так:
 Поскольку здесь у нас есть 2 буквы, p и r, у нас будет 2 столбца в начале таблицы истинности, помеченные p и r:
Поскольку здесь у нас есть 2 буквы, p и r, у нас будет 2 столбца в начале таблицы истинности, помеченные p и r:р
р
Т
Т
Т
Ф
Ф
Т
Ф
Ф
р
р
~р
р∧~р
(r∧~p)→r
Т
Т
Ф
Ф
Т
Т
Ф
Ф
Ф
Т
Ф
Т
Т
Т
Т
Ф
Ф
Т
Ф
Т
- Порядок операций гласит, что мы всегда делаем круглые скобки первыми .
- г∧(~р→г)
- Сначала мы начнем с написания таблицы со всеми возможными комбинациями значений истинности для каждой буквы в выражении.
- Порядок операций гласит, что мы всегда делаем круглые скобки первыми .
 Итак, смотрим, что находится внутри скобок: ~p→r.
Итак, смотрим, что находится внутри скобок: ~p→r.
Внутри скобок два символа: ~ и →.
Порядок операций гласит, что мы всегда делаем сначала отрицания .
Итак, мы помечаем первый пустой столбец как ~p.
Затем, поскольку p — единственная буква в выражении ~p, мы используем заданные значения истинности p в таблице, чтобы заполнить соответствующие значения истинности для ~p:р
р
Т
Т
Ф
Т
Ф
Ф
Ф
Т
Т
Ф
Ф
Т

- Первым значением истинности в столбце ~p является F, потому что когда p=T, ~p=F.
- Вторым значением истинности в столбце ~p является T, потому что когда p=T, ~p=F.
- Третье истинное значение в столбце ~p равно F, потому что когда p=F, ~p=T.
- Четвертым значением истинности в столбце ~p является T, потому что когда p=T, ~p=F.
- Теперь, когда мы позаботились о знаке ~ в выражении внутри круглых скобок, все, о чем нам осталось беспокоиться внутри круглых скобок, — это символ → в ~p→r. Символ → всегда объединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными утверждениями, но нас не волнует, насколько они сложны, до тех пор, пока у нас уже есть столбец в таблице истинности с этим логическим выражением вверху 9.0663 . В этом выражении символ → объединяет 2 выражения: ~p и r.
И ~p, и r находятся вверху столбцов в таблице истинности, поэтому мы можем использовать эти два столбца, чтобы заполнить столбец для ~p→r, просто используя определение символа →:р
р
~ стр.

Т
Т
Ф
Т
Т
Ф
Ф
Т
Ф
Т
Т
Т
Ф
Ф
Т
Ф
Когда вы работаете с условной связкой (→), вы должны пометить столбец, соответствующий первому оператору иначе, чем пометку второго столбца . При заполнении столбца условного утверждения убедитесь, что вам 9 лет.0662 не перепутать столбец для первого оператора со столбцом для второго оператора !
При заполнении столбца условного утверждения убедитесь, что вам 9 лет.0662 не перепутать столбец для первого оператора со столбцом для второго оператора !
В этих примерах мы различаем их, окрашивая столбец, содержащий , первый оператор , желтый , и столбец, содержащий , второй оператор , , голубой . Помните, что утверждение, содержащее символ → , является ложным только в том случае, если первое утверждение (то, что перед знаком →) является истинным и второй оператор (тот, что после знака →) false !- Первым значением истинности в столбце ~p→r является T, потому что, когда ~p=F и r=T, ~p→r=T.
- Вторым значением истинности в столбце ~p→r является T, потому что, когда ~p=F и r=F, ~p→r=T.
- Третьим значением истинности в столбце ~p→r является T, потому что, когда ~p=T и r=T, ~p→r=T.

- Четвертым значением истинности в столбце ~p→r является F, потому что, когда ~p=T и r=F, ~p→r=F.
- Теперь, когда мы позаботились о скобках, все, о чем нам осталось беспокоиться, это символ, оставшийся за скобками: это символ ∧ в r∧(~p→r). Символ ∧ всегда соединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными утверждениями, но нас не волнует, насколько они сложны, до тех пор, пока у нас уже есть столбец в таблице истинности с этим логическим выражением наверху . В этом выражении символ ∧ соединяет 2 выражения: r и ~p→r.
И r, и ~p→r находятся в верхней части столбцов таблицы истинности, поэтому мы можем использовать эти два столбца, чтобы заполнить столбец для r∧(~p→r), просто используя определение ∧ символ:р
р ~ стр.
~п→р
Т
Т Ф
Т
Т
Т
Ф Ф
Т
Ф
Ф
Т Т
Т
Т
Ф
Ф Т
Ф
Ф
- Первым значением истинности в столбце r∧(~p→r) является T, потому что, когда r=T и ~p→r=T, r∧(~p→r)=T.

- Вторым значением истинности в столбце r∧(~p→r) является F, потому что, когда r=F и ~p→r=T, r∧(~p→r)=F.
- Третьим значением истинности в столбце r∧(~p→r) является T, потому что, когда r=T и ~p→r=T, r∧(~p→r)=T.
- Четвертым значением истинности в столбце r∧(~p→r) является F, потому что, когда r=F и ~p→r=F, r∧(~p→r)=F.
р
р ~р
~п→р
г∧(~п→г)
Т
Т Ф
Т
Т
Т
Ф Ф
Т
Ф
Ф
Т Т
Т
Т
Ф
Ф Т
Ф
Ф
- Первым значением истинности в столбце r∧(~p→r) является T, потому что, когда r=T и ~p→r=T, r∧(~p→r)=T.

Поскольку здесь у нас есть 2 буквы, p и r, у нас будет 2 столбца в начале таблицы истинности, помеченные p и r:
р
р
Т
Т
Т
Ф
Ф
Т
Ф
Ф
- Порядок операций гласит, что мы всегда делаем круглые скобки первыми .
- ~(p∨q)↔r
- Сначала мы начнем с написания таблицы со всеми возможными комбинациями значений истинности для каждой буквы в выражении.
- Порядок операций гласит, что мы всегда делаем круглые скобки первыми .
 Итак, мы смотрим на то, что находится внутри скобок: p∨q.
Итак, мы смотрим на то, что находится внутри скобок: p∨q.
Внутри скобок у нас есть один символ: ∨.Символ ∨ всегда соединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными операторами, но нам все равно, насколько они сложны, , если у нас уже есть столбец в таблице истинности с этим логическим выражением вверху .
В этом выражении символ ∨ объединяет 2 выражения: p и q.
Оба столбца p и q находятся в верхней части столбцов таблицы истинности, поэтому мы можем использовать эти два столбца, чтобы заполнить столбец для p∨q, просто используя определение символа ∨:р
q
р
Т
Т
Т
Т
Т
Т
Ф
Т
Т
Ф
Т
Т
Т
Ф
Ф
Т
Ф
Т
Т
Т
Ф
Т
Ф
Т
Ф
Ф
Т
Ф
Ф
Ф
Ф
Ф
Помните, что утверждение, содержащее символ ∨, верно , если хотя бы одно из утверждений верно !- Первым значением истинности в столбце p∨q является T, потому что, когда p=T и q=T, p∨q=T.

- Вторым значением истинности в столбце p∨q является T, потому что, когда p=T и q=T, p∨q=T.
- Третье истинное значение в столбце p∨q равно T, потому что, когда p=T и q=F, p∨q=T.
- Четвертым значением истинности в столбце p∨q является T, потому что, когда p=T и q=F, p∨q=T.
- Пятое истинное значение в столбце p∨q равно T, потому что, когда p=F и q=T, p∨q=T.
- Шестое значение истинности в столбце p∨q равно T, потому что, когда p=F и q=T, p∨q=T.
- Седьмое истинное значение в столбце p∨q равно F, потому что, когда p=F и q=F, p∨q=F.
- Восьмое значение истинности в столбце p∨q равно F, потому что, когда p=F и q=F, p∨q=F.
- Первым значением истинности в столбце p∨q является T, потому что, когда p=T и q=T, p∨q=T.
- Теперь, когда мы позаботились обо всем, что находится внутри круглых скобок, мы можем позаботиться о символе ~, находящемся вне круглых скобок: ~(p∨q). Поскольку p∨q — это утверждение в выражении ~(p∨q), мы используем заданные значения истинности p∨q в таблице, чтобы заполнить соответствующие значения истинности для ~(p∨q):
стр.

q
р
p∨q
Т
Т
Т
Т
Ф
Т
Т
Ф
Т
Ф
Т
Ф
Т
Т
Ф
Т
Ф
Ф
Т
Ф
Ф
Т
Т
Т
Ф
Ф
Т
Ф
Т
Ф
Ф
Ф
Т
Ф
Т
Ф
Ф
Ф
Ф
Т

- Первым значением истинности в столбце ~(p∨q) является F, потому что, когда p∨q=T, ~(p∨q)=F.
- Вторым значением истинности в столбце ~(p∨q) является F, потому что, когда p∨q=T, ~(p∨q)=F.
- Третье истинное значение в столбце ~(p∨q) равно F, потому что, когда p∨q=T, ~(p∨q)=F.
- Четвертым значением истинности в столбце ~(p∨q) является F, потому что, когда p∨q=T, ~(p∨q)=F.
- Пятое значение истинности в столбце ~(p∨q) равно F, потому что, когда p∨q=T, ~(p∨q)=F.
- Шестое значение истинности в столбце ~(p∨q) равно F, потому что, когда p∨q=T, ~(p∨q)=F.
- Седьмое истинное значение в столбце ~(p∨q) равно T, потому что, когда p∨q=F, ~(p∨q)=T.
- Восьмое значение истинности в столбце ~(p∨q) равно T, потому что, когда p∨q=F, ~(p∨q)=T.
- Теперь, когда мы позаботились о скобках, все, о чем нам осталось побеспокоиться, — это символ, оставшийся за скобками: символ ↔ в ~(p∨q)↔r. Символ ↔ всегда соединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными операторами, но нам все равно, насколько они сложны, , если у нас уже есть столбец в таблице истинности с этим логическим выражением вверху .
 В этом выражении символ ↔ соединяет 2 выражения: ~(p∨q) и r.
В этом выражении символ ↔ соединяет 2 выражения: ~(p∨q) и r.
Оба ~(p∨q) и r находятся в верхней части столбцов таблицы истинности, поэтому мы можем использовать эти два столбца, чтобы заполнить столбец для ~(p∨q)↔r, просто используя определение символ ↔:р
q
р
p∨q
~(p∨q)
Т
Т
Т
Т
Ф
Ф
Т
Т
Ф
Т
Ф
Т
Т
Ф
Т
Т
Ф
Ф
Т
Ф
Ф
Т
Ф
Т
Ф
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Т
Ф
Т
Ф
Ф
Т
Ф
Т
Т
Ф
Ф
Ф
Ф
Т
Ф
- Первым значением истинности в столбце ~(p∨q)↔r является F, потому что, когда r=T и ~(p∨q)=F, ~(p∨q)↔r=F.

- Вторым значением истинности в столбце ~(p∨q)↔r является T, потому что, когда r=F и ~(p∨q)=F, ~(p∨q)↔r=T.
- Третьим значением истинности в столбце ~(p∨q)↔r является F, потому что, когда r=T и ~(p∨q)=F, ~(p∨q)↔r=F.
- Четвертым значением истинности в столбце ~(p∨q)↔r является T, потому что, когда r=F и ~(p∨q)=F, ~(p∨q)↔r=T.
- Пятым значением истинности в столбце ~(p∨q)↔r является F, потому что, когда r=T и ~(p∨q)=F, ~(p∨q)↔r=F.
- Шестое значение истинности в столбце ~(p∨q)↔r равно T, потому что, когда r=F и ~(p∨q)=F, ~(p∨q)↔r=T.
- Седьмым значением истинности в столбце ~(p∨q)↔r является T, потому что, когда r=T и ~(p∨q)=T, ~(p∨q)↔r=T.
- Восьмое значение истинности в столбце ~(p∨q)↔r равно F, потому что, когда r=F и ~(p∨q)=T, ~(p∨q)↔r=F.
р
q
р
p∨q
~(p∨q)
~(p∨q)↔r
Т
Т
Т
Т
Ф
Ф
Т
Т
Ф
Т
Ф
Т
Т
Ф
Т
Т
Ф
Ф
Т
Ф
Ф
Т
Ф
Т
Ф
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Т
Ф
Т
Ф
Ф
Т
Ф
Т
Т
Ф
Ф
Ф
Ф
Т
Ф
- Первым значением истинности в столбце ~(p∨q)↔r является F, потому что, когда r=T и ~(p∨q)=F, ~(p∨q)↔r=F.

Поскольку здесь у нас есть 3 буквы, p, q и r, у нас будет 3 столбца в начале таблицы истинности, помеченные p, q и r:
стр.
q
р
Т
Т
Т
Т
Т
Ф
Т
Ф
Т
Т
Ф
Ф
Ф
Т
Т
Ф
Т
Ф
Ф
Ф
Т
906:30 Ф
Ф
Ф
- Порядок операций гласит, что мы всегда делаем круглые скобки первыми .
- (~r∧(p→~q))→p
- Сначала мы начнем с написания таблицы со всеми возможными комбинациями значений истинности для каждой буквы в выражении.
- Порядок операций гласит, что мы всегда делаем скобки сначала .
 Итак, смотрим, что находится внутри скобок: p→~q.
Итак, смотрим, что находится внутри скобок: p→~q.
Внутри скобок два символа: → и ~.
Порядок операций гласит, что мы всегда делаем отрицания сначала .
Итак, мы помечаем первый пустой столбец как ~q.
Поскольку q — это утверждение в выражении ~q, мы используем заданные значения истинности q в таблице, чтобы заполнить соответствующие значения истинности для ~q:р
q
р
Т
Т
Т
Ф
Т
Т
Ф
Ф
Т
Ф
Т
Т
Т
Ф
Ф
Т
Ф
Т
Т
Ф
Ф
Т
Ф
Ф
Ф
Ф
Т
Т
Ф
Ф
Ф
Т
Напомним, что утверждение с символом ~ в нем является только истинным , если то, что следует за символом ~, является ложным , и наоборот .
- Первое истинное значение в столбце ~q равно F, потому что когда q=T, ~q=F.
- Второе истинное значение в столбце ~q равно F, поскольку при q=T ~q=F.
- Третье истинное значение в столбце ~q равно T, потому что когда q=F, ~q=T.
- Четвертым значением истинности в столбце ~q является T, потому что когда q=F, ~q=T.
- Пятое истинное значение в столбце ~q равно F, поскольку при q=T ~q=F.
- Шестое значение истинности в столбце ~q равно F, поскольку при q=T ~q=F.
- Седьмое истинное значение в столбце ~q равно T, потому что когда q=F, ~q=T.
- Восьмое истинное значение в столбце ~q равно T, потому что когда q=F, ~q=T.
- Теперь, когда мы позаботились об отрицании внутри самого внутреннего набора скобок, мы можем позаботиться о символе →, единственном оставшемся символе в выражении внутри скобок: p→~q. Символ → всегда объединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными операторами, но нам все равно, насколько они сложны, , если у нас уже есть столбец в таблице истинности с этим логическим выражением вверху .
 В этом выражении символ → объединяет 2 выражения: p и ~q.
В этом выражении символ → объединяет 2 выражения: p и ~q.
И p, и ~q находятся в верхней части столбцов таблицы истинности, поэтому мы можем использовать эти два столбца, чтобы заполнить столбец для p→~q, просто используя определение символа →:р
q
р
~q
Т
Т
Т
Ф
Ф
Т
Т
Ф
Ф
Ф
Т
Ф
Т
Т
Т
Т
Ф
Ф
Т
Т
Ф
Т
Т
Ф
Т
Ф
Т
Ф
Ф
Т
Ф
Ф
Т
Т
Т
Ф
Ф
Ф
Т
Т
Когда вы работаете с условной связкой (→), вы должны пометить столбец, соответствующий первому оператору иначе, чем пометку второго столбца . При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора !
При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора !
В этих примерах мы различаем их, окрашивая столбец, содержащий , первый оператор , , желтый , и столбец, содержащий , второй оператор , , голубой . Помните, что утверждение, содержащее символ →, является ложным только в том случае, если первое утверждение (то, что перед знаком →) является истинным , а второе утверждение (то, что после знаком →) является ложь !- Первым значением истинности в столбце p→~q является F, потому что, когда p=T и ~q=F, p→~q=F.
- Вторым значением истинности в столбце p→~q является F, потому что, когда p=T и ~q=F, p→~q=F.
- Третьим значением истинности в столбце p→~q является T, потому что, когда p=T и ~q=T, p→~q=T.

- Четвертым значением истинности в столбце p→~q является T, потому что, когда p=T и ~q=T, p→~q=T.
- Пятым значением истинности в столбце p→~q является T, потому что, когда p=F и ~q=F, p→~q=T.
- Шестое значение истинности в столбце p→~q равно T, потому что, когда p=F и ~q=F, p→~q=T.
- Седьмое значение истинности в столбце p→~q равно T, потому что, когда p=F и ~q=T, p→~q=T.
- Восьмое значение истинности в столбце p→~q равно T, потому что, когда p=F и ~q=T, p→~q=T.
- Теперь, когда мы позаботились о самом внутреннем наборе скобок, нам нужно посмотреть, что находится в следующем наборе скобок: ~r∧(p→~q).
В этом большом наборе скобок осталось 2 символа: символ ~ и символ ∧. Порядок операций говорит, что мы всегда делаем отрицания сначала .
Итак, мы помечаем первый пустой столбец как ~r.
Поскольку r — это утверждение в выражении ~r, мы используем заданные значения истинности r в таблице, чтобы заполнить соответствующие значения истинности для ~r:р
q
р
~q
п→~к
Т
Т
Т
Ф
Ф
Ф
Т
Т
Ф
Ф
Ф
Т
Т
Ф
Т
Т
Т
Ф
Т
Ф
Ф
Т
Т
Т
Ф
Т
Т
Ф
Т
Ф
Ф
Т
Ф
Ф
Т
Т
Ф
Ф
Т
Т
Т
Ф
Ф
Ф
Ф
Т
Т
Т

- Первым значением истинности в столбце ~r является F, поскольку при r=T ~r=F.
- Второе истинное значение в столбце ~r равно T, потому что когда r=F, ~r=T.
- Третье истинное значение в столбце ~r равно F, поскольку при r=T ~r=F.
- Четвертым значением истинности в столбце ~r является T, потому что, когда r=F, ~r=T.
- Пятое истинное значение в столбце ~r равно F, потому что при r=T ~r=F.
- Шестое истинное значение в столбце ~r равно T, потому что когда r=F, ~r=T.
- Седьмое истинное значение в столбце ~r равно F, поскольку при r=T ~r=F.
- Восьмое истинное значение в столбце ~r равно T, потому что когда r=F, ~r=T.
- Теперь, когда мы позаботились о знаке ~ в выражении внутри круглых скобок, все, о чем нам осталось беспокоиться в больших скобках, — это символ ∧ в ~r∧(p→~q). Символ ∧ всегда соединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными операторами, но нам все равно, насколько они сложны, , если у нас уже есть столбец в таблице истинности с этим логическим выражением вверху .
 В этом выражении символ ∧ объединяет 2 выражения: ~r и p→~q.
В этом выражении символ ∧ объединяет 2 выражения: ~r и p→~q.
И ~r, и p→~q находятся вверху столбцов в таблице истинности, поэтому мы можем использовать эти два столбца, чтобы заполнить столбец для ~r∧(p→~q), просто используя определение символ ∧:р
q
р
~q
п→~к
~r
Т
Т
Т
Ф
Ф
Ф
Ф
Т
Т
Ф
Ф
Ф
Т
Ф
Т
Ф
Т
Т
Т
Ф
Ф
Т
Ф
Ф
Т
Т
Т
Т
Ф
Т
Т
Ф
Т
Ф
Ф
Ф
Т
Ф
Ф
Т
Т
Т
Ф
Ф
Т
Т
Т
Ф
Ф
Ф
Ф
Ф
Т
Т
Т
Т
- Первым значением истинности в столбце ~r∧(p→~q) является F, потому что, когда ~r=F и p→~q=F, ~r∧(p→~q)=F.

- Вторым значением истинности в столбце ~r∧(p→~q) является F, потому что, когда ~r=F и p→~q=T, ~r∧(p→~q)=F.
- Третьим значением истинности в столбце ~r∧(p→~q) является F, потому что, когда ~r=T и p→~q=F, ~r∧(p→~q)=F.
- Четвертым значением истинности в столбце ~r∧(p→~q) является T, потому что, когда ~r=T и p→~q=T, ~r∧(p→~q)=T.
- Пятым значением истинности в столбце ~r∧(p→~q) является F, потому что, когда ~r=T и p→~q=F, ~r∧(p→~q)=F.
- Шестое значение истинности в столбце ~r∧(p→~q) равно T, потому что, когда ~r=T и p→~q=T, ~r∧(p→~q)=T.
- Седьмое значение истинности в столбце ~r∧(p→~q) равно F, потому что, когда ~r=T и p→~q=F, ~r∧(p→~q)=F.
- Восьмое значение истинности в столбце ~r∧(p→~q) равно T, потому что, когда ~r=T и p→~q=T, ~r∧(p→~q)=T.
- Первым значением истинности в столбце ~r∧(p→~q) является F, потому что, когда ~r=F и p→~q=F, ~r∧(p→~q)=F.
- Теперь, когда мы закончили со всеми скобками, у нас остался еще один символ: →, который соединяет два выражения ~r∧(p→~q) и p. Когда мы соединяем эти два выражения вместе с символом →, мы получаем окончательное выражение: (~r∧(p→~q))→p.
 Символ → всегда объединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными операторами, но нам все равно, насколько они сложны, , если у нас уже есть столбец в таблице истинности с этим логическим выражением вверху . В этом выражении символ → объединяет 2 выражения: ~r∧(p→~q) и P.
Символ → всегда объединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными операторами, но нам все равно, насколько они сложны, , если у нас уже есть столбец в таблице истинности с этим логическим выражением вверху . В этом выражении символ → объединяет 2 выражения: ~r∧(p→~q) и P.
Оба ~r∧(p→~q) и P находятся в верхних столбцах таблицы истинности, поэтому мы можем использовать эти два столбца, чтобы заполнить столбец для (~r∧(p→~q))→P, просто используя определение символа →:р
кв.
р
~q
п→~к
~р
~r∧(p→~q) Т
Т
Т
Ф
Ф
Ф
Ф
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Т
Т
Ф
Т
Т
Т
Ф
Ф
Т
Т
Ф
Ф
Т
Т
Т
Т
Т
Ф
Т
Т
Ф
Т
Ф
Ф
Т
Ф
Т
Ф
Ф
Т
Т
Т
Ф
Ф
Ф
Т
Т
Т
Ф
Ф
Т
Ф
Ф
Ф
Т
Т
Т
Т
Ф
Когда вы работаете с условной связкой (→), вы должны пометить столбец, соответствующий первому оператору иначе, чем пометку второго столбца . Убедитесь, что при заполнении столбца для условного оператора вы не путаете столбец для первого оператора со столбцом для второго оператора !
Убедитесь, что при заполнении столбца для условного оператора вы не путаете столбец для первого оператора со столбцом для второго оператора !
В этих примерах мы различаем их, окрашивая столбец, содержащий , первый оператор , желтый , и столбец, содержащий , второй оператор , , голубой . Помните, что утверждение, содержащее символ →, является ложным только в том случае, если первое утверждение (то, что перед знаком →) является истинным , а второе утверждение (то, что после знаком →) является ложь !- Первым значением истинности в столбце (~r∧(p→~q))→P является T, потому что, когда (~r∧(p→~q))=F и P=T, (~r∧(p →~q))→P=T.
- Вторым значением истинности в столбце (~r∧(p→~q))→P является T, потому что, когда (~r∧(p→~q))=F и P=T, (~r∧(p→ ~q))→P=T.
- Третьим значением истинности в столбце (~r∧(p→~q))→P является T, потому что, когда (~r∧(p→~q))=F и P=T, (~r∧(p→ ~q))→P=T.

- Четвертым значением истинности в столбце (~r∧(p→~q))→P является T, потому что, когда (~r∧(p→~q))=T и P=T, (~r∧(p→ ~q))→P=T.
- Пятым значением истинности в столбце (~r∧(p→~q))→P является T, потому что, когда (~r∧(p→~q))=F и P=F, (~r∧(p→ ~q))→P=T.
- Шестое значение истинности в столбце (~r∧(p→~q))→P равно F, потому что, когда (~r∧(p→~q))=T и P=F, (~r∧(p→ ~q))→P=F.
- Седьмое значение истинности в столбце (~r∧(p→~q))→P равно T, потому что, когда (~r∧(p→~q))=F и P=F, (~r∧(p→ ~q))→P=T.
- Восьмое значение истинности в столбце (~r∧(p→~q))→P равно F, потому что, когда (~r∧(p→~q))=T и P=F, (~r∧(p→ ~q))→P=F.
р
q
р
~q
п→~к
~р
~r∧(p→~q) (~r∧(p→~q))→p Т
Т
Т
Ф
Ф
Ф
Ф
Т
Т
Т
Ф
Ф
Ф
Т
Ф
Т
Т
Ф
Т
Т
Т
Ф
Ф
Т
Т
Ф
Ф
Т
Т
Т
Т
Т
Ф
Т
Т
Ф
Т
Ф
Ф
Т
Ф
Т
Ф
Ф
Т
Т
Т
Ф
Ф
Ф
Т
Т
Т
Ф
Ф
Т
Ф
Ф
Ф
Т
Т
Т
Т
Ф

Поскольку здесь у нас есть 3 буквы, p, q и r, у нас будет 3 столбца в начале таблицы истинности, помеченные p, q и r:
р
q
р
Т
Т
Т
906:30 Т
Т
Ф
Т
Ф
Т
Т
Ф
Ф
Ф
Т
Т
Ф
Т
Ф
906:30 Ф
Ф
Т
Ф
Ф
Ф
- Порядок операций гласит, что мы всегда делаем скобки сначала .
Готовы ли вы теперь попробовать составить свои собственные таблицы истинности?
Теперь вернитесь к Blackboard, чтобы ответить на вопросы второй лекции по логике: создание таблиц истинности!
[SL04] Комплексные таблицы истинности
§1.
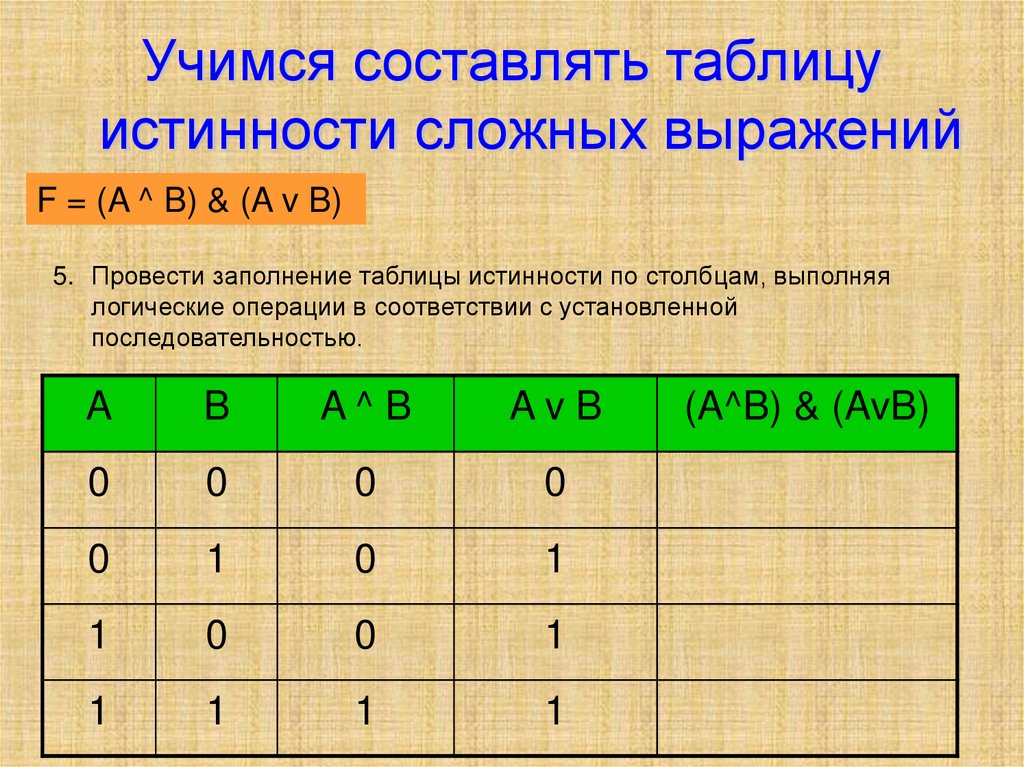 Что мы делаем?
Что мы делаем?В этом уроке вы узнаете, как нарисовать 90 465 полных (или полных) 90 466 таблиц истинности для более сложных WFF. Что мы хотим сделать, так это использовать таблицу истинности, чтобы сказать нам, когда WFF является истинным, а когда ложным. Вот аналогия, которая поможет вам понять, что мы хотим сделать.
Предположим, у нас есть две стрелки, и они могут указывать только вверх или вниз. Тогда есть только четыре возможных способа их выравнивания:
Теперь рассмотрим предложение «левая стрелка указывает вверх, а правая стрелка указывает вверх». Очевидно, что предложение истинно в первой ситуации и ложно в остальных трех ситуациях. Если мы рассмотрим другое предложение, например, «правая стрелка указывает вниз», то оно истинно во второй и четвертой ситуации. Наконец, как насчет такого предложения, как «стрелка влево указывает вверх, а стрелка влево указывает вниз»? Это противоречивое утверждение, и очевидно, что оно ложно во всех четырех ситуациях.
Точно так же, когда мы рисуем таблицу истинности для WFF в SL, мы пытаемся перечислить набор возможных ситуаций, чтобы определить, когда WFF истинна (если когда-либо) и когда она ложна (если вообще).
§2. Составление таблицы истинности
Чтобы нарисовать таблицу истинности для WFF, выполните следующую процедуру. Во-первых, помните, что в полной таблице истинности есть четыре области:
| Регион №1 | |
Регион № 3
|
Регион №4
|
Чтобы заполнить таблицу истинности для WFF, вам необходимо заполнить четыре региона в соответствии с этой процедурой:
Этап 1
Запишите WFF в области № 2.
Этап 2
Определите буквы предложений, которые появляются в WFF, и напишите их.
вниз один за другим в одной строке в регионе № 1.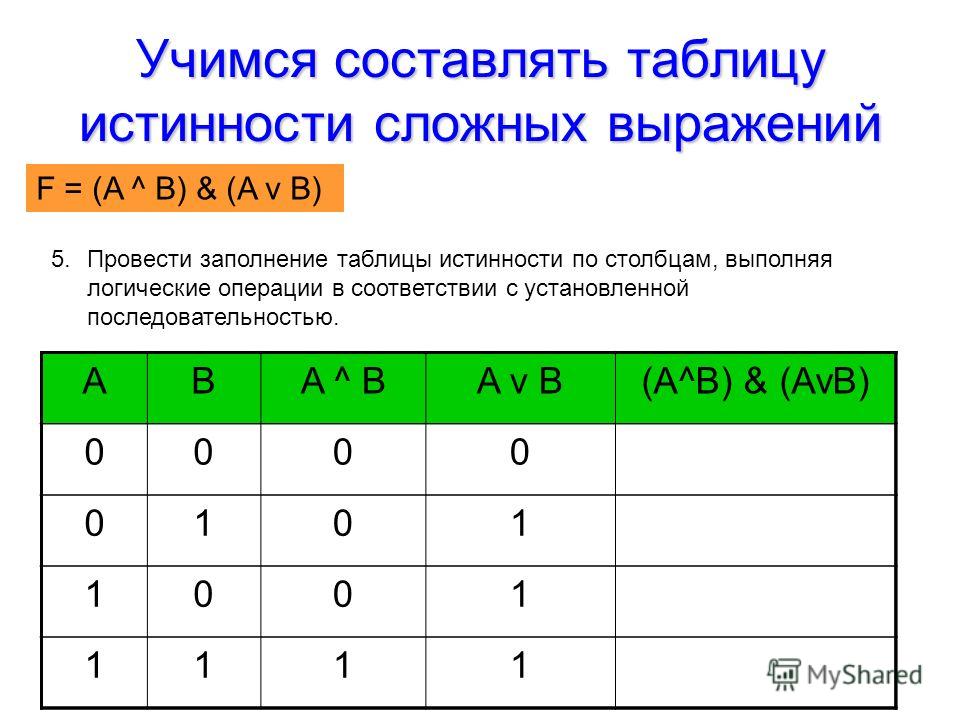 Вам нужно только
запишите письмо-предложение один раз, даже если оно состоит из нескольких
События в WFF.
Вам нужно только
запишите письмо-предложение один раз, даже если оно состоит из нескольких
События в WFF.
Так, например, при наличии WFF «(P→(PvQ))» таблица истинности будет выглядеть вот так после первых двух шагов:
Регион № 3
|
Регион №4
|
Этап 3
Область 3 представляет собой список всех возможных комбинаций значений истинности, которые могут принимать буквы предложения в области № 1. Каждая строка в области № 3 определяет комбинацию, и каждая комбинация называется 9.0465 присвоение значений истинности. Эти назначения соответствуют различным возможным ситуациям в примере со стрелкой вверху.
Если в области №1 n букв предложений, каждая из которых может иметь
значение истинности T или F, то мы знаем, что существует 2 n возможные назначения значений истинности (2 1 =2, 2 2 =4, 2 3 =8, 2 4 =16 и т.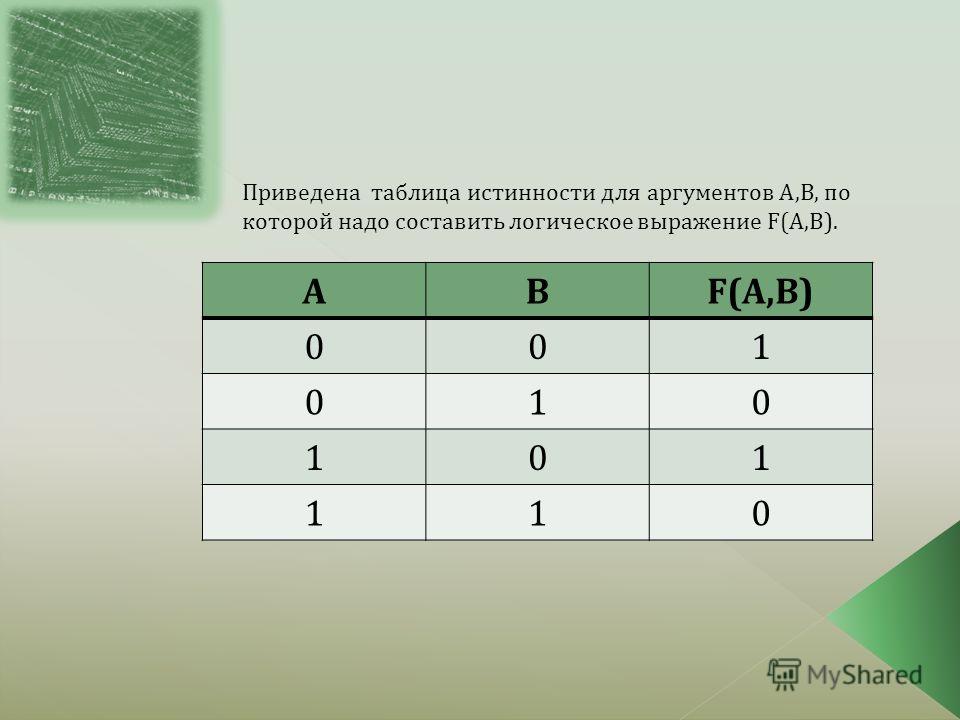 д.). Таким образом, в приведенной выше таблице истинности должно быть четыре назначения. Записываем их по одному на каждом
строка в области № 3:
д.). Таким образом, в приведенной выше таблице истинности должно быть четыре назначения. Записываем их по одному на каждом
строка в области № 3:
T F F T F F |
В каждом ряду пишем под каждым предложением букву истинностное значение, которое является истинностным значением, которое получает буква предложения под это задание. Таким образом, «TF» во второй строке указывает на присвоение где «P» — это T, а «Q» — это F, а «FT» в третьей строке указывает на присвоение, где «P» — это F, а «Q» — это T.
При написании заданий важно систематизировать
способ перечислить их все. Без такого метода легко промахнуться
некоторые из них, если в таблице истинности много строк.
Когда вы сравниваете таблицы истинности двух или более WFF, важно
использовать тот же метод для перечисления значений истинности в
такой же порядок.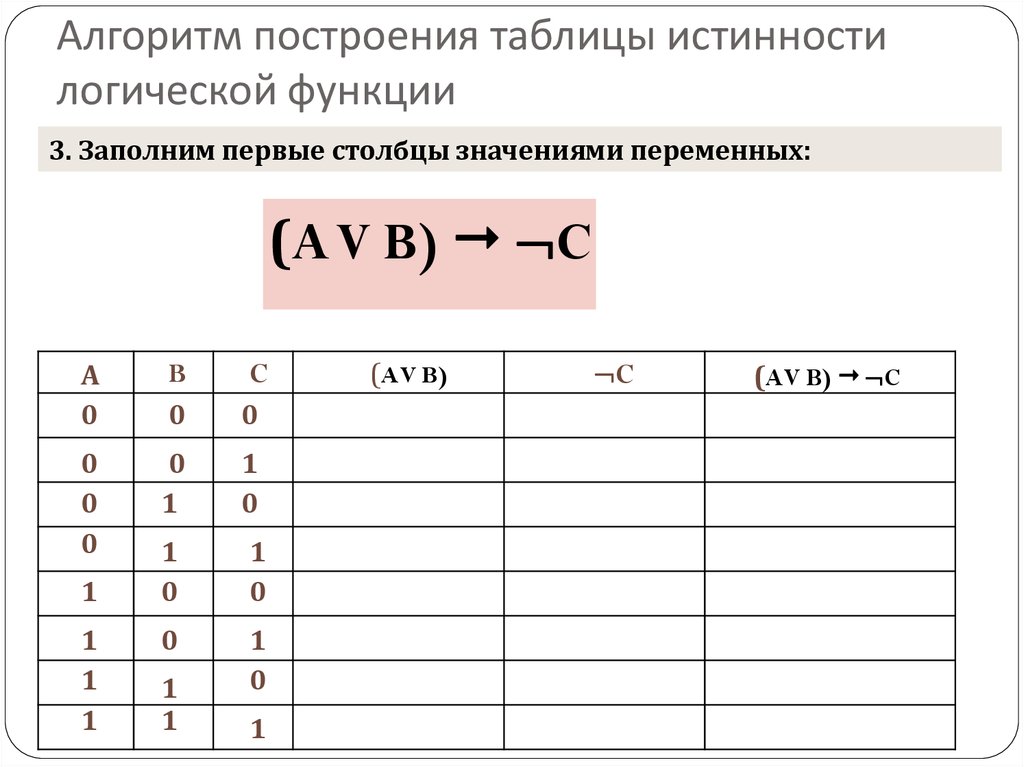
Стандартный метод следующим образом: начните с самой правой буквы предложения в регионе № 1. Напишите «T» под буквой в первом ряду области № 3, а затем «F» в второй ряд, чередуя в каждом ряду до последнего ряда. Затем перейдите ко второй букве предложения и снова начните с «Т». Но на этот раз чередуйте истинностное значение только каждые два ряда . Если там есть буква третьего предложения, чередующаяся между буквами «T» и «F» через каждые четыре ряды. В общем то для n -го письма предложения (начиная с справа), чередуйте «Т» и «Ф» через каждые 2 п -1 ряд.
Этап 4
Оставшаяся задача при заполнении таблицы истинности состоит в том, чтобы заполнить область № 4 путем вычисления истинностного значения WFF для каждого задания.
Во-первых, давайте определим длина WFF как количество символов SL
это содержит. Учитывается каждое появление соединительной буквы или буквы предложения.
как один символ, а открывающая и закрывающая скобки — разные символы.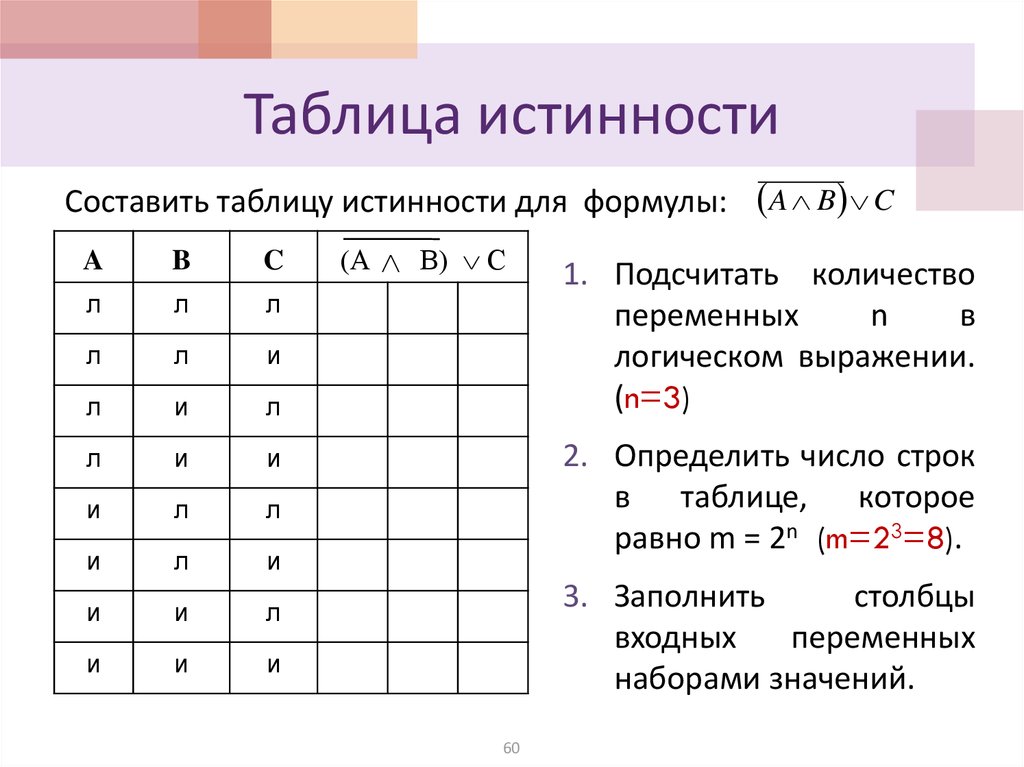 Таким образом, «P» имеет длину 1, «~~Q» имеет длину 3, а «((P&Q)→R)» имеет длину 9 (не 10).
Таким образом, «P» имеет длину 1, «~~Q» имеет длину 3, а «((P&Q)→R)» имеет длину 9 (не 10).
Затем мы применяем эту процедуру. Во-первых, напишите ниже каждая буква предложения WFF истинностное значение, которое оно имеет по каждому заданию:
T F F T F F | T T F F F T F F F |
Буквы предложений, конечно, являются WFF длины 1. Затем мы ищем
следующие кратчайшие WFF, которые являются частью всего WFF, и вычислить их
значения истинности по каждому заданию. Следующие кратчайшие WFF должны быть
длина 2, например «~Q», но поскольку таких WFF нет, следующий
кратчайший WFF есть «(PvQ)» длины 5. Запишем
его истинностное значение для каждого задания под его главный оператор .
Помните, что основным оператором WFF является появление связки, которая имеет
самый широкий размах.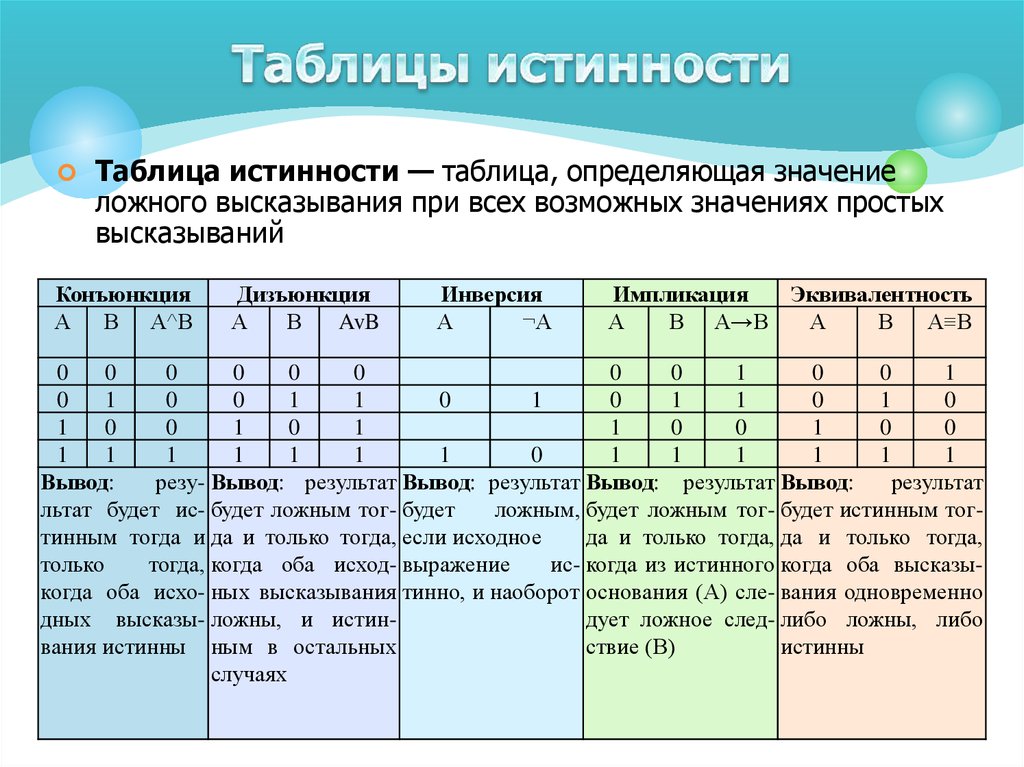
T F F T F F | T TTF F FTT F FFF |
Затем мы повторяем эту процедуру со следующим кратчайшим WFF, пока не получим закончил со всем WFF:
T F F T F F | T T TTF F T FTT F T FFF |
Последний столбец значений истинности, который мы записываем, указывает на значения истинности. всего WFF по каждому из заданий. Эта конкретная таблица истинности мы завершили показывает, что WFF верно во всех четырех возможных задания.
Если вы можете быстро произвести в уме вычисления истинностных значений, вы можете не записывать истинностные значения частей WFF и просто записывать истинностные значения всего WFF под каждым заданием.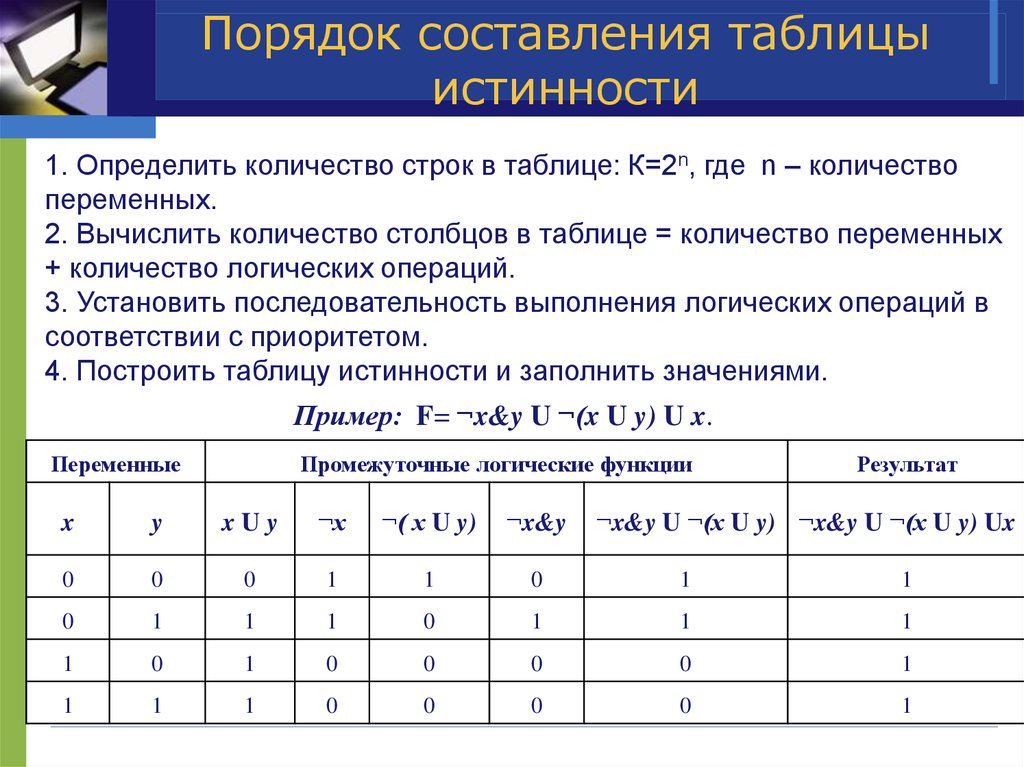 Тогда вы получите эту таблицу истинности.
Тогда вы получите эту таблицу истинности.
T F F T F F | T T T |
Нарисуйте следующие полные таблицы истинности, а затем нажмите WFF, чтобы проверить, правильно ли вы это сделали.
- (P&~Q)
- ((P&Q)→R)
- (~(P∨Q)→R)
- ~(~(П↔(~П∨Q))→~R)
- ~(S↔(~(P&Q)→R))
§3. Кронштейны
Теперь, когда вы знаете, как строить сложные таблицы истинности, вы можете понять, зачем нужны скобки. Например, (A&B→C) является двусмысленным между ((A&B)→C) и (A&(B→C)). Однако таблицы истинности двух WFF сильно различаются:
| A | B | C | ((A&B)→C) |
| T | T | T | T |
| T | T | F | F |
| T | F | T | T |
| T | F | F | T |
| F | T | T | T |
| F | T | F | T |
| F | F | T | T |
| F | F | F | T |
| A | B | C | (A&(B→C)) |
| T | T | T | T |
| T | T | F | F |
| T | F | T | T |
| T | F | F | T |
| F | T | T | F |
| F | T | F | F |
| F | Ф | Т | Ф |
| Ф | Ф | Ф | Ф |
Конечно, есть случаи, когда скобки не имеют значения.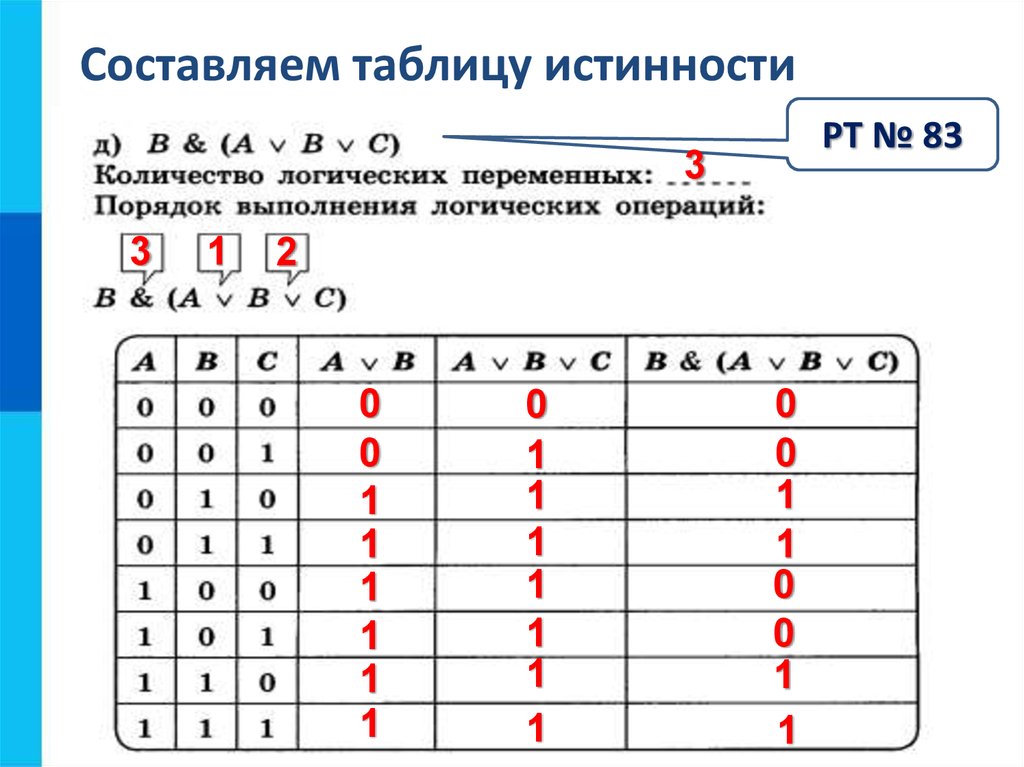 Например, должно быть очевидно, что с P&Q&R&S, независимо от того, где вы поместите скобки, чтобы превратить его в WFF, результирующая таблица истинности всегда будет одной и той же.
Например, должно быть очевидно, что с P&Q&R&S, независимо от того, где вы поместите скобки, чтобы превратить его в WFF, результирующая таблица истинности всегда будет одной и той же.
предыдущий урок следующий урок
2.8: Таблицы истинности — K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2146
На данный момент мы знаем эти символы для логики:
- \(\sim\) не (отрицание)
- \(\стрелка вправо\) если-то
- \(\поэтому\) поэтому
Еще два символа:
- \(\клин\) и
- \(\лор\) или
Мы бы написали «\(p\) и \(q\)» как \(p\клин q\) и «\(p\) или \(q\)» как \(p\lor q\) .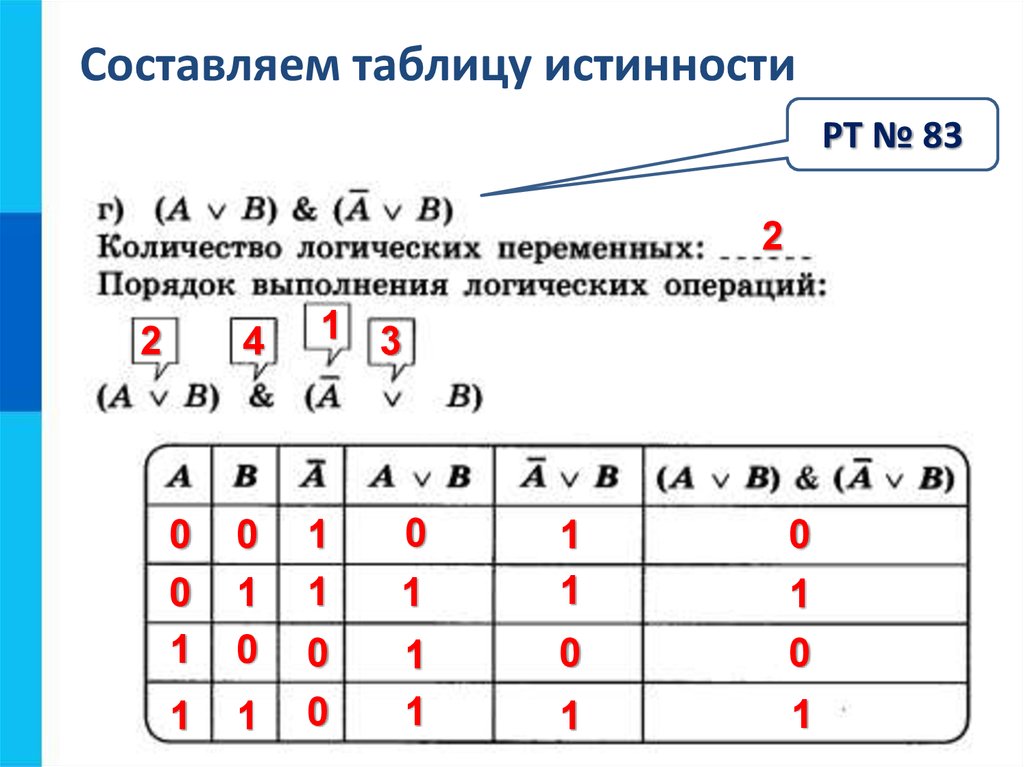
Таблицы истинности используют эти символы и представляют собой еще один способ анализа логики. Во-первых, давайте свяжем p и \sim p. Чтобы было проще, установите p как: Четное число. Следовательно, \sim p равно Нечетное число . Составьте таблицу истинности, чтобы узнать, верны ли они оба. Начните со всех «истин» p, истинных (T) или ложных (F).
Далее мы записываем соответствующие значения истинности для \(\sim p\). \(\sim p\) имеет значения истинности, противоположные \(p\). Итак, если \(p\) истинно, то \(\sim p\) ложно, и наоборот.
| стр | \sim p |
|---|---|
| Т | Ф |
| Ф | Т |
Резюме:
- Начать таблицы истинности со всеми возможными комбинациями истин.
 Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом.
Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом. - Выполните отрицание любой из переменных.
- Любые комбинации в скобках.
- Завершите выполнение того, о чем просила проблема.
Составление таблицы истинности
1. Нарисуйте таблицу истинности для \(p\), \(q\) и \(p \клин q\).
Сначала создайте столбцы для p и q. Заполните столбцы всеми возможными истинными и ложными комбинациями для этих двух.
| стр | к | |
|---|---|---|
| Т | Т | |
| Т | Ф | |
| Ф | Т | |
| Ф | Ф |
Обратите внимание на все комбинации p и q.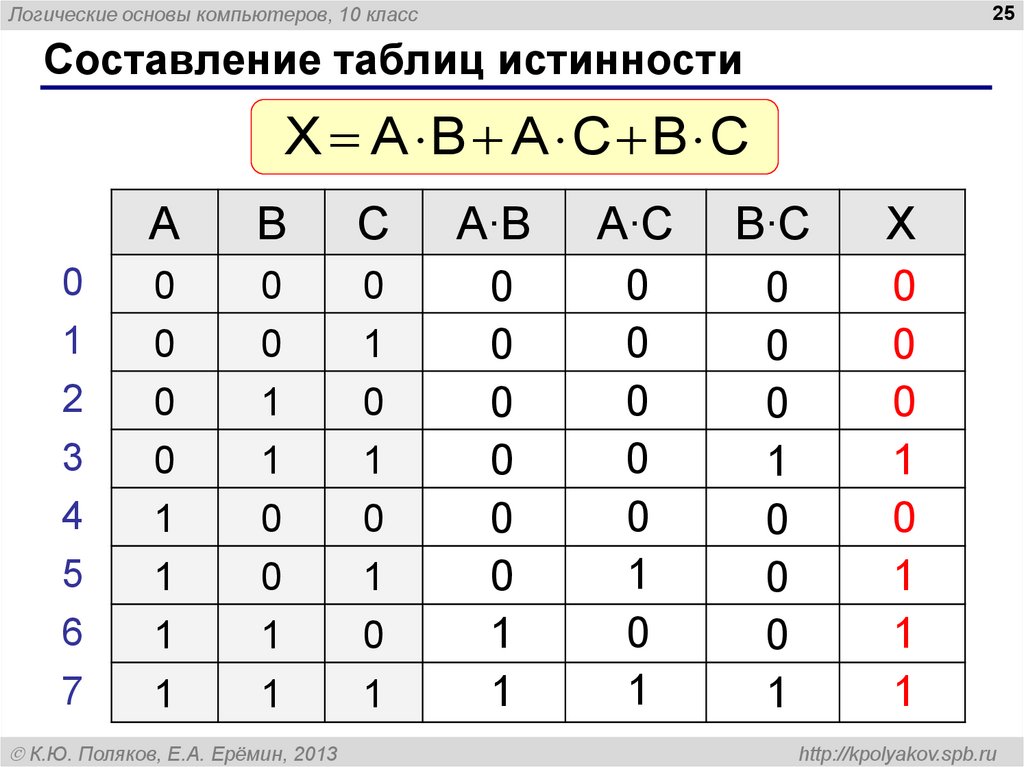 Каждый раз, когда у нас есть таблицы истинности с двумя переменными, это всегда , как мы заполняем первые два столбца.
Каждый раз, когда у нас есть таблицы истинности с двумя переменными, это всегда , как мы заполняем первые два столбца.
Далее нам нужно выяснить, когда \(p\wedge q\) истинно, основываясь на первых двух столбцах. p \wedge q может быть истинным только в том случае, если ОБА p и q истинны. Итак, заполненная таблица выглядит так:
Рисунок \(\PageIndex{1}\)Так всегда заполняется таблица истинности с двумя переменными и их столбцом «и».
2. Нарисуйте таблицу истинности для \(p\), \(q\) и \(p \lor q\).
Сначала создайте столбцы для \(p \lor q\) и \(q\), как в примере A.
| стр | к | |
|---|---|---|
| Т | Т | |
| Т | Ф | |
| Ф | Т | |
| Ф | Ф |
Далее нам нужно выяснить, когда \(p \или q\) истинно, основываясь на первых двух столбцах.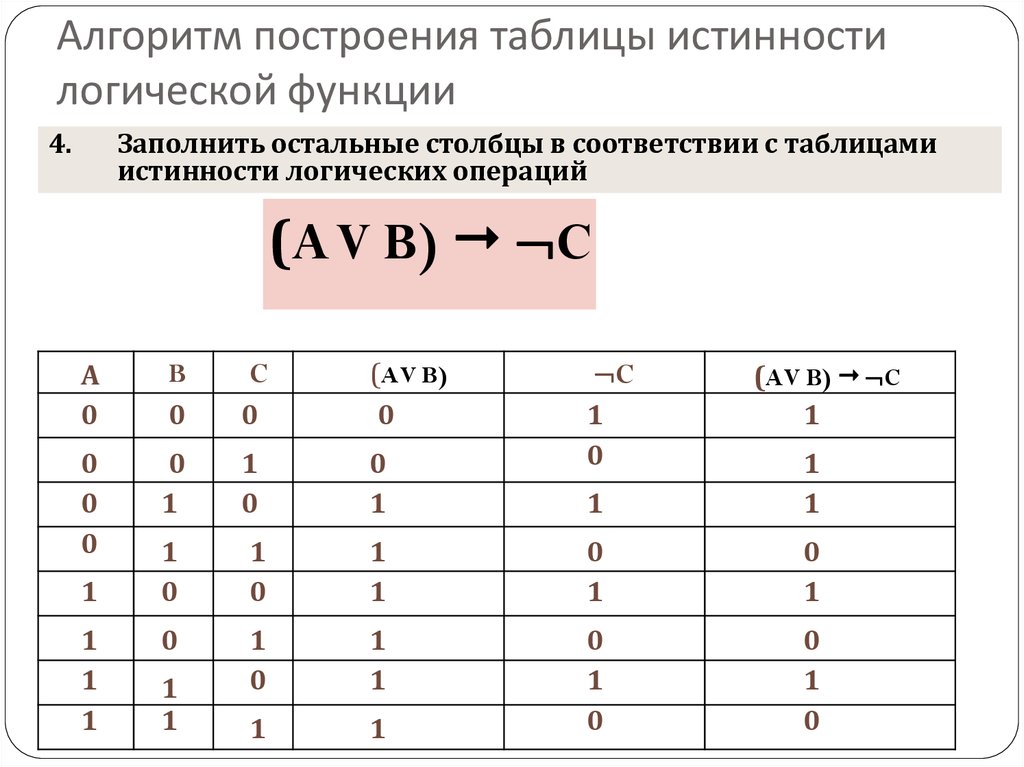 \(p \lor q\) истинно, если \(p\) ИЛИ \(q\) истинны, или оба истинны. Итак, заполненная таблица выглядит так:
\(p \lor q\) истинно, если \(p\) ИЛИ \(q\) истинны, или оба истинны. Итак, заполненная таблица выглядит так:
Разница между \(p \wedge q\) и \(p \lor q\) во второй и третьей строках. Для «и» оба \(p\) и \(q\) должны быть истинными, но для «или» только одно должно быть истинным.
Определение истинности переменных
Определите истинность для \(p \клин(\sim q \lor r)\).
Во-первых, есть три переменных, поэтому нам понадобятся все комбинации их истинности. Для трех переменных всегда есть 8 возможных комбинаций.
| \(р\) | \(к\) | \(р\) | |||
|---|---|---|---|---|---|
| Т | Т | Т | |||
| Т | Т | Ф | |||
| Т | Ф | Т | |||
| Т | Ф | Ф | |||
| Ф | Т | Т | |||
| Ф | Т | Ф | |||
| Ф | Ф | Т | |||
| Ф | Ф | Ф |
Далее адрес \(\sim q\).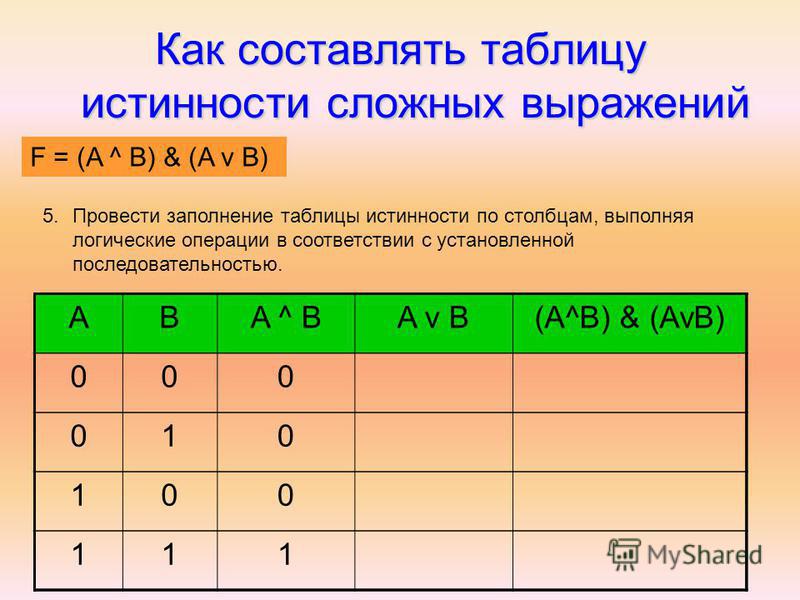 Это будут просто противоположности столбца \(q\).
Это будут просто противоположности столбца \(q\).
| \(р\) | \(к\) | \(р\) | \(\sim q\) | ||
|---|---|---|---|---|---|
| Т | Т | Т | Ф | ||
| Т | Т | Ф | Ф | ||
| Т | Ф | Т | Т | ||
| Т | Ф | Ф | Т | ||
| Ф | Т | Т | Ф | ||
| Ф | Т | Ф | Ф | ||
| Ф | Ф | Т | Т | ||
| Ф | Ф | Ф | Т |
Теперь давайте сделаем то, что указано в скобках, \(\sim q\lor r\). Помните, что для «или» должно быть верно только \(\sim q\) OR \(r\). Используйте только столбцы \(\sim q\) и \(r\) для определения значений в этом столбце.
Помните, что для «или» должно быть верно только \(\sim q\) OR \(r\). Используйте только столбцы \(\sim q\) и \(r\) для определения значений в этом столбце.
| \(р\) | \(к\) | \(р\) | \(\sim q\) | \(\sim q\lor r\) | |
|---|---|---|---|---|---|
| Т | Т | Т | Ф | Т | |
| Т | Т | Ф | Ф | Ф | |
| Т | Ф | Т | Т | Т | |
| Т | Ф | Ф | Т | Т | |
| Ф | Т | Т | Ф | Т | |
| Ф | Т | Ф | Ф | Ф | |
| Ф | Ф | Т | Т | Т | |
| Ф | Ф | Ф | Т | Т |
Наконец, мы можем решить всю проблему, \(p \wedge(\sim q \lor r)\).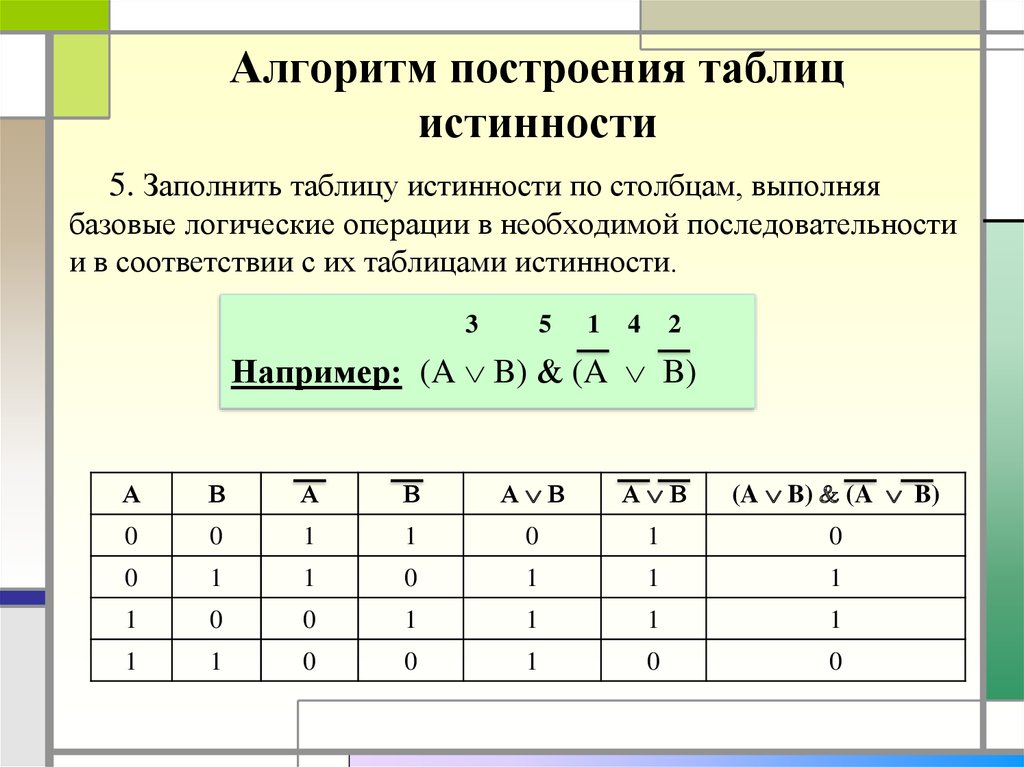 Используйте \(p\) и \(\sim q\lor r\) для определения значений. Помните, что для «и» оба \(p\) и \(\sim q\lor r\) должны быть истинными.
Используйте \(p\) и \(\sim q\lor r\) для определения значений. Помните, что для «и» оба \(p\) и \(\sim q\lor r\) должны быть истинными.
| \(р\) | \(к\) | \(р\) | \(\sim q\) | \(\sim q\lor r\) | \(p \клин(\sim q \lor r)\) |
|---|---|---|---|---|---|
| Т | Т | Т | Ф | Т | Т |
| Т | Т | Ф | Ф | Ф | Ф |
| Т | Ф | Т | Т | Т | Т |
| Т | Ф | Ф | Т | Т | Т |
| Ф | Т | Т | Ф | Т | Ф |
| Ф | Т | Ф | Ф | Ф | Ф |
| Ф | Ф | Т | Т | Т | Ф |
| Ф | Ф | Ф | Т | Т | Ф |
Напишите таблицу истинности для следующих переменных.
Пример \(\PageIndex{1}\)
\(p \wedge \sim p\)
Решение
Сначала создайте столбцы для \(p\), затем добавьте \(\sim p \) и, наконец, оценить \(p \клин \sim p\).
| \(р\) | \(\сим п\) | \(п \клин \сим п\) |
|---|---|---|
| Т | Ф | Ф |
| Ф | Т | Ф |
Пример \(\PageIndex{2}\)
\(\sim p \lor \sim q\)
Решение
Сначала создайте столбцы для \(p\) и \(q\ ), затем добавьте \(\sim p\) и \(\sim q\). Наконец, оцените \(\sim p \lor \sim q\).
Наконец, оцените \(\sim p \lor \sim q\).
| \(р\) | \(к\) | \(\сим п\) | \(\sim q\) | \(\sim p \lor \sim q\) |
|---|---|---|---|---|
| \(p \lor \sim q\) | Т | Ф | Ф | Ф |
| Т | Ф | Ф | Т | Т |
| Ф | Т | Т | Ф | Т |
| Ф | Ф | Т | Т | Т |
Пример \(\PageIndex{3}\)
\(p \wedge (q\lor \sim q)\)
Решение
Сначала создайте столбцы для p и q, затем добавьте \(\sim q\) и \(q\lor \sim q\).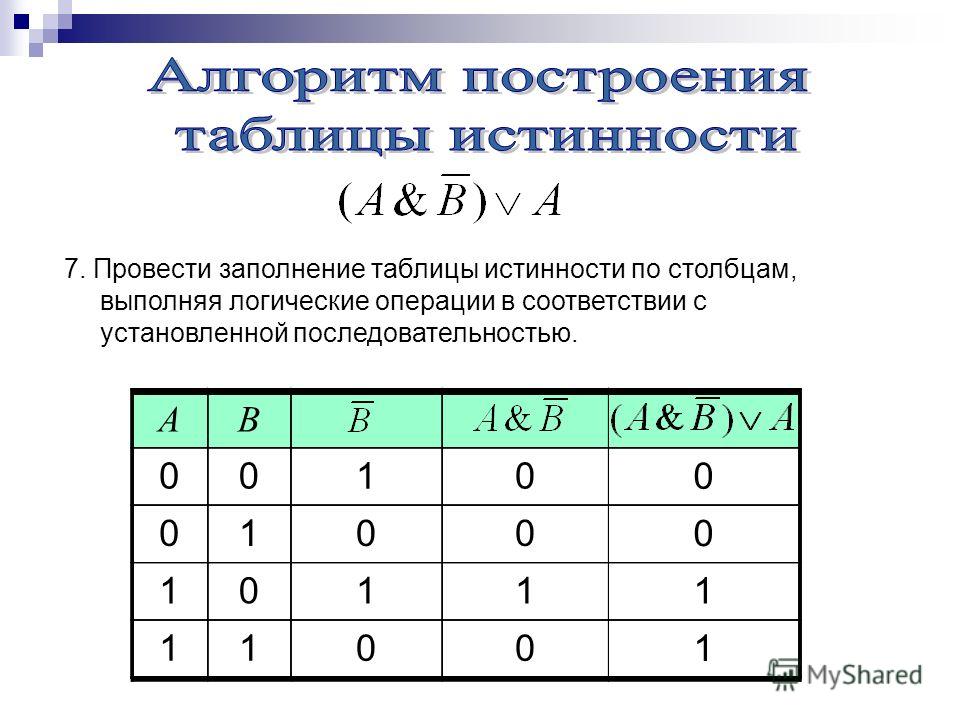 Наконец, оцените \(p\клин (q\lor \sim q)\).
Наконец, оцените \(p\клин (q\lor \sim q)\).
| \(р\) | \(к\) | \(\sim q\) | \(q\lor \sim q\) | \(p\клин (q\lor \sim q)\) |
|---|---|---|---|---|
| Т | Т | Ф | Т | Т |
| Т | Ф | Т | Т | Т |
| Ф | Т | Ф | Т | Ф |
| Ф | Ф | Т | Т | Ф |
Обзор
Напишите таблицу истинности для следующих переменных.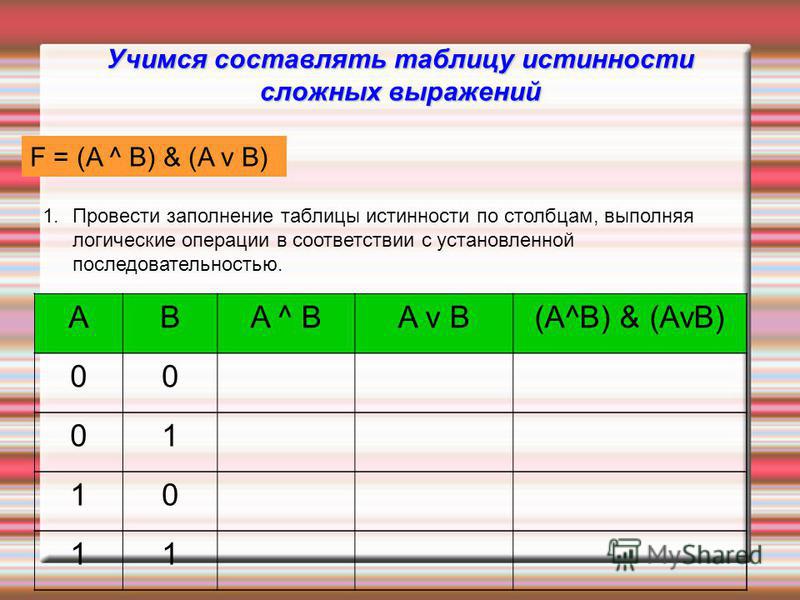
- \((p \клин q)\lor \sim r\)
- \(p \lor ( \sim q \lor r)\)
- \(p \клин (q \lor \sim r)\)
- Единственная разница между #1 и #3 заключается в размещении скобки. Чем отличаются таблицы истинности?
- Когда верно \(p \lor q \lor r\)?
- \(р \лор д \лор г\)
- \((p \lor q) \lor \sim r\)
- \(( \sim p \клин \sim q) \клин r\)
- \(( \sim p \lor \sim q) \клин г\)
Является ли следующий аргумент допустимым? Если да, то какой закон используется? СОВЕТ: Заявления могут быть не по порядку.
\(p \rightarrow q\)
\(r \rightarrow p\)
\(\следовательно r \rightarrow q\)
\(p \rightarrow q\)
\(r \rightarrow q\)
\(\следовательно p \rightarrow r\)
\(p \rightarrow \sim r\)
\(r \)
\(\следовательно \sim p\)
\(\sim q \rightarrow r\)
\(q \)
\(\следовательно \sim r\)
\(p \rightarrow (r \rightarrow s)\)
\(p \)
\(\следовательно r \rightarrow s\)
\(r \rightarrow q\)
\(r \rightarrow s \)
\(\следовательно q \rightarrow s\)
Дополнительные ресурсы
Видео: Таблицы истинности Принципы
Практика: Таблицы истинности 90
Эта страница под названием 2. 8: Таблицы правды распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
8: Таблицы правды распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа ООР или издатель
- СК-12
- Показать оглавление
- нет
- Теги
- источник@https://www.
 ck12.org/c/geometry
ck12.org/c/geometry
- источник@https://www.
17.10: Оценка дедуктивных аргументов с помощью таблиц истинности
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 41409
- Дэвид Липпман
- Колледж Пирса через OpenTextBookStore
Аргументы также можно анализировать с помощью таблиц истинности, хотя это может потребовать много работы.
Анализ аргументов с использованием таблиц истинности
Чтобы проанализировать аргумент с помощью таблицы истинности:
- Символически представить каждую посылку
- Создайте условный оператор, объединив все посылки в антецедент и используя заключение в качестве консеквента.

- Создайте таблицу истинности для утверждения. Если это всегда истинно, то аргумент действителен.
Пример 34
Рассмотрим аргумент
\(\begin{array} {ll} \text{Посылка:} & \text{Если вы купили хлеб, значит, вы пошли в магазин.} \\ \text{ Посылка:} & \text{Вы купили хлеб.} \\ \text{Вывод:} & \text{Вы пошли в магазин.} \end{array}\)
Решение
Хотя этот пример, очевидно, является правильным аргументом, мы можем проанализировать его, используя таблицу истинности, представив каждое из предпосылок символически. Затем мы можем сформировать условное утверждение, показывающее, что посылки вместе подразумевают заключение. Если таблица истинности является тавтологией (всегда истинной), то аргумент действителен.
Пусть \(b\) означает «вы купили хлеб», а s — «вы пошли в магазин». Тогда аргумент принимает вид:
\(\begin{array} {ll} \text{Предпосылка:} & b \rightarrow s \\ \text{Предпосылка:} & b \\ \text{Вывод:} & s \end{массив}\)
Чтобы проверить достоверность, мы смотрим, подразумевает ли комбинация обеих посылок заключение; правда ли, что \([(b \rightarrow s) \wedge b] \rightarrow s ?\)
\(\begin{array}{|c|c|c|}
\hline b & s & b \ стрелка вправо s \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline
\end {массив}\)
\(\begin{array}{|c|c|c|c|}
\hline b & s & b \rightarrow s & (b \rightarrow s) \wedge b \\
\ hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{ F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline
\end{массив}\)
\(\begin{массив}{| c|c|c|c|c|}
\hline b & s & b \rightarrow s & (b \rightarrow s) \wedge b & {[(b \rightarrow s) \wedge b] \rightarrow s} \ \
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T }\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline
\end{массив}\)
Поскольку правда table for \([(b \rightarrow s) \wedge b] \rightarrow s\) всегда верно, это допустимый аргумент.
Попробуйте сейчас 13
Определите, верен ли аргумент:
\(\begin{array} {ll} \text{Предпосылка:} & \text{Если у меня есть лопата, я могу вырыть яму.} \\ \text{Предпосылка:} & \text{Я выкопал яму.} \\ \text{Вывод:} & \text{Поэтому у меня была лопата.} \end{array}\)
- Ответить
Пусть у \(S=\) есть лопата, а у \(D=\operatorname{dig}\) яма. Первая посылка эквивалентна \(S \rightarrow D\). Вторая посылка — \(D\). Вывод \(S\). Мы тестируем \([(S \rightarrow D) \wedge D] \rightarrow S\)
\(\begin{array}{|c|c|c|c|c|}
\hline S & D & S \rightarrow D & (S \rightarrow D) \wedge D & {[(S \rightarrow D ) \клин D] \стрелка вправо S} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \ mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline
\end{массив}\)Это не тавтология, поэтому это неверный аргумент.

Пример 35
\(\begin{array} {ll} \text{Посылка:} & \text{Если я пойду в торговый центр, то куплю новые джинсы.} \\ \text{Посылка:} & \text{Если я куплю новые джинсы, я куплю к ним рубашку.} \\ \text{Вывод:} & \text{Если я пойду в торговый центр, я куплю рубашку.} \ конец{массив}\)
Решение
Пусть \(m=\) я иду в торговый центр, \(j=\) покупаю джинсы и \(s=\) покупаю рубашку.
Посылки и заключение можно сформулировать следующим образом:
\(\begin{array} {ll} \text{Посылка:} & m \rightarrow j \\ \text{Посылка:} & j \rightarrow s \\ \ text{Вывод:} & m \rightarrow s \end{array}\)
Мы можем построить таблицу истинности для \([(m \rightarrow j) \wedge(j \rightarrow s)] \rightarrow(m \rightarrow s) .\) Попробуйте воссоздать каждый шаг и посмотреть, как была построена таблица истинности.
\(\begin{array}{|c|c|c|c|c|c|c|c|}
\hline m & j & s & m \rightarrow j & j \rightarrow s & (m \ стрелка вправо j) \клин(j \стрелка вправо s) & m \стрелка вправо s & {[(m \стрелка вправо j) \клин(j \стрелка вправо s)] \стрелка вправо(m \стрелка вправо s)} \\
\hline \mathrm {T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{ T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \ mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{ T} \\
\hline
\end{array}\)
Из последнего столбца таблицы истинности мы видим, что это правильный аргумент.
Эта страница под названием 17.10: Оценка дедуктивных аргументов с помощью таблиц истинности распространяется под лицензией CC BY-SA 3.0 и была создана, изменена и/или курирована Дэвидом Липпманом (OpenTextBookStore) с помощью исходного содержимого, которое было отредактировано в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Дэвид Липпман
- Лицензия
- CC BY-SA
- Версия лицензии
- 3,0
- Теги
- источник@http://www.
 opentextbookstore.com/mathinsociety
opentextbookstore.com/mathinsociety
- источник@http://www.
генератор таблиц истинности · PyPI
генератор таблиц истинности — это инструмент, который позволяет создавать таблицы истинности. Это форк истин от tr3buchet.
Он объединяет некоторые запросы на извлечение в исходных и других внешних помощниках. Ниже приведены некоторые изменения и улучшения по сравнению с оригиналом:
- табулирование вместо устаревшего
в качестве основного инструмента для
представлять табличные данные в таблицах ASCII (версия PrettyTable все еще доступна).
- , поэтому существует множество форматов таблиц, таких как LaTeX, Org Tables, HTML и все остальные, указанные в табличных документах
- таблица теперь является Pandas DataFrame, поэтому вы можете сделать вывод более наглядным обращение с Pandas Styling. См. примеры ниже.
- новая функция
оценкаоценивающая предложение как тавтология, противоречие или непредвиденные обстоятельства.
- новый интерфейс командной строки (CLI) для печати таблицы истинности с терминала.
Установка
pip install генератор таблицы истинности
Использование
Импорт и синтаксис
Сначала импортируем пакет. ttg означает генератор таблиц истинности .
импортный тг
Таблица истинности имеет по одному столбцу для каждой входной переменной (например, p и q ), и один последний столбец, показывающий все возможные результаты логического операция, которую представляет таблица. Если на входе есть только один список строк, каждая строка считается входной переменной:
print(ttg.Truths(['p', 'q', 'r']))
+-----+-----+-----+ | р | д | р | |-----+-----+-----| | 1 | 1 | 1 | | 1 | 1 | 0 | | 1 | 0 | 1 | | 1 | 0 | 0 | | 0 | 1 | 1 | | 0 | 1 | 0 | | 0 | 0 | 1 | | 0 | 0 | 0 | +-----+-----+-----+
Можно передать второй список строк с созданными пропозициональными выражениями
с логическими операторами.
print(ttg.Truths(['p', 'q', 'r'], ['p и q и r', 'p или q или r', '(p или (~q)) => р']))
+-----+-----+-----+---+----------- ----+------+ | р | д | р | р и д и г | р или д или г | (p или (~q)) => r | |-----+-----+------+---+------------- --+--------------------| | 1 | 1 | 1 | 1 | 1 | 1 | | 1 | 1 | 0 | 0 | 1 | 0 | | 1 | 0 | 1 | 0 | 1 | 1 | | 1 | 0 | 0 | 0 | 1 | 0 | | 0 | 1 | 1 | 0 | 1 | 1 | | 0 | 1 | 0 | 0 | 1 | 1 | | 0 | 0 | 1 | 0 | 1 | 1 | | 0 | 0 | 0 | 0 | 0 | 0 | +-----+-----+------+---+------------- ----------+
Операторы и их представления:
- отрицание :
'не','-','~' - логическая дизъюнкция :
'или' - логическое ни :
'ни' - эксклюзивная дизъюнкция :
'xor','!=' - логическое соединение :
'и' - логическая И-НЕ :
'И-И' - материальное значение :
'=>','подразумевает' - логический двуусловный :
'='
Примечание : Используйте скобки! Особенно с оператором отрицания. Используйте таблицы
выше и ниже в качестве ссылки. Хотя правила приоритета используются, иногда
приоритет между конъюнкцией и дизъюнкцией не указан, что требует
предоставьте это явно в данной формуле со скобками.
Используйте таблицы
выше и ниже в качестве ссылки. Хотя правила приоритета используются, иногда
приоритет между конъюнкцией и дизъюнкцией не указан, что требует
предоставьте это явно в данной формуле со скобками.
Отображение слов (Истина/Ложь)
Если вы предпочитаете слова True и False вместо чисел 0 и 1, есть
третий параметр, логический тип, целых чисел , который может быть установлен на False :
print(ttg.Truths(['p', 'q'], ['p and q', 'p or q', ' (p или (~q)) => (~p)'], ints=False))
+-------+-------+------------+----------+-------- ---------------+ | р | д | р и д | р или д | (p или (~q)) => (~p) | |-------+-------+-----------+-----------+---------- -------------| | Правда | Правда | Правда | Правда | Ложь | | Правда | Ложь | Ложь | Правда | Ложь | | Ложь | Правда | Ложь | Правда | Правда | | Ложь | Ложь | Ложь | Ложь | Правда | +-------+-------+-----------+-----------+---------- -------------+
Параметры форматирования с помощью PrettyTable и Tabulate
Для получения дополнительных параметров форматирования создадим переменную таблицы истинности:
table = ttg. Truths(['p', 'q'], ['p => q', 'p = д'])
Truths(['p', 'q'], ['p => q', 'p = д'])
Команда print(table) отображает стандартную таблицу, как показано в примерах выше:
+-----+-----+----------+---- -----+ | р | д | р => д | р = д | |-----+-----+-----------+---------| | 1 | 1 | 1 | 1 | | 1 | 0 | 0 | 0 | | 0 | 1 | 1 | 0 | | 0 | 0 | 1 | 1 | +-----+-----+-----------+---------+
Команда print(table.as_prettytable()) отображает таблицу с помощью PrettyTable
пакет как на оригинальной версии этого пакета:
+---+---+--------+-------+ | р | д | р => д | р = д | +---+---+--------+-------+ | 1 | 1 | 1 | 1 | | 1 | 0 | 0 | 0 | | 0 | 1 | 1 | 0 | | 0 | 0 | 1 | 1 | +---+---+--------+-------+
Как видно, в выходных данных PrettyTable меньше пустых мест. Тем не менее Пакет PrettyTable имеет гораздо меньше параметров вывода и устарел. Так что я решил использовать пакет Tabulate в качестве стандарта.
Команда print(table.as_tabulate()) отображает таблицу с помощью Tabulate
упаковка. В первом столбце представлены номера строк (которые можно отключить с помощью
параметр
В первом столбце представлены номера строк (которые можно отключить с помощью
параметр index=False ):
+----+-----+-----+----------+---------+ | | р | д | р => д | р = д | |----+-----+-----+----------+---------| | 1 | 1 | 1 | 1 | 1 | | 2 | 1 | 0 | 0 | 0 | | 3 | 0 | 1 | 1 | 0 | | 4 | 0 | 0 | 1 | 1 | +----+-----+-----+----------+---------+
Используя Tabulate, мы можем использовать любой из доступных форматов. Давайте выведем LaTeX таблица без столбца с номером строки:
print(table.as_tabulate(index=False, table_format='latex'))
\begin{табличный}{cccc}
\hline
p & q & p =\ensuremath{>} q & p = q \\
\hline
1 и 1 и 1 и 1 \\
1 и 0 и 0 и 0 \\
0 и 1 и 1 и 0 \\
0 и 0 и 1 и 1 \\
\hline
\end{табличный}
Параметры форматирования с помощью Pandas
С помощью терминала IPython или ноутбука Jupyter можно отобразить Pandas
DataFrame с table.as_pandas() :
И этот вывод можно изменить с помощью Pandas Styling
Более сложные модификации можно выполнить с помощью функций, которые применяют изменения стиля. Примеры см. в учебном блокноте по стилям.
См. изображение ниже для причудливого примера с двумя строками и двумя столбцами.
выделены желтым фоном и разными цветами для True и False.
Примеры см. в учебном блокноте по стилям.
См. изображение ниже для причудливого примера с двумя строками и двумя столбцами.
выделены желтым фоном и разными цветами для True и False.
Функция оценки
Давайте посмотрим, как использовать функцию оценки с новой таблицей истинности:
table_val = ttg.Truths(['p', 'q'], ['p = q', 'p и (~p)', '(p и q) => p'])
печать (таблица_значение)
+-----+-----+---------+--------------+---------- --------+ | р | д | р = д | р и (~р) | (p и q) => p | |-----+-----+---------+---------------+------------ ------| | 1 | 1 | 1 | 0 | 1 | | 1 | 0 | 0 | 0 | 1 | | 0 | 1 | 0 | 0 | 1 | | 0 | 0 | 1 | 0 | 1 | +-----+-----+---------+---------------+------------ ------+
Без аргументов функция оценки классифицирует последний столбец как
тавтология, противоречие или случайность:
table_val.valuation()
«Тавтология»
Если в качестве аргумента используется целое число, функция классифицирует соответствующий столбец:
table_val. value(3)
value(3)
«Непредвиденные обстоятельства»
table_val.value(4)
«Противоречие»
CLI-утилита
Для тех, кто работает в терминале есть простой интерфейс командной строки
(CLI) для печати таблиц. Имя сценария ttg_cly.py и принимает
следующий синтаксис в соответствии с его использованием --help :
: ttg_cli.py [-h] [-p PROPOSITIONS] [-i INTS] переменные
позиционные аргументы:
переменные Список переменных e. грамм. "['р', 'к']"
необязательные аргументы:
-h, --help показать это справочное сообщение и выйти
-p ПРЕДЛОЖЕНИЯ, --propositions ПРЕДЛОЖЕНИЯ
Список предложений e. грамм. "['p или q', 'p и q']"
-i INTS, --ints INTS Истинно для 0 и 1; Ложь для слов
Как видно, список переменных является обязательным. Обратите внимание, что списки должны быть между " .
$ ttg_cli.py "['p', 'q', 'r']"
+-----+-----+-----+ | р | д | р | |-----+-----+-----| | 1 | 1 | 1 | | 1 | 1 | 0 | | 1 | 0 | 1 | | 1 | 0 | 0 | | 0 | 1 | 1 | | 0 | 1 | 0 | | 0 | 0 | 1 | | 0 | 0 | 0 | +-----+-----+-----+
В утилите CLI также есть опция -i для отображения слов вместо цифр:
$ ttg_cli. py "['p', 'q', 'r']" -i Ложь
py "['p', 'q', 'r']" -i Ложь
+-------+-------+-------+ | р | д | р | |-------+-------+-------| | Правда | Правда | Правда | | Правда | Правда | Ложь | | Правда | Ложь | Правда | | Правда | Ложь | Ложь | | Ложь | Правда | Правда | | Ложь | Правда | Ложь | | Ложь | Ложь | Правда | | Ложь | Ложь | Ложь | +-------+-------+-------+
Параметр -p должен стоять перед списком предложений:
$ ttg_cli.py "['p', 'q', 'r']" -p "['p или q', 'p и q или р']"
+-----+-----+-----+----------+----------------+ | р | д | р | р или д | p и q или r | |-----+-----+-----+-----------+----------------| | 1 | 1 | 1 | 1 | 1 | | 1 | 1 | 0 | 1 | 1 | | 1 | 0 | 1 | 1 | 1 | | 1 | 0 | 0 | 1 | 0 | | 0 | 1 | 1 | 1 | 1 | | 0 | 1 | 0 | 1 | 0 | | 0 | 0 | 1 | 0 | 1 | | 0 | 0 | 0 | 0 | 0 | +-----+-----+-----+-----------+----------------+
Со словами вместо чисел:
$ ttg_cli.py "['p', 'q', 'r']" -p "['p или q', 'p и q или r']" -i ЛОЖЬ
+-------+-------+-------+----------+------------ ----+ | р | д | р | р или д | p и q или r | |-------+-------+-------+----------+-------------- --| | Правда | Правда | Правда | Правда | Правда | | Правда | Правда | Ложь | Правда | Правда | | Правда | Ложь | Правда | Правда | Правда | | Правда | Ложь | Ложь | Правда | Ложь | | Ложь | Правда | Правда | Правда | Правда | | Ложь | Правда | Ложь | Правда | Ложь | | Ложь | Ложь | Правда | Ложь | Правда | | Ложь | Ложь | Ложь | Ложь | Ложь | +-------+-------+-------+----------+--------------- --+
Реальный вид таблицы зависит от конфигурации внешнего вида вашего терминала. Скриншоты зеленого на черном фоне с первой картинки в этом README
с моего терминала.
Скриншоты зеленого на черном фоне с первой картинки в этом README
с моего терминала.
Вклад
Приветствуется любой вклад.
Проблемы
Не стесняйтесь присылать вопросы относительно:
- рекомендации
- больше примеров для учебника
- запросов на улучшение и новые полезные функции
- ошибок кода
Запросы на вытягивание
- Прежде чем приступить к работе над запросом на вытягивание, сначала отправьте вопрос
- форк репозитория
- клонировать проект на свой компьютер
- зафиксировать изменения в собственной ветке
- верните свою работу на вилку
- отправьте запрос на вытягивание, чтобы ваши изменения можно было просмотреть
Лицензия
Apache 2.0, см. ЛИЦЕНЗИЯ
Ссылка
Если вы используете генератор таблиц истинности в научной публикации или на занятиях, пожалуйста, рассмотрите возможность цитирования как
FLS Bustamante, генератор таблиц истинности — создание таблиц истинности.


 Выражения для упрощения записи обозначают латинскими буквами A, B, C.
Выражения для упрощения записи обозначают латинскими буквами A, B, C.
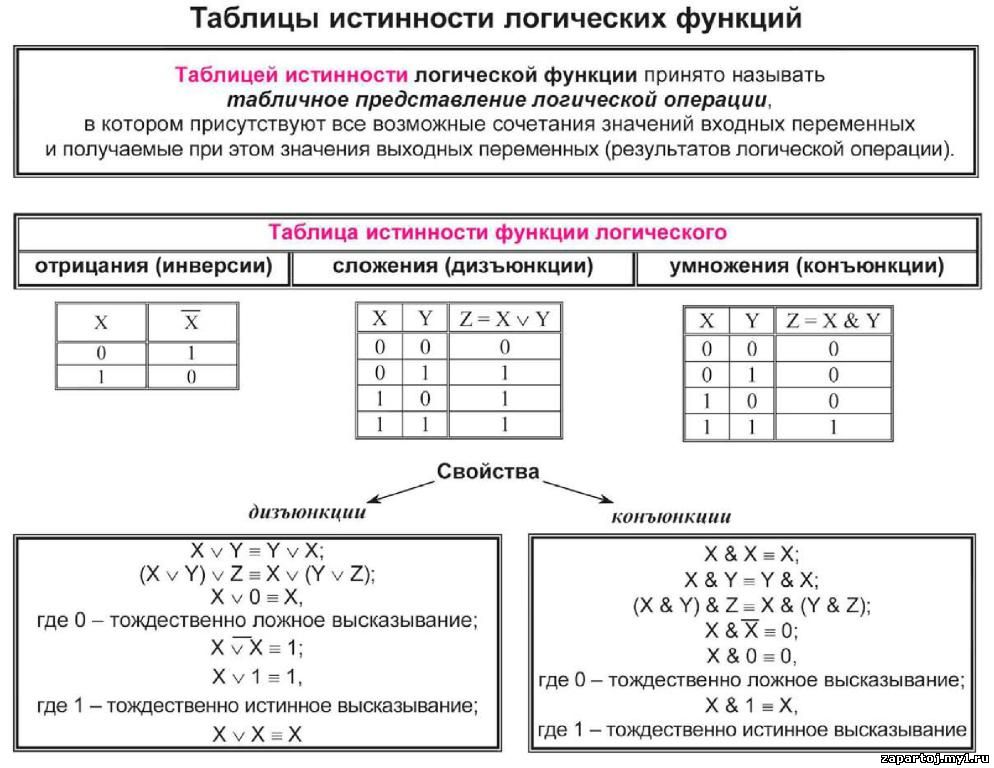
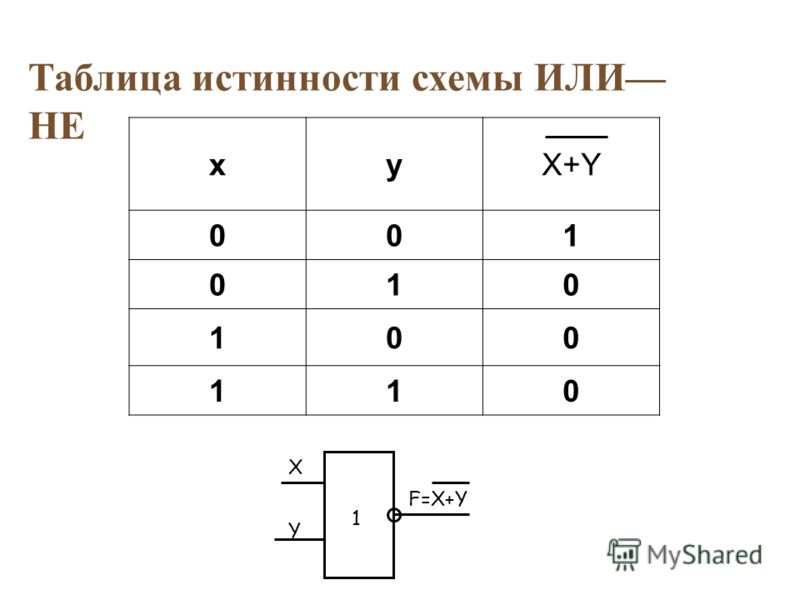

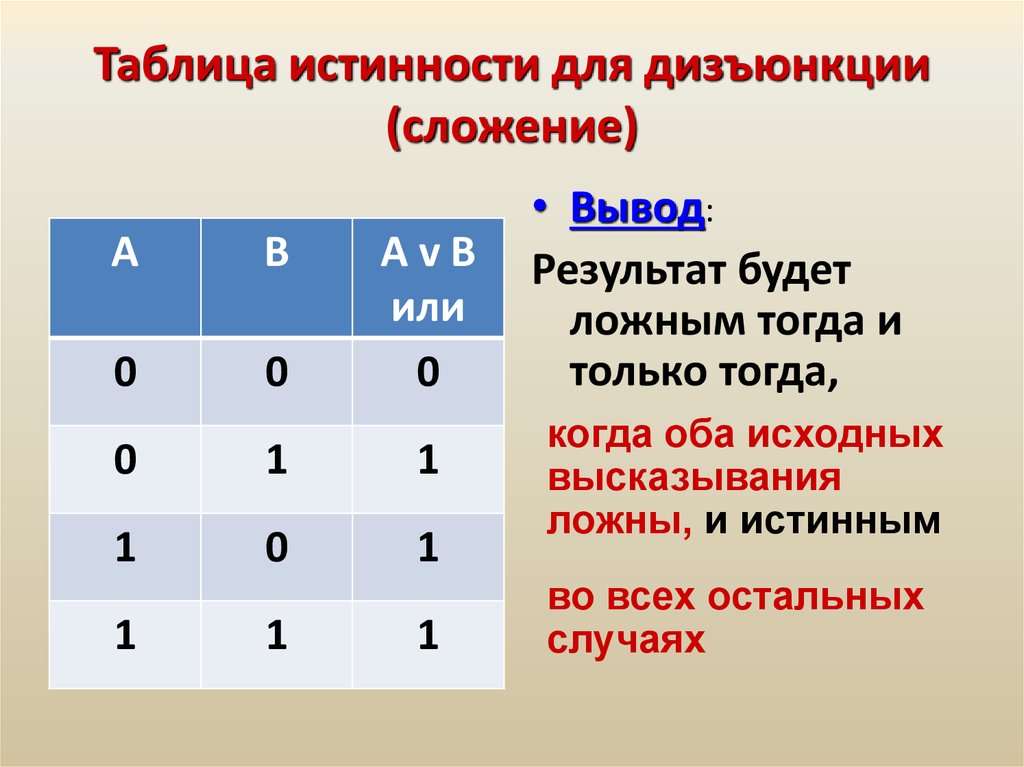
 Логические схемы
Логические схемы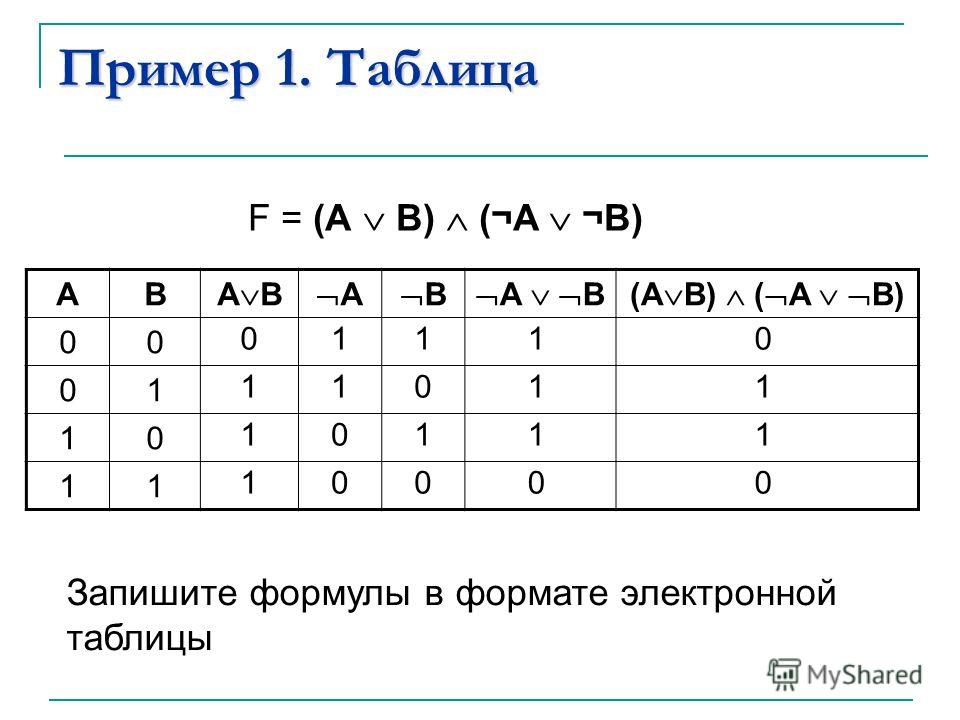 На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее присильном увеличении она поразит нас своей стройной архитектурой. Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них.
На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее присильном увеличении она поразит нас своей стройной архитектурой. Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них. Цепь на схеме 1 с последовательным соединением контактов соответствует логической операции «И». Цепь на схеме 2 с параллельным соединением контактов соответствует логической операции «ИЛИ». Цепь на схеме 3 (электромагнитное реле) соответствует логической операции «НЕ».
Цепь на схеме 1 с последовательным соединением контактов соответствует логической операции «И». Цепь на схеме 2 с параллельным соединением контактов соответствует логической операции «ИЛИ». Цепь на схеме 3 (электромагнитное реле) соответствует логической операции «НЕ».

 Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.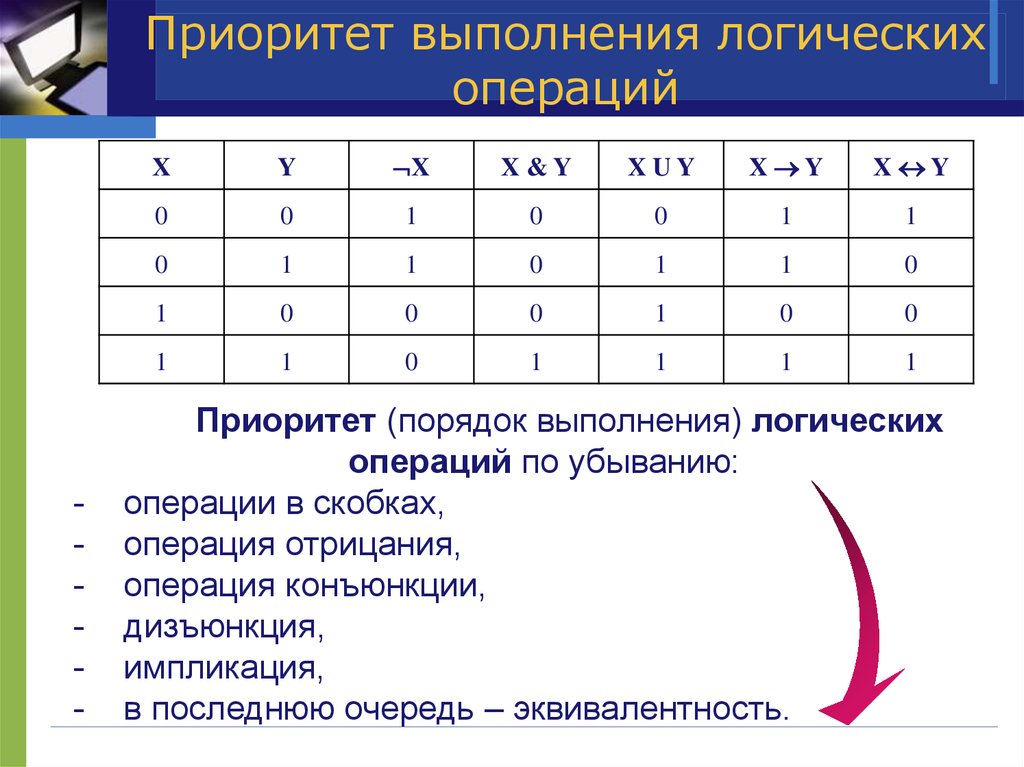 В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.
В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.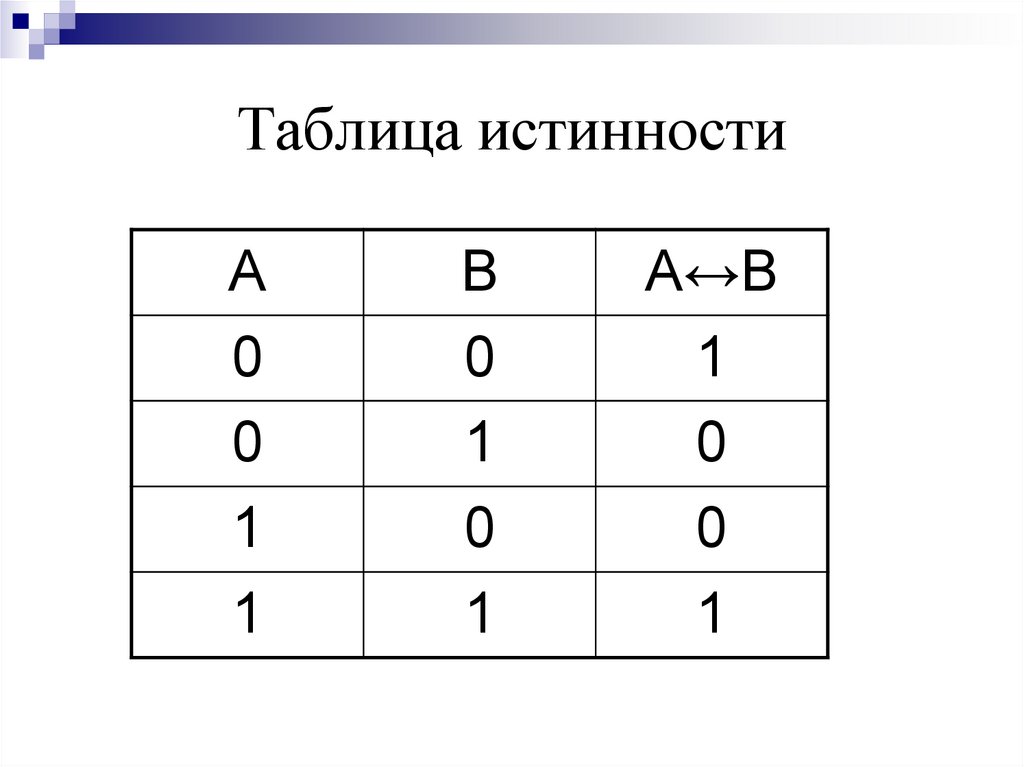
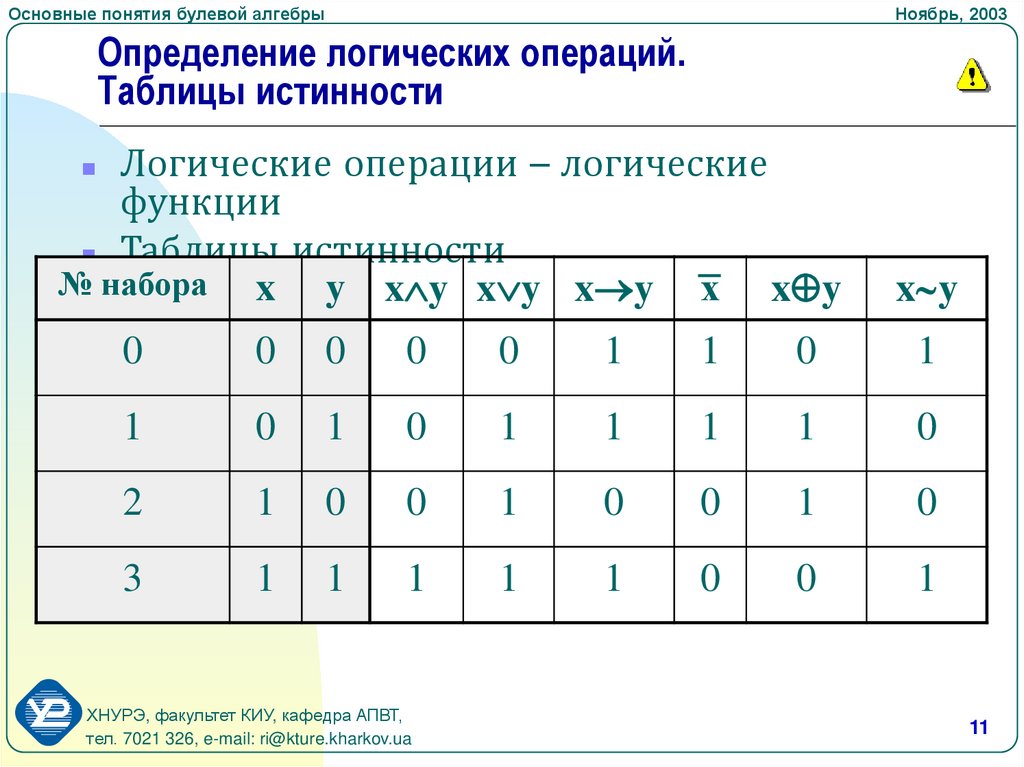

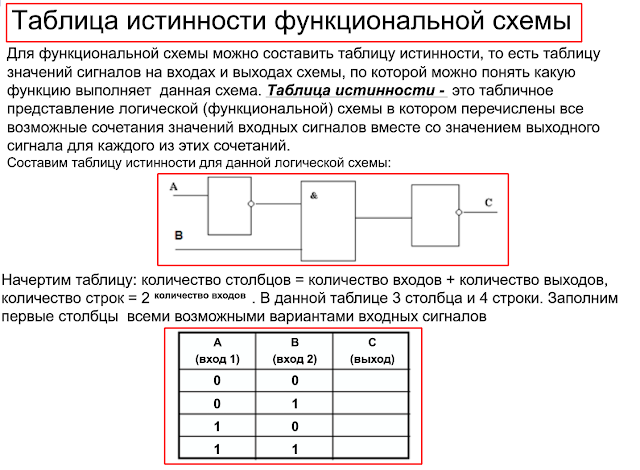 Итоги урока
Итоги урока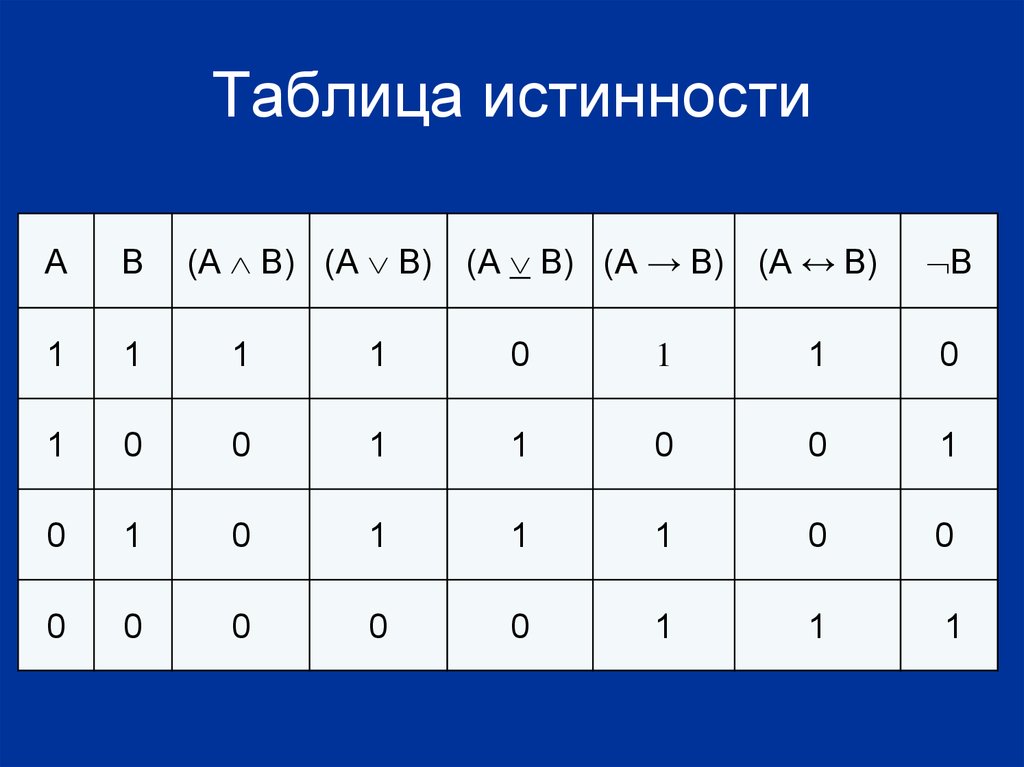 Логические законы и правила преобразования логических выражений
Логические законы и правила преобразования логических выражений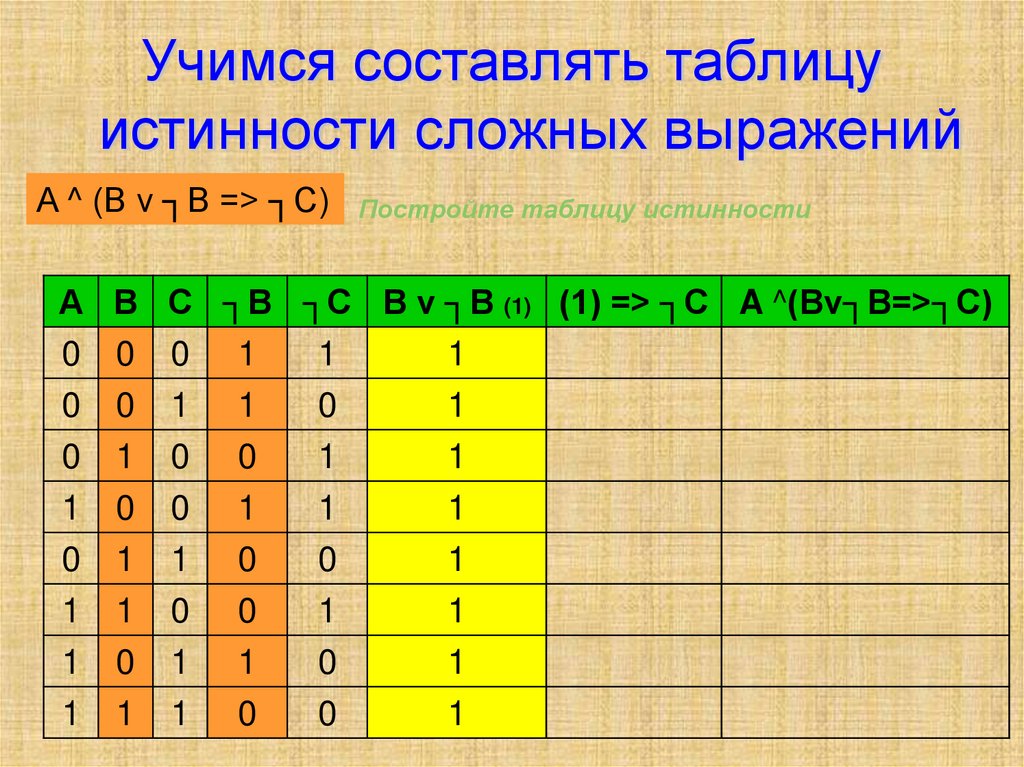 Проверка домашнего задания
Проверка домашнего задания
 Законы логики
Законы логики 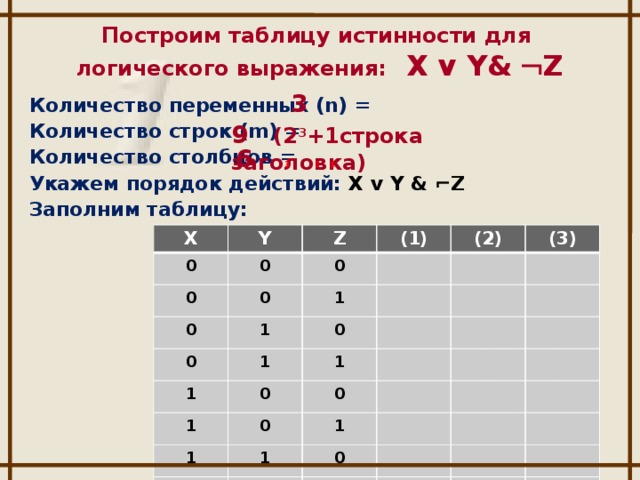 Ю. Ершовой
Ю. Ершовой : И. Л. Новожилов, В. Н. Самородова, Барнаул, 2009. 25 с
: И. Л. Новожилов, В. Н. Самородова, Барнаул, 2009. 25 с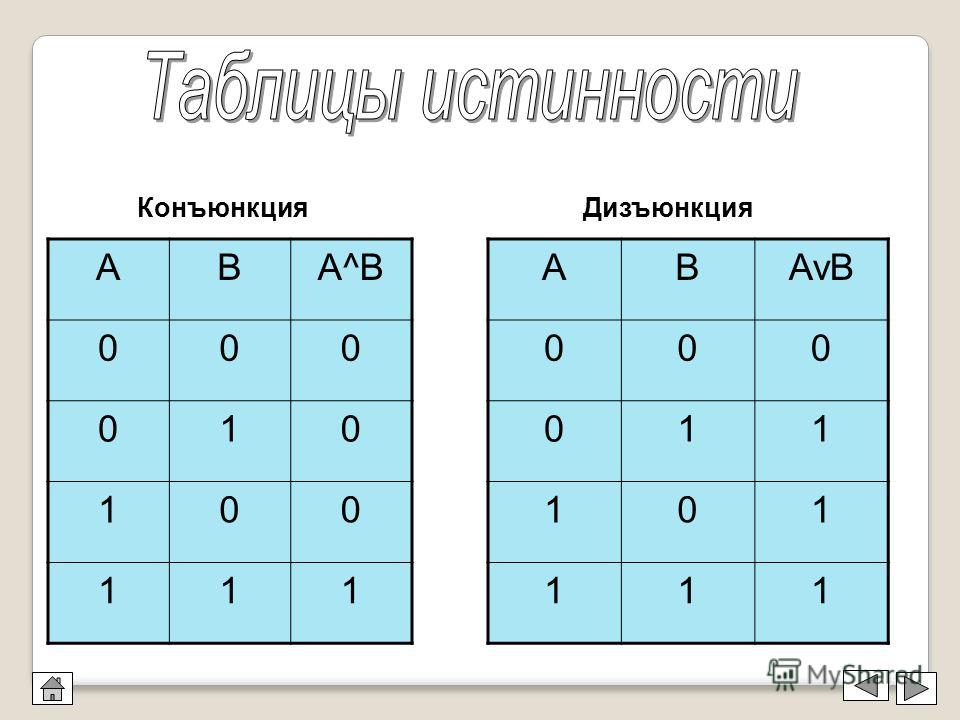 При изменении же порядка выполнения действий в описании логических операций используют скобки.
При изменении же порядка выполнения действий в описании логических операций используют скобки.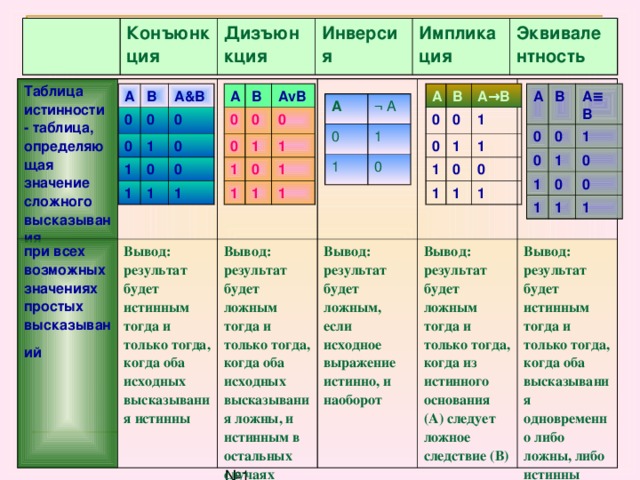 При этом учитывать, что если значение какого-то из аргументов функции в соответствующей строке таблицы будет равное нулю, то записывать его нужно в виде отрицания.
При этом учитывать, что если значение какого-то из аргументов функции в соответствующей строке таблицы будет равное нулю, то записывать его нужно в виде отрицания. lander.edu
lander.edu 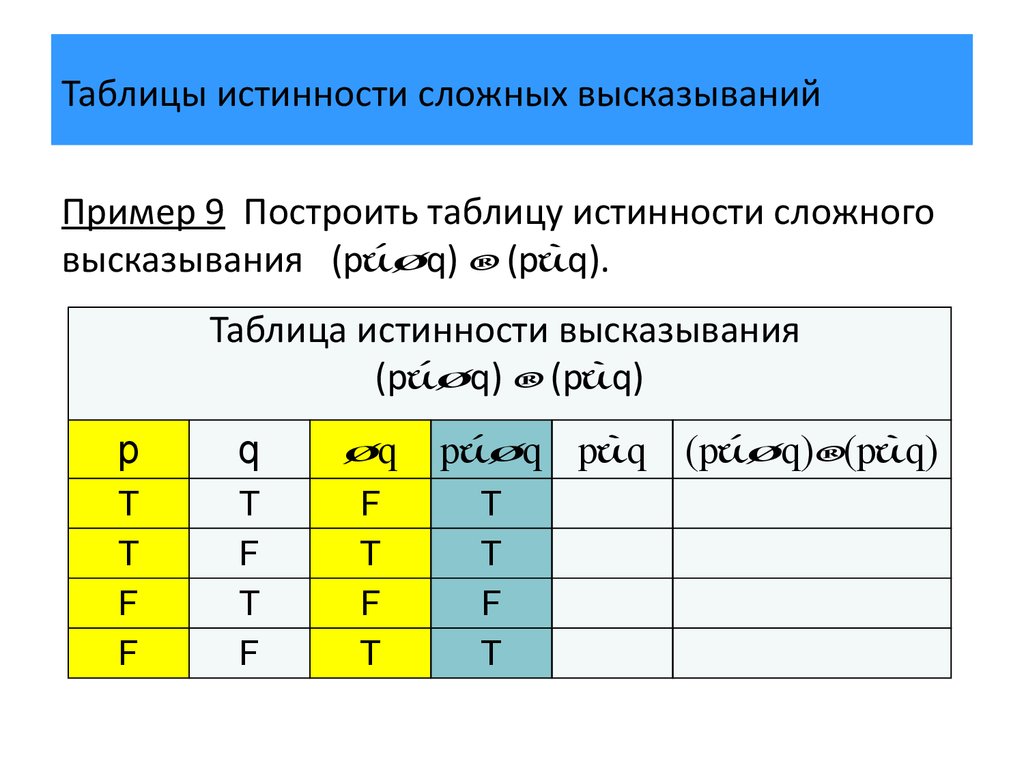

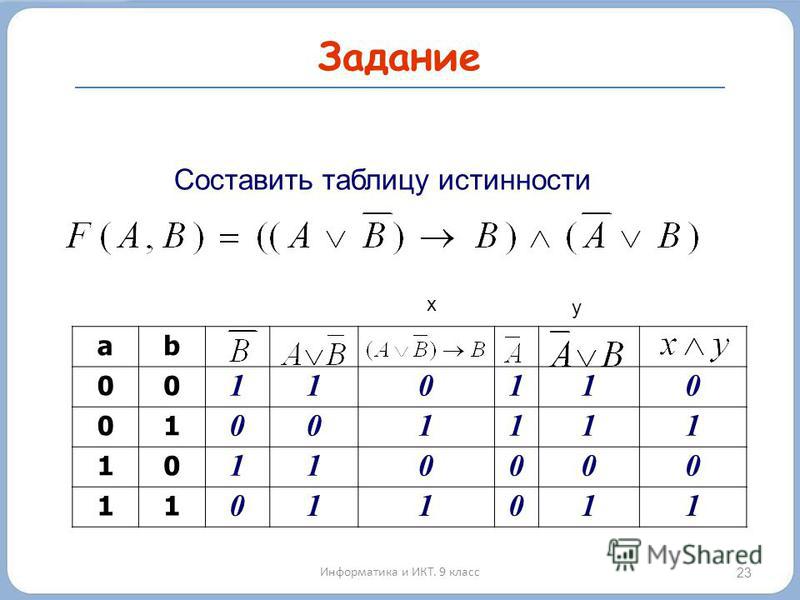
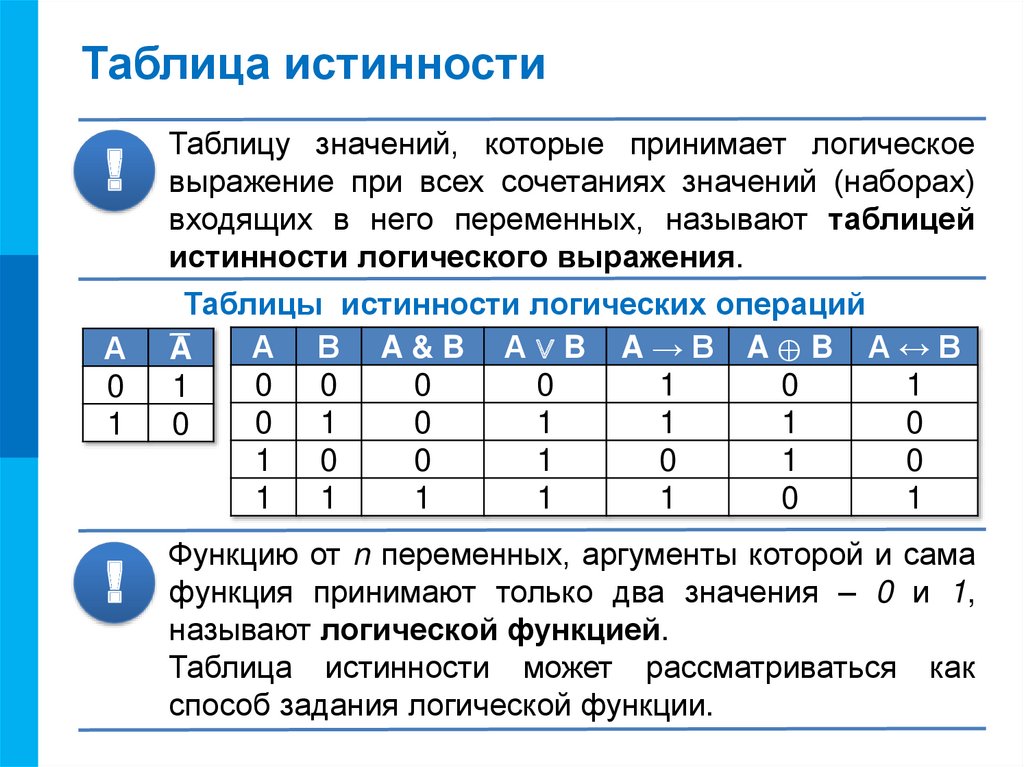
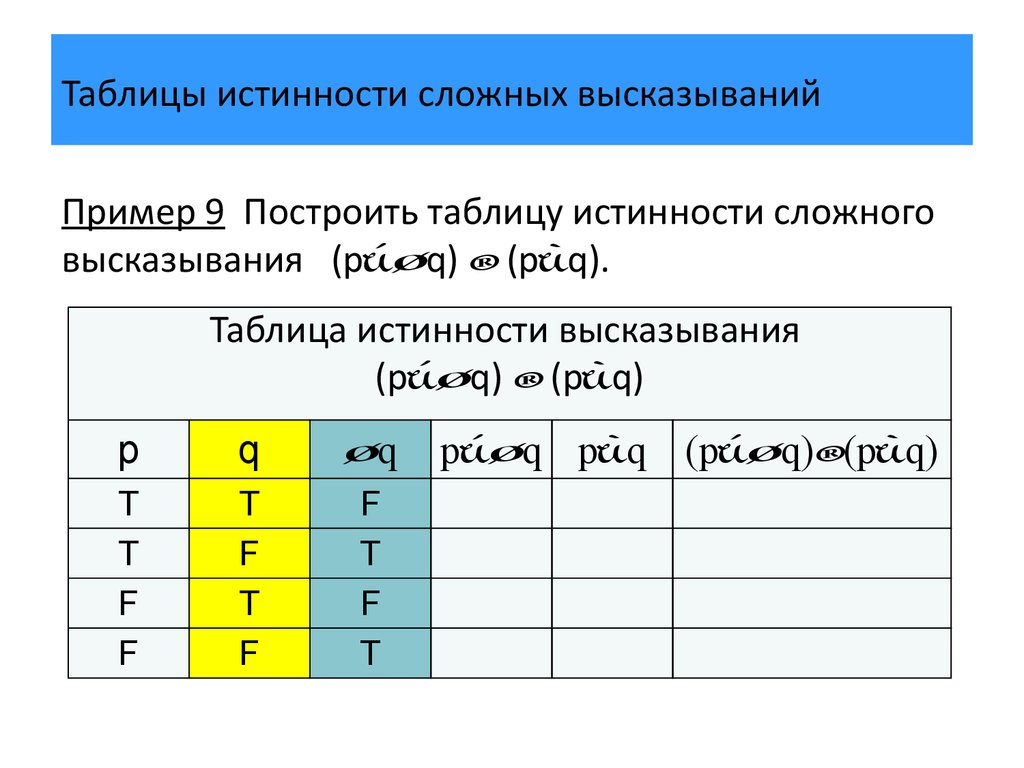
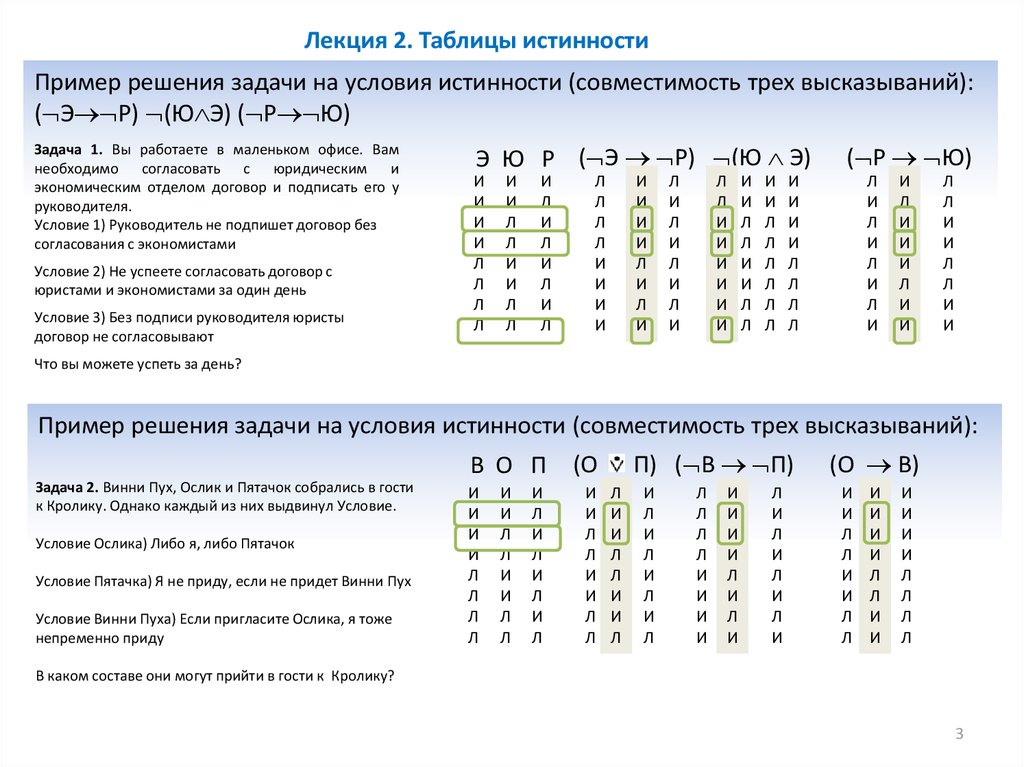
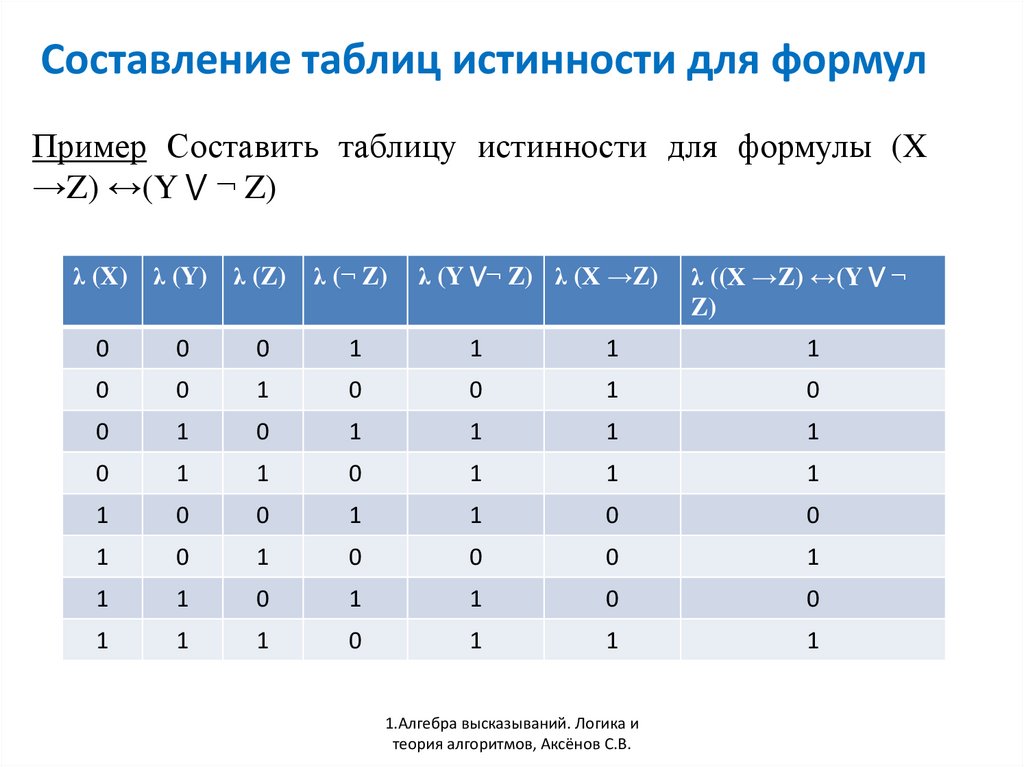
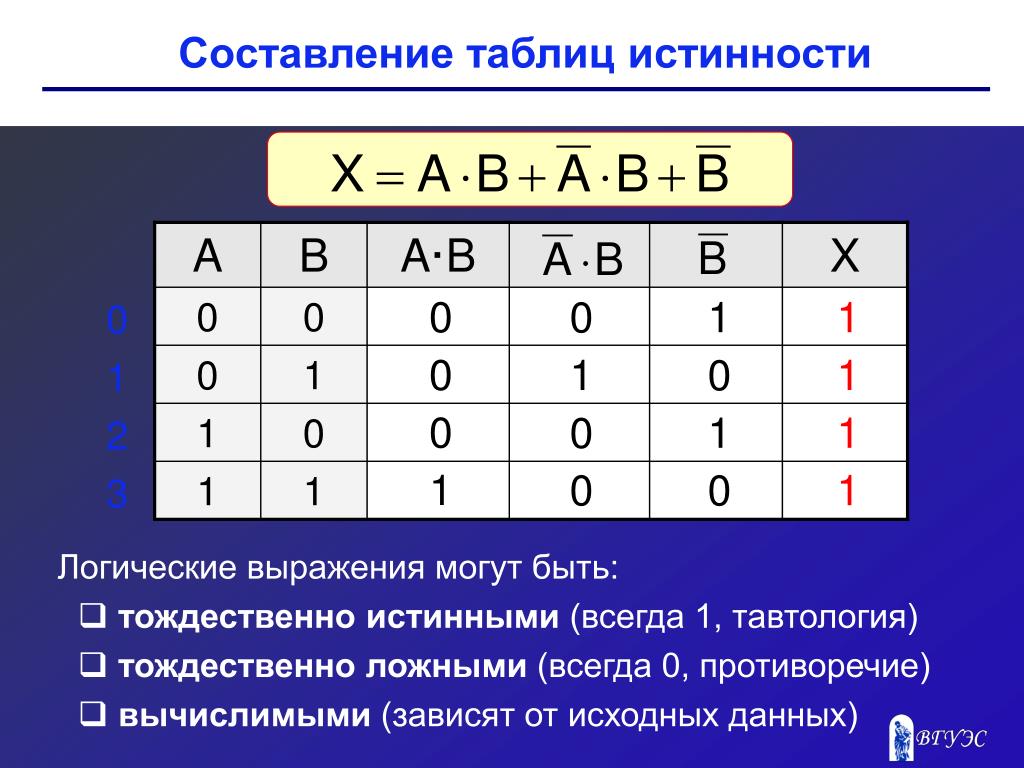
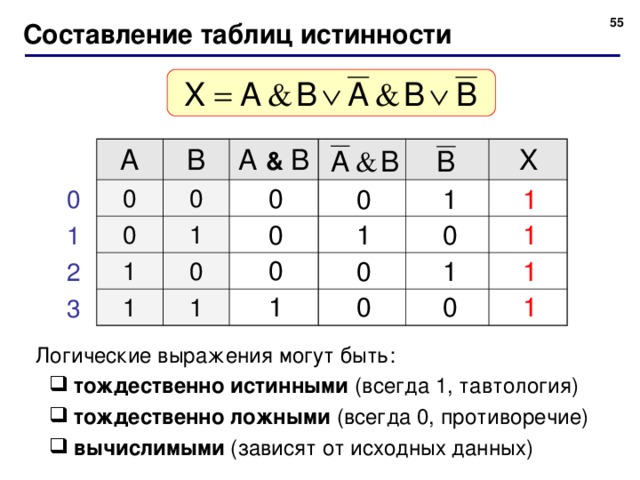
 При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора !
При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора ! 
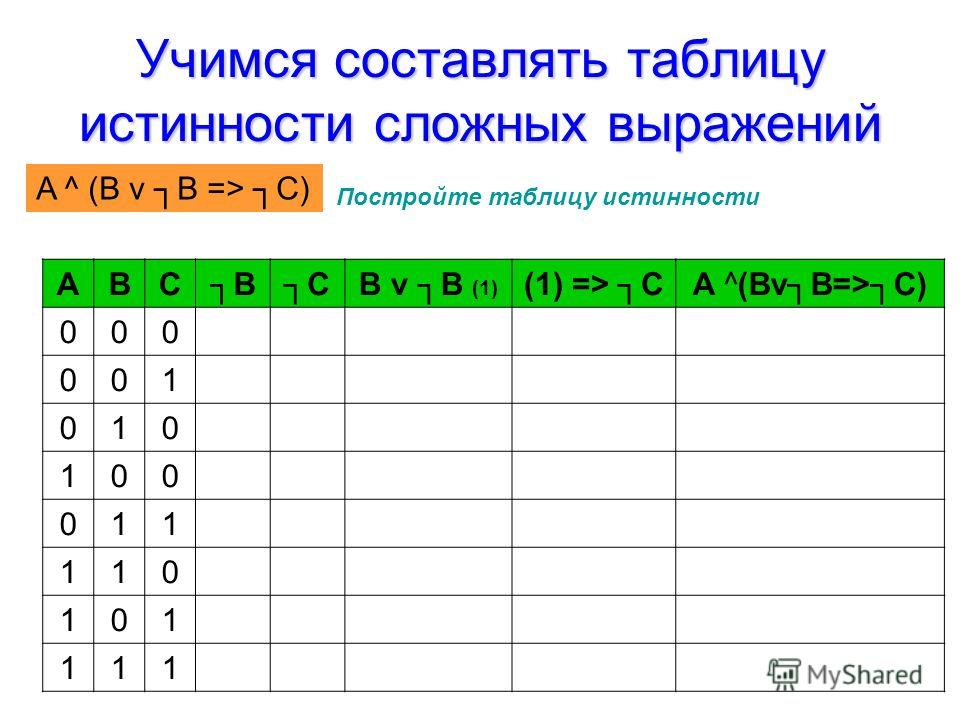 Поскольку здесь у нас есть 2 буквы, p и r, у нас будет 2 столбца в начале таблицы истинности, помеченные p и r:
Поскольку здесь у нас есть 2 буквы, p и r, у нас будет 2 столбца в начале таблицы истинности, помеченные p и r: Итак, смотрим, что находится внутри скобок: r∧~p.
Итак, смотрим, что находится внутри скобок: r∧~p. 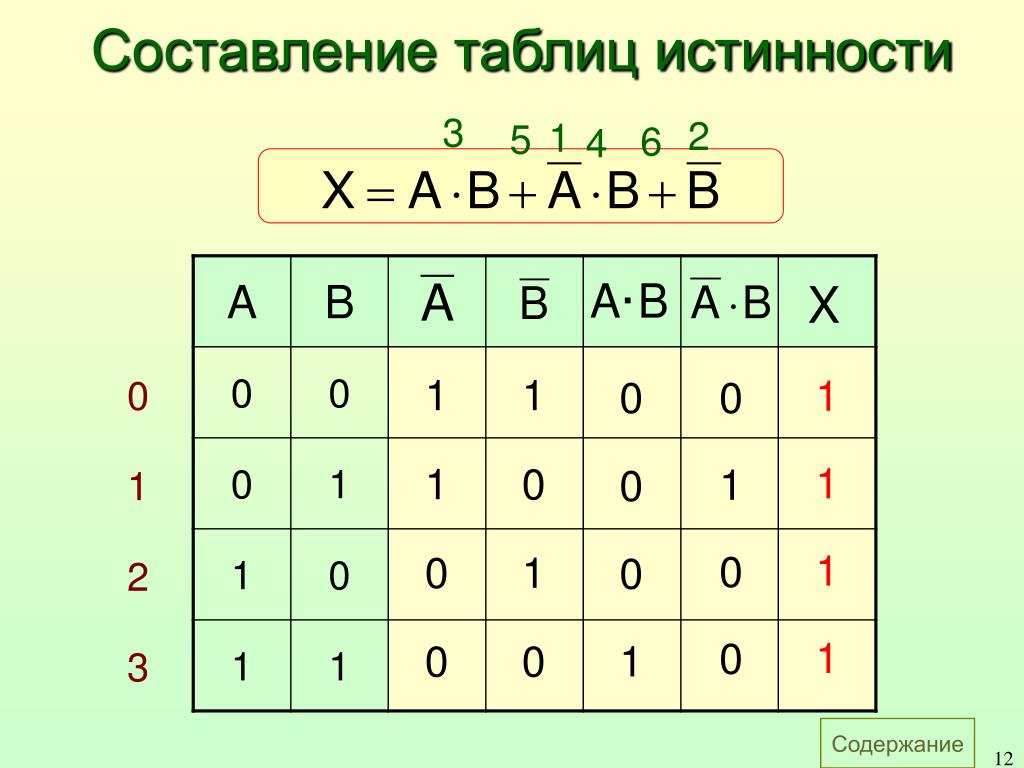

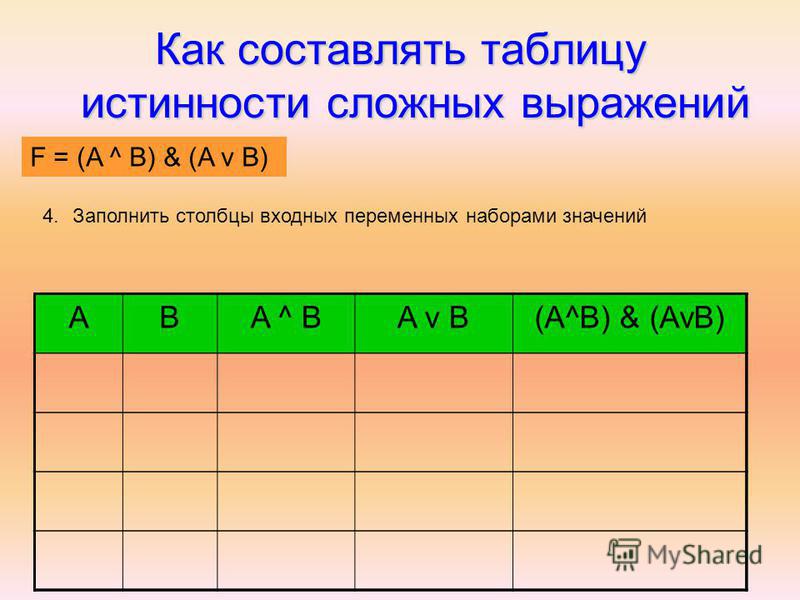
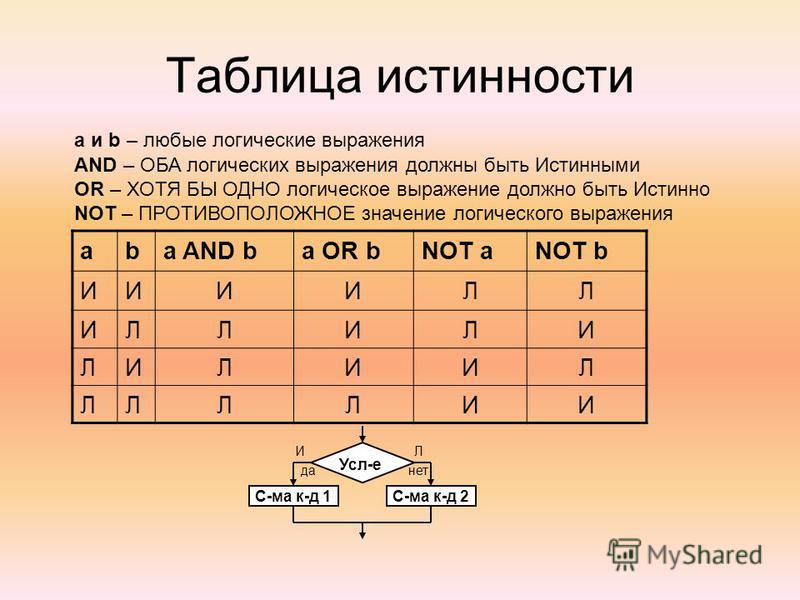
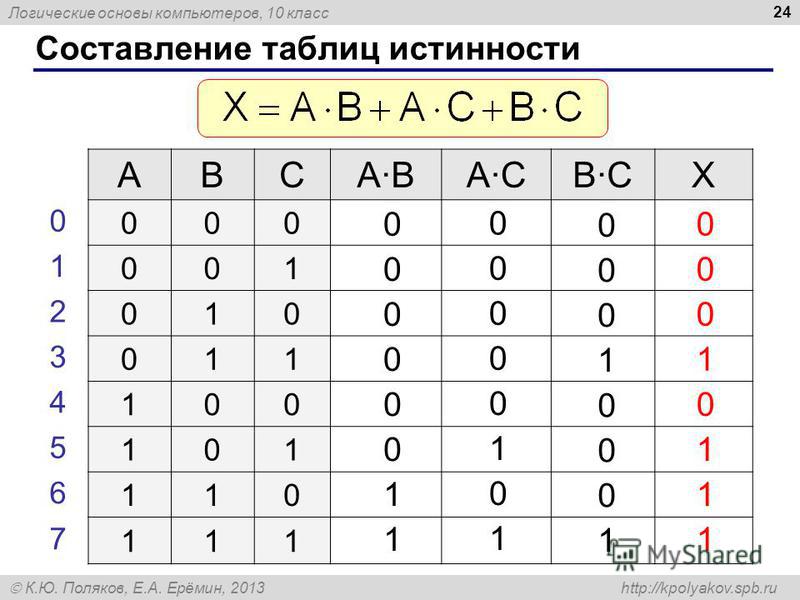 При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора !
При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора ! 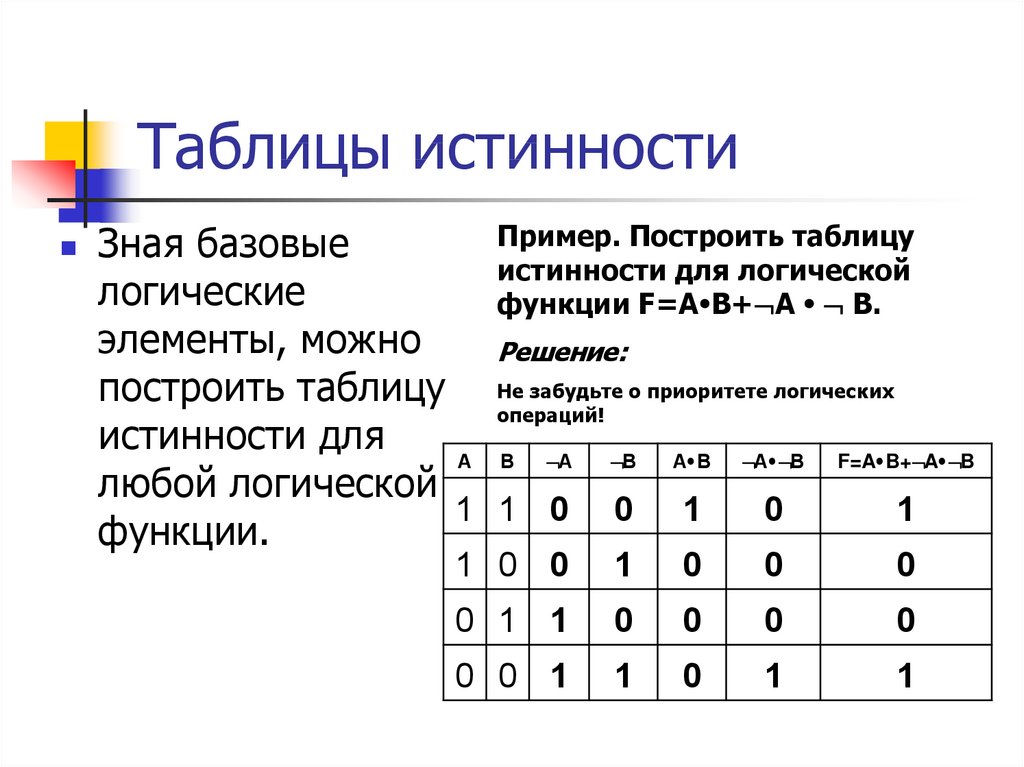

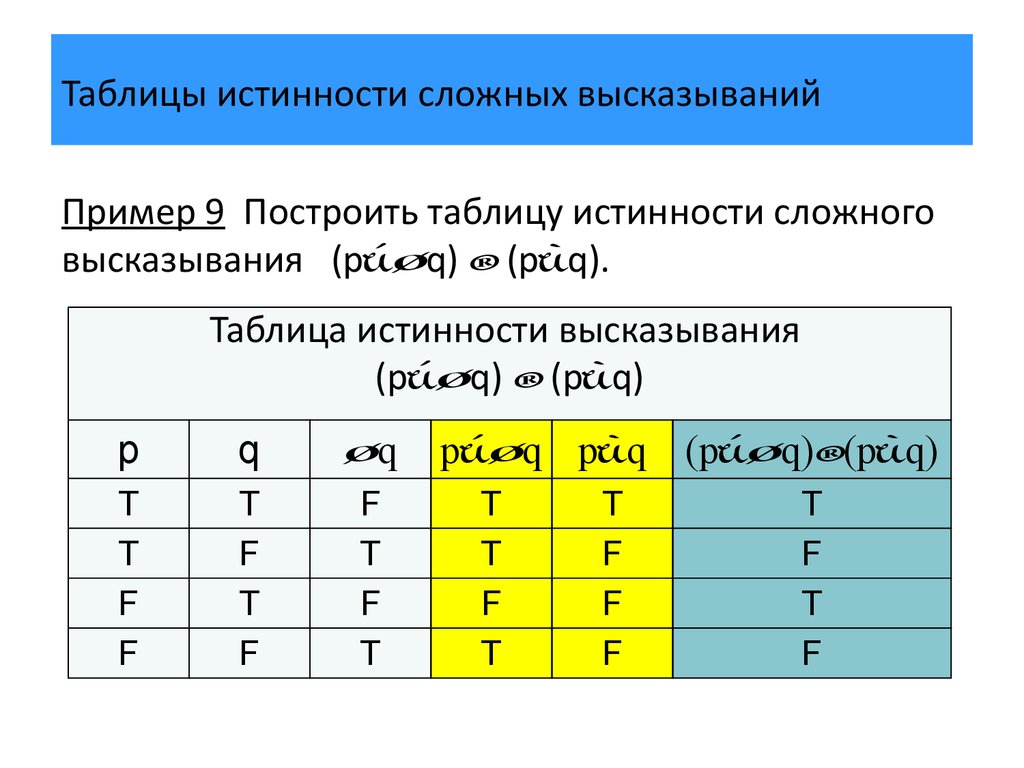 Итак, смотрим, что находится внутри скобок: ~p→r.
Итак, смотрим, что находится внутри скобок: ~p→r. 
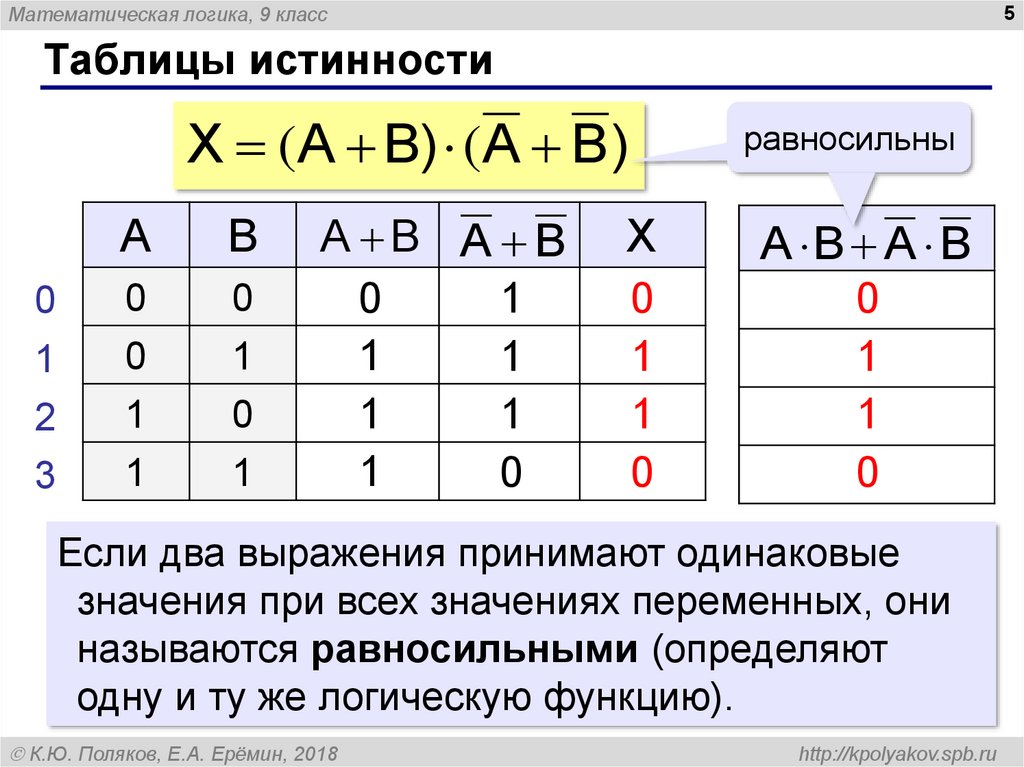
 При заполнении столбца условного утверждения убедитесь, что вам 9 лет.0662 не перепутать столбец для первого оператора со столбцом для второго оператора !
При заполнении столбца условного утверждения убедитесь, что вам 9 лет.0662 не перепутать столбец для первого оператора со столбцом для второго оператора ! 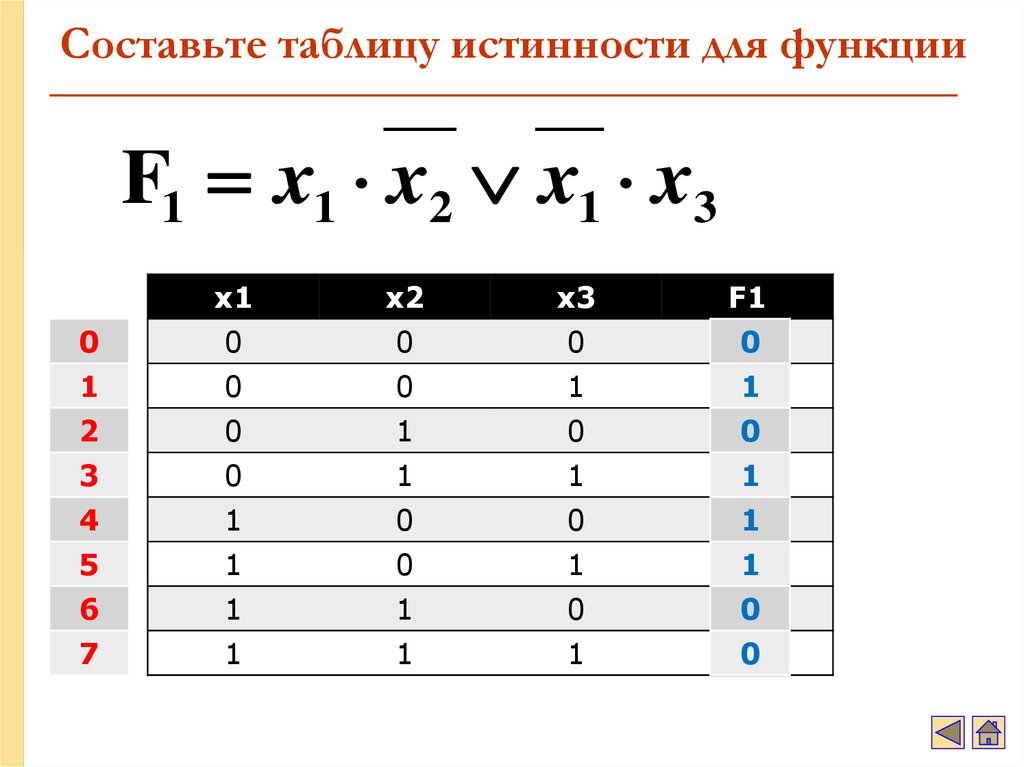
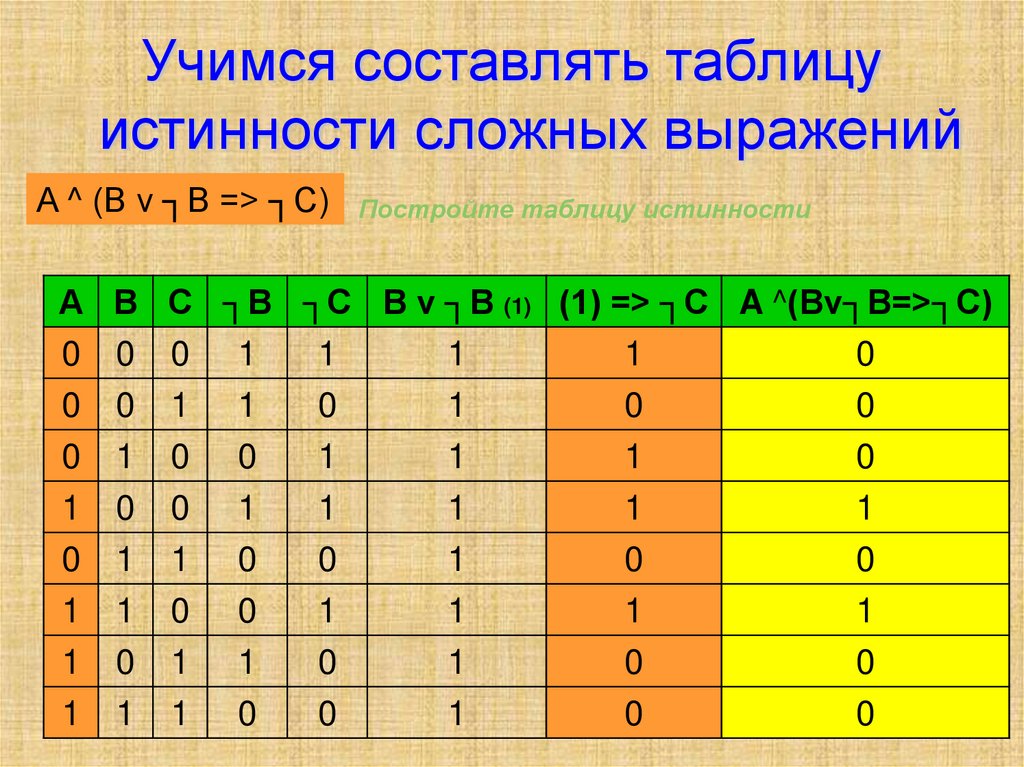
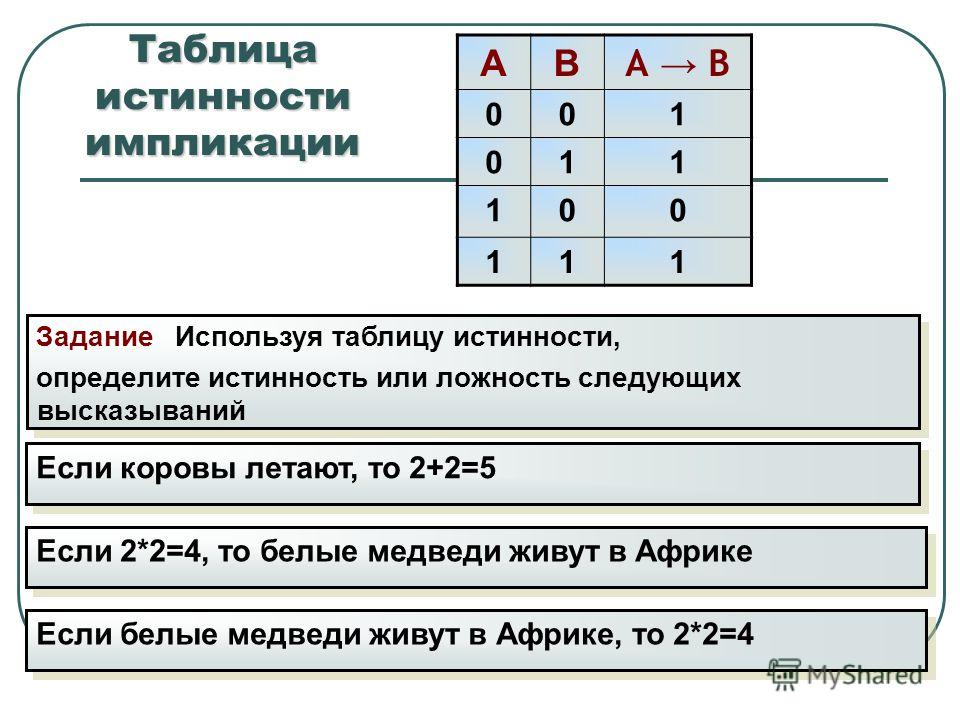
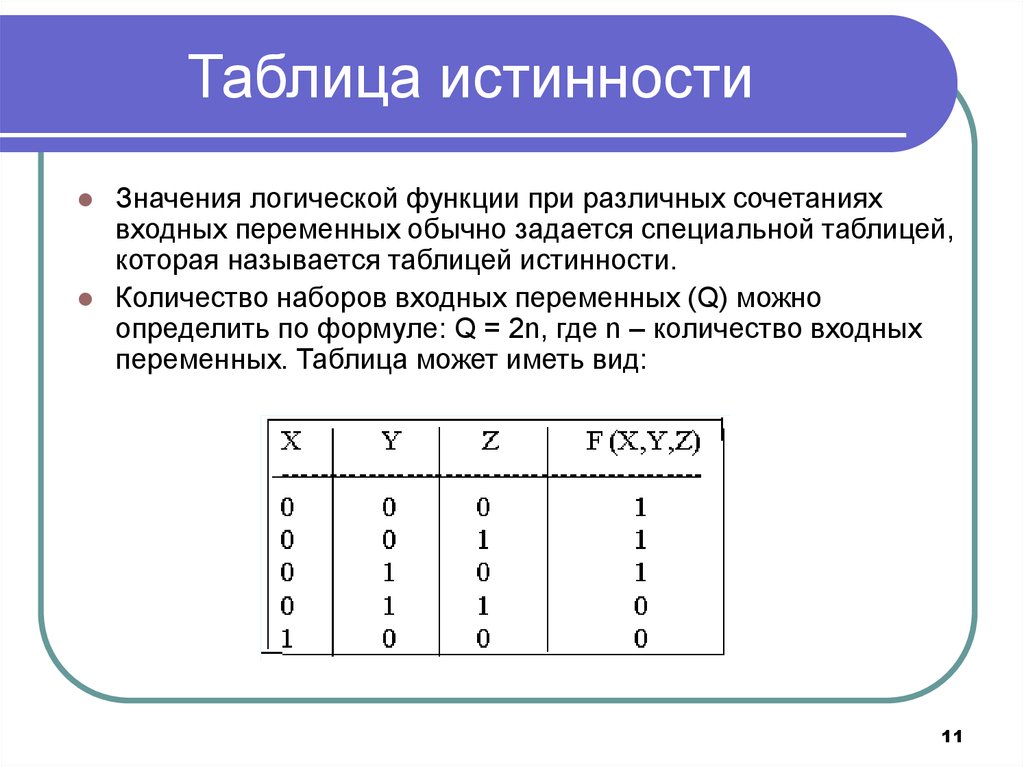 Итак, мы смотрим на то, что находится внутри скобок: p∨q.
Итак, мы смотрим на то, что находится внутри скобок: p∨q. 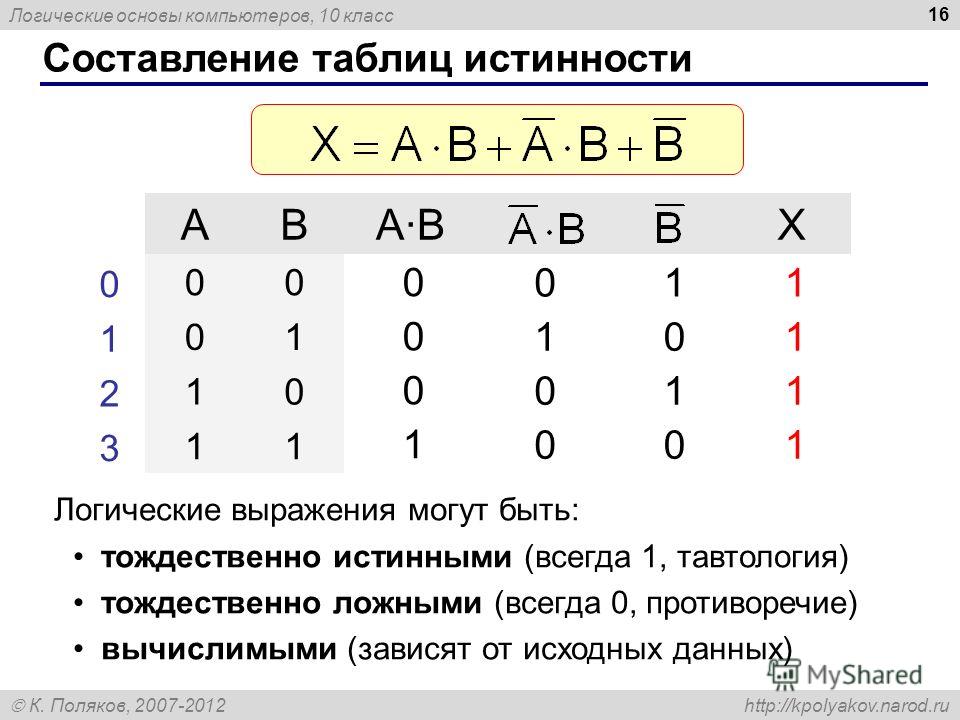
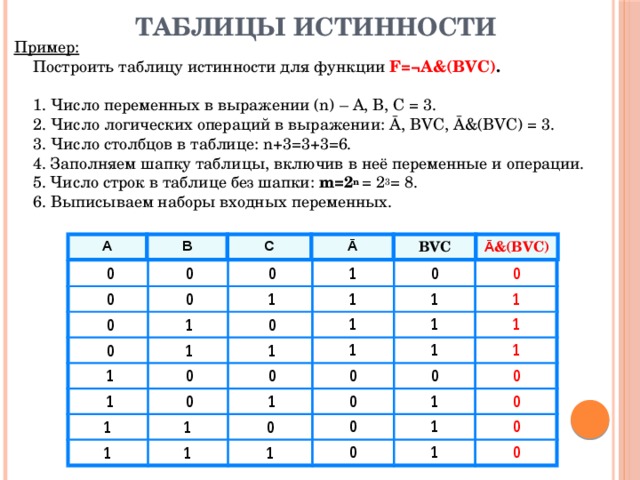
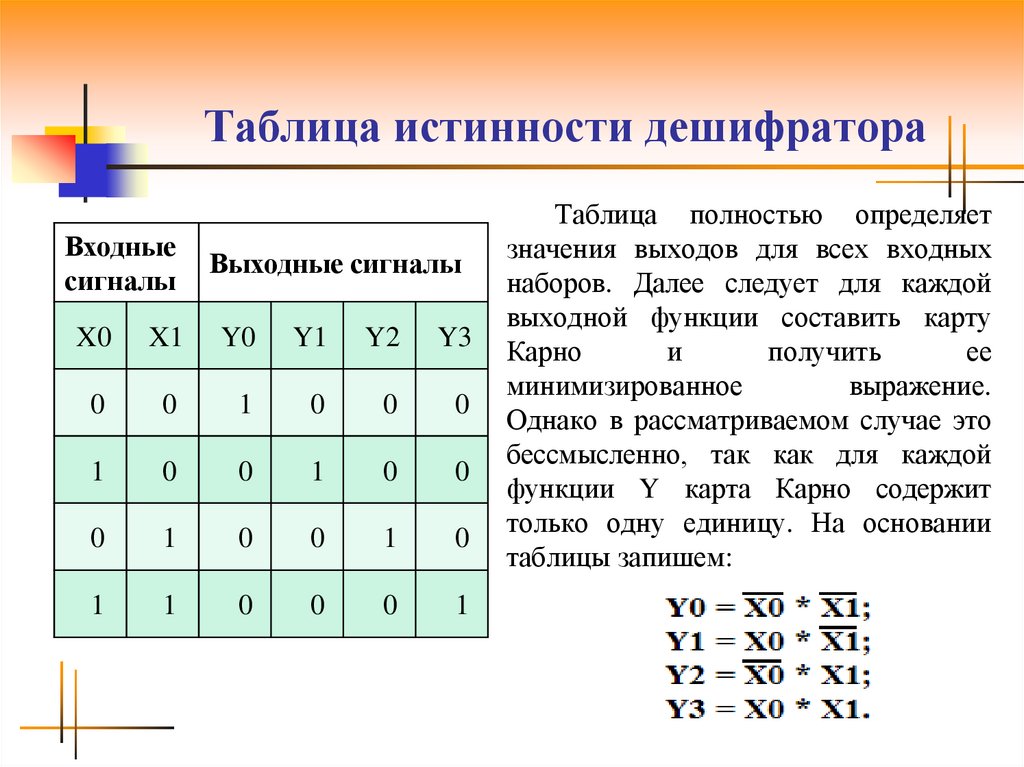
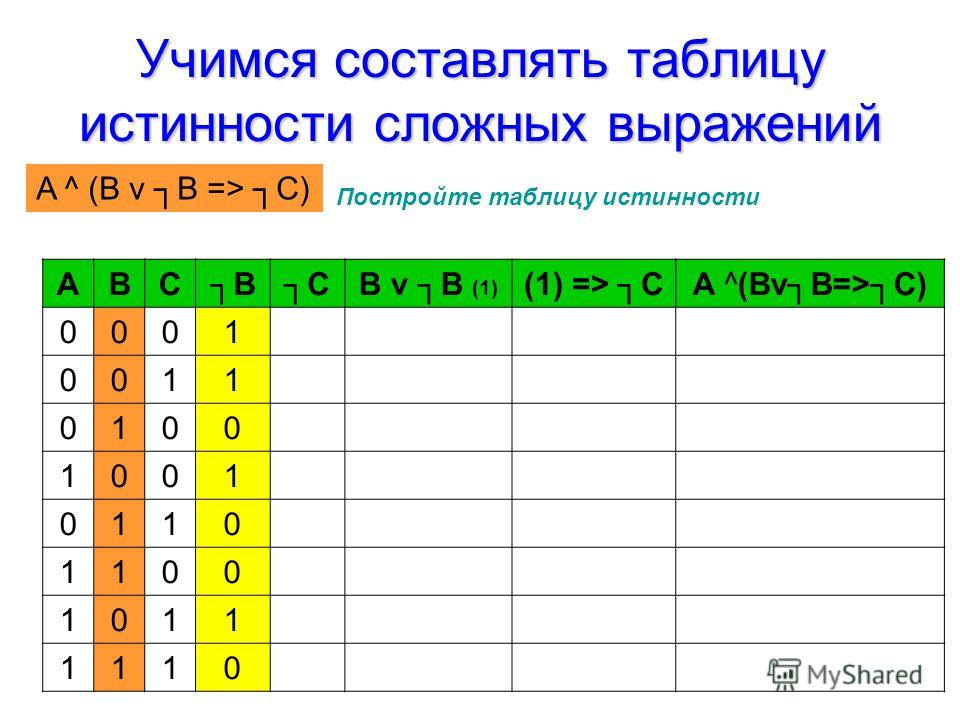 В этом выражении символ ↔ соединяет 2 выражения: ~(p∨q) и r.
В этом выражении символ ↔ соединяет 2 выражения: ~(p∨q) и r. 
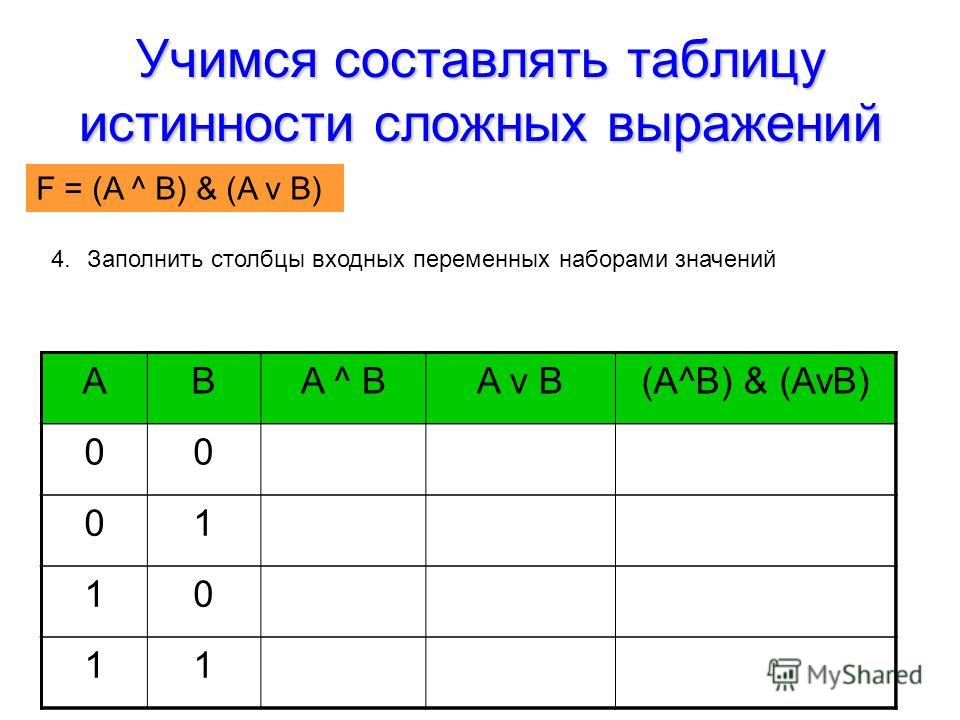
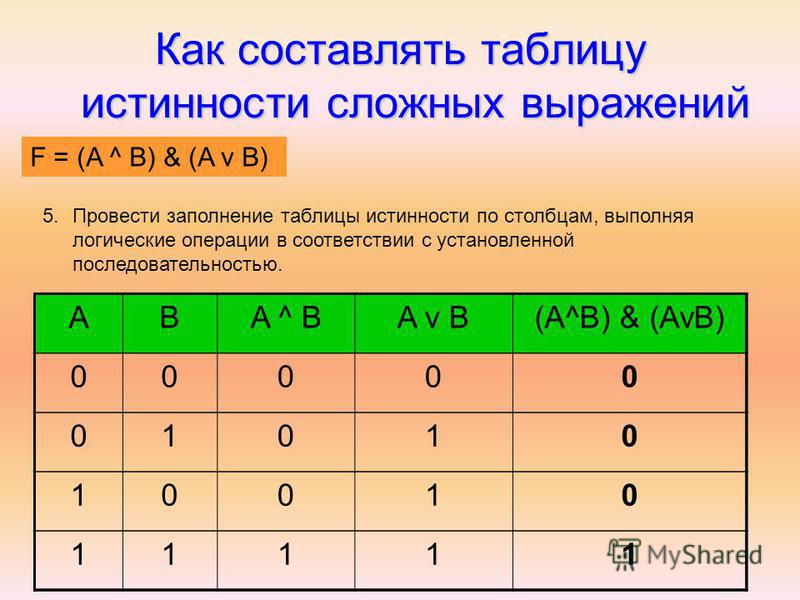 Итак, смотрим, что находится внутри скобок: p→~q.
Итак, смотрим, что находится внутри скобок: p→~q. 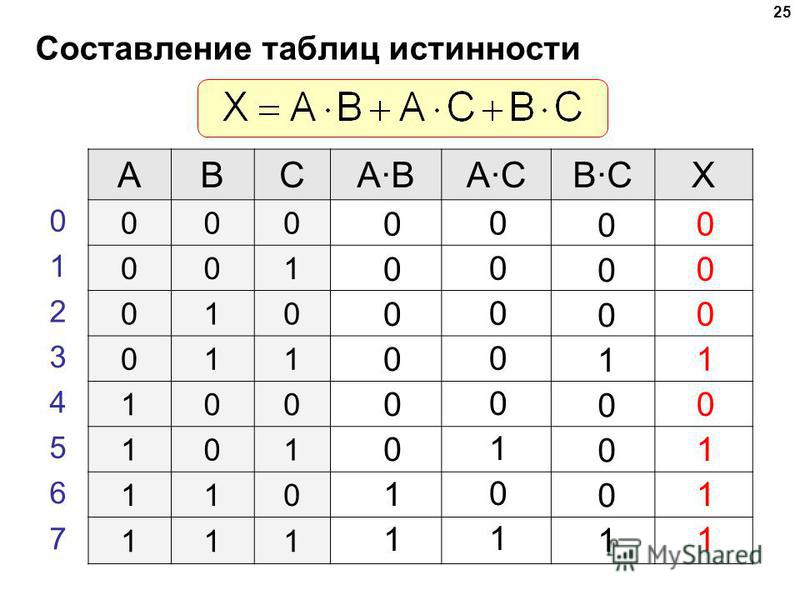
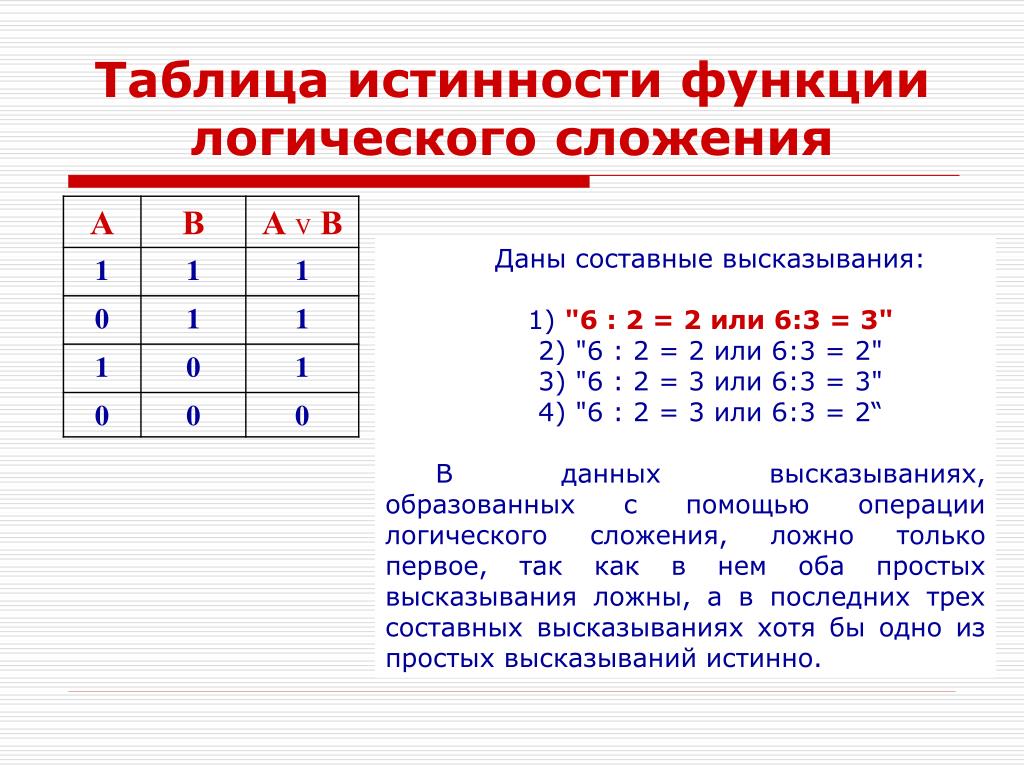 В этом выражении символ → объединяет 2 выражения: p и ~q.
В этом выражении символ → объединяет 2 выражения: p и ~q. 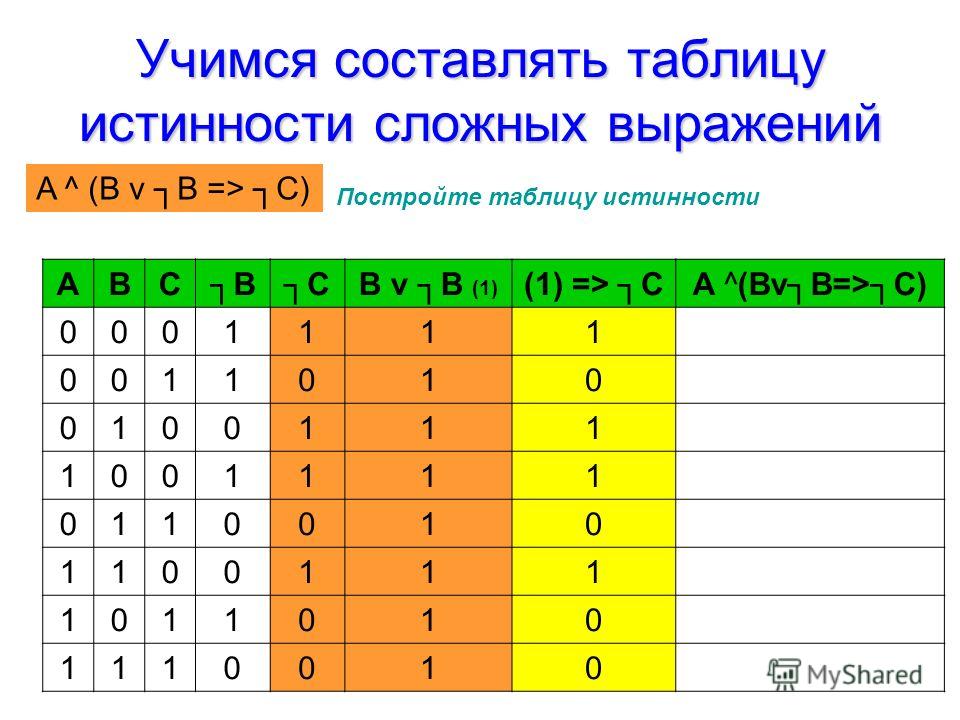 При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора !
При заполнении столбца условного оператора убедитесь, что вы не перепутали столбец первого оператора со столбцом второго оператора ! 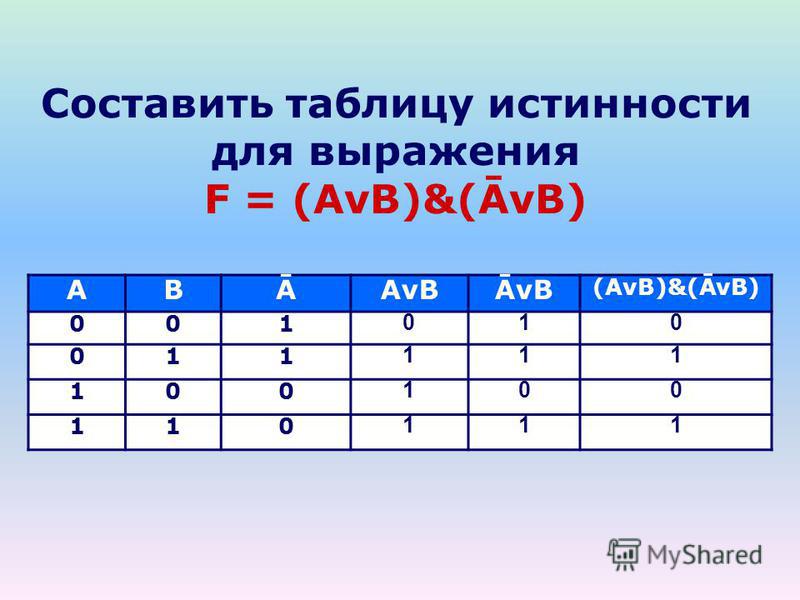
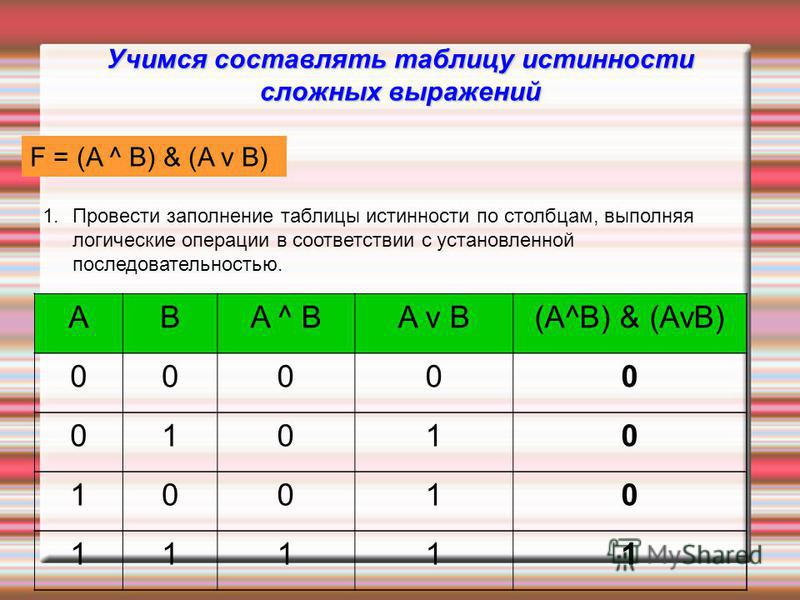
 В этом выражении символ ∧ объединяет 2 выражения: ~r и p→~q.
В этом выражении символ ∧ объединяет 2 выражения: ~r и p→~q. 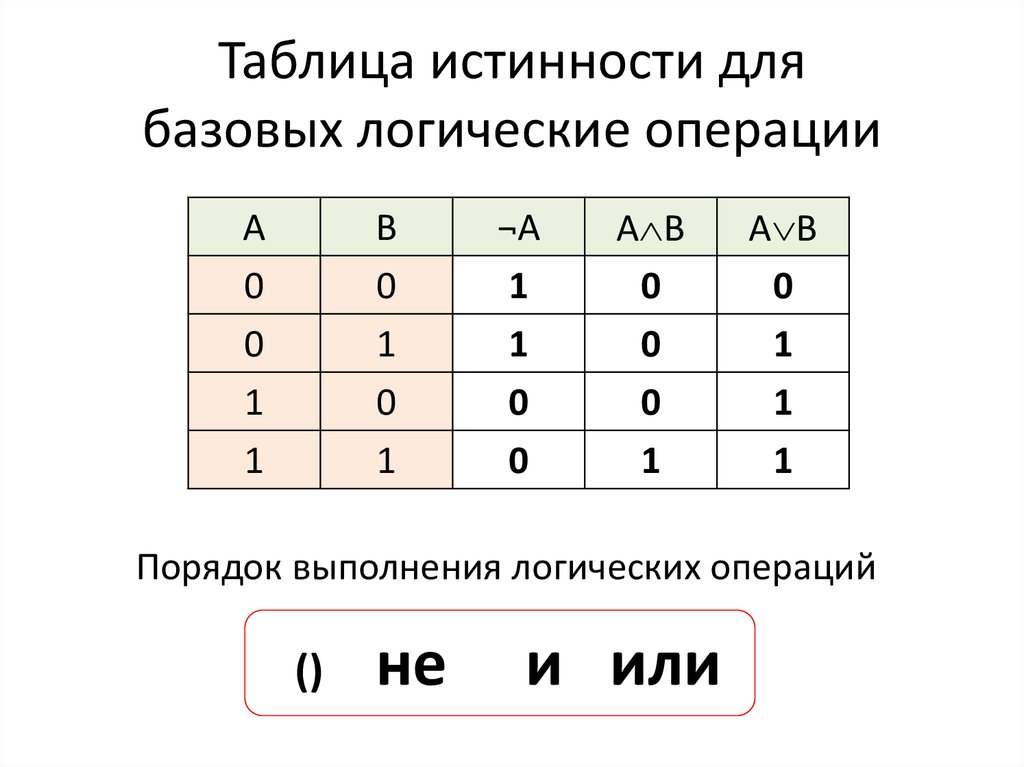
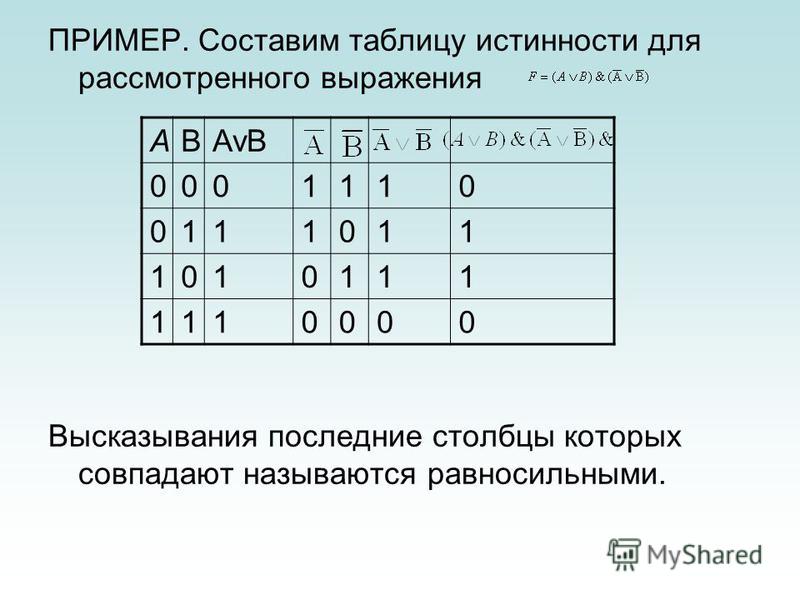 Символ → всегда объединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными операторами, но нам все равно, насколько они сложны, , если у нас уже есть столбец в таблице истинности с этим логическим выражением вверху . В этом выражении символ → объединяет 2 выражения: ~r∧(p→~q) и P.
Символ → всегда объединяет ровно два выражения; два выражения, которые он соединяет, сами по себе могут быть более сложными операторами, но нам все равно, насколько они сложны, , если у нас уже есть столбец в таблице истинности с этим логическим выражением вверху . В этом выражении символ → объединяет 2 выражения: ~r∧(p→~q) и P. 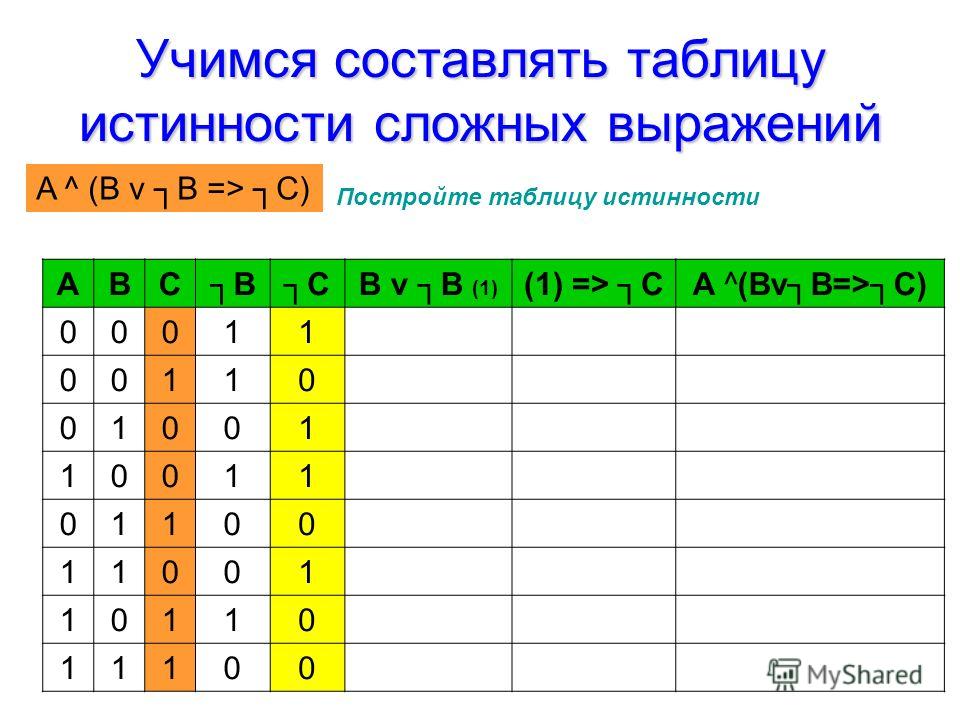 Убедитесь, что при заполнении столбца для условного оператора вы не путаете столбец для первого оператора со столбцом для второго оператора !
Убедитесь, что при заполнении столбца для условного оператора вы не путаете столбец для первого оператора со столбцом для второго оператора ! 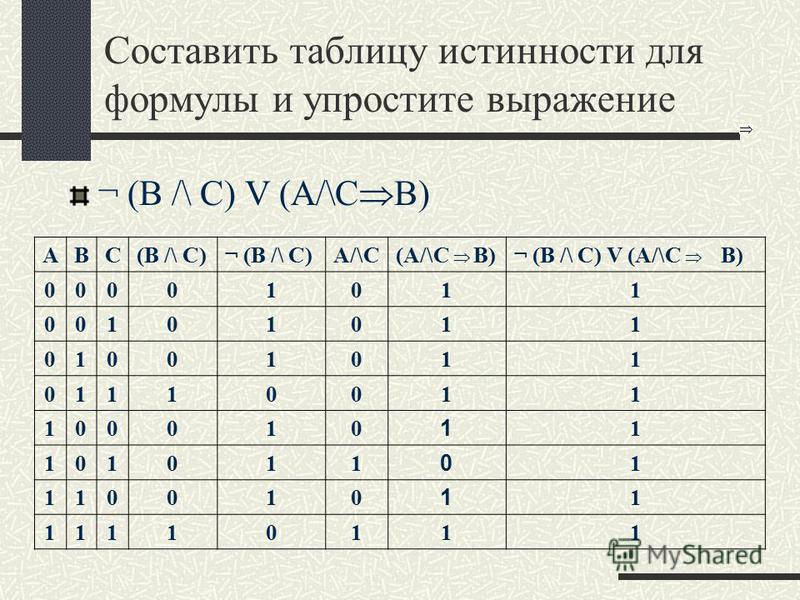
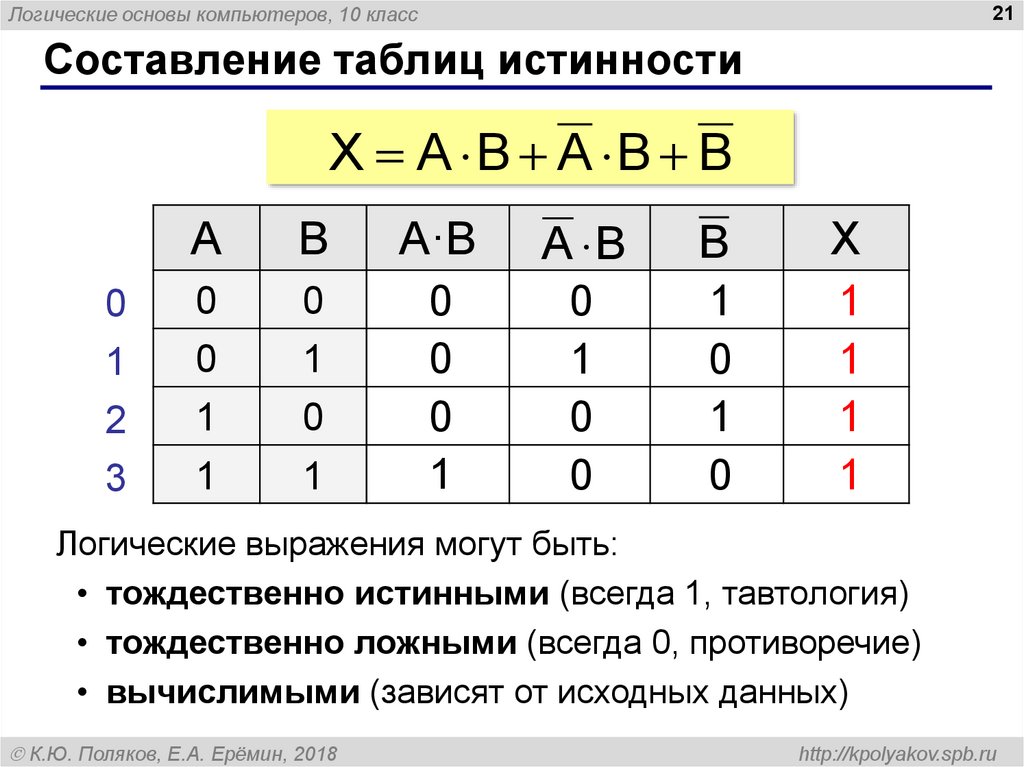 Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом.
Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом.