Логические операции и таблицы истинности
Похожие презентации:
Основы логики. Таблица истинности. Равносильные логические выражения
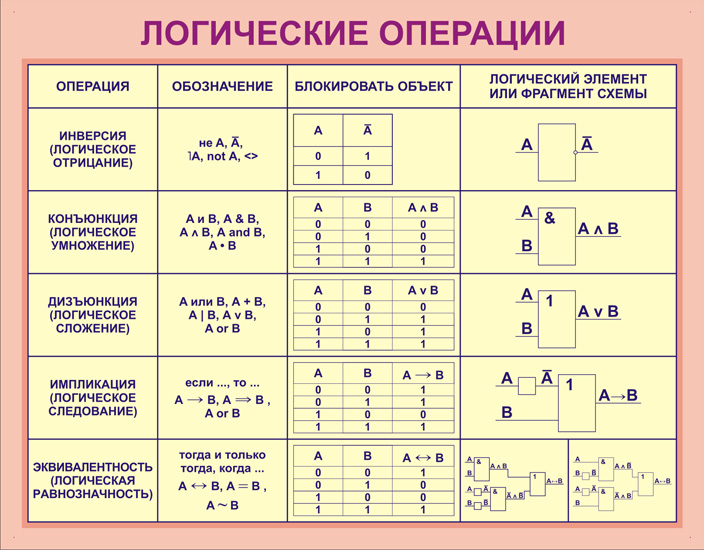
Логические операции
Базовые логические операции и функции. Таблицы истинности. Контактные схемы
Основы программирования на языке Python. Логическая операция
Алгебра логики и таблицы истинности. (лекция 4)
Логические операции
Логические операции
Логические операции компьютеров
Элементарные логические операции
Элементы математической логики
1. Логические операции и таблицы истинности
Учитель информатикиПоборцева Елена Валентиновна
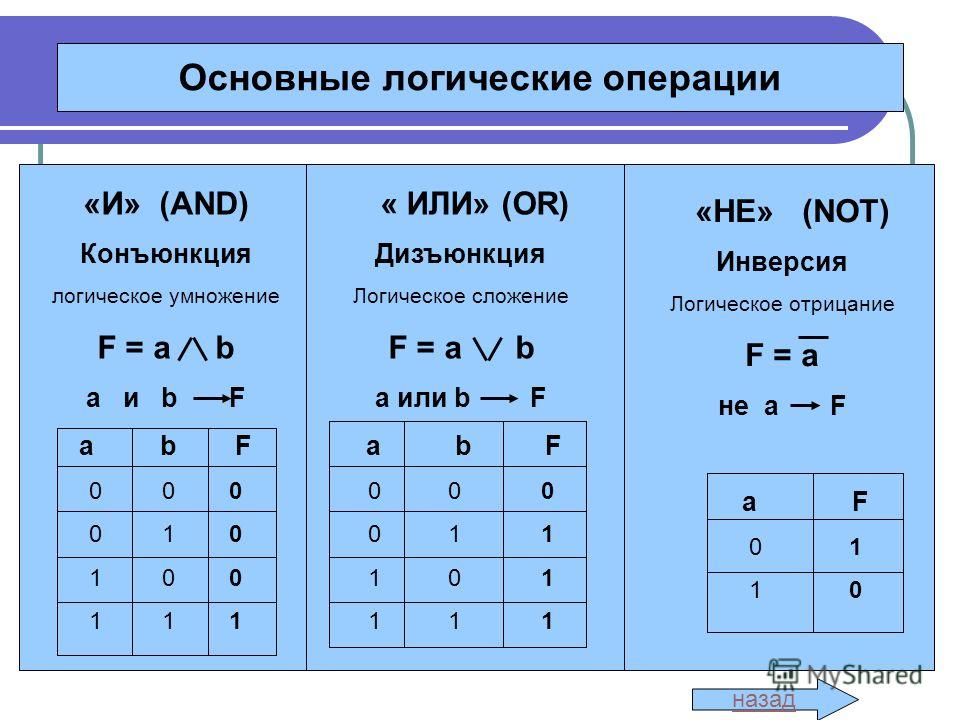
2. КОНЪЮНКЦИЯ
F = A & B.
Логическое умножение
КОНЪЮНКЦИЯ — это
новое сложное выражение
будет истинным только
тогда, когда истинны оба
исходных простых
выражения.
Конъюнкция определяет
соединение двух
логических выражений с
помощью союза И.
A
B
F
1
1
1
1
0
0
0
1
0
0
0
0
3.
 Примеры:
Примеры:10
10
10
10
делится на
не делится
делится на
не делится
2 и 5 больше 3
на 2 и 5 больше 3
2 и 5 не больше 3
на 2 и 5 не больше 3
► F=A&B
Задание: Определить, чему будет равно значение F
для каждого выражения.
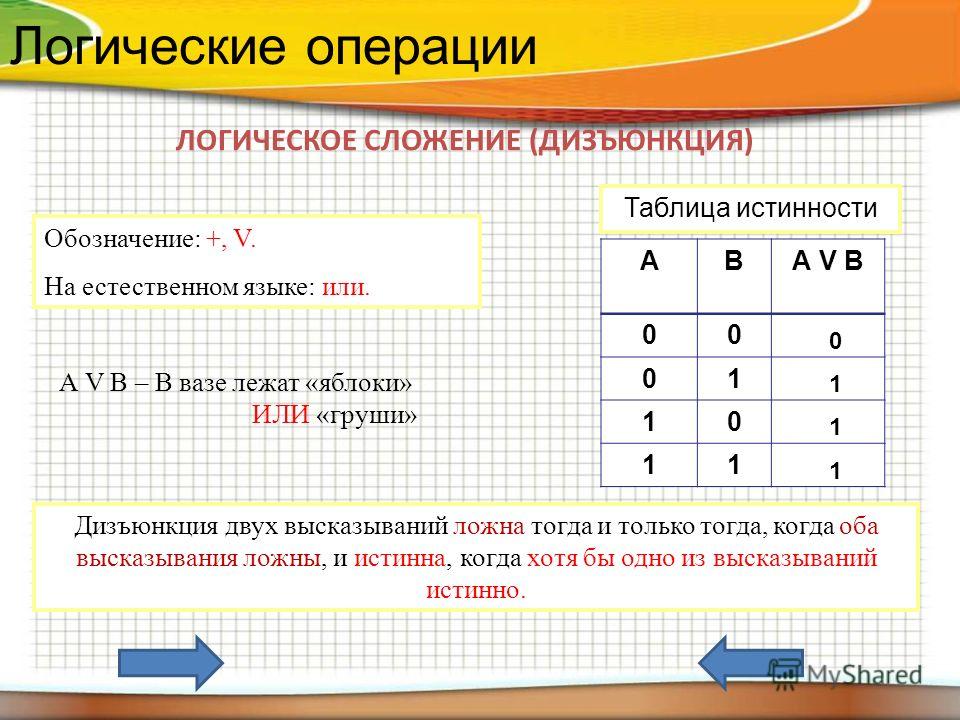
4. ДИЗЪЮНКЦИЯ
F=A+BЛогическое сложение –
ДИЗЪЮНКЦИЯ — это
новое сложное выражение
будет истинным тогда и
только тогда,
когда истинно хотя бы
одно из исходных (простых)
выражений.
► Дизъюнкция определяет
соединение двух
логических выражений с
помощью союза ИЛИ
A
B
F
1
1
1
1
0
1
0
1
1
0
0
0
5. Примеры:
► 10делится на
► 10 не делится
► 10 делится на
► 10 не делится
2 или 5 больше 3
на 2 или 5 больше 3
2 или 5 не больше 3
на 2 или 5 не больше 3
F=AVB
Задание: Определить, чему будет равно значение F для
каждого выражения.
6. ИНВЕРСИЯ
Логическое отрицание :
ИНВЕРСИЯ — если исходное
выражение истинно, то
результат отрицания будет
ложным, и наоборот, если
исходное выражение ложно,
то результат отрицания будет
истинным/
Данная операция означает,
что к исходному логическому
выражению добавляется
частица НЕ или слова
НЕВЕРНО, ЧТО
A
_
F=A
1
0
0
1
► Пример:
► Луна
— спутник Земли (А).
► Луна — не спутник Земли (не A)
_
F= A
8. Логическое следование (импликация)
Логическое следование (Импликация) образуется
соединением двух высказываний в одно с помощью союза
«если… то…».
Импликация записывается как посылка следствие; (остриё
всегда указывает на следствие).
F = A B, составное высказывание, образованное с помощью
операции: логическое следование (импликация)
Суждение, выражаемое импликацией, выражается также
следующими способами:
1. Посылка является условием, достаточным для выполнения следствия;
2. Следствие является условием, необходимым для истинности посылки.
9. «Житейский» смысл импликации.
«Житейский» смыслимпликации.
Для более лёгкого понимания смысла импликации и
запоминания ее таблицы истинности может
пригодиться житейская модель:
А — начальник. Он может приказать «работай» (1) или
сказать «делай что хочешь» (0).
В — подчиненный. Он может работать (1) или
бездельничать (0).
В таком случае импликация — не что иное, как
послушание подчиненного начальнику.
По таблице истинности легко проверить, что
послушания нет только тогда, когда начальник
приказывает работать, а подчиненный бездельничает.
10. ИМПЛИКАЦИЯ
Логическое
следование: ИМПЛИКАЦИЯ связывает два простых логических
выражения, из которых первое
является условием (А), а второе
(В)– следствием из этого условия.
Результатом ИМПЛИКАЦИИ
является ЛОЖЬ только тогда,
когда условие А истинно, а
следствие В ложно.
Обозначается A B
символом «следовательно» и
выражается словами ЕСЛИ … ,
ТО …
A
B
F
1
1
1
1
0
0
0
1
1
0
0
1
11. Примеры:
Если данный четырёхугольник квадрат, то около него
можно описать окружность
Если данный четырёхугольник не квадрат, то около
него можно описать окружность
Если данный четырёхугольник квадрат, то около него
нельзя описать окружность
Если данный четырёхугольник не квадрат, то около
него нельзя описать окружность
A B
Задание: Определить, чему будет равно значение F для каждого
выражения.
12. Порядок выполнения логических операций
► 1.инверсия
► 2. конъюнкция
► 3. дизъюнкция
► 4. импликация
Для изменения указанного порядка
выполнения операций используются
скобки.
13. Пример задания 1:
Символом F обозначено
одно из указанных ниже
логических выражений от
трех аргументов: X, Y, Z.
Дан фрагмент таблицы
истинности выражения F:
►Какое
1) ¬X ¬Y ¬Z
X
Y
Z
F
1
0
0
1
0
0
0
1
1
1
1
0
выражение соответствует F?
2) X Y Z
3) X Y Z
4) ¬X ¬Y ¬Z
14. Решение :
нужно для каждой строчки подставить заданные
значения X, Y и Z во все функции, заданные в
ответах, и сравнить результаты с соответствующими
значениями F для этих данных
если для какой-нибудь комбинации X, Y и Z результат
не совпадает с соответствующим значением F,
оставшиеся строчки можно не рассматривать,
поскольку для правильного ответа все три результата
должны совпасть со значениями функции F
первое выражение, равно 1 только при X=Y=Z=0 , поэтому это
неверный ответ (первая строка таблицы не подходит)
второе выражение, равно 1 только при X=Y=Z=1, поэтому это
неверный ответ (первая и вторая строки таблицы не подходят)
третье выражение, равно нулю при X=Y=Z=0, поэтому это
неверный ответ (вторая строка таблицы не подходит)
наконец, четвертое выражение, равно нулю только тогда, когда
X=Y=Z=1, а в остальных случаях равно 1, что совпадает с
приведенной частью таблицы истинности
X
Y
Z
F
таким образом, правильный ответ – 4
1) ¬X ¬Y ¬Z
2) X Y Z
3) X Y Z
1
0
0
1
0
0
0
1
1
1
1
0
4) ¬X ¬Y ¬Z
16.
 Пример задания 2:
Пример задания 2:Символом F обозначено
одно из указанных ниже
логических выражений от
трех аргументов: X, Y, Z.
Дан фрагмент таблицы
истинности выражения F:
X
Y
Z
F
1
0
0
1
0
0
0
0
1
1
1
0
Какое выражение соответствует F?
1) ¬X ¬Y ¬Z
2) X Y Z
3) X ¬Y ¬Z
4) X ¬Y ¬Z
17. Решение :
В столбце F есть единственная единица
для комбинации X=1, Y=Z=0,
простейшая функция, истинная (только)
для этого случая, имеет вид , она есть
среди приведенных ответов (ответ 3)
таким образом, правильный ответ – 3.
18. Пример задания 3:
Дан фрагмент таблицы
истинности выражения F
(см. таблицу справа).
Какое выражение
соответствует F?
1) (X ¬Y)→ Z
2) (X Y)→ ¬Z
X
Y
Z
F
0
0
0
0
0
1
1
1
1
0
0
1
3) X (¬Y → Z)
4) X Y ¬Z
19. Ответ к заданию 3:
► Найдиправильный ответ:
► 1, 2, 3, 4
English Русский Правила
С этим файлом связано 14 файл(ов). Среди них: пр1.docx, Лекция 4.pptx, РП_Математические методы.doc, Сам_работа_тема_1-3.docx, Каталог паттернов проектирования.docx, Лекция ГОСТ Р ИСО_МЭК 12207. Основные процессы и взаимосвязь меж, Стратегии, цели и сценирии внедрения.docx, Виды и план внедрения.docx, Лекция.doc, Лекция 1.docx, Дестабилизирующие факторы.docx, Савостьянов.docx, 1.docx, 208 Татаринский-Ерофеев, крутые пацаны МЧС-ники.docx и ещё 4 файл(а). Показать все связанные файлы Подборка по базе: Лекция 1. Базовые понятия управления проектами-1-3 (1).pdf, Лекция 4 Базовые конструкции языков программирования.doc, Звуковые схемы.docx, 7 дарис после операции.docx, План операций на 20 Сентября 2022 года Вторник.doc, задания и схемы.doc, Инструкционная карта к практическому занятию по теме Множества и, 5-6 Схемы.pptx, ДЛЯ ОТЧЕТА урок Определение последовательности технологических , Гинекологические операции.pptx Тема занятия: «Базовые логические операции и схемы.  Таблицы истинности». Таблицы истинности».Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов. Таблица истинности необходима для совершения логических операций. Она включает в себя n+1 столбцы и 2n строки, где n — число используемых переменных. В первых n столбцах представлены разные значения аргументов функции, а в n+1 столбце представлены значения функции, которые она принимает на данном наборе аргументов. Набором называется совокупность значений переменных. А = 0, В = 1. В случае, когда количество переменных n, число различных наборов будет равно 2N. Например, для трех переменных число разных наборов будет равно 23 = 8. Для создания таблиц истинности используются обозначения логических значений 0 (ложь) и 1 (истина). Можно встретить вариацию таблицы, в которой число столбцов равно n + число используемых логических операций. В подобной таблице в первые n столбцы, так же как и в первом варианте, вписаны наборы аргументов, а остальные столбцы заполнены значениями подфункций, которые входят в запись функции. Применение таблиц истинности чаще всего встречается в булевой алгебре и в цифровой электронной технике для описания работы логических схем. Логические операции — построение из одного или нескольких высказываний нового высказывания. Результатом может являться не только образование нового высказывания, но и изменение содержания или объема уже данных высказываний. В случае логической операции истинность значения нового высказывания всецело определяется истинностью значения исходных высказываний. К логическим операциям относятся конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, эквиваленция, антиконъюнкция, антидизъюнкция. Логическое выражение — это запись, принимающая логическое значение «истина» или «ложь». Их можно разделить на два типа: выражения, использующие операции сравнения и принимающие логические значения. Например, выражение a логические выражения, которые связаны с логическими величинами и операциями.  Например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина. Например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина.В логические выражения могут входить функции, алгебраические операции, операции сравнения и логические операции. Для таких случаев существует алгоритм выполнения действий. За исключением тех случаев, когда в логическом выражении присутствуют скобки, влияющие на порядок выполнения операций. вычисляется существующие функциональные зависимости; вычисляются алгебраические операции в обычном порядке; вычисляются операции сравнения в любом порядке; вычисляются логические операции начиная с операции отрицания. Следом вычисляется операция логического умножения, логического сложения, в последнюю очередь выполняются операции импликации и эквивалентности. Инверсия или логическое отрицание — это логическая операция, при выполнении которой из данного высказывания получается новое высказывание. Это высказывание является отрицанием исходного высказывания.  Если данное высказывание обозначается буквой A, то отрицание исходного высказывания обозначается следующим образом [A¯¯¯¯][A¯]. Кроме этого возможно использование условного обозначения ¬A¬A. Читаться это будет как «не А», «А ложно», «неверно, что А», «отрицание А». Унарной в данном случае называется операция, которая используется относительно одной величины. Конъюнкция — это логическое умножение. Эта операция, для которой требуются два и более логических величины. Конъюнкция соединяет логические высказывания при помощи связки «и». Связка изображается символом ∧. Конъюнкция может быть истинной только в том случае, если оба высказывания истинны. Например, A ∧ B, если A = ложь, а B = истина, является ложным. Дизъюнкция — логическое сложение. Эта логическая операция соединяет два и более высказываний с помощью связки «или». Эта связка обозначается как ∨. Логическое высказывание будет истинным, если истинно хотя бы одно из условий. Например, A ∨ B истинно, даже если А = истина, а В = ложь. Правила составления таблицы истинности Таблицу истинности можно построить для любого логического выражения. В этой таблице будут отражены все значения, которые принимает выражение при всех наборах значений входящих в него переменных. Строить таблицы истинности необходимо по следующему алгоритму: Вычислить число переменных в выражении (n). Вычислить общее количество логических операций в выражении. Определить последовательность, в которой будут выполняться логические операции. Установить количество столбцов в таблице — количество переменных и количество операций. Внести в шапку таблицы переменные и операции, соблюдая последовательность, определенную в пункте 3. Высчитать количество строк в таблице, используя формулу m = 2n Занести в таблицу наборы входных переменных.  Они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2n−1. Они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2n−1.Заполнить таблицу, совершая логические операции. Примеры построения таблицы истинности Пример 1. Построим таблицу истинности и решим выражение F=(A∨B)∧(¬A∨¬B)F=(A∨B)∧(¬A∨¬B). Будем пользоваться приведенным выше алгоритмом. Число переменных в выражении n = 2. Общее количество логических операций в выражении — 5. Последовательность выполнения логических операций — 1, 5, 2, 4, 3. Количество столбцов — 7. Логические переменные (А и В) + логические операции ∨∨, ∧∧, ¬¬, ∨∨ , ¬¬ = 2 +5 = 7. Количество строк — 5, исходя из m =2n, таким образом 22 = 4, 4+1 (строка заголовков столбцов) = 5. Заполним таблицу. Решение
После заполнения таблицы, ответ будет выглядеть следующим образом: F = 0 при A = B = 0 и A = B = 1 Пример 2. Число переменных в выражении n = 3. Общее количество логических операций в выражении — 3. Последовательность выполнения логических операций — 3, 2, 1. Количество столбцов — 6. Логические переменные (X, Y, Z) + логические операции∨∨, ∧∧, ¬ = 3 + 3 = 6. Количество строк — 9, исходя из m =2n, таким образом 23 = 8, 8+1 (строка заголовков столбцов) = 9. Заполним таблицу. Решение
После заполнения таблицы, ответ будет выглядеть следующим образом: F = 0, при X = Y = Z = 0; при X = Y = 0 и Z = 1. |
Таблицы истинности
Таблицы истинности
|
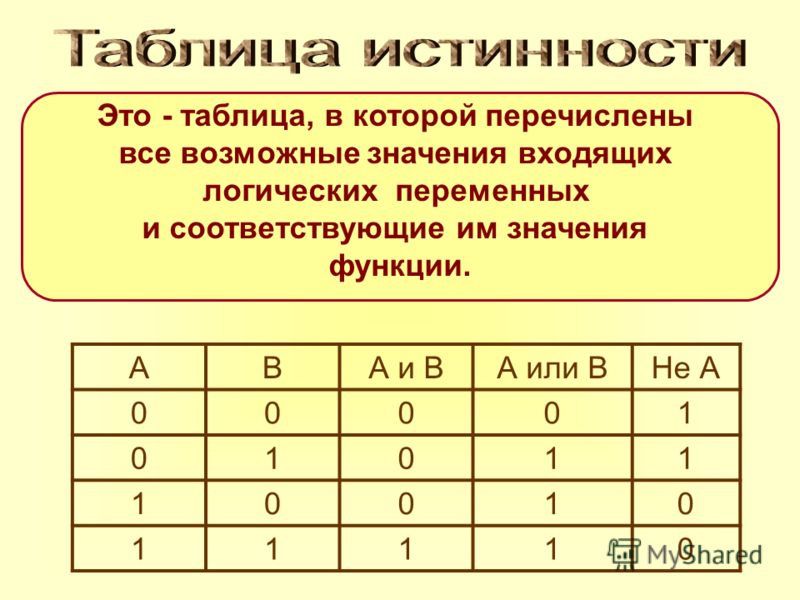
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений (наборах) входящих в него переменных, называют таблицей истинности логического выражения. |
Для того чтобы построить таблицу истинности логического выражения, достаточно:
1) определить число строк таблицы m = 2n, где n — число переменных в логическом выражении;
2) определить число столбцов таблицы как сумму чисел логических переменных и логических операций в логическом выражении;
3) установить последовательность выполнения логических операций с учётом скобок и приоритетов операций;
4) заполнить строку с заголовками столбцов таблицы истинности, занеся в неё имена логических переменных и номера выполняемых логических операций;
5) выписать наборы входных переменных с учётом того, что они представляют собой ряд целых n-разрядных двоичных чисел от 0 до 2n — 1;
6) провести заполнение таблицы истинности по столбцам, выполняя логические операции.
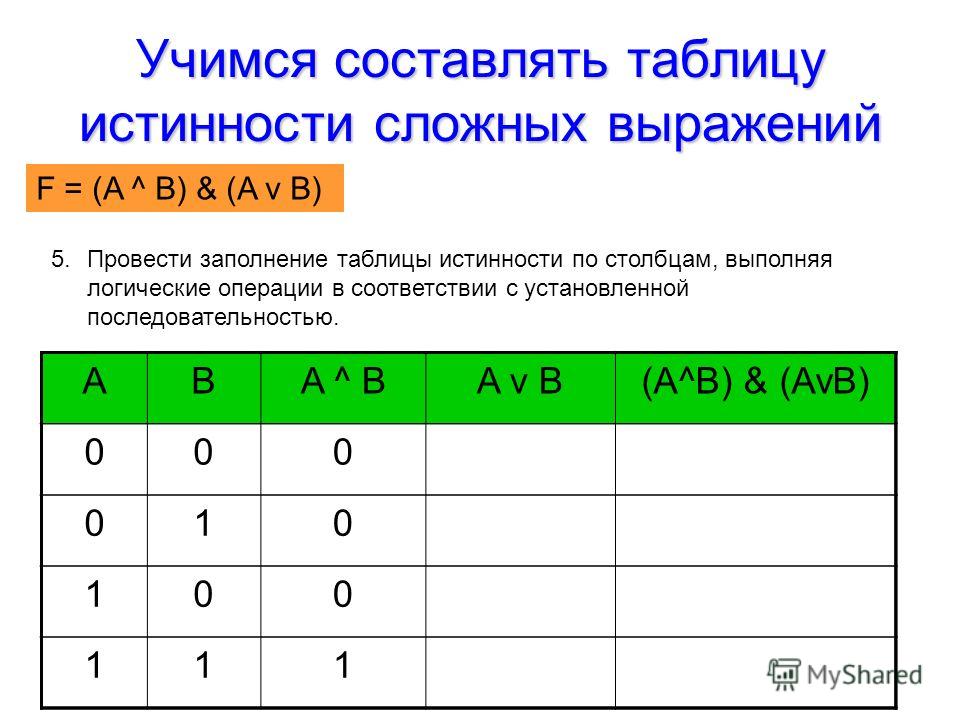
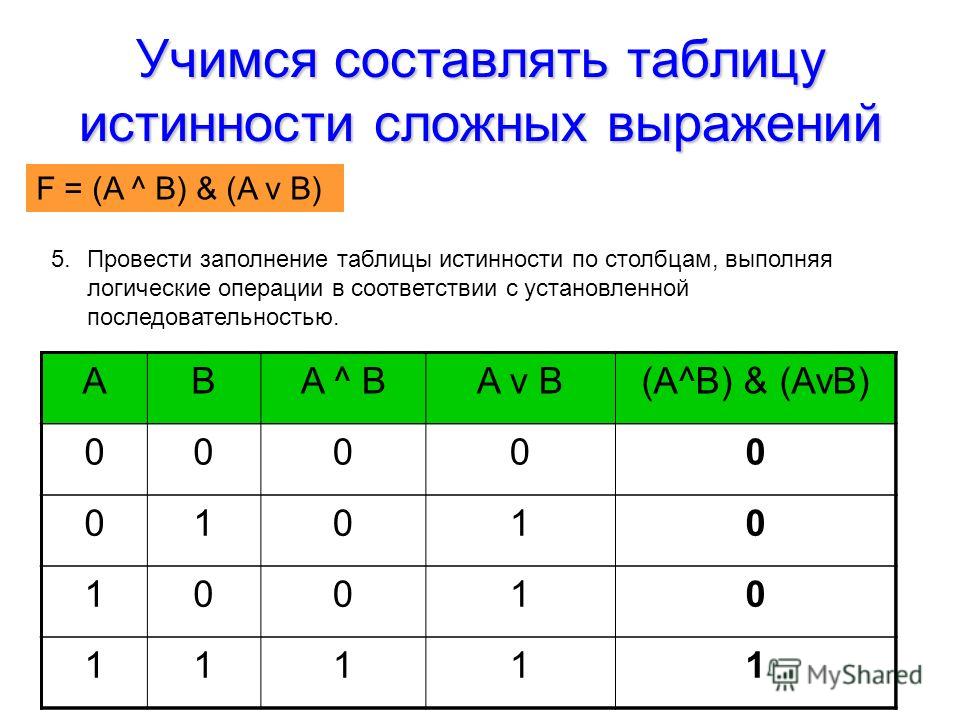
Пример 1. Построим таблицу истинности для логического выражения
В этом выражении две логические переменные и пять логических операций. Всего в таблице истинности будет пять строк (22 плюс строка заголовков) и 7 столбцов.
Начнём заполнять таблицу истинности с учётом следующего порядка выполнения логических операций: сначала выполняются операции отрицания (в порядке следования), затем операции конъюнкции (в порядке следования), последней выполняется дизъюнкция.
|
Логические выражения, зависящие от одних и тех же логических переменных, называются равносильными или эквивалентными, если для всех наборов входящих в них переменных значения выражений в таблицах истинности совпадают. |
Таблица истинности, построенная в предыдущем примере, доказывает равносильность выражений и А ↔ B.
Можно записать:
С помощью таблиц истинности докажите равносильность выражений А ↔ В и
|
Функцию от n переменных, аргументы которой и сама функция принимают только два значения — 0 и 1, называют логической функцией. Таблица истинности может рассматриваться как способ задания логической функции. |
Рассмотрим несколько примеров.
Пример 2. Известен фрагмент таблицы истинности для логического выражения F, содержащего логические переменные А, В и С.
Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
Ответить на поставленный вопрос можно, вычислив значение каждого логического выражения на каждом заданном наборе переменных и сравнив его с имеющимся значением F.
1) Логическое выражение соответствует данному фрагменту таблицы истинности:
2) Логическое выражение не соответствует данному фрагменту таблицы истинности, т.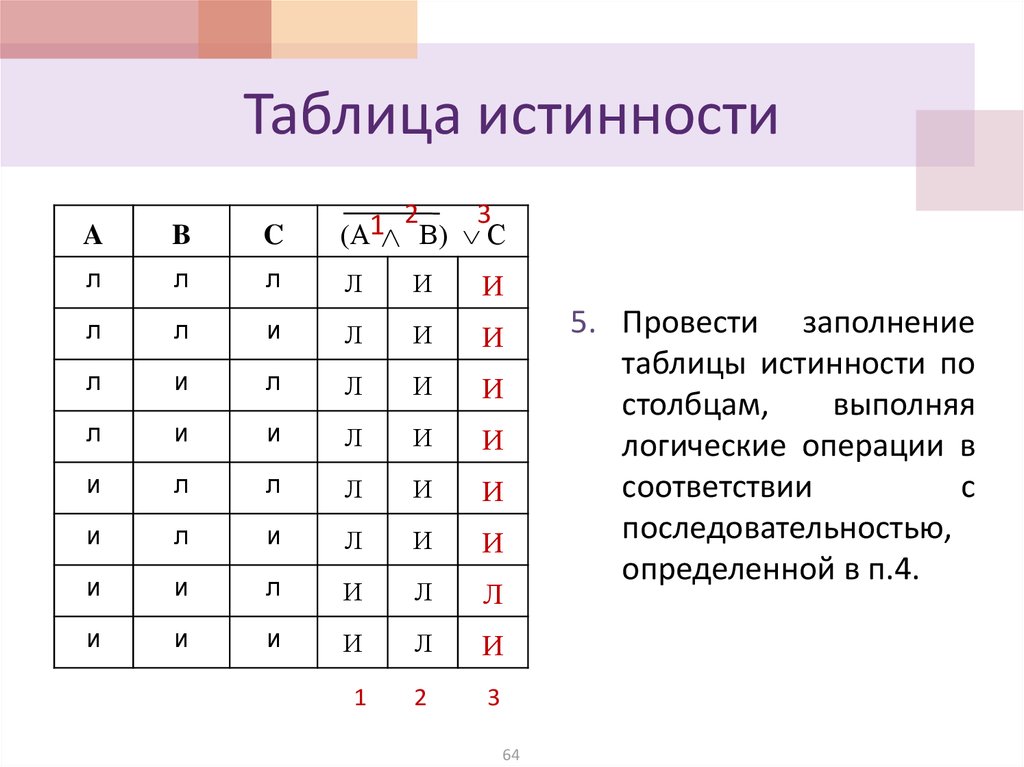 к. уже на первом наборе значение рассматриваемого логического выражения не совпадает со значением F. Проведение дальнейших вычислений не имеет смысла.
к. уже на первом наборе значение рассматриваемого логического выражения не совпадает со значением F. Проведение дальнейших вычислений не имеет смысла.
3) Логическое выражение не соответствует данному фрагменту таблицы истинности:
4) Логическое выражение
Итак, имеется два логических выражения, соответствующих заданному фрагменту таблицы истинности.
Можно ли утверждать, что в результате решения задачи мы нашли логическое выражение F?
Пример 3. Логическая функция F задаётся выражением:
Ниже приведён фрагмент таблицы истинности, содержащий все наборы переменных, на которых F истинна.
Определим, какому столбцу таблицы истинности функции F соответствует каждая из переменных х, у, z.
В исходном логическом выражении задействовано три логические переменные. Полная таблица истинности для этого выражения должна состоять из 8 (23) строк.
Наборам переменных, на которых логическое выражение истинно, соответствуют десятичные числа 0, 2, 3, 4 и 7.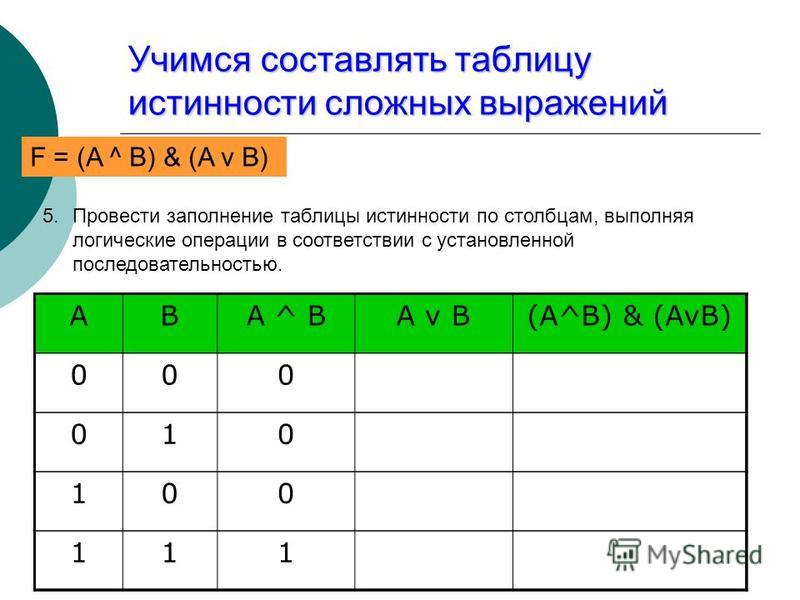
Следовательно, наборам переменных, на которых логическое выражение ложно, должны соответствовать десятичные числа 1, 5 и 6 (их двоичные коды 001, 101 и 110). Построим по этим данным вторую часть таблицы истинности:
Теперь выясним, при каких значениях х, у, z логическое выражение ложно: Логическое произведение ложно, если хотя бы один из операндов равен нулю. Таким образом, мы имеем две дизъюнкции, каждая из которых должна быть ложной. Это возможно только в случае равенства нулю каждого из операндов, входящих в дизъюнкцию. Подберём подходящие значения х, у и z, заполняя следующую таблицу:
Первая дизъюнкция равна нулю на наборе 011. Для равенства нулю второй дизъюнкции требуется, чтобы х = 1, у = 0, a z может быть и 0, и 1.
Сравним эту таблицу с восстановленным нами фрагментом исходной таблицы истинности, предварительно подсчитав, сколько раз каждая переменная принимает единичное значение.
Переменная у принимает единичное значение только один раз. Следовательно, ей соответствует второй столбец исходной таблицы. Из таблицы со значениями х, у и z следует, что при у = 1: х = 0, a z = 1. Следовательно, переменной z соответствует первый столбец, а переменной х — третий столбец исходной таблицы.
Следовательно, ей соответствует второй столбец исходной таблицы. Из таблицы со значениями х, у и z следует, что при у = 1: х = 0, a z = 1. Следовательно, переменной z соответствует первый столбец, а переменной х — третий столбец исходной таблицы.
Убедиться в правильности полученного ответа можно, полностью заполнив следующую таблицу:
Самое главное
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений (наборах) входящих в него переменных, называют таблицей истинности логического выражения.
Истинность логического выражения можно доказать путём построения его таблицы истинности.
Функцию от n переменных, аргументы которой и сама функция принимают только два значения — 0 и 1, называют логической функцией. Таблица истинности может рассматриваться как способ задания логической функции.
3.1: Предложения и логические операторы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 80504
- Al Doerr & Ken Levasseur
- University of Massachusetts Lowell
Propositions
Определение \(\PageIndex{1}\): Proposition
Предложение — это предложение, к которому может быть осмысленно применено одно и только одно из условий true или false .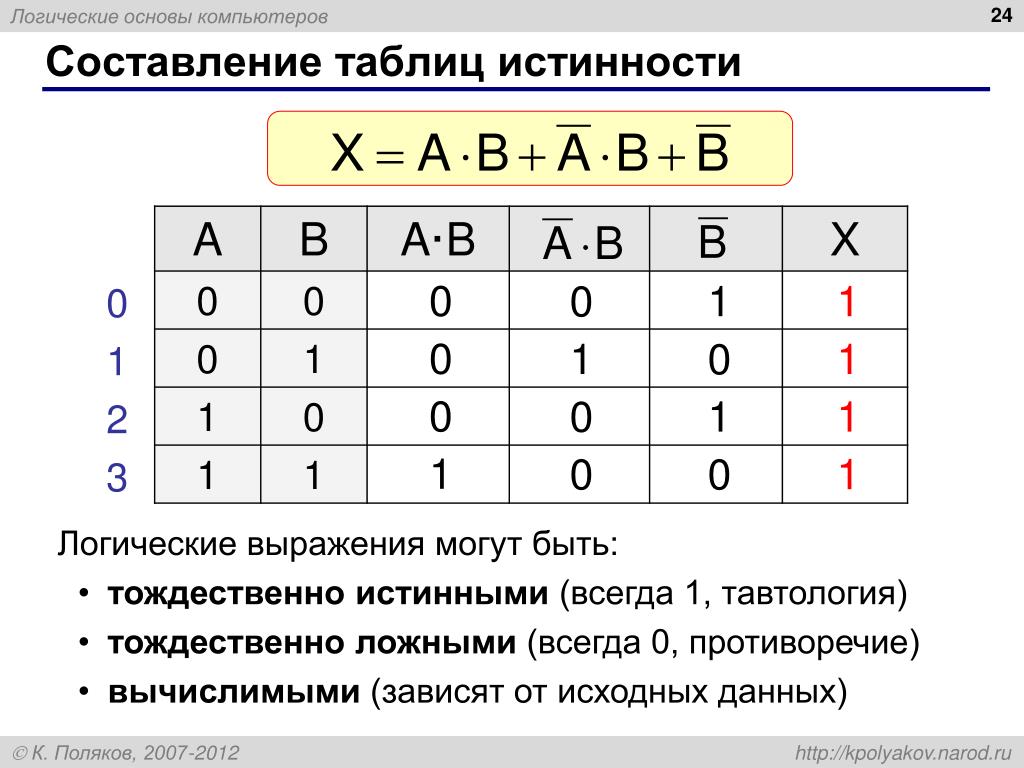
Пример \(\PageIndex{1}\): некоторые утверждения
«Четыре четные», «\(4 \in \{1,3, 5\}\)» и «\(43 > 21\) )» являются предложениями.
В традиционной логике декларативное утверждение с определенным значением истинности считается предложением. Хотя нашей конечной целью является обсуждение математической логики, мы не будем полностью отделяться от традиционной обстановки. Это естественно, потому что основные предположения или постулаты математической логики моделируются по образцу логики, которую мы используем в повседневной жизни. Поскольку в повседневной речи часто используются сложные предложения, мы ожидаем, что логические предложения содержат такие связки, как слово «и». Утверждение «Европа поддерживает жизнь или Марс поддерживает жизнь» является предложением и, следовательно, должно иметь определенное истинностное значение. Каким бы ни было это истинное значение, оно должно быть таким же, как истинное значение «Марс поддерживает жизнь или Европа поддерживает жизнь».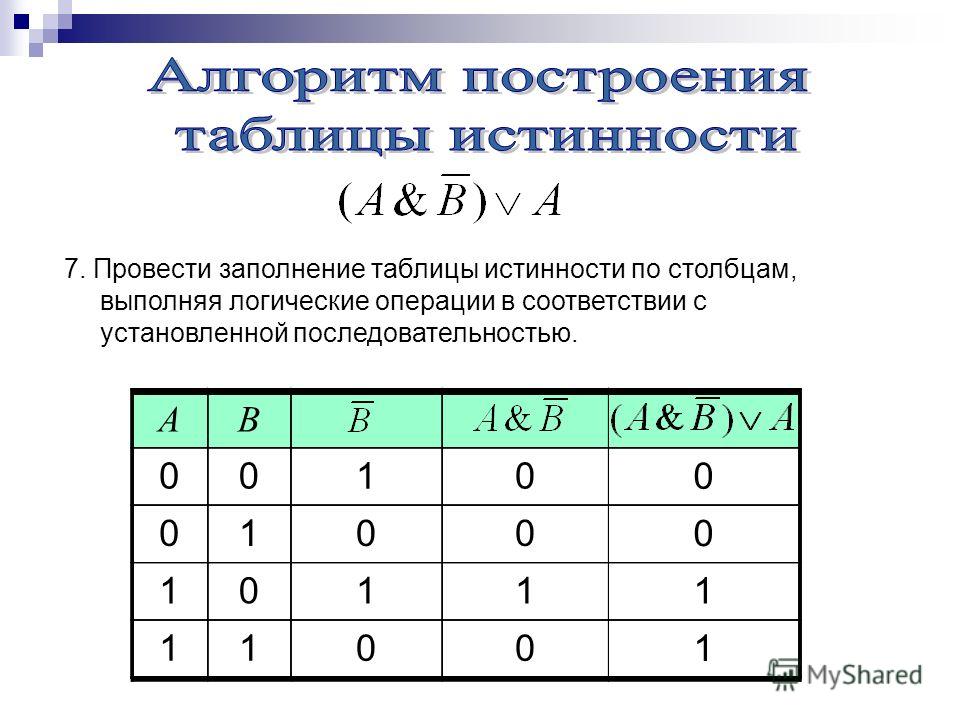
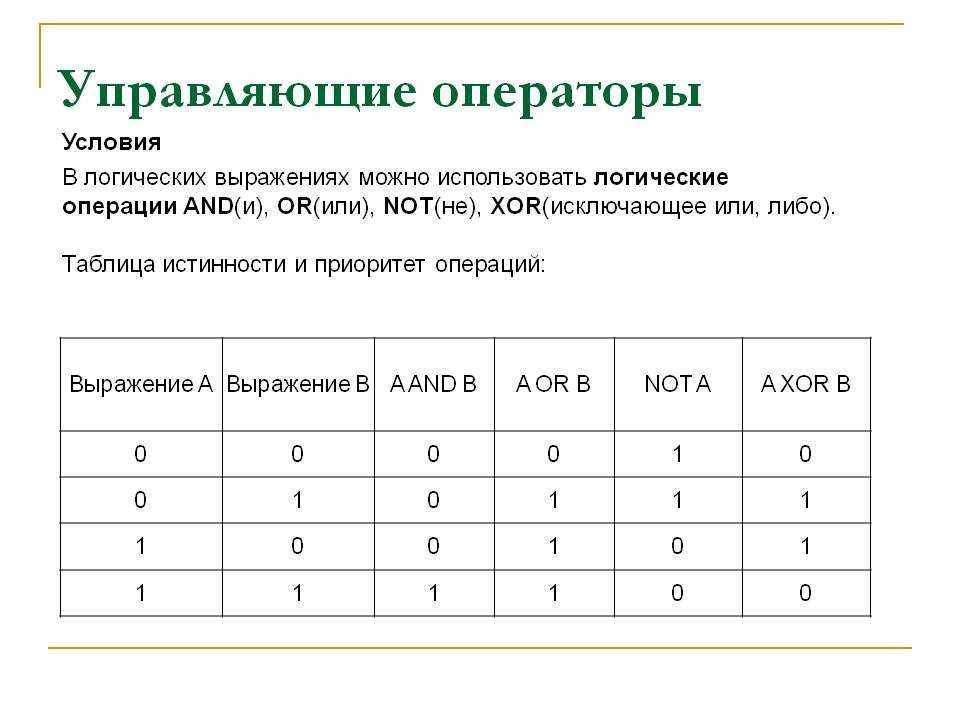
Логические операции
Существует несколько способов объединения простых операторов в составные. Слова/фразы и , или , не , если… то… , и
Определение \(\PageIndex{2}\): Логическая конъюнкция
Если \(p\) и \(q\) являются высказываниями, их конъюнкция \(p \textrm{ и } q\) (обозначается \( p \land q\)) определяется таблицей истинности
\begin{equation*} \begin{array}{ccc} p & q & p\land q \\ \hline 0 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \\ \end{array} \end{equation*}
Примечание \(\PageIndex{1}\)
- Чтобы прочитать эту правду таблицы, вы должны понимать, что любая строка представляет случай: один возможный набор значений для \(p\) и \(q\text{.
 }\)
}\) - Цифры 0 и 1 используются для обозначения ложных и истинных значений соответственно. Это согласуется со способом, которым многие языки программирования обрабатывают логические или логические переменные, поскольку один бит, 0 или 1, может представлять значение истинности.
- В каждом случае символ под \(p\) представляет истинное значение \(p\text{.}\) То же верно для \(q\text{.}\) Символ под \(p \ land q\) представляет его истинное значение для этого случая. Например, вторая строка таблицы истинности представляет случай, когда \(p\) ложно, \(q\) истинно, а результирующее значение истинности для \(p \land q\) ложно. Как и в повседневной речи, \(p \land q\) истинно только тогда, когда оба предложения истинны.
- Буквы \(x\text{,}\) \(y\) и \(z\) часто используются в алгебре для обозначения числовых переменных, \(p\text{,}\) \(q\ ) и \(r\) кажутся наиболее часто используемыми символами для логических переменных. Когда мы говорим, что \(p\) является логической переменной, мы имеем в виду, что любое предложение может занять место \(p\text{.
 }\)
}\) - И последнее замечание: порядок, в котором мы перечисляем случаи в таблице истинности, в этой книге стандартизирован. Если таблица истинности включает два простых предложения, числа под простыми предложениями можно интерпретировать как двузначные двоичные целые числа в возрастающем порядке: 00, 01, 10 и 11 для 0, 1, 2 и 3 соответственно.
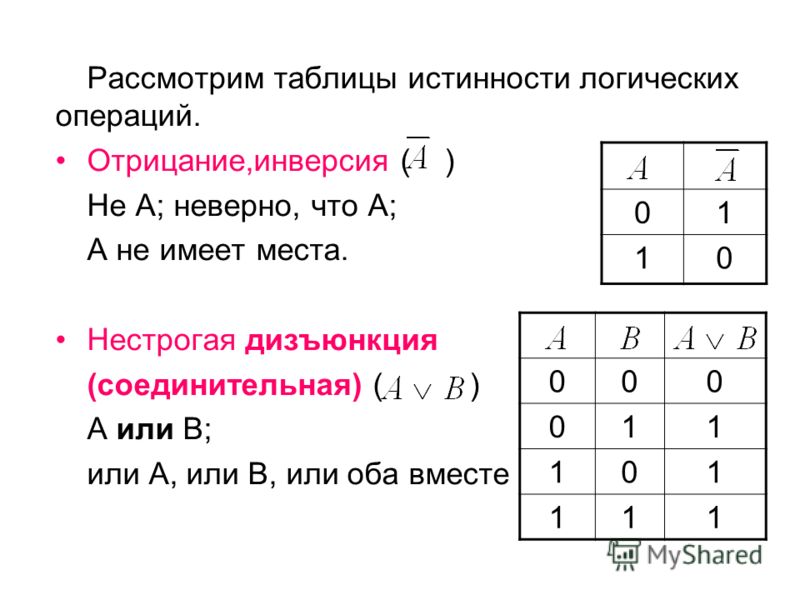
Определение \(\PageIndex{3}\): Логическая дизъюнкция
Если \(p\) и \(q\) являются предложениями, их дизъюнкция, \(p \textrm{ или } q\) (обозначается \( p \lor q\)), определяется таблицей истинности
\begin{equation*} \begin{array}{ccc} p & q & p\lor q \\ \hline 0 & 0 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\ \end{массив} \end{уравнение*}
Определение \(\PageIndex{4}\): логическое отрицание
Если \ (p\) есть предложение, его отрицание, \(\textrm{not } p\text{,}\) обозначается \(\neg p\text{,}\) и определяется таблицей истинности
\begin{equation*} \begin{array}{cc} p & \neg p \\ \hline 0 & 1 \\ 1 & 0 \\ \end{array} \end{equation*}
Примечание \ (\PageIndex{2}\)
Отрицание — единственный стандартный оператор, который действует на одно предложение; следовательно, необходимы только два случая.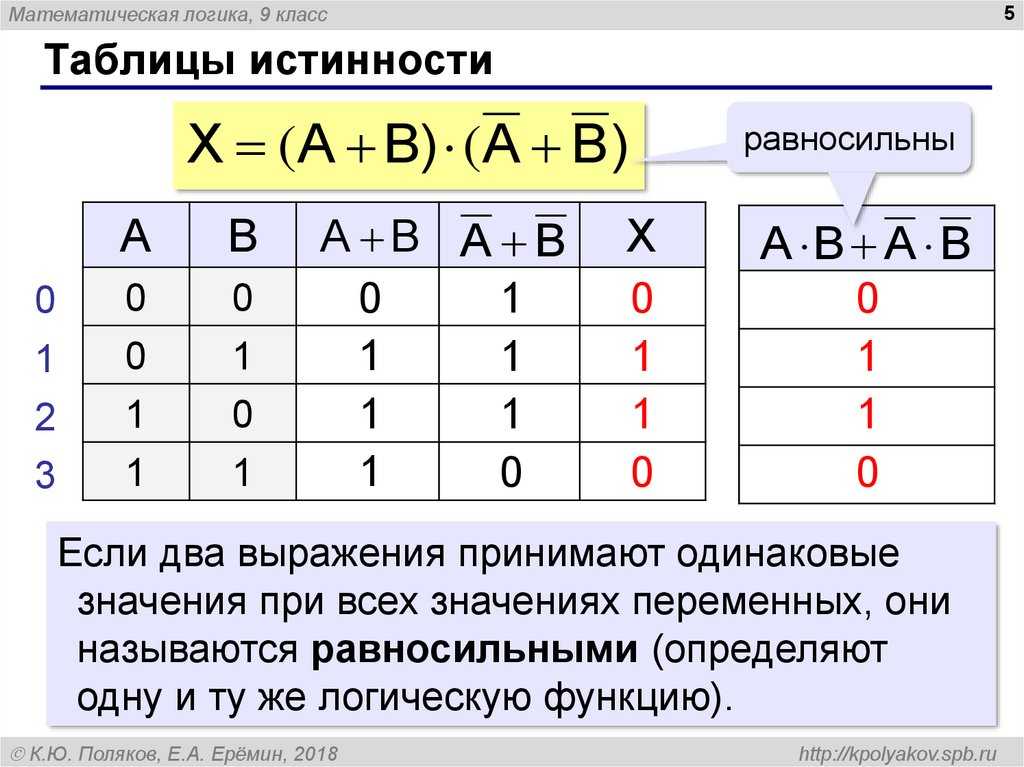
Рассмотрим следующие предложения из повседневной речи:
- Я уволюсь, если не получу повышения.
- Если я пройду финал, я закончу школу.
- Я пойду в кино, если моя машина заведется.
Все три суждения условны, их все можно переформулировать так, чтобы они соответствовали форме «Если Условие , то Заключение ». Например, первое утверждение можно переписать так: «Если я не получу повышения, я уволюсь».
Условное утверждение следует интерпретировать как гарантию; если условие истинно, то ожидается, что заключение будет истинным. Говорит не больше и не меньше.
Определение \(\PageIndex{5}\): условное выражение
Условное утверждение «Если \(p\), то \(q\text{,}\)», обозначаемое \(p \rightarrow q\text{,}\), определяется таблицей истинности
Таблица \(\ PageIndex{1}\: Таблица истинности для \(p\стрелка вправо q\)
| \(p\) | \(к\) | \(p\стрелка вправо q\) |
|---|---|---|
| \(0\) | \(0\) | \(1\) |
| \(0\) | \(1\) | \(1\) |
| \(1\) | \(0\) | \(0\) |
| \(1\) | \(1\) | \(1\) |
Пример \(\PageIndex{2}\): Анализ условного суждения
Предположим, ваш преподаватель сказал вам: «Если вы получите оценку 95 или выше на выпускном экзамене, вы получите пятерку на этом экзамене».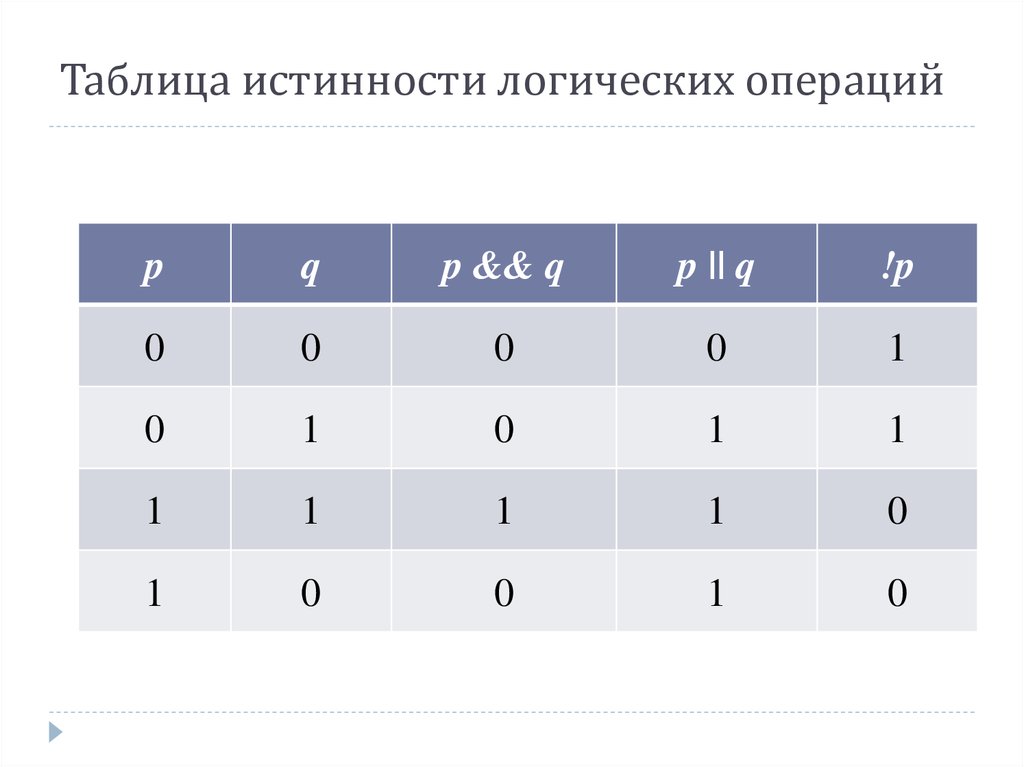 курс.» Ваш инструктор дал вам обещание. Если вы выполняете его условие, вы ожидаете, что вывод (получение пятерки) будет не за горами. Предположим, вам вернули итоговую оценку. Ваш инструктор сказал правду или он виновен во лжи?
курс.» Ваш инструктор дал вам обещание. Если вы выполняете его условие, вы ожидаете, что вывод (получение пятерки) будет не за горами. Предположим, вам вернули итоговую оценку. Ваш инструктор сказал правду или он виновен во лжи?
Случай I: Ваш итоговый балл за экзамен был меньше 95 (условие ложно), и вы не получили пятерку (заключение ложно). Инструктор сказал правду.
Случай II: Ваш итоговый балл на экзамене был ниже 95, но вы получили пятерку за курс. Инструктор сказал правду. (Возможно, ваш общий средний балл по курсу был превосходным.)
Случай III: Ваш итоговый экзаменационный балл был выше 95, но вы не получили пятерку. Преподаватель солгал.
Случай IV: Ваш итоговый балл за экзамен был выше 95, и вы получили пятерку. Инструктор сказал правду.
Подводя итог, единственный случай, когда условное суждение ложно, это когда условие истинно, а заключение ложно.
Порядок условия и заключения в условном суждении важен. Если поменять местами условие и заключение, получится другое предложение.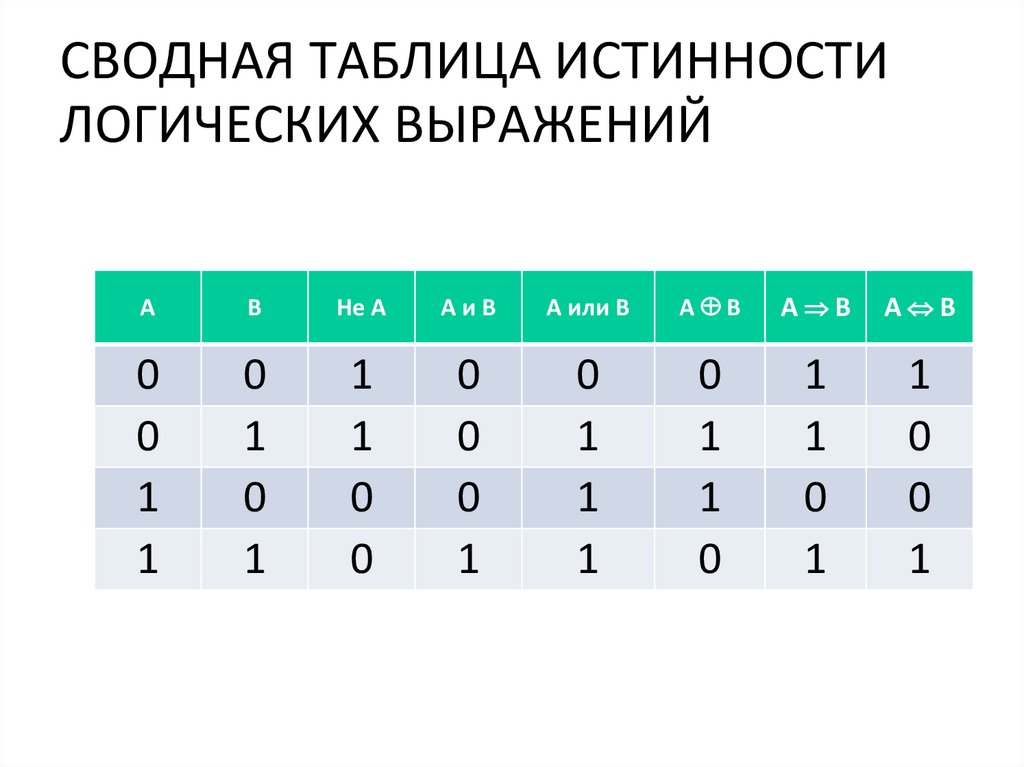
Определение \(\PageIndex{6}\): Обратное
Обратное предложение \(p \rightarrow q\) есть предложение \(q \rightarrow p\text{.}\)
Обратное выражение «Если вы получите оценку 95 или выше на выпускном экзамене, то вы получите пятерку по этому курсу»: «Если вы получите пятерку по этому курсу, то вы получите оценку 95 или выше. лучше на выпускном экзамене». Должно быть ясно, что эти два утверждения говорят о разных вещах.
Здесь есть предложение, связанное с \(p \rightarrow q\), которое имеет тот же логический смысл. Это противопоставление.
Определение \(\PageIndex{7}\): Противоположный
Противоположным высказыванию \(p \rightarrow q\) является высказывание \(\neg q \rightarrow \neg p\text{.}\)
Как мы увидим при обсуждении логических доказательств, мы можем доказать условное суждение, доказывая его противоположность, что может быть несколько проще.
Определение \(\PageIndex{8}\): Биусловное высказывание
Если \(p\) и \(q\) являются высказываниями, биусловное высказывание «\(p\) тогда и только тогда, когда \(q\text {,}\)», обозначаемый \(p \leftrightarrow q\text{,}\), определяется таблицей истинности
\begin{equation*} \begin{array}{ccc} p & q & p\leftrightarrow q \\ \hline 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \\ \end{массив} \end{уравнение*}
Обратите внимание, что \(p \leftrightarrow q\) истинно, когда \(p\) и \(q\) имеют одинаковые значения истинности.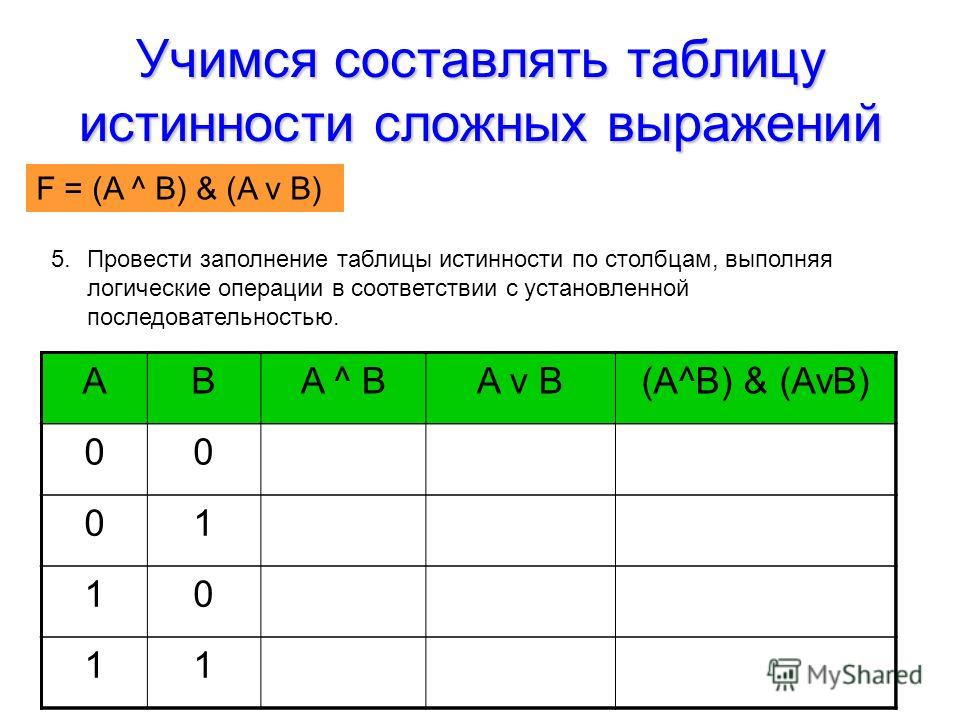 Обычно «если и только если» сокращают до «iff».
Обычно «если и только если» сокращают до «iff».
Несмотря на то, что «если… то…» и «…если и только если…» часто используются в повседневной речи, есть несколько альтернативных форм, о которых вам следует знать. Они сведены в следующие списки.
Все следующие эквиваленты «Если \(p\), то \(q\)»:
- \(p\) подразумевает \(q\text{.}\)
- \(q\) следует из \(p\text{.}\)
- \(p\text{,}\) только если \(q\text{.}\)
- \(q\text{,}\) если \(p\text{.}\)
- \(p\) достаточно для \(q\text{.}\)
- \(q\) необходимо для \(p\text{.}\)
Все следующие эквиваленты «\(p\) тогда и только тогда, когда \(q\)»:
- \(p\) необходимо и достаточно для \(q\text{.}\)
- \(p\) эквивалентно \(q\text{.}\)
- Если \(p\text{,}\), то \(q\text{,}\), а если \(q\text{,}\), то \(p\text{.}\)
- Если \(p\text{,}\), то \(q\) и наоборот.
Упражнения
Упражнение \(\PageIndex{1}\)
Пусть \(d\) = «Мне нравятся дискретные структуры», \(c\) = «Я пройду этот курс» и \(s\) = «Я буду выполнять свои задания». Выразите каждое из следующих утверждений в символической форме:
Выразите каждое из следующих утверждений в символической форме:
- Мне нравятся дискретные структуры, и я пройду этот курс.
- Я буду выполнять задания или не пройду этот курс.
- Неправда, что я люблю дискретные структуры и буду выполнять свои задания.
- Я не буду выполнять задание и не пройду этот курс.
- Ответить
- \(\displaystyle d\land c\)
- \(\displaystyle s\lor \neg c\)
- \(\displaystyle \neg (d\land s)\)
- \(\displaystyle \neg s\land \neg c\)
Упражнение \(\PageIndex{2}\)
Для каждого из следующих предложений определите простые предложения, выразите составное предложение в символической форме и определите, истинно оно или ложно:
- Мир плоский или ноль — четное целое число.
- Если 432 802 кратно 4, то 432 802 четно.

- 5 — простое число, а 6 не делится на 4.
- \(3 \in \mathbb{Z}\) и \(3 \in \mathbb{Q}\text{.}\)
- \(2/3 \in \mathbb{Z}\) и \(2/3 \in \mathbb{Q}\text{.}\)
- Сумма двух четных целых чисел четна, а сумма двух нечетных целых чисел нечетна.
Упражнение \(\PageIndex{3}\)
Пусть \(p =\)»\(2 \leq 5\)», \(q\) = «8 — четное целое число» и \(r \) = «11 — простое число». Выразите следующее в виде утверждения на английском языке и определите, верно оно или нет:
- \(\displaystyle \neg p \land q\)
- \(\displaystyle p\стрелка вправо q\)
- \(\displaystyle (p\land q)\to r\)
- \(\displaystyle p \rightarrow (q \lor (\neg r))\)
- \(\displaystyle p \rightarrow ((\neg q)\lor (\neg r))\)
- \(\displaystyle (\neg q) \rightarrow (\neg p)\)
- Ответить
- \(2>5\), а 8 — четное целое число.
 ЛОЖЬ.
ЛОЖЬ. - Если \(2\leqslant 5\), то 8 — четное целое число. Истинный.
- Если \(2\leqslant 5\) и 8 — четное целое число, то 11 — простое число. Истинный.
- Если \(2\leqslant 5\), то либо 8 — четное целое число, либо 11 — не простое число. Истинный.
- Если \(2\leqslant 5\), то либо 8 является нечетным целым числом, либо 11 не является простым числом. ЛОЖЬ.
- Если 8 не является четным целым числом, то \(2>5\text{.}\) Истинно.
- \(2>5\), а 8 — четное целое число.
Упражнение \(\PageIndex{4}\)
Перепишите каждое из следующих утверждений, используя другие условные формы:
- Если целое число кратно 4, то оно четное. 92\) является необходимым условием для \(x = y\text{.}\)
Упражнение \(\PageIndex{5}\)
Напишите обратное предложение из упражнения \(\PageIndex{4}\). Сравните истинность каждого предложения и его обратного.
- Ответить
Верно только обратное \(d\).

Эта страница под названием 3.1: Предложения и логические операторы распространяется по лицензии CC BY-NC-SA, автором, ремиксом и/или куратором этой страницы являются Эл Доерр и Кен Левассер.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Эл Дорр и Кен Левассер
- Лицензия
- CC BY-NC-SA
- Показать страницу TOC
- нет
- Теги

Таблицы истинности ADS и предложения, сгенерированные набором
Подраздел 3.2.1 Таблицы истинности
Рассмотрим составное предложение \(c= (p \land q)\lor (\neg q \land r)\text{,}\), где \(p\text{,}\) \(q\text{, }\) и \(r\) являются предложениями. Это пример предложения, порожденного \(p\text{,}\) \(q\text{,}\) и \(r\text{.}\). Мы определим эту терминологию позже в этом разделе. Поскольку каждое из трех простых утверждений имеет два возможных значения истинности, отсюда следует, что существует восемь различных комбинаций значений истинности, которые определяют значение для \(c\text{.}\). Эти значения могут быть получены из таблицы истинности для \ (c\text{.}\) Чтобы построить таблицу истинности, мы строим \(c\) из \(p\text{,}\) \(q\text{,}\) и \(r\) и от логических операторов. Результатом является приведенная ниже таблица истинности. Строго говоря, первые три столбца и последний столбец составляют таблицу истинности для \(c\text{. }\). Остальные столбцы представляют собой рабочее пространство, необходимое для построения до \(c\text{.}\)
}\). Остальные столбцы представляют собой рабочее пространство, необходимое для построения до \(c\text{.}\)
| \(p\) | \(к\) | \(р\) | \(p\land q\) | \(\отр\) | \(\neg q\land r\) | \((p\land q)\lor (\neg q\land r)\) |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 |
Обратите внимание, что первые три столбца таблицы истинности представляют собой перечисление восьми трехзначных двоичных целых чисел. n\) строк с первыми \(n\) столбцами, перечисление \(n\) цифр двоичных целых чисел. В нашем примере мы можем с первого взгляда увидеть, что ровно в четырех из восьми случаев \(с\) будет верным. Например, если \(p\) и \(r\) истинны, а \(q\) ложно (шестой случай), то \(c\) истинно.
n\) строк с первыми \(n\) столбцами, перечисление \(n\) цифр двоичных целых чисел. В нашем примере мы можем с первого взгляда увидеть, что ровно в четырех из восьми случаев \(с\) будет верным. Например, если \(p\) и \(r\) истинны, а \(q\) ложно (шестой случай), то \(c\) истинно.
Пусть \(S\) — любое множество предложений. Мы дадим два определения предложения, порожденного S. Первое немного неточно, но должно быть ясным. Второе определение называется рекурсивным определением . Если это вас сбивает с толку, используйте первое определение и вернитесь ко второму позже.
Подраздел 3.2.2 Предложения, порожденные множеством
Определение 3.2.2. Предложение, порожденное множеством.
Пусть \(S\) — любое множество предложений. Предложение, порожденное \(S\), представляет собой любую допустимую комбинацию предложений в \(S\) с конъюнкцией, дизъюнкцией и отрицанием. Или, если быть более точным,
Если \(p \in S\text{,}\), то \(p\) является предложением, порожденным \(S\text{,}\) и
Если \(x\) и \(y\) являются предложениями, порожденными \(S\text{,}\), то таковыми являются \((x)\text{,}\) \(\neg x\text {,}\) \(x\lor y\) и \(x\land y\text{.
 }\)
}\)
Примечание. Мы не включили в определение условные и биусловные конструкции, потому что они оба могут быть получены из конъюнкции, дизъюнкции и отрицания, как мы увидим позже.
Если \(S\) — конечное множество, то мы можем использовать несколько иную терминологию. Например, если \(S = \{p, q, r\}\text{,}\), мы можем сказать, что предложение порождено \(p, q\text{,}\) и \(r\ ) вместо \(\{p, q, r\}\text{.}\)
Обычно для толкования предложений используется следующая иерархия, при этом круглые скобки преобладают над этим порядком:
Внутри любого уровня иерархии работайте слева направо. Используя эти правила, \(p \land q \lor r\) означает \((p \land q)\lor r\text{.}\) Эти правила приоритета являются универсальными и в точности используются компьютером. языки для интерпретации логических выражений.
Пример 3.2.3. Примеры иерархии логических операций.
Несколько сокращенных выражений и их полностью заключенных в скобки версий:
\(p \land q \land r\) is \((p \land q) \land r\text{.
 }\)
}\)\(\neg p \lor \neg r\) is \((\neg p) \lor (\neg r)\text{.}\)
\(\neg \neg p\) равно \(\neg (\neg p)\text{.}\)
\(p \leftrightarrow q\land r\rightarrow s \) is \(p \leftrightarrow ((q\land r)\rightarrow s)\text{.}\)
Предложение, порожденное множеством \(S\), не обязано включать в свое выражение каждый элемент \(S\). Например, \(\neg q \land r\) является предложением, порожденным \(p, q\text{,}\) и \(r\text{.}\)
Упражнения 3.2.3 Упражнения
1.
Построить таблицы истинности:
\(\displaystyle p\lor p\)
\(\displaystyle p\land (\neg p)\)
\(\displaystyle p\lor (\neg p)\)
\(\displaystyle p \land p\)
Ответ.
\(\displaystyle \begin{array}{cc} р & р \ лор р \\ \hline 0 и 0 \\ 1 и 1 \\ \конец{массив}\)
\(\displaystyle \begin{массив}{ccc} p & \neg p & p\land (\neg p) \\ \hline 0 и 1 и 0 \\ 1 и 0 и 0 \\ \конец{массив}\)
\(\displaystyle \begin{массив}{ccc} p & \neg p & p\lor (\neg p) \\ \hline 0 и 1 и 1 \\ 1 и 0 и 1 \\ \конец{массив}\)
\(\displaystyle \begin{массив}{cc} р&р\земля р\\ \hline 0 и 0 \\ 1 и 1 \\ \конец{массив}\)
2.
Построить таблицы истинности:
\(\displaystyle \neg (p\land q )\)
\(\displaystyle p \land (\neg q)\)
\(\displaystyle (p \land q)\land r\)
\(\displaystyle (p \land q) \lor (q \land r)\lor (r \land p)\)
\(\displaystyle \text{ }\neg p\lor \neg q\)
\(\displaystyle p \lor q \lor r \lor s\)
3.
Перепишите следующее, убрав как можно меньше лишних скобок:
\(\displaystyle (\neg ((p) \land (r))) \lor (s)\)
\(\displaystyle ((p) \lor (q)) \land ((r) \lor (q))\)
Ответ.
\(\displaystyle \neg (p\land r) \lor s\)
\(\displaystyle (p\lor q) \land (r\lor q)\)
4.
В каком порядке выполняются операции в следующих предложениях?
\(\displaystyle p \lor \neg q \lor r\land \neg p\)
\(\displaystyle p \land \neg q \land r \land \neg p\)
5.
Определить количество строк в таблице истинности предложения, содержащего четыре переменные \(p, q, r, \textrm{ и } s\text{.}\) 94 = 16\) рядов.
6.
Если на листе бумаги 45 строк, и вы хотите зарезервировать по одной строке для каждой строки в таблице истинности, насколько большой может быть \(\lvert S\rvert \), если вы можете написать таблицы истинности предложений, сгенерированных \(S\) на листе бумаги?
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашняя страница > Логика > Символика Логика > Логические связки | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Философия 103: Введение в логику Конъюнкция, отрицание и дизъюнкция Abstract: Логические операции конъюнкции, отрицания и дизъюнкции (альтерации) обсуждаются относительно их табличных определений истинности.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Присылайте исправления или предложения по адресу webmaster@philosophy. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


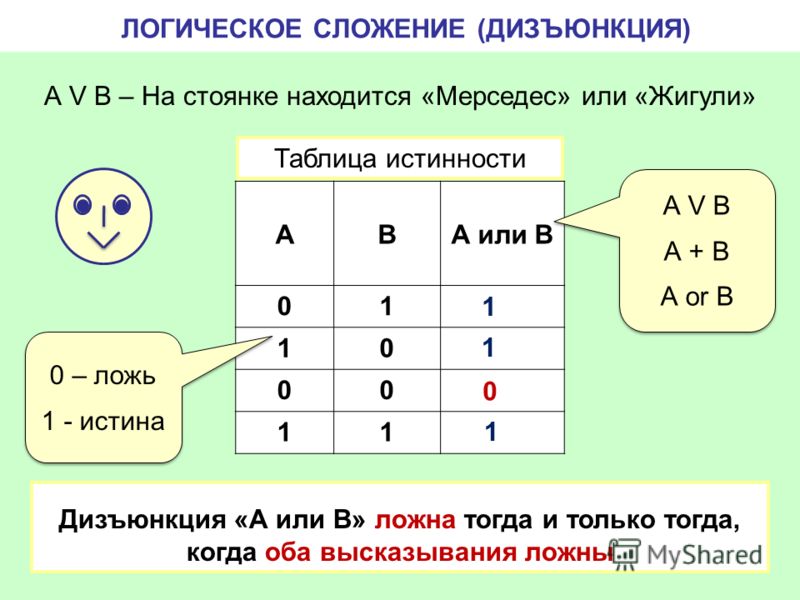 Таблицы истинности
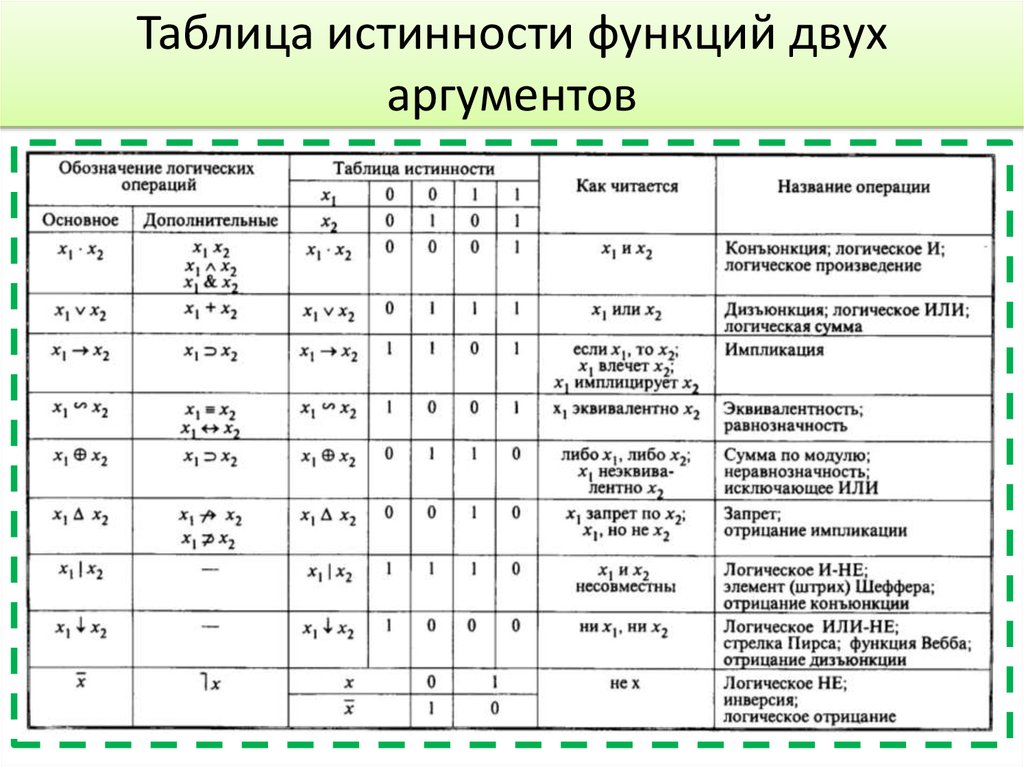
Таблицы истинности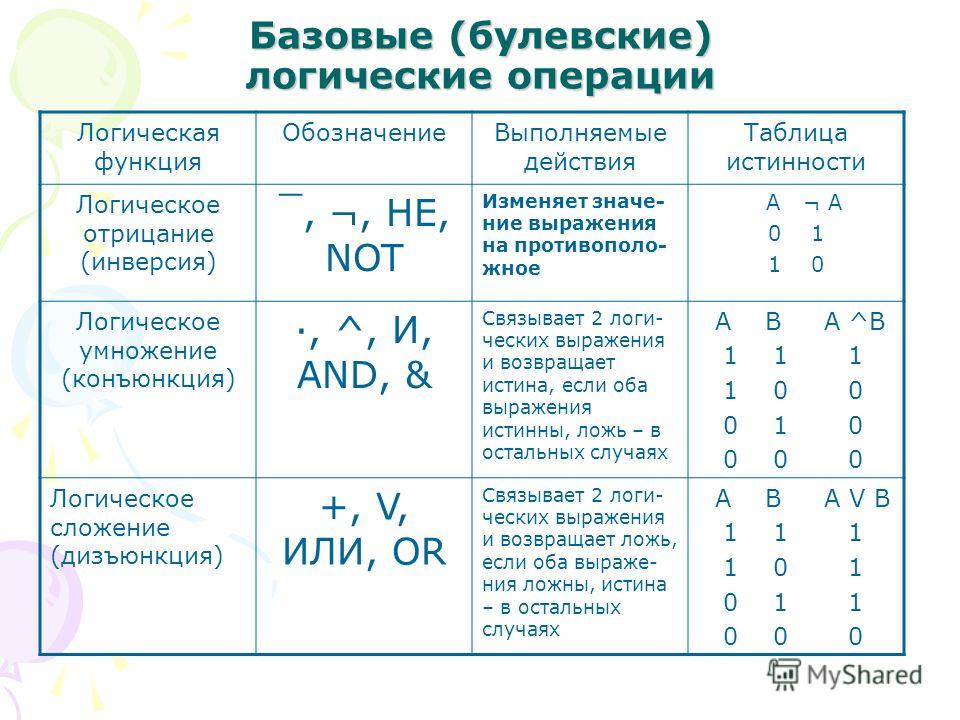 Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.
Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.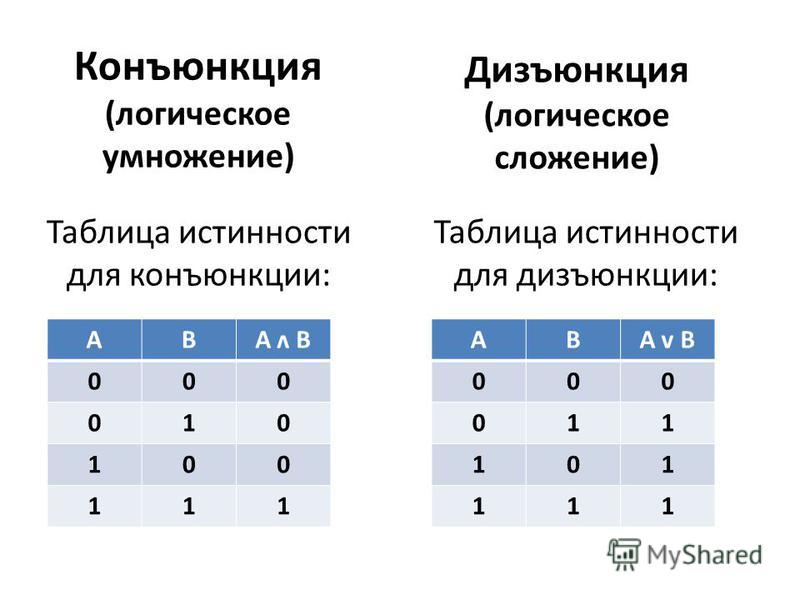 Высказывание будет ложным только в том случае, если ложны и А, и В.
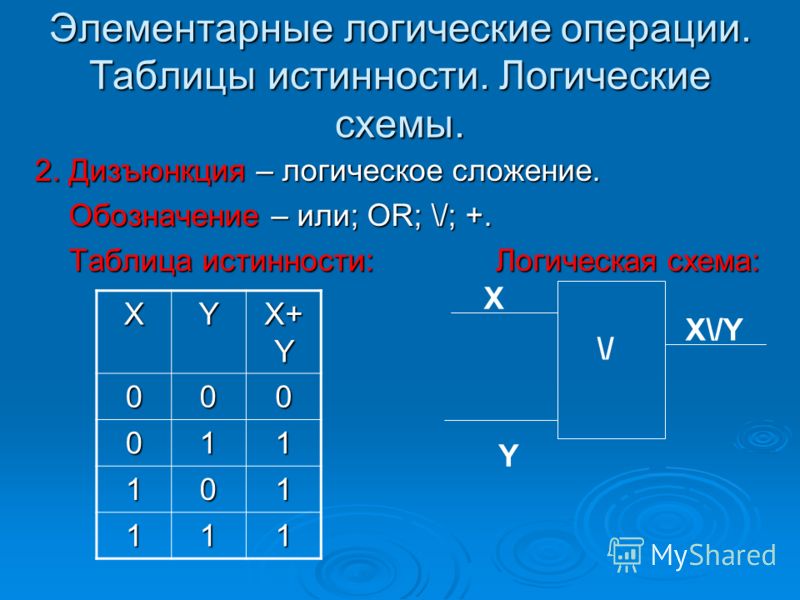
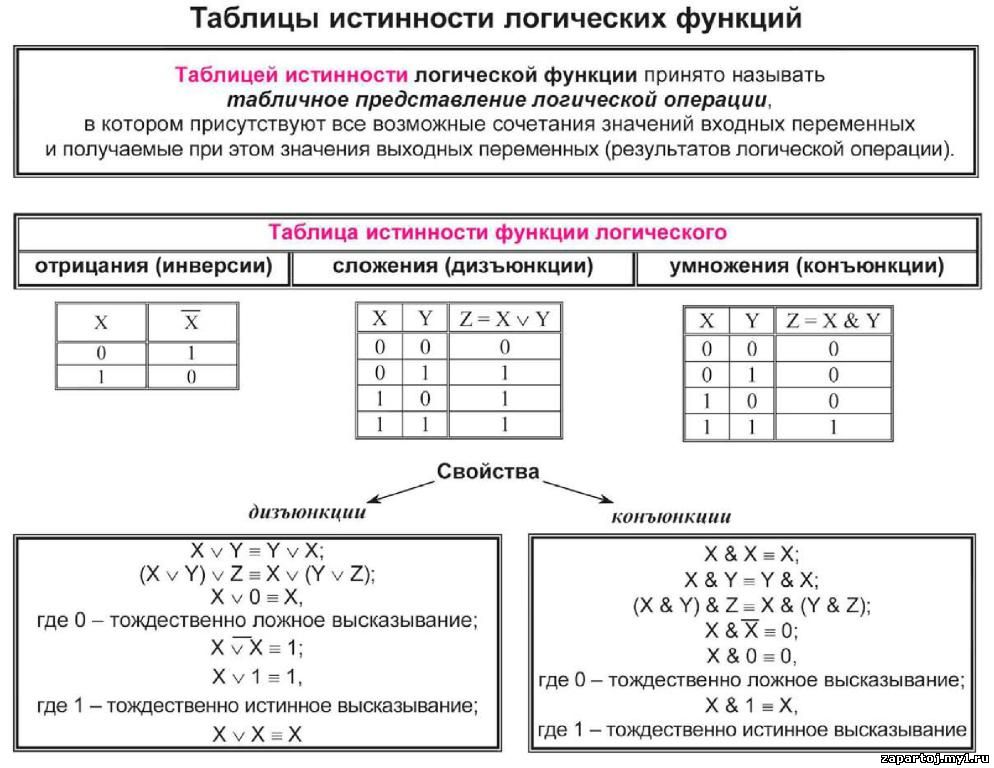
Высказывание будет ложным только в том случае, если ложны и А, и В.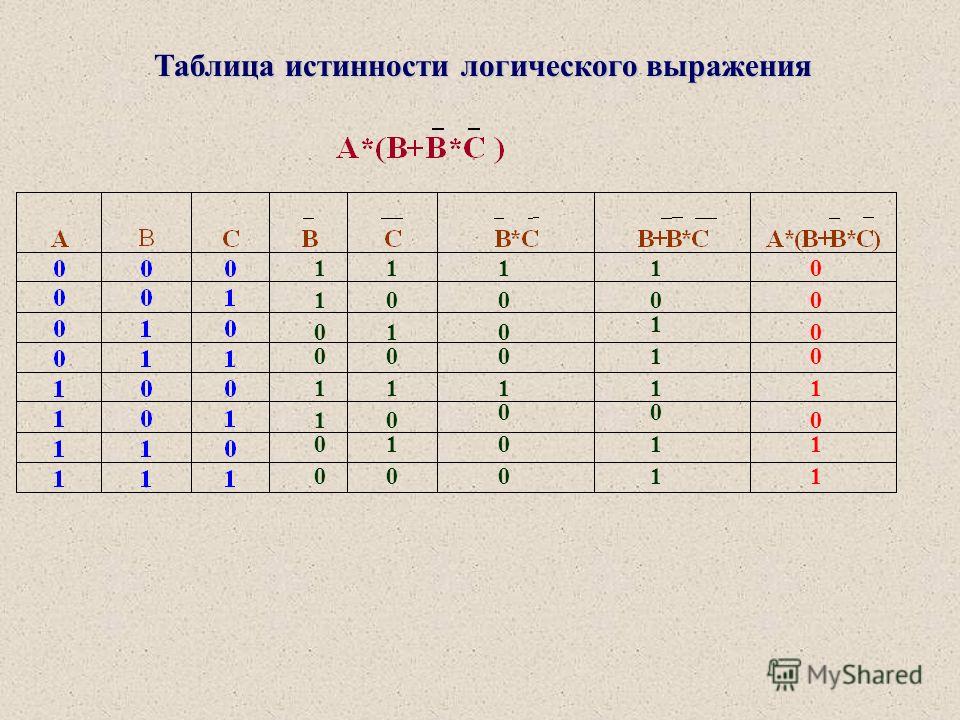 Построим еще одну таблицу истинности и решим выражение F=X∨Y∧¬ZF=X∨Y∧¬Z
Построим еще одну таблицу истинности и решим выражение F=X∨Y∧¬ZF=X∨Y∧¬Z
 }\)
}\) }\)
}\)
 ЛОЖЬ.
ЛОЖЬ.

 }\)
}\) }\)
}\)
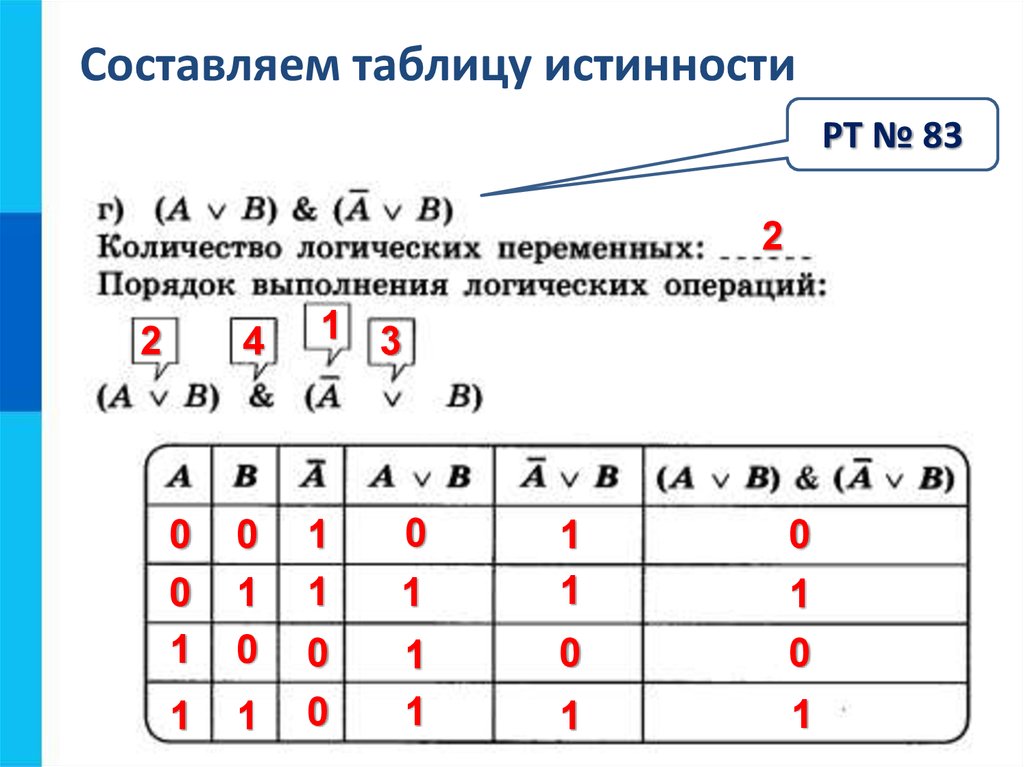 Эти случаи могут быть
перечислены следующим образом в так называемой таблице истинности .
Эти случаи могут быть
перечислены следующим образом в так называемой таблице истинности .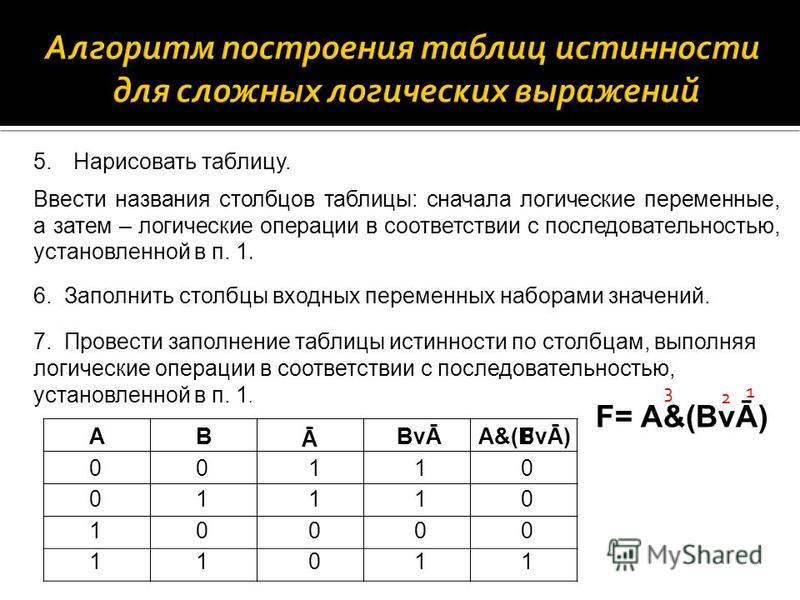 Его можно рассматривать как «минимальный
общее логическое значение» для соединенных утверждений.
Его можно рассматривать как «минимальный
общее логическое значение» для соединенных утверждений.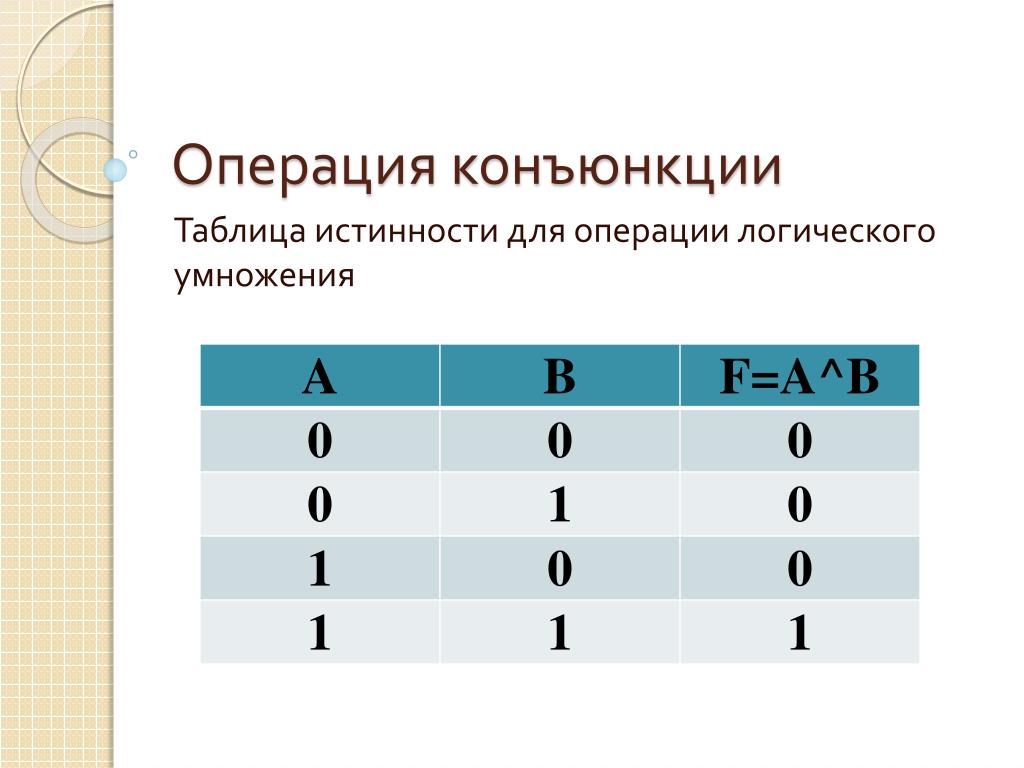
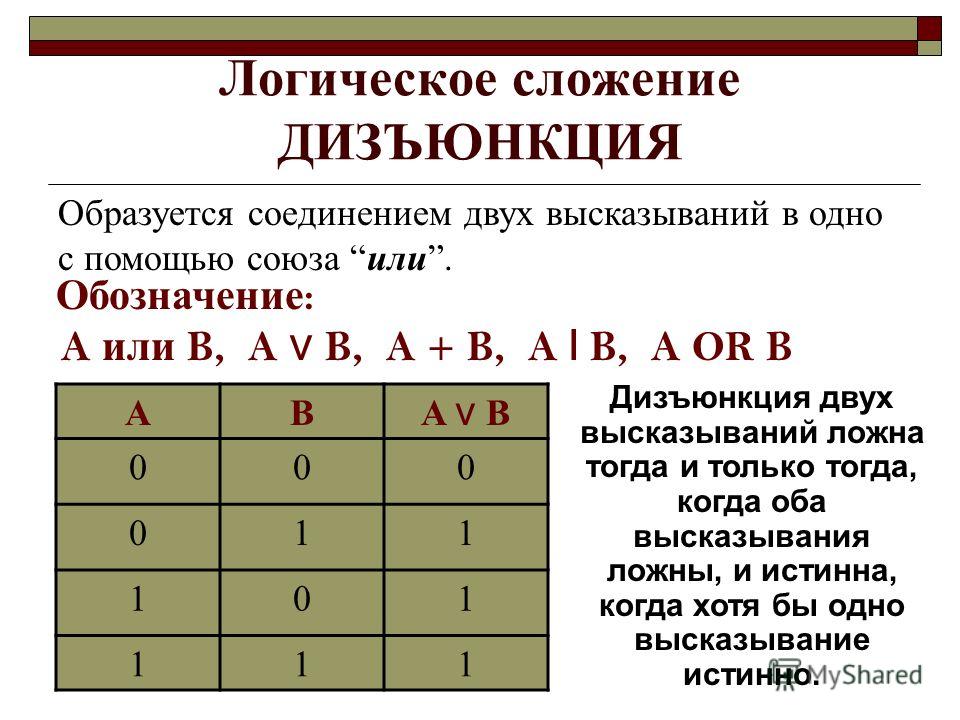
 которые ложны, только если оба утверждения (дизъюнкты) ложны.
которые ложны, только если оба утверждения (дизъюнкты) ложны.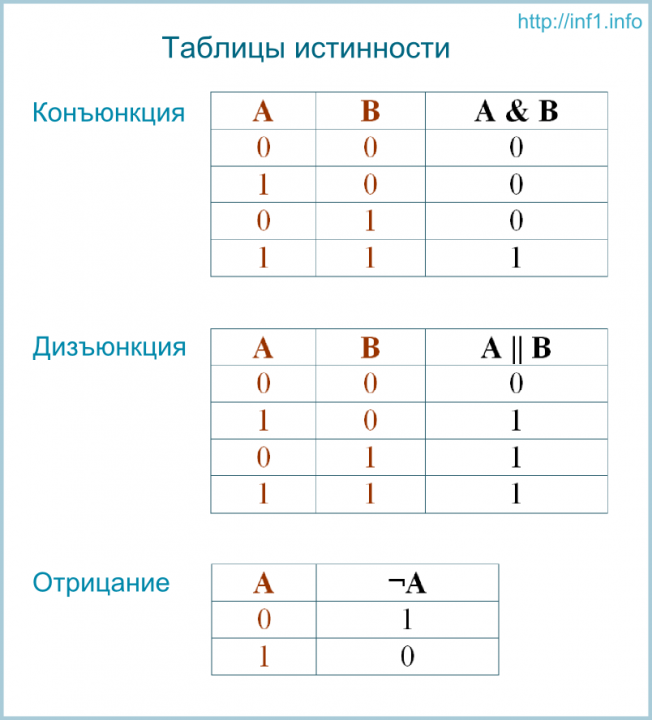 » Если в этом примере Джон не на
библиотека и Джон не учится, то истинность сложного утверждения
неверно:
» Если в этом примере Джон не на
библиотека и Джон не учится, то истинность сложного утверждения
неверно: