Принципы построения таблиц истинности
Оглавление
Время чтения:: 5 минут
492
Логическая функция одно из основополагающих понятий математической логики. Она зависит от логических переменных и принимает значения из множества, от которого находится в зависимости. Логические функции булевых переменных могут принимать только два значения – 1 или 0.
Понятие таблиц истинности
Задаваться логическая функция может числовым способом, словесным описанием, картами Карно, аналитическим выражением и с помощью таблиц истинности. В последнем случае все аргументы функции следует записать в левой части таблицы, а значения, которые им соответствуют, в правой.
Определения 1 — 2
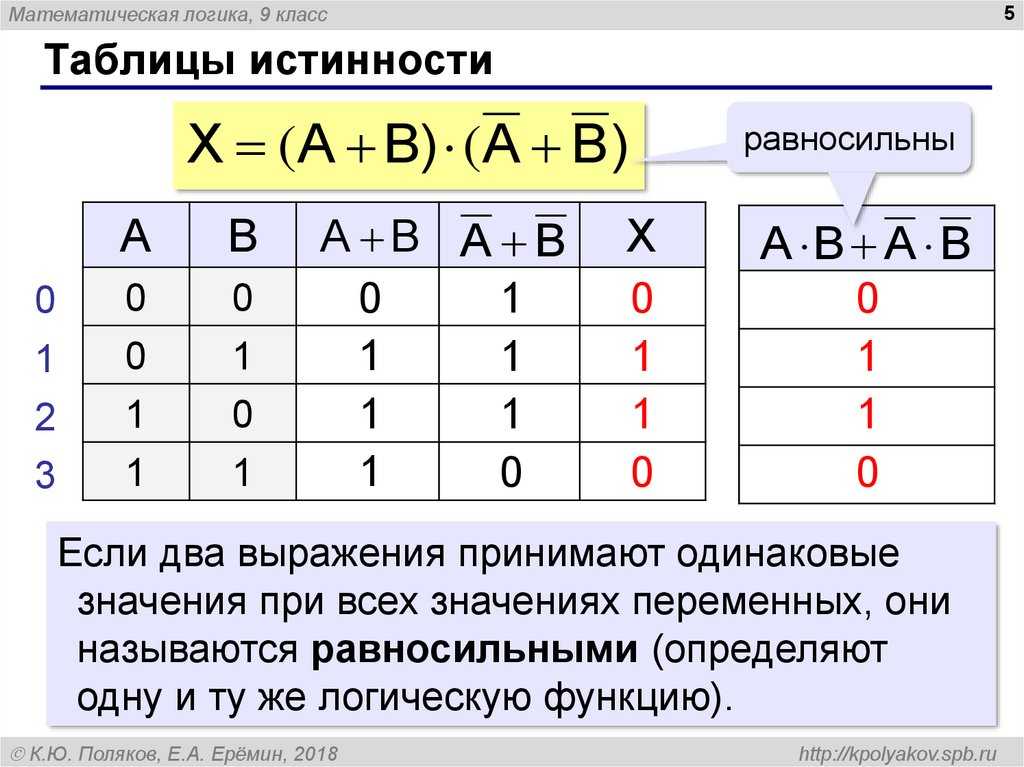
Таблица истинности – это таблица, просто и наглядно показывающая, какие значения будут у логического выражения при всевозможных наборах переменных функции.
Равносильными именуют те логические выражения с совпадающими последними столбцами таблицы истинности. Обозначают равносильные функции знаком «=».
Обозначают равносильные функции знаком «=».
Правила того, как следует проводить построение таблицы истинности
Несоблюдение хотя бы одного из них ведёт к очень грубой ошибке. Вот эти правила:
- Число строк таблицы должно совпадать с числом комбинаций всевозможных n логических переменных, то есть быть равным 2n;
- Количество столбцов таблицы должно равняться сумме числа логических переменных и числа логических операций;
- В построенный шаблон таблицы истинности должны вписываться все значения исходных переменных;
- Построение таблицы истинности выражения происходит по её столбцам, при этом обязательно учитываются правила логических операций.
Порядок действий при построении таблицы истинности для логических выражений
Порядок действий при построении таблицы истинности, какой бы ни была логическая функция, следующий:
- Определить, какое число строк и столбцов будет в будущей таблице. Делается подобное по формулам
X = n + m, Y = 2n+1.
Где n – число переменных, m – чило логических операций. - Заполнить самую верхнюю строку таблицы переменными и логическими операциями, идя слева направо. При этом приоритетность логических операций следует учитывать обязательно, иначе получится совсем не то, что нужно;
- В первых столбцах перечислить всевозможные комбинации входных значений;
- Выполняя заданные логические операции, заполнить все оставшиеся ячейки;
Ответом следует считать последний заполненный столбец таблицы.
О порядке логических операций
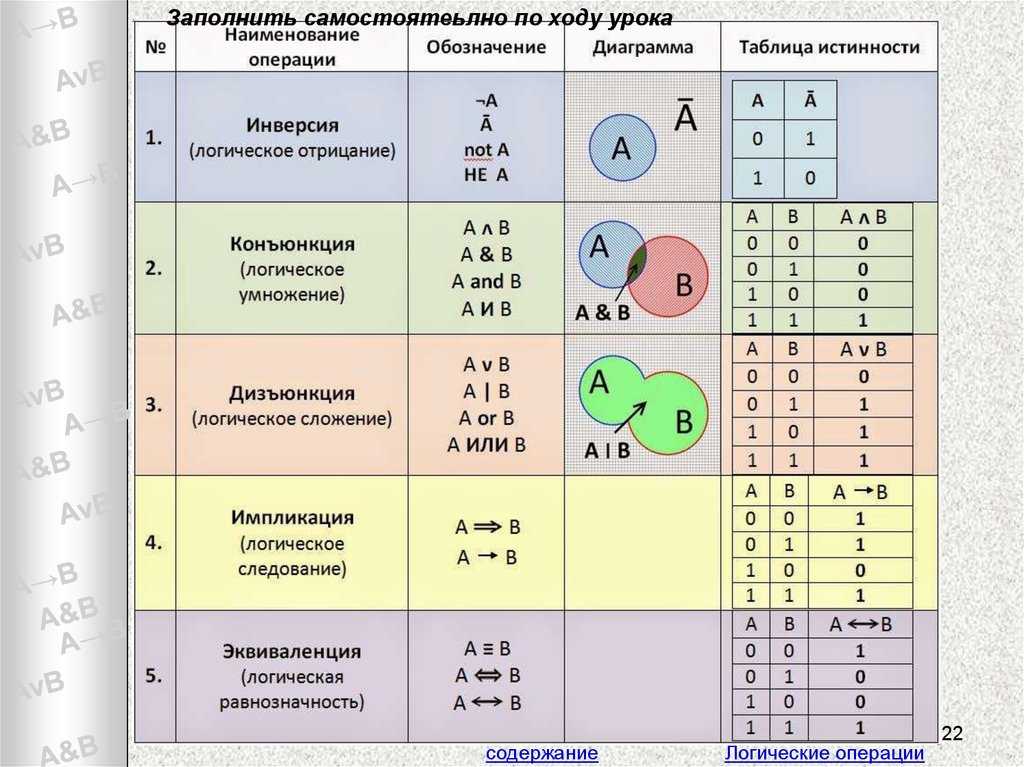
Лучше его представить списком. Логические операции выполняют в следующей последовательности: сначала идёт инверсия, затем конъюнкция, после этого дизъюнкция, после неё импликация, по её выполнении эквиваленция.
После них идут Штрих Шеффера и Стрелка Пирса. Первым может быть выполнено как то, так и другое.
Далее приведём несколько поучительных задач на построение таблиц истинности
Задачи 1 — 3
Сделать построение таблицы истинности для функции ((A→B) ∧ A) ↔ B
Решение:
- Определяем сколько будет у нас столбцов.
 Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.
Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6. - Определяем, сколько будет у на строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций. У нас будет 2n+1 = 22 + 1= 5;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В двух первых столбцах записываем возможные значения переменных;
- В далее идущих столбцах записываем, какие значения принимают промежуточные функции;
- В самом последнем из столбцов записываем итоговые значения функции.
- Определяем сколько будет у нас столбцов.
В результате всего этого у нас должно получиться:
Провести построение таблицы истинности функции (A ∨ B) ∧ – C
Решение:
- Определяем сколько будет столбцов. Количество переменных у нас 3, количество логических операций 3.

- Определяем, количество строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций.В итоге будет 2n+1 = 23 + 1= 9;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В два первые столбца вносим возможные значения наших переменных;
- В далее следующие столбцы записываем, какие значения принимают промежуточные функции;
- В последнем столбце записываем итоговые значения функции.
В итоге получим таблицу:
Сделать таблицу истинности для
(A ∧ B ↔ B ∧ C) ∨ (C → A)
Функция посложнее и таблица получится значительно больше, чем предыдущая.
- Считаем столбцы. Количество переменных 3, количество логических операций 6. Значит столбцов будет 3+6=9;
- Считаем строки. Их количество будет 23+1= 9;
- Заполняем первую строку таблицы;
- В первых столбцах записываем все допустимые значения наших переменных;
- В остающихся столбцах пишем, какие наша функция принимает промежуточные значения
- В последний столбец пишем итоговые значения данной нам функции.

В итоге у нас получается таблица:
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Построения функции, если известна её таблица истинности
Совершенной дизъюнктивной нормальной формой считают такую нормальную форму, в которой отсутствуют одинаковые элементарные конъюкции и все конъюкции включают один и тот же набор переменных, куда каждая из них входит не более одного раза.
Алгоритм действий для получения СДНФ по таблице истинности:
- Отметьте в таблице строки, в которых значение функции равняется 1
- Выпишете для каждой отмеченной строки конъюкцию всех переменных. Если переменная равна 1, в конъюкцию следует включить саму эту переменную. Если переменная равняется 0, то её отрицание;
- Все полученные конъюкции свяжите в дизъюкцию.
Аналогичным образом определяется СКНФ
В строках, в последнем столбце которых функция равна 0, запишите дизъюкции всех переменных. Если значение переменной в данной строке будет 0, в дизъюкцию следует включить саму эту переменную. Если значение функции равно 1, то включить нужно её отрицание.
Если значение переменной в данной строке будет 0, в дизъюкцию следует включить саму эту переменную. Если значение функции равно 1, то включить нужно её отрицание.
Правило + задача
СДНФ всегда равно СКНФ. СДНФ = СКНФ.
Дана таблица истинности:
Выделяем в ней цветом строку
Заполняем столбцы с СДНФ и с СКНФ
Записываем СДНФ
СДНФ = A & B
Записываем СКНФ
СКНФ = (A ∨ B) & (A ∨ B) & (A ∨ B)
Оценить статью (79 оценок):
Поделиться
Жанна Ивановна Конева — Магистр прикладной информатики
Популярные статьи
Выполнение любых работ по информатике
4. Логические выражения и таблицы истинности
13
4.1.Логические выражения
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.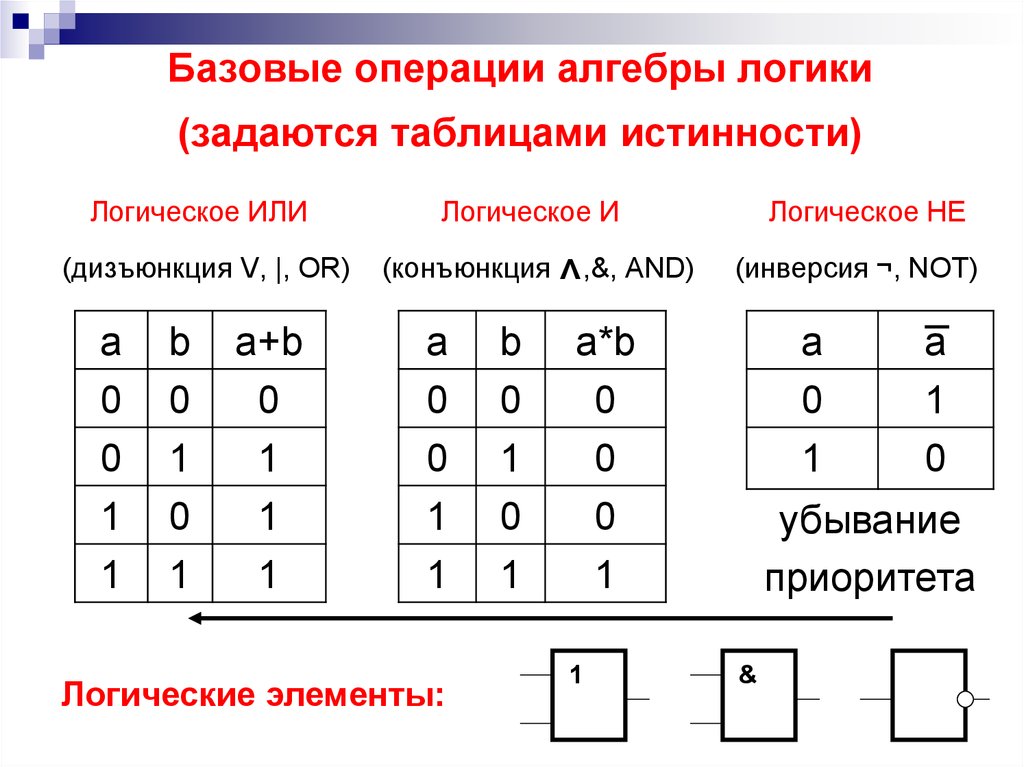
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание
«(2·2=5 или 2·2=4) и (2·2≠5 или 2·2≠4)».
Проанализируем составное высказывание. Оно содержит два простых высказывания:
А = «2•2=5»—ложно (0), В = «2•2=4»—истинно (1).
Тогда составное высказывание можно записать в следующей форме: «(А или В) и (Ā или В)».
Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:
инверсия, конъюнкция, дизъюнкция.
Для изменения указанного порядка могут использоваться скобки:
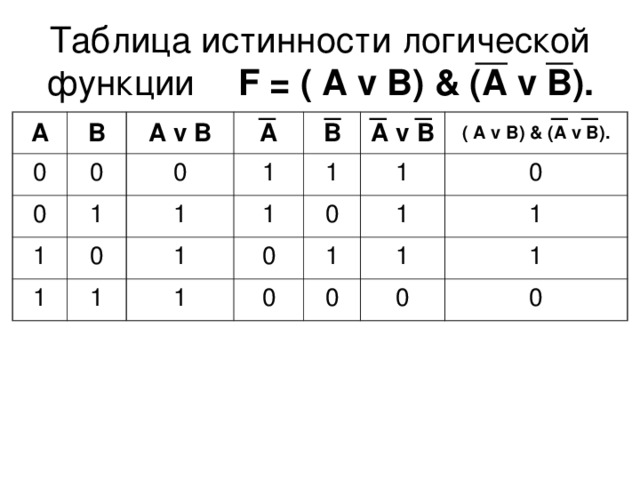
F = (A v В) & (Ā v В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.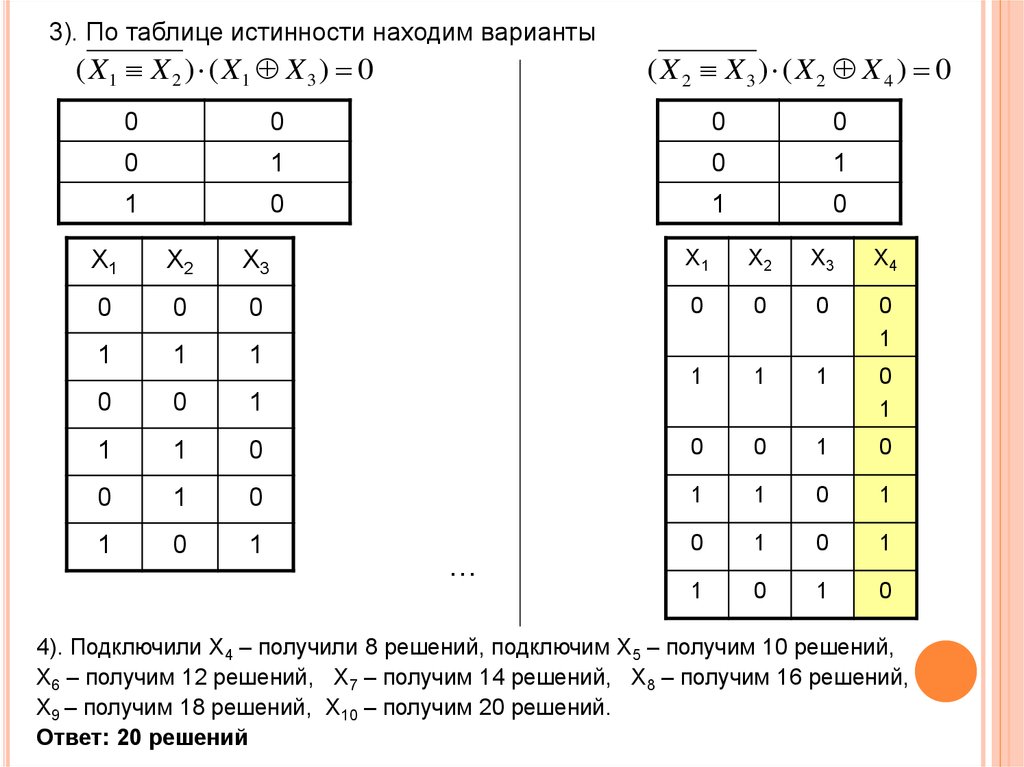
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F = (A v В) & (Ā v В) = (0 v 1) & (1 v 0) = 1 & 1 = 1.
14
4.2.Таблицы истинности
Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.
Простые высказывания обозначаются переменными (например, A и B).
При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:
1) необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
В нашем случае логическая функция имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;
2)необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;
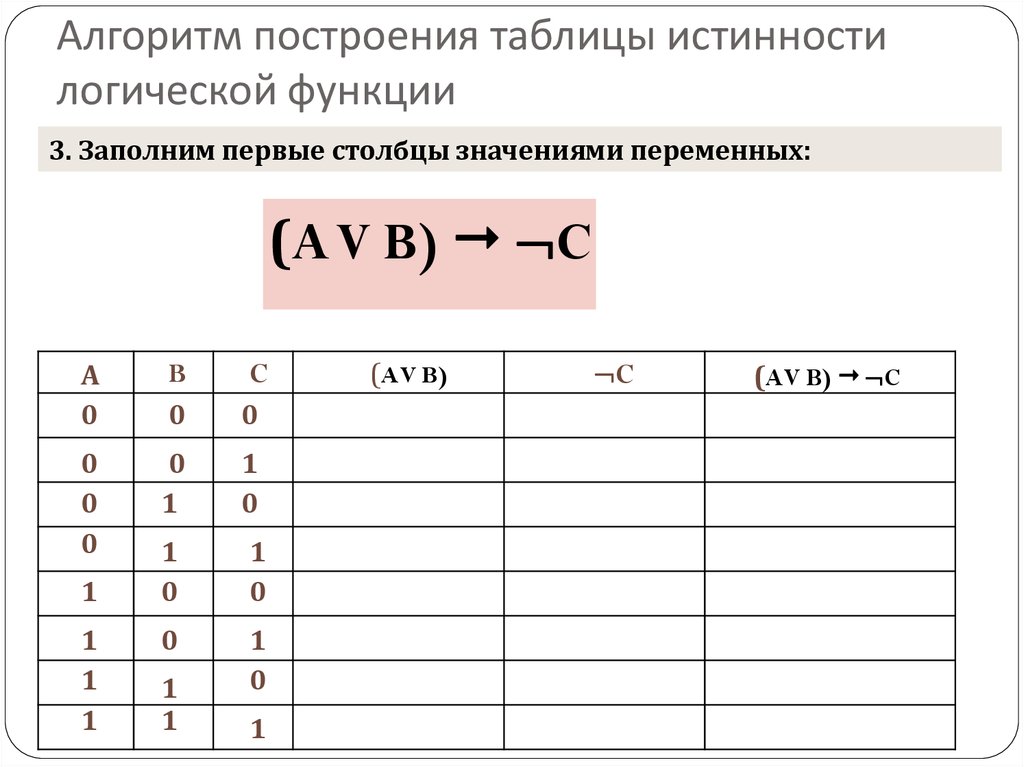
3)необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;
4)необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
15
Таблица 8 – Таблица истинности логической функции
4.3.Равносильные логические выражения
Логические выражения, у которых последние столбцы таблиц истинности сов-
падают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Докажем, что логические выражения равносильны. Построим сначала таблицу истинности логического выражения (табли-
Построим сначала таблицу истинности логического выражения (табли-
ца 9).
Таблица 9 – Таблица истинности логического выражения
А | В |
|
|
|
|
|
|
|
|
0 | 0 | 1 | 1 | 1 |
|
|
|
|
|
0 | 1 | 1 | 0 | 0 |
|
|
|
|
|
1 | 0 | 0 | 1 | 0 |
|
|
|
|
|
1 | 1 | 0 | 0 | 0 |
|
|
|
|
|
Теперь построим таблицу истинности логического выражения (таблица 10).
Таблица 10 – Таблица истинности логического выражения
А | В | А v В |
|
|
|
|
|
0 | 0 | 0 | 1 |
|
|
|
|
0 | 1 | 1 | 0 |
|
|
|
|
1 | 0 | 1 | 0 |
|
|
| |
1 | 1 | 1 | 0 |
|
|
|
|
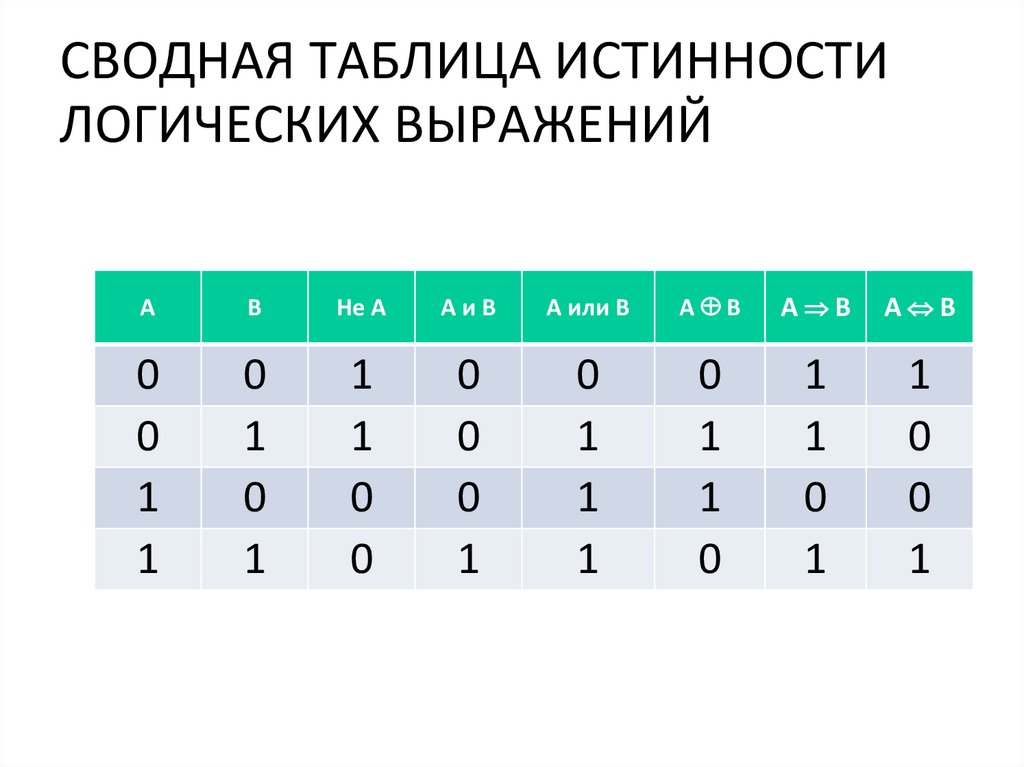
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:
=.
16
5. Построение таблиц истинности для сложных выражений
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений
переменных всего четыре: |
| ||
(0, 0), | (0, 1), | (1, 0), | (1, 1). |
Если формула содержит три переменные, то возможных наборов значений
переменных восемь: |
|
|
|
|
|
| |
(0, 0, 0), | (0, 0, 1), | (0, 1, 0), | (0, 1, 1), | (1, 0, 0), | (1, 0, 1), | (1, 1, 0), | (1, 1, 1). |
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Пример 1 1. Составим таблицу истинности для формулы, которая содержит две пере-
менные X и Y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 11:
Таблица 11 – Таблица истинности для формулы с переменными Х и У
Пример 2
Cоставить таблицу истинности сложного логического выражения: D = неA & (B+C).
А, В, С – три простых высказывания, поэтому:
количество строк = 23 +2 = 10 (n=3, т.к. на входе три элемента А, В, С) количество столбцов (таблица 12):
1)А,
2)В,
Таблицы истинности — KnowItAllNinja
Мы рассмотрели, как можно изобразить логические схемы в виде диаграмм с входами и выходами.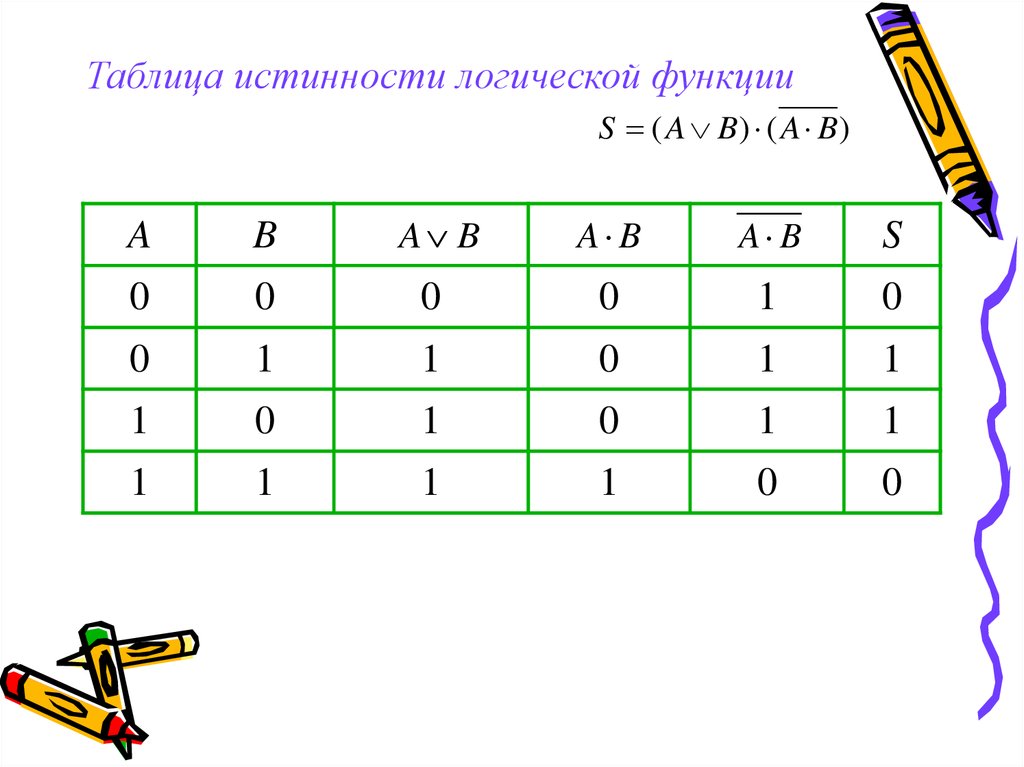 Другой способ представить их — нарисовать схему в виде таблицы истинности.
Другой способ представить их — нарисовать схему в виде таблицы истинности.
Таблица истинности представляет собой простую сетку, которая показывает все входные данные и все возможные выходные данные. Мы можем использовать их, чтобы понять, что делает наша схема. Это особенно полезно, когда мы начинаем комбинировать логические вентили.
Мы также можем выразить наши логические вентили с помощью булевой алгебры, где мы записываем логику наших вентилей в виде логического выражения.
В этом уроке мы узнаем о:
- Что такое таблицы истинности
- Таблица истинности для вентиля НЕ
- Таблица истинности для вентиля И
- Таблица истинности для вентиля ИЛИ
Медиа Приложения: Презентационное видео
1. Что такое таблицы истинности
Таблицы истинности используются для отображения выходных данных логического элемента и логических схем (где мы объединяем более одного логического элемента вместе).
Мы создаем их, рисуя таблицу со столбцами для каждого из входов и выходов в нашей логической схеме.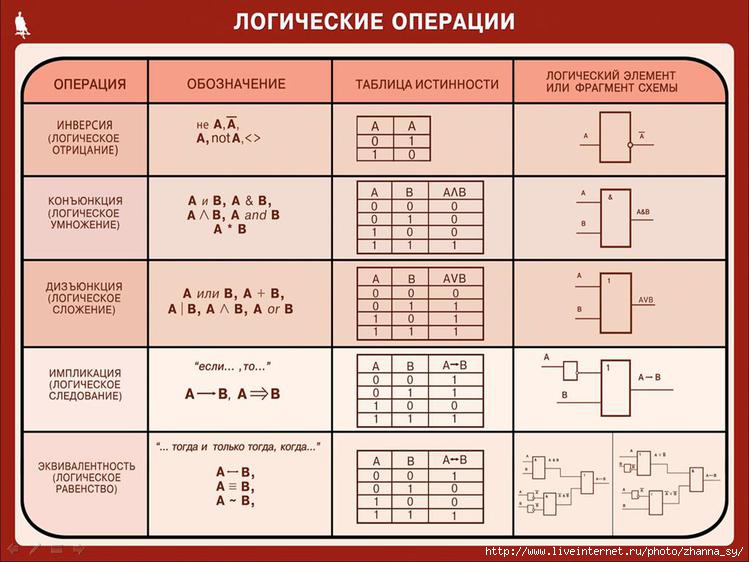 В таблице также должно быть достаточно строк для представления всех возможных комбинаций входных данных.
В таблице также должно быть достаточно строк для представления всех возможных комбинаций входных данных.
Например, если у вас есть два входа (которые всегда являются двоичными числами), то у нас могут быть следующие комбинации: четыре строки в нашей таблице истинности.
Таблицы истинности становятся чрезвычайно важными, когда мы начинаем проектировать более крупные схемы, чтобы помочь нам точно определить, какие выходные данные производятся этими комбинациями вентилей.
Дополнительные мысли
Мы часто выражаем схемы булевой логики с помощью булевой алгебры. Изучите, что это такое.
2. Таблица истинности для вентиля НЕ
Мы видели, как вентиль НЕ представлен в виде логической схемы. Это выглядит как на рисунке 1 ниже.
Рисунок 1. Шлюз НЕ.Существует только ОДИН возможный вход, который может быть либо 1, либо 0.
Мы рисуем это в виде таблицы истинности следующим образом: 1
Вот и все.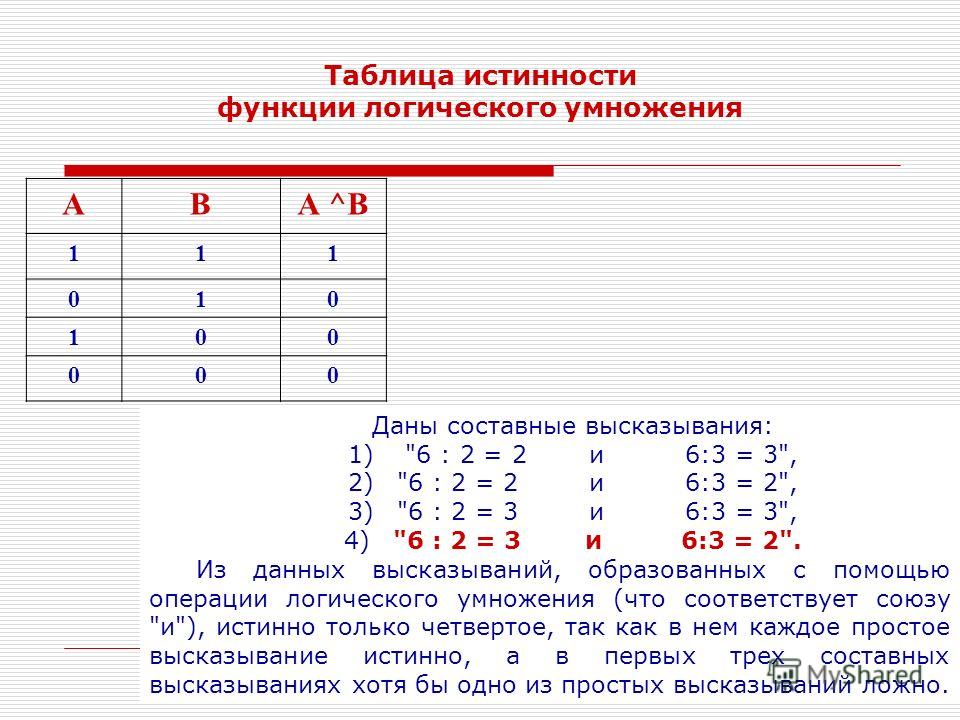 Если вы введете 1, на выходе будет 0. Если вы введете 0, на выходе будет 1.
Если вы введете 1, на выходе будет 0. Если вы введете 0, на выходе будет 1.
Таблица истинности имеет ОДИН вход, который может иметь ДВЕ ВОЗМОЖНЫЕ КОМБИНАЦИИ, поэтому в таблице истинности есть ДВЕ строки.
Если бы мы хотели записать это как логическое выражение, мы могли бы написать это как Q = NOT X.
Дополнительные мысли
Что произойдет, если вы объедините логический элемент НЕ с логическим элементом И или ИЛИ?
3. Таблица истинности для вентиля И
Мы видели, что схема И представляет собой два переключателя один за другим.
Свет будет гореть, только если ОБА переключателя замкнуты.
Рисунок 2 – схема И с обоими замкнутыми переключателями.Если свет горит, это означает, что у нас есть выход 1.
Мы нарисовали это как логический элемент И на логической схеме, как показано на рисунке 3.
Рисунок 3 – логический элемент И Для этой таблицы истинности мы можем видим, что у нас есть два входа с двумя возможными комбинациями, поэтому у нас есть ЧЕТЫРЕ строки в таблице истинности.
Чтобы построить таблицу истинности, нужно записать все возможные комбинации входных данных. Поскольку у нас есть два входа двоичных чисел, каждое из них может быть 1 или 0. Итак, все комбинации следующие:
| Вход X | Вход Y | Выход Q | 1 |
|---|---|---|
| 1 | 0 | |
| 0 | 1 | |
| 0 | 0 |
После того, как мы настроили нашу таблицу истинности с нашими входными данными, мы можем записать наши выходные данные. Помните, что с логическим элементом И мы получаем выход 1 только в том случае, если ОБА входа равны 1.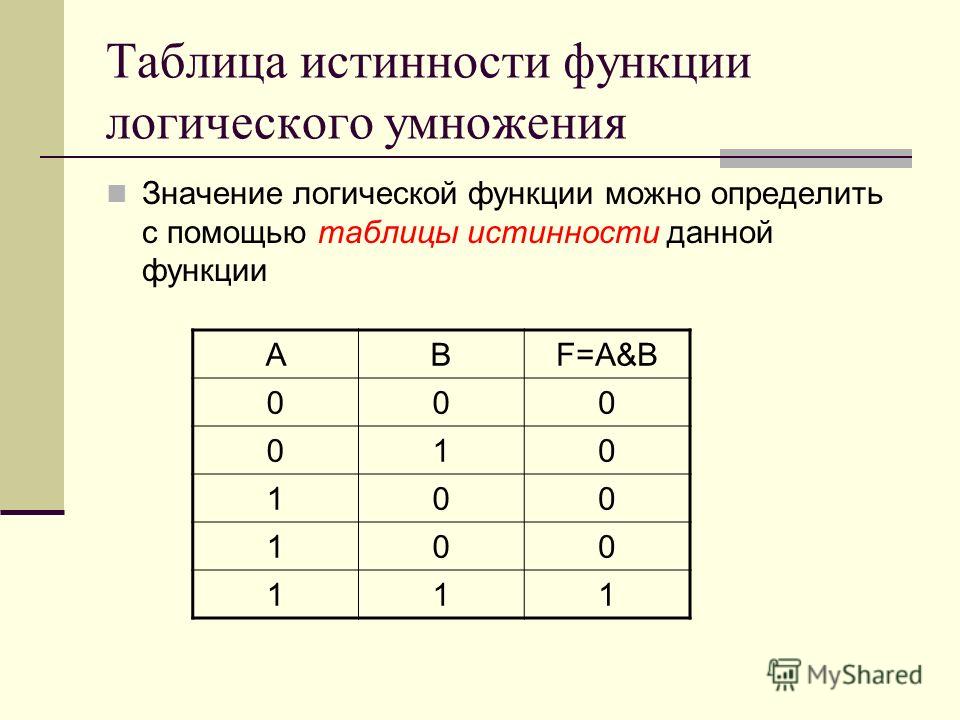 В противном случае выход равен 0.
В противном случае выход равен 0.
, если мы хотели написать это как логовое выражение, мы можем написать это как Q = x
Сколько строк у вас было бы, если бы у вас было 3 входа?
4. Таблица истинности для схемы ИЛИ
Мы видели, что схема ИЛИ представляет собой два переключателя, включенных параллельно.
Если замкнут ОДИН из выключателей, загорится свет.
Рисунок 4 – схема ИЛИ с одним замкнутым переключателем и одним разомкнутым переключателем.Мы нарисовали это как вентиль ИЛИ на логической схеме, как показано на рисунке 5.
Рисунок 5 – Логический вентиль ИЛИ Для этой таблицы истинности нам снова нужно записать все возможные комбинации входных данных. Поскольку он имеет два входа, он имеет те же комбинации, что и для логического элемента И.
Поскольку он имеет два входа, он имеет те же комбинации, что и для логического элемента И.
| Вход X | Вход Y | Выходные0121 |
|---|---|---|
| 0 | 1 | |
| 0 | 0 |
. Помните, что с вентилем ИЛИ мы получаем на выходе 1, если ОДИН ИЛИ ОБА входа равны 1. В противном случае выход равен 0.
 как Q = X OR Y.
как Q = X OR Y.Дополнительные мысли
Существует такая вещь, как вентиль исключающее ИЛИ. Чем это отличается от стандартных ворот ИЛИ?
Итоги урока
Итак, подведем итог тому, что мы узнали на этом уроке:
- Таблицы истинности — это способы суммирования вывода любого входа в логическую схему.
- При заполнении таблицы истинности мы должны сначала определить все возможные комбинации входных данных.
- Вывод таблицы истинности НЕ противоположен вводу.
- Выход таблицы истинности по И равен 1, когда оба входа равны 1, в противном случае он равен 0.
- Выход таблицы истинности по ИЛИ равен 0, когда оба входа равны 0, иначе он равен 1.
Продолжить …
анализ цепей — Реализация логического выражения и таблица истинности логической функции
спросил
Изменено 3 года, 8 месяцев назад
Просмотрено 242 раза
\$\начало группы\$
(a) Выражение для \$Z\$
\$Z=(B+\overline{C})A+B(C+\overline{D})+BD\$
\$Z=AB+A\overline{C}+BC+B\overline{ D}+BD\$
\$Z=AB+\overline{A}C+B\$
\$Z=B+A\overline{C}\$
(b) Таблица истинности
A B C | | Z ========== 0 0 0 || 0 0 0 1 || 0 0 1 0 || 1 0 1 1 || 1 1 0 0 || 1 1 0 1 || 0 1 1 0 || 1 1 1 1 || 1
(c) Карта Карно
| БК 00 01 11 10
------------------------
А 0 | 0 1 1 1
1 | 1 0 1 1
903:60 Я был уверен в том, о чем мне задавали последние два вопроса (d) и (e).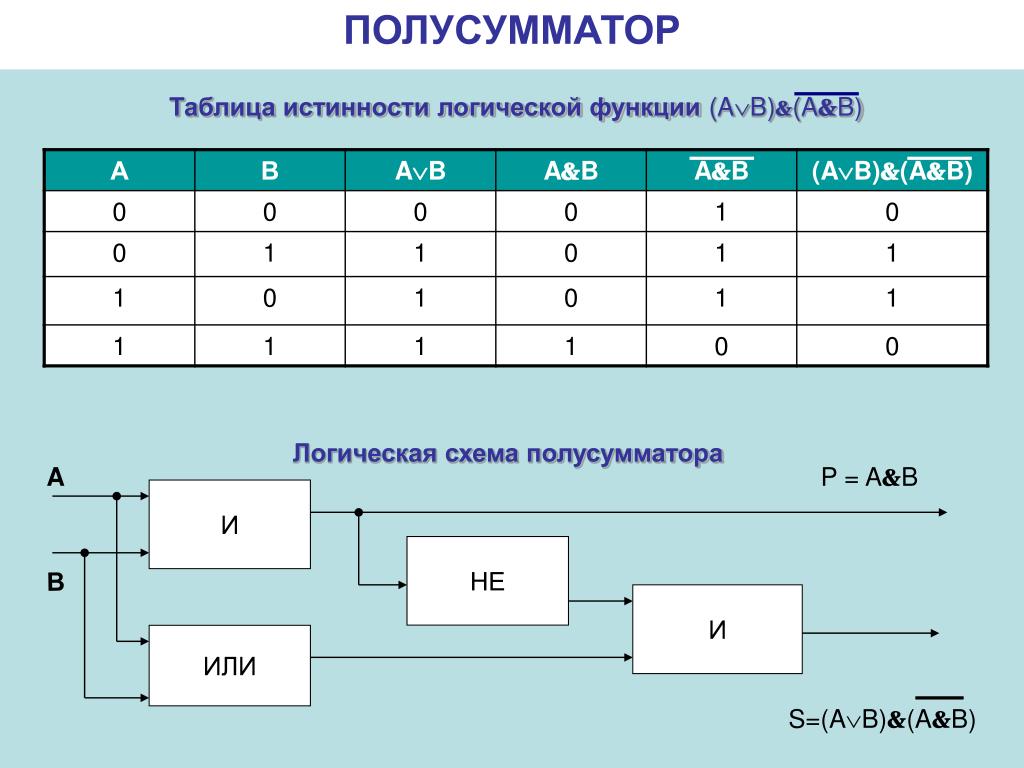 Может ли кто-нибудь дать некоторые рекомендации о том, как решить эти последние два вопроса? Заранее спасибо.
Может ли кто-нибудь дать некоторые рекомендации о том, как решить эти последние два вопроса? Заранее спасибо.
- анализ схем
- цифровая логика
- логические элементы
- булева алгебра
\$\конечная группа\$
3
\$\начало группы\$
Вы, наверное, уже знаете, что любой логический вентиль можно построить с помощью вентилей И-НЕ. Это часто делается, потому что вентили NAND легко построить.
В г) задача состоит в том, чтобы перестроить эту схему, только используя вентили И-НЕ.
В д) задача состоит в том, чтобы найти критический (он же самый длинный) путь в вашей схеме и вычислить его задержку распространения, используя заданную задержку распространения одиночных вентилей.
\$\конечная группа\$
\$\начало группы\$
Согласно ДеМоргану, логический элемент НЕ-И может использоваться для реализации операции типа ИЛИ.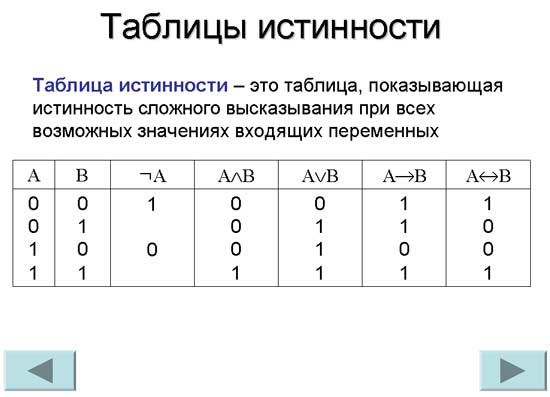



 Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.
Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.