03.4. Основные логические операции над высказываниями
Прежде чем перейти к определению логических операций и связок, посредством которых образуются сложные высказывания из простых, необходимо руководствоваться следующими допущениями.
1. Любое высказывание в классической логике имеет одно и только одно из двух значений истинности – «истину» или «ложь». С этой точки зрения истинностное значение будущих событий остается неопределенным.
2. Значение истинности сложного высказывания зависит исключительно от истинностных значений входящих в него простых высказываний. Поэтому истинностное значение сложного высказывания представляет собой функцию истинности от образующих его простых высказываний.
3. При образовании сложных высказываний учитывается лишь истинностное значение входящих в него простых высказываний, а не их смысл.
Определение логических операций
Простейшей из логических операций является Отрицание, с помощью которого из данного высказывания образуется противоречащее ему высказывание.
Для определения отрицания используется матрица (таблица) истинности, в которой в левой колонке даются два значения истинности («истина» и «ложь») первоначального высказывания, а в правой колонке – его отрицания (табл.
1). Истинность высказывания будет обозначаться буквой «и» или числом 1, ложь – буквой «л» и числом 0.
Если высказывание истинно, то противоречащее ему высказывание будет ложно, и, наоборот, если высказывание ложно, то противоречащее высказывание будет истинно.
Конъюнкция (логическое произведение) двух или нескольких простых высказываний образуется путем их объединения логической связкой «и». Например, если обозначить одно из простых высказываний буквой Х, а другое – У, тогда их конъюнкцией будет сложное высказывание «х и у» или «х Ù у», где знаком Ù обозначен конъюнктивный оператор (логическая связка). Простые высказывания, входящие в сложное, называются Конъюнктивными членами.
Конъюнкция будет считаться истинной, если и только если все ее конъюнктивные члены будут истинными. Наличие хотя бы одного ложного члена превращает всю конъюнкцию в ложное высказывание. Исходя из этого нетрудно построить таблицу истинности для конъюнкции (табл.
Дизъюнкция (логическая сумма) двух или нескольких простых высказываний образуется путем объединения их логической связкой «или». Союз «или» в языке чаще всего употребляется в исключающем смысле, когда происходит выбор между двумя альтернативами: либо одно, либо другое. Реже используется этот союз в неисключающем смысле, т. е. выражается словом «а также». В логике и математике связка «или» употребляется преимущественно в неисключающем смысле. Так, например, дизъюнкция «2 меньше 3 или 3 меньше 5» понимается в неисключающем смысле, так как не только 2, но и 3 меньше 5.
Неисключающая дизъюнкция считается ложной в том и только в том случае, когда все ее дизъюнктивные члены будут ложными. Поэтому достаточно одного истинного члена, чтобы дизъюнкция была истинной. Исключающая дизъюнкция истинна тогда, когда только один из ее членов является истинным, а другой – ложным. Она будет ложной, если оба ее члена одновременно истинны либо ложны. Оператор дизъюнкции обозначается символом Ú – для неисключающей дизъюнкции и символом Ú – для исключающей дизъюнкции.
Операция Импликации состоит в образовании сложного высказывания из двух простых высказываний посредством логической связки, обозначаемой словами «если…, то… » и приблизительно соответствующей условному предложению в естественном языке. В логике эту связку называют Импликацией, и мы будем обозначать ее стрелкой.
Условное высказывание состоит из двух простых высказываний. То из них, которое вводится словом «если», называется Антецедентом (предыдущим высказыванием), а также основанием, а начинающееся словом «то» – Консеквентом (последующим высказыванием) или следствием условного высказывания.
В науке и повседневном мышлении условные высказывания употребляются для установления связи между высказываниями, которые могут иметь различную форму. С помощью понятий антецедента и консеквента определяются необходимые и достаточные условия.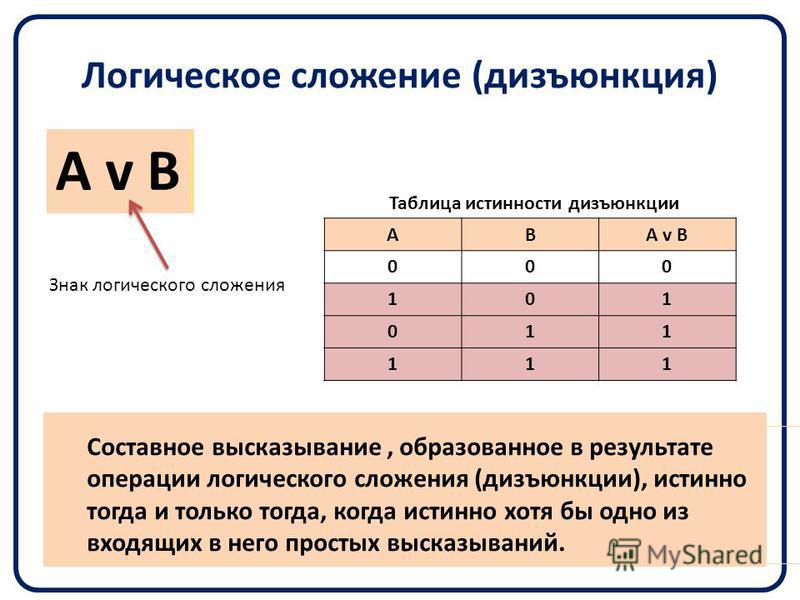
Так, антецедент есть достаточное условие (основание) для консеквента (следствия). Например, в высказывании «Если треугольник имеет равные стороны, то и все его углы будут равны» условие равенства сторон служит достаточным условием (основанием) для следствия – равенства его углов. Одновременно с этим можно сказать, что следствие является необходимым условием для основания, так как «Равенство углов треугольника есть необходимое условие для равенства его сторон».
В обычной речи часто не проводят различия между основанием и следствием, как логическим отношением, и причиной и следствием, как отношением реального мира. Убедиться в наличии причинной связи можно лишь путем конкретного исследования явлений окружающего нас мира. Если одно явление вызывает или порождает другое явление, то первое из них мы называем причиной, а второе – следствием. Так, нагревание стержня – причина – вызывает его удлинение – следствие. Эту зависимость мы устанавливаем эмпирически – путем наблюдения и измерения.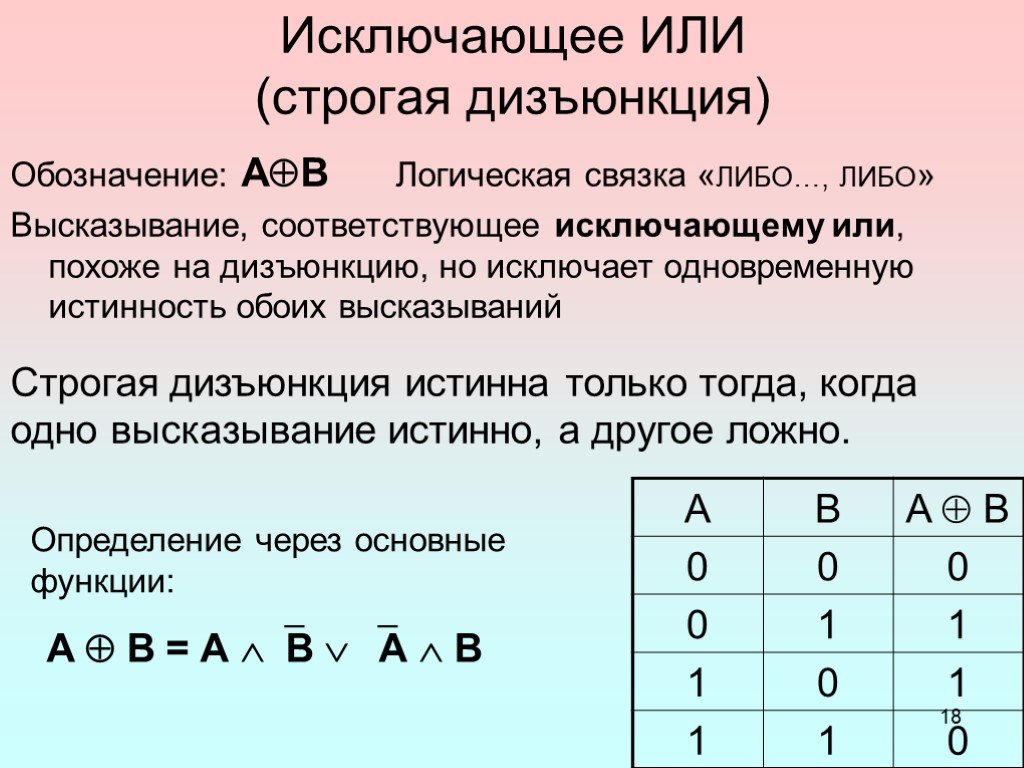
Условные высказывания употребляются для выражения самых разнообразных отношений между высказываниями, но не во всех случаях при этом учитывается их содержание и смысл. В современной логике обращается внимание исключительно на связь между высказываниями по значению их истинности, потому что задача логики состоит в том, чтобы гарантировать истинность заключения из истинных посылок, а для этого необходимо перенести истинность с посылок на заключение. В связи с этим в логической импликации абстрагируются (отвлекаются) от содержания и смысла и обращают внимание только на связь высказываний по значению их истинности. В результате можно рассматривать импликации, которые выглядят бессмысленными и парадоксальными с точки зрения обычного, здравого смысла.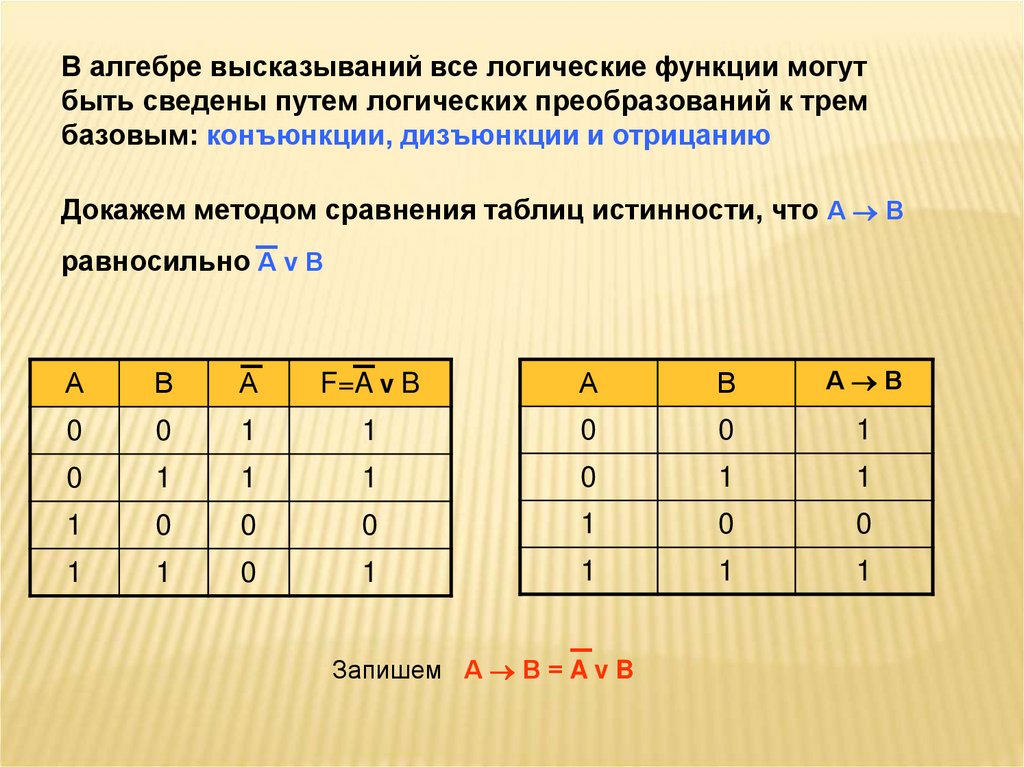
Таким образом, импликация учитывает все случаи распределения значений истинности и считается ложной только тогда, когда ее антецедент истинен, а консеквент ложен.
Например, импликация «Если 2 х 2 = 4, то Москва – небольшой город» является ложной, так как ее антецедент – истинное высказывание, а консеквент – ложное.
Отсюда ясно, что импликация выражает важнейшее свойство правильных рассуждений. Известно, что из истинных посылок нельзя получить ложное заключение, если рассуждать правильно. Этот фундаментальный принцип лежит в основе всей дедуктивной логики и сохраняется при определении операции импликации.
Распределение значений истинности высказываний для импликации представлено табл.4, где стрелка обозначает импликацию.
Резкое расхождение между употреблением условных высказываний в естественной речи и современной логике породило немало споров и дискуссий, в которых логиков обвиняли в том, что они не учитывают смысловой связи между высказываниями, и поэтому приходят к бессмыслице.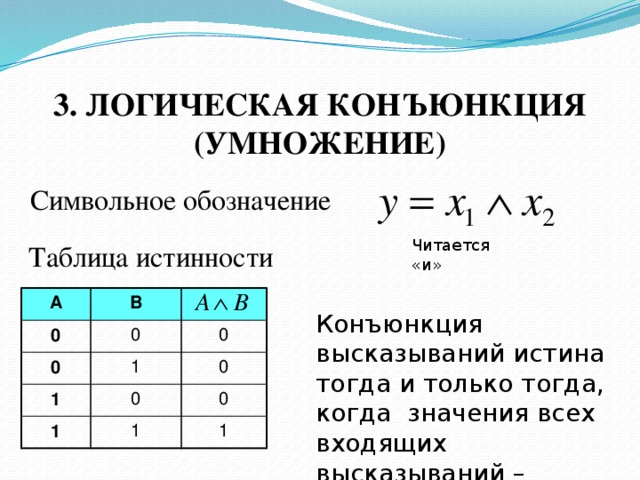
Операция Эквивалентности объединяет два высказывания, имеющие одинаковые значения истинности. Следовательно, будут эквивалентными, с одной стороны, истинные высказывания, а с другой – высказывания ложные. В противном случае высказывания считаются не эквивалентными. Исходя из этого легко построить таблицу истинности для эквивалентности, символом которой служит стрелка с противоположными концами (табл.
5).
Эквивалентность можно выразить на естественном языке словами «если и только если», и в таком виде она часто встречается в формулировке научных определений.
Кроме табличного определения логические операции (за исключением отрицания) можно определить через другие, с обязательным использованием отрицания. Действительно, применив табличный метод (табл. 6), можно убедиться, что выражения (х→у) и (Y → X) будут эквивалентными, т. е. (х→у) ↔ (у→X).
Каждая строка первой импликации и второй конверсной (обратной), полученной перестановкой отрицаний консеквента и антецедента первой, совпадают друг с другом. Следовательно указанные импликации будут эквивалентны.
С помощью таблиц истинности можно проверить, что и остальные логические операции можно определить через Другие две, причем второй операцией всегда будет отрицание. Например, дизъюнкцию можно выразить через конъюнкцию: (х Ú У) ↔ (X Ù Y).
Способ установления истинности сложных высказываний, образованных из простых с помощью таблицы, был предложен американским логиком Ч. С. Пирсом и оказался весьма удобным. Как мы видели, этот способ основывается на комбинации значений истинности простых высказываний и последующего определения истинности сложных высказываний, образованных с помощью операций отрицания, конъюнкции, дизъюнкции и импликации. Например, когда имеется два высказывания, то число различных комбинаций из их значений истинности будет равно 4, при трех – 8, при четырех – 16, а следовательно, при заданном числе П оно равно 2ⁿ. Отсюда нетрудно заметить, что определение истинности сложного высказывания сводится в сущности к вычислению ее на основе значений истинности простых высказываний. Это впечатление усилится, если мы обозначим истину как 1, а ложь как 0 и будем их комбинировать, чтобы образовать отрицание, конъюнкцию, дизъюнкцию и т. д. В качестве иллюстрации вычислим значение истинности следующего выражения: (Х Ú Y) →(X Ù Z).
При некотором навыке процесс вычисления можно ускорить, обратив главное внимание на основную операцию, которая связывает две части формулы. В приведенном примере (табл. 7) достаточно заметить, что ложная импликация возникает при истинном антецеденте и ложном консеквенте. Отсюда легко определить возможные значения Х и У в дизъюнкции (х Ú У), а также значения Х и Z в конъюнкции (х Ù Z). Такой сокращенный способ вычисления истинности сложного высказывания основывается на установлении главной логической операции в рассматриваемой формуле.
Законы логики высказываний
Такие законы представляют собой тождественно истинные высказывания, т. е. высказывания, остающиеся истинными при любых значениях входящих в них простых высказываний. В справедливости этого утверждения можно убедиться опять-таки с помощью таблиц истинности. В принципе все тождественно истинные высказывания являются законами логики (или исчисления высказываний).
Мы перечислим только основные из них.
• Закон тождества: если Х, то Х, т. е. Х → х.
• Закон упрощения: если Х и У, то Х, т. е. Х Ù у →х. То же самое относится к другому конъюнктивному члену:
X Ù Y → Y
• Закон эквивалентности: если из Х следует У, а из У следует Х, тогда высказывания эквивалентны, т. е.
X ↔ Y.
• Закон гипотетического силлогизма: если из Х следует У, А из У следует Z, то из Х следует Z, т. е.
((X → Y) Ù (Y → Z)) → (X → Z)
• Закон двойного отрицания: если из Х следует Не-х, то отрицание последнего приводит к первоначальному высказыванию:
(X) ↔ X
• Законы О. де Моргана дают возможность переходить от конъюнкции к дизъюнкции и, наоборот, от дизъюнкции к конъюнкции.
Они служат удобным средством для преобразования высказываний:
А) Отрицание конъюнкции высказываний эквивалентно дизъюнкции из отрицаний конъюнктивных членов:
(X Ù Y) ↔ (X Ú Y)
Б) Отрицание дизъюнкции эквивалентно конъюнкции отрицаемых членов дизъюнкции:
(X Ú Y) ↔ (X Ù Y)
• Закон «поглощения»: конъюнкция или дизъюнкция одинаковых высказываний эквивалентна самому высказыванию, т. е. повторяющийся член «поглощается»:
(X ÙX) → X и (X Ú X) → X.
• Коммутативные законы для конъюнкции и дизъюнкции разрешают перестановку их членов:
(X Ù Y) ↔ (X Ù Y) и (X Ú Y) ↔ (Y Ú X).
• Ассоциативные законы для конъюнкции и дизъюнкции позволяют по-разному сочетать члены, т. е. по-иному расставлять скобки:
X Ù (Y Ù Z) ↔ (X Ù Y) Ù Z или X Ú (Y Ú Z) ↔ (X Ú Y) Ú Z.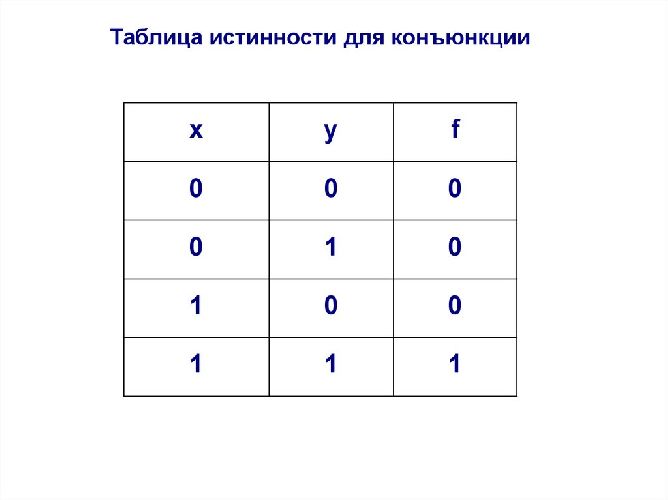
• Закон Контрапозиции разрешает прямую импликацию заменять обратной, в результате чего антецедент первой заменяется отрицанием консеквента второй, а ее консеквент – отрицанием антецедента. Проще говоря, при контрапозиции происходит перестановка членов импликации или их контрапозиция, но они берутся с отрицаниями:
(X → Y) ↔ (Y → X)
• Закон противоречия: два противоречащих друг другу высказывания, т. е. высказывание Х и его отрицание не-х, не могут быть вместе истинными:
(X Ù X)
Поскольку этот закон запрещает противоречия в рассуждении, то его часто называют также Законом непротиворечия, и последнее более правильно.
• Закон наслюненного третьего: Из двух противоречащих друг другу высказываний только одно является истинным. Тогда второе будет ложным и никакой третьей возможности не существует
X Ú X
Все эти законы можно непосредственно проверить с помощью таблиц истинности, но их желательно запомнить, чтобы каждый раз не обращаться к построению таблиц.
Можно было бы привести и другие законы, которые иногда применяются в рассуждениях, но они играют значительно меньшую роль. В принципе таких законов может быть бесчисленное множество. Все они должны содержать только переменные и логические постоянные и быть истинными в любой области (универсуме) рассуждения. При этом предполагается, что данная область непустая. В логике высказываний к постоянным относят логические коннекторы (связки), с помощью которых образуются сложные высказывания, а переменными являются простые высказывания.
Все перечисленные выше законы служат основой для правильных рассуждений, ибо опираясь на них, никогда нельзя получить ложного заключения из истинных посылок. Поэтому любое последовательное, непротиворечивое и правильное мышление всегда осуществляется в соответствии с законами логики, сознаем мы это или нет. В то же время среди перечисленных законов необходимо выделить самые основные, которые обычно называются Законами логики. К ним относятся законы тождества, противоречия и исключенного третьего, о которых пойдет речь в гл.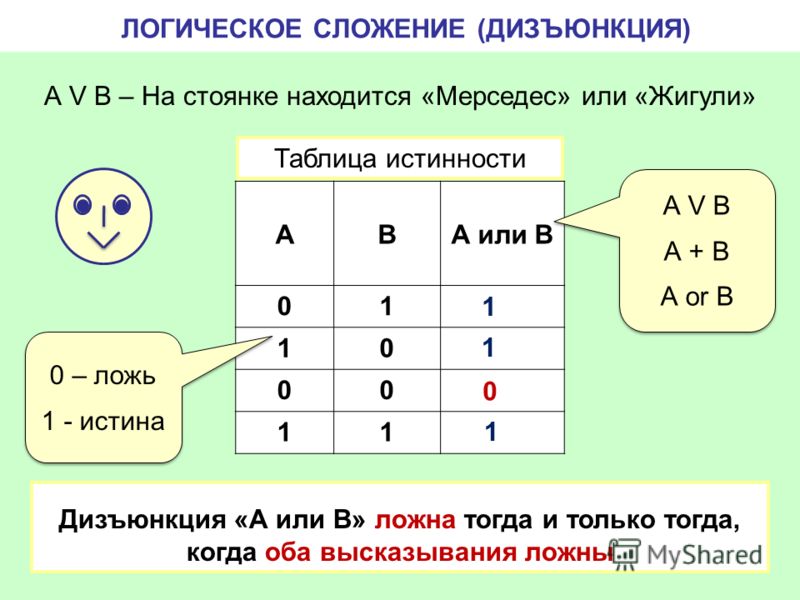
6.
Все законы исчисления высказываний, как в этом можно убедиться с помощью таблиц истинности, являются тождественно истинными (общезначимыми формулами). Какие бы истинностные значения не придавались входящим в них высказываниям, в конечном счете формула оказывается всегда истинной. Вот почему эти законы явно или неявно применяются в любом рассуждении, ибо именно с их помощью становится возможным преобразовать и упрощать имеющуюся информацию и приходить к определенным заключениям. Поясним это на примере закона контрапозиции. Если нам известно, что «треугольник Х равнобедренный», то отсюда следует высказывание У, утверждающее, что «углы при его основании равны». Но если эти углы не равны, то по закону контрапозиции можно заключить, что «треугольник не является равнобедренным», т. е. (Х → У) → (Y → X). Таким образом, этот вывод мы получаем чисто логически, не прибегая, например, к доказательству методом от противного.
Отсюда непосредственно видно, что законы логики высказываний, во-первых, облегчают наши рассуждения, во-вторых, значительно упрощают их, в-третьих, делают их более точными и удобозримыми, ибо с символами и формулами обращаться легче, чем с менее определенными и неточными словесными формулировками.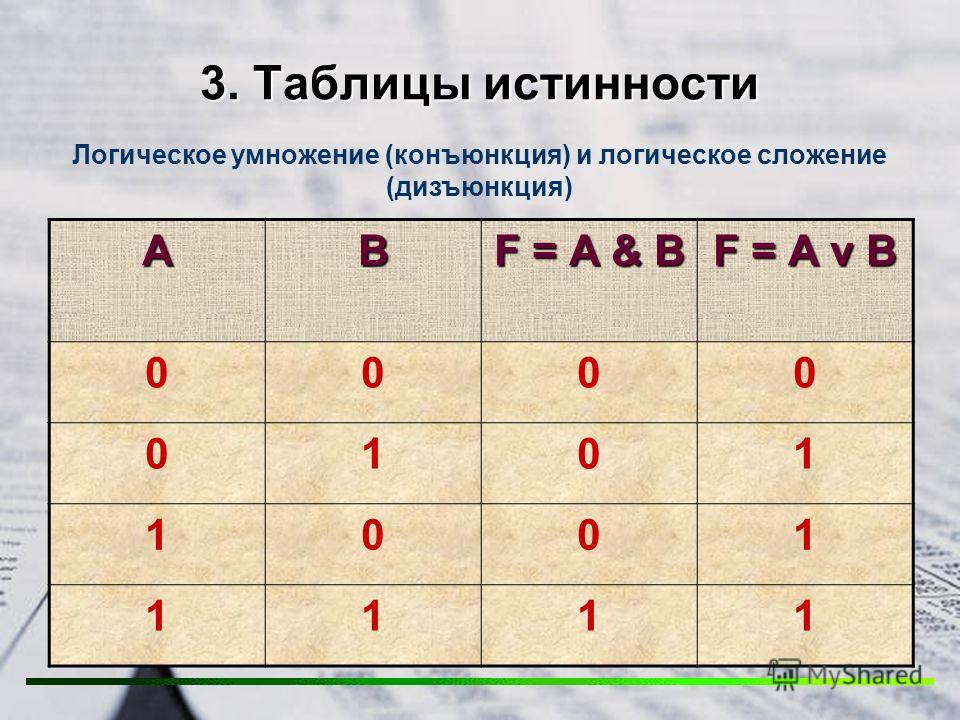
Поскольку законы исчисления высказываний являются такими же общезначимыми по своему характеру, как и основные законы логики, то в принципе они ничем не отличаются от них. Если мы продолжаем отличать их от основных законов логики, то это скорее дань традиции, хотя для характеристики разных систем такое различие продолжает сохранять свое значение. Так, конструктивную логику мы отличаем от классической по отсутствию в ней закона исключенного третьего.
| < Предыдущая | Следующая > |
|---|
Логика высказываний
Отрицание, конъюнкция (AND), дизъюнкция (OR), исключающее ИЛИ (XOR), импликация (если …, то …), эквиваленция (тогда и только тогда)
10 февраля 2021, автор: Елена Позднякова
Во вступлении к данной статье я хочу пояснить, зачем тема «Логика высказываний» нужна в курсе про нейросети:
1. Обучение одного нейрона удобно рассматривать на основе таблиц истинности для базовых логических операций (конъюнкция, дизъюнкция.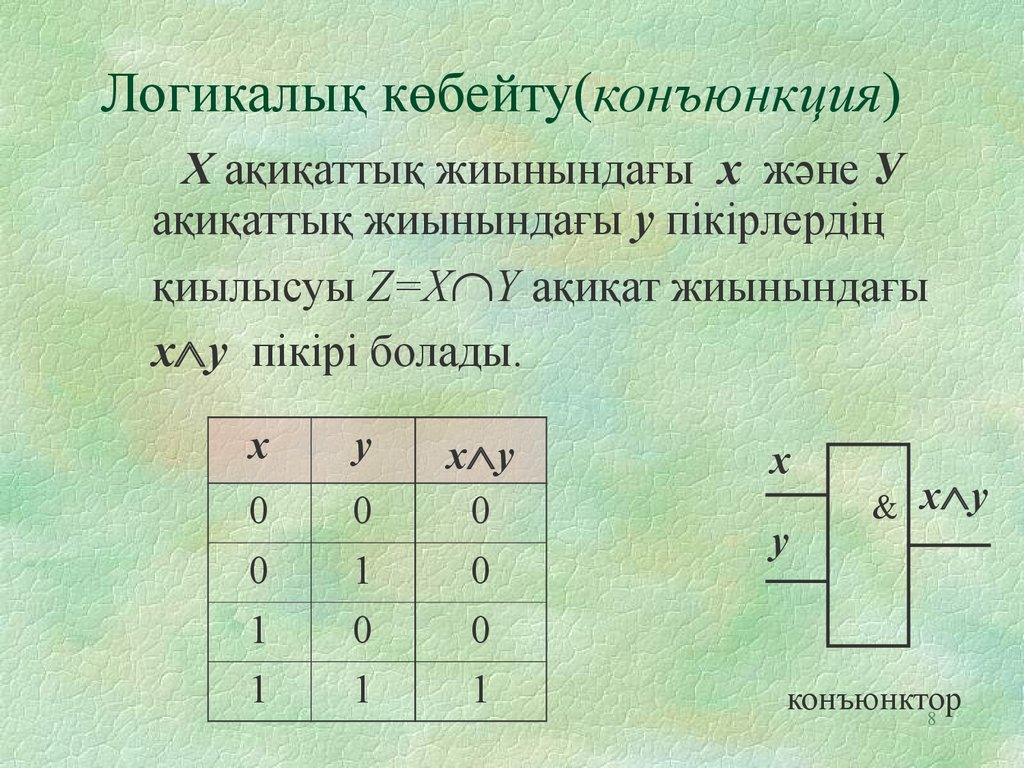
отрицание).
2. В состав темы «Логика высказываний» входит ужасный XOR (читается, как КСОР)«, который приостановил развитие нейросетей в 1969 году.
Причиной стало следующее.
Марвин Минский в своей совместной работе с Сеймуром Папертом «Перцептроны. Введение в вычислительную геометрию» раскритиковал перцептрон (это первая модель нейросети), который, по его словам, не может реализовать простейшую логическую функцию XOR: либо-либо.
На самом деле это не так, но известно об этом стало позже.
А тогда, после публикации названной книги, работы по нейронным сетям были свернуты во многих научных центрах и финансирование существенно урезано. Нейросети почти на 10 лет были забыты и заброшены.
3. И третья причина, почему «Логика высказываний» появилась здесь.
В курсе «На пути к нейросети» рассматривается создание нейросети, которая выполняет производные логические операции (XOR, импликация, эквиваленция), из базовых логических элементов путем их комбинации, без использования метода обратного распространения ошибки.
Оглавление
Оглавление:
¬ отрицание
∧ конъюнкция
∨ дизъюнкция
⊕ исключающее или
→ импликация
↔ эквиваленция
Единицы логических операций
Язык логики состоит из высказываний и логических связок.
Высказывание — это повествовательное предложение, относительно которого можно определенно сказать, истинно оно или ложно.
Обозначения:
1 — истина,
0 — ложь.
Синонимом высказывания является суждение.
Приведу некоторые выдержки из авторитетных источников по этому вопросу.
Из учебника для средней школы «Логика» (1954г):
Суждением называется мысль, которая утверждает или отрицает что-то относительно предметов и их признаков.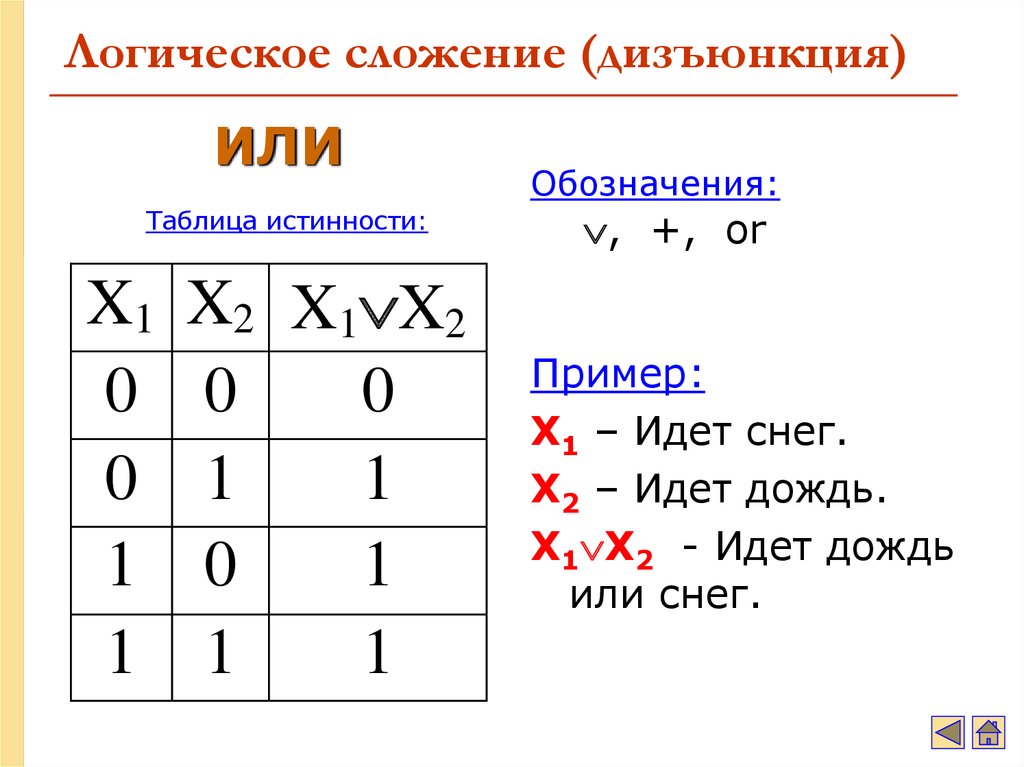
Суждение истинно в том случае, когда в суждении связано то, что действительно связано в окружающей действительности, или разъединено то, что разъединено в окружающей действительности.
Суждение ложно (не истинно), когда в суждении связано то, что не связано на самом деле в материальном мире, или разъединено то, что в действительности связано в материальном мире, ибо оно не соответствует предмету, который отображается в суждении.
Аристотель. Сочинения в 4-х томах. М: — «Мысль» (период издания: 1975-1984)
Аристотель писал, что относительно чего бы то ни было необходимо или утверждение, или отрицание, и что невозможно в одно и то же время быть и не быть
Обратите внимание, что в учебнике логики истинность суждения определена через связь с окружающей действительностью (нам это в дальнейшем еще пригодится!).
А теперь перейдем к логическим операциям.
Логические операции — это действия с высказываниями, как в математике.
Новые высказывания создаются путём соединения более простых. Соединение высказываний производится с помощью логических операторов.
Логические операторы — это специальные символы, которые изменяют или комбинируют логические значения высказываний (истина/ложь).
Базовыми логическими операторами являются:
¬ отрицание
∧ конъюнкция
∨ дизъюнкция.
Все остальные операторы являются производными от базовых и могут быть выражены с помощью них.
Вот некоторые производные логические операторы, которые мы рассмотрим:
⊕ исключающее ИЛИ
→ импликация
↔ эквиваленция.
Раздел математической логики, в котором изучаются логические операции над высказываниями называется алгебра логики.
Чаще всего используется двоичная логика, то есть, предполагается, что высказывания могут быть только истинными или ложными.
Однако, стоит упомянуть, что существуют и логики более высокой размерности, например, троичная логика (в данном материале она не рассматривается).
Логическое выражение — это одно или несколько высказываний, выраженных через переменные, каждое из которых имеет значение истинности, и связанных логическими операторами.
Сложное логическое выражение также имеет значение истинности: оно либо истинно, либо ложно, в зависимости от состава входящих высказываний и типа оператора.
Выполнить логическую операцию — это значит, определить значение истинности выражения.
Этих значений может быть только два: ИСТИНА (1), ЛОЖЬ (0).
Приоритет логических операций:
¬ отрицание
∧ конъюнкция
∨ дизъюнкция
⊕ исключающее или
→ импликация
↔ эквиваленция
¬ отрицание
Отрицание — унарныйлогический оператор, результатом которого является суждение, противоположное исходному.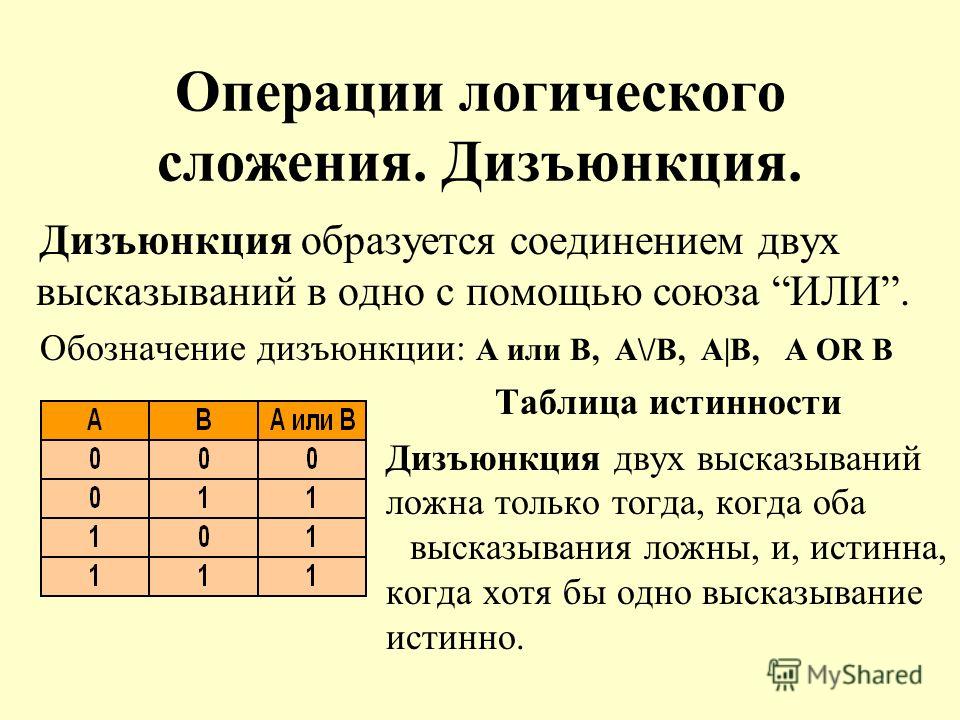
Смысл: неверно, что …
Пример:
Маша варит суп.
Неправильное отрицание: Маша не варит суп, Маша варит не суп, не Маша варит суп.
Правильное отрицание: неверно, что Маша варит суп.
Утверждение ¬A истинно тогда и только тогда, когда A ложно.
Таблица истинности отрицания:
∧ конъюнкция
Конъюнкция ( от лат. conjunctio — «соединение») — логический оператор, отражающий употребление союза «И» в сложных высказываниях.
Конъюнкция — это логическая операция, результат которой равен ИСТИНА тогда и только тогда, когда оба операнда имеют значение ИСТИНА.
Смысл: и то, и это одновременно.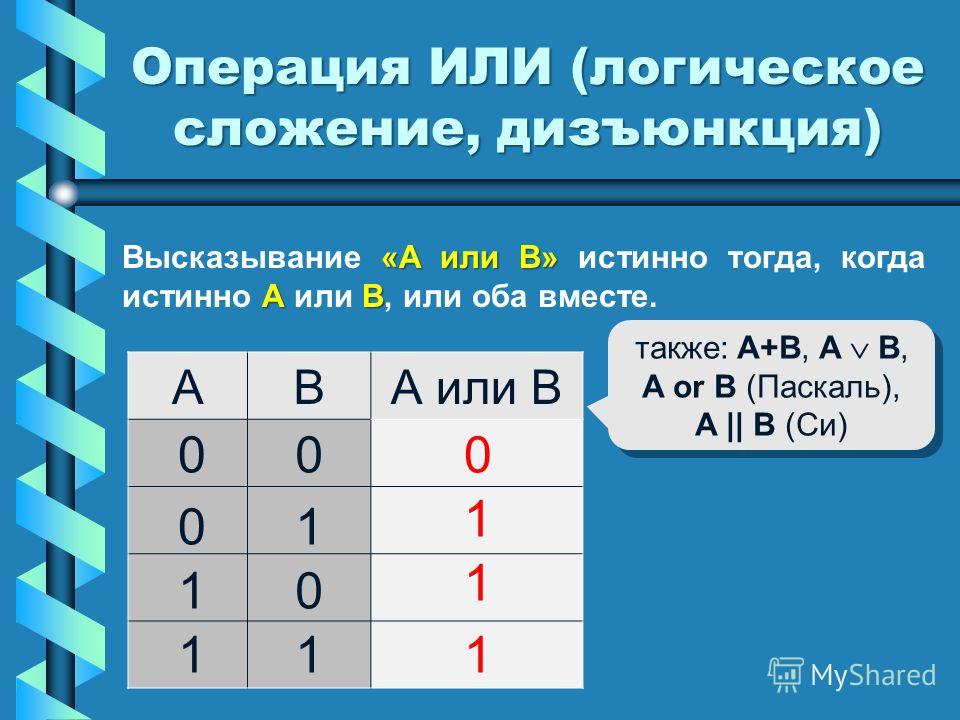
Конъюнкция может применяться к двум и большему числу операндов (бинарная, тернарная, n-арная).
Утверждение A ∧ B истинно, если и A, и B истинны, и ложно в противном случае.
Таблица истинности конъюнкции:
∨ дизъюнкция
Дизъюнкция( от лат. disjunctio — «разобщение») — логический оператор, отражающий употребление союза «ИЛИ» в сложных высказываниях. Дизъюнкция — это логическая операция, результат которой равен ЛОЖЬ тогда и только тогда, когда оба операнда имеют значение ЛОЖЬ.
Смысл: или то, или это, или оба сразу.
Утверждение A ∨ B истинно, если A или B (или оба) истинны, и ложно, если оба операнда ложны.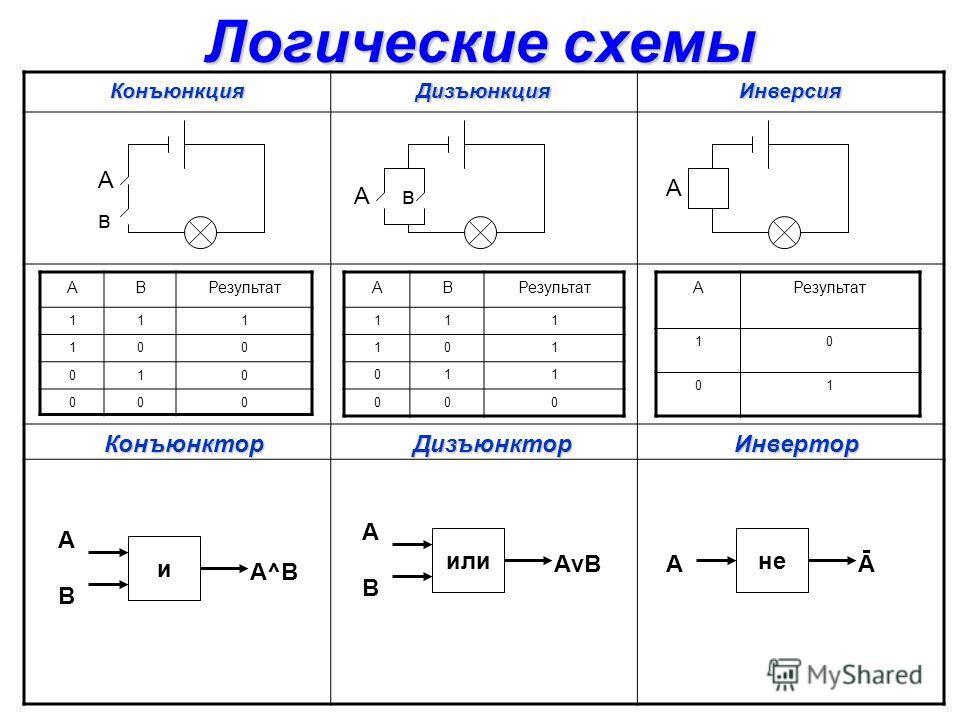
Таблица истинности дизъюнкции:
⊕ исключающее ИЛИ (XOR)
Исключающее ИЛИ — логический оператор, который истинен для двух переменных тогда и только тогда, когда один из аргументов истинен, а другой — ложен.
Смысл: или то, или это, но не оба сразу.
Утверждение A ⊕ B истинно, когда истинно либо A, либо B, но не оба.
Таблица истинности XOR:
Операцию XOR можно разложить на базовые логические операции: отрицание, конъюнкция, дизъюнкция:
A ⊕ B = (¬A ∧ B) ∨ (¬B ∧ A)
Читается так:
дизъюнкция двух конъюнкций:
конъюнкции отрицания A и В,
конъюнкции отрицания В и А.
Замена XOR на базовые функции:
→ импликация
Импликация — бинарная логическая связка, которая записывается формулой:
Посылка → Следствие,
где посылка является достаточным условием для выполнения следствия, а следствие является необходимым условием для истинности посылки.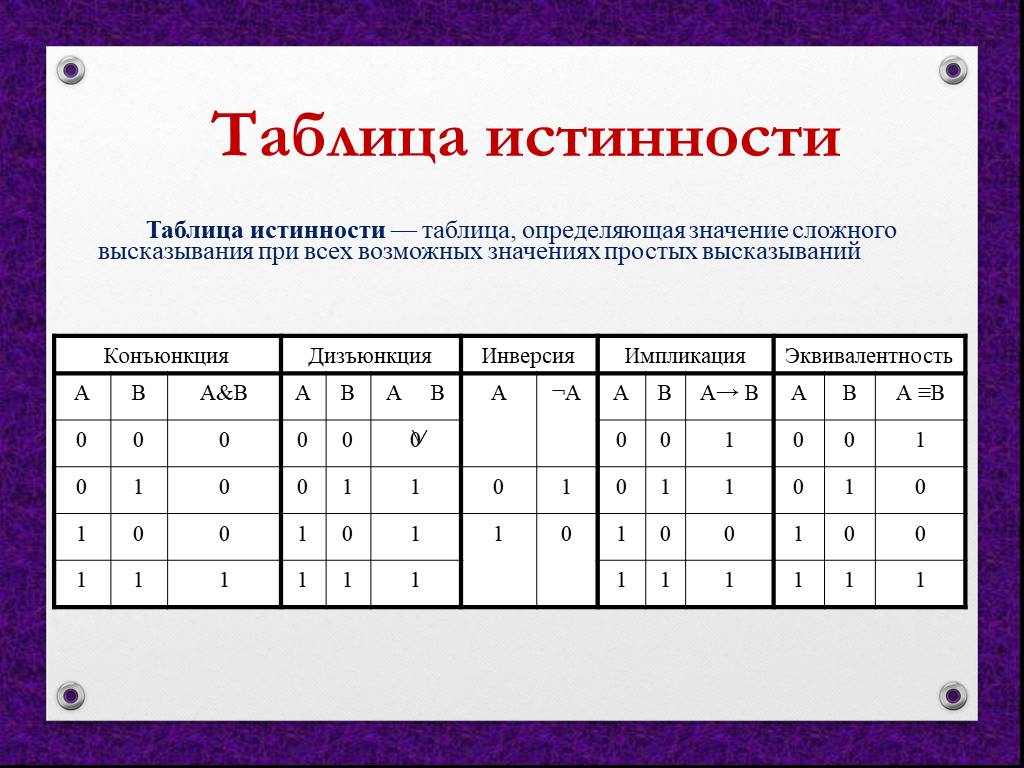
Импликация соответствует условному оператору «если …, то …»
Импликация не является коммутативной операцией (слагаемые нельзя менять местами).
Смысл: если А, то B.
Еще раз:
A → B (читаем: если А, то B)
где
А достаточное условие для В,
В необходимое условие для истинности А.
A → B ложно, только когда A истинно, а B ложно.
Таблица истинности импликации:
Пример импликации №1.
В этом примере мы учитываем смысл высказываний и смысловую причинно-следственную связь между посылкой и следствием:
Если прошел дождь, то на улице мокро.
А (посылка) = Прошел дождь.
В (следствие) = На улице мокро.
А достаточное условие для В: для того, чтобы на улице стало мокро, достаточно, чтобы прошел дождь.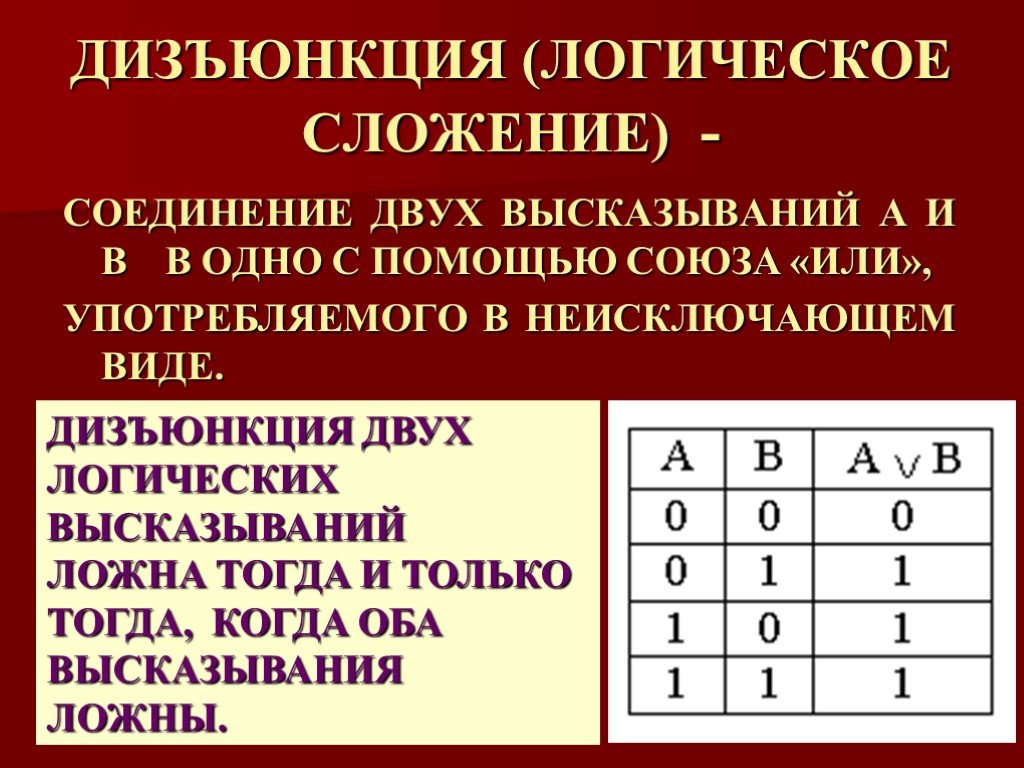
Но не необходимо! Например, вместо дождя могла проехать поливальная машина.
В необходимое условие для истинности А: если прошел дождь, то на улице мокро. Мокро — это необходимое условие, точнее, следствие. Такого не может быть, что прошел дождь, но улица сухая. Если улица сухая, значит, не было никакого дождя и высказывание «Прошел дождь» не может быть истинным.
Таблица истинности импликации «Если прошел дождь, то на улице мокро»:
До рассмотрения таблицы хочу обратить внимание вот на какой момент: в данном случае, в качестве истины или лжи выступает не собственно истина (отражающая окружающую действительность) и не собственно ложь (не отражающая окружающую действительность), а факт выполнения утверждений, указанных в изначальной импликации.
Прошел дождь — условие выполняется — значит, присваиваем значение 1(истина), не прошел дождь — условие не выполняется, значит, присваиваем значение 0 (ложь).
Пока вроде бы все логично?! 🙂
Уфф! Так хотелось обойтись без парадокса материальной импликации.
..
И, кажется, у меня получилось!
Временно. Обойти парадокс, конечно же, не удастся.
Просто я решила преподнести его на сладкое, после эквиваленции, потому что, на мой взгляд, этот препротивнейший парадокс распространяется и на эквиваленцию тоже (хотя никто и нигде об этом ни слова, ни полслова).
Еще пример (№2, пока опять без парадоксов).
Если этот человек — президент РФ, то он старше 35.
(данное требование к возрасту установлено в Конституции, статья 81).
А (посылка) = Этот человек президент РФ.
В (следствие) = Этот человек старше 35.
А достаточное условие для В: если человек является президентом, то он точно старше 35. Это достаточное условие, но не необходимое. Достаточно знать, что человек — президент, чтобы быть уверенным, что он старше 35.
При этом не все люди старше 35 — президенты.
В необходимое условие для истинности А: чтобы быть президентом, необходимо быть старше 35.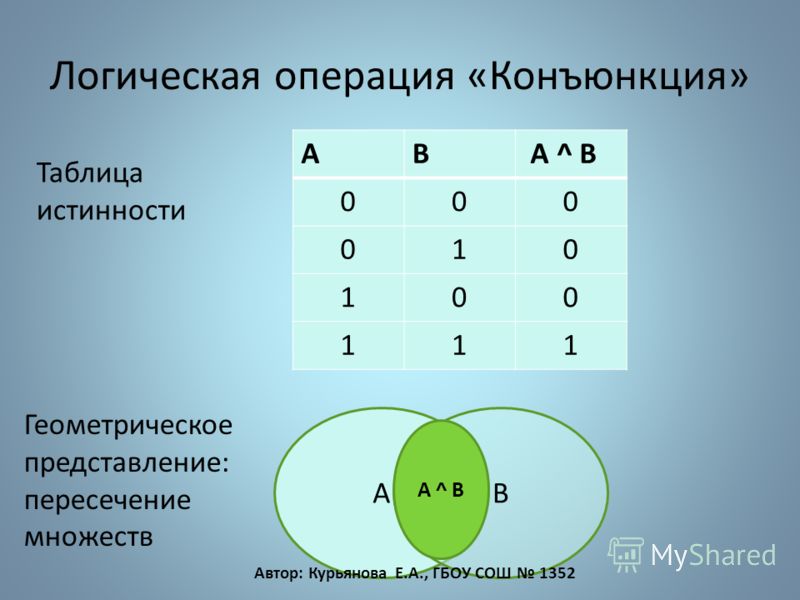
Без выполнения этого условия посылка А не может быть истинной.
Таблица истинности импликации
«Если этот человек — президент РФ, то он старше 35»:
А теперь предлагаю рассмотреть эти же 2 примера наглядно, на множествах, чтобы лучше понять соотношение необходимых и достаточных условий:
Как видите, в обоих случаях множество А является подмножеством множества В.
Именно поэтому А всегда есть В, но В не всегда есть А.
Импликацию можно разложить на базовые логические операции: отрицание, дизъюнкция:
A → B = ¬A ∨ B
Читается так:
дизъюнкция отрицания A и В.
Замена импликации на базовые функции:
↔ эквиваленция
Эквиваленцией двух высказываний А и В называется новое сложное высказывание, которое истинно тогда и только тогда, когда оба исходных высказывания одновременно истинны и одновременно ложны.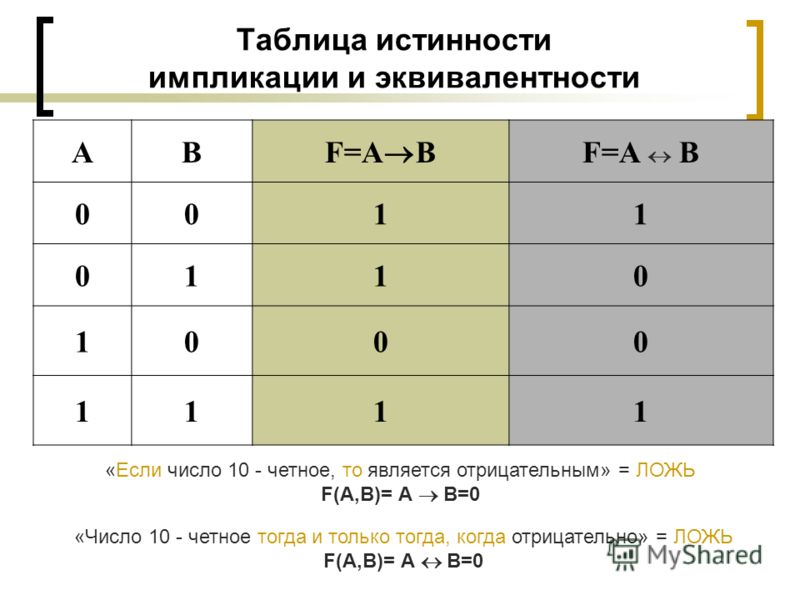
Синоним — эквивалентность.
Смысл: тогда и только тогда.
A ↔ B (читаем: А тогда и только тогда, когда В)
где
А необходимое и достаточное условие для В,
В необходимое и достаточное условие для А.
A ↔ B истинно, только если оба значения A и B ложны, либо оба истинны.
Таблица истинности эквиваленции:
Пример эквиваленции.
Две прямые параллельны тогда и только тогда, когда они не пересекаются.
А: Две прямые параллельны.
В: Две прямые не пересекаются.
А необходимое и достаточное условие для В, а В необходимое и достаточное условие для А.
Множества А и В равны. Графически это можно представить так:
Эквиваленцию можно разложить на базовые логические операции: отрицание, конъюнкция, дизъюнкция:
A ↔ B = (¬A ∧ ¬B) ∨ (A ∧ B)
Читается так:
дизъюнкция двух конъюнкций:
конъюнкции отрицания A и отрицания В,
конъюнкции А и В.
Замена эквиваленции на базовые функции:
А попробуйте сами заполнить!
Показать ответ
А теперь про парадокс материальной импликации
Предупреждение: всё сказанное ниже является личным мнением автора и не претендует на истину в последней инстанции.
Если у вас есть свои мысли на эту тему, приглашаю обсудить в комментариях.
Итак, возможно, что до сих пор вы никакого парадокса не заметили — и это потому, что когда я приводила примеры импликации, я умышленно ввела оговорку, что:
мы учитываем смысл высказываний и смысловую причинно-следственную связь между посылкой и следствием.
Действительно, если учитывать смысл и причинно-следственные связи, парадоксов не будет, но в классической логике содержание утверждений во внимание не принимается. Даже если исходные утверждения никак не связаны друг с другом по смыслу, составленное из них условное утверждение может быть истинным.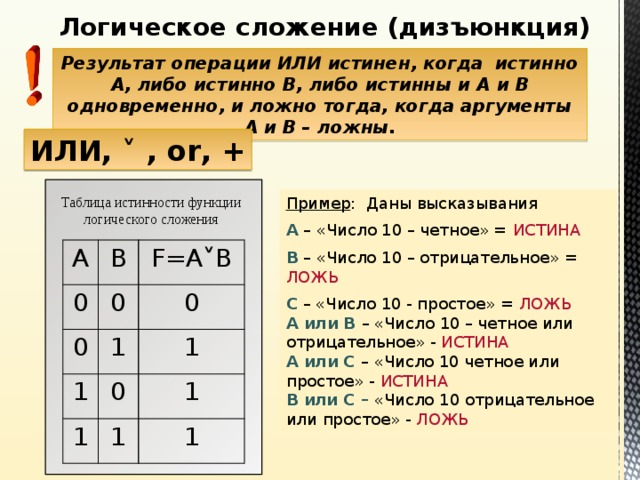
Теперь еще раз посмотрите на таблицу истинности импликации и особое внимание обратите на последние две строчки:
Как же так?
В предпоследней строчке мы видим, что если из ЛЖИ следует ИСТИНА, то результатом будет: ИСТИНА!
В последней строчке мы видим, что если из ЛЖИ следует ЛОЖЬ, то результатом будет: опять ИСТИНА.
А давайте подставим в эту конструкцию не связанные по смыслу выражения:
Если луна сделана из зеленого сыра, то 2х2=4.
Если луна сделана из зеленого сыра, то жирафы умеют летать.
Абсурд, но с технический точки зрения оба выражения являются истинными.
Итак, парадокс материальной импликации:
ИЗ ЛЖИ МОЖЕТ СЛЕДОВАТЬ ВСЁ, ЧТО УГОДНО: РЕЗУЛЬТАТ БУДЕТ ИСТИННЫМ.
Как это объяснить?
Дело в том, что истинность следования А → В (если А, то В), подтверждается отношениями между множествами А и В.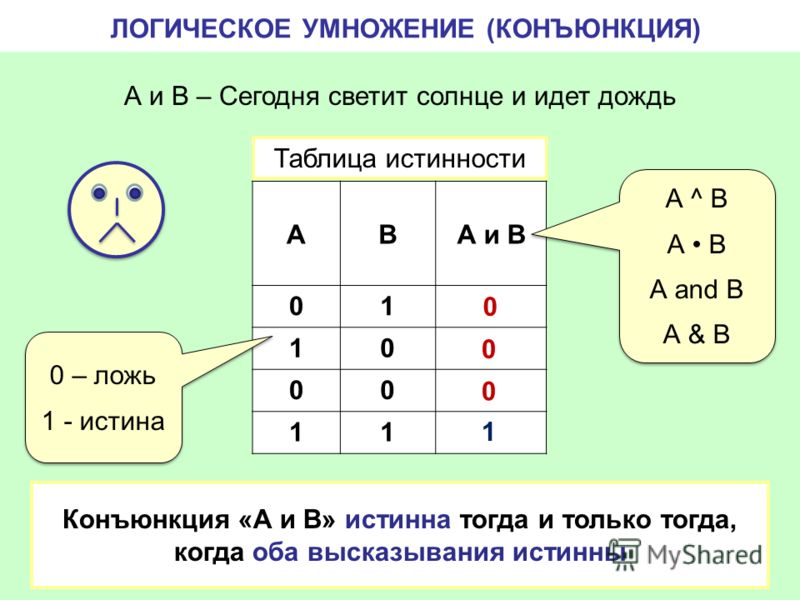
Множество А всегда является подмножеством множества В.
На математических символах это выглядит так: A ⊂ В.
Графически так:
А теперь давайте разберемся, что из себя представляет множество A, если оно является ложью.
Ложь — это значит, что мы имеем пустое множество, которое не содержит ни одного элемента.
Ну в самом деле: какая луна из зеленого сыра? Какие летающие жирафы?
Ложь, вранье, болтовня. Есть даже соответствующая фраза в разговорном языке: «Да это все пустое!» — И действительно, пустое. Множество не состоящее ни из одного элемента. Ноль. Пустота.
Пустое множество обозначается вот таким знаком: ∅ и обладает следующими свойствами:
- пустое множество является подмножеством любого множества ∅ ⊂ ∀а
- пустое множество является подмножеством самого себя ∅ ⊂ ∅
Вот почему следование из лжи (в смысле из пустого множества) является истиной.
Потому что это доказывается математически, с помощью операций над множествами, на основании свойств пустого множества.
Вы можете это увидеть даже графически (пустое множество обозначу точкой):
Таблица истинности импликации с графическим представлением
И никакого парадокса здесь, как видите, нет: обычная математика и операции над множествами.
И не бойтесь того, что из лжи следует истина. Эта операция абсолютно безопасна.
Если вы будете строить автоматическое доказательство какой-либо теоремы с использованием логических операторов (в том числе примените и импликацию, как оператор следования, — а куда ж без него в доказательствах!), то ложь на входе — это просто 0. В пустое множество невозможно передать никакое значение, потому что оно не содержит ни одного элемента. Там всегда будет пусто. Луна из зеленого сыра не появится, а жирафы не научатся летать.
А если вдруг они возьмут и научатся, то множество становится НЕ ПУСТЫМ, значит, оно приобретает значение ИСТИНА и таблица истинности импликации работает уже по-другому.
Парадокс эквиваленции.
В завершение темы хочу сказать, что в таблице истинности эквиваленции можно разглядеть такой же парадокс (0,0,1):
Ложь тогда и только тогда, когда ложь. Ведь это выражение имеет значение ИСТИНА!
«Луна сделана из зеленого сыра тогда и только тогда, когда жирафы умеют летать». Истина.
И опять же объяснение следует из свойств пустого множества: пустое множество не содержит ни одного элемента и равно самому себе ∅ = ∅.
Пустое множество луны из зеленого сыра равно пустому множеству летающих жирафов, потому что: ни луны из зеленого сыра, ни летающих жирафов не существует, — все эти множества пусты.
Дополнительные материалы и ссылки:
Плейлист «Логика высказываний»
на youtube канале Artificial Intelligence and Machine Learning
(Окуловский Юрий Сергеевич, доцент Уральского Федерального Университета)
Список логических символов (википедия)
Логика.
Учебник для средней школы, 1954 (С.Н. Виноградов, А.Ф.Кузьмин)
Ссылка 1 (в контакте)
Ссылка 2
Please enable JavaScript to view the comments powered by Disqus.
1.7 Таблицы истинности: отрицание, соединение, дизъюнкция
Цели обучения
- Что такое таблица истинности?
- Основные таблицы истинности для
- Отрицание
- Соединение
- Разъединение
- Порядок логических операций
- Соединение (отрицание, конъюнкция, дизъюнкция)
Поскольку сложно представить сложные утверждения, мы можем создать таблицу истинности , чтобы разбить сложное утверждение на простые утверждения и определить, являются ли они истинными или ложными. Таблица поможет отслеживать все значения истинности простых утверждений, составляющих сложное утверждение, что приведет к анализу всего утверждения.
Таблица истинности
Таблица, показывающая результирующее значение истинности сложного утверждения для всех возможных значений истинности простых утверждений.
Пример
Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите секционный 9».0035 или что-нибудь с фаэтоном». Постройте таблицу истинности, описывающую элементы условий этого утверждения и соблюдение условий.
Показать решение
Отрицание говорит нам: «Это не так, что…»
Соединение говорит нам: «И то, и другое… имеет место». Союзы истинны только тогда, когда оба союза истинны.
Дизъюнкция говорит нам, что «верно хотя бы одно…» Дизъюнкции ложны только тогда, когда ложны оба дизъюнкции.
Основные таблицы истинности
Обратите внимание, что столбец b имеет шаблон TFTF. Тогда столбец A имеет шаблон TTFF.
| и | б | [латекс]а\клин{б}[/латекс] |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Ф |
| Ф | Ф | Ф |
Думая о ситуациях «и», часто полезно представить сценарий.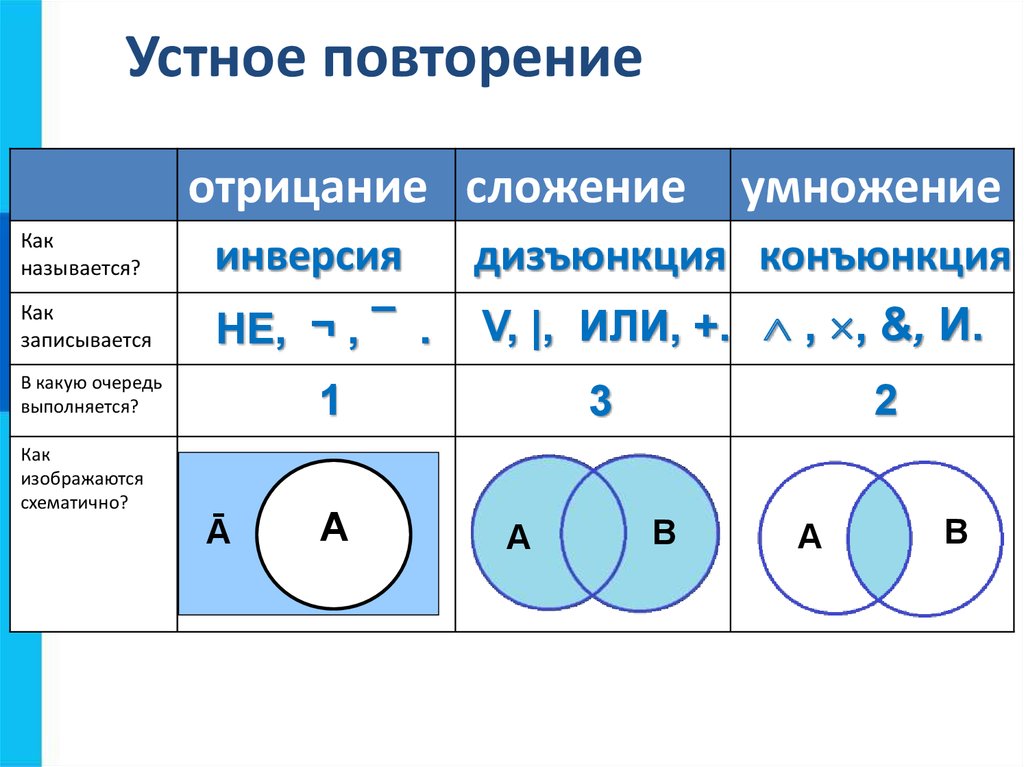
Представьте, что вы арендатор и заключили договор с арендодателем. Вы договорились, что будете выносить мусор и косить газон. Теперь, если А выносит мусор, а Б косит газон, вы выполняете свою часть сделки только тогда, когда делаете и то, и другое. Значения истинности будут ложными, за исключением случаев, когда вы выполняете оба действия, и в этом случае они будут истинными.
| и | б | [латекс]а\ви{б}[/латекс] |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
При обдумывании ситуаций «или» также полезно подумать о сценарии. Представьте, что вы арендатор (как в предыдущем примере), и ваш арендодатель попросил вас заплатить 1-го числа за плату 2-го числа. Предположим, что A заплатит за первое, а B заплатит за второе. Результат будет верным во всех сценариях, за исключением случаев, когда вы не платите ни в первый, ни во второй раз.
В этом случае результат ложный.
| и | [латекс]\sim{а}[/латекс] |
|---|---|
| Т | Ф |
| Ф | Т |
Я просто думаю о противоположном дне, когда дело доходит до отрицаний. Все противоположно тому, что было изначально.
Примечание:
Когда мы создаем таблицу истинности, нам нужно перечислить все возможные комбинации значений истинности для A и B. Обратите внимание, что первый столбец содержит 2 значения True (T), за которыми следуют 2 значения False (F). Во втором столбце чередуются T, F, T, F. Этот шаблон гарантирует, что будут учтены все 4 комбинации.
| А | Б |
| Т | Т |
| Т | Ф |
| Ф | Т |
| Ф | Ф |
Попробуйте
Это конец раздела.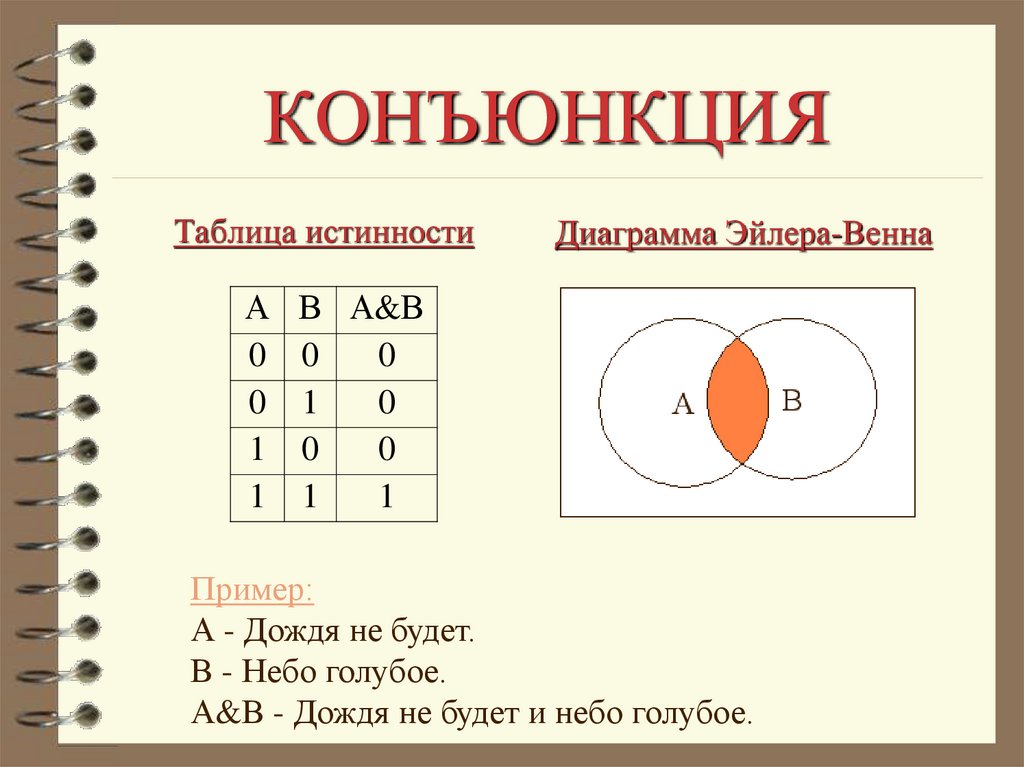
Закройте эту вкладку и перейдите к соответствующему заданию.
Логика, истинность Значения, отрицание, конъюнкция, дизъюнкция
Математическое предложение — это предложение, в котором констатируется факт или содержится законченная идея. Предложение, которое можно оценить как истинное или ложное, называется утверждением или закрытым предложением .
Важные термины в логических и математических утверждениях
Отрицание
Указывает на обратное, обычно используя слово вместо .
Символ для обозначения отрицания: ~
| Оригинал выписки | Отрицание заявления |
|---|---|
Сегодня понедельник.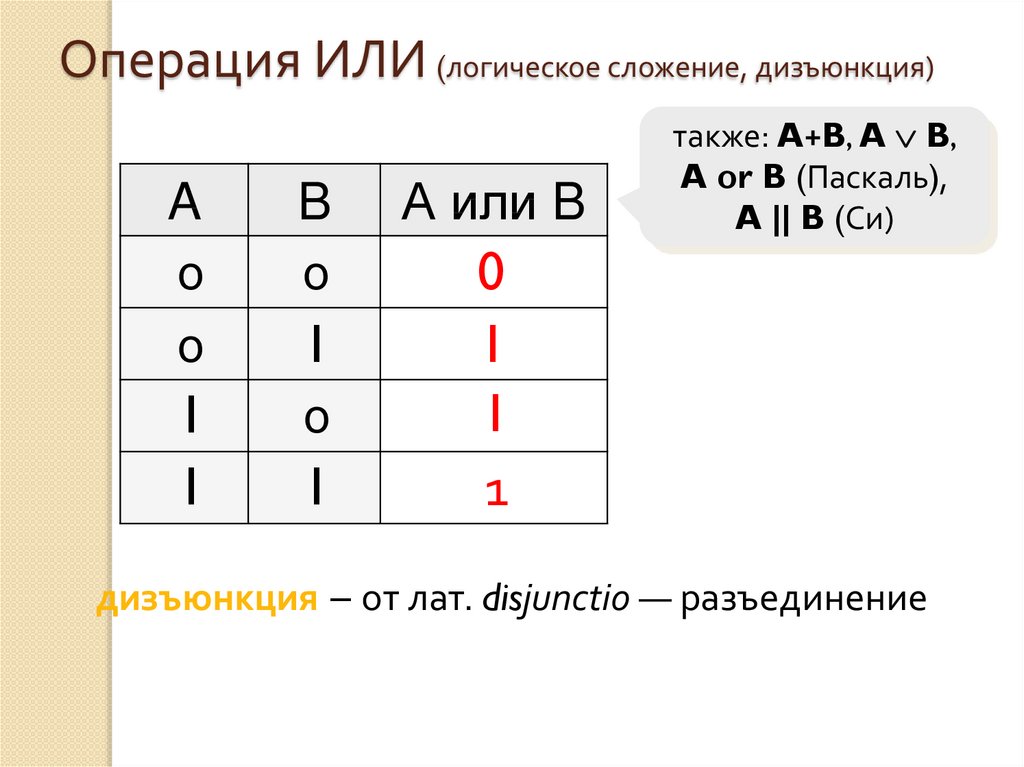 | Сегодня не понедельник. |
| Было весело. | Это было не весело. |
Соединение
В логике союз — это сложное предложение, образованное словом и соединяющее два простых предложения.
Символ для этого $$ Λ $$. (всякий раз, когда вы видите $$ Λ $$ , просто читайте «и»). Когда два простых предложения, p и q, соединяются в операторе соединения, союз символически выражается как p $$ Λ $$ q.
| Простые предложения | Составное предложение: Союз |
|---|---|
| р: Джо ест картошку фри. Вопрос: Мария пьет газировку. | p $$Λ $$ q : Джо ест картошку фри, и Мария пьет газировку. |
Разъединение
В логике дизъюнкция — это сложное предложение, образованное с помощью слова или для соединения двух простых предложений. Символ для этого $$ ν $$ . (всякий раз, когда вы видите, что $$ ν $$ читается как «или»). Когда два простых предложения, p и q, соединяются в операторе дизъюнкции, дизъюнкция выражается символически как p $$ ν$$ q.
Пневмония: способ запомнить символ дизъюнкции заключается в том, что этот символ ν выглядит как «r» в или , ключевом слове операторов дизъюнкции.
| Простые предложения | Составное предложение: дизъюнкция |
|---|---|
| р : Часы отстают. q : Время правильное. | p $$ ν $$ q : Часы отстают, или время правильное. |
Предупреждение и предостережение: Дизъюнкция может быть ложным утверждением только в том случае, если обе его половины ложны. Дизъюнкция истинна, если одно из утверждений верно или оба утверждения верны! Другими словами, утверждение «Часы отстают или время правильное» является ложным утверждением только в том случае, если обе его части ложны! Точно так же заявление «Mr. G преподает математику или мистер G преподает естественные науки» верно, если мистер G преподает уроки естествознания, а также уроки математики!
Условное
В логике условное высказывание представляет собой сложносочиненное предложение, которое обычно выражается ключевыми словами «Если. …то…». Используя переменные p и q для представления двух простых предложений, условное выражение «Если p, то q» символически выражается как p $$\rightarrow$$ q
| Простые предложения | Составное предложение: условное |
|---|---|
| р: Вы отсутствуете q : Вам нужно выполнить задание по макияжу. | р $$ \rightarrow $$ д : Если вы отсутствуете, , затем вам нужно выполнить задание по макияжу. |
Примечание : слово «тогда» не является обязательным, а условное предложение часто опускает слово «тогда». Приведенный выше пример можно было бы выразить так: если вы отсутствуете, вам нужно выполнить задание по восполнению.
Истинностные значения условных выражений
Единственный случай, когда условное выражение является ложным утверждением, это когда условие if истинно, а предложение then ложно.
Например, условное «Если ты пришел вовремя, значит, ты опоздал». ложно, потому что, когда предложение «если» истинно, предложение «тогда» ложно. ПОЭТОМУ, все утверждение ложно.
Пример ложного условия
| Если Пункт | Затем Пункт | Весь отчет |
|---|---|---|
| р | д | п д |
| ты опоздал | ты вовремя | Если вы опоздали, значит, вы вовремя. |
| Когда p истинно | , тогда q ложно | Все утверждение неверно |
| Правда | Ложь | Ложь |
Предупреждение и предостережение Противоположная ситуация не приводит к ложному утверждению. Ложное предложение «если» и истинное предложение «тогда» создают истинное утверждение. (Сначала кажется нелогичным!) См. пример в таблице ниже.
| Если Пункт | Затем Пункт | Весь отчет |
|---|---|---|
| р | д | п д |
| человек-кошка | тогда у квадратов есть углы | Если человек — кошка, то у квадратов есть углы. |
| Когда p ложно | q верно | Все утверждение верно. |
| Ложь | Правда | Правда |
Объяснение: Предложение if всегда ложно (люди не кошки), а предложение then всегда истинно (у квадратов всегда есть углы). И все утверждение верно.
Практика Проблемы Приведенные ниже практические задачи охватывают истинностные значения условных предложений, дизъюнкции, конъюнкции и отрицания.
Часть I.
Пусть представляют «Мы идем в школу в День памяти».
Пусть b означает «День памяти — это праздник».
Пусть c представляет «Мы работаем в День памяти».
Будьте готовы выразить каждое утверждение символически, а затем укажите истинность каждого математического утверждения.
Проблема 1
Заявление: Мы работаем в День памяти или День памяти является праздником.
| Заявление в символах | Достоверность деталей | Значение истинности всего утверждения |
|---|---|---|
| в ν б | Ф ν Т | Верное утверждение |
Проблема 2
Заявление: День памяти — это праздник, и мы не работаем в День памяти.
| Заявление в символах | Достоверность деталей | Значение истинности всего утверждения |
|---|---|---|
| б Λ ~с | Т Λ ~F = Т Λ Т | Верное утверждение |
Проблема 3
Заявление: Если мы идем в школу в День памяти, то мы работаем в День памяти.
| Заявление в символах | Достоверность деталей | Значение истинности всего утверждения |
|---|---|---|
| а с | Ф Ф | Верное утверждение |
Объяснение : это условное утверждение, а условие ‘if’ ложно, потому что мы , а не ходим в школу на мемориал. Кроме того, предложение «тогда» неверно, потому что мы делаем , а не работ в День памяти. Однако это утверждение является истинным утверждением во всей его полноте. Помните, что условие является ложным утверждением только тогда, когда истинное предложение «если» приводит к ложному предложению «тогда» (т. е. когда T
F) (пример ложного условного предложения)
Проблема 4
Заявление: «Мы не ходим в школу в День памяти» означает, что мы работаем в День памяти.
| Заявление в символах | Достоверность деталей | Значение истинности всего утверждения |
|---|---|---|
| ~ а с | ~ Ф Ф = Т Ф | Ложное утверждение |
Проблема 5
Заявление: Мы работаем в День памяти тогда и только тогда, когда мы идем в школу в День памяти.
| Заявление в символах | Достоверность деталей | Истинное значение всего утверждения |
|---|---|---|
| с а | Ф Ф | Верное утверждение |
Проблема 6
Заявление: Если мы не ходим в школу в День памяти, а День памяти является выходным, то мы не работаем в День памяти.
