сайт школы №127 — системы счисления_4
Важно и полезно Информация Школа сегодня Общение Питание Навигатор Детства Школьная группа ВК Большая перемена Госуслуги Статистика | системы счисления_4 Удобные для работы компьютера двоичные числа неудобны для человека в силу большой длины (большого количества цифр). Во-первых, длинные числа трудны для восприятия, во-вторых, они занимают слишком много места при выводе.
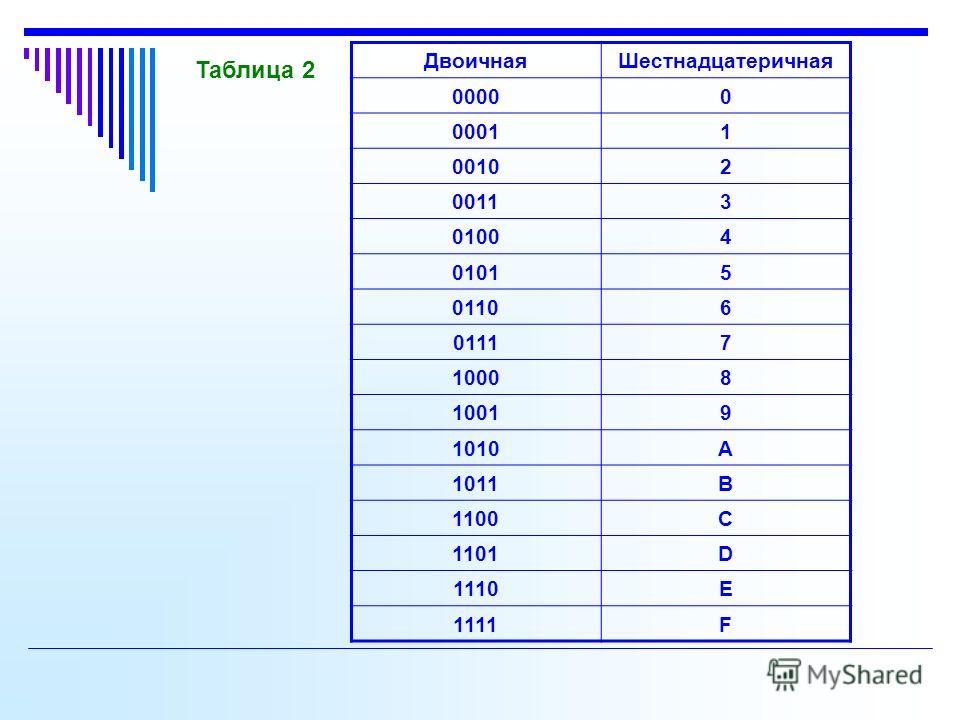
Видно, что наиболее короткую запись имеет шестнадцатеричное число (3 цифры вместо 11 у двоичного). Поэтому в настоящее время помимо двоичной системы счисления в компьютерах используют и шестнадцатиричную. Для решения задач нам поможет таблица чисел
ТРИАДА — группа из трех разрядов (нулей и единиц). ТЕТРАДА — группа из четырех разрядов (нулей и единиц). Из тетрад можно составить шестнадцать различных двоичных чисел (24=16) Алгоритм перевода чисел из двоичной системы счисления в восьмеричнуюN2 → N8
Алгоритм перевода чисел из двоичной системы счисления в шестнадцатеричнуюN2 → N16
Косвенные методы перевода(через промежуточную систему счисления) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Перевод чисел в различные системы счисления в Excel — TutorExcel.
RuПеревод чисел в различные системы счисления в Excel
Изучим стандартные способы перевода чисел в различные системы счисления в Excel: двоичную, восьмеричную, десятичную и шестнадцатеричную.
Помимо повсеместно распространенной и всем нам хорошо известной десятичной системы счисления также используются и системы с другими основаниями (отличными от 10), например, двоичная, троичная, восьмеричная и т.д.
Большинство из них имеют достаточно широкое применение практически во всех современных электронных устройствах, в программировании или компьютерной документации.
Системы счисления в Excel
В Excel есть возможность стандартными средствами переводить данные в четырех системах счисления:
Давайте подробно остановимся на основных вариантах преобразования данных.
Перевод числа из десятичной в двоичную систему в Excel
Для преобразования данных в двоичную запись в Excel существует стандартная функция ДЕС.
В.ДВ (имя функции получается как первые буквы от слов ДЕСятичное В ДВоичное, дополнительно разделенное точками):
ДЕС.В.ДВ(число; [разрядность])
Преобразует десятичное число в двоичное.
- Разрядность (необязательный аргумент) — количество знаков для использования в записи. Данный аргумент необходим если нужно приписать к двоичной записи данных ведущие нули. К примеру, число 1101 с разрядностью 7 будет иметь вид 0001101.
Обратите внимание, что Excel накладывает определенные ограничения на размер преобразуемых данных.
Двоичная запись не должна занимать более 10 знаков, поэтому десятичное число, соответственно, не должно быть больше 511 или меньше -512, иначе в качестве значения функция ДЕС.В.ДВ вернет ошибку.
Перевод числа из двоичной в десятичную систему в Excel
Для осуществления обратного перевода можно воспользоваться функцией ДВ.В.ДЕС:
ДВ.В.ДЕС(число)
Преобразует двоичное число в десятичное.
- Число (обязательный аргумент) — двоичное число, которое требуется преобразовать.
При этом разрядность в качестве аргумента функции для десятичной записи не используется.
Как и в случае с функцией ДЕС.В.ДВ при использовании ДВ.В.ДЕС существует ограничение на размер преобразуемых данных — не более 10 знаков в записи, в ином случае функция вернет значение ошибки.
Перевод в других системах счисления
Для других систем счисления (восьмеричной, шестнадцатеричной) также определен набор стандартных формул.
Для удобства мы составили таблицу со схемой выбора формулы для преобразования данных (в левом столбце указано откуда переводим данные, в верхней строчке — куда переводим):
Как и в примерах выше имена функций образуются по достаточно простому правилу — берутся первые буквы от названий систем в которых преобразуются данные и разделяются точками (ВОСЬМеричное В ШЕСТНадцатеричное и пр.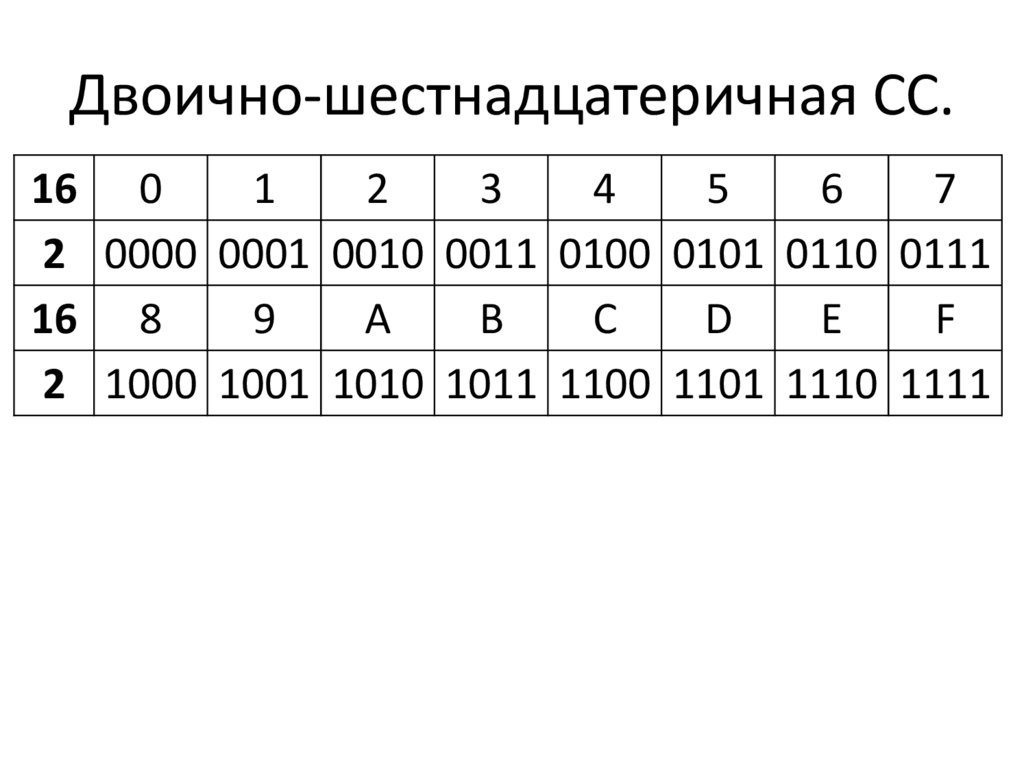
)
Арифметические операции с данными
Операции в Excel осуществляются в десятичной системе счисления, поэтому при применении арифметических действий (сложение, вычитание и т.д.) для преобразованных данных учитывайте, что конечный результат также будет записан в десятичной записи:
Чтобы избежать подобной проблемы, необходимо сначала перевести все данные в десятичный вид, произвести требуемые вычисления, а уже затем вновь преобразовать полученный результат в исходную систему счисления:
Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!
Поделиться с друзьями:
Поиск по сайту:
Математика,Функции
- ← Пузырьковая диаграмма в Excel
- Фильтр и сортировка ячеек по цвету в Excel →
Преобразователь двоичного кода в шестнадцатеричный
Преобразователь двоичного кода в шестнадцатеричныйГлавная›Преобразование›Преобразование чисел›Двоичный код в шестнадцатеричный
От BinaryDecimalOctalHexadecimalText
Кому BinaryDecimalOctalHexadecimalText
Введите двоичное число
Шестнадцатеричный номер
Десятичное число
Группировка цифр
Расчет
Преобразователь шестнадцатеричного кода в двоичный ►
Как преобразовать двоичный код в шестнадцатеричный
Преобразовать каждые 4 двоичных разряда (начиная с бита 0) в 1 шестнадцатеричный разряд с помощью этой таблицы:
| Двоичный | Шестигранник |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | А |
| 1011 | |
| 1100 | С |
| 1101 | Д |
| 1110 | Е |
| 1111 | Ф |
Пример
Преобразовать двоичное число 1101100 2 в шестнадцатеричное:
Преобразовать каждые 4 двоичных бита (из бита 0) в шестнадцатеричное число:
1101100 2 = 110 1100 = 6 C = 6C 16
Преобразователь шестнадцатеричного кода в двоичный
Напишите, как улучшить эту страницу
ПРЕОБРАЗОВАНИЕ ЧИСЕЛ
- ASCII, шестнадцатеричный, двоичный, десятичный преобразователь Преобразователь текста
- ASCII в двоичный код
- Преобразователь текста ASCII в шестнадцатеричный
- Базовый преобразователь
- Двоичный преобразователь
- Преобразователь двоичного текста в текст ASCII
- Преобразователь двоичного кода в десятичный
- Преобразователь двоичного кода в шестнадцатеричный
- Преобразователь даты в римские цифры
- Преобразователь десятичных чисел в дроби
- Преобразователь десятичных чисел в проценты
- Преобразователь десятичной системы в двоичную
- Преобразователь десятичного числа в восьмеричное
- Преобразователь десятичного числа в шестнадцатеричный
- Перевод градусов в град,мин,сек
- Перевод градусов,мин,сек в градусы
- Перевод градусов в радианы
- Преобразователь дроби в десятичную дробь
- Преобразователь дробей в проценты
- Шестнадцатеричный/десятичный/восьмеричный/двоичный преобразователь
- Преобразователь текста Hex в ASCII
- Преобразователь шестнадцатеричного кода в двоичный
- Преобразователь шестнадцатеричного кода в десятичный
- Преобразователь восьмеричных чисел в десятичные
- Преобразователь процентов в десятичные числа
- Преобразователь процентов в дроби
- Конвертер процентов в ppm Конвертер
- ppm в проценты Конвертер
- ppm в ppb Конвертер
- ppm в ppt Конвертер
- ppb в ppm Конвертер
- ppt в ppm Преобразователь
- частей на миллион
- Перевод радиан в градусы
- Преобразователь римских цифр
- Преобразователь экспоненциальной записи
RAPID TABLES
- Рекомендовать сайт
- Отправить отзыв
- О
Двоичный код в шестнадцатеричный — определение, этапы преобразования, преобразование с десятичной точкой, примеры
Преобразование двоичного кода в шестнадцатеричный — это еще один тип преобразования, который происходит в системе счисления.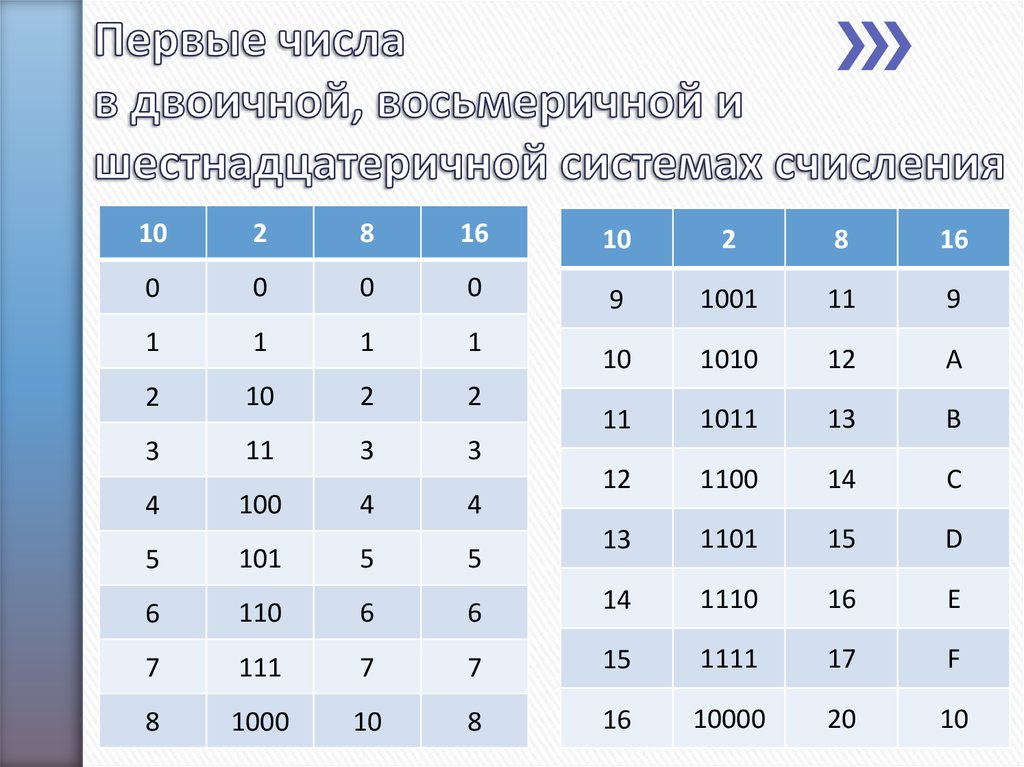
В математике существует 4 типа системы счисления: двоичная, восьмеричная, десятичная и шестнадцатеричная. Каждая из этих форм может быть преобразована в другой тип системы счисления с помощью таблицы преобразования или метода преобразования. Давайте рассмотрим различные способы преобразования двоичных чисел в шестнадцатеричные числа и решим несколько примеров для лучшего понимания.
| 1. | Что такое преобразование двоичного кода в шестнадцатеричный? |
| 2. | шагов для преобразования двоичного в шестнадцатеричный |
| 3. | Преобразование двоичного в шестнадцатеричное с десятичной точкой |
| 4. | Часто задаваемые вопросы о преобразовании двоичного кода в шестнадцатеричный код |
Что такое преобразование двоичного кода в шестнадцатеричный?
Преобразование двоичных чисел в шестнадцатеричные — это процесс преобразования двоичных чисел в шестнадцатеричные числа.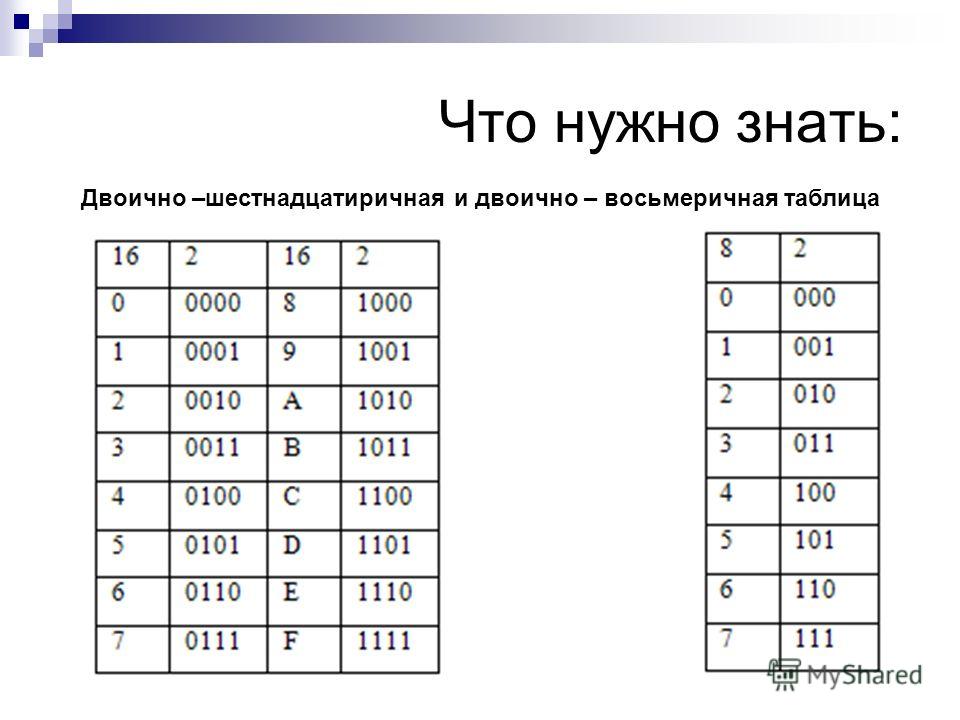
Двоичные числа имеют базовое число 2, а базовое число шестнадцатеричных — 16. Преобразование из двоичного в шестнадцатеричное происходит с помощью базовых чисел. Существуют способы, с помощью которых выполняется преобразование, первый — путем преобразования двоичного числа в десятичное число, а затем в шестнадцатеричное число. Во-вторых, с помощью двоичной таблицы преобразования в шестнадцатеричное. Прежде чем мы перейдем к методу преобразования, давайте посмотрим, что такое двоичный и шестнадцатеричный форматы.
Двоичная система счисления
Двоичная система счисления — одна из самых простых систем счисления, в которой цифры 0 и 1 используются только вместе с базовым числом 2. Двоичные числа в основном используются в компьютерах, которые очень удобны для инженеров, сетей и связи. специалиста, и во многих современных компьютерах. Цифры 0 и 1 называются битами, а 8 бит вместе составляют байт. Двоичная система счисления не работает с другими числами, такими как 2,3,4,5 и так далее.
Например: \(10110001_2, 11001101_2, 1011001_2 \) — некоторые примеры чисел в двоичной системе счисления.
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления — это позиционная система счисления в системе счисления, в которой используется базовое число 16 вместе с шестнадцатью цифрами/алфавитами: 0, 1, 2, 3, 4, 5, 6, 7. , 8, 9 и A, B, C, D, E, F. Здесь A-F шестнадцатеричной системы счисления означают соответственно числа 10-15 десятичной системы счисления. Каждая цифра в шестнадцатеричной системе счисления представляет степень основания (16). Например: \(4E7_{16}, 3F_{16}, 6D2C_{16}\) — некоторые примеры чисел в шестнадцатеричной системе счисления.
шагов для преобразования двоичного в шестнадцатеричный
Чтобы преобразовать двоичные числа в шестнадцатеричные, нам нужно использовать оба основных числа, то есть 2 для двоичных и 16 для шестнадцатеричных. Процесс преобразования происходит двумя способами. Первый метод заключается в использовании таблицы преобразования двоичного кода в шестнадцатеричный, где 1 шестнадцатеричное число эквивалентно 4 двоичным числам. Второй метод заключается в преобразовании шестнадцатеричного числа в десятичное, а затем в двоичное. Давайте рассмотрим оба метода подробно.
Способ 1. Преобразование двоичного в шестнадцатеричное с помощью таблицы преобразования
Один из самых простых и легких способов преобразования из двоичного в шестнадцатеричное — использование таблицы преобразования. Поскольку двоичные числа имеют только 0 и 1, которые называются битами, а шестнадцатеричные числа также являются позиционной системой счисления, каждые 4 бита или числа эквивалентны 1 шестнадцатеричному числу, которое также включает алфавиты от A до F. Таблица преобразования выглядит следующим образом:
Давайте рассмотрим пример для лучшего понимания.
Например: преобразовать \((00110110101)_{2}\) в шестнадцатеричное число.
Сначала мы группируем числа в набор из 4. Так как каждые 4 цифры в двоичном формате становятся одной 1 цифрой в шестнадцатеричном формате. Добавьте нули слева от последней цифры, если цифр недостаточно, чтобы составить набор из четырех:
0001 1011 0101
Взглянув на таблицу преобразования, мы можем найти эквивалентное шестнадцатеричное число.
0001 = 1 , 1011 = B , 0101 = 5
Складываем числа вместе, чтобы получить окончательное число.
Следовательно, \((00110110101)_{2}\) = \((1B5)_{16}\).
Метод 2: Преобразование двоичных чисел в шестнадцатеричные без таблицы преобразования
Двоичные числа можно также преобразовать в шестнадцатеричные без использования таблицы преобразования. Двоичные числа сначала преобразуются в десятичное, а затем в шестнадцатеричное число. Здесь базовое число десятичного числа равно 10. Двоичное число можно преобразовать в десятичное число, представив каждую цифру как произведение заданного числа 1 или 0 в соответствующей степени 2. И преобразовать из десятичного в шестнадцатеричный делим число 16 до тех пор, пока частное не станет равным нулю. Давайте посмотрим на пример для лучшего понимания.
Например: преобразовать \((0111000101001)_{2}\) в шестнадцатеричное число.
Сначала мы преобразуем двоичное число в десятичное. Для этого каждая цифра умножается на соответствующую степень двойки.
\((0111000101001)_{2}\) = 0 × 2 12 + 1 × 2 11 + 1 × 2 10 + 1 × 2 9 + 0 3 8 2 90 × 2 7 + 0 × 2 6 + 1 × 2 5 + 0 × 2 4 + 1 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
\((0111000101001)_{2}\) = 0 × 4096 + 1 × 2048 + 1 × 1024 + 1 × 512 + 0 × 256 + 0 × 128 + 0 × 64 + 1 × 32 + 0 × 16 + 1 × 8 + 0 × 4 + 0 × 2 + 1 × 1
\((0111000101001)_{2}\) = 0 + 2048 + 1024 + 512 + 0 + 0 + 0 + 32 + 0 + 8 + 0 + 0 + 1
\((0111000101001)_{2}\) = 3625
Следовательно, \((0111000101001)_{2}\) = \((3625)_{10}\).
После получения десятичного числа мы преобразуем это десятичное число в шестнадцатеричное число. Число делится на 16 до тех пор, пока частное не станет равным нулю.
3625/16 = 226 частное, остаток 9
226/16 = 14 частное, остаток 2
14/16 = 0 частное, остаток 14
Окончательное число получается путем расположения чисел снизу вверх, то есть 1429. Поскольку шестнадцатеричная система счисления имеет дело только с 0–9 в цифрах и 10–15 в алфавитах как A–F, поэтому число равно E29.
Следовательно, \((0111000101001)_{2}\) = \((E29)_{16}\).
Преобразование двоичного в шестнадцатеричное с десятичной точкой
Чтобы преобразовать двоичное число в шестнадцатеричное с десятичной точкой, мы используем метод, аналогичный тому, что использовался в предыдущем разделе. Мы используем таблицу преобразования для преобразования двоичных чисел в шестнадцатеричные. С десятичной точкой двоичное число также будет иметь дробную часть, которая считается после десятичной точки. При преобразовании десятичная точка не влияет на положение чисел. Давайте посмотрим на пример, чтобы понять это лучше.
Например: \((0100110.10110110)_{2}\)
Сначала мы группируем числа в набор из 4. Так как каждые 4 цифры в двоичном формате становятся одной 1 цифрой в шестнадцатеричном. Добавьте нули слева от последней цифры, если цифр недостаточно для составления набора из четырех:
0010 0110 . 1011 0110
Глядя на таблицу преобразования, упомянутую в предыдущем разделе, мы можем найти эквивалентное шестнадцатеричное число.
0010 = 2 , 0110 = 6 , 1011 = B , 0110 = 6
Складываем числа вместе, чтобы получить окончательное число. Десятичная точка будет в том же положении, что и в двоичном числе.
Следовательно, \((0100110.10110110)_{2}\) = \((26.B6)_{16}\).
Связанные темы
Ниже перечислены несколько интересных тем, связанных с преобразованием двоичного кода в шестнадцатеричный.
- Шестнадцатеричный код в двоичный
- Десятичный в восьмеричный
- Восьмеричный в десятичный
Часто задаваемые вопросы о преобразовании двоичного кода в шестнадцатеричный
Как преобразовать двоичный код в шестнадцатеричный?
Двоичное число в шестнадцатеричное — это форма преобразования, при которой двоичное число с основанием 2 преобразуется в шестнадцатеричное число с основанием 16.
