Таблица истинности онлайн
Назначение сервиса. Онлайн-калькулятор предназначен для построения таблицы истинности для логического выражения.Таблица истинности – таблица содержащая все возможные комбинации входных переменных и соответствующее им значения на выходе.
Таблица истинности содержит 2n строк, где n – число входных переменных, и n+m – столбцы, где m – выходные переменные.
- Решение онлайн
- Видеоинструкция
Инструкция. При вводе с клавиатуры используйте следующие обозначения:
| Клавиша | Оператор | |
|---|---|---|
| ! | ¬ | Отрицание (НЕ) |
| | | | | Штрих Шеффера (И-НЕ) |
| # | ↓ | Стрелка Пирса (ИЛИ-НЕ) |
| * | & | Конъюнкция (И) |
| + | v | Дизъюнкция (ИЛИ) |
| ^ | ⊕ | Исключающее ИЛИ, сумма по модулю 2 (XOR) |
| @ | → | Импликация (ЕСЛИ-ТО) |
| % | ← | Обратная импликация |
| = | ≡ (~, ↔) | Эквивалентность (РАВНО) |
Построение СКНФ
Построение СДНФ
Построение полинома Жегалкина
Построение карты Вейча-Карно
Минимизация булевой функции методом Квайна
Например, логическое выражение abc+ab~c+a~bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической схемы используйте этот сервис. y).
y).
Для создания любого логического устройства необходимо определить зависимость каждой из выходных переменных от действующих входных переменных такая зависимость называется переключательной функцией или функцией алгебры логики.
Функция алгебры логики называется полностью определённой если заданы все 2n её значения, где n – число выходных переменных.
Если определены не все значения, функция называется частично определённой.
Устройство называется логическим, если его состояние описывается с помощью функции алгебры логики.
Для представления функции алгебры логики используется следующие способы:
- словесное описание – это форма, которая используется на начальном этапе проектирования имеет условное представление.

- описание функции алгебры логики в виде таблицы истинности.
- описание функции алгебры логики в виде алгебраического выражения: используется две алгебраические формы ФАЛ:
а) ДНФ – дизъюнктивная нормальная форма – это логическая сумма элементарных логических произведений. ДНФ получается из таблицы истинности по следующему алгоритму или правилу:
1) в таблице выбираются те строки переменных для которых функция на выходе =1.
2) для каждой строки переменных записывается логическое произведение; причём переменные =0 записываются с инверсией.
3) полученное произведение логически суммируется.
ДНФ называется совершенной, если все переменные имеют одинаковый ранг или порядок, т.е. в каждое произведение обязательно должны включаться все переменные в прямом или инверсном виде.
б) КНФ – конъюнктивная нормальна форма – это логическое произведение элементарных логических сумм.
КНФ может быть получена из таблицы истинности по следующему алгоритму:
2) для каждого набора переменных записываем элементарную логическую сумму, причём переменные =1 записываются с инверсией.
3) логически перемножаются полученные суммы.
Fскнф=(X1 V X2 V X3) ∧ (X1 V X2 V X3) ∧ (X1 V X2 V X3) ∧ (X1 V X2 V X3)
КНФ называется совершенной, если все переменные имеют одинаковый ранг.
По алгебраической форме можно построить схему логического устройства, используя логические элементы.
Рисунок1- Схема логического устройства
Все операции алгебры логики определяются таблицами истинности значений.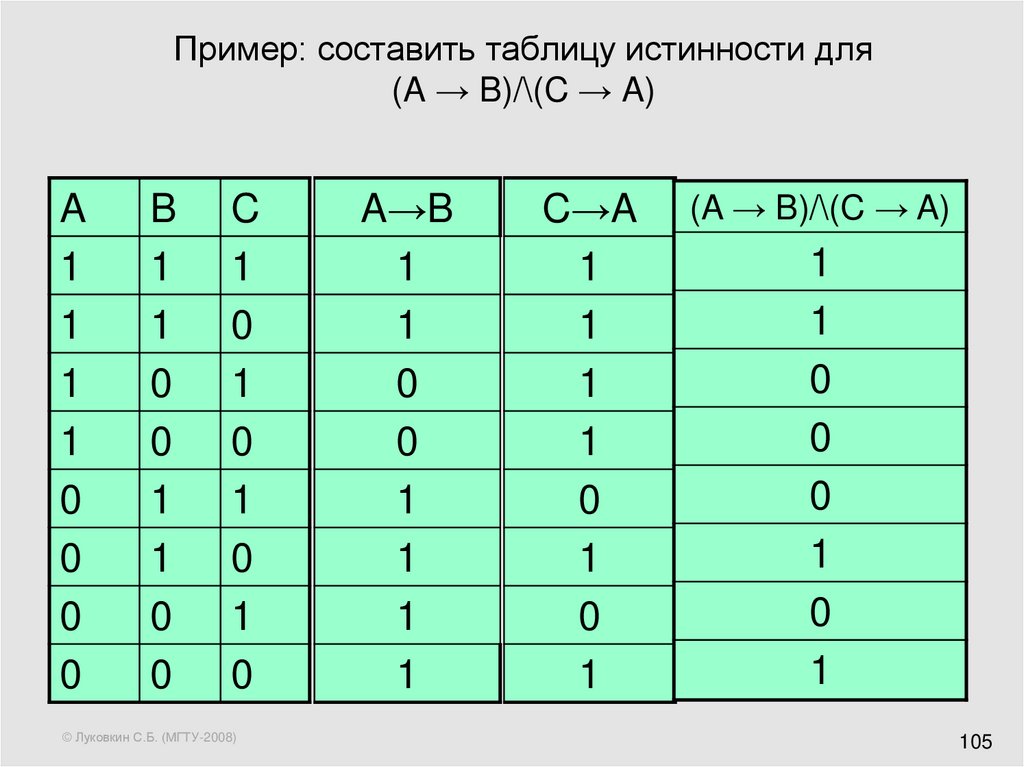 Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2N строк, так как существует 2N различных комбинаций возможных значений аргументов.
Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2N строк, так как существует 2N различных комбинаций возможных значений аргументов.
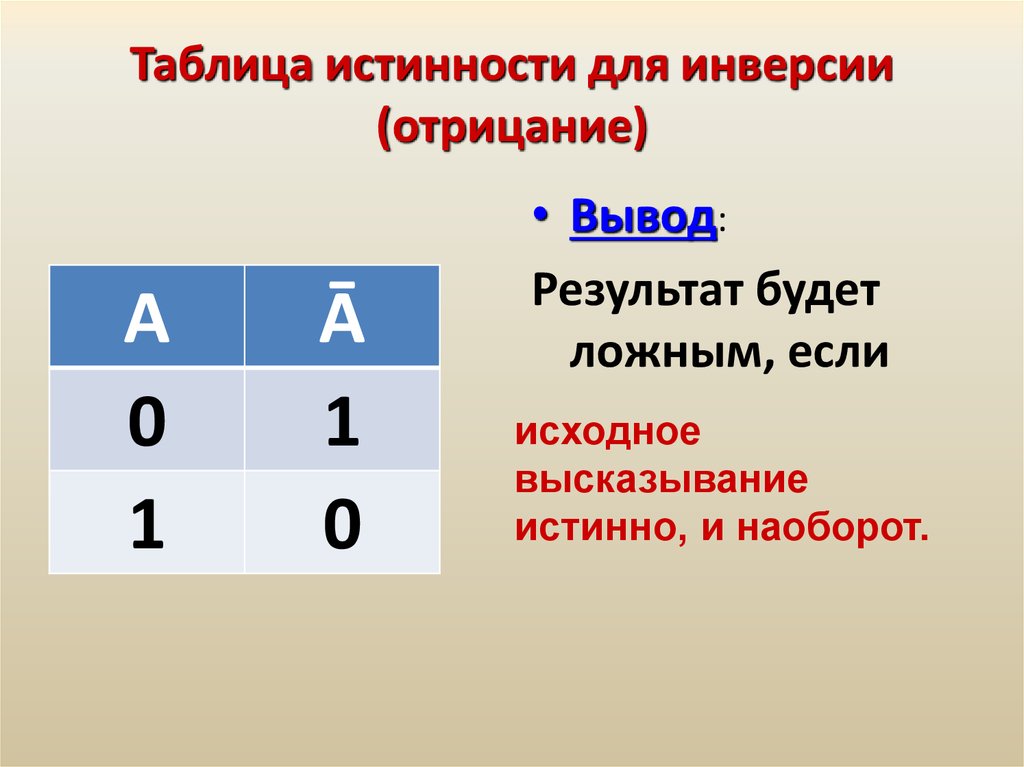
Операция НЕ — логическое отрицание (инверсия)
Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:- если исходное выражение истинно, то результат его отрицания будет ложным;
- если исходное выражение ложно, то результат его отрицания будет истинным.
не А, Ā, not A, ¬А, !A
Результат операции отрицания НЕ определяется следующей таблицей истинности:
| A | не А |
| 0 | 1 |
| 1 | 0 |
Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.
Операция ИЛИ — логическое сложение (дизъюнкция, объединение)
Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.Применяемые обозначения: А или В, А V В, A or B, A||B.
Результат операции ИЛИ определяется следующей таблицей истинности:
| A | B | А или B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В — ложны.
Операция И — логическое умножение (конъюнкция)
Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.Применяемые обозначения: А и В, А Λ В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:
| A | B | А и B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.
Операция «ЕСЛИ-ТО» — логическое следование (импликация)
Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.если А, то В; А влечет В; if A then В; А→ В.
Таблица истинности:
| A | B | А → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 |
Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
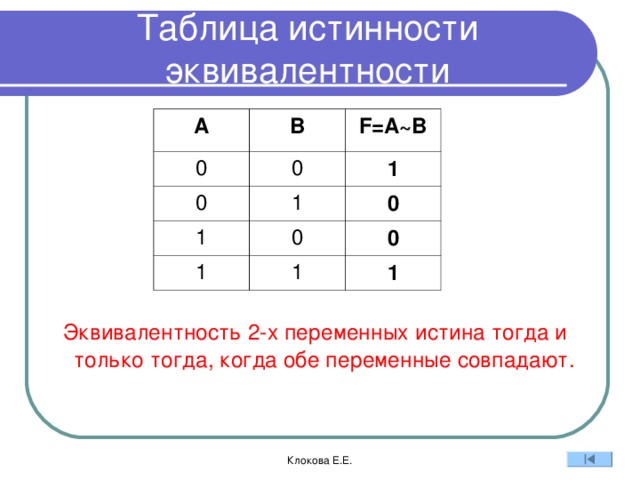
Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)
Применяемое обозначение: А ↔ В, А ~ В.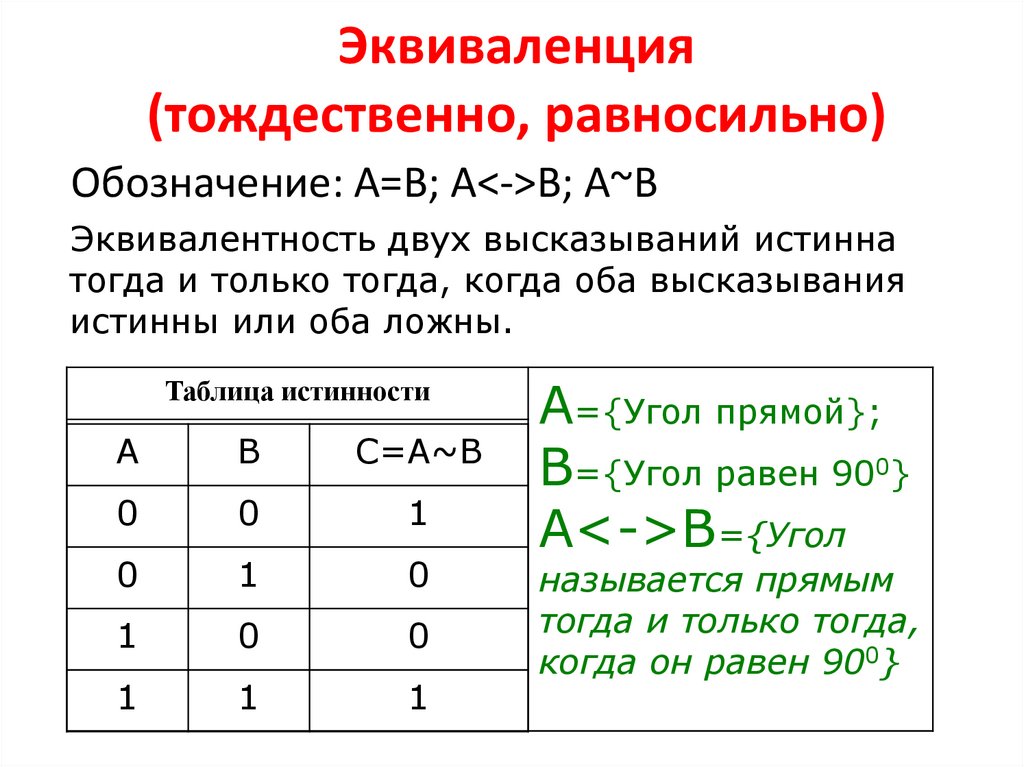
Таблица истинности:
| A | B | А↔B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.
Операция «Сложение по модулю 2» (XOR,
исключающее или, строгая дизъюнкция) Применяемое обозначение: А XOR В, А ⊕ В.
Таблица истинности:
| A | B | А⊕B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.

Приоритет логических операций
- Действия в скобках
- Инверсия
- Конъюнкция ( & )
- Дизъюнкция ( V ), Исключающее ИЛИ (XOR), сумма по модулю 2
- Импликация ( → )
- Эквивалентность ( ↔ )
Совершенная дизъюнктивная нормальная форма
Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:- Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x1,x2,…xn).
- Все логические слагаемые формулы различны.
- Ни одно логическое слагаемое не содержит переменную и её отрицание.
- Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
СДНФ можно получить или с помощью таблиц истинности или с помощью равносильных преобразований.
Для каждой функции СДНФ и СКНФ определены единственным образом с точностью до перестановки.
Совершенная конъюнктивная нормальная форма
Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:- Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x1,x2,…xn).
- Все элементарные дизъюнкции различны.
- Каждая элементарная дизъюнкция содержит переменную один раз.
- Ни одна элементарная дизъюнкция не содержит переменную и её отрицание.
Таблица истинности — Стоматология в Химках
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов.
Таблица истинности необходима для совершения логических операций. Она включает в себя n+1 столбцы и 2 n строки, где n — число используемых переменных. В первых n столбцах представлены разные значения аргументов функции, а в n+1 столбце представлены значения функции, которые она принимает на данном наборе аргументов.
Она включает в себя n+1 столбцы и 2 n строки, где n — число используемых переменных. В первых n столбцах представлены разные значения аргументов функции, а в n+1 столбце представлены значения функции, которые она принимает на данном наборе аргументов.
Набором называется совокупность значений переменных. А = 0, В = 1. В случае, когда количество переменных n, число различных наборов будет равно 2 N. Например, для трех переменных число разных наборов будет равно 2 3 = 8.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для создания таблиц истинности используются обозначения логических значений 0 (ложь) и 1 (истина).
Можно встретить вариацию таблицы, в которой число столбцов равно n + число используемых логических операций. В подобной таблице в первые n столбцы, так же как и в первом варианте, вписаны наборы аргументов, а остальные столбцы заполнены значениями подфункций, которые входят в запись функции. Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.
Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.
Применение таблиц истинности чаще всего встречается в булевой алгебре и в цифровой электронной технике для описания работы логических схем.
Логические операции — построение из одного или нескольких высказываний нового высказывания.
Результатом может являться не только образование нового высказывания, но и изменение содержания или объема уже данных высказываний. В случае логической операции истинность значения нового высказывания всецело определяется истинностью значения исходных высказываний.
К логическим операциям относятся конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, эквиваленция, антиконъюнкция, антидизъюнкция.
Логическое выражение — это запись, принимающая логическое значение «истина» или «ложь».
выражения, использующие операции сравнения и принимающие логические значения. Например, выражение aВ логические выражения могут входить функции, алгебраические операции, операции сравнения и логические операции. Для таких случаев существует алгоритм выполнения действий. За исключением тех случаев, когда в логическом выражении присутствуют скобки, влияющие на порядок выполнения операций.
Для таких случаев существует алгоритм выполнения действий. За исключением тех случаев, когда в логическом выражении присутствуют скобки, влияющие на порядок выполнения операций.
- вычисляется существующие функциональные зависимости; вычисляются алгебраические операции в обычном порядке; вычисляются операции сравнения в любом порядке; вычисляются логические операции начиная с операции отрицания. Следом вычисляется операция логического умножения, логического сложения, в последнюю очередь выполняются операции импликации и эквивалентности.
Инверсия
Инверсия или Логическое отрицание — это логическая операция, при выполнении которой из данного высказывания получается новое высказывание. Это высказывание является отрицанием исходного высказывания.
Унарной в данном случае называется операция, которая используется относительно одной величины.
Конъюнкция
Конъюнкция — это логическое умножение. Эта операция, для которой требуются два и более логических величины.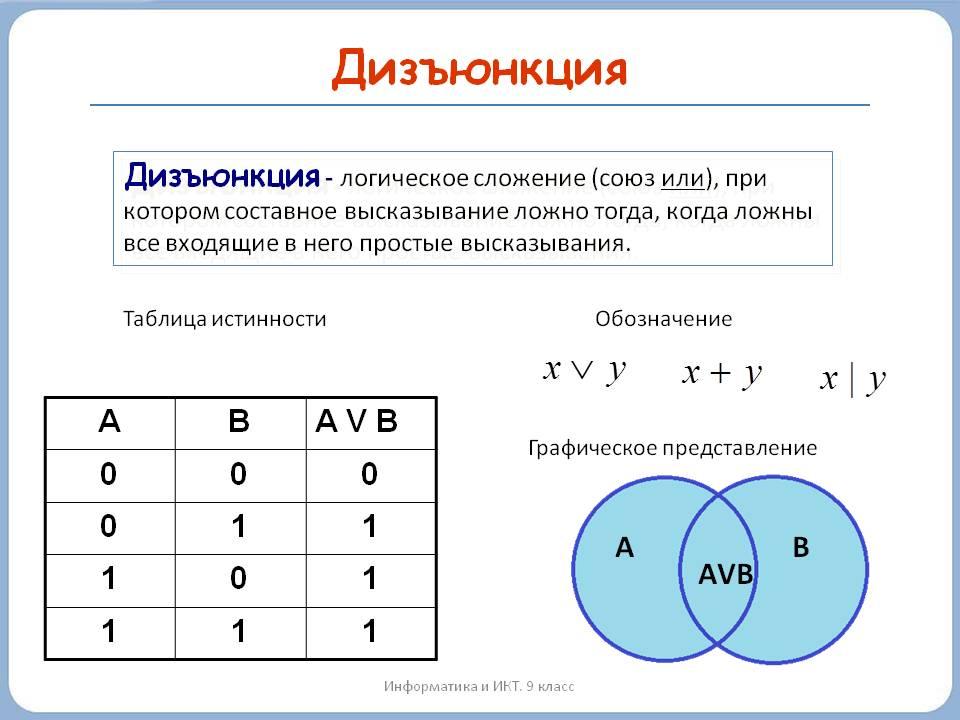 Конъюнкция соединяет логические высказывания при помощи связки «и». Связка изображается символом ∧.
Конъюнкция соединяет логические высказывания при помощи связки «и». Связка изображается символом ∧.
Конъюнкция может быть истинной только в том случае, если оба высказывания истинны. Например, A ∧ B, если A = ложь, а B = истина, является ложным.
Дизъюнкция
Дизъюнкция — логическое сложение. Эта логическая операция соединяет два и более высказываний с помощью связки «или». Эта связка обозначается как ∨.
Логическое высказывание будет истинным, если истинно хотя бы одно из условий. Например, A ∨ B истинно, даже если А = истина, а В = ложь. Высказывание будет ложным только в том случае, если ложны и А, и В.
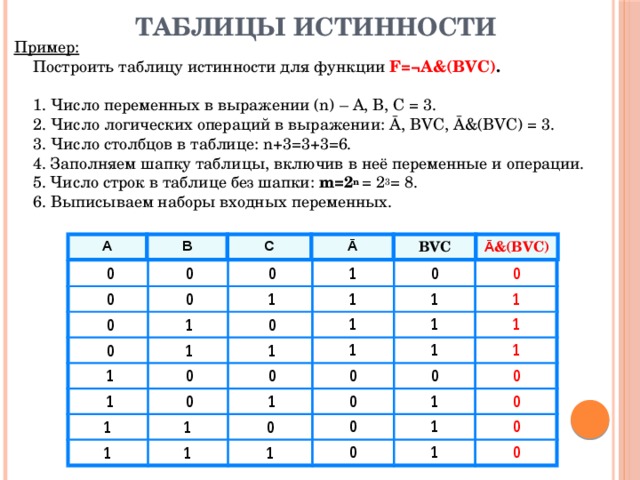
Правила составления таблицы истинности
Таблицу истинности можно построить для любого логического выражения. В этой таблице будут отражены все значения, которые принимает выражение при всех наборах значений входящих в него переменных.
Строить таблицы истинности необходимо по следующему алгоритму:
Вычислить число переменных в выражении (n).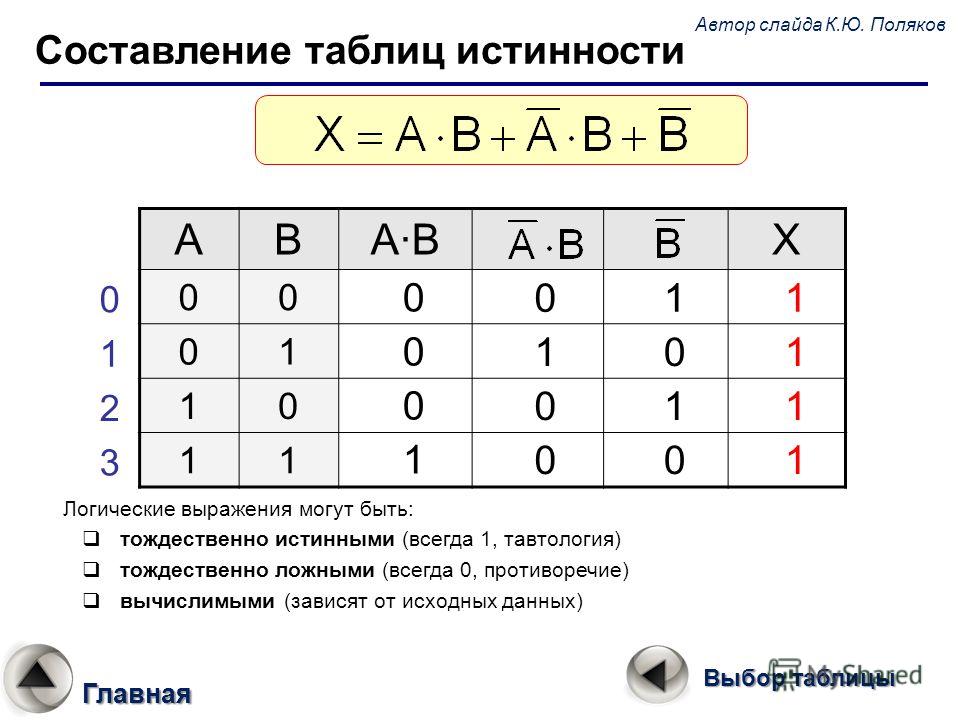 Вычислить общее количество логических операций в выражении. Определить последовательность, в которой будут выполняться логические операции. Установить количество столбцов в таблице — количество переменных и количество операций. Внести в шапку таблицы переменные и операции, соблюдая последовательность, определенную в пункте 3. Высчитать количество строк в таблице, используя формулу m = 2 n Занести в таблицу наборы входных переменных. Они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2 n −1. Заполнить таблицу, совершая логические операции.
Вычислить общее количество логических операций в выражении. Определить последовательность, в которой будут выполняться логические операции. Установить количество столбцов в таблице — количество переменных и количество операций. Внести в шапку таблицы переменные и операции, соблюдая последовательность, определенную в пункте 3. Высчитать количество строк в таблице, используя формулу m = 2 n Занести в таблицу наборы входных переменных. Они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2 n −1. Заполнить таблицу, совершая логические операции.
Примеры построения таблицы истинности
Задача
Построим таблицу истинности и решим выражение \( F = (A \vee B) \wedge (A \vee B)\) . Будем пользоваться приведенным выше алгоритмом.
Число переменных в выражении n = 2. Общее количество логических операций в выражении — 5. Последовательность выполнения логических операций — 1, 5, 2, 4, 3. Количество столбцов — 7. Логические переменные (А и В) + логические операции \(\vee\) , \(\wedge\) , \(\) , \(\vee\) , \(\) = 2 +5 = 7.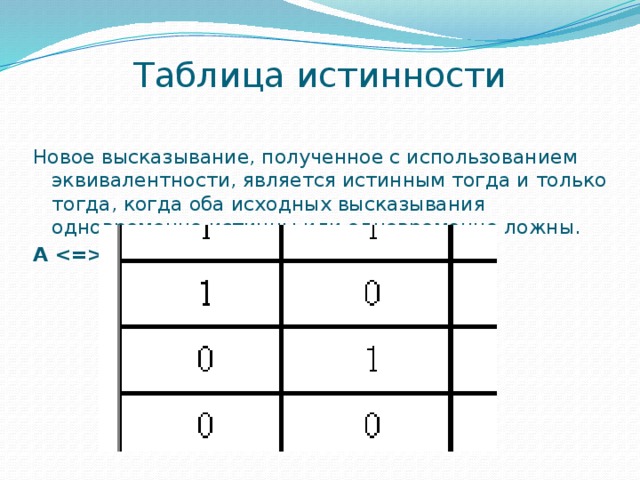 Количество строк — 5, исходя из m =2 n, таким образом 2 2 = 4, 4+1 (строка заголовков столбцов) = 5. Заполним таблицу.
Количество строк — 5, исходя из m =2 n, таким образом 2 2 = 4, 4+1 (строка заголовков столбцов) = 5. Заполним таблицу.
Решение
| А | В | \(А \vee В\) | А | В | \(А \vee В\) | \((A \vee B) \wedge (A \vee B)\) |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
После заполнения таблицы, ответ будет выглядеть следующим образом:
F = 0 при A = B = 0 и A = B = 1
Задача
Построим еще одну таблицу истинности и решим выражение \(F = X \vee Y \wedge Z\)
В случае, когда количество переменных n, число различных наборов будет равно 2 N.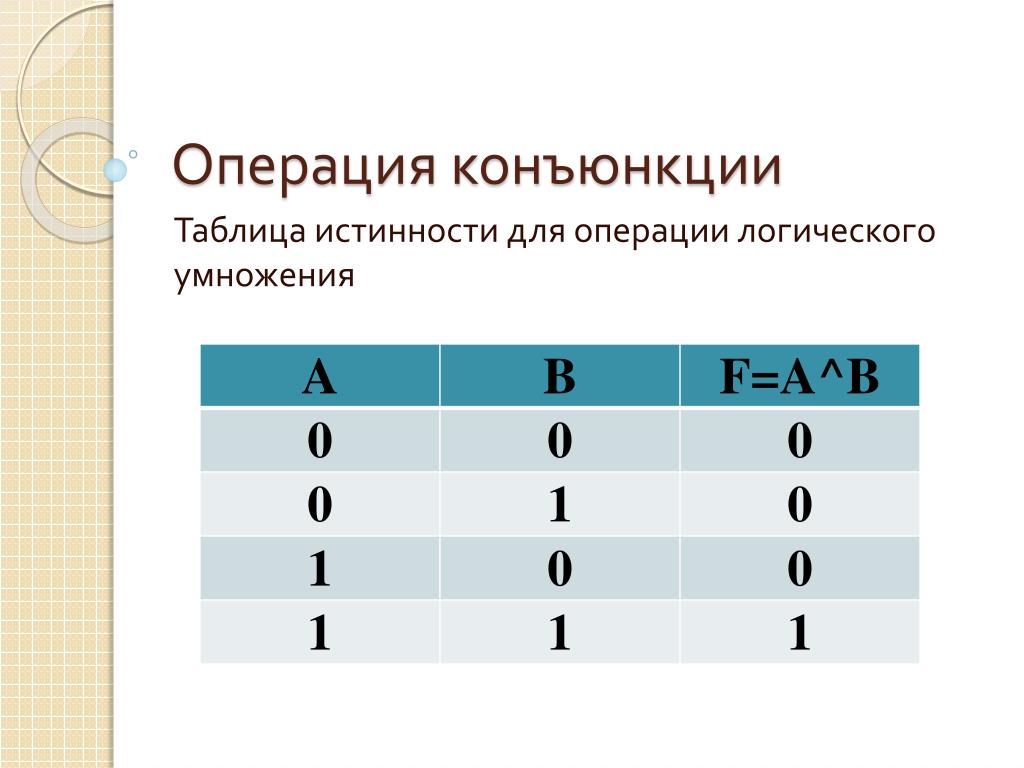
Wiki. fenix. help
22.05.2017 16:04:17
2017-05-22 16:04:17
Источники:
Https://wiki. fenix. help/informatika/tablitsa-istinnosti
Информатика: таблица истинности. Построение таблиц истинности » /> » /> .keyword { color: red; }
Таблица истинности информатикаСегодня мы поговорим о предмете под названием информатика. Таблица истинности, разновидности функций, порядок их выполнения – это наши основные вопросы, на которые мы постараемся найти ответы в статье.
Обычно данный курс преподается еще в средней школе, но большое количество учеников является причиной недопонимания некоторых особенностей. А если вы собрались посвятить этому свою жизнь, то просто не обойтись без сдачи единого государственного экзамена по информатике. Таблица истинности, преобразование сложных выражений, решение логических задач – это все может встретиться в билете. Сейчас мы рассмотрим более подробно данную тему и поможем вам набрать больше балов на ЕГЭ.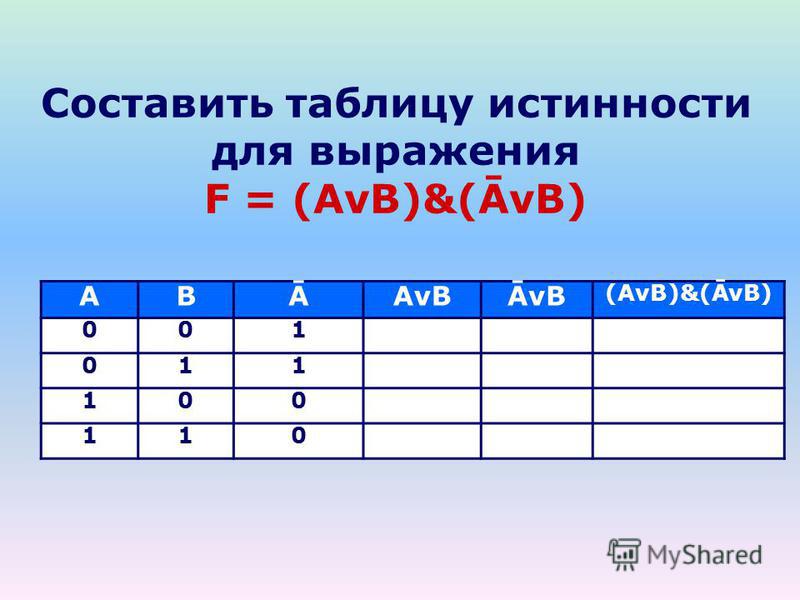
Предмет логики
Что же это за предмет — информатика? Таблица истинности – как ее строить? Зачем нужна наука логика? На все эти вопросы мы сейчас с вами ответим.
Информатика – это довольно увлекательный предмет. Он не может вызывать затруднения у современного общества, ведь все, что нас окружает, так или иначе, относится к компьютеру.
Основы науки логики даются преподавателями средней школы на уроках информатики. Таблицы истинности, функции, упрощение выражений – все это должны объяснять учителя информатики. Эта наука просто необходима в нашей жизни. Приглядитесь, все подчиняется каким-либо законам. Вы подбросили мяч, он подлетел вверх, но после этого упал опять на землю, это произошло из-за наличия законов физики и силы земного притяжения. Мама варит суп и добавляет соль. Почему когда мы его едим, нам не попадаются крупинки? Все просто, соль растворилась в воде, подчиняясь законам химии.
Теперь обратите внимание на то, как вы разговариваете.
- «Если я отвезу своего кота в ветеринарную клинику, то ему сделают прививку».
 «Сегодня был очень тяжелый день, потому что приходила проверка». «Я не хочу идти в университет, потому что сегодня будет коллоквиум» и так далее.
«Сегодня был очень тяжелый день, потому что приходила проверка». «Я не хочу идти в университет, потому что сегодня будет коллоквиум» и так далее.Все, что вы говорите, обязательно подчиняется законам логики. Это относится как к деловой, так и к дружеской беседе. Именно по этой причине необходимо понимать законы логики, чтобы не действовать наугад, а быть уверенным в исходе событий.
Функции
Для того чтобы составить таблицу истинности к предложенной вам задаче, необходимо знать логические функции. Что это такое? Логическая функция имеет некоторые переменные, которые являются утверждениями (истинными или ложными), и само значение функции должно дать нам ответ на вопрос: «Выражение истинно или ложно?».
Все выражения принимают следующие значения:
- Истина или ложь. И или Л. 1 или 0. Плюс или минус.
Здесь отдавайте предпочтение тому способу, который для вас является более удобным. Для того чтобы составить таблицу истинности, нам нужно перечислить все комбинации переменных. Их количество вычисляется по формуле: 2 в степени n. Результат вычисления – это количество возможных комбинаций, переменной n в данной формуле обозначается количество переменных в условии. Если выражение имеет много переменных, то можно воспользоваться калькулятором или сделать для себя небольшую таблицу с возведением двойки в степень.
Их количество вычисляется по формуле: 2 в степени n. Результат вычисления – это количество возможных комбинаций, переменной n в данной формуле обозначается количество переменных в условии. Если выражение имеет много переменных, то можно воспользоваться калькулятором или сделать для себя небольшую таблицу с возведением двойки в степень.
Всего в логике выделяют семь функций или связей, соединяющих выражения:
- Умножение (конъюнкция). Сложение (дизъюнкция). Следствие (импликация). Эквиваленция. Инверсия. Штрих Шеффера. Стрелка Пирса.
Первая операция, представленная в списке, имеет название «логическое умножение». Ее графически можно отметить в виде перевернутой галочки, знаками & или *. Вторая в нашем списке операция – логическое сложение, графически обозначается в виде галочки, +. Импликацию называют логическим следствием, обозначается в виде стрелки, указывающей от условия на следствие. Эквиваленция обозначается двухсторонней стрелкой, функция имеет истинное значение только в тех случаях, кода оба значения принимают либо значение «1», либо «0». Инверсию называют логическим отрицанием. Штрих Шеффера называют функцией, которая отрицает конъюнкцию, а стрелку Пирса – функцией, отрицающей дизъюнкцию.
Инверсию называют логическим отрицанием. Штрих Шеффера называют функцией, которая отрицает конъюнкцию, а стрелку Пирса – функцией, отрицающей дизъюнкцию.
Основные двоичные функции
Логическая таблица истинности помогает найти ответ в задаче, но для этого необходимо запомнить таблицы двоичных функций. В этом разделе они будут предоставлены.
Конъюнкция (умножение). Если два выражения истинны, то в результате мы получаем истину, во всех остальных случаях мы получаем ложь.
Таблица истинности как ее строить.
Autogear. ru
03.03.2017 10:27:23
2017-03-03 10:27:23
Источники:
Https://autogear. ru/article/319/401/informatika-tablitsa-istinnosti-postroenie-tablits-istinnosti/
Таблица истинности онлайн » /> » /> .keyword { color: red; }
Таблица истинности информатикаНапример, логическое выражение abc+ab~c+a~bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической схемы используйте этот сервис.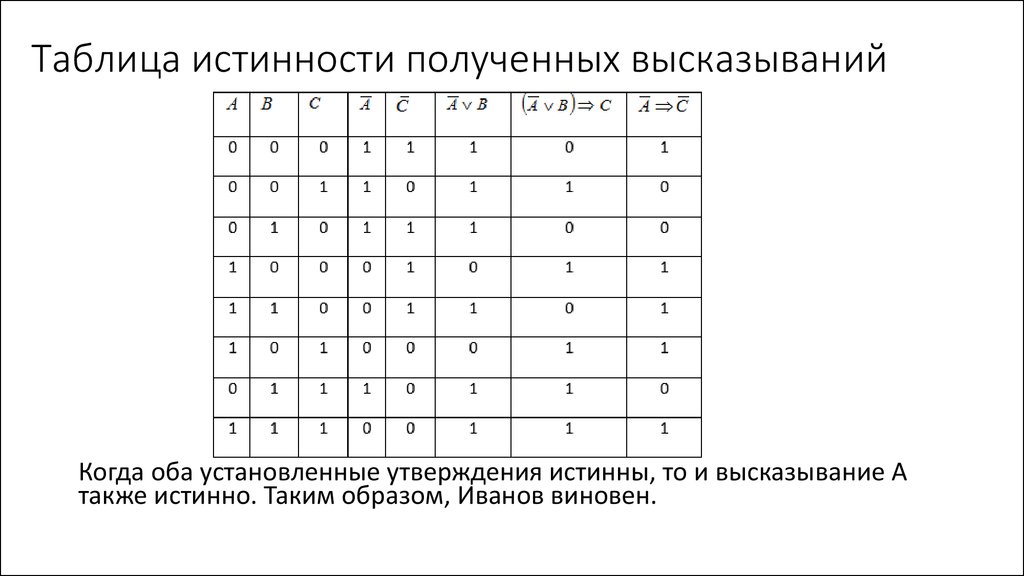 y) . Максимальное количество переменных равно 10 .
y) . Максимальное количество переменных равно 10 .
- словесное описание – это форма, которая используется на начальном этапе проектирования имеет условное представление. описание функции алгебры логики в виде таблицы истинности. описание функции алгебры логики в виде алгебраического выражения: используется две алгебраические формы ФАЛ:
А) ДНФ – дизъюнктивная нормальная форма – это логическая сумма элементарных логических произведений. ДНФ получается из таблицы истинности по следующему алгоритму или правилу:
1) в таблице выбираются те строки переменных для которых функция на выходе =1 .
2) для каждой строки переменных записывается логическое произведение; причём переменные =0 записываются с инверсией.
3) полученное произведение логически суммируется.
Fднф= X 1*Х2*Х3 ∨ Х1 x 2Х3 ∨ Х1Х2 x 3 ∨ Х1Х2Х3
ДНФ называется совершенной, если все переменные имеют одинаковый ранг или порядок, т. е. в каждое произведение обязательно должны включаться все переменные в прямом или инверсном виде.

Б) КНФ – конъюнктивная нормальна форма – это логическое произведение элементарных логических сумм.
КНФ может быть получена из таблицы истинности по следующему алгоритму:
1) выбираем наборы переменных для которых функция на выходе =0
2) для каждого набора переменных записываем элементарную логическую сумму, причём переменные =1 записываются с инверсией.
3) логически перемножаются полученные суммы.
Fскнф=(X1 V X2 V X3) ∧ (X1 V X2 V X 3) ∧ (X1 V X 2 V X3) ∧ ( X 1 V X2 V X3)
КНФ называется совершенной, если все переменные имеют одинаковый ранг.
Все операции алгебры логики определяются Таблицами истинности значений. Таблица истинности определяет результат выполнения операции для Всех возможныХ логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.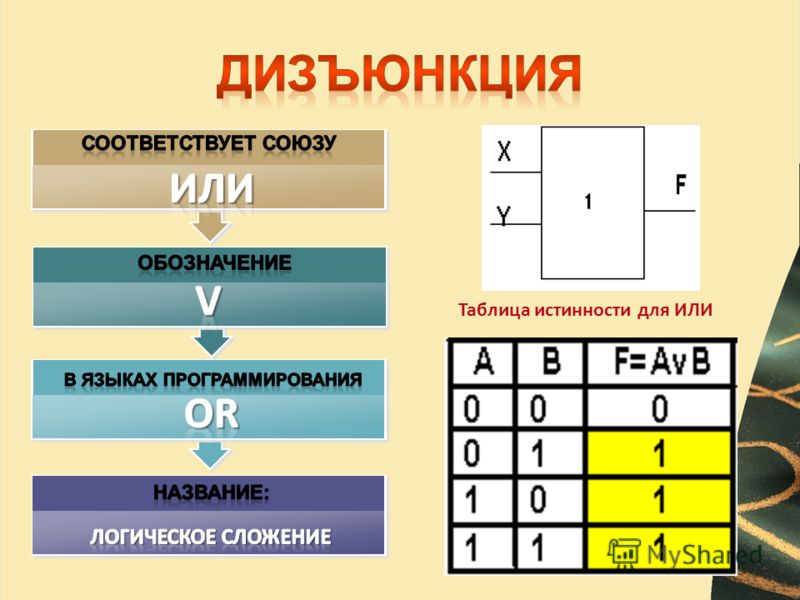 y) . Максимальное количество переменных равно 10 .
y) . Максимальное количество переменных равно 10 .
- словесное описание – это форма, которая используется на начальном этапе проектирования имеет условное представление. описание функции алгебры логики в виде таблицы истинности. описание функции алгебры логики в виде алгебраического выражения: используется две алгебраические формы ФАЛ:
А) ДНФ – дизъюнктивная нормальная форма – это логическая сумма элементарных логических произведений. ДНФ получается из таблицы истинности по следующему алгоритму или правилу:
1) в таблице выбираются те строки переменных для которых функция на выходе =1 .
2) для каждой строки переменных записывается логическое произведение; причём переменные =0 записываются с инверсией.
3) полученное произведение логически суммируется.
Fднф= X 1*Х2*Х3 ∨ Х1 x 2Х3 ∨ Х1Х2 x 3 ∨ Х1Х2Х3
ДНФ называется совершенной, если все переменные имеют одинаковый ранг или порядок, т. е. в каждое произведение обязательно должны включаться все переменные в прямом или инверсном виде.

Б) КНФ – конъюнктивная нормальна форма – это логическое произведение элементарных логических сумм.
КНФ может быть получена из таблицы истинности по следующему алгоритму:
1) выбираем наборы переменных для которых функция на выходе =0
2) для каждого набора переменных записываем элементарную логическую сумму, причём переменные =1 записываются с инверсией.
3) логически перемножаются полученные суммы.
Fскнф=(X1 V X2 V X3) ∧ (X1 V X2 V X 3) ∧ (X1 V X 2 V X3) ∧ ( X 1 V X2 V X3)
КНФ называется совершенной, если все переменные имеют одинаковый ранг.
Все операции алгебры логики определяются Таблицами истинности значений. Таблица истинности определяет результат выполнения операции для Всех возможныХ логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.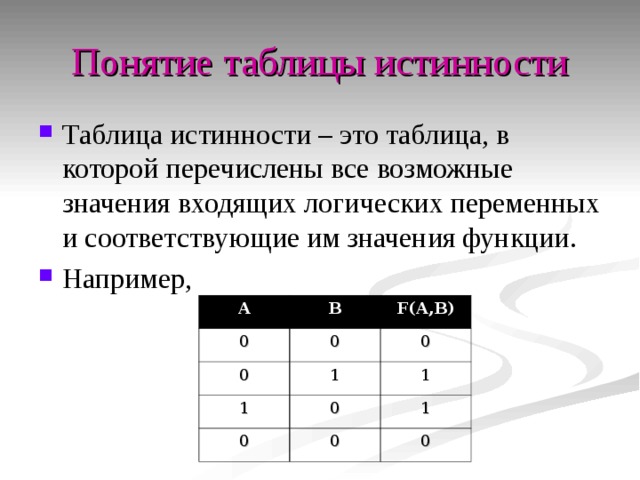
3 полученное произведение логически суммируется.
Math. semestr. ru
11.05.2019 6:56:03
2019-05-11 06:56:03
Источники:
Https://math. semestr. ru/inf/table. php
Презентация по информатике на тему Таблицы истинности 10 класс доклад, проект
ТАБЛИЦЫ ИСТИННОСТИ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
И АЛГЕБРЫ ЛОГИКИ
Ключевые слова
таблицы истинности
логическая функция
равносильные (эквивалентные) логические выражения
Таблица истинности
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений (наборах) входящих в него переменных, называют таблицей истинности логического выражения.
!
Таблицы истинности логических операций
Функцию от n переменных, аргументы которой и сама функция принимают только два значения – 0 и 1, называют логической функцией.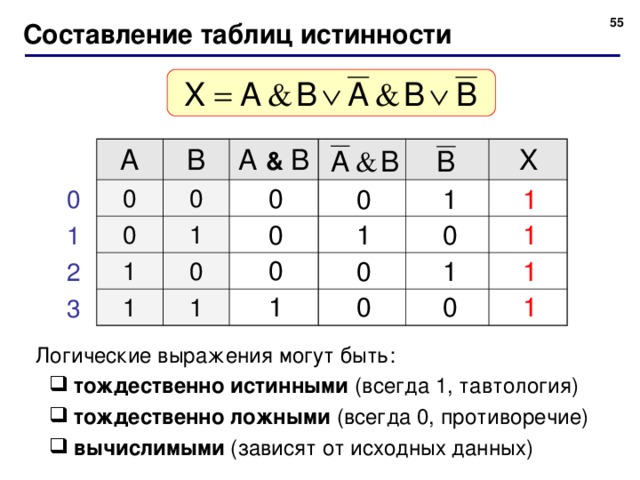
Таблица истинности может рассматриваться как способ задания логической функции.
!
Построение таблиц истинности
Пример построения таблицы истинности
Построим таблицу истинности для логического выражения
Сколько строк будет в таблице?
Сколько столбцов будет в таблице?
В этом выражении две переменные – А и В.
В таблице будет 5 строк (22 плюс строка заголовка).
В логическом выражении две логические переменные и пять логических операций. Итого 7 столбцов.
1
4
2
5
3
1
2
3
4
5
Строим таблицу из 5 строк и 7 столбцов.
Заполним заголовок таблицы с учётом приоритета логических операций (поря-док выполнения операций: инверсия, конъюнкция, дизъюнкция).
Заполним наборы входных переменных с учётом того, что они представляют собой ряд целых двухразрядных двоичных чисел от 0 до 3.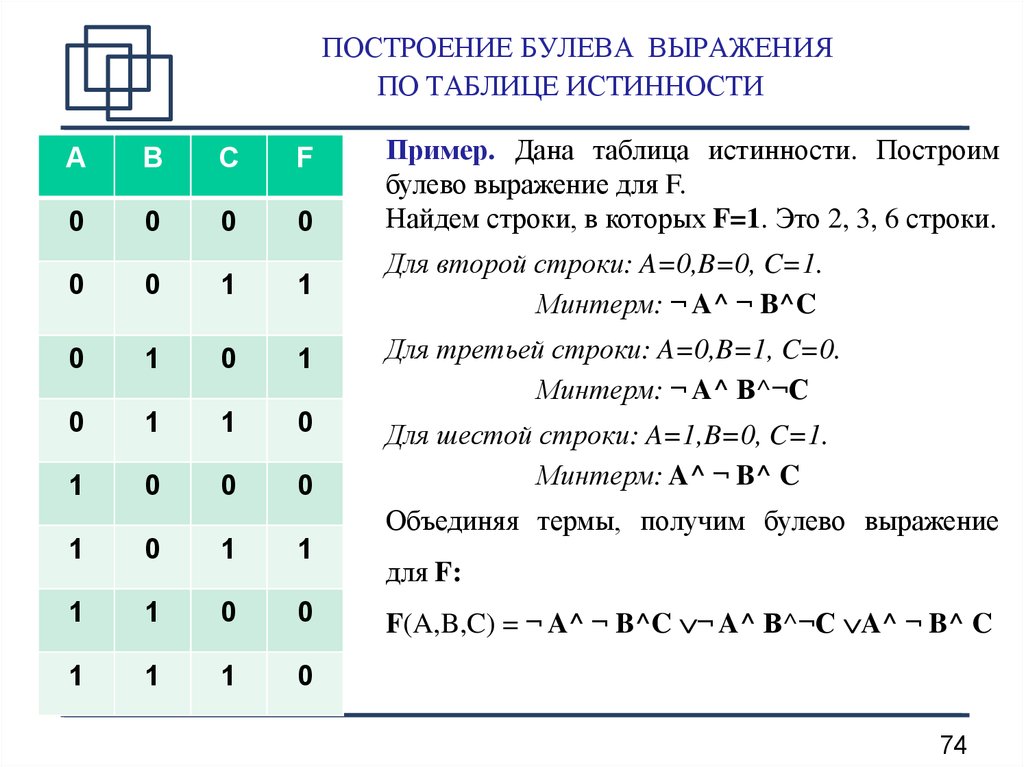
Заполним столбцы таблицы согласно правилам определения истинности логических операций.
Обратите внимание на последний стол-бец, содержащий конечный результат. Какой из рассмотренных логических операций он соответствует?
А
В
1
0
0
0
1
0
1
1
0
0
1
0
0
0
0
1
0
0
1
1
Эквивалентные выражения
Логические выражения, зависящие от одних и тех же логических переменных, называются равносильными или эквивалентными, если для всех наборов входящих в них переменных значения выражений в таблицах истинности совпадают.
!
Ответ
?
Анализ таблиц истинности
№ 1. Известен фрагмент таблицы истинности для логической функции F (А, В, С). Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
Известен фрагмент таблицы истинности для логической функции F (А, В, С). Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
а) (A ∨ С) & В
б) (A ∨ В) & (C → A)
в) (A & В ∨ С) & (В → A & С)
г) (A → В) ∨ (С ∨ A → В)
Ответить на поставленный вопрос можно, вычислив значение каждого логического вы-ражения на заданном наборе переменных и сравнив его с имеющимся значением F.
Вычисления будем производить построчно.
Таблица
Таблица
Таблица
Таблица
Ответ
Ответ: 2 (а, г)
а) (A ∨ С) & В
б) (A ∨ В) & (C → A)
в) (A & В ∨ С) & (В → A & С)
г) (A → В) ∨ (С ∨ A → В)
Анализ таблиц истинности
№ 1. Известен фрагмент таблицы истинности для логической функции F (А, В, С). Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
а) (A ∨ С) & В
1
1
1
1
1
0
1
2
а) (A ∨ С) & В
б) (A ∨ В) & (C → A)
в) (A & В ∨ С) & (В → A & С)
г) (A → В) ∨ (С ∨ A → В)
Анализ таблиц истинности
№ 1.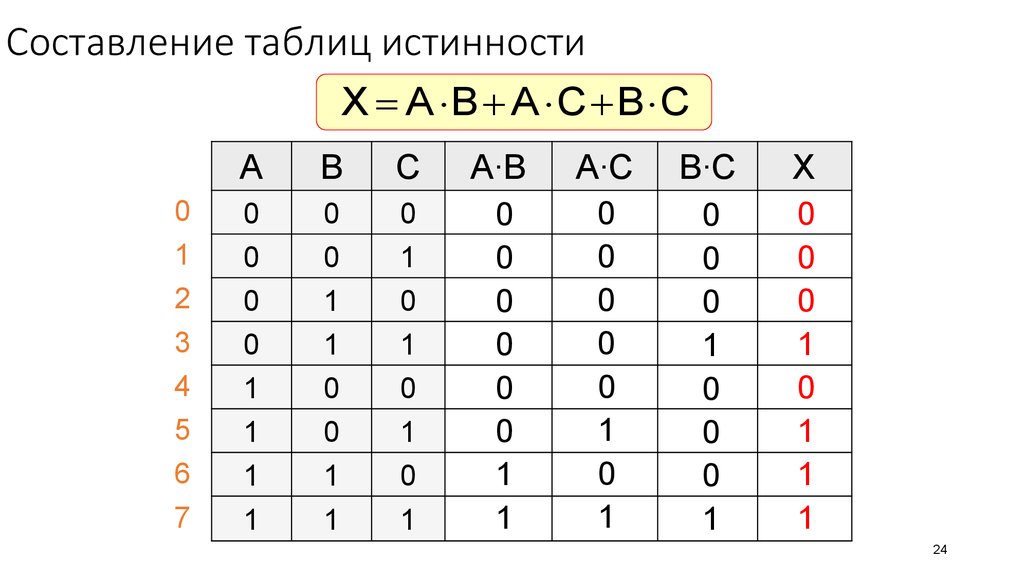 Известен фрагмент таблицы истинности для логической функции F (А, В, С). Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
Известен фрагмент таблицы истинности для логической функции F (А, В, С). Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
б) (A ∨ В) ∧ (C → A)
1
1
1
2
3
1
а) (A ∨ С) & В
б) (A ∨ В) & (C → A)
в) (A & В ∨ С) & (В → A & С)
г) (A → В) ∨ (С ∨ A → В)
Анализ таблиц истинности
№ 1. Известен фрагмент таблицы истинности для логической функции F (А, В, С). Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
в) (A ∧ В ∨ С) ∧ (В → A ∧ С)
0
1
1
2
3
1
4
5
1
1
а) (A ∨ С) & В
б) (A ∨ В) & (C → A)
в) (A & В ∨ С) & (В → A & С)
г) (A → В) ∨ (С ∨ A → В)
Анализ таблиц истинности
№ 1. Известен фрагмент таблицы истинности для логической функции F (А, В, С). Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
Известен фрагмент таблицы истинности для логической функции F (А, В, С). Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
г) (A → В) ∨ (С ∨ A → В)
0
1
1
2
3
0
4
0
1
1
1
1
1
1
1
1
Анализ таблиц истинности
№ 2. Дана логическая функция:
Справа приведён фрагмент таблицы истинности, содержащий все наборы переменных, на которых F истинна. Определите, какому столбцу таблицы соответствует каждая из переменных.
Ответ
Существуют разные подходы к решению подобных задач:
1) построение полной таблицы истинности
2) методом рассуждений
Решение
Решение
Анализ таблиц истинности
№ 2.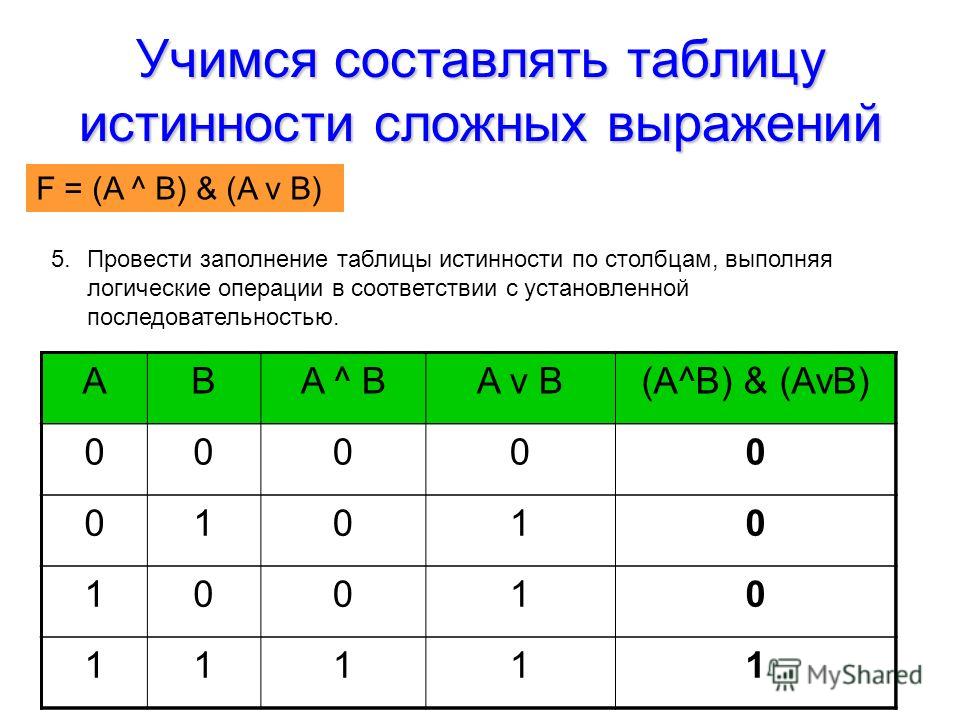
Решение:
Выясним, при каких значениях x, y, z функция F(x, y, z) = 0.
Конъюнкция («и») ложна, если хотя бы один из операндов равен нулю.
Дизъюнкция («или») ложна только в случае равенства нулю каждого из операндов, входящих в нее.
Подберём подходящие значения x, y и z, заполняя следующую таблицу:
0
1
1
Сколько строк в полной таблице истинности для данной функции?
Данная функция зависит от 3 логических переменных. Полная таблица истинности для нее должна состоять из 8 (23) строк.
При каких наборах переменных x, y, z функция F (x, y, z) = 0?
Наборы переменных, на которых функция ложна — 001, 101 и 110.
= 0
Анализ таблиц истинности
№ 2.
Решение:
Выясним, при каких значениях x, y, z функция F(x, y, z) = 0.
= 0
=0
Дизъюнкция («или») ложна только в случае равенства нулю каждого из операндов, входящих в нее.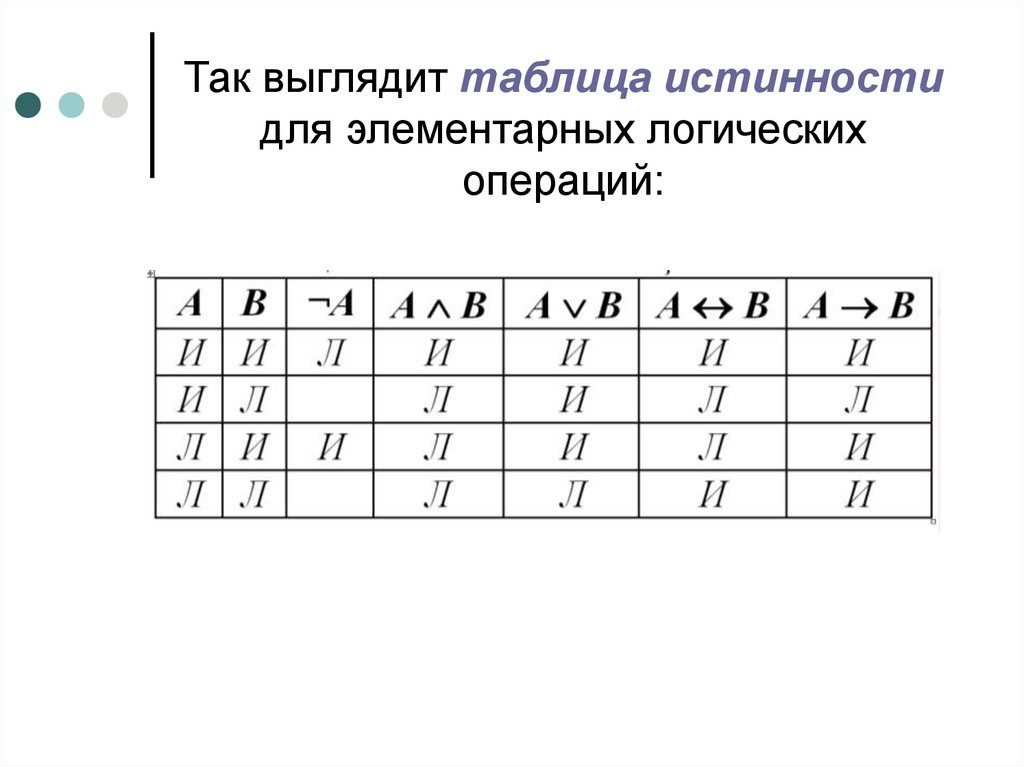
Конъюнкция («и») ложна, если хотя бы один из операндов равен нулю.
Сравним эту таблицу с восстановленным фрагментом исходной таблицы истин-ности.
x
x
y
z
y
Ответ: z, y, x
В данном примере два логических выра-жения связаны операцией «и».
Анализ таблиц истинности
Тогда в строках, где x = 1 значение y = 1.
№ 2.
Решение:
= 1
=1
0
1
x не 2-я переменная
x не 1-я переменная
y — 2-я переменная
z — 1-я переменная
Конъюнкция («и») истинна тогда и только тогда, когда каждый из операндов, входящих в нее, равен истине.
= 1
х не может быть
2-й переменной
х не может быть
1-й переменной
x
x
y – не может быть
1-й переменной
y
z
z
y
или
Ответ: z, y, x
Самое главное
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений (наборах) входящих в него переменных, называют таблицей истинности логического выражения.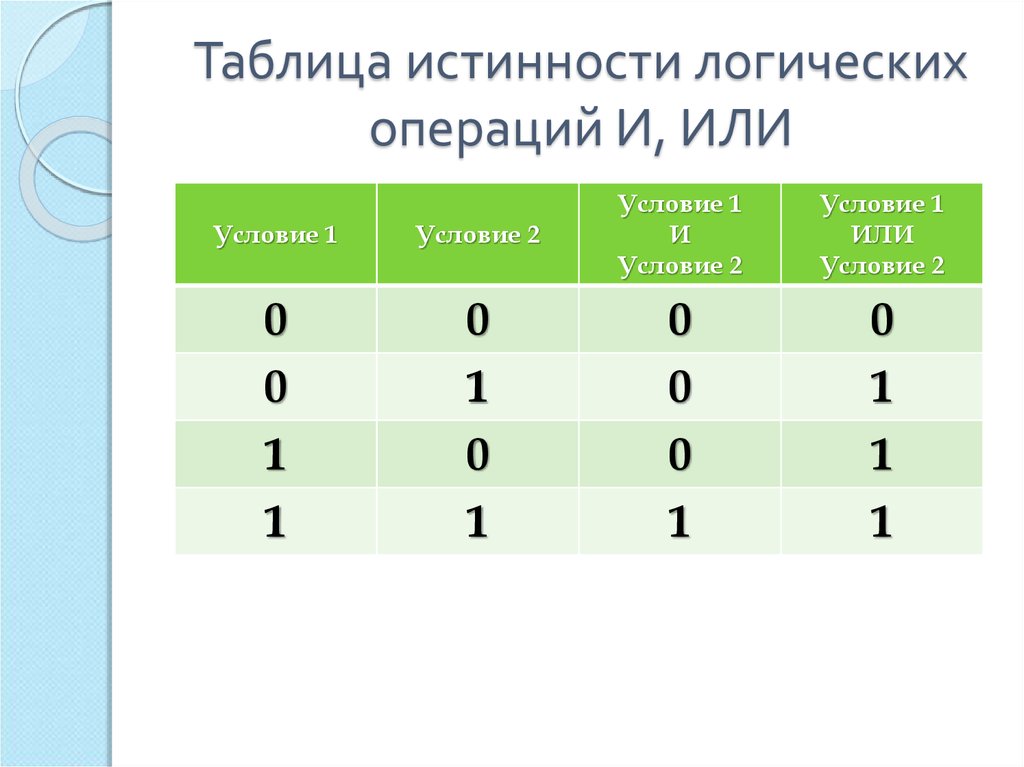
Истинность логического выражения можно доказать путём построения его таблицы истинности.
Функцию от n переменных, аргументы которой и сама функция принимают только два значения – 0 и 1, называют логической функцией.
Таблица истинности может рассматриваться как способ задания логической функции.
Вопросы и задания
№ 3. Проверьте правильность решения задания №2. Для этого составьте таблицу истинности.
Вопросы и задания
№ 4. Составлена таблица истинности для логического выражения, содержащего n переменных. Известно m — количество строк, в которых выражение принимает значение истина. Требуется выяснить, в скольких случаях логическое выражение примет значение ложь при следующих значениях n и m:
1) n = 4, m = 9
2) n = 8, m = 156
3) n = 12, m = 1596
Решение / Ответ
24 – 9 = 16 – 9 = 7
28 – 156 = 256 – 156 = 100
212 – 1596 = 4096 – 1596 = 2500
Задание 2 ЕГЭ по информатике 2023
За правильное выполненное задание получишь 1 балл. На решение отводится примерно 3 минуты.
На решение отводится примерно 3 минуты.
\lnot A, не A — отрицание, инверсия
A \land B, A и B — логическое умножение, конъюнкция
A \lor B, A или B — логическое сложение, дизъюнкция
A \to B -импликация, следование
A \equiv B — эквивалентность, равносильность
| Приоритет | Операция | Обозначение | |
| 1. Высший | НЕ | NOT | ¬,¯ |
| 2. Высокий | И | AND | &,*,Λ |
| 3. Средний | ИЛИ | OR | V, + |
| 4. Низкий | Следование | IMP | → |
| 5. Низший | Эквивалентность | EQU | ≡,↔ |
| A | B | ¬A | A Λ B | A V B | A → B | A ≡ B |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
Could not load xLike class!
Логическая функция F задаётся выражением (\lnot B \lor A \lor \lnot C) \land C.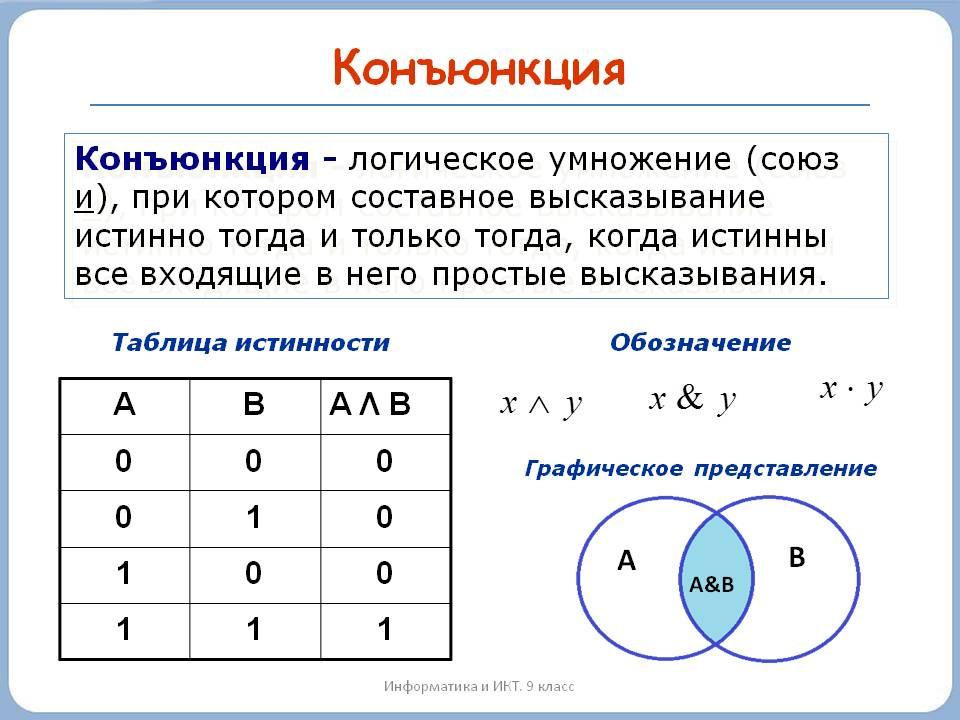 Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.
| ? | ? | ? | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы A, B, C в том порядке, в котором идут соответствующие им столбцы.
Обсуждение
Логическая функция F задаётся выражением (\lnot A \land B) \lor C \lor B . Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.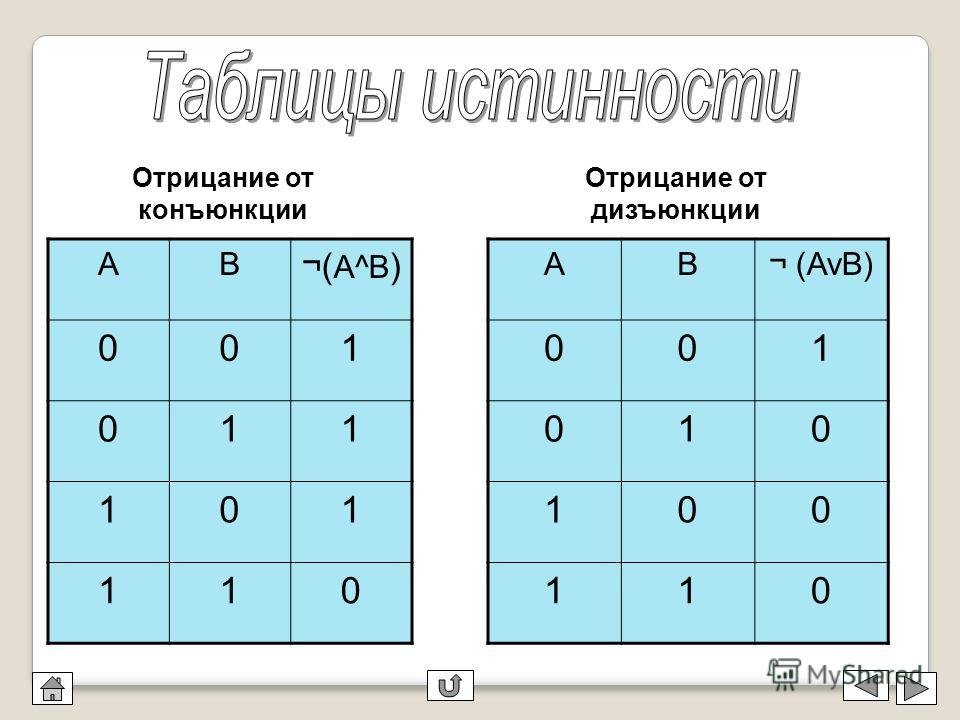
| ? | ? | ? | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы A, B, C в том порядке, в котором идут соответствующие им столбцы.
Обсуждение
Логическая функция F задаётся выражением (\lnot C \land A) \lor B \lor \lnot C . Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.
| ? | ? | ? | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы A, B, C в том порядке, в котором идут соответствующие им столбцы.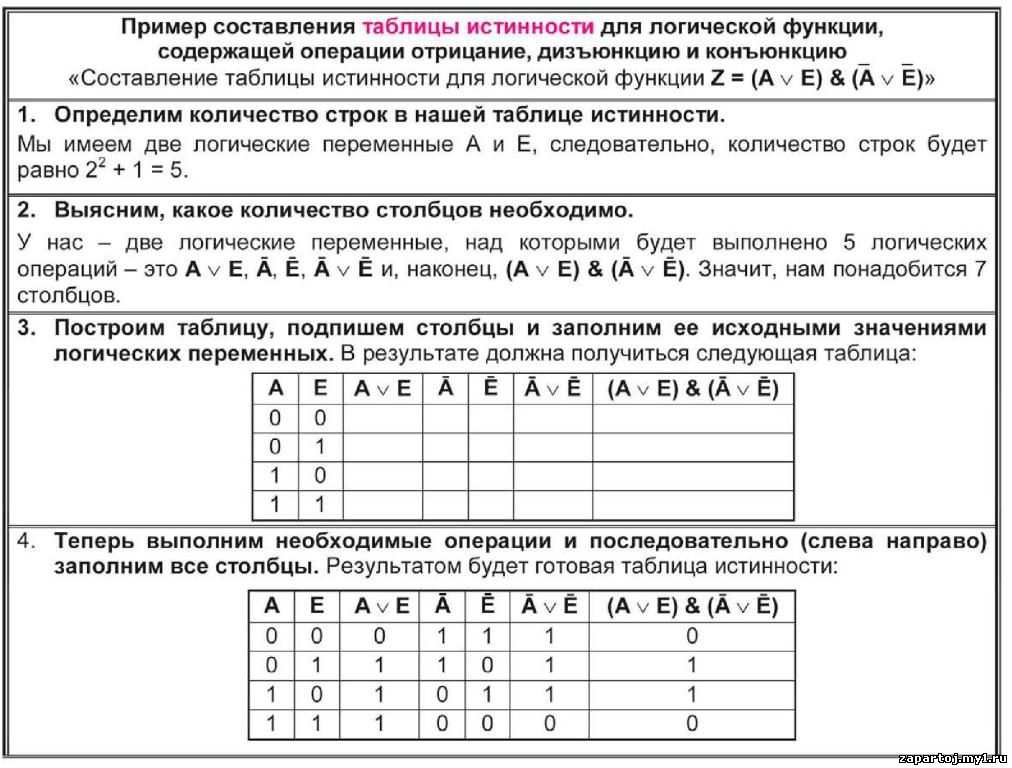
Обсуждение
Логическая функция F задаётся выражением (\lnot C \land A) \lor (C \land B \land A). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.
| ? | ? | ? | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы A, B, C в том порядке, в котором идут соответствующие им столбцы.
Обсуждение
Логическая функция F задаётся выражением C \to (A \land (B \lor C)). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.
| ? | ? | ? | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы A, B, C в том порядке, в котором идут соответствующие им столбцы.
Обсуждение
Начать
Построение таблиц истинности для логических выражений
Дата: 30.10.2020г
Класс: 8
Учитель: Муртазова Эльмира Вахитова
Ученики:_Мудаева Т.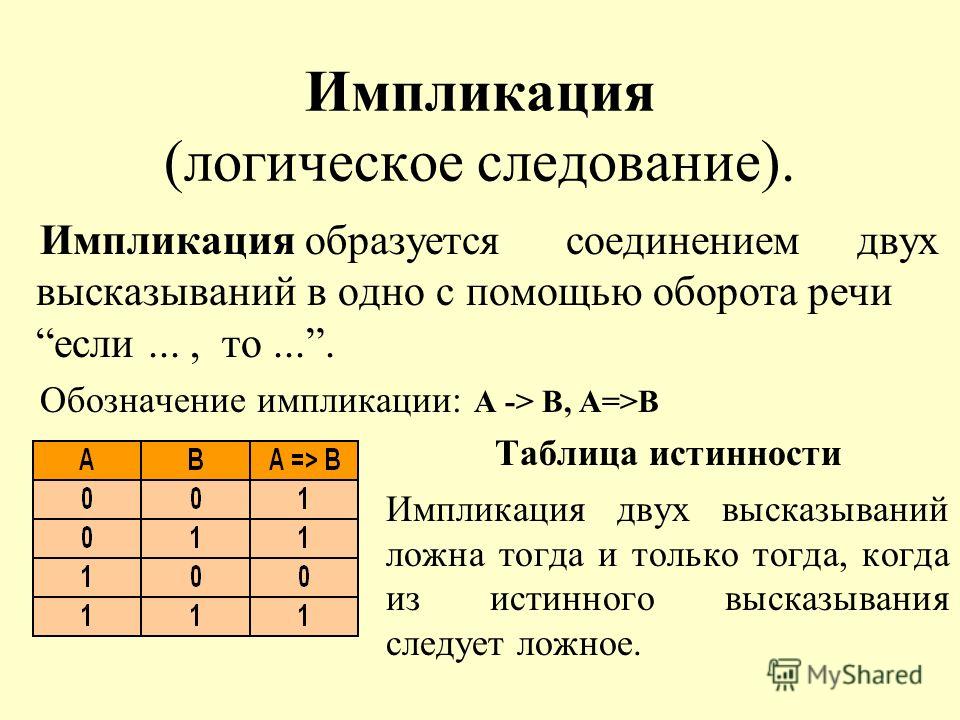 , Дайтаева И
, Дайтаева И
________________________________________________________________________________Автор учебника: Л. Л. Босова, А. Ю. Босова
Тема: «Построение таблиц истинности для логических выражений»
Цель урока: сформировать умения строить и заполнять таблицы истинности
Задачи:
Обучающие: изучить последовательность действий построения таблиц истинности, сформировать умение применять алгоритм заполнения таблиц истинности, научить находить значение логических выражений посредством построения таблиц истинности.
Развивающие: развивать логическое мышление и познавательный интерес к предмету, развивать внимание, память, речь учащихся.
Воспитательные: воспитывать культуру общения, формировать интеллектуальную и эмоциональную активность учащихся, воспитывать чувства ответственности за результаты своего труда.
Тип урока: урок изучения и первичного закрепления новых знаний.
План урока:
Организационный момент (2 мин.)
Повторение материала предыдущего урока, проверка ДЗ (5 мин.)
Объяснение нового материала (14 мин.)
Физкультминутка (2 мин.)
Закрепление разбор примера (5 мин.)
Задания для самостоятельной работы (8 мин.)
Подведение итогов, рефлексия (3 мин)
Домашнее задание (1 мин.)
Оборудование и программный материал:
ХОД УРОКА
I. Организационный момент
Здравствуйте ребята. Мы уже несколько уроков изучаем тему (главу) «Математические основы информатики». Слайд 1 И сегодня еще мы узнаем много нового. Вы готовы к этому?
Эпиграфом к уроку являются слова Б.Паскаля: “ВЕЛИЧИЕ ЧЕЛОВЕКА — В ЕГО СПОСОБНОСТИ МЫСЛИТЬ”. Слайд 2
На предыдущем уроке мы увидели, что логика достаточно крепко связана с нашей повседневной жизнью, а также увидели, что почти любое высказывание можно записать в виде формулы.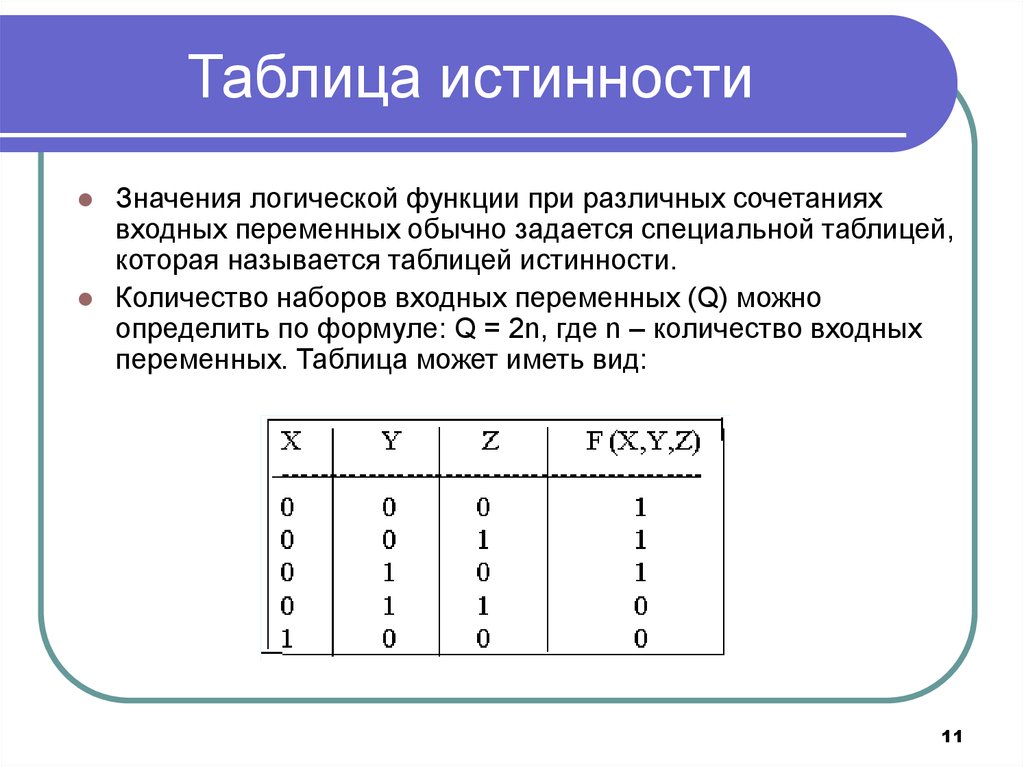 В
В
Рыбу ловят сачком, или ловят крючком, или мухой приманивают, или червячком
А V В V С V В
Давайте вспомним основные определения и понятия, выполните задания в Якласс (4 слайд):
Задания в Якласс
1. Числовые выражения (1 Б.)
Определи, является ли высказыванием: 5⋅2
является высказыванием
не является высказыванием
2. Предложение (2 Б.)
«Капитанская дочь» — самое весёлое стихотворение.
нельзя однозначно определить
истинное
ложное
(Повесть)
3. Высказывания в геометрии (2 Б.)
Определи, высказывание является ложным или истинным.
Площадь прямоугольника с длинами сторон c и d равна c⋅d.
нельзя однозначно определить
истинное
ложное
4. Основные понятия (1 Б.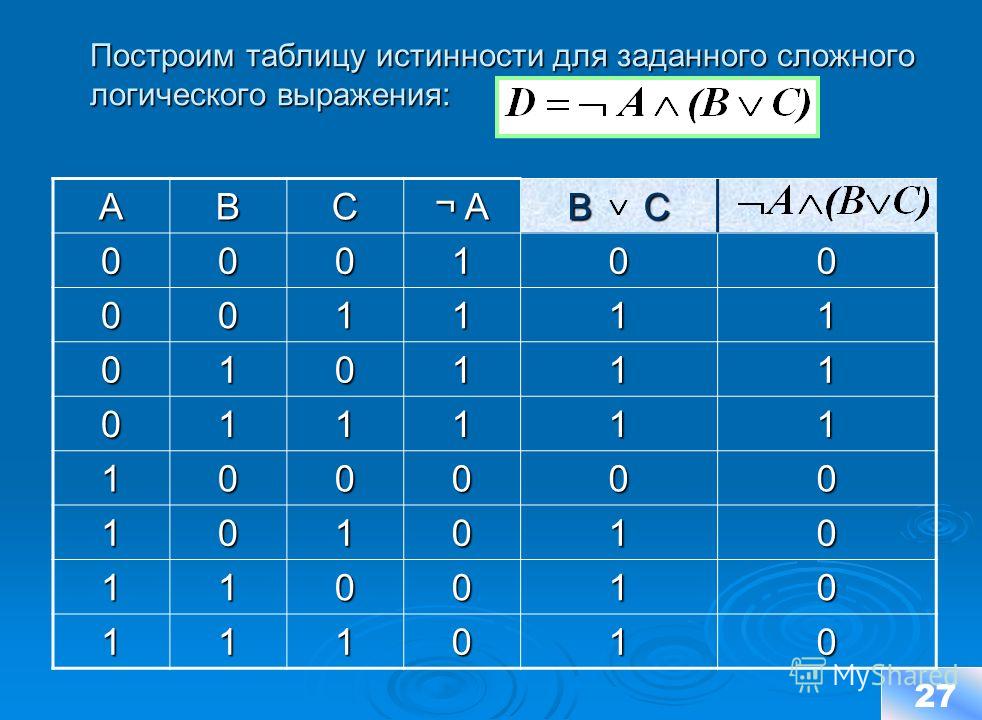 )
)
Выбери верный ответ.
В алгебре логики высказывания обозначают буквами и называют ________________________.
логические переменные
истинное высказывание
геометрия логики
математическое предложение
III. Объяснение нового материала
На Слайде 5 логическое выражение: F = X ИЛИ Y И (НЕ Z). Записать данное выражение, заменяя логические связки на знаки, которые используются для записи логических операций.
(F = X + Y * ¬Z)
Давайте найдем значение данного выражения при значениях переменных Х=1;У=1; Z=0.
Для нахождения значения функции необходимо подставить значении переменных в формулу.
Ответ: F=1+1*(не 0)= 1+1*1=1.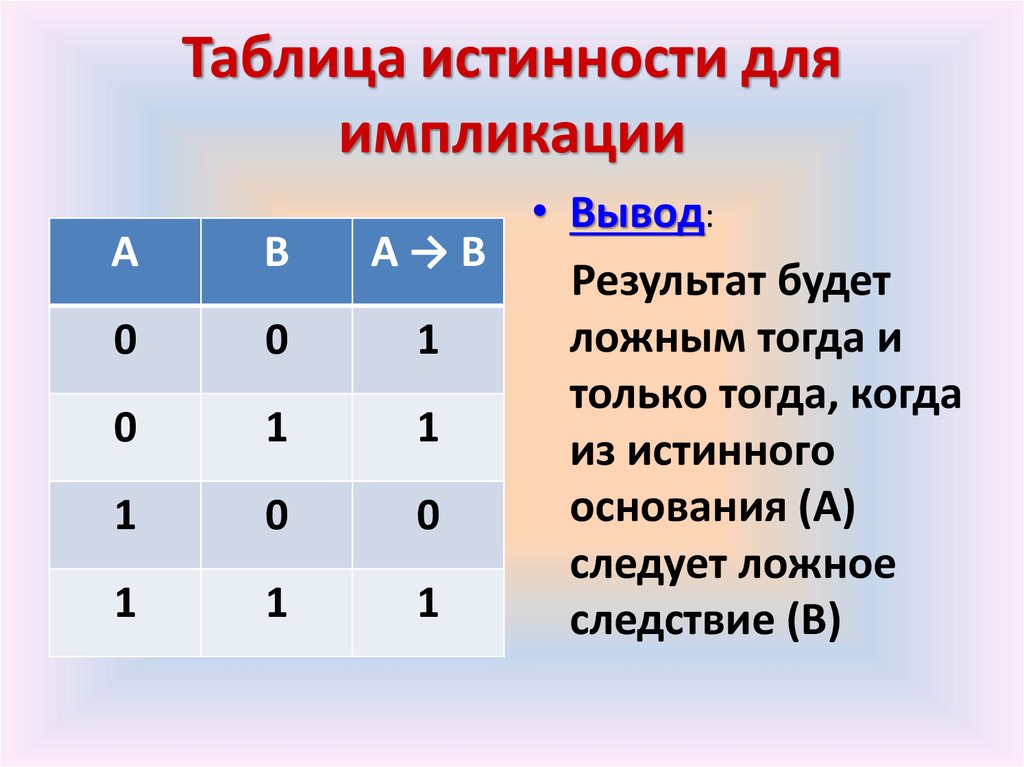
Это единственное значение, которое может принять наша функция? (Нет).
От чего зависит значения функции? (От значений переменных X,Y, Z)
Из ранее изученного материала, нам известно, что для нахождения значения функции логической операции: инверсия, конъюнкция, дизъюнкция мы использовали таблицу истинности. А кто может сформулировать тему нашего урока:
Слайд 7 «ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ»
Запишем тему урока в тетрадь. Давайте вместе с вами постараемся дать определение понятию ТАБЛИЦА ИСТИННОСТИ.
Слайд 8 Таблица истинности – это таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний
Для того, что бы построить ТИ необходимо пользоваться определенным алгоритмом: см.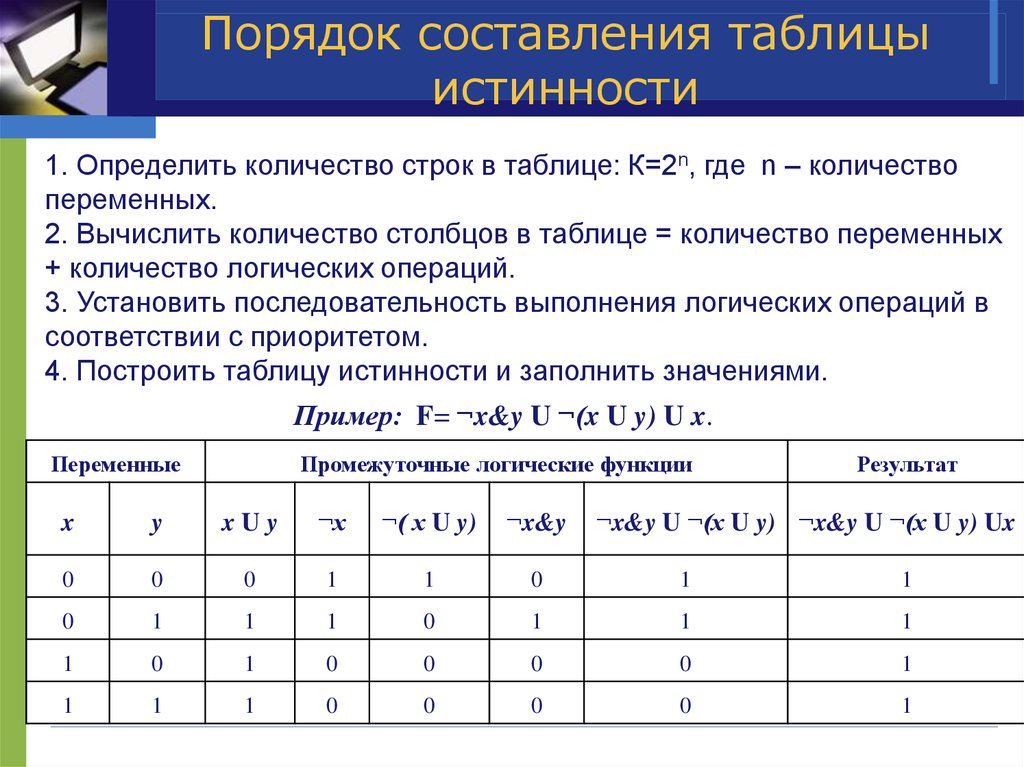 учебник с.29
учебник с.29
Приоритеты операций
скобки
отрицание
конъюнкция
дизъюнкция
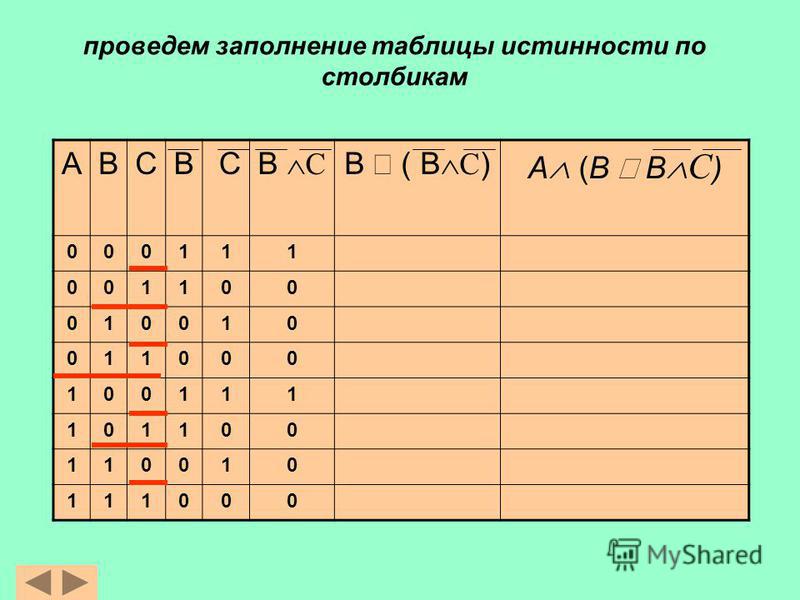
Пример: Для формулы A* (B * С) построить таблицу истинности (слайд 9)
Следуя пунктам алгоритма получаем: (слайд 10)
1. посчитаем n: 3
2. посчитаем общее число логических операций в выражении: 3
3. установим последовательность выполнения логических операций с учетом скобок и приоритетов
4. определим число столбцов в таблице: 3 + 3 = 6
5. заполним шапку таблицы, включив в нее и операции в соответствии с последовательностью, установленной в п. 3
6. определим количество строк в таблице (не считая шапки таблицы) m = 2n : 23 = 8
7. выписать наборы входных переменных:
1.разделить колонку значений первой переменной пополам и заполнить верхнюю часть «1», а нижнюю «0»;
2.разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «1» и «0», начиная с группы «1»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «1» или «0» до тех пор, пока группы «1» и «0» не будут состоять из одного символа.
продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «1» или «0» до тех пор, пока группы «1» и «0» не будут состоять из одного символа.
8. провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
A | B | C | B* | A* (B *) | |
1 | 1 | 1 | 0 | 0 | 0 |
1 | 1 | 0 | 1 | 1 | 1 |
1 | 0 | 1 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 1 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 0 | 0 |
IV. Физкультминутка
Физкультминутка
Гимнастика для глаз (слайд 12)
V. Закрепление новых знаний
Построить таблицы истинности для следующих выражений:
Слайд 13-14
(Задания выведены на слайде)
VI. Контроль знаний (если останется время)
Слайд 15-16
Вариант 1
Составить таблицу истинности для логического выражения
(А + В) * (¬А * А +В)
Вариант 2
Составить таблицу истинности для логического выражения
(А * В) + (¬ В+А)
VII. Рефлексия
Слайд 16
Личностное осмысление каждым учеником результатов урока
Что было наиболее трудным?
Что удалось лучше всего?
Сегодня на уроке мы научились определять истинность составных высказываний, но больше с математической точки зрения, так как вам были даны не сами высказывания, а формулы, отображающие их. На следующих уроках мы закрепим эти умения и постараемся их применить к решению логических задач.
На следующих уроках мы закрепим эти умения и постараемся их применить к решению логических задач.
VIII. Домашнее задание
Слайд 17
Домашняя работа:
§1.3.3
Составить таблицы истинности для логических выражений
Слайд 18 спасибо за урок
Приложение 1
Вариант 1
Составить таблицу истинности для логического выражения
(А + В) * (¬А * А +В)
Вариант 2
Составить таблицу истинности для логического выражения
(А * В) + (¬ В+А)
Приложение 2
Домашняя работа: §1.3.3, №8,10
Логические выражения и таблица истинности
Логические выражения и таблица истинности
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.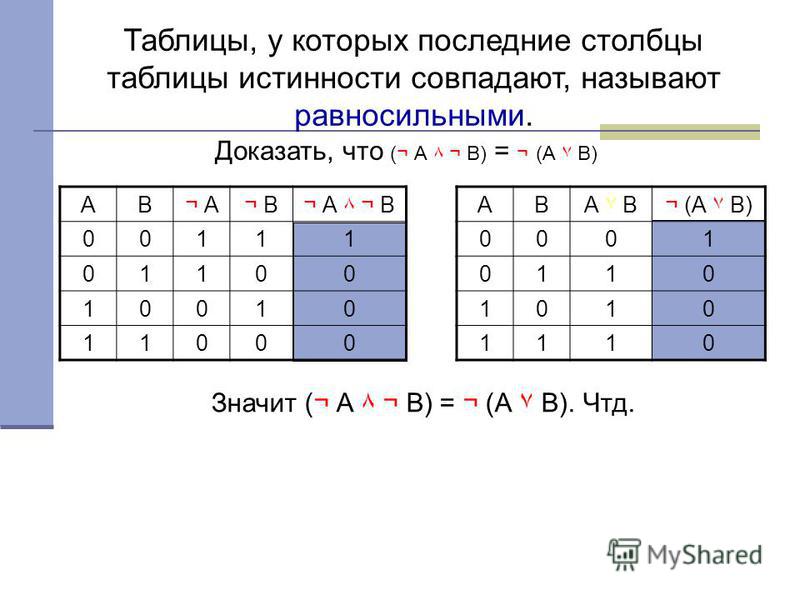
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2n, где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.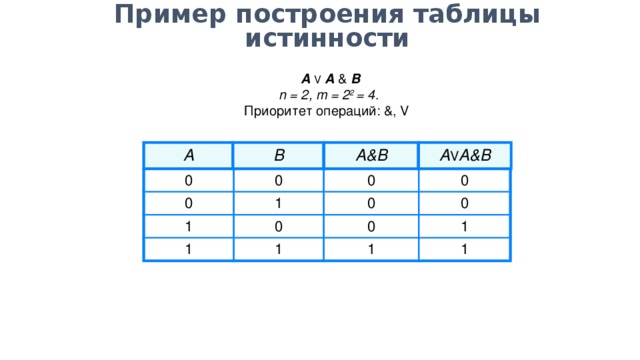
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
Пример 2. Определите истинность логического выражения F(А, В) = (А\/ В)/\(¬А\/¬В) .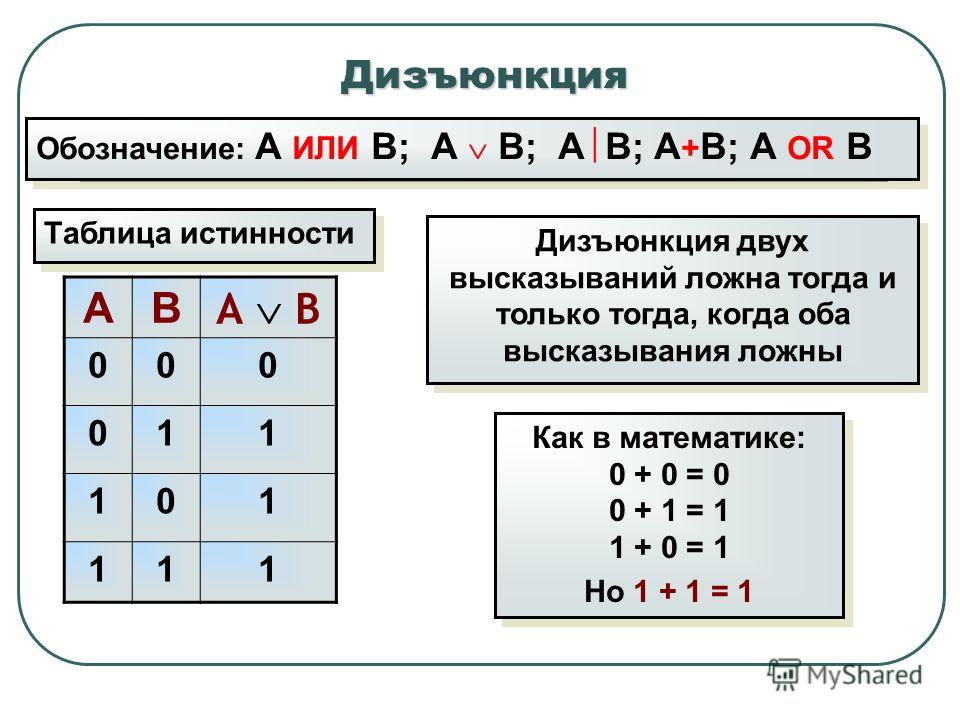
1. В выражении две переменные А и В (n=2).
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
А | В | А\/ В | ¬А | ¬В | ¬А\/¬В | F |
0 | 0 | 0 | 1 | 1 | 1 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 0 | 0 |
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Пример 3. Построёте таблицу истинности для логического выражения
F = (A\/ B) /\ ¬С
В данной функции три логические переменные – А, В, С
количество строк таблицы = 23 =8
В формуле 3 логические операции.
Расставляем порядок действий
1) А\/ В; 2) ¬С; 3) (AVB) /\ ¬С .
количество столбцов таблицы = 3 + 3 = 6
А | В | С | A\/B | ¬С | (A\/B) /\ ¬С |
0 | 0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 1 | 0 | 0 |
1 | 0 | 0 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 0 |
1 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 1 | 0 | 0 |
Пример 4.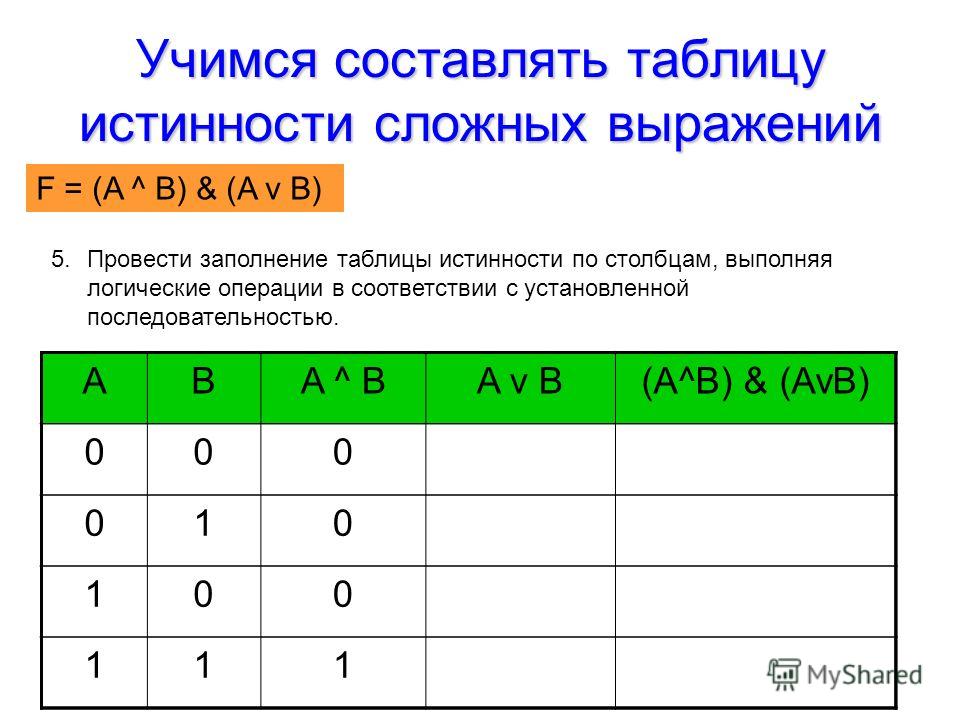 Определите истинность формулы: F = ((С \/В) В) /\ (А /\ В) = В.
Определите истинность формулы: F = ((С \/В) В) /\ (А /\ В) = В.
Построим таблицу истинности этой формулы.
Ответ: формула является тождественно истинной.
Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
X | Y | Z | F |
0 | 0 | 0 | 1 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 1 |
Какое выражение соответствует F?
1) ¬X/\¬Y/\Z 2) ¬X\/¬Y\/Z 3) X\/Y\/¬Z 4) X\/Y\/Z
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
X | Y | Z | F | ¬X | ¬Y | ¬Z | ¬X/\¬Y/\Z | ¬X\/¬Y\/Z | X\/Y\/¬Z | X\/Y\/Z |
0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z.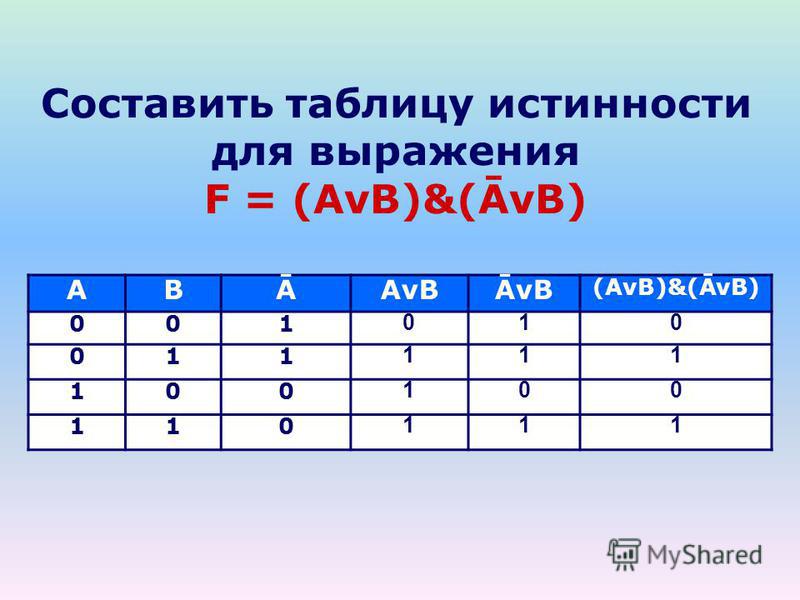 Следовательно, правильный ответ – 3.
Следовательно, правильный ответ – 3.
Ответ: 3
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
1) первое заданное выражение ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2) второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X\/Y\/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Ответ: 3
Доказательства таблицы истинности — Информатика
Из Информатики
Перейти к: навигация, поиск
Таблицы истинности используются для отображения всех возможных значений, которые может принимать данное логическое выражение.
Содержимое
- 1 Примеры
- 1.1 Определение И
- 1.2 Доказательство одного из законов Де Моргана
- 1.3 Опровержение логической ошибки
- 2 Назначение 1
- 3 Назначение 2
Определение И
Ниже приводится определение логической операции И.
| А | Б | А ∧ Б |
|---|---|---|
| ложный | ложь | ложь |
| ложный | правда | ложь |
| правда | ложь | ложь |
| правда | правда | верно |
Доказательство одного из законов Де Моргана
Таблицу истинности также можно использовать для доказательства логического тождества. Следующее доказывает закон Де Моргана, что ¬ (A ∧ B) эквивалентно (¬ A) ∨ (¬ B). Обратите внимание, что значения истинности для них (последние два столбца в таблице) всегда одинаковы.
Следующее доказывает закон Де Моргана, что ¬ (A ∧ B) эквивалентно (¬ A) ∨ (¬ B). Обратите внимание, что значения истинности для них (последние два столбца в таблице) всегда одинаковы.
| А | Б | А ∧ В | ¬ (А ∧ В) | (¬ А) ∨ (¬ В) |
|---|---|---|---|---|
| ложный | ложь | ложь | правда | верно |
| ложный | правда | ложь | правда | верно |
| правда | ложь | ложь | правда | верно |
| правда | правда | правда | ложь | ложь |
Опровержение логической ошибки
Таблицы истинности также можно использовать для опровержения логической ошибки. Например, одно заблуждение состоит в том, что предполагается, что имеет место обратное импликация. Если вы знаете, что (A → B) истинно, и вы знаете, что B истинно, то ошибкой будет заключение, что A также должно быть истинно.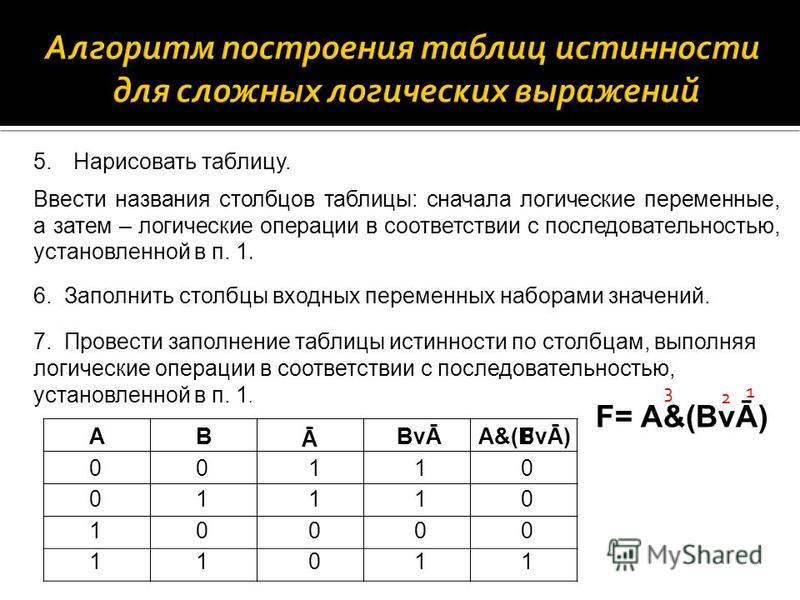 Обратите внимание, что утверждение «если животное является млекопитающим, то оно также является позвоночным» — верно. Если у нас есть животное, которое является позвоночным (например, собака), было бы ошибкой сейчас заключить, что животное также должно быть млекопитающим.
Обратите внимание, что утверждение «если животное является млекопитающим, то оно также является позвоночным» — верно. Если у нас есть животное, которое является позвоночным (например, собака), было бы ошибкой сейчас заключить, что животное также должно быть млекопитающим.
Мы покажем, что это логическая ошибка — независимо от утверждений A и B, только потому, что мы знаем, что A → B истинно, мы не должны вообще предполагать обратное также верно. Сначала напомним вам, что (A → B) эквивалентно ¬ A ∨ B. Мы хотим рассмотреть утверждение: ((A → B) ∧ B) → A. Если это выражение всегда верно, то мы могли бы полагайтесь на обратное, чтобы всегда использоваться. Сначала упростим выражение. Это эквивалентно ((¬ A ∨ B) ∧ B) → A. Это эквивалентно ¬ ((¬ A ∨ B) ∧ B) ∨ A. Мы можем помнить об этой формуле, когда оцениваем ее значение истинности для каждого возможное значение А и В.
Рассмотрим эту таблицу истинности.
| А | Б | А → В | ((А → В) ∧ В) → А |
|---|---|---|---|
| ложный | ложь | правда | верно |
| ложный | правда | правда | ложь |
| правда | ложь | ложь | верно |
| правда | правда | правда | верно |
Во второй строке мы видим, что последний столбец неверен.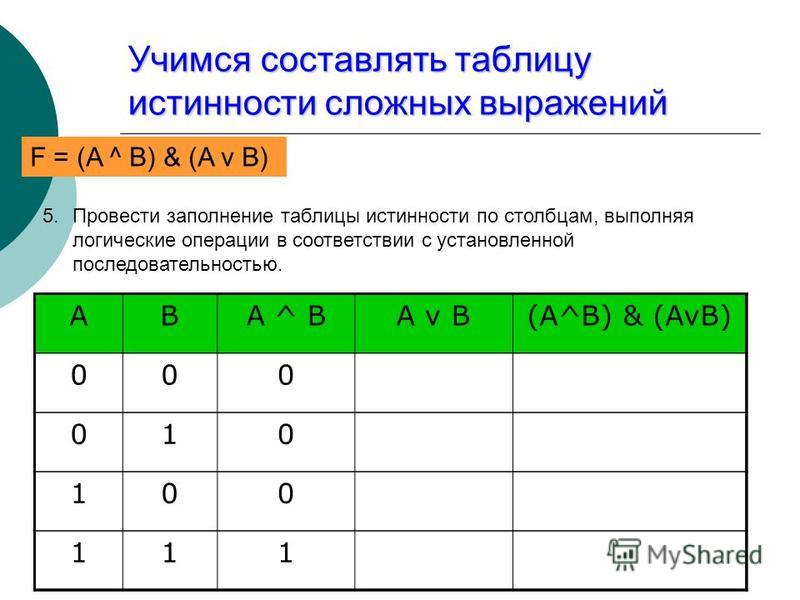 Именно здесь мы должны ожидать увидеть проблему — место, где B истинно, но мы не должны быть в состоянии сделать вывод, что A также должно быть истинным. Мы показали, что не всегда можно применить обратное.
Именно здесь мы должны ожидать увидеть проблему — место, где B истинно, но мы не должны быть в состоянии сделать вывод, что A также должно быть истинным. Мы показали, что не всегда можно применить обратное.
Вам будет назначена логическая идентичность, которую нужно доказать, и логическая ошибка, которую нужно опровергнуть. Для каждого из них вам разрешено и рекомендуется упрощать выражения, чтобы их было легче вычислять. Затем вы пишете таблицу истинности для каждой части, доказывая логическую идентичность и опровергая логическую ошибку. Включите такое же количество объяснений, как указано выше.
Если иное не указано вашим инструктором, вы можете отправлять свои решения в любом удобном для вас формате — текстовый документ, его изображения, обработанные на бумаге, физическая бумага, ссылка на блокнот OneNote. Если вы отправляете ссылку на электронный документ, убедитесь, что она настроена так, чтобы она была доступна вашему инструктору.
Пройдите проверку рейтинга Каждая часть должна быть правильной, чтобы получить 1/1 за эту часть. Сумма за задачи 2 балла. Вам нужно сдать и свою работу, а также проверить в лаборатории помощи, чтобы продемонстрировать свои доказательства. Вы можете использовать свою работу, которую сдаете, и должны обсудить доказательство с ГА. ГА сделает заметку, если вы не сможете это сделать, или если вам покажется, что вы не полностью понимаете процесс. Ваша письменная работа должна соответствовать правилам написания хороших доказательств — Proofs
Сумма за задачи 2 балла. Вам нужно сдать и свою работу, а также проверить в лаборатории помощи, чтобы продемонстрировать свои доказательства. Вы можете использовать свою работу, которую сдаете, и должны обсудить доказательство с ГА. ГА сделает заметку, если вы не сможете это сделать, или если вам покажется, что вы не полностью понимаете процесс. Ваша письменная работа должна соответствовать правилам написания хороших доказательств — Proofs
Примечание. Общая электронная таблица, которую GA используют для отправки информации на курсы Джеффа Кинна, — это ссылка, которая должна работать только для GA текущего семестра.
Ниже приведены дополнительные задачи, связанные с таблицами истинности и логикой. Некоторые из них взяты из Building Blocks for Theoretical Computer Science (сокращенно MCS).
- МКС Проблема 3.5. Это дает вам больше практики при проверке доказательств на наличие ошибок. Если у вас есть программа, которая создает таблицы истинности, вы можете использовать ее для этой задачи в части (а).

- Проблема MCS 3.8. Это дает вам некоторую практику работы с логическими формулами и рассуждения о них, а не просто использование таблиц истинности для доказательств (поскольку таблица истинности для этой задачи была бы громоздкой).
- Проблема MCS 3.11. Это дает вам возможность попрактиковаться в изучении логических формул для поиска примеров/контрпримеров истинностных назначений. Обратите внимание, что логическое выражение действительно , если оно всегда истинно. Для каждого ответа на этот вопрос вы должны указать причину, по которой вы даете правильный ответ; вам не нужно, чтобы это было формальным доказательством.
- Покажите, как можно использовать вентиль ИЛИ-НЕ для построения вентилей И, ИЛИ, НЕ, исключающее ИЛИ. Для каждого вам нужно дать выражение, используя только вентили НЕ-ИЛИ, и вам нужно дать обоснование того, почему это работает. Вашим обоснованием может быть таблица истинности или просто рассуждение о выражениях. Это не должно быть формальным доказательством, но оно должно убедить читателя в том, что ваши утверждения верны.
 Примечание. Вы можете использовать значения true и false в своих построениях. Если вы делаете конструкцию для NOT, вы можете использовать ее в последующих частях, не раскрывая ее полностью.
Примечание. Вы можете использовать значения true и false в своих построениях. Если вы делаете конструкцию для NOT, вы можете использовать ее в последующих частях, не раскрывая ее полностью.
Пройти проверку на рейтинг Вы должны быть в состоянии дать 90% ответов на отдельные части полностью правильно, и должны правильно определить те части, в правильности которых вы не уверены.
🖥 Информатика — Таблицы истинности и логика Утвержденные карточки
Похожие карточки
Пожалуйста, войдите, чтобы добавить в папки.
Войти
Вы создали 2 папки. Пожалуйста, обновитесь до Cram Premium, чтобы создавать сотни папок!
Обновление
- Перемешать
Включить
Выключить
- Алфавит
Включить
Выключить
- Передний Первый
Включить
Выключить
- Обе стороны
Включить
Выключить
- Читать
Включить
Выключить
Чтение. ..
..
Фронт
Диапазон карт для изучения
через
Кнопка воспроизведения
Кнопка воспроизведения
Прогресс
1/17
Нажмите, чтобы перевернуть
Используйте клавиши со стрелками ВЛЕВО и ВПРАВО для перемещения между карточками;
Используйте клавиши со стрелками ВВЕРХ и ВНИЗ, чтобы перевернуть карту;
H для показа подсказки;
А читает текст в речь;
- Делиться
- Распечатать
- Экспорт
- Клон
17 карточек в этом наборе
- Передняя часть
- Спина
Булева логика | Тип данных 1 или 0 (вкл. | |
Логический оператор | Только два состояния | |
Где находятся логические элементы | В ЦП | |
Три логических элемента | И, или, не | |
Логический вентиль И | ||
логический элемент ИЛИ | ||
логический вентиль НЕ | ||
Таблица правды | Показывает вывод всех возможных комбинаций входных данных логической функции | |
И Таблица истинности | ||
ИЛИ Таблица истинности | ||
Пример логического оператора ИЛИ | ||
Пример логического оператора И | Подъемная дверь | |
Объединение логических элементов И и НЕ | ||
И и НЕ Таблица истинности | ||
Количество входов | 9х (х = количество входов)||
НЕ Таблица истинности | ||
Логическое выражение | Утверждение, которое может быть как истинным, так и ложным, третьего варианта никогда не бывает |
Органический желеобразный фрактальный логический вентиль с бесконечной таблицей истинности
- Список журналов
- Научные отчеты
- PMC4471884
Научный представитель 2015; 5: 11265.
Published online 2015 Jun 18. doi: 10.1038/srep11265
, a, 1, 2 , 1 and b, 1
Author information Article notes Copyright и Информация о лицензии Заявление об отказе от ответственности
- Дополнительные материалы
Все логические вентили, изобретенные в течение столетия в широком диапазоне, являются конечными. По мере того, как проблема потока данных становится все более серьезной для индустрии обработки информации и связи, стремление к изучению радикальных концепций быстро растет. Здесь мы проектируем и синтезируем молекулу, в которой входная энергия передается по циклу внутри молекулярной системы, как осциллятор, затем мы используем молекулу для создания желе, которое действует как цепочка осцилляторов с фрактальной резонансной полосой. . Следовательно, с увеличением разрешения обнаружения в свободном пространстве между двумя энергетическими уровнями данной резонансной полосы появляется новая полоса, в силу фрактальной природы генерация более новых энергетических уровней никогда не прекращается.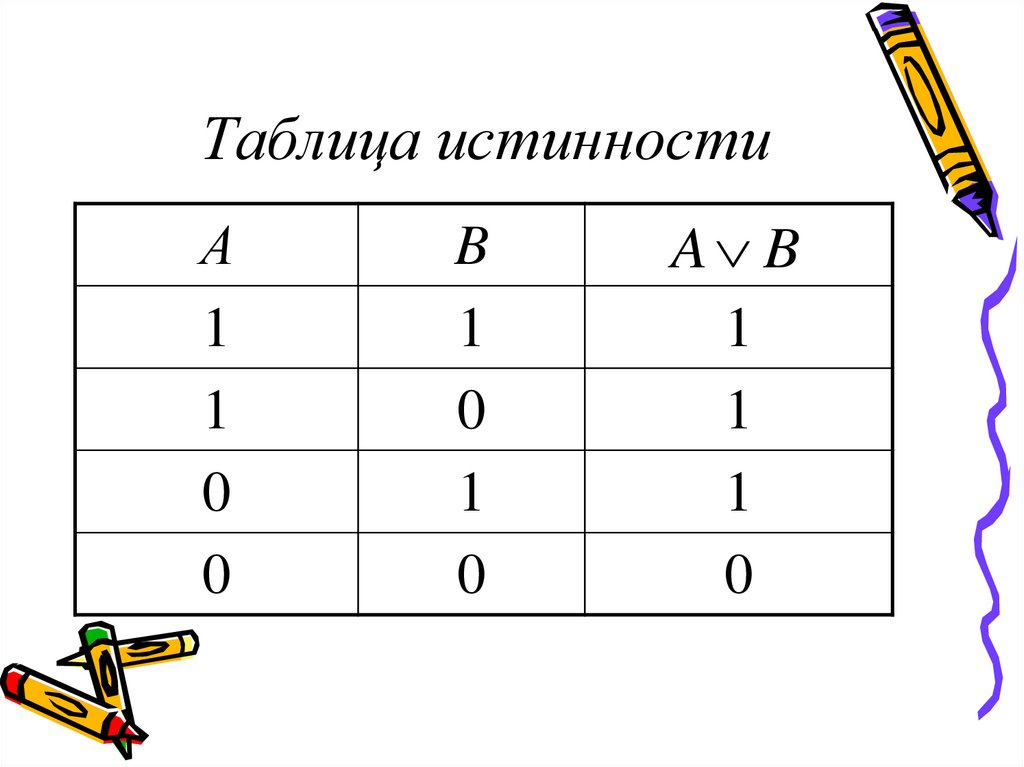 Это естественное свойство линейного цепного генератора. Когда мы сопоставляем каждый уровень энергии резонансной полосы органического желе в зависимости от pH и плотности желе, мы реализуем логический вентиль, таблица истинности которого конечна, но если мы увеличим любую маленькую часть, появится новая таблица истинности. . В принципе, масштабирование таблицы истинности будет продолжаться вечно. Таким образом, мы впервые изобретаем новый класс бесконечных логических элементов.
Это естественное свойство линейного цепного генератора. Когда мы сопоставляем каждый уровень энергии резонансной полосы органического желе в зависимости от pH и плотности желе, мы реализуем логический вентиль, таблица истинности которого конечна, но если мы увеличим любую маленькую часть, появится новая таблица истинности. . В принципе, масштабирование таблицы истинности будет продолжаться вечно. Таким образом, мы впервые изобретаем новый класс бесконечных логических элементов.
Лазерное травление, которое рисует миллионы логических элементов на кремнии, скоро перестанет уменьшаться, намного ниже предела вычислений 1 . Все пути, выходящие за рамки, например, обработки и запоминания в одном устройстве 2 ,3 ,4 , нефизического связывания 5 ,6 ,7 следуют одному и тому же принципу, — без сокращения размер устройства, больше информации не может быть упаковано и обработано в фиксированном пространстве (это тяготеет к закону Мура).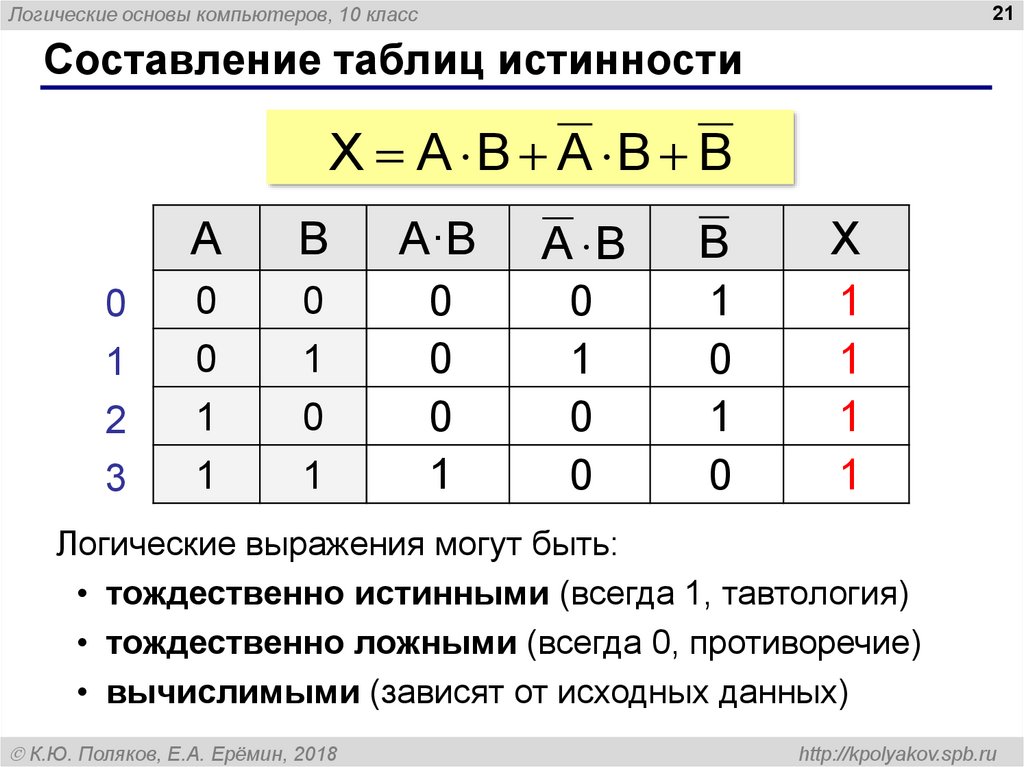 Принцип «бесконечной логики» 8 ,9 ,10 ,11 является как раз противоположным, если он будет реализован, он заменит «биты» континуумом, который критически необходим для истинной адаптивной логики 12 и часто рассматривается как прерогатива химических вычислений 13 ,14 ,15 . Хотя фракталы обещают дополнить технологические требования истинной «Бесконечной логики» 16 ,17 ,18 , не существует явных доказательств того, что охота достигла своего пика в биосистемах 19 ,20 ,21 ,22 ,23 . В физике диэлектриков теоретически показано, что в цепочке линейных осцилляторов в системе возникает фрактальное распределение уровней энергии 24 . Это означает, что, как и во фрактале Мандельброта, если увеличить часть резонансной полосы, появится новая полоса. Здесь мы используем этот принцип для разработки и синтеза нового материала, который демонстрирует аналогичное свойство, и реализуем бесконечную таблицу истинности.
Принцип «бесконечной логики» 8 ,9 ,10 ,11 является как раз противоположным, если он будет реализован, он заменит «биты» континуумом, который критически необходим для истинной адаптивной логики 12 и часто рассматривается как прерогатива химических вычислений 13 ,14 ,15 . Хотя фракталы обещают дополнить технологические требования истинной «Бесконечной логики» 16 ,17 ,18 , не существует явных доказательств того, что охота достигла своего пика в биосистемах 19 ,20 ,21 ,22 ,23 . В физике диэлектриков теоретически показано, что в цепочке линейных осцилляторов в системе возникает фрактальное распределение уровней энергии 24 . Это означает, что, как и во фрактале Мандельброта, если увеличить часть резонансной полосы, появится новая полоса. Здесь мы используем этот принцип для разработки и синтеза нового материала, который демонстрирует аналогичное свойство, и реализуем бесконечную таблицу истинности. Это делает тенденцию к непрерывной миниатюризации неактуальной, беспрецедентные технологии, представленные с гипотезой континуума с 1870-х годов 8 ,9 ,10 ,11 ,25 , как бесконечная плотность упаковки, универсальная программируемая материя 26 и временное разрешение за пределами любой измеримой машины устройства.
Это делает тенденцию к непрерывной миниатюризации неактуальной, беспрецедентные технологии, представленные с гипотезой континуума с 1870-х годов 8 ,9 ,10 ,11 ,25 , как бесконечная плотность упаковки, универсальная программируемая материя 26 и временное разрешение за пределами любой измеримой машины устройства.
Все машины, которые мы видим вокруг, состоят из логики с конечным числом состояний (0 и 1). Историческая ирония заключается в том, что логика с бесконечным числом состояний родился задолго до 25 конечная логика. Поскольку нам не удалось создать бесконечное состояние в конечной машине, обещания невероятных технологий остались в уравнениях, так и не увидев свет в лаборатории. Параметры, управляющие природой, состоят из бесконечных рядов, вызывая поиски детерминистического решения в случайных или хаотических химических системах, вдохновленных живыми машинами, и в синтетических химико-биологических термоядерных системах, обе проблемы в значительной степени доминировали в литературе по логическим вентилям ,21 ,22 ,23 .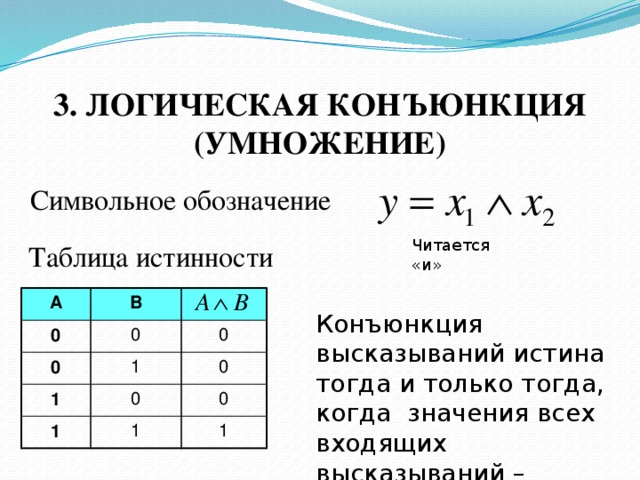 Более того, литература изобилует интерпретациями сложных биологических событий как логических ворот для изучения процесса принятия решений в природе простыми словами, однако то, что теряется одновременно, никогда не может быть восстановлено в последовательных дискретизированных конечных автоматах 28 . Таким образом, нам нужны базовые вычислительные элементы, которые могут хранить и обрабатывать бесконечные серии. Неспособность реализовать такое устройство привело к хаосу, когда знание входных данных генерирует выходные данные независимо от сложности. В моделях искусственного интеллекта детерминизм обеспечивается за счет манипулирования случайностью, что дает тонкие преимущества 9.0553 29 . Все приключения о случайности, хаосе и детерминизме имеют конечный логический скелет ( хаос и детерминизм онлайн текст A ), в отличие от бесконечной логики разрешение решения постоянно увеличивается до точного числа, но увеличение масштаба никогда не прекращается.
Более того, литература изобилует интерпретациями сложных биологических событий как логических ворот для изучения процесса принятия решений в природе простыми словами, однако то, что теряется одновременно, никогда не может быть восстановлено в последовательных дискретизированных конечных автоматах 28 . Таким образом, нам нужны базовые вычислительные элементы, которые могут хранить и обрабатывать бесконечные серии. Неспособность реализовать такое устройство привело к хаосу, когда знание входных данных генерирует выходные данные независимо от сложности. В моделях искусственного интеллекта детерминизм обеспечивается за счет манипулирования случайностью, что дает тонкие преимущества 9.0553 29 . Все приключения о случайности, хаосе и детерминизме имеют конечный логический скелет ( хаос и детерминизм онлайн текст A ), в отличие от бесконечной логики разрешение решения постоянно увеличивается до точного числа, но увеличение масштаба никогда не прекращается.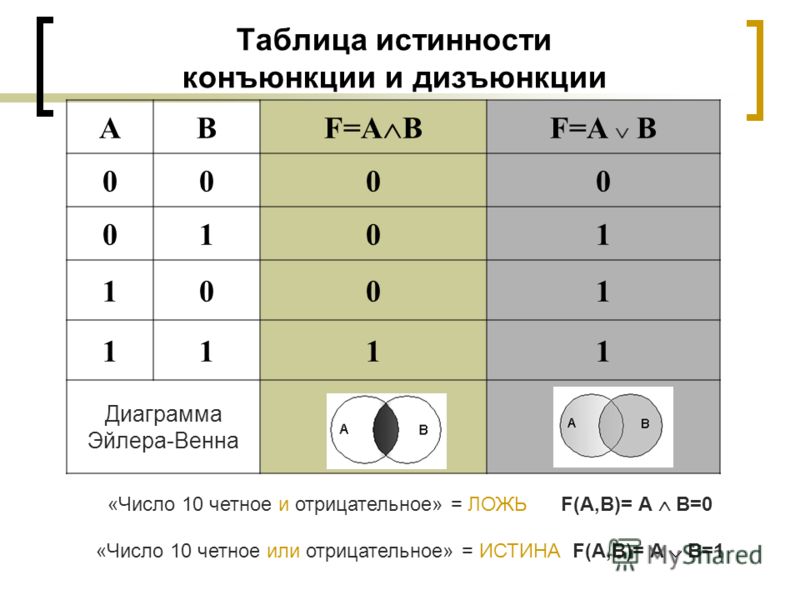 Таким образом, аргумент Гёделя о неполноте 30 переводится в бесконечный ряд, который должен продемонстрировать вычислительный элемент. За исключением фрактала, никакая другая инженерная концепция не может быть так близка к такому квазидетерминизму 23 , следовательно, в этом одиночном приключении создание такого фрактала в органической молекулярной системе было главной целью.
Таким образом, аргумент Гёделя о неполноте 30 переводится в бесконечный ряд, который должен продемонстрировать вычислительный элемент. За исключением фрактала, никакая другая инженерная концепция не может быть так близка к такому квазидетерминизму 23 , следовательно, в этом одиночном приключении создание такого фрактала в органической молекулярной системе было главной целью.
Теоретические расчеты (см. Методы) предполагают, что линейная цепочка осцилляторов порождает фрактальное распределение энергетических уровней. Следовательно, нам нужен электромагнитный молекулярный осциллятор, потенциально образующий цепь. Для периодических колебаний нам нужно как минимум три центра захвата энергии в молекуле. Поскольку ковалентная связь ослабляет первозданные молекулярные свойства, поэтому очень сложно синтезировать структуру со слабой связью с тремя легирующими добавками в подходящей матрице. Мы используем дендримерную матрицу 31 , чтобы использовать его фрактальную передачу энергии.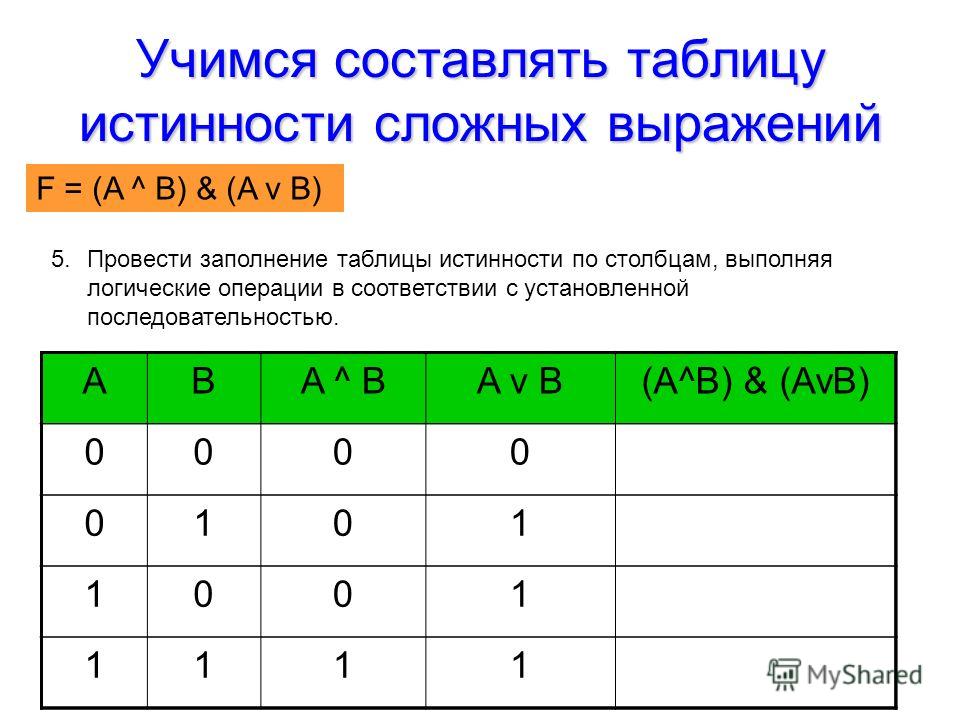 Затем мы добавляем молекулу датчика pH, молекулярный ротор, вращение которого можно настроить, изменяя плотность (M, см. фильм 1 и фильм 2 о динамике молекулярного ротора в теории и в СТМ), и добавляем многоуровневый электромагнитный переключатель 32 . ,33 внутри дендритной полости для создания треугольного пути передачи энергии. Затем дендритное производное превращается в желе, чтобы имитировать свойство линейной цепи, в котором, просто меняя pH и плотность, можно было управлять граничными значениями его линейных цепных колебаний. Таким образом, экспериментально реализуется бесконечная таблица истинности ( разница между фрактальными и обычными логическими вентилями: Таблица 1 онлайн ), удовлетворен спрос на бесконечный компьютер 34 .
Затем мы добавляем молекулу датчика pH, молекулярный ротор, вращение которого можно настроить, изменяя плотность (M, см. фильм 1 и фильм 2 о динамике молекулярного ротора в теории и в СТМ), и добавляем многоуровневый электромагнитный переключатель 32 . ,33 внутри дендритной полости для создания треугольного пути передачи энергии. Затем дендритное производное превращается в желе, чтобы имитировать свойство линейной цепи, в котором, просто меняя pH и плотность, можно было управлять граничными значениями его линейных цепных колебаний. Таким образом, экспериментально реализуется бесконечная таблица истинности ( разница между фрактальными и обычными логическими вентилями: Таблица 1 онлайн ), удовлетворен спрос на бесконечный компьютер 34 .
показывает общий дизайн дендритной наноплатформы. Самый важный шаг для создания универсального программируемого генератора — это выбор подходящей матрицы. показывает геометрию ветвей дендримера. Чем меньше сопряжение, тем выше подвижность ветвей. Полное сопряжение делает структуру плоской, ограничивая межплоскостной обмен энергией. Частичное сопряжение уравновешивает два ( молекулярная динамика отчетливо сопряженных ветвей в фильм 3 онлайн ). Прикрепленные к поверхности функциональные группы дендримера ограничивают случайность его динамики ветвления. Функционализация полусопряженных ветвей блокирует передачу энергии между ветвями, поэтому для эффективного треугольного пути передачи энергии подходит полностью несопряженная матрица ПАМАМ.
Чем меньше сопряжение, тем выше подвижность ветвей. Полное сопряжение делает структуру плоской, ограничивая межплоскостной обмен энергией. Частичное сопряжение уравновешивает два ( молекулярная динамика отчетливо сопряженных ветвей в фильм 3 онлайн ). Прикрепленные к поверхности функциональные группы дендримера ограничивают случайность его динамики ветвления. Функционализация полусопряженных ветвей блокирует передачу энергии между ветвями, поэтому для эффективного треугольного пути передачи энергии подходит полностью несопряженная матрица ПАМАМ.
Открыть в отдельном окне
( a ) Общий дизайн сложного многофункционального производного на основе дендримера.( б ). Слева направо 1,2,3,4 Молекулярные структуры (вверху) и их структуры с минимизацией энергии (внизу) показаны здесь для 1, 2 и 3 . 4. Первый, 1 и 2. Sp 2 гибридизированный конъюгированный дендример (инкапсуляция невозможна) 3 ПАМАМ-дендример 5-го поколения (неконъюгированный, Sp 3 дизайн полугибридного) 4 конъюгированная дендримерная структура, созданная линейной комбинацией Sp 2 и Sp 3 гибридные состояния.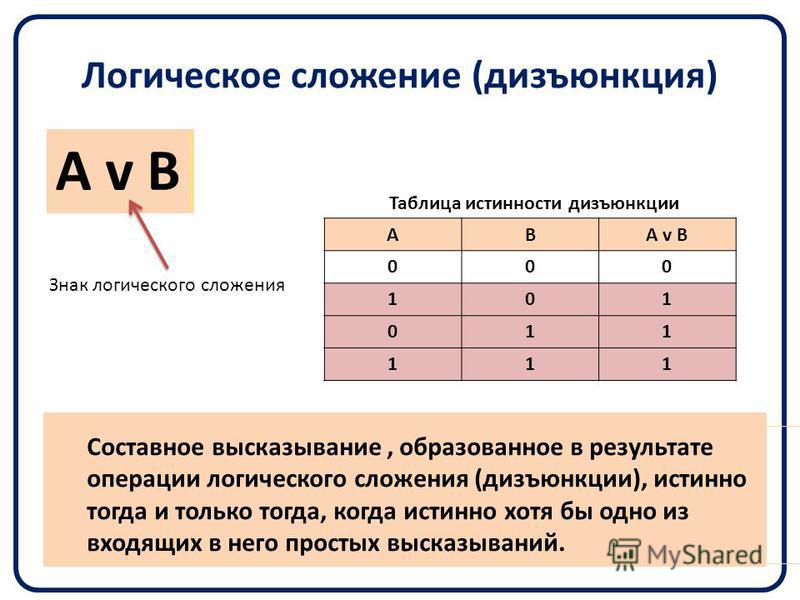 Для всех панелей заштрихованы потенциально активные плоскости, участвующие в переносе заряда по молекулярной структуре. ( c ) На первом этапе схема реакции для легирования двух молекул нильского красного C демонстрируется (исследование масс-спектроскопии MALDI-TOF подтверждает число), затем присоединяются четыре сенсорные молекулы (изотиоцианат S = NIR797) и на третьем этапе 32 молекулярные машины связаны с поверхностью PAMAM. ( d ) Линейная цепочка PCMS и фрактальная/бесконечная полоса резонанса (см. методы).
Для всех панелей заштрихованы потенциально активные плоскости, участвующие в переносе заряда по молекулярной структуре. ( c ) На первом этапе схема реакции для легирования двух молекул нильского красного C демонстрируется (исследование масс-спектроскопии MALDI-TOF подтверждает число), затем присоединяются четыре сенсорные молекулы (изотиоцианат S = NIR797) и на третьем этапе 32 молекулярные машины связаны с поверхностью PAMAM. ( d ) Линейная цепочка PCMS и фрактальная/бесконечная полоса резонанса (см. методы).
показывает протокол синтеза молекулы ПАМАМ 5-го поколения или P. Сначала внутрь добавляют молекулу Nile Red (C), чтобы получить PC, подключают 4 датчика pH NIR 797 S, а затем подключают 32 молекулярных ротора M (M представляет собой 2-метокси- фенилэтинил)-нафталин-1-иламин, разработанный и синтезированный нами), мы получаем PCMS (см. Методы и вспомогательную информацию онлайн). показывает, что линейная цепочка PCMS генерирует полосу фрактального резонанса, в которой находится бесконечное количество дискретных, но теоретически предсказуемых энергетических уровней (см.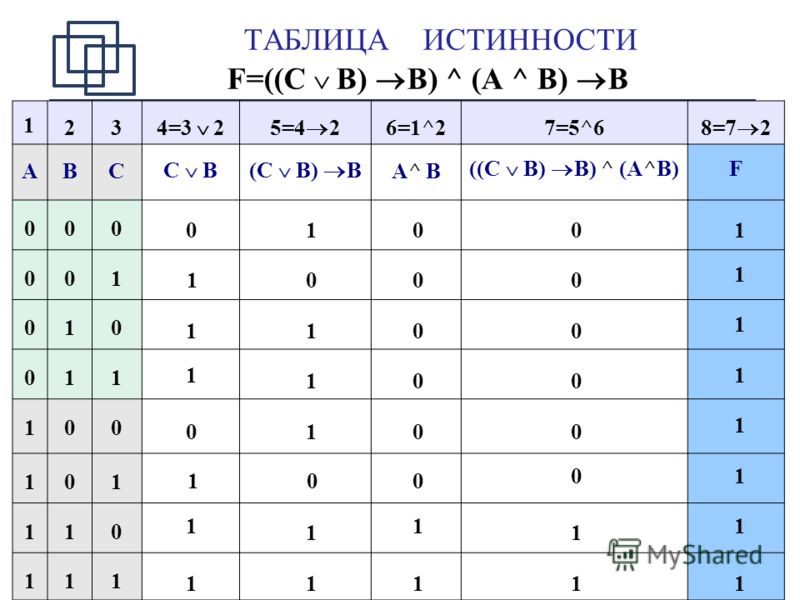 Методы расчета).
Методы расчета).
Чтобы подтвердить, что молекула PCMS является желаемым электромагнитным осциллятором, нам нужны экспериментальные и теоретические доказательства, которые говорят, что если входная энергия будет сначала захвачена S, затем C и затем M, то этот путь S → C → M универсальный, все маршруты, кроме этого, заблокированы. В эмиссионной спектроскопии с комбинированным возбуждением (CEES, см. Методы, онлайн-текст B) на графике CEES есть отчетливые пики для P, C, M и S. Поэтому, если мы постепенно изменяем pH или плотность, мы обнаружим, что пики высокой интенсивности на графике CEES перемещаются вдоль линии, как показано на рисунке, где мы видим, что пики для S, C и M становятся яркими последовательно. Мы демонстрируем треугольный путь передачи энергии в фильме 4 онлайн, где видно, что M и S обмениваются энергией только через C ().
Открыть в отдельном окне
( a-f ) ( a ) Спектр CEES для PAMAM; ( б ).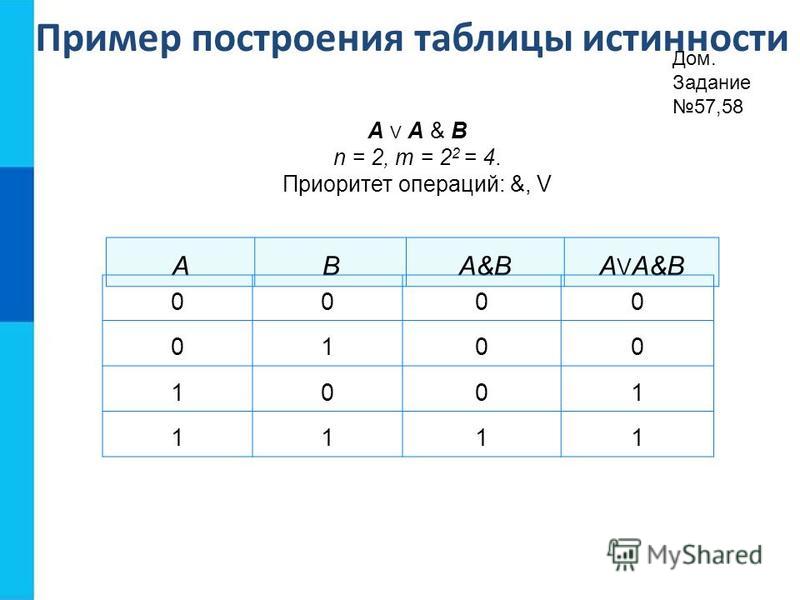 спектр CEES для NR-PAMAM; ( с ). спектр CEES для NR-PAMAM; ( д ). Спектр CEES для PAMAM-NR-NIR797; ( и ). CEES для PAMAM-NR-MM; ( ф ). Спектр CEES для PAMAM-NR-NIR797-MM. Обратите внимание, что эти данные зависят от плотности и pH. ( г ). Схема показывает двойной путь CS и MC ( h ) Потенциальная поверхность PCMS. Один лепесток увеличен ниже. (i) Изменение пиков с плотностью от 2 мг/мл до 10мг/мл ( j ) Пики отличаются от pH. 2 до PH 12.
спектр CEES для NR-PAMAM; ( с ). спектр CEES для NR-PAMAM; ( д ). Спектр CEES для PAMAM-NR-NIR797; ( и ). CEES для PAMAM-NR-MM; ( ф ). Спектр CEES для PAMAM-NR-NIR797-MM. Обратите внимание, что эти данные зависят от плотности и pH. ( г ). Схема показывает двойной путь CS и MC ( h ) Потенциальная поверхность PCMS. Один лепесток увеличен ниже. (i) Изменение пиков с плотностью от 2 мг/мл до 10мг/мл ( j ) Пики отличаются от pH. 2 до PH 12.
Теоретически мы отследили путь передачи энергии, имитируя изменение pH и плотности, поместив PCMS в потенциальный ящик и увеличив количество протонов и PCMS в этом ящике. По мере изменения электромагнитного потенциала (синий отрицательный и красный положительный) в PCMS () можно проследить путь S → C → M; один из четырех лепестков PCMS увеличен ниже, мы можем видеть дискретные, изолированные красные и синие области. Мы начертили дискретные уровни энергии для PCMS, P, C, M и S, а затем показали, как фрактальное распределение уровня энергии проявляется в зависимости от pH и плотности в фильме 5 онлайн.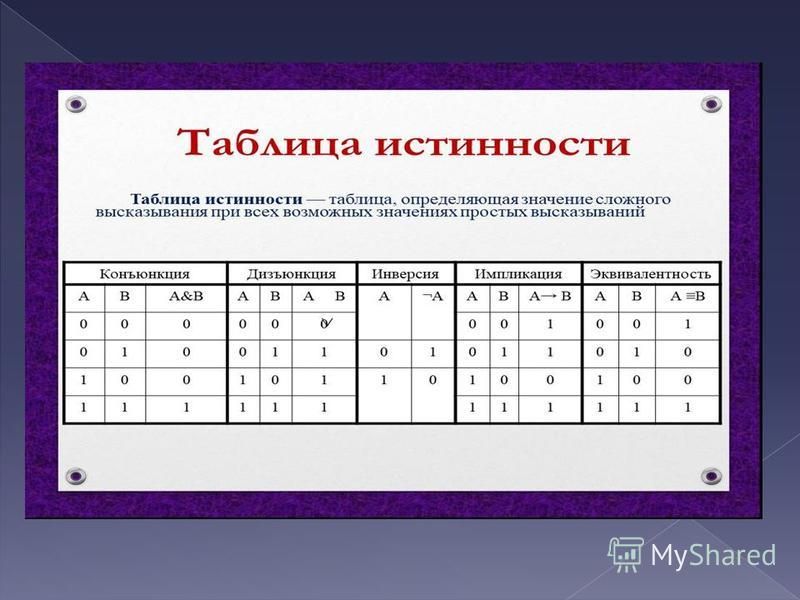 Одна из самых замечательных особенностей, которую читатель заметит в фильме 5, заключается в том, что распределение фрактальных уровней энергии для pH и плотности не совпадает по фазе, это классическое условие, подобное учебнику, для построения простого гармонического осциллятора. Таким образом, PCMS в растворе образует линейную цепочку осцилляторов, поскольку pH и плотность настраивают фотоиндуцированный резонанс 35 ,36 .
Одна из самых замечательных особенностей, которую читатель заметит в фильме 5, заключается в том, что распределение фрактальных уровней энергии для pH и плотности не совпадает по фазе, это классическое условие, подобное учебнику, для построения простого гармонического осциллятора. Таким образом, PCMS в растворе образует линейную цепочку осцилляторов, поскольку pH и плотность настраивают фотоиндуцированный резонанс 35 ,36 .
Кроме того, регулярность изменения интенсивности в зависимости от плотности (вверху) и pH (внизу) закладывает основу для проектирования логических элементов. При этом пики движутся по линии, изменение не случайно. Имеющиеся в продаже 14 датчиков с низким разрешением могут обнаруживать 14 точек возбуждения-эмиссии вдоль линии входа (из стакана). Мы варьировали pH и плотность и создали базу данных графиков CEES (онлайн-база данных pH-плотности CEES, отдельный pdf-файл 9).0316). Скажем, двигаясь вдоль изображенной линии в , мы находим четыре основные области, в которых движутся пики ().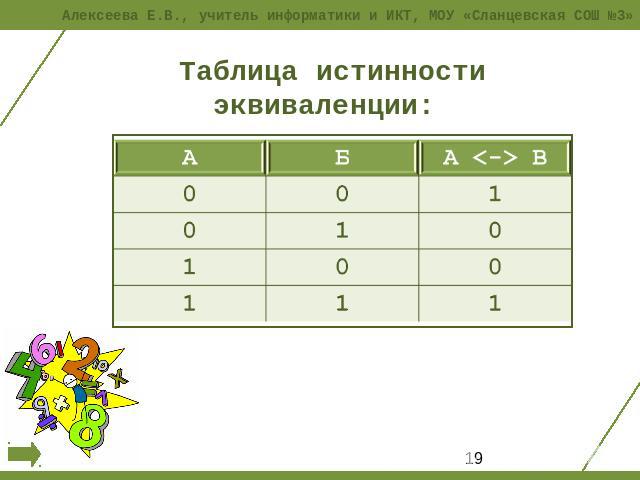 Если у нас есть датчик с разрешением 0,5 эВ, то осталось записать в четырех областях, мы могли бы обнаружить 1 + 5 + 6 + 2 = 14 шагов движения вдоль линии. Из этой строки мы выбираем три точки вывода для создания таблицы истинности. Для простоты построим таблицу истинности для логического элемента «два входа, три выхода», выходов может быть гораздо больше. В таблице в эВ показаны только 10 выходных точек. Поддерживая постоянный рН, мы изменили плотность и наблюдали изменение интенсивности флуоресценции при различных сенсорных выходах. Таблица показывает, что для значений от 0 до 4 можно было принять пять различных решений. Поскольку мы можем взять любую небольшую область из четырех, масштабируем эту область, просто увеличивая разрешение сенсора, и получаем четкие выходные данные. Keithley 6430 с предусилителем имеет 10 × 10 −18 эВ датчиков, следовательно, начиная с логического вентиля 2 × 3 с 10 значениями, мы можем масштабировать любую область pH или плотности, чтобы использовать область по крайней мере от 0,5 до 10 −5 эВ, т.
Если у нас есть датчик с разрешением 0,5 эВ, то осталось записать в четырех областях, мы могли бы обнаружить 1 + 5 + 6 + 2 = 14 шагов движения вдоль линии. Из этой строки мы выбираем три точки вывода для создания таблицы истинности. Для простоты построим таблицу истинности для логического элемента «два входа, три выхода», выходов может быть гораздо больше. В таблице в эВ показаны только 10 выходных точек. Поддерживая постоянный рН, мы изменили плотность и наблюдали изменение интенсивности флуоресценции при различных сенсорных выходах. Таблица показывает, что для значений от 0 до 4 можно было принять пять различных решений. Поскольку мы можем взять любую небольшую область из четырех, масштабируем эту область, просто увеличивая разрешение сенсора, и получаем четкие выходные данные. Keithley 6430 с предусилителем имеет 10 × 10 −18 эВ датчиков, следовательно, начиная с логического вентиля 2 × 3 с 10 значениями, мы можем масштабировать любую область pH или плотности, чтобы использовать область по крайней мере от 0,5 до 10 −5 эВ, т. е. мы можем масштабировать ту же таблицу истинности 10 6 раза как минимум, и, следовательно, это фрактальный логический вентиль ( фрактальный логический вентиль согласно CEES Фильм 5 онлайн ). Доступность бесконечного состояния зависит от эффективности измерительной системы.
е. мы можем масштабировать ту же таблицу истинности 10 6 раза как минимум, и, следовательно, это фрактальный логический вентиль ( фрактальный логический вентиль согласно CEES Фильм 5 онлайн ). Доступность бесконечного состояния зависит от эффективности измерительной системы.
Открыть в отдельном окне
CEES, слева направо pH 2, 4, 7, 9; плотность 2 мг/мл, линия проведена параллельно гребню комбинационного рассеяния, где движутся пики, масштаб такой же, как
( a ) ( b ). Схема траекторий движения пиков, показывает 14 точек вдоль линии ( c ) Логический вентиль с двумя входами и тремя выходами: таблица истинности.
Полуэмпирические расчеты и эксперимент показывают, что пики для пути M ↔ C ↔ S в CEES изменяются нелинейно в зависимости от pH и плотности. Пики по-разному смещаются в разных регионах, это позволяет пользователю использовать локальные энергетические состояния и применять разрешенные/ограниченные правила перехода.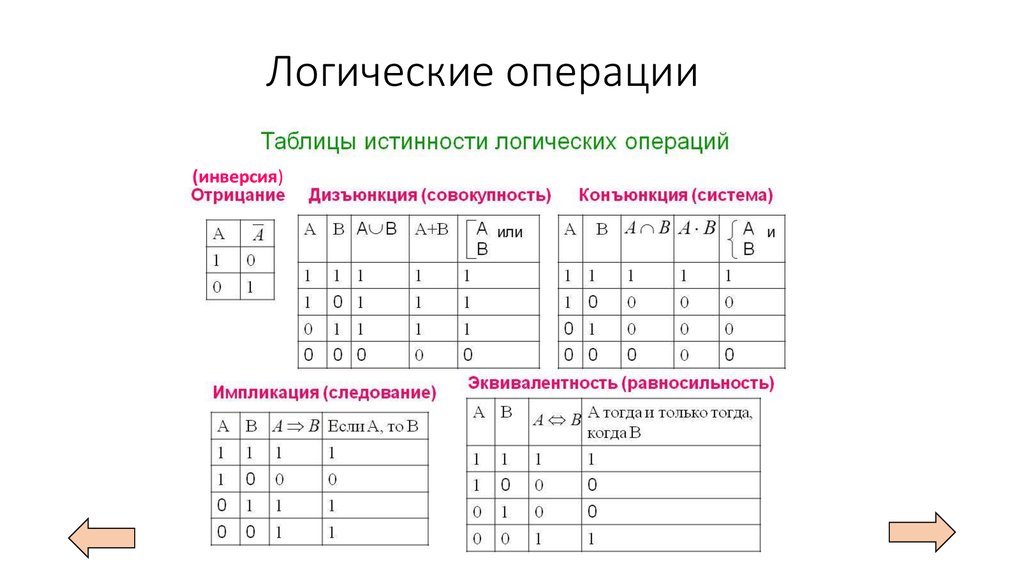 Молекулы ПКМС на Si/SiO 9Поверхность 0787 2 под РЭМ начинает самопроизвольное движение, как показано на ( колебания одной молекулы PCMS с высоким разрешением в Movie 6 онлайн ). Начальные шаблоны и схематические пути для трех рядов показывают, что выбран конкретный путь, несмотря на индуцированный шум. При увеличении количества ПКМС изменение входных условий самопроизвольно отражается на динамике измененного пути — система является адаптивной. Самое интересное, что вторая и третья строки показывают, что принятый путь меняется в зависимости от расположения входных данных, хотя количество PCMS остается прежним. Это напоминает хаотические вычисления, динамика закодирована в расположении входных данных, зная входные данные, мы можем получить выходные данные. показывает, что если мы продолжим увеличивать PCMS, принятые случайные движения, пытающиеся следовать четко определенному геометрическому пути, преобладающим будет временной цикл. Это важно, поскольку квазидетерминизм порождает хаос и детерминированный выбор, у нас есть более общий вычислительный элемент.
Молекулы ПКМС на Si/SiO 9Поверхность 0787 2 под РЭМ начинает самопроизвольное движение, как показано на ( колебания одной молекулы PCMS с высоким разрешением в Movie 6 онлайн ). Начальные шаблоны и схематические пути для трех рядов показывают, что выбран конкретный путь, несмотря на индуцированный шум. При увеличении количества ПКМС изменение входных условий самопроизвольно отражается на динамике измененного пути — система является адаптивной. Самое интересное, что вторая и третья строки показывают, что принятый путь меняется в зависимости от расположения входных данных, хотя количество PCMS остается прежним. Это напоминает хаотические вычисления, динамика закодирована в расположении входных данных, зная входные данные, мы можем получить выходные данные. показывает, что если мы продолжим увеличивать PCMS, принятые случайные движения, пытающиеся следовать четко определенному геометрическому пути, преобладающим будет временной цикл. Это важно, поскольку квазидетерминизм порождает хаос и детерминированный выбор, у нас есть более общий вычислительный элемент. Также читатели могли увидеть живую линейную цепочку осцилляторов PCMS, которая является основой полосы фрактального резонанса. Этот осциллятор можно было бы использовать для лечения рака и болезни Альцгеймера 9.0553 37 .
Также читатели могли увидеть живую линейную цепочку осцилляторов PCMS, которая является основой полосы фрактального резонанса. Этот осциллятор можно было бы использовать для лечения рака и болезни Альцгеймера 9.0553 37 .
Открыть в отдельном окне
Три строки показывают три временных профиля.
Первые два ряда Последовательные изображения четырех роев слева направо, временной интервал 20 секунд, масштабная линейка 8 нм. a ) Схема исходного расположения показана справа с траекторией движения; Третий ряд Последовательные изображения семи роев слева направо, временной интервал 20 секунд, масштабная линейка 6 нм. Схема начальной презентации показана справа. ( б ). Таблица, обобщающая геометрию и геометрию колебаний в зависимости от количества PCMS.
Период, временной цикл или ритм остаются постоянными даже при случайных движениях PCMS. Путь передачи энергии (M ↔ C ↔ S) — это ритм, закодированный в атомных аранжировках, которые PCMS восстанавливает под шумом, — ключ к его адаптивному поведению.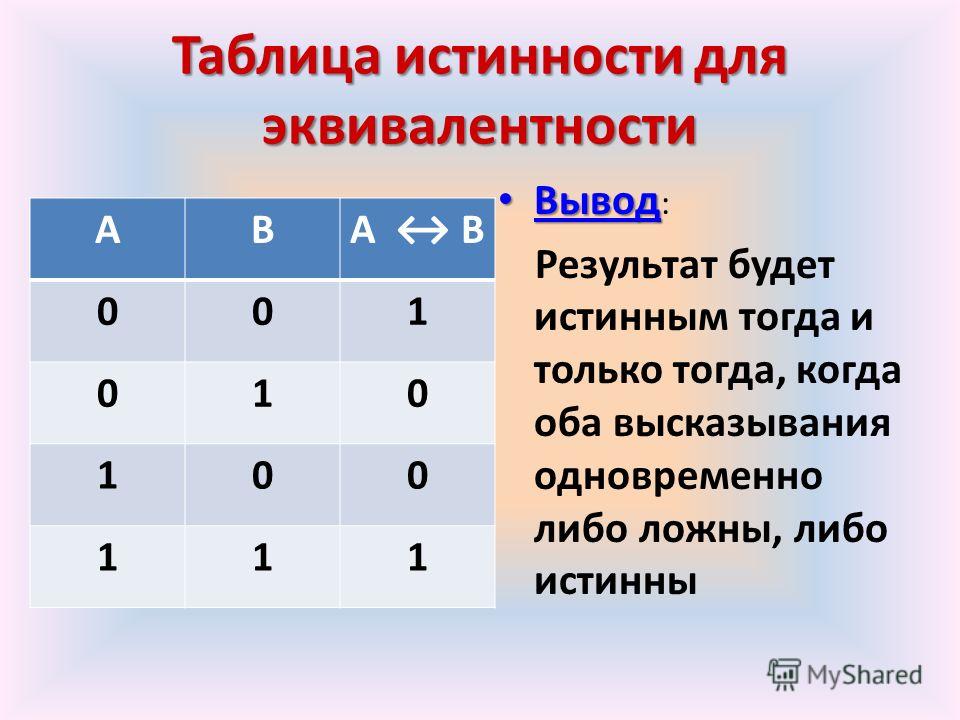 Это позволяет PCMS поддерживать заданную геометрическую траекторию на поверхности в условиях шума и логический выход флуоресценции в растворе даже при постоянном изменении диапазона pH и плотности, проверяя устойчивость системы к высокому разрешению. Беспрецедентное разрешение включает в себя уникальную функцию памяти; масштабирование для расширения любой части операционной матрицы, преобразование, скажем, матрицы плотности pH 10 × 10 в матрицу 1000 × 1000, таким образом, вложенная сеть содержит астрономически большие данные 38 . Даже для большой матрицы время на поиск определяется временным циклом наименьшей матрицы, это то, что мы называем «мгновенным принятием решения» — для наблюдателя, сидящего на мире самого низкого разрешения (Таблица 1 онлайн) 38 .
Это позволяет PCMS поддерживать заданную геометрическую траекторию на поверхности в условиях шума и логический выход флуоресценции в растворе даже при постоянном изменении диапазона pH и плотности, проверяя устойчивость системы к высокому разрешению. Беспрецедентное разрешение включает в себя уникальную функцию памяти; масштабирование для расширения любой части операционной матрицы, преобразование, скажем, матрицы плотности pH 10 × 10 в матрицу 1000 × 1000, таким образом, вложенная сеть содержит астрономически большие данные 38 . Даже для большой матрицы время на поиск определяется временным циклом наименьшей матрицы, это то, что мы называем «мгновенным принятием решения» — для наблюдателя, сидящего на мире самого низкого разрешения (Таблица 1 онлайн) 38 .
Теория того, как молекулярный осциллятор генерирует фрактальную энергетическую полосу: создание бесконечных энергетических уровней
Если мы синтезируем молекулярный осциллятор с одной резонансной частотой f 0 , осциллятор будет иметь более высокую модовую частоту колебаний f 1 и связь между ними f 1 /f 0 = n.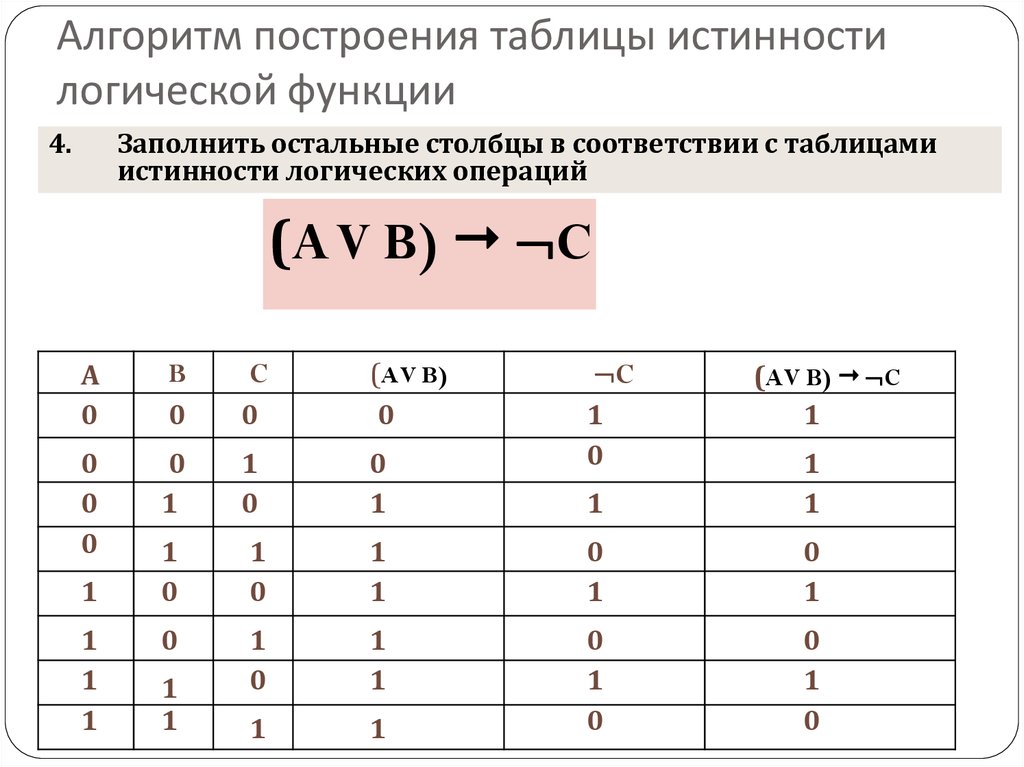 Теперь для вложенной сети сигналов, скажем, один сигнал инкапсулирует в нем 3 сигнала, и это продолжается, тогда сначала мы получаем f 1 = f 0 , затем f 1 = 3f 0 , затем f 1 = 9f 0 , поэтому в общем случае мы можем написать f n ,p = f 0 n r . Таким образом, спектр резонансных частот, обусловленный одной конкретной симметрией, может быть представлен в виде логарифмического фрактального спектра. Мы можем ясно видеть, что в цепочке осцилляторов продолжает появляться сингулярная часть формы волны. Если f 0 — основной резонанс одного осциллятора, а f — частота цепочки, тогда, используя простое выражение цепной дроби, мы получаем резонансный спектр или распределение собственных резонансных частот, f = f 0 exp(S), S = n 0 /z + z/(n 1 + z/(n 2 + z/(n 3 +….+z/n i ))). Теперь полоса, которую мы получаем для i = 1, похожа на полосу, которую мы получаем для i = 2 и так далее, так что это фрактал, спектр выглядит как гиперболическая функция.
Теперь для вложенной сети сигналов, скажем, один сигнал инкапсулирует в нем 3 сигнала, и это продолжается, тогда сначала мы получаем f 1 = f 0 , затем f 1 = 3f 0 , затем f 1 = 9f 0 , поэтому в общем случае мы можем написать f n ,p = f 0 n r . Таким образом, спектр резонансных частот, обусловленный одной конкретной симметрией, может быть представлен в виде логарифмического фрактального спектра. Мы можем ясно видеть, что в цепочке осцилляторов продолжает появляться сингулярная часть формы волны. Если f 0 — основной резонанс одного осциллятора, а f — частота цепочки, тогда, используя простое выражение цепной дроби, мы получаем резонансный спектр или распределение собственных резонансных частот, f = f 0 exp(S), S = n 0 /z + z/(n 1 + z/(n 2 + z/(n 3 +….+z/n i ))). Теперь полоса, которую мы получаем для i = 1, похожа на полосу, которую мы получаем для i = 2 и так далее, так что это фрактал, спектр выглядит как гиперболическая функция.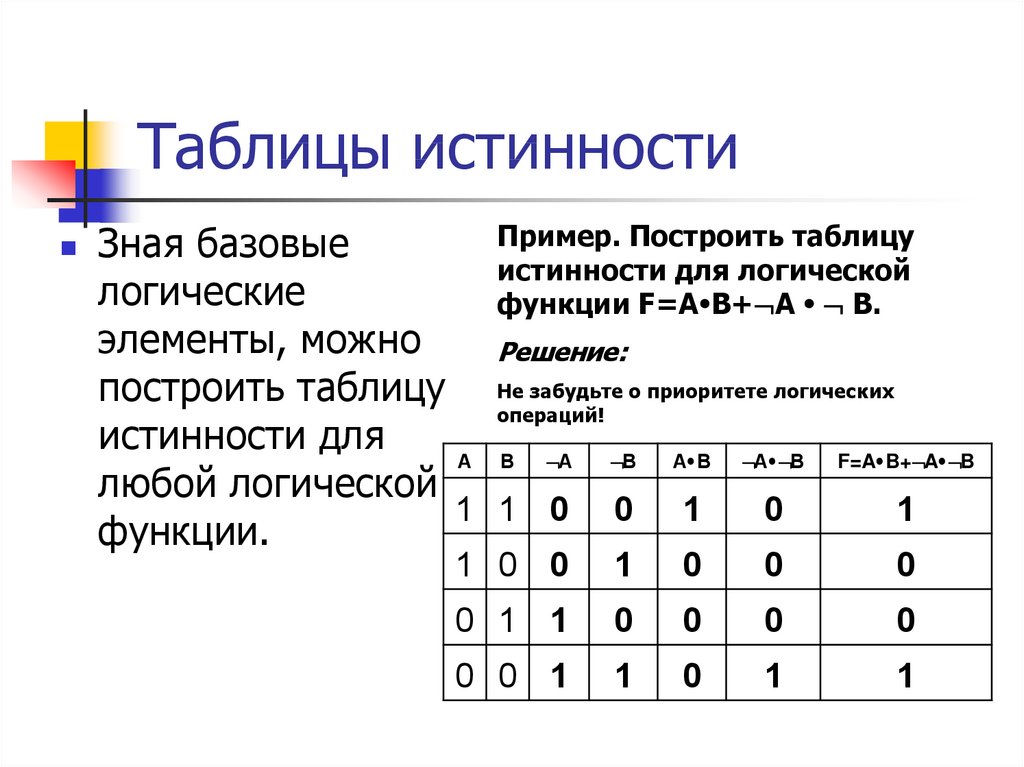 показывает полосу для f 1 /f 0 = 3.
показывает полосу для f 1 /f 0 = 3.
Синтез молекулярного ротора и четырех супрамолекулярных архитектур: синтез молекулярной машины (MM или M)
Реакционноспособная аминогруппа 1-амино-4-бромнафталина сначала защищена ди- трет-бутилдикарбонат (Boc) для облегчения сочетания Соногаширы с 2-этиниланизолом. В присутствии ацетата палладия в качестве катализатора и трифенилфосфена в качестве сокатализатора Boc-производное 1-амино-4-бромнафталина соединяется с 2-этиниланизолом с образованием Boc-производного 4-(2-метоксифенилэтинила). -нафталин-1-иламин, который при обработке гидратированным фторидом тетрабутиламмония приводил к 4-(2-метоксифенилэтинил)-нафталин-1-иламину (ММ). Резюме молекулярно-динамического моделирования, спектроскопическое подтверждение способности ротора содержится в вспомогательном онлайн-тексте A, а подробности синтеза — в онлайн-тексте B (см. рисунки S1–S9).онлайн).
Синтез ПК, ПМ, ПКМ, ПКС, ПКМС
Для синтеза ПР, ПКМ и ПКМС — сначала дендример ПАМАМ G5 (1:2) водный раствор карбоната натрия, раствор метанола берут при рН >9,5 , в присутствии нила -красные молекулы красителя, чтобы инкапсулировать две из них в глубокое ядро четырех дендритных полостей, мы получаем дендритный бокс [PAMAM5-NR] (PC, шаг I). Затем ФС помещают в 10% и 40% смесь диметилсульфоксида (ДМСО) и ацетонитрила, добавляют одной порцией раствор сенсора (изотиоцианат NIR797, S) в боратном буфере (50% от общего объема) и реакционную смесь. продолжают при комнатной температуре. Затем первичные аминогруппы на поверхности ПАМАМ соединяют с NIR79.7изотиоцианатного красителя, продукт реакции [PAMAM-NR]-NIR797изотиоцианат (PCS, стадия II) переносят на следующую стадию. Многокомпонентную смесь продукта PCS, MM, диизопропиламина и триэтиламина растворяют в сухом диметилсульфоксиде и к смеси медленно добавляют глутарилхлорид при температуре ниже 20°С. Реакцию проводят при комнатной температуре в течение 48 часов и собирают конечный продукт, [PAMAM-NLR]-NIR797изотиоцианат-MM (PCMS, стадия III). Для ПМС шаг I избегают, остальное остается прежним; для ПКМ вместо S, часть крепления М выполняется на ПК. На всех этапах продукты очищаются с помощью интенсивного диализа, MALDI-TOF, Raman, FTIR, NMR и пошаговой CEES-спектроскопии для подтверждения природы продукта (см.
Затем ФС помещают в 10% и 40% смесь диметилсульфоксида (ДМСО) и ацетонитрила, добавляют одной порцией раствор сенсора (изотиоцианат NIR797, S) в боратном буфере (50% от общего объема) и реакционную смесь. продолжают при комнатной температуре. Затем первичные аминогруппы на поверхности ПАМАМ соединяют с NIR79.7изотиоцианатного красителя, продукт реакции [PAMAM-NR]-NIR797изотиоцианат (PCS, стадия II) переносят на следующую стадию. Многокомпонентную смесь продукта PCS, MM, диизопропиламина и триэтиламина растворяют в сухом диметилсульфоксиде и к смеси медленно добавляют глутарилхлорид при температуре ниже 20°С. Реакцию проводят при комнатной температуре в течение 48 часов и собирают конечный продукт, [PAMAM-NLR]-NIR797изотиоцианат-MM (PCMS, стадия III). Для ПМС шаг I избегают, остальное остается прежним; для ПКМ вместо S, часть крепления М выполняется на ПК. На всех этапах продукты очищаются с помощью интенсивного диализа, MALDI-TOF, Raman, FTIR, NMR и пошаговой CEES-спектроскопии для подтверждения природы продукта (см. рисунки S1–S9).онлайн). Синтез ранее описанного PCM и описанного здесь PCMS принципиально различаются (подробности см. В Интернете).
рисунки S1–S9).онлайн). Синтез ранее описанного PCM и описанного здесь PCMS принципиально различаются (подробности см. В Интернете).
Эмиссионная спектроскопия с комбинированным возбуждением (CEES)
Эмиссионная спектроскопия с комбинированным возбуждением (CEES): регистрируется около 200 эмиссионных спектров на длинах волн возбуждения с интервалом 5 нм. Интенсивности на выходе представлены как функция длин волн возбуждения и излучения, преобразованных в энергии (эВ). На изоконтурном графике мы обнаруживаем пики; на каждом пике мы получаем три значения, энергию возбуждения (Ex), энергию излучения (Em) и в зависимости от отрицательного или положительного знака ΔE ( = Ex — Em), поглощаемую или излучаемую молекулярной структурой энергию в процессе излучения, используя раствор Рамана и молекулярную динамику, мы находим, какие атомные группы используют ΔE. Используя эту концепцию, мы оцениваем переходы полос для каждого отдельного события, пренебрегая областями выше рамановского хребта на 45 0 (поскольку Ex < Em), около 45 0 , ΔE~0, поглощения нет, вся приложенная энергия излучается.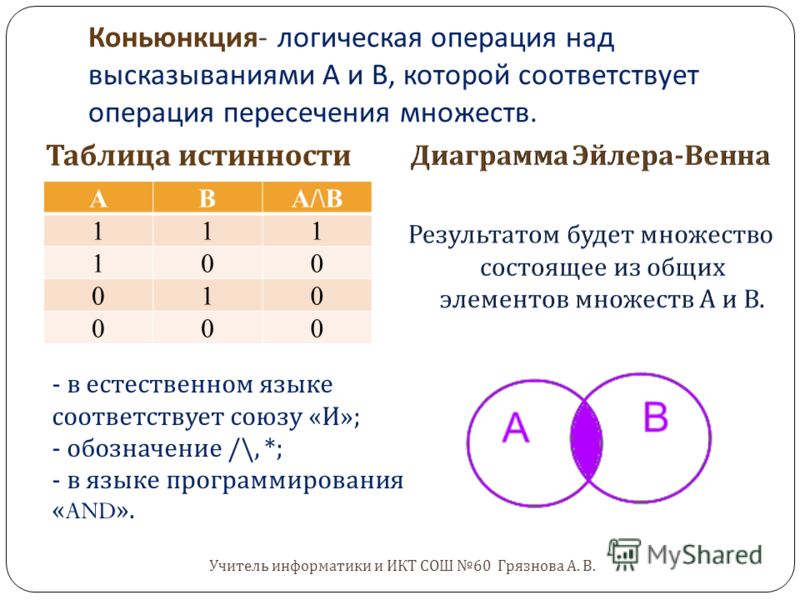 В CEES пик S (1,9 эВ, 4,5 эВ) скрыт на всех графиках CEES в этой статье, поскольку его интенсивность низка по сравнению с P, C и M.
В CEES пик S (1,9 эВ, 4,5 эВ) скрыт на всех графиках CEES в этой статье, поскольку его интенсивность низка по сравнению с P, C и M.
Теоретическое моделирование пути передачи энергии PCMS
Теоретическое моделирование для отслеживания путь передачи энергии осуществлялся по полуэмпирической методике АМ1 на МОПАС. Чтобы сымитировать эффект плотности, мы протестировали 60 различных конформаций и оценили изменение траектории стресса на PCMS. Для исследования pH мы использовали Hyperchem 10.0, где мы окружили PCMS ионами как потенциальную проблему с коробкой. Распределение относительного потенциала в зависимости от плотности протонов (H+) изучалось для имитации эксперимента по изменению pH.
Как цитировать эту статью : Ghosh, S. et al. Органический желеобразный фрактальный логический вентиль с бесконечной таблицей истинности. науч. Респ. 5 , 11265; doi: 10.1038/srep11265 (2015).
Дополнительные данные:
Нажмите здесь для просмотра.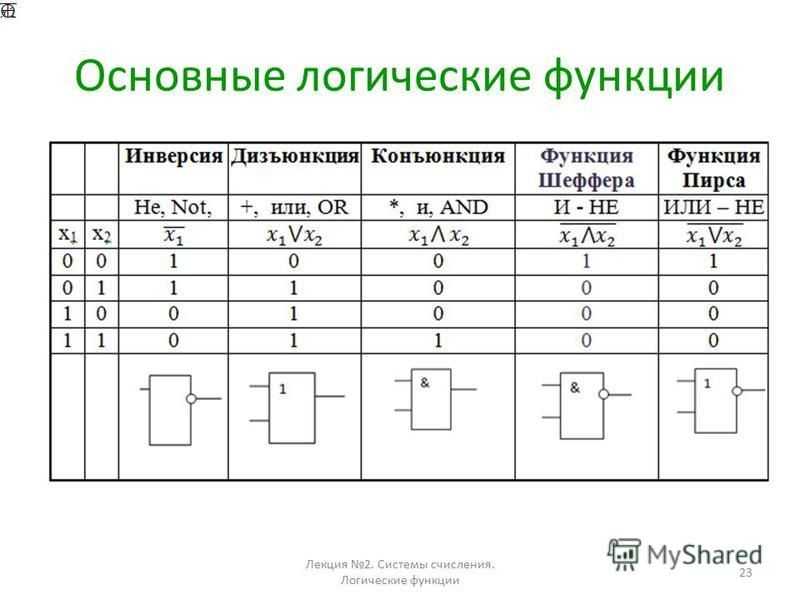 (771K, pdf)
(771K, pdf)
Дополнительный фильм 1:
Нажмите здесь для просмотра. (21M, avi)
Дополнительный фильм 2:
Щелкните здесь для просмотра. (16M, avi)
Дополнительный фильм 3:
Нажмите здесь для просмотра. (7,5M, wmv)
Дополнительный фильм 4:
Нажмите здесь для просмотра. (9,6M, avi)
Дополнительный фильм 5:
Нажмите здесь для просмотра. (2,8M, avi)
Дополнительный фильм 6:
Нажмите здесь для просмотра. (8.1M, avi)
Дополнительный онлайн-материал:
Нажмите здесь для просмотра. (2.3M, doc)
(2.3M, doc)
Работа выполнена при финансовой поддержке AFSOR.
Авторы заявляют об отсутствии конкурирующих финансовых интересов.
Вклад авторов С.Г. синтезировал и охарактеризовал А.Б. планировал исследование, Д.Ф. рассмотрел работу
- Bennett C.H. & Landauer R. Фундаментальные физические пределы вычислений. науч. Являюсь. 253, 48–56 (1985). [Google Scholar]
- Сиути П., Язбек Дж. и Лу Т. К. Разработка генетических схем, которые вычисляют и запоминают. Нац. Прото. 9, 1292–1300 (2014). [PubMed] [Google Scholar]
- Bandyopadhyay A. & Acharya S. 16-битная параллельная обработка молекулярной сборки. проц. Натл. акад. науч. США 105, 3668–3672 (2008). [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Biswas A.K., Atulasimha J. & Bandyopadhyay S.
Устойчивый к ошибкам энергонезависимый магнитоупругий универсальный логический вентиль со сверхнизким энергетическим запаздыванием. науч. Респ.
4, 7553 (2014).
 [Бесплатная статья PMC] [PubMed] [Google Scholar]
[Бесплатная статья PMC] [PubMed] [Google Scholar] - Tamsir A., Tabor J. J. & Voigt A. Надежные многоклеточные вычисления с использованием генетически закодированных вентилей НЕ-ИЛИ и химических проводов. Природа 469, 212–215 (2011). [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Bandyopadhyay A., Pati R., Sahu S., Fujita D. & Peper F. Массивно-параллельные вычисления на органическом молекулярном слое. Природа физ. 6, 369–375 (2010). [Google Scholar]
- Bandyopadhyay A., Sahu S. & Fujita D. Наименьшая искусственная молекулярная нейронная сеть для коллективной и оперативной обработки информации. заявл. физ. лат. 95, 113702 (2009). [Google Scholar]
- Калики Дж. Неразрешимая проблема алгебры таблиц истинности. Дж. Симб. Логика 19, 172–176 (1954). [Google Scholar]
- Грим П., Мар Г. и Денис П. С. Философский компьютер: исследовательские эссе по философскому компьютерному моделированию. [323] (MIT Press, Бостон, США, 1998). [Google Scholar]
- Карп С.
 Р.
Языки с выражениями бесконечной длины. (редакторы Brouwer I.E.J. и др. ) (North-Holland Publishing Co., Амстердам, 1964). [Google Scholar]
Р.
Языки с выражениями бесконечной длины. (редакторы Brouwer I.E.J. и др. ) (North-Holland Publishing Co., Амстердам, 1964). [Google Scholar] - Barwise K. J. Инфинитарная логика и допустимые множества. Дж. Симб. Логика 34, 226–252 (1969). [Академия Google]
- Ван Оттерло М. Frontiers in Artificial Intelligence and Applications, Vol 192 (eds Van Otterlo M.) [508] (Ios Press, STM Publishing House, 2009). [Google Scholar]
- Адамацкий А., Костелло Д. Л. и Бенджамин П. Дж. Экспериментальные логические вентили в реакционно-диффузионной среде: вентиль XOR и не только. физ. Преподобный Е 66, 046112 (2002). [PubMed] [Google Scholar]
- Лебендер Д. и Шнайдер Ф. В. Логические вентили, использующие нелинейную химическую реакцию. Дж. Физ. хим. 98, 7533–7537 (1994). [Google Scholar]
- Стейнбок О., Кеттунен П. и Шоуолтер К. Химические волновые логические элементы Дж. Физ. хим. 100, 18970–18975 (1996). [Google Scholar]
- Джентили П. Л., Хорват В.
 , Ванаг В. К. и Эпштейн И. Р.
Белоусова-Жаботинского «химический нейрон» как процессор бинарной и нечеткой логики. Междунар. Дж. Неконв. Комп.
8, 177–192 (2012). [Google Scholar]
, Ванаг В. К. и Эпштейн И. Р.
Белоусова-Жаботинского «химический нейрон» как процессор бинарной и нечеткой логики. Междунар. Дж. Неконв. Комп.
8, 177–192 (2012). [Google Scholar] - Копельман Р. Кинетика фрактальных реакций, Наука, 241, 1620–1625, (1988). [PubMed] [Google Scholar]
- Гордон Н. Л. Введение во фрактальную геометрию, 3-е изд. [71] (книга Тотема, 2000 г.). [Академия Google]
- Ауслендер С., Ауслендер Д., Мюллер М., Виланд М. и Фуссенеггер М. Программируемые одноклеточные биокомпьютеры млекопитающих. Природа 487, 123–127 (2012). [PubMed] [Google Scholar]
- Синха С. и Дитто В. Л. Вычисления с распределенным хаосом. физ. Преподобный Э. 59, 363–377 (1999). [PubMed] [Google Scholar]
- Casdagli M. Хаос и детерминированное против стохастического нелинейного моделирования. Дж. Роял Стат. соц. Серия Б 54, 303–328 (1991). [Google Scholar]
- Бабаи М.
Новый метод шифрования текста и изображений, основанный на теории хаоса и вычислениях ДНК.
 Нац. Комп.
12, 101–107 (2013). [Академия Google]
Нац. Комп.
12, 101–107 (2013). [Академия Google] - Пэн С.К. и др. Случайность против детерминированного хаоса: влияние на кластеры перколяции вторжения. физ. Преп. А 42, 4537–4542 (1990). [PubMed] [Google Scholar]
- Мюллер Х. Фрактальные скейлинговые модели резонансных колебаний в цепных системах гармонических осцилляторов. прог. физ. 2, 72–76 (2009). [Google Scholar]
- Добен Дж. В. Георг Кантор: его математика и философия бесконечного. [404] (Пресса Принстонского университета, 1990). [Google Scholar]
- МакЛеннан Б. Дж. Универсально программируемая интеллектуальная материя: систематический подход к нанотехнологиям (презентация на IEEE-Nano, 2002 г.). [Академия Google]
- Гуревич Ю. и Шелах С. Почти линейное время. LNCS 363, 108–118 (1989). [Google Scholar]
- Джожа Р. и Линден Н. О роли запутанности в ускорении квантовых вычислений. проц. Королевский соц. Лондон Серия А. Математика. физ. англ. науч. 459, 2011–2032 (2003). [Google Scholar]
- Маасс В.
 , Натшлегер Т. и Маркрам Х.
Вычисления в реальном времени без устойчивых состояний: новая структура нейронных вычислений на основе возмущений. Нейронный комп.
14, 2531–2560 (2002). [PubMed] [Академия Google]
, Натшлегер Т. и Маркрам Х.
Вычисления в реальном времени без устойчивых состояний: новая структура нейронных вычислений на основе возмущений. Нейронный комп.
14, 2531–2560 (2002). [PubMed] [Академия Google] - Джин. Ван Х. [От Фреге до Гёделя: Справочник по математической логике] в От Фреге до Гёделя: Справочник по математической логике. 1879–1931 (Harvard Univ. Press, Бостон, США, 2002). [Google Scholar]
- Гош С. и др. Наномолекулярная платформа: протокол для написания программы передачи энергии внутри молекулы для биоинспирированной супрамолекулярной инженерии. Доп. Функц. Мат. 24, 1364–1371 (2014). [Google Scholar]
- Bandyopadhyay A. & Wakayama Y. Происхождение отрицательного дифференциального сопротивления в молекулярных соединениях бенгальской розы. заявл. физ. лат. 90, 023512 (2007). [Google Scholar]
- Bandyopadhyay A., Sahu S., Fujita D. & Wakayama Y.
Новый подход к извлечению нескольких различных конформеров и одновременно существующих различных электронных свойств одной молекулы методом точечного контакта.
 физ. хим. хим. физ.
12, 2033 (2010). [PubMed] [Google Scholar]
физ. хим. хим. физ.
12, 2033 (2010). [PubMed] [Google Scholar] - Сергеев Ю. Д. Численное дифференцирование высшего порядка на Infinity Computer, Optimiz. лат. 5, 575–585 (2011). [Google Scholar]
- Dirksen A. & Cola L.D.C.R. Фотоиндуцированные процессы в дендримерах. Чими 6, 873–882 (2003). [Академия Google]
- Хауэр Дж., Бакап Т. и Мотцкус М. Усиление молекулярных мод за счет электронно-резонансного многоимпульсного возбуждения: дальнейший прогресс в области селективной химии мод. Дж. Хим. физ. 125, 061101 (2006). [PubMed] [Google Scholar]
- Гош С., и др. Резонансный язык колебаний футуристического нано-машинного модуля: устранение раковых клеток и бляшек болезни Альцгеймера Aβ, Curr. Тема мед. хим. 15, 534–541 (2015). [PubMed] [Google Scholar]
- Гош С. и др. Проектирование и создание компьютера, похожего на мозг: новый класс частотно-фрактальных вычислений с использованием беспроводной связи в надмолекулярной органической неорганической системе.
 Информация
5, 28–101 (2014). [Google Scholar]
Информация
5, 28–101 (2014). [Google Scholar]
Статьи из Scientific Reports предоставлены здесь Nature Publishing Group
Таблицы правды (… вы можете справиться с правдой)
Около восьми лет назад я работал над своим первым крупным коммерческим проектом программного обеспечения. Раньше я работал фрилансером, и у меня были в основном небольшие и скучные проекты. Однако в этом проекте участвовала команда из восьми человек плюс руководство, и временами он был на удивление сложным.
Однажды нам пришлось реализовать функцию, которая зависела от четырех независимых условий. Независимая в данном случае означает, что не было исключительных ветвей логики. Для его реализации понадобилось несколько веток с похожей, но не идентичной логикой. Я был немного напуган, потому что знал, что это будет один большой уродливый клубок вложенных операторов if / case, который невозможно сделать правильно с первой попытки и, вероятно, будет трудно протестировать.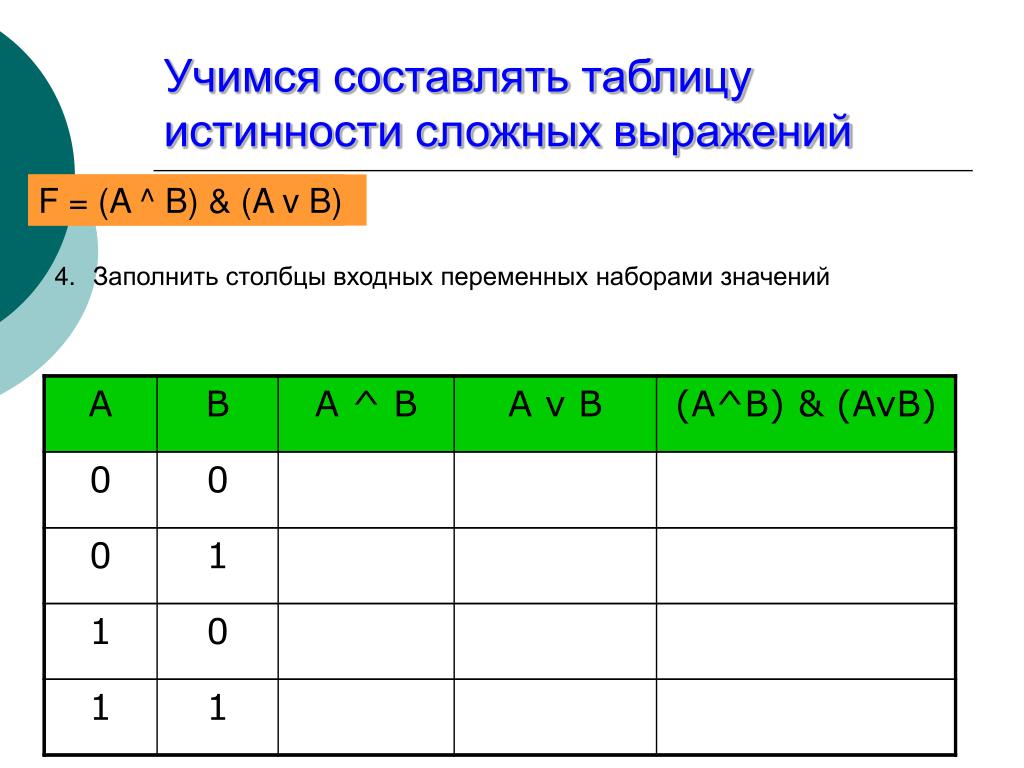
Затем появился наш руководитель разработки, опытный хакер старой школы, который сказал мне: «Давайте реализуем это с таблицей истинности!»
Сначала я не понял, о чем он говорит, а потом подумал, что это будет какое-то хитроумное низкоуровневое решение этой сложной проблемы, но оказалось, что все понятно и легко рассуждать.
С тех пор у меня было еще три или четыре случая, когда я использовал таблицы истинности для решения подобных сложных задач, и я всегда был благодарен за этот совет. Каждый раз, когда я предлагал использовать таблицы истинности в таких ситуациях, всегда находились коллеги, которые либо не знали о них, как и я семь лет назад, либо знали их теоретически, но никогда не применяли на практике.
Последний случай был совсем недавно в моем текущем проекте в Wooga, поэтому я подумал, что было бы неплохо поделиться концепцией со всеми, кто еще не знает, о чем я говорю.
Покажите мне таблицы
Если вы изучали информатику и/или философию, вы должны были видеть таблицы истинности на бумаге. Они часто используются, например, для описания поведения логических вентилей. Вот как будет выглядеть таблица истинности для вентиля И:
Они часто используются, например, для описания поведения логических вентилей. Вот как будет выглядеть таблица истинности для вентиля И:
А | Б | Выход ---|---|------- 0 | 0 | 0 1 | 0 | 0 0 | 1 | 0 1 | 1 | 1
Эта таблица говорит вам, что на выходе логического элемента И будет 1, только если на входе A И B 1.
В философии одни и те же таблицы используются для рассуждений о логических утверждениях в аргументах это недостаточно точно, я знаю, что вам не все равно :).
Практическое применение таблиц истинности
Для практического применения таблицы истинности имеют немного другую форму. Представьте, что у нас есть веб-сайт, на котором пользователи генерируют много контента, и у них есть возможность загрузить всю свою историю, которая настолько велика, что нам приходится ее обрабатывать и сжимать. Теперь приложение может находиться в нескольких разных состояниях, и только в одном из них пользователь может загрузить архив.
Давайте начнем с простого и скажем, что у нас есть две логические переменные, которые важны для определения состояния нашего приложения.
запрашиваемый_архив: правда | ЛОЖЬ обработка_завершена: правда | ЛОЖЬ
Для каждой переменной мы теперь назначаем уникальный двоичный флаг:
запрашиваемый_архив: 01 (десятичный: 1) processing_finished: 10 (десятичное число: 2)
Теперь таблица истинности будет выглядеть так:
запрошенный | обработка |
архив | закончил | результат | значение
----------|-------------|---------|----------------- ------------
00 | 00 | 00 | не запрошено, не обработано
01 | 00 | 01 | запрошено, но не обработано
00 | 10 | 10 | невозможно
01 | 10 | 11 | запрашивается и обрабатывается
Основная идея здесь состоит в том, чтобы оценить условия по отдельности и использовать двоичное ИЛИ для вычисления результирующего битового флага.
Как я уже сказал, это простой пример, который не требует строгой реализации таблицы истинности, но даже в этой ситуации таблица истинности в форме комментария над вложенным условным оператором может принести пользу следующему человеку, читающему ваш код.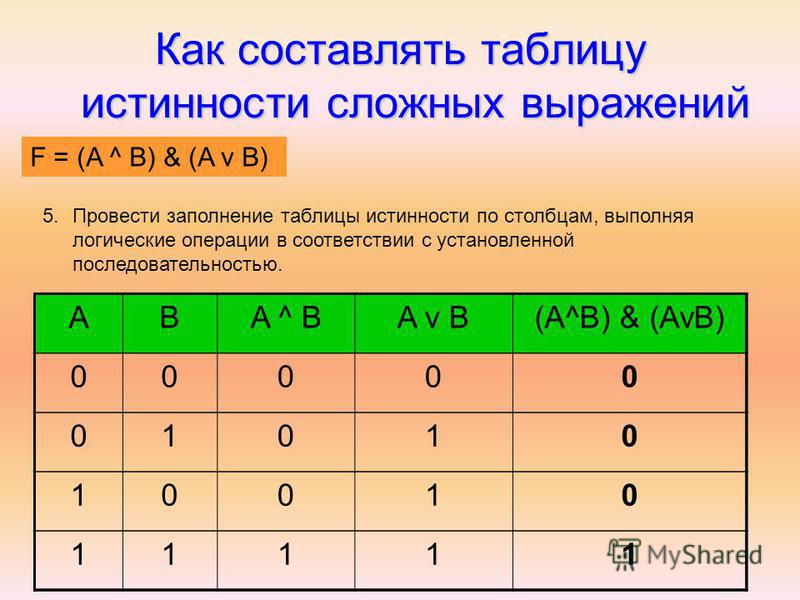
Также он предоставляет обзор всех возможных комбинаций и того, какие случаи действительно актуальны для вас. Вы знаете, какие модульные тесты писать, и можете быть уверены, что рассмотрели все.
Реализация
Хорошо, теперь давайте реализуем эту таблицу истинности. Мы уже знаем, какие у нас есть случаи и что они означают, поэтому первое, что нужно сделать, это присвоить им символические имена в вашем коде. В этом примере я буду использовать ruby, но он должен работать аналогичным образом на вашем любимом языке.
Для этого простого примера может показаться неочевидным, почему таблицы истинности хороши, но он уже иллюстрирует некоторые аспекты. Оценка условий изолирована в отдельные функции, которые вы можете очень легко протестировать.
Когда вы выполняете модульное тестирование функции archive_state и получаете неожиданное состояние, битовые флаги сообщают вам, какое именно из условий не оправдало ваших ожиданий.
Вы даете каждому состоянию символическое имя и избегаете вложенных условий.
Я знаю, я знаю, это выглядит безумно сложно, но это всего лишь пример, и как только вы добавите одно или несколько условий, станет намного яснее, почему я всегда предпочитаю таблицу истинности вложенным условиям.
Следующий пример кода взят из реального приложения erlang и снова посвящен определению состояния приложения. В зависимости от дня сезона, состояния пользовательских данных и состояния обработки мы должны делать разные вещи, и для одного из условий нет эксклюзивной ветки, что означает, что реализация будет болезненной. (Примечание: в первом есть скрытое четвертое условие, проверяющее, что сезон действительно закончился, так как все матчи были смоделированы в последний день сезона) 93 возможных комбинации, две из которых невозможны, мы точно знаем, какие случаи означают, что и что мы хотим сделать для каждой из них, мы также можем реализовать каждое условие в аккуратных и аккуратных функциях, которые легко тестируются, у нас есть символические имена и окончательный оператор case действительно читаем.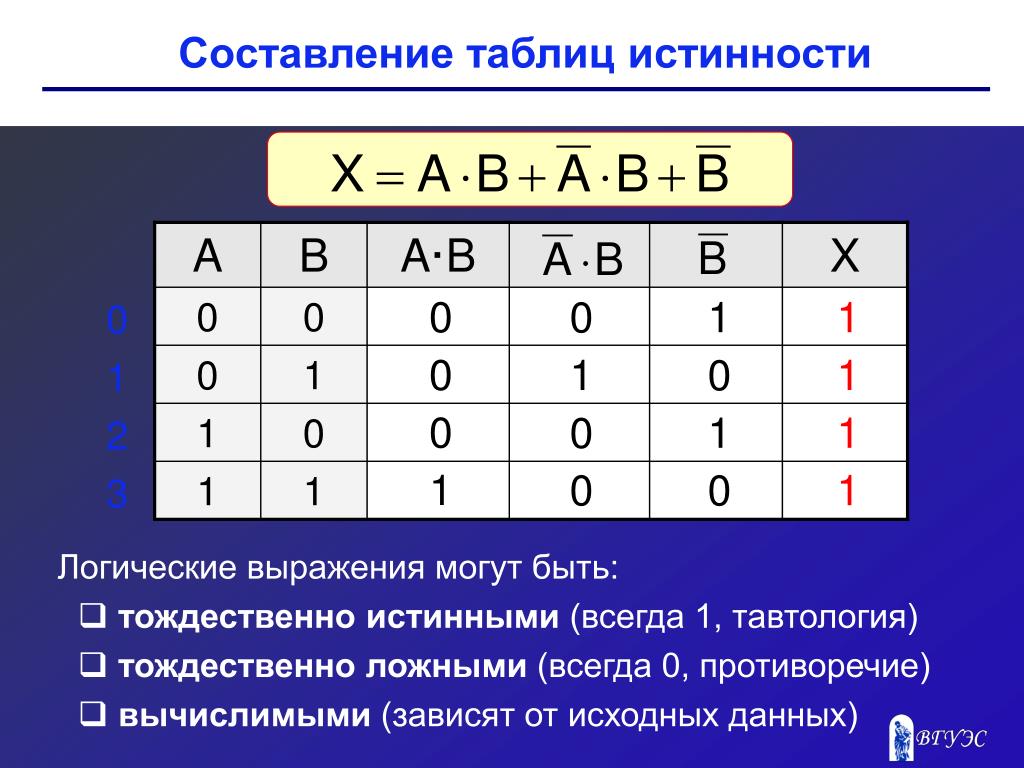
Без комментария, показывающего фактическую таблицу истинности, и без всех остальных комментариев весь этот фрагмент кода, конечно, был бы намного менее интуитивным, но с ними это самодостаточная документация.
Самое приятное то, что даже если у вас есть четыре или пять условий, сложность кода не увеличивается, просто требуется больше работы, чтобы записать начальную таблицу истинности из 16 или 32 возможностей, но реализация будет следовать той же схеме и оценочный оператор case по-прежнему будет легко читаться.
Лично я дошел до четырех условий, и когда я сталкивался с ситуацией, когда оцениваются пять условий, я сначала потратил несколько часов, пытаясь уменьшить количество условий, возможно, даже рефакторинг кода, но если у вас действительно такая сложная система , таблицы истинности — ваш лучший шанс реализовать это, не теряя рассудка.
Дайте мне знать в комментариях, если это было полезно.
Генератор таблиц истинности — Мгновенное создание логических таблиц истинности
Генератор таблиц истинности — Мгновенное создание логических таблиц истинности
Логический инструмент для создания таблицы истинности онлайн
Введите логическое выражение
Поделиться
Твитнуть
Как использовать ?
- Введите свое логическое выражение в поле поиска
- Использовать буквы для переменных, символы для логических операторов
- Нажмите кнопку «Получить таблицу истинности»
- Таблица истинности будет отображаться
- Нажмите кнопку «Расширенная таблица истинности» для операций с пропозициональной логикой
| Оператор | Символ для ввода | Пример |
|---|---|---|
| ИЛИ | | | А | Б | С |
| И | и | А и В и С |
| НЕ | ! 9 Б |
Таблица истинности
Таблица истинности представляет собой представление логического выражения в табличном формате. Он в основном используется в математике и информатике.
Он в основном используется в математике и информатике.
Представление выполняется с использованием двухзначной логики — 0 или 1. Вы также можете ссылаться на них как на True (1) или False (0). Он используется для просмотра выходного значения, сгенерированного из различных комбинаций входных значений.
Символы логических вентилей
Эти входные значения представляют собой различные переменные и символы (обычно называемые ЛОГИЧЕСКИМИ ВОРОТАМИ). Ниже приведены ВОРОТ и символы
- И (символически: &)
- ИЛИ (символически: +)
- НЕ (символически: !)
- НО (обозначает: НЕ ИЛИ)
- НЕ-И (Обозначает: Не-И)
Примеры таблиц истинности
В каждой таблице истинности каждое утверждение обычно представлено двоичной цифрой или переменной.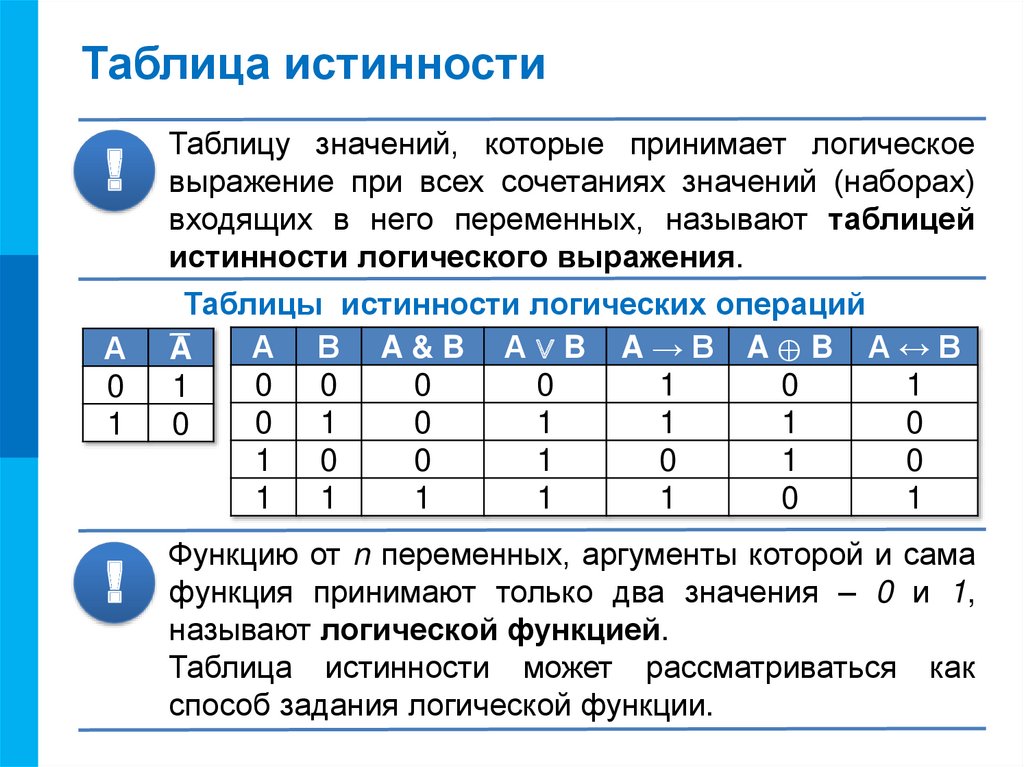 Для лучшего понимания взгляните на приведенные ниже примеры.
Для лучшего понимания взгляните на приведенные ниже примеры.
Таблица истинности шлюза OR
| Символ | А | Б | А+В |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 0 | 1 | 1 | |
| 1 | 1 | 1 |
Таблица истинности вентилей И
| Символ | А | Б | АБ |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
Таблица истинности логических элементов NAND
| Символ | А | Б | !(А. Б) Б) |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Таблица истинности шлюза NOR
| Символ | А | Б | !(А+В) |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 0 |
Таблица истинности шлюза НЕ
| Символ | А | !А |
|---|---|---|
| 0 | 1 | |
| 1 | 0 |
Генератор таблиц истинности
Таблица истинности представляет собой математическую таблицу и основу для всех вычислительных нужд.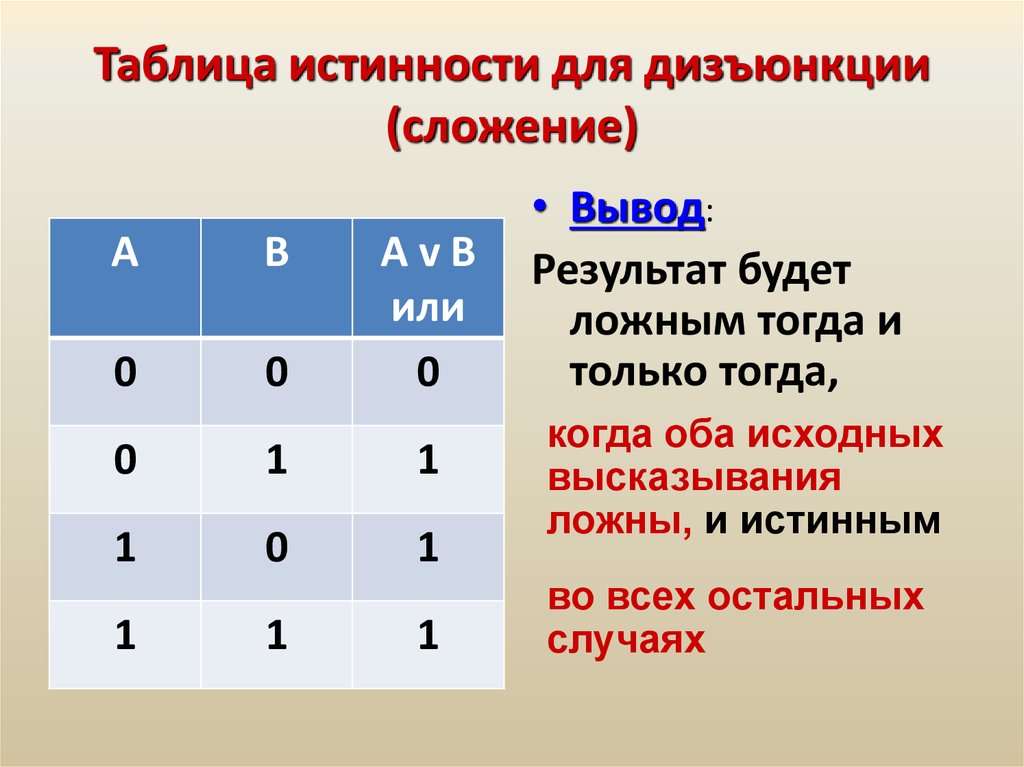 Он используется, чтобы выяснить, истинно ли пропозициональное выражение для всех допустимых входных значений.
Он используется, чтобы выяснить, истинно ли пропозициональное выражение для всех допустимых входных значений.
Создание таблицы истинности включает в себя простую логику, но иногда это может замедлить работу, особенно когда вы работаете над последним проектом. Это когда вы можете использовать генератор таблиц истинности.
Генератор таблиц истинности — это онлайн-инструмент, который используется для мгновенного создания логических таблиц истинности. Вы можете вводить логические операторы в различных форматах и получать точные результаты в виде символов логической логики.
Расширенная таблица истинности
Этот инструмент генерирует таблицы истинности для формул пропозициональной логики. Вы можете вводить логические операторы в нескольких различных форматах. Например, пропозициональная формула p ∧ q → ¬r может быть записана как р/\ q -> ~г, как p и q => не r, или как p && q -> !r. Связки ⊤ и ⊥ можно вводить как T и F.
FAQ
Таблица, показывающая все возможные комбинации переменных в выражении в символьной логике с их окончательным результатом как истинным или ложным.
Таблица истинности представляет собой разбивку логической функции путем перечисления всех возможных значений, которые может получить функция.
0 представляет false в булевых логических выражениях. 1 считается Истинным. .
Введение в булеву логику — GeeksforGeeks
Булева алгебра — это тип алгебры, который создается путем работы с двоичной системой. В 1854 году Джордж Буль, английский математик, предложил эту алгебру. Это вариант логики высказываний Аристотеля, в которой используются символы 0 и 1, или Истина и Ложь. Булева алгебра связана с бинарными переменными и логическими операциями.
Логическое выражение и переменные
Логическое выражение — это выражение, которое при вычислении дает логическое значение, истинное или ложное, единственный способ выразить логическое значение. Принимая во внимание, что логические переменные — это переменные, которые хранят логические числа. P + Q = R — логическая фраза, в которой P, Q, R — логические переменные, которые могут хранить только два значения: 0 и 1. Компьютер выполняет все операции, используя двоичные 0 и 1, поскольку компьютер понимает машинный язык (0/1 ). Булева логика, названная в честь Джорджа Буля, представляет собой тип алгебры, в которой все значения сводятся к одной из двух возможностей: 1 или 0. Чтобы эффективно понять булеву логику, мы должны сначала понять правила булевой логики, а также истину таблицы и логические вентили.
Компьютер выполняет все операции, используя двоичные 0 и 1, поскольку компьютер понимает машинный язык (0/1 ). Булева логика, названная в честь Джорджа Буля, представляет собой тип алгебры, в которой все значения сводятся к одной из двух возможностей: 1 или 0. Чтобы эффективно понять булеву логику, мы должны сначала понять правила булевой логики, а также истину таблицы и логические вентили.
Таблицы истинности
Таблица истинности представляет все разнообразие комбинаций входных и выходных значений в виде таблицы. В нем показаны все возможности ввода и вывода и, следовательно, сохраняется таблица истинности имени. В логических задачах, таких как булева алгебра и электронные схемы, обычно используются таблицы истинности. T или 1 означает «Истина», а F или 0 означает «Ложь» в таблице истинности.
Пример:
А B X = A.B T T T T F F F T F F F F
Логические вентили
Логический вентиль — это виртуальное или физическое устройство, выполняющее логическую функцию.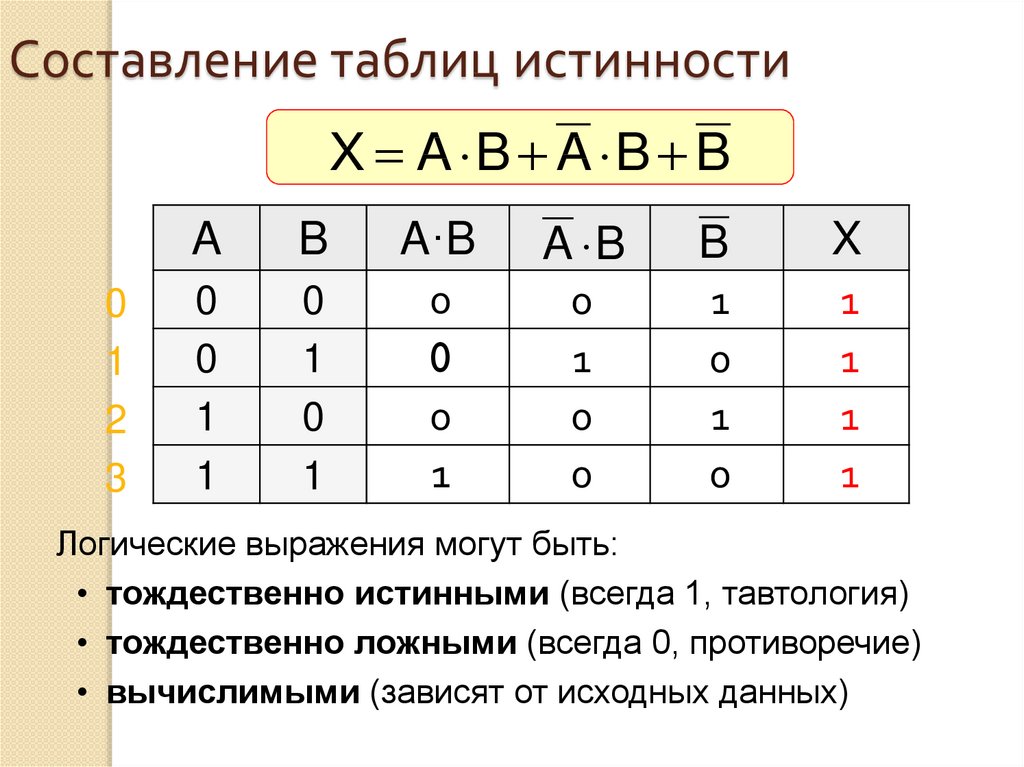 Они используются для создания логических схем. Логические элементы являются основными компонентами любой цифровой системы. Эта электрическая цепь может иметь только один выход и 1 или более входов. Связь между входом и выходом регулируется определенной логикой. Логические вентили И, ИЛИ, НЕ и т. д. являются примерами логических вентилей.
Они используются для создания логических схем. Логические элементы являются основными компонентами любой цифровой системы. Эта электрическая цепь может иметь только один выход и 1 или более входов. Связь между входом и выходом регулируется определенной логикой. Логические вентили И, ИЛИ, НЕ и т. д. являются примерами логических вентилей.
1. Элемент И (Продукт): Логический элемент с двумя или более входами и одним выходом называется элементом И. Правила логического умножения используются для работы вентиля И. Логический элемент И может иметь любое количество входов, хотя наиболее распространенными являются вентили И с двумя и тремя входами. Если на каком-либо из входов низкий уровень (0), на выходе этого вентиля также низкий уровень. Когда все входы имеют высокий уровень (1), выход также будет высоким.
Логическая схема:
Таблица истинности:
Для вентиля И выход X истинен тогда и только тогда, когда оба входа P и Q истинны. So the truth table of AND gate is as follows:
So the truth table of AND gate is as follows:
| P | Q | X = P.Q |
|---|---|---|
| T | T | T |
| T | F | F |
| Ф | Т | Ф |
| F | F | F |
2. Элемент ИЛИ (сумма): Логический элемент, выполняющий операцию логического ИЛИ, называется элементом ИЛИ. Если один или оба входа вентиля имеют высокий уровень, логическая операция ИЛИ выдает высокий уровень на выходе (1). (1). Если ни на одном из входов нет высокого уровня, результатом будет низкий уровень на выходе (0). Точно так же, как вентиль И может иметь неограниченное количество входных пробников, вентиль ИЛИ может иметь только один выходной пробник. Логический элемент ИЛИ находит максимум между двумя двоичными цифрами.
Логическая схема:
Таблица истинности:
Для вентиля ИЛИ выход X истинен тогда и только тогда, когда истинен любой из входов P или Q. So the truth table of OR gate is as follows:
So the truth table of OR gate is as follows:
| P | Q | X = P + Q |
|---|---|---|
| T | T | T |
| T | F | Т |
| Ф | Т | Т |
| F | F | F |
3. Логические элементы НЕ (дополнение): Инвертирующие логические элементы НЕ — это устройства, которые принимают только один вход с выходным уровнем, который обычно равен 1 низким до логического уровня 0, когда их единственный вход находится на логическом уровне 1, или, другими словами, они инвертируют свой входной сигнал. Выход вентиля НЕ возвращает высокий уровень только тогда, когда его вход находится на уровне логического 0. Выход ~ P (~ обозначает «нет») одного входного вентиля НЕ является истинным только тогда, когда вход P ложный или мы можем сказать «неправда». Его также называют обратным вентилем, поскольку он приводит к отрицанию входного логического выражения.
Логическая схема:
Таблица истинности:
Для вентиля НЕ выход X истинен тогда и только тогда, когда вход P ложен. So the truth table of NOT gate is as follows:
| P | ~P |
|---|---|
| T | F |
| F | T |
4. NAND Gate: Логический вентиль, известный как вентиль И-НЕ, выдает низкий уровень на выходе (0), только если все его входы истинны, и высокий уровень на выходе (1) в противном случае. В результате вентиль И-НЕ является инверсией вентиля И, и его схема создается путем соединения вентиля И и вентиля НЕ. NAND означает «не И» Gate, и это приводит к ложному результату только тогда, когда оба входа P и Q истинны. Вентиляторы И (вместе с вентилями ИЛИ-НЕ) известны как универсальные вентили, потому что они представляют собой форму логических вентилей, которые могут реализовывать любую логическую функцию без использования вентилей любого другого типа.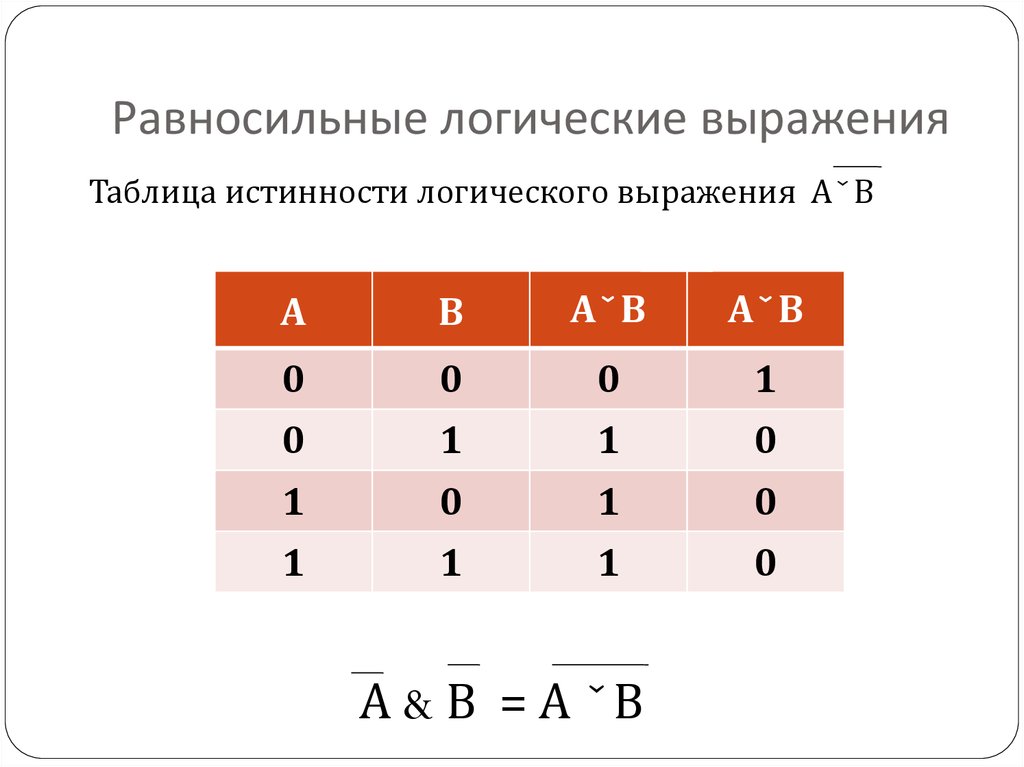
Логическая схема:
Таблица истинности:
Для вентиля И-НЕ выход X ложен тогда и только тогда, когда оба входа (т. е. P и Q) истинны. So the truth table of the NAND gate is as follows:
| P | Q | ~(P.Q) |
|---|---|---|
| T | T | F |
| T | F | Т |
| Ф | Т | T |
| F | F | T |
5. NOR GATE: Логический ворот, известный как NOR Gate (1). false, и низкий выход (0) в противном случае. В результате вентиль ИЛИ-НЕ является обратным вентилю ИЛИ, и его схема создается путем соединения вентилей ИЛИ и вентилей НЕ. NOR означает «не ИЛИ» Gate, и это приводит к истине только тогда, когда оба входа P и Q ложны.
Логическая схема:
Таблица истинности:
Для вентиля И-НЕ выход X истинен тогда и только тогда, когда оба входа (т. е. P и Q) ложны. So the truth table of NOR gate is as follows:
е. P и Q) ложны. So the truth table of NOR gate is as follows:
| P | Q | X = ~(P + Q) |
|---|---|---|
| T | T | F |
| T | Ф | Ф |
| Ф | Т | Ф |
| F | F | T |
и один выход. Только один из входов вентиля XOR должен быть истинным, чтобы выход был истинным. Выход вентиля XOR ложен, если оба его входа ложны, или истинен, если оба его входа истинны. Исключающее ИЛИ означает вентиль «исключающее ИЛИ», и он приводит к истине только тогда, когда любой из двух входов P и Q истинен, т. е. либо истинно P, либо истинно Q, но не оба одновременно.
Logical circuit:
Truth table:
| P | Q | X = P ⊕ Q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
7.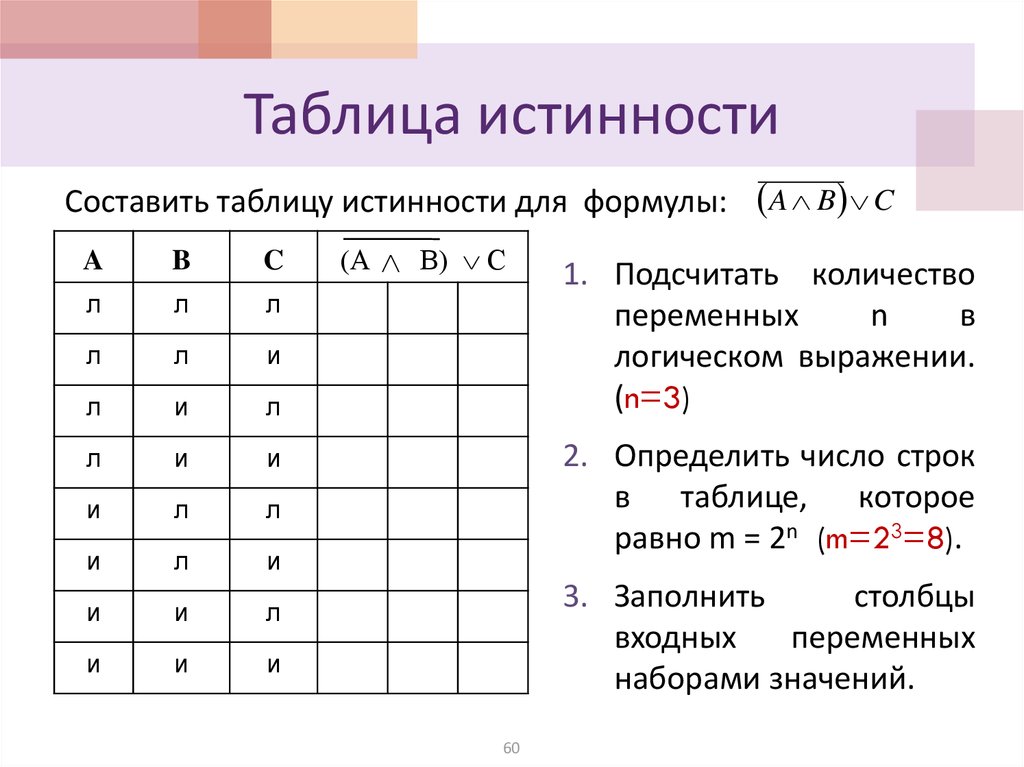 XNOR Gate: An NOR gate (also known as an Exclusive NOR gate) — это цифровой логический вентиль, который находится прямо напротив вентиля XOR. Он имеет два или более входа и один выход. Когда один из двух его входов истинен, но не оба, он вернет ложь. XNOR означает «Исключающее ИЛИ» Gate, и его результат истинен только тогда, когда оба его входа P и Q либо истинны, либо ложны.
XNOR Gate: An NOR gate (also known as an Exclusive NOR gate) — это цифровой логический вентиль, который находится прямо напротив вентиля XOR. Он имеет два или более входа и один выход. Когда один из двух его входов истинен, но не оба, он вернет ложь. XNOR означает «Исключающее ИЛИ» Gate, и его результат истинен только тогда, когда оба его входа P и Q либо истинны, либо ложны.
Logical circuit:
Truth table:
| P | Q | X = P XNOR Q | |||||
|---|---|---|---|---|---|---|---|
| T | T | T | |||||
| T | F | F | |||||
| F | T | F | |||||
| F | F | TA | .0003
Законы де МорганаЗакон Де Моргана гласит: Утверждение 1: Дополнение произведения (И) двух логических переменных (или выражений) равно сумме (ИЛИ) дополнения каждой логической переменной (или выражения) .
Доказательство: Утверждение: ~(P.Q) = (~P) + (~Q) Таблица истинности:
Мы можем ясно видеть, что значения истинности для ~(P.Q) равны значениям истинности для (~P) + (~Q), соответствующие тем же входным данным. Заявление 2: Дополнение суммы (ИЛИ) двух логических переменных (или выражений) равно произведению (И) дополнения каждой логической переменной (или выражения).
Доказательство Утверждение: ~(P+Q) = (~P).(~Q) Таблица истинности is :
| T |
Логические схемы
Электрическая схема, в которой мы можем подать один или несколько двоичных входов (предполагая два состояния, включено или выключено) и получить один двоичный выход, соответствующий входу, способом, который можно описать как функцию в символическая логика. Элементы И, ИЛИ и НЕ представляют собой базовые логические схемы, выполняющие логические функции — И, ИЛИ и НЕ соответственно.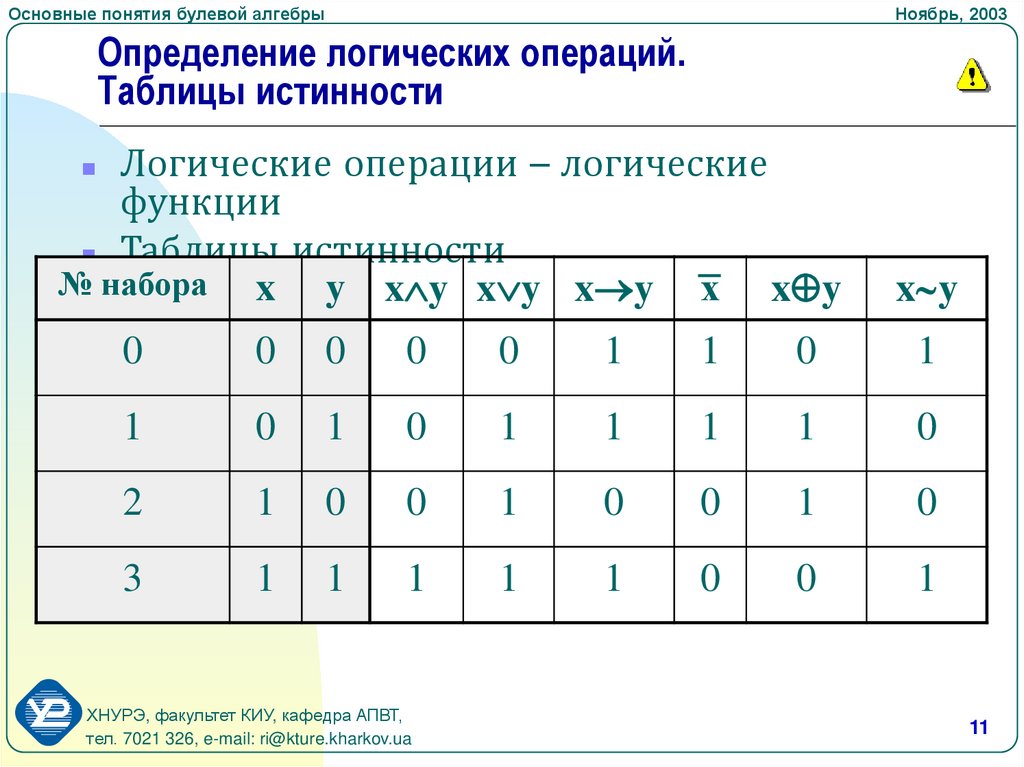 Компьютеры могут выполнять более сложные задачи со схемами, чем с одним вентилем.
Компьютеры могут выполнять более сложные задачи со схемами, чем с одним вентилем.
Пример: Цепочка из двух логических элементов является наименьшей схемой. Рассмотрим следующую схему:
Эта логическая схема предназначена для логического выражения: (P + Q).R.
Здесь используется первый логический элемент ИЛИ: входы P, Q и выход P + Q.
Затем используется логический элемент И: (P + Q), R является входом в него и (P + Q).R является выходом.
Итак, таблица истинности:
P Q R P + Q X = (P + Q).R T T T T T T T F T F T F T T T T F F T F F T T T Т F T F T F F F T F F F F F F F
Примеры вопросов
Вопрос 1.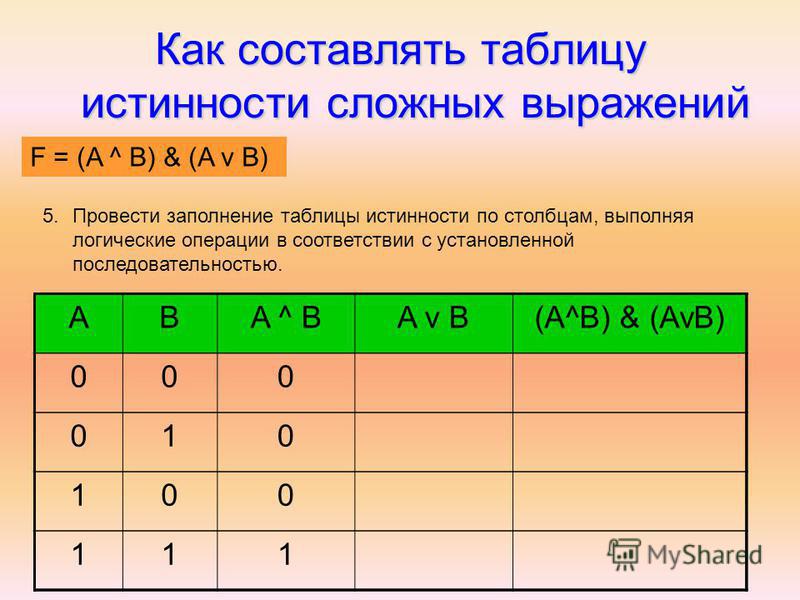 Что такое универсальные ворота?
Что такое универсальные ворота?
Решение:
Универсальные вентили — это логические вентили, которые могут реализовывать любую булеву функцию без необходимости использования каких-либо дополнительных вентилей. Универсальных ворот в цифровой электронике всего два:
1. Ворота И-НЕ и
2. Ворота НЕ-ИЛИ.
Question 2. Design the logical circuit for: A.B + B.C
Solution:
Question 3. What will be the Boolean expression for the following logic circuit :
Решение:
X = ~(P + Q).R + S
Вопрос 4. Проверьте с помощью таблицы истинности: P + P.Q = P
Решение:
The truth table for P + P.Q = P
P Q P.


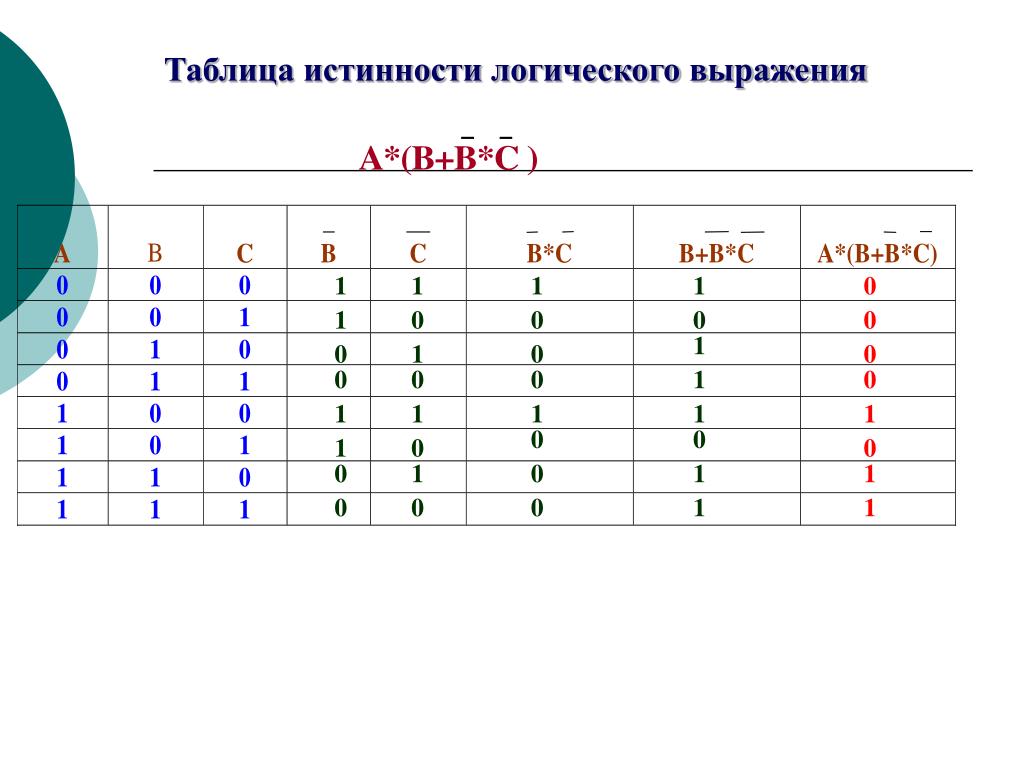
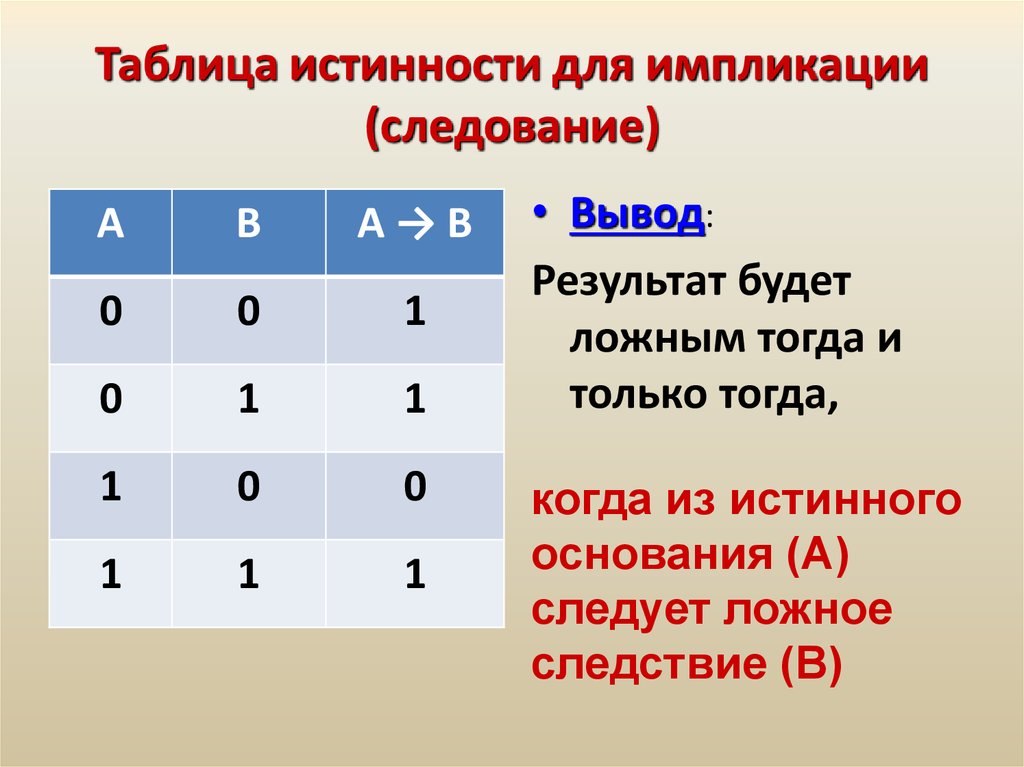

 Примечание. Вы можете использовать значения true и false в своих построениях. Если вы делаете конструкцию для NOT, вы можете использовать ее в последующих частях, не раскрывая ее полностью.
Примечание. Вы можете использовать значения true и false в своих построениях. Если вы делаете конструкцию для NOT, вы можете использовать ее в последующих частях, не раскрывая ее полностью. 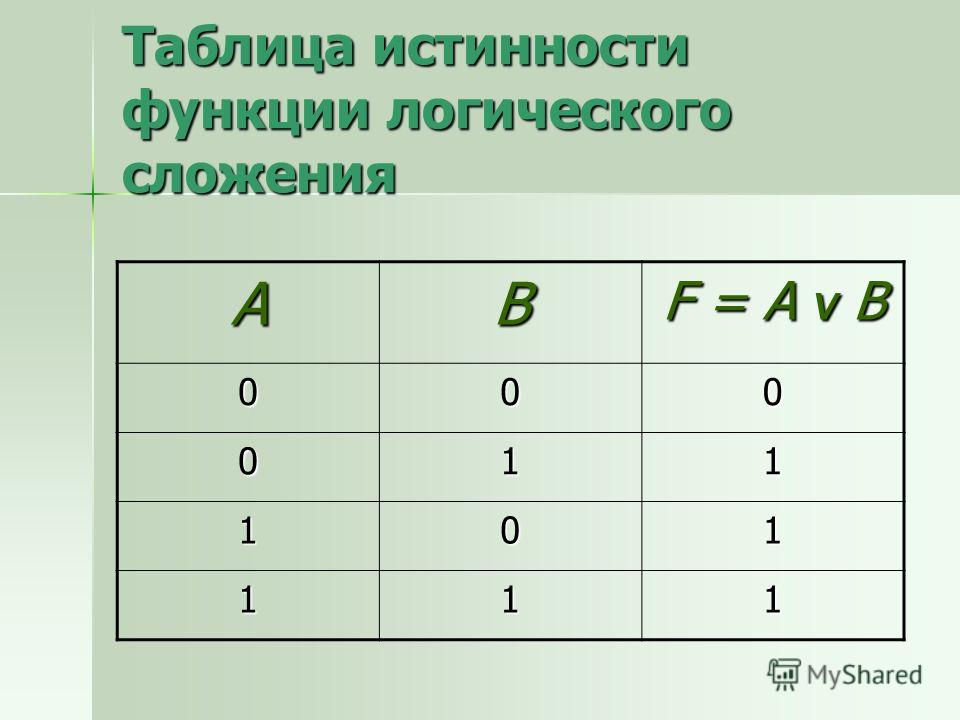 или выкл., истина или ложь)
или выкл., истина или ложь) [Бесплатная статья PMC] [PubMed] [Google Scholar]
[Бесплатная статья PMC] [PubMed] [Google Scholar] Р.
Языки с выражениями бесконечной длины. (редакторы Brouwer I.E.J. и др. ) (North-Holland Publishing Co., Амстердам, 1964). [Google Scholar]
Р.
Языки с выражениями бесконечной длины. (редакторы Brouwer I.E.J. и др. ) (North-Holland Publishing Co., Амстердам, 1964). [Google Scholar] , Ванаг В. К. и Эпштейн И. Р.
Белоусова-Жаботинского «химический нейрон» как процессор бинарной и нечеткой логики. Междунар. Дж. Неконв. Комп.
8, 177–192 (2012). [Google Scholar]
, Ванаг В. К. и Эпштейн И. Р.
Белоусова-Жаботинского «химический нейрон» как процессор бинарной и нечеткой логики. Междунар. Дж. Неконв. Комп.
8, 177–192 (2012). [Google Scholar] Нац. Комп.
12, 101–107 (2013). [Академия Google]
Нац. Комп.
12, 101–107 (2013). [Академия Google] , Натшлегер Т. и Маркрам Х.
Вычисления в реальном времени без устойчивых состояний: новая структура нейронных вычислений на основе возмущений. Нейронный комп.
14, 2531–2560 (2002). [PubMed] [Академия Google]
, Натшлегер Т. и Маркрам Х.
Вычисления в реальном времени без устойчивых состояний: новая структура нейронных вычислений на основе возмущений. Нейронный комп.
14, 2531–2560 (2002). [PubMed] [Академия Google] физ. хим. хим. физ.
12, 2033 (2010). [PubMed] [Google Scholar]
физ. хим. хим. физ.
12, 2033 (2010). [PubMed] [Google Scholar]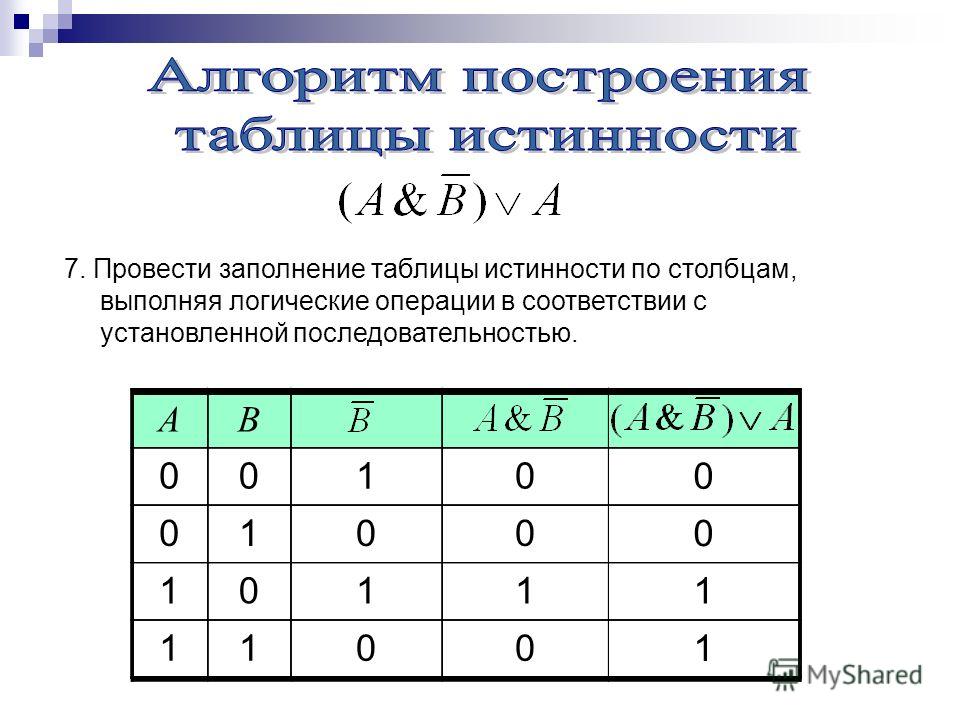 Информация
5, 28–101 (2014). [Google Scholar]
Информация
5, 28–101 (2014). [Google Scholar] 0 = P
0 = P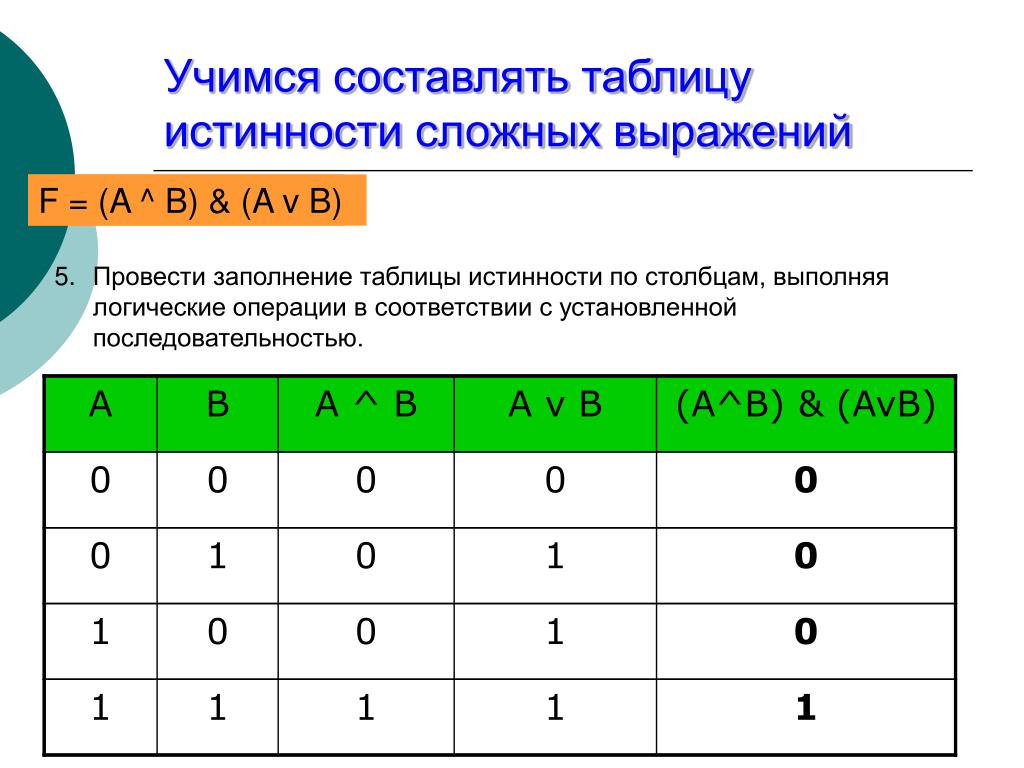 Q)
Q) (~Q)1
(~Q)1