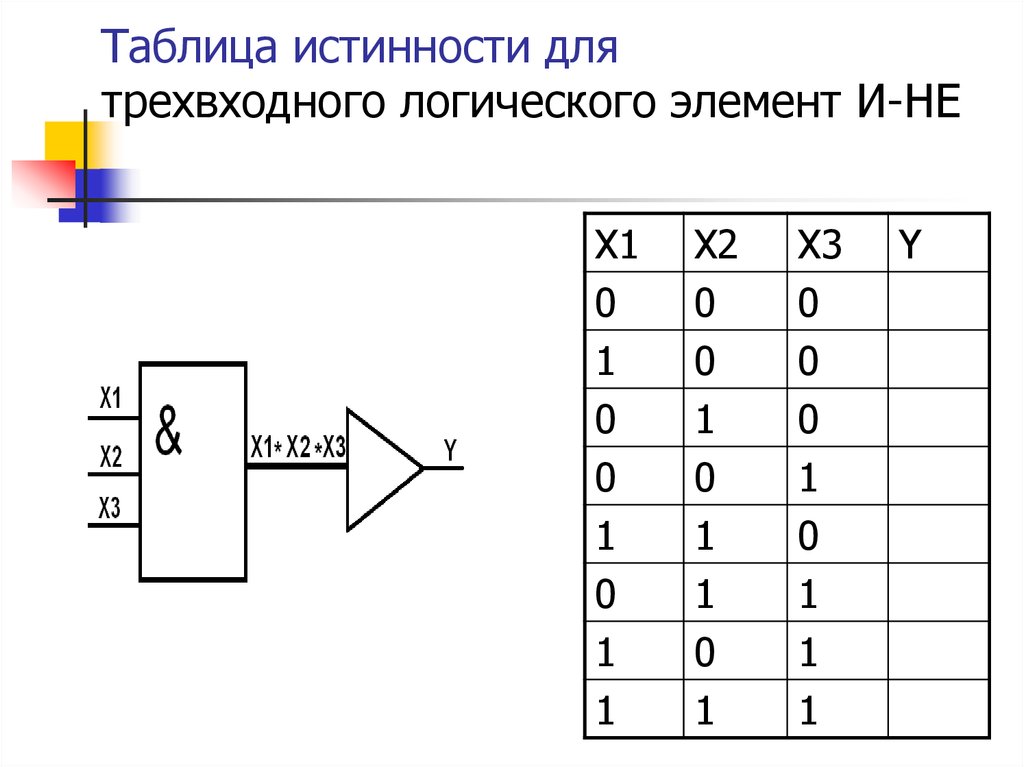
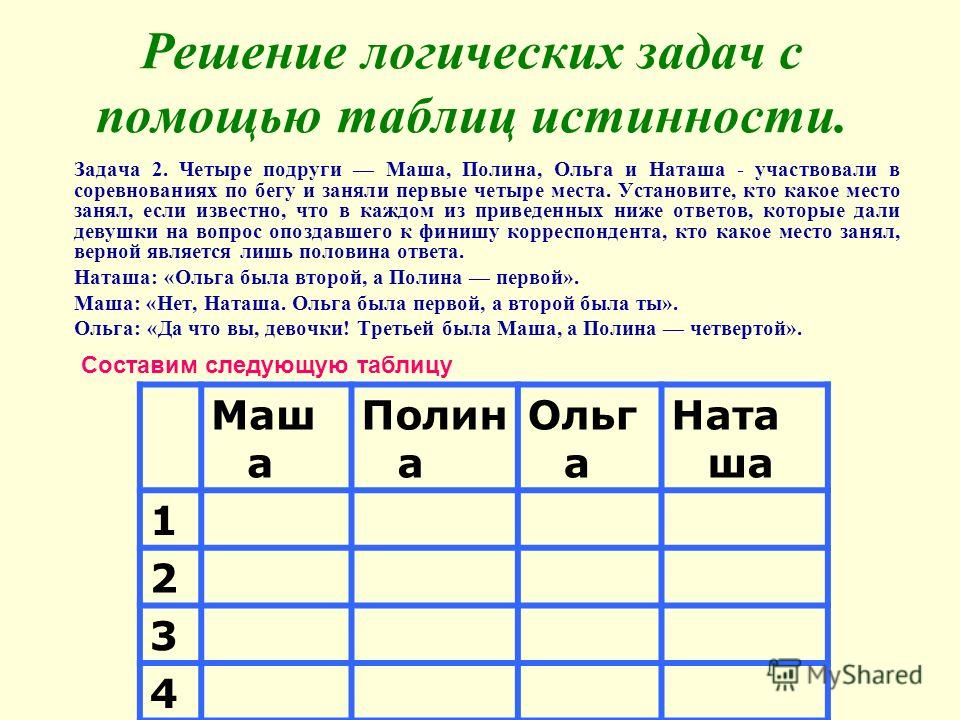
Таблицы истинности. Решение задач
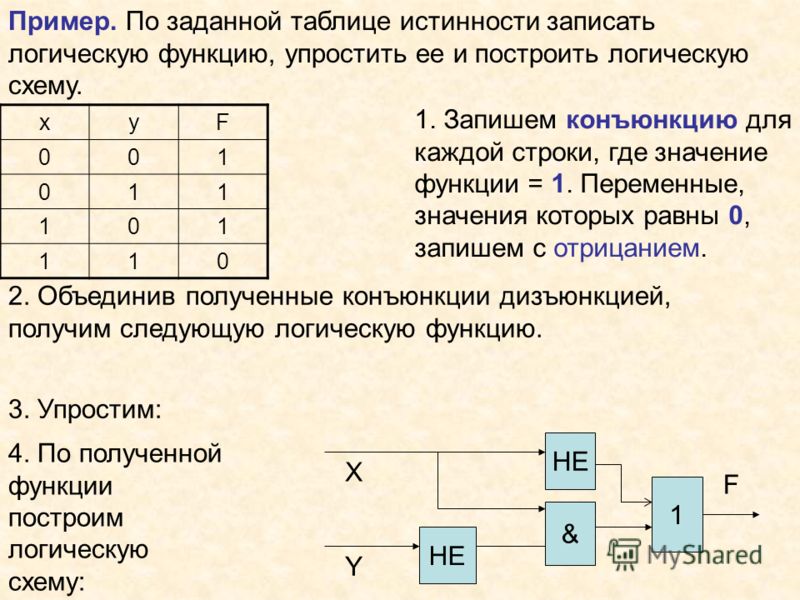
Задание 2. В следующем высказывании выделите простые, обозначив каждое из них буквой. Запишите с помощью букв и знаков логических операций каждое составное высказывание: Неверно, что Солнце движется вокруг Земли
А= Солнце движется вокруг Земли
НЕ А; NOT A; ¬A;
Задание 3. В следующем высказывании выделите простые, обозначив каждое из них буквой. Запишите с помощью букв и знаков логических операций каждое составное высказывание: Число 376 чётное и трёхзначное.
А= Число 376 чётное ; B= Число 376 трёхзначное
А И В; А & В; А • В; A AND В; A B
Задание 4 В следующем высказывании выделите простые, обозначив каждое из них буквой. Запишите с помощью букв и знаков логических операций каждое составное высказывание: Новый год мы встретим на даче или на Красной площади .
А= Новый год мы встретим на даче ;
B= Новый год мы встретим на Красной площади
А ИЛИ В; А OR В; А V В; А | В; A + В
1. В классе 35 учеников. Все они являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 — в районной. Сколько из них:
В классе 35 учеников. Все они являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 — в районной. Сколько из них:
Р.Б=20
Ш.Б=25
а) не являются читателями школьной библиотеки;
10
б) не являются читателями районной библиотеки;
10
15
10
15
в) являются читателями только школьной библиотеки;
15
г) являются читателями только районной библиотеки;
10
Всего 35
д) являются читателями обеих библиотек?
10
20+25=45
45-35=10
В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое, или то и другое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?
П=26
М=46
М=?
52-6-20=26
6
20
26
М=26+20=46
Всего 52
Ответ: 46 детей любит мороженое
В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек —.и математический, и физический, 5 — и математический, и химический, 3 — и физический, и химический кружки. Сколько учеников класса не посещают никакие кружки?
Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек —.и математический, и физический, 5 — и математический, и химический, 3 — и физический, и химический кружки. Сколько учеников класса не посещают никакие кружки?
М=18
Ф=14
6
Количество учеников, посещающие кружки:7+3+2+6+5+1+4=28
18-6-2-3=7
14-6-2-1=5
2
1
3
Количество учеников, не посещающие кружки: 36-28=8
10-3-2-1=4
Ответ: 8 учеников класса не посещают никакие кружки
Х=10
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4.
Т=11
К=25
6
Ц=17
Все учеников: 36-2=34
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
Т=11
К=25
6
10
Ц=17
Все учеников: 36-2=34
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
Т=11
К=25
6
4
10
Ц=17
Все учеников: 36-2=34
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
Т=11
К=25
6
?
4
10
Ц=17
Все учеников: 36-2=34
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
1)Для того, чтобы решить задачу, нам необходимо узнать, сколько учеников были только в цирке или в кино, или театры (т.е. области 1 или 3 или 7):
7: 34-(К+Т)=34-(25+11-6)=4
Т=11
К=25
2
3
1
2)Количество учеников, которые сходили в цирк : 4+5+6+7=17
4+5 Учащиеся, которые сходили и в кино, и в цирке =10
6: 17-10-4=3
5+6: Учащиеся, которые сходили и в театре, и в цирке =4
5: 4-3=1
5
4
6
7
Ц=17
Все учеников: 36-2=34
Ответ: 1 ученик побывал в театре, кино и цирке одновременно
Таблицы истинности
Простые и сложные высказывания
Высказывания бывают простые и сложные.
Высказывание называется простым , если никакая его часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с помощью логических операций .
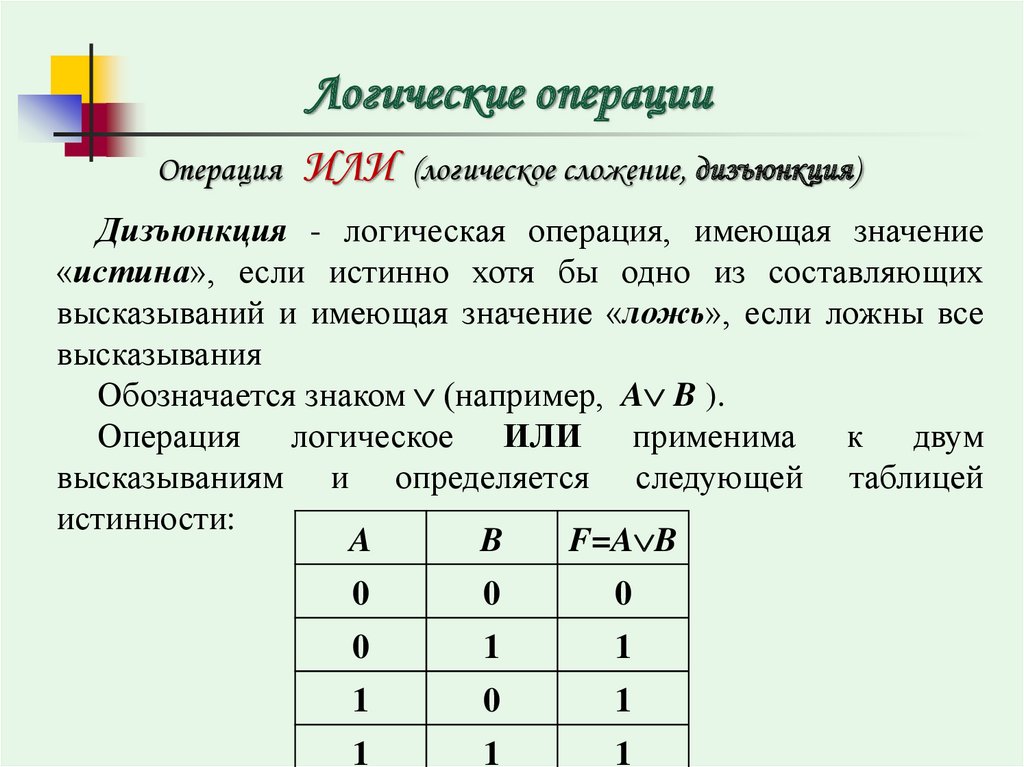
Название логической операции
Конъюнкция
Логическая связка
Дизъюнкция
«и»; «а»; «но»; «хотя»
«или»
Инверсия
«не»; «неверно, что»
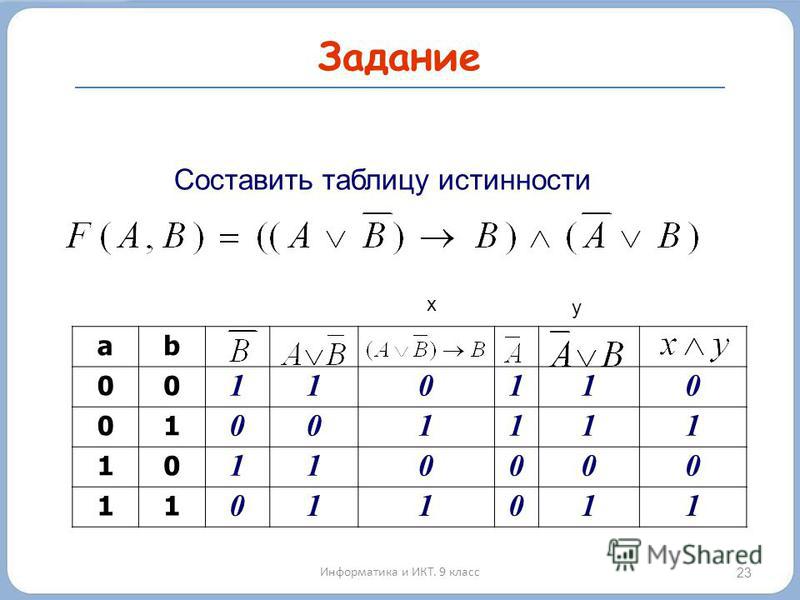
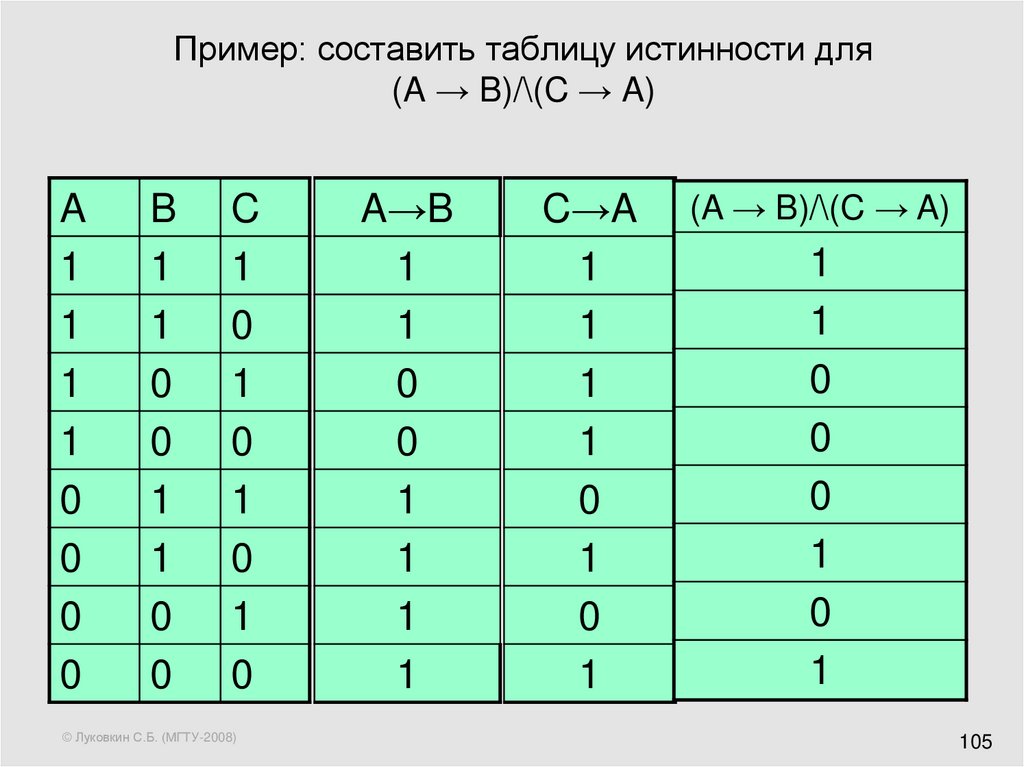
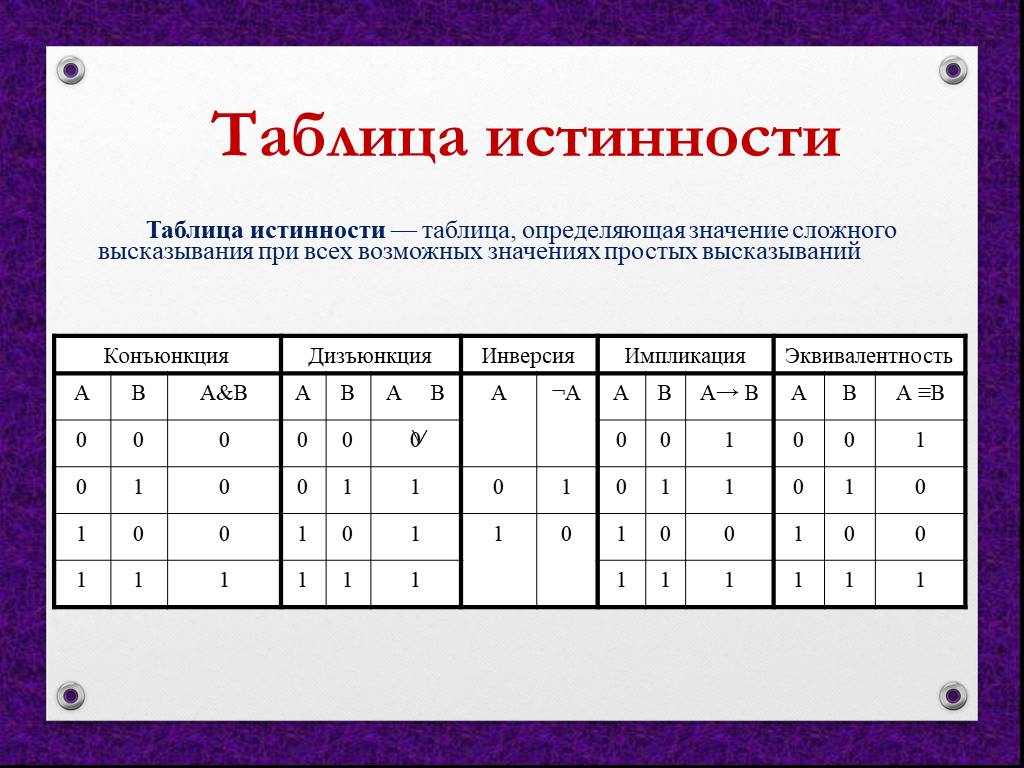
Решение логических выражений принято записывать в виде таблиц истинности .
Таблица истинности – таблица, в которой по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.
Для составления таблицы необходимо:
- Выяснить количество строк в таблице (вычисляется как 2 n +1, где n – количество переменных).
- Выяснить количество столбцов = количество переменных + количество логических операций.

- Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
- Заполнить таблицу истинности по столбцам.
Приоритет выполнения логических операций следующий: то, что в скобках , инверсия (отрицание), конъюнкция (умножение), дизъюнкция (сложение) .
С помощью таблиц истинности можно проверить истинность любых сложных высказываний.
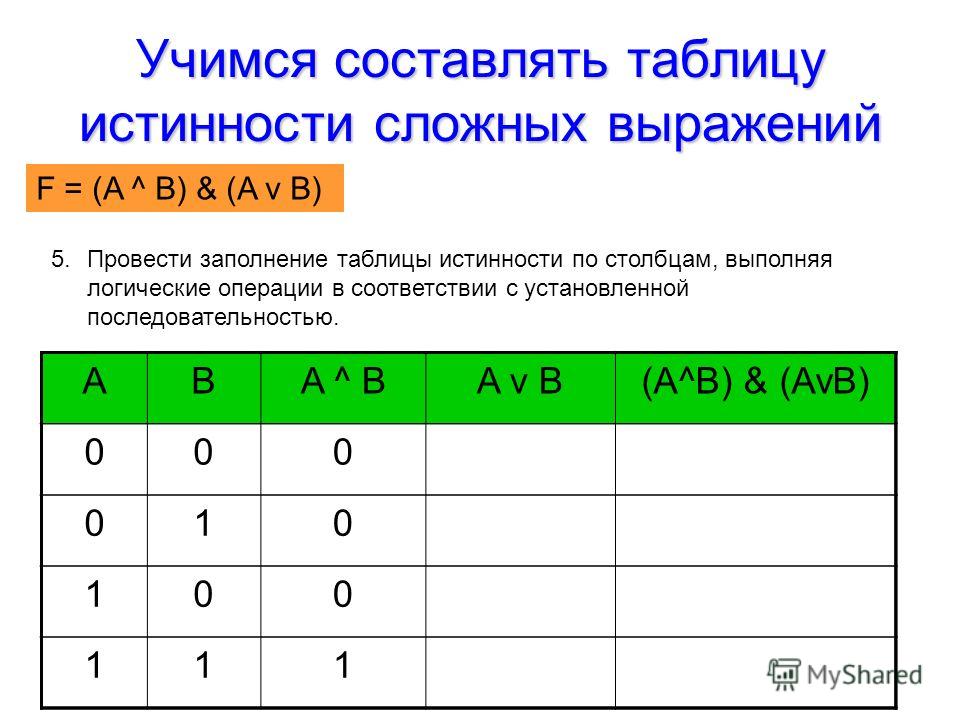
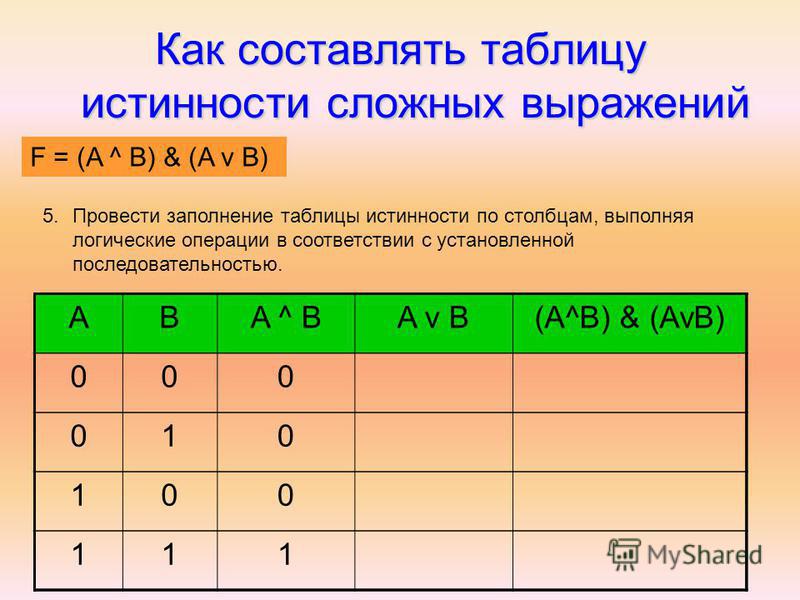
Построим таблицу истинности для выражения:
Количество строк = 2 2 (2 переменных)+ 1()заголовки столбцов=5.
Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (v, &, ¬, v, ¬ )=7
A
B
Построим таблицу истинности для выражения:
Построим таблицу истинности для выражения:
Решение логических задач с помощью таблиц истинности
- org/Person»>
Панов Валерий Алексеевич,
Разделы: Информатика
Классы: 8, 9, 10
Ключевые слова: информатика, логика, таблицы истинности, логические задачи
Цели:
- создание комфортных психологических условий для обучения;
- развитие, поощрение и стимулирование интересов у школьников к самостоятельной творческой деятельности;
- практическое применение знаний;
- систематизация знаний и умений учащихся по теме “Логика”.

Задачи:
Образовательные:
- обобщить и систематизировать знания учащихся по теме “Логика”;
- подготовить учащихся к контрольной работе;
- продолжить развитие навыков логического анализа;
- выработать умение корректно и логически безупречно формулировать определение понятий;
- продолжить решение логических задач;
- развивать умение строить логические выражения.
Развивающие:
- развитие внимания, наблюдательности, критичности;
- развитие активности и самостоятельности;
- развитие умений и навыков работы при решении логических задач.
Воспитательные:
- привитие интереса к приобретению новых знаний, умений и навыков;
- изучение основных исторических этапов развития логики и знакомство с историческими личностями, связанными с развитием данной науки с Древних времен и по сей день.

Оборудование урока:
- Интерактивная доска.
- Компьютер, проектор.
- Карточки с заданиями для учащихся.
- Тест.
- Презентации по теме урока.
План урока
| № | Вид работы | Время (мин) |
1 | Организационный момент | 1 |
2 | Опрос (презентация) | 5 |
3 | Диктант | 3 |
4 | Исправь ошибки / Тест | 5 |
5 | Работа в парах | 5 |
6 | Решение задач на Законы логики | 7 |
7 | Новая тема | 7 |
8 | Решение задач | 10 |
9 | Рефлексия | 2 |
10 | Д/з | 1 |
|
| 45 |
ХОД УРОКА
1. Оргмомент — 1 мин.2. Опрос (презентация) – 5 мин.
Оргмомент — 1 мин.2. Опрос (презентация) – 5 мин.- Кто заложил основы формальной логики?
- Что такое высказывание?
- Выберете из предложенных вариантов высказывания:
- Завтра будет дождь.
- Вчера было солнечно.
- Земля – спутник Юпитера.
- Петя вчера хотел бы пойти в кино.
- У кого есть сотовый телефон?
- Урок длится 45 минут.
- Ура, каникулы!
- Каким методом пользовался великий сыщик Шерлок Холмс? Дайте определение.
Записать высказывания:
- Не А и В.
- Отрицание А или не В.
- Из не В следует А и С.
- Если А то не С.
- Инверсия А или В эквивалентно не А и не В.
Тест – 5 мин. | Логические функции – 5 мин. |
1. Какой из перечисленных законов является переместительным для «И»?
- X+Y = Y+X
- X*Y=Y*X
- Х*(Y*Z)=(X*Y)*Z
- X+(Y+X)=(X+Y)+Z
- X*(Y+Z)= X*Y + X*Z
2. Какой из перечисленных законов является сочетательным для «И»?
- X+Y = Y+X
- X+Y*Z=(X+Y)*(X+Z)
- Х*(Y*Z)=(X*Y)*Z
- X+(Y+X)=(X+Y)+Z
- X*(Y+Z)= X*Y + X*Z
3. Какой из перечисленных законов является сочетательным для «ИЛИ»?
- X+Y = Y+X
- X+Y*Z=(X+Y)*(X+Z)
- Х*(Y*Z)=(X*Y)*Z
- X+(Y+X)=(X+Y)+Z
- X*(Y+Z)= X*Y + X*Z
Каждой группе выдается лист с заданием (таблица с простыми высказываниями и их обозначения).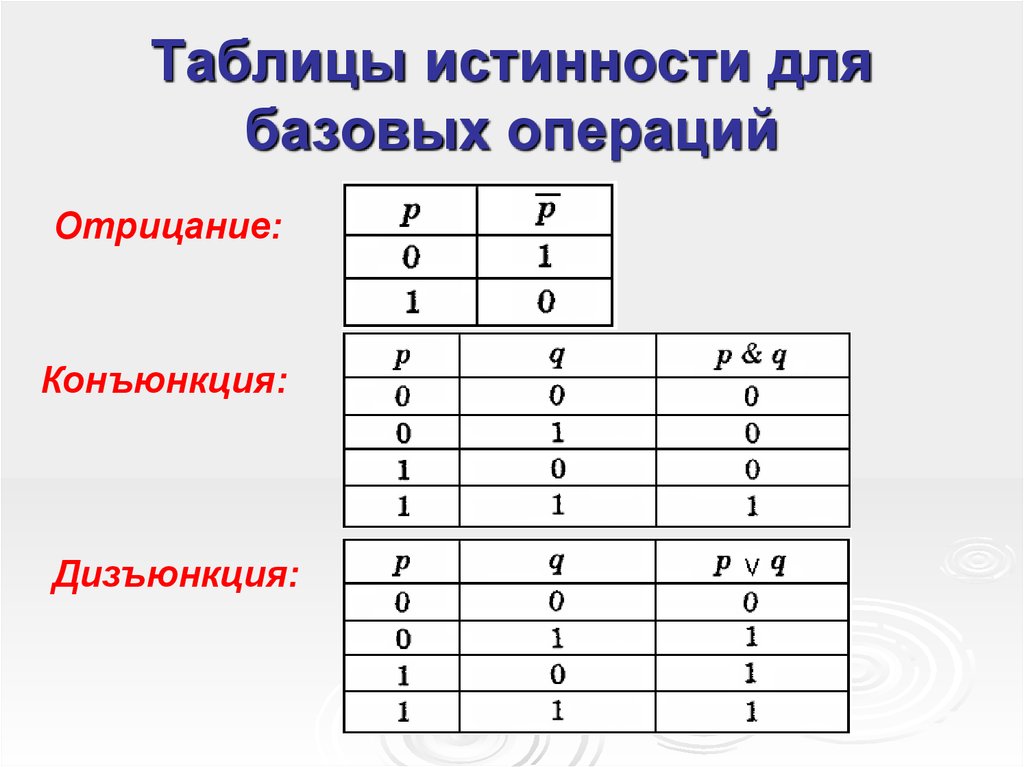 Необходимо записать сложные высказывания на языке алгебры логики.
Необходимо записать сложные высказывания на языке алгебры логики.
N | Ветер северный | T | Температура плюсовая |
S | Ветер южный | I | На деревьях иней |
D | Идёт дождь | U | На улице туман |
C | Идёт снег | P | Небо пасмурное |
M | На улице мороз | Z | Налипание снега на провода |
O | На улице оттепель | G | На дорогах гололедица |
1. «На улице мороз, небо пасмурное, но снег не идёт»;
«На улице мороз, небо пасмурное, но снег не идёт»;
2. «На улице температура плюсовая и туман или на деревьях иней»;
3. «Если северный ветер или идёт снег, то на улице мороз»;
4. «На дорогах нет гололедицы, если дует северный ветер при морозе»;
5. «На улице оттепель или на деревьях иней, если температура плюсовая»;
6. Решение задач на «Законы логики» — 7 мин.Упростить:
7. Новая тема – 7 мин.Нами это уже пройдено…
Мы рассмотрели с вами решение нескольких задач-софизмов:
- Ахилл и черепаха.
- Спичка длиннее столба.
- Зависит ли скорость свободного падения от массы тела.
- Парадокс парикмахера.
Методом логических рассуждений.
Для решения логической задачи методом таблиц истинности необходимо:
- «разобрать» задачу на простые высказывания и обозначить их;
- записать задачу на языке алгебры логики;
- составить таблицу истинности;
- сделать вывод.

Рассмотрим это на примере:
Задача 1. Кто из подозреваемых участвовал в преступлении, если известно:
1) если Иванов не участвовал или Петров участвовал, то Сидоров участвовал;
2) если Иванов не участвовал, то Сидоров не участвовал.
(объяснение с помощью презентации)
8. Закрепление. Решение задач – 10 мин.Задача 2. В нарушении правил обмена валюты подозреваются 4 работника банка А, В, С, Д.
Известно:
1) если А нарушил, то В нарушил;
2) если В нарушил, то и С нарушил или А нет
3) если Д не нарушил, то А нарушил, а С нет
4) если Д нарушил, то и А нарушил
Наш урок подошел к концу. Выразите свои ощущения после урока с помощью пословиц. Выберите из предложенных ту, которая соответствует вашему настроению.
- Без хорошего труда нет плода.
- Терпенье и труд все перетрут.
- И швец, и жнец, и на дуде игрец.

- Упорно трудиться — будет хлеб в закромах водиться.
- Трудовая денежка плотно лежит, чужая ребром торчит.
- Была б лишь охота — наладится каждая работа.
- Маленькое дело лучше большого безделья.
- Глаза страшатся, а руки делают.
- Не боги горшки обжигают.
- Хлеб даром не даётся.
Намечаются экскурсии в три города А, В и С. Руководитель фирмы сказал:
- «Неверно, что если будет экскурсия в город В, то не будет экскурсии в город С.
- Если будет экскурсия в город С, то не будет экскурсии в город А.»
В какие города будет проводиться экскурсия?
Приложение 1
Таблицы истинности в наборе правил
- Обновлено 30 июня 2022 г.

- 2 Минуты на чтение
Распечатать
Поделиться
Темный
Свет
Обзор
Использование таблиц истинности в наборах правил позволяет разработчикам избежать создания множества правил, которые имеют одинаковые условия, но отличаются только значением для оценки данных.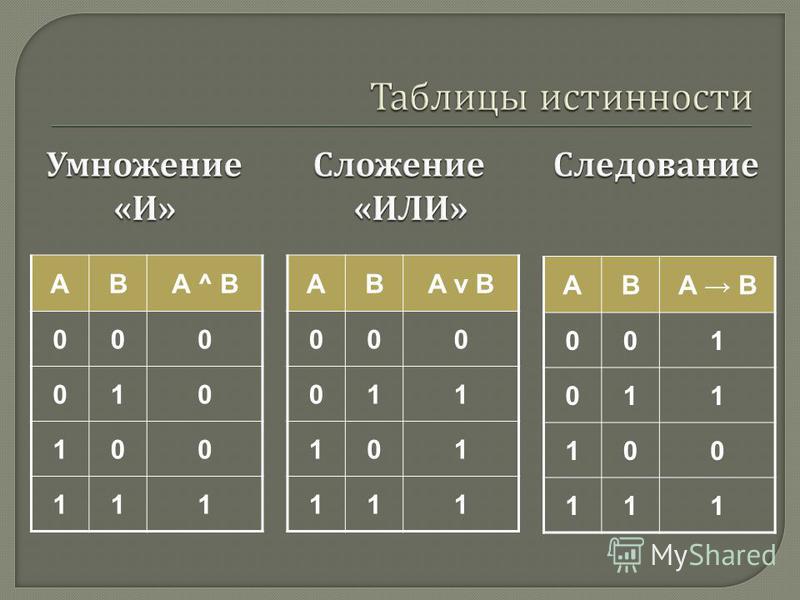
Пример
В этом примере извлекаются учетные записи, созданные в Решениях. Таблица истинности в наборе правил будет запущена, чтобы подтвердить, что у каждой учетной записи есть назначенная компания и должность. Выходные данные набора правил передаются правилу True/False, чтобы остановить поток при первом ложном ответе. Ниже приведен загружаемый пример для импорта в Decisions.
Таблицы истинности в наборе правил-18052020-102940.zip
- Создайте новый набор правил.
- Нажмите Настройка на верхней панели действий, чтобы открыть диалоговое окно Setup Rule Set . В категории RULE TYPES выберите Таблицы истинности и нажмите СОХРАНИТЬ, чтобы закрыть диалоговое окно.
- На верхней панели действий щелкните ДОБАВИТЬ ТАБЛИЦУ ИСТИННОСТИ и выберите Таблица истинности . Введите «Таблица истинности названий компаний и должностей» в поле «Имя» и нажмите «СОЗДАТЬ ТАБЛИЦУ ИСТИННОСТИ».

- Когда появится Rule Designer, нажмите [Select Data Element] и выберите Item > Company .
- Затем нажмите [Pick Verb] и выберите Is в категории Common > Evaluate и нажмите ЗАКРЫТЬ.
- Затем добавьте значения оценки (Decisions.com, That Other Company) в столбце Item.Company .
- Щелкните знак плюса рядом со столбцом Товар.Компания, чтобы добавить другое условие. Настройте это второе условие для оценки Item.JobTitle In List .
Затем установите оба флажка под Выходные данные по умолчанию . В этом примере в качестве константы будет использоваться статический список должностей (дизайнер, администратор). - Нажмите Сохранить и закройте окно Rule Designer.
- В проекте Designer создайте поток, щелкнув CREATE FLOW на глобальной панели действий и выбрав Flow в верхней части диалогового окна.

- Затем добавьте шаг Fetch Entities .
- При выбранном шаге «Выбор объектов» введите «account» в поле Введите имя в раскрывающемся списке и выберите Account [DecisionsFramework…] .
- Добавьте шаг для каждого элемента . Это можно найти, выполнив поиск foreach на панели инструментов шагов
- В категории DATA выберите Account как Type .
- Далее, в разделе Коллекция в категории ВХОДЫ нажмите РЕДАКТИРОВАТЬ. Затем выберите Entity Results и нажмите ГОТОВО.
- Затем щелкните путь Next на шаге «Для каждого элемента». Затем выберите Designer Entities > Rules и добавьте шаг Run Rule Set .
- В Flow Designer щелкните путь «Готово» для набора правил запуска. Добавьте шаг True False Rule из категории Designer Entities > Rules .

- В категории ВХОДЫ выберите Неизвестно и выберите Выбрать из потока .
Затем выберите FlowRuleSetResult.First.RuleResult и выберите ГОТОВО, чтобы закрыть окно. При выборе FlowRuleSetResult.First.RuleResult поток остановится при первом ложном результате. - Затем соедините путь False в правиле True False с шагом End , а путь True с шагом For Each Element.
Затем соедините путь No Results с шагом «Для каждого элемента». Затем соедините путь «Готово» от шага «Для каждого элемента» к пути «Конец». - Щелкните Сохранить, чтобы сохранить изменения в потоке.
Отладка
- Нажмите Отладка на верхней панели действий. Затем нажмите НАЧАТЬ ОТЛАДКУ.
Для получения дополнительной информации о правилах посетите форум решений.
Была ли эта статья полезной?
Таблицы истинности и анализ аргументов: примеры | Математика для гуманитарных наук |
Таблицы истинности
Поскольку сложные логические утверждения могут быть сложными для понимания, мы можем создать таблицу истинности , чтобы отслеживать, какие значения истинности для простых утверждений делают сложное утверждение истинным и ложным
Таблица истинности
Таблица, показывающая результирующее истинностное значение сложного утверждения для всех возможных истинностных значений простых утверждений.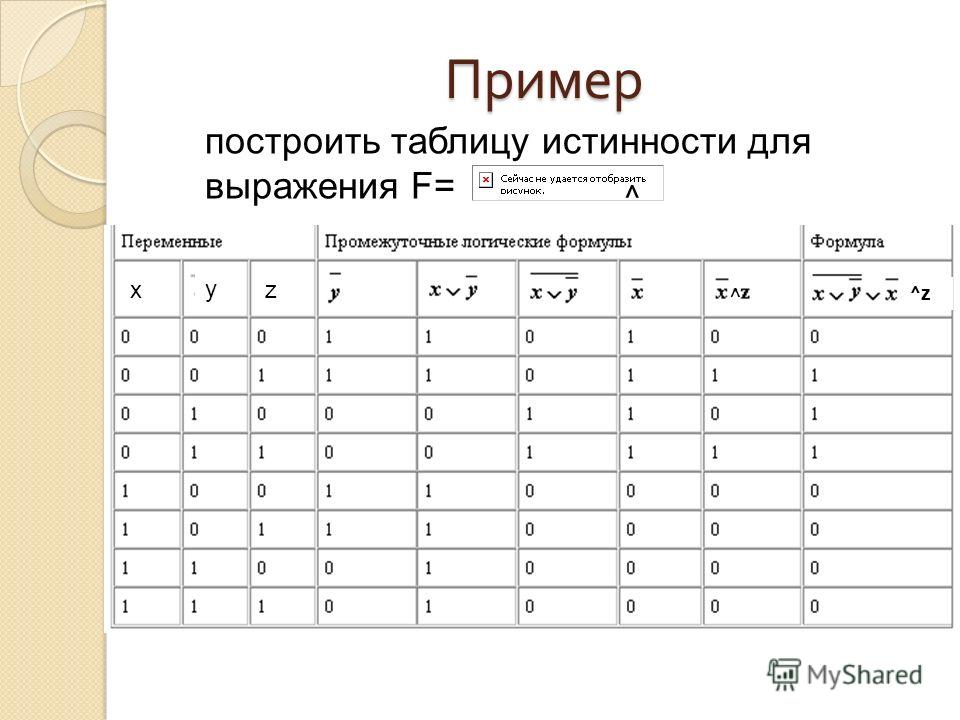
Пример 1
Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите секционный или что-нибудь с фаэтоном».
Это сложное утверждение состоит из двух более простых условий: «является секционным» и «имеет фаэтон». Для простоты давайте использовать S для обозначения «является секционным», а C для обозначения «имеет шезлонг». Условие S верно, если кушетка секционная.
Таблица истинности для этого будет выглядеть так:
| S | С | S или C |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
В таблице T используется для true, а F для false. В первой строке, если S истинно и C также истинно, то комплексное утверждение « S или C » истинно. Это будет секционная, в которой также есть шезлонг, что соответствует нашему желанию.
В первой строке, если S истинно и C также истинно, то комплексное утверждение « S или C » истинно. Это будет секционная, в которой также есть шезлонг, что соответствует нашему желанию.
Помните также, что или в логике не являются исключающими; если кушетка имеет обе функции, она соответствует условию.
Чтобы еще больше сократить наши обозначения, мы собираемся ввести некоторые символы, которые обычно используются для и , или и вместо .
Символы
Символ ⋀ используется для и : A и B обозначается как A ⋀ B .
Символ ⋁ используется для или : A или B обозначается A ⋁ B
Символ ~ используется для не : не А обозначается ~ А
Вы можете запомнить первые два символа, связав их с фигурами объединения и пересечения.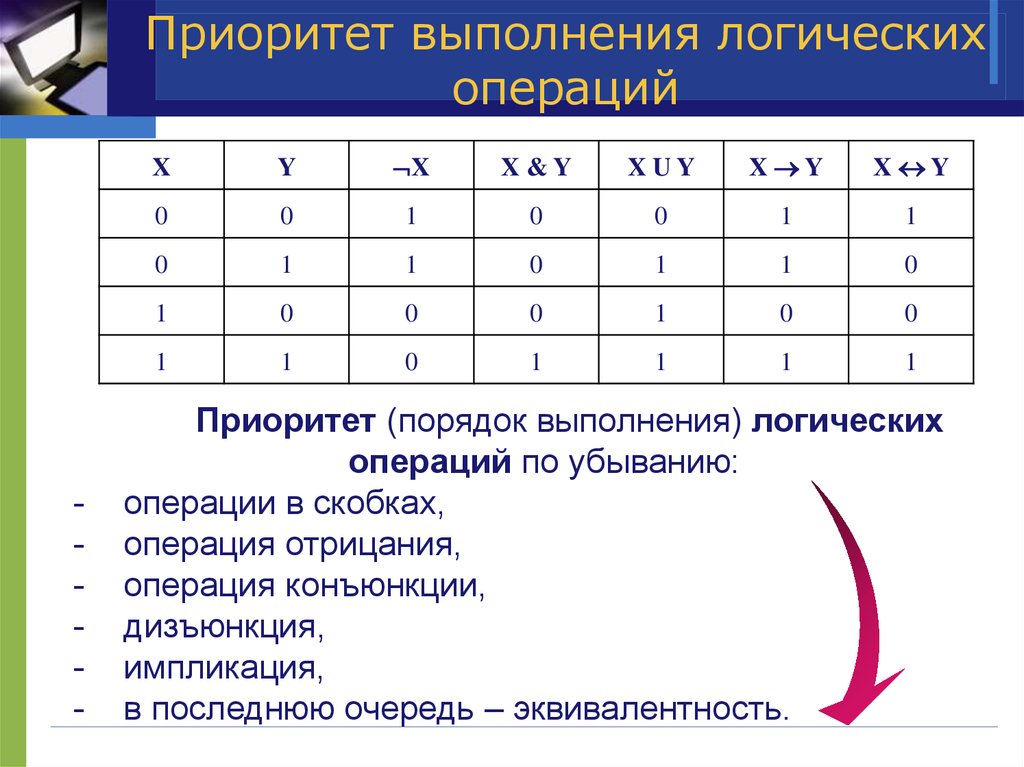 A ⋀ B будут элементами, которые существуют в обоих наборах, в A ⋂ B. Аналогично, A ⋁ B будут элементами, которые существуют в любом наборе, в A ⋃ B.
A ⋀ B будут элементами, которые существуют в обоих наборах, в A ⋂ B. Аналогично, A ⋁ B будут элементами, которые существуют в любом наборе, в A ⋃ B.
В В предыдущем примере таблица истинности на самом деле просто обобщала то, что мы уже знаем о том, как работают операторы или . Таблицы истинности для основных 9Операторы 0190 и , или и , а не показаны ниже.
Основные таблицы истинности
| А | Б | А ⋀ Б |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Ф |
| Ф | Ф | Ф |
| А | Б | А ⋁ В |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
| А | ~А |
|---|---|
| Т | Ф |
| Ф | Т |
Таблицы истинности становятся действительно полезными при анализе более сложных логических выражений.
Пример 2
Создайте таблицу истинности для утверждения A ⋀ ~( B ⋁ C )
Это помогает работать изнутри наружу при создании таблиц истинности и создавать таблицы для промежуточных операций. Начнем с перечисления всех возможных комбинаций значений истинности для A , В и С . Обратите внимание, что первый столбец содержит 4 T, за которыми следуют 4 F, второй столбец содержит 2 T, 2 F, затем повторяется, а последний столбец чередуется. Этот шаблон гарантирует рассмотрение всех комбинаций. Наряду с этими начальными значениями мы перечислим значения истинности для самого внутреннего выражения, B ⋁ C .
| А | Б | С | Б ⋁ С |
| Т | Т | Т | Т |
| Т | Т | Ф | Т |
| Т | Ф | Т | Т |
| Т | Ф | Ф | Ф |
| Ф | Т | Т | Т |
| Ф | Т | Ф | Т |
| Ф | Ф | Т | Т |
| Ф | Ф | Ф | Ф |
Затем мы можем найти отрицание B ⋁ C , работая с столбцом B ⋁ C , который мы только что создали.
| А | Б | С | В ⋁ С | ~( Б ⋁ С ) |
| Т | Т | Т | Т | Ф |
| Т | Т | Ф | Т | Ф |
| Т | Ф | Т | Т | Ф |
| Т | Ф | Ф | Ф | Т |
| Ф | Т | Т | Т | Ф |
| Ф | Т | Ф | Т | Ф |
| Ф | Ф | Т | Т | Ф |
| Ф | Ф | Ф | Ф | Т |
Наконец, мы находим значения A и ~( B ⋁ C )
| A | Б | С | В ⋁ С | ~( Б ⋁ С ) | А ⋀ ~( В ⋁ С ) |
| Т | Т | Т | Т | Ф | Ф |
| Т | Т | Ф | Т | Ф | Ф |
| Т | Ф | Т | Т | Ф | Ф |
| Т | Ф | Ф | Ф | Т | Т |
| Ф | Т | Т | Т | Ф | Ф |
| Ф | Т | Ф | Т | Ф | Ф |
| Ф | Ф | Т | Т | Ф | Ф |
| Ф | Ф | Ф | Ф | Т | Ф |
Оказывается, это сложное выражение верно только в одном случае: если А истинно, В ложно и С ложно.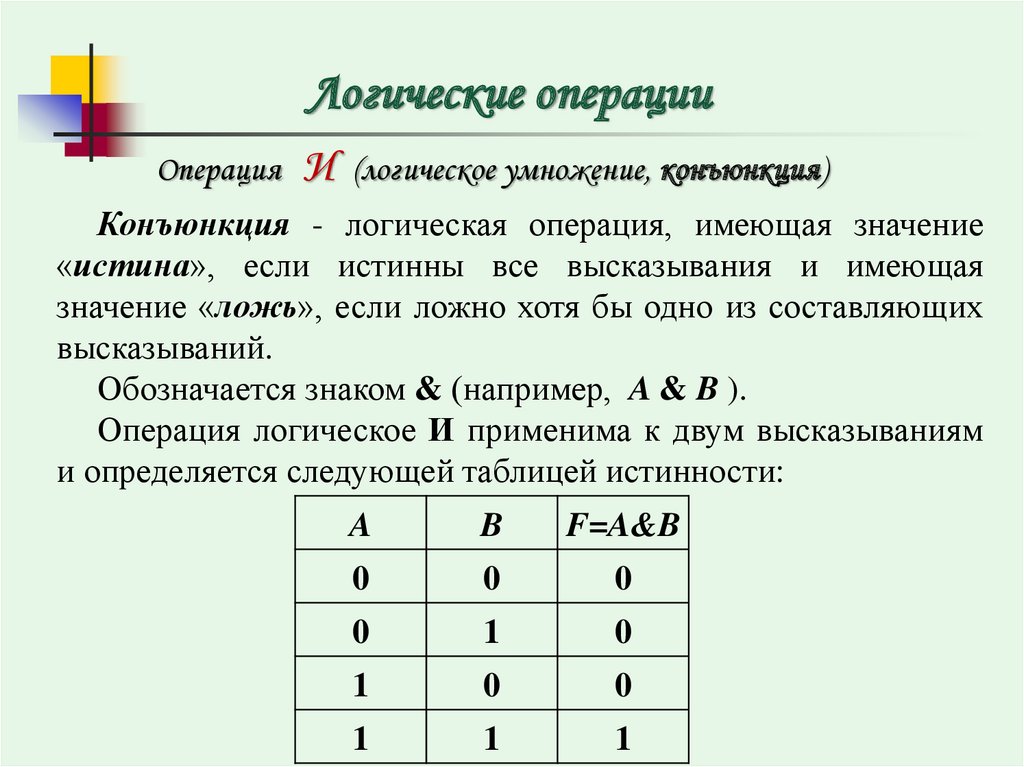
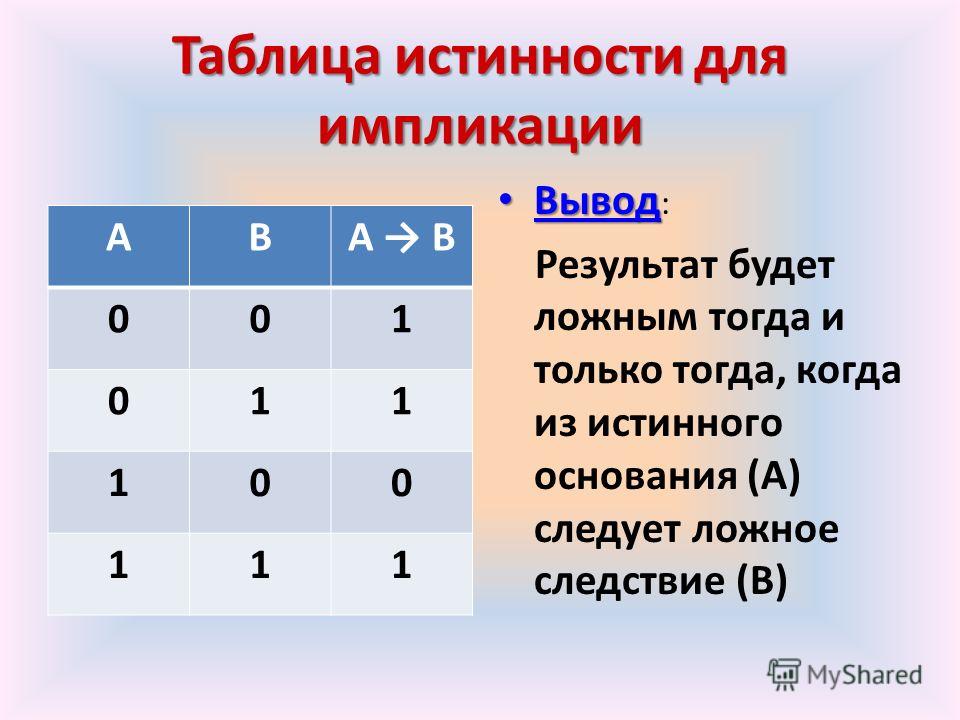
Когда мы обсуждали условия ранее, мы обсуждали тип, при котором мы предпринимаем действие на основе значения условия. Теперь мы собираемся поговорить о более общей версии условного предложения, иногда называемой импликацией .
Последствия
Импликации — это логические условные предложения, утверждающие, что высказывание p , называемое антецедентом, подразумевает следствие q .
Импликации обычно записываются как p → q
Последствия аналогичны условным операторам, которые мы рассматривали ранее; p → q обычно записывается как «если p, то q» или «p, следовательно, q». Разница между импликациями и условными предложениями заключается в том, что условные предложения, которые мы обсуждали ранее, предполагают действие — если условие истинно, то в результате мы предпринимаем какое-то действие. Импликации — это логическое утверждение, предполагающее, что следствие должно логически следовать, если антецедент истинен.
Пример 3
Английское высказывание «Если идет дождь, то на небе облака» является логическим следствием. Это правильный аргумент, потому что если антецедент «идет дождь» истинен, то следствие «на небе облака» также должно быть истинным.
Обратите внимание, что утверждение ничего не говорит нам о том, чего ожидать, если не идет дождь. Если антецедент ложен, то импликация становится нерелевантной.
Пример 4
Друг говорит вам, что «если вы загрузите эту фотографию в Facebook, вы потеряете работу». Возможны четыре исхода:
- Вы загружаете изображение и сохраняете свою работу
- Вы загрузили картинку и потеряли работу
- Вы не загружаете картинку и сохраняете свою работу
- Вы не загрузите картинку и потеряете работу
Есть только один возможный случай, когда ваш друг солгал — первый вариант, когда вы загружаете картинку и сохраняете свою работу. В последних двух случаях ваш друг ничего не сказал о том, что произойдет, если вы не загрузите изображение, поэтому вы не можете заключить, что его заявление недействительно, даже если вы не загрузили изображение и все равно потеряли работа.
В последних двух случаях ваш друг ничего не сказал о том, что произойдет, если вы не загрузите изображение, поэтому вы не можете заключить, что его заявление недействительно, даже если вы не загрузили изображение и все равно потеряли работа.
В традиционной логике импликация считается достоверной (истинной) до тех пор, пока нет случаев, в которых антецедент истинен, а следствие ложно. Важно помнить, что символическая логика не может охватить все тонкости английского языка.
Значения истинности для следствий
| р | q | р → q |
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Т |
| Ф | Ф | Т |
Пример 5
Постройте таблицу истинности для утверждения ( m ⋀ ~ p ) → r
Начнем с построения таблицы истинности для антецедента.
| м | стр | ~ р | м ⋀ ~ р |
| Т | Т | Ф | Ф |
| Т | Ф | Т | Т |
| Ф | Т | Ф | Ф |
| Ф | Ф | Т | Ф |
Теперь мы можем построить таблицу истинности для импликации
| м | р | ~ р | м ⋀ ~ р | р | ( м ⋀ ~ р ) → р |
| Т | Т | Ф | Ф | Т | Т |
| Т | Ф | Т | Т | Т | Т |
| Ф | Т | Ф | Ф | Т | Т |
| Ф | Ф | Т | Ф | Т | Т |
| Т | Т | Ф | Ф | Ф | Т |
| Т | Ф | Т | Т | Ф | Ф |
| Ф | Т | Ф | Ф | Ф | Т |
| Ф | Ф | Т | Ф | Ф | Т |
В этом случае, когда m истинно, p ложно, а r ложно, тогда антецедент m ⋀ ~ p будет истинным, но следствие ложным, что приведет к недопустимому импликации; каждый другой случай дает правильное следствие.
Для любой импликации есть три связанных утверждения: обратное, обратное и контрапозитивное.
Связанные заявления
Первоначальное значение: «Если р , то Q »: P → Q
. Позвоночник — «IF Q Затем P »: Q . Затем P »: Q . P »: Q . «Если не p , то не Q »: ~ P → ~ Q
Контрапозитор — «если нет Q , то не P »: ~ Q , то не P »: ~ Q , тогда не P »: ~ Q Q Q Q . Рассмотрим снова верный вывод: «Если идет дождь, значит, в небе облака». Обратное: «Если на небе облака, значит, идет дождь». Это, конечно, не всегда верно. Обратное: «Если не идет дождь, то на небе нет облаков». Точно так же это не всегда верно. Противоположным было бы: «Если на небе нет облаков, значит, не идет дождь». Это утверждение верно и эквивалентно исходному выводу. Глядя на таблицы истинности, мы видим, что исходное условное и контрапозитивное логически эквивалентны, а обратное и обратное логически эквивалентны. Условное утверждение и его противоположность логически эквивалентны. Обратное и обратное утверждение логически эквивалентны. Логический аргумент — это утверждение о том, что набор предпосылок поддерживает вывод. Существует два основных типа аргументов: индуктивные и дедуктивные аргументы. Индуктивный 9Аргумент 0047 использует набор конкретных примеров в качестве посылок и использует их, чтобы предложить общий вывод. дедуктивный аргумент использует набор общих утверждений в качестве своих предпосылок и использует их, чтобы предложить конкретную ситуацию в качестве вывода. Аргумент «когда я пошел в магазин на прошлой неделе, я забыл свой кошелек, и когда я пошел сегодня, я забыл свой кошелек. Я всегда забываю свою сумочку, когда иду в магазин» — это индуктивный аргумент. Помещения: Я забыл свой кошелек на прошлой неделе Я забыл свой кошелек сегодня Вывод: Я всегда забываю свой кошелек Обратите внимание, что посылки — это конкретные ситуации, а заключение — это общее утверждение. Аргумент «каждый день в течение последнего года самолет пролетает над моим домом в 2 часа дня. Каждый день в 14:00 над моим домом будет летать самолет» — более сильный индуктивный аргумент, поскольку он основан на большем наборе доказательств. Индуктивный аргумент никогда не сможет доказать истинность вывода, но он может предоставить как слабое, так и сильное доказательство того, что оно может быть верным. Многие научные теории, такие как теория большого взрыва, никогда не могут быть доказаны. Вместо этого они представляют собой индуктивные аргументы, подкрепленные широким спектром доказательств. Обычно в науке идея считается гипотезой до тех пор, пока она не будет тщательно проверена, после чего она становится теорией. Дедуктивный аргумент является более верным или нет, что облегчает его оценку. Дедуктивный аргумент считается действительным, если все посылки верны, а вывод логически следует из этих посылок. Другими словами, посылки истинны, и заключение обязательно следует из этих посылок. Аргумент «Все кошки — млекопитающие, а тигр — кошка, значит, тигр — млекопитающее» — верный дедуктивный аргумент. Помещения: Все кошки млекопитающие Тигр кошка Вывод: Тигр — это млекопитающее Обе посылки верны. Чтобы проанализировать аргумент с помощью диаграммы Венна Помещение: Все пожарные знают CPR Посылка: Джилл знает СЛР Вывод: Джилл — пожарный Из первой посылки мы знаем, что все пожарные входят в группу тех, кто знает СЛР. Поскольку вывод не обязательно следует из посылок, это неверный аргумент, независимо от того, действительно ли Джилл является пожарным. Важно отметить, что для оценки обоснованности аргумента не важно, действительно ли Джилл пожарный; нас интересует только то, достаточно ли посылок для доказательства вывода. В дополнение к этим категориальным посылкам стиля в форме «все ___», «некоторые ____» и «нет ____», также часто встречаются посылки, являющиеся импликациями. Помещение: Если вы живете в Сиэтле, вы живете в Вашингтоне. Посылка: Маркус не живет в Сиэтле Вывод: Маркус не живет в Вашингтоне Из первой посылки мы знаем, что множество людей, живущих в Сиэтле, находится внутри множества людей, живущих в Вашингтоне. Рассмотрим аргумент «Вы женатый мужчина, поэтому у вас должна быть жена». Это неверный аргумент, так как есть, по крайней мере, в некоторых частях мира, мужчины, которые женаты на других мужчинах, так что посылки недостаточно, чтобы подразумевать заключение. Некоторые аргументы лучше анализировать с помощью таблиц истинности. Рассмотрим аргумент: Посылка: Если вы купили хлеб, то вы пошли в магазин Посылка: Вы купили хлеб Вывод: Вы пошли в магазин Хотя мы надеемся, что этот пример является довольно очевидным обоснованным аргументом, мы можем проанализировать его, используя таблицу истинности, представив каждую из предпосылок символически. Мы получим B, означающее «вы купили хлеб», а S — «вы пошли в магазин». Тогда аргумент принимает вид: Предпосылка: B → S Предпосылка: B Вывод: S 4
Чтобы проверить достоверность, мы смотрим, подразумевает ли комбинация обеих посылок заключение; правда ли, что [( B → S ) ⋀ B ] → S ? Поскольку таблица истинности для [( B → S ) ⋀ B ] → S всегда верна, это правильный аргумент. Чтобы проанализировать аргумент с помощью таблицы истинности: Предпосылка: Если я пойду в торговый центр, то я куплю новые джинсы Предпосылка: Если я куплю новые джинсы, я куплю к ним рубашку Вывод: Если мне нужно торговый центр, я куплю рубашку. Пусть M = я иду в торговый центр, J = я покупаю джинсы и S = я покупаю рубашку. Посылки и заключение можно сформулировать так: Premise: M → J Premise: J → S Conclusion: M → S We can construct a truth table for [( M → J ) ⋀ ( J → S )] → ( M → S ) Из таблицы истинности мы видим, что это правильный аргумент. Пример 6
Значение Конверс Обратный Противоположный р q р → q q → стр ~ р → ~ q ~ к → ~ к Т Т Т Т Т Т Т Ф Ф Т Т Ф Ф Т Т Ф Ф Т Ф Ф Т Т Т Т Эквивалентность
Аргументы
Типы аргументов
Пример 7
 В данном случае это достаточно слабый аргумент, так как он основан всего на двух случаях.
В данном случае это достаточно слабый аргумент, так как он основан всего на двух случаях. Пример 8
Оценка индуктивных аргументов
 Все общеизвестные научные теории, такие как теория гравитации Ньютона, выдержали годы испытаний и доказательств, хотя иногда их необходимо корректировать на основе новых данных. Для гравитации это произошло, когда Эйнштейн предложил общую теорию относительности.
Все общеизвестные научные теории, такие как теория гравитации Ньютона, выдержали годы испытаний и доказательств, хотя иногда их необходимо корректировать на основе новых данных. Для гравитации это произошло, когда Эйнштейн предложил общую теорию относительности. Оценка дедуктивных аргументов
Пример 9
 Чтобы увидеть, что посылки должны логически вести к заключению, можно использовать диаграмму Венна. Из первой посылки мы можем заключить, что множество кошек является подмножеством множества млекопитающих. Из второй посылки нам говорят, что тигр находится в множестве кошек. Отсюда на диаграмме Венна видно, что тигр также находится внутри множества млекопитающих, так что вывод верен.
Чтобы увидеть, что посылки должны логически вести к заключению, можно использовать диаграмму Венна. Из первой посылки мы можем заключить, что множество кошек является подмножеством множества млекопитающих. Из второй посылки нам говорят, что тигр находится в множестве кошек. Отсюда на диаграмме Венна видно, что тигр также находится внутри множества млекопитающих, так что вывод верен. Анализ аргументов с помощью диаграмм Венна
[2] Пример 10
 Из второй посылки мы знаем, что Джилл является членом этого большего множества, но у нас недостаточно информации, чтобы узнать, является ли она также членом меньшего подмножества, то есть пожарных.
Из второй посылки мы знаем, что Джилл является членом этого большего множества, но у нас недостаточно информации, чтобы узнать, является ли она также членом меньшего подмножества, то есть пожарных. Пример 11
 Из второй посылки мы знаем, что Маркус не входит в набор Сиэтла, но у нас недостаточно информации, чтобы узнать, живет ли Маркус в Вашингтоне или нет. Это неверный аргумент.
Из второй посылки мы знаем, что Маркус не входит в набор Сиэтла, но у нас недостаточно информации, чтобы узнать, живет ли Маркус в Вашингтоне или нет. Это неверный аргумент. Пример 12
Пример 13
 Затем мы можем рассмотреть импликацию о том, что посылки вместе подразумевают вывод. Если таблица истинности является тавтологией (всегда истинной), то аргумент действителен.
Затем мы можем рассмотреть импликацию о том, что посылки вместе подразумевают вывод. Если таблица истинности является тавтологией (всегда истинной), то аргумент действителен. Б С В → С ( В → С ) ⋀ В [( Б → С ) ⋀ Б ] → С Т Т Т Т Т Т Ф Ф Ф Т Ф Т Т Ф Т Ф Ф Т Ф Т 
Анализ аргументов с использованием таблиц истинности
Пример 14
M Дж С М → Дж Дж → Ю ( М → Дж ) ⋀ ( Дж → С ) М → С [( M → J ) ⋀ ( J → S )] → ( M → S ) Т Т Т Т Т Т Т Т Т Т Ф Т Ф Ф Ф Т Т Ф Т Ф Т Ф Т Т Т Ф Ф Ф Т Ф Ф Т Ф Т Т Т Т Т Т Т Ф Т Ф Т Ф Ф Т Т Ф Ф Т Т Т Т Т Т Ф Ф Ф Т Т Т Т Т