Таблица истинности или
Поиск по сайту. Главная страница. Лекционный материал. Лабораторный практикум.
Поиск данных по Вашему запросу:
Таблица истинности или
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- лабы по информатике, егэ
- Логика. Основные сведения.
- Примерные ответы на профильные билеты
- лабы по информатике, егэ
- Урок информатики по теме «Основы логики, таблицы истинности»
- Информатика.
10 класс
- Построение таблиц истинности
- Логические элементы
лабы по информатике, егэ
Решение логических выражений принято записывать в виде таблиц истинности — таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.
Установить последовательность выполнения логических операций. Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных. Заполнить таблицу истинности по столбцам. Записать ответ. Построим таблицу и заполним ее по столбцам:.
Проверьте себя эталон ответов. Обратите внимание! Наборы входных переменных, во избежание ошибок, рекомендуется перечислять следующим образом:. Тавтология — тождественно истинная формула , или формула принимающая значение » истина » » 1 » при любых входящих в нее значениях переменных.
Противоречие — тождественно ложная формула , или формула принимающая значение » ложь » » 0 » при любых входящих в нее значениях переменных. Равносильные формулы — две формулы А и В принимающие одинаковые значения, при одинаковых наборах значений входящих в них переменных.
Равносильность двух формул алгебры логики обозначается символом. Логика Электронное учебное пособие. Содержание Входной контроль Раздел 1. Основы логики Итоговый тест Раздел 2. Упражнение 8 Постройте таблицы истинности для следующих логических выражений: 1.
Логика. Основные сведения.
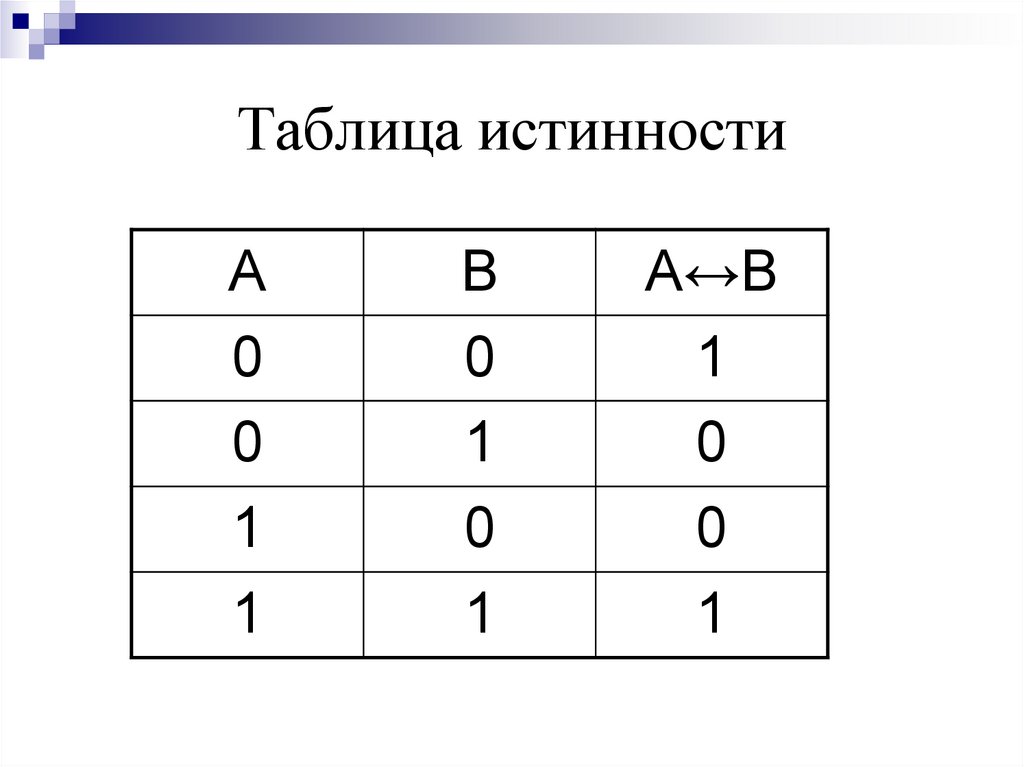
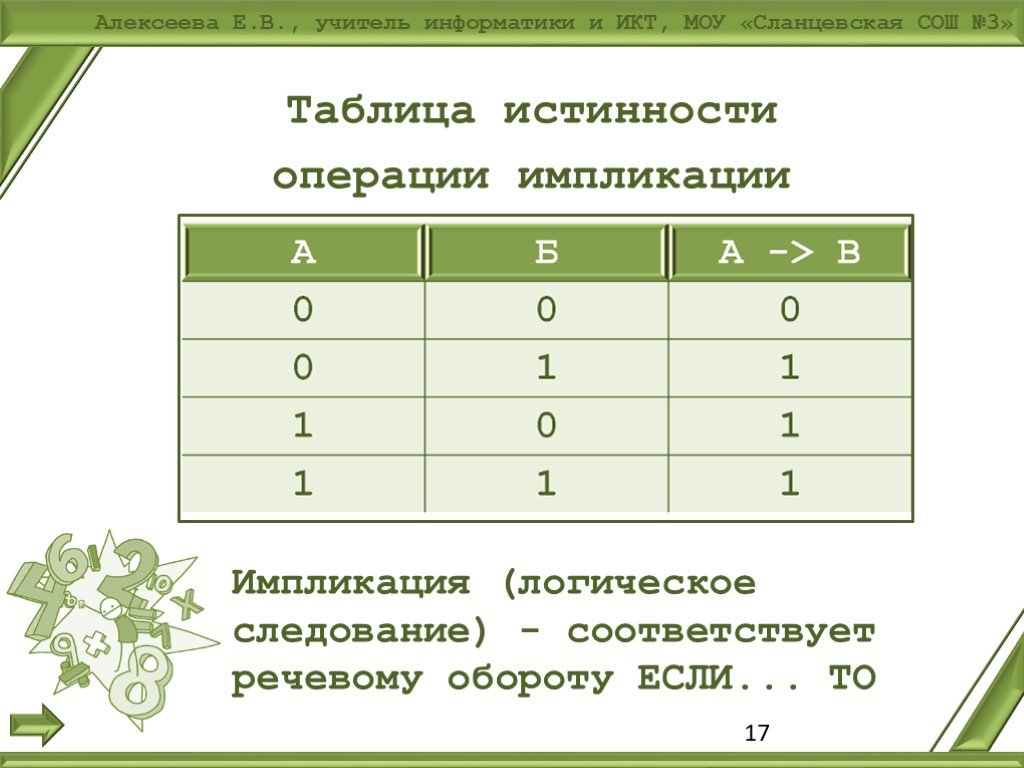
На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи. Таблица истинности операции ИЛИ дизъюнкция. Таблица истинности операции Импликация если…, то…. Таблица истинности операции Эквивалентность тогда и только тогда, …. О преобразованиях логических операций читайте здесь. Каждое из логических выражений F и G содержит 5 переменных.
Содержание: Объяснение задания 2 ЕГЭ по информатике. Таблицы истинности и порядок выполнения логических операций. Решение заданий 2 ЕГЭ.
Примерные ответы на профильные билеты
В прошлом уроке были рассмотрены условия истинности для категорических атрибутивных высказываний в силлогистике. Мы показали, что разные типы высказываний при одних условиях истинны, а при других — ложны. При этом нам ни разу не встречались высказывания, которые были бы всегда истинны или всегда ложны. Между тем, такие высказывания бывают. Первые называются логическими законами, а вторые — логическими противоречиями.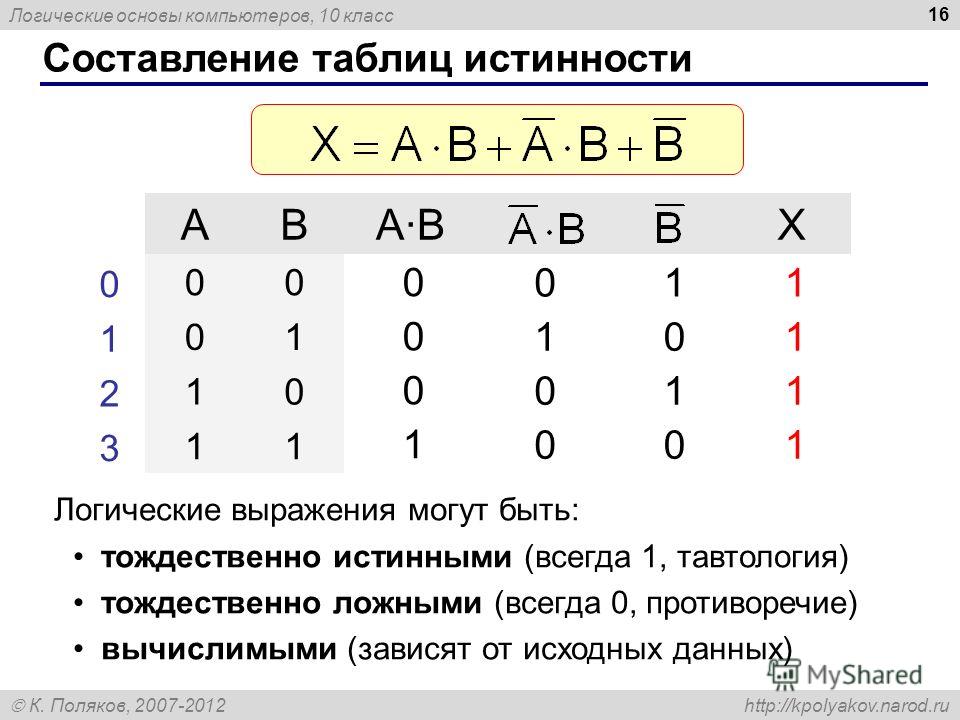
лабы по информатике, егэ
Каждое составное высказывание можно выразить в виде формулы логического выражения , в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции. Для записи составного высказывания в виде логического выражения на формальном языке языке алгебры логики в составном высказывании нужно выделить простые высказывания и логические связи между ними. Проанализируем составное высказывание. Теперь необходимо записать высказывание в форме логического выражения с учетом последовательности выполнения логических операций. При выполнении логических операций определен следующий порядок их выполнения: инверсия, конъюнкция, дизъюнкция.
Самостоятельно доказать первую часть распределительного закона, используя таблицу истинности 2.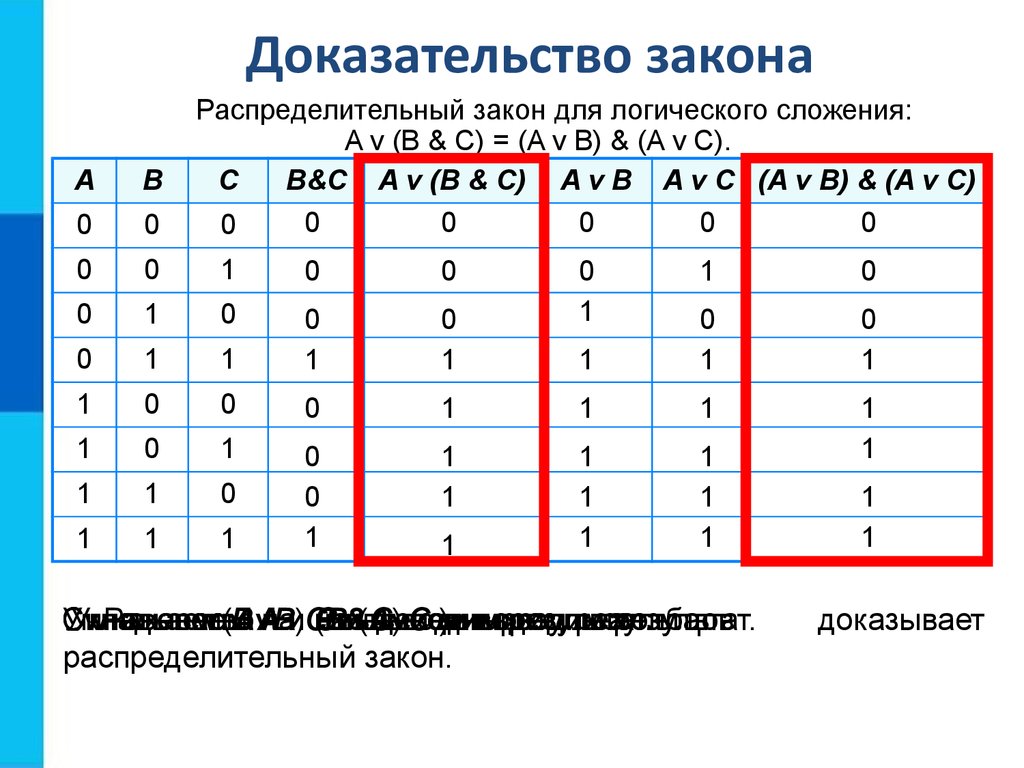
Урок информатики по теме «Основы логики, таблицы истинности»
Таблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, у которой значения переменных и значение самой функции выражают истинность. Таблицы истинности применяются для определения значения какого-либо высказывания для всех возможных случаев значений истинности высказываний, которые его составляют. Таблицы истинности нередко используются в цифровой технике и булевой алгебре, чтобы описать работу логических схем. Таблицы истинности для основных функций.
Информатика. 10 класс
Основные сведения. Логические значения, логические связки и логические выражения. Свойства логических выражений и таблиц истинности. Эквивалентные преобразования логических выражений. Такие высказывания утверждают что-то о свойствах объекта или об отношениях между объектами чаще всего — между двумя объектами. Высказывание может быть истинным верным или ложным неверным. Например, Коля может на самом деле быть старше, чем Петя тогда высказывание 3 истинно.
ВЫСКАЗЫВАНИЯ И ЛОГИЧЕСКИЕ СВЯЗКИ. В этом разделе рассматриваются таблицы истинности, знакомство с которыми будет для нас первым.
Построение таблиц истинности
Таблица истинности или
Опорный конспект по теме «Логические значения, операции, выражения» для самостоятельного изучения и подготовки к контрольным работам, экзаменам и ГИА. Код ОГЭ: 1. Логические значения, операции, выражения.
Логические элементы
Табличное задание функций встречается не только в логике, но и в логических функциях. Таблицы оказались довольно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики. Материал из Википедии — свободной энциклопедии.
Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений истинности или ложности и логических операций над ними.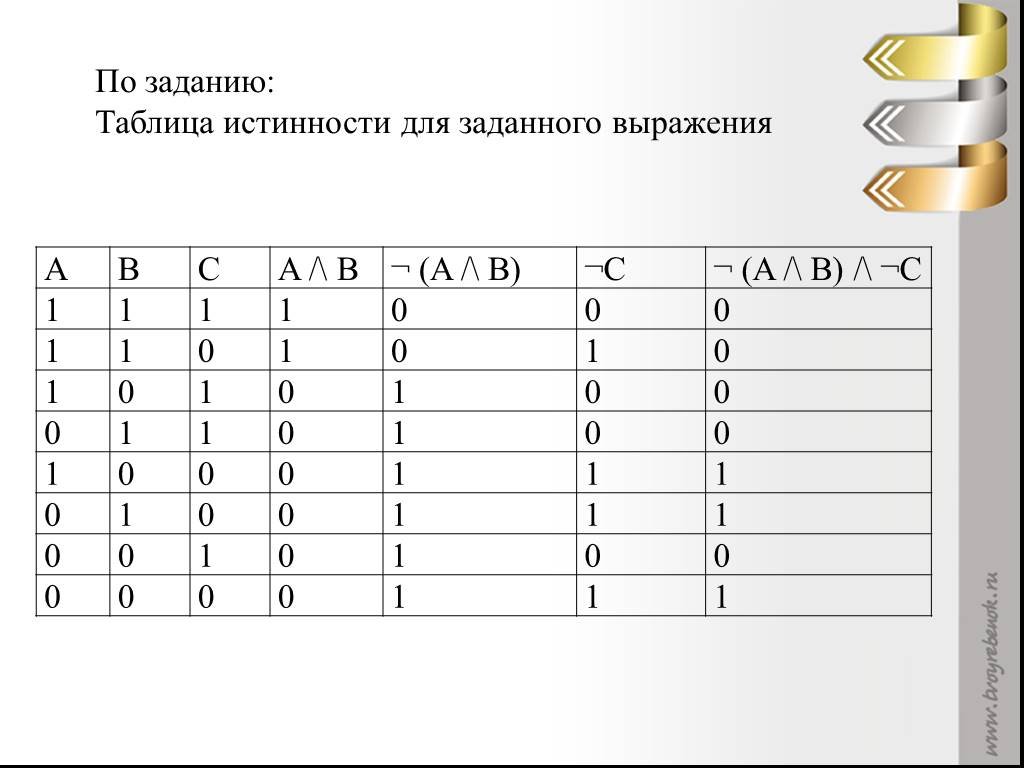
Перечень вопросов, рассматриваемых в теме: высказывание, логическая переменная, логические операции отрицание, конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквиваленция , логические выражения, предикаты и их множества истинности, таблицы истинности и их анализ. Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений истинности или ложности , и логические операции над ними. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами. В году Клод Шеннон применил алгебру логики для описания процесса функционирования релейно-контактных и электронно-ламповых схем. Логическое высказывание — это повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. Высказывания, образованные из других высказываний, называются составными.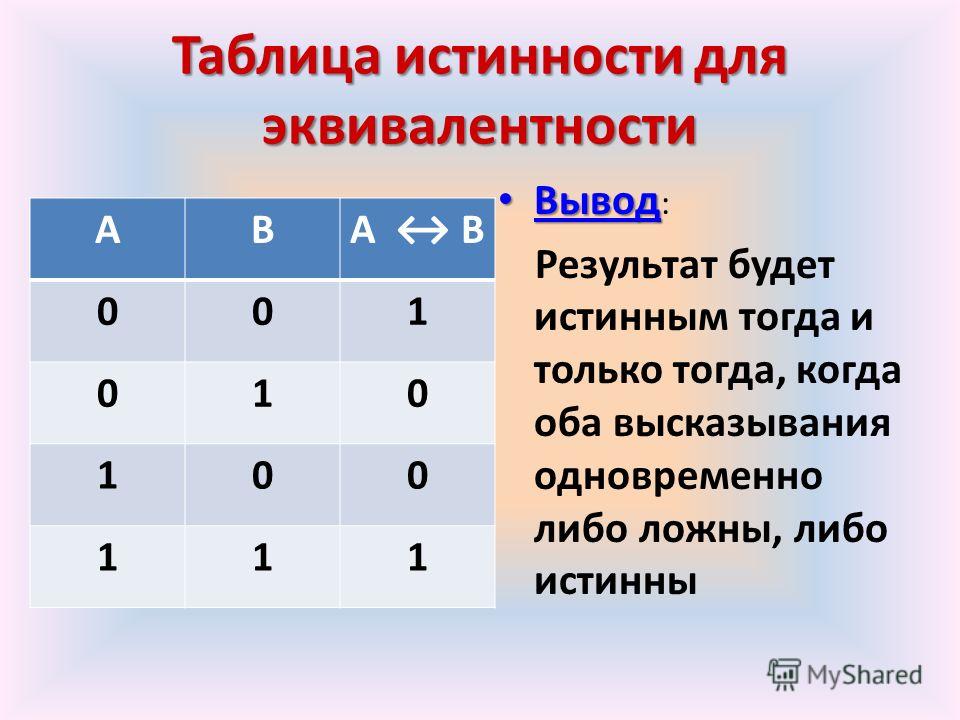
На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб!
Таблицы истинности
Таблицы истинности
|
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений (наборах) входящих в него переменных, называют таблицей истинности логического выражения. |
Для того чтобы построить таблицу истинности логического выражения, достаточно:
1) определить число строк таблицы m = 2n, где n — число переменных в логическом выражении;
2) определить число столбцов таблицы как сумму чисел логических переменных и логических операций в логическом выражении;
3) установить последовательность выполнения логических операций с учётом скобок и приоритетов операций;
4) заполнить строку с заголовками столбцов таблицы истинности, занеся в неё имена логических переменных и номера выполняемых логических операций;
5) выписать наборы входных переменных с учётом того, что они представляют собой ряд целых n-разрядных двоичных чисел от 0 до 2n — 1;
6) провести заполнение таблицы истинности по столбцам, выполняя логические операции.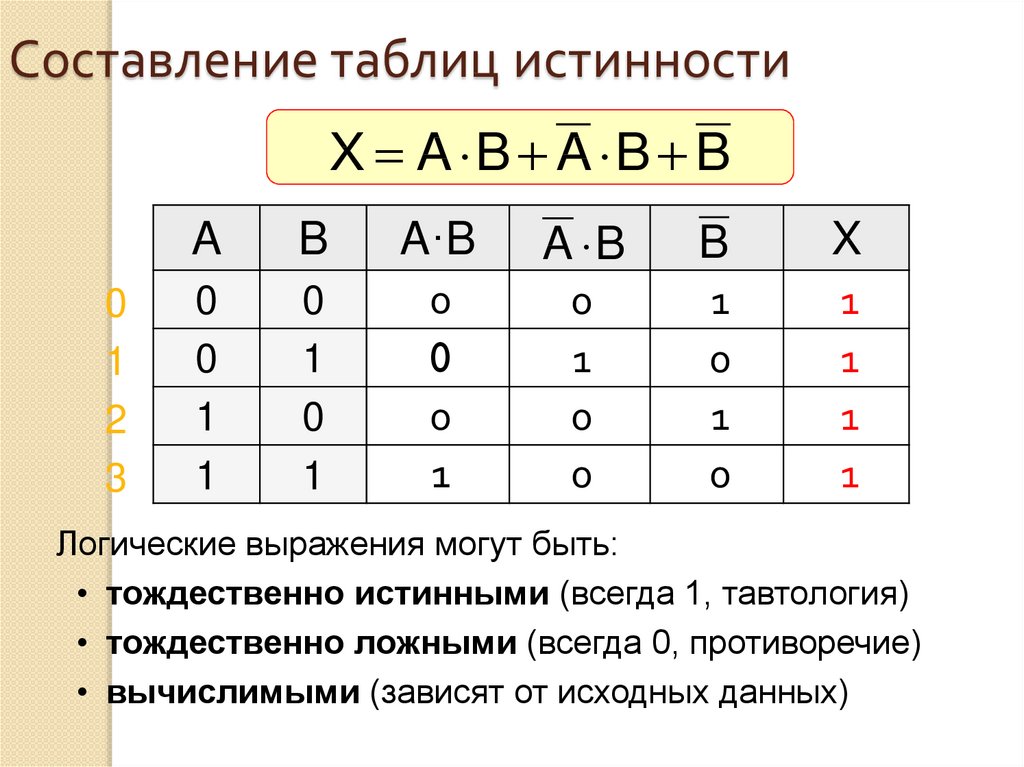
Пример 1. Построим таблицу истинности для логического выражения
В этом выражении две логические переменные и пять логических операций. Всего в таблице истинности будет пять строк (22 плюс строка заголовков) и 7 столбцов.
Начнём заполнять таблицу истинности с учётом следующего порядка выполнения логических операций: сначала выполняются операции отрицания (в порядке следования), затем операции конъюнкции (в порядке следования), последней выполняется дизъюнкция.
Обратите внимание на последний столбец, содержащий конечный результат. Какой из рассмотренных логических операций он соответствует?
|
Логические выражения, зависящие от одних и тех же логических переменных, называются равносильными или эквивалентными, если для всех наборов входящих в них переменных значения выражений в таблицах истинности совпадают. |
Таблица истинности, построенная в предыдущем примере, доказывает равносильность выражений и А ↔ B.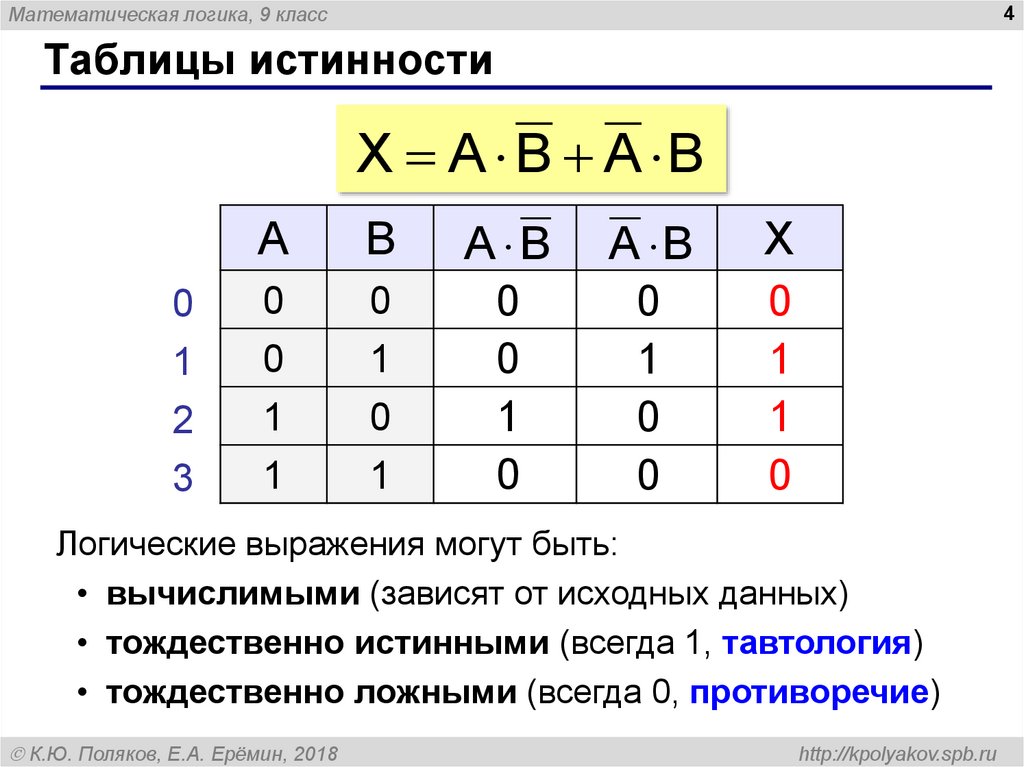
Можно записать:
С помощью таблиц истинности докажите равносильность выражений А ↔ В и
|
Функцию от n переменных, аргументы которой и сама функция принимают только два значения — 0 и 1, называют логической функцией. Таблица истинности может рассматриваться как способ задания логической функции. |
Рассмотрим несколько примеров.
Пример 2. Известен фрагмент таблицы истинности для логического выражения F, содержащего логические переменные А, В и С.
Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
Ответить на поставленный вопрос можно, вычислив значение каждого логического выражения на каждом заданном наборе переменных и сравнив его с имеющимся значением F.
1) Логическое выражение соответствует данному фрагменту таблицы истинности:
2) Логическое выражение не соответствует данному фрагменту таблицы истинности, т.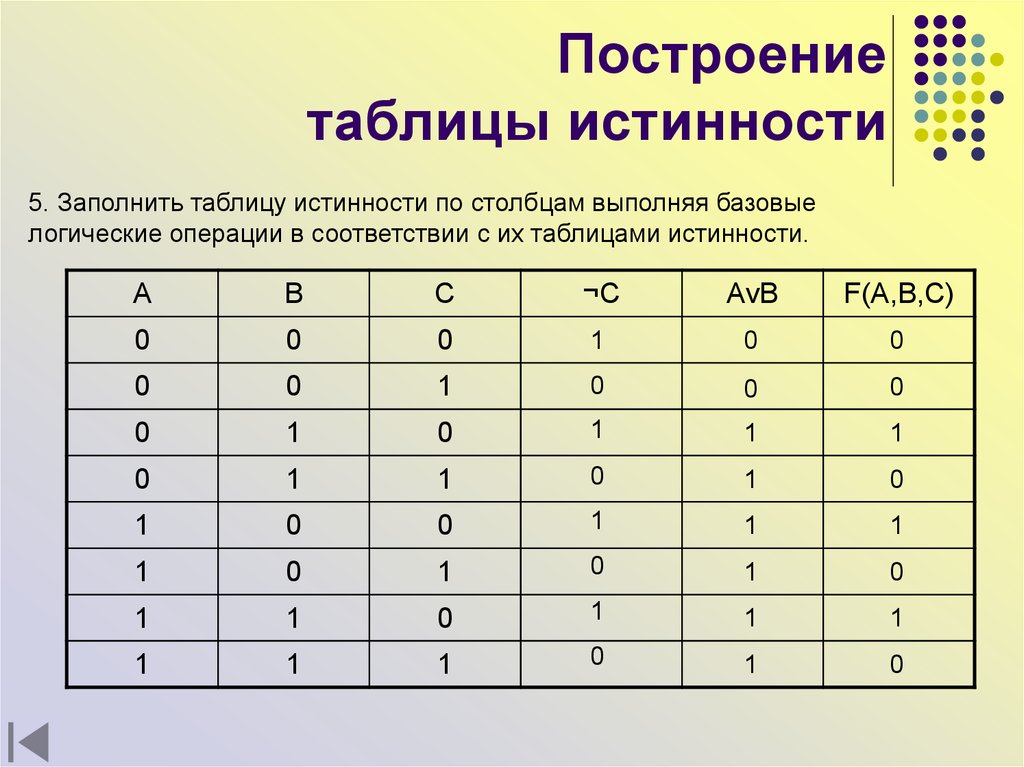 к. уже на первом наборе значение рассматриваемого логического выражения не совпадает со значением F. Проведение дальнейших вычислений не имеет смысла.
к. уже на первом наборе значение рассматриваемого логического выражения не совпадает со значением F. Проведение дальнейших вычислений не имеет смысла.
3) Логическое выражение не соответствует данному фрагменту таблицы истинности:
4) Логическое выражение
Итак, имеется два логических выражения, соответствующих заданному фрагменту таблицы истинности.
Можно ли утверждать, что в результате решения задачи мы нашли логическое выражение F?
Пример 3. Логическая функция F задаётся выражением:
Ниже приведён фрагмент таблицы истинности, содержащий все наборы переменных, на которых F истинна.
Определим, какому столбцу таблицы истинности функции F соответствует каждая из переменных х, у, z.
В исходном логическом выражении задействовано три логические переменные. Полная таблица истинности для этого выражения должна состоять из 8 (23) строк.
Наборам переменных, на которых логическое выражение истинно, соответствуют десятичные числа 0, 2, 3, 4 и 7.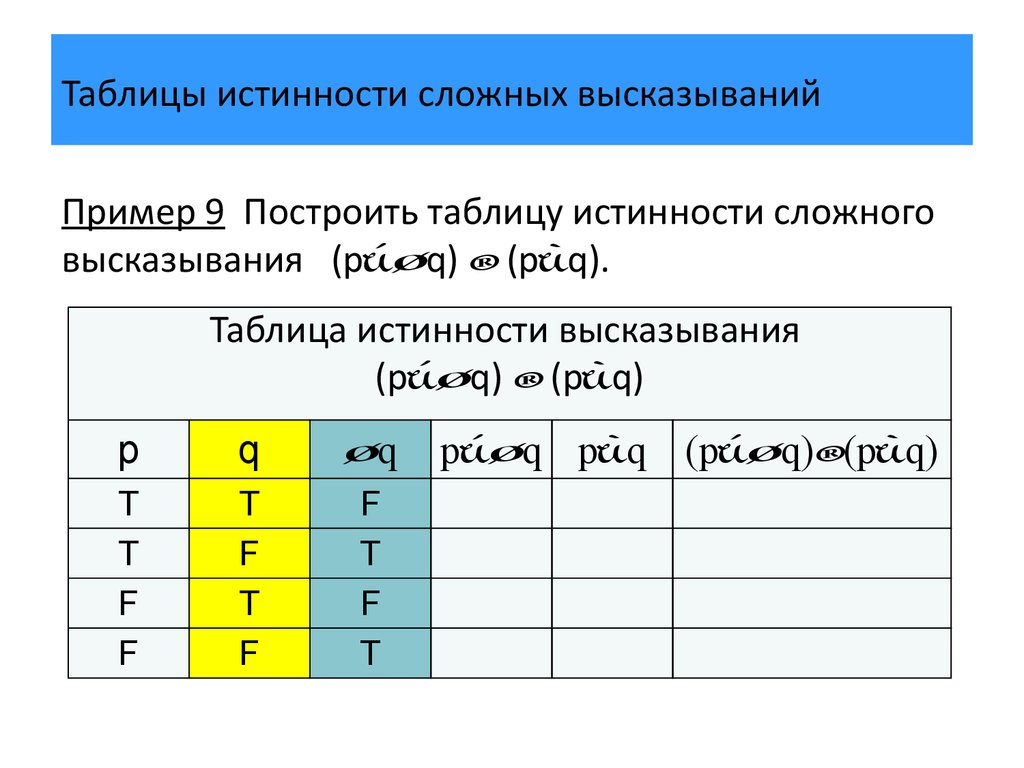
Следовательно, наборам переменных, на которых логическое выражение ложно, должны соответствовать десятичные числа 1, 5 и 6 (их двоичные коды 001, 101 и 110). Построим по этим данным вторую часть таблицы истинности:
Теперь выясним, при каких значениях х, у, z логическое выражение ложно: Логическое произведение ложно, если хотя бы один из операндов равен нулю. Таким образом, мы имеем две дизъюнкции, каждая из которых должна быть ложной. Это возможно только в случае равенства нулю каждого из операндов, входящих в дизъюнкцию. Подберём подходящие значения х, у и z, заполняя следующую таблицу:
Первая дизъюнкция равна нулю на наборе 011. Для равенства нулю второй дизъюнкции требуется, чтобы х = 1, у = 0, a z может быть и 0, и 1.
Сравним эту таблицу с восстановленным нами фрагментом исходной таблицы истинности, предварительно подсчитав, сколько раз каждая переменная принимает единичное значение.
Переменная у принимает единичное значение только один раз. Следовательно, ей соответствует второй столбец исходной таблицы. Из таблицы со значениями х, у и z следует, что при у = 1: х = 0, a z = 1. Следовательно, переменной z соответствует первый столбец, а переменной х — третий столбец исходной таблицы.
Следовательно, ей соответствует второй столбец исходной таблицы. Из таблицы со значениями х, у и z следует, что при у = 1: х = 0, a z = 1. Следовательно, переменной z соответствует первый столбец, а переменной х — третий столбец исходной таблицы.
Убедиться в правильности полученного ответа можно, полностью заполнив следующую таблицу:
Самое главное
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений (наборах) входящих в него переменных, называют таблицей истинности логического выражения.
Истинность логического выражения можно доказать путём построения его таблицы истинности.
Функцию от n переменных, аргументы которой и сама функция принимают только два значения — 0 и 1, называют логической функцией. Таблица истинности может рассматриваться как способ задания логической функции.
булева алгебра — Как составить таблицу истинности
Задавать вопрос
спросил
Изменено 6 лет, 10 месяцев назад
Просмотрено 173 раза
$\begingroup$
Да, это домашнее задание, но мне нужна помощь только в его настройке, после того, как я его настрою, вопрос состоит из 7 частей:
Мы хотим построить функцию Y = 2X + 3, где X обозначает 3-битный значение без знака (x2x1x0) и Y = y4.
.y0 — это 5-битное аппаратное значение. Постройте его таблицу истинности, где входные биты равны x2, x1 и x0, а выходные биты от y4 до y0.
Домашнее задание требует кучу других вещей, которые я могу получить. Я просто не понимаю вопроса, как создать таблицу истинности на основе функции и этих входных битов?
Должна ли таблица истинности выглядеть примерно так?
х2 х1 х0 у4 у3 у2 у1 у0 0 0 0 0 0 0 1 1 0 0 1 0 0 1 0 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 1 0 1 0 1 1 0 1 1 1 0 0 1 1 1 1 1 1 1 1 0 0 0 1
- булева-алгебра
- цифровые схемы
$\endgroup$
$\begingroup$
Для каждого из восьми входов вы вычисляете результат. Вы получите таблицу с восемью строками и столбцами $3+5=8$, содержащую три входных бита и пять выходных битов.
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Глава 3. Логические элементы и логические схемы
Введение
Электрические схемы в компьютерах имеют небольшие устройства управления памятью, называемые логическими элементами. Логические вентили вводят двоичные значения и также выводят двоичное значение. Последовательность логических вентилей также известна как логическая схема, и они предназначены для выполнения определенной функции. Проверка вывода осуществляется по таблице истинности . Мы используем Logic Gates для управления потоком трафика, а также для включения и выключения. Логические ворота можно найти во всех устройствах, таких как компьютеры и кондиционеры. Существует много типов вентилей, таких как вентиль НЕ и И, которые имеют разные выходы, некоторые имеют 2, а другие имеют 1 выход
Логические вентили
Вот примеры вентилей:
- НЕ ШЛЮЗ
- И ВОРОТ
- ИЛИ ВОРОТ
- ВОРОТ НЕ-И
- НОРМАЛЬНЫЕ ВОРОТА
- ВОРОТА ИСКЛЮЧАЮЩЕГО ИЛИ
Таблицы истинности
Таблицы истинности используются для отслеживания выходных данных логических вентилей или схем.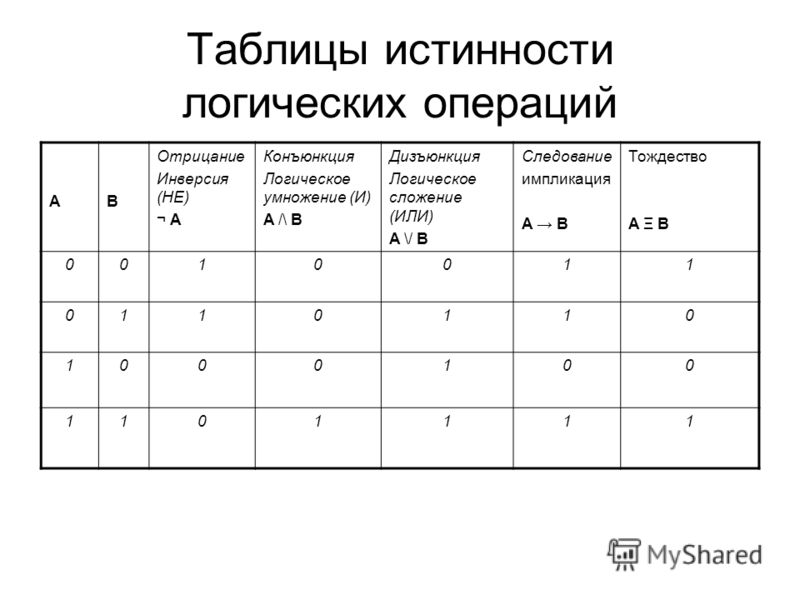 Ворота НЕ — это единственные вентили, имеющие один выход, а все остальные вентили имеют два выхода. Таблицы истинности строятся из двоичных значений (1 и 0), которые используются для создания различных комбинаций для разных вентилей.
Ворота НЕ — это единственные вентили, имеющие один выход, а все остальные вентили имеют два выхода. Таблицы истинности строятся из двоичных значений (1 и 0), которые используются для создания различных комбинаций для разных вентилей.
Логический вентиль — основа цифровой схемы, управляющей потоком электронных сигналов
Цифровая схема — схема, в которой электронные сигналы имеют одно из двух значений: высокое напряжение (1) или низкое напряжение (0)
Напряжение — разность потенциалов на электрическом компоненте, необходимая для протекания через него электричества
Микропроцессор — интегральная схема, выполняющая те же функции, что и процессор
Таблица истинности — способ отображения каждого результата логических вентилей
Логическое выражение:
Все вентили могут быть записаны в алгебраической записи, например вентиль И может быть записан как A.B=Y, что означает A и B = Y.
. = точка означает И Операция
+ = плюс означает ИЛИ Операция
Строка над выражениями означает = НЕ Операция
Видео ниже объясняет логическую алгебру:
youtube.com/embed/2zRJ1ShMcgA?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en&autohide=2&wmode=transparent» allowfullscreen=»true» sandbox=»allow-scripts allow-same-origin allow-popups allow-presentation»>Логические схемы
они могут выполнять функцию, чтобы выяснить, какую функцию они выполняют, вы можете составить для нее таблицу истинности. В этой таблице истинности у вас должны быть входы, например, если есть только 2 входа, тогда у вас будут только значения (0 0) (1 0) (0 1) и (1 1), промежуточные значения (которые являются значениями которые вы получаете в «середине» или когда у вас есть логический вентиль, они могут быть помечены любой буквой, которую вы хотите, но не повторяйте никакие буквы) и выводом (в основном записывается как X). Когда у вас есть один вход, например 0 1 в вентиль И, он выведет 0, этот 0, если больше не осталось вентилей, будет выходом, если их больше, чем это промежуточное значение.
Логические схемы в реальной жизни можно найти в любой электронике, от кондиционеров до телевизоров, однако количество используемых логических элементов может отличаться.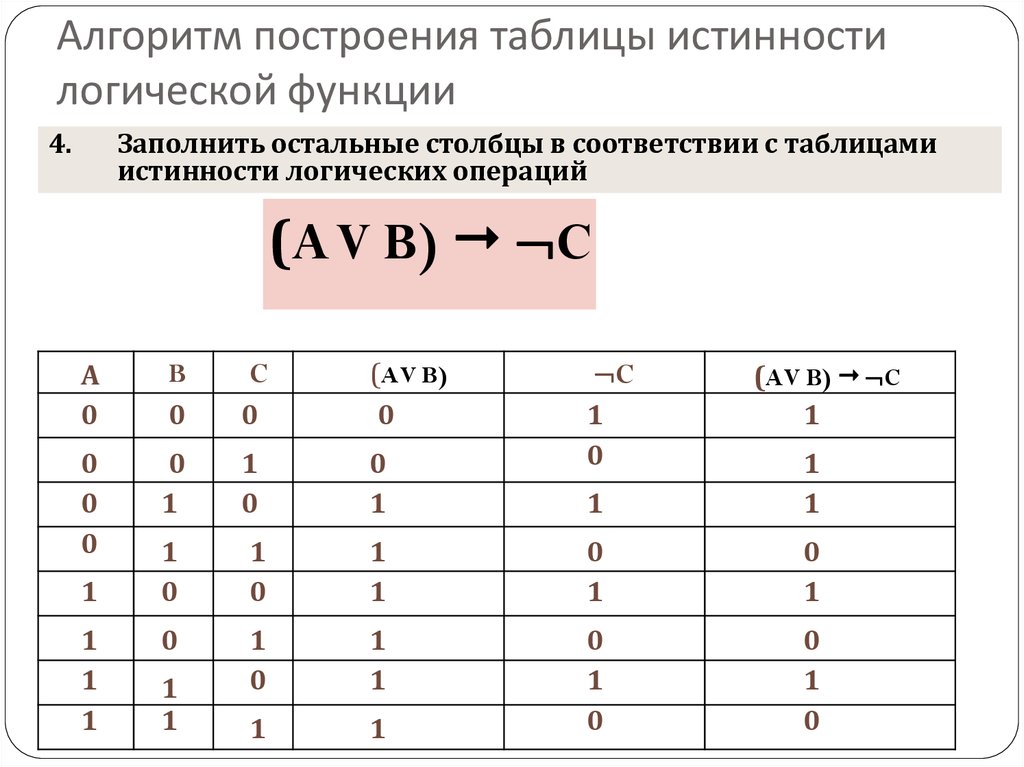


 10 класс
10 класс .y0 — это 5-битное аппаратное значение.
Постройте его таблицу истинности, где входные биты равны x2, x1 и x0, а
выходные биты от y4 до y0.
.y0 — это 5-битное аппаратное значение.
Постройте его таблицу истинности, где входные биты равны x2, x1 и x0, а
выходные биты от y4 до y0.