Таблица истинности — презентация онлайн
Похожие презентации:
Основы логики. Таблица истинности. Равносильные логические выражения
Алгебра логики и таблицы истинности. (лекция 4)
Таблицы истинности
Логика высказываний. Таблицы истинности
Таблицы истинности
Элементы алгебры логики. Математические основы информатики. Таблицы истинности
Элементы алгебры логики. Математические основы информатики. Таблицы истинности
Таблицы истинности
Таблицы истинности
Базовые логические операции и функции. Таблицы истинности. Контактные схемы
1. ТАБЛИЦЫ ИСТИННОСТИ
МКТАБЛИЦЫ ИСТИННОСТИ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
И АЛГЕБРЫ ЛОГИКИ
2. Ключевые слова
МККлючевые слова
• таблицы истинности
• логическая функция
• равносильные (эквивалентные)
логические выражения
3. Таблица истинности
МКТаблица истинности
!
А
0
1
!
Таблицу значений, которые принимает логическое
выражение при всех сочетаниях значений (наборах)
входящих в него переменных, называют таблицей
истинности логического выражения.

Таблицы истинности логических операций
А В A&B А∨B A→B A⊕B A↔B
A
0
0
0
0
1
0
1
1
0
1
0
1
1
1
0
0
1
0
0
1
0
1
0
1
1
1
1
1
0
1
Функцию от n переменных, аргументы которой и сама
функция принимают только два значения – 0 и 1,
называют логической функцией.
Таблица истинности может рассматриваться как
способ задания логической функции.
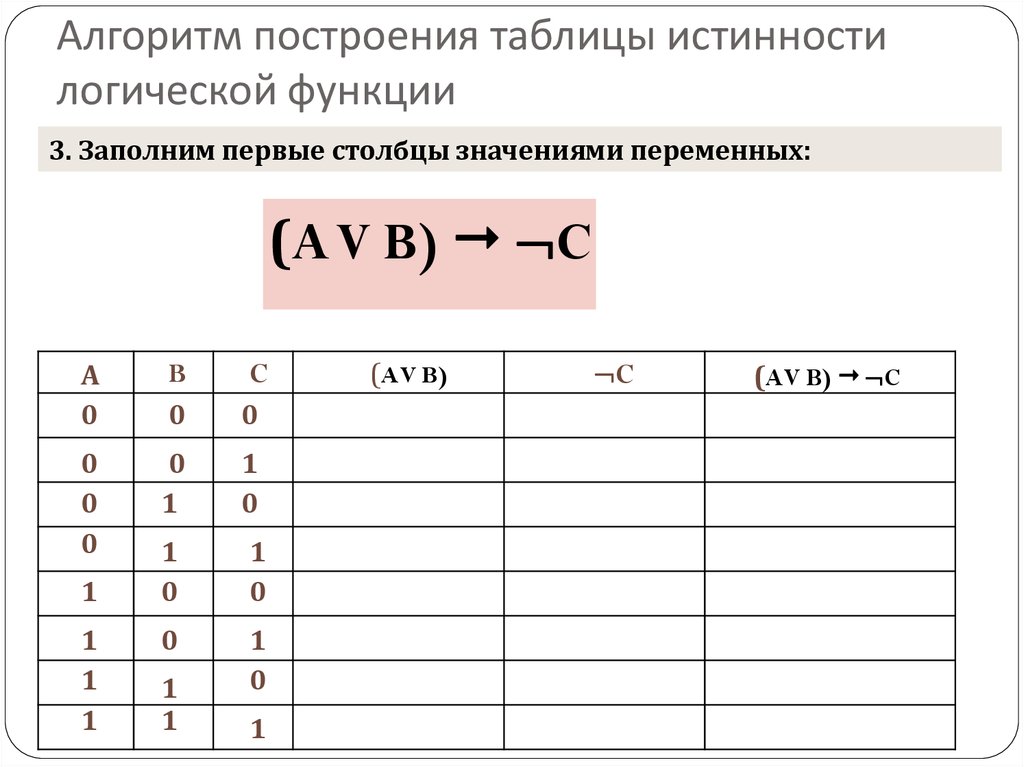
4. Построение таблиц истинности
МКПостроение таблиц истинности
Определить количество строк таблицы m = 2n , где n количество переменных в логическом выражении
Определить число столбцов таблицы — сумма количества логических переменных и операций в выражении
Установить последовательность выполнения логических операций с учётом скобок и приоритетов операций
Заполнить строку с заголовками столбцов таблицы
истинности (имена переменных, номера операций)
Выписать наборы входных переменных (ряд целых
n-разрядных двоичных чисел от 0 до 2n – 1)
Провести заполнение таблицы истинности по столбцам,
выполняя логические операции
5.
 Пример построения таблицы истинностиМК
Пример построения таблицы истинностиМКПример построения таблицы истинности
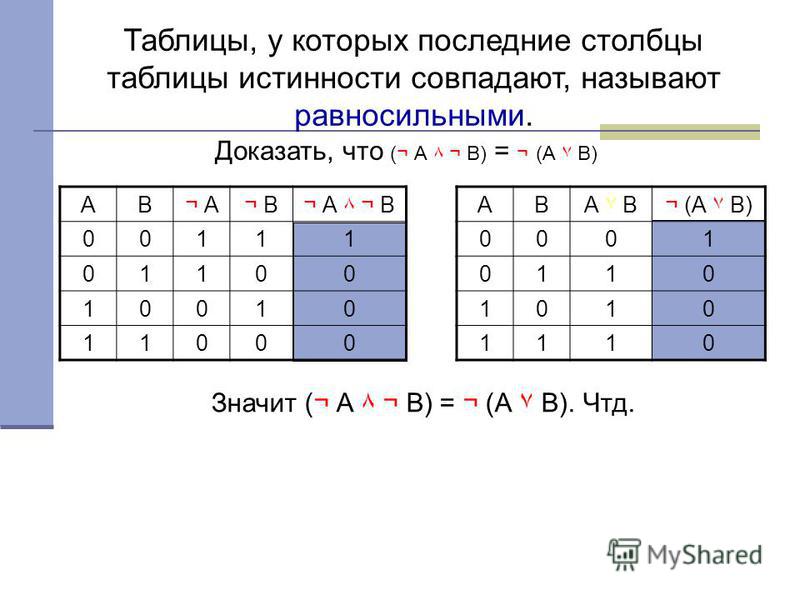
Построим таблицу истинности для логического выражения
3
5 1 4 2
A&B∨A&B
Сколько
строк
А
В будет1 в таблице?
2
3
4
5
В этом выражении две переменные – А и В.
0
0
1
0
1
1
В таблице
будет 5 строк
(22 1плюс строка
заголовка).
1
0
0
0
0
0
1
Сколько столбцов будет в таблице?
В логическом
две
переменные
0
1 логические
0
0
0и
1
0 выражении
пять логических операций. Итого 7 столбцов.
1
1
0
0
1
0
1
Строим
таблицу
наборы
из входных
5 на
строк
ипеременных
7 столбцов.
заголовок
таблицы
ссогласно
учётом
Заполним
столбцы
таблицы
Обратите
внимание
последний
столс
учётом
того,
чтоконечный
они
представляют
приоритета
логических
операций
(поряправилам
определения
истинности
бец,
содержащий
результат.
собой
целых
двухразрядных
док
операций:
инверсия,
логических
операций.
Какойвыполнения
изряд
рассмотренных
логических
двоичных
чисел
от 0 до 3.
конъюнкция,
дизъюнкция).
операций
он
соответствует?
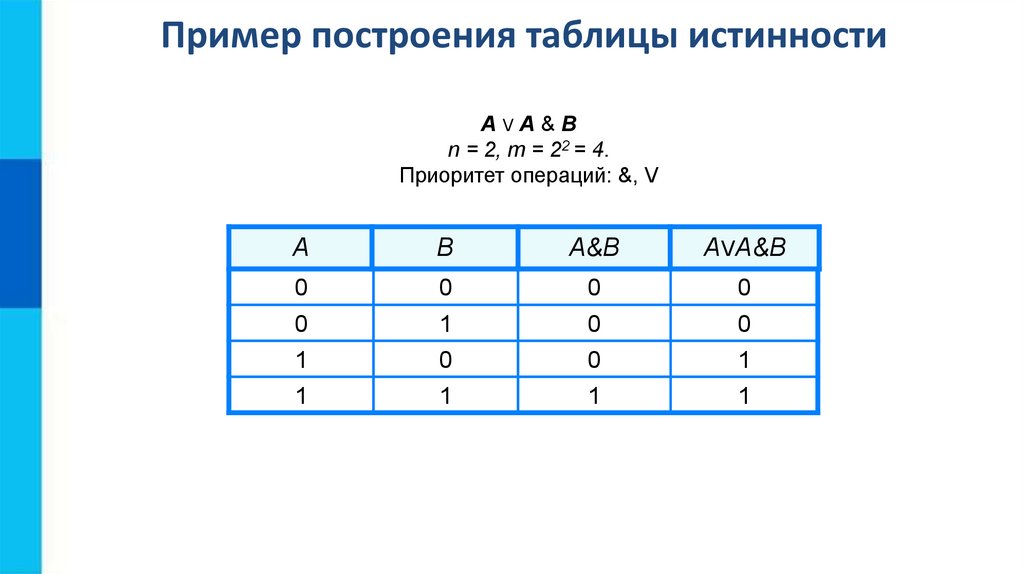
6. Эквивалентные выражения
МКЭквивалентные выражения
!
?
Логические выражения, зависящие от одних и тех же
логических переменных, называются равносильными или эквивалентными, если для всех наборов
входящих в них переменных значения выражений в
таблицах истинности совпадают.
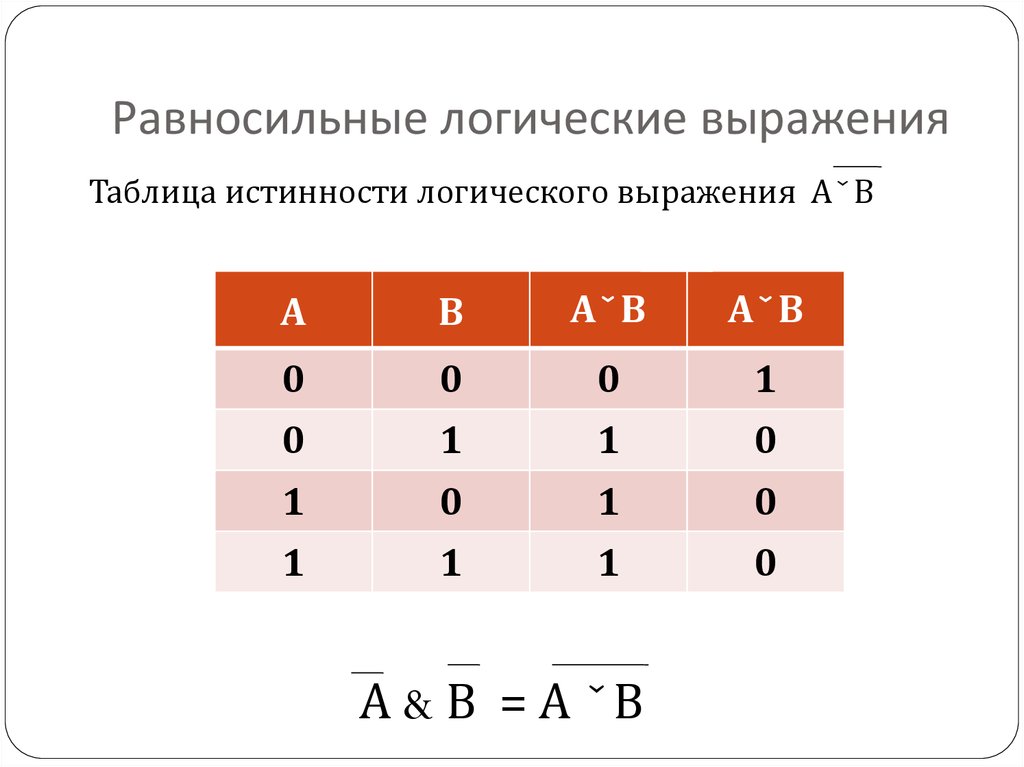
А
В
А ∧A
В→
∨ A
B∧ В
A
А↔
∨B
B
0
0
11
1
0
1
10
0
1
1
0
00
1
1
11
Ответ
0
1
С помощью таблиц истинности докажите
равносильность выражений A → B и А ∨ B.
7. Анализ таблиц истинности
МК?
Анализ таблиц истинности
№ 1. Известен фрагмент таблицы истинности для логической функции F (А, В, С).
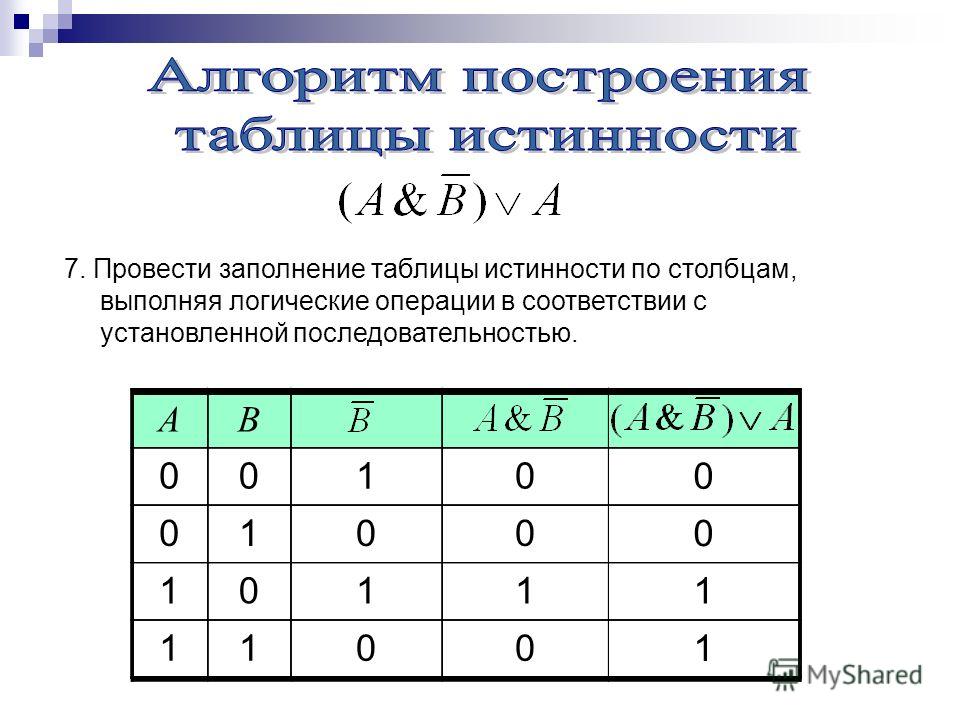 Сколько из приведённых ниже
Сколько из приведённых нижелогических выражений соответствуют этому фрагменту?
Таблица
а) (A ∨ С) & В
А В С F
б) (A ∨ В) & (C → A)
Таблица
1
0
1
0
в) (A & В ∨ С) & (В → A & С)
Таблица
1
1
0
1
г) (A → В) ∨ (С ∨ A → В)
Таблица
1
1
1
1
Ответ: 2 (а, г)
Ответить на поставленный вопрос можно,
вычислив значение каждого логического выражения на заданном наборе переменных и
сравнив его с имеющимся значением F.
Вычисления будем производить построчно.
Ответ
8. Анализ таблиц истинности
МК?
Анализ таблиц истинности
№ 2. Дана логическая функция:
F (x, y, z) = (x ∨ y ∨ z ) & (x ∨ y).
Справа приведён фрагмент таблицы
истинности, содержащий все наборы
переменных, на которых F истинна.
Определите, какому столбцу таблицы
соответствует каждая из переменных.
?z
?y
?x
F
0
0
0
1
0
1
0
1
0
1
1
1
1
0
0
1
1
1
1
1
Существуют разные подходы к решению подобных задач:
1) построение полной таблицы истинности
Решение
2) методом рассуждений
Решение
Ответ
9.
 Анализ таблиц истинностиМК
Анализ таблиц истинностиМКСамое главное
Таблицу значений, которые принимает логическое
выражение при всех сочетаниях значений (наборах)
входящих в него переменных, называют таблицей
истинности логического выражения.
Истинность логического выражения можно доказать путём
построения его таблицы истинности.
Функцию от n переменных, аргументы которой и сама
функция принимают только два значения – 0 и 1, называют
логической функцией.
Таблица истинности может рассматриваться как способ
задания логической функции.
10. Анализ таблиц истинности
МК?
Вопросы и задания
№ 3. Проверьте правильность решения
задания №2. Для этого составьте таблицу
истинности.
F (x, y, z) = (x ∨ y ∨ z ) & (x ∨ y).
z
y
x
F
0
0
0
1
0
1
0
1
0
1
1
1
1
0
0
1
1
1
1
1
English Русский Правила
Таблицы истинности — интернет энциклопедия для студентов
ОПРЕДЕЛЕНИЕ
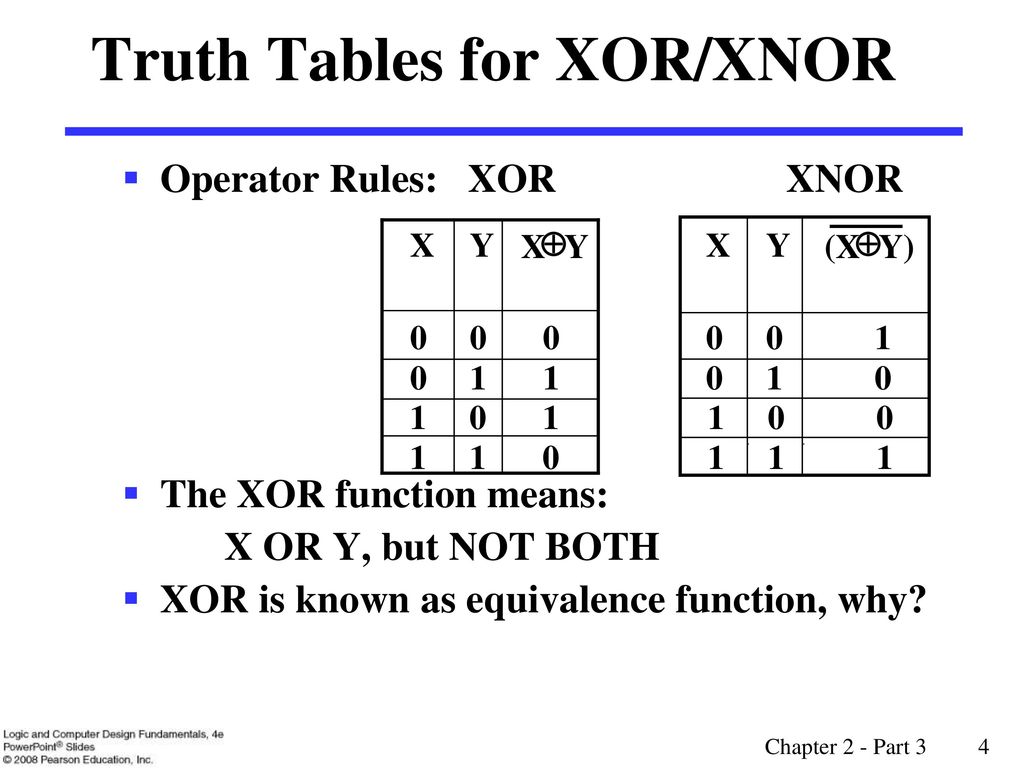
Они могут быть либо истинными, либо ложными (1 или 0). Для функции, содержащей две переменные, существует только четыре набора переменных значений:
\(\ (1,1),(1,0),(0,1),(0,0) \)
Значения логических функций определяются с помощью таблицы истинности.
Таблицы истинности для основных двоичных логических функций
1. Конъюнкция (логическое умножение) представляет собой сложное логическое выражение, которое истинно, только если оба простых выражения истинны.
Обозначение:\(\ A \wedge B \)
\(\ \begin{array}{|c|c|c|} \hline A&B&A \wedge B\\ \hline 1&1&1\\ \hline 1&0&0\\ \hline 0&1&0\\ \hline 0&0&0\\ \hline \end{array} \)
2. Дизъюнкция (логическое добавление) представляет собой сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений является истинным и ложным, если оба простых логических выражения являются ложными.
Обозначение: \(\ A \vee B \)
\(\ \begin{array}{|c|c|c|} \hline А&В&A \vee B\\ \hline 1&1&1\\ \hline 1&0&1\\ \hline 0&1&1\\ \hline 0&0&0\\ \hline \end{array} \)
3.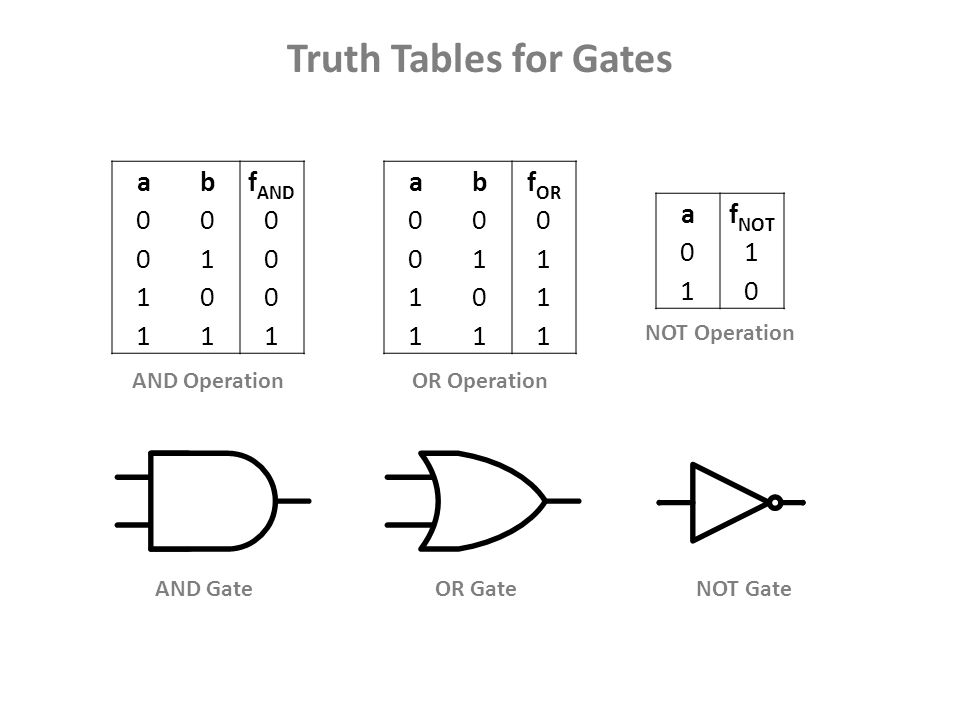
Обозначение:\(\ A \rightarrow B \)
\(\ \begin{array}{|c|c|c|} \hline А&В&A \rightarrow B\\ \hline 1&1&1\\ \hline 1&0&0\\ \hline 0&1&1\\ \hline 0&0&1\\ \hline \end{array} \)
4. Эквивалентность — это сложное логическое утверждение, которое верно только для тех же значений истинности простых выражений, включенных в него.
Обозначение:\(\ A \leftrightarrow B \)
\(\ \begin{array}{|c|c|c|} \hline A&B&A \leftrightarrow B\\ \hline 1&1&1\\ \hline 1&0&0\\ \hline 0&1&0\\ \hline 0&0&1\\ \hline \end{array} \)
5. Логическое отрицание (инверсия) делает истинное утверждение ложным и, наоборот, ложное утверждение истинно.
Обозначение:\(\ \neg A(A) \)
\(\ \begin{array}{|c|c|} \hline A&\neg A\\ \hline 1&0\\ \hline 0&1\\ \hline \end{array} \)
6. Ход Шаффера — это операция, которая отрицает конъюнкцию, т. е. Значение ложно тогда и только тогда, когда оба простых выражения истинны.
Ход Шаффера — это операция, которая отрицает конъюнкцию, т. е. Значение ложно тогда и только тогда, когда оба простых выражения истинны.
Обозначение:\(\ A | B \)
\(\ \begin{array}{|c|c|c|} \hline A&B&A | B\\ \hline 1&1&0\\ \hline 1&0&1\\ \hline 0&1&1\\ \hline 0&0&1\\ \hline \end{array} \)
7. Стрелка Пирса — это операция, которая отрицает соединение, т. е. Значение истинно тогда и только тогда, когда оба простых выражения являются ложными.
Обозначение: \(\ A \downarrow B \)
\(\ \begin{array}{|c|c|c|} \hline А&В&A \downarrow B\\ \hline 1&1&0\\ \hline 1&0&0\\ \hline 0&1&0\\ \hline 0&0&1\\ \hline \end{array} \)
Процедура выполнения логических операций
При построении таблицы истинности необходимо учитывать порядок логических операций:
1. Инверсия
2. Конъюнкция
3. Дизъюнкция
4. Последствия
5. Эквивалентность
6. Шеффирский удар
7.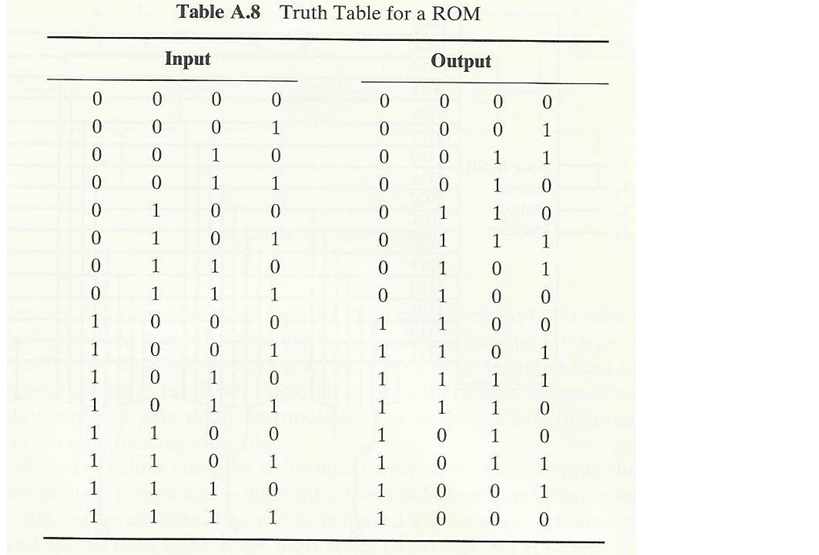 Стрелка Пирс
Стрелка Пирс
Для двух последних операций приоритет не определен.
Комментарий. Если вам необходимо изменить указанный порядок логических операций, используются скобки.
Примеры решения проблем
ПРИМЕР 1
Задача Создать таблицу истинности для функции \(\ ((A \rightarrow B) \wedge A) \leftrightarrow \overline{B} \)
Решение. Давайте сделаем таблицу истинности для данной функции, которая содержит две переменные \(\ A \) и \(\ В \). В первых двух столбцах таблицы мы пишем четыре возможные пары значений этих переменных, в последующих столбцах — значения промежуточные функции и в последнем столбце — значение функций. В результате мы получаем таблицу:
\(\ \begin{array}{|c|c|c|c|c|c|} \hline A&B&A \rightarrow B&(A \rightarrow B) \wedge A&\overline{B}&((A \rightarrow B) \wedge A) \leftrightarrow \overline{B}\\ \hline 1&1&1&1&0&0\\ \hline 1&0&0&0&1&0\\ \hline 0&1&1&0&0&1\\ \hline 0&0&1&0&1&0\\ \hline \end{array} \)
ПРИМЕР 2
\(\ (A \wedge B \leftrightarrow B \wedge C) \vee(C \rightarrow A) \)
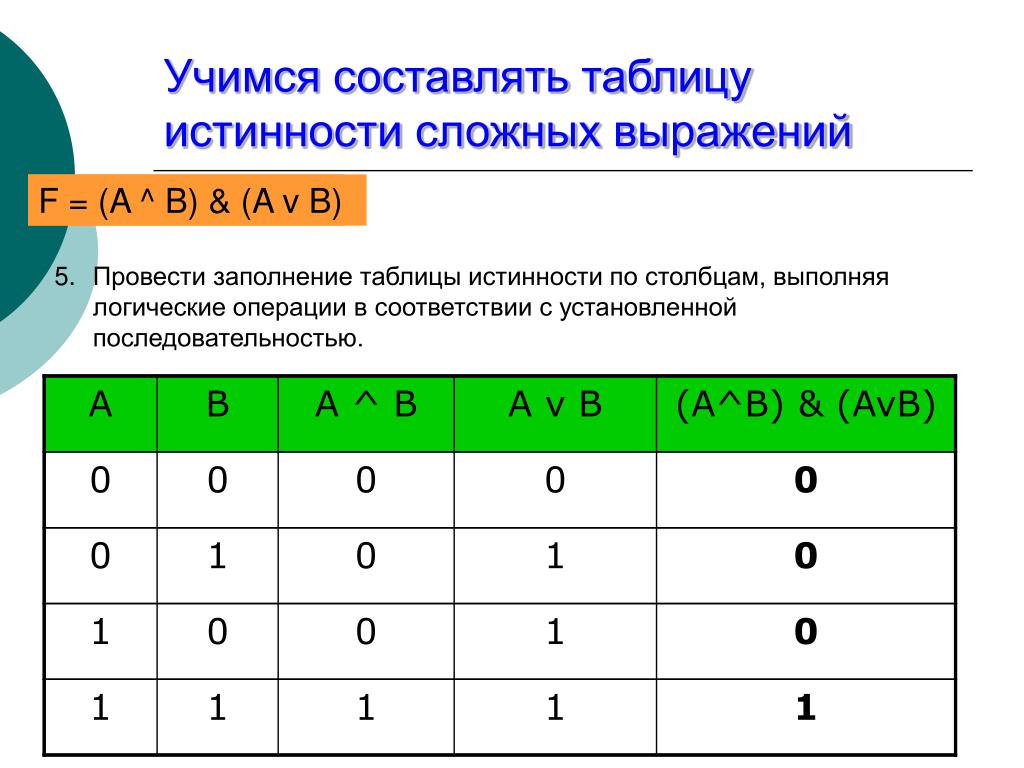
Давайте создадим таблицу истинности для данной функции, которая содержит три переменные \(\ A \), \(\ B \) и \(\ C \). Множества возможных переменных будут 8, и мы напишем их в первых трех столбцах таблицы, в последующих столбцах значения Промежуточных функций, а в последнем столбце — значения функций.
Промежуточные функции:
I — \(\ A \wedge B \)
II — \(\ B \wedge C \)
III — \(\ (A \wedge B \leftrightarrow B \wedge C) \)
IV — \(\ C \)
V — \(\ C \rightarrow A \)
VI — \(\ (A \wedge B \leftrightarrow B \wedge C) \vee(C \rightarrow A) \)
\(\ \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline A&B&C&I&II&III&\mathrm{IV}&\mathrm{V}&\mathrm{VI}\\ \hline 1&1&1&1&1&1&0&1&1\\ \hline 1&1&0&1&0&0&1&1&1\\ \hline 1&0&1&0&0&1&0&1&1\\ \hline 1&0&0&0&0&1&1&1&1\\ \hline 0&1&1&0&1&0&0&1&1\\ \hline 0&1&0&0&0&1&1&0&1\\ \hline 0&0&1&0&0&1&0&1&1\\ \hline 0&0&0&0&0&1&1&0&1\\ \hline \end{array} \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
1
Конфликтология
15
Этика
9
Формулы дифференцирования Таблица котангенсов Таблица тангенсов Таблица Брадиса Таблица факториалов
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
О таблицах истинности — Таблицы истинности
- Обновлено 16 июня 2022 г.

- 2 Минуты на чтение
Распечатать
Поделиться
Темный
Свет
Обзор
A Таблица истинности — это тип правила, которое сравнивает пользовательские данные с несколькими комбинациями входных данных, используемых в условиях, для вывода правильного результата или результата. Каждая строка настроена с несколькими правилами операторов на основе входных данных, используемых в таблице истинности. Эти Правила оператора затем приводят к набору результатов. Если в таблице истинности возвращено несколько строк, будут разные комбинации, которые логика будет оценивать при сравнении входных данных пользователя.
Каждая строка настроена с несколькими правилами операторов на основе входных данных, используемых в таблице истинности. Эти Правила оператора затем приводят к набору результатов. Если в таблице истинности возвращено несколько строк, будут разные комбинации, которые логика будет оценивать при сравнении входных данных пользователя.
Столбцы представляют данные ввода/вывода в каждой строке. Например, таблица истинности с именем и адресом электронной почты в качестве входных данных будет иметь один столбец для правила утверждения имени и другой для адреса электронной почты, а затем столбец результатов для этой строки.
На приведенном ниже снимке экрана Марка, Модель и Год являются входными данными для Правила с условиями, настроенными для каждой строки. Вводимые пользователем данные сравниваются с каждой строкой для поиска строки, в которой данные соответствуют критериям, которые затем выводят соответствующие данные.
Дополнительные сведения о создании таблицы истинности см.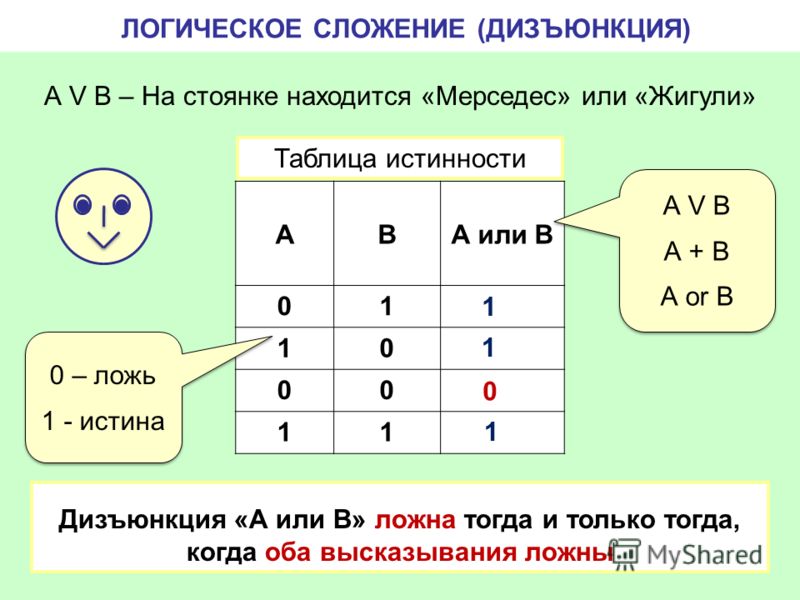 в следующей статье: Создание таблицы истинности.
в следующей статье: Создание таблицы истинности.
Типы поведения вывода
- Правило возврата данных (одиночное) : Возвращает одну переменную в поток.
- Правило действия : Передает значение и выполняет поток.
- Правило возврата данных (множественный, составной тип) : Создает новый тип данных на основе полей, указанных в возвращаемых данных. Это позволяет разработчику динамически создавать типы данных для вывода таблицы истинности на основе определенных полей.
- Правило возврата данных (несколько) : Возвращает несколько переменных в поток.
Варианты использования
Таблицы истинности можно использовать для самых разных вариантов использования. Таблицы истинности лучше всего использовать для случаев, в которых используются правила , в которых используются вложенные операторы «если». Одна из таких реализаций может включать проверку данных, таких как оценка того, когда следует утвердить аренду автомобиля для компании, путем просмотра времени аренды автомобиля, стоимости для компании и должности лица, запрашивающего аренду. Таким образом, если запрос сделан человеком X, и если он арендован на X дней и стоит компании X долларов, то запрос будет одобрен.
Таким образом, если запрос сделан человеком X, и если он арендован на X дней и стоит компании X долларов, то запрос будет одобрен.
Благодаря тому, что их можно создавать с использованием внутренних или внешних данных, они могут быть полезны для отслеживания данных, относящихся к Системе и/или Учетным записям этой Системы, таким как разрешения Учетной записи. Этого можно добиться, оценив конкретное разрешение в качестве входных данных и сравнив его с учетными записями в системе, которые имеют эти разрешения в качестве выходных данных. Это может быть введено статически через конструктор правил или динамически путем создания таблицы истинности извне через отчет.
Была ли эта статья полезной?
Что дальше
- Действия таблицы истинности
Таблицы истинности ADS и предложения, сгенерированные набором
Подраздел 3.
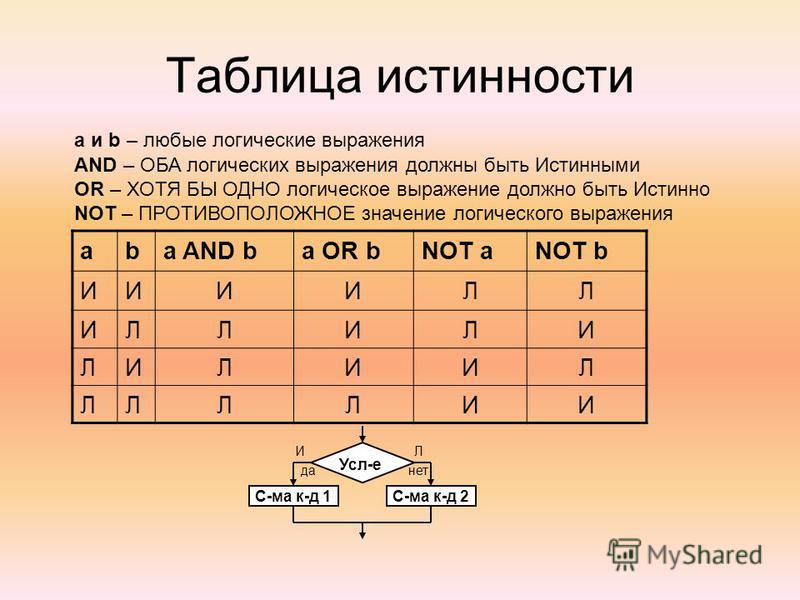 2.1 Таблицы истинности
2.1 Таблицы истинностиРассмотрим сложное предложение \(c= (p \land q)\lor (\neg q \land r)\text{,}\), где \(p\text{,}\) \(q\text{, }\) и \(r\) являются предложениями. Это пример предложения, порожденного \(p\text{,}\) \(q\text{,}\) и \(r\text{.}\). Мы определим эту терминологию позже в этом разделе. Поскольку каждое из трех простых утверждений имеет два возможных значения истинности, отсюда следует, что существует восемь различных комбинаций значений истинности, которые определяют значение для \(c\text{.}\). Эти значения могут быть получены из таблицы истинности для \ (c\text{.}\) Чтобы построить таблицу истинности, мы строим \(c\) из \(p\text{,}\) \(q\text{,}\) и \(r\) и от логических операторов. Результатом является приведенная ниже таблица истинности. Строго говоря, первые три столбца и последний столбец составляют таблицу истинности для \(c\text{.}\). Остальные столбцы представляют собой рабочее пространство, необходимое для построения до \(c\text{.}\)
Таблица 3.2.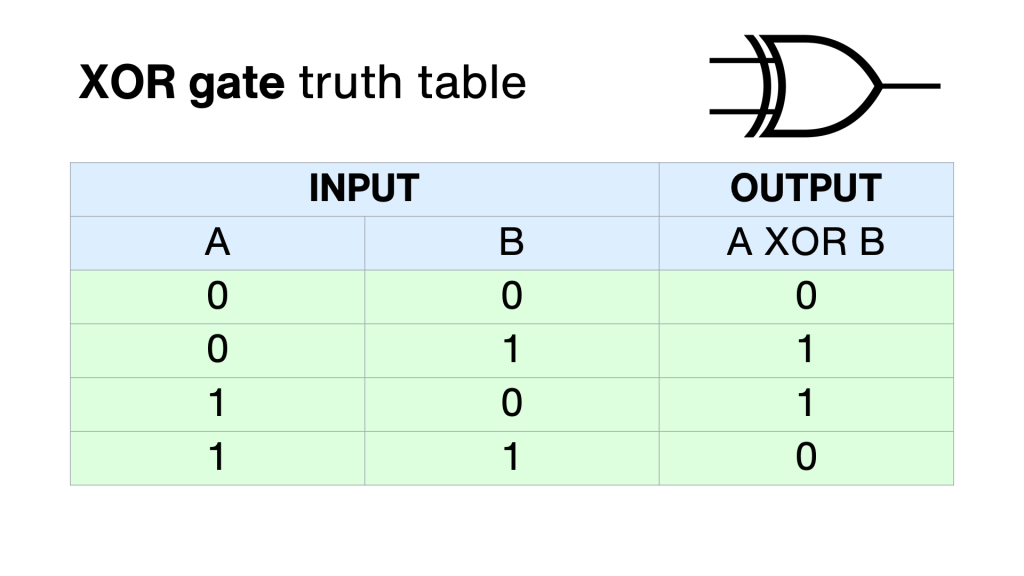 1. Таблица истинности для \(c= (p \land q)\lor (\neg q \land r)\)
1. Таблица истинности для \(c= (p \land q)\lor (\neg q \land r)\)| \(p\) | \(к\) | \(р\) | \(р\земля д\) | \(\отр д\) | \(\neg q\land r\) | \((p\land q)\lor (\neg q\land r)\) |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 |
Обратите внимание, что первые три столбца таблицы истинности представляют собой перечисление восьми трехзначных двоичных целых чисел. n\) строк с первыми \(n\) столбцами перечисление \(n\) цифр двоичных целых чисел. В нашем примере мы можем с первого взгляда увидеть, что ровно в четырех из восьми случаев \(с\) будет верным. Например, если \(p\) и \(r\) истинны, а \(q\) ложно (шестой случай), то \(c\) истинно.
n\) строк с первыми \(n\) столбцами перечисление \(n\) цифр двоичных целых чисел. В нашем примере мы можем с первого взгляда увидеть, что ровно в четырех из восьми случаев \(с\) будет верным. Например, если \(p\) и \(r\) истинны, а \(q\) ложно (шестой случай), то \(c\) истинно.
Пусть \(S\) — любое множество предложений. Мы дадим два определения предложения, порожденного S. Первое немного неточно, но должно быть ясным. Второе определение называется рекурсивным определением . Если это вас сбивает с толку, используйте первое определение и вернитесь ко второму позже.
Подраздел 3.2.2 Предложения, порожденные множеством
Определение 3.2.2. Предложение, порожденное множеством.
Пусть \(S\) — любое множество предложений. Предложение, порожденное \(S\), представляет собой любую допустимую комбинацию предложений в \(S\) с конъюнкцией, дизъюнкцией и отрицанием. Или, если быть более точным,
Если \(p \in S\text{,}\), то \(p\) является предложением, порожденным \(S\text{,}\) и
Если \(x\) и \(y\) являются предложениями, порожденными \(S\text{,}\), то таковыми являются \((x)\text{,}\) \(\neg x\text {,}\) \(x\lor y\) и \(x\land y\text{.
 }\)
}\)
Примечание. Мы не включили в определение условные и биусловные конструкции, потому что они оба могут быть получены из конъюнкции, дизъюнкции и отрицания, как мы увидим позже.
Если \(S\) — конечное множество, то мы можем использовать несколько иную терминологию. Например, если \(S = \{p, q, r\}\text{,}\), мы можем сказать, что предложение порождено \(p, q\text{,}\) и \(r\ ) вместо \(\{p, q, r\}\text{.}\)
Обычно для интерпретации предложений используется следующая иерархия, при этом круглые скобки преобладают над этим порядком:
Внутри любого уровня иерархии работайте слева направо. Используя эти правила, \(p \land q \lor r\) означает \((p \land q)\lor r\text{.}\) Эти правила приоритета являются универсальными и в точности языки для интерпретации логических выражений.
Пример 3.2.3. Примеры иерархии логических операций.
Несколько сокращенных выражений и их полностью заключенных в скобки версий:
\(p \land q \land r\) is \((p \land q) \land r\text{.
 }\)
}\)\(\neg p \lor \neg r\) is \((\neg p) \lor (\neg r)\text{.}\)
\(\neg \neg p\) равно \(\neg (\neg p)\text{.}\)
\(p \leftrightarrow q\land r\rightarrow s \) is \(p \leftrightarrow ((q\land r)\rightarrow s)\text{.}\)
Предложение, порожденное набором \(S\), не обязано включать каждый элемент \(S\) в свое выражение. Например, \(\neg q \land r\) является предложением, порожденным \(p, q\text{,}\) и \(r\text{.}\)
Упражнения 3.2.3 Упражнения
1.
Построить таблицы истинности:
\(\displaystyle p\lor p\)
\(\displaystyle p\land (\neg p)\)
\(\displaystyle p\lor (\neg p)\)
\(\displaystyle p \land p\)
Ответ.
\(\displaystyle \begin{массив}{cc} р & р \ лор р \\ \hline 0 и 0 \\ 1 и 1 \\ \конец{массив}\)
\(\displaystyle \begin{массив}{ccc} p & \neg p & p\land (\neg p) \\ \hline 0 и 1 и 0 \\ 1 и 0 и 0 \\ \конец{массив}\)
\(\displaystyle \begin{массив}{ccc} p & \neg p & p\lor (\neg p) \\ \hline 0 и 1 и 1 \\ 1 и 0 и 1 \\ \конец{массив}\)
\(\displaystyle \begin{массив}{cc} р&р\земля р\\ \hline 0 и 0 \\ 1 и 1 \\ \конец{массив}\)
2.
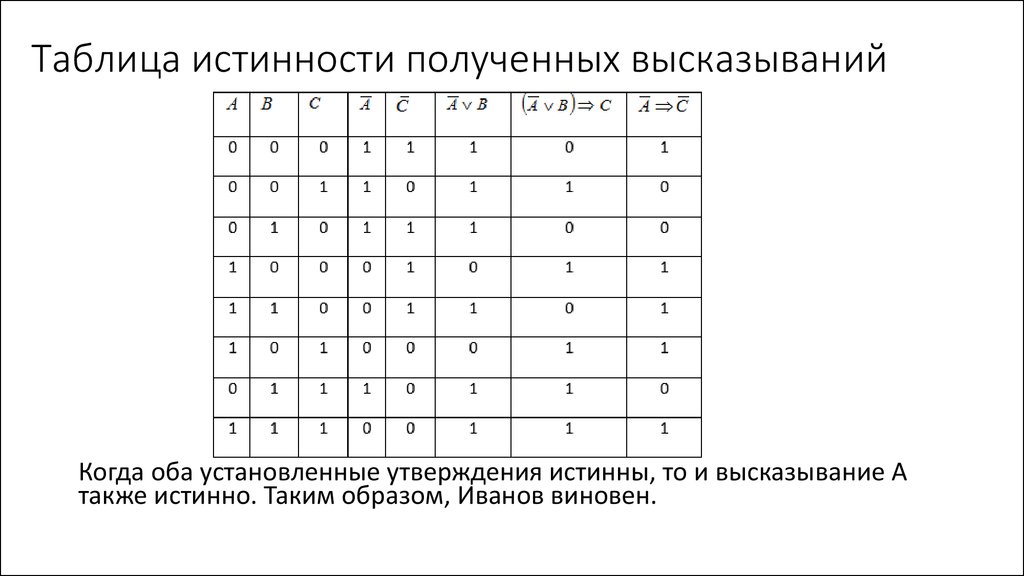
Построить таблицы истинности:
\(\displaystyle \neg (p\land q )\)
\(\displaystyle p \land (\neg q)\)
\(\displaystyle (p \land q)\land r\)
\(\displaystyle (p \land q) \lor (q \land r)\lor (r \land p)\)
\(\displaystyle \text{ }\neg p\lor \neg q\)
\(\displaystyle p \lor q \lor r \lor s\)
3.
Перепишите следующее, убрав как можно меньше лишних скобок:
\(\displaystyle (\neg ((p) \land (r))) \lor (s)\)
\(\displaystyle ((p) \lor (q)) \land ((r) \lor (q))\)
Ответ.
\(\displaystyle \neg (p\land r) \lor s\)
\(\displaystyle (p\lor q) \land (r\lor q)\)
4.
В каком порядке выполняются операции в следующих предложениях?
\(\displaystyle p \lor \neg q \lor r\land \neg p\)
\(\displaystyle p \land \neg q \land r \land \neg p\)
5.



 }\)
}\) }\)
}\)