Информатика — Логические выражения и таблицы истинности. Справочник.
Приведенный ниже список НЕ претендует на полноту, но, надеемся, достаточно представителен.
5.1. Общие свойства
1) Для набора из n логических переменных существует ровно 2n различных значений.
2) Таблица истинности для логического выражения от n переменных содержит n+1 столбец (по одному столбцу на каждую переменную + 1 столбец на значение выражения) и 2n строк.
5.2.Дизъюнкция
1) Если хоть одно из подвыражений, к которым применяется дизъюнкция, истинно на некотором наборе значений переменных, то и вся дизъюнкция истинна для этого набора значений.
2) Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже истинна.
3) Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже ложна.
4) Значение дизъюнкции не зависит от порядка записи подвыражений, к которым она применяется.
5.3. Конъюнкция
1) Если хоть одно из подвыражений, к которым применяется конъюнкция, ложно на некотором наборе значений переменных, то и вся конъюнкция ложна для этого набора значений.
2) Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то конъюнкция этих выражений тоже истинна.
3) Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то конъюнкция этих выражений тоже ложна.
4) Значение конъюнкции не зависит от порядка записи подвыражений, к которым она применяется.
5.4. Простые дизъюнкции и конъюнкции
Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.
1) Простая конъюнкция принимает значение 1 (истина) ровно на одном наборе значений переменных.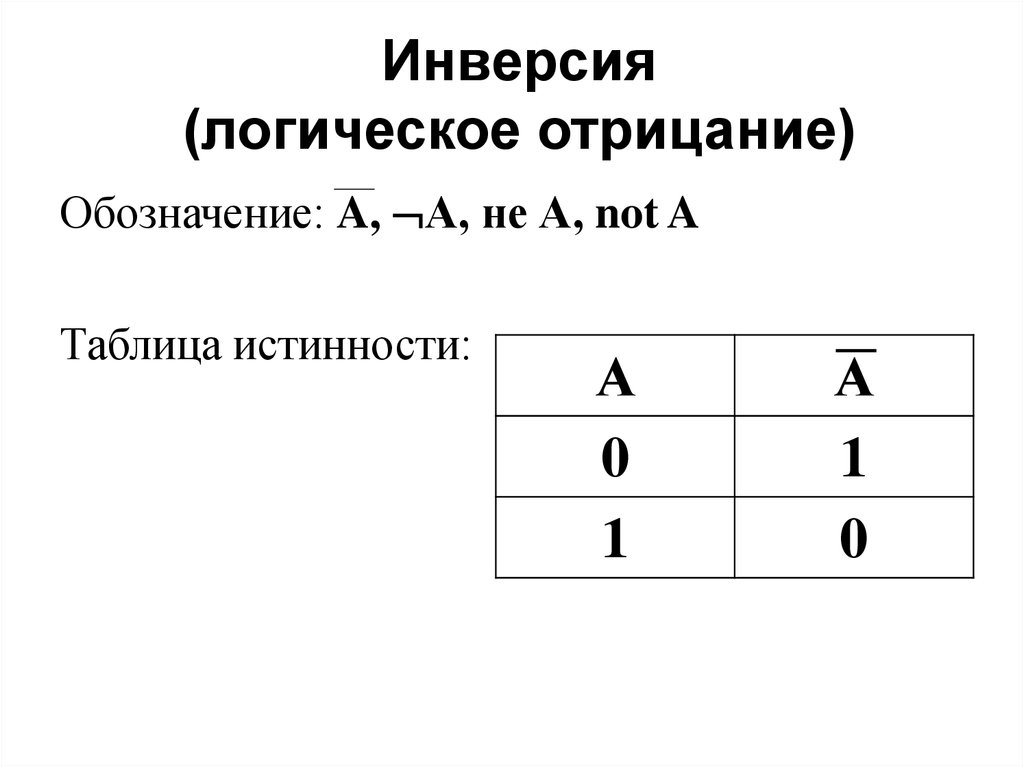
2) Простая дизъюнкция принимает значение 0 (ложь) ровно на одном наборе значений переменных.
5.5. Импликация
1) Импликация A →B равносильна дизъюнкции (¬А) \/ В. Эту дизъюнкцию можно записать и так: ¬А \/ В.
2) Импликация A →B принимает значение 0 (ложь) только если A=1 и B=0. Если A=0, то импликация A→B истинна при любом значении B.
5.6. Эквивалентность
1) Эквивалентность A ≡ B равносильна конъюнкции двух импликаций: A→B и B→A. Эту конъюнкцию можно записать так: (A→B)/\ (B→A)
2) Эквивалентность A ≡ B принимает значение 1 (истина) тогда и только тогда, когда значения переменных A и B одинаковы, т.е. A=B=1 или A=B=0.
Поэтому эквивалентность A ≡ B равносильна выражению (A/\B) \/ ((¬А) /\ (¬В) ).
3) Эквивалентность A ≡ B принимает значение 0 (истина) тогда и только тогда, когда значения переменных A и B различны, т.е. A=0, а B=1 или A=1, а B=0.
Поэтому эквивалентность A ≡ B равносильна выражению ¬ ( (A/\¬B) \/ (А /\¬В) )
Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны
жүктеу/скачать 0.
|
1 2 3 4 5 6 7 8 9 10 11
- Бұл бет үшін навигация:
- Название логической операции Логическая связка
- Конъюнкция (логическое умножение)
- Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
|
Тема 2.5. Арифметико-логические основы работы компьютера Тема 2.5. Арифметико-логические основы работы компьютера Алгебра логики. Понятие, основные логические операции. Таблицы истинности Сложные (составные) высказывания строятся из простых с помощью логических операций.
Конъюнкция (логическое умножение) Рассмотрим два высказывания: A = «Основоположником алгебры логики является Джордж Буль», B = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике».  Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания. Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Для записи конъюнкции используются следующие знаки: И, ˆ, ⋅, & (амперсанд). Например: A и B, AˆB, A⋅B, A&B (коды программирования). Конъюнкцию можно описать в виде таблицы, которую называют В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы A и B), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: 00,01,10,11. В последнем столбце записан результат выполнения логической операции для соответствующих операндов. жүктеу/скачать 0.52 Mb. Достарыңызбен бөлісу: |
1 2 3 4 5 6 7 8 9 10 11
©emirsaba.org 2022
[Решено] Таблицы истинности 1: соединение, дизъюнкция, условное выражение, отрицание и…
Получите больше от подписки*
- Доступ к более чем 100 миллионам учебных ресурсов по конкретным курсам
- Круглосуточная помощь опытных наставников по более чем 140 предметам
- Полный доступ к более чем 1 миллиону решений для учебников
*Вы можете изменить, приостановить или отменить в любое время
Вопрос от ConstablePartridge177
Таблицы истинности 1: соединение, дизъюнкция, условное выражение, отрицание и биусловное выражение
Буквы p и q обозначают утверждения. Значение истинности утверждения либо истинно, либо ложно, «T» или «F». Таблица истинности показывает все возможные комбинации назначений значений истинности p и q и проверки достоверности.
Значение истинности утверждения либо истинно, либо ложно, «T» или «F». Таблица истинности показывает все возможные комбинации назначений значений истинности p и q и проверки достоверности.
Сначала назначаются возможные исходы p и q. Это делается путем заполнения столбца p, а затем столбца q сверху вниз, как показано на рисунке. (Обратите внимание, что под «p» читается T,T,F,F, а под «q» чередуются T,F,T,F.) 9q
t t t
t f f
ft f
f f f
Конъюнкция: Читая слева направо во второй строке таблицы, мы видим, что только когда оба p и q истинны и является составным высказыванием «p и к» правда. Утверждение неверно в каждом из оставшихся трех случаев.
2. Разделение: p или q
P Q P v Q
T T T
T F T
F T T
F F F
Дизъюнкция: Применяя правила вывода и чтения слева направо, мы видим, что «p или q» ложно только тогда, когда оба p и q ложны (в последней строке). Это демонстрирует включительно смысл «или». Пока одно или ОБА из p и q истинны, утверждение «p или q» истинно.
Это демонстрирует включительно смысл «или». Пока одно или ОБА из p и q истинны, утверждение «p или q» истинно.
3. Условный: Если p, то q
p q Если p > q
T T T
T F F
F T T
F F T
Условное выражение ложно только тогда, когда антецедент (p) истинен, а следствие (q) ложно (строка 3).
4. Отрицание: ~p
При всех отрицаниях присваивается противоположное значение истинности.
p ~p
T F
F T
5. Биусловный: p тогда и только тогда, когда q
p q p = q
T T T 9q» (не p и q), присвоения значений истинности из столбца 2 «q» должны сравниваться с присвоениями значений истинности из столбца 3 «~p». (Но в некоторых примерах, таких как второй пример, столбец 1 будет сравниваться с столбец 3 и один пример будут сравнивать столбцы 3 и 4, причины, почему должны быть очевидны, когда вы доберетесь до задач.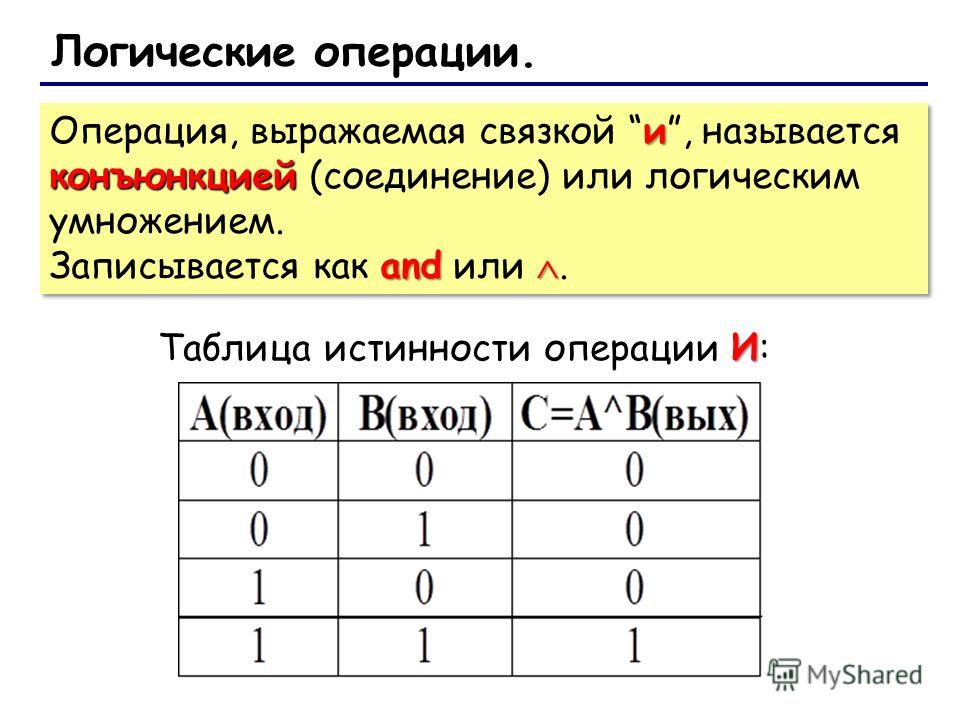
T T T F F
T F F F
F T T T T T T
F F T F
P или нет Q
P Q ~ Q P V ~ Q
P Тогда не Q
P p тогда не q
p q ~p ~q ~p > ~q
P тогда и только тогда, когда не q
p q ~q p = ~q
Искусство и гуманитарные науки Философия
Ответ и объяснение
Решено проверенным экспертом
Ответил kajalpandey12345678
Donec aliquet. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam la
acinia pulvinar tortor nec facilisis.
ce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis
Донец Аликет. Lorem
Lorem
Получите полный доступ к Course Hero
Изучите более 16 миллионов пошаговых ответов из нашей библиотеки
Подпишитесь, чтобы посмотреть ответ
Пошаговое объяснение
фасилизис. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Нам ла
1 Приложение
jpg
Другой ответ
Ответил krtan1
acinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetu
Получите полный доступ к Course Hero
Изучите более 16 миллионов пошаговых ответов из нашей библиотеки
Подпишитесь, чтобы просмотреть ответ
rises
ur laoreet. Nam risus ante, da
Nam risus ante, da
, ultrices ac magna. Fusce dui
ur laoreet. Нам рис
облегчение. Pellentesque dapibus efficitur
а. Fusce dui lectus, congue vel laoreet ac,
molestie consequat, ultrices ac magna. Fusc
ур laoreet. Nam risus ante, dapibus a moles
s a molestie conquat, ultrices ac magna
или nec facilisis. Pell
itur laoreet. Nam risus ante,
ongue vel laoreet ac, dictum
lestie consequat, ultrices ac
inia pulvinar tortor nec facil
iscing elit. Nam lacinia pulvi
ipiscing elit. Nam lacinia pulvinar t
логика — Таблица истинности логической дизъюнкции
спросил
Изменено 7 лет, 10 месяцев назад
Просмотрено 577 раз
$\begingroup$
Таблица истинности логической дизъюнкции показывает, что есть только одна ситуация, когда результат может быть ложным, когда оба утверждения ложны. Пока одно утверждение истинно, результат также верен.
Пока одно утверждение истинно, результат также верен.
Для меня это имеет смысл, но мне интересно, почему это так. Разве не было бы в равной степени правильным, если бы ложное преобладало над истинным. Верное утверждение, по-видимому, имеет некоторую управляющую силу без какой-либо особой причины.
Например, учитывая предложения:
p.Я играю за бейсбольную команду (присвоено False)
q.Я играю за футбольную команду (присваивается True)
$$ p \lor q$$
не будет рассматривается как истинное или ложное составное утверждение в английском языке, так какова же причина этого приоритета в логике высказываний?
Будем признательны за любую помощь.
- логика
- исчисление высказываний
$\endgroup$
4
$\begingroup$
Вы правы в том, что в пропозициональной логике нет причин иметь такой приоритет.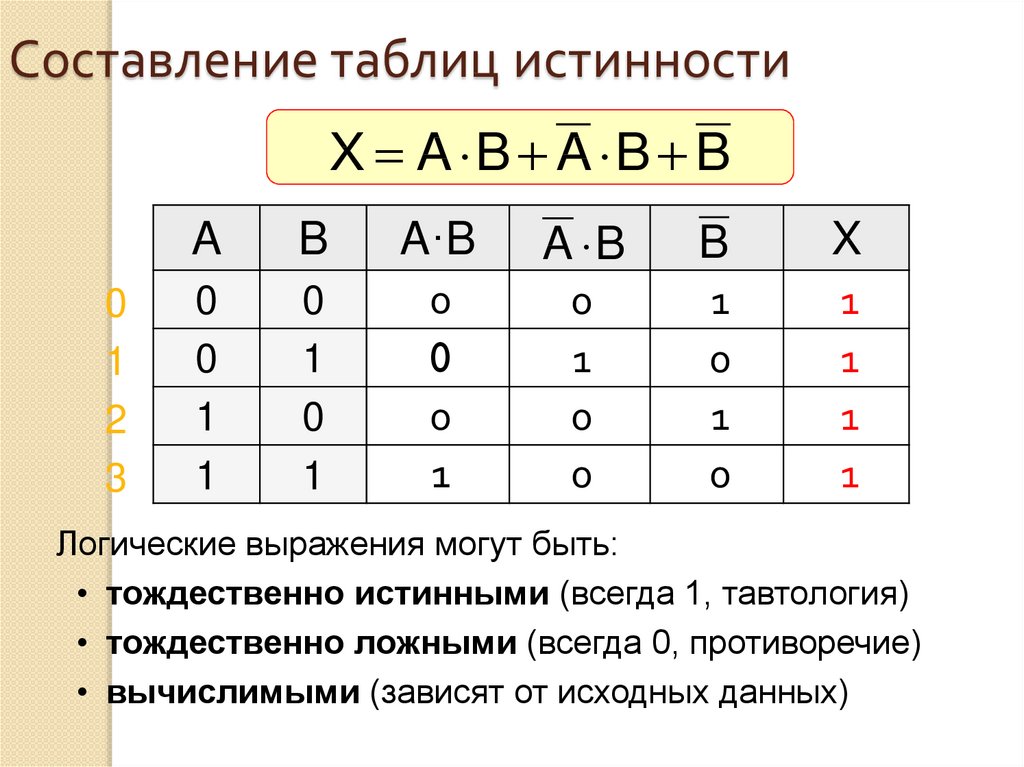
Следовательно, у нас есть оба определения конъюнкции и дизъюнкции:
$$p \lor q \leadsto \text{По крайней мере, одно из следующих }\color{red}{\text{true}}: p, п.\\ p \land q \leadsto \text{По крайней мере, одно из следующих значений равно }\color{red}{\text{false}}: p, q.$$
Обратите внимание, что ложное в соединении превалирует над истинным. Как видите, пара дизъюнкция/конъюнкция вместе не отдает никакого предпочтения истинному или ложному.
Педантичные лингвистические конструкции, подобные приведенным выше, могут показаться излишними, но они помогают уточнить значение символического выражения, особенно в таких потенциально запутанных случаях, как дизъюнкция.
Дизъюнкция немного особенная из-за так называемой эксклюзивной или конструкции:
$$p \oplus q \leadsto \text{Истинно либо $p$, либо $q$.}$$
, что явно исключает возможность того, что $p$ и $q$ оба истинны. К инклюзивному характеру $\lor$ нужно привыкнуть; однако через некоторое время вы можете обнаружить, что отвечаете на вопрос: «Вы пили чай или воду?» с «Да», как указано coffeemath в комментариях.


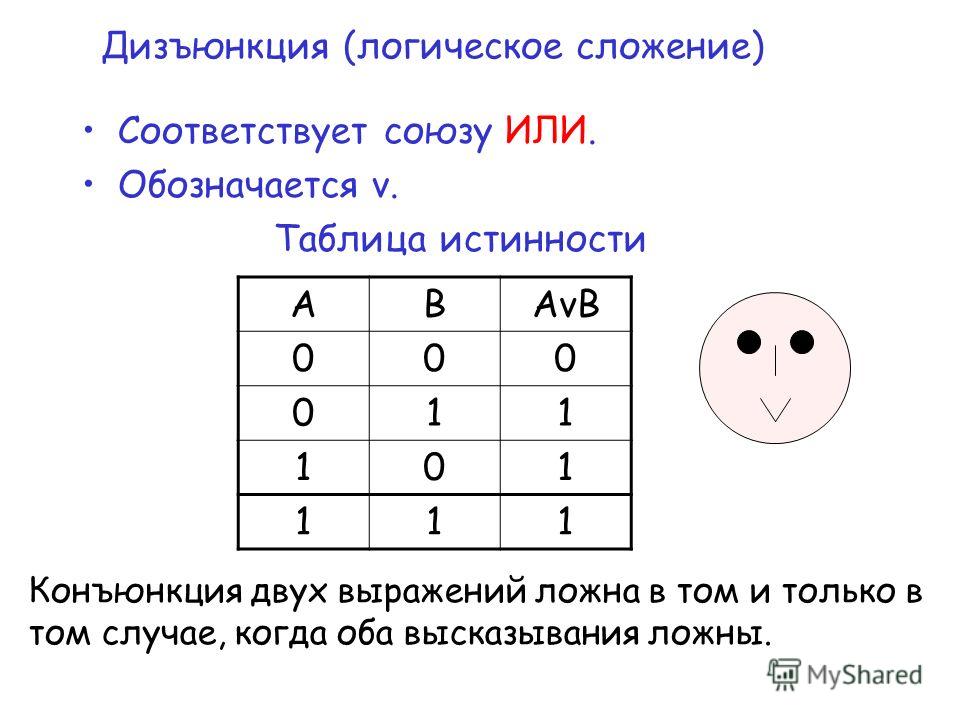 52 Mb.
52 Mb. Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.
Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.