Минимизация логических функций. Практика и теория | Курсовые работы Информатика
Скачай Минимизация логических функций. Практика и теория и еще Курсовые работы в формате PDF Информатика только на Docsity! ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ГОРОДА МОСКВЫ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА МОСКВЫ «КОЛЛЕДЖ АВТОМАТИЗАЦИИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ № 20» КУРСОВАЯ РАБОТА по МДК01.02 Цифровая схемотехника специальность 09.02.01. Компьютерные системы и комплексы Тема: «Минимизация логических функций» Группа КСК412 Выполнил/а/ студент Демидов Д.Е. (подпись) (ФИО) Руководитель Кричфалуши В.И. (подпись) (ФИО) Оценка ______________ Москва, 2021 ОГЛАВЛЕНИЕ ВВЕДЕНИЕ 1. ПОНЯТИЕ ЛОГИЧЕСКОЙ ФУНКЦИИ 5 1.1АЛГОРИТМ СИНТЕЗА КОМБИНАЦИОННЫХ СХЕМ 1.1.1 Канонический метод……………………………………………………………………………… 1.1.2 Карты Карно 1.1.3 Алгоритм построения Карт Карно 1.1.4 Использование Карт Карно 1.1.5 Реализация Решения 1.
1.6 Упрощение Карт Карно 1.1.7 Правило Карт Карно 2. МЕТОД КВАЙНА МАК-КЛАКСИ 2.1 Процедура минимизации Квайна Мак-Клакси 3. ПРИМЕРЫ ДЛЯ РЕАЛИЗАЦИИ ФУНКЦИИ Пример 1. Пример 2. Пример 3. Пример 4 20 ВЫВОД. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ. 1. ПОНЯТИЕ ЛОГИЧЕСКОЙ ФУНКЦИИ Логическая операция — это специальный символ или слово, связывающее две или более фраз информации. Он чаще всего используется для проверки того, является ли определенная связь между фразами истинной или ложной. В вычислительной технике логические операции необходимы, потому что они моделируют то, как информация проходит через электрические цепи, например, внутри центрального процессора. Эти типы операций называются булевыми. Элементы схемы, которые ведут себя в соответствии с булевой логикой, называются логическими элементами. Они названы в честь английского математика Джорджа Буля, который изобрел булеву алгебру и широко считается основателем теории компьютерных наук. Они также могут быть представлены как 1 и 0. Обычно 1 представляет истину, а 0-ложь, но может быть и наоборот.
B истинно только в том случае, если оба A и B истинны. Таблица 3 Таблица истинности для конъюнкции A B A ∧ B 0 0 0 0 1 0 1 0 0 1 1 1 4) Оператор «ИЛИ-НЕ»: Другими словами, если его входы представляют собой комбинацию правда и ложь, то выход ИЛИ-НЕ является правда. Если его входы все истинно или все ложно, выход элемента исключающее ИЛИ является ложным. Таблица 4 Таблица истинности для отрицания дизъюнкции A B A ∨ B 0 0 0 0 1 1 A B A ∨ B 1 0 1 1 1 0 5) Оператор «И-НЕ»: Другими словами, если его входы представляют собой комбинацию истинно и ложь, то выход «И-НЕ» является ложным. Если все его входы истинны или ложны, то выход «И-НЕ» истинен. Таблица 5 Таблица истинности для отрицания конъюнкции A B A ∧ B 0 0 1 0 1 0 1 0 0 1 1 1 1.1 АЛГОРИТМ СИНТЕЗА КОМБИНАЦИОННЫХ СХЕМ Основной задачей синтеза комбинационных схем является построение оптимальной схемы по физическому описанию, под которым понимается 3) 4 входные схемы с входами A B C и D требуют карт с 24 = 16 ячейками; Рис 4. 4 входа и 16 ячеек Следует заметить, что эта нумерация ребер не соответствует обычной последовательности двоичного счета, а использует последовательность кода Грея, в которой только один бит, изменяется от одной ячейки к другой.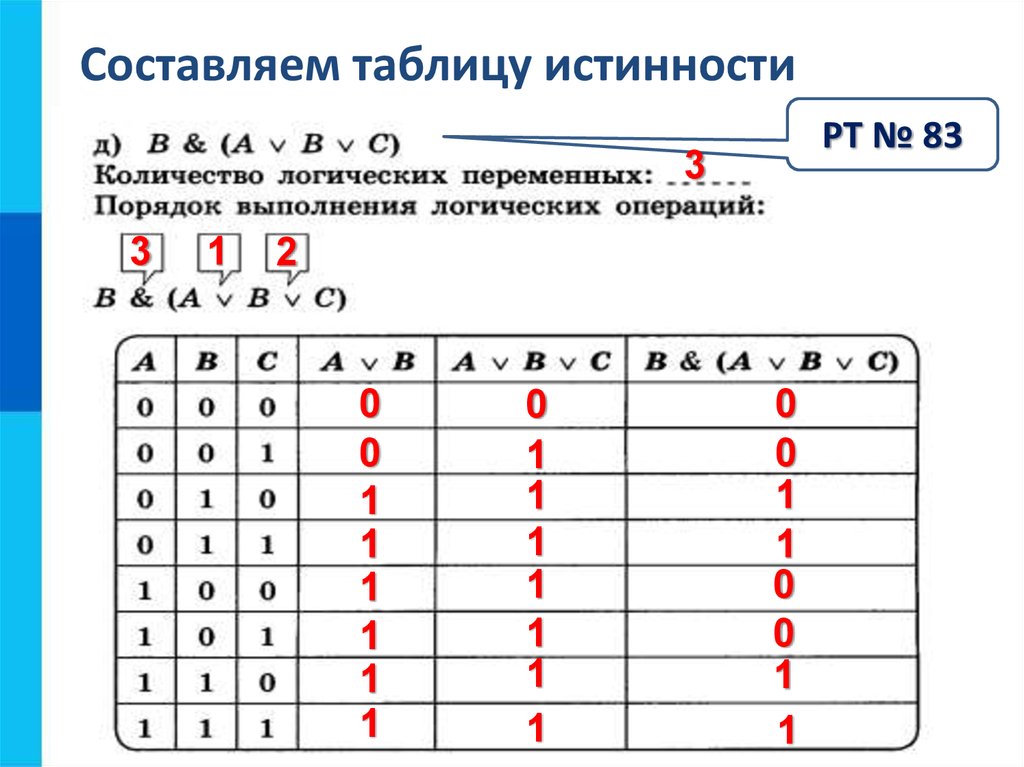
1.1.4 Использование Карт Карно: Карта Карно может быть заполнена данными либо из таблицы истинности, либо из булевого уравнения. В качестве примера в Таблице 6 показана таблица истинности для примера “кассовой комнаты” с 3 входами, вместе с логическими выражениями, полученными из каждой комбинации входов, которая приводит к выходу логической единицы. Таблица 6 Таблица истинности для “кассовой комнаты” A B C X Логическая операция 0 0 0 0 — 0 0 1 0 — 0 1 0 1 B 0 1 1 1 B∧ C 1 0 0 0 — 1 0 1 1 A ∧C 1 1 0 1 B∧ C 1 1 1 1 A ∧ B ∧ C Это приводит к Булеву уравнению для неупрощенной схемы: X=B ∨ BC ∨ AC ∨ AB∨ ABC Эта таблица будет служить для отображения процесса переноса данных из таблицы 6 в ячейки карты Карно. Этот процесс показан шаг за шагом на таблицах 7, 8, 9, 10, 11 и 12. 1.1.5 Реализация решения: 1) Из строки 3 таблицы 6 входы AMC имеют значение 010, что дает логическую 1 на выходе (X) и дает логическое выражение B в столбце Логическая операция. Таблица 7 Первый процесс решения. Метод Карт Карно \ BC A 00 01 11 10 0 1 1 2) В строке 4 таблицы 6 входы ABC имеют значения 011, что создает логическую 1 на выходе (X) и дает логическое выражение BC в столбце Логическая операция.
Следовательно, 1 помещается в ячейку карты, соответствующую A = 0 и BC = 11, как показано в таблице 8. Таблица 8 – Второй процесс решения. Метод Карт Карно \ BC A 00 01 11 10 0 1 1 1 3) В строке 5 таблицы 6 вывод (X) равен 0, поэтому эта строка игнорируется. Однако в строке 6 входы ABC имеют значения 101, что дает логическую 1 на выходе (X) и дает логическое выражение AC в столбце Логическая операция. Следовательно, 1 помещается в ячейку карты, соответствующую A = 1 и ВС = 01, как показано в таблице 9. Таблица 9 Третий процесс решения. Метод Карт Карно \ BC A 00 01 11 10 0 1 1 1 1 4) В строке 7 таблицы 6 входы AВC имеют значения 110, что дает логическую единицу на выходе (X) и дает логическое выражение AВ в столбце Логическая операция. Следовательно, 1 помещается в ячейку карты, соответствующую A = 1 и ВC = 10, как показано в таблице 10. Таблица 10 Четвёртый процесс решения. Метод Карт Карно \ BC A 00 01 11 10 0 1 1 1 1 1 5) Наконец, в строке 8 таблицы 6 входы AВC имеют значения 111, что дает логическую единицу на выходе (X) и дает логическое выражение AВC в столбце Логическая операция.
Следовательно, 1 помещается в ячейку карты, соответствующую A = 1 и ВC = 11, как показано в таблице 11. Таблица 11 Пятый процесс решения. Метод Карт Карно \ BC A 00 01 11 10 0 1 1 1 1 1 1 6) Все строки таблицы истинности, которые создали логическую единицу, теперь введены в карту, а те строки, которые дали 0, могут быть проигнорированы, поэтому оставшиеся три ячейки остаются пустыми. Позже A 00 01 11 10 0 1 1 1 1 1 1 Следующая задача — упростить исходное булево уравнение для этой схемы: X=B ∨ BC ∨ AC ∨ AB∨ ABC Преобразование двух групп в карте Карно в булевы выражения осуществляется путем обнаружения того, какой вход или входы (A, B или C) НЕ изменяются в каждой группе. Шаг 1: Взяв сначала (синюю) группу из 4, обратите внимание, что она охватывает две строки по вертикали и, следовательно, содержит строки A = 0 и A = 1, поэтому A изменяется внутри группы и не может появиться в выражении. Синяя группа также охватывает два столбца и поэтому содержит BC=11 и BC=10.Здесь C = и 1, и 0, но B=1 в обоих столбцах.
Поэтому единственным входным сигналом, который не изменяется в синей группе, является B, следовательно, логическое выражение для синей группы просто B. Шаг 2: Глядя на (зеленую) группу из 2, A не меняется, но BC изменяется с 01 на 11. Объединение результатов упрощения путем “И” любых неизменяемых входных данных в одной группе и “ИЛИ” различных групп дает упрощенное логическое уравнение для всей схемы: X=B ∨ AC Основное преимущество использования карты Карно для упрощения схемы состоит в том, что в методе Карно используется меньше правил, и эти правила можно применять систематически, а не интуитивно, как в случае с булевой алгеброй. 2. МЕТОД КВАЙНА-МАККЛАКСИ Метод Куайна-Маккласки полезен для минимизации логических выражений для более крупных количество переменных по сравнению с минимизацией Карно или Булевой алгеброй. В этой работе я попытался собрать воедино все компьютерные коды, которые доступны в Интернете, отредактировал и модифицировал их, а также переписал некоторые части. Метод Куайна- Маккласки был реализован с использованием компьютерных языков, таких как C и C ++, с некоторыми вариациями.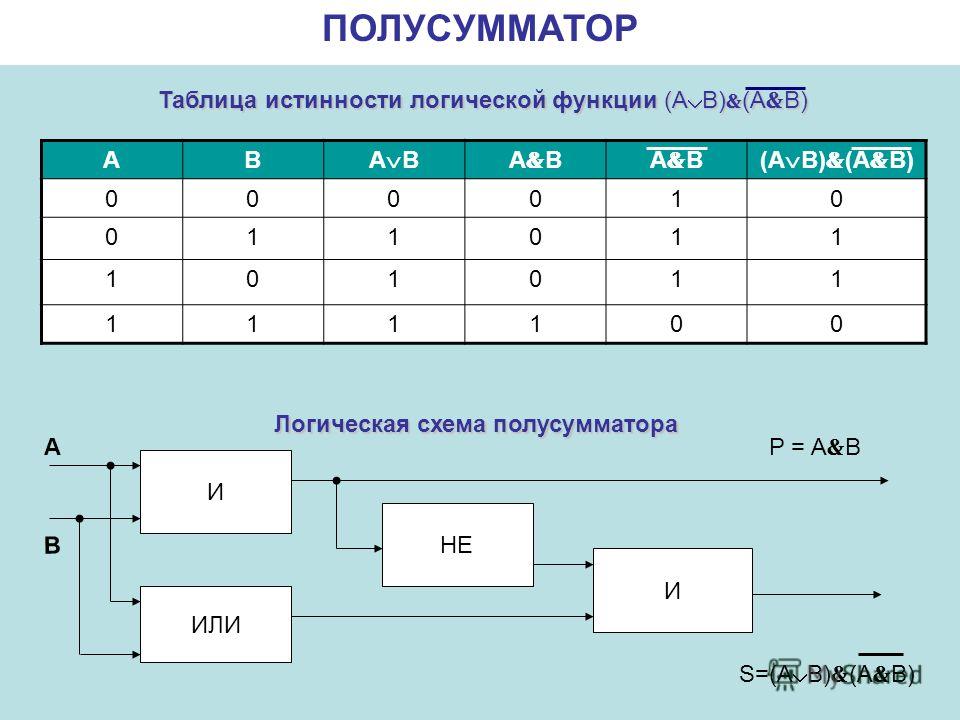
Алгоритм Куайна-Маккласки метод простых импликант — это метод, используемый для минимизации логических функций. Его разработали W.V. Куайн и Эдвард Дж. Маккласки в 1956 году. Функционально оно идентично картированию Карно, но табличное форма делает его более эффективным для использования в компьютерных алгоритмах, а также дает детерминированный способ проверить, что минимальная форма логической функции была достигнута. Иногда его называют методом табуляции. Метод состоит из двух этапов: 1. Нахождение всех простых импликант функции. 2. Использовать эти простые импликанты в диаграмме простых импликантов, чтобы найти необходимое простое число. Импликанты функции, а также другие основные импликанты, которые необходимы для покрытия функция. 2.1 Процедура минимизации Куайна-Маккласки: По сути, это табличный метод минимизации, который подходит для компьютеров. Порядок процедуры, следующий: Шаг 1. Описать отдельные термины данного выражения в их эквивалентных двоичных формах. Шаг 2: Сформировать таблицу, сгруппировав числа с эквивалентным количеством единиц в них, т.
е. сначала числа без 1, затем числа с единицей, а затем числа с двумя 1 и т. д Шаг 3. Сравнить каждое число в верхней группе с каждым минтермом следующей, более низкой группы. Если два числа одинаковые во всех позициях, кроме одного, поставьте галочку знак () справа от обоих чисел, чтобы показать, что они были парными и покрыт. Затем ввести вновь образованное число в следующий столбец (новую таблицу). Новое число — это старые числа, но там, где различаются буквальные значения, отображается «x» и помещается в позицию этого литерала. Шаг 4: Используя (3) выше, нужно сформировать вторую таблицу и повторить процесс еще раз, пока не прекратится возможное сопряжение. При втором повторении сравните числа с числами в следующую группу, имеющую такую же позицию «x». Шаг 5: Термины, которые не были охвачены, являются основными импликантами, объединяются в “ИЛИ”, чтобы сформировать окончательную функцию. Пример: Минимизируйте приведенную ниже функцию методом Куайна- Маккласки: Таблица 14 Задание f(A, B, C, D) A BC D+¿AB C D+¿ ABC D+¿ A B C D+¿ A B C D+¿ AB C D+¿ ABC D+¿ ABCD + ABCD + Двоичны й 0000 0101 0110 1001 1010 1101 1110 1111 0111 минтеро м 0 5 6 9 10 13 14 15 7 Без 1 0 2 2 2 2 3 3 4 3 Группа 1 2 2 2 2 3 3 4 3 Это можно записать в виде суммы минтермов следующим образом: f (A, B, C, D) =∑ m(0 ,5,6,9,10,13,14,15) Шаг 1: Сформировать таблицу функций согласно номеру 1 в каждом по таблице 15.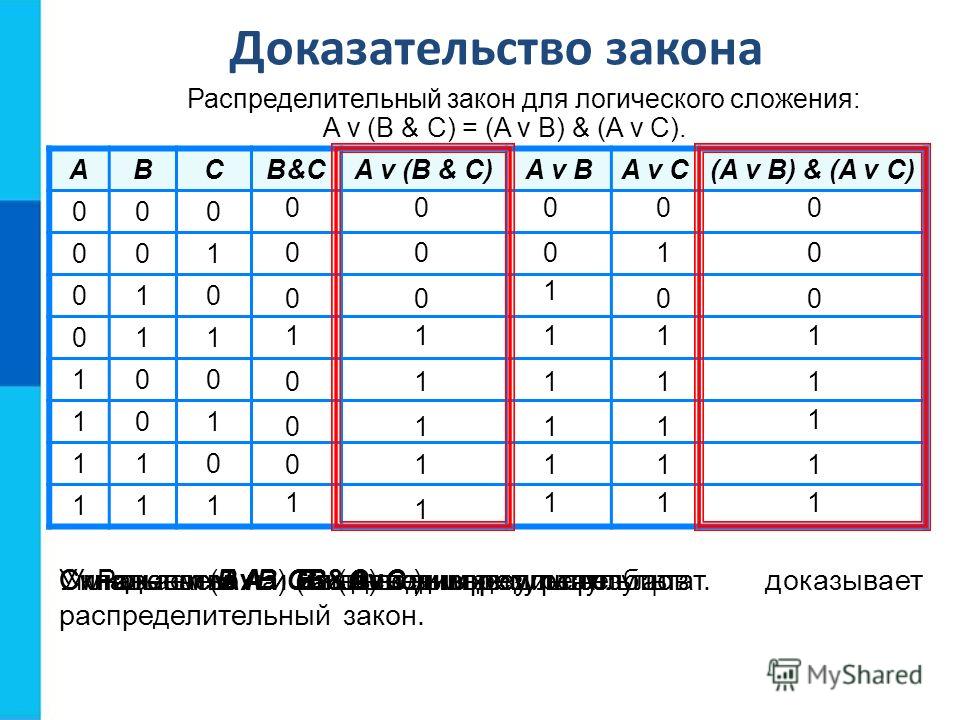
Таблица 15 Таблица функций Шаг 2: Начнем объединять каждый элемент первой группы m0 со следующей, однако, поскольку нет единиц, это и следующая группа чисел с одной единицей, то единицы отсутствуют, поэтому их нельзя разделить на пары. Начнем с соединения элементов m5 ,m7, m13, m14, и m6 с m7, m13, m14 и так далее. Если они образуют пару, запишем их в отдельной таблице минтермов этой пары, то есть m5 ,m7 соединяют 0101 и 0111, следовательно, проделываем так со всеми остальными m. В итоге должно быть так: Таблица 16 Объединение элементов Шаг 3: Теперь повторим ту же процедуру, объединяя каждый элемент группы в пары с элементами следующей группы для элементов, у которых «x» находится в той же позиции. Например, «5,7» соответствует «13,15», чтобы получить x1x1. Эти элементы помещаются в таблицу 15, как показаны, и отмечены указанные выше элементы в таблице 14. Элементы, которые производят один и тот же паттерн ABCD, удаляются. Поскольку 9,13 и 10,14 в таблице 14 не образуют пары, они являются простыми импликантами и с m0 из таблицы 15.
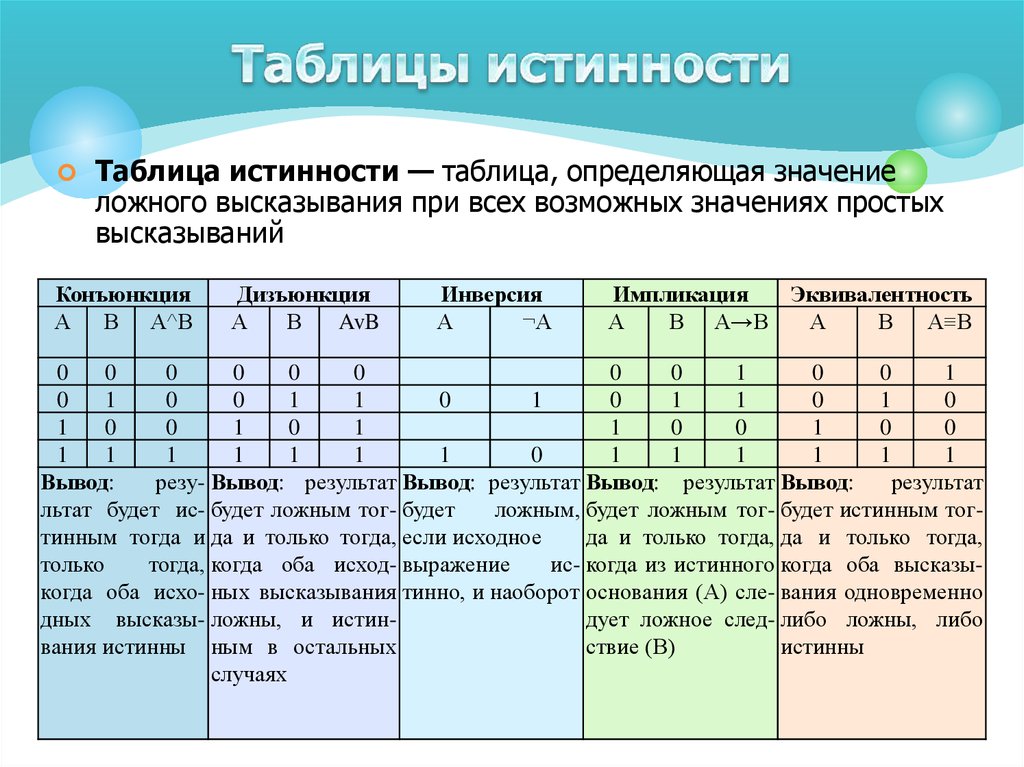Следовательно, можно записать минимизированную СОП как: a + b + c + d + r или f(A, B, C, D) =A BC D+AC D+ AC D+BD+BC. Проверим этот результат для нашего с использованием подхода карты Карно. Импликанты с двумя квадратами: Таблица 17 Импликанты с двумя квадратами Парные м-мы ¿(z→ x¿→ ( y∨ z→ x )=¿(z→ x¿→ ( y∨ z→ x )=¿ =( z∧ x )∨ z∨ y∨ x=x ∨ y ∨ z По минимальной ДНФ построим нашу релейно-контактную функцию: Рисунок 8 Релейно-контактная функция Пример 4: Реализовать функцию ¿ в Tinkercad и Electronics Workbench: РЕШЕНИЕ: Для того, чтобы реализовать нашу функцию, необходимо составить для нее таблицу истинности. Таблица 19 Таблица истинности для функции X Y Z x y x∨ y (x∨ y )∗z ¿ y∗z ¿ 0 0 0 1 1 1 0 1 0 1 0 0 1 1 1 1 1 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 0 0 1 0 0 0 1 0 0 1 0 1 1 0 1 0 1 0 0 1 1 1 1 1 0 0 0 1 0 1 0 1 1 1 1 0 0 1 1 0 0 0 Следующим этапом является создание самой комбинационной схемы, создадим ее: Рисунок 9 Комбинационная схема Теперь можно выполнить наше задание в Tinkercad’e: Пусть x=0, y=0; z=0, на лампочке мы должны получить 1, то есть, она должна загореться: Рисунок 10 Реализация функции в Tinkercad’e Для полного убеждения предположим, что x;y;z имеют такие значения: 0;1;1.
На выходе мы должны получить 0, лампа должна погаснуть. Убеждаемся в этом на рисунке 11. Рисунок 11 Реализация функции в Tinkercad’e Как видно, схема работает, задание можно считать выполненным. Для более доступного убеждения, переключатели светодиодов вы можете проверить самостоятельно. Для проверки есть таблица 18 (проверять нужно последний столбец). Функция, выполненная при помощи генератора слов, абсолютно так же совпадает и в Electronics Workbench: Рисунок 12 реализация функции в EWB при помощи генератора слов
Основы логики презентация, доклад
Основы логики
Основные понятия и операции формальной логики
Логические выражения и их преобразование
Построение таблиц истинности логических выражений
Основные логические устройства компьютера
Понятие логики
Слово логика обозначает совокупность правил, которым подчиняется процесс мышления.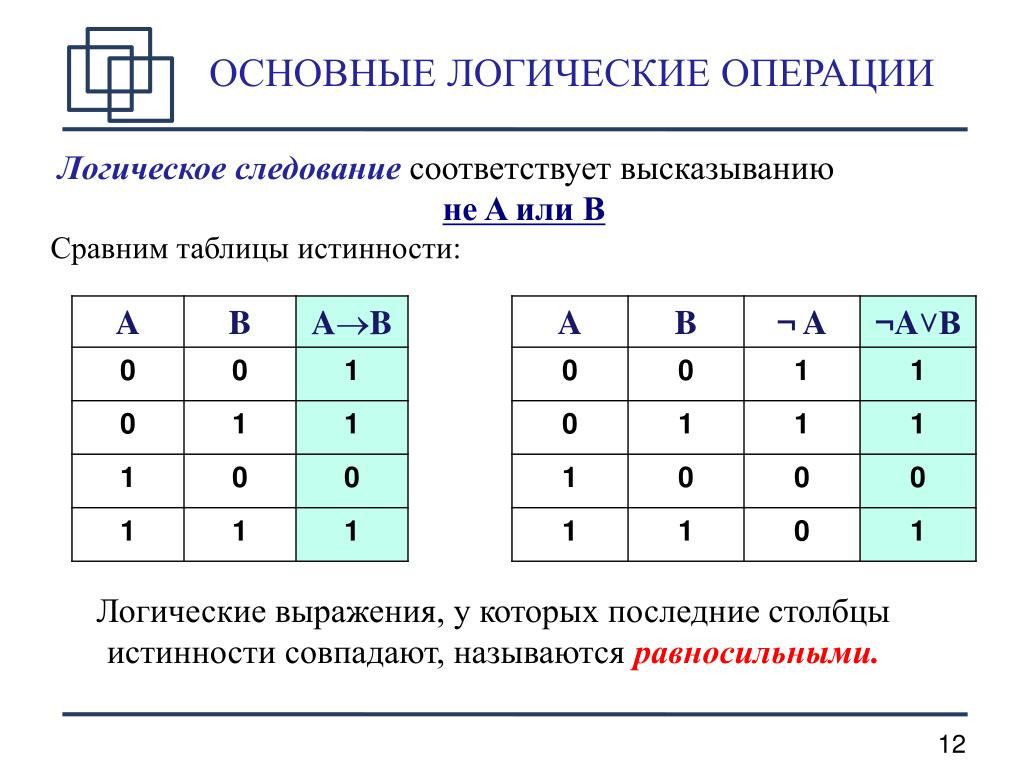
Логика очень древняя наука. Еще в античные времена была известна формальная логика, позволяющая делать заключение о правильности какого-либо суждения не по его фактическому содержанию, а только по форме его построения.
Законы логики
1. Закон исключения третьего.
Был известен уже в древности. Его содержательная трактовка такова: «Во время своих странствований Платон был в Египте ИЛИ не был Платон в Египте». В такой трактовке это и любое другое выражение будут правильны (тогда говорили: истинно). Ничего другого быть не может: Платон либо был, либо не был в Египте – третьего не дано.
Если сказать: «Во время своих странствий Платон был в Египте И не был Платон в Египте, то очевидно, что любое высказывание, имеющее такую форму, всегда будет ложно.
3. Закон отрицания: «Если НЕ верно, что Платон Не БЫЛ в Египте, то значит, Платон БЫЛ в Египте».
Этапы развития логики (1)
Первый этап развития логики связан с работами древних ученых и философов, живших до н.
Аристотель впервые дал систематическое изложение логики, он пытался найти ответ на вопрос «как мы рассуждаем», изучал правила мышления, анализировал его. Так возникла формальная логика.
До 19 века ее законы сохраняли форму высказываний на разговорном языке.
Этапы развития логики (2)
Второй этап – появление
математической или символьной
логики. Основы ее были заложены
французским ученым Рене
Декартом и немецким ученым
Вильгельмом Лейбницем.
Но окончательно эту идею в 1847 г. развил англичанин Джорж Буль, преподаватель провинциального университета в маленьком городе Корке на юге Англии, который и считается основоположником математической логики, как самостоятельной дисциплины.
(Булева алгебра). Однако прошло еще почти 100 лет, прежде чем в 1938 году американский математик и инженер Клод Шеннон обнаружил, что созданная Булем алгебра приложима не только к логике, но и к теории электрических цепей, к любым переменным, которые могут принимать только два значения, самое главное, она лежит в основе всех операций ЭВМ.
Алгебра логики
Алгебра логики очень проста, так как каждая переменная может принимать только два значения: истинно или ложно. Трудность изучения алгебры логики возникает из-за того, что для обозначения переменных применяют символы 1 и 0, которые по написанию совпадают с обычными арифметическими 1 и 0.
Но совпадение только внешнее, так как смысл они имеют совсем иной. Логическая 1 не есть одна штука чего-то реального, это знак того, что свершилось какое-то событие, например, Платон был в Египте.. логическая 1 означает, что какое-то событие истинно, в противоположность этому логический 0 означает, что высказывание не соответствует истине, т.
Возможно, что лучше было бы иметь специальные символы-иероглифы для логических истинно и ложно, но сейчас говорить об этом не приходится, т.к. алгебра логики уже сложилась, ее надо принимать такой , какова она есть.
Высказывания
В основе работы логических схем и устройств ПК лежит специальный математический аппарат – математическая логика. Она изучает вопросы применения математических методов для решения логических задач и построения логических схем.
Высказывание – это повествовательное предложение, о котором можно сказать, что оно истинно или ложно.
Например,
Земля – планета Солнечной системы истинно 2 + 8
Примеры
А вот примеры, не являющиеся высказываниями:
Уходя, гасите свет.
Да здравствует мыло душистое и полотенце пушистое.
Высказывания, приведенные выше, являются простыми. Сложное высказывание получается путем объединения простых высказываний связками – союзами И, ИЛИ и частицей НЕ. Значение истинности сложных высказываний зависит от истинности входящих в них простых высказываний и объединяющих их связок.
Например, даны четыре простых высказывания:
На улице идет дождь.
На улице светит солнце.
На улице пасмурная погода.
На улице идет снег.
Задание
Составьте два сложных высказывания, одно из которых в любой ситуации будет ложно, а другое всегда истинно, обязательно используя все предложенные простые высказывания.
Логические операции
Алгебра логики очень проста еще и потому, что имеет только три логические функции: операции ИЛИ, И, НЕ.
Любое устройство, выполняющее действия над двоичными числами, можно рассматривать как функциональный преобразователь.
Причем входные числа – значения входных логических переменных, а выходное число – значение логической функции, которое получено в результате выполнения определенных операций. Таким образом, этот преобразователь реализует некоторую логическую функцию.
Таблица истинности
Значения логической функции при различных сочетаниях входных переменных обычно задается специальной таблицей, которая называется таблицей истинности.
Количество наборов входных переменных (Q) можно определить по формуле: Q = 2n, где n – количество входных переменных. Таблица может иметь вид:
Логические операции
В алгебре высказываний, как и в обычной алгебре, вводится ряд операций. Связки И, ИЛИ и НЕ заменяются логическими операциями: конъюнкцией, дизъюнкцией и инверсией.
Это основные логические операции, при помощи которых можно записать любую логическую функцию.
Логическая операция И (КОНЪЮНКЦИЯ )
Обозначается знаком ∧ или &,
Иначе называется ЛОГИЧЕСКОЕ УМНОЖЕНИЕ.
Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания истинны.
Пример. A∧B∧C = 1, если А=1, В=1, С=1.
Таблица истинности конъюнкции имеет вид:
A B A ∧ B
————————
0 0 0
1 0 0
1 1 1
ИЛИ
Логическая операция ИЛИ (ДИЗЪЮНКЦИЯ)
Обозначается знаком ∨,
Иначе называется ЛОГИЧЕСКОЕ СЛОЖЕНИЕ.
Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны..
Пример, A∨B∨C = 0, если А=0, В=0, С=0.
Таблица истинности дизъюнкции имеет вид:
А В А∨В
———————————
0 0 0
0 1 1
1 0 1
1 1 1
НЕ
Логическая операция НЕ (ИНВЕРСИЯ)
Обозначается черточкой над именем переменной,
Иначе называется ОТРИЦАНИЕ.
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
Таблица истинности имеет вид:
А Ā
—————
1 0
0 1
В алгебре высказываний любую логическую функцию можно выразить через основные логические операции. По формуле логической функции легко рассчитать таблицу истинности, необходимо только учитывать порядок выполнения логических операций (приоритет) и скобки.
Логические выражения и их преобразование
Построение таблиц истинности логических выражений
В алгебре логики, как и в элементарной, справедливы законы – переместительный, сочетательный и распределительный.
Операции выполняются слева направо с учетом скобок. Приоритет логических операций:
ИНВЕРСИЯ,
КОНЪЮНКЦИЯ,
ДИЗЪЮНКЦИЯ.
Таким образом, сохраняется тот же порядок как в обычной алгебре: сначала все умножения, а потом сложения.
Основные логические устройства компьютера
При проектировании и разработке ЭВМ выбирается набор элементов, из которых составляются схемы функциональных устройств. Элементы интегральных схем, реализующие логические операции над двоичными переменными называют логическими элементами. Это триггеры, регистры, сумматоры
Триггер
Основной элемент ЭВМ – триггер – устройство, имеющее два устойчивых состояния, 0 и 1. Триггер используется для хранения одного бита информации.
Из логических элементов и триггеров создаются схемы узлов ЭВМ, функционально предназначенные для выполнения операций запоминания, преобразования, пересылки машинных слов или их частей. К ним относятся регистр, сумматор, счетчик, дешифратор, мультиплексор, таймер и т.д.
Регистр
Регистр – узел ЭВМ, предназначенный для хранения одного машинного слова.
Он представляет совокупность триггеров, число которых соответствует числу разрядов в слове и схем, обеспечивающих выполнение ряда операций:
сброс (установка в 0),
передача и прием слова,
сдвиг слова и т.д.
в соответствии с типом хранящегося машинного слова регистрам присваиваются наименования, например, регистр команд, индексный регистр, регистр адреса и т.д.
Сумматор
Сумматор, узел АЛУ, посредством которого осуществляется суммирование чисел.
На принципиальных электрических схемах логические элементы изображаются прямоугольниками с обозначением входов и выходов.
Математическая логика | Skerritt.blog
Логика использовалась тысячи лет, от философии до математики, а теперь и до искусственного интеллекта. Логика связана с истинностью и ложностью утверждений. Логика, которую мы будем изучать, будет отвечать на вопрос: «когда утверждение следует из набора утверждений?»
Примечание для читателя
Ранее я писал здесь о логике, и поэтому эта статья будет относительно короткой, когда дело доходит до объяснения все про логику.
Если вы хотите понять логику, пожалуйста, прочитайте статью, которую я написал о логике. Это просто расширение того, что мы узнали.
Логика высказываний
Предложения могут быть только истинными или ложными.
Интерпретация
Интерпретация присваивает пропозициональному утверждению истинностное значение Истина или Ложь. True или False могут быть представлены как 0 и 1 соответственно.
Пропозициональные символы
Существует около 500 000 способов представления логических символов, вот наиболее распространенные способы 9или И или , Что он делает
Принимает >1 входных данных и, если оба входных значения истинны, выводит истину.
Дизъюнкция, «ИЛИ»
Символ в логике
В, или, «ИЛИ» Что он делает
Принимает > 1 входных данных, если какой-либо из входных данных верен, то и выходные данные верны.
Эквивалентность
Символ в логике <=> или ≡
Символ в электронике Нет, это концепция, а не ворота.
Что он делает A и B должны принимать одно и то же значение истинности
Таблица истинности
A B A <=> B 1 1 = 1 0 1 = 0 1 0 = 0 0 0 = 1
Значение5
Символ в логике => или «если a, то b»
Символ в электронике Нет
Что он делает Если A истинно, то верно и B https://www.dyclassroom.com/boolean-алгебра/пропозициональная-логика-истина-таблица Извините за смену картинок. Ранее в этой таблице истинности была ошибка.
Истинность в интерпретации
Учитывая интерпретацию I, мы можем вычислить истинностное значение любой формулы P в соответствии с I. То есть, учитывая версию формулы, мы можем вычислить истинностное значение.
если I(P) = 1, то мы говорим, что P истинно при интерпретации I. если I(P) = 0, то мы говорим, что P ложно при интерпретации I.
Логические задачи
Этот раздел может помочь читателю в понимании логических головоломок.
На острове есть два типа жителей: рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Вы отправляетесь на остров и встречаете А и Б. А говорит, что «Б — рыцарь» Б говорит, что «Мы двое противоположных типов»
Что такое А и Б?
Итак, у нас есть 2 варианта, р: «А — рыцарь»; и q: «B — рыцарь»
У нас есть 2 варианта, потому что один из них должен быть рыцарем. Либо и A, и B — лжецы, что делает B рыцарем, поскольку он сказал правду, значит, он солгал, либо A — рыцарь и говорит правду, что B — рыцарь.
Варианты для лица A p истинно, то есть утверждение «A — рыцарь» истинно. P => Q p ложно, то есть утверждение «A — рыцарь» ложно. ¬P => ¬Q
Варианты для человека B q истинно, тогда q => ¬p q ложно, тогда ¬q => ¬p
Теперь нам просто нужно построить таблицу истинности для этих значений
p q ¬p ¬q p => q ¬p => ¬q q => ¬p ¬q => ¬p 0 0 1 1 1 1 1 1 = 1
Тогда мы остановимся здесь, потому что мы нашли удовлетворительную интерпретацию, согласно которой они оба являются лжецами.
Semantic Conseqeuence
Примечание. Слайды лекций для этого не помогли, и для этого нет звука. Пожалуйста, напишите мне, что это такое.
Цифровые логические схемы
Современные компьютеры используют для работы логические вентили. Вы должны иметь представление о логических элементах из приведенного выше.
Общие правила организации цепей
Никогда не объединяйте два входных провода
Если есть 2 отдельных входа, A и B, вы не можете объединить их в один провод.
Один входной провод можно разделить на части и использовать как вход для двух отдельных ворот
Если у вас есть один вход A, его можно разделить на 2 отдельных провода.
Выходной провод можно использовать как вход
Выход провода можно использовать как вход.
Ни один выход гейта не может в конечном итоге вернуться к этому гейту
Ни один гейт не может зациклиться сам на себе.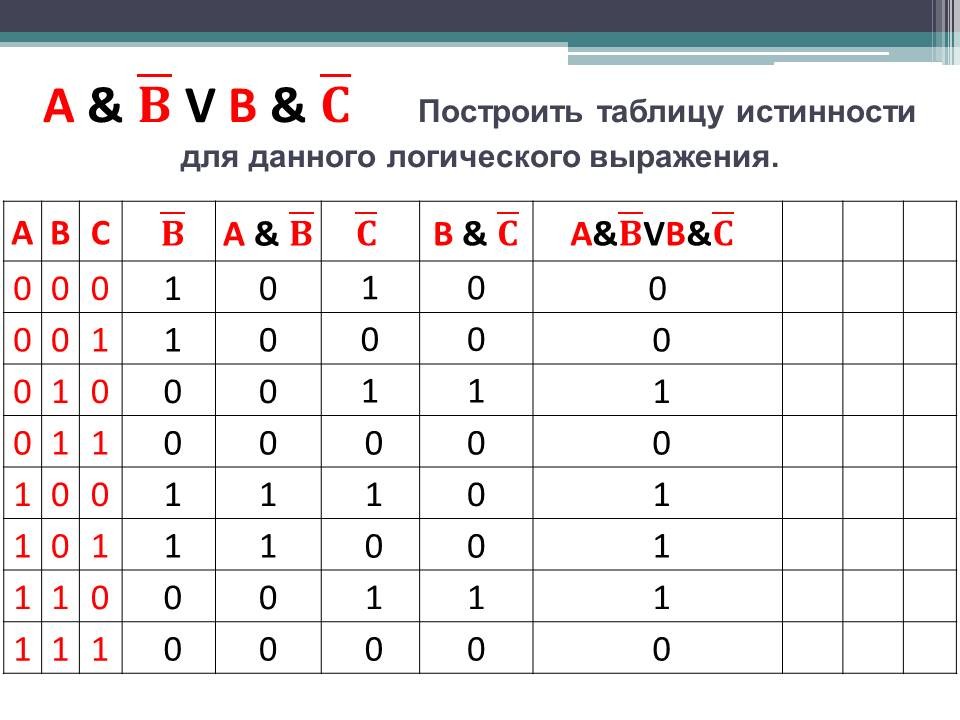
Построение логических схем из таблиц
Имея таблицу, подобную приведенной ниже, как бы мы построили для нее логическую схему? Сначала разберемся, где оно равно 1 (истинно), а потом уже оттуда формализуем в математической логике, из математической логики сможем вывести для него схему. Иногда проще сразу догадаться, какие логические вентили используются.
Эквивалентность схемы
Две схемы эквивалентны, если они производят одинаковый результат при одинаковых входных данных
Эквивалентность формул
2 формулы эквивалентны, если они содержат одно и то же значение истинности при всех возможных интерпретациях.
О логической эквивалентности
Символ «≡» используется для обозначения отношения эквивалентности.
Факты
≡ рефлексивно ≡ транзитивно ≡ симметрично
Упрощение формул предложений
Есть несколько правил, которые мы можем использовать для упрощения пропозициональных формул.
Коммуникативное право
AB = BA, A + B = B + A
Примеры: 6 * 2 = 12 и 2 * 6 = 12 3 + 4 = 7 и 4 + 3 = 7
Ассоциативный закон
a(bc) = ab(c) = abc
Примеры: (2 + 4) + 5 = 6 + 5 = 11 2 + (4 + 5) = 2 + 9 = 11
Распределительный закон
a(b+c) = ab + ac
Пример: 3 × (2 + 4) = 3 * 6 = 18 3 × 2 + 3 × 4 = 6 + 12 = 18
Законы Деморгана
(A ∪ B)’ = (A)’ ∩ (B)’ Первый закон гласит, что дополнением объединения двух множеств является пересечение дополнений.
(A ∩ B)’ = (A)’ ∪ (B)’ Второй закон гласит, что дополнение пересечения двух множеств есть объединение дополнений.
Чтобы получить хороший пост в блоге о понимании этих законов, нажмите (здесь)[https://brilliant.org/wiki/de-morgans-laws/]
Прочие правила
Не Не А = А А или А и В = А А или не А и В = А и В (А или В) (А или С) = А или В и С
Что делать дальше С этого момента повернуть преобразовать схему в логическое выражение и упростить ее, используя приведенные выше правила.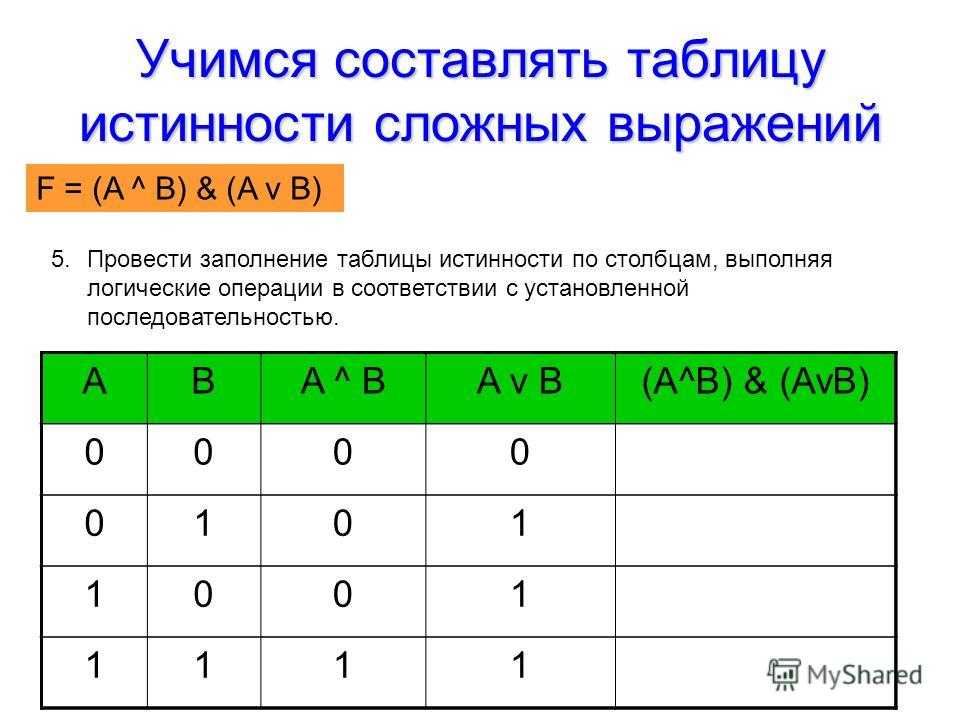
Если это все еще сбивает с толку, возможно, это видео поможет: https://www.youtube.com/watch?v=59BbncMjL8I
Логические функции
Arity Арность логической функции — это количество аргументов функции. занимает
9, v или ¬.
Расширенные логические вентили
В этом разделе мы еще немного познакомимся с логическими вентилями, рассмотрев семейство неисключающих вентилей.
XOR
Символ в логике
Нет Что он делает
Логический элемент XOR принимает >1 входных данных и выполняет исключающую дизъюнктию. Выход вентиля XOR истинен только в том случае, если один из его входов отличается от другого входа.
И-НЕ
Символ в логике
Нет Что он делает
Элемент И-НЕ принимает >1 входов, а выход противоположен элементу И. Вывод истинен, когда один или несколько, но не все входные данные ложны.
Универсальность XOR и NAND
Все булевы функции могут быть созданы с использованием вентилей XOR или NAND.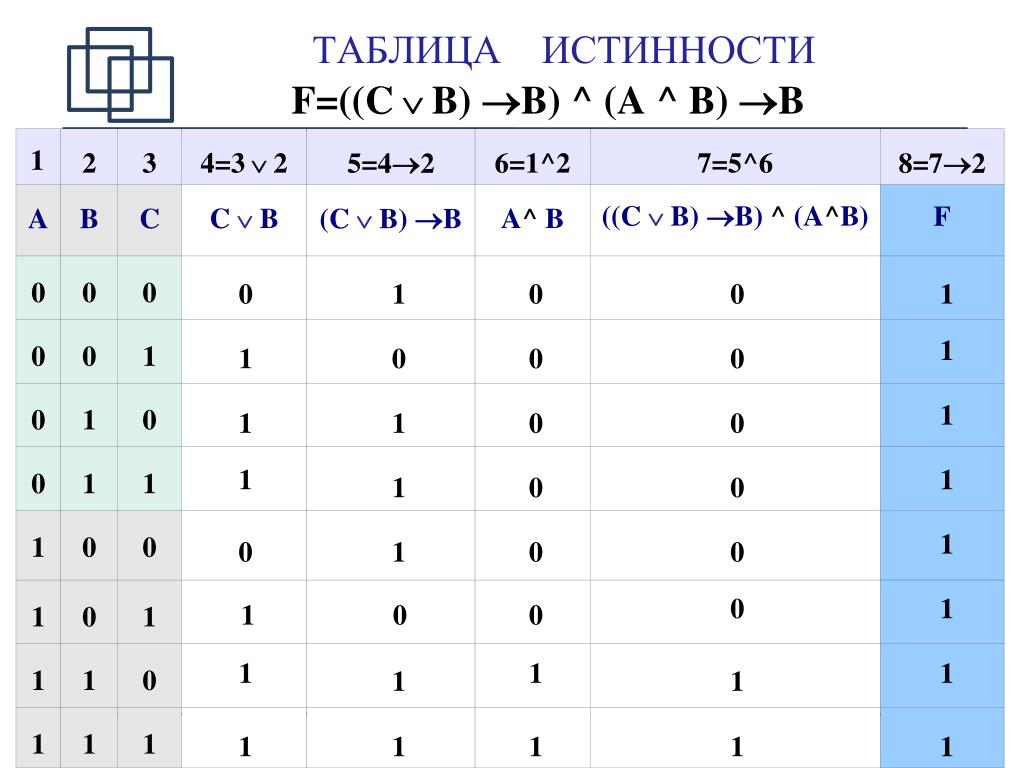
Двоичная система счисления
Двоичная система счисления состоит из 0 и 1. В качестве альтернативы вы можете запомнить степени 2. 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024… А затем, чтобы преобразовать число в двоичное, скажем, 6, вы строите это из разные силы. Итак, 6 — это 011, а затем переверните это, 110 9.0003
Двоичное сложение
Кое-что, что вам нужно знать о двоичном коде 0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 в двоичном виде так же, как вы можете добавить обычные числа. Попробуйте выполнить это упражнение
011
полусумматор
Полусумматор — это тип двоичного сумматора в электронике, который складывает два одиночных двоичных разряда и обеспечивает выход плюс значение переноса. Примечание. Полусумматор Бориса слишком сложен, вы можете добиться того же, заменив 3 его логических вентиля одним вентилем XOR.
Таблица истинности Полный сумматор
Полный сумматор позволяет как вносить, так и выносить.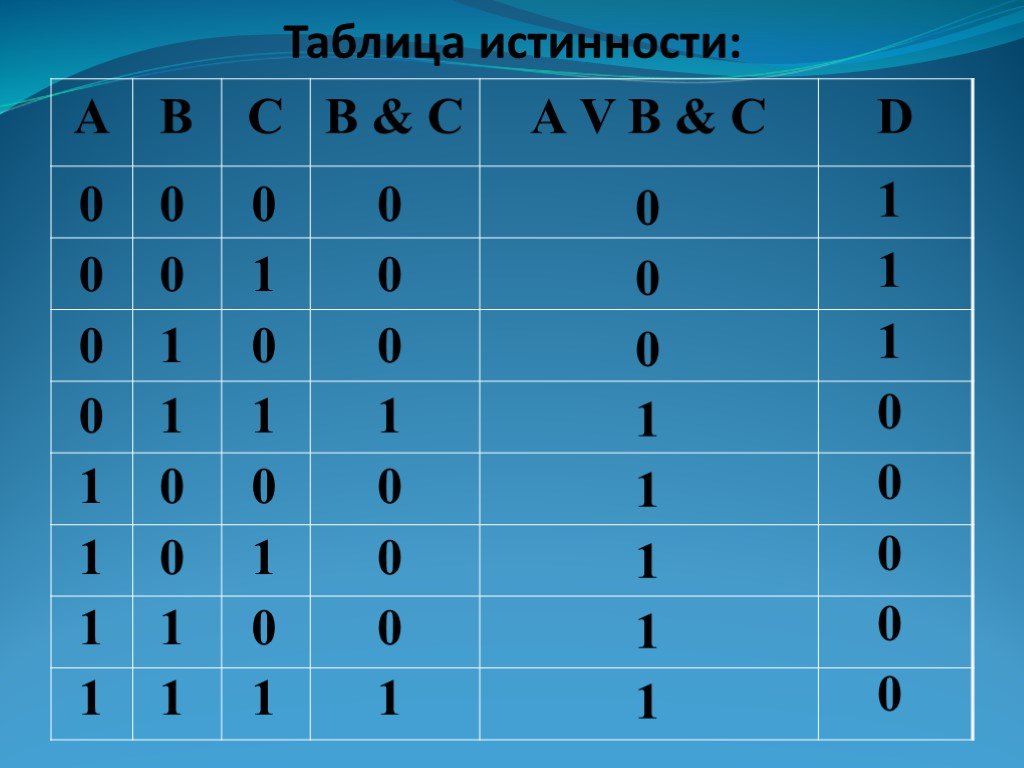
Посмотрите это видео для лучшего понимания. нужно знать, что происходит внутри него, только входы и выходы. 4-битный сумматор
Используя нотацию черного ящика, мы можем создать 4-битный сумматор
http://www.electronics-tutorials.ws/combination/comb_7.html
Компьютерное представление отрицательных целых чисел
Для представления целых чисел используется фиксированное количество битов: 8, 16, 32 или 64 бита. Беззнаковое целое может занимать все доступное пространство.
Вы можете «подписать» двоичное число, чтобы указать, является ли оно отрицательным или нет. Например, число 10 может быть представлено в 8-битном виде как 00001010, а -10 может быть представлено в 8-битном виде как 10001010
. Но иногда это вызывает проблемы, например, 10000000 представляет -0. Чтооо?? Отрицательный 0? Да! Это верно, и это именно та проблема, которую это вызывает.
Здесь в игру вступает дополнение 2.
Дополнение до двух
Преобразование десятичной дроби в дополнение до двух
Преобразовать число в двоичное, игнорируя пока знак.
.
Итак, 5 — это 0101, а -5 — это 0101.Если число положительное, то все готово, дальше идти не нужно. В противном случае…
Если число отрицательное, то:
Итак, 5 — это 0101, а -5 — это 0101.- Найдите дополнение (например, преобразуйте все 0 в 1 и все 1 в 0)
- Добавьте 1 к дополнению
- 1101 1100 с переносом 1, который идет до упора влево, его можно игнорировать.
Первоначально опубликовано на brandonskerritt.github.io 25 ноября 2017 г. спросил
Изменено 12 лет, 2 месяца назад
Просмотрено 10 тысяч раз
Я пытаюсь понять, как это сделать.
Насколько я понимаю, набор логических вентилей называется «функционально завершенным», если некоторая комбинация вентилей может использоваться для выполнения каждой из основных логических операций И, ИЛИ и НЕ.
Утверждается, что вентиль И-НЕ функционально завершен.
Чего я не понимаю, так это того, как построить ворота ИЛИ как ворота И. построить вентиль И из вентиля И-НЕ и т. д.. должна ли формула, которую я придумал, иметь такой же выход?
Х' = Х НЕ-И 1 Х + Y = ? Х * Y = ?
с использованием таблицы истинности, как X’ = X NAND 1?
Я не уверен, что означает X NAND 1. Я так понимаю, что 1 фиксируется как y?
Я запутался, когда увидел вентиль между двумя входами, такими как x NAND y
Как составить таблицу истинности для x+y = NAND?
или по другому сделать?
- логическая логика
- логическое выражение
4
Просто перейдите по определению:
X НЕ-И Y = ~ (X И Y) = ~X ИЛИ ~Y
Подставьте Y = 1 и вы получите
X НЕ-И 1 = ~X ИЛИ ~1 = ~X ИЛИ 0 = ~X = X’
Редактировать:
Эта статья в Википедии очень хороша и информативна, чтобы вы поняли, как создавать другие вентили, используя вентиль NAND.
Надеюсь, это поможет.
http://en.wikipedia.org/wiki/NAND_logic
1
Да, X NAND 1 похоже на X NAND Y , где Y зафиксировано как 1. Вещь, с которой вы сравниваете X, не обязательно должна называться Y; это может быть любая переменная, любая константа или результат другого сравнения. Все, что имеет значение, это то, является ли значение 0 или 1, в конце концов.
Пример:
Х | Y | 1 | Х ИЛИ У ---+---+---+-------- 0 | 0 | 1 | 0 0 | 1 | 1 | 1 1 | 0 | 1 | 1 1 | 1 | 1 | 1
Теперь вы можете сделать X И Y , X AND 1 или X AND (X OR Y) просто путем сравнения чисел в первом столбце с числами во втором, третьем или четвертом столбцах соответственно.
Что касается конкретно NAND , просто помните, что это означает противоположность AND . На самом деле это означает «не и».
Таким образом, если вы И объединили две вещи вместе и получили 0, то И-НЕ объединив те же две вещи вместе, вы получите 1.
Тем не менее, ваш последний вопрос не имеет особого смысла. Нет такой вещи, как X+Y = НЕ-И . X , Y и X+Y являются значениями; NAND — ворота. Нельзя сравнивать числа с воротами. Ваш вопрос заключается в том, чтобы использовать вентили NAND для сравнения вещей снова и снова, пока вы не получите столбец нулей и единиц, который выглядит так же, как X + Y .
РЕДАКТИРОВАТЬ:
Хорошо, давайте посмотрим на ваш вопрос: «используя таблицу истинности, как X’ = X NAND 1?»
Х | Х' | 1 | Х И 1 | X NAND 1 — это то же самое, что противоположность X AND 1. ---+----+---+---------------+----------------------- -------------------------- 0 | 1 | 1 | 0 И 1 = 0 | 1 (напротив 0) 0 | 1 | 1 | 0 И 1 = 0 | 1 (напротив 0) 1 | 0 | 1 | 1 И 1 = 1 | 0 (напротив 1) 1 | 0 | 1 | 1 И 1 = 1 | 0 (напротив 1)
И глядя на каждый столбец, мы видим, что X' имеет те же значения, что и X NAND 1
22
NAND в основном является обратным AND:
Таблица истинности
A B A NAND B A AND B A OR B A NOR B 0 0 1 0 о 1 0 1 1 0 1 0 1 0 1 0 1 0 1 1 0 1 1 0
Составляя правильные комбинации с использованием этих и остальных логических операторов, вы должны быть в состоянии построить любой из них в терминах других
0
Быстрые таблицы истинности:
НЕ-И 1 0 0 1 1 1 0 1 ИЛИ 1 0 0 1 0 1 1 1 НЕТ 1 0 0 1
Функциональная завершенность означает, что, имея стопку полных ворот, вы можете построить ворота любого другого типа.
