«архитектура электронно-вычислительных машин и вычислительные системы»

Практическая работа № 1 4

Тема: Разработка структурной схемы ПК 4

Практическая работа № 2 6

Тема: Перевод чисел из одной системы счисления в другую 6

Практическая работа № 3 13

Тема: Представление информации в ЭВМ 13

Цель работы: научиться переводить числа в те системы счисления, которые использует ЭВМ, подсчитывать объем занимаемой данными информации и уметь переводить значения количества информации из одних единиц измерения в другие. 13

Теоретический материал: 13

Задания: 16

VI. 17

VII. Перевести данные из Кбайт в бит и из бит в Кбайт 18

Самостоятельно: 18

Контрольные вопросы: 18

Практическая работа № 4 19

Выполнение операций над числами в естественной и нормальной 19

формах 19

Контрольные вопросы: 31

Практическая работа № 5 32

Тема: Работа логических узлов ЭВМ 32

Практическая работа № 6 40

Тема: Работа и особенности логических элементов 40

Практическая работа № 7 45

Тема: Построение последовательности машинных операций для 45

реализации простых вычислений 45

Практическая работа № 8 48

Тема: Построение общей структуры ПК с подсоединенными 48

периферийными устройствами 48

1. Принципы фон Неймана 48

2.Роль центрального процессора 48

Практическая работа № 9 50

Тема: Параллельные и последовательные порты 50

Практическая работа № 10 52

Тема: Архитектура системной платы 52

Практическая работа № 11 56

Тема: Внутренние интерфейсы системной платы 56

Практическая работа № 12 61

Тема: Системные ресурсы 61

Практическая работа № 13 65

Тема: Интерфейсы периферийных устройств 65

Практическая работа № 14 75

Тема: Интерфейсы периферийных устройств IDSE и SCSI 75

Практическая работа № 15 78

Тема: Устройство накопителя на ГМД 78

Практическая работа № 16 81

Тема: Устройство накопителя на ЖМД 81

Практическая работа № 17 86

Тема: Устройство накопителей информации на CD, DVD, флэш-памяти 86

Практическая работа № 18 91

Тема: Устройства ввода информации 91

Практическая работа №19 96

Тема: Устройства вывода информации 96

Практическая работа № 20 101

Тема: Архитектура вычислительной системы 101

Практическая работа № 21 105

Тема: Выбор вычислительной системы 105

Устройство 107

Изображение устройства 107

Модель 107

Цена(в руб) 107

Процессор 107

Материнская плата 107

ОП 107

Жёсткий диск 107

Видеокарта 107

Кулер 107

Звуковая карта 107

Практическая работа № 22-23 108

Тема: Типовая структура ВС 108

Список рекомендованной литературы 112

Каталог: sveden -> files
files -> 1.

Цели дисциплины
files -> Направления научно-исследовательской деятельности ноу впо «мгта» и Липецкого филиала ноу впо «мгта» и база для ее осуществления
files -> 1. общая характеристика направления подготовки дипломированного специалиста
files -> Педагогика и психология высшей школы для аспирантов бгсха им. В. Р. Филиппова
files -> Направления научно-исследовательской деятельности ноу впо «мгта» и Липецкого филиала ноу впо «мгта» и база для ее осуществления
files -> «История»
files -> «Философия»

десятичная, двоичная, таблица перевода чисел

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Арифметика Позиционные системы счисления

Система счисления – это способ записи чисел с помощью определенных знаков.

Давайте рассмотрим самые распространенные позиционные системы – в зависимости от местоположения (разряда) в записи числа один и тот же знак имеет различные значения.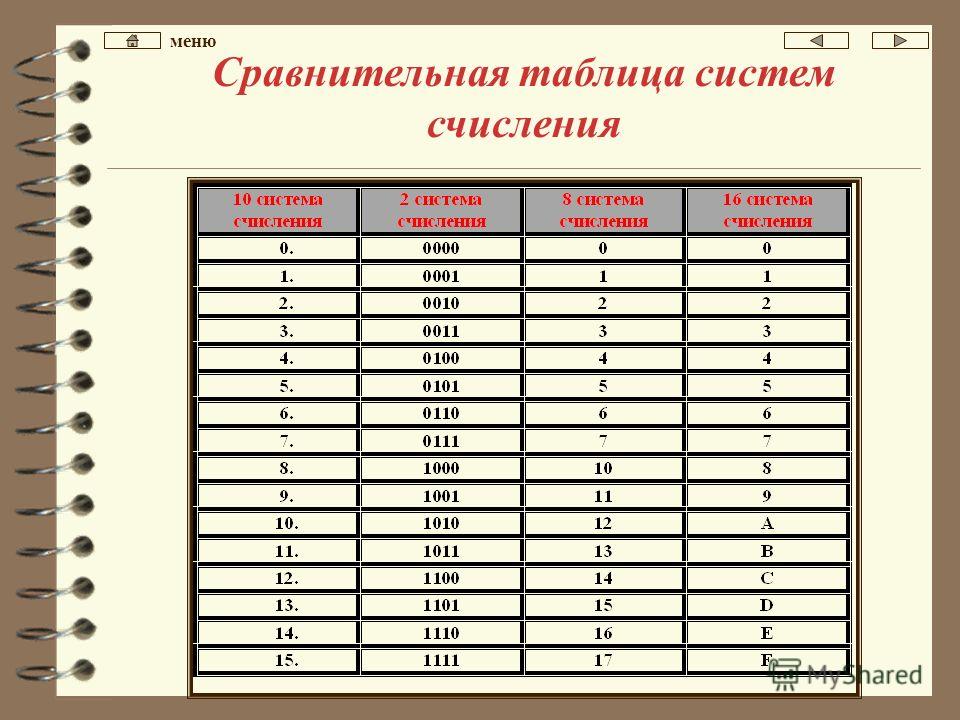

Целое число “x” в позиционной системе счисления можно выразить следующим образом:

• b – основание системы
• a_k – цифры числа (0 ≤ a_k ≤ b-1)
• k – количество разрядов

Развернутая форма записи целого числа:

• Двоичная система счисления: основание – 2
• Восьмеричная система счисления: основание – 8
• Десятичная система счисления: основание -10
• Шестнадцатеричная система счисления: основание – 16
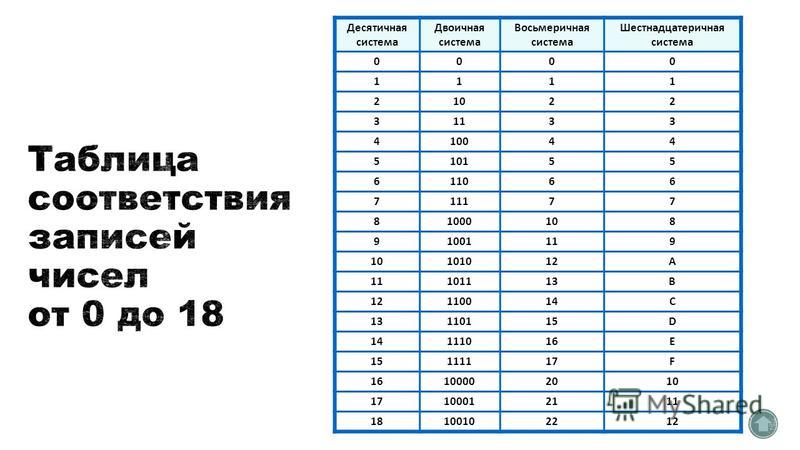
• Таблица соответствия чисел систем счисления

Двоичная система счисления: основание – 2

Используется в дискретной математике, информатике и программировании. Содержит только две цифры – 0 и 1. Число, записанное в данной системе, обозначается буквой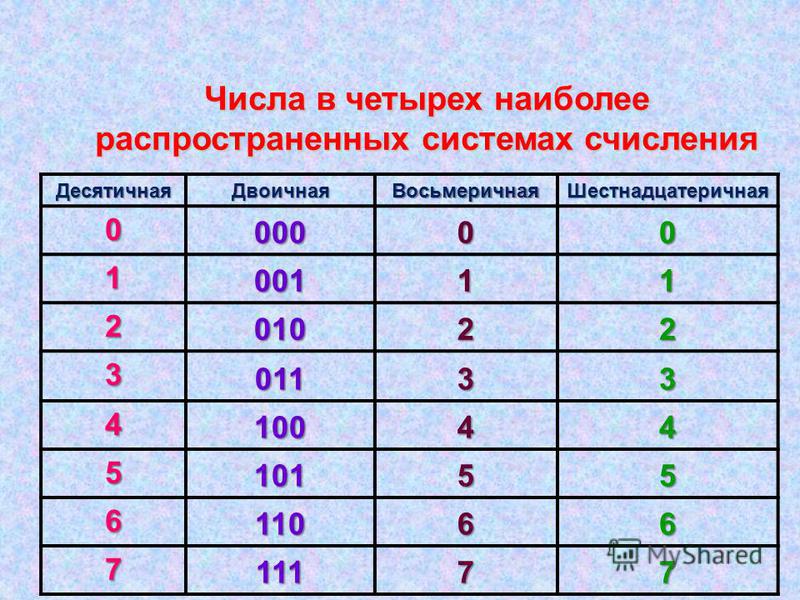

B на конце (префикс).

Примеры:

• 10101₂ = 10101B = 1×2⁴+0×2³+1×2²+0×2¹+1×2⁰ = 16+4+1= 21
• 10111₂ = 10111B = 1×2⁴+0×2³+1×2²+1×2¹+1×2⁰ = 16+4+2+1= 23
• 100011₂ = 100011B = 1×2⁵+0×2⁴+0×2³+0×2²+1×2¹+1×2⁰ =32+2+1= 35

Восьмеричная система счисления: основание – 8

Для записи числа используются восемь цифр – от 0 до 7.

Примеры:

• 27₈ = 2×8¹+7×8⁰ = 16+7 = 23
• 30₈ = 3×8¹+0×8⁰ = 24
• 4307₈ = 4×8³+3×8²+0×8¹+7×8⁰= 2247

Десятичная система счисления: основание -10

Самая распространенная система, которая используется повсеместно. Содержит цифры от 0 до 9.

Пример:

2538₁₀ = 2×10³+5×10²+3×10¹+8×10⁰

Шестнадцатеричная система счисления: основание – 16

Используются цифры от 0 до 9, а также буквы от A до F.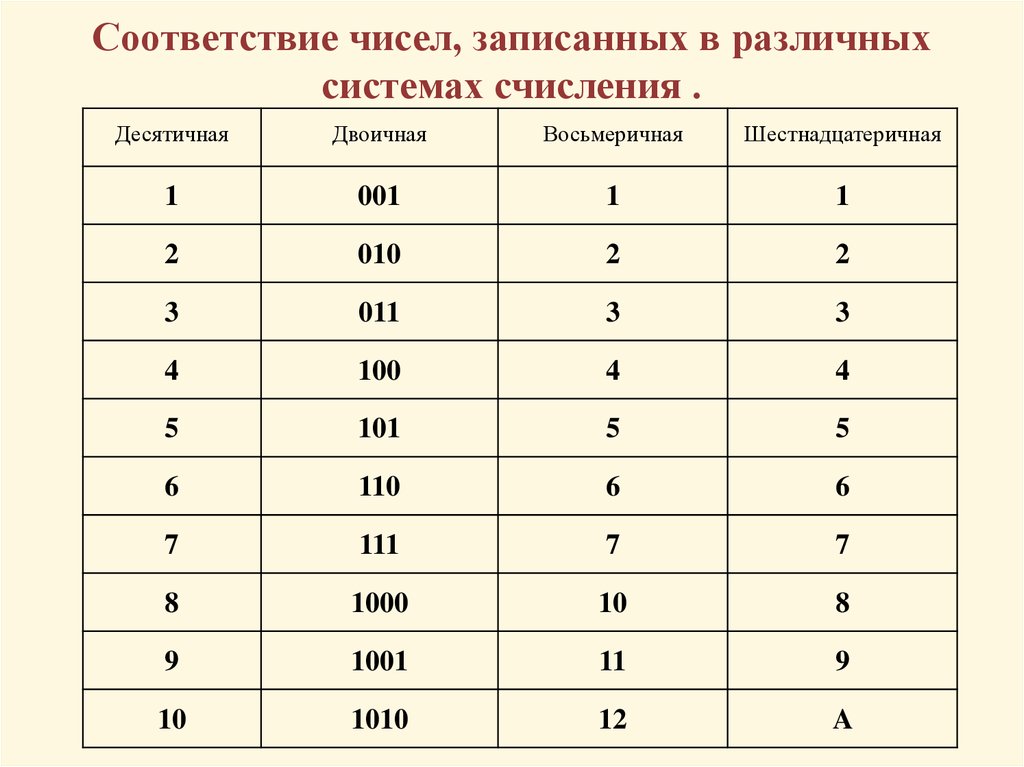 Для обозначения чисел служит префикс H. Система применяется в информатике и программировании.

Примеры:

• 28₁₆ = 28H = 2×16¹+8×16 ⁰ = 40
• 2F₁₆ = 2FH = 2×16¹+15×16⁰ = 47
• BC12₁₆ = BC12H = 11×16³+12×16²+1×16¹+2×16⁰= 48146

Таблица соответствия чисел систем счисления

Двоичная система	Восьмеричная система	Десятичная система	Шестнадцатеричная система
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	13
20	10100	24	14
21	10101	25	15
22	10110	26	16
23	10111	27	17
24	11000	30	18
25	11001	31	19
26	11010	32	1A
27	11011	33	1B
28	11100	34	1C
29	11101	35	1D
30	11110	36	1E
31	11111	37	1F
32	100000	40	20

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Объяснение систем нумерации | Library.

Automationdirect.com

Существует несколько типов систем нумерации, обычно используемых в оборудовании автоматизации: двоичная, шестнадцатеричная, восьмеричная, двоично-десятичная и с плавающей запятой (действительная). Как их использовать может быть запутанным. В этой статье с нашей веб-страницы технической поддержки объясняются различные системы нумерации.

Двоичные числа

Компьютеры, включая ПЛК, используют систему нумерации с основанием 2, называемую двоичной или логической. В базе 2 есть только две допустимые цифры: 0 и 1 (ВЫКЛ и ВКЛ). Вы могли бы подумать, что система счисления, построенная на базе 2 только с двумя возможными значениями, будет сложной, но это можно сделать с помощью кодирования, используя несколько цифр.

Каждая цифра в системе счисления по основанию 2, на которую ссылается компьютер, называется битом. Когда четыре бита сгруппированы вместе, они образуют то, что известно как полубайт. Восемь бит или два полубайта — это байт.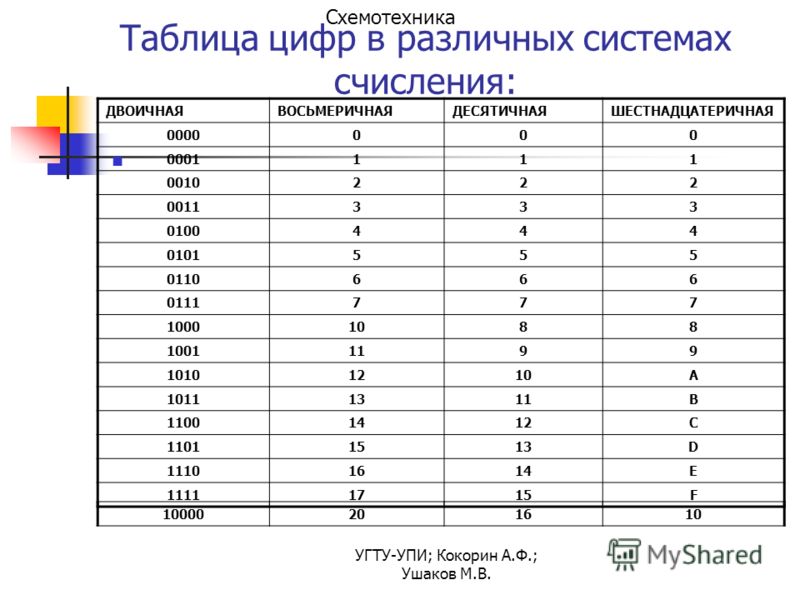 Шестнадцать бит – или два байта – это слово (таблица 1). Тридцать два бита или два слова — это двойное слово.

Двоичные числа не являются для нас «естественными», так как мы выросли, используя систему счисления с основанием 10, в которой используются числа 0-9. В этой статье различные базы будут показаны в виде числа с индексом. Например, десятичное число 10 будет равно 10 9.0018 10 .

В таблице 2 показано, как числа с основанием 2 соотносятся с их десятичными эквивалентами.

Часть 1001 ₂  будет равна десятичному числу 9 или (1*2 ³  + 1*2 ⁰ ) или (8 ₁₀  + 1 _{10 9 10 ). Байт 11010101 2 будет равен 213 10 или (1*2 ⁷ + 1*2 ⁶ + 1*2 ⁴ + 1*2 ² + 1*2 ⁰ ) или (128 10  + 64 10  + 16 10  + 4 10  +1 10 ).}

Шестнадцатеричные числа

Как вы, наверное, заметили, двоичную систему счисления не очень легко интерпретировать. Для нескольких битов это легко, но большие числа обычно занимают много места при их записи, и трудно отслеживать позицию бита при преобразовании. Вот где использование альтернативной системы нумерации может быть преимуществом. Одной из первых используемых систем счисления была шестнадцатеричная или сокращенно Hex.

HEX-это система нумерации, которая использует базу 16. Числа 0-9 ₁₀ представлены нормально, но число 10 ₁₀ по 15 _{представляются нормально, но число 10 10 по 15 . 10  представлены буквами от A до F соответственно (таблица 3). Это хорошо работает с двоичной системой, так как каждый полубайт (1111 2 ) равен 15 10 . Следовательно, для 16-битного слова у вас может быть возможное шестнадцатеричное значение FFFF 9.0018 16} . См. пример в Таблице 4.

Преобразование шестнадцатеричных чисел в десятичные работает почти так же, как и двоичные.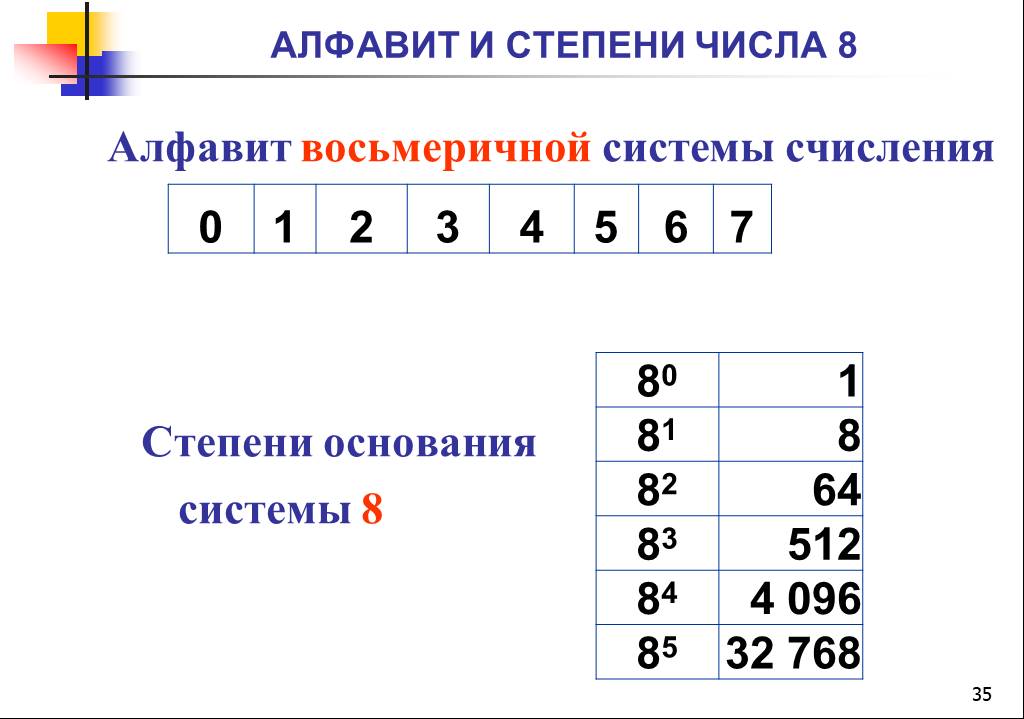 C2 ₁₆ будет равно 194 ₁₀ или (12*16 ¹ + 2*16 ⁰ ) или (192 ₁₀ +2 _{19 ). A6D4 16 будет равен 42708 10 или (10*16 ³ +6*16 ² +13*16 ¹ +4 ⁰ ) или (40960 10 +15366). 10  + 208 10  +4 10 ).}

Восьмеричные числа

Восьмеричная система счисления аналогична шестнадцатеричной системе в интерпретации битов (Таблица 5). Разница заключается в том, что максимальное значение Octal равно 7, так как это основание 8.

Например, 63 ₈ равно 51 ₁₀ или (6*8 ¹  + 3*8 ⁰ ) или (48 ₁₀  +3 ₁₀ ).

Числа в двоично-десятичной системе счисления

Система счисления в двоично-десятичной системе счисления, как и восьмеричная и шестнадцатеричная, основана на данных, закодированных битами (таблица 6). Это основание 10 (десятичное), но это двоично-десятичное число. Как мы увидим позже, между BCD и Binary существует большая разница.

Одним из преимуществ двоично-десятичного кода является то, что он читается как десятичное число, тогда как 867 двоично-десятичный означает 867 десятичное число. Преобразование не требуется. Однако, как и во всем, что связано с компьютером, есть проблемы, о которых стоит беспокоиться.

Вещественные числа (с плавающей запятой)

Термины «Вещественное» и «Плавающая запятая» описывают числа с плавающей запятой IEEE-754. Большинство ПЛК используют 32-битный формат для чисел с плавающей запятой (действительных) (таблица 7).

Формула и раскладка номера следующая:
Число = 1.M*2(E-127)
Число = число, которое должно быть преобразовано в число с плавающей запятой
M = Мантисса
E = Экспонента

Вычисление формата действительного числа является очень сложной операцией. Если вас интересует процесс преобразования, в Интернете есть множество документов, в которых подробно описаны все детали.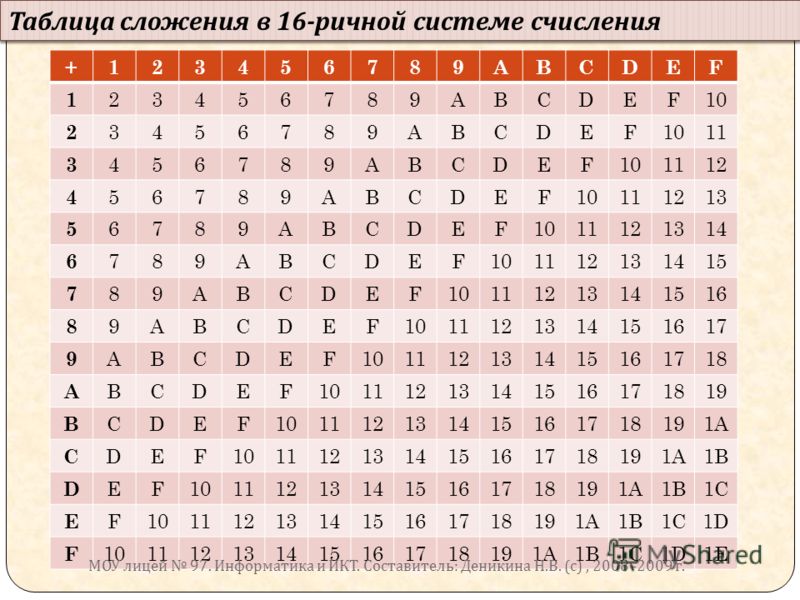

Возможно, вы заметили, что для формата действительных чисел не указано ни минимальное, ни максимальное значение. Диапазон от отрицательной бесконечности до положительной бесконечности. Сказав это и заметив, что для создания каждого числа можно использовать только 32 бита, легко предположить, что не все числа могут быть представлены. Это на самом деле так. Формату Real присуща степень погрешности.

Я уверен, вам интересно, сколько ошибок может существовать, и если ошибок много, то почему используется этот формат? Это действительно зависит от приложения. Для большинства приложений ПЛК, если вы не стремитесь к 100% точности, формат Real не вызовет особых проблем. В большинстве случаев внутреннюю ошибку можно игнорировать, но важно знать, что она существует.

BDC/двоичный/десятичный/шестнадцатеричный/восьмеричный – в чем разница?

Иногда возникает путаница в связи с различиями между типами данных, используемыми в ПЛК. Хотя данные хранятся одинаковым образом (0 и 1), существуют различия в том, как их интерпретирует ПЛК.

Хотя все форматы основаны на системе нумерации по основанию 2 и данных с битовым кодированием, формат данных отличается. В таблице 8 показаны битовые комбинации и значения для различных форматов.

Несоответствие типов данных

Несоответствие типов данных является распространенной проблемой при использовании интерфейса оператора. Диагностика может быть сложной задачей, пока вы не определите симптомы. Поскольку ПЛК использует двоично-десятичный формат в качестве собственного формата, многие люди склонны думать, что он взаимозаменяем с двоичным форматом (целое число без знака). В какой-то степени это верно, но не в данном случае. Таблица 9показывает, как различаются двоично-десятичные и двоичные числа.

Как видно из таблицы, BCD и Binary используют один и тот же битовый шаблон, пока вы не дойдете до десятичного числа 10. Когда вы дойдете до 10, битовый шаблон изменится. Битовая комбинация BCD для десятичного числа 10 фактически равна значению 16 в двоичном формате, что приводит к скачку числа на шесть цифр при просмотре в виде BCD.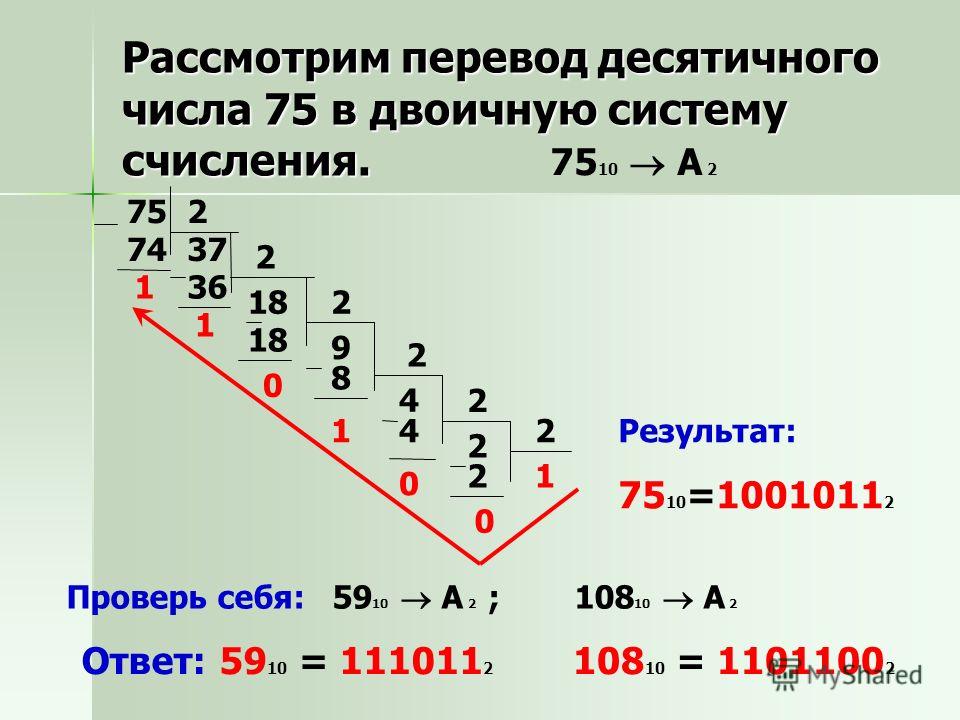 При больших числах ошибка увеличивается. Двоичные значения от 10 до 15 Decimal фактически недействительны для типа данных BCD.

Давайте посмотрим на большее число, показанное в таблице 10.

В качестве двоично-десятичного числа значение равно 4096. Если мы интерпретируем преобразованное двоично-десятичное число как двоичное, десятичное значение будет 16534. Точно так же, если мы интерпретируем двоичное число как двоично-десятичное, десятичное значение будет 1000.

Знаковые и беззнаковые целые числа

До сих пор мы имели дело только с беззнаковыми типами данных. Теперь поговорим о знаковых типах данных (отрицательных числах). Представление BCD нельзя использовать для подписанных типов данных.
Чтобы указать, что число отрицательное или положительное, мы должны присвоить ему бит. Обычно это старший значащий бит (MSB), как показано в таблице 11. Для 16-битного числа это бит 15. Это означает, что для 16-битных чисел мы имеем диапазон от -32 767 до 32 767.

У нас есть два способа кодирования отрицательного числа: дополнение до двух и знак величины плюс. Эти два метода несовместимы.

Пока значение положительное (бит 15 выключен), правила работают аналогично двоичному. Если бит 15 включен, то мы должны знать, какой метод кодирования использовался.

Знак Величины Плюс расшифровать проще всего. В основном отрицательное число имеет тот же формат, что и положительное число, за исключением того, что бит 15 включен (таблица 12).

Дополнение до двух немного сложнее. Формула состоит в том, чтобы инвертировать двоичное значение и добавить единицу (таблица 13).  

Очевидно, что системы нумерации различаются и в то же время схожи. Очень важно знать, какая система используется, чтобы правильно запрограммировать приложение. Методический и логический подход к пониманию используемой системы счисления делает интерпретацию данных менее сложной.

 

Первоначально опубликовано: 1 сентября 2005 г.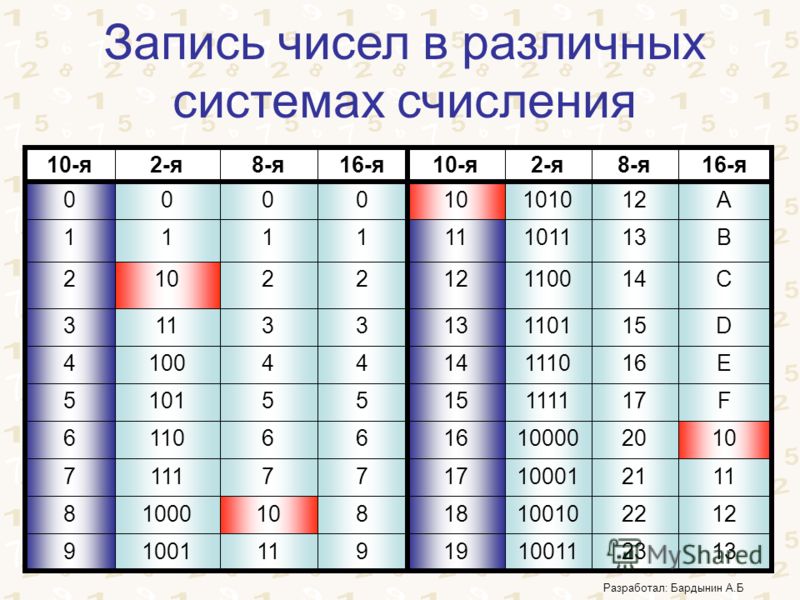 / Пересмотрено 22 января 2021 г.

Шестнадцатеричные числа: 16 с основанием

Шестнадцатеричные числа: 16 с основанием

4 двоичные цифры могут быть представлены 1 шестнадцатеричной цифрой.

Шестнадцатеричное
Если мы запишем большое число в виде двоичного числа, оно может быть довольно длинным.
Используется шестнадцатеричное (шестнадцатеричное) основание 16, поскольку каждые 4 двоичных разряда могут быть представлены одной шестнадцатеричной цифрой.
В двоичной системе с основанием 2 2 цифры: 0, 1.
В десятичной системе с основанием 10 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В шестнадцатеричном формате с основанием 16 имеется 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

В таблице ниже показано соответствующие десятичные, двоичные и шестнадцатеричные значения:

Десятичное число	Двоичный	Шестнадцатеричный
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	А
11	1011	Б
12	1100	С
13	1101	Д
14	1110	Е
15	1111	Ф

Чтобы преобразовать двоичное число в шестнадцатеричное, сначала разбейте его на группы по 4, начиная справа.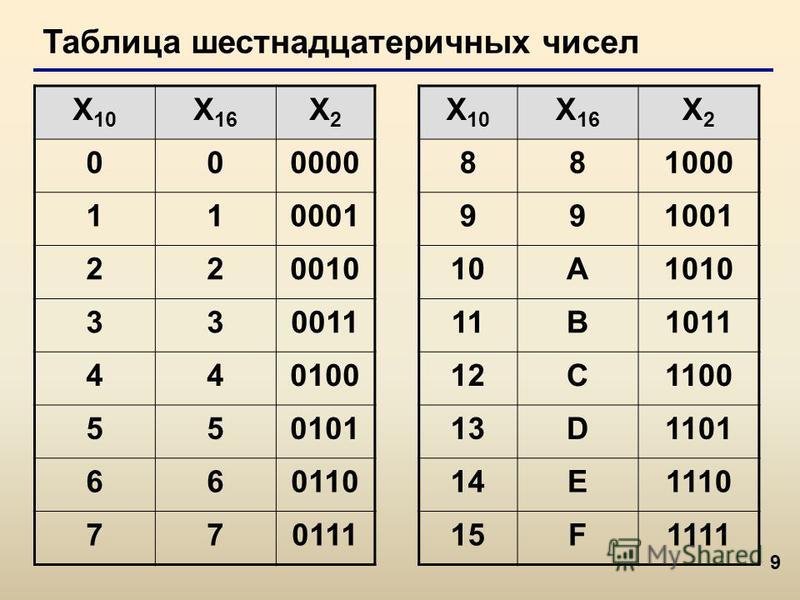 Вы всегда можете добавить 0 слева без изменения значения числа. Если в самой левой группе нет 4 цифр, просто добавьте нули слева, чтобы получить группу из 4. Затем замените каждую группу из 4 соответствующей шестнадцатеричной цифрой из таблицы выше.
Пример: преобразовать 10110111110112 в шестнадцатеричное (по основанию 16)
Разбить на группы по 4, начиная СПРАВА: 0001,0110,1111,1011
Записать шестнадцатеричное число для каждой группы по 4:
0001,0110,1111,1041 10001
6         F       B
Вот так: 10110111110112 = 16FB16
Значения разрядов в шестнадцатеричном формате начинаются с разряда единиц справа, затем умножаются на 16 для каждого разряда, перемещающегося влево:

909025 9 3 048,56 9 3 048,62	65 536	4096	256	16	1
165	164	163	162	161	160

Ниже показано шестнадцатеричное число 16FB со значениями разрядов:

4096	256	16	1
1	6	Ф	Б

Десятичное значение: 1×4096 + 6×256 + 15×16 + 11×1.