iMath Wiki — Алгебра логики. Основные логические операции и их таблицы истинности. Основные законы алгебры логики.
Мы выяснили, как информация представляется в памяти вычислительных устройств и установили алгоритмы проведения операций над этими представлениями.
Теперь, давайте попробуем разобраться, как именно реализуются операции над двоичными представлениями. Для этого, для начала, нам придется разобраться с алгеброй логики.
Алгебра логики является частью дискретной математики – раздела математики, изучающего свойства структур конечного характера.
Сама алгебра логики изучает свойства функций, у которых значения как аргументов, так и самих функций ограничены двумя значениями, например, \(\{0,1\}\).
Отцом алгебры логики считается английский математик Джордж Буль (1815-1864), поэтому алгебру логики иногда называют булевой алгеброй.
Долгое время алгебра логики была известна лишь узкому кругу специалистов, и только в 1938 году американский математик Клод Шеннон (1916-2001), стоявший у истоков современной информатики, показал, что алгебра логики применима для описания самых разных процессов, в том числе релейных и транзисторных схем.
Исследования в области алгебры логики связаны с формальной логикой, а точнее, с понятием высказывания. Высказывание – это некое лексическое образование, которое устанавливает свойства и взаимосвязи между объектами. Высказывания могут быть истинными, если они адекватно описывают объекты, или ложными в противном случае.
Так, примерами высказываний могут служить такие фразы, как “сегодня идет дождь”, или “завтра я не пойду в институт”.
Определение истинности высказывания не всегда тривиально. Так, например:
Великая теорема Ферма
Для любого натурального числа \(n>2\) уравнение \[ a^n + b^n = c^n\] Не имеет решений в целых ненулевых числах \(a,\,b,\,c\)
Как известно, сформулированная Пьером Ферма в 1637 году, была окончательно доказана только в 1994.
Введем не совсем формальное, но достаточное для наших целей определение
- Высказывание
- это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.
Это определение было предложено Аристотелем.
Проблема языковых образований в рамках алгебры логики в том, что они могут иметь весьма своеобразную структуру. Например, фраза “это высказывание является ложным” не может считаться высказыванием, поскольку бессмысленно говорить о его истинности или ложности. Причиной парадокса является структура фразы: она ссылается сама на себя. Подобные парадоксы могут быть устранены введением следующего определения:
- Элементарное высказывание
- это такое высказывание, никакая часть которого не является высказыванием.
Следует заметить, что высказыванием в строгом смысле является только утверждение о конкретных объектах. Если речь идет о неких переменных, например, “x – рациональное число”, то мы говорим о неких функциях, имеющих значение “истина” или “ложь”. Такие функции называются предикатами.
Так же следует заметить, что алгебра логики отвлекается от смыслового содержания высказываний, и занимается скорее связями между высказываниями. Если мы договоримся считать за аксиому, что “солнце светит ночью”, то есть, договоримся что это высказывание истинно, то в рамках нашей аксиоматики сможем делать какие-то обоснованные выводы. Эти выводы, конечно, не будут иметь много общего с действительностью.
Примерами таких отвлеченных, на первый взгляд, систем, может служить, например, геометрия Лобачевского, которая имеет не слишком много общего с нашим псевдоевклидовым пространством.
Различные языковые связки, такие, как “не”, “если …, то …”, “или”, “и”, и т.п. позволяют строить из элементарных высказываний более сложные.
В алгебре логики существуют соответствующие подобным связкам операции.
Введем некоторые из них.
- Конъюнкция, или логическое умножение
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Конъюнкция обозначается различными способами, в частности, амперсандом \(a \,\&\,b\), точкой \(a \cdot b\), или “крышкой” \(a \wedge b\), и соответствует языковой связке “и”. Мы будем в основном использовать амперсанд.
Поскольку оба исходных высказывания имеют по два возможных значения, и конъюнкция имеет два возможных значения, мы можем записать это определение в виде
- Дизъюнкция, или логическое сложение
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда хотя бы одно из исходных высказываний истинно.
Дизъюнкция соответствует союзу “или”, и обозначается плюсом \(a+b\), или “галочкой” \(a\vee b\). Мы будем использовать в основном второй вариант.
Таблица истинности дизъюнкции, по определению:
- Строгая дизъюнкция, или сложение по модулю 2
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда
Строгая дизъюнкция соответствует связке “либо …, либо …”, и обозначается плюсом в кружочке \(a\oplus b\), или треугольником \(a\vartriangle b\). Будем в основном пользоваться первым обозначением.
Таблица истинности, по определению:
- Импликация
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда первое из исходных высказываний (условие) истинно, а второе (следствие
Импликация соответствует связке “если …, то …”, и обозначается стрелкой \(a \rightarrow b\), или \(a \Rightarrow b\)
Таблица истинности, по определению:
Импликация, на первый взгляд, имеет не очевидное определение: как вдруг из ложных условий получается истинное следствие. Однако, в математике это никакая не новость. Например, возьмем очевидно ложное утверждение “один равен двум”:
\[1 = 2\] \[2 = 1\]
Складывая эти равенства, получим очевидно истинный результат:
\[3=3.\]
С другой стороны, из заведомо истинных посылок формально нельзя вывести ложный результат (конечно, человеческий фактор никто не отменял, но человеческий фактор выходит за пределы рассмотрения формальной логики).
- Эквивалентность
- логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Эквивалентность соответствует связке “тогда и только тогда, когда”, и обозначается \(a \Leftrightarrow b\), или \(a \equiv b\), или \(a \sim b\), или \(a \leftrightarrow b\). Будем в основном пользоваться первыми двумя обозначениями.
Таблица истинности, по определению:
- Инверсия, или отрицание
- логическая операция, ставящая в соответствие элементарному высказыванию новое высказывание, являющееся истинным тогда и только тогда, исходное ложно.
Инверсия соответствует связке “не”, и обозначается \(\neg a\), или \(\;\overline{a}\;\), или \(!a\). Будем в основном пользоваться первыми двумя обозначениями.
Таблица истинности, по определению:
В заключение, таблица истинности основных логических операций:
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
Законы алгебры логики
Введем некоторые определения, аналогичные алгебре действительных чисел, для алгебры логики.
- Логическая переменная
- Переменная, значением которой может быть любое высказывание. Обозначать будем маленькими латинскими буквами.
- Логическая формула
- любая переменная, а так же любая из констант “0” (“ложь”) и “1” (“истина”)
- Любая комбинация логических формул, составленная с помощью логических операций.
- Эквивалентные формулы
- такие формулы, которые зависят от одного и того же набора переменных, и при одинаковых значениях этих переменных, формулы так же имеют одинаковые значения. Обозначать будем знаком равенства.
Существуют следующие “законы” алгебры логики, определяющие некий набор эквивалентных формул:
- Законы коммутативности
- \[x \,\&\,y = y \,\&\,x\] \[x \vee y = y\vee x\]
- Законы ассоциативности
- \[ (x \,\&\,y) \,\&\,z = x \,\&\,(y \,\&\,z)\] \[ (x \vee y) \vee z = x \vee(y \vee z)\]
- Законы поглощения
- \[x\vee 0 = x\] \[x\,\&\,1 = x\]
- Законы дистрибутивности
- \[ x\,\&\,(y\vee z) = (x\,\&\,y) \vee(x\,\&\,z)\] \[ x\vee(y\,\&\,z) = (x \vee y) \,\&\,(x\vee z)\]
- Закон противоречия
- \[ x \,\&\,\;\overline{x}\; = 0\]
- Закон исключения третьего
- \[ x \vee\;\overline{x}\; = 1\]
- Закон равносильности
- \[ x \,\&\,x = x\] \[ x \vee x = x \]
- Закон двойного отрицания
- \[\;\overline{\;\overline{x}\;}\; = x \]
- Законы де Моргана
- \[ \;\overline{x\,\&\,y}\; = \;\overline{x}\; \vee\;\overline{y}\; \] \[ \;\overline{x\vee y}\; = \;\overline{x}\; \,\&\,\;\overline{y}\; \]
- Законы поглощения
- \[ x\vee(x\,\&\,y) = x\] \[ x\,\&\,(x\vee y) = x\]
Все перечисленные законы элементарно доказываются составлением таблиц истинности.
Например, первый закон де Моргана:
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
3 и 6 столбец одинаковы, следовательно, соответствующие формулы эквивалентны.
Введем еще одно определение
- Тавтология
- логическая формула, которая всегда истинна.
Например, тавтологией является формула, выражающая закон исключения третьего.
Оказывается, алгебра логики хорошо подходит для решения логических задач. Решение логических задач, конечно, умеренно бессмысленное времяпрепровождение (исключая случаи, когда на их примере рассматриваются более сложные вопросы), однако это хороший способ поработать с алгеброй логики и осмыслить основные концепции.
Итак, формальный способ решения логических задач:
- Из условий задачи выделяются простые высказывания и обозначаются как логические переменные.
- Условия задачи записываются в виде логических формул
- Составляется единое логическое выражение, соответствующее условию задачи. По условию задачи оно является истинным.
- Полученное выражение упрощается, либо составляется таблица истинности для него (либо и то, и другое)
- Выбирается решение задачи (случаи, когда условие истинно)
- Решение формулируется в исходных терминах задачи.
Пример: (источник)
На весеннем фестивале, четыре садовника показывали выращенные ими розы.
Всего розы были четырех цветов и у каждого садовника было по две розы.
Известно, что
- У первого была желтая роза
- У второго не было красной розы
- У третьего была синяя роза, но не было зеленой
- У одного из садовников с зеленой розой не было красной
- Ни у одного из садовников с желтой розой не было зеленой
- Ни у кого нет роз двух одинаковых цветов
Введем переменные, в которых название переменной соответствует цвету, а индекс – садовнику (номеру). Это автоматически учитывает условие “Ни у кого нет роз двух одинаковых цветов”. Тогда условия задачи запишутся в виде:
- \(y_1\)
- \(\;\overline{r_2}\;\)
- \(b_3 \,\&\,\;\overline{g_3}\;\)
- \((g_1\rightarrow\;\overline{r_1}\;) \oplus(g_2\rightarrow\;\overline{r_2}\;)\oplus(g_3\rightarrow\;\overline{r_3}\;)\oplus(g_4\rightarrow\;\overline{r_4}\;)\)
- \((y_1\rightarrow\;\overline{g_1}\;) \,\&\,(y_2\rightarrow\;\overline{g_2}\;)\,\&\,(y_3\rightarrow\;\overline{g_3}\;)\,\&\,(y_4\rightarrow\;\overline{g_4}\;)\)
Дополнительно, у каждого садовника по условиям задачи по две розы: Поэтому, если у садовника есть розы двух цветов, то роз двух других цветов у него нет. Учтем подразумеваемые импликации постфактум.
Далее для простоты записи, амперсанды опускаются (если между переменными нет ничего – значит там амперсанд). В случае отсутствия скобок, сначала применяется конъюнкция, потом все остальное.
Рассматривая последнее условие:
\((y_1\rightarrow\;\overline{g_1}\;) (y_2\rightarrow\;\overline{g_2}\;)(y_3\rightarrow\;\overline{g_3}\;)(y_4\rightarrow\;\overline{g_4}\;)\)
Первая импликация истинна, только если \(\;\overline{g_1}\;\) истинно. Предпоследняя импликация истинна всегда, \(\;\overline{g_3}\;\). Можем переписать в виде:
\(y_1 \;\overline{g_1}\; (y_2\rightarrow\;\overline{g_2}\;) (y_4\rightarrow\;\overline{g_4}\;)\)
Рассмотрим предпоследнее условие
\[ (g_1 \rightarrow\;\overline{r_1}\;) \oplus(g_2 \rightarrow\;\overline{r_2}\;) \oplus(g_3 \rightarrow\;\overline{r_3}\;) \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]
Первая импликация всегда истинна, поскольку \(\;\overline{g_1}\;\), вторая всегда истинна, поскольку \(\;\overline{r_2}\;\), третья всегда истинна, поскольку \(\;\overline{g_3}\;\). Получаем:
\[ 1 \oplus 1 \oplus 1 \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]
\[ 1 \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]
Легко показать, что \(1 \oplus x = \;\overline{x}\;\). Тогда условие принимает вид
\[ \;\overline{g_4 \rightarrow\;\overline{r_4}\;}\; \]
Импликацию можно представить в виде \(x \rightarrow y = \;\overline{x}\; \vee y\)
Применяя закон де Моргана,
\[ r_4 g_4 \]
Записывая все условия вместе:
\[ y_1 \;\overline{g_1}\; \;\overline{r_2}\; (\;\overline{y_2}\; \vee\;\overline{g_2}\;) (\;\overline{y_4}\; \vee\;\overline{g_4}\;) b_3 \;\overline{g_3}\; g_4 r_4 \]
Учитывая \(g_4 (\;\overline{y_4}\; \vee\;\overline{g_4}\;) = g_4 \;\overline{y_4}\;\),
\[ y_1 \;\overline{g_1}\; \;\overline{r_2}\; (\;\overline{y_2}\; \vee\;\overline{g_2}\;) b_3 \;\overline{g_3}\; \;\overline{y_4}\; g_4 r_4 \]
Известно, что зеленые розы должны быть у двух садовников:
\[ \;\overline{g_1}\; \;\overline{g_2}\; g_3 g_4 \vee\;\overline{g_1}\; g_2 \;\overline{g_3}\; g_4 \vee\;\overline{g_1}\; g_2 g_3 \;\overline{g_4}\; \vee g_1 \;\overline{g_2}\; \;\overline{g_3}\; g_4 \vee g_1 \;\overline{g_2}\; g_3 \;\overline{g_4}\; \vee g_1 g_2 \;\overline{g_3}\; \;\overline{g_4}\; \]
А так как \(\;\overline{g_3}\;\) и \(\;\overline{g_1}\;\)
\[ \;\overline{g_1}\; g_2 \;\overline{g_3}\; g_4 \]
Получаем \(g_2\), тогда \(g_2 (\;\overline{y_2}\; \vee\;\overline{g_2}\;) = g_2 \;\overline{y_2}\;\)
Аналогично для желтых:
\[ y_1 \;\overline{y_2}\; y_3 \;\overline{y_4}\; \]
Получаем \(y_3\). Поскольку \(y_3 b_3\), можно утверждать \(\;\overline{r_3}\; \;\overline{g_3}\;\)
Для красных тогда:
\[ r_1 \;\overline{r_2}\; \;\overline{r_3}\; r_4 \]
Получаем \(r_1\). Поскольку \(r_1 y_1\), можем утверждать \(\;\overline{b_1}\; \;\overline{g_1}\;\)
Для синих:
\[ \;\overline{b_1}\; b_2 b_3 \;\overline{b_4}\; \]
Получаем \(b_2\).
Итого
\[ y_1 r_1 g_2 b_2 b_3 y_3 g_4 r_4 \]
Основные законы алгебры логики
Для преобразования функций, упрощения формул, полученных при формализации условий логических задач, в алгебре логики производятся эквивалентные преобразования, опирающиеся на основные логические законы. Некоторые из этих законов формулируются и записываются так же, как аналогичные законы в арифметике и алгебре, другие выглядят непривычно.
Законы алгебры логики называют иногда теоремами.
В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул.
В справедливости всех законов можно убедиться, построив таблицы истинности для левой и правой частей записанного закона. После упрощения выражения с применением законов алгебры логики таблицы истинности совпадают.
Справедливость части законов можно доказать, применяя инструментарий таблиц истинности.
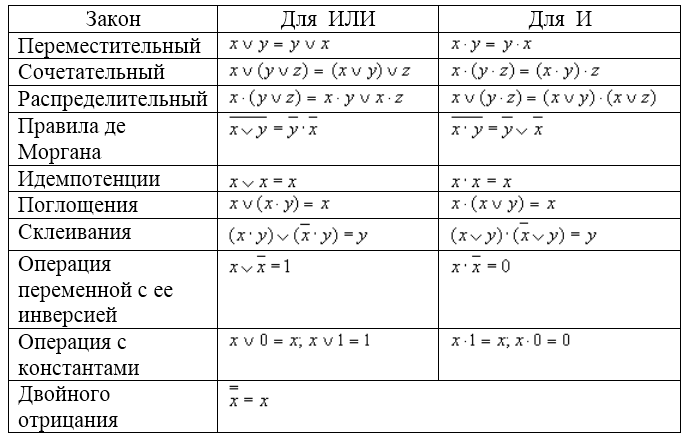
Рисунок 1.
Примеры
- Составим таблицу истинности для выражения

Рисунок 2.
В первые два столбца таблицы запишем четыре возможных пары значений $x$ и $y$, в последующих столбцах — значения промежуточных выражений, а в последнем столбце — значение исходного выражения. В результате получим таблицу:
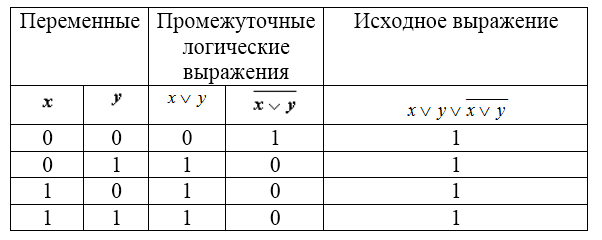
Рисунок 3.
Упростим исходное выражение, используя основные законы алгебры логики:
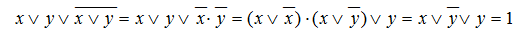
Рисунок 4.
(закон Де Моргана, распределительный закон для И, закон идемпотенции, операция переменной с её инверсией).
Из таблицы видно, что при всех наборах значений переменных $x$ и $y$ формула на рис.2 принимает значение $1$, то есть является тождественно истинной.
- Составим таблицу истинности для выражения:

Рисунок 5.
, которое содержит две переменные $x$ и $y$. В первые два столбца таблицы запишем четыре возможных пары значений $x$ и $y$, в последующих столбцах — значения промежуточных выражений, а в последнем столбце — значение исходного выражения. В результате получим таблицу:
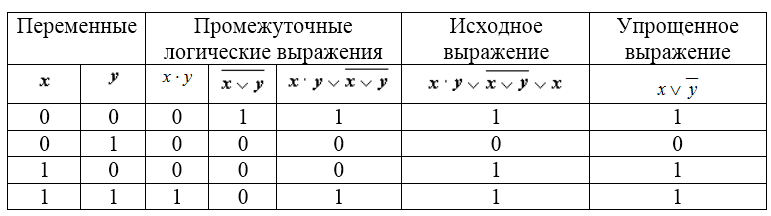
Рисунок 6.
Из таблицы видно, что Исходное выражение принимает такие же значения, что и Упрощенное выражение на соответствующих значениях переменных $x$ и $y$.
Упростим выражение на рис.5, применяя основные законы алгебры логики.
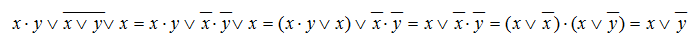
Рисунок 7.
(закон Де Моргана, закон поглощения, распределительный закон для И).
- Составим таблицу истинности для выражения

Рисунок 8.
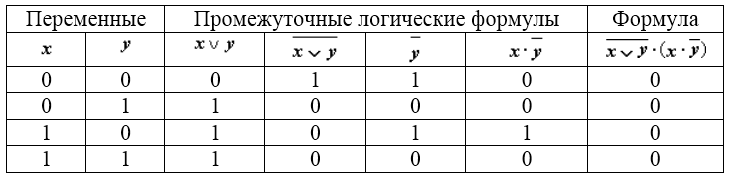
Рисунок 9.
Из таблицы видно, что при всех наборах значений переменных $x$ и $y$ формула на рис.8 принимает значение $0$, то есть является тождественно ложной.
Упростим выражение, применяя законы алгебры логики:
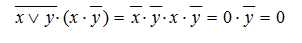
Рисунок 10.
- Упростим выражение:

Рисунок 11.
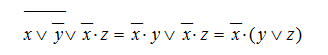
Рисунок 12.
(закон Де Могргана, распределительный).
Составим таблицу истинности для выражения на рис.11:
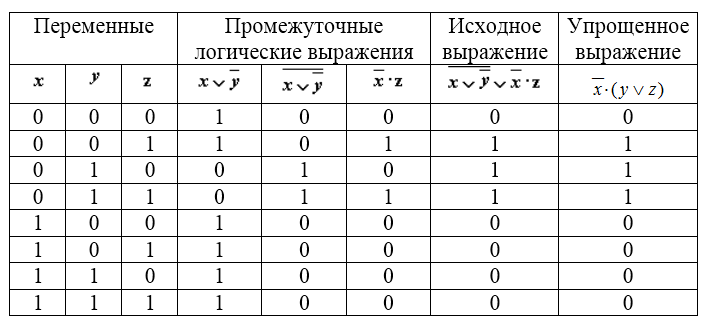
Рисунок 13.
Из таблицы видно, что выражение на рис.11 в некоторых случаях принимает значение $1$, а в некоторых — $0$, то есть является выполнимым.
(правило де Моргана, выносим за скобки общий множитель, правило операций переменной с её инверсией).
- Упростить выражение используя законы алгебры логики:

Рисунок 15.
(повторяется второй сомножитель, что возможно используя закон идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания).
- Упростить выражение используя законы алгебры логики:

Рисунок 16.
(вводим вспомогательный логический сомножитель
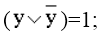
Рисунок 17.
Логика. Таблицы истинности. Законы алгебры логики
Тема: Логические основы ЭВМ
Урок 1: Логические функции и таблицы истинности
Мы закончили тему «Арифметические основы ЭВМ». Познакомились с системами счисления.
Какая система счисления применяется в компьютере? (двоичная)
Почему? (существует 2 устойчивых состояния: ток течет – ток не течет, напряжение высокое – низкое, участок магнитного диска намагничен – не намагничен, на лазерном диске «выпуклость» и «впадина», от которых луч лазера отражается – не отражается)
Как выполняются арифметические операции в двоичной с.с.? Сложить два числа (обращая внимание на «запоминание» переносов)
1 1 1
1001
+1011
10100
А как же эти действия выполняются в компьютере?! Неужели компьютер таким же образом считает 1+1=10, 0 пишем, 1 в уме. Где же и как компьютер пишет, как именно запоминает «в уме»? Наша задача разобраться в этом.
На какой элементной базе строились ЭВМ различных поколений? Сколько поколений ЭВМ существует? (4 поколения: I – на электронных лампах; II – на транзисторах; III – на микросхемах; IV – большие интегральные схемы, микропроцессоры). А еще раньше – были построены счетные машины на электромеханических реле (Марк-1). А еще ранее в 1823 году Ч.Бэббидж пытался построить ЭВМ на основе гидравлических систем.
Основоположником древнейшей науки ЛОГИКИ был великий древнегреческий ученый Аристотель.
Логика – это наука о формах и способах мышления.
Мышление всегда осуществляется в каких-либо формах. Основными формами мышления являются понятие, суждение и умозаключение.
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта. Т.е. понятие выделяет существенные признаки объекта, которые отличают его от других объектов.
Например, понятие «компьютер» объединяет множество электронных устройств, которые предназначены для обработки информации, в числе которых монитор и клавиатура. Даже по этому короткому описанию компьютер трудно спутать с другими объектами, например, с механизмами, служащими для перемещения по дорогам и хранящимися в гаражах, которые объединяются понятием «автомобиль»
Свое понимание окружающего мира человек формулирует в виде высказываний. Высказывание строится на основе понятий и по форме является повествовательным предложением.
Высказывание может быть либо истинным, либо ложным. Истинным будет высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Например, «Процессор является устройством обработки информации» — истинное высказывание. «Процессор является устройством печати» — ложное высказывание. Иногда истинности того или иного высказывания является относительной.
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о процессах, предметах, их свойствах и отношениях между ними.
Высказывание может быть либо истинным, либо ложным.
Например:
– высказывание «В нашем классе сейчас горит свет» – истинно.
– высказывание «Кошки умеют летать» – ложно (для нормальных кошек).
Высказывание «X>Y» истинно при одних значениях Х и Y и ложно при других значениях. Поэтому «X>Y» – высказыванием не является. Не являются высказыванием и вопрос «Который час?», и восклицание «Какая прелесть!».
Простые высказывания можно объединять в сложные с помощью связок.
х
0
1
1
0
Пусть есть высказывание х «В нашем классе сейчас горит свет». Оно истинно.Построим отрицание этого высказывания с помощью связки НЕ: «В нашем классе сейчас не горит свет». Оно ложно.
Или высказывание «Кошки умеют летать». Оно ложно. Отрицание этого высказывания: «Кошки не умеют летать» — истинно.
Функция, которая строится с помощью частицы «НЕ» называется ОТРИЦАНИЕ или ИНВЕРСИЯ.
Обозначается y= или y= ¬ х
или y= ¬ х
y
x&y
0
0
0
0
1
0
1
0
0
1
1
1
Есть два высказывания:
х: «Ручка состоит из корпуса»
у: «Ручка состоит из стержня»
Объединим эти высказывания связкой «И»: «Ручка состоит из корпуса и стержня». Рассмотрим таблицу истинности для этого сложного высказывания:
Функция, которая строится с помощью частицы «И» называется КОНЪЮНКЦИЯ или Логическое умножение.
Обозначается z= x&y или z= xy или z= xy
хy
xVy
0
0
0
0
1
1
1
0
1
1
1
1
Рассмотрим другие два высказывания:х: «На улице идет дождь»
у: «На улице идет снег»
Объединим эти высказывания связкой «ИЛИ»: «На улице идет дождь или снег». Рассмотрим таблицу истинности для этого сложного высказывания:
Функция, которая строится с помощью частицы «И» называется ДИЗЪЮНКЦИЯ или Логическое сложение.
Обозначается z= xy z= x+y
хy
xy
0
0
1
0
1
1
1
0
0
1
1
1
Рассмотрим еще два высказывания:х: «На улице идет дождь»
у: «Улицы мокрые»
Объединим эти высказывания связкой «ЕСЛИ … ТО …»: «Если на улице идет дождь, то улицы мокрые». Рассмотрим таблицу истинности для этого сложного высказывания:
Функция, которая строится с помощью связки «ЕСЛИ … ТО …» называется ИМПЛИКАЦИЕЙ.
Обозначается z= xy
хy
xy
0
0
1
0
1
0
1
0
0
1
1
1
Рассмотрим следующие два высказывания:х: «Вася выучит уроки»
у: «Рак на горе свиснет»
Объединим эти высказывания связкой «ТОГДА И ТОЛЬКО ТОГДА …»: «Вася выучит уроки тогда и только тогда, когда рак на горе свиснет». Рассмотрим таблицу истинности для этого сложного высказывания:
Функция, которая строится с помощью связки «ТОГДА И ТОЛЬКО ТОГДА …» называется ЭКВИВАЛЕНТНОСТЬЮ.
Обозначается z= xy; x~y; x≡y;
хy
x y xy
y xy
0
0
0
0
1
1
1
0
1
1
1
0
Рассмотрим еще два высказывания:х: «На футбольном матче я сижу на северной трибуне»
у: «На футбольном матче я сижу на южной трибуне»
Объединим эти высказывания связкой «ЛИБО … ЛИБО …»: «На футбольном матче я сижу либо на северной трибуне, либо на южной трибуне». Рассмотрим таблицу истинности для этого сложного высказывания:
Функция, которая строится с помощью связкой «ЛИБО … ЛИБО …» называется СТРОГОЙ ДИЗЪЮНКЦИЕЙ или СЛОЖЕНИЕМ ПО МОДУЛЮ ДВА.
Обозначается z= x y или z= xy
y или z= xy
Порядок выполнения логических операций (в порядке убывания приоритета их выполнения):
Д
 ействия в скобках
ействия в скобкахИнверсия ()
Конъюнкция ( или &)
Дизъюнкция ()
Строгая дизъюнкция (сложение по модулю два) (
 или )
или )Импликация ()
Эквивалентность ()
Задание 1: Построить таблицу истинности для функции:
х y x (y)
Решение:
Определяем количество переменных (2: x и y)
Определяем количество наборов (комбинаций 0 и 1 для такого количества переменных равно 2n, где n – количество переменных, в нашем случае n = 2: 22=4)
Определяем порядок выполнения действий:
1 4 3 2
(х y) x (y)
Составляем таблицу и заполняем ее:
y
1
(х y)
2
(y)
3
x (y)
4
(1)(3)
0
0
1
1
1
1
0
1
1
0
1
1
1
0
0
1
1
1
1
1
1
0
0
1
Задание 2: Построить таблицу истинности для функции:
х (y) z x
Решение:
Определяем количество переменных (3: x,y и z)
Определяем количество наборов (2n для n = 3: 23=8)
Определяем порядок выполнения действий:
2 1 3 4
х (y) z x
Составляем таблицу и заполняем ее:
y
z
1
y
2
х (y)
3
x (y) z
4
(3)(x)
2-й способ
х
y
z
3
x (y) z
4
(3)(x)
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
1
1
0
0
0
0
0
1
1
0
0
1
0
0
1
1
0
1
1
0
0
0
1
1
0
1
1
1
1
1
1
0
1
1
1
1
1
0
0
0
0
1
1
1
0
0
1
1
1
1
0
0
0
1
1
1
1
0
1
Покажем, как можно упростить построение таблицы истинности для этой функции: функция конъюнкция («И», логическое умножение) будет иметь значение 1, когда равны 1 все переменные, т.е. х=1,  =1 (т.е. у=0) и z=1. Т.о. можно сразу же записать столбец 3:
=1 (т.е. у=0) и z=1. Т.о. можно сразу же записать столбец 3:
Кстати, обратите внимание, что в приведенном примере получено значение, полностью совпадающее с переменной х. Это должно навести нас на мысль, что должны быть способы упрощения логических выражений. Такие способы есть. Это материал следующего урока.
Итак, мы познакомились с основными логическими функциями, их обозначениями и таблицами истинности.
Дом. задание.
Выучить все функции, слова-связки, которые им соответствуют, их таблицы истинности.
Построить таблицы истинности для следующих функций:
(х y z) x
(х y) (y z)
Урок 2: Преобразование логических выражений. Законы алгебры логики.
Основные законы алгебры логики.
Переместительный (коммутативный) закон
X v Y = Y v X; X & Y = Y & X
Сочетательный (ассоциативный) закон
X v (Y v Z) = (X v Y) v Z; X & (Y & Z) = (X & Y) & Z
Распределительный (дистрибутивный) закон
X & (Y v Z) = X & Y v X & Z
В отличие от математики, в которой есть только один распределительный закон для умножения, в алгебре логики есть и второй распределительный закон для сложения:
X v (Y & Z) = (X v Y) & (X v Z) (! Докажите этот закон с помощью таблиц истинности!)
Операции с константами:

X 0 = X; X 1 = 1
X & 1 = X; X & 0 = 0
Операции с переменной и ее инверсией (отрицанием)
X v  = 1 — исключение третьего (Х Х = 1)
= 1 — исключение третьего (Х Х = 1)
X &  = 0 — противоречие (Х Х = 0)
= 0 — противоречие (Х Х = 0)
Двойное отрицание
 = Х ((Х) = Х)
= Х ((Х) = Х)
Правила де Моргана (чтобы “разбить” “длинную” инверсию, нужно поставить инверсии над каждой переменной, входящей в операцию, а знак операции изменить на противоположный). _____ _ _ ______ _ _
X v Y = X & Y; X & Y = X v Y
[ (X Y) = X Y; (X Y) = X Y ]
(! Докажите эти законы с помощью таблиц истинности!)
Идемпотентность (убрать лишнее)
X v X = X; X & X = X
Поглощение X v (X & Y) = X; X & (X v Y) = X
Дополнительные формулы
A → B = ¬ A B или в других обозначениях A → B = 
A ~ B = (¬ A B) ( A ¬B) = (¬ A ¬B) ( A B)
или в других обозначениях A ↔ B = 
 (т.к.
(т.к.  )
) (т.к.
(т.к.  )
)
Задача: упростить выражение: 
Применяем закон де Моргана:

2-й раз применяем закон де Моргана:

Снова применяем закон де Моргана для каждой «длинной» инверсии:

Применяем закон двойного отрицания для b и c:

Применяя сочетательный закон для сложения, и учитывая, что умножение является более приоритетной операцией, чем сложение, убираем скобки и получаем ответ:

2-й способ решения данной задачи:
Применяем закон де Моргана для конъюнкции (умножения):

Применяем закон де Моргана для 1-й скобки и закон двойного отрицания для 2-й скобки:

Применяя сочетательный закон для сложения, и учитывая, что умножение является более приоритетной операцией, чем сложение, убираем скобки и получаем ответ:

Дом. задание.
Выучить все законы алгебры логики.
Доказать распределительный закон и 2 правила де Моргана с помощью таблиц истинности
Индивидуальные задания на упрощение логических выражений (выдает учитель)
Булева алгебра (алгебра логики)
На этом уроке знакомимся с алгеброй логики (булевой алгеброй). Одним из её основателей стал английский математик Джордж Буль (1815-1864), который был из довольно бедной семьи, а в юности зарабатывал переводами сочинений древнегреческих философов. За этим занятием его и посетила мысль о том, что высказываниям можно присваивать значения 1 («истина») и 0 «ложь».
Итак, алгебра логики (булева алгебра) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики позволяет закодировать любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими подобно обычным числам в математике.
Создание алгебры логики в середине ХIХ века в трудах Джорджа Буля представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Пусть функция 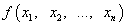 от
n переменных и любой из её аргументов могут принимать значения только из множества {0, 1}. Тогда эта
функция называется логической, или булевой, или переключательной,
или функцией алгебры логики. Описанную функцию часто называют также
булевым вектором. Количество функций от n переменных
равно 2 в степени n. То же самое можно сказать и иначе: число различных n-мерных
булевых векторов равно 2 в степени n. А число различных функций алгебры логики от этих векторов
равно уже
от
n переменных и любой из её аргументов могут принимать значения только из множества {0, 1}. Тогда эта
функция называется логической, или булевой, или переключательной,
или функцией алгебры логики. Описанную функцию часто называют также
булевым вектором. Количество функций от n переменных
равно 2 в степени n. То же самое можно сказать и иначе: число различных n-мерных
булевых векторов равно 2 в степени n. А число различных функций алгебры логики от этих векторов
равно уже 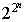 .
.
Значениям переменной в булевой алгебре соответствуют состояниям элементов микросхем компьютера или любого другого электронного устройства: сигнал присутствует (логическая «1») или сигнал отсутствует (логический «0»).
На логических элементах, реализующих булевы функции, строятся логические схемы электронных устройств.
Законы булевой алгебры применяются и в программировании — при написании сложных логических условий и сложных запросов к базе данных. Один пример со скриптом на PHP приведён здесь (это статья о системе многокритериального поиска по сайту с базой данных). Ещё один пример — применение алгебры логики в создании многоуровневого меню сайта, в котором были бы открыты все пункты всех уровней, по которому пролегает путь к конечному открытому пункту меню.
Часто оказывается, что изначально построенное логическое выражение можно упростить, используя аксиомы, теоремы и законы алгебры логики.
Логические функции одной переменной
| Переменная | Логические функции | |||
| x | 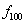 | 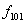 | 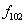 | 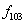 |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Логические функции двух переменных
Ниже дана таблица истинности для логических функций от двух переменных.
В логических схемах функции могут быть реализованы с произвольных количеством входных переменных, примеры — в материале Логические схемы и таблицы истинности.
Ответить на контрольные вопросы, а затем посмотреть ответы
Контрольный вопрос 1. Даны две переменные x1 и x2. Число различных булевых векторов и различных ФАЛ от полученных векторов равны соответственно:
- 8 и 16
- 8 и 32
- 4 и 8
- 4 и 16
Контрольный вопрос 2. Какие из функций не являются ФАЛ одной переменной (и одна, и вторая в варианте ответа):
- отрицание и сложение по модулю два
- эквивалентность и повторение x
- отрицание и импликация
- функция Шеффера и эквивалентность
- запрет по x2 и отрицание
Правильные ответы на вопрос 1 и вопрос 2.
Любую булеву функцию с произвольным количеством аргументов можно построить через подстановку элементарных функции вместо аргументов (суперпозицию). Набор простейших функций, с помощью которого можно выразить любые другие, сколь угодно сложные логические функции, называется функционально полным набором, или логическим базисом.
Инверсия (логическое отрицание, «НЕ»)
 .
.
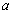 | 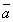 |
| 0 | 1 |
| 1 | 0 |
Конъюнкция (логическое умножение, «И»)
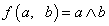 .
.
Дизъюнкция (логическое сложение, «ИЛИ»)
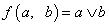 .
.
В булевом базисе обычно строятся логические схемы, которые реализуют сколь угодно сложные логические функции, примеры — в материале Логические схемы и таблицы истинности.
В качестве исходного описания сложных логических функций обычно используется таблица истинности, однако упрощение функций удобнее производить в аналитической форме. При аналитической записи функция алгебры логики представляется либо в виде логической суммы элементарных логических произведений (дизъюнкции элементарных конъюнкций), либо в виде логического произведения элементарных логических сумм (конъюнкции элементарных дизъюнкций). Первая форма записи имеет название дизъюнктивной нормальной формы (ДНФ), вторая — конъюнктивной нормальной формы (КНФ). В этих названиях термин «нормальная» означает отсутствие общей инверсии (отрицания) над несколькими перемнными сразу.
Дизъюнктивная нормальная форма
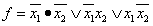 .
.
Конъюнктивная нормальная форма
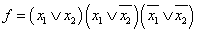 .
.
Применяются следующие способы описания логических функций:
- словесный;
- табличный;
- числовой;
- аналитический;
- координатный;
- графический.
Пример табличного описания функций алгебры логики. В верхней таблице под набором подразумевается набор значений логических переменных (1 или 0), а f — это значение функции алгебры логики, заданной определённой формулой. Нижняя таблица несёт в себе более подробную информацию о наборах, поскольку в ней указаны значения переменных.
| Номер набора | f |
| 0 | 0 |
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 1 |
| 6 | 0 |
| 7 | 1 |
| X1 | X2 | X3 | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Приведённые выше таблицы имеют название таблиц истинности. Такие таблицы в практике необходимо строить для любой, сколь либо сложной булевой функции. Примеры таблиц истинности для булевых функций, реализованных в логических схемах — в материале Логические схемы и таблицы истинности.
Пример числового описания логических функций
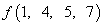 или
или 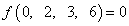 .
.
Пример аналитического описания логических функций
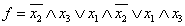
Пример координатного описания логических функций
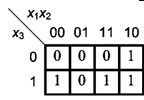
Карта Карно
Пример графического описания логических функций
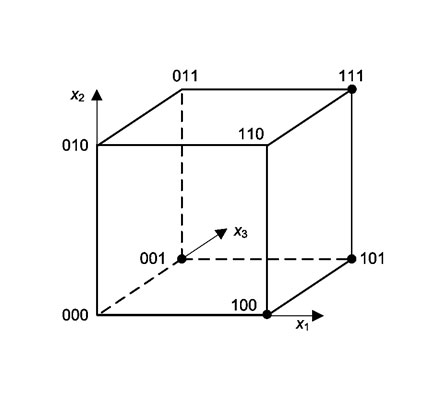
Аксиомы конъюнкции
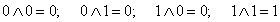 .
.
Аксиомы дизъюнкции
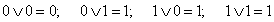 .
.
Аксиомы отрицания
если 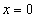 ,
то
,
то 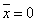 ; если
; если 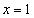 ,
то
,
то 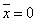 .
.
Теоремы исключения констант
 .
.
Теоремы идемпотентности (тавтологии, повторения)
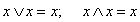 .
.
для n переменных
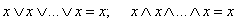 .
.
Теорема противоречия
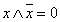 .
.
Теорема «исключённого третьего»
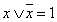 .
.
Теорема двойного отрицания (инволюции)
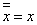 .
.
Ассоциативный (сочетательный) закон
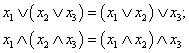 .
.
Коммутативный (переместительный) закон
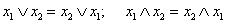 .
.
Дистибутивный (распределительный) закон
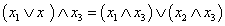 .
.
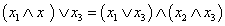 .
.
Законы де Моргана (законы общей инверсии или дуальности)
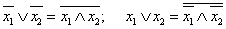 .
.
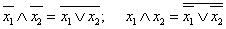 .
.
Закон поглощения (элиминации)
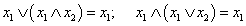 .
.
Закон склеивания (исключения)
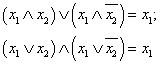 .
.



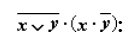
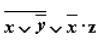
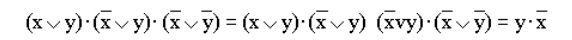
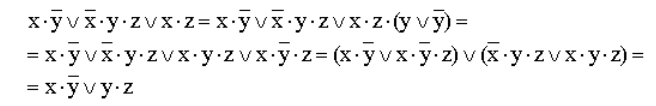
 ействия в скобках
ействия в скобках
 = Х ((Х) = Х)
= Х ((Х) = Х)





