Презентация по информатике на тему «Таблица истинности»
Сегодня поговорим о таблицах истинности, их построение и для чего они нужны.
Что же такое таблица истинности?
Таблица истинности — таблица, описывающая логическую функцию.
Логическая функция – это функция, у которой значения переменных и значение функции выражают логическую истинность.
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
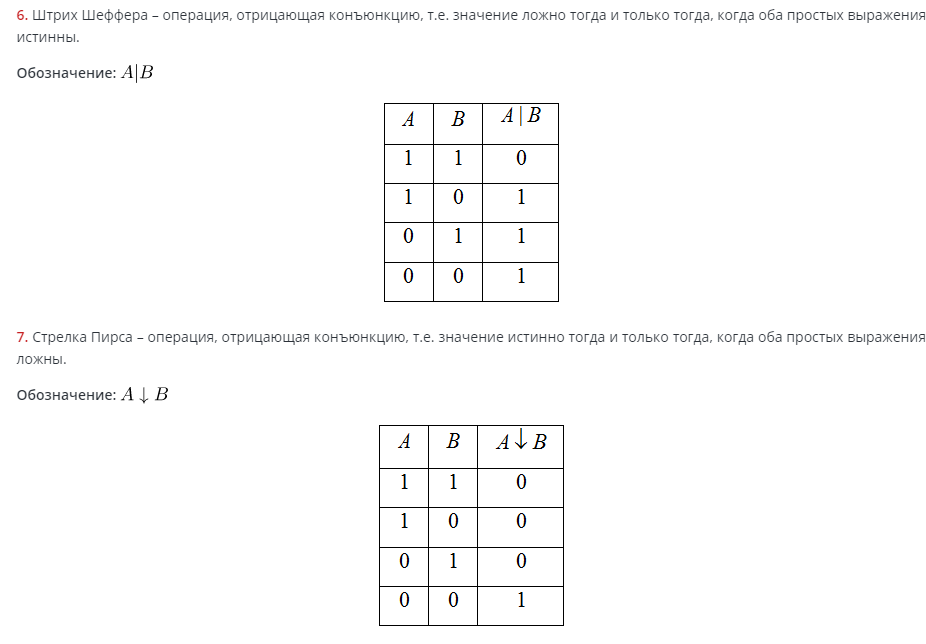
Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций: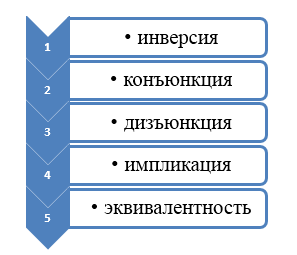
Логические операции и таблицы истинности:
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно.
Обозначение: F = A & B. А˄В
Таблица истинности для конъюнкции
2) Логическое сложение или дизъюнкция: Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны.
Обозначение: F = A v B.
Таблица истинности для дизъюнкции
3) Логическое отрицание или инверсия:Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬A. 
Таблица истинности для инверсии
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
5) Логическая равнозначность или эквивалентность:Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
«A ↔ B» истинно тогда и только тогда, когда А и B равны.
Обозначение: F = A ↔ B.
Таблица истинности для эквивалентности
«A ⊕ B» истинно тогда, когда истинно А или B, но не оба одновременно.
Эту операцию также называют «сложение по модулю два».
Обозначение: F = A ⊕ B.
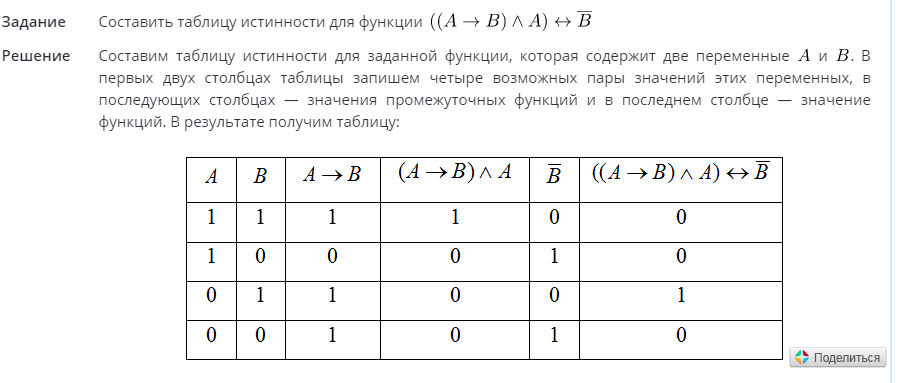
а) A & B ∨ ¬ A & B
б) (A ∨ B) & (¬ A ∨ B)
а) A & B ∨ ¬ A & B
б) (A ∨ B) & (¬ A ∨ B)
а) A & B ∨ ¬ A & B
б) (A ∨ B) & (¬ A ∨ B)
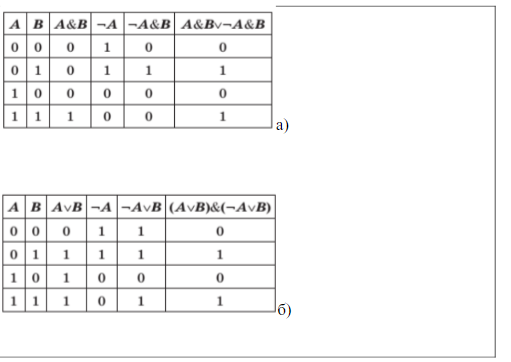

Таблица истинности — это… Что такое Таблица истинности?
Таблица истинности — это таблица, описывающая логическую функцию.
Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» ( либо , либо ).
Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.
Таблицы истинности для основных двоичных логических функций
Таблицы истинности для некоторых троичных логических функций
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| Минимум | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| Максимум Минус. | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 0 |
| x | 2 | 1 | 0 | 2 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| Webb(x,y) | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 2 | 1 |
См. также
Примечания
Литература
- Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. — М.: Наука, 1966. — (Математическая логика и основания математики).
Ссылки
Таблица истинности — это… Что такое Таблица истинности?
Таблица истинности — это таблица, описывающая логическую функцию.
Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» ( либо , либо ).
Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.
Таблицы истинности для основных двоичных логических функций
Таблицы истинности для некоторых троичных логических функций
| x | 2 | 1 | 0 | 2 | 1 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| Минимум | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| Максимум Минус. | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| Webb(x,y) | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 2 | 1 |
См. также
Примечания
Литература
- Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. — М.: Наука, 1966. — (Математическая логика и основания математики).
Ссылки
Таблица истинности — Википедия. Что такое Таблица истинности
Материал из Википедии — свободной энциклопедииТаблица истинности — это таблица, описывающая логическую функцию.
Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (true{\displaystyle true} либо false{\displaystyle false}, 1{\displaystyle 1} либо 0{\displaystyle 0}).
Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.
Таблицы истинности для основных двоичных логических функций
В программировании:
- Конъюнкция = AND = И = ∧{\displaystyle \land } = &
- Дизъюнкция = OR = ИЛИ = ∨{\displaystyle \lor } = |
- Сложение по модулю 2 = XOR = ИСКЛЮЧАЮЩЕЕ ИЛИ = ⊕{\displaystyle \oplus } = ~
- Отрицание = NOT = НЕ = ¬{\displaystyle \neg } = !
Таблицы истинности для некоторых троичных логических функций
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| min(x,y) | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| max(x,y) | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| F2TN22310 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 2 | 1 |
См. также
Примечания
Литература
- Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. — М.: Наука, 1966. — (Математическая логика и основания математики).

