Таблица соответствия кодов — представлений чисел. (Десятичные от 1 до 255 и соответствующие восьмеричные, шестнадцатиричные, двоичные, ASCII коды).

Dec/ десяти чный	Oct/ восьмер ичный	hex/ шестна дцатер ичный	Bin/ двоич ный	ASCII симв	пояснение	ввод с клавиатуры	Dec/ десяти чный	Oct/ восьмер ичный	hex/ шестна дцатер ичный	Bin/ двоич ный	ASCII симв
0	000	0	00000000	NUL	Пустой ASCII символ	[email protected]	64	100	40	01000000	@
1	001	1	00000001	SOH	Начало заголовка	CTRL-A	65	101	41	01000001	A
2	002	2	00000010	STX	Начало текста	CTRL-B	66	102	42	01000010	B
3	003	3	00000011	ETX	Конец текста	CTRL-C	67	103	43	01000011	C
4	004	4	00000100	EOT	Конец передачи	CTRL-D	68	104	44	01000100	D
5	005	5	00000101	ENQ	Запрос	CTRL-E	69	105	45	01000101	E
6	006	6	00000110	ACK	Подтвержд. получения	CTRL-F	70	106	46	01000110	F
7	007	7	00000111	BEL	Звуковой сигнал	CTRL-G	71	107	47	01000111	G
8	010	8	00001000	BS**	Обратный ход каретки	CTRL-H	72	110	48	01001000	H
9	011	9	00001001	TAB**	Горизонт. табуляция	CTRL-I	73	111	49	01001001	I
10	012	A	00001010	LF**	Начало строки	CTRL-J	74	112	4A	01001010	J
11	013	B	00001011	VT	Вертикальная табуляция	CTRL-K	75	113	4B	01001011	K
12	014	C	00001100	FF	Начало формы	CTRL-L	76	114	4C	01001100	L
13	015	D	00001101	CR**	Возврат каретки	CTRL-M	77	115	4D	01001101	M
14	016	E	00001110	SO	Передача	CTRL-N	78	116	4E	01001110	N
15	017	F	00001111	SI	Прием	CTRL-O	79	117	4F	01001111	O
16	020	10	00010000	DLE	Закр. канала связи	CTRL-P	80	120	50	01010000	P
17	021	11	00010001	DC1	Упр. устройством 1	CTRL-Q	81	121	51	01010001	Q
18	022	12	00010010	DC2	Упр. устройством 2	CTRL-R	82	122	52	01010010	R
19	023	13	00010011	DC3	Упр. устройством 3	CTRL-S	83	123	53	01010011	S
20	024	14	00010100	DC4	Упр. устройством 4	CTRL-T	84	124	54	01010100	T
21	025	15	00010101	NAK	Отрицание получения	CTRL-U	85	125	55	01010101	U
22	026	16	00010110	SYN	Синхронизация	CTRL-V	86	126	56	01010110	V
23	027	17	00010111	ETB	Конец пакета	CTRL-W	87	127	57	01010111	W
24	030	18	00011000	CAN	Отмена	CTRL-X	88	130	58	01011000	X
25	031	19	00011001	EM	Закрытие среды	CTRL-Y	89	131	59	01011001	Y
26	032	1A	00011010	SUB	Замена	CTRL-Z	90	132	5A	01011010	Z
27	033	1B	00011011	ESC	Завершение	CTRL-[	91	133	5B	01011011	[
28	034	1C	00011100	FS	Разделитель файлов	CTRL-\	92	134	5C	01011100	\
29	035	1D	00011101	GS	Разделитель групп	CTRL-]	93	135	5D	01011101	]
30	036	1E	00011110	RS	Разделитель записей	CTRL-^	94

Двоичный код — Википедия

Материал из Википедии — свободной энциклопедии

Слово «Wikipedia», закодированное двоичным ASCII-кодом.

Двои́чный код — это способ представления данных в виде кода, в котором каждый разряд принимает одно из двух возможных значений, обычно обозначаемых цифрами 0 и 1. Разряд в этом случае называется двоичным разрядом.

В случае обозначения цифрами «0» и «1», возможные состояния двоичного разряда наделяются качественным соотношением «1» > «0» и количественными значениями чисел «0» и «1».

Двоичный код может быть непозиционным и позиционным. Позиционный двоичный код лежит в основе двоичной системы счисления, широко распространенной в современной цифровой технике.

Из комбинаторики известно, что, в случае непозиционного кода, количество комбинаций (кодов) n-разрядного кода является числом сочетаний с повторениями, равно биномиальному коэффициенту:

(n+k−1k)=(−1)k(−nk)=(n+k−1)!k!(n−1)!{\displaystyle {n+k-1 \choose k}=(-1)^{k}{-n \choose k}={\frac {\left(n+k-1\right)!}{k!\left(n-1\right)!}}}, [возможных состояний (кодов)], где:

n{\displaystyle n} — количество элементов в данном множестве различных элементов (количество возможных состояний, цифр, кодов в разряде),
k{\displaystyle k} — количество элементов в наборе (количество разрядов).
В двоичной системе кодирования (n=2) количество возможных состояний (кодов) равно :

(n+k−1)!k!(n−1)!=(2+k−1)!k!(2−1)!=(k+1)!k!1!=k+1{\displaystyle {\frac {\left(n+k-1\right)!}{k!\left(n-1\right)!}}={\frac {\left(2+k-1\right)!}{k!\left(2-1\right)!}}={\frac {\left(k+1\right)!}{k!1!}}=k+1}, [возможных состояний (кодов)], то есть

описывается линейной функцией:

Nkp(k)=k+1{\displaystyle N_{kp}(k)=k+1}, [возможных состояний (кодов)], где

k{\displaystyle k} — количество двоичных разрядов.
Например, в одном 8-битном байте (k=8) количество возможных состояний (кодов) равно:

Nkp(k)=k+1=8+1=9{\displaystyle N_{kp}(k)=k+1=8+1=9}, [возможных состояний (кодов)].

В случае позиционного кода, число комбинаций (кодов) k-разрядного двоичного кода равно числу размещений с повторениями:

Np(k)=A¯(2,k)=A¯2k=2k{\displaystyle N_{p}(k)={\bar {A}}(2,k)={\bar {A}}_{2}^{k}=2^{k}}, где

 k{\displaystyle \ k} — число разрядов двоичного кода.

Используя два двоичных разряда можно закодировать четыре различные комбинации: 00 01 10 11, три двоичных разряда — восемь: 000 001 010 011 100 101 110 111, и так далее.
При увеличении разрядности позиционного двоичного кода на 1, количество различных комбинаций в позиционном двоичном коде удваивается.

Двоичные коды являются комбинациями двух элементов и не являются двоичной системой счисления, но используются в ней как основа. Двоичный код также может использоваться для кодирования чисел в системах счисления с любым другим основанием. Пример: в двоично-десятичном кодировании (BCD) используется двоичный код для кодирования чисел в десятичной системе счисления.
При кодировании алфавитноцифровых символов (знаков) двоичному коду не приписываются весовые коэффициенты, как это делается в системах счисления, в которых двоичный код используется для представления чисел, а используется только порядковый номер кода из множества размещений с повторениями.

В системах счисления k-разрядный двоичный код, (k-1)-разрядный двоичный код, (k-2)-разрядный двоичный код и т. д. могут отображать одно и то же число. Например, 0001, 001, 01, 1 — одно и то же число — «1» в двоичных кодах с разным числом разрядов — k.

В таблице показаны первые 16 двоичных чисел и их соответствие десятичным и шестнадцатиричным числам.

Десятичное число	Шестнадцатеричное число	Двоичное число
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Пример «доисторического» использования кодов[править | править код]

Инки имели свою счётную систему кипу, которая физически представляла собой верёвочные сплетения и узелки. Генри Эртан обнаружил, что в узелках заложен некий код, более всего похожий на двоичную систему счисления^[1].

Сводная таблица ASCII — QuestHint

Символ	10-ный	16-ричный	двоичный	Символ	10-ный	16-ричный	двоичный
(null)	0	00	00000000	0	48	30	00110000
	1	01	00000001	1	49	31	00110001
	2	02	00000010	2	50	32	00110010
	3	03	00000011	3	51	33	00110011
	4	04	00000100	4	52	34	00110100
	5	05	00000101	5	53	35	00110101
	6	06	00000110	6	54	36	00110110
	7	07	00000111	7	55	37	00110111
	8	08	00001000	8	56	38	00111000
	9	09	00001001	9	57	39	00111001
	10	0A	00001010	:	58	3A	00111010
	11	0B	00001011	;	59	3B	00111011
	12	0C	00001100	<	60	3C	00111100
	13	0D	00001101	=	61	3D	00111101
	14	0E	00001110	>	62	3E	00111110
	15	0F	00001111	?	63	3F	00111111
	16	10	00010000	@	64	40	01000000
	17	11	00010001	A	65	41	01000001
	18	12	00010010	B	66	42	01000010
	19	13	00010011	C	67	43	01000011
	20	14	00010100	D	68	44	01000100
	21	15	00010101	E	69	45	01000101
	22	16	00010110	F	70	46	01000110
	23	17	00010111	G	71	47	01000111
	24	18	00011000	H	72	48	01001000
	25	19	00011001	I	73	49	01001001
	26	1A	00011010	J	74	4A	01001010
	27	1B	00011011	K	75	4B	01001011
	28	1C	00011100	L	76	4C	01001100
	29	1D	00011101	M	77	4D	01001101
	30	1E	00011110	N	78	4E	01001110
	31	1F	00011111	O	79	4F	01001111
пробел	32	20	00100000	P	80	50	01010000
!	33	21	00100001	Q	81	51	01010001
«	34	22	00100010	R	82	52	01010010
#	35	23	00100011	S	83	53	01010011
$	36	24	00100100	T	84	54	01010100
%	37	25	00100101	U	85	55	01010101
&	38	26	00100110	V	86	56	01010110
‘	39	27	00100111	W	87	57	01010111
(	40	28	00101000	X	88	58	01011000
)	41	29	00101001	Y	89	59	01011001
*	42	2A	00101010	Z	90	5A	01011010
+	43	2B	00101011	[	91	5B	01011011
,	44	2C	00101100	\	92	5C	01011100
—	45	2D	00101101	]	93	5D	01011101
.	46	2E	00101110	^	94	5E	01011110
/	47	2F	00101111	_	95	5F	01011111
`	96	60	01100000	Щ	153	99	10011001
a	97	61	01100001	Ъ	154	9A	10011010
b	98	62	01100010	Ы	155	9B	10011011
c	99	63	01100011	Ь	156	9C	10011100
d	100	64	01100100	Э	157	9D	10011101
e	101	65	01100101	Ю	158	9E	10011110
f	102	66	01100110	Я	159	9F	10011111
g	103	67	01100111	а	160	A0	10100000
h	104	68	01101000	б	161	A1	10100001
i	105	69	01101001	в	162	A2	10100010
j	106	6A	01101010	г	163	A3	10100011
k	107	6B	01101011	д	164	A4	10100100
l	108	6C	01101100	е	165	A5	10100101
m	109	6D	01101101	ж	166	A6	10100110
n	110	6E	01101110	з	167	A7	10100111
o	111	6F	01101111	и	168	A8	10101000
p	112	70	01110000	й	169	A9	10101001
q	113	71	01110001	к	170	AA	10101010
r	114	72	01110010	л	171	AB	10101011
s	115	73	01110011	м	172	AC	10101100
t	116	74	01110100	н	173	AD	10101101
u	117	75	01110101	о	174	AE	10101110
v	118	76	01110110	п	175	AF	10101111
w	119	77	01110111	№	176	B0	10110000
x	120	78	01111000	Ђ	177	B1	10110001
y	121	79	01111001	Ѓ	178	B2	10110010
z	122	7A	01111010	Ё	179	B3	10110011
{	123	7B	01111011	Є	180	B4	10110100
|	124	7C	01111100	Ѕ	181	B5	10110101
}	125	7D	01111101	І	182	B6	10110110
~	126	7E	01111110	Ї	183	B7	10110111
	127	7F	01111111	Ј	184	B8	10111000
А	128	80	10000000	Љ	185	B9	10111001
Б	129	81	10000001	Њ	186	BA	10111010
В	130	82	10000010	Ћ	187	BB	10111011
Г	131	83	10000011	Ќ	188	BC	10111100
Д	132	84	10000100	Ґ	189	BD	10111101
Е	133	85	10000101	Ў	190	BE	10111110
Ж	134	86	10000110	Џ	191	BF	10111111
З	135	87	10000111	А	192	C0	11000000
И	136	88	10001000	Б	193	C1	11000001
Й	137	89	10001001	В	194	C2	11000010
К	138	8A	10001010	Г	195	C3	11000011
Л	139	8B	10001011	Д	196	C4	11000100
М	140	8C	10001100	Е	197	C5	11000101
Н	141	8D	10001101	Ж	198	C6	11000110
О	142	8E	10001110	З	199	C7	11000111
П	143	8F	10001111	И	200	C8	11001000
Р	144	90	10010000	Й	201	C9	11001001
С	145	91	10010001	К	202	CA	11001010
Т	146	92	10010010	Л	203	CB	11001011
У	147	93	10010011	М	204	CC	11001100
Ф	148	94	10010100	Н	205	CD	11001101
Х	149	95	10010101	О	206	CE	11001110
Ц	150	96	10010110	П	207	CF	11001111
Ч	151	97	10010111	Р	208	D0	11010000
Ш	152	98	10011000	С	209	D1	11010001
Т	210	D2	11010010	щ	233	E9	11101001
У	211	D3	11010011	ъ	234	EA	11101010
Ф	212	D4	11010100	ы	235	EB	11101011
Х	213	D5	11010101	ь	236	EC	11101100
Ц	214	D6	11010110	э	237	ED	11101101
Ч	215	D7	11010111	ю	238	EE	11101110
Ш	216	D8	11011000	я	239	EF	11101111
Щ	217	D9	11011001	ј	240	F0	11110000
Ъ	218	DA	11011010	Ј	241	F1	11110001
Ы	219	DB	11011011	т	242	F2	11110010
Ь	220	DC	11011100	у	243	F3	11110011
Э	221	DD	11011101	ф	244	F4	11110100
Ю	222	DE	11011110	х	245	F5	11110101
Я	223	DF	11011111	ц	246	F6	11110110
р	224	E0	11100000	ч	247	F7	11110111
с	225	E1	11100001	ш	248	F8	11111000
т	226	E2	11100010	щ	249	F9	11111001
у	227	E3	11100011	ъ	250	FA	11111010
ф	228	E4	11100100	ы	251	FB	11111011
х	229	E5	11100101	ь	252	FC	11111100
ц	230	E6	11100110	э	253	FD	11111101
ч	231	E7	11100111	ю	254	FE	11111110
ш	232	E8	11101000		255	FF	11111111

Двоично-десятичный код — Википедия

Материал из Википедии — свободной энциклопедии

Перевод десятичных цифр в двоично-десятичный код

Двоично-десятичный код (англ. binary-coded decimal), BCD, 8421-BCD  — форма записи рациональных чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода.

Например, десятичное число 311₁₀ будет записано в двоичной системе счисления в двоичном коде как 1 0011 0111₂, а в двоично-десятичном коде как 0011 0001 0001_BCD.

При помощи 4 бит можно закодировать 16 цифр. Из них используются 10. Остальные 6 комбинаций в двоично-десятичном коде являются запрещёнными. Таблица соответствия двоично-десятичного кода и десятичных цифр:

Двоично-десятичный код также применяется в телефонной связи. В этом случае кроме десятичных цифр кодируются символы ‘*’ или ‘#’, или любые другие. Для записи этих символов в двоично-десятичном коде используются запрещенные комбинации:

Преимущества[править | править код]

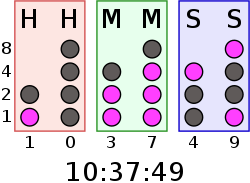Часы с двоично-десятичной системой индикации. В этих часах каждая колонка отображает десятичное число в двоично-десятичной системе.

• Упрощён вывод чисел на индикацию — вместо последовательного деления на 10 требуется просто вывести на индикацию каждый полубайт. Аналогично, проще ввод данных с цифровой клавиатуры.
• Для дробных чисел (как с фиксированной, так и с плавающей запятой) при переводе в человекочитаемый десятичный формат и наоборот не теряется точность.
• Упрощены умножение и деление на 10, а также округление.

По этим причинам двоично-десятичный формат применяется в калькуляторах — калькулятор в простейших арифметических операциях должен выводить в точности такой же результат, какой подсчитает человек на бумаге.

Недостатки[править | править код]

• Требует больше памяти.
• Усложнены арифметические операции. Так как в 8421-BCD используются только 10 возможных комбинаций 4-битового поля вместо 16, существуют запрещённые комбинации битов: 1010(10₁₀), 1011(11₁₀), 1100(12₁₀), 1101(13₁₀), 1110(14₁₀) и 1111(15₁₀).

Поэтому, при сложении и вычитании чисел формата 8421-BCD действуют следующие правила:

1. При сложении двоично-десятичных чисел каждый раз, когда происходит перенос бита в старший полубайт, необходимо к полубайту, от которого произошёл перенос, добавить корректирующее значение 0110 (= 6₁₀ = 16₁₀ — 10₁₀: разница количеств комбинаций полубайта и используемых значений).
2. При сложении двоично-десятичных чисел каждый раз, когда встречается недопустимая для полубайта комбинация (число, большее 9), необходимо к каждой недопустимой комбинации добавить корректирующее значение 0110 с разрешением переноса в старшие полубайты.
3. При вычитании двоично-десятичных чисел, для каждого полубайта, получившего заём из старшего полубайта, необходимо провести коррекцию, отняв значение 0110.

Пример операции сложения двоично-десятичных чисел:

Требуется: Найти число A = D + C, где D = 3927, C = 4856

Решение: Представим числа D и C в двоично-десятичной форме:
D = 3927₁₀ = 0011 1001 0010 0111_BCD
C = 4856₁₀ = 0100 1000 0101 0110_BCD

Суммируем числа D и С по правилам двоичной арифметики:

       *         ** 
  0011 1001 0010 0111
+ 0100 1000 0101 0110
  ___________________
= 1000 0001 0111 1101 - Двоичная сумма
+      0110      0110 - Коррекция
  ___________________
  1000 0111 1000 0011

‘*’ — тетрада, из которой был перенос в старшую тетраду

‘**’ — тетрада с запрещённой комбинацией битов

В тетраду, помеченную символом *, добавляем шестёрку, так как по правилам двоичной арифметики перенос унёс с собой 16, а по правилам десятичной арифметики должен был унести 10. В тетраду, помеченную символом **, добавляем шестёрку и разрешаем распространение переноса, так как комбинация битов 1101 (что соответствует десятичному числу 13) является запрещённой.

В системе кодирования «2 из 5»^[en] одна десятичная цифра кодируется 5 битами, из которых 2 бита установлены в 1, а 3 бита — в 0, что даёт ровно 10 комбинаций. Такая система обеспечивает лучшее обнаружение ошибок, поскольку изменение одного бита всегда даст недопустимую комбинацию; также всегда обнаруживаются однонаправленные изменения (несколько изменений 0→1 или 1→0). Кодирование «2 из 5» использовалось в компьютерах серий IBM 7070, IBM 7072 и IBM 7074; также применяется в некоторых странах для маркирования почты штрих-кодом.

Уплотнённые десятичные числа^[en] позволяют разместить 3 десятичные цифры в 10 битах (2¹⁰=1024 комбинации, что достаточно для 3 десятичных цифр), причём кодирование устроено так, что преобразование между 10-битным кодом и тремя отдельными десятичными цифрами можно осуществить с помощью простой и быстрой логической схемы. Такое кодирование используется в десятичных числах с плавающей запятой, описанных в стандарте IEEE 754-2008.

Кодирование информации. Двоичное кодирование. Единицы измерения информации

Тема: Информация вокруг нас

Урок: Кодирование информации. Двоичное кодирование. Единицы измерения информации

На данном уроке будут рассмотрены следующие вопросы:

1. Кодирование как изменение формы представления информации.

2. Как компьютер распознает информацию?

3. Как измерить информацию?

4. Единицы измерения информации.

 

В мире кодов 

Зачем люди кодируют информацию? 

1. Скрыть ее от других (зеркальная тайнопись Леонардо да Винчи, военные шифровки).

2. Записать информацию короче (стенография, аббревиатура, дорожные знаки).

3. Для более легкой обработки и передачи (азбука Морзе, перевод в электрические сигналы — машинные коды).

Кодирование — это представление информации с помощью некоторого кода.

Код — это система условных знаков для представления информации. 

 

Способы кодирования информации 

1. Графический (см. Рис. 1) (с помощью рисунков и знаков). 

Рис. 1. Система сигнальных флагов (Источник)

 

2. Числовой (с помощью чисел).

Например: 11001111 11100101.

 

3. Символьный (с помощью символов алфавита).

Например: НКМБМ ЧГЁУ. 

Декодирование — это действие по восстановлению первоначальной формы представления информации. Для декодирования необходимо знать код и правила кодирования.

Средством кодирования и декодирования служит кодовая таблица соответствия. Например, соответствие в различных системах счисления — 24 — XXIV, соответствие алфавита каким-либо символам (Рис. 2). 

Рис. 2. Пример шифра (Источник)

 

Примеры кодирования информации 

Примером кодирования информации является азбука Морзе (см. Рис. 3). 

 

Рис. 3. Азбука Морзе (Источник)

 

В азбуке Морзе используется всего 2 символа — точка и тире (короткий и длинный звук).

Еще одним примером кодирования информации является флажковая азбука (см. Рис. 4). 

Рис. 4. Флажковая азбука (Источник)

 

Также примером является азбука флагов (см. Рис. 5). 

Рис. 5. Азбука флагов (Источник)

 

Всем известный пример кодирования — нотная азбука (см. Рис. 6). 

Рис. 6. Нотная азбука (Источник)

 

Рассмотрим следующую задачу:

Используя таблицу флажковой азбуки (см. Рис. 7), необходимо решить следующую задачу: 

Рис. 7

Старший помощник Лом сдает экзамен капитану Врунгелю. Помогите ему прочитать следующий текст (см. Рис. 8): 

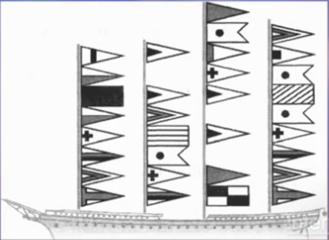
Рис. 8

Представление информации происходит в различных формах в процессе восприятия окружающей среды живыми организмами и человеком, в процессах обмена информацией между человеком и человеком, человеком и компьютером, компьютером и компьютером. 

Кодирование — это операция преобразования знаков или групп знаков одной знаковой системы в знаки или группы знаков другой знаковой системы. 

Примером может служить язык жестов (см. Рис. 9). 

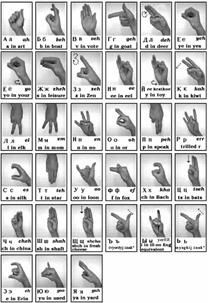
Рис. 9. Азбука жестов (Источник) 

Вокруг нас существуют преимущественно два сигнала, например:

— Светофор: красный — зеленый;

— Вопрос: да — нет;

— Лампа: горит — не горит;

— Можно — нельзя;

— Хорошо — плохо;

— Истина — ложь;

— Вперед — назад;

— Есть — нет;

— 1 — 0. 

Всё это сигналы, обозначающие количество информации в 1 бит.

1 бит — это такое количество информации, которое позволяет нам выбрать один вариант из двух возможных.

Компьютер — это электрическая машина, работающая на электронных схемах. Чтобы компьютер распознал и понял вводимую информацию, ее надо перевести на компьютерный (машинный) язык.

Алгоритм, предназначенный для исполнителя, должен быть записан, то есть закодирован, на языке, понятном компьютеру.

Это электрические сигналы: проходит ток или не проходит ток.

Машинный двоичный язык — последовательность «0» и «1». Каждое двоичное число может принимать значение 0 или 1.

Каждая цифра машинного двоичного кода несет количество информации, равное 1 бит. 

Устройства	1	0
Электронные схемы	Проводят электрический ток	Не проводят электрический ток
Участок поверхности магнитного носителя (жесткий диск, дискета)	Намагничен	Размагничен
Участок поверхности лазерного диска	Отражает луч	Не отражает луч

Двоичное число, которое представляет наименьшую единицу информации, называется бит. Бит может принимать значение либо 0, либо 1. Наличие магнитного или электронного сигнала в компьютере означает 1, отсутствие 0.

Строка из 8 битов называется байт. Эту строку компьютер обрабатывает как отдельный символ (число, букву).

Рассмотрим пример. Слово ALICE состоит из 5 букв, каждая из которых на языке компьютера представлена одним байтом (см. Рис. 10). Стало быть, Alice можно измерить как 5 байт. 

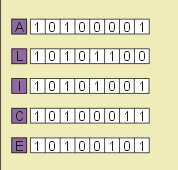
Рис. 10. Двоичный код (Источник) 

Кроме бита и байта, существуют и другие единицы измерения информации.

Название	Сокращенное обозначение	Размер в байтах	Степень
Килобайт	Кбайт, Kb	1 024	210
Мегабайт	Мбайт, Mb	1 048 576	220
Гигабайт	Гбайт, Gb	1 079 741 824	230
Терабайт	Тбайт, Tb	1 099 511 627 776	240

 

Список литературы

1. Босова Л.Л. Информатика и ИКТ: Учебник для 5 класса. – М.: БИНОМ. Лаборатория знаний, 2012.

2. Босова Л.Л. Информатика: Рабочая тетрадь для 5 класса. – М.: БИНОМ. Лаборатория знаний, 2010.

3. Босова Л.Л., Босова А.Ю. Уроки информатики в 5-6 классах: Методическое пособие. – М.: БИНОМ. Лаборатория знаний, 2010.

 

Рекомендованные ссылки на ресурсы интернет 

1. Учительский портал (Источник).

2. Фестиваль «Открытый урок» (Источник).

3. Информатика в школе (Источник).

 

Домашнее задание 

1. §1.6, 1.7 (Босова Л.Л. Информатика и ИКТ: Учебник для 5 класса).

2. Стр. 28, задания 1, 4; стр. 30, задания 1, 4, 5, 6 (Босова Л.Л. Информатика и ИКТ: Учебник для 5 класса).

Что такое двоичный код | Vunderkind.Info

Задача сегодняшней публикации – разобраться в том, что такое двоичный код, для каких целей и где используется двоичный код и зачем вообще он нужен.

Двоичный код – это система обозначений из двух элементов, различные комбинации которых служат для представления (кодировки) информации.

В качестве элементов системы наиболее часто выступают цифры «0» и «1». Но в действительности обозначения могут быть произвольными, исходя из характера сведений, которые требуется кодировать.

Главное – чтобы соответствующие элементы обозначали взаимоисключающие либо противоположные по значению данные.

Великолепным примером двоичного кода могут служить любые пары антонимов, к примеру, «да/нет», «белое/черное», «включено/выключено» и т.д.

Для описания двоичного кода используется понятие разряда (более точно – двоичного разряда), объединяющего целочисленную группу элементов двоичного кода.

Например, в системе, использующей базовые элементы 0 и 1, два двоичных разряда могут быть представлены следующими четырьмя комбинациями: 00, 01, 10 и 11.

Три двоичных разряда могут иметь следующий вид: 000, 001, 010, 011, 100, 101, 110 и 111.

Число двоичных разрядов может быть сколь угодно большим в зависимости от характера решаемых задач и объема кодируемой информации.

Форма представления данных с помощью двоичных разрядов характерна для позиционного двоичного кода, лежащего в основе двоичной системы счисления, применяемой сплошь и рядом во всех типах вычислительной техники.

Увеличение разрядности на единицу приведет к удвоению числа комбинаций в позиционном двоичном коде.

При двух символах (смотри примеры выше) мы имеем 4 комбинации, при трех – 8 комбинаций, при четырех – 16 комбинаций, при n символах – 2ⁿ комбинаций.

С помощью двух символов можно закодировать практически любую информацию. Доказательством тому служат современные компьютеры, работа которых невозможна без такой кодировки.

Характерная особенность систем счисления, использующих разрядный двоичный код, заключается в возможности обозначения одного и того же числа различной комбинацией символов, отличающихся между собой по разрядности.

Например, в двоичной системе счисления единицу можно представить по-разному: 1, 01, 001, 0001 и т.д.

Нумерация двоичных разрядов осуществляется справа налево.

Если взять двоичный код 01011, то первый разряд будет иметь значение 1, второй разряд – 1, третий разряд – 0, четвертый – 1 и пятый разряд – 0:

Примеры двоичного кода

С помощью трех двоичных разрядов можно обозначить восемь десятичных чисел от 0 до 7:

0 = 000
1 = 001
2 = 010
3 = 011
4 = 100
5 = 101
6 = 110
7 = 111

Эта таблица отражает перевод десятичных чисел в двоичный код.

Фото 1. Выключатели — прекрасный пример двоичного кода

Поскольку число двоичных разрядов ничем не ограничено, с помощью такой кодировки можно зашифровать любое привычное нам десятичное число.

Чтобы перевести двоичный код обратно в десятичный, нужно 1-ый разряд двоичного кода умножить на 1 (или на 2⁰), 2-ой разряд – на 2 (или на 2¹), третий разряд – на 4 (или на 2²), n-ый разряд — на 2^n-1, а затем сложить полученные значения.

Примеры:

111 → 1 * 2² + 1 * 2¹ + 1 * 2⁰ = 4 + 2 + 1 = 7

101 → 1 * 2² + 0 * 2¹ + 1 * 2⁰ = 4 + 0 + 1 = 5

Зачем нужен двоичный код

Основное назначение двоичного кода – шифрование и кодирование информации.

Его главные преимущества – минимальное число символов, используемых для кодирования информации, и удобство – с машинной точки зрения – оперирования зашифрованными с их помощью данными.

Допустим, нам необходимо закодировать фразу «ХОЛОДНОЕ ЛЕТО».

Установим произвольные соответствия букв двоичному коду: Х – 000, О – 001, Л – 010, Д – 011, Н – 100, Е – 101, Т – 111.

Фото 2. Двоичный код лежит в основе двоичной системы счисления

Тогда закодированная фраза примет следующий вид: 000001010001011100001101010101111001 (36 символов).

Если получатель зашифрованного кода знает, что в основе кодировки каждой буквы лежат три двоичных разряда, то расшифровать фразу ему не составит никакого труда.

В данном случае мы имеем дело с однозначно декодируемым кодом (то есть код может быть расшифрован одним единственным способом).

Для сокращения длины кода может применяться неравномерный двоичный код.

Тогда кодировщик сознательно отступает от принципа разрядности, присваивая буквам произвольное число разрядов.

Например, если Х будет иметь обозначение 01, О – 00, Л – 100, Д – 101, Н – 110, Е – 111, Т – 1111, то фразе «ХОЛОДНОЕ ЛЕТО» будет соответствовать строка 01001000010111000111100111111100 (32 символа).

В данной фразе будет однозначно декодироваться фрагмент «ХОЛОДНО», после чего дешифровщику придется ломать голову над выбором приемлемой трактовки кода: «Е ЛЕТО», «Е ЛЕЕЛ», «Е ЛТЕО», «ТОЕЕЛ» и т.д.

Данный пример указывает на проблемы с использованием непродуманных комбинаций двоичного кода.

При правильном же подборе кодов неравномерный двоичный код позволяет не только сократить объем передаваемого сообщения, но и начать его дешифровку после поступления уже первых нескольких символов, не дожидаясь пока сообщение будет получено в полном объеме.

Виды двоичных кодов

Представление в памяти компьютера целочисленных значений производится с помощью беззнакового двоичного кода, основанного на представлении двоичных разрядов степенями двойки.

При этом значение минимального числа в n-разрядном двоичном коде будет равно 0, а максимального вычисляться по формуле 2ⁿ-1.

К примеру, для шестнадцатиразрядного кода допустимыми будут значения чисел от 0 до 65535.

На практике приходится решать задачи посложнее.

Фото 3. С помощью двоичного кода можно закодировать все что угодно

Машине или компьютеру достаточно трудно объяснить разницу между положительными и отрицательными числами. Отдельного представления требуют и числа с плавающей запятой, дробные или трансцендентные числа.

Инженеры придумали способ, как обходить эти проблемы, не выходя за пределы использования двоичного кода. Для решения озвученных проблем используется знаковый двоичный код.

В частности, для определения знака числа используется старший разряд в слове.

Если слово начинается с символа «0», значит число положительное (имеет знак «+»), если с символа «1», значит оно – отрицательное (имеет знак «-»).

При использовании шестнадцатиразрядного кода в таком случае мы сможем зашифровать числа в диапазоне от -32767 до +32767.

Недостаток знакового двоичного кода кроется в необходимости раздельной обработки цифрового и знакового разрядов, что заставляет разработчиков программного обеспечения прибегать к усложненным алгоритмам обработки данных.

Как следствие, программный код увеличивается в объеме, а скорость его работы замедляется.

Видео о двоичном коде:

Единично-десятичный код

Каждый разряд десятичного числа записывается в единичном коде, при этом между символами единично-десятичного кода, отображающими один разряд десятичного кода, ставится пробел.

Этот код неравномерный, но может быть преобразован в равномерный. Для этого каждый разряд десятичного числа кодируется равномерным единичным кодом. Примеры единично-десятичного кода представлена в табл. 4.4.

 Таблица 4.4

Примеры единично-десятичного кода

Десятичное число	Кодовые комбинации единично-десятичного кода
2 3 4	11 111 1111
3 1 5	111 1 11111

 

13.Двоичный нормальный (натуральн ый) код

Этот код имеет широкое распространение в различных областях цифровой техники. Он называется нормальным (натуральным) потому, что весовой коэффициент младшего разряда у него равен единице, а весовой коэффициент каждого последующего разряда по сравнению с предыдущим возрастает в два раза.

Максимально возможное число комбинаций двоичного кода N=2ⁿ, где n – количество разрядов. Вес старшего разряда равен 2^n-1. Таблица четырёхразрядного двоичного натурального кода представлена в табл. 4.5.

 Таблица 4.5

Таблица четырёхразрядного двоичного натурального кода

Десятичное число	Двоичный натуральный код
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1
10	1	0	1	0
11	1	0	1	1
12	1	1	0	0
13	1	1	0	1
14	1	1	1	0
15	1	1	1	1

Достоинства двоичного кода:

1. Высокая надежность передачи кодовых символов по сравнению с кодами, имеющими большее основание.

2. Простота аппаратной реализации кодовых комбинаций. 

Недостаток – плохая ассоциативная значимость кодовых комбинаций для человека по сравнению с десятичным кодом.

Двоично-десятичные коды

Каждый разряд десятичного числа записывается в виде комбинаций двоичного кода, десятичный разряд отображается четырьмя двоичными разрядами.

 Таблица 4.6

Примеры двоично-десятичного кода с весовыми коэффициентами 8-4-2-1

Десятичное число	Десятки				Единицы
0	0	0	0	0	0	0	0	0
9	0	0	0	0	1	0	0	1
10	0	0	0	1	0	0	0	0
25	0	0	1	0	0	1	0	1
99	1	0	0	1	1	0	0	1

 

Четыре двоичных разряда, отображающие один десятичный разряд, называются тетрадой. Число тетрад двоично-десятичного кода равно числу отображаемых десятичных разрядов.

Двоично-десятичный код соединяет в себе достоинства двоичного кода с лучшей ассоциативностью для человека. Лучшая ассоциативная значимость формируется благодаря тому, что пользователь легко может запомнить девять ненулевых кодовых комбинаций двоичного кода, используемых для отображения одного десятичного разряда. Именно поэтому данный код получил широкое распространение.

Приведенный выше в табл. 4.6 пример двоично-десятичного кода дан для весовых коэффициентов 8-4-2-1, применяемых для кодирования одного десятичного разряда. Эти весовые коэффициенты однозначно определяют любое десятичное число.

Иногда применяют двоично-десятичные коды с другими весовыми коэффициентами, например 2-4-2-1 или 4-2-2-1. С помощью этих весовых коэффициентов одно и тоже десятичное число можно записать несколькими кодовыми комбинациями (табл. 4.7).

Таблица 4.7

Таблица двоично-десятичных кодов

Десятичное число	Весовые коэффициенты
	2-4-2-1		4-2-2-1
	Первый вариант	Второй вариант	Первый вариант	Второй вариант
2	0010	1000	0100	0010
3	0011	1001	0011	0101
4	0100	1010	0110	1000
5	0101	1011	1001	0111
6	0110	1100	1100	1010
7	0111	1101	1011	1101

Код 4-2-2-1 обладает свойством самодополняемости, которое означает, что кодовая комбинация, полученная из исходной путем замены 0 на 1 и 1 на 0 (инвертированный код) в каждом разряде, всегда дополняет исходное число до 9 (1111). Благодаря этому свойству указанные коды и получили распространение в телемеханике.

Двоично-десятичный код с весами 7-4-2-1 в каждой кодовой комбинации имеет не более двух единиц, что позволяет использовать это свойство для повышения помехоустойчивости передачи.