PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.
 1 Электростатика
1 Электростатика - 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 4.
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.
 6 СТО
6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
|
Заглавная страница
КАТЕГОРИИ: Археология Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 10 из 12Следующая ⇒
Сила тока: .
. Вектор направлен как и вектор . 10.3. ЭДС источника . φ1 = φ2, если траектория замкнута. . где q — заряд, над которым сторонние силы совершили работу Aст.сил. . Единица ЭДС — такая же, как и единица потенциала — вольт. Закон Ома для участка цепи
R — сопротивление проводника. .
, ρ — удельное сопротивление (из таблиц). . Закон Ома в дифференциальной форме Закон Ома (10.4) для элементарного объема проводника. См. (9.7) Используя (10.2) получим:
Закон Джоуля-Ленца в дифференциальной форме Количество тепла, выделяемое в элементарном объеме с сопротивлением R при прохождении тока I в течении времени dt:
См. (10.2), (10.4), (10.5). Закон Ома для неоднородного участка цепи Неоднородный участок — участок, содержащий ЭДС.
dA12 переходит в джоулево тепло I2Rdt (10.6): , Закон Ома для неоднородного участка цепи: .
Магнетизм. Уравнения Максвелла Магнитное поле в вакууме Магнитное поле в веществе Уравнения Максвелла Магнитное поле в вакууме Движущийся заряд — источник магнитного поля, индикатор магнитного поля — другой движущийся заряд
Проводник с током создает только магнитное поле, другой проводник с током реагирует только на магнитное поле
Рамка с током как регистратор магнитного поля. Вектор магнитной индукции
Вращающий момент (7.1) .
11.3.1. Линии магнитной индукции: а) замкнуты, т.к. в природе нет магнитных зарядов; Закон Био-Савара-Лапласа
Модуль вектора : . Применение закона Био-Савара-Лапласа для нахождения магнитного поля прямого тока Независимо от положения на проводнике все направлены в одну сторону — от нас. Значит, — без векторов! Для бесконечного проводника α1 = 0, α2 = π, Сos α1 — Сos α2 = 2 . Теорема о циркуляции вектора В Циркуляция вектора В по произвольному контуру равна алгебраической сумме токов, охватываемых контуром, помноженной на μ0. 11.5.1. Циркуляция вектора — это интеграл вида: ⇐ Предыдущая3456789101112Следующая ⇒ Читайте также: Техника нижней прямой подачи мяча Комплекс физических упражнений для развития мышц плечевого пояса Стандарт Порядок надевания противочумного костюма Общеразвивающие упражнения без предметов |
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 712; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Презентация «Электрический ток и сила тока» по учебнику Касьянов В.А. профильный уровень
Электрический ток Сила тока.
Физика 11 класс
Под ред. В.А. Касьянова
Движение зарядов в проводнике
Проводник — железнодорожный служащий, сопровождающий пассажирский вагон в пути и обслуживающий пассажиров.
Но это не тема нашего урока!
Проводник (электричество) — вещество, проводящее электрический ток, или элемент электрической цепи, изготовленный из такого вещества.
Движение зарядов в проводнике
Для существования электрического тока необходимы свободные заряды – носители заряда, например заряженные частицы: положительные и отрицательные ионы, электроны.
Количество протонов меньше количества электронов – отрицательный ион
Количество протонов равно количеству электронов – нейтральный атом.
Количество протонов больше количества электронов – положительны ион
Свободный электрон -это электрон, потерявший связь со своим атомом и поэтому может перемещаться по всему проводнику.
Движение зарядов в проводнике
Электрический ток – упорядоченное (направленное) движение заряженных частиц.
Условия существования постоянного электрического тока
Из просмотренного видеофрагмента можно выделить два условия возникновения и существования электрического тока:
- Наличиее свободных зарядов.
- Постоянное во времени электрическое поле (разность потенциалов)
Электрический ток
В проводнике помещенном в электрическое поле происходит наложение упорядоченного движения зарядов на хаотическое.
Аналогия:
Листовки сброшенные с самолета. Каждая из них летит хаотично, но все вместе они двигаются к земле.
За направление тока принимают направление упорядоченного движения положительно заряженных частиц. (от «+» к «-»)
Сила тока
Одно из действий тока: тепловое.
Сила тока
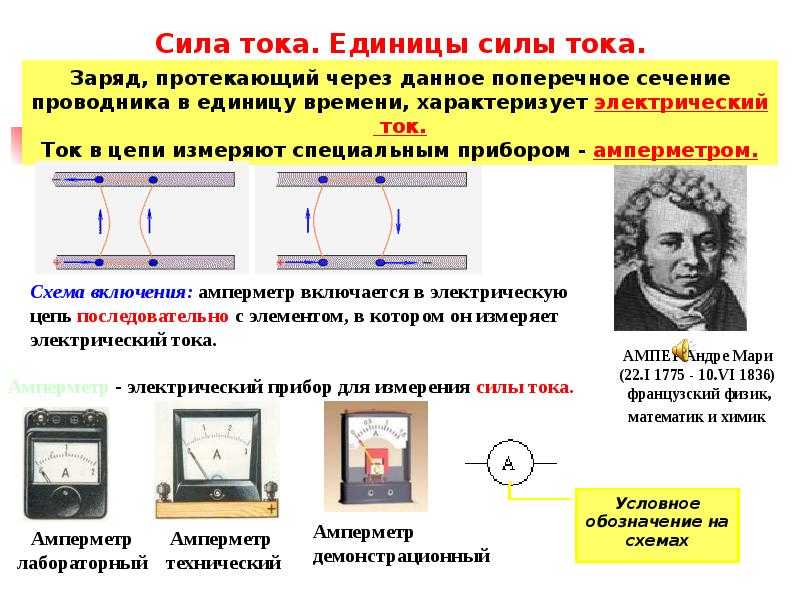
Чем больше зарядов (количество электричества) проходит через поперечное сечение проводника за 1 сек, тем ярче проявляется действие тока (нагрев, магнит т.д.). Тем больше сила тока .
Сила тока в данный момент времени – скалярная физическая величина, равная пределу отношения электрического заряда, прошедшего через поперечное сечение проводника, к промежутку времени его прохождения:
Используем при решении задач
Строгое определение
Сила тока
Из строгого определения силы тока следует, что сила тока это производная от заряда
Единица силы тока – ампер (А):
1 А= 1 Кл/с
Андре Мари (22. 1.1775, Лион, — 10.6.1836, Марсель), французский физик и математик, один из основоположников электродинамики
1.1775, Лион, — 10.6.1836, Марсель), французский физик и математик, один из основоположников электродинамики
Как-то раз он шел по парижской улице и производил сложные подсчеты в голове. Вдруг перед Ампером оказалась черная доска, точно такая, как в университетской аудитории! Профессор достал из кармана кусок мела и стал писать формулы. Доска сдвинулась с места, Ампер пошел за ней, продолжая свои вычисления. Доска начала набирать скорость; профессор побежал за ней, спеша окончить расчет… Наконец, Ампера отвлек веселый смех прохожих, раздававшийся со всех сторон. Он остановился, а доска унеслась за угол! Оказалось, что ученый писал свои формулы… на задней стенке черной кареты
Связь силы тока со скоростью упорядоченного движения
Рассмотрим, как зависит сила тока от скорости упорядоченного движения свободных зарядов.
Выделим участок проводника площадью сечения S и длиной Δl (рис. 1). Заряд каждой частицы q 0
Введем обозначения:
v – скорость упорядоченного движения (скорость с которой все заряды двигаются от одного полюса к другому)
S – площадь сечения проводника.
– расстояние которое проходят заряды со скоростью v за время
n – концентрация зарядов (количество зарядов в 1 м 3 )
Тогда получается, что заряд который пройдет через сечение 2 за время :
Связь силы тока со скоростью упорядоченного движения
Если скорость упорядоченного движения не меняется, то не меняется и сила тока
Постоянный электрический ток – ток, сила тока и направление которого не изменяется со временем.
Зависимость силы тока от времени I(t) для постоянного тока
I
t
Площадь под графиком зависимости силы тока от времени равна заряду, протекающему через сечение проводника
Задачи
Задача 1.
Какой заряд пройдет через поперечное сечение проводника за 1 мин если сила тока в проводнике 2 А?
Задачи
Задача 1.
Какой заряд пройдет через поперечное сечение проводника за 1 мин если сила тока в проводнике 2 А?
Дано:
Сила тока
t=60 c
I=2 А
q -?
— заряд
, но пусть будет…
Задачи
Задача 2.
Задачи
Задача 2.
Для решения задачи нужно вспомнить правило дискретности заряда
Дано:
e- заряд электрона = 1,6*10 -19 Кл,
N-количество электронов
t=1 c
I=1,6 А
Сила тока
N -?
— заряд
, но пусть …..
Задачи
Задача 3.
Сила тока, протекающего по проводнику в течении года, равна 1 А, найдите массу электронов, проходящих за этот промежуток времени сквозь поперечное сечение проводника. Отношение заряда электрона к его массе e/m e =1,76*10 11 Кл/кг.
Отношение заряда электрона к его массе e/m e =1,76*10 11 Кл/кг.
Задачи
Задача 3.
Сила тока, протекающего по проводнику в течении года, равна 1 А, найдите массу электронов, проходящих за этот промежуток времени сквозь поперечное сечение проводника. Отношение заряда электрона к его массе e/m e =1,76*10 11 Кл/кг.
Дано:
Дано:
t=1 год
=31,536*10 6 c
Масса всех электронов
I=1 А
N – количество всех электронов, прошедших за год по проводнику. Возьмем из предыдущей задачи.
m -?
, но интереснее …..
За весь год всего 18 г электронов…..
Задачи
Задача 4.
В проводнике, площадь поперечного сечения которого 1 мм 2 , сила тока 1,6 А. Концентрация электронов в проводнике 10 28 м -3 при температуре 20˚С. Найдите среднюю скорость направленного движения электронов и сравните ее с тепловой скоростью.
Концентрация электронов в проводнике 10 28 м -3 при температуре 20˚С. Найдите среднюю скорость направленного движения электронов и сравните ее с тепловой скоростью.
Задачи
Задача 4.
В проводнике, площадь поперечного сечения которого 1 мм 2 , сила тока 1,6 А. Концентрация электронов в проводнике 10 28 м -3 при температуре 20˚С. Найдите среднюю скорость направленного движения электронов и сравните ее с тепловой скоростью.
Дано:
Дано:
S=1 мм 2
=1*10 -6 м 2
I=1,6 А
n=10 28 м -3
=293 K
T= 20˚С
=1 мм/с
v д -?
v-?
=11,5*10 4 м/с
Задачи
Задача 5.
За 4 с сила тока в проводнике линейно возросла с 1 до 5 А. Постройте график зависимости силы тока от времени. Какой заряд прошел через поперечное сечение проводника за это время?
Задачи
Задача 5.
За 4 с сила тока в проводнике линейно возросла с 1 до 5 А. Постройте график зависимости силы тока от времени. Какой заряд прошел через поперечное сечение проводника за это время?
I,A
5
1
t,c
4
Площадь синей трапеции и есть заряд прошедший через сечение проводника.
Что такое плотность тока
Электрические провода, находящиеся под напряжением, постоянно испытывают определенную нагрузку. Поэтому очень часто возникает вопрос, что такое плотность тока и каким образом она влияет на качество электроснабжения. Фактически данная величина характеризует степень электрической нагрузки проводников. Она позволяет предотвратить излишние потери при прокладке кабельных линий. Во время использования устройств с высокой частотой, следует учитывать наличие дополнительных электродинамических эффектов.
Во время использования устройств с высокой частотой, следует учитывать наличие дополнительных электродинамических эффектов.
Плотность электрического тока
Под действием электрического поля начинается упорядоченное перемещение зарядов, известное всем, как электрический ток. Обычно для движения зарядов используется какая-либо среда, которая называется проводником и является носителем тока.
Плотность тока совместно с другими факторами характеризует движение зарядов. Формула плотности тока дает описание электрического заряда, переносимого в течение 1 секунды через определенное сечение проводника, направленного перпендикулярно этому току.
Таким образом, с физической точки зрения плотность тока — это заряды, в определенном количестве протекающие через установленную единицу площади в период единицы времени. Данный параметр является векторной величиной и представляется в виде соотношения силы тока и площади поперечного сечения проводника, по которому и протекает этот ток. Модульное значение плотности тока будет равно: j = I/S. В этой формуле j является модулем вектора, I – силой тока, S – площадью поперечного сечения.
Модульное значение плотности тока будет равно: j = I/S. В этой формуле j является модулем вектора, I – силой тока, S – площадью поперечного сечения.
Векторы плотности тока и скорости движения токообразующих зарядов имеют одинаковое направление, если заряды обладают положительным значением и противоположное – когда они отрицательные.
В чем измеряется плотность тока? В качестве единицы измерения используется А/мм2. Данная величина применяется на практике, в основном, для принятия решения о выборе того или иного проводника в соответствии с его способностями выдерживать те или иные нагрузки. плотность играет важную роль, поскольку каждый проводник обладает сопротивлением. В результате потерь тока происходит нагрев проводника. Чрезмерные потери приводят к критическому нагреванию, вплоть до расплавления жил.
Для предотвращения подобных ситуаций, каждый потребитель рассчитывается на определенную плотность, по которой подбирается и оптимальное сечение проводника. Во время проектирования, помимо расчетных формул, используются уже готовые таблицы, содержащие все необходимые исходные данные, на основе которых можно получить конечный результат.
Следует помнить, что у разных проводников неодинаковая плотность электрического тока. В современных условиях практикуется использование преимущественно медных проводов, где это значение не превышает 6-10 А/мм2. Это приобретает особую актуальность в условиях длительной эксплуатации, когда проводка должна работать в облегченном режиме. Повышенные нагрузки допускаются, но лишь на короткий период времени.
Сила тока и плотность
Для того чтобы понять, как работает та или иная электрическая величина, необходимо знать условия и степень их взаимодействия между собой. Большое значение имеет зависимость силы и плотности тока в проводнике. Перед тем как рассматривать эту зависимость следует более подробно остановиться на понятии электрического тока.
Под действием определенных факторов в металлах, выступающих в роли основных проводников, образуется направленное движение заряженных частиц. Как правило, это электроны, обладающие отрицательным зарядом. Существуют и другие проводники, называемые электролитами, в которых направленное движение создается ионами, которые могут быть положительными или отрицательными. Третий вид проводников представляет собой различные газы, где электрический ток создается не только электронами, но и с помощью положительных и отрицательных ионов. Величину плотности тока можно определить в любом проводнике, но более наглядно это будет на примере металлов.
Третий вид проводников представляет собой различные газы, где электрический ток создается не только электронами, но и с помощью положительных и отрицательных ионов. Величину плотности тока можно определить в любом проводнике, но более наглядно это будет на примере металлов.
Условно электрический ток имеет направление, совпадающее с направлением движения положительно заряженных частиц. Для его создания и существования необходимо соблюдение двух основных условий. В первую очередь, это сами заряженные частицы, которые могут свободно перемещаться в проводнике под действием сил электрического поля. Соответственно, необходимо само электрическое поле, способное существовать в проводнике в течение длительного времени под действием источника тока.
Сила (I) и плотность (j) электрического тока являются его основными характеристиками. Сила тока считается скалярной физической величиной, определяемой как отношение заряда ∆q, проходящего через поперечное сечение проводника в течение некоторого времени ∆t, к данному временному промежутку. В виде формулы это будет выглядеть следующим образом: I = ∆q/∆t. Единицей измерения силы тока служит ампер. Это позволит в дальнейшем решить вопрос, как найти плотность тока.
В виде формулы это будет выглядеть следующим образом: I = ∆q/∆t. Единицей измерения силы тока служит ампер. Это позволит в дальнейшем решить вопрос, как найти плотность тока.
Существует связь силы тока со скоростью свободных зарядов, находящихся в упорядоченном движении. Определить эту зависимость можно на примере участка проводника, имеющего площадь сечения S и длину ∆l. Заряд каждой частицы принимается за q0, а объем проводника ограничивается сечениями № 1 и № 2. В этом объеме количество частиц составляет nS∆l, где n является концентрацией частиц. Величина их общего заряда составляет: ∆q = q0nS∆l. Упорядоченное движение свободных зарядов осуществляется со средней скоростью hvi. Следовательно за установленный промежуток времени ∆t = ∆I/ hvi все частицы, находящиеся в этом объеме, пройдут через сечение № 2. В результате, сила тока составит I = ∆q/∆t, как уже и было отмечено.
Сила тока имеет непосредственную связь с плотностью тока j представляющей собой векторную физическую величину. Ее модуль определяется как отношение силы тока I и площади поперечного сечения проводника. Плотность формула отражает как j = I/S. Вектор плотности тока совпадает с вектором скорости упорядоченно движущихся положительно заряженных частиц. Постоянный ток обладает плотностью, имеющей стабильное значение на всем поперечном сечении проводника. Таким образом, плотность и сила тока самым тесным образом связаны между собой.
Ее модуль определяется как отношение силы тока I и площади поперечного сечения проводника. Плотность формула отражает как j = I/S. Вектор плотности тока совпадает с вектором скорости упорядоченно движущихся положительно заряженных частиц. Постоянный ток обладает плотностью, имеющей стабильное значение на всем поперечном сечении проводника. Таким образом, плотность и сила тока самым тесным образом связаны между собой.
Литература
Занятие 11
РАСЧЁТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Учебная цель: научиться применять законы Ома и правила Кирхгофа к расчёту электрических цепей. Выработать навыки самостоятельного решения задач на данную тему.
Основная: Детлаф А.А., Яворский Б. М. Курс физики.
М.: Высшая школа, 1989,-Гл.19, §19.1 – 19.3.
М. Курс физики.
М.: Высшая школа, 1989,-Гл.19, §19.1 – 19.3.
Дополнительная: Савельев И.В. Курс общей физики. М.: Наука, 1989. – Т.2, гл.5, §31 –36.
Контрольные вопросы для подготовки к занятию
Что называется электрическим током проводимости?
Дайте определение силы тока, напишите определяющую формулу. Единица измерения силы тока.
Какой ток называется постоянным?
Что называется плотностью тока? Запишите определяющую формулу. Единица измерения плотности тока.
Запишите формулу связи силы тока и плотности электрического тока.
Запишите выражение, устанавливающее связь силы и плотности электрического тока со средней скоростью <v> упорядоченного движения заряженных частиц в проводнике.
Дайте определение ЭДС и её единицы измерения.

Сформулируйте и запишите закон Ома для участка однородной цепи.
Дайте определение электрического сопротивления. От чего оно зависит? Единица измерения.
Запишите закон Ома для участка неоднородной цепи и поясните физический смысл величин, входящих в него.
Сформулируйте и запишите закон Ома для замкнутой цепи.
Напишите формулы для вычисления общего сопротивления n участков цепи при их последовательном и параллельном соединении.
Сформулируйте, запишите и поясните правила Кирхгофа.
Сформулируйте правила выбора знаков для токов и ЭДС.
Краткие теоретические сведения и основные формулы
Электрическим
током проводимости (электрическим
током) называется упорядоченное
(направленное) движение электрически
заряженных частиц относительно среды
(т. е. внутри макроскопических тел).
е. внутри макроскопических тел).
Количественно электрический ток характеризуется скалярной величиной – силой тока I и векторной величиной – плотностью электрического тока .
Сила тока I – скалярная величина, определяемая электрическим зарядом, переносимым через поперечное сечение проводника в единицу времени:
(11.1)
Электрический ток, направление движения электрических зарядов в котором и сила тока не изменяются со временем, называется постоянным. Для постоянного тока
(11.2)
Единицa измерения силы тока – ампер (А).
Плотность электрического тока – векторная характеристика тока, равная по модулю электрическому заряду, проходящему за единицу времени через единичную площадку, перпендикулярную направлению упорядоченного движения заряженных частиц:
(11. 3)
3)
где dSn – площадь проекции плоскости на направление, перпендикулярное направлению упорядоченного движения заряженных частиц.
При равномерном распределении плотности электрического тока по сечению проводника сила тока в нём
(11.4)
где S – площадь поперечного сечения проводника.
В общем случае сила тока через поверхность S равна:
(11.5)
где — проекция плотностиэлектрического тока на нормаль к площадкеdS.
Плотность тока, согласно закону Ома в дифференциальной форме, определяется по формуле
(11.6)
где — удельная проводимость материала.
Следовательно,
вектор плотности электрического тока
сонаправлен с вектором напряженности
электрического поля в данной точке, то
есть совпадает с направлением
упорядоченного движения положительных
зарядов. Поэтому за направление силы
тока принимается направление упорядоченного
движения положительно заряженных
частиц.
Поэтому за направление силы
тока принимается направление упорядоченного
движения положительно заряженных
частиц.
Единица плотности тока – ампер на метр в квадрате ().
Сила и плотность тока связаны со средней скоростью <v> упорядоченного движения зарядов в проводнике следующей зависимостью:
(11.7)
(11.8)
где n – концентрация носителей тока; е – элементарный электрический заряд.
Направленное
движение электрических зарядов возможно
только при наличии электрического поля,
энергия которого каким-то образом
восполнялась и расходовалась бы на их
упорядоченное движение. Поэтому в
замкнутой цепи наряду с участками, на
которых положительные носители движутся
в сторону убывания потенциала, должны
иметься участки, на которых перенос
положительных зарядов происходит в
направлении возрастания потенциала,
то есть против сил электростатического
поля (пунктирная часть рис. 11.1). Перемещение
носителей на этих участках возможно
лишь с помощью сил неэлектрического
происхождения, называемых сторонними
силами. Сторонние силы могут действовать
либо на всём протяжении цепи, либо на
её отдельных участках.
11.1). Перемещение
носителей на этих участках возможно
лишь с помощью сил неэлектрического
происхождения, называемых сторонними
силами. Сторонние силы могут действовать
либо на всём протяжении цепи, либо на
её отдельных участках.
Сторонние силы, перемещая электрические заряды, совершают работу.
Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС), действующей в цепи или на её участке:
(11.9)
ЭДС, как и потенциал, измеряется в вольтах.
Закон Ома для участка однородной цепи:
сила тока, текущего по однородному (в смысле отсутствия сторонних сил) проводнику, пропорциональна падению напряжения U на этом проводнике:
(11.10)
где R – электрическое сопротивление проводника.
Электрическое
сопротивление проводника – характеристика
электрических свойств проводника,
определяемая отношением постоянного
напряжения между его началом и концом
к силе протекающего по нему тока.
Сопротивление зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан, и температуры.
Для однородного цилиндрического проводника
(11.11)
где l – длина проводника; S – площадь его поперечного сечения; — коэффициент, зависящий от свойств материала и называемый удельным электрическим сопротивлением, Ом.м.
Что такое плотность электрического тока единица ее измерения
Автор Сфера закона На чтение 13 мин Просмотров 2 Опубликовано
Содержание
- Электрический ток и его плотность
- Плотность электрического тока
- Плотность тока — что это такое и в чем измеряется
- Виды электротока, условия протекания
- Плотность тока и мощность
- Закон Ома
- Единица измерения плотности электротока
- Формула вычисления
- 4-вектор плотности тока
- Видео
- Что такое плотность тока
- Плотность электрического тока
- Сила тока и плотность
Электрический ток и его плотность
Электрическим током называют направленное движение свободно заряженных частиц под действием электрического поля.
Как правило движение зарядов происходит в некоторой среде (веществе или вакууме), являющейся проводником для электрического тока. Движущимися в среде заряженными частицами могут быть электроны (в металлах, полупроводниках) или ионы (в жидкостях и газах).
Рис. 1 Электрический ток
Для возникновения и протекания электрического тока в любой токопроводящей среде необходимо выполнение двух условий:
- Наличие в среде свободных носителей заряда;
- Наличие электрического поля.
Для поддержания электрического поля, например в проводнике, к его концам необходимо подключить какой-либо источник электрической энергии (батарейку или аккумулятор). Поле в проводнике создается зарядами, которые накопились на электродах источника тока под действием сил (химических, механических и т.д.).
За направление тока условно принято принимать направление движения положительных зарядов. Следовательно, условно принятое направление тока обратно направлению движения электронов – основных отрицательных электрических носителей заряда в металлах и полупроводниках.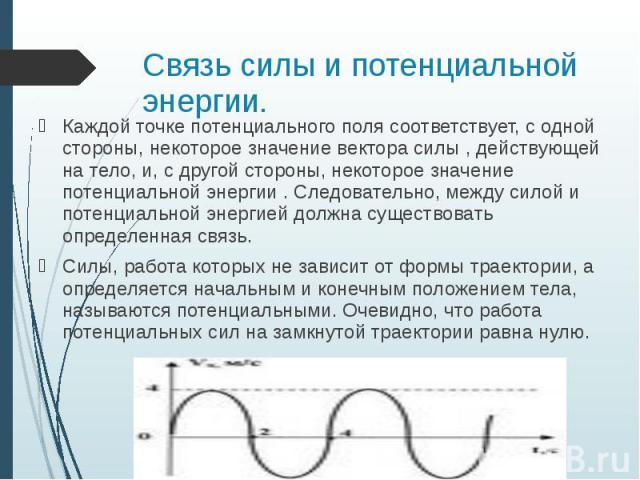
Понять явление электрического тока достаточно сложно так как его невозможно увидеть глазами. Для лучшего понимания процессов в электронике проведем аналогию между электрическим током в проводнике и водой в тонкой трубочке. В трубочке есть вода (носители заряда в проводнике), но она неподвижна, если трубочка лежит на горизонтальной поверхности и уровень высот ее концов (значения потенциалов электрического поля) одинаковый. Если трубочку наклонить так, что один конец станет выше другого (появится разность потенциалов), вода потечет по трубочке (электроны придут в движение).
Способность вещества проводить электрический ток под действием электрического поля называется электропроводностью. Каждому веществу соответствует определенная степень электропроводности. Ее значение зависит от концентрации в веществе носителей заряда – чем она выше, тем больше электропроводность. В зависимости от электропроводности все вещества делятся на три большие группы: проводники, полупроводники и диэлектрики.
Электрический ток может менять направление и величину во времени (переменный ток) или оставаться неизменным (постоянный) (рисунок 2).
Рис. 2. Постоянный и переменный электрические токи
Количественной мерой электрического тока служит сила тока I, которая определяется числом электронов (зарядов) q, проходящих через импровизированное поперечное сечение проводника в единицу времени t (рисунок 3).
Рис. 3. Сила тока в проводнике
Для постоянного тока представленное выше выражение можно записать в виде
Ток в системе СИ измеряется в амперах, [А]. Току в 1 А соответствует ток, при котором через поперечное сечение за 1 секунду проходит электрический заряд, равный 1 Кл.
Плотность электрического тока
Под плотностью тока j понимается физическая величина, равная отношению тока I к площади поперечного сечения S проводника. При равномерном распределении тока по поперечному сечению проводника.
При равномерном распределении тока по поперечному сечению проводника.
Плотность тока в системе СИ измеряется в амперах на миллиметр квадратный, [А/мм 2 ].
Рассмотрим плотность тока в проводнике с разным поперечным сечением. Например, соединены два проводника с различными сечениями: первый толстый провод с большим поперечным сечением S1 второй тонкий провод с сечением S2. К концам которых приложено постоянное напряжение (рисунок 5) в следствии чего через них протекает постоянный ток с одинаковой силой тока.
Рис.5 Плотность тока в проводниках с различными сечениями.
Предположим, что сила тока через поперечное сечение толстого проводника S1 и тонкого провода S2 различная. Из этого предположения вытекает, что за каждую единицу времени через сечения S1 и S2 протекают различные значения электрического заряда. Следовательно, в объёме провода, расположенного между двумя указанными сечениям происходит непрерывное скапливание зарядов, и напряженность электрического поля изменялась бы, чего не может быть, так как при изменении электрического поля ток был бы непостоянен. В проводах с различным сечением при одном и том же токе плотность тока обратно пропорциональна площади поперечного сечения.
В проводах с различным сечением при одном и том же токе плотность тока обратно пропорциональна площади поперечного сечения.
Плотность тока — векторная величина.
Рис. 4. Графическая интерпретация плотности тока j
Направление вектора совпадает с направлением положительно заряженных зарядов и, следовательно, с направлением самого тока I.
Если концентрация носителей тока равна n, каждый носитель имеет заряд e и скорость его движения в проводнике равна v (рисунок 3), то за время dt через поперечное сечение S проводника переносится заряд
В этом случае величину силы тока I можно представить в виде зависимости
Сила тока через произвольную поверхность определяется через поток вектора плотности тока, как интеграл по произвольной (в общем случае) поверхности S (рисунок 6)
Рис. 6. Сила тока через произвольную поверхность S
6. Сила тока через произвольную поверхность S
От величины плотности тока зависит важный показатель – качество электропередачи. Фактически этот показатель зависит от степени нагрузки проводника (хотя и не только от нее). В зависимости от значения плотности тока принято выбирать сечение проводов – это связано с наличием у проводников сопротивления, в результате которого происходит нагрев жил проводника вплоть до его расплавления и выхода из строя.
Источник
Плотность тока — что это такое и в чем измеряется
Проходя по длине проводникового элемента, электроток распределяется по его поверхности неравномерно. Плотность электрического тока характеризует распределение токовых зарядов по поперечному сечению проводящего материала.
Виды электротока, условия протекания
Частицы, несущие заряд, могут перемещаться в толще проводника беспорядочно или целенаправленно двигаться в определенном направлении. Во втором случае говорят о наличии электрического тока. Основная его характеристика – наличие вектора перемещения. Вектор токового движения идентичен направлению заряженных частиц.
Основная его характеристика – наличие вектора перемещения. Вектор токового движения идентичен направлению заряженных частиц.
Важно! Токовый ход может быть постоянным и переменным. В первом случае поток частиц перемещается четко в одном направлении по прямой, без колебаний и возмущений. Во втором – имеют место синусоидальные колебания с определенной частотой. Для трансформации (выпрямления) переменного электротока применяют специальные устройства. Вообще для существования константного тока требуется, чтобы с одного конца проводникового элемента все время имел место избыток отрицательно заряженных частиц, а со второго – дефицит. Также требуется сила, которая будет эти заряды перемещать.
Переменный ток, в противоположность постоянному, не требует соблюдения полярности. В отличие от постоянного, он имеет частоту – так называется количество смен направления перемещения частиц за единицу времени. В стандартной бытовой сети число таких смен равно 50 в секунду. Различные приборы, питающиеся от аккумуляторных элементов и батарей, а также бытовая техника, ноутбуки, стационарные компьютеры потребляют постоянный электроток. Сама батарея является генератором постоянного токового хода, но его можно инвертировать в переменный с помощью специальных устройств.
Различные приборы, питающиеся от аккумуляторных элементов и батарей, а также бытовая техника, ноутбуки, стационарные компьютеры потребляют постоянный электроток. Сама батарея является генератором постоянного токового хода, но его можно инвертировать в переменный с помощью специальных устройств.
Ток, вызываемый электрополем, принято называть током проводимости. Элементарные частицы, переносящие заряд, отличаются у разных типов проводниковых материалов. В случае металлических элементов это свободные электроны, у части полупроводниковых материалов – целенаправленно движущиеся ионы. В электролитах (в том числе применяемых в аккумуляторных батареях) ионы с плюсовым и минусовым зарядами движутся в разные стороны. Последнее характерно для всех проводников, представляющих собой жидкости.
В конвекционном электротоке электроны перемещаются под действием инерции. Еще одна разновидность тока – протекающий в вакуумных условиях (такое явление применяется в электронных лампочках). Основными характеристиками электротока являются сила и плотность тока.
Плотность тока и мощность
Работа, которую электрополе совершает над источниками токового движения, может быть охарактеризована плотностью мощности (она равна энергии, деленной на произведение объема проводника и временного периода). Самый распространенный путь данной мощности – рассеивание во внешнее пространство в качестве тепловой энергии. Но некоторая ее доля может превращаться в механическую энергию (например, при работе электрического двигателя) или в разные типы излучения.
Закон Ома
Для токопроводящей среды, обладающей изотропными характеристиками, данный закон имеет следующий вид:
где j – плотность идущего электротока, Е – полевая напряженность в рассматриваемой точке (скалярная величина, как и предыдущая), а σ – удельная проводимость средового окружения.
Что касается работы электрополя для такой среды (w), то она может быть выражена следующими формулами:
w= E2* σ=j2/σ=p*j2 (p здесь – удельное сопротивление).
Выражение для работы в этом случае примет вид:
w=E* σ *E=j*p*j (E и j в данном случае – скалярные величины).
В матрице справа налево умножают столбчатый вектор на строчной и на матрицу. Тензорные величины р и σ генерируют релевантные им квадратичные формы.
Единица измерения плотности электротока
Для выражения плотностной величины применяется производная от единиц измерения токовой силы (Ампер) и площади поперечного разреза (квадратный метр), а также дольных и кратных указанным. Обычно плотность измеряется в амперах, разделенных на квадратный метр (А/м2). Вместо слова «плотность» иногда используют «насыщенность электрического тока».
Важно! Поскольку величина имеет направление, она относится к категории векторных (или скалярных). Этот вектор проходит вдоль оси электрического тока.
Формула вычисления
Рассматриваемая величина находится в обратной зависимости от размеров сечения (чем больше площадь, тем меньше плотность тока) и временного периода прохождения электрозаряда и в прямой – от величины этого заряда.
Это можно записать так:
j=Δq/ΔtΔS (q тут – элементарно малый заряд, t – бесконечно малый промежуток времени, а S – площадь сечения).
Так как токовая сила выражается как частное заряда и временного промежутка его прохода, формулу можно записать и так:
Формула плотности тока с опорой на параметры перемещающихся зарядов будет выглядеть так:
j=q*n*V (V тут – скорость, а n – концентрация электронных частиц).
4-вектор плотности тока
Данное обозначение из теории относительности призвано обобщать явление плотности на пространственно-временной континуум, оперирующий четырьмя измерениями. Такой четырехвектор включает в себя трехвекторное выражение токовой плотности (скалярной величины) и имеющей объем плотности электрического заряда. Использование четырехвектора дает возможность формулировать электродинамические уравнения ковариантным образом.
Рассматриваемая величина необходима для описания концентрации и равномерности распределения заряженных микрочастиц по проводниковому материалу, в котором существует та или иная форма электротока. При оперировании с выражениями, содержащими величину, нужно не забывать о ее скалярности.
При оперировании с выражениями, содержащими величину, нужно не забывать о ее скалярности.
Видео
Источник
Что такое плотность тока
Электрические провода, находящиеся под напряжением, постоянно испытывают определенную нагрузку. Поэтому очень часто возникает вопрос, что такое плотность тока и каким образом она влияет на качество электроснабжения. Фактически данная величина характеризует степень электрической нагрузки проводников. Она позволяет предотвратить излишние потери при прокладке кабельных линий. Во время использования устройств с высокой частотой, следует учитывать наличие дополнительных электродинамических эффектов.
Плотность электрического тока
Под действием электрического поля начинается упорядоченное перемещение зарядов, известное всем, как электрический ток. Обычно для движения зарядов используется какая-либо среда, которая называется проводником и является носителем тока.
Плотность тока совместно с другими факторами характеризует движение зарядов. Формула плотности тока дает описание электрического заряда, переносимого в течение 1 секунды через определенное сечение проводника, направленного перпендикулярно этому току.
Таким образом, с физической точки зрения плотность тока — это заряды, в определенном количестве протекающие через установленную единицу площади в период единицы времени. Данный параметр является векторной величиной и представляется в виде соотношения силы тока и площади поперечного сечения проводника, по которому и протекает этот ток. Модульное значение плотности тока будет равно: j = I/S. В этой формуле j является модулем вектора, I – силой тока, S – площадью поперечного сечения.
Векторы плотности тока и скорости движения токообразующих зарядов имеют одинаковое направление, если заряды обладают положительным значением и противоположное – когда они отрицательные.
В чем измеряется плотность тока? В качестве единицы измерения используется А/мм2. Данная величина применяется на практике, в основном, для принятия решения о выборе того или иного проводника в соответствии с его способностями выдерживать те или иные нагрузки. плотность играет важную роль, поскольку каждый проводник обладает сопротивлением. В результате потерь тока происходит нагрев проводника. Чрезмерные потери приводят к критическому нагреванию, вплоть до расплавления жил.
Данная величина применяется на практике, в основном, для принятия решения о выборе того или иного проводника в соответствии с его способностями выдерживать те или иные нагрузки. плотность играет важную роль, поскольку каждый проводник обладает сопротивлением. В результате потерь тока происходит нагрев проводника. Чрезмерные потери приводят к критическому нагреванию, вплоть до расплавления жил.
Для предотвращения подобных ситуаций, каждый потребитель рассчитывается на определенную плотность, по которой подбирается и оптимальное сечение проводника. Во время проектирования, помимо расчетных формул, используются уже готовые таблицы, содержащие все необходимые исходные данные, на основе которых можно получить конечный результат.
Следует помнить, что у разных проводников неодинаковая плотность электрического тока. В современных условиях практикуется использование преимущественно медных проводов, где это значение не превышает 6-10 А/мм2. Это приобретает особую актуальность в условиях длительной эксплуатации, когда проводка должна работать в облегченном режиме. Повышенные нагрузки допускаются, но лишь на короткий период времени.
Повышенные нагрузки допускаются, но лишь на короткий период времени.
Сила тока и плотность
Для того чтобы понять, как работает та или иная электрическая величина, необходимо знать условия и степень их взаимодействия между собой. Большое значение имеет зависимость силы и плотности тока в проводнике. Перед тем как рассматривать эту зависимость следует более подробно остановиться на понятии электрического тока.
Под действием определенных факторов в металлах, выступающих в роли основных проводников, образуется направленное движение заряженных частиц. Как правило, это электроны, обладающие отрицательным зарядом. Существуют и другие проводники, называемые электролитами, в которых направленное движение создается ионами, которые могут быть положительными или отрицательными. Третий вид проводников представляет собой различные газы, где электрический ток создается не только электронами, но и с помощью положительных и отрицательных ионов. Величину плотности тока можно определить в любом проводнике, но более наглядно это будет на примере металлов.
Условно электрический ток имеет направление, совпадающее с направлением движения положительно заряженных частиц. Для его создания и существования необходимо соблюдение двух основных условий. В первую очередь, это сами заряженные частицы, которые могут свободно перемещаться в проводнике под действием сил электрического поля. Соответственно, необходимо само электрическое поле, способное существовать в проводнике в течение длительного времени под действием источника тока.
Сила (I) и плотность (j) электрического тока являются его основными характеристиками. Сила тока считается скалярной физической величиной, определяемой как отношение заряда ∆q, проходящего через поперечное сечение проводника в течение некоторого времени ∆t, к данному временному промежутку. В виде формулы это будет выглядеть следующим образом: I = ∆q/∆t. Единицей измерения силы тока служит ампер. Это позволит в дальнейшем решить вопрос, как найти плотность тока.
Существует связь силы тока со скоростью свободных зарядов, находящихся в упорядоченном движении. Определить эту зависимость можно на примере участка проводника, имеющего площадь сечения S и длину ∆l. Заряд каждой частицы принимается за q0, а объем проводника ограничивается сечениями № 1 и № 2. В этом объеме количество частиц составляет nS∆l, где n является концентрацией частиц. Величина их общего заряда составляет: ∆q = q0nS∆l. Упорядоченное движение свободных зарядов осуществляется со средней скоростью hvi. Следовательно за установленный промежуток времени ∆t = ∆I/ hvi все частицы, находящиеся в этом объеме, пройдут через сечение № 2. В результате, сила тока составит I = ∆q/∆t, как уже и было отмечено.
Определить эту зависимость можно на примере участка проводника, имеющего площадь сечения S и длину ∆l. Заряд каждой частицы принимается за q0, а объем проводника ограничивается сечениями № 1 и № 2. В этом объеме количество частиц составляет nS∆l, где n является концентрацией частиц. Величина их общего заряда составляет: ∆q = q0nS∆l. Упорядоченное движение свободных зарядов осуществляется со средней скоростью hvi. Следовательно за установленный промежуток времени ∆t = ∆I/ hvi все частицы, находящиеся в этом объеме, пройдут через сечение № 2. В результате, сила тока составит I = ∆q/∆t, как уже и было отмечено.
Сила тока имеет непосредственную связь с плотностью тока j представляющей собой векторную физическую величину. Ее модуль определяется как отношение силы тока I и площади поперечного сечения проводника. Плотность формула отражает как j = I/S. Вектор плотности тока совпадает с вектором скорости упорядоченно движущихся положительно заряженных частиц. Постоянный ток обладает плотностью, имеющей стабильное значение на всем поперечном сечении проводника. Таким образом, плотность и сила тока самым тесным образом связаны между собой.
Таким образом, плотность и сила тока самым тесным образом связаны между собой.
Источник
Подробные пояснения и задачи – Lambda Geeks
В статье рассматривается взаимосвязь между крутящим моментом и скоростью вращающегося тела и ее решаемые проблемы.
Крутящий момент и скорость характеризуют вращательное движение. Угловая скорость – это скорость вращения, а крутящий момент – это сила, рассчитанная на вращательное движение. Мощность связывает крутящий момент со скоростью, объясняя, сколько энергии распределяется, когда тело вращается из-за приложенной силы.
Каждое вращающееся тело имеет заданную выходную мощность, при этом его скорость и крутящий момент изменяются.
Выходная мощность определяется произведением приложенной силы и линейного расстояния, пройденного за единицу времени . Математически,
P = Fd/t ………………(*)
Когда сила F приложена к телу на определенном расстоянии r от его оси вращения, действующий на него крутящий момент определяется выражением,
𝜏 = r * F
F = 𝜏/r ………….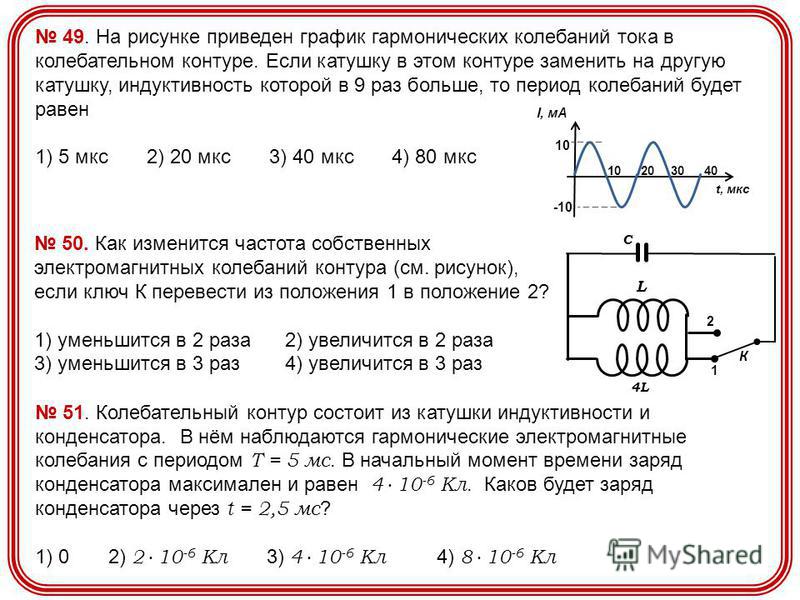 .(1)
.(1)
Соотношение между линейным расстоянием d и угловым расстоянием θ равно,
d=r *θ…………………..(2)
Подстановка (1) и (2) в (*),
(3) тела. т. е. ω = θ/tP = 𝜏 ω …………………….(4)
Итак, крутящий момент и скорость связаны через мощность as,
𝜏 =P/ω ……………………(5)
Крутящий момент обратно пропорционален скорости и прямо пропорционален мощности .
Читать о том, как найти крутящий момент?
Если тело имеет мощность 50 Вт и вращается со скоростью 10 рад/с, какой крутящий момент действует на него?Дано :
P = 50 Вт
ω = 10 рад/с
Найти : :0003
𝜏 = ?
Formula :
𝜏 = p/ ω
Solution :
The torque acting on the body is calculated as,
𝜏 = P/ ω
Substituting all значений,
𝜏 = 50/10
𝜏 = 5
Крутящий момент, действующий на кузов, равен 5 Нм.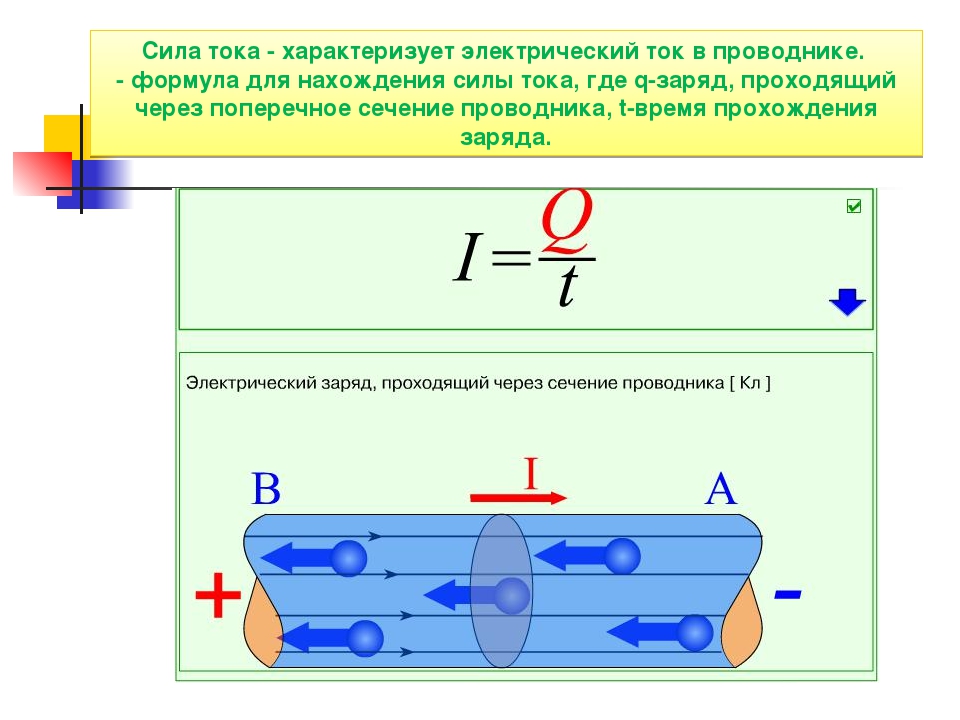
Указано :
𝜏 = 50 нм
P = 150 Вт
T = 10 S
, чтобы найти : θ =?
Formula :
𝜏 = P/ ω
Решение :
Угловое расстояние, пройденное автомобильными колесами. ω = θ/t
𝜏 = P/ θ
Перестановка,
θ = P/T𝜏
Заменить все значения,
θ = 150/50 * 10
θ = 1500/50
θ = 30
Угольное расстояние, пройденное колесом автомобиля, составляет 30 рад/с. .
Соотношение крутящего момента и скорости в двигателе постоянного токаМомент и скорость обратно пропорциональны двигателю постоянного тока.
Подобно тому, как моторные устройства преобразуют электрическую энергию в механическую, двигатель постоянного тока также включает преобразование электрической энергии в энергию вращения. На двигатель подается определенное напряжение, которое создает крутящий момент на выходном валу, так что двигатель начинает вращаться с угловой скоростью.
На двигатель подается определенное напряжение, которое создает крутящий момент на выходном валу, так что двигатель начинает вращаться с угловой скоростью.
Крутящий момент, скорость и мощность являются важными параметрами, которые отображают производительность двигателя постоянного тока, который включает преобразование энергии . Скорость двигателя постоянного тока определяется входным напряжением, необходимым для создания крутящего момента на его валу.
Как видите, транспортному средству требуется меньший крутящий момент для движения с более высокой скоростью по прямой дороге. Но конкретное транспортное средство требует большого крутящего момента при движении по наклонной дороге. Это когда его скорость падает, но мощность остается постоянной.
На корпус двигателя постоянного тока действуют два крутящих момента; один — крутящий момент нагрузки , а другой — индуцированный крутящий момент . Крутящий момент нагрузки представляет собой механическую нагрузку, воздействующую на вал, в то время как индуцированный крутящий момент создается входным током для управления крутящим моментом нагрузки на определенной скорости.
Крутящий момент нагрузки представляет собой механическую нагрузку, воздействующую на вал, в то время как индуцированный крутящий момент создается входным током для управления крутящим моментом нагрузки на определенной скорости.
При движении по наклонной дороге момент нагрузки на вал становится больше, чем индуктивный момент. Следовательно, скорость мотора на такой дороге становится меньше. Именно поэтому крутящий момент и угловая скорость обратно пропорциональны двигателю постоянного тока .
Крутящий момент от скорости вращенияДля каждого двигателя постоянного тока имеется график зависимости крутящего момента от скорости, и его наклон иллюстрирует его характеристики.
Наклон, совпадающий в точке на оси Y, называется ‘ крутящий момент опрокидывания ’ 𝜏 s ; что показывает максимальный крутящий момент при отсутствии угловой скорости . Точно так же точка на оси X, где наклон совпадает, называется ‘ скорость без нагрузки ’ ω n ; что показывает максимальную скорость 90 195, поскольку крутящий момент не применяется.
Точно так же точка на оси X, где наклон совпадает, называется ‘ скорость без нагрузки ’ ω n ; что показывает максимальную скорость 90 195, поскольку крутящий момент не применяется.
в двигателе постоянного тока
Линейная кривая соединяет две максимальные точки на графике, что приводит к уравнениям крутящего момента и скорости в двигателе постоянного тока = as,
𝜏 с – ω/ 𝜏 с ω н ………….6
ω = (𝜏 s – 𝜏)ω n / 𝜏 s ……………..7
Прямоугольную область можно нарисовать под кривой крутящий момент-скорость с одним углом начала графика, а другая совпадает с кривой, изображающей мощность двигателя постоянного тока .
Зависимость крутящего момента и скорости Поскольку крутящий момент и скорость обратно пропорциональны, его мощность должна быть максимальной в точке, где ω = 0,5 ω n и 𝜏 = 0,5/ 𝜏 с .
Фиксированная выходная мощность двигателя постоянного тока можно оценить, подставив (6) и (7) в (4).
Мощность двигателя постоянного тока также измеряется в лошадиных силах и показывает, сколько энергии двигатель может выдать за единицу времени. Согласно уравнениям (4) и (8), мы понимаем, что мощность напрямую связана с крутящим моментом и скоростью. Таким образом, чем больше мощность двигателя, тем быстрее он может работать .
Читать о крутящем моменте против силы
Двигатель постоянного тока вращается со скоростью 30 рад/с, когда на его вал не действует крутящий момент. Его скорость снижается до 20 рад/с, когда входной ток создает крутящий момент. Двигатель останавливается, когда индуцированный крутящий момент достигает своего максимального значения 10 Нм. Каково первоначальное значение крутящего момента, создаваемого двигателем постоянного тока?Дано :
𝜏 с = 10 Нм
ω= 20 рад/с
ω 9022
Найти:
𝜏 = ?
Formula :
𝜏 = 𝜏 S — ω/𝜏 S ω N
Решение :
TOUCKED INDED INDECED DC SACEDULED DC SACEDULED DC.
𝜏 = 𝜏 S — ω/𝜏 S ω N
Заменить все значения,
𝜏 = 10–20/10*30
𝜏 = 10 — 6,66
𝜏 = 3.4
𝜏 = 10 — 6,66
𝜏 = 3,4
𝜏 = 1066
0003
Крутящий момент двигателя постоянного тока составляет 3,4 Нм.
Двигатель постоянного тока движется со скоростью 50 рад/с при индуцируемом крутящем моменте 20 Нм. Рассчитайте мощность двигателя постоянного тока, когда он останавливается при крутящем моменте 30 Н.GIV EN
𝜏 = 20 нм
ω = 50 рад/с
𝜏 S = 30 нм
, чтобы найти : P =?
Формула :
P = 𝜏 S 2 — 𝜏 S 𝜏 — ω𝜏 S + ω𝜏
Решение :
Мощность DC мотоцикл вычисляется As,
P = n. 9029.904 9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029. — 𝜏 S 𝜏- ω𝜏 S + ω𝜏
9029.904 9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029.9029. — 𝜏 S 𝜏- ω𝜏 S + ω𝜏
Заменить все значения,
P = 30 2 — 30 * 20 -50 * 20 — 50 * 30 0003
P = 900 — 60 — 100 +. 150
P = 890 Вт
Мощность двигателя постоянного тока рассчитывается как
1 л.с. = 745,7 Вт.
Итак, P = 890/745,7 л.с.
P= 1,19 л.с.
Мощность двигателя постоянного тока 1,19 л.с.
Разница в крутящем моменте и скорости
| Крутящий момент | Скорость |
| Это связано с ротом. | Относится к скорости вращения. |
| Влияет на ускорение объекта, когда сила приложена от его оси вращения. | Влияет на движение объекта при приложении силы. |
При максимальном крутящем моменте на объекте его скорость равна нулю. | При максимальной скорости на объекте его крутящий момент равен нулю. |
| Измеряется в Ньютонах . Метр (Нм) шт. | Измеряется в единицах радиан на время (рад/с) . |
Читать о зависимости скорости от скорости
AB-032: Двигатели постоянного тока – напряжение от скорости. Выходная скорость против. Крутящий момент
Двигатели постоянного тока — напряжение по сравнению с. Выходная скорость против. Крутящий момент
Соотношение между напряжением, крутящим моментом и выходной скоростью является частой темой обсуждения между нашими клиентами и инженерами по продажам Precision Microdrives.
Целью следующей статьи является обсуждение и уточнение взаимосвязи между этими параметрами и методами их использования вместе с другими ресурсами, чтобы понять все возможности наших двигателей постоянного тока и мотор-редукторов.
Определения терминов, используемых в нашем техпаспорте, можно найти ниже со ссылками, щедро разбросанными по всей статье для дальнейшего чтения.
Крутящий момент и скорость
Крутящий момент можно определить как «крутящую силу», которая имеет тенденцию вращать объект вокруг точки опоры. Что касается двигателей постоянного тока и мотор-редукторов, мы обычно будем называть «номинальный крутящий момент» «номинальной нагрузкой», чтобы избежать путаницы в наших значениях. В конечном счете, эти два термина представляют одно и то же значение — вращательное усилие, приложенное к выходному валу.
Говоря о скорости, мы обычно имеем в виду угловую скорость выходного вала наших двигателей постоянного тока и мотор-редукторов (обычно в оборотах в минуту). В зависимости от приложения этот параметр будет влиять на скорость выполнения конкретной функции и может существенно повлиять на общую производительность устройства.
Зачем менять крутящий момент?
Наиболее очевидным преимуществом изменения крутящего момента является поддержание постоянной скорости при изменении нагрузки двигателя с учетом взаимозависимого характера скорости, крутящего момента и напряжения.
Хотя этот пример может быть устаревшим, аудиокассеты — отличный способ объяснить, как в некоторых приложениях необходимо изменять крутящий момент, чтобы соответствовать изменяющейся нагрузке. По мере воспроизведения кассеты и перемещения аудиозаписи с одного шпинделя на другой нагрузка на приводной двигатель будет изменяться. Тем не менее, воспроизведение должно оставаться с постоянной скоростью, иначе это повлияет на высоту тона звука.
Также бывают случаи, когда нагрузка двигателя резко меняется между операциями, а не медленно, как в примере с кассетой. Это часто происходит со шкивами и подъемниками: двигатель останавливается в крайнем случае, когда груз прикрепляется или снимается. Здесь поддержание постоянной скорости не так важно, как способность двигателя выдерживать различные крутящие нагрузки, поскольку для перемещения более тяжелого объекта требуется больший выходной крутящий момент, чем для легкого объекта или без нагрузки.
Все эти приложения имеют общую тему переменной нагрузки, прикрепленной к двигателю. Если ваше приложение предполагает фиксированную нагрузку, то, вероятно, вам будет интереснее варьировать скорость.
Если ваше приложение предполагает фиксированную нагрузку, то, вероятно, вам будет интереснее варьировать скорость.
Свяжитесь с нами по телефону
Поговорите с членом нашей команды.
Каталог двигателей
Ищете нашу продукцию?
Надежные, экономичные миниатюрные механизмы и двигатели, отвечающие вашим требованиям.
Зачем менять скорость?
Возможность изменять скорость двигателя при поддержании постоянного крутящего момента важна для многих приложений по разным причинам.
Примером приложения, требующего переменной скорости и постоянного крутящего момента, является проигрыватель аудио компакт-дисков, поскольку обычно наблюдается, что в одних точках компакт-диск будет вращаться быстрее, чем в других. Это связано с тем, что информация хранится в спиральных круговых дорожках на диске, а длина/окружность дорожек прямо пропорциональна количеству информации, хранящейся на них. Это означает, что скорость должна быть уменьшена по мере того, как лазер считывает данные с крайних дорожек, потому что за один оборот поступает больше информации. И наоборот, скорость увеличивается по мере того, как лазер считывает самые внутренние дорожки, поскольку окружности спирали меньше и, следовательно, содержат меньше информации за один оборот.
И наоборот, скорость увеличивается по мере того, как лазер считывает самые внутренние дорожки, поскольку окружности спирали меньше и, следовательно, содержат меньше информации за один оборот.
Без возможности регулировать скорость двигателя (с напряжением) при поддержании этого постоянного крутящего момента было бы очень сложно считывать и воспроизводить эту информацию с постоянной скоростью.
Этот же принцип может быть применен к большому количеству приложений и часто имеет решающее значение для их успешной работы. Многие из наших двигателей постоянного тока и мотор-редукторов могут работать при самых разных скоростях и нагрузках, что позволяет нашим клиентам изучить возможности своего проекта и, как правило, найти подходящее решение с одним двигателем.
Как читать типовую таблицу характеристик производительности
Таблица типичных рабочих характеристик находится на первой странице каждого из наших технических паспортов. Этот график является чрезвычайно полезным инструментом, иллюстрирующим типичное поведение отдельного двигателя.
Как мы уже обсуждали ранее, многие из наших клиентов ищут двигатель или мотор-редуктор, который будет работать с заданной скоростью и нагрузкой. Одним из лучших мест для поиска решения является наш онлайн-каталог, и мы всегда можем помочь порекомендовать подходящие двигатели и обсудить варианты настройки. Поскольку скорость двигателя в двигателях постоянного тока и редукторных двигателях в основном определяется нагрузкой и напряжением привода, значение «Номинальная скорость» в техпаспорте берется при «Номинальном напряжении» и «Номинальной нагрузке». Это означает, что значения скорости, указанные в технических характеристиках, берутся в контролируемых и конкретных условиях и не отражают всех возможностей какого-либо отдельного двигателя. Именно здесь типичная диаграмма производительности является полезным инструментом для просмотра более широкого диапазона возможностей двигателя.
108-106 Motor Performance Graph Графики для наших двигателей постоянного тока и мотор-редукторов предполагают фиксированное напряжение и показывают, как потребляемый ток, мощность, КПД и скорость двигателя зависят от изменения нагрузки. Каждый из затронутых параметров имеет свою независимую линию производительности и соответствующую шкалу по оси Y.
Каждый из затронутых параметров имеет свою независимую линию производительности и соответствующую шкалу по оси Y.
Синяя линия на диаграмме типичных характеристик 108-106 (выше) показывает скорости, при которых двигатель будет работать от точки холостого хода до крутящего момента (около 0,725 мНм) и позволяет нам исследовать производительность двигателя, а также понять взаимосвязь между скоростью и крутящим моментом для отдельного двигателя.
Например; если клиенту требуется постоянная скорость и крутящий момент 1900 об/мин и 0,65 мНм соответственно, в разделе «ключевые характеристики» (выше) листа данных будет указано, что 108-106 не подходит, поскольку в нем указано:
. Номинальная нагрузка – 0,15 мН·м
Номинальная скорость нагрузки – 12 600 об/мин
Однако после проверки диаграммы производительности при нагрузке 0,65 мНм по оси X синяя линия производительности (скорость) указывает на соответствующей оси Y, что скорость будет равна 1900 об/мин. Изображение выше иллюстрирует это и демонстрирует, что 108-106 действительно подходит для клиентов, исходя из их требований к фиксированной скорости и крутящему моменту. Эту диаграмму также можно расширить, чтобы проиллюстрировать диапазон возможностей двигателя, если он будет использоваться с динамической нагрузкой/скоростью.
Эту диаграмму также можно расширить, чтобы проиллюстрировать диапазон возможностей двигателя, если он будет использоваться с динамической нагрузкой/скоростью.
Связь между скоростью, крутящим моментом и напряжением
Теперь, когда мы обсудили, как читать диаграмму производительности, мы можем взглянуть на взаимосвязь между скоростью и крутящим моментом. В этом разделе мы обрисуем взаимосвязь между скоростью и крутящим моментом и объясним пределы каждого из них, прежде чем рассматривать дальнейшее влияние напряжения на эти параметры.
N/L скорость и момент опрокидывания на графиках производительности двигателяЕсли предположить, что двигатель приводится в действие при фиксированном напряжении, есть две точки, которые описывают пиковую производительность двигателя на каждом конце. «Холостой ход» (N/L) и «опрокидывающий момент»
- Момент остановки представляет собой точку, в которой двигатель достигает максимальной рабочей нагрузки. В этот момент вал больше не будет вращаться, и двигатель будет находиться в «заглохшем» состоянии.
 Обратите внимание, что двигатель не должен работать с остановкой, так как это почти наверняка приведет к преждевременному выходу из строя.
Обратите внимание, что двигатель не должен работать с остановкой, так как это почти наверняка приведет к преждевременному выходу из строя. - Скорость холостого хода — это максимальная выходная скорость, которой двигатель достигает при заданном напряжении. В этот момент двигатель работает свободно и без внешней нагрузки
Наши двигатели постоянного тока и мотор-редукторы могут работать в любом диапазоне между этими пределами до остановки. Если мы посмотрим на синюю линию производительности, связь между скоростью и крутящим моментом довольно легко понять — крутящий момент обратно пропорционален скорости двигателя — начиная с точки холостого хода/полной скорости и, по мере увеличения нагрузки, скорость уменьшается пропорционально, пока двигатель не заглохнет.
Хотя диаграмма производительности показывает, как скорость влияет на применение различных нагрузок, она не указывает на то, что скорость наших двигателей постоянного тока также прямо пропорциональна приложенному напряжению.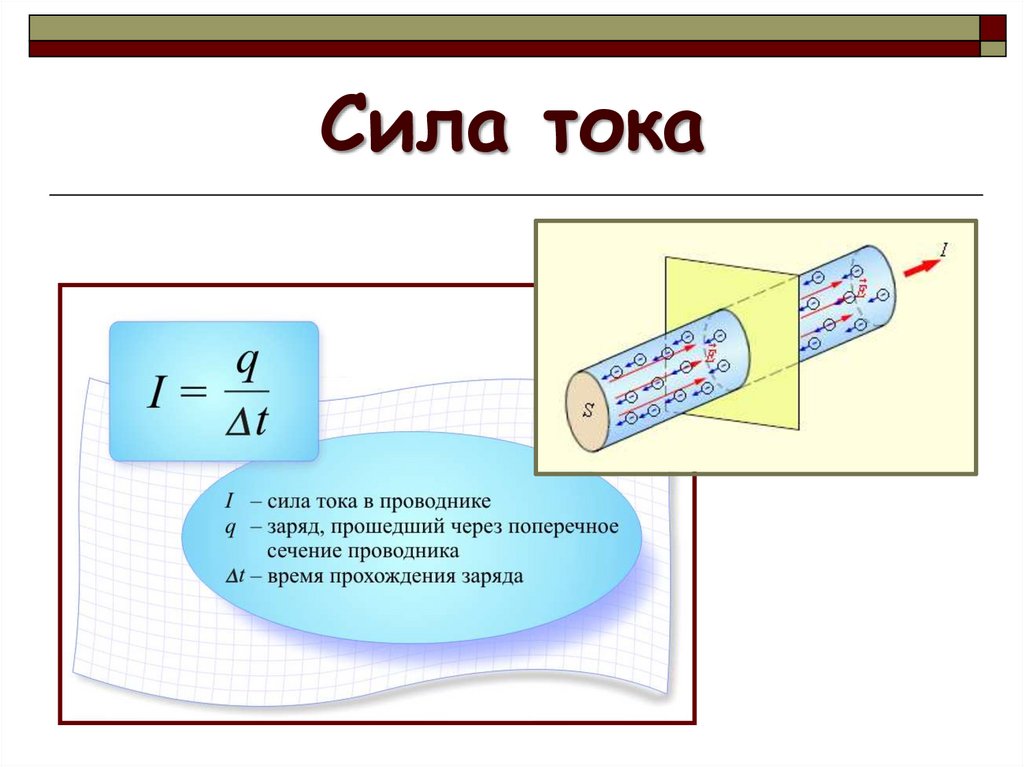 Теорию, лежащую в основе этого принципа, можно найти здесь. Короче говоря, это означает, что мы можем управлять скоростью двигателя независимо от крутящего момента, и это позволяет нам поддерживать постоянную скорость для переменной нагрузки, а также поддерживать постоянный крутящий момент при изменении скорости двигателя.
Теорию, лежащую в основе этого принципа, можно найти здесь. Короче говоря, это означает, что мы можем управлять скоростью двигателя независимо от крутящего момента, и это позволяет нам поддерживать постоянную скорость для переменной нагрузки, а также поддерживать постоянный крутящий момент при изменении скорости двигателя.
Этот принцип используется для обеспечения правильного воспроизведения нашего проигрывателя компакт-дисков и кассеты и, вероятно, будет включать систему обратной связи с обратной связью, которая будет измерять скорость двигателя и регулировать напряжение возбуждения, чтобы либо поддерживать постоянную скорость при переменной нагрузке, либо обеспечивать переменная скорость для фиксированной нагрузки.
Как мы можем изменить производительность двигателя
Существует несколько методов настройки характеристик двигателя, будь то специальное решение, адаптированное к потребностям клиента, или простая регулировка режима работы двигателя. Некоторые распространенные модификации перечислены ниже:
- Обмотки: Путем изменения количества витков в катушках двигателя и/или площади поперечного сечения используемого провода можно управлять сопротивлением клемм, рабочим напряжением/током и индуктивностью клемм.
 Это означает, что как электрические, так и механические характеристики двигателя могут быть легко адаптированы к конкретной спецификации.
Это означает, что как электрические, так и механические характеристики двигателя могут быть легко адаптированы к конкретной спецификации. - Передаточные числа коробки передач: коробки передач являются эффективным методом точного изменения характеристик двигателя постоянного тока с использованием одной или нескольких ступеней редуктора. Несмотря на то, что мы поставляем мотор-редукторы со склада, многие из наших клиентов хотели бы разработать свой собственный набор шестерен. Если вы хотите поэкспериментировать со своими собственными зубчатыми цепями, простые уравнения для шестерен можно найти в AB-024. Тем не менее, мы можем предложить нестандартные редукторы и модификации стандартных деталей, поэтому, пожалуйста, не стесняйтесь обращаться к инженеру, если вы хотите обсудить ваши требования и варианты, которые мы можем предложить.
- Управляющее напряжение: это может быть простой и экономичный способ управления производительностью наших двигателей. Есть несколько способов, которыми вы можете настроить управляющее напряжение для вашего двигателя, включая ШИМ и даже специальные микросхемы драйвера.
 Ранее мы обсуждали эти темы более подробно по следующим ссылкам – 1 и 2
Ранее мы обсуждали эти темы более подробно по следующим ссылкам – 1 и 2 - . Выбор материала. Используемые материалы могут существенно повлиять на общую производительность вашего мотор-редуктора. Некоторые из возможных вариантов здесь перечислены ниже
- Материал редуктора: общая точка отказа микроредукторов возникает на последней ступени редуктора. Это точка приложения наибольшей силы при приложении нагрузки к двигателю. В этом случае редуктор может выйти из строя задолго до того, как будет достигнут момент остановки двигателя, и потенциальные возможности не будут использованы полностью. В этом случае на последней ступени (ступенях) можно добавить более мощные шестерни, чтобы можно было достичь более высокого крутящего момента и более широкого диапазона производительности. На практике это использовалось с 206-108, который глохнет примерно на 17 мНм из-за отказа шестерни. На графике характеристик это характеризуется резкой остановкой на линии крутящий момент-скорость задолго до приближения к остановке (0 об/мин).
 Вставляя металлическую шестерню на последнем этапе, достигается крутящий момент примерно 34 мНм, что удваивает возможности двигателя по крутящему моменту и открывает более широкий спектр возможностей. Ему был присвоен номер детали 206-10C 9.0578
Вставляя металлическую шестерню на последнем этапе, достигается крутящий момент примерно 34 мНм, что удваивает возможности двигателя по крутящему моменту и открывает более широкий спектр возможностей. Ему был присвоен номер детали 206-10C 9.0578 - Смазочные материалы. Температура окружающей среды и рабочая температура в значительной степени влияют на эффективность мотор-редуктора и общую производительность выходного вала. В то время как электрический КПД двигателя часто может увеличиваться при низких температурах, эффективность редуктора и эффективность смазки могут снижаться, что приводит к снижению общей производительности. Распространенным методом уменьшения этого эффекта является использование специальной низкотемпературной смазки. Это может повысить КПД редуктора и, следовательно, производительность двигателя на выходе. Это означает, что диапазон температур, указанный в техпаспорте, не является абсолютным пределом, и существует несколько способов его расширения. Если возникнут вопросы, инженеры Precision Microdrives будут рады помочь
- Энкодеры: если вам требуется больший контроль над вашим мотор-редуктором или вы используете его в приводе позиционирования, вам может потребоваться энкодер.
 Это типичная модификация, которую мы можем предложить, начиная от простых тахометров для измерения скорости, инкрементных энкодеров для позиционирования по одному эталону и заканчивая абсолютными энкодерами для точного позиционирования выходного вала. Эти энкодеры также можно использовать в управлении с обратной связью для поддержания скорости при изменении крутящего момента, изменения скорости для постоянного крутящего момента или любой комбинации этих двух способов (примеры обсуждались ранее в этой статье). Пожалуйста, свяжитесь с инженером Precision Microdrives, если вам нужна дополнительная информация о том, что мы можем поставить
Это типичная модификация, которую мы можем предложить, начиная от простых тахометров для измерения скорости, инкрементных энкодеров для позиционирования по одному эталону и заканчивая абсолютными энкодерами для точного позиционирования выходного вала. Эти энкодеры также можно использовать в управлении с обратной связью для поддержания скорости при изменении крутящего момента, изменения скорости для постоянного крутящего момента или любой комбинации этих двух способов (примеры обсуждались ранее в этой статье). Пожалуйста, свяжитесь с инженером Precision Microdrives, если вам нужна дополнительная информация о том, что мы можем поставить
Любая комбинация вышеперечисленного может быть использована вместе для достижения широкого диапазона мощностей наших мотор-редукторов. Таким образом, даже если вы не можете найти диаграмму производительности мотор-редуктора, соответствующую вашим требованиям, свяжитесь с нашими инженерами, поскольку мы можем найти множество способов удовлетворить ваши требования.
Ограничения
Как и все хорошее, есть ограничения на то, чего можно достичь. Целью этого раздела является описание некоторых связанных ограничений, возникающих при модификации мотор-редуктора.
- Обмотки: К сожалению, без значительных модификаций и затрат на разработку провода с определенной площадью поперечного сечения иногда трудно обеспечить точные характеристики при требуемом сопротивлении на клеммах, рабочем напряжении/токе и индуктивности на клеммах. В этом случае требования часто выполняются очень точно, и отклонения могут быть незначительными. Здесь также действуют ограничения по размерам, поскольку для обмоток имеется очень ограниченное пространство. На практике это означает, что определенные механические/электрические характеристики не могут быть достигнуты с данным двигателем из-за доступного пространства оболочки для обмоток и требуемой площади поперечного сечения/количества проводов обмотки. Разумеется, компания Precision Microdrives будет рада оценить осуществимость вашего запроса, поэтому, пожалуйста, не стесняйтесь обращаться к нам с вашими требованиями
- Свойства материалов: Свойства материалов также являются ограничением при рассмотрении достижимых модификаций наших двигателей.

Как уже говорилось, смазочные материалы для низких температур можно использовать для улучшения характеристик материала при определенных температурах, однако существуют очевидные физические ограничения для конкретных материалов. К заметным ограничивающим свойствам относятся коэффициент теплового расширения, прочность материала, температуры плавления и многие другие. Если у вас есть какие-либо вопросы, связанные с этим, пожалуйста, свяжитесь с нами
В этом разделе мы обсудили несколько очевидных ограничений, возникающих при модификации мотор-редуктора. Во многих случаях эти ограничения можно преодолеть, если менее важные параметры более гибкие. Поэтому, пожалуйста, обратитесь к нашим инженерам, чтобы оценить, что можно реализовать в вашем приложении.
Заключение
В этой статье мы обсудили некоторые причины, по которым пользователь может изменять скорость и крутящий момент двигателя, и рассмотрели конкретные примеры для каждой ситуации. Это побудило нас рассмотреть пределы скорости и крутящего момента для наших мотор-редукторов при постоянном напряжении. Здесь мы поняли, что при фиксированном напряжении наши двигатели могут работать в широком диапазоне скоростей и крутящих моментов между точкой холостого хода (полная скорость) и точкой максимальной нагрузки (опрокидывание).
Здесь мы поняли, что при фиксированном напряжении наши двигатели могут работать в широком диапазоне скоростей и крутящих моментов между точкой холостого хода (полная скорость) и точкой максимальной нагрузки (опрокидывание).
Мы также обсудили, как читать «таблицу типичных рабочих характеристик», чтобы понять весь диапазон возможностей крутящего момента и скорости данного двигателя (при его номинальном напряжении). Отсюда мы увидели, что соотношение между скоростью и крутящим моментом обратно пропорционально от точки холостого хода до крутящего момента, и обсудили, как мы можем отрегулировать управляющее напряжение, чтобы поддерживать постоянную скорость или крутящий момент, когда другая переменная является динамической.
Последний раздел этого бюллетеня был посвящен описанию некоторых методов управления двигательной активностью. Некоторые из этих методов легко реализуются, и с ними можно экспериментировать при тестировании, в то время как другие являются постоянными модификациями, которые могут быть предусмотрены для конкретной спецификации. Если вы хотите рассмотреть варианты, которые у вас есть для вашего проекта, свяжитесь с одним из наших инженеров, чтобы обсудить ваши требования и варианты, которые мы можем вам предложить.
Если вы хотите рассмотреть варианты, которые у вас есть для вашего проекта, свяжитесь с одним из наших инженеров, чтобы обсудить ваши требования и варианты, которые мы можем вам предложить.
Информационный бюллетень
Подпишитесь на получение новых блогов, тематических исследований и ресурсов прямо на ваш почтовый ящик.
Зарегистрироваться
ИмяПервое Последний
Электронная почта (обязательно)
Согласие с условиями (обязательно)Я прочитал и согласен с Условиями и политикой конфиденциальности Precision Microdrives
Согласие на обсуждение (обязательно)Я рад, что Precision Microdrives получил мои данные, чтобы мы могли обсудить мой запрос
Узнать больше
Прецизионные микроприводы
Нужен ли вам компонент двигателя или полностью проверенный и испытанный сложный механизм — мы здесь, чтобы помочь. Узнайте больше о нашей компании.
- Почему PMD
- О нас
- Двигатели
- Механизмы
- Карьера
Фундаментальная проблема электронной мобильности
Внедрение электромобилей ускоряется благодаря технологическим усовершенствованиям, катализируемым государственной политикой и стимулами, направленными на достижение нулевого уровня выбросов. В 2020 году количество электромобилей в мире достигло 10 миллионов, но они составляют лишь 1% всех транспортных средств. По прогнозам, к 2030 году более четверти всех автомобилей, продаваемых в мире, будут электромобилями. Барьеры, стоящие перед внедрением электромобилей, в том числе инфраструктура зарядки, беспокойство по поводу запаса хода, а также стоимость и доступность моделей электромобилей, хорошо известны. Однако фундаментальная проблема, стоящая перед электрификацией мобильности, — это компромисс между скоростью и крутящим моментом.
В 2020 году количество электромобилей в мире достигло 10 миллионов, но они составляют лишь 1% всех транспортных средств. По прогнозам, к 2030 году более четверти всех автомобилей, продаваемых в мире, будут электромобилями. Барьеры, стоящие перед внедрением электромобилей, в том числе инфраструктура зарядки, беспокойство по поводу запаса хода, а также стоимость и доступность моделей электромобилей, хорошо известны. Однако фундаментальная проблема, стоящая перед электрификацией мобильности, — это компромисс между скоростью и крутящим моментом.
Соотношение крутящего момента и скорости — фундаментальная проблема электромобилей — легко описать, но решить экономически эффективно оказалось сложно. Транспортное средство должно уметь передвигаться, подниматься и спускаться с холмов, останавливаться на светофорах и разгоняться на автомагистралях, но при этом все это нужно делать за разумное время. Способность автомобиля приводить в движение колеса, подниматься в гору и ускоряться на шоссе зависит от крутящего момента.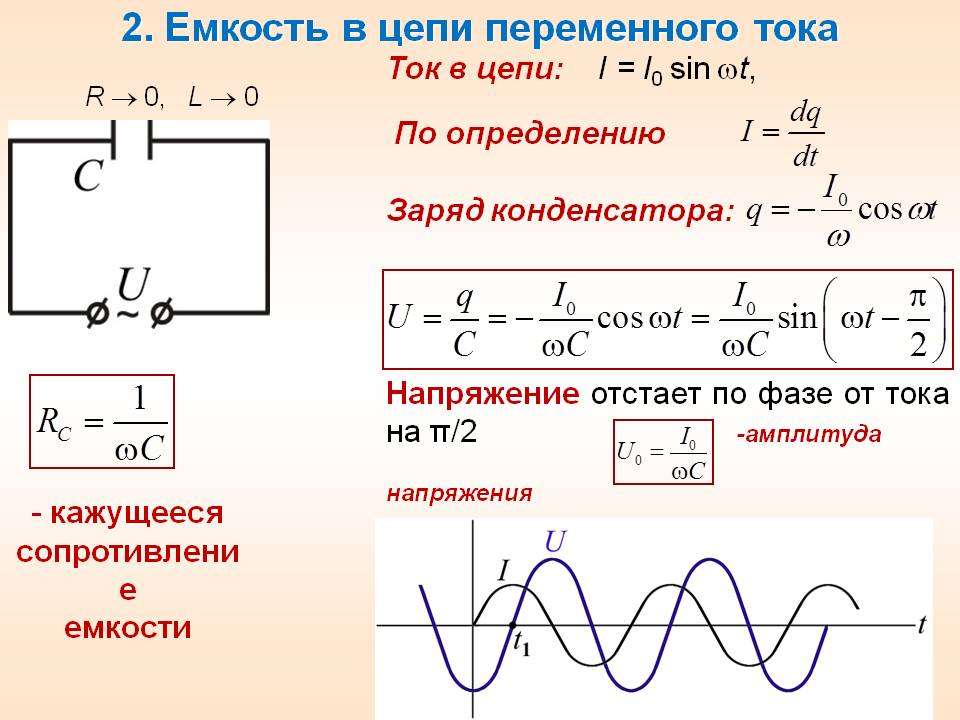 Насколько быстро он может двигаться, и время, необходимое для перемещения из одной точки в другую, зависит от скорости. Таким образом, фундаментальная проблема, которую должны решить все электромобили, заключается в том, какой крутящий момент и скорость необходимы для выполнения задач, для которых предназначен автомобиль. Это осложняется тем, что скорость и крутящий момент обратно пропорциональны. Это проблема соотношения крутящего момента и скорости.
Насколько быстро он может двигаться, и время, необходимое для перемещения из одной точки в другую, зависит от скорости. Таким образом, фундаментальная проблема, которую должны решить все электромобили, заключается в том, какой крутящий момент и скорость необходимы для выполнения задач, для которых предназначен автомобиль. Это осложняется тем, что скорость и крутящий момент обратно пропорциональны. Это проблема соотношения крутящего момента и скорости.
Как определяются скорость и крутящий момент в электродвигателе
Скорость
Скорость двигателя определяется как скорость вращения двигателя и измеряется в оборотах в минуту или об/мин. Другими словами, скорость определяется как количество оборотов двигателя за 1 минуту.
Крутящий момент
Выходной крутящий момент двигателя представляет собой величину силы вращения, которую развивает двигатель, и измеряется в ньютон-метрах или Нм. Проще говоря, крутящий момент — это крутящая сила двигателя, но его может быть труднее понять, чем его эквивалентную скорость, поэтому давайте углубимся.
Требуемый крутящий момент определяется тремя факторами
1. Сопротивление качению
Сопротивление качению — это сила трения/противодействия, которую транспортное средство должно преодолевать из-за качения между колесами и поверхностью, по которой движется транспортное средство. Сопротивление качению зависит от материала шин и шероховатости поверхности. Чем выше сопротивление между шиной и дорогой, тем больше силы/крутящего момента необходимо двигателю для движения.
2. Сопротивление уклону
Сопротивление уклону — это сила тяжести, которая тянет автомобиль назад, когда он поднимается по наклонной поверхности. Чем круче подъем/холм, тем больше силы/крутящего момента требуется двигателю для подъема.
3. Сила ускорения
Сила ускорения помогает транспортному средству достичь заданной скорости из состояния покоя за определенный период времени. Крутящий момент двигателя имеет прямую зависимость от силы ускорения. Чем выше крутящий момент, тем меньше времени требуется автомобилю для достижения заданной скорости.
Общее тяговое усилие
Общее тяговое усилие — это общая сила, необходимая для движения транспортного средства с требуемыми показателями производительности, и представляет собой сумму трех сил, перечисленных выше. Таким образом, величина крутящего момента, который должен развить двигатель, определяется тем, насколько сильно транспортное средство имеет трение с дорогой, сколько требуется движения в гору и под гору и как быстро водитель хотел бы перейти от нуля до полной скорости. .
Взаимосвязь крутящего момента и скорости: аналогия
Какой простой способ понять взаимосвязь крутящего момента и скорости? Представьте себе сценарий, в котором человека попросили забить длинный гвоздь в стену. Сколько раз человек ударяет гвоздем по головке за одну минуту, это скорость, насколько сильно каждый контакт с гвоздем, это крутящий момент. Однако у человека ограниченное количество энергии, и увеличение силы каждого удара или увеличение количества ударов в минуту приведет к более высокому потреблению энергии и заставит человека быстрее утомляться.
Теперь давайте определим две гипотетические ситуации, где в первом сценарии цель состоит в том, чтобы максимизировать количество ударов в минуту, а во втором сценарии цель состоит в том, чтобы как можно сильнее забить гвоздь один раз. В первом сценарии человек должен был бы поддерживать небольшое расстояние между гвоздем и молотком и, по сути, шевелить рукой, чтобы записать наибольшее количество ударов. Во втором сценарии человек должен был бы сделать полный ход, чтобы достичь пиковой силы.
Два сценария иллюстрируют обратную зависимость между скоростью и крутящим моментом, а также ограничения, которые существуют, когда целью является максимизация обоих. В зависимости от общей силы человека или номинальной мощности двигателя скорость и крутящий момент должны быть сбалансированы для достижения определенных целей.
Какая связь между крутящим моментом и скоростью?
В электродвигателе соотношение крутящего момента и скорости определяется формулой: механическая мощность равна скорости, умноженной на крутящий момент .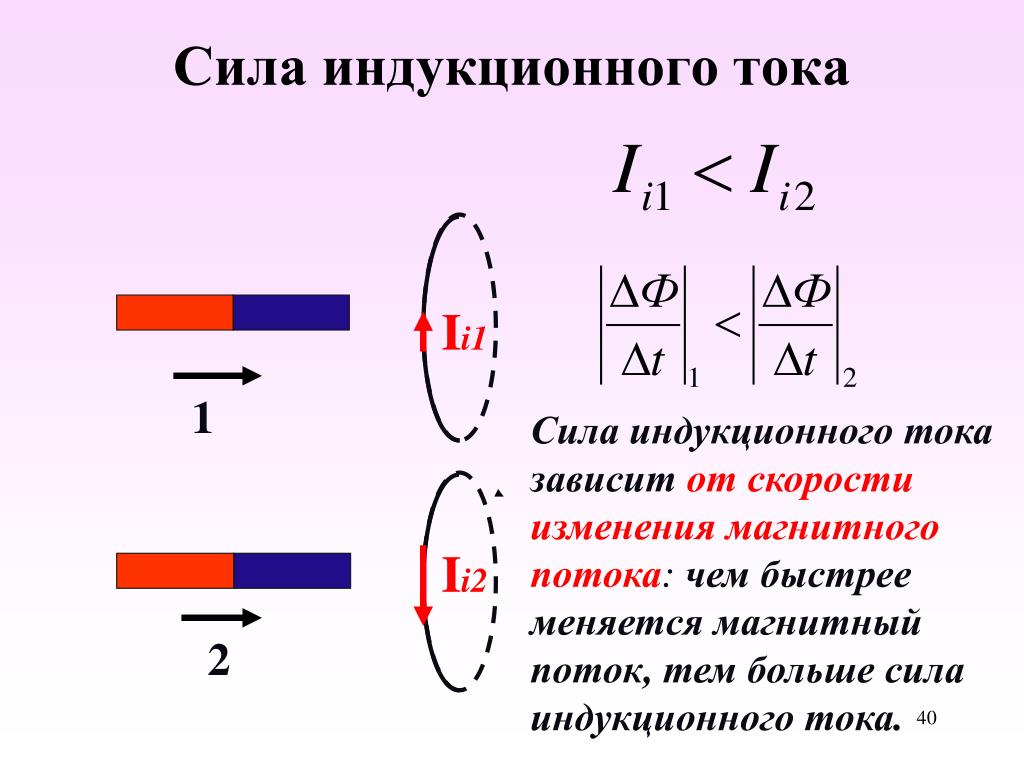 Соотношение крутящего момента и скорости обратно пропорционально, поскольку номинальная выходная мощность двигателя является фиксированной величиной. По мере увеличения выходной скорости доступный выходной крутящий момент пропорционально уменьшается. По мере увеличения выходного крутящего момента выходная скорость пропорционально уменьшается. Хотя скорость определяет максимальную скорость электродвигателя, больший крутящий момент позволяет системе достигать максимальной скорости за меньшее время. Динамические требования для предполагаемого применения будут определять, что лучше: больший крутящий момент или большая скорость.
Соотношение крутящего момента и скорости обратно пропорционально, поскольку номинальная выходная мощность двигателя является фиксированной величиной. По мере увеличения выходной скорости доступный выходной крутящий момент пропорционально уменьшается. По мере увеличения выходного крутящего момента выходная скорость пропорционально уменьшается. Хотя скорость определяет максимальную скорость электродвигателя, больший крутящий момент позволяет системе достигать максимальной скорости за меньшее время. Динамические требования для предполагаемого применения будут определять, что лучше: больший крутящий момент или большая скорость.
Как производители электромобилей балансируют между скоростью и крутящим моментом?
Существует несколько распространенных способов, которыми сегодня производители электромобилей пытаются управлять соотношением крутящего момента и скорости.
Увеличенный размер двигателя
Увеличить номинальный размер двигателя означает выбрать более высокую номинальную мощность, чем это необходимо для обеспечения того, чтобы транспортное средство могло работать во всем диапазоне применений.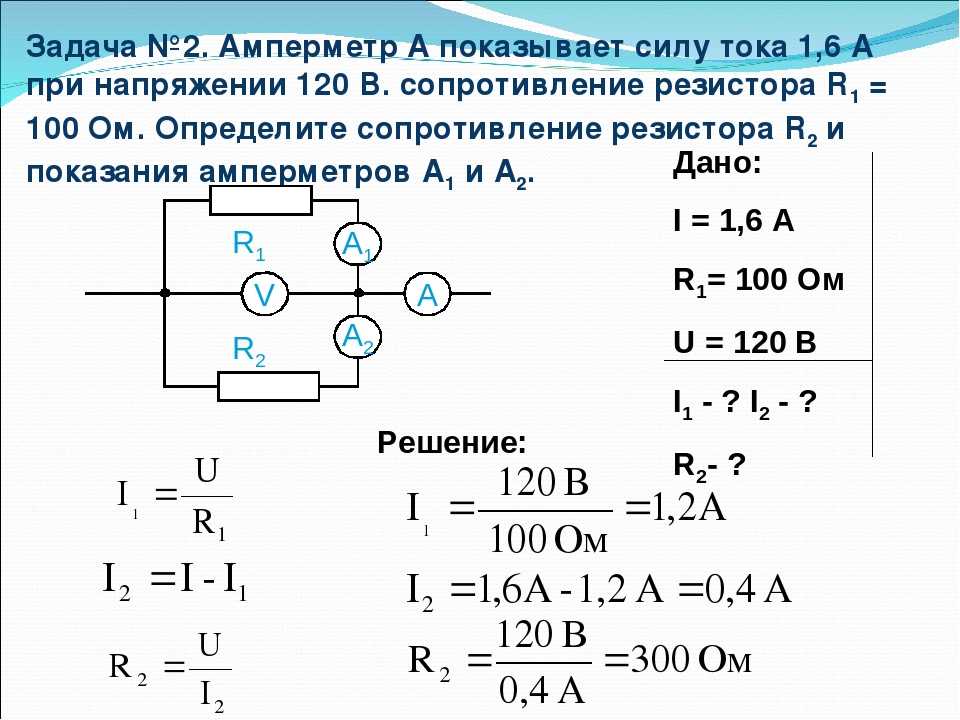 Однако электродвигатели больших размеров имеют более высокую начальную стоимость, более высокие эксплуатационные расходы и приводят к потерям энергии.
Однако электродвигатели больших размеров имеют более высокую начальную стоимость, более высокие эксплуатационные расходы и приводят к потерям энергии.
Использование двигателя мощностью 400 кВт на полной мощности для приложения, которое может быть достигнуто с двигателем мощностью 200 кВт на полной мощности, даст хорошие результаты с точки зрения запуска приложения, но будет потреблять больше электроэнергии и, следовательно, быстрее разряжать батарею. сократить запас хода автомобиля и потребовать компонентов с более высокой номинальной мощностью, что приведет к дальнейшему увеличению затрат и снижению эффективности системы. Это один из современных способов, которым производители электромобилей управляют соотношением крутящего момента и скорости.
Несколько двигателей
Производители транспортных средств также могут увеличить выходную мощность системы, включив в систему несколько двигателей, чтобы расширить рабочий диапазон и сбалансировать соотношение скорости и крутящего момента.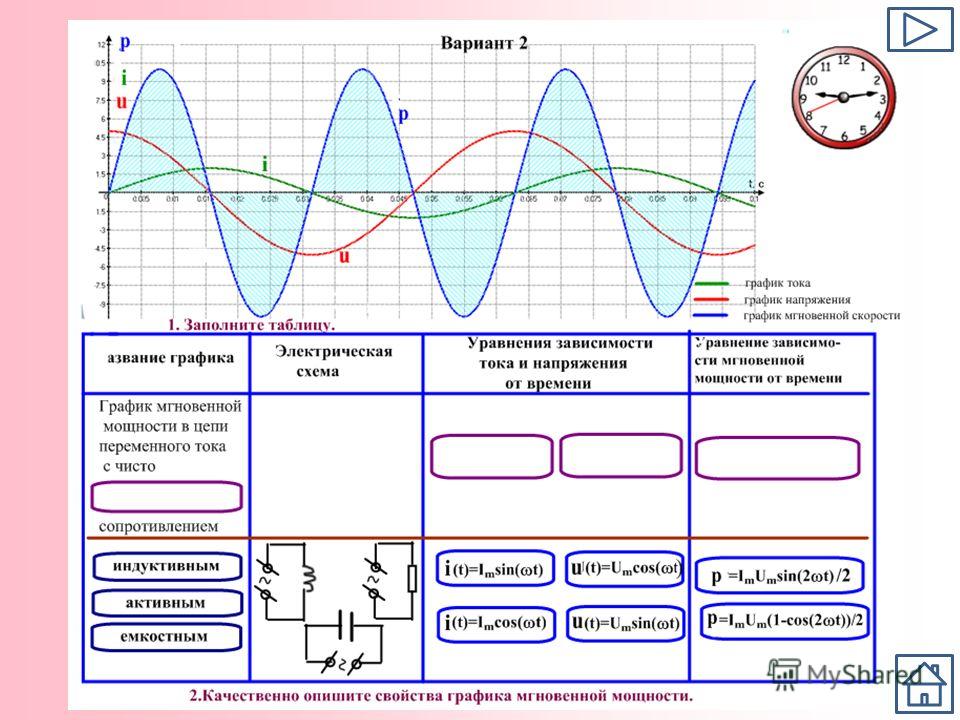 Производители электромобилей используют несколько двигателей для более высокой производительности, оптимальной механической компоновки и улучшенной тяги по более высокой цене. Компании традиционно выбирают двухдвигательную конфигурацию с асинхронным двигателем и двигателем с постоянными магнитами (ПМ). Двигатель с постоянными магнитами обычно используется транспортным средством для повышения дальности и эффективности, но асинхронный двигатель включается, когда транспортное средство должно быстро разогнаться. Преимущество асинхронного двигателя заключается в том, что он имеет минимальный крутящий момент для свободного хода, а это означает, что если он отстает и не используется, потери будут минимальными. Существуют также автомобили с 3 и 4 двигателями, которые предлагают превосходную производительность в дополнение к другим преимуществам, таким как лучшая управляемость и тяга.
Производители электромобилей используют несколько двигателей для более высокой производительности, оптимальной механической компоновки и улучшенной тяги по более высокой цене. Компании традиционно выбирают двухдвигательную конфигурацию с асинхронным двигателем и двигателем с постоянными магнитами (ПМ). Двигатель с постоянными магнитами обычно используется транспортным средством для повышения дальности и эффективности, но асинхронный двигатель включается, когда транспортное средство должно быстро разогнаться. Преимущество асинхронного двигателя заключается в том, что он имеет минимальный крутящий момент для свободного хода, а это означает, что если он отстает и не используется, потери будут минимальными. Существуют также автомобили с 3 и 4 двигателями, которые предлагают превосходную производительность в дополнение к другим преимуществам, таким как лучшая управляемость и тяга.
Этот подход к обработке отношения крутящего момента и скорости также имеет свои недостатки. Несколько конструкций двигателей имеют свои оговорки. Дополнительные двигатели стоят дороже и увеличивают вес системы. Кроме того, необходимость в более крупной батарее, компонентах с более высокой номинальной мощностью и более высоком энергопотреблении нескольких двигателей еще больше увеличивает вес и стоимость системы. Комбинация приводит либо к уменьшению запаса хода, либо к увеличению общей стоимости владения.
Дополнительные двигатели стоят дороже и увеличивают вес системы. Кроме того, необходимость в более крупной батарее, компонентах с более высокой номинальной мощностью и более высоком энергопотреблении нескольких двигателей еще больше увеличивает вес и стоимость системы. Комбинация приводит либо к уменьшению запаса хода, либо к увеличению общей стоимости владения.
Механический редуктор
Еще одним решением для достижения правильного баланса крутящего момента и скорости для данного применения является включение механической коробки передач. Механический редуктор — это устройство, используемое для увеличения выходного крутящего момента или изменения скорости двигателя. Редуктор состоит из ряда встроенных шестерен, которые изменяют крутящий момент и скорость между электродвигателем и нагрузкой в зависимости от передаточных чисел.
Механический редуктор имеет длительный срок службы и поддерживает огромную силу; однако коробки передач имеют высокую стоимость и тяжелые по сравнению с другими компонентами автомобиля.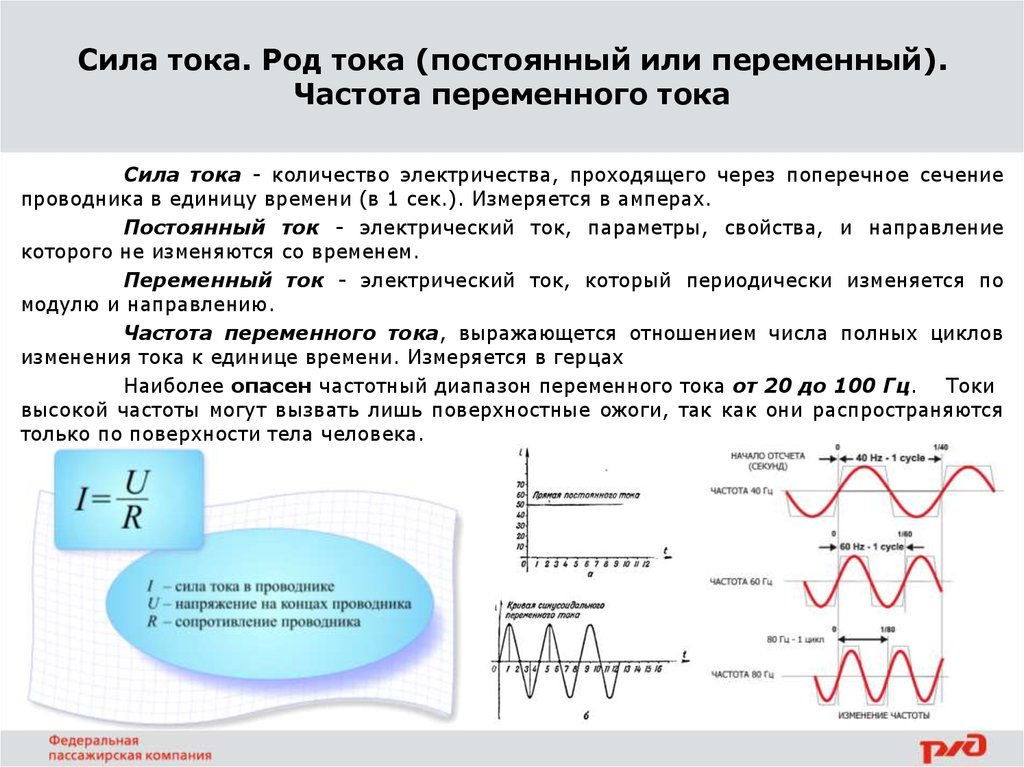 Существует также потеря эффективности, когда мощность преобразуется механическими компонентами. Эти факторы приводят к снижению общей эффективности системы и увеличению стоимости дополнительных компонентов. Это еще один подход к управлению соотношением крутящего момента и скорости в электромобилях.
Существует также потеря эффективности, когда мощность преобразуется механическими компонентами. Эти факторы приводят к снижению общей эффективности системы и увеличению стоимости дополнительных компонентов. Это еще один подход к управлению соотношением крутящего момента и скорости в электромобилях.
Принятие компромисса между крутящим моментом и скоростью
Другой альтернативой фундаментальной проблеме балансировки скорости и крутящего момента является принятие системных ограничений, когда речь идет о некоторых приложениях. Гоночный мотоцикл, например, предназначен для работы и, таким образом, может развивать невероятную скорость, но не может буксировать дом на колесах, поскольку у него нет необходимого крутящего момента для этого приложения. С другой стороны, полуприцеп оптимизирован для высокого крутящего момента и может тянуть чрезмерный вес, но не может развивать высокие скорости, которые может развить легковой автомобиль. Не имея лучших технологических решений, производители иногда просто принимают ограничения соотношения крутящего момента и скорости.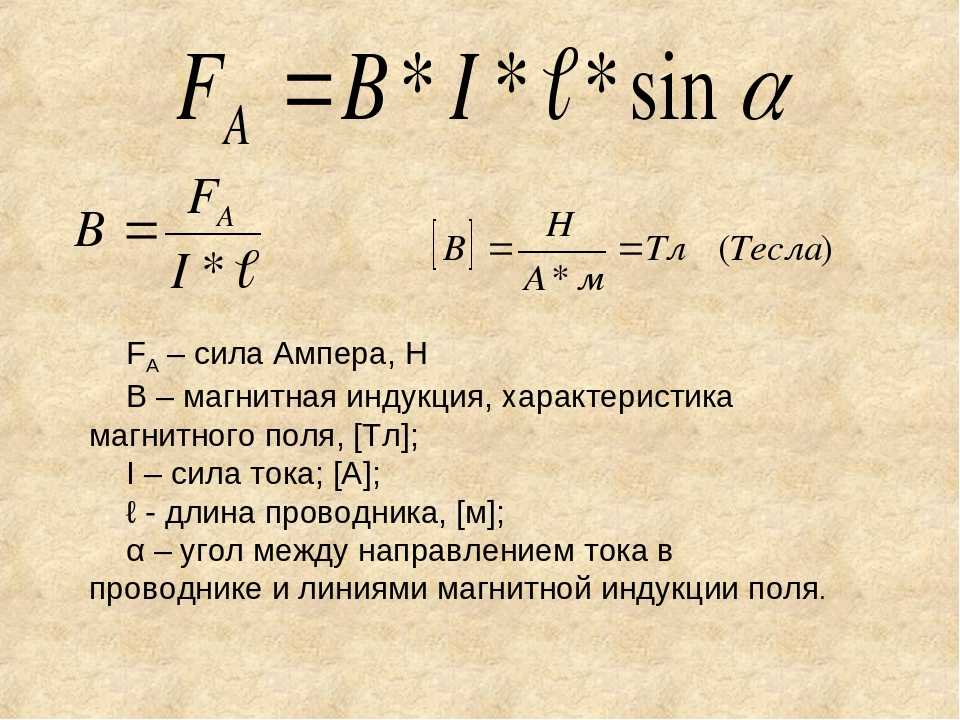
Новое решение для компромисса между крутящим моментом и скоростью: Coil Driver™
В технологии Coil Driver™ существует новый способ управления соотношением крутящего момента и скорости. Оснащенный передовой силовой электроникой, Coil Driver™ может управлять любым двигателем переменного тока с повышенной производительностью в широком диапазоне приложений вплоть до пиковой мощности и предлагает современное решение для компромисса между скоростью и крутящим моментом. Coil Driver от Exro — это новый динамический контроллер, который позволяет использовать несколько настроек мощности в одном двигателе. Этот контроллер заменяет стандартный контроллер электродвигателя и эффективно создает интеллектуальный электронный редуктор внутри двигателя. Это достигается за счет включения двух режимов работы в одном двигателе, один из которых оптимизирован для низкой скорости и высокого крутящего момента, а другой оптимизирован для высокой скорости и низкого крутящего момента.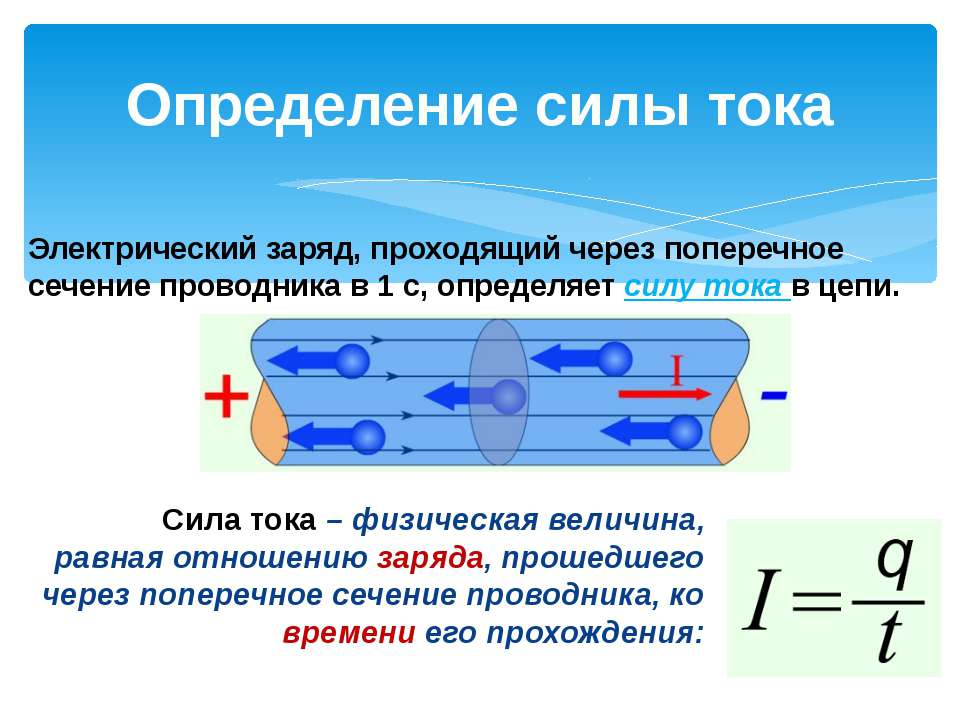 Coil Driver™ оптимизирует двигатель в режиме реального времени, плавно и по запросу, что позволяет оптимизировать эффективность для каждого режима работы, что приводит к более рациональному потреблению энергии, повышению производительности и снижению стоимости системы.
Coil Driver™ оптимизирует двигатель в режиме реального времени, плавно и по запросу, что позволяет оптимизировать эффективность для каждого режима работы, что приводит к более рациональному потреблению энергии, повышению производительности и снижению стоимости системы.
Exro Technologies также представила новое приложение для своей запатентованной технологии Coil Driver™, которая может значительно снизить стоимость и сложность, связанные с развертыванием инфраструктуры электромобилей в масштабе. Зарядное устройство Coil Drive убирает встроенное зарядное устройство, удаляет внешний выпрямитель переменного/постоянного тока, обеспечивает универсальную быструю зарядку переменного тока и добавляет возможности транспортного средства ко всему (V2X).
Технологические достижения Exro Technologies не только решают фундаментальную проблему соотношения крутящего момента и скорости в электромобилях, но и устраняют барьеры, связанные с внедрением электромобилей.
Электрический ток | безграничная физика |
Аккумулятор
Батарея — это устройство, которое преобразует химическую энергию непосредственно в электрическую энергию.
Цели обучения
Опишите функции и определите основные компоненты батареи
Ключевые выводы
Ключевые моменты
- Батарея накапливает электрический потенциал в результате химической реакции. Когда он подключен к цепи, этот электрический потенциал преобразуется в кинетическую энергию, когда электроны движутся по цепи.
- Напряжение или разность потенциалов между двумя точками определяется как изменение потенциальной энергии заряда q, перемещенного из точки 1 в точку 2, деленное на заряд.
- Напряжение батареи является синонимом ее электродвижущей силы или ЭДС. Эта сила отвечает за поток заряда через цепь, известную как электрический ток.
Ключевые термины
- батарея : Устройство, вырабатывающее электричество в результате химической реакции между двумя веществами.
- ток : Скорость потока электрического заряда во времени.

- напряжение : Величина электростатического потенциала между двумя точками в пространстве.
Символ батареи на принципиальной схеме : Это символ батареи на принципиальной схеме. Он возник как схематический рисунок самого раннего типа батареи, вольтовой батареи. Обратите внимание на положительный катод и отрицательный анод. Эта ориентация важна при рисовании принципиальных схем, чтобы изобразить правильный поток электронов.
Батарея — это устройство, которое преобразует химическую энергию непосредственно в электрическую энергию. Он состоит из ряда гальванических элементов, соединенных последовательно проводящим электролитом, содержащим анионы и катионы. Одна полуэлемент включает электролит и анод или отрицательный электрод; другая половина элемента включает электролит и катод или положительный электрод. В окислительно-восстановительной (восстановительно-окислительной) реакции, которая питает аккумулятор, катионы восстанавливаются (присоединяются электроны) на катоде, а анионы окисляются (электроны удаляются) на аноде. Электроды не касаются друг друга, а электрически связаны электролитом. В некоторых элементах используются два полуэлемента с разными электролитами. Разделитель между полуячейками позволяет ионам течь, но предотвращает смешивание электролитов.
Электроды не касаются друг друга, а электрически связаны электролитом. В некоторых элементах используются два полуэлемента с разными электролитами. Разделитель между полуячейками позволяет ионам течь, но предотвращает смешивание электролитов.
Каждая полуячейка обладает электродвижущей силой (или ЭДС), определяемой ее способностью проводить электрический ток изнутри клетки наружу. Суммарная ЭДС клетки представляет собой разность между ЭДС ее полуячеек или разность между восстановительными потенциалами полуреакций.
Электрическая движущая сила на клеммах элемента известна как напряжение на клеммах (разность) и измеряется в вольтах. Когда батарея подключена к цепи, электроны от анода проходят через цепь к катоду по прямой цепи. Напряжение батареи является синонимом ее электродвижущей силы или ЭДС. Эта сила отвечает за поток заряда через цепь, известную как электрический ток.
Аккумулятор накапливает электрический потенциал в результате химической реакции. Когда он подключен к цепи, этот электрический потенциал преобразуется в кинетическую энергию, когда электроны движутся по цепи. Электрический потенциал определяется как потенциальная энергия на единицу заряда ( q ). Напряжение или разность потенциалов между двумя точками определяется как изменение потенциальной энергии заряда q , перемещенного из точки 1 в точку 2, деленное на заряд. В перестановке это математическое соотношение может быть описано как:
Электрический потенциал определяется как потенциальная энергия на единицу заряда ( q ). Напряжение или разность потенциалов между двумя точками определяется как изменение потенциальной энергии заряда q , перемещенного из точки 1 в точку 2, деленное на заряд. В перестановке это математическое соотношение может быть описано как:
ΔPE=qΔV\Delta \text{PE} =\text{q}\Delta \text{V}ΔPE=qΔV
Напряжение — это не то же самое, что энергия. Напряжение – это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между клеммами аккумулятора), но один из них хранит гораздо больше энергии, чем другой. Автомобильный аккумулятор может передавать больше заряда, чем аккумулятор мотоцикла, хотя оба являются аккумуляторами на 12 В.
Идеальные и настоящие батареи : Краткое введение в идеальные и реальные батареи для студентов, изучающих схемы.
Измерение тока и напряжения в цепях
Электрический ток прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению в цепи.
Цели обучения
Описать взаимосвязь между электрическим током, напряжением и сопротивлением в цепи
Ключевые выводы
Ключевые моменты
- Простая цепь состоит из источника напряжения и резистора.
- Закон Ома дает соотношение между током I , напряжением В и сопротивлением R в простой цепи: I = В / R .
- Единицей СИ для измерения скорости потока электрического заряда является ампер, который равен заряду, протекающему через некоторую поверхность со скоростью один кулон в секунду.
Ключевые термины
- электрический ток : движение заряда по цепи
- ом : в Международной системе единиц производная единица электрического сопротивления; электрическое сопротивление устройства, на котором разность потенциалов в один вольт вызывает ток в один ампер; символ: Ом
- ампер : Единица электрического тока; стандартная базовая единица в Международной системе единиц.
 Аббревиатура: амп. Символ: А.
Аббревиатура: амп. Символ: А.
Чтобы понять, как измерять ток и напряжение в цепи, вы также должны иметь общее представление о том, как работает цепь и как связаны ее электрические измерения.
Что такое напряжение? : Это видео помогает получить концептуальное представление о напряжении.
Электрическая цепь — это тип сети с замкнутым контуром, который обеспечивает обратный путь для тока. Простая электрическая цепь состоит из источника напряжения и резистора и может быть схематически представлена следующим образом:
Простая электрическая цепь : простая электрическая цепь, состоящая из источника напряжения и резистора
По закону Ома ток I , или движение заряда, протекающего через большинство веществ, прямо пропорционально приложенному к нему напряжению В . Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется сопротивлением R . Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току. Следовательно, закон Ома можно записать следующим образом:
Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется сопротивлением R . Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току. Следовательно, закон Ома можно записать следующим образом:
I=V/R\text{I} = \text{V}/\text{R}I=V/R
, где I — ток через проводник в амперах, V — разность потенциалов, измеренная на проводнике в вольтах, а R — сопротивление проводника в омах (Ом). Точнее, закон Ома гласит, что R в этом отношении постоянна, не зависит от тока. Используя это уравнение, мы можем рассчитать ток, напряжение или сопротивление в данной цепи.
Например, если бы у нас была батарея на 1,5 В, которая была подключена по замкнутой цепи к лампочке с сопротивлением 5 Ом, какой ток протекает по цепи? Чтобы решить эту проблему, мы просто подставим данные значения в закон Ома: I = 1,5 В/5 Ом; I = 0,3 ампера.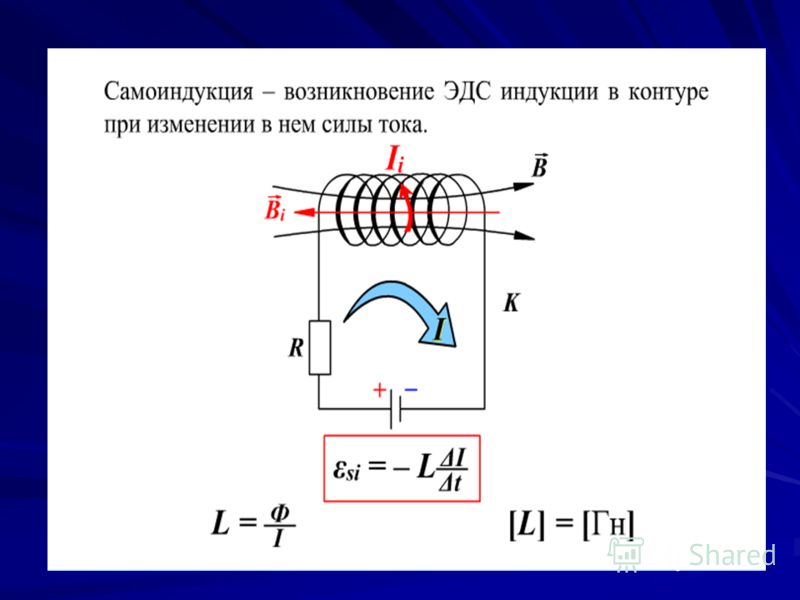 Если мы знаем ток и сопротивление, мы можем изменить уравнение закона Ома и решить для напряжения В :
Если мы знаем ток и сопротивление, мы можем изменить уравнение закона Ома и решить для напряжения В :
В=IR\text{V} = \text{IR}V=IR
A Вид под микроскопом: дрейф Скорость
Скорость дрейфа — это средняя скорость, которую частица достигает благодаря электрическому полю.
Цели обучения
Свяжите скорость дрейфа со скоростью свободных зарядов в проводниках
Ключевые выводы
Ключевые моменты
- В проводниках существует электрическое поле, которое заставляет электроны дрейфовать в направлении, противоположном полю. Скорость дрейфа представляет собой среднюю скорость этих свободных зарядов.
- Выражение для связи между током и скоростью дрейфа можно получить, рассматривая количество свободных зарядов в отрезке проволоки.
- I = qnAv связывает скорость дрейфа с током, где I — ток через провод с площадью поперечного сечения изготовлен из материала с плотностью свободного заряда n .
 Каждый из носителей тока имеет заряд q и движется с дрейфовой скоростью величины v .
Каждый из носителей тока имеет заряд q и движется с дрейфовой скоростью величины v .
Ключевые термины
- дрейфовая скорость : Средняя скорость свободных зарядов в проводнике.
Скорость дрейфа
Известно, что электрические сигналы распространяются очень быстро. Телефонные разговоры, переносимые токами по проводам, проходят большие расстояния без заметных задержек. Свет загорается, как только щелкаешь выключателем. Большинство электрических сигналов, переносимых током, распространяется со скоростью порядка 10 8 м/с, что составляет значительную часть скорости света. Интересно, что отдельные заряды, составляющие ток, в среднем движутся гораздо медленнее, обычно дрейфуя со скоростью порядка 10 −4 м/с.
Высокая скорость электрических сигналов обусловлена тем, что сила между зарядами быстро действует на расстоянии. Таким образом, когда свободный заряд попадает в проводник, входящий заряд отталкивает другие заряды впереди себя, которые, в свою очередь, отталкивают заряды дальше по линии. Возникающая в результате ударная волна электрического тока движется по системе почти со скоростью света. Точнее, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.
Возникающая в результате ударная волна электрического тока движется по системе почти со скоростью света. Точнее, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.
Электроны, движущиеся через проводник : Когда заряженные частицы попадают в этот объем проводника, такое же количество быстро вынуждено покинуть его. Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только входит один заряд, другой почти сразу уходит, быстро перенося сигнал вперед.
Скорость дрейфа
Хорошие проводники имеют большое количество свободных зарядов. В металлах свободными зарядами являются свободные электроны. Расстояние, которое может пройти отдельный электрон между столкновениями с атомами или другими электронами, весьма мало. Таким образом, траектории электронов кажутся почти случайными, как движение атомов в газе.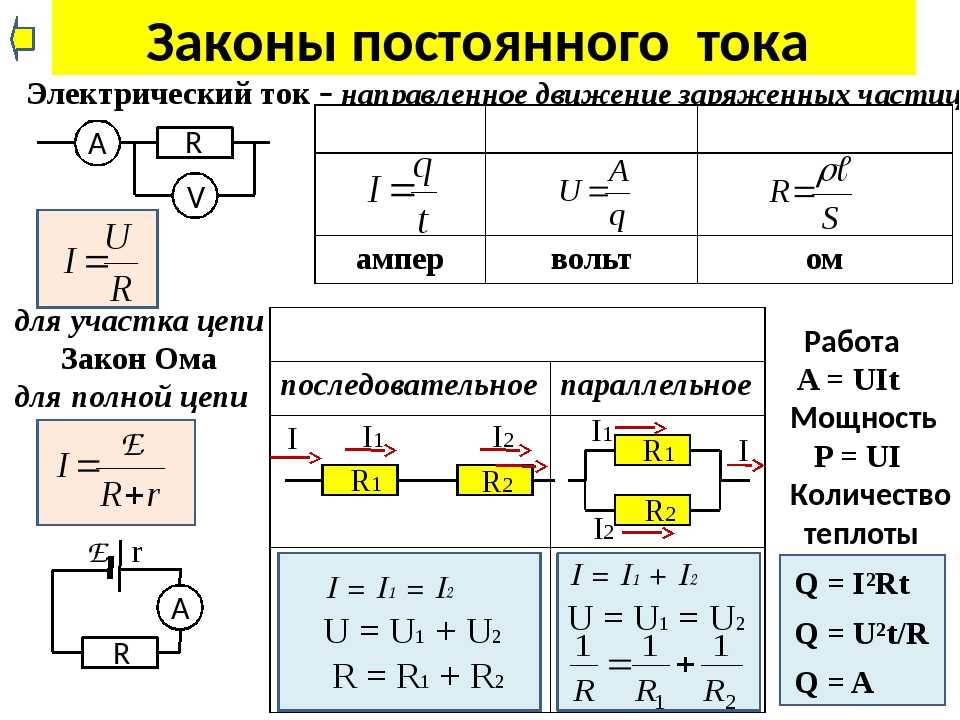 Однако в проводнике существует электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). Скорость дрейфа v d — средняя скорость свободных зарядов после приложения поля. Скорость дрейфа довольно мала, так как очень много свободных зарядов. Зная плотность свободных электронов в проводнике (количество электронов в единице объема), можно рассчитать скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.
Однако в проводнике существует электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). Скорость дрейфа v d — средняя скорость свободных зарядов после приложения поля. Скорость дрейфа довольно мала, так как очень много свободных зарядов. Зная плотность свободных электронов в проводнике (количество электронов в единице объема), можно рассчитать скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.
Скорость дрейфа : Свободные электроны, движущиеся в проводнике, часто сталкиваются с другими электронами и атомами. Показан путь одного электрона. Средняя скорость свободных зарядов называется дрейфовой скоростью и направлена в направлении, противоположном электрическому полю для электронов. Столкновения обычно передают энергию проводнику, что требует постоянной подачи энергии для поддержания постоянного тока.
Можно получить выражение для связи между током и скоростью дрейфа, рассматривая количество свободных зарядов в отрезке проволоки. Количество свободных зарядов на единицу объема обозначается символом n и зависит от материала. Ax — это объем сегмента, так что количество свободных зарядов в нем равно nAx . Плата ΔQ в этом сегменте, таким образом, составляет qnAx , где q — сумма платы на каждом носителе. (Напомним, что для электронов q составляет 1,60×10-19°С. ) Ток — это заряд, перемещаемый в единицу времени. Таким образом, если все первоначальные заряды покидают этот отрезок за время t, то ток равен:
Количество свободных зарядов на единицу объема обозначается символом n и зависит от материала. Ax — это объем сегмента, так что количество свободных зарядов в нем равно nAx . Плата ΔQ в этом сегменте, таким образом, составляет qnAx , где q — сумма платы на каждом носителе. (Напомним, что для электронов q составляет 1,60×10-19°С. ) Ток — это заряд, перемещаемый в единицу времени. Таким образом, если все первоначальные заряды покидают этот отрезок за время t, то ток равен:
I=ΔQ/Δt=qnAx/Δt\text{I} = \Delta \text{Q}/\Delta \text{ t} = \text{qnAx}/\Delta \text{t}I=ΔQ/Δt=qnAx/Δt
Примечательно, что x/Δt — модуль скорости дрейфа v d , так как заряды движутся среднее расстояние x за время t. Перестановка членов дает: I = qnAv d , где I — сила тока через провод площадью поперечного сечения А , изготовленный из материала с плотностью свободного заряда n . Каждый из носителей тока имеет заряды q и движется с дрейфовой скоростью величины v d .
Каждый из носителей тока имеет заряды q и движется с дрейфовой скоростью величины v d .
Плотность тока – это электрический ток на единицу площади поперечного сечения. Он измеряется в амперах на квадратный метр.
Лицензии и атрибуты
Содержимое по лицензии CC, опубликованное ранее
- Курирование и доработка. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, конкретное указание авторства
- OpenStax College, College Physics. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Аккумулятор (электричество). Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Аккумулятор (электричество).
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - напряжение. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- батарея. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- ток. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Идеальные и настоящие батареи. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Аккумулятор (электричество). Предоставлено : Википедия. Лицензия : CC BY: Атрибуция
- Предоставлено : Свет и Материя. Лицензия : CC BY: Атрибуция
- Напряжение.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Электрический ток. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Электрический ток. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- ампер. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Ом. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- электрический ток. Предоставлено : Викисловарь.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Идеальные и настоящие батареи. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Аккумулятор (электричество). Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Электрическая цепь. Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Что такое напряжение?. Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
- Электрический ток. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Безграничный. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Идеальные и настоящие батареи. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Аккумулятор (электричество). Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Электрическая цепь. Предоставлено : Википедия. Лицензия : CC BY: Attribution
- Что такое напряжение?. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- OpenStax College, College Physics.
 26 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
26 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Колледж физики. 26 октября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
Взаимосвязь между изменением направления, скорости и мощности у спортсменов национальных олимпийских команд мужского и женского пола по гандболу
. 2018 Октябрь; 32 (10): 2987-2994.
doi: 10.1519/JSC.0000000000002494.
Лукас А. Перейра 1 , София Нимфий 2 , Роналдо Кобал 1 , Катя Китамура 1 , Луис А.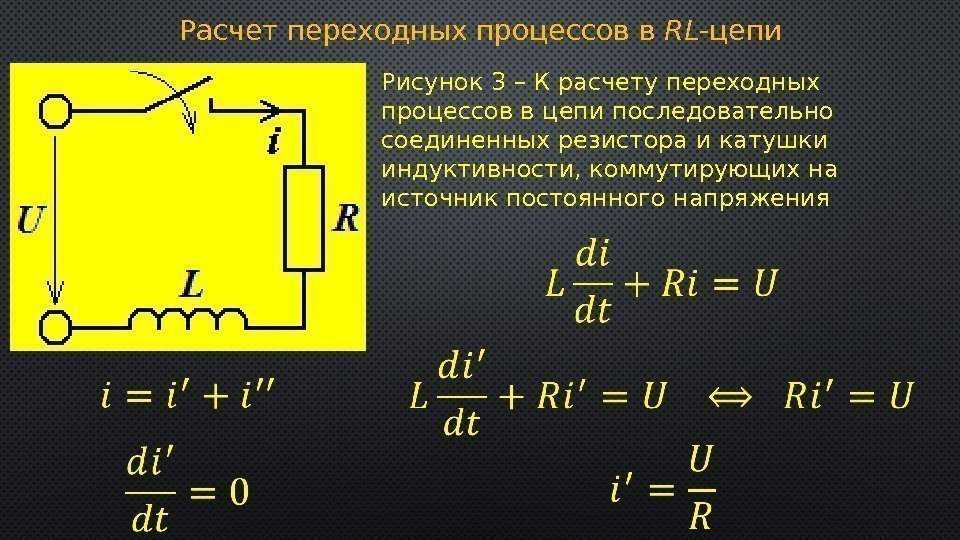 Л. Туриско 3 , Рита К Орси 3 , Сезар С. Каль-Абад 1 , Иринеу Лотурко 1
Л. Туриско 3 , Рита К Орси 3 , Сезар С. Каль-Абад 1 , Иринеу Лотурко 1
Принадлежности
- 1 NAR-Nucleus of High Performance in Sport, Сан-Паулу, Сан-Паулу, Бразилия.
- 2 Центр физических упражнений и спортивных наук, Школа медицины и здравоохранения, Университет Эдит Коуэн, Джоондалуп, Западная Австралия, Австралия.
- 3 Бразильская конфедерация гандбола, Аракажу, Сержипи, Бразилия.
- PMID: 29481446
- DOI:
10.
 1519/ОАО.0000000000002494
1519/ОАО.0000000000002494
Лукас А. Перейра и др. J Прочность Конд Рез. 2018 Октябрь
. 2018 Октябрь; 32 (10): 2987-2994.
doi: 10.1519/JSC.0000000000002494.
Авторы
Лукас А. Перейра 1 , София Нимфий 2 , Роналдо Кобал 1 , Катя Китамура 1 , Луис А. Л. Туриско 3 , Рита К Орси 3 , Сезар С. Каль-Абад 1 , Иринеу Лотурко 1
Принадлежности
- 1 NAR-Nucleus of High Performance in Sport, Сан-Паулу, Сан-Паулу, Бразилия.

- 2 Центр физических упражнений и спортивных наук, Школа медицины и здравоохранения, Университет Эдит Коуэн, Джоондалуп, Западная Австралия, Австралия.
- 3 Бразильская конфедерация гандбола, Аракажу, Сержипи, Бразилия.
- PMID: 29481446
- DOI: 10.1519/ОАО.0000000000002494
Абстрактный
Перейра, Л.А., Нимфиус, С., Кобал, Р., Китамура, К., Туриско, ЛАЛ, Орси, Р.К., Кал-Абад, К.С., и Лотурко, И. Взаимосвязь между изменением направления, скорости и мощности у мужчин и женщин на национальных олимпийских играх. Команда гандболистов. J Прочность Сопротивление 32(10): 2987-2994, 2018-Цели этого исследования состояли в том, чтобы (а) оценить взаимосвязь между выбранными скоростными и силовыми способностями (определяемыми спринтом на 20 м, прыжком в контрдвижении без нагрузки [CMJ] и прыжком в приседе [SJ] и приседания с прыжком с нагрузкой [JS]) и производительность в двух различных протоколах изменения направления (COD) (зигзагообразный тест и Т-тест) и (b) определяют величину разницы между женщинами и мужчинами-спортсменами национальной олимпийской сборной Бразилии. Пятнадцать мужчин и 23 женщины элитных гандболистов вызвались провести следующие оценки: SJ и CMJ; Зигзагообразный тест и Т-тест; спринт на 20 м с разделением на 5, 10 и 20 м; и средняя тяговая мощность в JS. Корреляция продукта-момента Пирсона (p ≤ 0,05) была выполнена для определения взаимосвязи между тестами ХПК (тест Зигзаг и Т-тест) и показателями скорости и мощности (спринт, SJ, CMJ и JS). Различия между мужскими и женскими показателями определялись с помощью логического вывода.
Команда гандболистов. J Прочность Сопротивление 32(10): 2987-2994, 2018-Цели этого исследования состояли в том, чтобы (а) оценить взаимосвязь между выбранными скоростными и силовыми способностями (определяемыми спринтом на 20 м, прыжком в контрдвижении без нагрузки [CMJ] и прыжком в приседе [SJ] и приседания с прыжком с нагрузкой [JS]) и производительность в двух различных протоколах изменения направления (COD) (зигзагообразный тест и Т-тест) и (b) определяют величину разницы между женщинами и мужчинами-спортсменами национальной олимпийской сборной Бразилии. Пятнадцать мужчин и 23 женщины элитных гандболистов вызвались провести следующие оценки: SJ и CMJ; Зигзагообразный тест и Т-тест; спринт на 20 м с разделением на 5, 10 и 20 м; и средняя тяговая мощность в JS. Корреляция продукта-момента Пирсона (p ≤ 0,05) была выполнена для определения взаимосвязи между тестами ХПК (тест Зигзаг и Т-тест) и показателями скорости и мощности (спринт, SJ, CMJ и JS). Различия между мужскими и женскими показателями определялись с помощью логического вывода.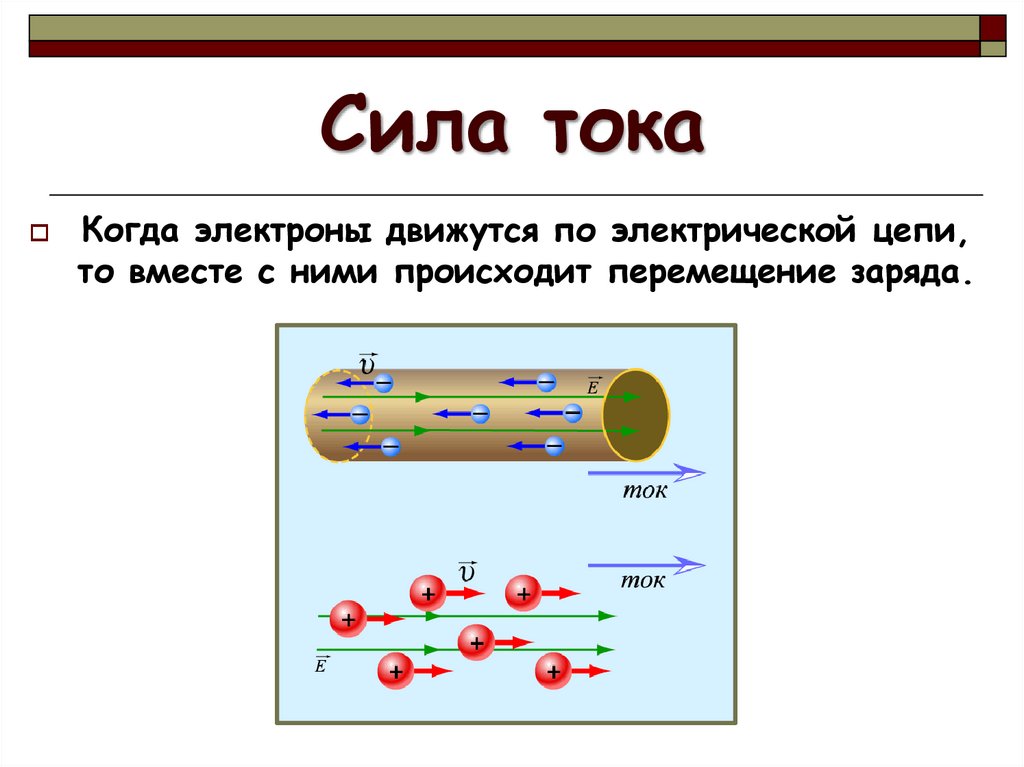 Между тестами ХПК и скоростно-силовыми способностями наблюдались значимые корреляции от умеренных до очень больших. Более того, спортсмены-мужчины почти наверняка продемонстрировали более высокие результаты, чем спортсменки-женщины, по всем оцениваемым переменным. Результаты текущего исследования показывают, что различные скоростно-силовые качества сильно коррелируют с показателями, полученными при различных оценках ХПК (значения r варьируются от 0,38 до 0,84 и от 0,34 до 0,84 для корреляции между тестами скорости и мощности с тестом Зигзаг и Т-тестом). тест соответственно). Однако уровень этих ассоциаций может сильно различаться в зависимости от механических требований каждой соответствующей задачи ХПК. Хотя тесты ХПК могут быть трудными для проведения во время соревновательных сезонов, из-за сильной корреляции, представленной здесь, регулярное использование тестов вертикального прыжка с этими спортсменами кажется эффективной и прикладной альтернативой. Кроме того, можно сделать вывод, что правильное развитие прыжковых способностей с нагрузкой и без нагрузки может улучшить физические качества, связанные с показателями ХПК, у спортсменов-гандболистов.
Между тестами ХПК и скоростно-силовыми способностями наблюдались значимые корреляции от умеренных до очень больших. Более того, спортсмены-мужчины почти наверняка продемонстрировали более высокие результаты, чем спортсменки-женщины, по всем оцениваемым переменным. Результаты текущего исследования показывают, что различные скоростно-силовые качества сильно коррелируют с показателями, полученными при различных оценках ХПК (значения r варьируются от 0,38 до 0,84 и от 0,34 до 0,84 для корреляции между тестами скорости и мощности с тестом Зигзаг и Т-тестом). тест соответственно). Однако уровень этих ассоциаций может сильно различаться в зависимости от механических требований каждой соответствующей задачи ХПК. Хотя тесты ХПК могут быть трудными для проведения во время соревновательных сезонов, из-за сильной корреляции, представленной здесь, регулярное использование тестов вертикального прыжка с этими спортсменами кажется эффективной и прикладной альтернативой. Кроме того, можно сделать вывод, что правильное развитие прыжковых способностей с нагрузкой и без нагрузки может улучшить физические качества, связанные с показателями ХПК, у спортсменов-гандболистов.
Похожие статьи
Прогностические факторы элитного спринта: влияние механических свойств мышц и функциональных параметров.
Лотурко И., Кобал Р., Китамура К., Фернандес В., Моура Н., Сикейра Ф., Кал Абад К.С., Перейра Л.А. Лотурко I и др. J Прочность Конд Рез. 2019 апр; 33 (4): 974-986. doi: 10.1519/JSC.0000000000002196. J Прочность Конд Рез. 2019. PMID: 303
Силовые и силовые показатели паралимпийских и олимпийских спортсменов-дзюдоистов с нарушениями зрения из национальной сборной Бразилии: сравнительное исследование.
Лотурко И., Накамура Ф.Ю., Винклер К., Браганса Дж.Р., да Фонсека Р.А., Мораес-Фильо Дж., Заккани В.А., Кобал Р., Кэл Абад К.С., Китамура К., Перейра Л.А., Франчини Э.
 Лотурко I и др.
J Прочность Конд Рез. 2017 март; 31 (3): 743-749. doi: 10.1519/JSC.0000000000001525.
J Прочность Конд Рез. 2017.
PMID: 27379958
Лотурко I и др.
J Прочность Конд Рез. 2017 март; 31 (3): 743-749. doi: 10.1519/JSC.0000000000001525.
J Прочность Конд Рез. 2017.
PMID: 27379958Различия в скорости и силовых возможностях между женской национальной сборной колледжа и национальной олимпийской сборной по гандболу.
Перейра Л.А., Каль Абад К.С., Кобал Р., Китамура К., Орси Р.С., Рамирес-Кампильо Р., Лотурко И. Перейра Л.А. и соавт. Джей Хам Кинет. 2018 сен 24; 63: 85-94. doi: 10.2478/hukin-2018-0009. Электронная коллекция 2018, 31 августа. Джей Хам Кинет. 2018. PMID: 30279944 Бесплатная статья ЧВК.
Понимание способности к изменению направления в спорте: обзор исследований силовых тренировок.
Бругелли М., Кронин Дж., Левин Г.
 , Чауачи А.
Бругелли М. и соавт.
Спорт Мед. 2008;38(12):1045-63. doi: 10.2165/00007256-200838120-00007.
Спорт Мед. 2008.
PMID: 120
Обзор.
, Чауачи А.
Бругелли М. и соавт.
Спорт Мед. 2008;38(12):1045-63. doi: 10.2165/00007256-200838120-00007.
Спорт Мед. 2008.
PMID: 120
Обзор.Изменчивость соревновательной деятельности элитных спортсменов: систематический обзор.
Малката Р.М., Хопкинс В.Г. Малката Р.М. и соавт. Спорт Мед. 2014 Декабрь; 44 (12): 1763-74. doi: 10.1007/s40279-014-0239-x. Спорт Мед. 2014. PMID: 25108349 Обзор.
Посмотреть все похожие статьи
Цитируется
На пути к новой парадигме тренировок с отягощениями с помощью мониторинга скорости: критический и сложный рассказ.
Гонсалес-Бадильо Х.Дж., Санчес-Медина Л., Рибас-Серна Х., Родригес-Роселл Д.
 Гонсалес-Бадильо Дж. Дж. и др.
Открытый мед. спорт. 2022 16 сентября; 8 (1): 118. doi: 10.1186/s40798-022-00513-z.
Открытый мед. спорт. 2022.
PMID: 36114395
Бесплатная статья ЧВК.
Обзор.
Гонсалес-Бадильо Дж. Дж. и др.
Открытый мед. спорт. 2022 16 сентября; 8 (1): 118. doi: 10.1186/s40798-022-00513-z.
Открытый мед. спорт. 2022.
PMID: 36114395
Бесплатная статья ЧВК.
Обзор.Альтернативы общепринятым подходам к обучению изменению направления деятельности: предварительный обзор.
Бухманн Р., Штуэлькен М., Сэйерс М. Бухманн Р. и соавт. BMC Sports Sci Med Rehabil. 2022 3 августа; 14 (1): 151. doi: 10.1186/s13102-022-00544-9. BMC Sports Sci Med Rehabil. 2022. PMID: 35922872 Бесплатная статья ЧВК.
Различия в профилях сила-скорость при прыжке с контрдвижением и приседаниях на маховом колесе и ассоциации с разным изменением направления в тестах элитных каратистов.
Смайла Д.
 , Спудич Д., Козинц Ж., Шарабон Н.
Смайла Д. и соавт.
Фронт Физиол. 2022 21 июня; 13:828394. doi: 10.3389/fphys.2022.828394. Электронная коллекция 2022.
Фронт Физиол. 2022.
PMID: 35800347
Бесплатная статья ЧВК.
, Спудич Д., Козинц Ж., Шарабон Н.
Смайла Д. и соавт.
Фронт Физиол. 2022 21 июня; 13:828394. doi: 10.3389/fphys.2022.828394. Электронная коллекция 2022.
Фронт Физиол. 2022.
PMID: 35800347
Бесплатная статья ЧВК.Силовые способности и эффективность приема подачи юных волейболисток.
Павлик Д., Дзюбек В., Роговский Л., Струзик А., Рокита А. Павлик Д. и др. Appl Bionics Biomech. 2022 1 июня; 2022:4328761. дои: 10.1155/2022/4328761. Электронная коллекция 2022. Appl Bionics Biomech. 2022. PMID: 35694275 Бесплатная статья ЧВК.
Влияние физических и технических аспектов на изменение направления движения игроков в регби: предварительное исследование.
Freitas TT, Alcaraz PE, Calleja-González J, Arruda AFS, Guerriero A, Mercer VP, Pereira LA, Carpes FP, McGuigan MR, Loturco I.
 Фрейтас ТТ и др.
Общественное здравоохранение Int J Environ Res. 2021 дек 20;18(24):13390. дои: 10.3390/ijerph282413390.
Общественное здравоохранение Int J Environ Res. 2021.
PMID: 34948999
Бесплатная статья ЧВК.
Фрейтас ТТ и др.
Общественное здравоохранение Int J Environ Res. 2021 дек 20;18(24):13390. дои: 10.3390/ijerph282413390.
Общественное здравоохранение Int J Environ Res. 2021.
PMID: 34948999
Бесплатная статья ЧВК.
Просмотреть все статьи «Цитируется по»
термины MeSH
Учебное пособие по двигателю постоянного тока. Расчеты двигателей постоянного тока без сердечника
Ниже приведен метод определения параметров двигателя на примере двигателя постоянного тока без сердечника 2668W024CR. Сначала мы объясним более эмпирический подход, затем проведем теоретический расчет.
Одним из широко используемых методов графического отображения характеристик двигателя является использование кривых крутящий момент-скорость. Хотя использование кривых крутящий момент-скорость гораздо более распространено в технической литературе для более крупных машин постоянного тока, чем для небольших устройств без сердечника, этот метод применим в любом случае.
Обычно кривые крутящий момент-скорость строятся путем построения графика скорости двигателя, тока двигателя, механической выходной мощности и КПД в зависимости от крутящего момента двигателя. В следующем обсуждении будет описано построение набора кривых крутящий момент-скорость для типичного двигателя постоянного тока на основе серии измерений необработанных данных.
Номинальное напряжение 2668W024CR составляет 24 В. Если у вас есть несколько основных элементов лабораторного оборудования, вы можете измерить кривые крутящий момент-скорость для двигателя постоянного тока без сердечника серии 2668 CR в заданной рабочей точке.
Шаг 1: Измерьте основные параметры
Многие параметры можно получить непосредственно с помощью контроллера движения, например, одного из контроллеров движения FAULHABER MC3. Большинство производителей контроллеров предлагают программное обеспечение, такое как FAULHABER Motion Manager, которое включает в себя функцию записи кривой, отображающую напряжение, ток, положение, скорость и т. д. Они также могут предоставить точный моментальный снимок работы двигателя в мельчайших деталях. Например, контроллеры движения семейства MC3 (MC 5004, MC 5005 и MC 5010) могут измерять множество параметров движения. Это, вероятно, самый быстрый метод получения данных для построения кривой крутящий момент-скорость, но это не единственный метод.
д. Они также могут предоставить точный моментальный снимок работы двигателя в мельчайших деталях. Например, контроллеры движения семейства MC3 (MC 5004, MC 5005 и MC 5010) могут измерять множество параметров движения. Это, вероятно, самый быстрый метод получения данных для построения кривой крутящий момент-скорость, но это не единственный метод.
Если контроллер с возможностью записи трассировки недоступен, мы также можем использовать базовое лабораторное оборудование для определения характеристик двигателя в условиях останова, номинального состояния и без нагрузки. Используя источник питания, настроенный на 24 В, запустите 2668W024CR без нагрузки и измерьте скорость вращения с помощью бесконтактного тахометра (например, стробоскопа). Кроме того, измерьте ток двигателя в этом состоянии без нагрузки. Токовый пробник идеально подходит для этого измерения, так как он не добавляет сопротивления последовательно с работающим двигателем. Используя нагрузку с регулируемым крутящим моментом, такую как тормоз мелких частиц или динамометр с регулируемым гистерезисом, к валу двигателя может быть присоединена нагрузка.
Теперь увеличьте крутящий момент двигателя до точки, при которой происходит остановка. В остановленном состоянии измерьте крутящий момент от тормоза и ток двигателя. Для этого обсуждения предположим, что муфта не добавляет нагрузки к двигателю и что нагрузка от тормоза не включает неизвестные фрикционные компоненты. В этот момент также полезно измерить терминальное сопротивление двигателя. Измерьте сопротивление, прикоснувшись к клеммам двигателя омметром. Затем прокрутите вал двигателя и выполните еще одно измерение. Измерения должны быть очень близки по значению. Продолжайте вращать вал и сделайте не менее трех измерений. Это гарантирует, что измерения не проводились в точке минимального контакта с коммутатором.
Теперь мы измерили:
N 0 = Скорость без нагрузки
I 0 = ток без нагрузки
H = Респин
Шаг 2. Постройте график зависимости тока от крутящего момента и скорости от крутящего момента
Вы можете построить график с крутящим моментом двигателя на оси абсцисс (горизонтальная ось), скоростью на левой оси ординаты (вертикальная ось) и током на правой стороне ординаты. Масштабируйте оси на основе измерений, сделанных на первом шаге. Проведите прямую линию от левого начала графика (нулевой крутящий момент и нулевой ток) к току останова на правой стороне ординаты (момент останова и ток останова). Эта линия представляет собой график зависимости тока двигателя от крутящего момента двигателя. Наклон этой линии представляет собой текущую константу k I , которая представляет собой константу пропорциональности для отношения между током двигателя и крутящим моментом двигателя (в единицах тока на единицу крутящего момента или А/мН·м). Обратной величиной этого наклона является постоянная крутящего момента k M (в единицах крутящего момента на единицу тока или мНм/А).
Масштабируйте оси на основе измерений, сделанных на первом шаге. Проведите прямую линию от левого начала графика (нулевой крутящий момент и нулевой ток) к току останова на правой стороне ординаты (момент останова и ток останова). Эта линия представляет собой график зависимости тока двигателя от крутящего момента двигателя. Наклон этой линии представляет собой текущую константу k I , которая представляет собой константу пропорциональности для отношения между током двигателя и крутящим моментом двигателя (в единицах тока на единицу крутящего момента или А/мН·м). Обратной величиной этого наклона является постоянная крутящего момента k M (в единицах крутящего момента на единицу тока или мНм/А).
Где:
k I = постоянная тока
k M = постоянная момента
Для целей данного обсуждения предполагается, что двигатель не имеет внутреннего трения. На практике момент трения двигателя M R определяется путем умножения постоянной крутящего момента k M двигателя на измеренный ток холостого хода I 0 . Линия крутящего момента в зависимости от скорости и линия крутящего момента в зависимости от тока затем начинаются не от левой вертикальной оси, а со смещением по горизонтальной оси, равным расчетному моменту трения.
Линия крутящего момента в зависимости от скорости и линия крутящего момента в зависимости от тока затем начинаются не от левой вертикальной оси, а со смещением по горизонтальной оси, равным расчетному моменту трения.
Где:
M R = Момент трения
Шаг 3: График зависимости мощности от крутящего момента и эффективности от крутящего момента
В большинстве случаев можно добавить две дополнительные вертикальные оси для построения зависимости мощности и эффективности от крутящего момента. Вторая вертикальная ось обычно используется для эффективности, а третья вертикальная ось может использоваться для мощности. Для упрощения этого обсуждения КПД в зависимости от крутящего момента и мощность в зависимости от крутящего момента будут нанесены на тот же график, что и графики зависимости скорости от крутящего момента и тока от крутящего момента (пример показан ниже).
Составьте таблицу механической мощности двигателя в различных точках от холостого хода до момента остановки.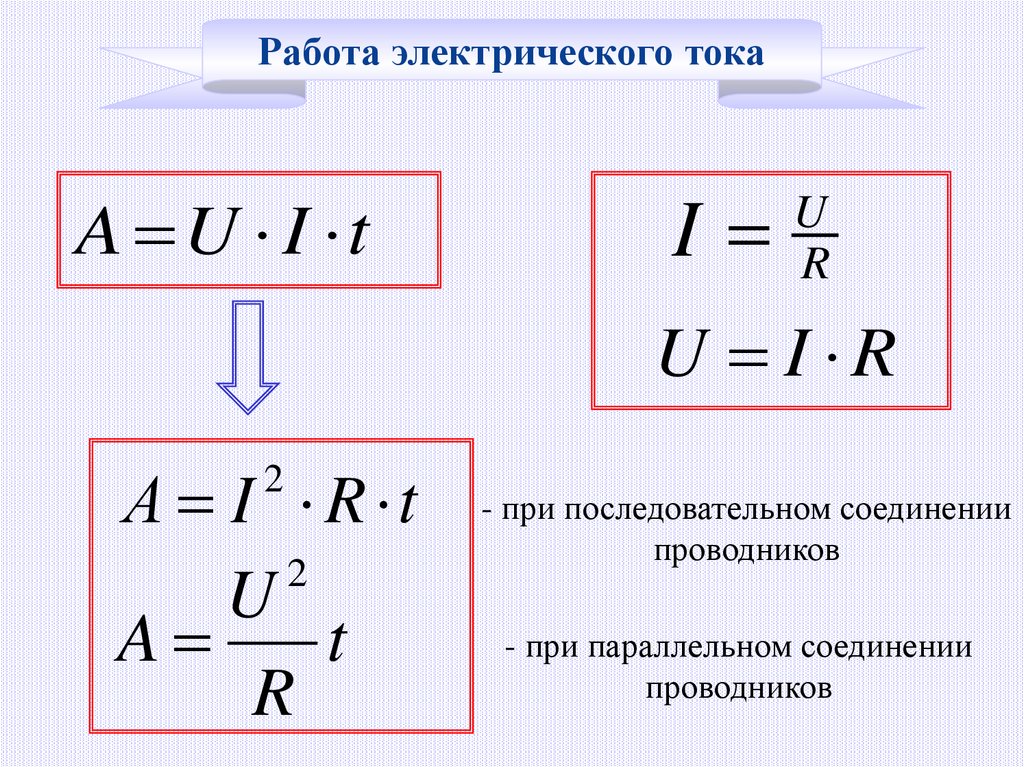 Поскольку выходная механическая мощность — это просто произведение крутящего момента и скорости с поправочным коэффициентом для единиц измерения (см. раздел о расчете начальной требуемой мощности), мощность можно рассчитать, используя ранее построенную линию зависимости скорости от крутящего момента.
Поскольку выходная механическая мощность — это просто произведение крутящего момента и скорости с поправочным коэффициентом для единиц измерения (см. раздел о расчете начальной требуемой мощности), мощность можно рассчитать, используя ранее построенную линию зависимости скорости от крутящего момента.
Пример таблицы расчетов для двигателя 2668W024CR показан в Таблице 1. Затем каждая расчетная точка для мощности наносится на график. Результирующая функция представляет собой параболическую кривую, как показано ниже на графике 1. Максимальная механическая мощность возникает примерно при половине крутящего момента срыва. Скорость в этот момент составляет примерно половину скорости холостого хода.
Составьте таблицу КПД двигателя в различных точках от скорости холостого хода до крутящего момента. Задано напряжение, приложенное к двигателю, и нанесен ток при различных уровнях крутящего момента. Произведение тока двигателя и приложенного напряжения представляет собой потребляемую двигателем мощность.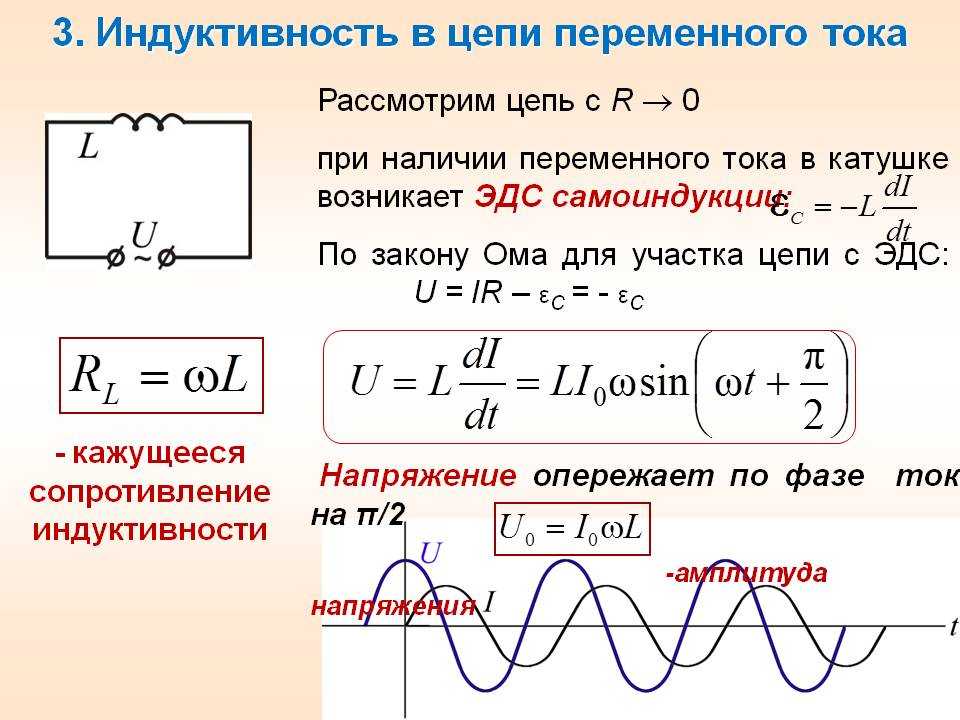 В каждой точке, выбранной для расчета, КПД η двигателя представляет собой выходную механическую мощность, деленную на потребляемую электрическую мощность. Опять же, примерная таблица для двигателя 2668W024CR показана в таблице 1, а примерная кривая — на графике 1. Максимальный КПД достигается примерно при 10% крутящего момента двигателя.
В каждой точке, выбранной для расчета, КПД η двигателя представляет собой выходную механическую мощность, деленную на потребляемую электрическую мощность. Опять же, примерная таблица для двигателя 2668W024CR показана в таблице 1, а примерная кривая — на графике 1. Максимальный КПД достигается примерно при 10% крутящего момента двигателя.
Определения графика
- Синий = скорость против крутящего момента ( N против M )
- Красный = ток против крутящего момента ( I против M )
- Green = Effectiality Vs. η по сравнению с M )
- Коричневый = мощность по отношению к крутящему моменту ( P по сравнению с M )
Характеристики двигателя
Примечание. Обратите внимание на изменение всех четырех сплошных графиков в результате увеличения сопротивления в медных обмотках и ослабления выходного крутящего момента из-за повышения температуры. Таким образом, ваши результаты могут немного отличаться в зависимости от того, холодный или теплый двигатель, когда вы строите графики.
Таким образом, ваши результаты могут немного отличаться в зависимости от того, холодный или теплый двигатель, когда вы строите графики.
| Load current | 2,79 A |
| Load voltage | 24,11 V |
| Motor winding temperature | 140,23 °C |
| Motor housing temperature | 105 ,03 °C |
| Motor speed | 7370 min -1 |
| Required load torque | 68 mNm |
| Output power | 52,48 W |
| Эффективность (общая) | 77,97 % |
Примечание. Из-за нехватки места приведен пример расчета для одной точки.
Теоретический расчет параметров двигателя
Другим полезным параметром при выборе двигателя является постоянная двигателя. Правильное использование этого показателя качества существенно сократит итерационный процесс выбора двигателя постоянного тока. Он просто измеряет внутреннюю способность преобразователя преобразовывать электрическую энергию в механическую.
Он просто измеряет внутреннюю способность преобразователя преобразовывать электрическую энергию в механическую.
Максимальный КПД достигается примерно при 10% крутящего момента двигателя. Знаменатель известен как резистивная потеря мощности. С помощью некоторых алгебраических преобразований уравнение можно упростить до:
Пожалуйста, имейте в виду, что k m (постоянная двигателя) не следует путать с k M (постоянная крутящего момента). Обратите внимание, что нижний индекс константы двигателя записывается строчными буквами « м », в то время как нижний индекс константы крутящего момента использует заглавные буквы « M 9».0006».
Для щеточного или бесщеточного двигателя постоянного тока относительно небольшого размера зависимости, управляющие поведением двигателя в различных обстоятельствах, могут быть получены из законов физики и характеристик самих двигателей. Правило напряжения Кирхгофа гласит: «Сумма повышений потенциала в контуре цепи должна равняться сумме падений потенциалов». Применительно к двигателю постоянного тока, соединенному последовательно с источником питания постоянного тока, правило напряжения Кирхгофа может быть выражено как «Номинальное напряжение питания от источника питания должно быть равно по величине сумме падения напряжения на сопротивлении обмоток и противо-ЭДС, создаваемой двигателем».
Применительно к двигателю постоянного тока, соединенному последовательно с источником питания постоянного тока, правило напряжения Кирхгофа может быть выражено как «Номинальное напряжение питания от источника питания должно быть равно по величине сумме падения напряжения на сопротивлении обмоток и противо-ЭДС, создаваемой двигателем».
Где:
U = источник питания в V
I = ток в
R = сопротивление терминала в ω
U E = Back-EMF в V
генерируемая двигателем, прямо пропорциональна угловой скорости двигателя. Константа пропорциональности – это константа противо-ЭДС двигателя.
Где:
ω = угловая скорость двигателя
k E = постоянная противо-ЭДС двигателя
Таким образом, путем замены:
Константа противо-ЭДС двигателя обычно указывается производителем двигателя в В/об/мин или мВ/об/мин. Чтобы получить осмысленное значение противо-ЭДС, необходимо указать скорость двигателя в единицах, совместимых с заданной константой противо-ЭДС.
Чтобы получить осмысленное значение противо-ЭДС, необходимо указать скорость двигателя в единицах, совместимых с заданной константой противо-ЭДС.
«Сумма повышений потенциала в петле цепи должна равняться сумме падений потенциалов».
(правило напряжения Кирхгофа)
Постоянная двигателя зависит от конструкции катушки, силы и направления силовых линий в воздушном зазоре. Хотя можно показать, что обычно указанные три константы двигателя (константа противо-ЭДС, константа крутящего момента и константа скорости) равны, если используются соответствующие единицы измерения, расчет облегчается заданием трех констант в общепринятых единицах измерения.
Крутящий момент, создаваемый ротором, прямо пропорционален току в обмотках якоря. Константа пропорциональности – это константа крутящего момента двигателя.
Где:
M m = крутящий момент, развиваемый двигателем
k M = постоянный крутящий момент двигателя крутящий момент двигателя плюс крутящий момент нагрузки (из-за внешней механической нагрузки):
Где:
M R = момент трения двигателя
M L = крутящий момент нагрузки сумма момента трения и момента нагрузки.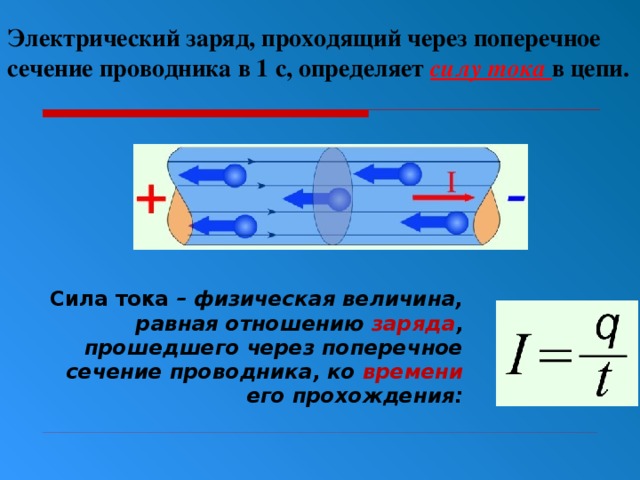 Константа пропорциональности представляет собой наклон кривой крутящий момент-скорость. Производительность двигателя лучше, когда этот наклон имеет меньшее значение. Чем круче падение наклона, тем хуже производительность, которую можно ожидать от данного двигателя без сердечника. Это соотношение можно рассчитать по формуле:
Константа пропорциональности представляет собой наклон кривой крутящий момент-скорость. Производительность двигателя лучше, когда этот наклон имеет меньшее значение. Чем круче падение наклона, тем хуже производительность, которую можно ожидать от данного двигателя без сердечника. Это соотношение можно рассчитать по формуле:
Where:
Δn = Change in speed
ΔM = Change in torque
M H = Stall torque
n 0 = No-Load speed
An alternative approach to deriving это значение для скорости, n :
С помощью исчисления мы дифференцируем обе части относительно M , что дает:
или
Хотя мы не показываем здесь отрицательный знак, подразумевается, что результат даст уменьшающийся (отрицательный) наклон.
Пример теоретического расчета двигателя
Давайте немного углубимся в теоретические расчеты.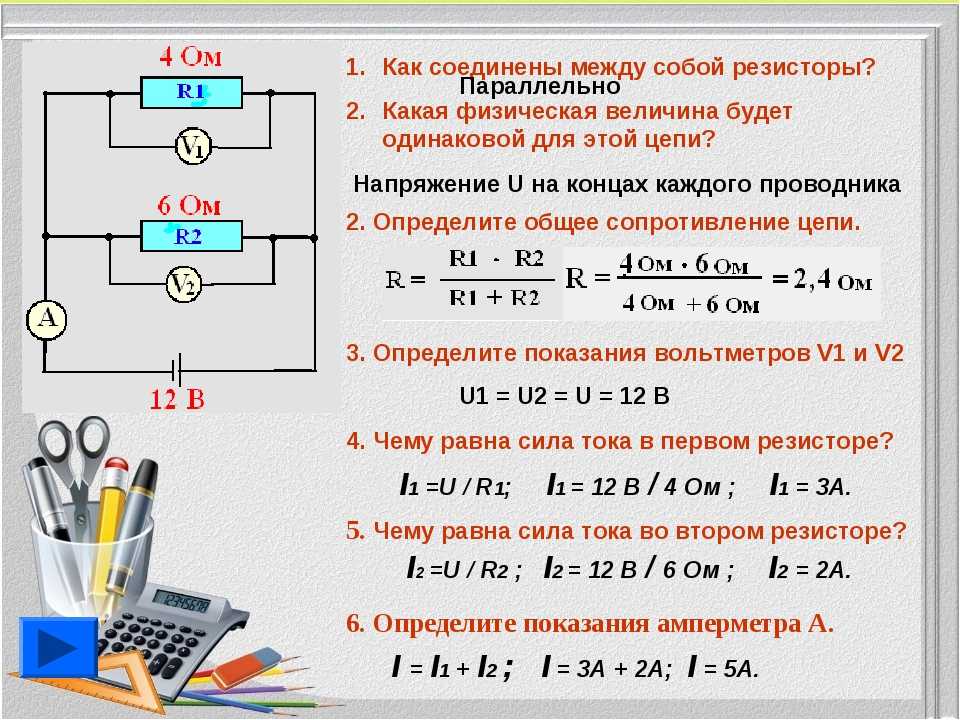 Двигатель постоянного тока без сердечника 2668W024CR должен работать с напряжением 24 В, подаваемым на клеммы двигателя, и с крутящим моментом 68 мН·м. Найдите результирующую постоянную двигателя, скорость двигателя, ток двигателя, КПД двигателя и выходную мощность. Из паспорта двигателя видно, что скорость холостого хода двигателя при 24 В составляет 7 800 мин -1 . Если крутящий момент не соединен с валом двигателя, двигатель будет работать на этой скорости.
Двигатель постоянного тока без сердечника 2668W024CR должен работать с напряжением 24 В, подаваемым на клеммы двигателя, и с крутящим моментом 68 мН·м. Найдите результирующую постоянную двигателя, скорость двигателя, ток двигателя, КПД двигателя и выходную мощность. Из паспорта двигателя видно, что скорость холостого хода двигателя при 24 В составляет 7 800 мин -1 . Если крутящий момент не соединен с валом двигателя, двигатель будет работать на этой скорости.
Во-первых, давайте получим общее представление о работе двигателя, рассчитав постоянную двигателя k m . В этом случае мы получаем константу 28,48 мНм/А. «Согласно техпаспорту двигателя, электрическое сопротивление составляет 1,03 Ом в холодном состоянии для варианта 24 В».
Скорость двигателя под нагрузкой — это просто скорость холостого хода за вычетом снижения скорости из-за нагрузки. Константа пропорциональности для соотношения между скоростью двигателя и крутящим моментом двигателя представляет собой наклон кривой зависимости крутящего момента от скорости, определяемый отношением скорости холостого хода двигателя к крутящему моменту двигателя. В этом примере мы рассчитаем снижение скорости (без учета влияния температуры), вызванное крутящим моментом 68 мНм, путем исключения единиц мНм:
В этом примере мы рассчитаем снижение скорости (без учета влияния температуры), вызванное крутящим моментом 68 мНм, путем исключения единиц мНм:
Теперь путем замены:
Скорость двигателя под нагрузкой должна быть приблизительно равна:
Ток двигателя под нагрузкой представляет собой сумму тока холостого хода и тока, возникающего под нагрузкой.
Константа пропорциональности, относящая ток к нагрузке крутящего момента, представляет собой константу крутящего момента ( k M ) . Это значение составляет 28,9 мНм/А. Взяв обратную величину, мы получим постоянную тока k I , которая может помочь нам рассчитать ток при нагрузке. В этом случае нагрузка составляет 68 мН·м, а ток, вытекающий из этой нагрузки (без учета тепловыделения), примерно равен:
Общий ток двигателя можно приблизительно определить путем суммирования этого значения с током двигателя без нагрузки. В техническом описании ток холостого хода двигателя указан как 78 мА.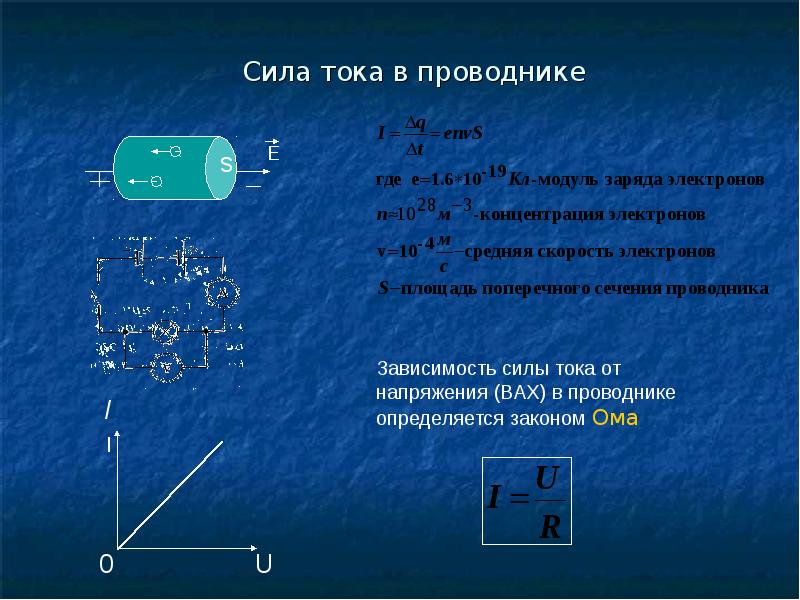 После округления общий ток примерно равен:
После округления общий ток примерно равен:
Выходная механическая мощность двигателя представляет собой просто произведение скорости двигателя и крутящего момента с поправочным коэффициентом для единиц (при необходимости). Таким образом, выходная мощность двигателя будет приблизительно равна:
Механическая мощность, потребляемая двигателем, является произведением приложенного напряжения и полного тока двигателя в амперах. В этом приложении:
Так как эффективность η это просто выходная мощность, деленная на входную мощность, давайте рассчитаем ее в нашей рабочей точке:
Оценка температуры обмотки двигателя во время работы:
Ток I , протекающий через сопротивление R , приводит к потере мощности в виде тепла I 2 · R . В случае двигателя постоянного тока произведение квадрата полного тока двигателя на сопротивление якоря представляет собой потери мощности в виде тепла в обмотках якоря.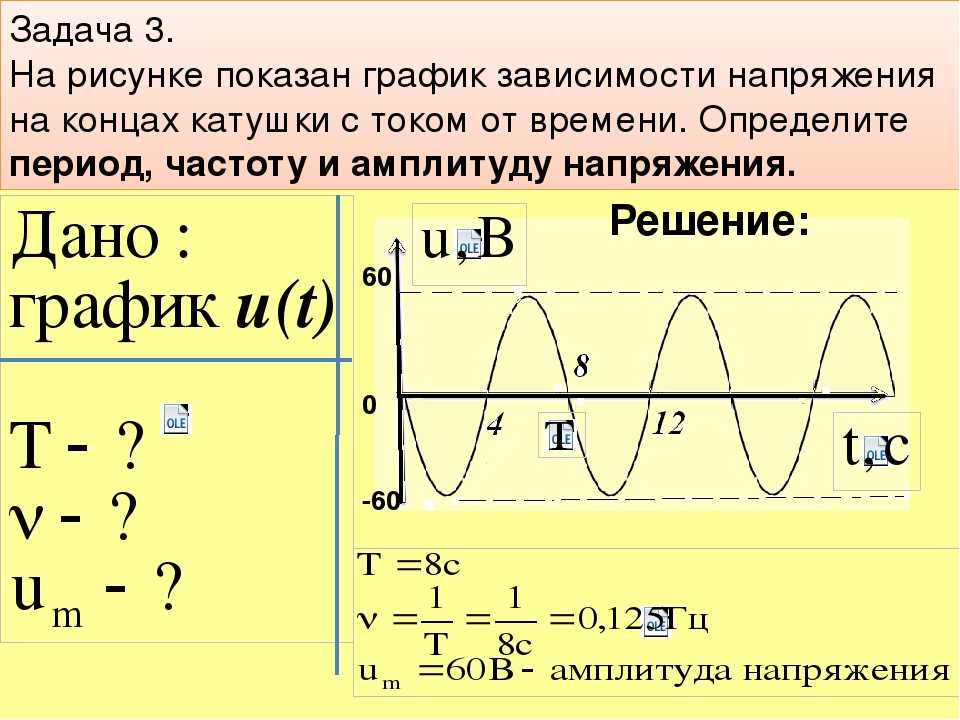 Например, если общий ток двигателя 0,203 А, а сопротивление якоря 14,5 Ом, потери мощности на тепло в обмотках составляют:
Например, если общий ток двигателя 0,203 А, а сопротивление якоря 14,5 Ом, потери мощности на тепло в обмотках составляют:
Тепло, возникающее в результате I 2 · R потерь в катушке, рассеивается за счет теплопроводности через компоненты двигателя и поток воздуха в воздушном зазоре. Легкость, с которой это тепло может быть рассеяно в двигателе (или любой системе), определяется тепловым сопротивлением.
Термическое сопротивление (которое является обратной величиной теплопроводности) показывает, насколько хорошо материал сопротивляется передаче тепла по определенному пути. Производители двигателей обычно указывают способность двигателя рассеивать тепло, обеспечивая тепловое сопротивление R й значений. Например, алюминиевая пластина большого сечения будет иметь очень низкое тепловое сопротивление, в то время как значения для воздуха или вакуума будут значительно выше. В случае двигателей постоянного тока существует тепловой путь от обмоток двигателя к корпусу двигателя и второй тепловой путь между корпусом двигателя и окружающей средой двигателя (окружающий воздух и т. д.). Некоторые производители двигателей указывают тепловое сопротивление для каждого из двух тепловых путей, в то время как другие указывают только их сумму как общее тепловое сопротивление двигателя. Значения термического сопротивления указаны в приросте температуры на единицу потерь мощности. Всего I 2 · R потери в змеевике (источнике тепла) умножаются на тепловые сопротивления для определения установившейся температуры якоря. Повышение температуры двигателя в установившемся режиме ( T ) определяется как:
д.). Некоторые производители двигателей указывают тепловое сопротивление для каждого из двух тепловых путей, в то время как другие указывают только их сумму как общее тепловое сопротивление двигателя. Значения термического сопротивления указаны в приросте температуры на единицу потерь мощности. Всего I 2 · R потери в змеевике (источнике тепла) умножаются на тепловые сопротивления для определения установившейся температуры якоря. Повышение температуры двигателя в установившемся режиме ( T ) определяется как:
Где:
ΔT = Изменение температуры в К
I = Ток через обмотки двигателя в А обмотки двигателя в Ом
R th2 = Тепловое сопротивление от обмоток к корпусу в К/Вт
R th3 = Термическое сопротивление корпуса к окружающей среде в К/Вт
Продолжим наш пример, используя двигатель 2668W024CR, работающий с током 2,458 А в обмотках двигателя, с сопротивлением якоря 1,03 Ом, а тепловое сопротивление между обмоткой и корпусом 3 К/Вт и тепловое сопротивление между корпусом и окружающей средой 8 К/Вт. Повышение температуры обмоток определяется по приведенной ниже формуле; мы можем заменить Ploss на I 2 · R :
Повышение температуры обмоток определяется по приведенной ниже формуле; мы можем заменить Ploss на I 2 · R :
Поскольку шкала Кельвина использует тот же приращение единицы, что и шкала Цельсия, мы можем просто заменить значение Кельвина, как если бы оно было значением Цельсия. Если предположить, что температура окружающего воздуха составляет 22°C, то конечную температуру обмоток двигателя можно приблизительно представить как:
Где:
T теплый = Температура обмотки
Важно убедиться, что конечная температура обмоток не превышает номинальное значение двигателя, указанное в паспорте. В приведенном выше примере максимально допустимая температура обмотки составляет 125°C. Поскольку расчетная температура обмотки составляет всего 90,4°C, тепловое повреждение обмоток двигателя не должно быть проблемой в этом приложении.
Подобные расчеты можно было бы использовать для ответа на вопрос другого типа. Например, приложение может потребовать, чтобы двигатель работал с максимальным крутящим моментом, в надежде, что он не будет поврежден в результате перегрева. Предположим, требуется запустить двигатель с максимально возможным крутящим моментом при температуре окружающего воздуха 22°C. Разработчик хочет знать, какой крутящий момент двигатель может обеспечить без перегрева. Опять же, в техническом описании двигателя постоянного тока без сердечника 2668W024CR указана максимальная температура обмотки 125°C. Таким образом, поскольку температура окружающей среды составляет 22°C, максимально допустимое повышение температуры ротора составляет: 125°C – 22°C = 103°C
Например, приложение может потребовать, чтобы двигатель работал с максимальным крутящим моментом, в надежде, что он не будет поврежден в результате перегрева. Предположим, требуется запустить двигатель с максимально возможным крутящим моментом при температуре окружающего воздуха 22°C. Разработчик хочет знать, какой крутящий момент двигатель может обеспечить без перегрева. Опять же, в техническом описании двигателя постоянного тока без сердечника 2668W024CR указана максимальная температура обмотки 125°C. Таким образом, поскольку температура окружающей среды составляет 22°C, максимально допустимое повышение температуры ротора составляет: 125°C – 22°C = 103°C
Теперь мы можем рассчитать увеличение сопротивления катушки из-за рассеяния тепловой мощности:
Где:
α Cu = Температурный коэффициент меди в единицах К нагрева катушки и магнита за счет рассеивания мощности от потерь I 2 · R сопротивление катушки увеличилось с 1,03 Ом до 1,44 Ом. Теперь мы можем пересчитать новую константу крутящего момента k M для наблюдения за влиянием повышения температуры на производительность двигателя:
Теперь мы можем пересчитать новую константу крутящего момента k M для наблюдения за влиянием повышения температуры на производительность двигателя:
Где:
α M = Температурный коэффициент магнита в единицах К Постоянная ЭДС k E и наблюдайте за результатами. Из формулы, которую мы вывели выше:
Как мы видим, константа крутящего момента ослабевает в результате повышения температуры, как и константа противо-ЭДС! Таким образом, сопротивление обмотки двигателя, постоянная крутящего момента и постоянная противо-ЭДС оказывают негативное влияние по той простой причине, что они являются функциями температуры.
Мы могли бы продолжить расчет дополнительных параметров из-за более горячих катушки и магнита, но наилучшие результаты дает выполнение нескольких итераций, что лучше всего делать с помощью количественного программного обеспечения. Поскольку температура двигателя продолжает расти, каждый из трех параметров будет изменяться таким образом, что ухудшаются характеристики двигателя и увеличиваются потери мощности. При непрерывной работе двигатель может даже достичь точки «теплового разгона», что потенциально может привести к повреждению двигателя, не подлежащему ремонту. Это может произойти, даже если первоначальные расчеты показали приемлемое повышение температуры (используя значения R и k M при температуре окружающей среды).
При непрерывной работе двигатель может даже достичь точки «теплового разгона», что потенциально может привести к повреждению двигателя, не подлежащему ремонту. Это может произойти, даже если первоначальные расчеты показали приемлемое повышение температуры (используя значения R и k M при температуре окружающей среды).
Обратите внимание, что максимально допустимый ток через обмотки двигателя можно увеличить, уменьшив тепловое сопротивление двигателя. Термическое сопротивление между ротором и корпусом R th2 в основном определяется конструкцией двигателя. Тепловое сопротивление между корпусом и окружающей средой R th3 можно значительно снизить за счет добавления радиаторов. Термическое сопротивление двигателя для небольших двигателей постоянного тока обычно указывается для двигателя, подвешенного на открытом воздухе. Поэтому обычно имеет место некоторый отвод тепла в результате простой установки двигателя в теплопроводящую раму или шасси.


 6 СТО
6 СТО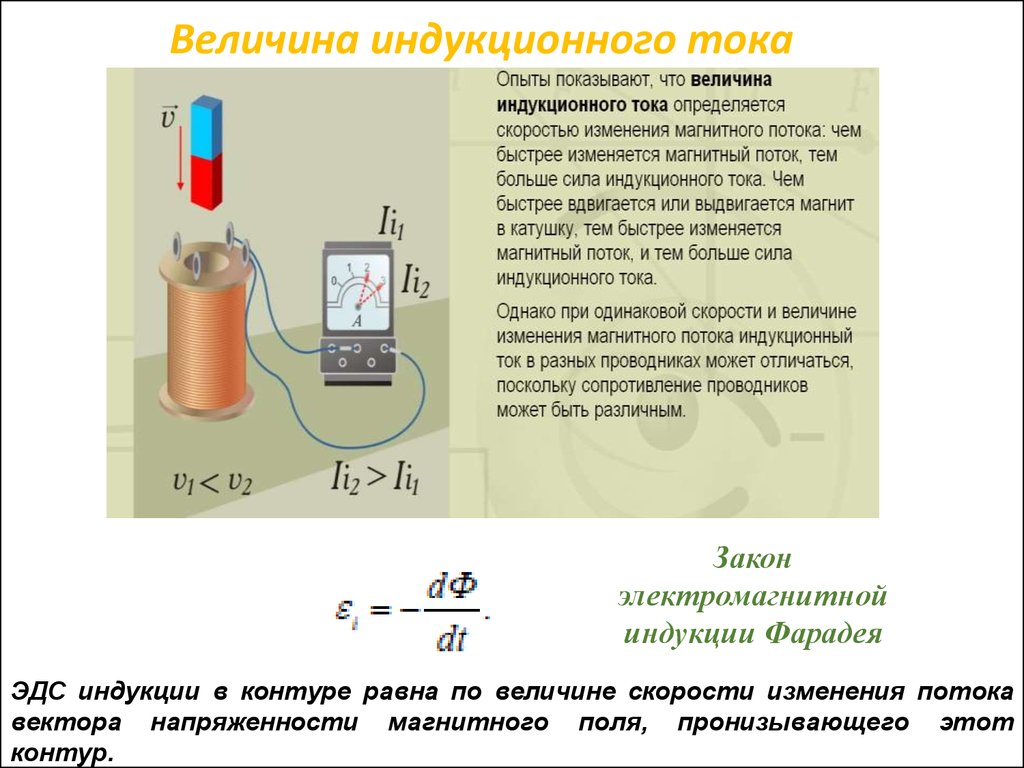


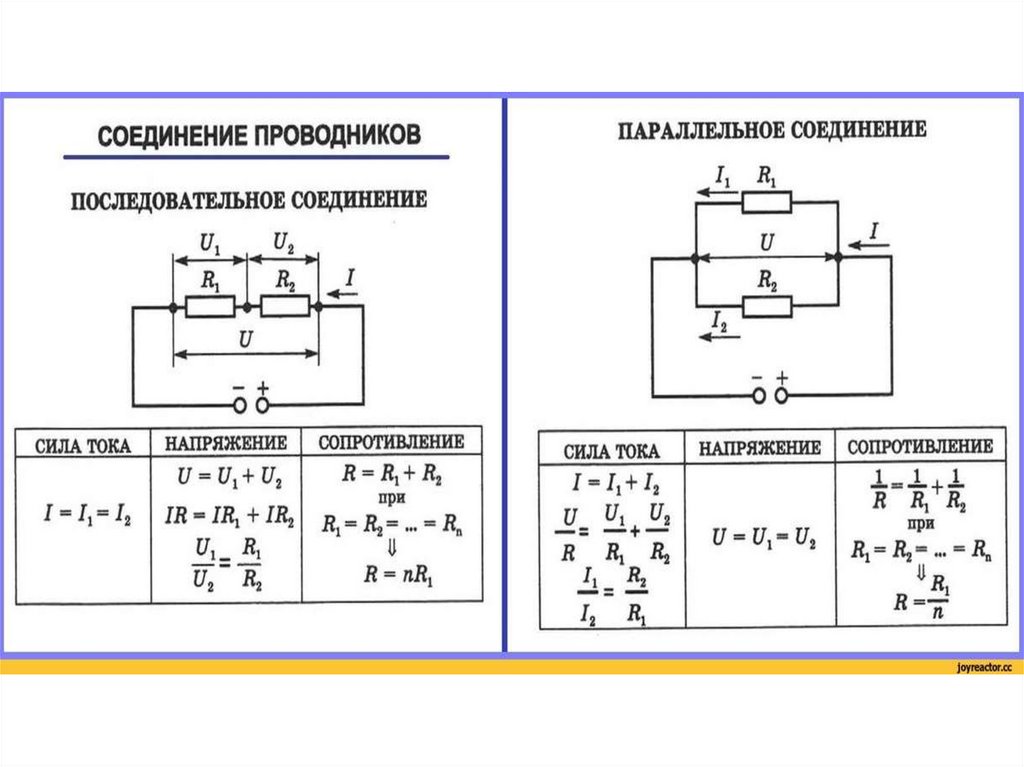 3.7):
,
и магнитное поле с индукцией . На заряд q2 действуют две силы: — электрическая, см. (9.3.5), — магнитная сила, или сила Лоренца, см. (11.7). Если q
3.7):
,
и магнитное поле с индукцией . На заряд q2 действуют две силы: — электрическая, см. (9.3.5), — магнитная сила, или сила Лоренца, см. (11.7). Если q Модуль вектора магнитной индукции пропорционален максимальному вращающему моменту:
.
Модуль вектора магнитной индукции пропорционален максимальному вращающему моменту:
.
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.019 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.019 с.)
 Обратите внимание, что двигатель не должен работать с остановкой, так как это почти наверняка приведет к преждевременному выходу из строя.
Обратите внимание, что двигатель не должен работать с остановкой, так как это почти наверняка приведет к преждевременному выходу из строя. Это означает, что как электрические, так и механические характеристики двигателя могут быть легко адаптированы к конкретной спецификации.
Это означает, что как электрические, так и механические характеристики двигателя могут быть легко адаптированы к конкретной спецификации.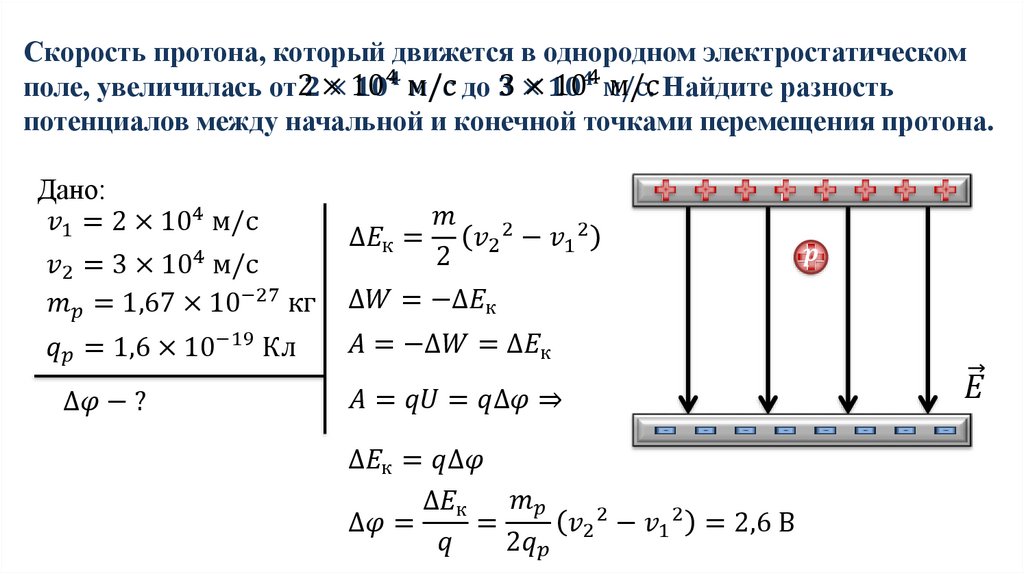 Ранее мы обсуждали эти темы более подробно по следующим ссылкам – 1 и 2
Ранее мы обсуждали эти темы более подробно по следующим ссылкам – 1 и 2 Вставляя металлическую шестерню на последнем этапе, достигается крутящий момент примерно 34 мНм, что удваивает возможности двигателя по крутящему моменту и открывает более широкий спектр возможностей. Ему был присвоен номер детали 206-10C 9.0578
Вставляя металлическую шестерню на последнем этапе, достигается крутящий момент примерно 34 мНм, что удваивает возможности двигателя по крутящему моменту и открывает более широкий спектр возможностей. Ему был присвоен номер детали 206-10C 9.0578 Это типичная модификация, которую мы можем предложить, начиная от простых тахометров для измерения скорости, инкрементных энкодеров для позиционирования по одному эталону и заканчивая абсолютными энкодерами для точного позиционирования выходного вала. Эти энкодеры также можно использовать в управлении с обратной связью для поддержания скорости при изменении крутящего момента, изменения скорости для постоянного крутящего момента или любой комбинации этих двух способов (примеры обсуждались ранее в этой статье). Пожалуйста, свяжитесь с инженером Precision Microdrives, если вам нужна дополнительная информация о том, что мы можем поставить
Это типичная модификация, которую мы можем предложить, начиная от простых тахометров для измерения скорости, инкрементных энкодеров для позиционирования по одному эталону и заканчивая абсолютными энкодерами для точного позиционирования выходного вала. Эти энкодеры также можно использовать в управлении с обратной связью для поддержания скорости при изменении крутящего момента, изменения скорости для постоянного крутящего момента или любой комбинации этих двух способов (примеры обсуждались ранее в этой статье). Пожалуйста, свяжитесь с инженером Precision Microdrives, если вам нужна дополнительная информация о том, что мы можем поставить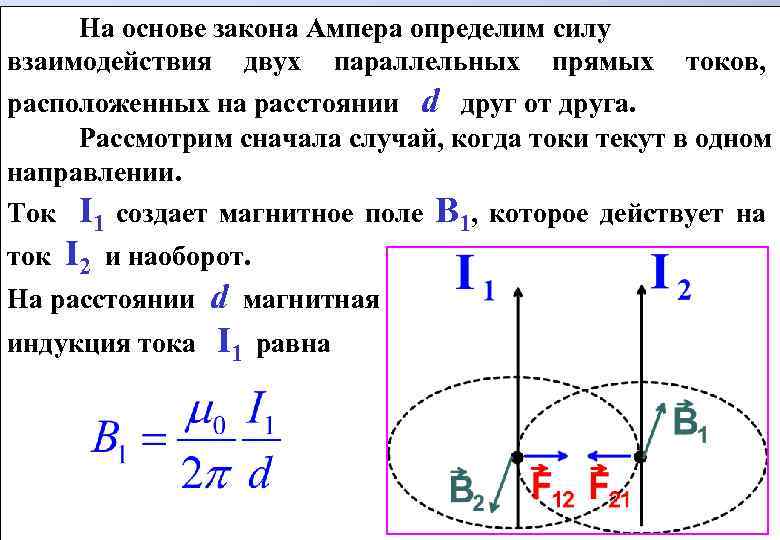

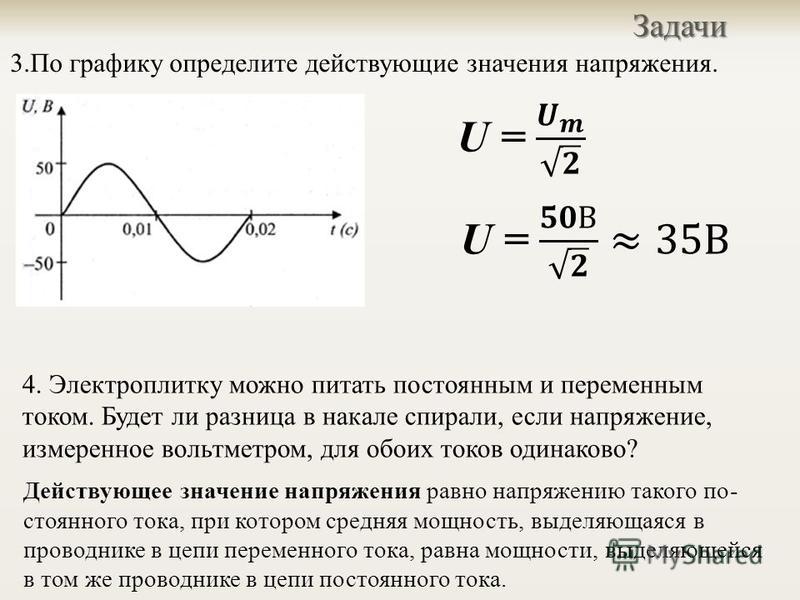 Аббревиатура: амп. Символ: А.
Аббревиатура: амп. Символ: А. Каждый из носителей тока имеет заряд q и движется с дрейфовой скоростью величины v .
Каждый из носителей тока имеет заряд q и движется с дрейфовой скоростью величины v . Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike 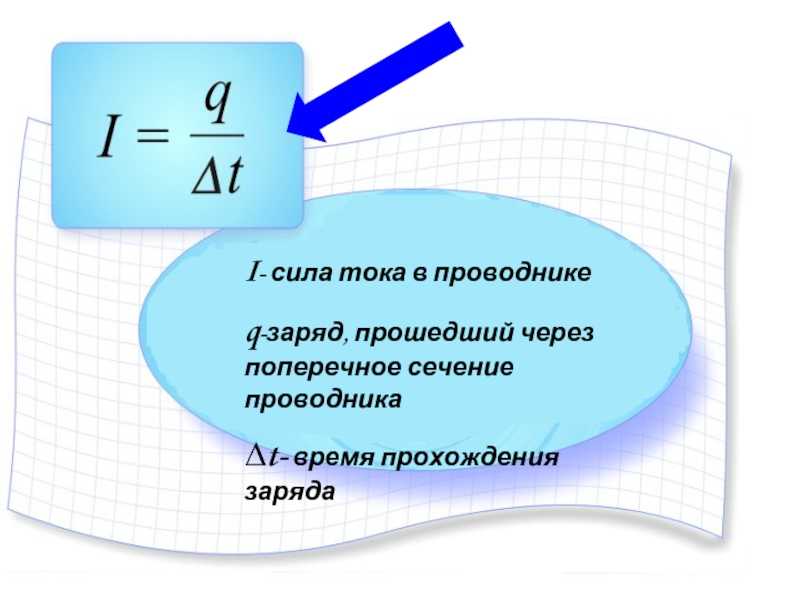 Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution  26 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
26 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция 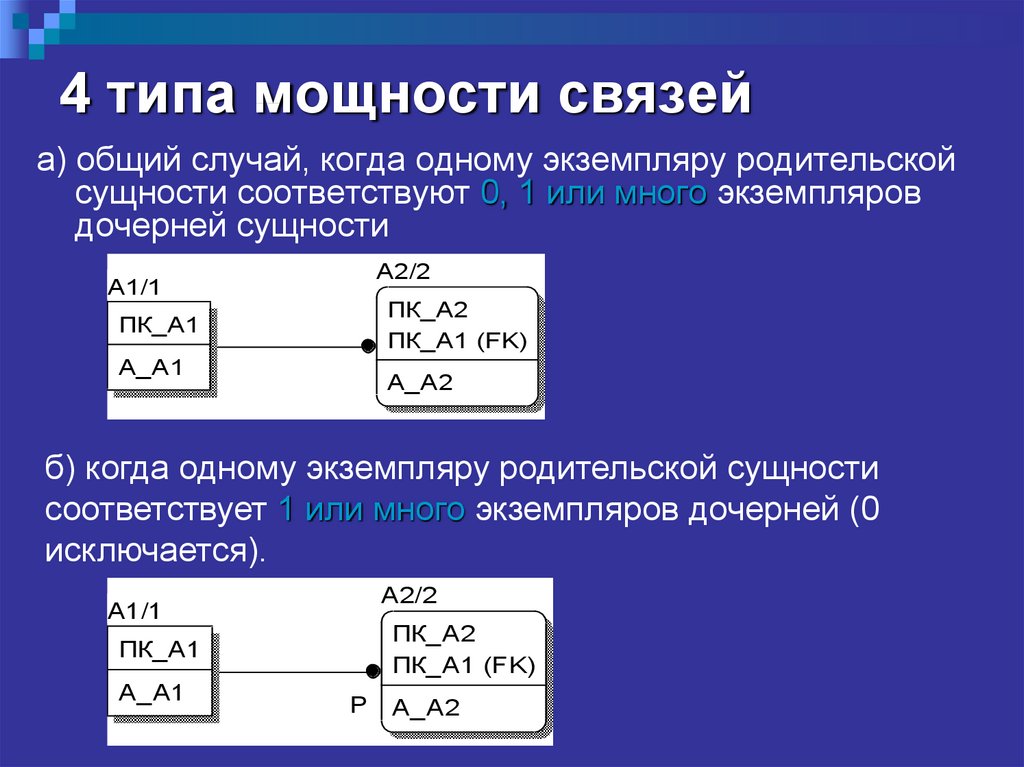 1519/ОАО.0000000000002494
1519/ОАО.0000000000002494
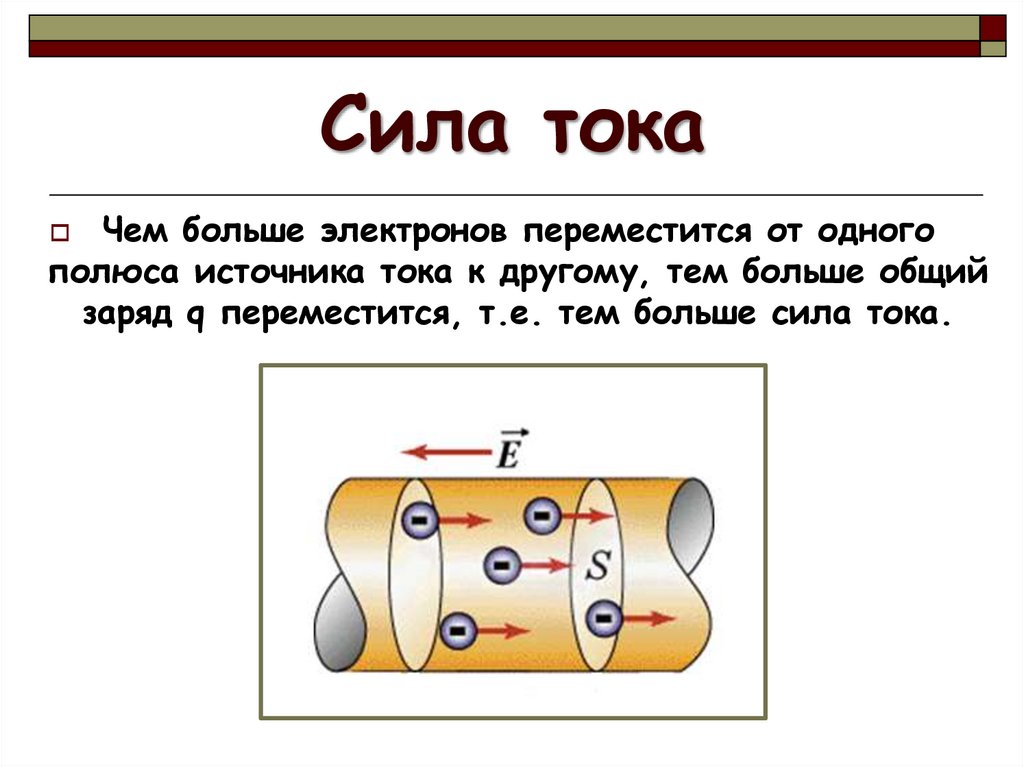 Лотурко I и др.
J Прочность Конд Рез. 2017 март; 31 (3): 743-749. doi: 10.1519/JSC.0000000000001525.
J Прочность Конд Рез. 2017.
PMID: 27379958
Лотурко I и др.
J Прочность Конд Рез. 2017 март; 31 (3): 743-749. doi: 10.1519/JSC.0000000000001525.
J Прочность Конд Рез. 2017.
PMID: 27379958 , Чауачи А.
Бругелли М. и соавт.
Спорт Мед. 2008;38(12):1045-63. doi: 10.2165/00007256-200838120-00007.
Спорт Мед. 2008.
PMID: 120
Обзор.
, Чауачи А.
Бругелли М. и соавт.
Спорт Мед. 2008;38(12):1045-63. doi: 10.2165/00007256-200838120-00007.
Спорт Мед. 2008.
PMID: 120
Обзор. Гонсалес-Бадильо Дж. Дж. и др.
Открытый мед. спорт. 2022 16 сентября; 8 (1): 118. doi: 10.1186/s40798-022-00513-z.
Открытый мед. спорт. 2022.
PMID: 36114395
Бесплатная статья ЧВК.
Обзор.
Гонсалес-Бадильо Дж. Дж. и др.
Открытый мед. спорт. 2022 16 сентября; 8 (1): 118. doi: 10.1186/s40798-022-00513-z.
Открытый мед. спорт. 2022.
PMID: 36114395
Бесплатная статья ЧВК.
Обзор. , Спудич Д., Козинц Ж., Шарабон Н.
Смайла Д. и соавт.
Фронт Физиол. 2022 21 июня; 13:828394. doi: 10.3389/fphys.2022.828394. Электронная коллекция 2022.
Фронт Физиол. 2022.
PMID: 35800347
Бесплатная статья ЧВК.
, Спудич Д., Козинц Ж., Шарабон Н.
Смайла Д. и соавт.
Фронт Физиол. 2022 21 июня; 13:828394. doi: 10.3389/fphys.2022.828394. Электронная коллекция 2022.
Фронт Физиол. 2022.
PMID: 35800347
Бесплатная статья ЧВК. Фрейтас ТТ и др.
Общественное здравоохранение Int J Environ Res. 2021 дек 20;18(24):13390. дои: 10.3390/ijerph282413390.
Общественное здравоохранение Int J Environ Res. 2021.
PMID: 34948999
Бесплатная статья ЧВК.
Фрейтас ТТ и др.
Общественное здравоохранение Int J Environ Res. 2021 дек 20;18(24):13390. дои: 10.3390/ijerph282413390.
Общественное здравоохранение Int J Environ Res. 2021.
PMID: 34948999
Бесплатная статья ЧВК.