Вращательное движение твёрдого тела — Физика

Лекция № 3

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА

План

1. Абсолютное твёрдое тело. Вращательное движение. Угловая скорость и угловое ускорение, их связь с линейными скоростями и ускорениями вращающегося твёрдого тела.

2. Момент инерции тела. Кинетическая энергия вращающегося твёрдого тела.

3. Вычисление моментов инерции. Теорема Штейнера. Свободные оси.

4. Момент силы. Момент импульса.

5. Уравнение моментов. Уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси.

6. Гироскопы. Гироскопический эффект.

1. Абсолютно твёрдое тело. Абсолютно твёрдым телом называется такое тело, деформацией которого в условиях данной задачи можно пренебречь. Расстояние между любыми двумя точками тела остаётся неизменным.

Всякое движение твёрдого тела можно разложить на два основных вида движения – поступательное и вращательное.

Вращательным называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Введём понятие угловой скорости и углового ускорения. Пусть твёрдое тело вращается вокруг неподвижной в данной системе отсчёта оси  и за время  совершает бесконечно малый поворот (рис. 3.1).

Соответствующий угол поворота будем характеризовать вектором , модуль которого равен углу поворота, а направление совпадает с осью , причём так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора .

Рис. 3.1

Из рис. 3.1 следует, что . Вектор  как бесконечно малую величину можно считать по модулю равным соответствующей дуге окружности , его направление соответствует правилу правого винта по отношению к векторам  и

         Разделим обе части на :

         .                                               (*)

Производная угла поворота по времени называется угловой скоростью.

Вектор  совпадает по направлению с вектором . Изменение вектора  со временем характеризуют вектором углового ускорения:

         Из выражения * получаем связь линейной  и угловой скоростей:

                                                (**)

То есть скорость  любой точки А твёрдого тела, вращающегося вокруг неподвижной оси с угловой скоростью , равна векторному произведению  на радиус-вектор  точки А относительно произвольной точки на оси вращения.

         Если выбрать в качестве точки отсчёта для радиус-вектора центр окружности вращения (точка О), при неизменном радиусе окружности  выражение (**) можно записать в скалярном виде:

Продифференцируем это выражение по времени: , отсюда получаем связь тангенциального и углового ускорений:

         Нормальное ускорение можно представить как

         Модуль полного ускорения:

         2. Момент инерции тела. Определим кинетическую энергию вращения твёрдого тела (рис. 3.2). Разделим его мысленно на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки (). Обозначим массу i-го элемента , а скорость этого элемента .

Кинетическая энергия этого элемента

.

Просуммировав кинетическую энергию всех элементов, получим кинетическую энергию вращательного движения тела:

         .

         Линейная скорость  связана с угловой скоростью вращения тела  (постоянна для всех точек тела).

.

Определение. Моментом инерции материальной точки относительно оси z называется произведение массы этой точки на квадрат её расстояния от оси вращения:

Определение. Моментом инерции твёрдого тела относительно некоторой оси z называется сумма моментов инерций материальных точек относительно данной оси.

В соответствии с этими определениями:

(Сравните с выражением для кинетической энергии поступательного движения , очевидно соответствие ).

Физический смысл момента инерции. Момент инерции во вращательном движении играет такую же роль, как масса при поступательном движении, характеризует меру инертности тела при вращательном движении. Чем больше момент инерции тела, тем труднее при прочих равных условиях привести его во вращательное движение. Момент инерции определяется не только массой, но и тем, как эта масса распределена относительно оси вращения.

Соотношение  является приближённым, причём тем более точным, чем меньше элементарные массы . Задача нахождения моментов инерции сводится к интегрированию.

(Интегрирование ведётся по всей массе тела ).

3. Вычисление моментов инерции. 1. Кольцо (полый цилиндр)             (рис. 3.3). В случае достаточно тонких стенок вся масса сосредоточена на расстоянии  от центра.

Относительно оси, проходящей через центр кольца:

,

.

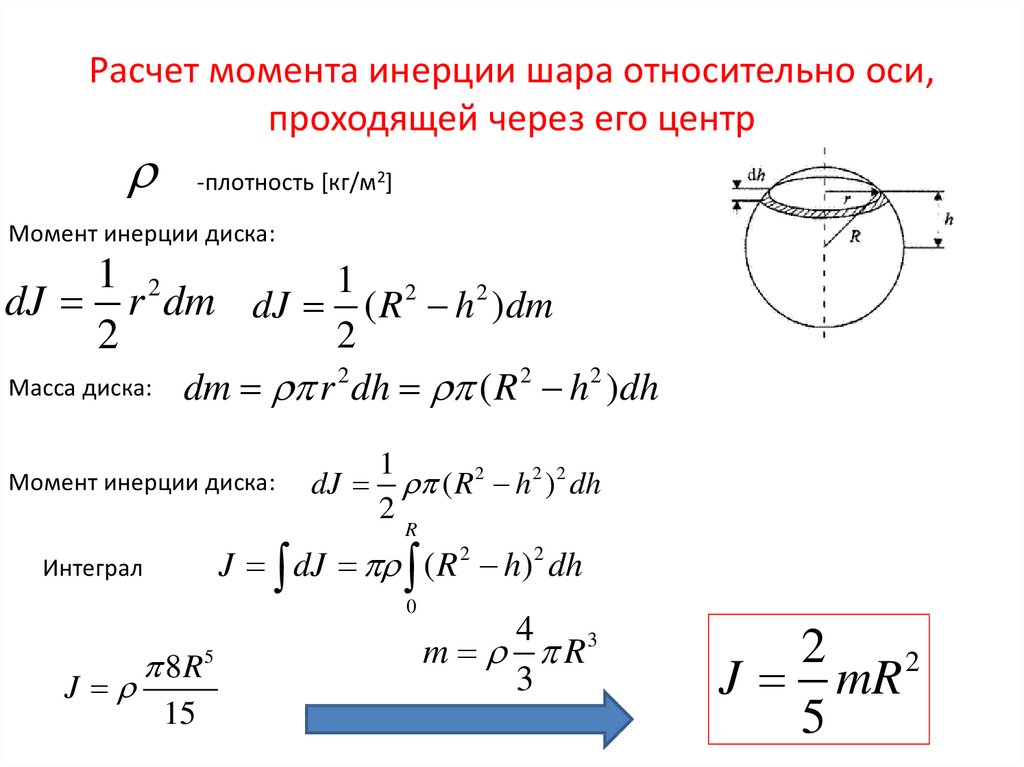
2. Однородный диск (сплошной цилиндр)

Дано: радиус диска, масса диска.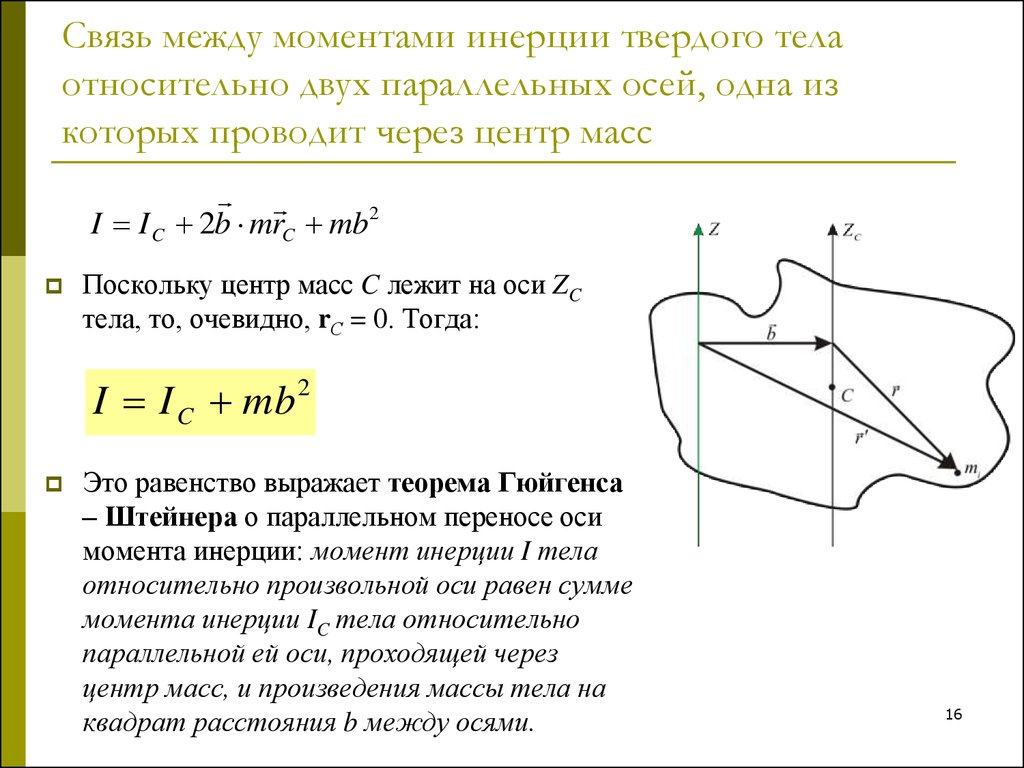

Найти: момент инерции диска относительно оси, проходящей через центр диска.

Разобьём диск (рис. 3.4) на кольца с радиусом , толщиной . По определению момента инерции . Пусть поверхностная плотность диска , тогда масса кольца , где площадь кольца, . Интегрируя по радиусу, находим момент инерции диска:

=,

3. Тонкий однородный стержень

Дано: масса стержня, длина стержня.

Найти:  (момент инерции относительно оси ОО, проходящей через конец стержня перпендикулярно ему) (рис. 3.5).

Рис. 3.5

Ввиду одномерного характера задачи выражение  можно заменить на , где , тогда .

Теорема Штейнера (без вывода)

Постановка задачи. Известен момент инерции произвольного тела массой  относительно оси, проходящей через его центр тяжести  (рис. 3.6). Требуется найти, каков момент инерции  относительно какой-либо оси , параллельной первой и находящейся на расстоянии  от неё.

Теорема. Момент инерции тела относительно произвольной оси z равен сумме момента инерции относительно оси, проходящей через центр масс тела С и параллельной данной, и произведения массы тела на квадрат расстояния между осями a:

.

Пример применения теоремы Штейнера.

Требуется найти момент инерции тонкого однородного стержня массой  и длиной  относительно перпендикулярной к нему оси , проходящей через центр стержня (рис. 3.7).

Рис. 3.7

Решение:

Воспользуемся полученным ранее выражением для момента инерции стержня относительно оси, проходящей через его конец:

. Используя теорему Штейнера, получаем:

 отсюда .

Свободные оси

Определение. Ось вращения тела, положение которой в пространстве остаётся неизменным без действия на неё внешних сил, называется свободной.

Можно доказать, что в любом теле существует три взаимно перпендикулярных оси, проходящие через центр масс тела, которые могут служить свободными осями. Они называются главными осями инерции тела. Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней. Вращение вокруг главных осей с наибольшим и наименьшим (экстремальными) моментами инерции оказывается устойчивым, а вращение вокруг оси со средним моментом – неустойчивым. Этот факт является достаточно важным при проектировании конструкций с вращающимися частями.

4. Момент силы. Пусть О – какая-либо точка, относительно которой рассматривается момент вектора силы. Обозначим  радиус-вектор, проведённый из этой точки к точке приложения силы  (Рис. 3.8).

Рис. 3.8

Определение. Моментом силы  относительно точки О называется векторное произведение радиуса-вектора на силу :

Раскрывая векторное произведение, получим  где  плечо силы (длина перпендикуляра, опущенного из точки О на линию действия силы).

В соответствии с определением векторного произведения вектор  направлен перпендикулярно плоскости, в которой лежат векторы  и  в соответствии с правилом правого винта (буравчика).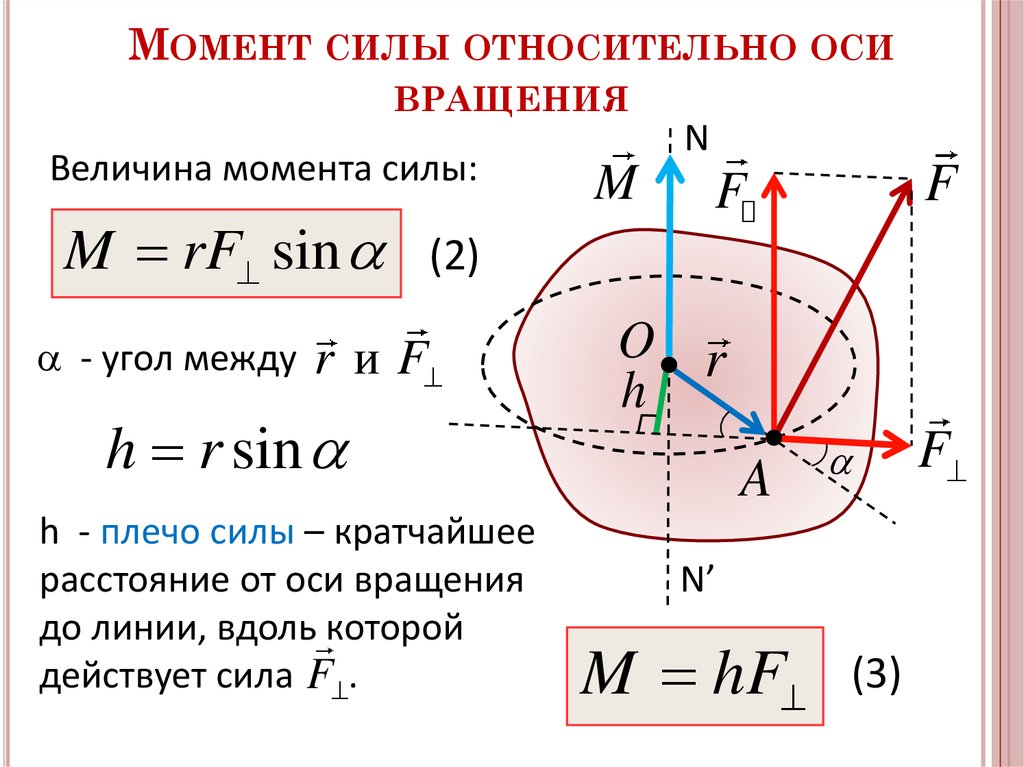

Определение. Момент силы относительно оси , проходящей через точку О, есть проекция на эту ось вектора момента силы  относительно точки, лежащей на этой же оси.

 как проекция на ось является скалярной величиной.

Момент импульса

Пусть материальная точка массой  движется со скоростью  относительно точки О, а радиус-вектор этой материальной точки, проведённый из точки О (рис. 3.9).

Определение. Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора  на вектор импульса :

Направление  перпендикулярно плоскости, в которой лежат векторы  и , в соответствии с правилом правого винта, например момент импульса электрона, двигающегося по круговой орбите в боровской модели атома.

Свяжем момент импульса с моментом инерции и угловой скоростью. Пусть радиус-вектор  некоторой частицы массой лежит в плоскости рис. 3.10, скорость  перпендикулярна ей («от нас»), частица движется по окружности радиусом .

Модуль момента импульса . Линейную скорость  можно связать с угловой  относительно оси  как , тогда . Проекция вектора  на ось вращения равна

 . Как видно из рис. 3.10, , т.е.

Для системы материальных точек (твёрдого тела) выражение связи ,  и  формально такое, как и для материальной точки:

Но под  здесь подразумевается сумма моментов инерции материальных точек системы:

Можно показать (см., например, в [1]), что для однородного тела, симметричного относительно оси вращения, суммарный момент импульса тела . Он направлен вдоль оси вращения в ту же сторону, что и , т.е.

(Для несимметричного тела в общем случае  не совпадает по направлению с вектором ).

         5. Уравнение моментов. В дальнейших преобразованиях условимся для упрощения записи индекс 0 у ,  и других величин не писать, но подразумевать, что он есть.

         Продифференцируем выражение для момента импульса материальной точки: . .

Учтём, что , а .

         Рассмотрим первое слагаемое (см. в лекции № 1 «Векторное произведение»).

= (так как угол между  и  равен нулю).

         Второе слагаемое в выражении для

 (по определению момента силы).

          В результате получаем:

Уравнение моментов (оно связывает момент импульса с моментом силы).

         Производная по времени момента импульса материальной точки относительно точки О равна моменту действующей силы относительно точки О.

Уравнение моментов для твёрдого тела

         Рассмотрим систему частиц, на которую действуют как внутренние, так внешние силы. Моментом импульса  системы относительно точки О называется сумма моментов импульса  отдельных частиц . Дифференцирование по времени даёт, что

.                                                   

Для каждой из частиц можно написать уравнение моментов

,

где момент внутренних сил, а  момент внешних сил, действующих на -ю частицу.  (по 3-му закону Ньютона, так как внутренние силы образуют пары, равные по величине, противоположные по направлению и действующие вдоль одной прямой, т.е. образуют равные по величине и противоположно направленные моменты сил).

Получаем

         Обозначим =, получаем окончательно

     

Производная по времени от момента импульса механической системы относительно некоторой точки О равна суммарному моменту относительно той же точки всех внешних сил, приложенных к системе (уравнение моментов).

Уравнение динамики вращательного движения твёрдого тела

относительно неподвижной оси

         В проекции на ось  предыдущее уравнение запишется:

а так как , то , если , то . Так как проекция углового ускорения на ось , то получим уравнение динамики вращательного движения относительно оси Z и сравним с уравнением динамики для поступательного движения (2-й закон Ньютона).

Соответствие очевидно:

Замечание: если вокруг оси  вращается однородное симметричное тело, то , и тогда очевидно:

(Угловое ускорение  совпадает по направлению с вектором момента силы).

            6. Гироскопы (от греч. круг, смотрю, наблюдаю).

Гироскопом называется массивное симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии.

Рассмотрим поведение гироскопа на примере волчка (рис. 3.11). Опыт показывает, что если ось вращающегося волчка наклонена к вертикали, то волчок не падает, а совершает так называемое прецессионное движение (прецессию) – т.е. его ось описывает конус вокруг вертикали с некоторой угловой скоростью , причём чем больше скорость  вращения волчка, тем меньше угловая скорость прецессии ().

Из уравнения моментов следует:

Приращение  совпадает по направлению с моментом внешних сил, относительно точки О. Момент силы тяжести , как видно из рис. 3.11, перпендикулярен моменту импульса, т.е. , следовательно, приращение момента импульса . В результате вектор  (и ось волчка) будут поворачиваться вместе с вектором  вокруг вертикали, описывая круговой конус с углом полураствора .

         Найдём связь между ,  и :

          или в векторном виде , сравнивая с , получаем уравнение для угловой скорости прецессии.

Из уравнения видно, что момент силы определяет угловую скорость прецессии, а не ускорение. Это означает, что мгновенное устранение момента  приводит к мгновенному исчезновению и прецессии, т.е. прецессия не обладает инерцией.

Гироскопический эффект

         Рассмотрим эффект, возникающий при вынужденном вращении оси гироскопа. Пусть ось гироскопа укреплена в -образной подставке, которую мы будем поворачивать вокруг оси  (рис. 3.12).

Рис. 3.12

Если момент импульса гироскопа  направлен вправо, то при таком повороте за время  вектор  получит приращение вектор, направленный перпендикулярно . Согласно уравнению  это означает, что на гироскоп действует момент силы , совпадающий по направлению с вектором . Момент  обусловлен возникновением пары сил , действующих на ось гироскопа со стороны подставки.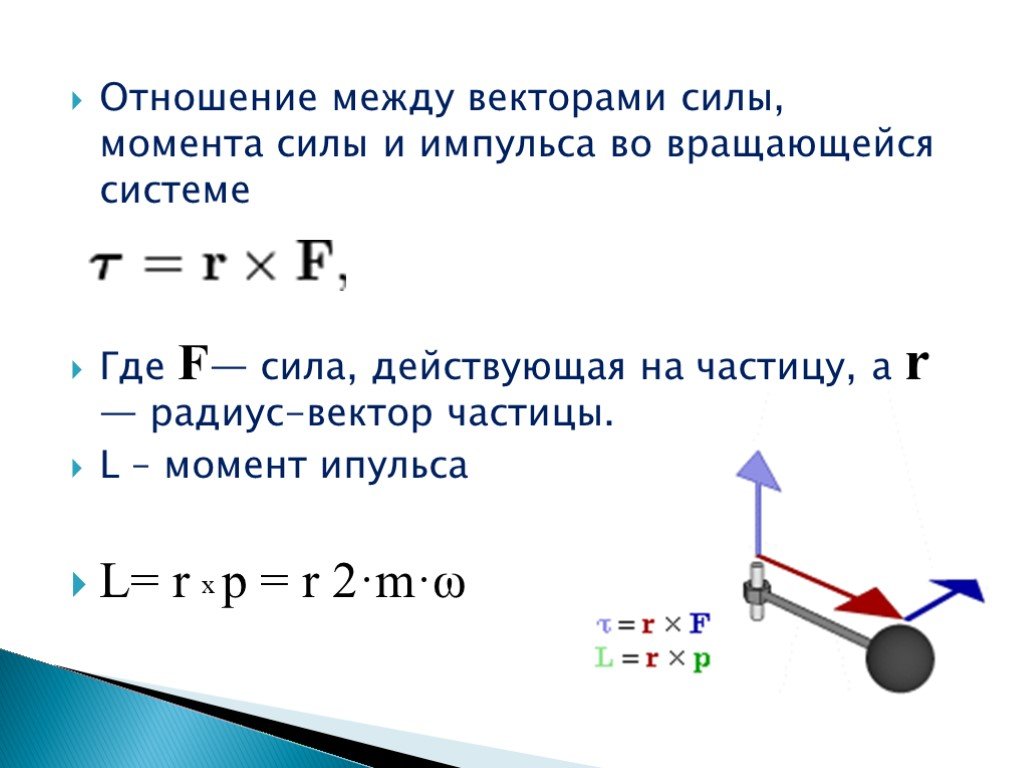 Ось гироскопа, в свою очередь, в соответствии с 3-им законом Ньютона будет действовать на подставку с силами . Эти силы называются гироскопическими. Они создают гироскопический момент . Появление гироскопических сил называют гироскопическим эффектом.

Замечание: в узком смысле гироскопическим эффектом иногда называют движение волчка не в сторону действия силы, а перпендикулярно к ней.

         Примеры возникновения гироскопического эффекта: гироскопическое давление на подшипники у роторов турбин, компрессоров на кораблях, самолётах при поворотах, виражах.

         Гироскопы являются основными узлами в гирокомпасах, в которых используется свойство гироскопов с тремя степенями свободы: его ось стремится устойчиво сохранить в мировом пространстве приданное ей первоначальное направление. Если ось направить на какую-либо звезду, то при любых перемещениях прибора и случайных толчках она будет указывать на эту звезду.

Вопросы для самоконтроля

1. Какое движение называется вращательным?

2. Как определяют угловую скорость и угловое ускорение?

3. Что является мерой инертности при вращательном движении?

4. Дайте определение момента инерции материальной точки и момента инерции твёрдого тела.

5. Как вычисляют моменты инерции для сплошного цилиндра и тонкого стержня?

6. Сформулируйте теорему Штейнера.

7. Что называется свободной осью? Какие оси называют главными осями инерции?

8. Дайте определения момента силы и момента импульса материальной точки относительно некоторой точки.

9. Как связан момент импульса с моментом инерции и угловой скоростью?

Если Вам понравилась эта лекция, то понравится и эта — Специфические особенности личности учителя и воспитателя.

10. Выведите уравнение моментов.

11. Запишите уравнение динамики вращательного движения относительно оси .

12. Что называется гироскопом?

13. Что такое прецессия? От чего зависит скорость прецессии?

14. Что называется гироскопическим эффектом?

Момент инерции. Теорема Штейнера. Кинетическая энергия вращательного движения твердого тела. (Лекция 5)

Похожие презентации:

Динамика вращательного движения твердого тела. Лекция 5

Уравнение вращения твердого тела вокруг неподвижной оси. Момент инерции

Динамика вращательного движения твердого тела

Динамика вращательного движения твердого тела. Основное уравнение динамики вращательного движения. Момент инерции твердого тела

Динамика твердого тела

Механика твердого тела. Динамика вращений

Динамика движения твердого тела

Динамика твердого тела. Уравнения движения твердого тела

Динамика поступательного и вращательного движения твердого тела

Динамика вращения твердого тела. Кинетическая энергия вращательного движения твердого тела. Лекция 7

1. Лекция 5

1
Контрольный вопрос
Две частицы обладают одинаковыми кинетическими
энергиями. Величины их импульсов соотносятся как:
а) p1 < p2,
б) p1 = p2,
в) p1 > p2,
г) невозможно определить.
2
p
T
2m
Масса тел неизвестна – г).
2
Содержание предыдущей лекции
Механическая энергия
• Столкновение тел.
Кинематика и динамика вращательного движения
• Кинематика вращательного движения: угловая скорость и
угловое ускорение, их связь с линейной скоростью и
ускорением.
• Момент силы. Уравнение моментов.
3
Содержание сегодняшней лекции
Кинематика и динамика вращательного движения
• Момент инерции. Теорема Штейнера. Кинетическая энергия
вращательного движения твердого тела.
• Основное уравнение динамики вращательного движения
твердого тела с закрепленной осью вращения.

• Момент импульса тела. Закон сохранения момента
импульса.
• Гироскопические силы. Гироскопы и их применение в
технике.
Релятивистская механика
• Принцип относительности Галилея.
4
Момент силы относительно точки
Момент силы относительно точки –
характеристика способности силы вращать тело
вокруг точки, относительно которой он рассчитывается.
M o (F )
5
Момент силы относительно оси
Возможность произвольного вращения тела
относительно точки О.
M rF
Реальность:
поворот тела под действием силы
вокруг оси,
перпендикулярной к плоскости,
в которой лежат сила F и точка О,
т.е. вокруг оси, совпадающей с
направлением момента силы
относительно данной точки.
6
Момент силы относительно оси
M
Проекция вектора
на некоторую ось,
проходящую через точку О,
относительно которой определен вектор M ,
называется моментом силы относительно этой оси:
M z r F пр z .
M z rF
пр z
M o (F )
7
M rF
M o (F )
Момент силы относительно оси
F FII FR F
M M II M R M
M z M z II M z R M z
M z 0 0 M z RF
r
r
M z RF
8
M z RF
Момент силы относительно оси
r
r
Момент силы относительно оси z – характеристика
способности силы вращать тело вокруг этой оси.
Поворот тем успешнее, чем больше
тангенциальная
составляющая силы F и плечо R.
9
Пара сил
Пара сил – две равные по модулю, но
противоположно направленные силы,
не действующие вдоль одной прямой.
Плечо пары сил –
расстояние l между прямыми,
вдоль которых действуют силы.
10
Уравнение моментов
M r1 F1 r2 F2 .
F1 F2 .
M r1F2 r2 F2 r2 r1 F2 r12 F2 .
r12 r2 r1
Суммарный момент
образующих пару сил
— вектор, проведенный
из точки
приложения силы F1 в точку
приложения силы F2 .
11
Уравнение моментов
Независимость выражения
M r12 F2
от выбора точки О.
Следствие:
момент пары сил относительно
любой точки одинаков.
12
M r12 F2
Уравнение моментов
Направление вектора момента пары сил
— перпендикулярно плоскости,
в которой лежат силы.
Равенство численного значения
вектора момента пары сил
произведению модуля любой из сил на плечо.
13
Уравнение моментов
Действие сил взаимодействия между
частицами вдоль одной и той же прямой.
Равенство по модулю и противоположное
направление вдоль одной и той же прямой
моментов сил взаимодействия
относительно произвольной точки О.
Уравновешивание моментов
внутренних сил друг другом,
в частности, для твердого тела
M внутр 0.
14
Момент инерции
Абсолютно твердое тело – система частиц (материальных
точек) с неизменным расстоянием между ними.
Момент инерции тела относительно некоторой оси –
величина, равная сумме произведений элементарных масс,
из которых состоит данное тело,
на квадраты их расстояний от некоторой оси,
I m R .
2
i i
Равенство момента инерции тела
сумме моментов инерции его частей.
15
Момент инерции
Плотность однородного тела –
характеристика распределения массы m в его объеме V,

m /V .
Плотность неоднородного тела
m dm
lim
.
V 0 V
dV
16
I mi Ri2 .
Момент инерции
mi i Vi .
I i Ri2 Vi .
Если = соnst, то
Наиболее точное решение —
I R Vi .
2
i
I R 2 dm R 2 dV .
17
Теорема Штейнера
Момент инерции I тела относительно произвольной оси
равен сумме моментов инерции IC данного тела
относительно оси, параллельной данной и проходящей
через центр масс тела, и произведения массы тела m на
квадрат расстояния а между осями:
I I C ma 2 .
18
Теорема Штейнера
Доказательство
Предположение:
Ось С проходит через
центр масс тела.
Ось О параллельна оси С.
Оси перпендикулярны
к плоскости экрана.
а – расстояние между осями.
19
Теорема Штейнера
Ri a Ri
2 2
2
Ri a Ri a 2aRi Ri
2
I mi Ri a mi 2a mi Ri mi Ri2
2
2a mi Ri 0
2
— ось С проходит через центр масс.
I ma I C
2
20
Кинетическая энергия
вращательного движения твердого тела
Вращение тела вокруг
неподвижной оси z.
Кинетическая энергия i-й
элементарной массы
2
i i
mv 1
Ti
mi 2 Ri2 .
2
2
Кинетическая энергия тела
вращающегося вокруг неподвижной оси
1 2
T Ti mi Ri2 I 2 / 2.
2
21
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Аналогия со вторым законом Ньютона
для поступательного движения частицы.
Частица массы m движется по
окружности радиуса
r под действием
касательной силы Ft и радиальной силы Fr .
22
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Связь между модулями
касательного ускорения at частицы
и вызвавшей это ускорение
касательной силой Ft
Ft mat .
Момент действующей на частицу касательной силы
относительно центра окружности
M Ft r (mat )r.
23
M Ft r (mat )r.
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Связь между модулями касательного
ускорения и углового ускорения
at r .
Момент действующей на частицу касательной силы
относительно центра окружности
M Ft r mat r (mr )r (mr 2 ) I .
I mr 2 — момент инерции частицы относительно
оси z, проходящей через центр окружности.
24
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Момент действующей на частицу касательной силы
относительно центра окружности
прямо пропорционален ее угловому ускорению
M I .
25
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Бесконечно большое количество материальных точек
(частиц) массы dm и бесконечно малого размера –
аналог твердого тела произвольной формы.
Действие на частицу тела,
вращающегося относительно
фиксированной оси, касательной силы
dFt (dm)a t .
26
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Момент касательной силы, действующий относительно оси
вращения и связанный с касательной силой dFt ,

dM rdFt a t rdm.
at r
Равенство углового ускорения для всех частиц.
dM r 2 dm.
27
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Момент касательной силы,
действующий относительно оси вращения на тело в целом,
M r dm r dm.
2
2
Момент инерции тела относительно оси вращения,
проходящей через точку О,
I r 2 dm.
28
Основное уравнение
динамики вращательного движения твердого тела
с закрепленной осью вращения
Прохождение линии действия
радиальной силы
через ось вращения тела.
Равенство нулю плеча и момента
радиальной силы.
Справедливость выражения M I .
с учетом как касательных, так и радиальных компонент силы.
29
Момент импульса тела
Момент импульса отдельно взятой
i-ой частицы относительно точки О,
лежащей на оси вращения,
Li
Li ri pi ri mi vi .
ri vi
Li mi ri vi mi ri Ri .
30
Li mi ri vi mi ri Ri
Момент импульса тела
Li
Угол i –
острый для любой частицы тела.
Lzi Li cos i mi ri Ri cos i
mi ri cos i Ri mi Ri2 i .
31
Момент импульса тела
Для всего тела
Lz Lzi m R z z mi Ri .
2
2
i i
Li
I m R .
2
i i
Lz I z .
Аналогия:
pz mvz .
32
Закон сохранения момента импульса
M M i ri Fi
i
i
L Li ri pi
i
i
M внутр 0
Для всякой системы частиц (тела)
d
L M внешн .
dt
33
d
L M внешн .
dt
Lz I z .
Закон сохранения момента импульса
d
Lz M z внешн
dt
z
I z M z внешн
— проекция углового ускорения на ось z.
Аналогия:
m z Fz .
34
Закон сохранения момента импульса
Однородное тело, симметричное относительно оси вращения,
— совпадение по направлению момента импульса
относительно точки О, лежащей
на оси вращения,
и вектора .
L I .
Общий случай несимметричного тела невыполнение данного уравнения.
35
Закон сохранения момента импульса
d
L M внешн .
dt
Если M внешн 0,
d
L 0 и L постоянен.
то
dt
Постоянство во времени момента импульса
замкнутой системы материальных точек.
36
Закон сохранения момента импульса
d
Lz M z внешн
dt
Если
M
z внешн
d
0, то Lz 0 и Lz постоянна.
dt
Постоянство во времени проекции момента импульса
замкнутой системы материальных точек на некоторую ось.
37
Контрольный вопрос
Труба и цилиндр, обладающие
одинаковыми радиусами, массой и длиной (высотой),
вращаются относительно их продольных центральных осей
с одинаковой угловой скоростью.
Большей вращательной кинетической энергией обладает:
а) полая труба,
б) сплошной цилиндр,
в) они обладают одинаковыми значениями
вращательной кинетической энергии,
г) невозможно определить.
38

English     Русский Правила

Знать связь между крутящим моментом и моментом инерции

Мы знаем, что крутящий момент вентилятора называется крутящим моментом, и существует прямая зависимость между крутящим моментом и моментом инерции.

Так вот, при включении кнопки вентилятора, когда вентилятор начинает вращаться, его момент силы или крутящий момент изменяется обратно пропорционально ускорению. Здесь это соотношение можно рассматривать как сестру второго закона движения Ньютона. Момент инерции — это вращательная масса вентилятора, а крутящий момент — его вращательная сила или его вращающая сила.

В физике и механике крутящий момент является вращательным, но эквивалентен линейной силе. Его также называют моментом, моментом силы, силой вращения или эффектом поворота, в зависимости от области или категории исследования. Эта концепция возникла в результате исследований, проведенных Архимедом по использованию рычагов. Крутящий момент — это крутящая сила, которая вызывает эффективный процесс вращения в любом механизме. Точка, в которой вращается конкретный объект, называется осью вращения. Математически крутящий момент можно записать как T = F * r * sin(theta), и он измеряется в ньютон-метрах.

Связь между инерцией и крутящим моментом

Согласно первому закону движения Ньютона, тело остается в покое или в состоянии движения, если оно не приводится в движение внешней силой. Например, конденсатор переменного тока, а стиральная машина остается в покое, если мы не включаем кнопку питания, и позволяем ей вращаться с помощью электричества.

Итак, мы видим, что все вращающиеся электроприборы остаются в покое, и при воздействии вращающего действия или крутящего момента каждая частица в системе, имеющая свои индивидуальные вращательные массы, начинает вращаться вокруг своей оси вращения. Итак, вот как мы можем понять взаимосвязь между крутящим моментом и инерцией, применяя первый закон движения Ньютона.

До сих пор мы понимали связь крутящего момента с инерцией и моментом инерции. Теперь выведем связь между крутящим моментом и моментом инерции.

Понятие, используемое во вращательном движении

Согласно механике вращательного движения, каждое твердое тело, совершающее вращательное движение вокруг неподвижной оси, совершает движение с равномерным угловым ускорением, т. е. под действием крутящего момента или момента силы.

Получение зависимости между крутящим моментом и моментом инерции

Предположим, что частица «Q» массы «m» вращается вокруг оси вращения, где она описывает дугу по окружности радиуса «r». Теперь, согласно второму закону движения Ньютона, имеем:

F = ma

Где а — ускорение, с которым вращается тело.

Теперь,\[a=\frac{F}{m}\]…….(a)

Если мы говорим, что частица движется по окружности со смещением ‘s’, то мы можем переписать уравнение для линейное ускорение как двойная производная от углового перемещения следующим образом:

\[a=\frac{d}{dt}\frac{d(s)}{dt}\]……..(1)

ускорение каждой частицы будет a1, a2, a3,…., an.

Для тела, совершающего вращательное движение, соотношение: ‘s = r’, применим это в уравнении (1):

\[a=\frac{d}{dt}\frac{rd(\ theta )}{dt}\]…….(2)

Также мы знаем соотношение между линейным и угловым ускорением, для которого напишем то же самое:

\[a=r\alpha \]…… (3)

Из уравнения (2) мы получаем уравнение (3), так как мы видим, что скорость изменения углового смещения является угловой скоростью, давайте посмотрим, как это происходит:

\[r\frac{d\ theta }{dt}=\omega \]

And,

\[\frac{d\omega }{dt}=\alpha \]

Здесь угловое ускорение частицы Q. Таким образом, мы также получили уравнение (3). Теперь переходим к следующему шагу:

Сила и момент силы

Нам известно еще одно соотношение между силой, приложенной к телу, и крутящим моментом, и оно выглядит следующим образом: 92\].….(6)

Где

m = масса частицы «Q», а r — квадрат расстояния частицы от оси вращения или просто радиус вращения, таким образом, подставляя значение уравнение (6) в (5), получаем:

\[\tau =I\alpha \]…..(7)

Итак, уравнение (7) и есть искомое уравнение, для которого мы проделали все эти математические вывод. Уравнение (7) описывает предельное соотношение между моментом инерции и крутящим моментом.

Мы можем переписать уравнение (7) в векторной форме как:

\[\vec{\tau }=I\vec{\alpha }\]

Мы называем это уравнение основным законом вращательного движения или законом вращательного движения. Теперь давайте определим приведенное выше уравнение:

Определение основного закона вращательного движения

Если α = 1, то τ = I * 1.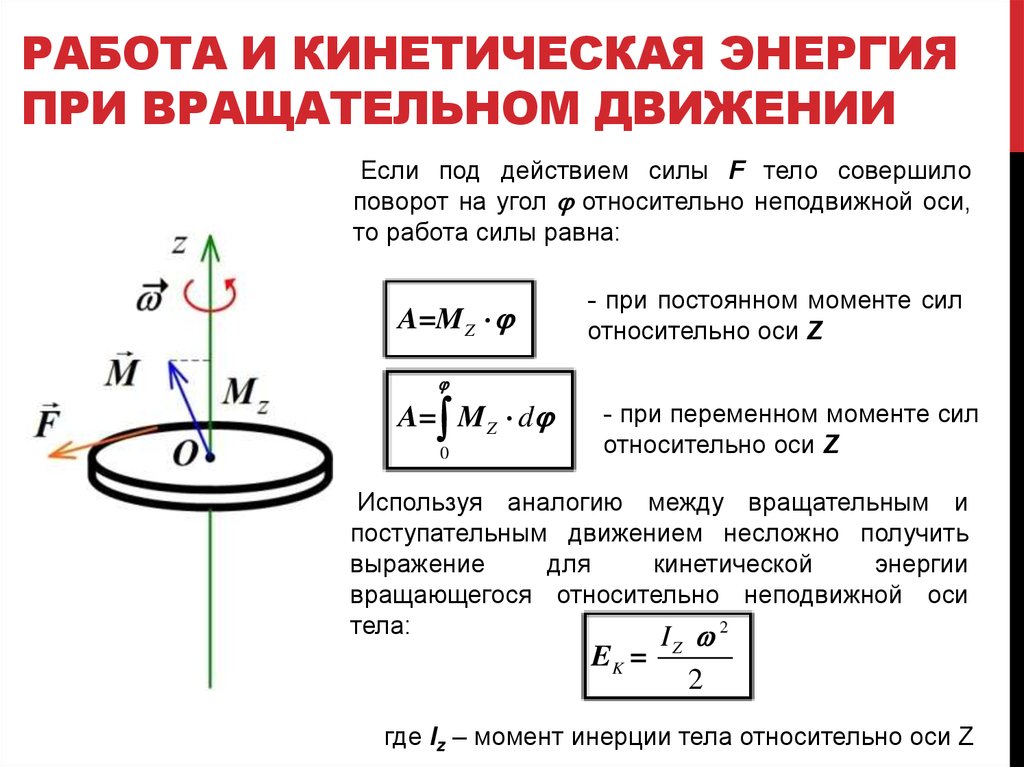 Из этого утверждения мы можем сказать, что момент инерции и крутящий момент, приложенные к телу равны друг другу при отсутствии углового ускорения.

Поскольку количество частиц в системе равно n, и каждая частица подчиняется уравнению (7), закон вращательного движения применим ко всем без исключения частицам системы.

Динамика вращательного движения: инерция вращения

Цели обучения

К концу этого раздела вы сможете:

• Понимать взаимосвязь между силой, массой и ускорением.
• Изучите поворотный эффект силы.
• Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, линейным ускорением и угловым ускорением.

Если вам когда-либо приходилось крутить велосипедное колесо или толкать карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 1. Фактически, ваша интуиция надежно предсказывает многие факторы, вовлеченный. Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.

Рисунок 1. Для вращения колеса велосипеда требуется сила. Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если надавить на спицу ближе к оси, угловое ускорение будет меньше.

Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу F к точке массой м , которая находится на расстоянии r от точки вращения, как показано на рисунке 2. Поскольку сила перпендикулярна r , ускорение[latex]a=\frac{F}{m}[/latex] получается в направлении Ф . Мы можем изменить это уравнение так, что F = ma , а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что a = rα , и подставим это выражение в F = ma , что даст

F = мра

Напомним, что крутящий момент — это вращательная эффективность силы. В этом случае, поскольку F перпендикулярна r , крутящий момент равен просто τ = Fr . Итак, если мы умножим обе части приведенного выше уравнения на r , мы получим крутящий момент в левой части. То есть

rF = mr ² α

или

τ = mr ² α .

Это последнее уравнение является вращательным аналогом второго закона Ньютона ( F = ma ), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr ²  аналогично массе (или инерции). . Величина mr ²  называется вращательной инерцией или моментом инерции точки массой m на расстоянии r от центра вращения.

Рис. 2. Объект поддерживается горизонтальным столом без трения и прикреплен к точке поворота шнуром, создающим центростремительную силу. Сила F приложена к объекту перпендикулярно радиусу r , заставляя его ускоряться относительно точки поворота. Сила удерживается перпендикулярно р.

Создание соединений: динамика вращательного движения

Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.

Инерция вращения и момент инерции

Прежде чем мы сможем рассмотреть вращение чего-либо, кроме точечной массы, подобной той, что изображена на рис. {2}[/латекс]. Здесь I аналогичен м в поступательном движении. Из-за расстояния r момент инерции любого объекта зависит от выбранной оси. На самом деле вычисление I выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одном и том же расстоянии от его оси. Следовательно, момент инерции обруча вокруг своей оси равен MR ² , где M — его полная масса, а R — его радиус. (мы используем M и R для всего объекта, чтобы отличить их от m и r для точечных масс.) Во всех других случаях мы должны обращаться к рисунку 3 (обратите внимание, что таблица представляет собой произведение искусства, форма которого а также формулы) для формул для I , которые были получены путем интегрирования по непрерывному телу. Обратите внимание, что I имеет единицы массы, умноженные на квадрат расстояния (кг⋅м ² ), как и следовало ожидать из его определения.

Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением:

, где net τ — это суммарный крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Отношение в сети τ = Iα,  [латекс]\альфа =\фракция {\текст{сеть}{\тау}}{I}[/латекс]  – это вращательный аналог второго закона Ньютона, применимый очень широко. Это уравнение действительно справедливо для любого крутящего момента, примененного к любому объекту относительно любой оси .

Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его распределение массы относительно оси, вокруг которой она вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.

Эксперимент на вынос

Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо. (Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.

Стратегия решения задач по динамике вращения

1. Изучите ситуацию, чтобы определить, участвуют ли крутящий момент и масса во вращении . Нарисуйте тщательный набросок ситуации.
2. Определить интересующую систему .
3. Нарисуйте свободную диаграмму тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
4. Примените net τ = Iα, α = net τI, вращательный эквивалент второго закона Ньютона, для решения задачи . Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
5. Как всегда, проверьте решение, чтобы убедиться, что оно разумно .

Выполнение соединений

В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.

Рис. 3. Некоторые инерции вращения.

Пример 1. Расчет влияния распределения массы на карусель

Рассмотрим отца, толкающего игровую карусель на рис. 4. Он прикладывает силу 250 Н к краю карусели весом 50,0 кг. карусель радиусом 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.

Рис. 4. Отец толкает игровую карусель за ее край и перпендикулярно ее радиусу для достижения максимального крутящего момента.

Стратегия

Угловое ускорение задается непосредственно выражением [латекс]\альфа =\frac{\text{net}\tau}{I}[/latex]:

[латекс]\alpha =\frac {\tau}{I}[/latex]

Чтобы найти α , мы должны сначала вычислить крутящий момент τ (который одинаков в обоих случаях) и момент инерции I 9{2}}[/латекс].

Решение для (b)

Мы ожидаем, что угловое ускорение системы будет меньше в этой части, потому что момент инерции больше, когда ребенок находится на карусели. Чтобы найти общий момент инерции I , сначала найдем момент инерции ребенка I _c , считая ребенка эквивалентным точечной массе на расстоянии 1,25 м от оси. Тогда

I _c = MR ²  = (18,0 кг)(1,25 м) ²  = 28,13 кг ⋅ м ² .

Суммарный момент инерции равен сумме моментов инерции карусели и ребенка (относительно одной оси). Чтобы оправдать эту сумму для себя, рассмотрите определение I :

I = 28,13 кг ⋅ м ² + 56,25 кг ⋅ м ² = 84,38 кг ⋅ м ^2.

Подстановка известных значений в уравнение для α дает 9{2}}[/латекс].

Обсуждение

Как и ожидалось, угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, и только 8,89 рад/с, когда на ней находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.

Проверьте свое понимание

Крутящий момент является аналогом силы, а момент инерции является аналогом массы. Сила и масса — физические величины, зависящие только от одного фактора. Например, масса связана исключительно с количеством атомов различных типов в объекте. Являются ли крутящий момент и момент инерции такими же простыми?

Решение

Нет. Крутящий момент зависит от трех факторов: величины силы, направления силы и точки приложения. Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти величины вращения зависят от большего количества факторов.

Резюме раздела

• Крутящий момент — это вращающая способность силы. В этом случае, поскольку F перпендикулярно r , крутящий момент равен просто τ = rF . Если мы умножим обе части приведенного выше уравнения на r , мы получим крутящий момент в левой части. То есть,

  rF = MR ² α

  или

  τ = мр ² α .

Концептуальные вопросы

1. Момент инерции длинного стержня, закрученного вокруг оси через один конец, перпендикулярный его длине, равен ML ² /3. Почему этот момент инерции больше, чем если бы вы вращали точечную массу M  в месте расположения центра масс стержня ( L /2)? (Это будет ML ² /4. )

2. Почему момент инерции обруча с массой M и радиусом R больше момента инерции диска, имеет ту же массу и радиус? Почему момент инерции сферической оболочки массой M и радиус R больше, чем у твердого шара той же массы и радиуса?

3. Приведите пример, в котором малая сила вызывает большой крутящий момент. Приведите другой пример, в котором большая сила действует на малый крутящий момент.

4. При уменьшении массы гоночного велосипеда наибольшая выгода достигается за счет уменьшения массы шин и колесных дисков. Почему это позволяет гонщику достичь большего ускорения, чем такое же уменьшение массы рамы велосипеда?

Рис. 5.

5. Шарик скользит вверх по пандусу без трения. Затем его катят без проскальзывания и с той же начальной скоростью вверх по другому пандусу без трения (с тем же углом наклона). В каком случае она достигает большей высоты и почему?

Задачи и упражнения

1. В этой задаче рассматриваются дополнительные аспекты Примера 1: Расчет влияния распределения массы на карусель. а) Сколько времени потребуется отцу, чтобы придать карусели угловую скорость 1,50 рад/с? б) Сколько оборотов он должен совершить, чтобы развить эту скорость? в) Если он приложит тормозящую силу 300 Н в радиусе 1,35 м, сколько времени потребуется ему, чтобы остановить их?

2. Рассчитайте момент инерции конькобежца, зная следующую информацию. (a) Фигурист весом 60,0 кг аппроксимирован цилиндром с радиусом 0,110 м. (b) Фигурист с вытянутыми руками примерно представляет собой цилиндр весом 52,5 кг, радиусом 0,110 м и двумя руками длиной 0,900 м, каждая из которых весит 3,75 кг и выходит прямо из цилиндра, как стержни, вращающиеся вокруг своей оси. заканчивается.

3. Трехглавая мышца задней поверхности плеча разгибает предплечье. Эта мышца профессионального боксера действует с силой 2,00 × 10 ³ Н с эффективным перпендикулярным плечом рычага 3,00 см, обеспечивающим угловое ускорение предплечья 120 рад/с ² . Каков момент инерции предплечья боксера?

4. {2}[/latex]  Что сила, действующая на мышцу, если ее эффективное перпендикулярное плечо рычага равно 1,90 см?

5. Предположим, вы прикладываете силу 180 Н по касательной к точильному камню массой 75,0 кг (сплошной диск) радиусом 0,280 м. а) Какой крутящий момент приложен? б) Чему равно угловое ускорение при пренебрежимо малом противодействии трения? в) Чему равно угловое ускорение, если на расстоянии 1,50 см от оси действует противодействующая сила трения 20,0 Н?

6. Рассмотрим колесо мотоцикла массой 12,0 кг, показанное на рис. 6. Предположим, что оно приблизительно представляет собой кольцевое кольцо с внутренним радиусом 0,280 м и внешним радиусом 0,330 м. Мотоцикл стоит на центральной подножке, так что колесо может свободно вращаться. а) Если приводная цепь действует с силой 2200 Н на радиусе 5,00 см, чему равно угловое ускорение колеса? б) Каково тангенциальное ускорение точки на внешней кромке шины? в) Через какое время, начиная с состояния покоя, достигается угловая скорость 80,0 рад/с?

Рис. 6. Момент инерции колеса мотоцикла примерно равен моменту инерции кольцевого кольца.

7. Зорх, заклятый враг Супермена, решает замедлить вращение Земли до одного раза в 28,0 часов, применяя противодействующую силу на экваторе и параллельно ему. Супермена это не сразу беспокоит, потому что он знает, что Зорч может приложить силу только 4,00 × 10 ⁷ Н (немного больше, чем тяга ракеты Сатурн-5). Как долго Зорх должен давить этой силой, чтобы достичь своей цели? (Этот период дает Супермену время, которое он может посвятить другим злодеям.) Четко покажите, как вы следуете шагам, приведенным в0111 Стратегия решения задач по динамике вращения , раздел (выше).

8. Автомобильный двигатель может развивать крутящий момент 200 Н∙м. Рассчитайте угловое ускорение, возникающее, если 95,0% этого крутящего момента приложено к приводному валу, оси и задним колесам автомобиля, учитывая следующую информацию. Автомобиль подвешен так, что колеса могут свободно вращаться. Каждое колесо действует как диск массой 15,0 кг с радиусом 0,180 м. Стенки каждой шины действуют как кольцевое кольцо массой 2,00 кг с внутренним радиусом 0,180 м и внешним радиусом 0,320 м. Протектор каждой шины действует как обруч весом 10,0 кг и радиусом 0,330 м. Ось весом 14,0 кг действует как стержень с радиусом 2,00 см. Приводной вал весом 30,0 кг действует как стержень с радиусом 3,20 см. 9{2}[/латекс]. а) Сколько времени потребуется ей, чтобы точно повернуть вспять? б) Что неразумного в результате? (c) Какие посылки являются неразумными или непоследовательными?

11. Необоснованные результаты  В рекламе утверждается, что 800-килограммовому автомобилю помогает его 20,0-килограммовый маховик, который может разогнать автомобиль из состояния покоя до скорости 30,0 м/с. Маховик представляет собой диск радиусом 0,150 м. (a) Рассчитайте угловую скорость, которую должен иметь маховик, если 95,0 % энергии его вращения используется для разгона автомобиля. б) Что неразумного в результате? (c) Какая посылка неразумна или какая посылка несовместима?

Глоссарий

крутящий момент:

поворотная эффективность силы

инерция вращения:

сопротивление изменению вращения.