Скорость электромагнитных волн. Связь скорости и волны с длиной волны и частотой колебания. заранее спасибо!

длина волны есть частное от деления скорости на частоту. Если волна пробегает в секунду 100 метров, при этом ее частота 50 Гц (50 колебаний в секунду) , то в 100 метрах уложится 50 колебаний, и значит 1 колебание занимает 2 метра.

Электромагнитные волны, возбуждаемые различными излучающими объектами, — заряженными частицами, атомами, молекулами, антеннами и пр. В зависимости от длины волны различают гамма-излучение, рентгеновское, ультрафиолетовое излучение, видимый свет, инфракрасное излучение, радиоволны и низкочастотные электромагнитные колебания. Может показаться удивительным, что внешне столь разные физические явления имеют общую основу. В самом деле, что общего между кусочком радиоактивного вещества, рентгеновской трубкой, ртутной газоразрядной лампой, лампочкой фонарика, теплой печкой, радиовещательной станцией и генератором переменного тока, подключенным к линии электропередачи? Как, впрочем, и между фотопленкой, глазом, термопарой, телевизионной антенной и радиоприемником. Тем не менее, первый список состоит из источников, а второй — из приемников электромагнитного излучения. Воздействия разных видов излучения на организм человека тоже различны: гамма- и рентгеновское излучения пронизывают его, вызывая повреждение тканей, видимый свет вызывает зрительное ощущение в глазу, инфракрасное излучение, падая на тело человека, нагревает его, а радиоволны и электромагнитные колебания низких частот человеческим организмом и вовсе не ощущаются. Несмотря на эти явные различия, все названные виды излучений — в сущности разные стороны одного явления. <img src=»//otvet.imgsmail.ru/download/f2a957f068f7a6b171eeb91df2792303_i-11.jpg» > РАСПРОСТРАНЯЮЩАЯСЯ ВОЛНА. Расстояние l между любыми двумя точками, колеблющимися в одной фазе, называется длиной волны. Эта величина связана со скоростью с электромагнитной волны и частотой колебаний f соотношением l = c/f. Фазовая скорость электромагнитного излучения в вакууме равна скорости света.

Коротше так. Дивись, якщо розглядати поширення Електромагнітних хвиль у вакуумі, то їх швидкість 299792456,2 м/с. А от в речовині (в кисні, у воді, у прозорих криталах тощо) — вона падає.

Интерференция волн — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 августа 2017; проверки требуют 17 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 августа 2017; проверки требуют 17 правок.

Картина интерференции большого количества круговых когерентных волн, в зависимости от длины волны и расстояния между источниками

Интерференция волн (лат. interferens, от inter — между + -ferens — несущий, переносящий) — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.^[1] Сопровождается чередованием максимумов (пучностей) и минимумов (узлов) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера.

При интерференции энергия волн перераспределяется в пространстве.^[1] Это не противоречит закону сохранения энергии потому, что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн.^[2]

При наложении некогерентных волн средняя величина квадрата амплитуды (то есть интенсивность результирующей волны) равна сумме квадратов амплитуд (интенсивностей) накладывающихся волн. Энергия результирующих колебаний каждой точки среды равна сумме энергий её колебаний, обусловленных всеми некогерентными волнами в отдельности.

Именно отличие результирующей интенсивности волнового процесса от суммы интенсивностей его составляющих и есть признак интерференции.^[3]

Расчёт результата сложения двух сферических волн[править | править код]

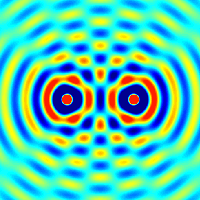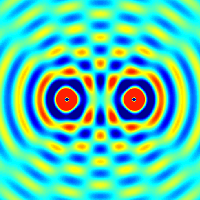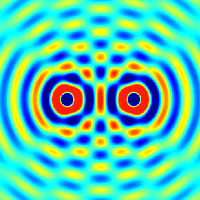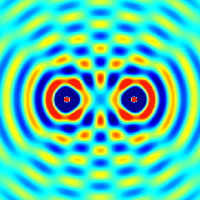Интерференция волн от двух точечных когерентных источников сферических волн. Синим и красным/желтым обозначены минимумы и максимумы

Если в некоторой однородной и изотропной среде два точечных источника возбуждают сферические волны, то в произвольной точке пространства M может происходить наложение волн в соответствии с принципом суперпозиции (наложения): каждая точка среды, куда приходят две или несколько волн, принимает участие в колебаниях, вызванных каждой волной в отдельности. Таким образом волны не взаимодействуют друг с другом и распространяются независимо друг от друга.

Две одновременно распространяющиеся синусоидальные сферические волны s1{\displaystyle s_{1}} и s2{\displaystyle s_{2}}, созданные точечными источниками B₁ и B₂, вызовут в точке M колебание, которое, по принципу суперпозиции, описывается формулой s=s1+s2{\displaystyle s=s_{1}+s_{2}}. Согласно формуле сферической волны:

s1=A1r1sin⁡(ω1t−k1r1+α1)=A1r1sin⁡Φ1{\displaystyle s_{1}={A_{1} \over r_{1}}\sin(\omega _{1}t-k_{1}r_{1}+\alpha _{1})={A_{1} \over r_{1}}\sin \Phi _{1}},

s2=A2r2sin⁡(ω2t−k2r2+α2)=A2r2sin⁡Φ2{\displaystyle s_{2}={A_{2} \over r_{2}}\sin(\omega _{2}t-k_{2}r_{2}+\alpha _{2})={A_{2} \over r_{2}}\sin \Phi _{2}},

где

Φ1=ω1t−k1r1+α1{\displaystyle \Phi _{1}=\omega _{1}t-k_{1}r_{1}+\alpha _{1}} и Φ2=ω2t−k2r2+α2{\displaystyle \Phi _{2}=\omega _{2}t-k_{2}r_{2}+\alpha _{2}} — фазы распространяющихся волн

k1{\displaystyle k_{1}} и k2{\displaystyle k_{2}} — волновые числа (k=ωv=2πλ{\displaystyle k={\omega \over v}={2\pi \over \lambda }})

ω1{\displaystyle \omega _{1}} и ω2{\displaystyle \omega _{2}} — циклические частоты каждой волны

α1{\displaystyle \alpha _{1}} и α2{\displaystyle \alpha _{2}} — начальные фазы,

r1{\displaystyle r_{1}} и r2{\displaystyle r_{2}} — расстояния от точки М до точечных источников B₁ и B₂

В результирующей волне s=s1+s2=Arsin⁡Φ{\displaystyle s=s_{1}+s_{2}={A \over r}\sin \Phi }, амплитуда Ar{\displaystyle {A \over r}} и фаза Φ{\displaystyle \Phi } определяются формулами:

Ar=(A1r1)2+(A2r2)2+2A1r1A2r2cos⁡(Φ2−Φ1){\displaystyle {A \over r}={\sqrt {\left({A_{1} \over r_{1}}\right)^{2}+\left({A_{2} \over r_{2}}\right)^{2}+2{A_{1} \over r_{1}}{A_{2} \over r_{2}}\cos(\Phi _{2}-\Phi _{1})}}},

Φ=arctg⁡A1r1sin⁡Φ1+A2r2sin⁡Φ2A1r1cos⁡Φ1+A2r2cos⁡Φ2{\displaystyle \Phi =\operatorname {arctg} {{{A_{1} \over r_{1}}\sin \Phi _{1}+{A_{2} \over r_{2}}\sin \Phi _{2}} \over {{A_{1} \over r_{1}}\cos \Phi _{1}+{A_{2} \over r_{2}}\cos \Phi _{2}}}}

Условием интерференции является когерентность двух волн. Волны и возбуждающие их источники когерентны, если разность фаз волн Φ2−Φ1{\displaystyle \Phi _{2}-\Phi _{1}} не зависит от времени. Если разность фаз волн Φ2−Φ1{\displaystyle \Phi _{2}-\Phi _{1}} изменяется с течением времени, то такие волны некогерентны. В формуле для разности фаз только первый член зависит от времени:

Φ2−Φ1=(ω2−ω1)t−(k2r2−k1r1)+(α2−α1){\displaystyle \Phi _{2}-\Phi _{1}=(\omega _{2}-\omega _{1})t-(k_{2}r_{2}-k_{1}r_{1})+(\alpha _{2}-\alpha _{1})}, где k1=ω1v{\displaystyle k_{1}={\omega _{1} \over v}}, k2=ω2v{\displaystyle k_{2}={\omega _{2} \over v}},

v{\displaystyle v} — скорость распространения волны в данной среде. Таким образом, две синусоидальные волны когерентны, если их частоты одинаковы (ω1=ω2{\displaystyle \omega _{1}=\omega _{2}}), и некогерентны, если условие не выполняется. Для когерентных волн (ω1=ω2=ω{\displaystyle \omega _{1}=\omega _{2}=\omega }) при условии α2−α1=0{\displaystyle \alpha _{2}-\alpha _{1}=0} разность фаз равна:

Φ2−Φ1=−ωv(r2−r1)=−k(r2−r1){\displaystyle \Phi _{2}-\Phi _{1}=-{\omega \over v}(r_{2}-r_{1})=-k(r_{2}-r_{1})}.

Амплитуда колебаний в результирующей волне максимальна (Ar=A1r1+A2r2){\displaystyle \left({A \over r}={A_{1} \over r_{1}}+{A_{2} \over r_{2}}\right)} во всех точках среды, для которых

k(r2−r1)=2mπ{\displaystyle k(r_{2}-r_{1})=2m\pi }, где m=0,±1,±2,…{\displaystyle m=0,\pm 1,\pm 2,…}(m-целое), или

r2−r1=mλ{\displaystyle r_{2}-r_{1}=m\lambda }, (так как k=2πΔ{\displaystyle k={2\pi \over \Delta }}).

Величина r2−r1=Δ{\displaystyle r_{2}-r_{1}=\Delta } называется геометрической разностью хода волн от их источников B₁ и B₂, до рассматриваемой точки среды.

Амплитуда колебаний в результирующей волне минимальна (Ar=|A1r1−A2r2|){\displaystyle \left({A \over r}={\begin{vmatrix}{A_{1} \over r_{1}}-{A_{2} \over r_{2}}\end{vmatrix}}\right)} во всех точках среды, для которых

k(r2−r1)=(2m−1)π{\displaystyle k(r_{2}-r_{1})=(2m-1)\pi }, где m=1,2,…{\displaystyle m=1,2,…} (m-натуральное), или

Δ=r2−r1=(2m−1)λ2{\displaystyle \Delta =r_{2}-r_{1}=(2m-1){\lambda \over 2}}.

При наложении когерентных волн квадрат амплитуды и энергия результирующей волны отличны от суммы квадратов амплитуд и суммы энергий накладываемых волн.

• Яворский Б. М., Селезнев Ю. А., Справочное руководство по физике., М., Наука., 1984

Стоячая волна — Википедия

Пример стоячей волны (чёрная линия), возникшей в результате интерференции двух гармонических волн (красная и синяя линии) одинаковой частоты и амплитуды, распространяющихся во встречных направлениях. Красные точки обозначают узлы — точки или области в пространстве, в которых амплитуда колебательного процесса минимальна и равна разности амплитуд интерферирующих волн (амплитуда стоячей волны в узлах равна нулю). Посередине между каждой парой соседних узлов располагается пучность — точка или область в пространстве, в которой амплитуда максимальна и равна сумме амплитуд интерферирующих волн (амплитуда стоячей волны в пучностях вдвое больше амплитуды каждой из интерферирующих волн). Фаза колебательного процесса стоячей волны при переходе через узел меняется на 180° (говорят, что колебания синфазны в пространстве с точностью до 180°). В данном примере расстояние между соседними узлами составляет половину длины волны интерферирующих волн, значение коэффициента стоячей волны (отноношение амплитуд колебаний в пучности и узле) стремится к бесконечности.

Стоя́чая волна́ — явление интерференции волн, распространяющихся в противоположных направлениях, при котором перенос энергии ослаблен или отсутствует^[1].

Стоячая волна (электромагнитная) — периодическое изменение амплитуды напряженности электрического и магнитного полей вдоль направления распространения, вызванное интерференцией падающей и отраженной волн^[2].

Стоячая волна — колебательный (волновой) процесс в распределённых колебательных системах с характерным устойчивым в пространстве расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Такой колебательный процесс возникает при интерференции нескольких когерентных волн.

Например, стоячая волна возникает при отражении волны от преград и неоднородностей в результате взаимодействия (интерференции) падающей и отражённой волн. На результат интерференции влияют частота колебаний, модуль и фаза коэффициента отражения, направления распространения падающей и отраженной волн друг относительно друга, изменение или сохранение поляризации волн при отражении, коэффициент затухания волн в среде распространения. Строго говоря, стоячая волна может существовать только при отсутствии потерь в среде распространения (или в активной среде) и полном отражении падающей волны. В реальной же среде наблюдается режим смешанных волн, поскольку всегда присутствует перенос энергии к местам поглощения и излучения. Если при падении волны происходит её полное поглощение, то отраженная волна отсутствует, интерференции волн нет, амплитуда волнового процесса в пространстве постоянна. Такой волновой процесс называют бегущей волной.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе^[3]; в природе — волны Шумана. Для демонстрации стоячих волн в газе используют трубу Рубенса.

• 

  Двумерная стоячая волна на упругом диске. Основная мода.

• 

  Более высокая мода стоячей волны на упругом диске.

В случае гармонических колебаний в одномерной среде стоячая волна описывается формулой:

u=u0cos⁡kxcos⁡(ωt−φ){\displaystyle u=u_{0}\cos kx\cos(\omega t-\varphi )},

где u — возмущения в точке х в момент времени t, u0{\displaystyle u_{0}} — амплитуда стоячей волны, ω{\displaystyle \omega } — частота , k — волновой вектор, φ{\displaystyle \varphi } — фаза.

Стоячие волны являются решениями волновых уравнений. Их можно представить себе как суперпозицию волн, распространяющихся в противоположных направлениях.

При существовании в среде стоячей волны, существуют точки, амплитуда колебаний в которых равна нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания имеют максимальную амплитуду, называются пучностями.

Стоячие волны возникают в резонаторах. Конечные размеры резонатора накладывают дополнительные условия на существование таких волн. В частности, для систем конечных размеров волновой вектор (а, следовательно, длина волны) может принимать лишь определенные дискретные значения. Колебания с определенными значениями волнового вектора называются модами.

Например, различные моды колебаний зажатой на концах струны определяют её основной тон и обертоны.

Математическое описание стоячих волн[править | править код]

В одномерном случае две волны одинаковой частоты, длины волны и амплитуды, распространяющиеся в противоположных направлениях (например, навстречу друг другу), будут взаимодействовать, в результате чего может возникнуть стоячая волна. Например, гармоничная волна, распространяясь вправо, достигая конца струны, производит стоячую волну. Волна, что отражается от конца, должна иметь такую же амплитуду и частоту, как и падающая волна.

Рассмотрим падающую и отраженную волны в виде:

y1=y0sin⁡(kx−ωt){\displaystyle y_{1}\;=\;y_{0}\,\sin(kx-\omega t)}

y2=y0sin⁡(kx+ωt){\displaystyle y_{2}\;=\;y_{0}\,\sin(kx+\omega t)}

где:

• y₀ — амплитуда волны,
• ω{\displaystyle \omega } — циклическая (угловая) частота, измеряемая в радианах в секунду,
• k — волновой вектор, измеряется в радианах на метр, и рассчитывается как 2π{\displaystyle 2\pi } поделённое на длину волны λ{\displaystyle \lambda },
• x и t — переменные для обозначения длины и времени.

Поэтому результирующее уравнение для стоячей волны y будет в виде суммы y₁ и y₂:

y=y0sin⁡(kx−ωt)+y0sin⁡(kx+ωt).{\displaystyle y\;=\;y_{0}\,\sin(kx-\omega t)\;+\;y_{0}\,\sin(kx+\omega t).}

Используя тригонометрические соотношения, это уравнение можно переписать в виде:

y=2y0cos⁡(ωt)sin⁡(kx).{\displaystyle y\;=\;2\,y_{0}\,\cos(\omega t)\;\sin(kx).}

Если рассматривать моды x=0,λ/2,3λ/2,…{\displaystyle x=0,\lambda /2,3\lambda /2,…} и антимоды x=λ/4,3λ/4,5λ/4,…{\displaystyle x=\lambda /4,3\lambda /4,5\lambda /4,…}, то расстояние между соседними модами / антимодами будет равно половине длины волны λ/2{\displaystyle \lambda /2}.

Для того, чтобы получить стоячие волны как результат решения однородного дифференциального волнового уравнения (Даламбера)

(∇2−1v2∂2∂t2)u=0{\displaystyle \left(\nabla ^{2}-{\frac {1}{v^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)u=0}

необходимо соответствующим образом задать его граничные условия (например, закрепить концы струны).

В общем случае неоднородного дифференциального уравнения

(∇2−1v2∂2∂t2)u=f0u,{\displaystyle \left(\nabla ^{2}-{\frac {1}{v^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)u=f_{0}u,}

где f0{\displaystyle f_{0}} — выполняет роль «силы», с помощью которой осуществляется смещение в определенной точке струны, стоячая волна возникает автоматически.

• Джо Вулфи «Струны, стоячие волны и гармоники»

Радиолиния нейтрального водорода — Википедия

Материал из Википедии — свободной энциклопедии

Радиолиния нейтрального водорода, также линия 21 см или линия HI — запрещённая линия (в смысле электродипольного приближения) нейтрального атомарного водорода. Важнейшая радиолиния в радиоастрономии.

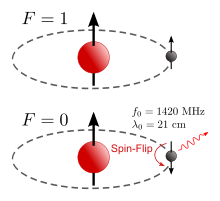
Запрещённая линия нейтрального водорода обусловлена взаимодействием магнитных моментов электрона и протона в атоме водорода. Энергия атома водорода при параллельном расположении магнитных моментов электрона и протона несколько больше, чем при антипараллельном, поэтому при спонтанном изменении ориентации магнитного момента электрона на противоположную атом излучает квант электромагнитного излучения с длиной волны 21,1 см (частота 1420,40575 МГц). Параллельно с излучением радиолинии происходит и обратный процесс — возбуждение атомов водорода электромагнитными квантами с бо́льшими энергиями, например, оптическими, либо в актах соударения атомов. Поэтому в межзвёздном атомарном водороде устанавливается динамическое равновесие между актами излучения радиоквантов и возбуждением атомов оптическими квантами и соударениями.

Такой самопроизвольный переход в каждом отдельном атоме происходит крайне редко — в среднем один раз за 11 миллионов лет (1 км³ водорода при плотности 1 атом/см³ излучает всего 3 кванта в секунду), и энергия каждого кванта крайне мала из-за низкой частоты (hν ≈ 0,941171·10⁻²⁴ Дж, или 5,87433 мкэВ), поэтому интенсивность радиоизлучения межзвёздной среды на единицу объёма ничтожно мала. К примеру, мощность излучения всего нейтрального водорода Солнечной системы в пределах орбиты Плутона не превышает 100 Вт. Однако в галактических масштабах мощность радиоизлучения нейтрального водорода становится заметной (например, мощность излучения всего нейтрального водорода нашей Галактики в десятки раз больше светимости Солнца), что позволяет обнаруживать его на галактических расстояниях. Это излучение крайне важно для изучения методами радиоастрономии распределения нейтрального водорода в Галактике, движения его облаков.

Значение линии нейтрального водорода в радиоастрономии[править | править код]

Линия нейтрального водорода является важнейшей в радиоастрономии. Более половины массы межзвёздного вещества составляет нейтральный водород. Его можно исследовать только по излучению в линии 21 см. Поэтому наблюдения излучения с длиной волны 21 см даёт очень ценные, часто уникальные, сведения о распределении нейтрального водорода в космическом пространстве. Принципиальная возможность излучения межзвёздным водородом радиолинии 21 см показана в 1945 году X. К. ван де Хюлстом. В 1948 году советский астрофизик И. С. Шкловский рассчитал ожидаемую интенсивность излучения межзвёздного водорода и показал, что она достаточна для того, чтобы его можно было обнаружить методами радиоастрономии. В 1951 году радиолиния нейтрального водорода была экспериментально обнаружена почти одновременно Х. Юэном и Э. Парселлом в США и Х. Мюллером и Я. Оортом в Нидерландах. Исследование излучения нейтрального водорода позволили получить информацию о структуре галактики: выяснилось, что большая часть нейтрального водорода сосредоточена в очень тонком (по сравнению с диаметром) слое толщиной около 220 парсек в плоскости Галактики. В распределении водорода отчётливо выделяются спиральные рукава, которые прослеживаются до больших расстояний. Измерение доплеровского смещения позволяет измерить скорость облаков нейтрального водорода относительно Земли (в том числе и красное смещение дальних галактик).

Длина волны 21 см, как самая распространённая во Вселенной, выбрана в качестве рабочей для поисков внеземных цивилизаций по программе SETI.