Свойства векторного произведения векторов.

1. Векторы и операции над ними. Компланарность, коллинеарность векторов.

Базис. Координаты вектора в базисе и действия с координатами.

Вектор – это Направленный отрезок.

Векторы, лежащие на одной или на параллельных прямых, называются Коллинеарными.

Векторы, лежащие в одной или в параллельных плоскостях, называются Компланарными. (Рис. 1 и 2).

Рис. 1 Рис. 2

Операции над векторами:

1. Суммой двух векторов A и B называется вектор C = a + b, начало которого совпадает с началом вектора A, а конец – с концом вектора B при условии, что начало вектора B совпадает с концом вектора A (рис. 3–а). Это правило сложения векторов называется еще “Правилом треугольника”.

Рис. 3–а Рис. 3–б

Вектор C = a + b можно построить также по “Правилу параллелограмма”: в точке O совместим начала векторов 

A И B и на этих векторах, как на сторонах, построим параллелограмм. Вектор, совпадающий с диагональю этого параллелограмма с началом в точке O, и является вектором C (рис. 3–а).

С умма векторов обладает как Переместительным свойством (рис. 3–б):

A + B = B + A

Так и Сочетательным (рис. 4):

(a + b) + c = a + (b + c).

Рис. 4

2) Умножение вектора на число-Произведением вектора A на число L называется вектор 

C = LA, удовлетворяющий следующим условиям:

1.  ;

2. A коллинеарен вектору A;

3.  , если   > 0 и  , если   < 0.

3)Вычитание векторов- это такой вектор С = А-В

Базис — это такой набор векторов, из которого линейной комбинацией (умножением на число и сложением друг с другом) можно получить любой другой вектор пространства.

Положение координатных осей можно задать с помощью единичных векторов  , направленных соответственно по осям  . Векторы   называются основными или базисными ортами и определяют базис   в трехмерном пространстве.

2. Системы координат: декартова прямоугольная, полярная, цилиндрическая,

сферическая. Связь полярных, цилиндрических и сферических координат декартовыми.

Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс  , вторая – осью ординат  , третья – осью аппликат  ; точка   ‑ начало координат (Рис. 4.4).

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. 

 

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом.

Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается  r ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом и обозначается  ф, равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

Выражение декартовых прямоугольных координат через полярные

x=ρcosφ,y=ρsinφ,(ρ≥0,0≤φ≤2π)

Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой z ), которая задаёт высоту точки над плоскостью.

Связь между декартовыми прямоугольными и цилиндрическими координатами: x=ρcosφ,y=ρsinφ,z=z, (ρ≥0,0≤φ≤2π).

Сферические координаты.  

Положение точки М в сферической системе координат задается тройкой чисел  r,  φ  и  θ, где  r – расстояние от начала координат до точки  M  ;  φ – угол, образованный проекцией радиус-вектора  на плоскость О

ху с положительным направлением оси  Ох ;  θ – угол между положительным направлением оси Ozи радиус-вектором точки М .

Связь между декартовыми прямоугольными и сферическими координатами

x=rcosφcosθ,y=rsinφcosθ,z=rsinθ

 (r≥0,0≤φ≤2π,−π2≤θ≤π2).

3. Простейшие задачи аналитической геометрии в декартовой системе координат: координаты вектора, деление отрезка в данном отношении.

Пусть в пространстве заданы две точки B1(α1,β1,γ1) и B2(α2,β2,γ2), определяющие вектор B1B2¯. Из точки O, которая является началом координат, проведем два направленных отрезка OB1¯ и OB2¯.

Данный рисунок представляет собой геометрическую интерпретацию нахождения разности двух векторов, которой мы и воспользуемся для выведения формулы. Также для удобства введем базисные векторы i, j, k и, разложив по ним вектора OB1¯ и OB2¯, получим:

B1B2¯=OB2¯−OB1¯=α2i+β2j+γ2k−(α1i+β1j+γ1k)==α2i+β2j+γ2k−α1i−β1j−γ1k==(α2i−α1i)+(β2j−β1j)+(γ2k−γ1k)==(α2−α1)i+(β2−β1)j+(γ2−γ1)k.

Отсюда видно, что для того, чтобы найти координаты вектора, необходимо из каждой координаты конца вычесть соответствующую координату начала:

B1B2¯=(α2−α1,β2−β1,γ2−γ1).

Для случая на плоскости формула примет следующий вид:B1B2¯=(α2−α1,β2−β1), где положение точек B1(α1,β1) и B2(α2,β2) определяется двумя координатами.

2.  Деление отрезка в данном отношении.

2 Отношением, в котором точка М делит отрезок АВ (рис. 3.1) называется число   .

Если точка М находится между точками А и В, то величины направленных отрезков   и   будут одного и того же знака независимо от выбора направления на прямой АВ. В этом случае число l будет больше нуля. Если же точка М находится за пределами отрезка 

АВ, то число l меньше нуля.

Координаты точки М, делящей отрезок АВ в отношении   можно найти по формулам:

 

4.  Координаты центра масс системы материальных точек.

координаты центра масс системы есть некоторая сумма произведений масс на радиус-вектора каждой точки, деленное на полную массу системы

 r¯¯C=(r¯¯1m1+ r¯¯2m2)/(m1+m2)

5. Проекция вектора на ось. Свойства проекции. Направляющие косинусы.

Проекцией 

вектора   на ось l называется длина вектора  ,   взятая со знаком «+», если вектор   и ось  l  сонаправлены,  и  со знаком «–»,  если   и l  противоположно направлены.  

Если в качестве оси l взять некоторый другой вектор  , то получим проекцию вектора   на вектор  .

Рассмотрим некоторые основные свойства проекций:

1)     проекция вектора   на ось l равна произведению модуля вектора   на косинус угла  между вектором и осью, то есть  ;

2)     проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой; 

3)     проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Направляющие косинусы вектора (в пространстве) – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. В общем случае для вектора с координатами (a; b; c) направляющие косинусы равны:

где a, b, g – углы, составляемые вектором с осями x, y, z соответственно.

Сумма квадратов направляющих косинусов равна 1.

6. Скалярное произведение векторов (определение, свойства, выражение в прямоугольных координатах).

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Свойства:

7. Векторное произведение векторов (определение, свойства, выражение в прямоугольных координатах).

Векторное произведение — это вектор, который перпендикулярен плоскости, построенной по двум другим векторам

Векторное произведение двух векторов обозначается квадратными скобками:

 

 

 

1. Геометрический смысл векторного произведения векторов.

 

 Векторным произведением вектора   на вектор   является

вектор  , длина его численно соответствует площади параллелограмма, который построен на векторах   и  .

 Площадь треугольника, строящегося на векторах   и    соответствует одной второй модуля

векторного произведения векторов   и    :

2. Вектор   перпендикулярен векторам   и  , то есть    и  ;

 

3. Вектор   направлен таким образом, что поворот от вектора   к вектору    происходит

против часовой стрелки, если смотришь с конца вектора   (в таком случае тройка векторов  ,   и    – правая).

      4. Длина вектора  равна | | * | | sin<( , ).

 

      5. Векторное произведения двух не нулевых векторов   и    = 0 тогда и только тогда, когда

эти вектора коллинеарны.

       6. Вектор  , равен векторному произведению не нулевых векторов   и    и перпендикулярен

им.

 

      7. 

 

      8. 

 

      9. 

Выражение векторного произведения через координаты.

Используем таблицу векторного произведения векторов i , j и k :

Если направление самого короткого пути от 1 вектора ко 2 совпадает с направлением стрелки, то

произведение векторов равно 3 вектору, а если оно не одинаково — 3 вектор приобретает знак «—».

 

Окончательную формулу легко выразить еще короче:

 

8. Приложения векторного произведения: вычисление площади треугольника (на

плоскости и в пространстве).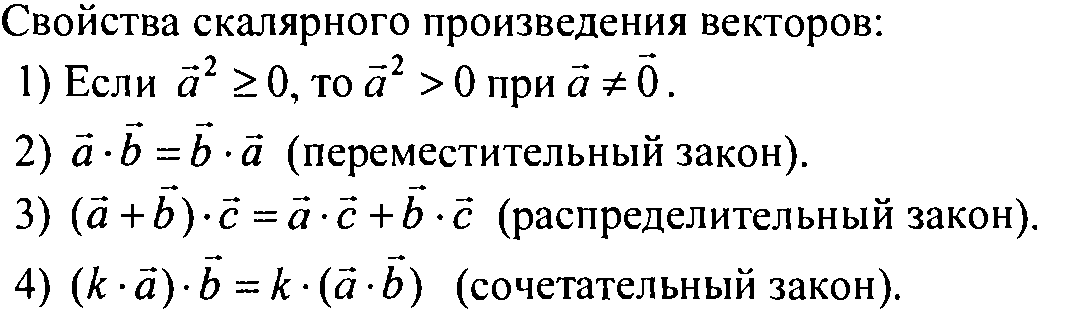

Модуль векторного произведения векторов равен удвоенной площади треугольника.

Вычисление площади треугольника:

1.найти векторное произведение.

2.найти длину получившегося вектора

(2)

(1)

9. Смешанное произведение, связь с объемом параллелепипеда, выражение в

координатах. Вычисление объема тетраэдра.

Смешанное произведение определяется для трех векторов, заданных в трехмерном пространстве.

Рассмотрим произведение векторов , и , составленное следующим образом: . Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

Доказательство. Построим параллелепипед, ребрами которого являются векторы , , и вектор .

Имеем: , , где — площадь параллелограмма, построенного на векторах и , для правой тройки векторов и для левой, где — высота параллелепипеда. Получаем: , т.е. , где — объем параллелепипеда, образованного векторами , и .

Пусть заданы векторы , , . Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:

Векторы , и компланарны тогда и только тогда, когда их смешанное произведение равно нулю ( , , )

Объем тетраэдра :

10.Двойное векторное произведение. Формула [[a, b], c] = b(a, c) − a(b, c) .

Двойным векторным или векторно-векторным произведением трех векторов называется выражение вида или Для двойного векторного произведения надо сначала умножить векторно два вектора и , а затем полученное произведение еще раз умножают векторно на третий вектор . Двойное векторное произведение выражается формулами

Правило: Двойное векторное произведение равно произведению среднего вектора на скалярное произведение двух других, минус крайний вектор в скобке, умноженный на скалярное произведение двух других. Если векторы заданы своими проекциями

то двойное векторное произведение будет равно:

11. Преобразование декартовых прямоугольных координат на плоскости (поворот и параллельный перенос).

В каждом случае координаты точки в старой и новой системах координат связаны формулой (1).

Поэтому достаточно найти вектор переноса начала координат и матрицу перехода от базиса к базису .

а) При параллельном переносе системы координат базис не изменяется, поэтому матрица перехода является единичной: . Находим координаты вектора переноса начала координат: . Тогда формула при параллельном переносе:

б) При повороте системы координат на угол начало новой системы координат совпадает с началом старой, поэтому вектор переноса нулевой: . Разлагая новые базисные векторы по старому базису, получаем Составим матрицу перехода, записывая координаты векторов по столбцам: .

Т огда формула для поворота системы координат:

Обратные преобразования:

Без a и b.

12.Уравнения линий и поверхностей: явное и параметрическое задание. Алгебраические линии и поверхности. Теорема об инвариантности порядка.

Поверхности:

— параметрические уравнения.

— явное уравнение.

Параметрические уравнении линий:

    

Линия на координатной плоскости называется алгебраической, если в некоторой декартовой прямоугольной системе координат уравнение линии является алгебраическим.

Алгебраической поверхностью называется множество всех точек М(x,y,z) геометрического пространства, координаты которых в декартовой прямоугольной системе координат удовлетворяют алгебраическому уравнению

Степень целой рациональной функции называется порядком алгебраической поверхности.

Поверхности, заданные относительно декартовой системы координат уравнениями

,

Эти уравнения называются общими уравнениями поверхности первого и второго порядка.

Теорема об инвариантности порядка.

Если в некоторой ДСК кривая задается ур-нием порядка n, то в любой другой системе координат эта линия задается ур-нием такого же вида, такого же порядка.

Инвариантно-т.е. независимо от выбора системы координат.

(расстояние)

середина отрезка (координат)

формулы деления отрезка в данном отношении.

13.Плоскость в пространстве. Различные виды уравнений: общее уравнение, уравнение по вектору нормали и точке, уравнение по трем точкам, уравнение в отрезках, параметрические уравнения плоскости..

14.Уравнения прямой в пространстве (канонические, параметрические, по 2 точкам). Уравнение прямой как пересечение пары плоскостей. Взаимное расположение двух прямых.

Канонические уравнения прямой:

Если известна некоторая точка пространства , принадлежащая прямой, и направляющий вектор  данной прямой, то  канонические уравнения этой прямой выражаются формулами:

Приведённая запись предполагает, что координаты направляющего вектора  не равны нулю.

Уравнение по двум точкам:

Если известны две точки пространства , то уравнения прямой, проходящей через данные точки, выражаются формулами:

Свойства скалярного произведения. Кратко, с примерами



Для произвольных векторов  и любого числа  справедливы следующие свойства:

1)  – переместительный или коммутативный закон

2)  – распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.

3)  – сочетательный или ассоциативный закон скалярного произведения относительно множителя (константу можно вынести из скалярного произведения)

Зачастую всевозможные свойства (которые ещё и доказывать надо!) воспринимаются студентами как ненужный хлам, который лишь необходимо вызубрить и сразу после экзамена благополучно забыть. Казалось бы, чего тут важного – все и так с первого класса знают, что от перестановки множителей произведение не меняется: . Должен предостеречь, в высшей математике с подобным подходом легко «наломать дров». Так, например, переместительное свойство не является справедливым для алгебраических матриц. Неверно оно и для векторного произведения векторов. Поэтому, в любые свойства, которые вам встретятся, как минимум, нужно вникать, чтобы понять, что можно делать, а чего нельзя.

Задача 17

Найти скалярное произведение векторов  и , если известно, что

Решение: сначала проясним ситуацию с вектором . Что это вообще такое? Сумма векторов  и  представляет собой вполне определенный вектор, который и обозначен через . Такая же история с вектором  – это сумма векторов  и

Итак, по условию требуется найти скалярное произведение . По идее, нужно применить рабочую формулу , но беда в том, что нам неизвестны длины векторов  и угол между ними. Зато в условии даны аналогичные параметры для векторов , поэтому мы пойдём другим путём:

(1) Поставляем выражения векторов .

(2) Используя дистрибутивное свойство, раскрываем скобки по правилу умножения многочленов: чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена. 

(3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов: . Во втором слагаемом используем перестановочность скалярного произведения: .

(4) Приводим подобные слагаемые: .

(5) В первом слагаемом используем формулу скалярного квадрата . В последнем слагаемом работает та же штука: . Второе слагаемое раскладываем по стандартной формуле .

(6) Подставляем исходные данные  и ВНИМАТЕЛЬНО проводим окончательные вычисления.

Ответ:

Отрицательное значение скалярного произведения констатирует тот факт, что угол между векторами  является тупым.

Задача типовая, вот пример для самостоятельного решения:

Задача 18

Найти скалярное произведение векторов  и , если известно, что .

Теперь ещё одно распространённое задание, как раз на новую формулу длины вектора . Обозначения тут будут совпадать, поэтому для ясности я перепишу её с другой буквой:

Задача 19

Найти длину вектора , если .

Сначала решение, затем комментарии:

(1) Поставляем выражение вектора .

(2) Используем формулу длины: , при этом в качестве вектора «вэ» у нас выступает целое выражение .

(3) Используем школьную формулу квадрата суммы :
 – обратите внимание, как она здесь любопытно сработала, фактически это квадрат разности , и, по сути, так оно и есть. Переставим векторы местами:  – получилось то же самое с точностью до перестановки слагаемых. 

(4) Дальнейшее уже знакомо из двух предыдущих задач.

Ответ:

Коль скоро речь шла о длине, то не забываем указать размерность – «единицы».

Задача 20

Найти длину вектора , если .

Это пример для самостоятельного решения.

Продолжаем выжимать полезные вещи из скалярного произведения:

1.6.5. Как найти угол между векторами?

1.6.3. Скалярный квадрат вектора

| Оглавление |



Автор: Aлeксaндр Eмeлин

20.3 Свойства векторов | Векторы и скаляры

Авторизоваться

Предыдущий 20.2 Графическое представление векторов

Следующий 20. 4 Методы сложения векторов

20.3 Свойства векторов (ESAGN)

Векторы — это математические объекты, и сейчас мы изучим некоторые их математические свойства.

Если два вектора имеют одинаковую величину (размер) и одинаковое направление, то мы называем их равными каждому другой. Например, если у нас есть две силы, \(\vec{F_{1}} = \text{20}\text{ N}\) в направлении вверх и \(\vec{F_{2}} = \text{20}\text{ N}\) в направлении вверх , то мы можем сказать, что \(\vec{F_{1}} = \vec{F_{2}}\).

Равенство векторов

Два вектора равны, если они имеют одинаковые величины и одинаковые направление.

Точно так же, как скаляры, которые могут принимать положительные или отрицательные значения, векторы также могут быть положительными или отрицательными. А отрицательный вектор — это вектор, который указывает в направлении , противоположном к ссылка положительная направление . Например, если в конкретной ситуации мы определяем восходящее направление как опорное положительное направление, то сила \(\vec{F_{1}} = \text{30}\text{ N}\) вниз будет отрицательной вектор и также может быть записан как \(\vec{F_{1}} = -\text{30}\text{N}\). В этом случае отрицательный знак (\(-\)) указывает, что направление \(\vec{F_{1}}\) противоположно направлению эталонного положительного направления.

Отрицательный вектор

Отрицательный вектор — это вектор, который имеет направление , противоположное , относительно опорного положительного направления.

Как и скаляры, векторы можно складывать и вычитать. Далее мы рассмотрим, как это сделать.

временный текст

Сложение и вычитание векторов (ЭСАГО)

Добавление векторов

При добавлении векторов нужно учитывать оба их величины и направления.

Например, представьте себе следующее. Вы с другом пытаетесь передвинуть тяжелую коробку. Вы стоите за ним и толкнуть вперед с силой \(\vec{{F}_{1}}\) и ваш друг стоит впереди и тянет его к себе с силой сила \(\vec{{F}_{2}}\). Две силы действуют в одном и том же направлении (т. е. вперед), и, таким образом, общая сила, действующая на коробку:

Очень легко понять концепцию сложения векторов с помощью действия, использующего смещение вектор.

Смещение — это вектор, описывающий изменение положения объекта. Это вектор, который указывает из начального положения в конечное положение.

Добавление векторов

Материалы

малярная лента

Метод

Наклейте полосу малярного скотча горизонтально на пол. Это будет вашей отправной точкой.

Задача 1 :

Сделать \(\text{2}\) шагов вперед. Используйте кусок малярной ленты, чтобы отметить конечную точку и обозначьте его A . Затем сделайте еще \(\text{3}\) шагов вперед. Использовать маскировку лентой, чтобы отметить ваше конечное положение как B . Убедитесь, что вы пытаетесь сохранить свои шаги все равно длина!

Задача 2 :

Вернитесь на исходную линию. Теперь сделайте \(\text{3}\) шагов вперед. Используйте кусок малярной ленты, чтобы отметить вашу конечную точку и обозначьте ее B . Затем сделайте еще \(\text{2}\) шагов вперед и используйте новый кусок клейкой ленты, чтобы обозначить ваше конечное положение как A .

Обсуждение

Что вы заметили?

1. В Задаче 1 первые \(\text{2}\) шаги вперед представляют собой вектор смещения, а вторые \(\text{3}\) шагов вперед также образуют вектор смещения. Если бы мы не остановились после первого \(\text{2}\) шагов, всего мы сделали бы \(\text{5}\) шагов в прямом направлении. Поэтому, если мы сложим векторы смещения для \(\text{2}\) шагов и \(\text{3}\) шагов, мы должны получить всего \(\text{5}\) шагов в прямом направлении.

2. Не имеет значения, делаете ли вы \(\text{3}\) шагов вперед, а затем \(\text{2}\) шагов вперед, или два шага, за которыми следует еще один \(\text{3}\) шаг вперед. Ваша конечная позиция такая же! порядок добавления значения не имеет!

Мы можем изобразить добавление вектора графически, основываясь на описанной выше деятельности. Нарисуйте вектор для первых двух шагов вперед, за которым следует вектор со следующими тремя шагами вперед.

Мы добавляем второй вектор в конец первого вектора, так как это то место, где мы сейчас находимся после первого вектор подействовал. Вектор от хвоста первого вектора (начальная точка) к началу второго вектор (конечная точка) является суммой векторов.

Как вы сами можете убедиться, порядок добавления векторов не имеет значения. В приведенном выше примере, если вы решили сначала сделать \(\text{3}\) шагов вперед, а затем еще \(\text{2}\) шагов вперед, конечный результат все равно будет \(\text{5}\) шагов вперед.

Вычитание векторов

Вернемся к проблеме с тяжелым ящиком, который вы и ваш друг пытаетесь передвинуть. если бы ты не сначала общайтесь должным образом, вы оба можете подумать, что вы должны двигаться в своем собственном направлении! Представить вас встаньте за ящик и потяните его на себя с силой \(\vec{{F}_{1}}\) а ваш друг стоит у перед ящиком и тянет его к себе с силой \(\vec{{F}_{2}}\). В этом случае две силы находятся в напротив направлений. Если мы определим направление, в котором движется ваш друг, как положительных , то сила, которую вы прилагаете, должна быть минус , так как она действует в противоположном направлении. Мы можем написать общая сила, действующая на коробку, как сумма отдельных сил:

То, что вы здесь сделали, это на самом деле вычитание двух векторов! Это то же самое, что сложить два вектора, которые имеют противоположные направления.

Как и раньше, мы можем красиво проиллюстрировать вычитание векторов с помощью векторов смещения. Если вы возьмете \(\text{5}\) шагов вперед, а затем вычтите \(\text{3}\) шагов вперед, у вас останется только два шага вперед:

Что вы физически сделали, чтобы вычесть \(\text{3}\) шагов? Сначала вы сделали \(\text{5}\) шагов вперед, но затем вы сделали \(\text{3}\) шагов назад , чтобы приземлиться назад всего на \(\text{2}\) шагов вперед. Что смещение назад представлено стрелкой, указывающей влево (назад) длиной \(\text{3}\). Конечным результатом сложения этих двух векторов является \(\text{2}\) шагов вперед:

Таким образом, вычитание вектора из другого равносильно добавлению вектора в противоположном направлении (т. е. вычитание \(\text{3}\) шагов вперед аналогично добавлению \(\text{3}\) шагов назад).

Вычитание вектора из другого равносильно добавлению вектора в противоположном направлении.

Результирующий вектор

Окончательная величина, которую вы получите при сложении или вычитании векторов, называется результирующей . вектор . Другими словами, отдельные векторы можно заменить равнодействующими – общими эффект тот же.

Результирующий вектор

Результирующий вектор является единственным вектором, эффект которого такой же, как у отдельных векторов, действующих вместе.

Мы можем проиллюстрировать концепцию результирующего вектора, рассмотрев наши две ситуации с использованием сил для передвинуть тяжелую коробку. В первом случае (слева) вы и ваш друг применяете силы в одном и том же направлении. направление. Результирующая сила будет суммой двух сил, приложенных в этом направлении. В секунду случае (справа) силы приложены в противоположных направлениях. Результирующий вектор снова будет суммой из двух приложенных сил, однако после выбора положительного направления одна сила будет положительной, а другое будет отрицательным, а знак результирующей силы будет зависеть только от того, какое направление вы выбрали в качестве положительный. Для наглядности посмотрите на схемы ниже.

Силы приложены в одном направлении

(положительное направление вправо)

Силы приложены в противоположных направлениях

(положительное направление вправо)

Существует специальное имя для вектора, который имеет ту же величину, что и результирующий вектор, но противоположное направление: уравновешенное . Если вы добавите результирующий вектор и уравновешивающих векторов вместе, ответ всегда равен нулю, потому что уравновешивающий аннулирует результирующий out.

Эквилибрант

Равновесным является вектор, имеющий ту же величину , но направление, противоположное результирующий вектор.

Если вы посмотрите на изображения тяжелого ящика ранее, уравновешивающие силы для двух ситуаций будут выглядеть так:

Предыдущий 20.2 Графическое представление векторов

Оглавление

Следующий 20.4 Методы сложения векторов

Свойства сложения векторов | Свойства добавления вектора

Вектор — это величина, которая имеет как направление, так и величину. Вектор — это направленный отрезок, который обозначается цифрой 9.0007

\(\begin{array}{l}\overline{AB}\end{array} \)

или

\(\begin{array}{l}\vec{a}\end{array} \)

. Стрелки представляют направление вектора. Точка A, где начинается

\(\begin{array}{l}\vec{a}\end{array} \)

, называется начальной точкой, а точка B, где

\(\begin{array}{ l}\vec{a}\end{array} \)

концов называется конечной точкой. Расстояние между начальной и конечной точкой вектора AB называется длиной или величиной вектора и обозначается буквой «а» или 9.0006 \(\begin{array}{l}|\vec{a}|\end{array} \)

или

\(\begin{array}{l}|\overline{AB}|\end{array} \)

. Кроме того, длина или величина вектора не может быть отрицательной. В этой статье мы собираемся подробно изучить два важных свойства сложения векторов.

Мы знаем, что сложение векторов представляет собой сумму двух или более векторов. Два важных закона, связанных со сложением векторов, — это закон треугольника и закон параллелограмма. Точно так же свойства, связанные с добавлением векторов:

• Коммутативное имущество
• Ассоциативное свойство

Теперь давайте подробно обсудим два свойства сложения векторов.

Коммутативное свойство сложения векторов

Коммутативное свойство сложения векторов гласит, что «Для любых двух векторов

\(\begin{array}{l}\vec{a}\end{array} \)

и

\(\begin{array}{ l}\vec{b}\end{array} \)

,

\(\begin{array}{l}\vec{a}\end{array} \)

+

\(\begin{array}{ l}\vec{b}\end{массив} \)

=

\(\begin{array}{l}\vec{b}\end{массив} \)

+

\(\begin{array}{l}\vec{a}\end{массив} \)

».

Доказательство:

Рассмотрим параллелограмм ABCD, как показано на рисунке.

Пусть

\(\begin{array}{l}|\overline{AB}|\end{array} \)

=

\(\begin{array}{l}\vec{a}\end{array } \)

и

\(\begin{array}{l}|\overline{BC}|\end{array} \)

=

\(\begin{array}{l}\vec{b}\end {массив} \)

.

Теперь, используя треугольный закон сложения векторов из треугольника ABC, мы можем записать:

\(\begin{массив}{l}\overline{AC}=\vec{a}+\vec{b}\end{массив} \)

Поскольку противоположные стороны параллелограмма параллельны и равны, мы имеем

\(\begin{array}{l}|\overline{AD}|\end{array} \)

=

\(\begin{ array}{l}|\overline{BC}|\end{массив} \)

=

\(\begin{массив}{l}\vec{b}\end{массив} \)

.

Теперь снова используем закон треугольника из треугольника ADC, получаем

\(\begin{массив}{l}|\overline{AC}|\end{массив} \)

=

\(\begin{массив}{l}|\overline{AD}|\end{массив} \)

+

\(\begin{array}{l}|\overline{DC}|\end{array} \)

=

\(\begin{array}{l}\vec{b}\end{array} \)

+

\(\begin{массив}{l}\vec{a}\end{массив} \)

.

Следовательно,

\(\begin{array}{l}\vec{a}+\vec{b}\end{array} \)

=

\(\begin{array}{l}\vec{b }+\vec{a}\end{массив} \)

.

Таким образом, коммутативность сложения векторов доказана.

Также читайте : Законы вектора Дополнение

Ассоциативное свойство векторного сложения

Ассоциативное свойство сложения векторов гласит, что «для любых трех векторов

\(\begin{array}{l}\vec{a}\end{array} \)

,

\(\begin{array}{ l}\vec{b}\end{array} \)

и

\(\begin{array}{l}\vec{c}\end{array} \)

,

\(\begin{array}{ l}(\vec{a}+\vec{b})+\vec{c}= \vec{a}+(\vec{b}+\vec{c})\end{массив} \)

” .

Доказательство:

Предположим, что векторы

\(\begin{array}{l}\vec{a}\end{array} \)

,

\(\begin{array}{l}\vec{b}\end{array } \)

и

\(\begin{array}{l}\vec{c}\end{array} \)

представлены

\(\begin{array}{l}\overline{PQ}\end{array} \)

,

\(\begin{array}{l}\overline{QR}\end{array} \)

и

\(\begin{array}{l}\overline{RS}\end{array } \)

как показано на рисунке.

Таким образом,

\(\begin{array}{l}\vec{a}+\vec{b} = \overline{PQ}+\overline{QR} = \overline{PR}\end{array} \)

Аналогично,

\(\begin{array}{l}\vec{b}+\vec{c} = \overline{QR}+\overline{RS} = \overline{QS}\end{array} \)

Следовательно,

\(\begin{array}{l}(\vec{a}+\vec{b})+\vec{c} = \overline{PR}+\overline{RS} = \overline{PS}\end {массив} \)

и

\(\begin{array}{l}\vec{a}+(\vec{b}+\vec{c}) = \overline{PQ}+\overline{QS} = \overline{PS}\end {массив} \)

(т.