Формулы алгебры логики мы будет обозначать большими N, M, … Например, следующие выражения являются формулами алгебры логики:

, .

С целью упрощения формул, условимся, что операция конъюнкции «сильнее» операции дизъюнкции, импликации и эквивалентности, т. е. если нет скобок, то вначале выполняется операция конъюнкции.

Формула алгебры логики определяет некоторую булеву функцию, значение которой совпадает со значениями данной формулы для всех наборов значений переменных.

Две формулы N и M называются Равносильными, если они определяют одну и ту же булеву функцию (запись N=M будет означать, что формулы N и M равносильны).

Действительно, построим таблицы истинности для данных формул.

Из таблицы видно, что формулы и определяют одну и ту же булеву функцию и, следовательно, являются равносильными.

Очевидно, что отношение равносильности формул алгебры логики является:

1. рефлексивным, т. е. N=N для любой формулы N;

2. симметричным, т. е. если N=M, то M=N для любых формул N и M;

3. транзитивным, т. е. если N=M и M=J, то N=J для любых формул N, M,J.

Таким образом, отношение равносильности является отношением эквивалентности.

Если какую-нибудь формулу N1, являющуюся частью формулы N заменить формулой N2, равносильной N1, то полученная формула окажется равносильной N. Это свойство лежит в основе преобразования формул с целью их упрощения или приведения к определенной форме.

При преобразовании формул алгебры логики используются свойства логических операций, которые будут рассмотрены ниже.

2.2 Законы алгебры логики. Приведем перечень важнейших равносильностей (законов) алгебры логики. Эти равносильности выражают свойства логических операций.

1. — закон тождества;

2. — закон противоречия;

3. — закон исключительного третьего;

4.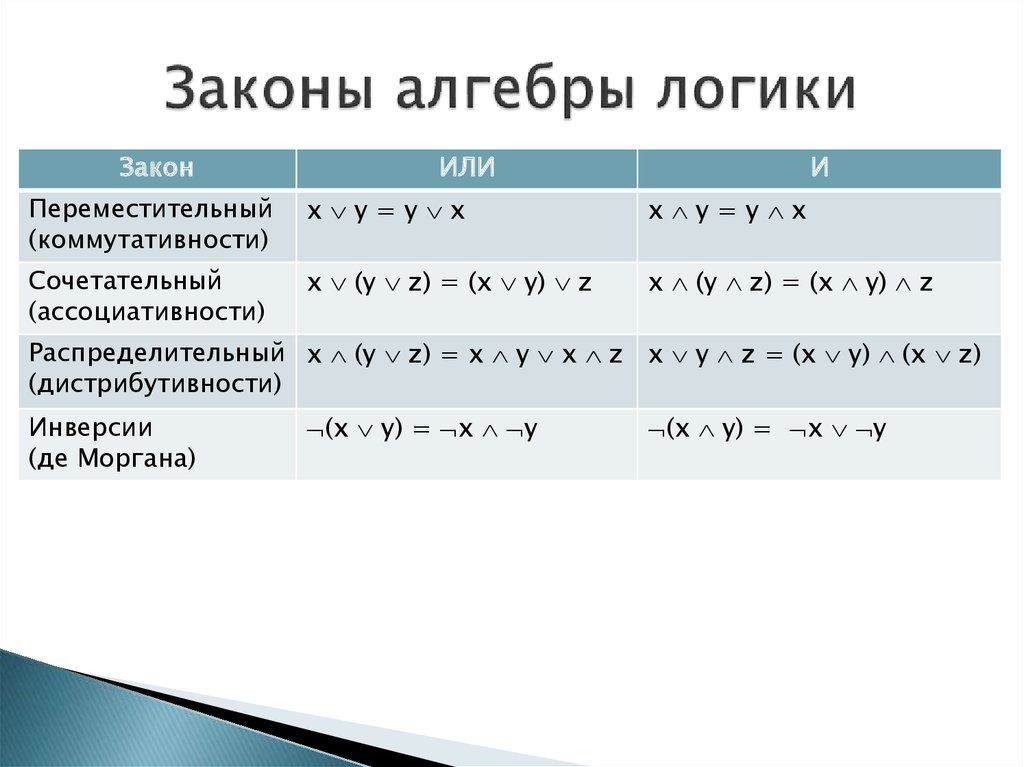 — закон двойного отрицания;

5. , — законы идемпотентности;

6. , — законы коммутативности;

7. , — законы дистрибутивности;

8. , — законы ассоциативности;

9. , — законы де Моргана;

10. ,

11. ,

12. , — законы поглощения;

13. , — законы склеивания.

Перечисленные законы алгебры логики доказываются с помощью таблицы истинности. В качестве примера докажем справедливость закона .

Из таблицы видно, что формулы и определяют одну и ту же булеву функцию. Следовательно, они равносильны.

Логические операции – конъюнкция, дизъюнкция, импликация и эквивалентность, вообще говоря, не являются независимыми друг от друга. В самом деле,

,

,

Первые две равносильности легко доказываются с помощью таблиц истинности. Две последние равносильности докажем с помощью законов де Моргана и двойного отрицания:

; .

Итак, справедливы следующие утверждения:

1) импликацию и эквивалентность можно выразить через конъюнкцию, дизъюнкцию и отрицание;

2) конъюнкцию можно выразить через дизъюнкцию и отрицание;

3) дизъюнкцию можно выразить через конъюнкцию и отрицание;

4) все операции посредством равносильных выражений можно заменить двумя: конъюнкцией и отрицанием или дизъюнкцией и отрицанием.

Естественно возникает следующий вопрос. Для чего вводить пять логических операций, когда можно обойтись двумя? Использование лишь двух операций существенным образом усложнило бы запись, что привело бы к громоздким формулам. Однако в некоторых приложениях математической логики удобно ограничиться двумя операциями. Аналогичная ситуация имеет место в арифметике. Всякое натуральное число можно записать с помощью цифр 0 и 1. Однако записи чисел и выкладки в двоичной системе громоздки. К этой системе прибегают лишь в некоторых случаях.

Множество булевых функций, рассматриваемое вместе с операциями отрицания, конъюнкции и дизъюнкции, называют Булевой алгеброй. Законы 1-13 являются Основными законами булевой алгебры.

Обратим внимание на характер соответствий между равносильностями, объединенными в пару под номерами (5-13). В этих соответствиях проявляется так называемый закон двойственности.

Назовем формулу алгебры логики Двойственной к формуле , если =.

Будем говорить, что операция конъюнкции двойственна операции дизъюнкции и наоборот.

Как показано в пункте 2.2, всякая формула алгебры логики может быть приведена равносильными преобразованиями к формуле, содержащей только операции конъюнкции, дизъюнкции и отрицания.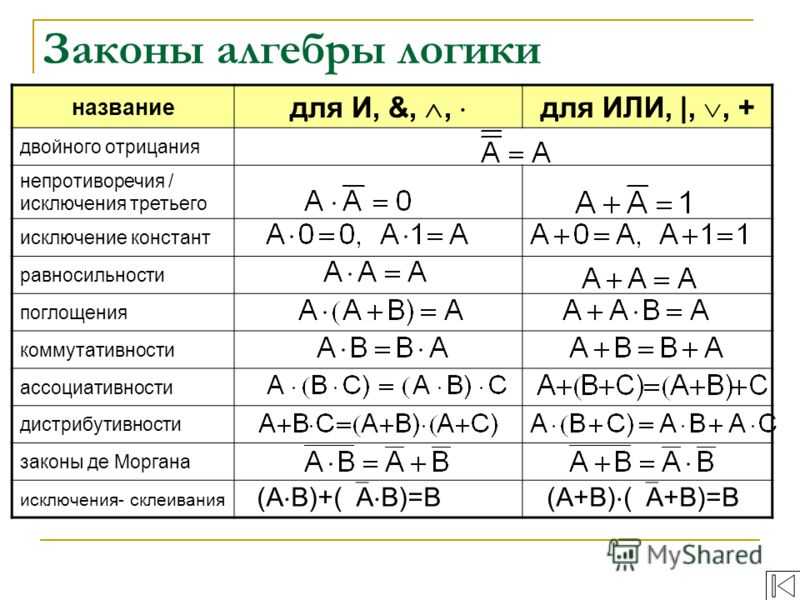 Поэтому, учитывая законы де Моргана и двойного отрицания, две формулы алгебры логики N и M, содержащие только операции конъюнкции, дизъюнкции и отрицания, будут двойственными, если одна получается из другой заменой каждой операции на двойственную и 1 заменяется на 0, а 0 на 1.

Например, формула двойственная к формуле , а формула двойственная к формуле .

Теперь сформулируем закон двойственности.

Теорема 2. Если формулы алгебры логики N и M равносильны, то и двойственные им формулы N* и M* равносильны.

Докажем данный закон. Пусть N(X1,X2,…,XN) = M(X1,X2,…,XN). Согласно определению двойственной формулы

и .

Так как N(X1,X2,…,XN) и M(X1,X2,…,XN) принимают одинаковые значения при любых значениях переменных X1,X2,…,XN, то

=.

Отсюда следует, что

.

Так как формулы и равносильны соответственно формулам и , то они равносильны между собой.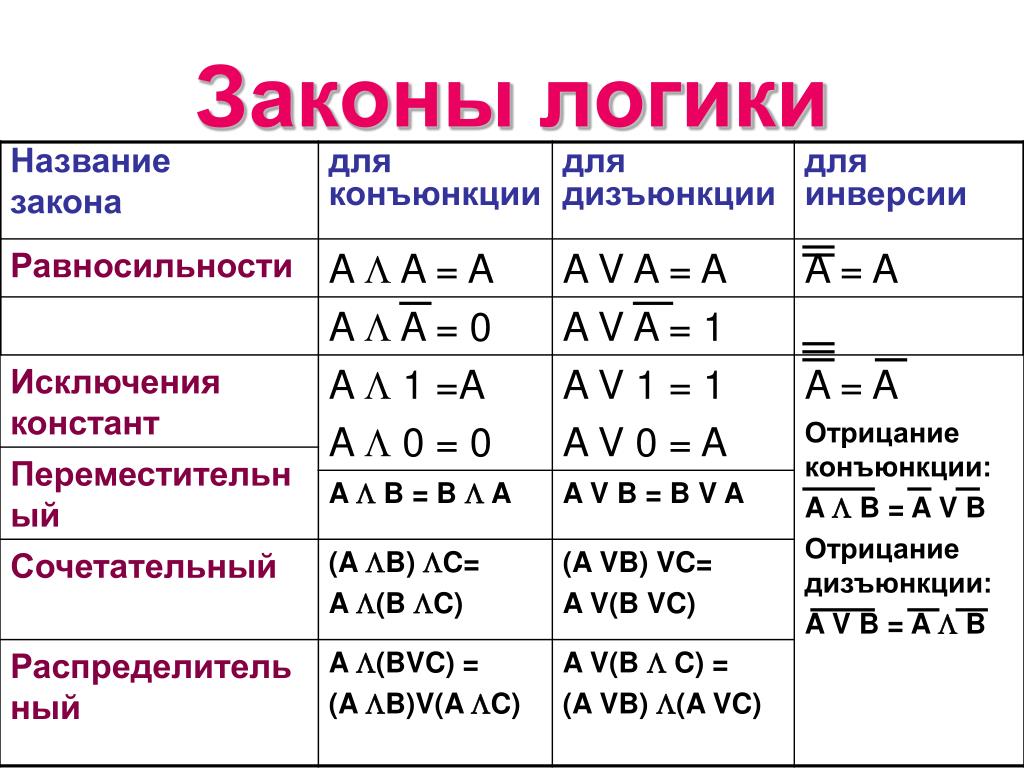

Принцип двойственности позволяет сократить усилие на вывод равносильностей.

Пример 2. Из равносильности вытекает равносильность . Из равносильности вытекает равносильность .

7.4: Булевы алгебраические свойства — Workforce LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• Tony R. Kuphaldt
• Schweitzer Engineering Laboratories via All About Circuits

Коммутативное свойство

Другой тип математического тождества, называемый «свойством» или «законом», описывает, как различные переменные соотносятся друг с другом в системе чисел.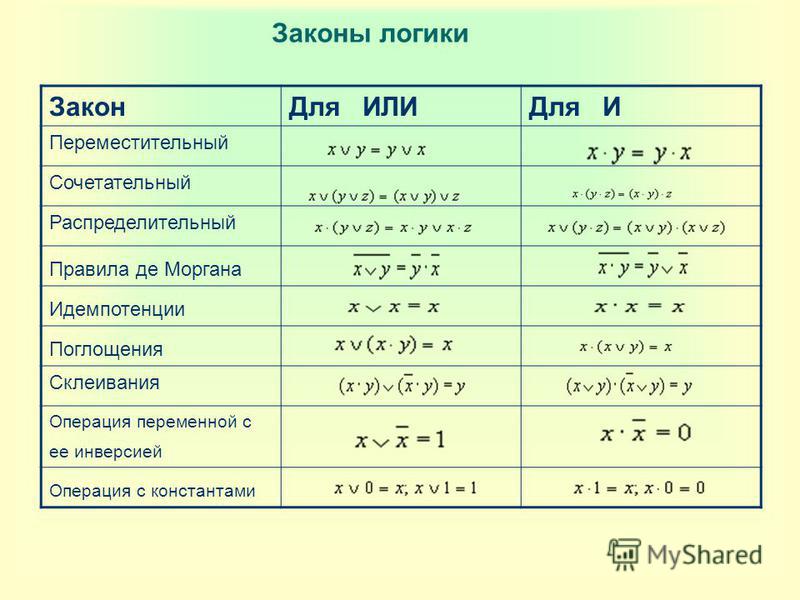 Одно из этих свойств известно как коммутативное свойство , и оно одинаково применимо к сложению и умножению. По сути, свойство коммутативности говорит нам, что мы можем изменить порядок переменных, которые либо складываются вместе, либо перемножаются вместе, не изменяя истинности выражения:

Ассоциативное свойство

Наряду с коммутативными свойствами сложения и умножения у нас есть ассоциативное свойство , опять же одинаково хорошо применимое к сложению и умножению. Это свойство говорит нам, что мы можем ассоциировать группы сложенных или перемноженных переменных вместе со скобками, не изменяя истинности уравнений.

Распределительное свойство

Наконец, у нас есть дистрибутивное свойство , иллюстрирующее, как расширить логическое выражение, образованное произведением суммы, и в обратном порядке показывает нам, как члены могут быть факторизованы из логических сумм произведений:

Подводя итог, вот три основные свойства: коммутативность, ассоциативность и дистрибутивность.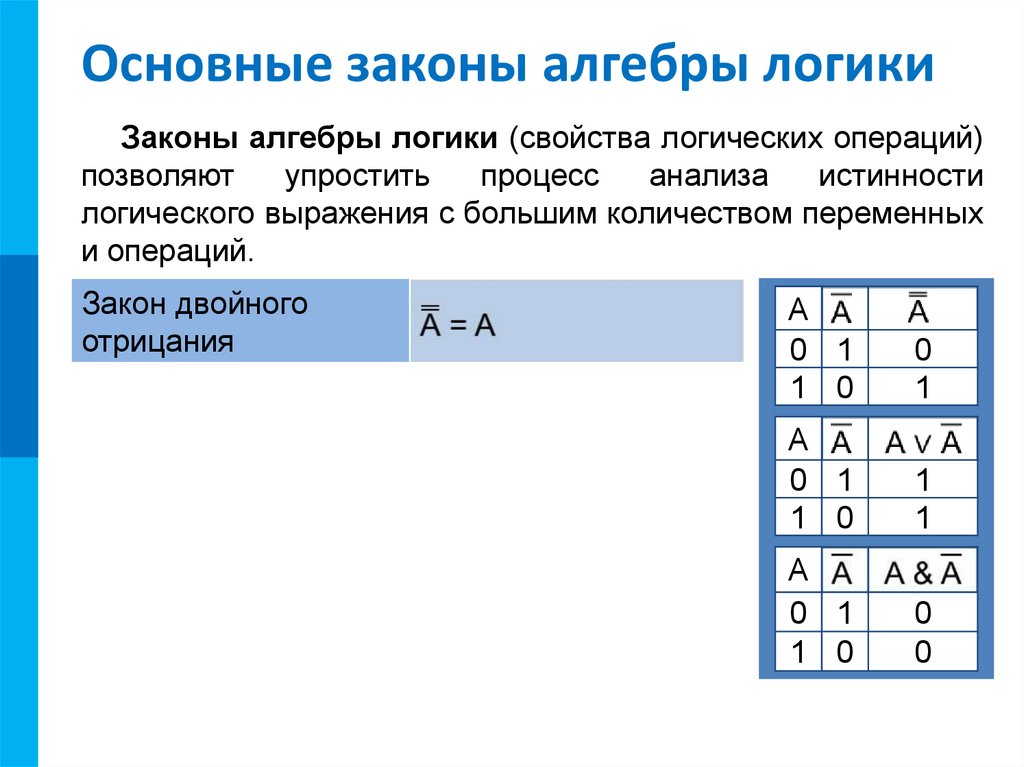

Эта страница под названием 7.4: Булевы алгебраические свойства распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Тони Р. Купхалдтом (Все о цепях) посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Тони Р. Купхалдт

   Лицензия

   ГНУ ФДЛ

   Версия лицензии

   1,3

2. Теги

   1. источник@https://www. allaboutcircuits.com/textbook/digital/

Логические и доказательные свойства равенства

• Главная /
• Геометрия /
• Логика и доказательство /
• Темы /
• Качество равенства /
• Свойства равенства

• Качество равенства /
• Свойства равенства

Темы

• Введение
• Темы
• Построение математических операторов
• Условные операторы
• Качество равенства
• Свойства равенства
• Арифметические свойства
• Доказательства
• Типы доказательств
• Примеры
• Упражнения
• Задачи Math Shack
• Викторины
• Условия
• Раздаточный материал
• Лучшее из Интернета
• Содержание

•  НАЗАД
• СЛЕДУЮЩИЙ

Так как же узнать, что две вещи равны? Мы полагаемся в первую очередь на недвижимость, и мы не говорим о недвижимости. Имеются в виду свойства рефлексивности, симметрии и транзитивности. Они играют особую роль в геометрии, поэтому их очень важно помнить.

Рефлексивное свойство утверждает, что A = A . Это что-то глубокое, чувак.

Думайте о рефлексивном свойстве как о гибком свойстве . Возьмем, к примеру, акробата. Он будет акробатом, если будет стоять или сидеть на собственной голове. Неважно, насколько он гибкий; он все равно будет акробатом.

Рефлексивное свойство может показаться очевидным (и это так), но оно все же полезно, особенно при работе с геометрическими фигурами. И это намного проще, чем свернуться в клубок.

Симметричное свойство утверждает, что если A = B , то B = A . (Вы заметили, что это тоже условный оператор?) Это в основном полезно для реорганизации наших выражений на странице, поскольку позволяет нам переворачивать операторы через знак равенства.

Переходное свойство утверждает, что если A = B и B = C , то A = C . Это занимает место там с рефлексивностью в том, как часто это используется в геометрии. Чтобы запомнить это, просто постройте небольшой поезд, который выглядит как A = B = C , и сделайте вывод, что паровоз равен вагону.