сумматор по модулю 2n+1 — патент РФ 2018926
Изобретение относится к вычислительной технике и микроэлектронике и может быть использовано при построении устройств, работающих в системе остаточных классов. Сумматор по модулю 2n+1 содержит (n+1)-разрядный двоичный сумматор, n элементов ЗАПРЕТ и 2n+1 элементов ИСКЛЮЧАЮЩЕЕ ИЛИ. На его входы потупают (n+1)-разрядные приведенные операнды X и Y, значения которых принадлежат множеству { 0, 1 …, 2n}. На выходах формируется (n+1)-разрядный двоичный код результата операции сложения по модулю 2n+1 входных операндов R = X + Y mod (2n+1).. Достоинством сумматора по модулю 2n+1 является высокое быстродействие и простая конструкция. 1 ил.
Рисунок 1
Формула изобретения
СУММАТОР ПО МОДУЛЮ 2n+1, содержащий первый элемент ЗАПРЕТ, отличающийся тем, что содержит элементы ЗАПРЕТ с второго по n-й, 2n + 1 элементов ИСКЛЮЧАЮЩЕЕ ИЛИ и (n + 1)-разрядный двоичный сумматор, i-й (i = 1, 2) вход j-го (j=) разряда которого соединен с j-м разрядом i-го операнда, выход переноса (n + 1)-разрядного двоичного сумматора соединен с первым входом первого элемента ИСКЛЮЧАЮЩЕЕ ИЛИ, второй вход которого соединен с выходом первого элемента ЗАПРЕТ и первым выходом сумматора по модулю 2
Описание изобретения к патенту
Изобретение относится к вычислительной технике и микроэлектронике и может быть использовано при построении устройств, работающих в системе остаточных классов.
Известен сумматор по модулю 2n-1, который содержит в каждом разряде элементы И, ИЛИ, ИЛИ-НЕ, РАВНОЗНАЧНОСТЬ и НЕРАВНОЗНАЧНОСТЬ [1].
Недостатком сумматора является невозможность выполнения сложения по модулю 2n+1.
Наиболее близким по функциональным возможностям и конструкции техническим решением к предлагаемому является сумматор по модулю 2n+1 при n = 2 (сумматор по модулю пять), содержащий пятнадцать элементов И, восемь элементов ИЛИ, три элемента ИЛИ-НЕ, элемент И-НЕ и элемент ЗАПРЕТ [2].
Недостатком известного сумматора по модулю 2n+1 являются низкие функциональные возможности, так как он не выполняет сложение чисел по модулю 2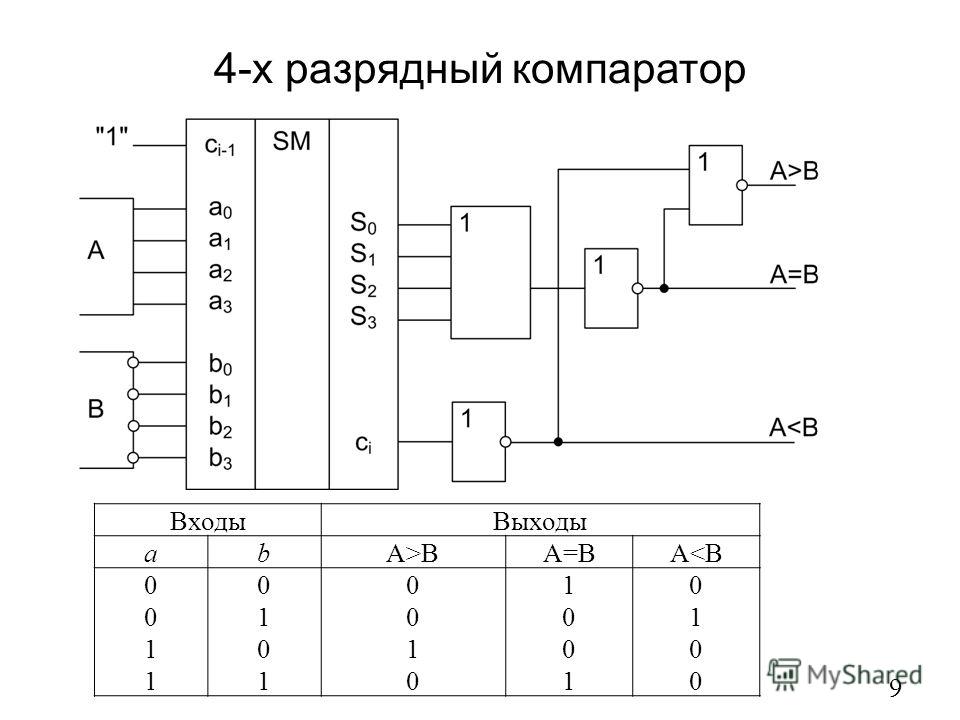
На чертеже представлена схема предлагаемого сумматора по модулю 2n+1 при n = 4.
При n = 4 сумматор по модулю 24 + 1 = =17 содержит пятиразрядный двоичный сумматор 1, n = 4 элементов ЗАПРЕТ 21…24, 2n+1 = 9 элементов ИСКЛЮЧАЮЩЕЕ ИЛИ 31. . .39, n = 5 входов первого операнда 41…45, n = 5 входов второго операнда 51…55, n = 5 выходов 6
В общем случае сумматор по модулю 2n+1 содержит n элементов ЗАПРЕТ, 2n+1 элементов ИСКЛЮЧАЮЩЕЕ ИЛИ и (n+1)-разрядный двоичный сумматор, i-й (i = 1, 2) вход j-го (j= разряда которого соединен с j-м разрядом i-го операнда. Выход переноса (n+1)-разрядного двоичного сумматора соединен с первым входом первого элемента ИСКЛЮЧАЮЩЕЕ ИЛИ, второй вход которого соединен с выходом первого элемента ЗАПРЕТ и первым выходом сумматора по модулю 2n+1. Выход первого элемента ЗАПРЕТ соединен с первым входом (k+1)-го (k= элемента ИСКЛЮЧАЮЩЕЕ ИЛИ, выход которого соединен с (k+1)-м выходом сумматора по модулю 2
Выход первого элемента ЗАПРЕТ соединен с первым входом (k+1)-го (k= элемента ИСКЛЮЧАЮЩЕЕ ИЛИ, выход которого соединен с (k+1)-м выходом сумматора по модулю 2
Сумматор по модулю 2n+1 работает следующим образом.
На входы (n+1)-разрядного двоичного сумматора поступают (n+1)-разрядные операнды X = 2nx1 + 2n-1x2 +.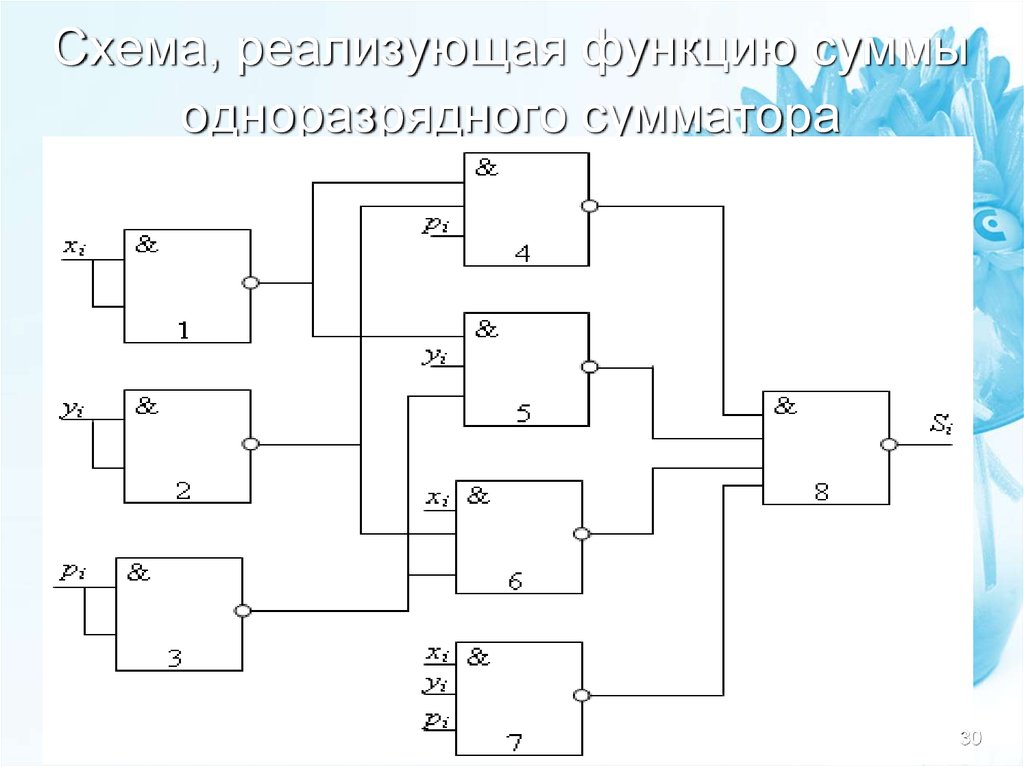 ..+xn+1 и Y = 2ny1 + 2n-1y2+…+Yn+1, значения которых принадлежат множеству {0, 1,…,2}, Xj {0, 1}, Yj {0, 1}, j = . На выходе (n+1)-разрядного двоичного сумматора вычисляется сумма S = X + Y = 2n+1 CR + 2ns1 + 2n-1s2 +…+ sn+1
..+xn+1 и Y = 2ny1 + 2n-1y2+…+Yn+1, значения которых принадлежат множеству {0, 1,…,2}, Xj {0, 1}, Yj {0, 1}, j = . На выходе (n+1)-разрядного двоичного сумматора вычисляется сумма S = X + Y = 2n+1 CR + 2ns1 + 2n-1s2 +…+ sn+1
Двоичные разряды результата операции сложения по модулю 2n+1 входных операндов R = X + Y mod (2n+1) = 2nr1 + 2n-1r2 +…+ rn+1формируются комбинационной схемой из сигнала CR и Sj согласно следующим соотношениям:
(1) где z = r1 CR
Так, при n = 4 на входы 41…45 и 51…55 пятиразрядного двоичного сумматора 1 поступают пятиразрядные операнды X = =16x1 + 8x2 + 4x При этом 0 Х 16, 0 Y16 xt {0, 1}, Yt {0, 1},t=. На выходе двоичного сумматора 1 вычисляется сумма S = X + Y = 32CR + 16s1 + + 8s2 + 4s3 + 2s4 + s5. Причем 0 S 32, CR {0, 1}, st {0, 1},t=.
При этом 0 Х 16, 0 Y16 xt {0, 1}, Yt {0, 1},t=. На выходе двоичного сумматора 1 вычисляется сумма S = X + Y = 32CR + 16s1 + + 8s2 + 4s3 + 2s4 + s5. Причем 0 S 32, CR {0, 1}, st {0, 1},t=.
Как следует из соотношений (1), двоичные разряды результата операции сложения по модулю семнадцать R = X + Y mod 17= = 16r
r1= s1,;
r2= z s2 s;
r3= z s3 s;
r4=z s4 s;
r5= z s5 s1, где z = r1 CR.
Достоинством предлагаемого сумматора по модулю 2n+1 является высокое быстродействие и простая конструкция.
Быстродействие заявляемого сумматора по модулю 2
T = tsм + 3t, где tsм — быстродействие (n+1)-разрядного двоичного сумматора;
t — задержка на вентиль.
Сигнал переноса CR в (n+1)-разрядном двоичном сумматоре может быть сформирован двухвходовым элементом И согласно соотношению CR = x1y1, поскольку X 2n и Y 2n. Кроме того, при использовании инверсного значения первого разряда суммы (n+1)-разрядного двоичного сумматора элементы ЗАПРЕТ могут быть однозначно заменены элементами ИЛИ-НЕ без изменения связей в предлагаемом сумматоре по модулю 2n+1.
Сумматор — Википедия
Возможно, эта статья содержит оригинальное исследование. Добавьте ссылки на источники, в противном случае она может быть выставлена на удаление. |
Сумма́тор в кибернетике — это устройство, преобразующее информационные сигналы (аналоговые или цифровые) в сигнал, эквивалентный сумме этих сигналов[1]; устройство, производящее операцию сложения.
Содержание
- 1 История
- 2 Классификация сумматоров
- 2.1 По способу реализации
- 2.1.1 По принципу действия
- 2.2 По архитектуре
- 2.3 По способу действия
- 2.4 По способу организации переноса[5][6]
- 2.5 По системе счисления
- 2.1 По способу реализации
- 3 Двоичный сумматор
- 3.1 Десятичный сумматор
- 4 Направления развития сумматоров
- 5 См. также
- 6 Примечания
- 7 Литература
- 8 Ссылки
Подробнее см. История компьютера
См. также: История АВМ
- 1623 год и 1624 год — Вильгельм Шиккард в двух письмах Кеплеру описывает считающие часы, в которых одной из трёх главных частей был механический десятичный 6-разрядный сумматор[2].

- 1645 год — Паскаль создал механическую суммирующую машину «Паскалину» с механическим десятичным сумматором.
- 1673 год — Лейбниц создал механический калькулятор, в котором был механический цифровой десятичный сумматор на механическом счётчике.
- 1938 год — в телефонной компании Bell Laboratories создали первый электронный двоичный сумматор, автором идеи был Джордж Штибиц.[3]
Классификация сумматоровПравить
В зависимости от формы представления информации различают сумматоры аналоговые и цифровые[1].
По способу реализацииПравить
- механические.
- электромеханические.
- электронные.
- пневматические.
По принципу действияПравить
- На счётчиках, считающие количества импульсов входного сигналах.
- Функциональные, выдающие на выходах значения логической функции суммы по модулю и логической функции разряда переноса:
- логические, каждый раз вычисляющие функцию разряда суммы по модулю и функцию разряда переноса
- табличные, с таблицами заранее вычисленных значений функции разряда суммы по модулю и значений функции разряда переноса записанных:
- в ПЗУ, ППЗУ (аппаратные) (надёжнее и дешевле логических, так как вместо полупроводников, выполняющих логические вычисления, в ПЗУ используются проводники и изоляторы («прошивки»))[4] или
- в ОЗУ (аппаратные и программные).

Табличные сумматоры впервые были применены в калькуляторах построенных на реле в США до второй мировой войны.
По архитектуреПравить
- Четвертьсумматоры — бинарные (двухоперандные) сумматоры по модулю без разряда переноса, характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма по модулю.
- Полусумматоры — бинарные (двухоперандные) сумматоры по модулю с разрядом переноса, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма по модулю в данном разряде, а на другом — перенос в следующий (старший) разряд.
- Полные сумматоры — тринарные (трёхоперандные) сумматоры по модулю с разрядом переноса, характеризующиеся наличием трёх входов, на которые подаются одноимённые разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма по модулю в данном разряде, а на другом — перенос в следующий (более старший разряд).
 Такие сумматоры изначально ориентированы только на показательные позиционные системы счисления[источник не указан 4413 дней].
Такие сумматоры изначально ориентированы только на показательные позиционные системы счисления[источник не указан 4413 дней]. - Накапливающие сумматоры — снабжённые собственной внутренней памятью.
По способу действияПравить
- Последовательные (одноразрядные), в которых обработка разрядов чисел ведётся поочерёдно, разряд за разрядом, на одном и том же одноразрядном оборудовании.
- Параллельно-последовательные, в которых одновременно параллельно последовательно складываются несколько разрядов пары чисел.
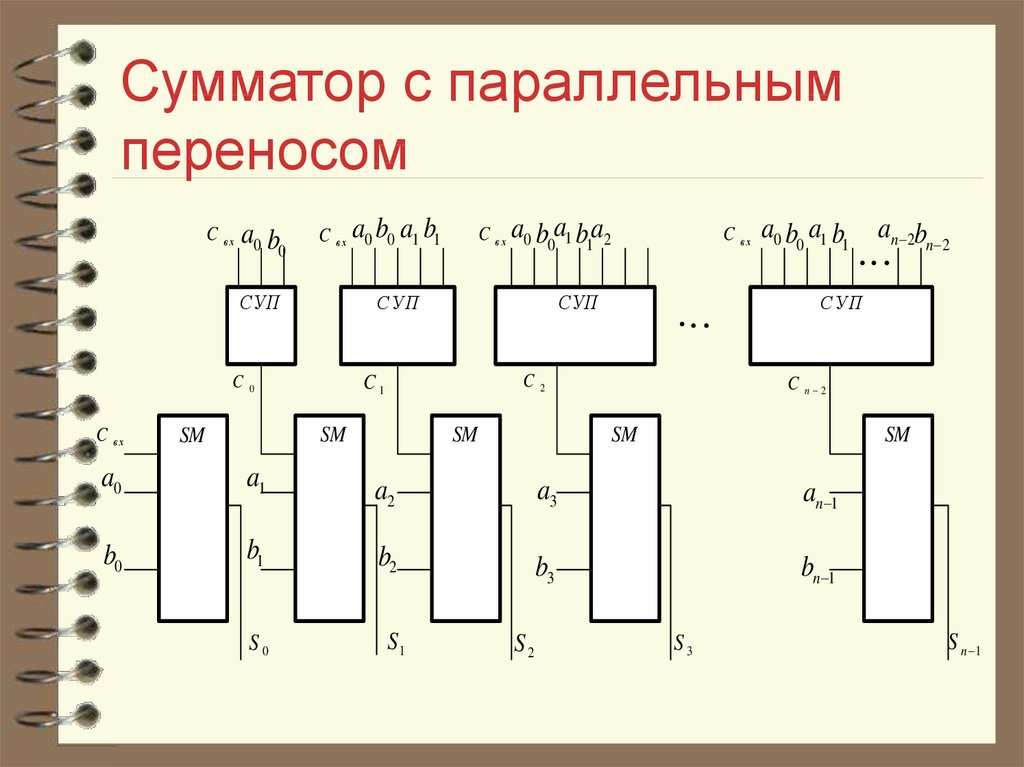
- Параллельные (многоразрядные), в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется своё оборудование.
По способу организации переноса
[5][6]Править- С последовательным переносом (Ripple-carry adder, Схема последовательного переноса).
- С ускоренным групповым переносом (с предвидением переноса) (Carry-lookahead adders, CLA-adders).

- С пропуском переноса (Carry-skip adder)[7].
- Сумматор с условным сложением (Conditional sum adder).
- С переключением переноса (с выбором переноса[8]) (Carry-select adder).
- С сохранением переноса (Carry-save adder).
По системе счисленияПравить
- Двоичные
- Троичные
- Четверичные
- Восьмеричные
- Десятеричные (десятичные)
- Шестнадцатеричные
Двоичный сумматорПравить
Двоичный сумматор может быть описан тремя способами:
- табличным, в виде таблицы истинности,
- аналитическим, в виде формулы (СДНФ),
- графическим, в виде логической схемы.
Так как формулы и схемы могут тождественно преобразовываться, то, одной таблице истинности двоичного сумматора могут соответствовать множества различных логических формул и логических схем. Поэтому, с точки зрения получения результата без учёта затрат времени на вычисление суммы, табличный способ определения двоичного сумматора является основным. Обычное табличное и обычное формульное описание сумматора не учитывают времена задержек в реальных логических элементах и не годятся для определения быстродействия реальных сумматоров.
Обычное табличное и обычное формульное описание сумматора не учитывают времена задержек в реальных логических элементах и не годятся для определения быстродействия реальных сумматоров.
Рис.1. Логическая схема трёхступенчатого двоичного сумматора на двух полусумматорах и логическом элементе 2ИЛИ.
Простейшая схема сумматора на логических элементах «И», «НЕ» и «ИЛИ». Анимация работы логических элементов сумматора.
| x0=A | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| x1=B | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| x2=Pi−1{\displaystyle P_{i-1}} | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | Название действия (функции) | Номер функции |
| Si{\displaystyle S_{i}} | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | Бит суммы по модулю 2 | F3,150 |
| Pi{\displaystyle P_{i}} | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | Бит переноса | F3,232 |
Единица переноса возникает в 4 случаях из 8.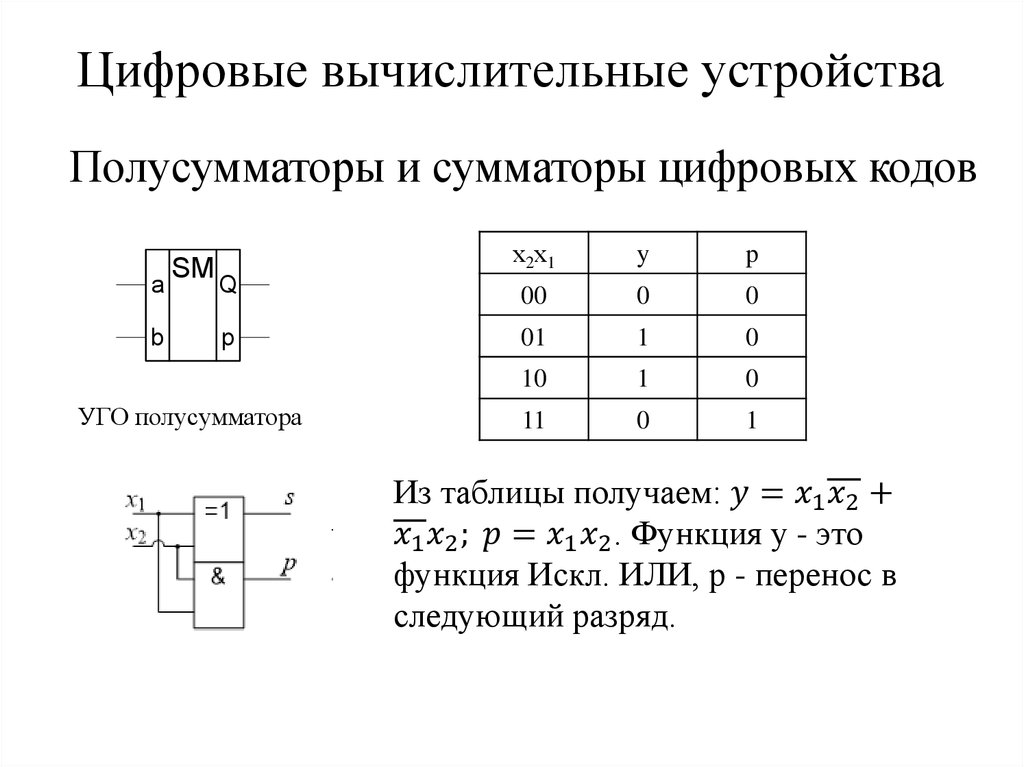
СДНФ суммы по модулю 2:
Si=f(x2,x1,x0)=(x2¯⋅x1¯⋅x0)∨(x2¯⋅x1⋅x0¯)∨(x2⋅x1¯⋅x0¯)∨(x2⋅x1⋅x0){\displaystyle S_{i}=\mathbf {f} (x_{2},x_{1},x_{0})=({\overline {x_{2}}}\cdot {\overline {x_{1}}}\cdot {x_{0}})\vee ({\overline {x_{2}}}\cdot {x_{1}}\cdot {\overline {x_{0}}})\vee ({x_{2}}\cdot {\overline {x_{1}}}\cdot {\overline {x_{0}}})\vee ({x_{2}}\cdot {x_{1}}\cdot {x_{0}})}
СДНФ бита переноса:
Pi=f(x2,x1,x0)=(x2¯⋅x1⋅x0)∨(x2⋅x1¯⋅x0)∨(x2⋅x1⋅x0¯)∨(x2⋅x1⋅x0){\displaystyle P_{i}=\mathbf {f} (x_{2},x_{1},x_{0})=({\overline {x_{2}}}\cdot {x_{1}}\cdot {x_{0}})\vee ({x_{2}}\cdot {\overline {x_{1}}}\cdot {x_{0}})\vee ({x_{2}}\cdot {x_{1}}\cdot {\overline {x_{0}}})\vee ({x_{2}}\cdot {x_{1}}\cdot {x_{0}})}
Схема, которая обеспечивает сложение двух однобитных чисел А и В без получения бита переноса из предыдущего разряда называют полусумматором.
Полусумматор имеет 4 сигнальных линии: два входа для сигналов, представляющих одноразрядные двоичные числа А и В, и два выхода: сумма А и В по модулю 2 (S) и сигнал переноса в следующий разряд (P).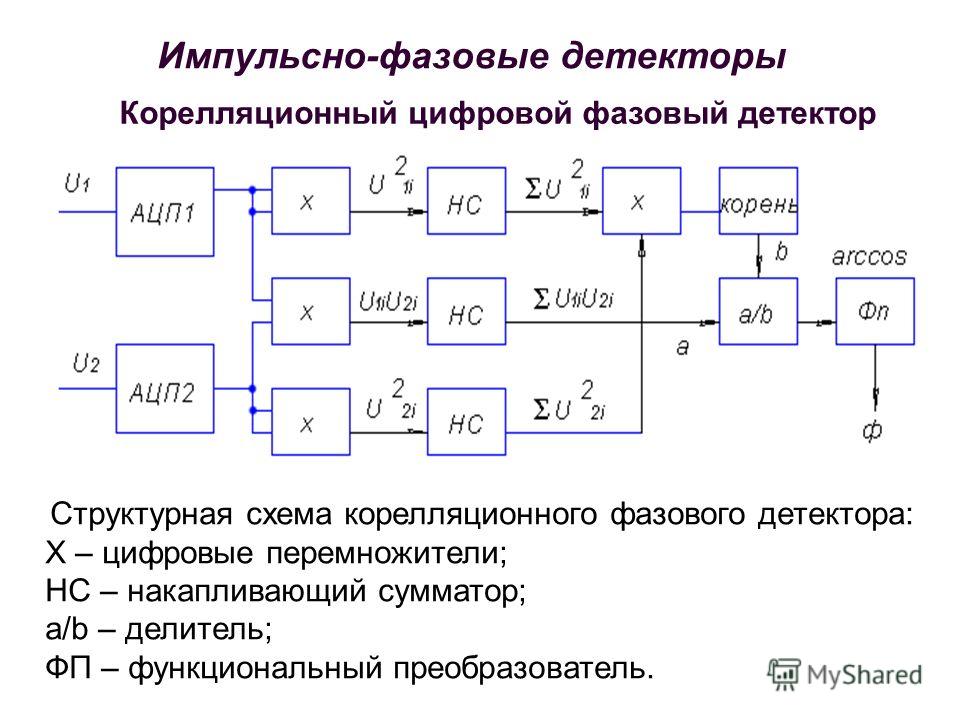 При этом S наименее значимый бит, а P наиболее значимый бит.
При этом S наименее значимый бит, а P наиболее значимый бит.
Объединив два полусумматора и добавив дополнительную схему ИЛИ, можно создать трёхступенчатый полный сумматор с дополнительным входом Pi-1 (на рисунке 1), который принимает сигнал переноса из предыдущей схемы. Первая ступень на полусумматоре осуществляет сложение двух двоичных чисел и вырабатывает первый частный бит переноса, вторая ступень на полусумматоре осуществляет сложение результата первой ступени с третьим двоичным числом и вырабатывает второй частный бит переноса, третья ступень на логическом элементе 2ИЛИ вырабатывает результирующий бит переноса в старший разряд.
Схема полного сумматора может быть использована в качестве «строительных блоков» для построения схем многоразрядных сумматоров, путём добавления одноразрядных полных сумматоров. Для каждой цифры, которую схема должна быть в состоянии обрабатывать, используется один полный сумматор.
В сумматоре на рис.1 время вычисления суммы по модулю 2 равно 2dt, время вычисления переноса равно 3dt, где dt — время задержки в одном типовом логическом элементе.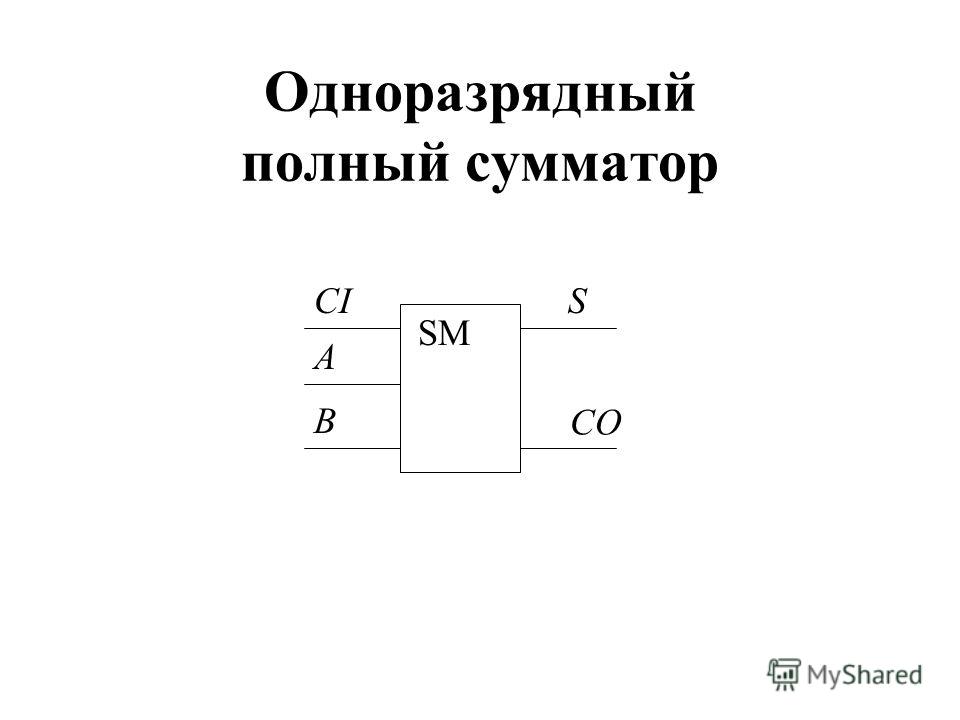 В m-разрядном сумматоре в худшем случае (единицы переноса во всех разрядах) до последнего разряда сигнал переноса проходит через m-1 разряд, а сумма будет готова ещё через 2dt, поэтому максимальное время сложения равно:
В m-разрядном сумматоре в худшем случае (единицы переноса во всех разрядах) до последнего разряда сигнал переноса проходит через m-1 разряд, а сумма будет готова ещё через 2dt, поэтому максимальное время сложения равно:
- 3dt(m−1)+2dt=(3m−1)dt{\displaystyle 3dt(m-1)+2dt=(3m-1)dt} .
Максимальные времена выполнения сложения и вычисления переноса для большего числа разрядов приведены в таблице 1:
Таблица 1.
| число разрядов сумматора | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
|---|---|---|---|---|---|---|---|
| время выполнения сложения, dt | 2 | 5 | 11 | 23 | 47 | 95 | 191 |
| время вычисления переноса, dt | 3 | 6 | 12 | 24 | 48 | 96 | 192 |
Двоичный одноразрядный полный сумматор является полной тринарной (трёхоперандной) двоичной логической функцией с бинарным (двухразрядным) выходом.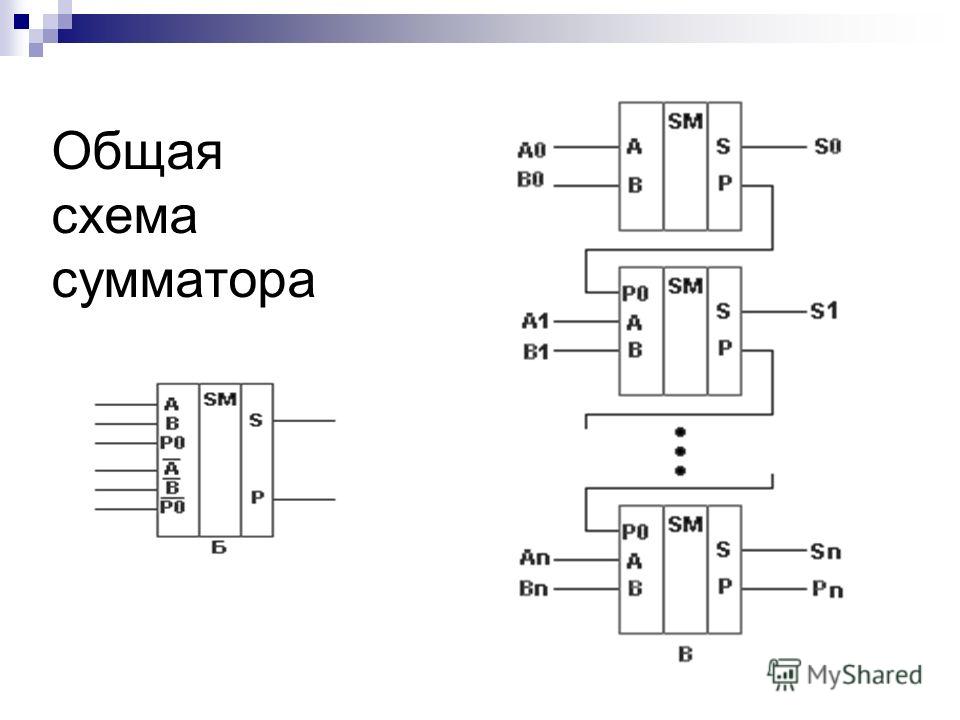 Все три операнда и оба выходных разряда однобитные.
Все три операнда и оба выходных разряда однобитные.
Десятичный сумматорПравить
Десятичный сумматор можно задать в виде двух таблиц:
с нулём в переносе из предыдущего разряда:
| + | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
и с единицей в переносе из предыдущего разряда:
| + | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
или в виде одной таблицы, в которой единица переноса из предыдущего разряда смещает на одну колонку вправо:
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
C соответствующей прошивкой как десятичный сумматор (десятеричный) могут работать шестнадцатеричный сумматор и двадцатисемиричный сумматор-вычитатель на ПЗУ.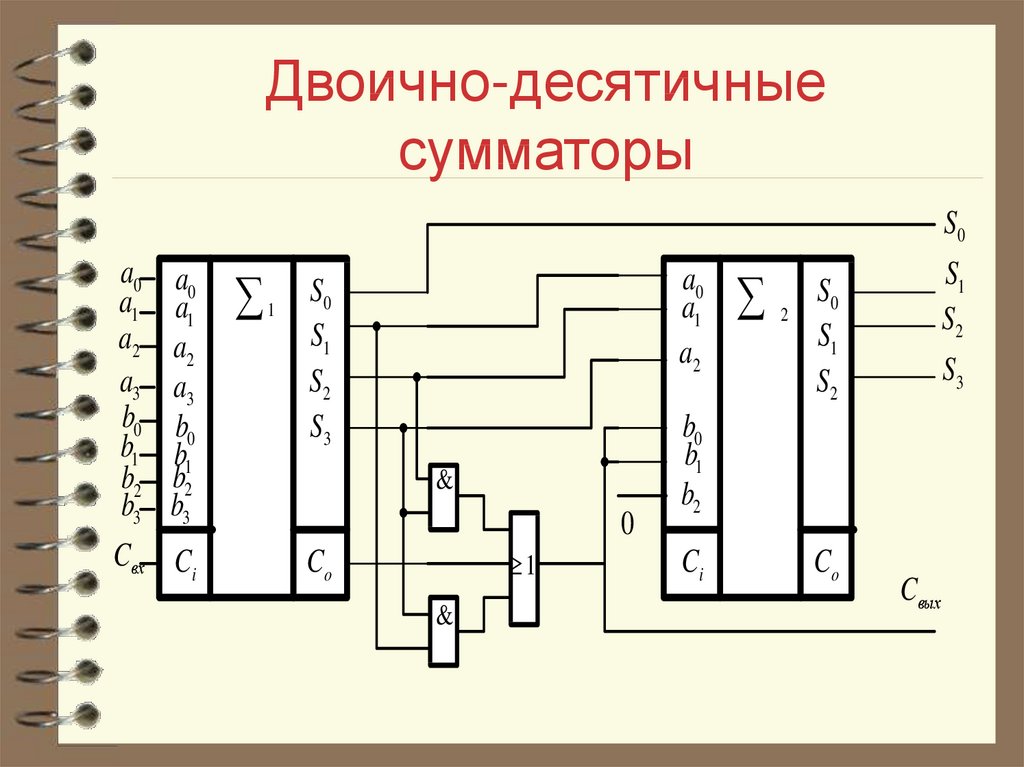
Направления развития сумматоровПравить
Быстродействия параллельных сумматоров вполне достаточно для быстрого сложения небольшого количества чисел фиксированной длины. Так как поразрядное сложение по природе своей последовательно, то при очень большом количестве сложений более выгодно перенастроить то же самое оборудование (АЛУ) для одновременного или не очень одновременного параллельного выполнения нескольких последовательных сложений.
Например, параллельный 64-разрядный двоичный сумматор из 64 двоичных сумматоров со сложными схемами ускоренного переноса сложит 1 пару 64-битных чисел в лучших схемах приблизительно за 5dt, а 32 пары 64-битных чисел приблизительно за 32*5dt=160dt.
32 последовательных двоичных сумматора без схем ускоренного переноса бит за битом сложат 32 пары 64-битных чисел приблизительно за 64*2dt=128dt.
32 последовательных четверичных сумматора без схем ускоренного переноса сложат 32 пары 64-битных чисел приблизительно за (64/lg24)*2dt=64dt.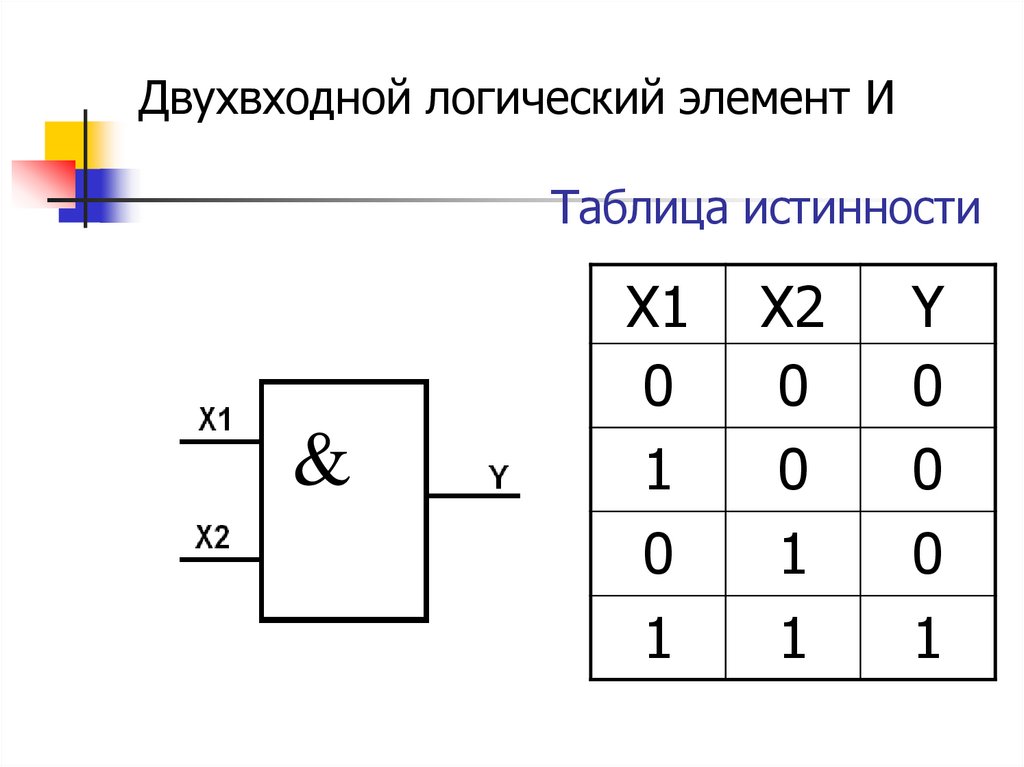
32 последовательных шестнадцатеричных сумматора без схем ускоренного переноса сложат 32 пары 64-битных чисел приблизительно за (64/lg216)*2dt=32dt.
32 последовательных двухсотпятидесятишестиричных сумматора без схем ускоренного переноса сложат 32 пары 64-битных чисел приблизительно за (64/lg2256)*2dt=16dt, т.е. приблизительно в десять раз быстрее, чем параллельный 64-битный сумматор со схемами ускоренного переноса.
32 последовательных четыретысячидевяностошестиричных сумматора без схем ускоренного переноса сложат 32 пары 64-битных чисел приблизительно за (64/lg24096)*2dt=10,67dt.
- Аналоговый сумматор
- Полусумматор
- Дифференциатор
- Алгебра Буля
- Сложение по модулю 2
- Троичная логика
- Вычитатель
- Схема ускоренного переноса
- АЛУ
- ↑ 1 2 Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е.
 — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5.
— Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5. - ↑ Считающие часы Вильгельма Шиккарда
- ↑ Архивированная копия (неопр.). Дата обращения: 7 марта 2011. Архивировано 9 октября 2009 года. Страницы истории. 1938 год
- ↑ Сумматор, 4-битный, полный, параллельногрупповой (табличный), на ПЗУ
- ↑ Hardware algorithms for arithmetic modules
- ↑ Adder Designs
- ↑ 3 Сложение и вычитание двоичных чисел. Двоичные сумматоры. Стр.30. Рис.12.Схема сумматора с пропуском переноса carry-skip adder
- ↑ Таненбаум Э.- Архитектура компьютера. стр.130
- Угрюмов Е. П. Элементы и узлы ЭЦВМ. М.: Высшая школа, 1976. — 232 с.
- Угрюмов Е. П. Цифровая схемотехника. — СПб.: БХВ-Петербург, 2001. — 528 с.
- Жан М. Рабаи, Ананта Чандракасан, Боривож Николич.
 11. Проектирование арифметических блоков: Сумматор // Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-е изд. — М.: Вильямс, 2007. — С. 912. — ISBN 0-13-090996-3.
11. Проектирование арифметических блоков: Сумматор // Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-е изд. — М.: Вильямс, 2007. — С. 912. — ISBN 0-13-090996-3.
- Сумматор — статья из Большой советской энциклопедии.
- Сумматор — статья из Большой советской энциклопедии.
В статье есть список источников, но не хватает сносок. Без сносок сложно определить, из какого источника взято каждое отдельное утверждение. Вы можете улучшить статью, проставив сноски на источники, подтверждающие информацию. Сведения без сносок могут быть удалены. |
арифметика — запутался в XOR и сложении по модулю $2$
спросил
Изменено 1 год, 5 месяцев назад
Просмотрено 32к раз
$\begingroup$
Насколько я понимаю, когда вы что-то выполняете XOR, результатом является сумма двух чисел по модулю $2$.
Почему тогда $4 \oplus 2 = 6$, а не $0$? $4+2=6$, $6%2$ не равно $6$. Должно быть, я что-то упускаю из того, что означает «сложение по модулю 2», но что?
100 // 4
010 // Исключающее ИЛИ против 2
110 = 6 // почему не ноль, если xor = sum mod 2?
- арифметика
$\endgroup$
0
$\begingroup$
Путаница здесь из-за пропущенного слова. Правильное утверждение: «Результат операции XOR двух бит такой же, как и при добавлении этих двух бит mod 2».
Например, $(0+1)\bmod 2 = 1\bmod 2 = 1=(0\text{ XOR }1)$
и
$(1+1) \bmod 2= 2\bmod 2 = 0 = (1\текст{исключающее ИЛИ}1)$
$\endgroup$
$\begingroup$
Исключающее ИЛИ двух однобитных чисел является их суммой по модулю 2.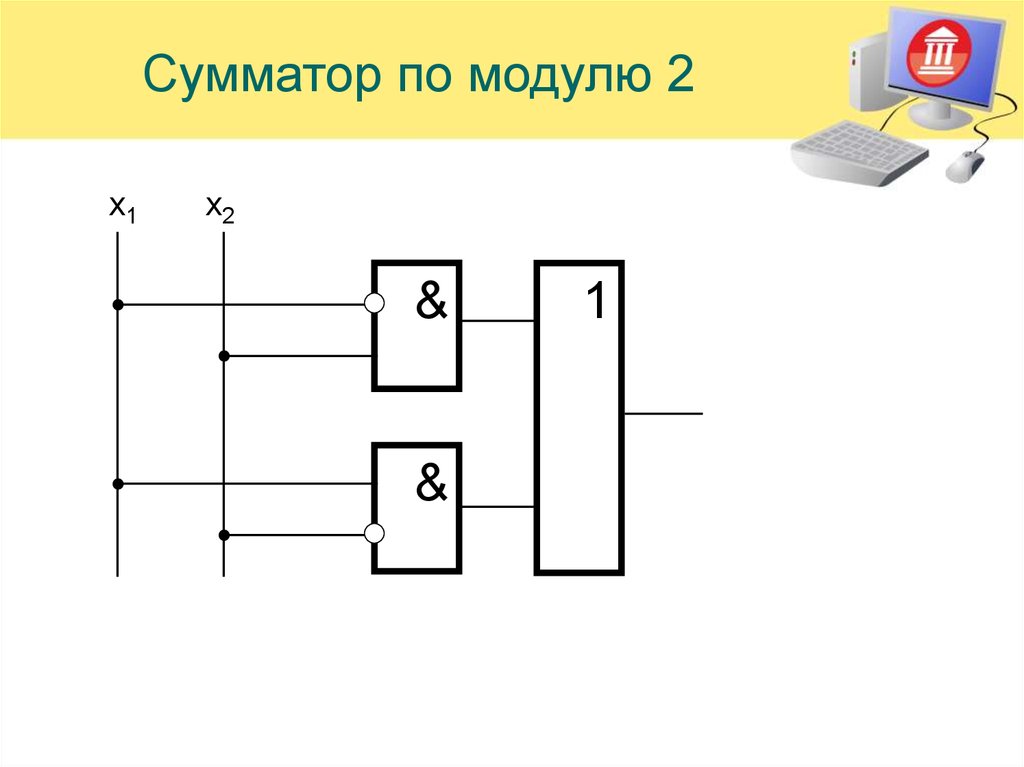 n-1$ включительно.
n-1$ включительно.
$\endgroup$
$\begingroup$
Вы путаете операции над одним битом с операциями над байтом или словом. (Несколько битов) Один бит представляет 0 или 1 в зависимости от его значения. Если вы добавите два бита и проигнорируете перенос, вы добавите «mod2». 0+0 = 0 0+1 = 1 1+0 = 1 1+1 переполняется или переносится, и у вас есть 0
это точно так же, как XOR
Однако это НЕ верно для слов. Рассмотрим откусывание (4 бита) 0110 + 0111 = 6 + 7 = 13 = 1101 0110 xили 0111 = 0001 = 1
$\endgroup$
$\begingroup$
Я думаю, вы неправильно понимаете собственность.
Я считаю, что свойство больше касается логического результата функции XOR, а не числового значения.
Я имею в виду, что каждое «число», которое вы добавляете, на самом деле является просто логическим значением True (1) или False (0), и сложение их вместе по модулю 2 аналогично XOR этих значений.
Эта страница может прояснить это дальше: Магия XOR
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Модуль 2 Принцип действия Сложение по модулю 2, вычитание по модулю 2, умножение по модулю 2, деление по модулю 2
Источник: Интернет
Автор: Пользователь Модуль 2 — это двоичный алгоритм, ядро технологии калибровки CRC, поэтому, прежде чем анализировать алгоритм CRC, мы должны понять правила работы по модулю 2. Так же, как и арифметика, модуль 2 также включает модуль 2 плюс, модуль 2 минус, умножение по модулю 2 и модуль 2 в дополнение к четырем бинарным операциям. Кроме того, операция по модулю 2 также использует тот же оператор, что и арифметический, что означает «+» для деления по модулю 2 плюс, «-» для деления по модулю 2 минус, «X» или «•» Представляет умножение по модулю 2, «÷» или «/». » означает 2 друг от друга. В отличие от арифметики, операция по модулю 2 не учитывает перенос и заимствование , то есть сложение по модулю 2 является двоичным сложением без переноса, вычитание по модулю 2 является операцией двоичного вычитания без заимствования. Таким образом, когда используются фазы двух битов, значения двух битов определяют результат операции, и на них не влияет предыдущая операция, и они не будут затронуты в следующий раз.
Таким образом, когда используются фазы двух битов, значения двух битов определяют результат операции, и на них не влияет предыдущая операция, и они не будут затронуты в следующий раз.
① Операция сложения по модулю 2 определяется как:
0+0=0 0+1=1 1+0=1 < Span class= "Apple-converted-space" > 1+1=0
Например, 0101+0011= 0110, расчет столбца по вертикали:
0 1 0 1
+0 0 1 1
тая iníbeedside =0 0-1=1 1- 0=1 1-1=0
Например, 0110-0011=0101, расчет по вертикали столбца:
0 1 1 0
-0 0 1 1
тая ─Find
0x0=00×1=0 1×0=0 1×1=< Span lang= "en-US" >1
Многобитное двоичное умножение по модулю 2 аналогично многобитовому двоичному умножению в общем смысле, где разница в добавлении переноса, когда последний накапливает промежуточные результаты (или частичный продукт), и по модулю 2 метод обработки промежуточных результатов с использованием сложения по модулю 2. Например, 1011×101=100111, вычисление столбца по вертикали:
Например, 1011×101=100111, вычисление столбца по вертикали:
&NBSP;&NBSP;&NBSP; 1 0 1 1
x 1 0 1
─дии добья
1 0 1 1
0 0 0
1 0 1 0 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1000. 1
────────
1 0 0 1 1 1
④ операция деления по модулю 2 определяется как: деление также похоже на многобитное двоичное деление в общем смысле, но в них используются разные правила определения частного в задаче. Последнее в соответствии с двоичным вычитанием с заимствованием, в соответствии с остатком вычитания числа, достаточно, чтобы определить, является ли частное 1 или 0, если достаточно, чтобы уменьшить 1, в противном случае дело 0. Многобитный режим 2 использует деление по модулю 2 вычитания без заимствования двоичного вычитания, поэтому нет смысла рассматривать, достаточно ли остатка для вычитания числа. На самом деле, в операции CRC всегда гарантируйте, что первый делитель равен 1, тогда частное деления по модулю 2 является первой и первой цифрой остатка результата операции деления по модулю 2 OK < Span lang= "en- нас".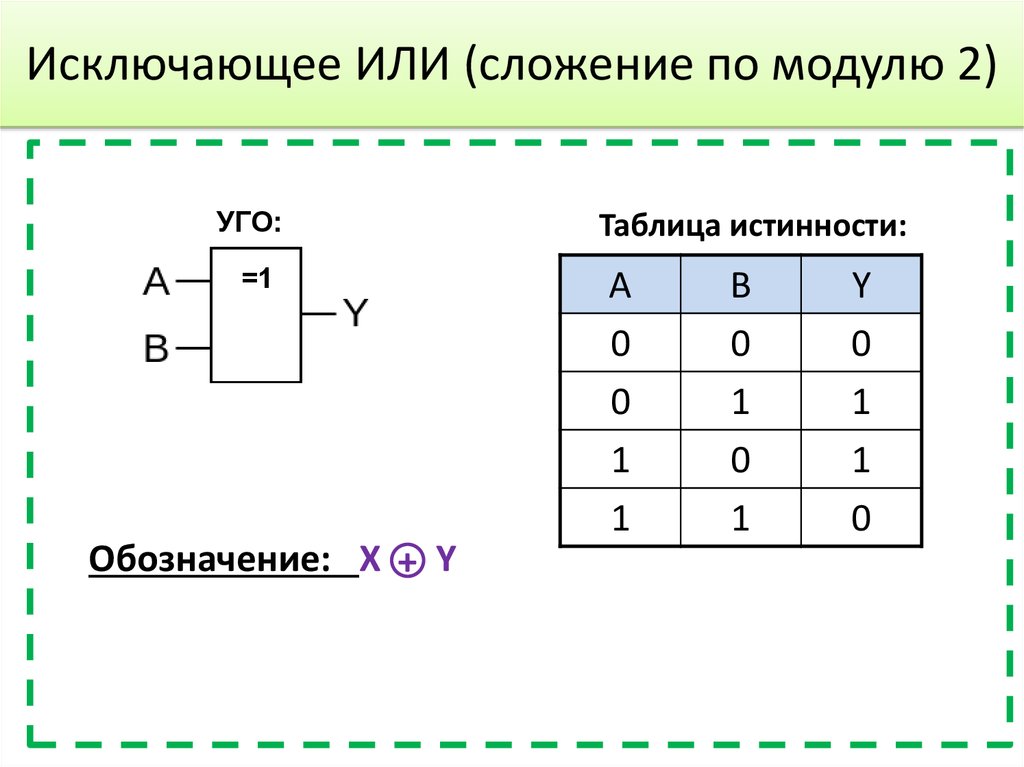


 (5 ноября 2016)
(5 ноября 2016)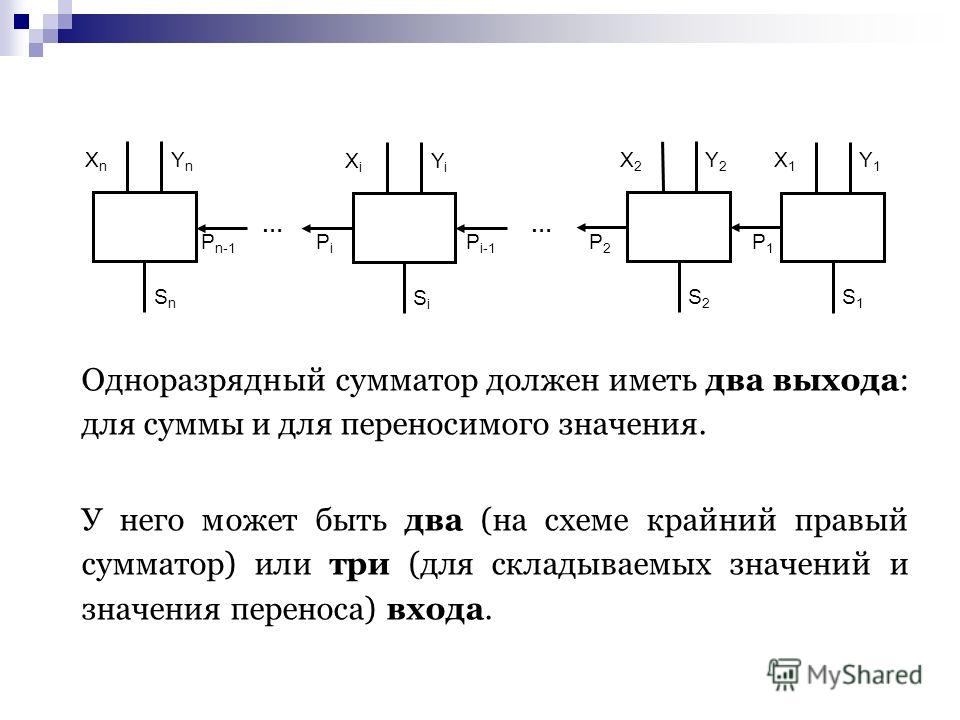

 Такие сумматоры изначально ориентированы только на показательные позиционные системы счисления[источник не указан 4413 дней].
Такие сумматоры изначально ориентированы только на показательные позиционные системы счисления[источник не указан 4413 дней].
 — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5.
— Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5. 11. Проектирование арифметических блоков: Сумматор // Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-е изд. — М.: Вильямс, 2007. — С. 912. — ISBN 0-13-090996-3.
11. Проектирование арифметических блоков: Сумматор // Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-е изд. — М.: Вильямс, 2007. — С. 912. — ISBN 0-13-090996-3.