Сумматор на ОУ — Типы, виды, описание работы

Что такое сумматор

В общем смысле слова, сумматор — это какое-либо устройство, которое что-либо суммирует и выдает на выходе сумму этих воздействий. Сумматор можно представить в виде какого-либо неизвестного нам ящика, на который поступает входные воздействия и на выходе такого ящика выдается их сумма.

В электронике сумматоры делятся на две группы:

• сумматоры аналоговых сигналов
• сумматоры цифровых сигналов

В этой статье мы будем разбирать аналоговые сумматоры.

Аналоговый сумматор

Думаю, все из вас помнят осциллограмму постоянного напряжения

Если, допустим, цена нашего квадратика 1 В, то на данной картинке мы видим постоянное напряжение амплитудой в 1 В. Суммировать постоянное напряжение — одно удовольствие. Для этого достаточно сложить амплитуды этих сигналов в любой момент времени.

На рисунке ниже мы видим два сигнала A и B и сумму этих сигналов: A+B. Если сигнал A = 2 В, сигнал B = 1 В, то сумма этих сигналов составит 3 В.

Все то же самое касается и сигналов с отрицательной полярностью

Как вы видите, при сложении сигналов с равной амплитудой, но разной полярности, мы в сумме получаем 0. То есть эти два сигнала взаимно себя скомпенсировали: 1 +(-1)=0. Все становится намного веселее, если мы начинаем складывать сигналы, которые меняются во времени, то есть переменные сигналы. Они могут быть как периодические, так и непериодические. 

Давайте для начала рассмотрим самый простой пример. Пусть у нас будут два синусоидальных сигнала с одинаковыми амплитудами, частотами и фазами. Подадим их на сумматор. Что получится в итоге?

Получим синусоиду с амплитудой в два раза больше. Как вообще она получилась? Вычисления производятся довольно просто. Каждая точка синусоиды A+B  — это сложение точек в одинаковый момент времени синусоид А и B. Для наглядности мы взяли 3 точки: t₁ , t₂  и t₃ .

Как вы видите, в момент времени t₁ у нас амплитуда сигнала А была равна 1 В, амплитуда сигнала В тоже 1 В. В сумме их результат в момент времени t₁ будет равен 2 В, что мы и видим на сигнале A+B. В момент времени t₂ амплитуда сигнала A была 0 В, амплитуда сигнала В тоже 0 В. Как нетрудно догадаться, 0+0=0, что мы и видим на сигнале A+B в момент времени t₂ . Ну а в момент времени t₃ амплитуда сигнала А = -1 В, амплитуда сигнала В = -1 В, в результате их сумма -1+(-1) = — 2 В, что мы как раз и видим на синусоиде А+B в момент времени t₃ . Отсюда напрашивается вывод: для сложения сигналов надо суммировать амплитуды сигналов в одинаковые моменты времени.

А давайте сместим фазу одного из сигналов на 180 градусов, относительно другого, но при этом амплитуды и частоты сигналов оставим без изменения. Про такие сигналы говорят, что они находятся в противофазе. Как думаете, чему будет равняться их сумма? Долго не думая, смещаем второй сигнал на 180 градусов и суммируем их амплитуды в каждый момент времени.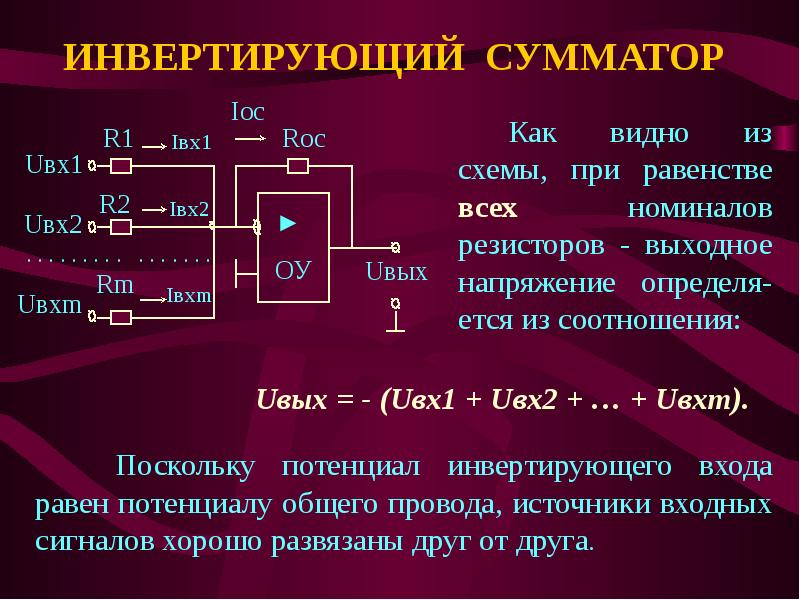 Нетрудно догадаться, что их сумма будет равняться нулю, что мы и видим на рисунке ниже.

Сложение двух сигналов в программном симуляторе

Но что, если нам надо сложить в теории два каких-нибудь два сложных сигнала с разными фазами, амплитудами, частотами? Здесь проще всего прибегнуть как различным симуляторам. Один из них — это Proteus. С помощью него я могу сложить два любых сигнала и посмотреть их сумму. Для этого выбираю синусоидальный генератор

потом виртуальный осциллограф

Собираю схему

Щелкаю два раза на генератор и задаю его параметры

Давайте сложим два наших синусоидальных сигнала с одинаковыми амплитудами, фазами и частотами, как во втором примере

Прописываем амплитуду и частоту каждого сигнала, остальное ничего не трогаем. Потом нажимаем «пуск»

Потом нажимаем правой кнопкой мыши на наш виртуальный осциллограф и нажимаем Digital Oscilloscope

Сигнал с канала B я немного сдвинул вниз, иначе он совпадает с сигналом А.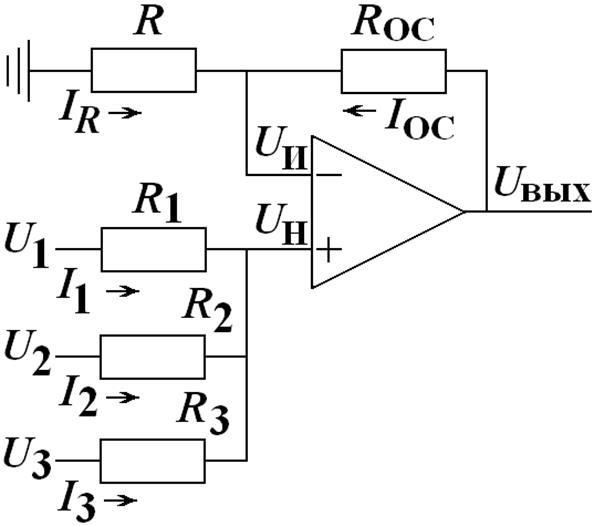 Оно и неудивительно, так как это два идентичных сигнала.

Для того, чтобы найти их сумму, нам достаточно нажать на кнопку A+B

Получаем сумму двух сигналов

В таком виртуальном осциллографе можно складывать любые два сигнала.

Давайте сложим два таких сигнала

Нажимаем A+B и получаем вот такую сумму сигналов

А давайте сдвинем синусоидальный сигнал на 90 градусов по фазе. Имеем

В результате сумма сигналов будет

На моем реальном цифровом осциллографе тоже имеется такая функция

Здесь на примере ниже я суммирую два сигнала: синусоидальный и прямоугольный.  Зеленая осциллограмма — это сумма двух этих сигналов.

Сумматор на ОУ

Инвертирующий сумматор

Как мы уже говорили еще в начале статьи: сумматор — это схема, которая суммирует два и более сигналов. Базовая схема сумматора на ОУ выглядит вот так:

Как и у инвертирующего усилителя, в схеме есть одна особенность. В точке E, где соединяются резисторы, находится потенциал виртуальной земли, о котором мы говорили еще в прошлой статье. Еще эту точку называют точкой суммирования сигналов.

Поэтому, сколько бы мы входных сигналов не подавали на такой сумматор, они не будут влиять друг на друга.

Не будем здесь делать сложные математические выкладки, а просто предоставим вам готовую формулу расчета выходного напряжения U_вых .

Как не трудно догадаться, для сложения двух сигналов

Формула примет вот такой вид:

Откуда в формуле знак «минус»? Так как эта схема сумматора построена на схеме инвертирующего усилителя, то на выходе будет сигнал со знаком «минус».

Как можно просто сложить два сигнала без всякого усиления?

Как вы заметили, выходное напряжение будет со знаком «минус». Добавив после такого сумматора инвертирующий усилитель на ОУ с  R₃ = R₄ , можно добиться того, что у нас на выходе сигнал будет без знака «минус».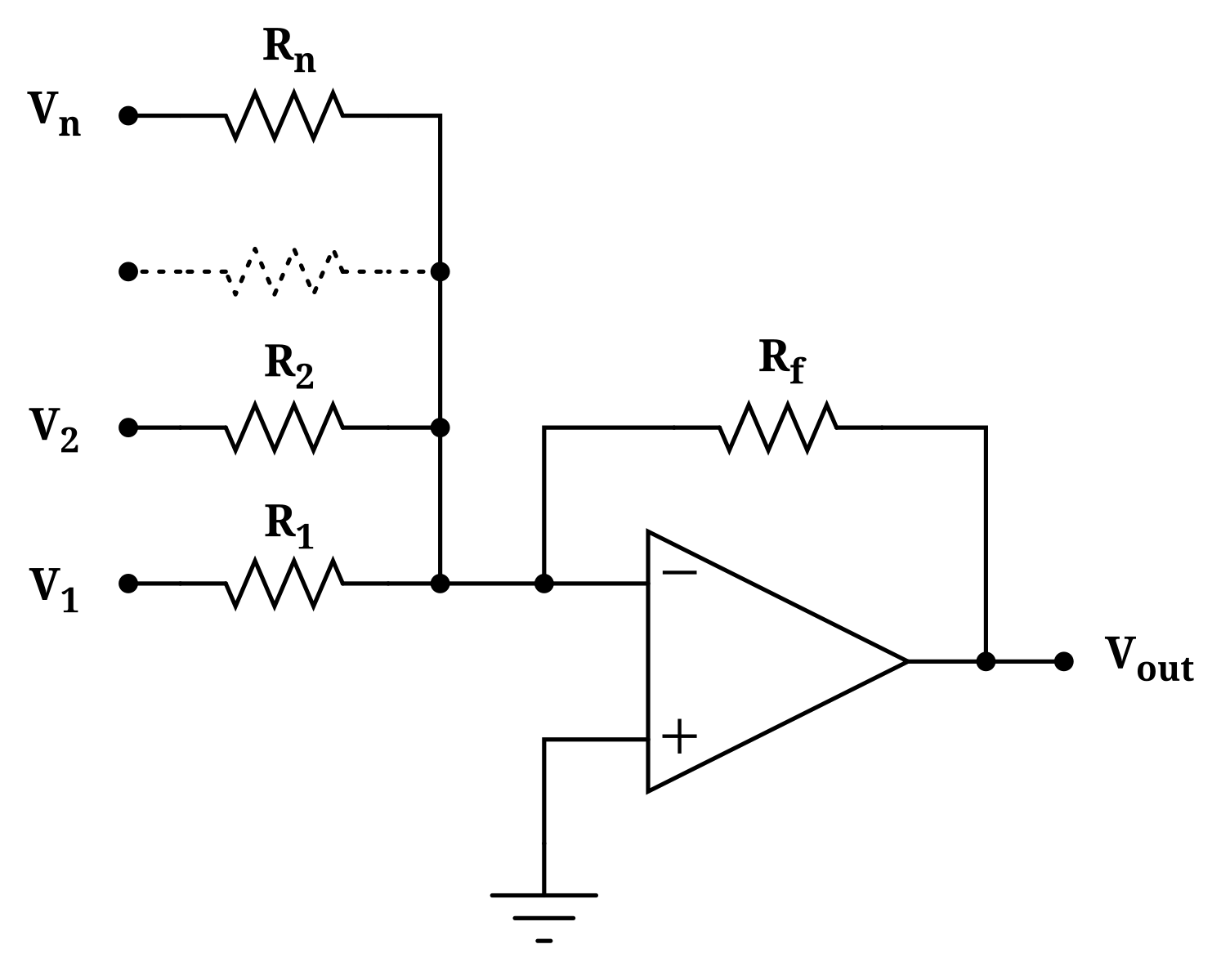 То есть мы получим неинвертирующий сумматор.

 

Неинвертирующий сумматор

Базовая схема будет выглядеть вот так:

Формулы для расчета

 

Поэтому, сумматор для двух сигналов будет выглядеть вот так:

Если взять R₅ = R₂ = R_3, то у нас будет простой сумматор с единичным коэффициентом усиления, который на выходе даст просто сумму двух входных сигналов. 

где

Причем должно выполняться условие:

то есть в нашем случае отношение этих резисторов должно равняться 2.

Компенсационный резистор в схеме сумматора

Для борьбы с током смещения, в схему также добавляется компенсационный резистор.

Для схемы с двумя входными сигналами он вычисляется по простой формуле

Если входов больше, то его значение вычисляется по формуле

Как работает сумматор на ОУ на примере

Симуляция работы инвертирующего сумматора

Давайте рассмотрим работу нашего сумматора на ОУ в симуляторе Proteus.

На вход такого сумматора будет подавать синусоидальные сигналы с амплитудой в 1 В, но с разной частотой. На in1 у нас будет сигнал с частотой в 50 Гц, на in2 сигнал с частотой в 100 Гц и на in3 сигнал с частотой в 150 Гц. Как вы видите, все 3 резистора после сигналов имеют одинаковый номинал в 1 кОм для удобства расчета коэффициента усиления. То есть все сигналы будут усиливаться одинаково. Резистор R2 имеем номинал в 2 кОм. Это значит, что коэффициент усиления на выходе будет равен 2. То есть сумма сигналов будет помножена на коэффициент 2 и инвертирована.

Итак, для того, чтобы посмотреть сигналы как на экране осциллографа, можно также воспользоваться инструментом аналоговым анализатором

на рабочем поле появится окно Analogue Analysis

Для того, чтобы анализировать входы, просто переносим в наше окошко входы in1, in2, in3 и выход out, удерживая левую кнопку мыши

В результате увидим это

Разворачиваем окно

Потом нажимаем пробел и в большом окне уже видим все наши сигналы: и входные, и выходной. (нажмите на картинку, откроется в новом окне)

черная осциллограмма — это и есть сумма всех трех синусоид усиленная в 2 раза, но со знаком «минус».

В чистом виде на выходе ОУ у нас будет только черная осциллограмма. Она является суммой всех входных сигналов, помноженная на 2, но со знаком «минус».

Работа неинвертирующего сумматора

Итак, давайте соберем простой нормальный сумматор для, который бы просто складывал сигналы и на выходе выдавал нормальный неинвертированный сигнал. Для того, чтобы создать такой сумматор, наш коэффициент усиления должен быть равен единице, а на выходе мы должны инвертировать такой сигнал. Настало время использовать схему для неинвертирующего сумматора

Итак, все что мы хотим — это просто сложить три сигнала и посмотреть их сумму. И все! Не надо ничего усиливать и инвертировать. Поэтому, наша схема будет выглядеть вот так:

В этой схеме первый каскад на ОУ суммирует входные сигналы, а второй каскад просто инвертирует получившийся сигнал. В каждом усилителе коэффициент передачи равен 1, поэтому, никакого усиления сигнала в данной схеме не происходит.

Итак, осциллограмма со всеми сигналами

Если оставить на экране только осциллограмму выходного сигнала

Тот же самый эффект мы можем получить и с помощью схемы на одном ОУ, о которой я упоминал выше:

 

Давайте на его входы подадим два одинаковых синусоидальных сигнала, но в противофазе. То есть мы должны получить что-то типа этого

Проверяем симуляцию и видим, что сумма двух одинаковых сигналов в противофазе действительно равняется нулю

АЧХ и ФЧХ сумматора

Все вы помните, что реальный ОУ — это не идеальный радиоэлемент. С ростом частоты его усилительные свойства начинают падать. Для того, чтобы рассмотреть, как ведет себя сумматор на ОУ, давайте построим виртуальную АЧХ для математической модели ОУ LM358, который мы задействуем в схеме сумматора. На два входа мы будем подавать сигнал с одного и то же генератора.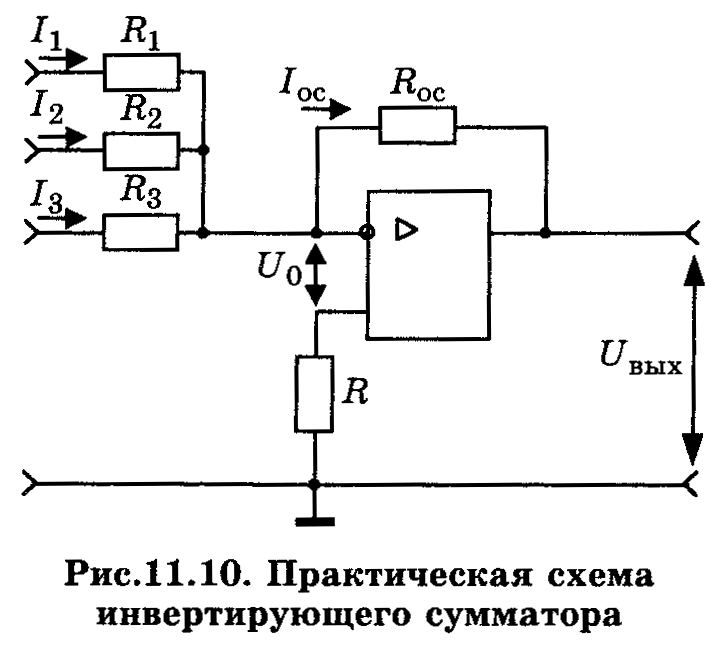 То есть в данном случае у нас на входы подаются два абсолютно идентичных сигнала.

Как можно увидеть на виртуальном графике АЧХ, полоса пропускания такого сумматора на уровне в -3 дБ от максимального уровня сигнала составляет 347 кГц.

Частота единичного усиления уже будет равняться 600 кГц

Если рассмотреть ФЧХ, то можно также заметить, что после 10 кГц начинает меняться фаза сигнала

Поэтому, при разработке всегда учитывайте неидеальность характеристик ОУ, которые также можно посмотреть в даташите.

Сравнение неинвертирующих сумматоров

Давайте сравним схему неинвертирующего сумматора на двух ОУ

и неинвертирующего сумматора на одном ОУ

Для более удобной симуляции мы на них будем подавать и суммировать один и тот же сигнал синусоидальный сигнал

Давайте рассмотрим, что же случится с выходным сигналами на ФЧХ. Как можно увидеть, сигнал  неинвертирующего сумматора с двумя ОУ будет запаздывать по фазе больше, чем с одним ОУ.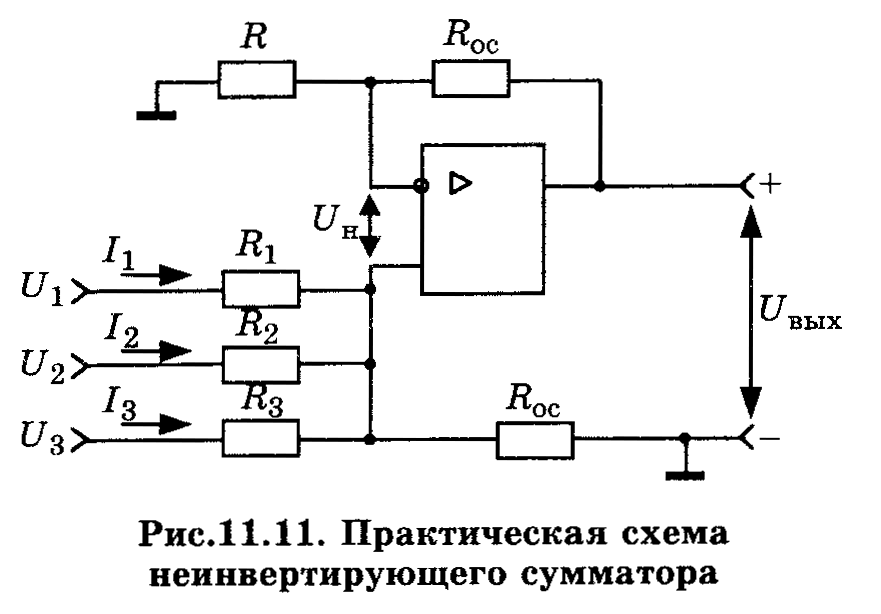 Это объясняется тем, что каждый ОУ вносит небольшую задержку.

Плюсы и минусы инвертирующего и неинвертирующего сумматора

Не забывайте, что инвертирующий сумматор на выходе будет давать сумму сигналов со знаком «минус», умноженных на коэффициент усиления. Неинвертирующий сумматор выдаст на выходе просто сумму сигналов умноженных на коэффициент усиления. Также инвертирующий сумматор проще построить и рассчитать. Если вы создаете какой-либо микшер на основе сумматора, то для человеческого уха нет никакой разницы, инвертируемый сигнал на выходе или нет. Поэтому, в этом случае будет проще применить инвертирующий сумматор.

Применение аналогового сумматора

В настоящее время аналоговый сумматор используется в схемах, где надо суммировать два и более аналоговых сигналов. Это могут быть микшеры звукового диапазона, где надо объединить выходные сигналы от микрофонов, а также от устройств, которые создают различные спецэффекты и которые потом можно добавить к основной звуковой дорожке. Вся прелесть микшеров на ОУ заключается в том, что входные сигналы никак не влияют друг на друга. А также это могут быть схемы операционной обработки сигналов для выполнения арифметической обработки сигналов (сложение/вычитание).

при участии JEER

Рекомендую посмотреть классное видео про сумматор:

26. Схема сумматора на оу.

К суммирующим схемам относятся сумматоры и схемы вычитания. Эти схемы используются для решения алгебраических уравнений и в устройствах аналоговой обработки сигналов. Сумматором называется устройство, на выходе которого сигналы, подаваемые на его входы, суммируются. Сумматоры строятся с использованием инвертирующих и неинвертирующих усилителей.

Инвертирующий сумматор

С хема инвертирующего сумматора с тремя входными сигналами приведена на рис.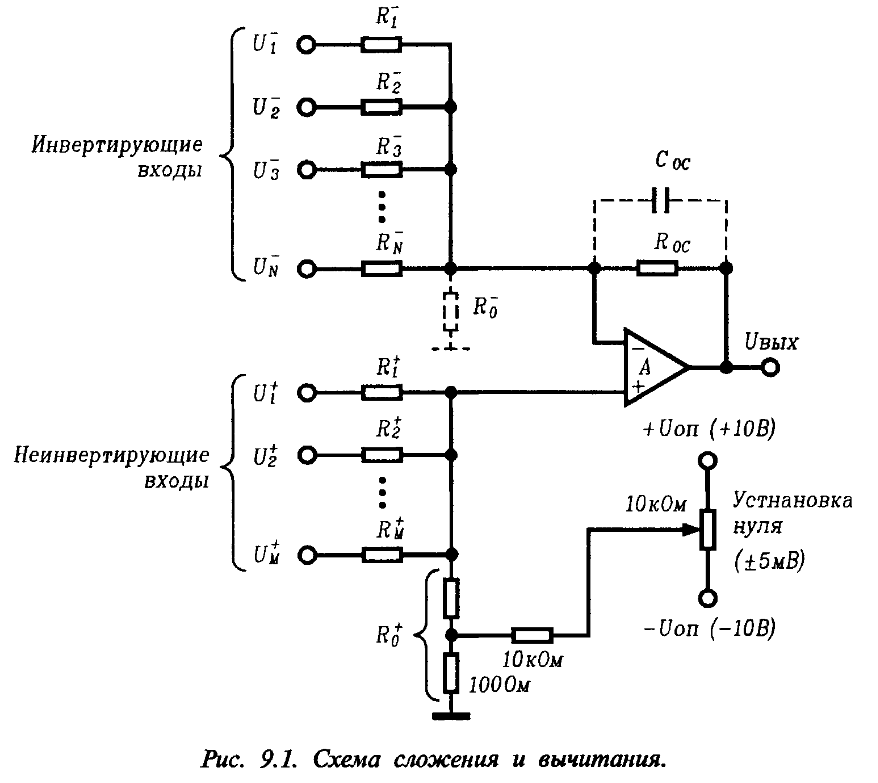 11.10. Для простоты рассуждений принимаем, что R1=R2=R3=Roc.

П оскольку у идеального ОУ K_U→∞, Rвx →∞, а ток смещения очень мал по сравнению с током обратной связи, то согласно закона Кирхгофа I1+I2+I3=Iос. (11.19) Вследствие того, что инвертирующий вход имеет практически нулевой потенциал, то в нем отсутствует взаимное влияние входных сигналов. Выражение (11.19) может быть представлено в виде Следовательно на выходе получается инвертированная сумма входных напряжений. Если R1≠R2≠R3, то на выходе получается инвертированная сумма входных напряжений (11.20) с различными масштабными коэффициентами. Инвертирующий сумматор объединяет в себе функции сумматора и усилителя при сохранении простоты схемы. Резистор R служит для компенсации сдвига нуля на выходе ОУ, вызванного временными и температурными колебаниями входного тока. Сопротивление R выбирают токай величины, чтобы эквивалентные сопротивления, подключенные ко входам ОУ были одинаковы: R=Roc ||R1||R2||R3 .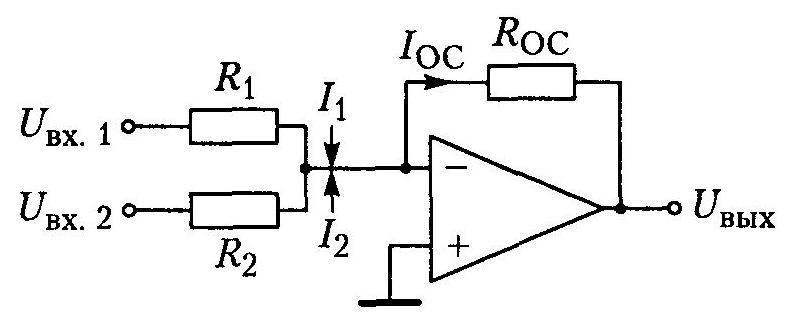

Неинвертирующий сумматор

Схема неинвертирующего сумматора, который строится на базе неинвертирующего усилителя, приведена на рис. 11.11. Так как при U0=0 напряжения на инвертирующем и неинвертиющем входах равны, то

Учитывая, что RвxОУ по неинвертирующему входу очень велико, то входной ток равен 0. Согласно закона Кирхгофа можно записать

Если же в схеме (рис. 11.11) еще подаются сигналы на инвертирующие входы, то схема выполняет операцию сложения- вычитания. Для правильной работы сумматора необходимо сбалансировать инвертирующий и неинвертирующий коэффициент усиления, т.е. обеспечить равенство сумм коэффициентов усиления инвертирующей и неинвертирующей частей схемы.

Дифференцирующий усилитель (дифференциатор) предназначен для получения входного сигнала пропорционального скорости изменения входного. При дифференцировании сигнала ОУ должен пропускать только переменную составляющую входного напряжения, а коэффициент усиления дифференцирующего звена должен возрастать при увеличении скорости изменения входного напряжения. Схема дифференциатора, на входе которого включен конденсатор С, а в цепи ОС – резистор, представлена на рис. 11.13. Полагая, что ОУ идеальный, ток через резистор обратной связи можно считать равным току через конденсатор Iс+Ir=0,

, тогда

Рассмотренный дифференциатор используется редко из-за следующих недостатков:

1. Низкого входного сопротивления на высоких частотах, определяемого емкостью С;

2. Относительно высокого уровня шумов на выходе обусловленного большим усилением на высоких частотах;

3 . Склонности к самовозбуждению. (данная схема может быть неустойчивой в области частот, где частотная характеристика дифференциатора (кривая 1 на рис .11.14), имеющая подъем 20 дБ/дек, пересекается с АЧХ скорректированного ОУ, имеющего спад −20дБ/ дек (кривая 2 на рис. 11.14). Амплитудно-частотная характеристика разомкнутой системы в некоторой части частотного диапазона имеет

спад –40 дБ/дек, который определяется разностью наклона кривых 1 и 2, а фазовый сдвиг ϕ = –180°, что и указывает на возможность самовозбуждения. )

Чтобы избежать проявления этих недостатков дифференциатора принимаются следующие схемотехнические решения:

1. Резистор обратной связи шунтируется конденсатором, ёмкость которого выбирается такой, чтобы участок АЧХ ОУ со спадом -20 дБ/дек начинался на частоте более высокой, чем максимальная частота полезного дифференциального сигнала. Это приводит к уменьшению высокочастотных составляющих шума в выходном сигнале. Такой участок начинается на частоте f=1/(2πRocCoc).

2. Последовательно со входным конденсатором С включается резистор, который ограничивает коэффициент усиления на высоких частотах дифференциатора. Это обеспечивает динамическую устойчивость и снижает входной ёмкостной ток от источника сигнала.

3. Использование ОУ с низким напряжением смещения и малыми входными токами, а также конденсаторов с малыми токами утечек и малошумящих резисторов.

Практическая схема дифференциатора и его АЧХ приведены на

рис. 11.15. Введение резистора R приводит к появлению на частотной характеристике (кривая 1 на рис.

11.15,б) горизонтального участка, где не происходит дифференцирования на частотах, превышающих частоту

Инвертирующий и неинвертирующий суммирующий усилитель

В этом уроке мы узнаем о суммирующем усилителе, его конфигурациях, типах суммирующих усилителей (инвертирующих и неинвертирующих) и некоторых областях применения суммирующего усилителя.

Одним из важных применений операционного усилителя является суммирующий усилитель, также известный как сумматор. Как следует из названия, суммирующий усилитель представляет собой схему на основе операционного усилителя, в которой суммируются несколько входных сигналов разного напряжения.

Для получения информации об основах операционных усилителей см. Основы операционных усилителей.

Описание

Введение

Многие приложения в электронных схемах требуют добавления или объединения двух или более аналоговых сигналов в один сигнал. Одним из лучших примеров таких требований являются приложения для записи музыки и вещания. В случае типичной настройки записи музыки у нее есть несколько входов от нескольких микрофонов, а выход — стерео (левый и правый).

Здесь пригодится суммирующий усилитель, так как он объединяет несколько входов в один общий сигнал без шума и помех. По этой причине суммирующий усилитель также называют сумматором напряжения, поскольку его выход представляет собой сложение напряжений, присутствующих на его входной клемме.

Инвертирующий суммирующий усилитель

Наиболее часто используемый суммирующий усилитель представляет собой расширенную версию конфигурации инвертирующего усилителя, т. е. несколько входов подаются на инвертирующий вход операционного усилителя, а неинвертирующий вход подключается к земле. Из-за этой конфигурации выход схемы сумматора напряжения не совпадает по фазе на 180 ^или  относительно входа.

Общая конструкция суммирующего усилителя показана на следующей схеме. Обычная схема инвертирующего усилителя имеет только одно напряжение/вход на инвертирующем входе.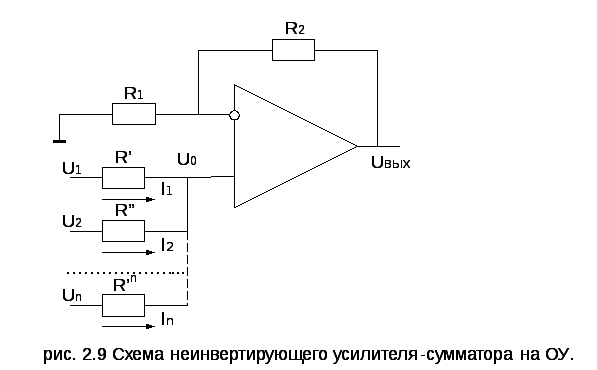 Если к инвертирующему входу подключено больше входных напряжений, как показано, результирующий выход будет суммой всех приложенных входных напряжений, но инвертированных.

Прежде чем анализировать приведенную выше схему, давайте обсудим важный момент в этой установке: концепцию виртуального заземления. Поскольку неинвертирующий вход вышеуказанной схемы подключен к земле, инвертирующий вход операционного усилителя находится на виртуальной земле. В результате инвертирующий входной узел становится идеальным узлом для суммирования входных токов.

Принципиальная схема суммирующего усилителя показана на рисунке выше. Вместо использования одного входного резистора все источники входного сигнала имеют свои собственные входные резисторы. Такая схема усиливает каждый входной сигнал. Коэффициент усиления для каждого входа определяется отношением резистора обратной связи R _f к входному сопротивлению в соответствующей ветви.

Расчет выходного напряжения инвертирующего суммирующего усилителя

Пусть R ₁ — входное сопротивление, а V ₁ — входное напряжение первого канала.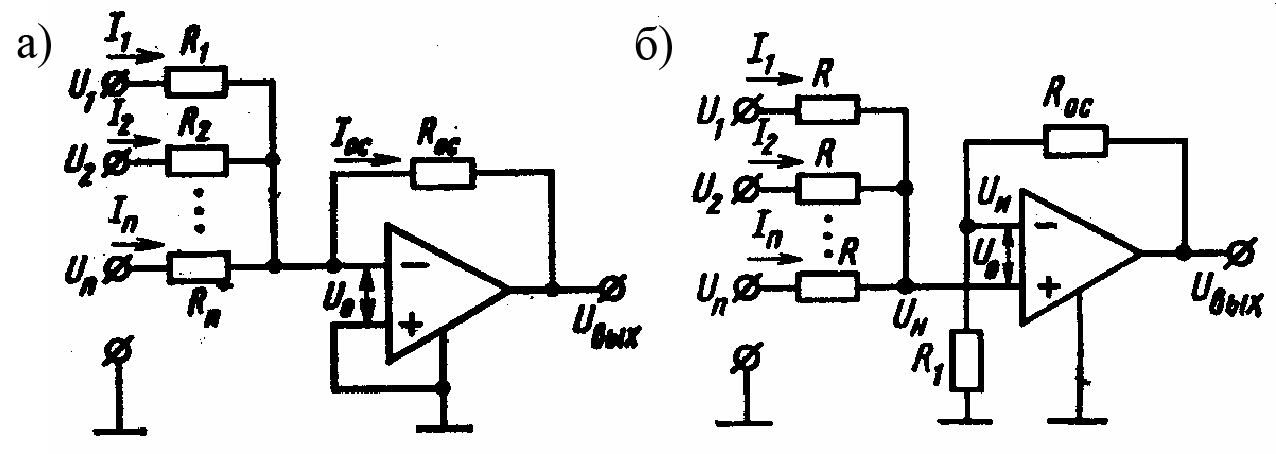 Аналогично, R ₂ – V ₂ для второго канала, R ₃ – V ₃ для третьего канала и так далее до R _n – V _n для n ^{th 900 20 канал.}

Уже было сказано, что суммирующий усилитель — это, по сути, инвертирующий усилитель с более чем одним напряжением на инвертирующем входе. Выходное напряжение для каждого канала может быть рассчитано индивидуально, и окончательное выходное напряжение будет суммой всех отдельных выходов.

Чтобы рассчитать выходное напряжение определенного канала, мы должны заземлить все остальные каналы и использовать базовую формулу выходного напряжения инвертирующего усилителя для каждого канала.

Если заземлены все каналы, кроме первого, то выход для первого канала определяется как:

Где – (R _f / R ₁ ) – коэффициент усиления по напряжению для первого канала (A _В1 ).

Аналогично, если все каналы заземлены, кроме второго канала, то выход для второго канала определяется как:

Где — (R _f / R ₂ ) — коэффициент усиления по напряжению для второго канала (A _V2 ).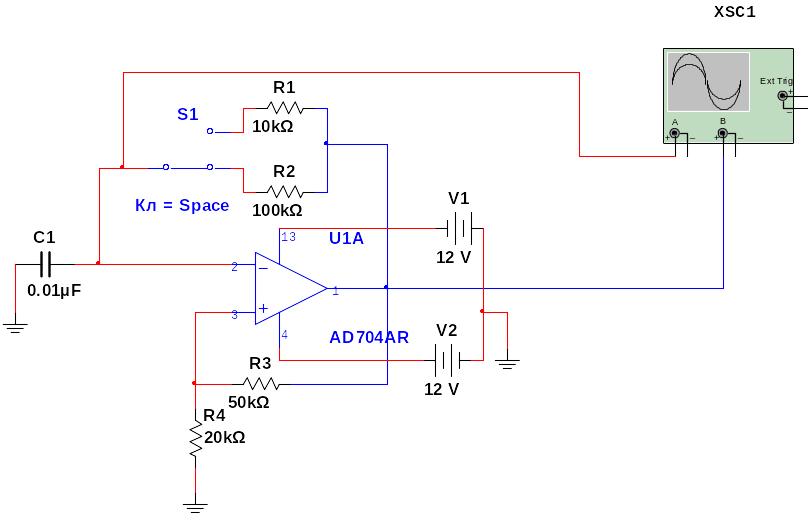

Аналогично, выходной сигнал для n ^{-го канала} определяется как:п ) В _п

А — (R _f / R _n ) — коэффициент усиления по напряжению для n ^-го канала (A _Vn ).

Выходной сигнал представляет собой алгебраическую сумму отдельных выходов или, другими словами, сумму всех входов, умноженную на их соответствующие коэффициенты усиления.

 В _ВЫХ = В _ВЫХ1 + В _ВЫХ2 + . . . + В _ВЫХ

 В _ВЫХ = – [(R _f / R ₁ ) V ₁ + (R _f / R ₂ ) V ₂ + . . . + (R _f / R _n ) V _n ]

 В _ВЫХ = В ₁ А _В1 + В ₂ А _В2 + . . . + В _н А _Вн

В суммирующем усилителе, если входные сопротивления не равны, схема называется масштабирующим суммирующим усилителем.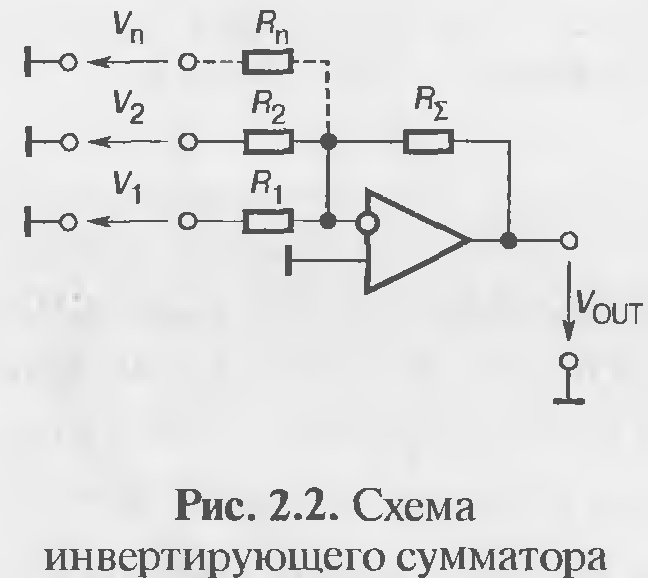

Но если все входные сопротивления выбраны равными, то говорят, что суммирующий усилитель имеет равновзвешенную конфигурацию, где коэффициент усиления для каждого входного канала одинаков.

Иногда необходимо просто добавить входные напряжения без их усиления. В таких ситуациях значение входного сопротивления R ₁ , R ₂ , R ₃ и т. д. необходимо выбирать равным значению резистора обратной связи R _f . В результате коэффициент усиления усилителя будет равен единице. Следовательно, выходное напряжение будет суммой входных напряжений.

Теоретически мы можем подать на вход суммирующего усилителя столько входных сигналов, сколько потребуется. Однако следует отметить, что все входные токи суммируются, а затем возвращаются обратно через резистор R9.0029 f

, поэтому мы должны знать номинальную мощность резисторов.

Неинвертирующий суммирующий усилитель

Неинвертирующий суммирующий усилитель также может быть сконструирован с использованием конфигурации неинвертирующего усилителя операционного усилителя. Здесь входные напряжения подаются на неинвертирующую входную клемму операционного усилителя, а часть выходного сигнала возвращается на инвертирующую входную клемму через обратную связь делителя напряжения и смещения.

Схема неинвертирующего суммирующего усилителя показана на следующем рисунке. Для удобства следующая схема состоит всего из трех входов, но можно добавить больше входов.

Прежде всего, несмотря на то, что это тоже суммирующий усилитель, расчеты не такие прямые, как у инвертирующего суммирующего усилителя, потому что в неинвертирующем суммирующем усилителе нет преимущества виртуального узла суммирования земли.

Расчет выходного напряжения неинвертирующего суммирующего усилителя

Чтобы понять работу неинвертирующего суммирующего усилителя, мы должны разделить схему на две части:

• Входной резистор/источник Раздел
• Секция неинвертирующего усилителя

Если V _IN представляет собой комбинацию всех входных сигналов, то она применяется к неинвертирующему выводу операционного усилителя. Из приведенной выше схемы мы можем рассчитать выходное напряжение неинвертирующего усилителя с V

IN в качестве входа и R _f и R _i в качестве резисторов делителя обратной связи следующим образом:

 V _OUT = V _В (1 + (Р _ф / Р _и ))

Поскольку выходное напряжение вычислено, теперь мы должны определить значение V _IN . Если V ₁ , V ₂ и V ₃ являются тремя основными входными источниками и R ₁ , R ₂ и R ₃ являются их входными сопротивлениями, то V _{IN1 9 0030, В ИН2 и V IN3 являются входами соответствующих каналов, когда другие соответствующие каналы заземлены. Итак,}

 V _IN  = V _IN1 + V _IN2 + В _IN3

Поскольку концепция виртуальной земли здесь не применяется, все каналы будут влиять на другие каналы. Давайте вычислим часть V _IN1 V _IN , и с помощью простой математики мы можем легко получить два других значения, то есть V _IN2 и V _IN3 .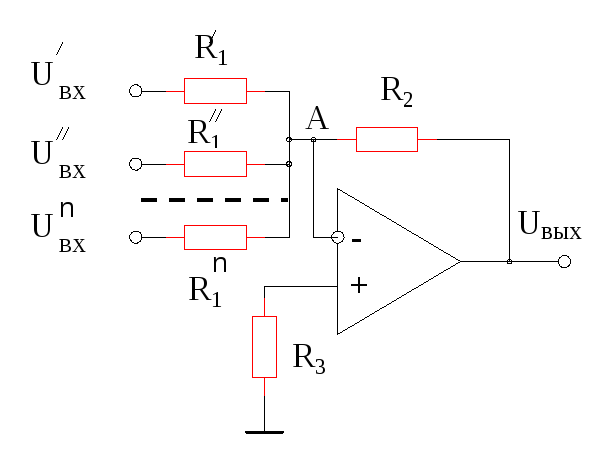

Переходя к V _IN1 , когда V ₂ и V ₃ заземлены, их соответствующие резисторы нельзя игнорировать, так как они образуют сеть делителя напряжения. Итак,

 V _IN1 = V ₁ [(R ₂ || R ₃ ) / (R ₁ + (R ₂ || R 9002 9 3 ))]

Аналогичным образом можно вычислить два других значения V _IN2 и V _IN3 как

 V _IN2 = V ₂ [(R ₁ || R 900 29 3 ) / (Р ₂ + (R ₁ || R ₃ ))]

 В _IN3 = В ₃ [(R ₁ || R ₂ ) / (R ₃ + (R ₁ || R ₂ ))]

Итак,

 В _ИН  = В _ИН1 + В _ИН2 + В _ИН3

 V _IN = V ₁ [(R ₂ || R ₃ ) / (R ₁ + (R ₂ || R 9002 9 3 ))] + В ₂ [(R ₁ || R ₃ ) / (R ₂ + (R ₁ || R ₃ ))] + V ₃ [(R _{1 9003 0 ||R 2 ) / (Р 3 + (Р 1 || Р 2 ))]}

Наконец, мы можем вычислить выходное напряжение V _OUT как

 V _OUT = V _IN (1 + (R _f / R _i ))

 V _OUT = (1 + (R _f / R _i )) {V ₁ [(R ₂ || R ₃ ) / (R 9 0029 1 + (Р ₂ || R ₃ ))] + V ₂ [(R ₁ || R ₃ ) / (R ₂ + (R ₁ || R ₃ ))] + V ₃ [(R ₁ || R ₂ ) / (Р ₃ + (R ₁ || R ₂ ))]}

Если мы рассмотрим специальное условие с равными весами, когда все резисторы имеют одинаковые номиналы, то выходное напряжение будет: В ₁ + В ₂ + В ₃ ) / 3)

Подход к проектированию неинвертирующей суммирующей схемы начинается с проектирования неинвертирующего усилителя с требуемым коэффициентом усиления по напряжению. Затем входные резисторы подбираются как можно большего размера, чтобы соответствовать типу используемого операционного усилителя.

Сумматор напряжения Пример

Три аудиосигнала управляют суммирующим усилителем, как показано на следующей схеме. Какое выходное напряжение?

Коэффициент усиления по напряжению замкнутого контура для каждого канала можно рассчитать как:

 A _CL1 = – (R _f / R ₁ ) = – (100 кОм / 20 кОм) = – 5

 A _CL2 = – (R _f / R ₂ ) = – (100 кОм / 10 кОм) => ACL2 = – 10

 A _CL3 = – (R _f / R ₃ ) = – (100 кОм / 50 кОм) => ACL3 = – 2

Выходное напряжение усилителя суммирования приведено, как

V _OUT = (A _CL1 V ₁ + A _CL2 V ₁ + A + A _CL2 В ₁ + A + A _CL2 V ₁ + A0029 КЛ3 В ₁ )

                          = – [(5 * 100 мВ) + (10 * 200 мВ) + (2 * 300 мВ)]

 = – (0,5 В + 2 В + 0,6 В)

 В _ВЫХ = – 3,1 В

Применение суммирующего усилителя

Аудиомикшер

Суммирующий усилитель является полезной схемой, когда необходимо добавить или объединить два или более сигналов, например, в приложениях для микширования звука. Звуки различных музыкальных инструментов могут быть преобразованы в определенный уровень напряжения с помощью преобразователей и подключены в качестве входа к суммирующему усилителю.

Эти различные источники сигналов будут объединены суммирующим усилителем, и объединенный сигнал будет отправлен на аудиоусилитель. Примерная принципиальная схема суммирующего усилителя в качестве аудиомикшера показана на рисунке ниже.

Суммирующий усилитель может работать как многоканальный аудиомикшер для нескольких аудиоканалов. Никаких помех (обратной связи с одного канала на вход другого канала) не будет, потому что каждый сигнал подается через резистор, другой конец которого подключен к клемме заземления.

Цифро-аналоговый преобразователь (ЦАП)

Цифро-аналоговый преобразователь (ЦАП) преобразует двоичные данные, поступающие на его вход, в эквивалентное аналоговое значение напряжения. Приложения промышленного управления в режиме реального времени часто используют микрокомпьютеры. Эти микрокомпьютеры выводят цифровые данные, которые необходимо преобразовать в аналоговое напряжение для управления двигателями, реле, исполнительными механизмами и т. д.

В простейшей схеме цифро-аналогового преобразователя используется суммирующий усилитель и сеть взвешенных резисторов. Типичная схема 4-битного ЦАП с суммирующим усилителем показана на рисунке ниже.

Входами показанного выше суммирующего усилителя являются двоичные данные Q _A , Q _B , Q _C и Q _D , которые обычно равны 5 В для представления логической 1 и 0 В для представления логической 1. логический 0.

Если входные резисторы в каждой ветви выбраны таким образом, что значение каждого входного резистора в два раза превышает значение резистора в предыдущей входной ветви, то цифровое логическое напряжение на входе создаст выходной сигнал, равный взвешенная сумма приложенных входных напряжений.

Точность такой схемы цифро-аналогового преобразователя ограничена точностью значений используемых резисторов и различиями в представлении логических уровней.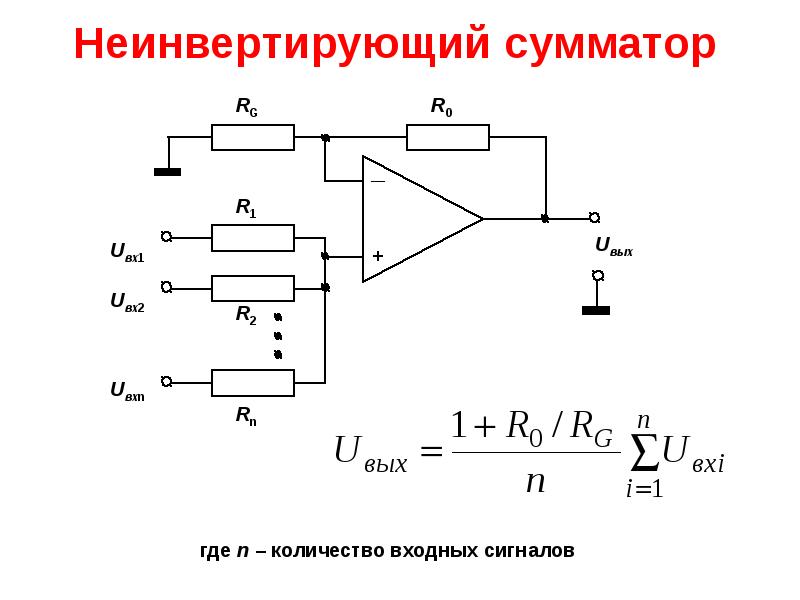

Сдвиг уровня

Другим важным применением суммирующего усилителя является смещение уровня. Суммирующий усилитель с двумя входами может действовать как регулятор уровня, где один вход представляет собой сигнал переменного тока, а второй вход — сигнал постоянного тока.

Сигнал переменного тока будет компенсирован входным сигналом постоянного тока. Одно из основных применений такого сдвига уровня — генераторы сигналов для управления смещением постоянного тока.

Заключение

Полное руководство для начинающих по суммирующим усилителям, также известным как сумматорные схемы. Вы изучили некоторые основы суммирующего усилителя, инвертирующего и неинвертирующего суммирующего усилителя, расчет выходного напряжения, примерную схему и несколько важных приложений.

Суммирующий усилитель или сумматор на операционном усилителе

7 месяцев назад 11 января 2022 г. 4973 просмотра

Операционные усилители имеют так много интересных применений, и мы создали множество схем с операционными усилителями. Операционный усилитель. В этой статье мы изучим еще одно приложение для операционных усилителей, добавляющее два или более входных напряжения, и эта схема называется суммированием или сумматором операционных усилителей. Здесь мы должны показать схему сумматора с использованием операционного усилителя LM358.

Купить на Amazon

Аппаратный компонент

Следующие компоненты необходимы для изготовления схемы суммирующего усилителя

S. №	Компонент	Значение	Кол-во
1	Цифровой мультиметр DMM для тестирования	–	1
2	Два источника входного напряжения (их сумма должна быть < напряжения питания)	–	1
3	Сдвоенные операционные усилители	LM358	1
4	Resis	1 кОм	4
5	Источник питания (для операционных усилителей +Vcc и -Vcc )	9 В пост. тока	1

LM358 Распиновка

Подробное описание цоколевки, размеров и технических характеристик загрузите в техпаспорте LM358

Суммирование Цепь усилителя

Работа схемы

Инвертирующий сумматор аналогичен вышеописанному усилителю, в котором поддерживаются любые входные напряжения инвертирующего вывода, но где основное внимание уделяется неинвертирующему выводу, но на их инвертирующем выводе имеется несколько входов, отличающихся от входа Схема инвертирующего сумматора. Здесь можно увидеть схему инвертирующего сумматора с двумя входами на инвертирующем входе.

Неинвертирующий терминал заземлен. И напряжение в точке B будет таким же, как напряжение в точке A, 0 В, как видно в структуре с обратной связью, что указывает на то, что ток I1 и I2 будет проходить в резисторе Rf (более высокий потенциал), а не в инвертирующем вывод (нижний потенциал) ОУ. Производство выходного напряжения теперь представляет собой сумму входов и является отрицательным, поскольку вход обеспечивает неинвертирующий вывод.