Сумматор — Википедия

Сумма́тор — в кибернетике — устройство, преобразующее информационные сигналы (аналоговые или цифровые) в сигнал, эквивалентный сумме этих сигналов^[1]; устройство, производящее операцию сложения.

В зависимости от формы представления информации различают сумматоры аналоговые и цифровые^[1].

По способу реализации[править | править код]

По принципу действия[править | править код]

• На счётчиках, считающие количества импульсов входного сигналах.
• Функциональные, выдающие на выходах значения логической функции суммы по модулю и логической функции разряда переноса:
  • логические, каждый раз вычисляющие функцию разряда суммы по модулю и функцию разряда переноса
  • табличные, с таблицами заранее вычисленных значений функции разряда суммы по модулю и значений функции разряда переноса записанных:
    • в ПЗУ, ППЗУ (аппаратные) (надёжнее и дешевле логических, так как вместо полупроводников, выполняющих логические вычисления, в ПЗУ используются проводники и изоляторы («прошивки»)) ^[4] или
    • в ОЗУ (аппаратные и программные).
      

Табличные сумматоры впервые были применены в калькуляторах построенных на реле в США до второй мировой войны.

По архитектуре[править | править код]

• Четвертьсумматоры — бинарные (двухоперандные) сумматоры по модулю без разряда переноса, характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма по модулю.
• Полусумматоры — бинарные (двухоперандные) сумматоры по модулю с разрядом переноса, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма по модулю в данном разряде, а на другом — перенос в следующий (старший) разряд.
• Полные сумматоры — тринарные (трёхоперандные) сумматоры по модулю с разрядом переноса, характеризующиеся наличием трёх входов, на которые подаются одноимённые разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма по модулю в данном разряде, а на другом — перенос в следующий (более старший разряд). Такие сумматоры изначально ориентированы только на показательные позиционные системы счисления^{[источник не указан 3324 дня]}.
• Накапливающие сумматоры — снабжённые собственной внутренней памятью.

По способу действия[править | править код]

• Последовательные (одноразрядные), в которых обработка разрядов чисел ведётся поочерёдно, разряд за разрядом, на одном и том же одноразрядном оборудовании.
• Параллельнопоследовательные, в которых одновременно параллельно последовательно складываются несколько разрядов пары чисел.
• Параллельные (многоразрядные), в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется своё оборудование.

По способу организации переноса^[5][6][править | править код]

По системе счисления[править | править код]

Двоичный сумматор может быть описан тремя способами:

1. табличным, в виде таблицы истинности,
2. аналитическим, в виде формулы (СДНФ),
3. графическим, в виде логической схемы.

Так как формулы и схемы могут тождественно преобразовываться, то, одной таблице истинности двоичного сумматора могут соответствовать множества различных логических формул и логических схем. Поэтому, с точки зрения получения результата без учёта затрат времени на вычисление суммы, табличный способ определения двоичного сумматора является основным. Обычное табличное и обычное формульное описание сумматора не учитывают времена задержек в реальных логических элементах и не годятся для определения быстродействия реальных сумматоров.

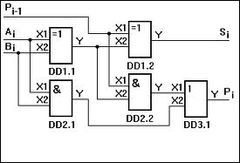Рис.1. Логическая схема трёхступенчатого двоичного сумматора на двух полусумматорах и логическом элементе 2ИЛИ.

x0=A	1	0	1	0	1	0	1	0
x1=B	1	1	0	0	1	1	0	0
x2=Pi−1{\displaystyle P_{i-1}}	1	1	1	1	0	0	0	0	Название действия (функции)	Номер функции
Si{\displaystyle S_{i}}	1	0	0	1	0	1	1	0	Бит суммы по модулю 2	F3,150
Pi{\displaystyle P_{i}}	1	1	1	0	1	0	0	0	Бит переноса	F3,232

Единица переноса возникает в 4 случаях из 8.

СДНФ суммы по модулю 2:
Si=f(x2,x1,x0)=(x2¯⋅x1¯⋅x0)∨(x2¯⋅x1⋅x0¯)∨(x2⋅x1¯⋅x0¯)∨(x2⋅x1⋅x0){\displaystyle S_{i}=\mathbf {f} (x_{2},x_{1},x_{0})=({\overline {x_{2}}}\cdot {\overline {x_{1}}}\cdot {x_{0}})\vee ({\overline {x_{2}}}\cdot {x_{1}}\cdot {\overline {x_{0}}})\vee ({x_{2}}\cdot {\overline {x_{1}}}\cdot {\overline {x_{0}}})\vee ({x_{2}}\cdot {x_{1}}\cdot {x_{0}})}

СДНФ бита переноса:
Pi=f(x2,x1,x0)=(x2¯⋅x1⋅x0)∨(x2⋅x1¯⋅x0)∨(x2⋅x1⋅x0¯)∨(x2⋅x1⋅x0){\displaystyle P_{i}=\mathbf {f} (x_{2},x_{1},x_{0})=({\overline {x_{2}}}\cdot {x_{1}}\cdot {x_{0}})\vee ({x_{2}}\cdot {\overline {x_{1}}}\cdot {x_{0}})\vee ({x_{2}}\cdot {x_{1}}\cdot {\overline {x_{0}}})\vee ({x_{2}}\cdot {x_{1}}\cdot {x_{0}})}

Схема, которая обеспечивает сложение двух однобитных чисел А и В без получения бита переноса из предыдущего разряда называют полусумматором. Полусумматор имеет 4 сигнальных линии: два входа для сигналов, представляющих одноразрядные двоичные числа А и В, и два выхода: сумма А и В по модулю 2 (S) и сигнал переноса в следующий разряд (P). При этом S наименее значимый бит, а P наиболее значимый бит.

Объединив два полусумматора и добавив дополнительную схему ИЛИ, можно создать трёхступенчатый полный сумматор с дополнительным входом P

i-1 (на рисунке 1), который принимает сигнал переноса из предыдущей схемы. Первая ступень на полусумматоре осуществляет сложение двух двоичных чисел и вырабатывает первый частный бит переноса, вторая ступень на полусумматоре осуществляет сложение результата первой ступени с третьим двоичным числом и вырабатывает второй частный бит переноса, третья ступень на логическом элементе 2ИЛИ вырабатывает результирующий бит переноса в старший разряд.

Схема полного сумматора может быть использована в качестве «строительных блоков» для построения схем многоразрядных сумматоров, путём добавления одноразрядных полных сумматоров. Для каждой цифры, которую схема должна быть в состоянии обрабатывать, используется один полный сумматор.

В сумматоре на рис.1 время вычисления суммы по модулю 2 равно 2dt, время вычисления переноса равно 3dt, где dt — время задержки в одном типовом логическом элементе. В m-разрядном сумматоре в худшем случае (единицы переноса во всех разрядах) до последнего разряда сигнал переноса проходит через m-1 разряд, а сумма будет готова ещё через 2dt, поэтому максимальное время сложения равно:

3dt(m−1)+2dt=(3m−1)dt{\displaystyle 3dt(m-1)+2dt=(3m-1)dt}.

Максимальные времена выполнения сложения и вычисления переноса для большего числа разрядов приведены в таблице 1:

Таблица 1.

число разрядов сумматора	1	2	4	8	16	32	64
время выполнения сложения, dt	2	5	11	23	47	95	191
время вычисления переноса, dt	3	6	12	24	48	96	192

Двоичный одноразрядный полный сумматор является полной тринарной (трёхоперандной) двоичной логической функцией с бинарным (двухразрядным) выходом. Все три операнда и оба выходных разряда однобитные.

Десятичный сумматор[править | править код]

Десятичный сумматор можно задать в виде двух таблиц:
с нулём в переносе из предыдущего разряда:

+	0	0	0	0	0	0	0	0	0	0
+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

и с единицей в переносе из предыдущего разряда:

+	1	1	1	1	1	1	1	1	1	1
+	0	1	2	3	4	5	6	7	8	9
0	1	2	3	4	5	6	7	8	9	10
1	2	3	4	5	6	7	8	9	10	11
2	3	4	5	6	7	8	9	10	11	12
3	4	5	6	7	8	9	10	11	12	13
4	5	6	7	8	9	10	11	12	13	14
5	6	7	8	9	10	11	12	13	14	15
6	7	8	9	10	11	12	13	14	15	16
7	8	9	10	11	12	13	14	15	16	17
8	9	10	11	12	13	14	15	16	17	18
9	10	11	12	13	14	15	16	17	18	19

или в виде одной таблицы, в которой единица переноса из предыдущего разряда смещает на одну колонку вправо:

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10	11
2	2	3	4	5	6	7	8	9	10	11	12
3	3	4	5	6	7	8	9	10	11	12	13
4	4	5	6	7	8	9	10	11	12	13	14
5	5	6	7	8	9	10	11	12	13	14	15
6	6	7	8	9	10	11	12	13	14	15	16
7	7	8	9	10	11	12	13	14	15	16	17
8	8	9	10	11	12	13	14	15	16	17	18
9	9	10	11	12	13	14	15	16	17	18	19

C соответствующей прошивкой как десятичный сумматор (десятеричный) могут работать шестнадцатеричный сумматор и двадцатисемиричный сумматор-вычитатель на ПЗУ.

Быстродействия параллельных сумматоров вполне достаточно для быстрого сложения небольшого количества чисел фиксированной длины.
Так как поразрядное сложение по природе своей последовательно, то при очень большом количестве сложений более выгодно перенастроить то же самое оборудование (АЛУ) для одновременного или не очень одновременного параллельного выполнения нескольких последовательных сложений.

Например, параллельный 64-разрядный двоичный сумматор из 64 двоичных сумматоров со сложными схемами ускоренного переноса сложит 1 пару 64-битных чисел в лучших схемах приблизительно за 5dt, а 32 пары 64-битных чисел приблизительно за 32*5dt=160dt.
32 последовательных двоичных сумматора без схем ускоренного переноса бит за битом сложат 32 пары 64-битных чисел приблизительно за 64*2dt=128dt.
32 последовательных четверичных сумматора без схем ускоренного переноса сложат 32 пары 64-битных чисел приблизительно за (64/lg₂4)*2dt=64dt.
32 последовательных шестнадцатиричных сумматора без схем ускоренного переноса сложат 32 пары 64-битных чисел приблизительно за (64/lg₂16)*2dt=32dt.
32 последовательных двухсотпятидесятишестиричных сумматора без схем ускоренного переноса сложат 32 пары 64-битных чисел приблизительно за (64/lg₂256)*2dt=16dt, т.е. приблизительно в десять раз быстрее, чем параллельный 64-битный сумматор со схемами ускоренного переноса.
32 последовательных четыретысячидевяностошестиричных сумматора без схем ускоренного переноса сложат 32 пары 64-битных чисел приблизительно за (64/lg₂4096)*2dt=10,67dt.

• Угрюмов Е. П. Элементы и узлы ЭЦВМ. М.: Высшая школа, 1976. — 232 с.
• Угрюмов Е. П. Цифровая схемотехника. — СПб.: БХВ-Петербург, 2001. — 528 с.
• Жан М. Рабаи, Ананта Чандракасан, Боривож Николич. 11. Проектирование арифметических блоков: Сумматор // Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-е изд. — М.: Вильямс, 2007. — С. 912. — ISBN 0-13-090996-3.

Цифровые арифметические схемы — CoderLessons.com

В этой главе давайте поговорим об основных арифметических схемах, таких как двоичный сумматор и двоичный вычитатель. Эти схемы могут работать с двоичными значениями 0 и 1.

Двоичный сумматор

Самая основная арифметическая операция – сложение. Схема, которая выполняет сложение двух двоичных чисел, называется двоичным сумматором . Во-первых, давайте реализуем сумматор, который выполняет сложение двух битов.

Полумесяц

Половина сумматора представляет собой комбинационную схему, которая выполняет сложение двух двоичных чисел A и B, состоящих из одного бита . Он выдает две выходные суммы, S & carry, C.

Таблица истинности Half сумматора показана ниже.

входные		Выходы
	В	С	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Когда мы добавляем два бита, результирующая сумма может иметь значения в диапазоне от 0 до 2 в десятичном виде. Мы можем представить десятичные цифры 0 и 1 одним битом в двоичном виде. Но мы не можем представить десятичную цифру 2 с одним битом в двоичном виде. Итак, нам требуется два бита для представления его в двоичном виде.

Пусть, sum, S – младший значащий бит и перенос, C – старший значащий бит полученной суммы. Для первых трех комбинаций входов, carry, C равен нулю, а значение S будет равно нулю или единице в зависимости от количества единиц, присутствующих на входах. Но, для последней комбинации входных данных, carry, C равен единице, а sum равен нулю, поскольку результирующая сумма равна двум.

Из таблицы Truth мы можем напрямую записать логические функции для каждого вывода как

S=A oplusB

C=AB

Мы можем реализовать вышеуказанные функции с 2-входным вентилем Ex-OR и 2-входным вентилем AND. Принципиальная электрическая схема полумесяца показана на следующем рисунке.

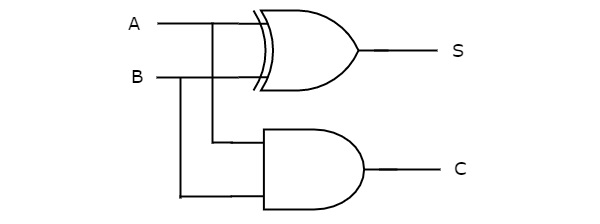
В приведенной выше схеме два входных логических элемента ИЛИ-И и два входных И логических элемента И дают сумму, S и перенос, C соответственно. Следовательно, Half-сумматор выполняет сложение двух битов.

Полный сумматор

Полный сумматор представляет собой комбинационную схему, которая выполняет сложение трех битов A, B и C _в . Где A & B – два параллельных значащих бита, а C _in – бит переноса, который генерируется из предыдущего этапа. Этот полный сумматор также выдает две выходные суммы, S & carry, C _out , которые аналогичны полумесяцу.

Таблица истинности полного сумматора показана ниже.

входные			Выходы
	В	С в	C out	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Когда мы добавляем три бита, результирующая сумма может иметь значения в диапазоне от 0 до 3 в десятичном виде. Мы можем представить десятичные цифры 0 и 1 одним битом в двоичном виде. Но мы не можем представлять десятичные цифры 2 и 3 одним битом в двоичном виде. Итак, нам требуется два бита для представления этих двух десятичных цифр в двоичном виде.

Пусть, sum, S – младший значащий бит и перенос, C _out – старший значащий бит из результирующей суммы. Легко заполнить значения выходов для всех комбинаций входов в таблице истинности. Просто посчитайте количество единиц на входах и запишите эквивалентное двоичное число на выходах. Если C _in равен нулю, то полная таблица истинности сумматора такая же, как в таблице истинной половины сумматора.

Мы получим следующие логические функции для каждого вывода после упрощения.

S=A oplusB oplusCin

cout=AB+ left(A oplusB right)cin

Сумма S равна единице, когда на входах присутствует нечетное число единиц. Мы знаем, что вентиль Ex-OR производит вывод, который является нечетной функцией. Таким образом, мы можем использовать либо два входа Ex-OR с 2 входами, либо один вентиль Ex-OR с 3 входами, чтобы получить сумму S. Мы можем реализовать перенос C _, используя два вентиля И с двумя входами И и один вентиль ИЛИ. Принципиальная электрическая схема полного сумматора показана на следующем рисунке.

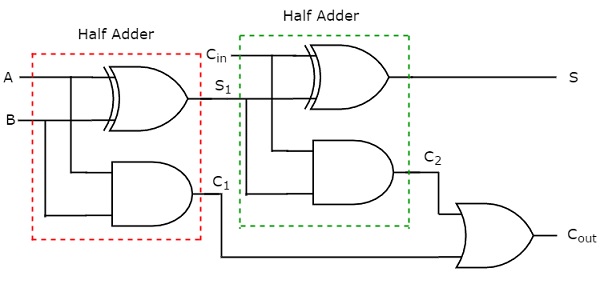
Этот сумматор называется полным сумматором, потому что для реализации одного полного сумматора нам нужны два полумесяца и один вентиль ИЛИ. Если C _in равно нулю, то Полное сумматор становится Полумесяным. Мы можем легко проверить это из приведенной схемы или из булевых функций выходов полного сумматора.

4-битный двоичный сумматор

4-разрядный двоичный сумматор выполняет сложение двух 4-разрядных чисел . Пусть 4-битные двоичные числа, A=A3A2A1A0 и B=B3B2B1B0. Мы можем реализовать 4-битный двоичный сумматор одним из следующих двух способов.

• Для суммирования двух старших значащих битов используйте один половинный сумматор и три полных сумматора.

• Используйте четыре полных сумматора для однородности. Поскольку начальный перенос C _in равен нулю, полный сумматор, который используется для добавления младших значащих битов, становится половинным сумматором.

Для суммирования двух старших значащих битов используйте один половинный сумматор и три полных сумматора.

Используйте четыре полных сумматора для однородности. Поскольку начальный перенос C _in равен нулю, полный сумматор, который используется для добавления младших значащих битов, становится половинным сумматором.

Пока мы рассматривали второй подход. Блок-схема 4-битного двоичного сумматора показана на следующем рисунке.

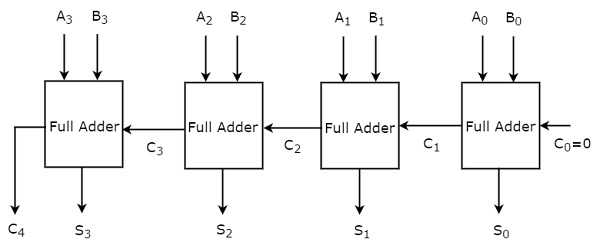
Здесь 4 полных сумматора расположены каскадом. Каждый полный сумматор получает соответствующие биты двух параллельных входов A и B. Выходной сигнал переноса одного полного сумматора будет входом переноса последующего полного сумматора более высокого порядка. Этот 4-битный двоичный сумматор производит результирующую сумму, имеющую не более 5 бит. Итак, проводить последний этап Полный сумматор будет MSB.

Таким образом, мы можем реализовать любой двоичный сумматор более высокого порядка, просто каскадируя необходимое количество полных сумматоров. Этот двоичный сумматор также называется сумматором с волновым переносом (двоичным), потому что перенос распространяется (колебания) от одного этапа к следующему этапу.

Бинарный вычитатель

Схема, которая выполняет вычитание двух двоичных чисел, известна как двоичный вычитатель . Мы можем реализовать двоичный вычитатель следующими двумя способами.

• Каскад Полные вычитатели
• Метод дополнения 2

В первом методе мы получим n-битный двоичный вычитатель путем каскадного вычитания ‘n’ полных вычитателей. Итак, сначала вы можете реализовать Half-вычитатель и Full-вычитатель, аналогично Half-сумматору и полному сумматору. Затем вы можете реализовать n-битный двоичный вычитатель, каскадируя ‘n’ полных вычитателей. Итак, у нас будут две отдельные схемы для двоичного сложения и вычитания двух двоичных чисел.

Во втором методе мы можем использовать один и тот же двоичный сумматор для вычитания двух двоичных чисел, просто выполнив некоторые изменения во втором входе. Итак, внутренне двоичная операция сложения имеет место, но на выходе получается вычитание.

Мы знаем, что вычитание двух двоичных чисел A & B может быть записано как,

AB=A+ left(2′s::compmentofB right)

 RightarrowAB=A+ left(1′s:комплиментofB right)+1

4-разрядный двоичный вычитатель

4-разрядный двоичный вычитатель производит вычитание двух 4-разрядных чисел . Пусть 4-битные двоичные числа, A=A3A2A1A0 и B=B3B2B1B0. Внутренне работа 4-разрядного двоичного вычитателя аналогична работе 4-разрядного двоичного сумматора. Если нормальные биты двоичного числа A, дополненные биты двоичного числа B и начального переноса (заимствования), C _в качестве единицы применяются к 4-разрядному двоичному сумматору, то он становится 4-разрядным двоичным вычитающим веществом. Блок-схема 4-разрядного двоичного вычитателя показана на следующем рисунке.

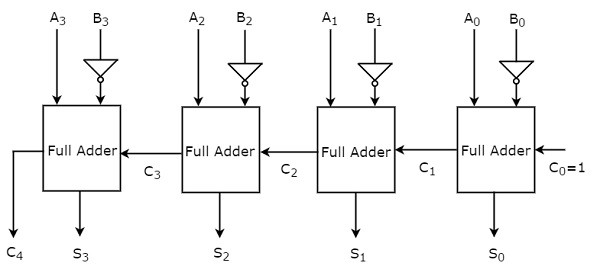
Этот 4-разрядный двоичный вычитатель выдает выходной сигнал, имеющий не более 5 бит. Если двоичное число A больше двоичного числа B, то значение MSB на выходе равно нулю, а оставшиеся биты содержат величину AB. Если двоичное число A меньше двоичного числа B, то MSB выходного значения равно единице. Итак, возьмите 2-е дополнение вывода, чтобы получить величину AB.

Таким образом, мы можем реализовать любой двоичный вычитатель более высокого порядка, просто каскадируя необходимое количество полных сумматоров с необходимыми модификациями.

Двоичный сумматор / вычитатель

Схема, которую можно использовать для сложения или вычитания двух двоичных чисел в любое время, называется двоичным сумматором / вычитателем . И двоичный сумматор, и двоичный вычитатель содержат набор полных сумматоров, которые каскадируются. Входные биты двоичного числа A непосредственно применяются как в двоичном сумматоре, так и в двоичном вычитателе.

Есть два различия в входах полных сумматоров, которые присутствуют в двоичном сумматоре и двоичном вычитателе.

• Входные биты двоичного числа B непосредственно применяются к полным сумматорам в двоичном сумматоре, тогда как дополненные биты двоичного числа B применяются к полным сумматорам в двоичном вычитателе.

• Первоначальный перенос, C ₀ = 0, применяется в 4-разрядном двоичном сумматоре, тогда как начальный перенос (C ₀₎ 1 применяется в 4-разрядном двоичном вычитателе.

Входные биты двоичного числа B непосредственно применяются к полным сумматорам в двоичном сумматоре, тогда как дополненные биты двоичного числа B применяются к полным сумматорам в двоичном вычитателе.

Первоначальный перенос, C ₀ = 0, применяется в 4-разрядном двоичном сумматоре, тогда как начальный перенос (C ₀₎ 1 применяется в 4-разрядном двоичном вычитателе.

Мы знаем, что вентиль Ex-OR с 2 входами производит выход, который совпадает с выходом первого входа, когда другой вход равен нулю. Точно так же это производит вывод, который является дополнением первого ввода, когда другой ввод – один.

Поэтому мы можем применить входные биты двоичного числа B к 2-входным вентилям Ex-OR. Другим входом для всех этих ворот Ex-OR является C ₀ . Таким образом, исходя из значения C ₀ , вентили Ex-OR создают либо нормальные, либо дополненные биты двоичного числа B.

4-разрядный двоичный сумматор / вычитатель

4-разрядный двоичный сумматор / вычитатель производит либо сложение, либо вычитание двух 4-разрядных чисел на основе значения начального переноса или заимствования, 𝐶 ₀ . Пусть 4-битные двоичные числа, A=A3A2A1A0 и B=B3B2B1B0. Работа 4-разрядного двоичного сумматора / вычитателя аналогична работе 4-разрядного двоичного сумматора и 4-разрядного двоичного сумматора.

Примените обычные биты двоичных чисел A и B и начальный перенос или заимствование, C ₀ от внешнего к 4-битному двоичному сумматору. Блок-схема 4-битного двоичного сумматора / вычитателя показана на следующем рисунке.

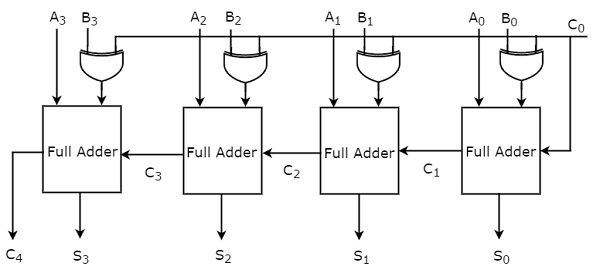
Если начальный перенос, 𝐶 ₀ равен нулю, то каждый полный сумматор получает нормальные биты двоичных чисел A & B. Таким образом, 4-разрядный двоичный сумматор / вычитатель выдает выход, который является сложением двух двоичных чисел A & B.

Если начальный заем равен ₀ , то каждый полный сумматор получает нормальные биты двоичного числа A и дополненные биты двоичного числа B. Таким образом, 4-битный двоичный сумматор / вычитатель выдает результат, который является вычитанием двух двоичных номера A и B.

Следовательно, с помощью дополнительных шлюзов Ex-OR одна и та же схема может использоваться как для сложения, так и для вычитания двух двоичных чисел.

9.5. Многоразрядные сумматоры

Используя     полный сумматор можно построить суммирующее устройство для сложения многоразрядных двоичных чисел А и В.

Различают многоразрядные последовательные и параллельные сумматоры.

9.5.1. Последовательный многоразрядный сумматор

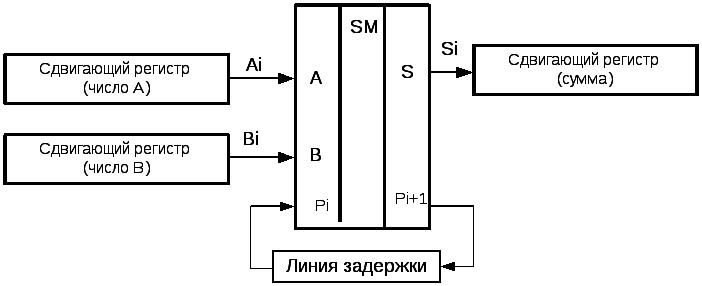
Последовательный многоразрядный сумматор состоит из оноразрядного сумматора на входы а и в которого из сдвигающих регистров, в которых хранятся n-разрядные числа А и В, подаются по тактам разряд за разрядам коды этих чисел, начиная с младшего разряда.

Сформированная сумма накапливается в сдвигающем регистре суммы. Возникающий перенос с задержкой на элементе задержки на один такт поступает на вход сумматора только в следующем такте, когда на входы а и в будут поданы следующие разряды чисел А и В.

Схема последовательного сумматора представлена на Рис.9.4.

Достоинством последовательного сумматора является простота схемы, требующая минимального количества оборудования, недостатком – низкое быстродействие, т.к. для сложения кодов n-разрядных чисел требуется, учитывая возможность переполнения, n-1 такт работы.

Рис.9.4. Последовательный многоразрядный сумматор

9.5.2. Параллельный многоразрядный сумматор с последовательным переносом

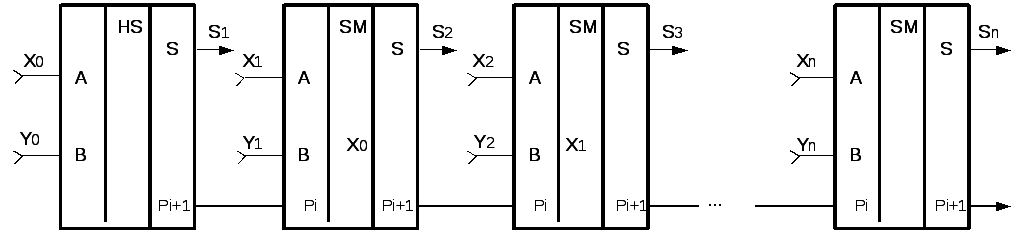
В этом сумматоре (Рис.9.5) операция суммирования производится одновременно за один такт во всех разрядах чисел А и В, которые поступают на входы паралледьным кодом.

Параллельный многоразрядный сумматор состоит из одного полусумматора (суммирование младших разрядов А и В) и n-1 полных сумматоров, где n – разрядность складываемых чисел.

Рис.9.5. Параллельный многоразрядный сумматор

Длительность формирования результата в таком сумматоре определяется временем установления выходных сигналов (сумма и перенос) в каждом из одноразрядных сумматоров после установления сигнала на его входах.

Надо учитывать, что если на входы Xi и Yi всех разрядов сигналы поступают в момент начала такта, то на вход Pi сигнал переноса поступает с некоторой задержкой, которая определяется длительностью переходных процессов tзд в сумматоре предыдущего разряда.

При наиболее неблагоприятном сложении, т.е. если , например, Х = 111…11, а Y = 000…01, произойдет перенос 1 через все сумматоры, т.е. время установления результата будет равно

Туст.рез. = tзд * (n-1) .

При большой разрядности чисел Туст.рез. может быть большим, следовательно длительность времени подачи чисел X,Y на входы одноразрядных сумматоров должна быть больше Туст.рез.

Для ускорения процесса формирования переноса используют дополнительные комбинационные схемы, позволяющие формировать перенос параллельно во всех разрядах.

9.5.3. Параллельный многоразрядный сумматор с параллельным переносом

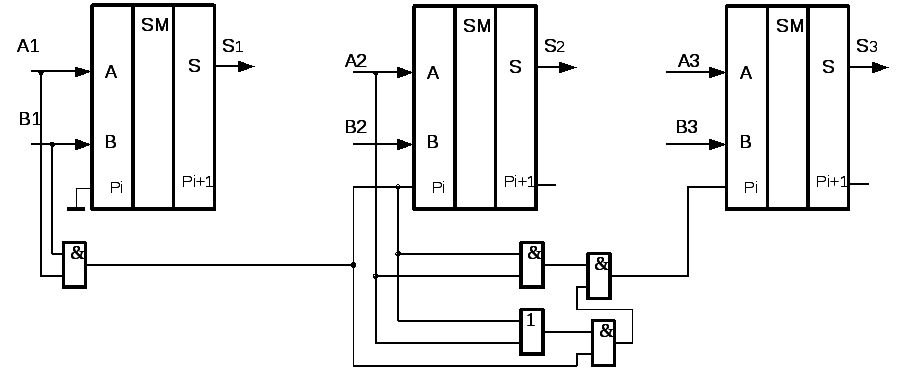
Принцип построения таких сумматоров заключается в том, что значение каждого разряда суммы получается в результате параллельного анализа соответствующих разрядов слагаемых.

Параллельные сумматоры с одновременным переносом бывают двух типов:

Принцип формирования параллельного переноса показан на Рис. 9.6.

Рис.9.6. Принцип формирования параллельного переноса

2.4.2. Комбинационные двоичные сумматоры

Двоичный сумматор (рис. 2.16) представляет собой логическое устройство, формирующее сумму S n-разрядных двоичных чисел А и В. При этом также создается сигнал переноса P в следующий (I + 1) разряд.

В

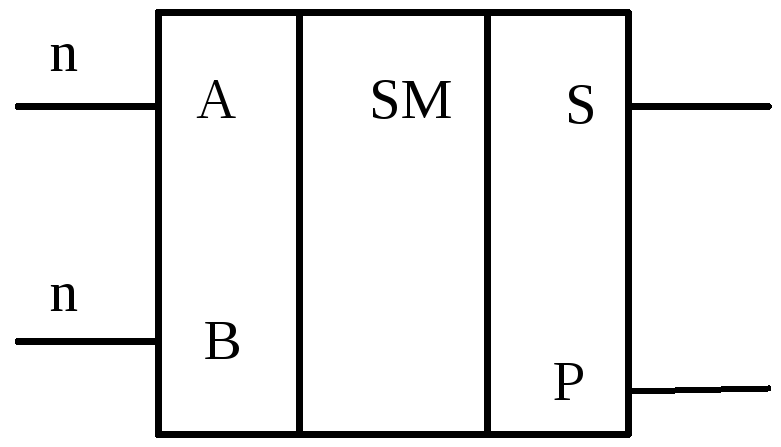
Рис. 2.16

основе построения многоразрядного сумматора лежит одноразрядный сумматор, представляющий собой устройство суммирования трех одноразрядных чисел: одноименных разрядов двух двоичных чисел и сигнала переноса от суммы предыдущих разрядов.

Таблица истинности одноразрядного сумматора (табл. 2.14), построенная по правилам суммирования двоичных чисел, приведена применительно к процедуре сложения k-х разрядов а_k, b_k и сигнала переноса P_k–1.

Т а б л и ц а 2.14                         

Pi–1	ak	bk	Sk	Pk
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Для получения алгебраических выражений выходных функций сумматора приведены их карты Карно (рис. 2.17, 2.18), анализ которых показывает, что функция поразрядного суммирования S_k не минимизируется, а функция переноса P_k может быть упрощена путем склеивания соседних клеток:

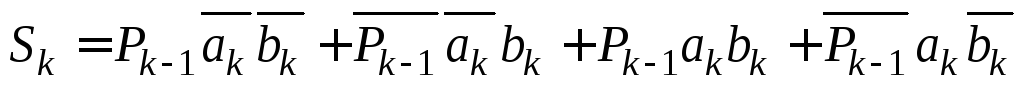        (2.9)

или

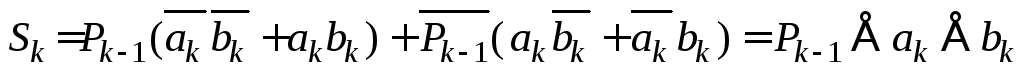   ? (2.10)

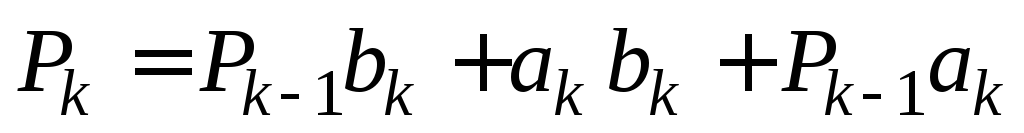/ (2.11)

Итоговое выражение для функции S_kназывается суммой по модулю 2 для трех переменных (напомним, что сумма по модулю 2 для двух переменных адекватна функции «исключительное или» и обозначается как М2).

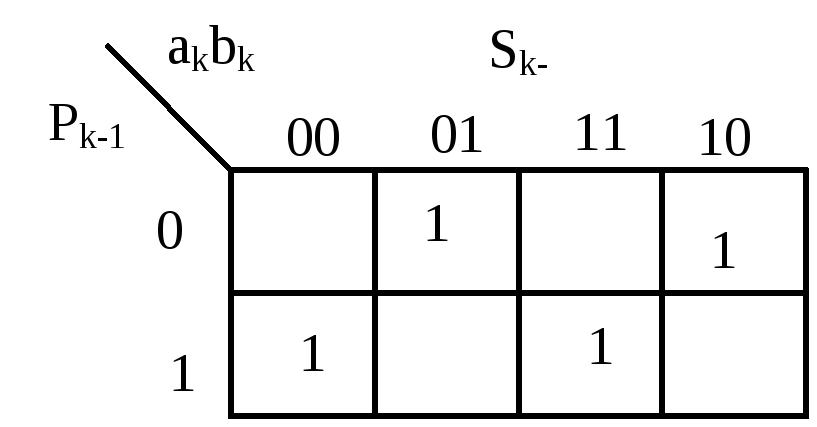
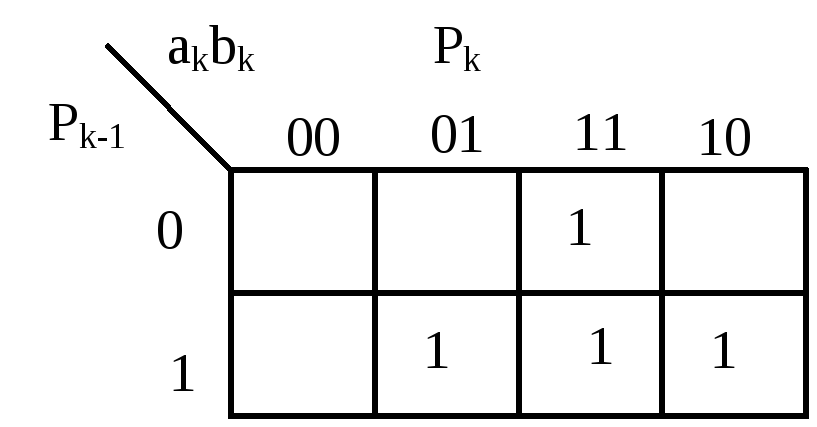
Рис. 2.17 Рис. 2.18

Выражение (2.11) отражает закон функционирования так называемого мажоритарного элемента, работающего по принципу два из трех: выходной сигнал истинен, если истинны, по крайней мере, два из трех входных сигнала, что эффективно используется при резервировании устройства передачи цифровой информации.

Вариант реализации одноразрядного сумматора с использованием схем М2 и схемы 3-2И-ИЛИ показан на рис. 2.19.

Многоразрядный сумматор состоит из нескольких одноразрядных сумматоров (условно изображен на рис. 2.20 применительно к четырехразрядному сумматору). Входными сигналами здесь являются сигнал переноса cr от предыдущего сумматора (или другой внешний сигнал), а также сигналы от одноименных разрядов двоичных чисел А и В. Результат сложения выделяется на выходе в виде многоразрядного слова CRS₃S₂S₁S₀ с разрядностью на единицу большую разрядности входных чисел. В свою очередь путем каскадного включения сумматоров конечной разрядности можно построить сумматор еще большей разрядности. Так, например, чтобы осуществить суммирование двух восьмиразрядных чисел, необходимо иметь два четырехразрядных сумматор и выход переноса CR первого из них соединить со входом сr второго.

Рассмотренный сумматор называется последовательным, поскольку операция сложения в нем выполняется последовательно разряд за разрядом начиная с младшего, что вызывает задержку выходного сигнала переноса. Существуют и параллельные сумматоры с более сложным построением, когда выходной перенос

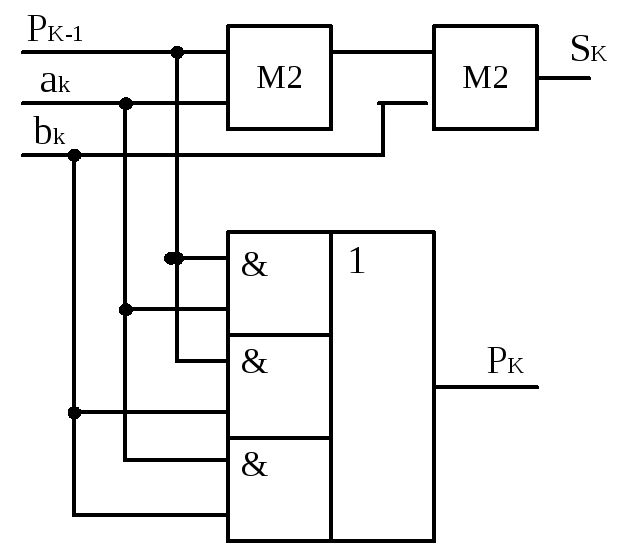
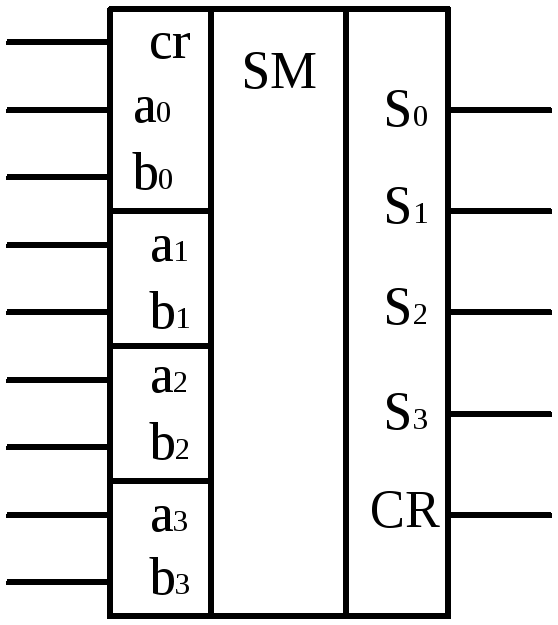
Рис. 2.19 Рис. 2.20

каждого разряда вырабатывается независимо от переноса соседнего младшего разряда, но при этом существенно уменьшается время задержки на выходе сумматора.

Помимо суммирования сумматоры находят применение и при реализации ряда других функциональных и арифметических задач. В числе их преобразование двоично-десятичного кода в двоичный и обратно, компараторы (схемы сравнения чисел) и др. Покажем это на следующих примерах.

1. Преобразователь двухразрядного двоично-десятичного кода в двоичный. Схема этого преобразователя, состоящая из двух четырехразрядных сумматоров, изображена на рис. 2.21.

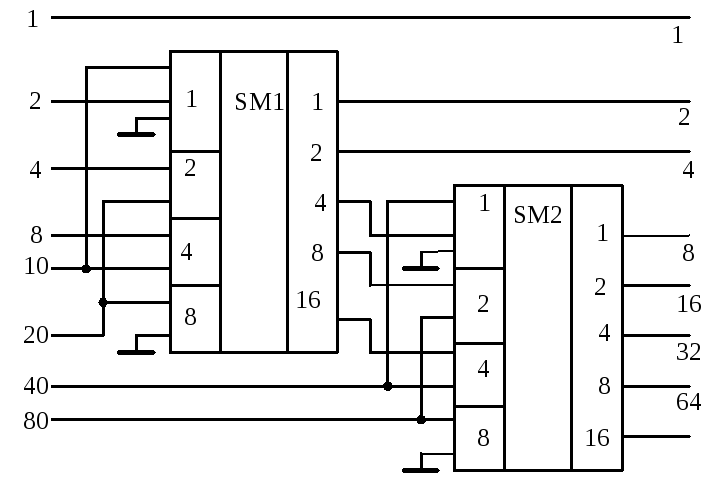
Рис. 2.21

Вспомним, что в двоично-десятичной системе каждая десятичная цифра представляется двоичным эквивалентом. Например, двухразрядное десятичное число (его максимальное значение равно 99) запишется в виде двух тетрад с четырьмя двоичными разрядами в каждой: X₂X₁ = x₇x₆x₅x₄x₃x₂x₁x₀ = x₇80 + x₆40 + + x₅20 + x₄10 + x₃8 + x₂4 + x₁2 + x₀1 = x₇2³10 + x₆2²10 + + x₅2¹10 + x₄2⁰10⁰ + x₃2³ + x₂2² +x₁2¹ + x₀2⁰, где x₇ – x₀ принимают значение нуль или единица._. Двоичный же эквивалент числа будет иметь на один разряд меньше, т. е. X₂X₁ = = y₆y₅y₄y₃y₂y₁y₀ = y₆2⁶ + y₅2⁵ + e₄2⁴ + y₃2³ + y₂2² + y₁2¹ + y₀2⁰, где также y₆–y₀ равны нулю или единице.

Для перехода от двоично-десятичного представления числа к его двоичному эквиваленту заметим, что 80 = 2⁶ + 2⁴, 40 = 2⁵ + 2³, 20 = 2⁴ + 2², 10 = 2³ + 2¹, т. е. все эти числа могут быть выражены через степени числа два. Легко видеть, что младший разряд (2⁰) преобразуемых кодов совпадает. Другие же разряды двоичного кода получаются в результате суммирования одноименных двоичных разрядов, из которых состоят числа 80, 40, 20, 10. Этот принцип и отражен в схеме рис. 2.21.

2. Компаратор. Компаратор – это цифровое устройство, предназначенное для сравнения чисел, представленных в виде двоичных кодов. Здесь возможны следующие ситуации:

а) Двоичные числа А и В одинаковы

Возьмем инверсию от всех разрядов числа В, т. е. создадим новое число 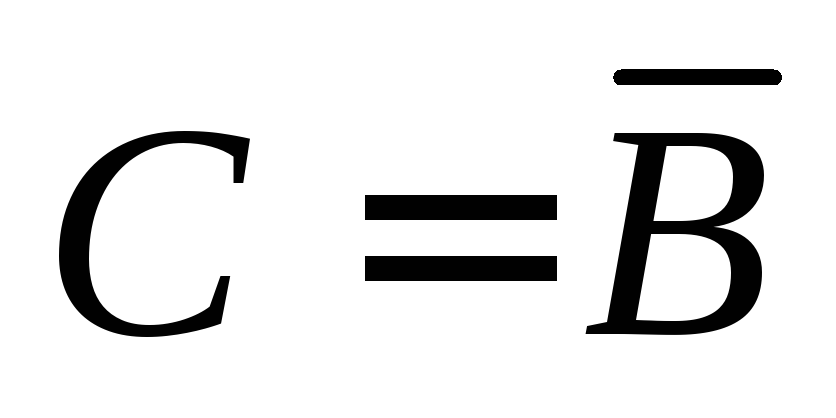, и просуммируемА и В. На всех выходах сумматора, кроме выхода переноса, окажутся единичные значения, что позволяет установить равенство чисел.

б) Число А > B

Сумма числа А и инверсии числа В вызовет на всех выходах сумматора появление единичных значений.

в) Число А < В

Для установления этого неравенства достаточно убедиться, что не выполняются пункты «а» и «б».

В заключение приведем примеры нескольких типов сумматоров: К155ИМ1 – одноразрядный, К155ИМ2 – двухразрядный, К564ИМ1 – четырехразрядный двоичные сумматоры.

Сумматоры

Сумматоры.

Сумматоры — устройства, осуществляющие основную арифметическую операцию — суммирование чисел в двоичном коде. Простейший случай — суммирование двух одноразрядных чисел: О + 0 = 0, 1 + 0 = 1, О + 1 = 1 и 1 + 1 = 10. В последнем случае выходное число 10 (в десятичной записи это 2) оказалось двоичным двухразрядным. Появившаяся в старшем разряде суммы единица называется единицей переноса.

На рисунке показана реализация схемы полусумматора для суммирования двух одноразрядных чисел, состоящая из элементов исключающее ИЛИ и И. Схема имеет два выходных провода: суммы ∑ и переноса С. Таблица состояний полусумматора показана на рисунке.

Полный сумматор должен иметь вход для приема сигнала переноса С_n (здесь n — число разрядов в суммируемых словах). Схема полного сумматора двух одноразрядных слов показана на рисунке, а состояние сумматора показаны в таблице. В последнем столбце таблицы результаты суммирования даны в десятичной форме. В присутствии входной единицы переноса С_n сумма чисел А и В увеличивается на 1.

Полные сумматоры многоразрядных чисел составляются из одноразрядных и могут складывать многоразрядные числа двумя способами: параллельным или последовательным.

На рисунке показана структура пятиразрядного параллельного сумматора. Здесь поразрядно (в параллель) суммируются два пятиразрядных слова: разряд АО с разрядом ВО, A1 с В1 и так далее до А5 с С5. При этом в каждом элементарном сумматоре получаются парциальные суммы ∑O, ∑1 — ∑5 и сигналы внутреннего переноса C_n+1, которые последовательно поступают на вход переноса С_{n, более старшего сумматора. Шестой выходной провод содержит сигнал переноса Сn+1 = С6 (единица в шестом разряде). Таким образом, полная выходная сумма сумматора составляет 111111, т.е. 63 в десятичном эквиваленте.}

Данное устройство нетрудно сделать любой длины, однако суммирование будет закончено лишь тогда, когда истечет время распространения сигналов переноса С_n через всю цепь одноразрядных сумматоров. Большое время распространения сигнала ограничивает применение параллельных сумматоров. Такой перенос иногда называю пульсирующим.

Последовательный двоичный сумматор содержит три n-разрядных регистра: регистры слагаемых А и В и регистр суммы ∑. Суммируемые слова загружаются в регистры А и В поразрядно. С такой же скоростью один такт — один разряд происходит и суммирование, т.е. заполнение регистра суммы ∑. Дополнительный D-триггер необходим для запоминания на один такт разряда С_n для переноса его в разряд С_n+1. Регистры последовательных сумматоров могут иметь параллельную загрузку. Если необходимо, чтобы переменные числа В прибавлялись к постоянному числу А, регистр числа А надо запустить в режиме рециркуляции (штриховая линия на рисунке).

Параллельные, комбинаторные (безрегистровые) сумматоры Обеспечивают наибольшую скорость суммирования, если снабжаются схемой, ускоренного переноса СУП. В результате действия СУП разряд C_n+1 появляется на выходе одновременно c разрядами суммы ∑.

НОУ ИНТУИТ | Лекция | Комбинационные микросхемы. Часть 2

Аннотация: В лекции рассказывается о комбинационных микросхемах: сумматорах, преобразователях кодов, одновибраторах и генераторах, об их алгоритмах работы, параметрах, типовых схемах включения, а также о реализации на их основе некоторых часто встречающихся функций.

Сумматоры

Микросхемы сумматоров (английское Adder), как следует из их названия, предназначены для суммирования двух входных двоичных кодов, то есть выходной код будет равен арифметической сумме двух входных кодов. Например, если один входной код — 7 (0111), а второй — 5 (0101), то суммарный код на выходе будет 12 (1100). Сумма двух двоичных чисел с числом разрядов N может иметь число разрядов (N + 1). Например, при суммировании чисел 13 (1101) и 6 (0110) получается число 19 (10011). Поэтому количество выходов сумматора на единицу больше количества разрядов входных кодов. Этот дополнительный (старший) разряд называется выходом переноса.

На схемах сумматоры обозначаются буквами SM. В отечественных сериях код, обозначающий микросхему сумматора, — ИМ.

Сумматоры бывают одноразрядные (для суммирования двух одноразрядных чисел), 2-х разрядные (суммируют 2-х разрядные числа) и 4-х разрядные (суммируют 4-х разрядные числа). Чаще всего применяют именно 4-разрядные сумматоры. На рис. 6.1 показаны для примера 2-разрядный и 4-разрядный сумматоры. Микросхема ИМ6 отличается от ИМ3 только повышенным быстродействием и номерами используемых выводов микросхемы, функция же выполняется та же самая.

Рис. 6.1. Примеры микросхем сумматоров

Помимо выходных разрядов суммы и выхода переноса, сумматоры имеют вход расширения (другое название — вход переноса) С для объединения нескольких сумматоров с целью увеличения разрядности. Если на этот вход приходит единица, то выходная сумма увеличивается на единицу, если же приходит нуль, то выходная сумма не увеличивается. Если используется одна микросхема сумматора, то на ее вход расширения С необходимо подать нуль.

Для примера в табл. 6.1 приведена полная таблица истинности 2-разрядного сумматора ИМ2. Как видно из таблицы, выходной 3-разрядный код (Р, S1, S0) равен сумме входных 2-разрядных кодов (А1, А0) и (В1, В0), а также сигнала С. Нулевые разряды — младшие, первые разряды — старшие. Полная таблица истинности 4-разрядного сумматора будет чрезмерно большой, поэтому она не приводится. Но суть работы остается точно такой же, как и в случае 2-разрядного сумматора.

Сумматоры могут использоваться также для суммирования чисел в отрицательной логике (когда логической единице соответствует электрический нуль, и наоборот, логическому нулю соответствует электрическая единица). Но в этом случае входной сигнал переноса С также становится инверсным, поэтому при использовании одной микросхемы сумматора на вход С надо подать электрическую единицу (высокий уровень напряжения). Инверсным становится и выходной сигнал переноса Р, низкий уровень напряжения на нем (электрический нуль) соответствует наличию переноса. То есть получается, что сумматор абсолютно одинаково работает как с положительной, так и с отрицательной логикой.

Таблица 6.1. Таблица истинности микросхемы 2-разрядного сумматора ИМ2

Входы				Выходы
				C=0			C=1
A1	A0	B1	B0	P	S1	S0	P	S1	S0
0	0	0	0	0	0	0	0	0	1
0	0	0	1	0	0	1	0	1	0
0	0	1	0	0	1	0	0	1	1
0	0	1	1	0	1	1	1	0	0
0	1	0	0	0	0	1	0	1	0
0	1	0	1	0	1	0	0	1	1
0	1	1	0	0	1	1	1	0	0
0	1	1	1	1	0	0	1	0	1
1	0	0	0	0	1	0	0	1	1
1	0	0	1	0	1	1	1	0	0
1	0	1	0	1	0	0	1	0	1
1	0	1	1	1	0	1	1	1	0
1	1	0	0	0	1	1	1	0	0
1	1	0	1	1	0	0	1	0	1
1	1	1	0	1	0	1	1	1	0
1	1	1	1	1	1	0	1	1	1

Рассмотрим пример. Пусть нам надо сложить два числа 5 и 7 в отрицательной логике. Числу 5 в положительной логике соответствует двоичный код 0101, а в отрицательной — код 1010. Числу 7 в положительной логике соответствует двоичный код 0111, а в отрицательной — код 1000. При подаче на вход сумматора кодов 1010 (десятичное число 10 в положительной логике) и 1000 (десятичное число 8 в положительной логике) получаем сумму 10 + 8 = 18, то есть код 10010 в положительной логике. С учетом входного сигнала переноса С=1 (отсутствие входного переноса в отрицательной логике) выходной код сумматора получится на единицу больше: 18 + 1 = 19, то есть 10011. При отрицательной логике это будет соответствовать числу 01100, то есть 12 при отсутствии выходного переноса. В результате получили 5+7=12.

Сумматор может вычислять не только сумму, но и разность входных кодов, то есть работать вычитателем. Для этого вычитаемое число надо просто поразрядно проинвертировать, а на вход переноса С подать единичный сигнал (рис. 6.2).

Рис. 6.2. 4-х разрядный вычитатель на сумматоре ИМ6 и инверторах ЛН1

Например, пусть нам надо вычислить разность между числом 11 (1011) и числом 5 (0101). Инвертируем поразрядно число 5 и получаем 1010, то есть десятичное 10. Сумматор при суммировании 11 и 10 даст 21, то есть двоичное число 10101. Если сигнал С равен 1, то результат будет 10110. Отбрасываем старший разряд (выходной сигнал Р) и получаем разность 0110, то есть 6.

Еще пример. Пусть надо вычислить разность между числом 12 (1100) и числом 9 (1001). Инвертируем поразрядно 9, получаем 0110, то есть десятичное 6. Находим сумму 12 и 6, получаем 18, а с учетом С = 1 получаем 19, то есть двоичное 10011. В четырех младших разрядах имеем 0011, то есть десятичное 3.

Каскадировать сумматоры для увеличения разрядности очень просто. Надо сигнал с выхода переноса сумматора, обрабатывающего младшие разряды, подать на вход переноса сумматора, обрабатывающего старшие разряды (рис. 6.3). При объединении трех 4-разрядных сумматоров получается 12-разрядный сумматор, имеющий дополнительный 13-й разряд (выход переноса Р).

Рис. 6.3. Каскадирование сумматоров ИМ6 для увеличения разрядности

Неопределенные состояния на выходах сумматора могут возникать при любом изменении любого из входных кодов (рис. 6.4). Выходной код суммы может принимать в течение короткого времени значения, никак не связанные с входными кодами, а на выходе переноса могут появляться короткие паразитные импульсы. Это связано прежде всего с неодновременным изменением разрядов входных кодов. Чтобы избежать влияния этих неопределенных состояний на дальнейшую схему, необходимо предусматривать синхронизацию или стробирование выходных сигналов. Но для этого надо располагать информацией о моментах изменения входных кодов, которая имеется далеко не всегда.

Рис. 6.4. Неопределенные состояния на выходах сумматора при изменении входных кодов

Задержки сумматора ИМ6 от входов до выходов суммы примерно вдвое превышает задержку логического элемента, а от входов до выхода переноса — примерно в полтора раза. Задержки сумматора ИМ3 больше задержек ИМ6 почти вдвое. Поэтому в схемах, где важно быстродействие, лучше использовать ИМ6. Особенно это существенно при каскадировании для увеличения разрядности, так как там задержки отдельных микросхем суммируются. Точные величины задержек надо смотреть в справочниках.

28.4 Одноразрядный двоичный сумматор

Рассмотрим, например, построение одноразрядного сумматора с использованием схем двоичных полусумматоров (рисунок 28.2, а). Для этой цели необходимо два полусумматора и элемент ИЛИ.

Условное графическое обозначение одноразрядного сумматора приведено на рисунке 28.2 б, описание работы приведено в таблице 28.2.

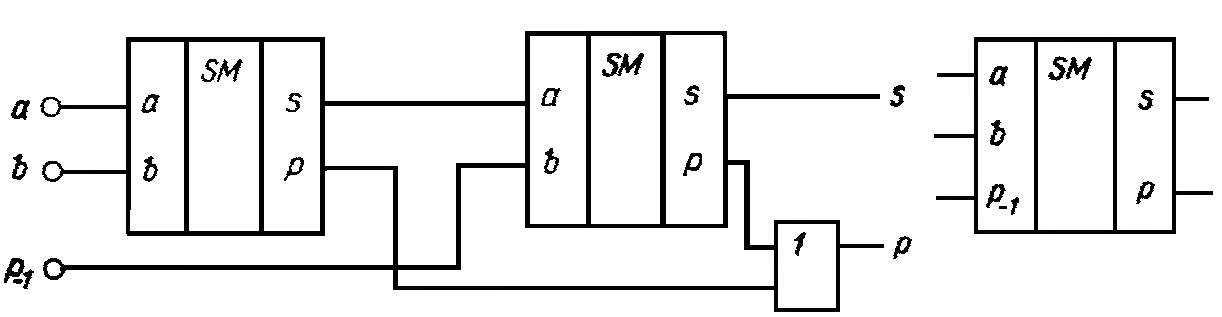
а) б)

Рисунок 28.2 – Внутренняя структурная схема (а) и УГО (б)

одноразрядного двоичного сумматора

Таблица 28.2 – Таблица истинности сложения разрядов многоразрядных двоичных чисел

a	b	p-1	s	p
0	0	0	0	0
0	1	0	1	0
1	0	0	1	0
1	1	0	0	1
0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	1	1	1

28.5 Многоразрядный сумматор параллельного действия

В этом сумматоре, согласно данному ранее определению, операции суммирования должны выполняться одновременно по всем разрядам исходных двоичных чисел. Из этого следует, что такой сумматор должен иметь отдельные аппаратные средства для выполнения суммирования в каждом разряде.

На рисунке 28.3 приведена типовая структурная схема 4-хразрядного сумматора, выполненного с использованием трех одноразрядных сумматоров и одного полусумматора. Разряды кодов слагаемых подаются на соответствующие входы сумматоров, выходы суммы которых подсоединяются к первым входам ЛЭ И, используемых в качестве выходных ключей, на вторые входы которых подается сигнал Z, определяющий момент считывания результата. Выход сигнала переноса сумматора нулевого разряда подается на вход переноса сумматора первого разряда и т.д.

Из сказанного следует, что для получения на выходе сигнала, равного реальной сумме входных чисел, необходимо, чтобы сигнал переноса последовательно сформировался на выходах сумматоров всех разрядов. Следовательно, не зависимо от того, что для суммирования в каждом разряде используется отдельный сумматор, реальное время выполнения операции в данной схеме определяется последовательным переносом сигнала p из разряда в разряд. Поэтому результат, который может быть снят с выхода схемы через время, равное времени суммирования в одном разряде, не будет являться реальным значением искомой суммы.

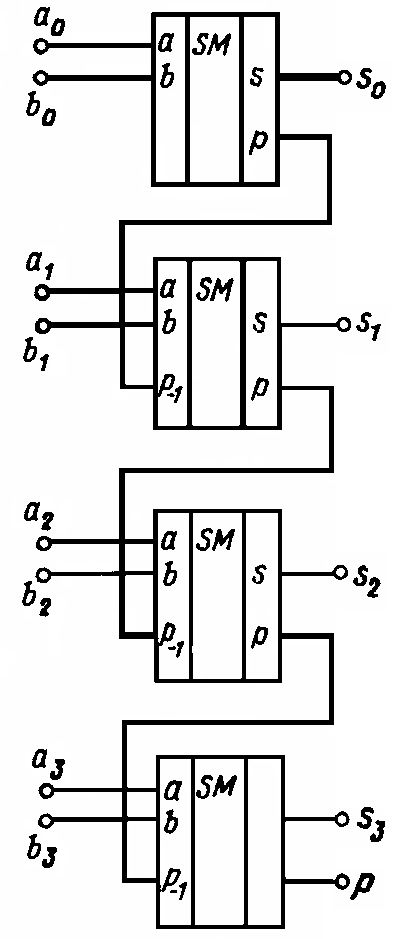
Рисунок 28.3 – Структурная схема многоразрядного сумматора

параллельного действия

Для исключения получения ложного результата на выходе схемы установлены элементы И. Сигнал Z на входах этих элементов должен появляться не ранее, чем вслед за последовательной передачей сигнала переноса по всем разрядам сумматоров.

Следует отметить, что реально схемы многоразрядных сумматоров строятся только с применением одноразрядных сумматоров, что позволяет, используя их последовательное включение, увеличить разрядность кодов слагаемых.

Для дальнейшего увеличения разрядности можно каскадировать сумматоры. Надо сигнал с выхода переноса сумматора, обрабатывающего младшие разряды, подать на вход переноса сумматора, обрабатывающего старшие разряды (рисунок 28.4). При объединении трех 4-разрядных сумматоров получается 12-разрядный сумматор, имеющий дополнительный 13-й разряд (выход переноса Р).

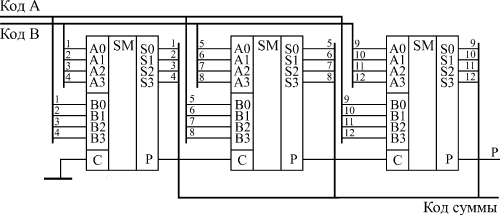
Рисунок 28.4 – Каскадирование сумматоров

для увеличения разрядности

Сумматор может вычислять не только сумму, но и разность входных кодов, то есть работать вычитателем. Для этого вычитаемое число надо просто поразрядно проинвертировать, а на вход переноса С подать единичный сигнал (рисунок 28.5).

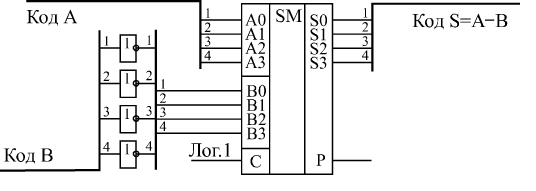
Рисунок 28.5 – 4-хразрядный вычитатель на сумматоре

и инверторах

Например, пусть нам надо вычислить разность между числом 11 (1011) и числом 5 (0101). Инвертируем поразрядно число 5 и получаем 1010, то есть десятичное 10. Сумматор при суммировании 11 и 10 даст 21, то есть двоичное число 10101. Если сигнал С равен 1, то результат будет 10110. Отбрасываем старший разряд (выходной сигнал Р) и получаем разность 0110, то есть 6.

Микросхемы, выполняющие функции сумматора, кодируются буквами ИМ.

Лекция № 29

ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ЦИФРОВЫЕ УСТРОЙСТВА.

ТРИГГЕРЫ