Проекция вектора на ось. Два свойства проекции

Пусть на плоскости или в пространстве заданы ось l с единичным вектором е и произвольный вектор а.

Ортогональной проекцией (или просто проекцией) вектора а на ось l называется число, равное произведению длины вектора а на косинус угла между векторами е и а.

Проекция вектора а на ось l обозначается символом пр_l а или пр_е а.

Таким образом, по определению

пр_l а = | a | cos\(\widehat{(e, a)}\).

Отложим вектор а от точки О оси l.

Если угол между векторами е и а острый (рис. 50, а), то проекция вектора а на ось l равна длине отрезка ОА₁ и где А₁ — проекция точки А на прямую l.

Действительно,

$$ пр_l a = |a|cos\widehat{(e, a)}=|OA|cos\widehat{AOA_1}=|OA_1| $$

Если угол между векторами е и а тупой (рис. 50,б), то проекция вектора а на ось l равна длине отрезка ОА₁ и взятой со знаком минус.

В самом деле,

$$ пр_l a = |a|cos\widehat{e, a}=|OA|cos\widehat{BOA}= -|OA|cos\widehat{A_{1}OA} = -|OA_1| $$

Если вектор а перпендикулярен оси l, то \(\widehat{(e, a)}\) = 90° и пр_l а = | a | cos 90° = 0.

Рассмотрим два важных свойства проекции вектора на ось.

Свойство 1. Для любых векторов а и b справедливо равенство

пр_l (а + b) = пр_l а + пр_l b, где l — произвольная ось.

Это свойство позволяет заменять проекцию суммы векторов суммой их проекций и наоборот.

Свойство 2. Для любого вектора а и любого числа k справедливо равенство

пр_l ka = k пр_l a,

где l — произвольная ось.

Это свойство позволяет выносить и вносить числовой множитель за знак проекции.

Справедливость этих свойств следует из правил действий над векторами, заданными своими координатами.

В самом деле, пусть l — произвольная ось с началом отсчета О и единичным вектором е. Введем прямоугольную систему координат следующим образом (рис. 51).

Примем точку О за начало координат, а вектор е — за первый базисный вектор (i = e). В качестве других базисных векторов j и k возьмем любые два единичных перпендикулярных друг другу вектора, лежащих в плоскости перпендикулярной оси l.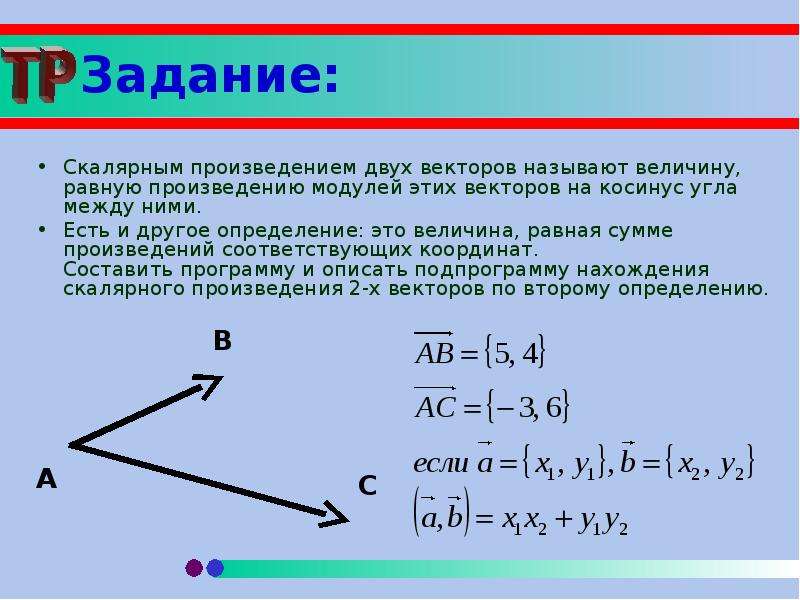

Пусть вектор а = \(\overrightarrow{OA}\) имеет координаты х, у, z. Тогда, по определению проекции,

пр_l а = | a | cos\(\widehat{(i, a)}\).

Но | a | cos\(\widehat{(i, a)}\) = x, т. е. проекция любого вектора на ось l равна абсциссе этого вектора в выбранном нами базисе.

Так как абсцисса суммы векторов равна сумме абсцисс слагаемых векторов, то, следовательно, и проекция суммы векторов на ось l равна сумме проекций этих векторов на ось l.

Точно так же и проекция произведения вектора на число равна произведению этого числа на проекцию вектора, так как при умножении вектора на число его абсцисса умножается на это число.

Сумма, разность векторов, произведение вектора на число. Свойства этих операций.

Линейные операции над векторами.

Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.

b

a+b

a Замечание. Такое правило сложения векторов называют правилом треугольника.

Свойство 1. a + b = b + a.

Свойство 2. (a+b)+c=a+(b+c).

Свойство

3. Для любого вектора а существует нулевой вектор О такой, что а+О=а.

Свойство 4. Для каждого вектора а существует противоположный ему вектор а^/ такой, что а+а^/=О.

Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.

a a—b

b

Произведением ka вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением а при k>0 и противоположное а при k<0.

Свойство 1. k(a + b) = ka + kb.

Свойство 2. (k + m)a = ka + ma.

Свойство 3. k(ma) = (km)a.

Следствие. Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b

= ka.

55. Угол между векторами.

Угол между векторами

56. Вычисление ортогональной проекции.

Так как , каждый вектор однозначно раскладывается в сумму векторов и . Вектор х₁ называется ортогональной проекцией х на .Легко видеть, что х₂ – ортогональная проекция х на .

Найдем ортогональную проекцию х на в предположении, что в задан некоторый ортогональный базис h₁,…,h_k. Дополним этот базис до ортогонального базиса в пространстве ε, присоединив к нему произвольный ортогональный базис h

k₊₁,…,h_n из . Так как сумма и прямая, искомое разложение вектора х единственно, и мы, группируя слагаемые в формуле:

получаем: .

Если k = 1, проекция имеет вид х₁ = ((х, h)/|h|²)h, и мы видим, что правая часть формулы – сумма проекций на ортогональные одномерные пространства, натянутые на h₁,…,h_k. Так же истолковывается формула , а значит, равенство Парсеваля является обобщением теоремы Пифагора.

Из (х₁

, х₂) = 0 следует .

Длина |х₂| ортогональной проекции х на обладает следующим свойством минимальности, обобщающую теорему о длине перпендикуляра и наклонной из элементарной геометрии.

Предположение: Пусть х₁ – ортогональная проекция х на . Тогда для любого вектора , отличного от х₁, выполнено

.

Доказательство. Обозначив х₁ – у через z, имеем: .

Но (z, x₂) = 0, так как , и, следовательно,

Отсюда непосредственно вытекает доказываемое утверждение.

57. Ортогональная проекция суммы векторов и произведения вектора на число.

58. Линейная комбинация векторов, линейно независимые вектора.

    Условия линейной зависимости векторов.

Линейной комбинацией векторов а_1, а₂,…,а_n называется выражение вида: k₁a₁ + k₂a₂ +…+ k_na_n, где k_i – числа.

Векторы а_1, а₂,…,а_n называются линейно зависимыми, если существует такая линейная комбинация k₁a₁ + k₂a₂ +…+ k_na_n = 0. (2),

при k

i не равных нулю одновременно, т.е. k₁² + k₂² +…+ k_n² ≠ 0.

Если же равенство (2) возможно только при всех k_i = 0, векторы называются линейно независимыми.

Замечание 1. Если система векторов содержит нулевой вектор , то она линейно зависима.

Замечание 2. Если среди n векторов какие-либо (n-1) линейно зависимы, то и все n векторов линейно зависимы. (Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.)

Замечание 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

Замечание 3. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.

Замечание 4. Необходимым и достаточным условием линейной зависимости трех векторов является их компланарность.

Замечание 5. Любые четыре вектора в трехмерном пространстве линейно зависимы.

Закон сложения векторов в виде параллелограмма — Формула, Утверждение

Закон сложения векторов в виде параллелограмма

— это метод, который используется для нахождения суммы двух векторов в теории векторов. Мы изучаем два закона сложения векторов — треугольный закон сложения векторов и параллелограммный закон сложения векторов. Закон сложения векторов параллелограмма используется для сложения двух векторов, когда векторы, которые должны быть сложены, образуют две смежные стороны параллелограмма путем соединения хвостов двух векторов. Тогда сумма двух векторов определяется диагональю параллелограмма, проходящей через хвост двух векторов.

В этой статье мы рассмотрим закон параллелограмма сложения векторов, его формулу, формулировку и доказательство. Мы научимся применять закон с помощью различных примеров для лучшего понимания концепции.

1.	Что такое параллелограммный закон сложения векторов?
2.	Закон параллелограмма формулы сложения векторов
3.	Закон параллелограмма векторного сложения Доказательство
4.	Некоторые частные случаи закона сложения векторов параллелограмма
5.	Часто задаваемые вопросы о законе сложения векторов параллелограмма

Что такое параллелограммный закон сложения векторов?

Закон параллелограмма сложения векторов представляет собой процесс геометрического сложения векторов. Этот закон гласит: «Два вектора можно расположить как смежные стороны параллелограмма так, что их хвосты соединяются друг с другом, а сумма двух векторов равна диагонали параллелограмма, хвост которого совпадает с двумя векторами».

Рассмотрим векторы P и Q на рисунке ниже. Чтобы найти их сумму:

• Шаг 1: Нарисуйте векторы P и Q так, чтобы их хвосты касались друг друга.
• Шаг 2: Завершите параллелограмм, нарисовав две другие стороны.
• Шаг 3: Диагональ параллелограмма, хвост которого совпадает с векторами P и Q , представляет собой сумму двух векторов. то есть Р + Р = Р.

☛Примечание: Здесь вектор R называется результирующим вектором (из P и Q ).

Закон векторов параллелограмма Формула

Рассмотрим два вектора P и Q с углом θ между ними. Сумма векторов

P и Q определяется вектором R , результирующим вектором суммы с использованием закона сложения векторов параллелограмма. Если результирующий вектор R составляет угол β с вектором P , тогда формулы для его величины и направления:

• |R| = √(P ² + Q ² + 2PQ cos θ)
• β = тангенс ^-1 [(Q sin θ)/(P + Q cos θ)]

Мы увидим доказательство этих формул в следующем разделе.

Закон параллелограмма векторного сложения Доказательство

Давайте сначала посмотрим формулировку закона параллелограмма векторов:

Формулировка закона сложения векторов параллелограмма : Если два вектора могут быть представлены двумя соседними сторонами параллелограмма, проведенного из точки, то их результирующий вектор суммы полностью представлен диагональю параллелограмма, проведенного из той же точки .

Теперь, чтобы доказать формулу закона параллелограмма, рассмотрим два вектора P и Q , представленные двумя смежными сторонами OB и OA параллелограмма OBCA соответственно. Угол между двумя векторами равен θ. Сумма этих двух векторов представлена ​​диагональю, проведенной из той же вершины O параллелограмма, результирующий вектор суммы R , который составляет угол β с вектором P .

Продлить вектор P до D так, чтобы CD был перпендикулярен OD. Так как OB параллелен AC, то угол AOB равен углу CAD, поскольку они являются соответствующими углами, т. е. угол CAD = θ. Теперь сначала выведем формулу модуля результирующего вектора R (сторона ОС). Обратите внимание, что

• | Р | = Р
• | Q | = Q
• | Р | = Р

В прямоугольном треугольнике OCD по теореме Пифагора имеем

OC ² = OD ² + DC ²

⇒ OC ^{2 901 21 = (OA + AD) 2 + DC 2 — (1)}

В прямоугольном треугольнике CAD имеем

cos θ = AD/AC и sin θ = DC/AC

⇒ AD = AC cos θ и DC = AC sin θ

⇒ AD = Q cos θ и DC = Q sin θ — (2)

Подставляя значения из (2) в (1), имеем

R ² = (P + Q cos θ) ² + (Q sin θ) ²

⇒ R ² = P ² + Q ² cos ² θ + 2PQ cos θ + Q ² sin ² θ

⇒ R ² = P ² + 2PQ cos θ + Q ² (cos ² θ + sin ² θ)

⇒ R ² = P ² + 2PQ cos θ + Q ² [cos ² θ + sin ² θ = 1]

⇒ R = √( стр. ² + 2PQ cos θ + Q ² ) → Величина результирующего вектора R

Далее определим направление результирующего вектора. В правом треугольнике ODC имеем

тангенс β = DC/OD

⇒ тангенс β = Q sin θ/(OA + AD) [Из (2)]

⇒ тангенс β = Q sin θ/(P + Q cos θ) [Из (2)]

⇒ β = tan ^-1 [(Q sin θ)/(P + Q cos θ)] → Направление результирующего вектора R

Некоторые частные случаи закона сложения векторов параллелограмма

Теперь мы знаем формулу для определения величины и направления суммы двух векторов. Рассмотрим несколько частных случаев и подставим значения в формулу:

Когда два вектора параллельны (в одном направлении)

Если векторы P и Q параллельны, то θ = 0°. Подставляя это в формулу закона параллелограмма векторов, имеем

| Р | = R = √(P ² + 2PQ cos 0 + Q ² )

= √(P ² + 2PQ + Q ² ) [Поскольку cos 0 = 1]

= √(P + Q) ² 90 005

= P + Q

β = tan ^-1 [(Q sin 0)/(P + Q cos 0)]

= tan ^-1 [(0)/(P + Q cos 0)] [Поскольку sin 0 = 0]

= 0°

Когда два вектора действуют в противоположных направлениях

Если векторы P и Q действуют в противоположных направлениях, то мы имеем θ = 180°. Подставляя это в формулу закона параллелограмма сложения векторов, имеем

| Р | = √(P ² + 2PQ cos 180° + Q ² )

= √(P ² — 2PQ + Q ² ) [Поскольку cos 180° = -1]

= √(P — Q) ² или √(Q — P) ²

= P — Q или Q — P

β = tan ^-1 [(Q sin 180°)/(P + Q cos 180° )]

= tan ^-1 [(0)/(P + Q cos 0)] [Поскольку sin 180° = 0]

= 0° или 180°

Когда два вектора перпендикулярны

Если векторов P и Q перпендикулярны друг другу, тогда имеем θ = 90°. По закону сложения векторов параллелограмма имеем

| Р | = √(P ² + 2PQ cos 90° + Q ² )

= √(P ² + 0 + Q ² ) [Поскольку cos 90° = 0] 900 05

= √(P ² + Q ² )

β = tan ^-1 [(Q sin 90°)/(P + Q cos 90°)]

= tan ^-1 [Q/(P + 0) ] [Поскольку cos 90° = 0]

= тангенс ^-1 (Q/P)

Важные замечания о законе параллелограмма сложения векторов:

• Чтобы применить закон сложения векторов параллелограмма, два вектора соединяются хвостами друг друга и образуют смежные стороны параллелограмма.
• Если два вектора параллельны, то величина их результирующего вектора может быть определена простым сложением величин двух векторов.
• Закон треугольника и правило параллелограмма сложения векторов эквивалентны и дают то же значение, что и результирующий вектор.

☛ Похожие темы:

• Калькулятор добавления векторов
• Обработка векторов, указанных в форме i-j
• Неравенство треугольников в векторах
• Вычитание двух векторов

Часто задаваемые вопросы о законе сложения векторов параллелограмма

Государственный параллелограмм Закон сложения векторов в векторной алгебре?

Закон параллелограмма сложения векторов используется для сложения двух векторов путем создания параллелограмма, в котором два вектора являются смежными сторонами (таким образом, что оба они имеют одну и ту же начальную точку). Затем сумма двух векторов определяется диагональю параллелограмма, начинающейся в той же точке, что и два заданных вектора.

Что такое формула закона параллелограмма векторов?

Сумма векторов P и Q определяется вектором R , результирующим вектором суммы. Пусть β будет углом между R и P , тогда формулы для его величины и направления R будут следующими: cos θ)

β = тангенс ^-1 [(Q sin θ)/(P + Q cos θ)]

Когда использовать параллелограммный закон сложения векторов?

Правило сложения векторов в виде параллелограмма используется, когда необходимо определить сумму двух векторов. Этот закон гласит, что сумма двух векторов является диагональю параллелограмма, образованного двумя векторами как смежными сторонами.

Как использовать параллелограммный закон сложения векторов?

Закон параллелограмма гласит, что сумма двух векторов, которые, будучи расположены как смежные стороны параллелограмма (и начинаются в одной и той же точке), являются диагональю параллелограмма, которая также начинается в той же точке.

Как представить результирующий вектор в правиле параллелограмма?

Для любых двух векторов P и Q:

• Величина результирующего вектора R равна, R = √(P ² + Q ^{2 9012 1 + 2PQ cos θ)}
• Направление R с P есть, β = tan ^-1 [(Q sin θ)/(P + Q cos θ)]

Как складывать векторы вместе

Автор: Steven Holzner and

Обновлено: 26 марта 2016 г.

Из книги: Учебник по физике I для чайников с онлайн-практикой

Учебник по физике I для чайников с онлайн-практикой

Посмотреть книгу Купить на Amazon

Вы часто просили добавлять векторы при решении задач по физике. Чтобы добавить два вектора, вы помещаете их голову к хвосту, а затем находите длину и величину результата. Порядок, в котором вы добавляете два вектора, не имеет значения.

Например, предположим, что вы направляетесь на большой конгресс по физике, и вам сказали, что вы должны пройти 20 миль на север, а затем 20 миль на восток, чтобы добраться туда. Под каким углом от вашего текущего местоположения находится конференц-центр и как далеко он находится?

Вы можете записать эти два вектора следующим образом (где восток проходит вдоль положительной оси x ):

(0, 20)

(20, 0)

В этом случае вам нужно сложить эти два вектора, и вы можете сделать это, просто добавив их x и y компоненты по отдельности:

Посчитайте, и ваш результирующий вектор равен (20, 20). Вы только что завершили сложение векторов. Но вопрос задает вектор в терминах величины/угла, а не в координатах. Итак, какова величина вектора от вас к соглашению о физике? Вы можете увидеть ситуацию на следующем рисунке, где у вас есть x и y и вы хотите найти v .

Находка v не так сложно, потому что вы можете использовать теорему Пифагора:

Подставьте цифры, чтобы получить

Итак, конгресс находится в 28,3 милях от нас. А угол тета? Вы знаете

тета = тангенс ^–1 ( y / x ) = тангенс ^–1 (20/20) = 45 градусов

И все — теперь вы знаете, что конвенция находится на расстоянии 28,3 мили под углом 45 градусов.

Пример вопроса

1. Сложите два вектора на следующем рисунке. Один имеет звездную величину 5,0 и угол 45 градусов, а другой имеет звездную величину 7,0 и угол 35 градусов.

   Правильный ответ: звездная величина 12,0, угол 39 градусов.

   1. Разложите два вектора на их компоненты. Для первого вектора примените уравнение v _x = v cos тета, чтобы найти координату x . Это 5,0, потому что 45 градусов = 3,5.

   2. Примените уравнение v _y = v sin тета, чтобы найти y координата первого вектора. Это 5,0 минус 45 градусов или 3,5. Таким образом, первый вектор равен (3.5, 3.5) в координатной форме.

   3. Для второго вектора примените уравнение v _x = v cos тета, чтобы найти координату x . Это 7,0, потому что 35 градусов = 5,7.

   4. Примените уравнение v _y = v sin тета, чтобы найти y координата второго вектора. Это 7,0 минус 35 градусов = 4,0. Таким образом, второй вектор равен (5.7, 4.0) в координатной форме.

   5. Чтобы сложить два вектора, сложите их в виде координат: (3.5, 3.5) + (5.7, 4.0) = (9.2, 7.5).

   6. Преобразование (9.2, 7.5) в форму величины/угла. Примените уравнение тета = тангенс ^–1 ( y / x ), чтобы найти угол, который равен тангенс ^–1 (7,5/9,2) = тангенс ^–1 (0,82) = 39градусов.

   7. Применить уравнение

      , чтобы найти величину, которая равна

      .

      Преобразование в две значащие цифры дает 12.

Практические вопросы

1. Добавьте вектор с величиной 13,0 и углом 27 градусов к вектору с величиной 11,0 и углом 45 градусов.

2. Добавьте вектор с величиной 16,0 и углом 56 градусов к вектору с величиной 10,0 и углом 25 градусов.

3. Добавьте два вектора: первый вектор имеет величину 22,0 и угол 19 градусов, а второй вектор имеет величину 19,0 и угол 48 градусов.

4. Добавьте вектор с величиной 10,0 и углом 257 градусов к вектору с величиной 11,0 и углом 105 градусов.

Ниже приведены ответы на практические вопросы:

1. Величина 23,7, угол 35 градусов

   1. Для первого вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 13,0 x cos 27 градусов = 11,6.

   2. Используйте уравнение v _y = v sin theta , чтобы найти координату y первого вектора: 13,0 x sin 27 градусов, или 5,90. Таким образом, первый вектор равен (11.6, 5.90) ​​в координатной форме.

   3. Для второго вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 11,0 x cos 45 градусов = 7,78.

   4. Используйте уравнение v _y = v sin theta , чтобы найти координату y второго вектора: 11,0 x sin 45 градусов = 7,7 8. Итак, второй вектор равен (7.78, 7.78) в координатной форме.

   5. Сложите два вектора в виде координат: (11.6, 5.90) + (7,78, 7,78) = (19,4, 13,7).

   6. Преобразовать (19.4, 13.7) в форму величины/угла. Используйте уравнение тета = тангенс ^–1 ( y / x ), чтобы найти угол: тангенс ^–1 (13,7/19,4) = тангенс ^–1 (0,71) = 35 градусов.

   7. Применить уравнение

      , чтобы найти величину, которая равна

      .

2. Величина 25,1, угол 44 градуса

   1. Для первого вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 16,0 x cos 56 градусов = 8,95.

   2. Используйте уравнение v _y = v sin theta , чтобы найти координату y первого вектора: 16,0 x sin 56 градусов или 13 .3. Таким образом, первый вектор равен (8.95, 13.3) в координатной форме.

   3. Для второго вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 10,0 x cos 25 градусов = 9,06.

   4. Используйте уравнение v _y = v sin theta , чтобы найти координату y второго вектора: 10,0 x sin 25 градусов = 4,23. Таким образом, второй вектор равен (9.06, 4.23) в координатной форме.

   5. Добавьте два вектора в виде координат: (8.95, 13,3) + (9,06, 4,23) = (18,0, 17,5).

   6. Преобразование вектора (18.0, 17.5) в форму величины/угла. Используйте уравнение тета = тангенс ^–1 ( y / x ), чтобы найти угол: тангенс ^–1 (17,5/18,0) = тангенс ^–1 (0,97) = 44 градуса.

   7. Применить уравнение

      , чтобы найти величину, которая равна

      .

3. Величина 39,7, угол 32 градуса

   1. Для первого вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 22,0 x cos 19 градусов = 20,8.

   2. Используйте уравнение v _y = v sin theta , чтобы найти координату y первого вектора: 22,0 x sin 19 градусов, или 7,16. Таким образом, первый вектор равен (20.8, 7.16) в координатной форме.

   3. Для второго вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 19,0 x cos 48 градусов = 12,7.

   4. Используйте уравнение v _y = v sin theta , чтобы найти координату y второго вектора: 19,0 x sin 48 градусов = 14. 1. Таким образом, второй вектор равен (12.7, 14.1) в координатной форме.

   5. Сложите два вектора в виде координат: (20.8, 7.16) + (12.7, 14.1) = (33.5, 21.3).

   6. Преобразование вектора (33.5, 21.3) в форму величины/угла. Используйте уравнение тета = тангенс ^–1 ( y / x ), чтобы найти угол: тангенс ^–1 (21,3/33,5) = тангенс ^–1 (0,64) = 32 градуса.

   7. Применить уравнение

      , чтобы найти величину, которая равна

      .

4. Величина 5,2, угол 170 градусов

   1. 1. Для первого вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 10,0 x cos 257 градусов = -2,25.

   2. Используйте уравнение v _y = v sin theta , чтобы найти координату y первого вектора: 10,0 x sin 257 градусов, или -9,74. Итак, первый вектор равен (–2,25, –9,74) в координатной форме.

   3. Для второго вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 11,0 x cos 105 градусов = -2,85.

   4. Используйте уравнение v _y = v sin theta , чтобы найти координату y второго вектора: 11,0 x sin 105 градусов = 10,6. Таким образом, второй вектор равен (–2,85, 10,6) в координатной форме.