Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Определение 1

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

R→=F1→+F2→+F3→+…+Fn→=∑i=1nFi→.

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

Определение 2

Для сложения 2-х сил используют правило параллелограмма (рисунок 1).

Рисунок 1. Сложение 2-х сил по правилу параллелограмма

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R→=F1→2+F2→2+2F1→2F2→2cos α

Определение 3

При необходимости сложения более 2-х сил используют правило многоугольника

: от конца
1-й силы необходимо провести вектор, равный и параллельный 2-й силе; от конца 2-й силы необходимо провести вектор, равный и параллельный 3-й силе и т. д.

Рисунок 2. Сложение сил правилом многоугольника

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4-х сил: F1→, F2→, F3→, F4→. Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Определение 4

Линией действия силы называют прямую, проходящую через вектор силы. 

Рисунок 3. Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3).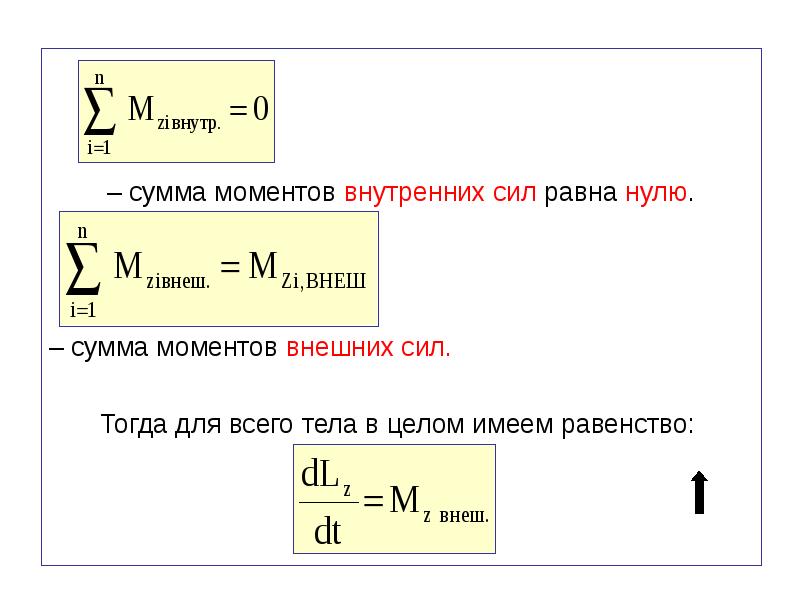 Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0: ∑i=1nFi→=0→. В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Разложение вектора силы по направлениям

Определение 5

Разложение сил на две составляющие – это замена одной силы 2-мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2, приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

• направления 2-х составляющих сил;
• модуль и направление одной из составляющих сил;
• модули 2-х составляющих сил.

Пример 1

Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b. Отрезок FA и отрезок FB изображают искомые силы.

Рисунок 4. Разложение вектора силы по направлениям

Пример 2

Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2-й проекции (рисунок 5 а ).

Рисунок 5. Нахождение проекции вектора силы по заданным векторам

Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F2→ силы F→.

Итак, 2-й способ решения: прибавим к силе силу, равную -F1→ (рисунок 5 в). В итоге получаем искомую силу F→.

Пример 3

Три силы F1→=1 Н; F2→=2 Н; F3→= 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а) и составляют углы с горизонталью α=0°; β=60°; γ=30° соответственно. Необходимо найти равнодействующую силу.

Решение

Рисунок 6.

Нахождение равнодействующей силы по заданным векторам

Нарисуем взаимно перпендикулярные оси ОХ и OY таким образом, чтобы ось ОХ совпадала с горизонталью, вдоль которой направлена сила F1→. Сделаем проекцию данных сил на координатные оси (рисунок 6 б). Проекции F2y и F2x отрицательны. Сумма проекций сил на координатную ось ОХ равняется проекции на данную ось равнодействующей: F1+F2cosβ-F3cosγ=Fx=4-332≈-0,6 Н.

Точно также для проекций на ось OY: -F2sin β+F3sin γ=Fy=3-232≈-0,2 Н.

Модуль равнодействующей определим с помощью теоремы Пифагора:

F=Fx2+Fy2=0,36+0,04≈0,64 Н.

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в):

tg φ=FyFx=3-234-33≈0,4.

Пример 4

Сила F=1 кН приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Рисунок 7. Нахождение составляющих силы F по направлениям стержней кронштейна

Дано:

F=1 кН=1000 Н

Пускай стержни прикручены к стене в точках А и С. На рисунке 7 б изображено разложение силы F→ на составляющие вдоль направлений АВ и ВС. Отсюда понятно, что

F1→=Ftg β≈577 Н;

F2→=Fcos β≈1155 Н.

Ответ: F1→=557 Н; F2→=1155 Н.

Автор: Роман Адамчук

Преподаватель физики

Формула равнодействующей всех сил в физике

Формула равнодействующей всех сил в физике

Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($\overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $\overline{F}$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.

Определение и формула равнодействующей всех сил

В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:

\[\overline{F}=m\overline{a}\ \left(1\right),\]

где $m$ — масса тела, на которое действует сила $\overline{F}$; $\overline{a}$ — ускорение, которое сила $\overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.

На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. \circ )\ }}\approx 26,5\ \left(Н\right).\]

Ответ. $F=26,5$ Н

Пример 2

Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?

Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:

\[\overline{F}={\overline{F}}_1+{\overline{F}}_2+{\overline{F}}_3+{\overline{F}}_4\left(2.1\right).\]

Найдем равнодействующую сил ${\overline{F}}_1$ и ${\overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:

\[F_{12}=F_1-F_2=17-11=6\ \left(H\right).\]

Так как $F_1>F_2$, то сила ${\overline{F}}_{12}$ направлена в туже сторону, что и сила ${\overline{F}}_1$.

Найдем равнодействующую сил ${\overline{F}}_3$ и ${\overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:

\[F_{34}=F_3-F_4=18-10=8\ \left(Н\right).\]

Направление силы ${\overline{F}}_{34}$ совпадает с направлением вектора ${\overline{F}}_3$, так как ${\overline{F}}_3>{\overline{F}}_4$. 2}=10\ \left(Н\right).\]

Ответ. $F$=10 Н

Читать дальше: формула равнодействующей силы.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

В статике сумма сил равна нулю

Урок: В статике сумма сил равна нулю.

Термин статика относится к объекту или системе, находящейся в статическом равновесии. Объект или система неподвижны, потому что все силы равны нулю.

Второй закон Ньютона:

ΣF = Σ(ma) = m ₁ a ₁ + m ₂ a ₂ + m ₃ a ₃ + • • • + m _п а _n

Сумма сил равна произведению массы на ускорение. Второй закон говорит нам, что если объект или система неподвижны, ускорение равно нулю. Поэтому сумма векторных сил должна быть равна нулю.

Пример. Рассмотрим стол с четырьмя ножками и объект массой 200 кг, неподвижно покоящийся в центре стола:

 Масса объекта = 200 кг
______________
  | | Масса стола = 100 кг
  | |
  | | Какие силы действуют на
                 нижняя часть каждой ножки стола?
 

Сила, действующая вверх на ноги, определяется путем уравновешивания этих сил в уравнении, заданном законом Ньютона:

ΣF = ma = 0 = — (200 кг X 9,81 м/с ² ) — (100 кг X 9,81 м/с ² ) + (сила _опора X 4)

Гравитация действует вниз на 200-килограммовый объект и 100-килограммовый стол. Следовательно, мы можем заменить ускорение свободного падения (на Земле) g (9,81 м/с ² ) вместо a.

Сила _опора = ((200 кг X 9,81 м/с ² ) + (100 кг X 9,81 м/с ² )) / 4

Единица кг•м/с ² эквивалентна единице силы, называемой ньютоном (Н). Таким образом, при умножении килограммы сокращаются.

Сила _опора = (1962 Н + 981 Н) / 4

Сила _ноги = 735,75 Н

Это означает, что каждая ножка оказывает на пол направленное вниз усилие в 735,75 ньютонов, и одновременно пол воздействует на каждую ножку стола вверх с такой же силой.

Обратите внимание, что очень важно соблюдать единое соглашение о знаках на протяжении всего анализа. Соглашение о знаках обычно выбирается в более сложных задачах, чтобы упростить общий объем алгебры, необходимый для анализа уравнений по осям x, y и z. Мы выбрали положительные значения для обозначения сил, направленных вверх, и отрицательные значения для обозначения сил, направленных вниз, но мы могли бы использовать и противоположные значения, если бы были последовательны.

Следствие для крутящего момента[править | изменить источник]

Урок: В статике сумма крутящих моментов равна нулю.

Сумма всех вращательных сил или крутящих моментов, обозначаемая заглавной греческой буквой тау (T{\displaystyle \mathrm {T}}), также равна нулю. Обычно используемыми единицами измерения крутящего момента являются фут•фунты (ft•lb) и ньютон•метры (Н•м).

Второй закон Ньютона (применительно к крутящим моментам):

ΣT {\ displaystyle \ mathrm {T}} = Σ (ωI) = ω ₁ I ₁ + ω ₂ I ₂ + ω ₃ я ₃ + • • • + ω _n I _n

Сумма крутящих моментов равна массе вращения (или моменту инерции I), умноженному на угловое ускорение (обозначается строчной греческой буквой омега, ω ). Второй закон говорит нам, что если объект или система неподвижны, то угловое ускорение равно нулю. Поэтому сумма векторов моментов должна быть равна нулю.

Крутящие моменты также могут быть рассчитаны как сила, умноженная на расстояние:

ΣT {\ displaystyle \ mathrm {T}} = Σ (Fd) = F ₁ d ₁ + F ₂ d ₂ + F ₃ d ₃ + • • • + F _n d _n

Пример. Рассмотрим невесомый рычаг с двумя прикрепленными грузами. и один безмассовый носитель:

 | + Вес объекта 1 = 10 фунтов
 | /| Расстояние от точки опоры = 10 футов
 | / |
 | Р/ | Расстояние поддержки
Вт| E/|S w1 от точки опоры = 7 футов
А| В/ |У
л| E/ |P Вес объекта 2 = 80 фунтов
л| л/| |P Расстояние от точки опоры = 4 фута
 | / w2 |О
 | / |R Какие силы действуют на
   |/ |T  безмассовый рычаг ?
   ПОЛ
 

Сначала напишем уравнение статического крутящего момента для системы:

ΣT {\ displaystyle \ mathrm {T}} = Σ (Fd) = F ₁ d ₁ + F _S d _S + F ₂ d 9001 1 2 = 0

Силы 1 и 2 на самом деле являются весами двух объектов:

ΣT {\ displaystyle \ mathrm {T}} = Σ (Fd) = w ₁ d ₁ + F _S d _S + w ₂ д ₂ = 0

Заменить известными значениями:

ΣT {\ displaystyle \ mathrm {T}} = Σ (Fd) = (-10 фунтов) (10 футов) + F _S (7 футов) + (-80 фунтов) (4 фута) = 0

Решите для F _S :

ΣT {\ displaystyle \ mathrm {T}} = Σ (Fd) = (-100 ft•lb) + F _S (7 футов) + (-320 ft•lb) = 0

F _S (7 футов) = (420 фут•фунт)

F _S = (420 ft•lb)/(7 ft) = 60 lb

Таким образом, сила в 60 фунтов действует на рычаг вверх от опоры, чтобы уравновесить крутящие моменты на рычаге. Так как общий вес на рычаге равен 90 фунтов и 60 из этих фунтов противодействуют опоре, остальные 30 фунтов должны воздействовать вверх на рычаг в точке опоры в нижнем, левом углу.

Обратите внимание, что нам не нужно было использовать точку опоры как точку отсчета всех расстояний, мы могли выбрать любую точку вдоль рычага. Однако, как и в случае с силами, необходимо использовать последовательное соглашение о знаках. В этом случае положительные значения могут использоваться для крутящих моментов по часовой стрелке (CW), измеренных с одной точки зрения, а отрицательные крутящие моменты могут использоваться для крутящих моментов против часовой стрелки (CCW), измеренных с той же точки обзора. Можно было бы использовать и противоположную систему, если бы мы были последовательны.

Также обратите внимание, что в приведенном ранее примере таблицы указано, что объект находится в центре таблицы. Если нет, то уравновешивание крутящих моментов (в двух направлениях) приведет к большей силе, поддерживаемой одними ножками стола, и меньшей — к другим. Например, если бы объект находился прямо над одной из ножек, то весь его вес поддерживался бы этой ногой в дополнение к одной четвертой веса стола. Тогда остальные ножки будут поддерживать только одну четвертую веса стола каждая.

Ньютоновская механика — Какова правильная математическая форма уравнения суммы сил?

спросил 5 лет, 6 месяцев назад

Изменено 2 года, 4 месяца назад

Просмотрено 1к раз

$\begingroup$

Я сдал работу по второму закону физики в форме, которую нашел в учебнике. Он описал Второй закон как «Сумму сил»:

$$\sum_i F_i=ma$$ Мой учитель говорит, что это неверно, потому что закон силы является «векторным» законом. Я смущен этим, потому что я думал, что результат суммы был скаляром. Как правильно думать об уравнении «сумма сил»? Почему мой учебник дает эту форму, если она неверна?

• ньютоновская механика
• силы
• векторы

$\endgroup$

1

$\begingroup$

Математический вектор подчиняется двум законам алгебры.

• Скалярный закон — Умножение скалярной величины $\lambda$ на вектор $\mathbf{a}$ представляет собой вектор, в котором каждый элемент умножается (отдельно).

$$ \lambda \mathbf{a} =\lambda \pmatrix{a_1 \\ a_2 \\ \vdots \\ a_n} = \pmatrix{\lambda a_1 \\ \lambda a_2 \\ \vdots \\ \lambda a_n } $$

• Закон сложения — Сложение двух векторов $\mathbf{a}$ и $\mathbf{b}$ представляет собой вектор, в который добавляется каждый элемент (отдельно). $$ \mathbf{a} + \mathbf{b} = \pmatrix{a_1 \\ a_2 \\ \vdots \\ a_n} +\pmatrix{b_1 \\ b_2 \\ \vdots \\ b_n} = \pmatrix{a_1 +b_1\a_2+b_2\\vdots\a_n+b_n}$$

Вектор силы, вектор скорости или вектор ускорения подчиняются тем же законам математического вектора.

Таким образом, сумма сил представляет собой вектор, в котором каждая компонента ($x$, $y$ и $z$) складывается отдельно.

$$ \mathbf{F}_1 + \mathbf{F}_2 = \pmatrix{F_{1x} + F_{2x} \\ F_{1y} + F_{2y} \\ F_{1z} + F_{ 2z} } $$

Итак, правильная форма второго закона Ньютона:

$$ \sum_i \mathbf{F}_i = m\, \mathbf{a}_{\rm C} $$, где точка C — центр масс. Это прямой результат определения линейного импульса как $$\mathbf{p} = m\, \mathbf{v}_{\rm C} $$ и второго закона $$\sum_i \mathbf{F} _i = \frac{\rm d}{{\rm d}t} \mathbf{p}$$

$\endgroup$

5

$\begingroup$

Вы оба правы, когда работаете в инерциальной системе отсчета и интересующая вас система имеет постоянную массу: 9Н$.

В классических системах $N=3$.

Примечание: $S$ также является вектором, хотя я намеренно опустил знак $\vec{}$.

---

В общем случае второй закон имеет вид $\vec{F} = \frac{d\vec{P}}{dt}$, где $\vec{P}= m \vec{V}$ — импульс, а $\vec{V}$ — скорость.

$\endgroup$

1

$\begingroup$

Сила — это вектор. Поэтому вам нужно сделать векторное сложение, т.е. вам нужно учитывать направление каждой силы. Возможно, вам придется разбить каждую силу на ее горизонтальную и вертикальную составляющие, а затем добавить их соответственно (не забывая направления).