Формула равнодействующей силы, F

В соответствии с первым законом Ньютона в инерциальных системах отсчета тело может изменять свою скорость только, если на него действуют другие тела. Количественно взаимное действие тел друг на друга выражают с помощью такой физической величины, как сила (). Сила может изменять скорость тела, как по модулю, так и по направлению. Сила является векторной величиной, у нее есть модуль (величина) и направление. Направление равнодействующей силы определяет направление вектора ускорения тела, на которое действует рассматриваемая сила.

Основной закон, при помощи которого определяют направление и величину равнодействующей силы – это второй закон Ньютона:

   

где m – масса тела, на которое действует сила ; – ускорение, которое сила сообщает рассматриваемому телу. Сущность второго закона Ньютона состоит в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Необходимо помнить, что второй закон Ньютона работает для инерциальных систем отсчета.

В том случае, если на тело действует несколько сил, то их совместное действие характеризуют при помощи равнодействующей силы. Допустим, что на тело действует одновременно несколько сил, при этом тело перемещается с ускорением, равным векторной сумме ускорений, которые появились бы при воздействии каждой из сил в отдельности. Силы, действующие на тело, и приложенные к одной его точке необходимо складывать по правилу сложения векторов. Векторная сумма всех сил, действующих на тело в один момент времени, называется равнодействующей силой ():

   

Выражение (2) можно считать формулой для вычисления равнодействующей силы. Равнодействующая сила – это гипотетический (искусственный) параметр, который вводят для того, чтобы удобнее было производить расчеты.

При действии на тело нескольких сил, второй закон Ньютона записывают как:

   

Равнодействующая всех сил, действующих на тело, может быть равна нулю, в том случае, если происходит взаимная компенсация сил, приложенных к телу. В таком случае тело движется с постоянной скоростью или находится в покое.

При изображении сил, действующих на тело, на чертеже, в случае равноускоренного перемещения тела, равнодействующую силу, направленную по ускорению следует изображать длиннее, чем противоположно ей направленную силу (сумму сил). В случае равномерного движения (или покоя) дина векторов сил, направленных в противоположные стороны одинакова.

Для нахождения равнодействующей силы, следует изобразить на чертеже все силы, которые необходимо учитывать в задаче, действующие на тело. Складывать силы следует по правилам сложения векторов.

Примеры решения задач по теме «Равнодействующая сила»

Законы сложения сил в механике

При одновременном действии на одно тело нескольких сил тело движется с ускорением, являющимся векторной суммой ускорений, которые бы возникли под действием каждой силы в отдельности. Действующие на тело силы, приложенные к одной точке, складываются по правилу сложения векторов.

Векторная сумма всех сил, одновременно действующих на тело, называется равнодействующей силой и определяется правилом векторного сложения сил: $\overrightarrow{R}={\overrightarrow{F}}_1+{\overrightarrow{F}}_2+{\overrightarrow{F}}_3+\dots +{\overrightarrow{F}}_n=\sum^n_{i=1}{{\overrightarrow{F}}_i}$.

Равнодействующая сила оказывает на тело такое же действие, как сумма всех приложенных к нему сил.

При этом модуль суммы двух сил находим по теореме косинусов:

\[\left|\overrightarrow{R}\right|=\sqrt{{\left|{\overrightarrow{F}}_1\right|}^2+{\left|{\overrightarrow{F}}_2\right|}^2+2{\left|{\overrightarrow{F}}_1\right|}^2{\left|{\overrightarrow{F}}_2\right|}^2{cos \alpha \ }}\]

Если нужно сложить более двух сил, приложенных в одной точке, то пользуются правилом многоугольника:~ из конца первой силы проводят вектор, равный и параллельный второй силе; из конца второй силы — вектор, равный и параллельный третьей силе и так далее.

Рисунок 2. Сложение сил по правилу многоугольника

Замыкающий вектор, проведённый из точки приложения сил к концу последней силы, по величине и направлению равен равнодействующей. На рис.2 это правило проиллюстрировано на примере нахождения равнодействующей~~четырёх сил ${\overrightarrow{F}}_1,\ {\overrightarrow{F}}_2,{\overrightarrow{F}}_3,{\overrightarrow{F}}_4$. Заметим, что при этом складываемые векторы не обязательно должны принадлежать одной плоскости.

Результат действия силы на материальную точку зависит только от ее модуля и направления. Твердое же тело имеет определенные размеры. Поэтому одинаковые по модулю и направлению силы вызывают различные движения твердого тела в зависимости от точки приложения. Прямая, проходящая через вектор силы, называется линией действия силы.

Рисунок 3. Сложение сил, приложенных к разным точкам тела

Если силы приложены к разным точкам тела и действуют не параллельно друг другу, то равнодействующая приложена к точке пересечения линий действия сил (рис.3).

Точка находится в равновесии, если векторная сумма всех сил, действующих на нее, равна нулю: $\sum^n_{i=1}{{\overrightarrow{F}}_i}=\overrightarrow{0}$. В этом случае равна нулю и сумма проекций этих сил на любую ось координат.

Замену одной силы двумя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила, называют разложением сил. Разложение сил производят, как и их сложение, по правилу параллелограмма.

Задача разложения одной силы (модуль и направление которой известны) на две, приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, если известны:

1. направления обеих составляющих сил;
2. модуль и направление одной из составляющих сил;
3. модули обеих составляющих сил.

Пусть, например, мы хотим разложить силу $F$ на две составляющие, лежащие в одной плоскости с F и направленные вдоль прямых а и b (рис.4). Для этого достаточно из конца вектора, изображающего F, провести две прямые, параллельные a и b. Отрезки $F_A$ и $F_B$ изобразят искомые силы.

Рисунок 4. Разложение вектора силы по направлениям

Другой вариант этой задачи — нахождение одной из проекций вектора силы по заданным векторам силы и второй проекции. (рис.5 а).

Рисунок 5. Нахождение проекции вектора силы по заданным векторам

Задача сводится к построению параллелограмма по диагонали и одной из сторон, известному из планиметрии. На рис.5б построен такой параллелограмм и указана искомая составляющая ${\overrightarrow{F}}_2$ силы ${\overrightarrow{F}}$.

Второй способ решения: прибавить к силе силу, равную — ${\overrightarrow{F}}_1$ (рис.5в).В результате получим искомую силу ${\overrightarrow{F}}_2$.

Сила. Сложение сил – FIZI4KA

1. Ускорения взаимодействующих тел обратно пропорциональны их массам: ​\( \frac{a_1}{a_2}=\frac{m_2}{m_1} \)​. Преобразовав это равенство, получаем:​ \( m_1a_1=m_2a_2 \)​. В правой и в левой частях равенства стоят одинаковые величины для двух взаимодействующих тел, причем значения ускорений тел не зависят от условий их взаимодействия. Следовательно, можно считать, что произведение массы тела и его ускорения характеризует взаимодействие тел и это произведение равно силе, действующей на тело со стороны другого взаимодействующего с ним тела, т.е.: ​\( \vec{F}=m\vec{a} \)​.

Силой называют физическую величину, характеризующую взаимодействие тел и равную произведению массы тела и его ускорения. Поскольку ускорение векторная величина, а масса скалярная, то сила — векторная величина: \( \vec{F}=m\vec{a} \).

2. Единица силы, в отличие от единицы массы, является производной единицей СИ. ​\( [\,F\,]=[\,m\,][\,a\,] \)​; ​\( [\,F\,] \)​ = 1кг · 1 м/с². \( [\,F\,] \) = 1 Н (1 ньютон).

Один ньютон — это такая сила, которая телу массой 1 кг сообщает ускорение 1 м/с².

3. Результат действия силы зависит от её модуля, направления и точки приложения. Например, дверную ручку прикрепляют как можно дальше от петель, на которых она висит, поскольку, чем ближе к петлям подействовать силой, тем труднее дверь открыть.

4. Прибором для измерения силы служит динамометр. В соответствии с законом Гука удлинение пружины прямо пропорционально силе упругости, поэтому по удлинению пружины можно судить о приложенной к пружине силе, которая равна силе упругости.

5. Обычно на тело действуют несколько сил. Например, на тело, падающее в воздухе, действуют сила тяжести и сила сопротивления воздуха; на груз, висящий на нити, действуют сила тяжести и сила упругости нити.

При этом действие каждой силы не зависит от действия других, т.е. каждая сила сообщает телу такое ускорение, какое она сообщила бы ему в отсутствие действия других сил. Это утверждение носит название принципа независимости действия сил. Поэтому при расчёте ускорения движения тела все действующие на него силы заменяют одной силой.

Равнодействующей силой называют силу, которая оказывает на тело такое же действие, как и все действующие на него силы вместе.

Равнодействующую силу находят по правилу сложения векторов, она равна геометрической сумме действующих на тело сил.

Если силы, действующие на тело, направлены по одной прямой в одну сторону, то ​\( \vec{F}=\vec{F}_1+\vec{F}_2 \)​, а модуль равнодействующей равен сумме модулей действующих сил ​\( F=F_1+F_2 \)​ (рис. 30).

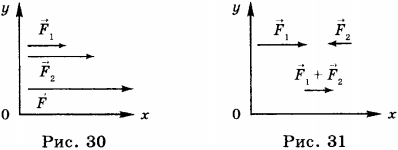
Если силы, действующие на тело, направлены в разные стороны, то \( \vec{F}=\vec{F}_1+\vec{F}_2 \), а модуль равнодействующей равен разности модулей действующих сил: \( F=F_1-F_2 \) (рис. 31 ).

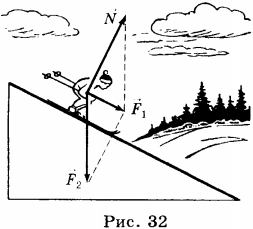
Если силы направлены под углом друг к другу, то равнодействующая равна диагонали параллелограмма, построенного на действующих на тело силах как на сторонах, или стороне треугольника, начало которой совпадает с началом вектора ​\( \vec{F}_1 \)​, а конец с концом вектора \( \vec{F}_2 \) (рис. 32).

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Ускорение движения парашютиста с раскрытым парашютом определяется его взаимодействием

1) только с Землёй
2) только с Землёй и с воздухом
3) только с Землёй и с парашютом
4) с Землёй, воздухом и парашютом

2. Сила — это мера

1) быстроты движения
2) инертности
3) взаимодействия
4) быстроты изменения скорости

3. Какие из приведённых ниже величин всегда совпадают по направлению?

1) сила и скорость
2) сила и перемещение
3) сила и ускорение
4) ускорение и перемещение

4. На рисунке а) показаны направления силы, действующей на тело, и его скорости. Какой из четырёх векторов, приведённых на рисунке б), указывает направление ускорения, с которым движется это тело?

1) 1
2) 2
3) 3
4) 4

5. На тело, находящееся на полу движущегося лифта, действуют сила тяжести 90 Н и сила упругости со стороны пола лифта, равная 75 Н. Чему равна равнодействующая этих сил и как она направлена?

1) 45 Н, направлена в ту же сторону, что и сила тяжести
2) 45 Н, направлена в ту же сторону, что и сила упругости
3) 125 Н, направлена в ту же сторону, что и сила тяжести
4) 125 Н, направлена в ту же сторону, что и сила упругости

6. На тело действуют две силы модули которых, — ​\( F_1 \)​ = 30 Н и \( F_2 \) = 40 Н, направленные под углом 90° друг к другу. Чему равна равнодействующая этих сил?

1) 70 Н
2) 50 Н
3) 40 Н
4) 10 Н

7. Чему равна равнодействующая сил, действующих на тело (рис.), если ​\( \vec{F}_1 \)​ = 4 Н, \( \vec{F}_2 \) = 16 Н, \( \vec{F}_3 \) = 22 Н, \( \vec{F}_4 \) = 6 Н?

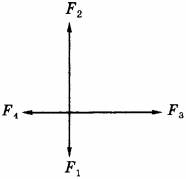
1) 48 Н
2) 34 Н
3) 28 Н
4) 20 Н

8. Чему равна сила, под действием которой тело массой 8 кг получает ускорение 4 м/с²?

1) 32 Н
2) 8 Н
3) 2 Н
4) 0,5 Н

9. Результат действия силы зависит от

А. Её направления
Б. Точки приложения

Правильный ответ:

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

10. На наклонной плоскости покоится брусок, на который действуют сила тяжести ​\( \vec{F} \)​, сила реакции опоры \( \vec{N} \) и сила трения покоя \( \vec{F}_{тр} \). Чему равна равнодействующая этих сил?

1) 0
2) ​\( F+N+F_{тр} \)​
3) ​\( F_{тр} \)​
4) ​\( F + N \)​

11. Установите соответствие между физическими величинами в левом столбце и их единицами в правом столбце. В таблице под номером физической величины левого
столбца запишите соответствующий номер выбранной вами единицы величины из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) масса
Б)сила
B)ускорение

ЕДИНИЦА ВЕЛИЧИНЫ
1) Ньютон (Н)
2) метр в секунду в квадрате (м/с²)
3) килограмм (кг)

12. Из приведённых высказываний выберите два верных и запишите их номера.

1) Из двух тел разной массы при действии на них одинаковой силы большее ускорение приобретет тело большей массы.
2) Сила равна произведению массы тела и его ускорения.
3) Направление движения тела всегда совпадает с направлением силы.
4) Сила — причина ускорения тела.

Часть 2

13. На автомобиль массой 1 т действуют сила тяги 1700 Н и сила трения 200 Н. С каким ускорением движется автомобиль?

Ответы

Сила. Сложение сил

5 (100%) 1 vote

Формула равнодействующей всех сил в физике

Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($\overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $\overline{F}$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.

Определение и формула равнодействующей всех сил

В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:

\[\overline{F}=m\overline{a}\ \left(1\right),\]

где $m$ — масса тела, на которое действует сила $\overline{F}$; $\overline{a}$ — ускорение, которое сила $\overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.

На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($\overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:

\[\overline{F}={\overline{F}}_1+{\overline{F}}_2+\dots +{\overline{F}}_N=\sum\limits^N_{i=1}{{\overline{F}}_i}\ \left(2\right).\]

Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.

Основной закон динамики поступательного движения при наличии нескольких сил

Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:

\[\sum\limits^N_{i=1}{{\overline{F}}_i}=m\overline{a}\left(3\right).\]

$\overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.

При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.

Когда нах

Сила, второй закон Ньютона — ЗФТШ, МФТИ

Сила является мерой взаимодействия (взаимного действия). Если действие велико (мало), то говорят о большой (малой) силе. Сила обозначается буквой $$F$$ (первая буква слова force).

При взаимодействии чем больше сила, тем больше ускорение тела, на которое эта сила действует. Следовательно, ускорение прямо пропорционально действующей силе: a∼Fa\sim F.

Но уже говорилось о том, что ускорение зависит от массы тела: a∼1ma \sim \frac 1m

Обощая эти зависимости получим:

\[a = \frac{F}{m}, \quad \mathrm{или}\quad F = ma.\]

Теперь рассмотрим свойства силы, устанавливаемые опытным путём:

1) Результат действия (проявления) силы зависит от направления действующей силы, следовательно, сила – величина векторная.

2)  Результат действия (проявления) силы зависит от величины приложенной силы .

3)  Результат действия (проявления) силы зависит от точки приложения силы.

4) За единицу силы принято значение такой силы, которая вызывает ускорение 1 м/с21\ \mathrm{м}/\mathrm{с}^2 у тела массой 1 кг1\ \mathrm{кг}. Единицу силы назвали в честь Исаака Ньютона 1 нью’тон. (Произносить фамилию считается правильным таким образом, как произносится фамилия в том государстве, где проживал или проживает учёный.)

[F→]=1 Н=1 кг·мс2  (ньютон).[\overset{\rightarrow}{F}] = 1\ \mathrm{Н} = 1\ \mathrm{кг}\cdot\frac{\mathrm{м}}{\mathrm{с}^2}\quad \mathrm{(ньютон)}.

5) Если на тело одновременно действуют несколько сил, то каждая сила действует независимо от других. (Принцип суперпозиции сил). Тогда все силы необходимо сложить векторно и получить результирующую силу (рис. 4).

Рис. 4

Из приведённых свойств силы следует, как обобщение опытных фактов, второй закон Ньютона:

Второй закон Ньютона: Сумма всех сил, действующих на тело, равна произведению массы тела на ускорение, сообщаемое этой суммой сил:

∑F→=ma→.\boxed{\sum \vec{F} = m\vec{a}}.

Данное выражение можно представить и в другой форме: так как a→=v→к-v→0t\vec a = \frac{\vec v_\mathrm{к} — \vec v_0}{t}, то второй закон Ньютона примет вид: ∑F→=mv→к-v→0t\sum \vec F = m\frac{\vec v_\mathrm{к} — \vec v_0}{t}.

Произведение массы тела и его скорости называют импульсом тела:

p→=mv→\vec p = m\vec v,

тогда получим новое выражение для второго закона Ньютона:

∑F→=mv→к-mv→0t=p→к-p→0t=Δp→t\boxed{\sum \vec F = \frac{m\vec v_\mathrm{к} — m\vec v_0}{t}} = \frac{\vec p_\mathrm{к} — \vec p_0}{t} = \frac{\Delta \vec p}{t}.

∑F→=p→к-p→0t\boxed{\sum \vec F = \frac{\vec p_\mathrm{к} — \vec p_0}{t}} — второй закон Ньютона в импульсной форме для среднего значения силы. Здесь p→к-p→0=Δp→\vec p_\mathrm{к} — \vec p_0 = \Delta \vec p — изменение импульса тела, t -t\ — время изменения импульса тела.

∑F→=dp→dt -\boxed{\sum \vec F = \frac{d\vec p}{dt}}\ — второй закон Ньютона в импульсной форме для мгновенного значения силы.

Из второго закона в частности следует, что ускорение тела, подвергающегося действию нескольких сил, равно сумме ускорений, сообщаемых каждой силой:

a→=∑a→i=a→1+a→2+…+a→i=∑F→m=F→1+F→2+…+F→im=F→1m+F→2m+…+F→im\boxed{\vec a = \sum \vec a_i = \vec a_1 + \vec a_2 + \dots + \vec a_i = \frac{\sum \vec F}{m} = \frac{\vec F_1 + \vec F_2 + \dots + \vec F_i}{m} = \frac{\vec F_1}{m} + \frac{\vec F_2}{m} + \dots + \frac{\vec F_i}{m}}.

Первая форма записи второго закона (∑F→=ma→)(\sum \vec F = m\vec a) справедлива только при малых скоростях по сравнению со скоростью света. И, разумеется, выполняется второй закон Ньютона только в инерциальных системах отсчёта. Так же следует отметить, что второй закон Ньютона справедлив для тел неизменной массы, конечных размеров и движущихся поступательно.

Второе (импульсное) выражение имеет более общий характер и справедливо при любых скоростях.

Как правило, в школьном курсе физики сила со временем не меняется. Однако последняя импульсная форма записи позволяет учесть зависимость силы от времени, и тогда изменение импульса тела будет найдено с помощью определённого интеграла на исследуемом интервале времени. В более простых случаях (сила изменяется со временем по линейному закону) можно брать среднее значение силы.


Рис. 5

Иногда очень полезно знать, что произведение F→·t\vec F \cdot t называют импульсом силы, и его значение F→·t=Δp→\vec F \cdot t = \Delta \vec p равно изменению импульса тела.

Для постоянной силы на графике зависимости силы от времени можем получить, что площадь фигуры под графиком равна изменению импульса (рис. 5).

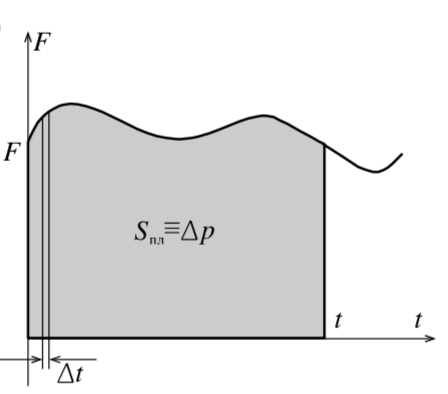
Но даже если сила будет изменяться со временем, то и в этом случае, разбивая время на малые интервалы Δt\Delta t такие, что величина силы на этом интервале остаётся неизменной (рис. 6), а потом, суммируя полученные «столбики», получим:

Площадь фигуры под графиком F(t)F(t) численно равна изменению импульса.

В наблюдаемых природных явлениях сила, как правило, меняется со временем. Мы же часто, применяя простые модели процессов, считаем силы постоянными. Сама же возможность использования простых моделей появляется из возможности подсчёта средней силы, т. е. такой постоянной силы, у которой площадь под графиком от времени будет равна площади под графиком реальной силы.

Рис. 6

Следует добавить ещё одно очень важное следствие второго закона Ньютона, связанное с равенством инертной и гравитационной масс.









Неразличимость гравитационной и инертной масс означает, что и ускорения, вызванные гравитационным взаимодействием (законом всемирного тяготения) и любым другим тоже неразличимы.

Пример 2. Мяч массой 0,5 кг0,5\ \mathrm{кг} после удара, длящегося 0,02 с0,02\ \mathrm{с}, приобретает скорость 10 м/с10\ \mathrm{м}/\mathrm{с}. Найти среднюю силу удара.

Решение. В данном случае рациональнее выбрать второй закон Ньютона в импульсной форме, т. к. известны начальная и конечная скорости, а не ускорение, и известно время действия силы. Также следует отметить, что сила, действующая на мяч, не остаётся постоянной. По какому закону меняется сила со временем, неизвестно. Для простоты мы будем пользоваться предположением, что сила постоянная, и её мы будем называть средней.

Тогда ∑F→=Δp→t\sum \vec F = \frac{\Delta \vec p}{t}, т. е. F→ср·t=Δp→\vec F_\mathrm{ср}\cdot t = \Delta \vec p. В проекции на ось, направленной вдоль линии действия силы, получим: Fср·t=pк-p0=mvкF_\mathrm{ср}\cdot t = p_\mathrm{к}-p_0 = mv_\mathrm{к}. Окончательно для искомой силы получим:

\[F_\mathrm{ср} = \frac{mv_\mathrm{к}}{t}.\]

Количественно ответ будет таким: Fср=0,5 кг·10 мс0,02 с=250 НF_\mathrm{ср} = \frac{0,5\ \mathrm{кг}\cdot 10\ \frac{\mathrm{м}}{\mathrm{с}}}{0,02\ \mathrm{с}} = 250\ \mathrm{Н}.

Результирующая сила — урок. Физика, 7 класс.

Если на тело одновременно действует несколько сил, тогда состояние тела или его движение определяет результирующая сила — сумма всех сил.

Если силы действуют в одном направлении, результирующая сила равна сумме сил.

F1→F2→    Fрез=F1+F2

Сила тяги обеих лошадей суммируется

 

Обрати внимание!

Если силы действуют в противоположных направлениях, результирующая сила равна разности сил — от большей силы отнимают меньшую, результирующая сила действует в направлении большей силы.

Например, при движении автомобиля на него действуют две силы: сила тяги \(Fт\), создаваемая двигателем и направленная в сторону движения, и сила трения \(Fтр\) с поверхностью дороги, которая направлена в противоположном направлении (силу сопротивления воздуха не учитываем).   

 

Fрез=Fт−Fтр

Fтр→ Fт→   Fрез=Fтр−Fт

В этом случае движение автомобиля будет замедленным, так как сила трения больше, чем сила тяги.

 

 

Если сила тяги одинакова с силой трения, тогда автомобиль двигается с постоянной скоростью.

Эти силы компенсируют друг друга. Сумма всех сил равна нулю, и автомобиль двигается без ускорения.

 

Fрез=0

1-й закон Ньютона:

Если на тело не действуют силы или они уравновешены, тогда тело остаётся неподвижным или двигается равномерно и прямолинейно.

Когда автомобиль стоит на дороге, он находится в статическом равновесии. На него действуют две силы — сила притяжения (гравитации) и сила упругоcти опоры (дороги), которые компенсируют друг друга, их сумма равна нулю.

Каждое тело стремится оказывать сопротивление изменению скорости, оказывая сопротивление силе, вызывающей ускорение.

Стремление тела сопротивляться изменению скорости называют инерцией. Масса является мерой инерции (чем больше масса, тем больше инерция тела). 

 

Обрати внимание!

Из-за инерции тормозной путь у автобуса длиннее, чем у легкового автомобиля!

Слободянюк А.И. Физика 10/4.7 — PhysBook

Содержание книги

Предыдующая страница

§4. Основные законы динамики

4.7 Статика – законы равновесия тел.

Рассмотрим, при каких условиях тело может находиться в состоянии покоя, естественно, в какой либо инерциальной системе отсчета. На основании законов динамики И.Ньютона можно сформулировать два обязательных условия равновесия.

1. Векторная сумма внешних сил, действующих на тело, должна быть равна нулю. Нами было показано, что ускорение центра масс тела полностью определяется внешними силами, действующими на рассматриваемое тело. Если эта сумма равна нулю, то ускорение центра масс тела равна нулю. Поэтому можно выбрать такую систему отсчета, в которой центр масс покоится. Заметим, что при вычислении суммы векторов, нас не интересуют точки приложения различных сил, нам важны только величины и направления этих сил. Поэтому, говорят, что при рассмотрении поступательного движения все векторы сил можно переносить параллельно самому себе.

Так как центр масс твердого тела жестко связан с самим телом, то при покоящемся центре масс, тело может только вращаться вокруг оси, проходящей через центр масс. Для того, чтобы тело не начало вращаться, необходимо выполнение второго условия равновесия.

2. Сумма моментов внешних сил, действующих на тело, должна быть равна нулю. Согласно определению, момент силы зависит не только от величины и направления этой силы, но и от оси вращения. Поэтому, говоря о покоящемся теле, встает вопрос, относительно какой оси должны вычисляться моменты действующих сил. Ответ на данный вопрос следующий – для покоящегося тела суммарный момент равен нулю для любой мыслимой оси вращения! К счастью, при рассмотрении условий равновесия нет необходимости рассматривать все возможные оси вращения (что в принципе невозможно). Можно показать, что если векторная сумма сил равна нулю и сумма моментов сил относительно какой-либо оси равна нулю, то и сумма моментов сил относительно любой другой параллельной оси также равна нулю.

Проиллюстрируем это положение простым примером. Пусть силы, действующие на тело, лежат в одной плоскости и параллельны друг другу (рис. 53). Введем систему координат XOY, одна из осей которой X перпендикулярна направлению действия сил и проходит через ось вращения O. Обозначим координаты точек приложения сил x₁, x

₂, x₃… , тогда суммарный момент сил относительно этой оси равен

\(~M = x_1 F_1 + x_2 F_2 + x_3 F_3 + \ldots\) .

Вычислим момент сил относительно оси O’, отстоящей от оси O на расстоянии a

\(~M’ = (x_1 + a) F_1 + (x_2 + a) F_2 + (x_3 + a) F_3 + \ldots = x_1 F_1 + x_2 F_2 + x_3 F_3 + \ldots + a (F_1 + F_2 + F_3 + \ldots) = M + a (F_1 + F_2 + F_3 + \ldots)\) .

Как следует из полученного соотношения, при (F₁ + F₁ + F₂ + F₃ + … ) = 0 M’ = M. То есть, если сумма сил равна нулю, то суммарные моменты сил, относительно всех параллельных осей, равны.

Практически важным является случай, когда не тело действуют две силы, равные по величине и противоположные по направлению, но приложенные к разным точкам (в этом случае говорят о паре сил). Момент пары сил не зависит от оси вращения и равен M = aF (где F — модуль каждой силы, a — расстояние между линиями действия сил).

Следующая страница